Simulation of Spatiotemporal Variations in Cotton Lint Yield in the Texas High Plains
Abstract
:1. Introduction
2. Materials and Methods
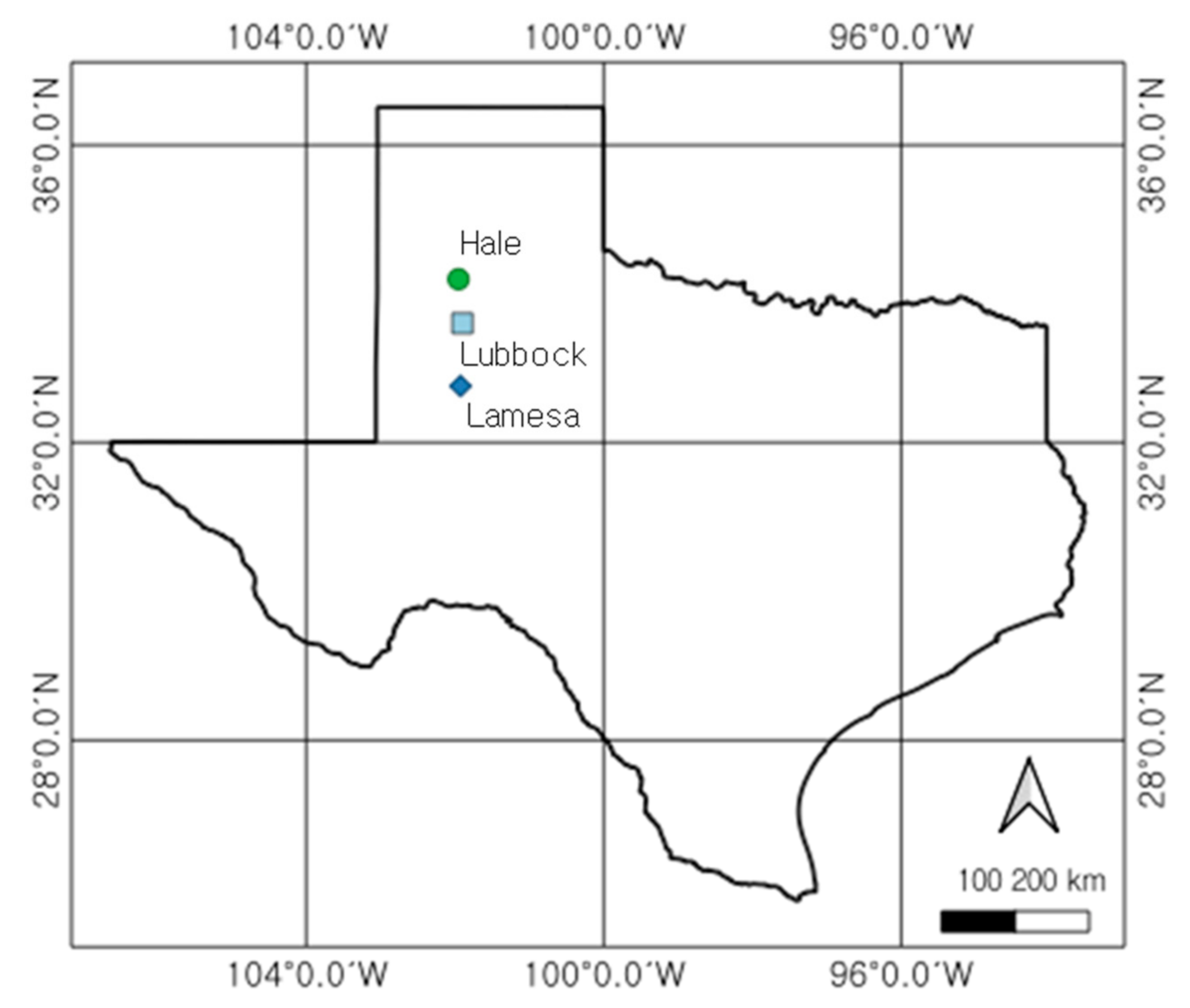
2.1. Study Site Description
2.2. Cotton Data
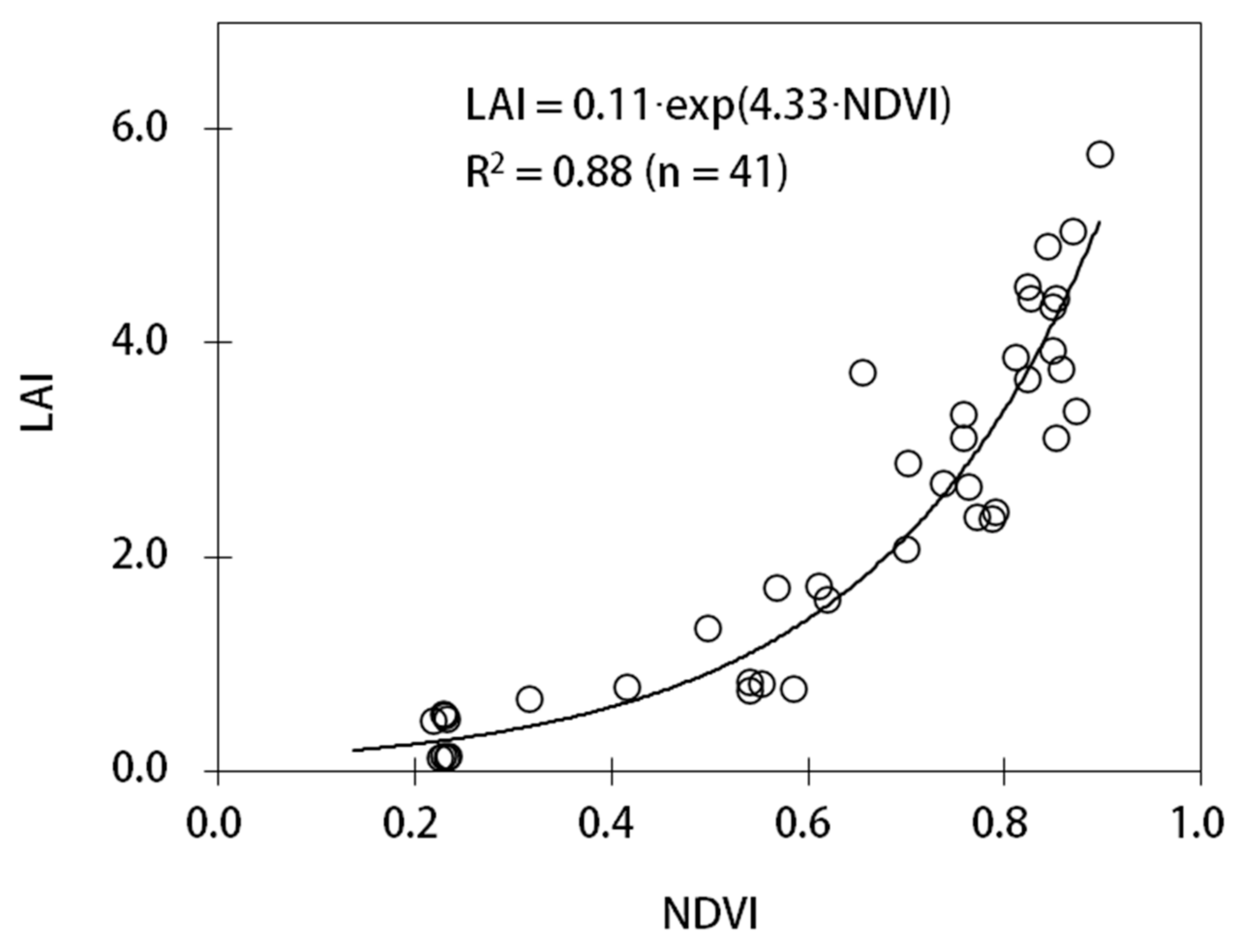
2.3. Proximal Sensing and Satellite Data
2.4. Model Calculation and Evaluation
Q = β × R × (1 − exp (−k × LAI))
P1 = Max [1 – a × exp (b × D), 0]
∆Rm = fm × M
P2 = Max [1 – a × exp (b × fGD), 0],
fGD = GDDpm − (Pa × GDDm)/(GDDm − GDDr/Pb)
3. Results
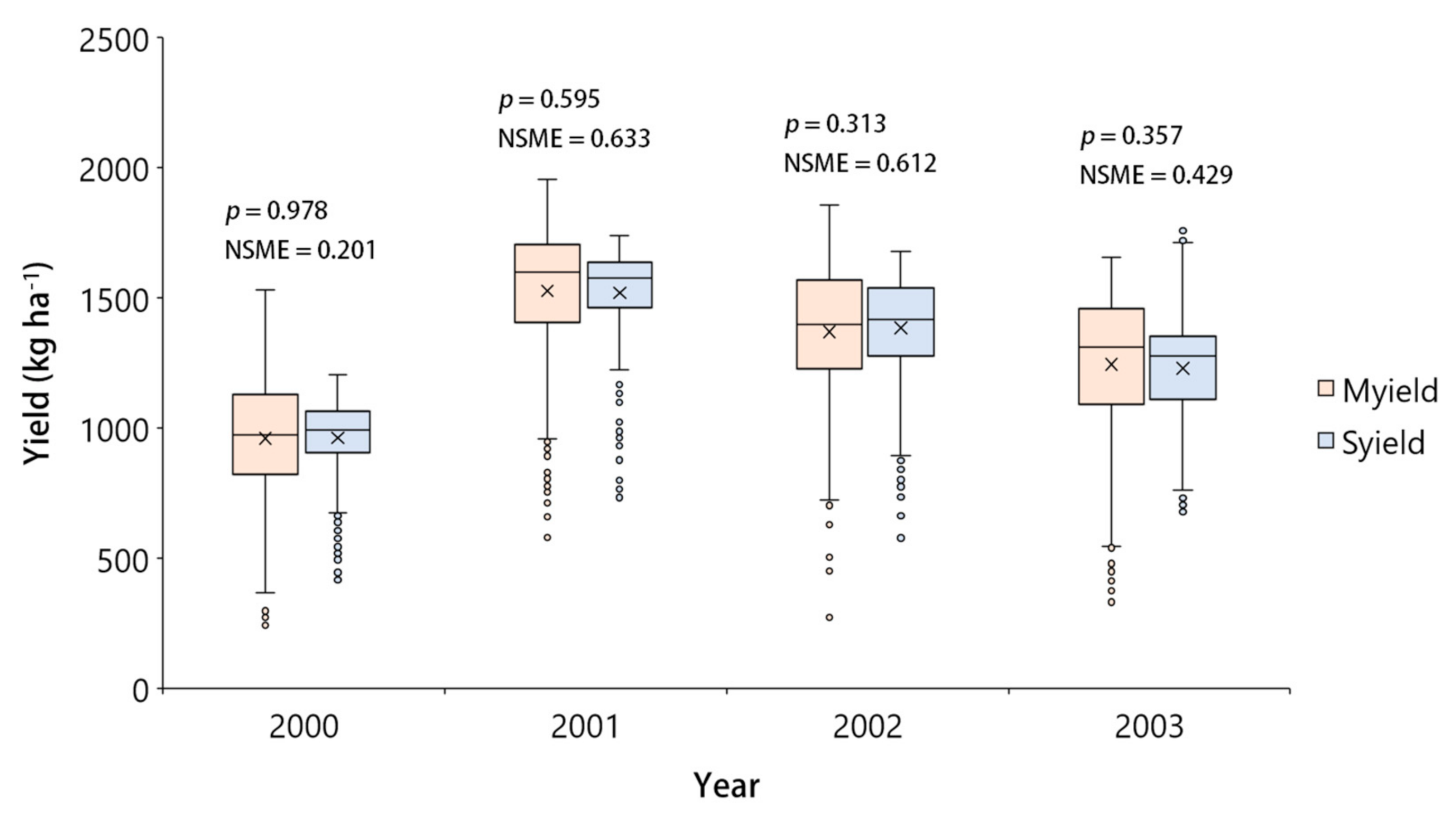
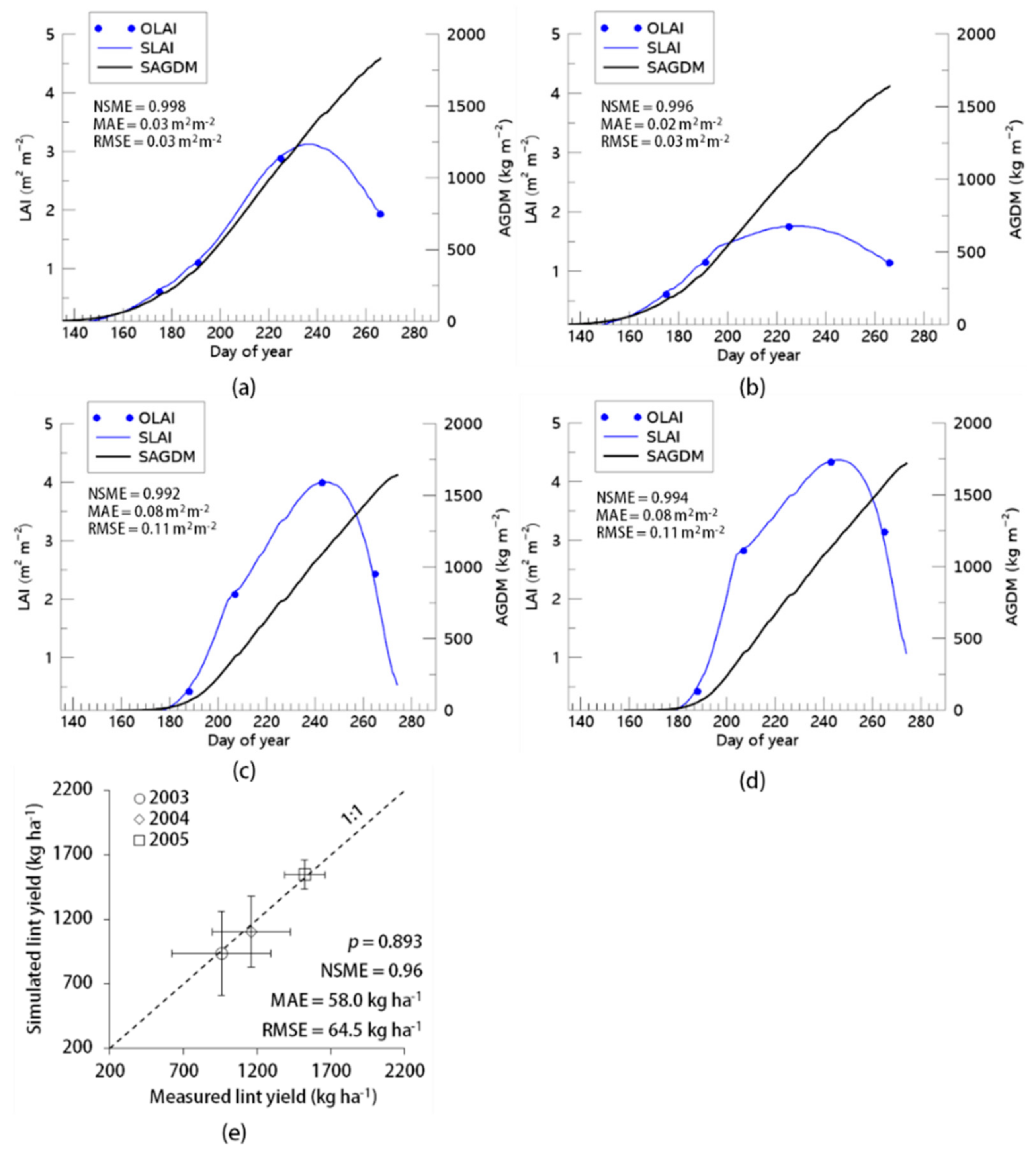
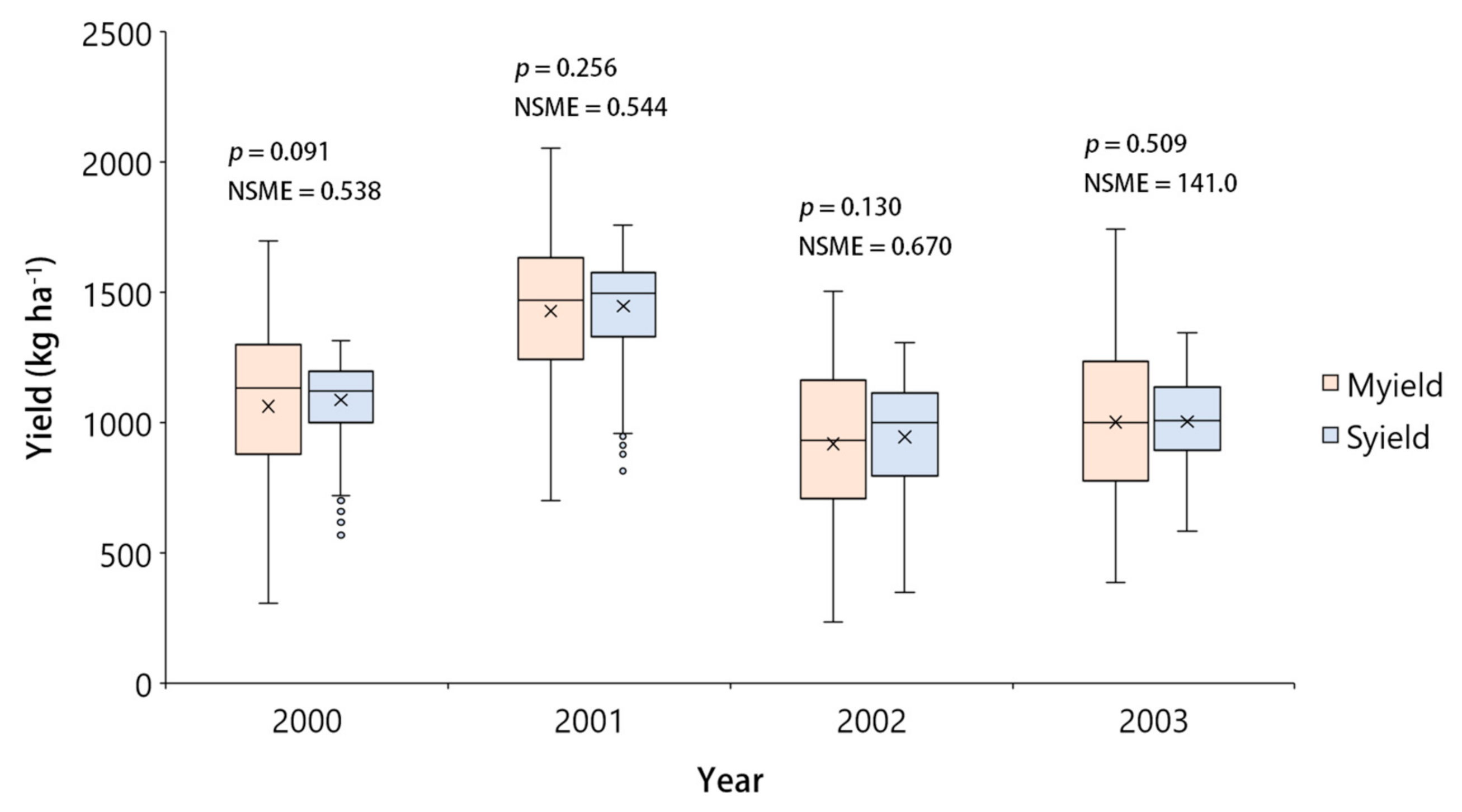
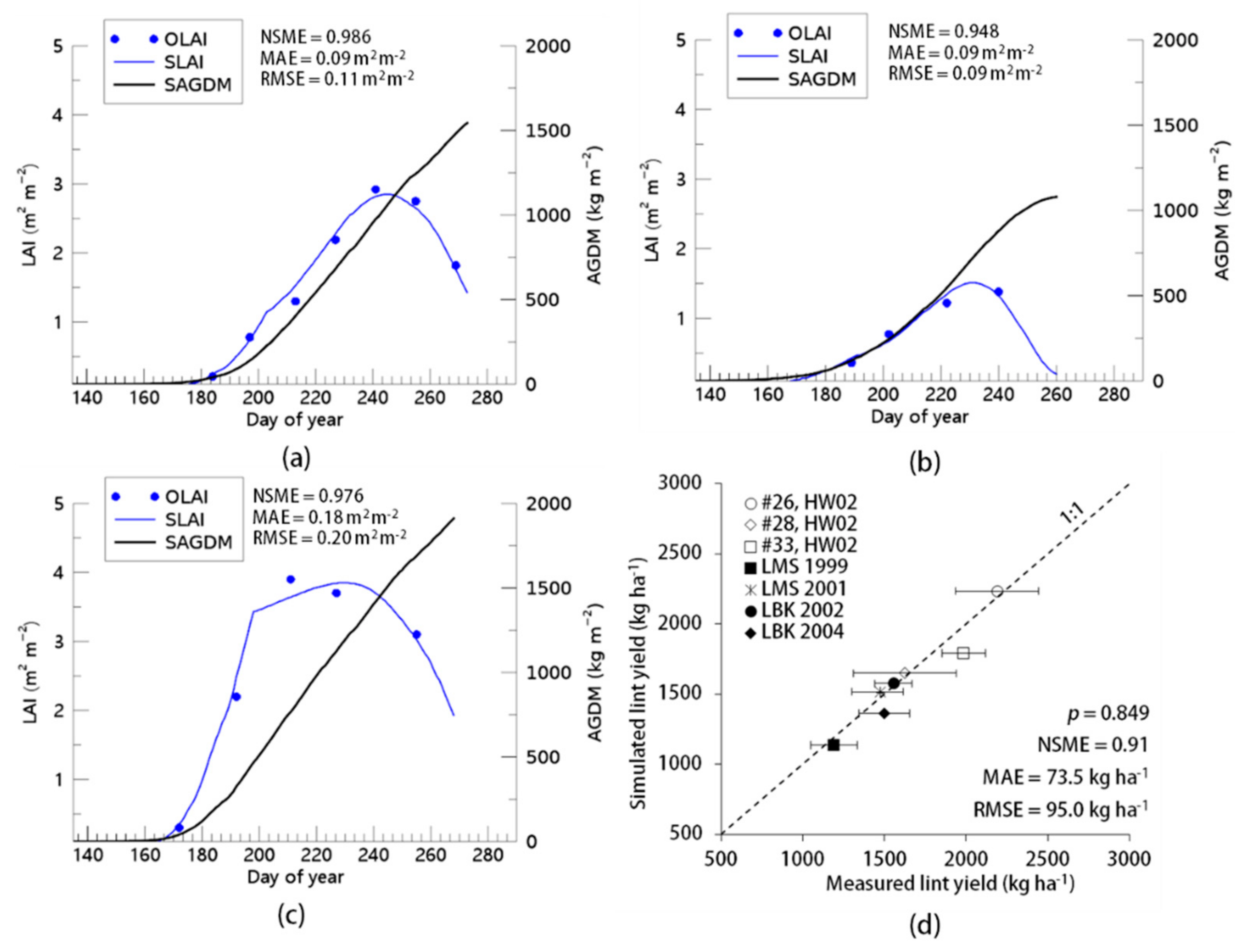
3.1. Model Evaluation
3.2. Geographical Projection
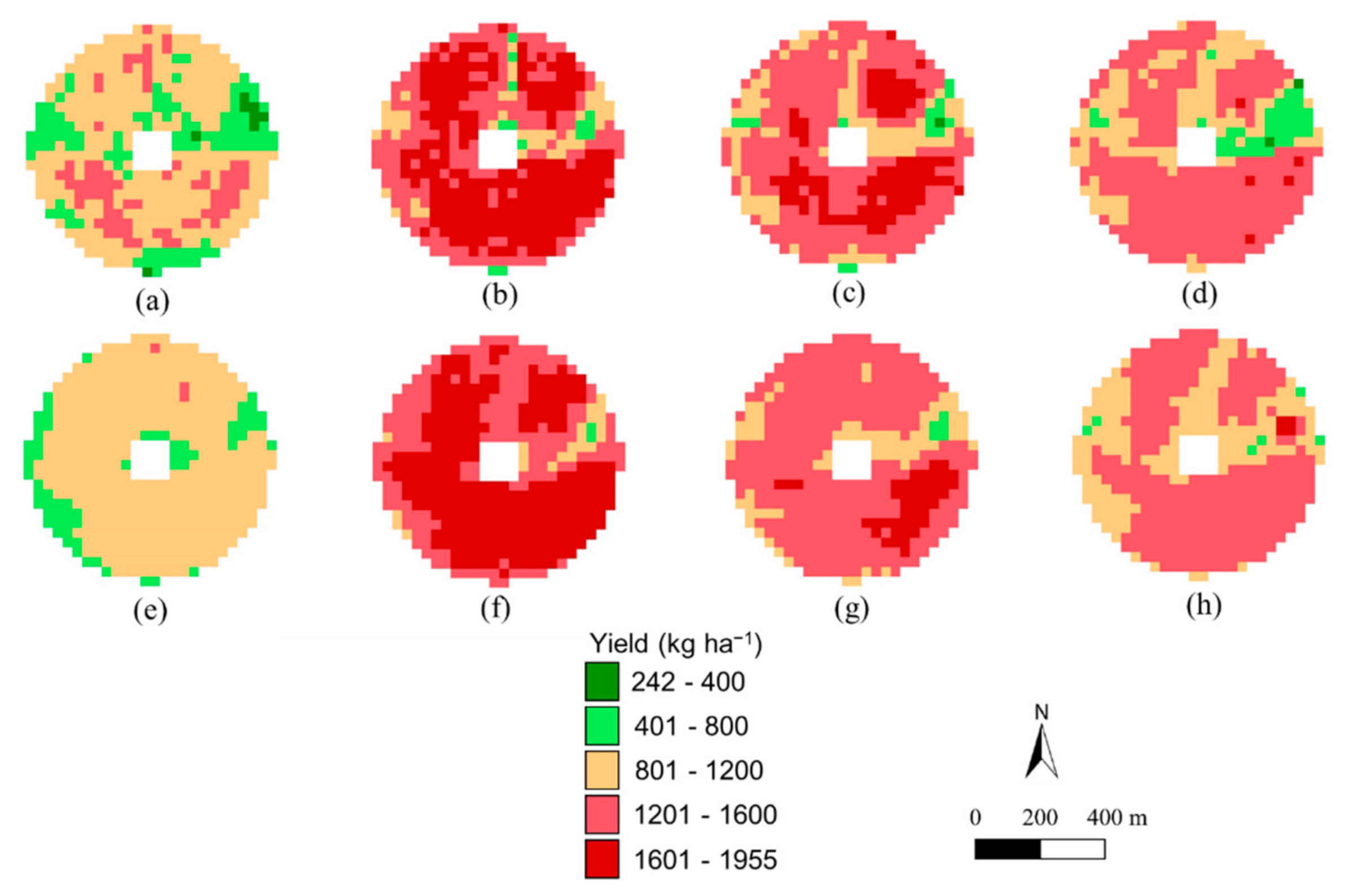
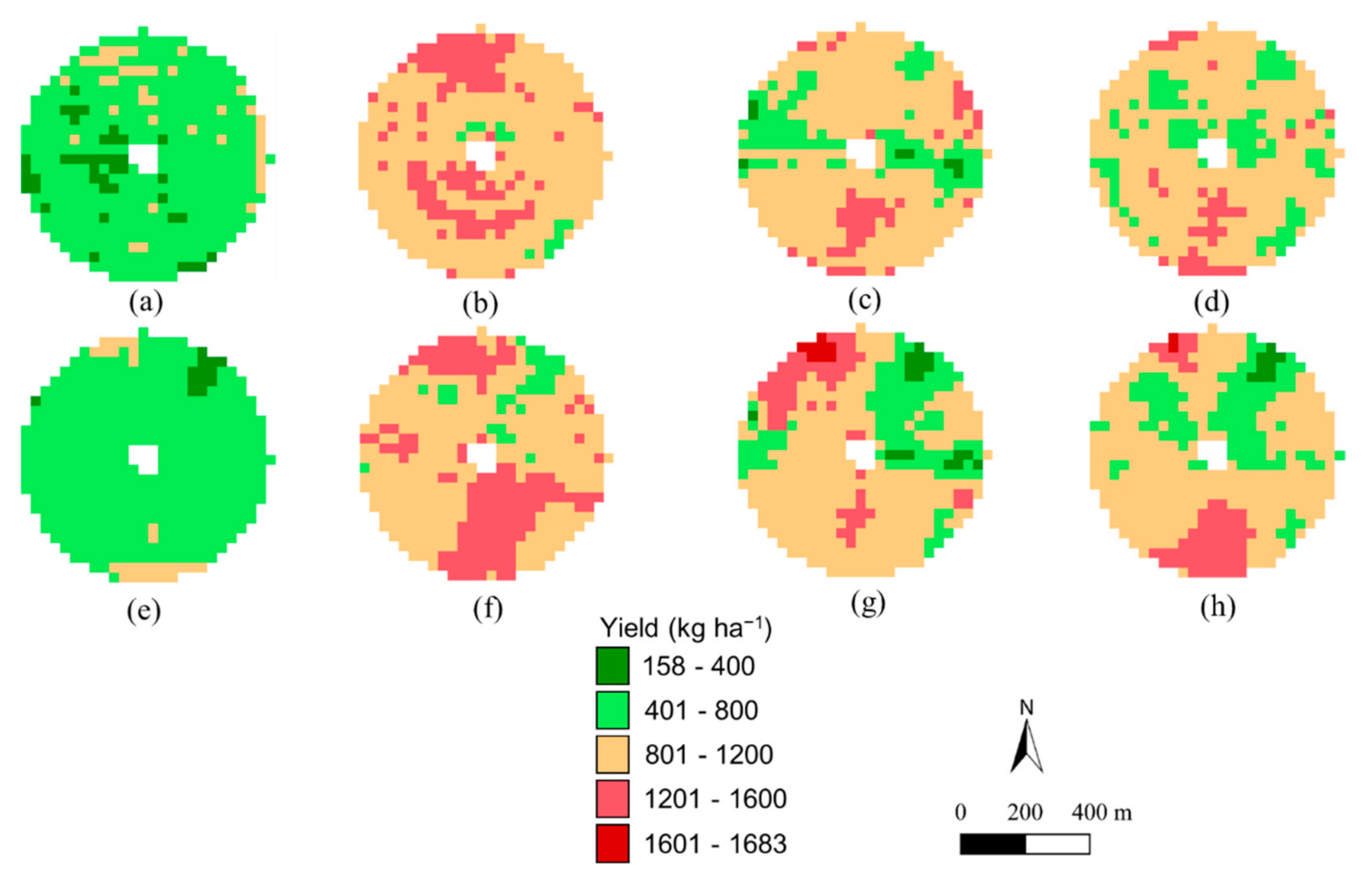

| Field # | Year | Mean (Median) ± 1 SD | p | MAE | RMSD | NSME | |
|---|---|---|---|---|---|---|---|
| Simulated | Observed | ||||||
| kg ha−1 | Unitless | kg ha−1 | Unitless | ||||
| 26 | 2000 | 961.5 (994.1) ± 146.3 | 961.2 (975.1) ± 237.4 | 0.978 | 168.6 | 212.1 | 0.201 |
| 2001 | 1518.9 (1576.2) ± 178.0 | 1526.7 (1597.7) ± 266.4 | 0.595 | 117.8 | 161.2 | 0.633 | |
| 2002 | 1384.8 (1417.1) ± 196.9 | 1369.6 (1397.3) ± 264.3 | 0.313 | 121.8 | 164.5 | 0.612 | |
| 2003 | 1230.0 (1277.0) ± 183.9 | 1243.8 (1312.6) ± 270.3 | 0.357 | 132.1 | 204.2 | 0.429 | |
| 28 | 2000 | 1088.1 (1122.8) ± 160.8 | 1063.2 (1131.8) ± 296.0 | 0.091 | 160.8 | 200.9 | 0.538 |
| 2001 | 1446.8 (1496.3) ± 184.8 | 1428.9 (1471.8) ± 297.9 | 0.256 | 157.7 | 201.1 | 0.544 | |
| 2002 | 945.3 (1001.6) ± 233.9 | 919.7 (933.4) ± 295.9 | 0.130 | 134.8 | 169.8 | 0.670 | |
| 2003 | 1038.6 (1045.8) ± 190.3 | 1049.4 (1053.4)± 311.2 | 0.509 | 141.0 | 172.1 | 0.694 | |
| 30 | 2000 | 604.4 (613.9) ± 143.4 | 604.6 (595.7) ± 109.3 | 0.979 | 139.5 | 173.9 | −1.535 |
| 2001 | 1104.5 (1101.6) ± 146.0 | 1107.9 (1121.9) ± 185.4 | 0.749 | 141.7 | 180.3 | 0.053 | |
| 2002 | 949.7 (980.3) ± 208.9 | 953.1 (974.3) ± 267.3 | 0.823 | 190.4 | 243.8 | 0.167 | |
| 2003 | 952.7 (941.9) ± 167.4 | 950.2 (944.8) ± 235.0 | 0.848 | 122.9 | 155.7 | 0.561 | |
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | Symbol or Acronym | Unit | Value |
|---|---|---|---|
| Radiation use efficiency | ε | g MJ−1 | 3.49 |
| Light extinction coefficient | k | - | 0.9 |
| Specific leaf area | S | m2 g−1 | 0.01 |
| Base temperature | Tb | °C | 15.6 |
| Leaf area index at transplanting | L0 | m2 m−2 | 0.02 |
| Partitioning parameter A | a | - | 0.1 |
| Partitioning parameter B | b | - | 0.00125 |
| Leaf senescence parameter | c | - | 0.00125 |
| Lint partitioning coefficient A | Pa | - | 2 |
| Lint partitioning coefficient B | Pb | - | 3 |
| Field Location | Year | Cultivar | L0 | a | b | c |
|---|---|---|---|---|---|---|
| #26, HW | 2002 | Paymaster 2326 BG/RR | 0.00022 | 0.2607 | 0.0014 | 0.0185 |
| #28, HW | 2002 | Paymaster 2326 BG/RR | 0.00026 | 0.3338 | 0.0012 | 0.0408 |
| #33, HW | 2002 | Paymaster 2326 BG/RR | 0.00041 | 0.3515 | 0.0011 | 0.0429 |
| TAMUAR | 1999 | Paymaster 2326 RR | 0.00228 | 0.4821 | 0.0007 | 0.0416 |
| TAMUAR | 2001 | Paymaster 2326 RR | 0.00028 | 0.0901 | 0.0022 | 0.0086 |
| PSWCL | 2002 | Paymaster 2326 BG/RR | 0.01528 | 0.3856 | 0.0012 | 0.0002 |
| PSWCL | 2004 | Paymaster 2326 BG/RR | 0.01939 | 0.4529 | 0.0008 | 0.0223 |

References
- Martin, J.D.; Leonard, W.H.; Stamp, D.L.; Waldren, R.P. Principles of Field Crop Production, 4th ed.; Pearson: New York, NY, USA, 2005. [Google Scholar]
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing; Guilford Press: New York, NY, USA, 2011. [Google Scholar]
- Dorigo, W.A.; Zurita-Milla, R.; De Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Ustin, S.L.; Whiting, M.L. Temporal and spatial relationships between within-field yield variability in cotton and high-spatial hyperspectral remote sensing imagery. Agron. J. 2005, 97, 641–653. [Google Scholar] [CrossRef] [Green Version]
- Kern, A.; Barcza, Z.; Marjanović, H.; Árendás, T.; Fodor, N.; Bónis, P.; Bognár, P.; Lichtenberger, J. Statistical modelling of crop yield in Central Europe using climate data and remote sensing vegetation indices. Agric. For. Meteorol. 2018, 260–261, 300–320. [Google Scholar] [CrossRef]
- Labus, M.P.; Nielsen, G.A.; Lawrence, R.L.; Engel, R.; Long, D.S. Wheat yield estimates using multi-temporal NDVI satellite imagery. Int. J. Remote Sens. 2002, 23, 4169–4180. [Google Scholar] [CrossRef]
- Delécolle, R.; Maas, S.; Guérif, M.; Baret, F. Remote sensing and crop production models: Present trends. ISPRS J. Photogramm. Remote Sens. 1992, 47, 145–161. [Google Scholar] [CrossRef]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Moulin, S.; Bondeau, A.; Delecolle, R. Combining agricultural crop models and satellite observations: From field to regional scales. Int. J. Remote Sens. 1998, 19, 1021–1036. [Google Scholar] [CrossRef]
- Nguyen, V.C.; Jeong, S.; Ko, J.; Ng, C.T.; Yeom, J. Mathematical integration of remotely-sensed information into a crop modelling process for mapping crop productivity. Remote Sens. 2019, 11, 2131. [Google Scholar] [CrossRef] [Green Version]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Hijmans, R.J.; Guiking-Lens, I.; Van Diepen, C. WOFOST 6.0: User’s Guide for the WOFOST 6.0 Crop Growth Simulation Model; D.L.O. Winand Staring Centre: Wageningen, The Netherlands, 1994; p. 145. [Google Scholar]
- Zhang, X.; Zhang, Q. Monitoring interannual variation in global crop yield using long-term AVHRR and MODIS observations. ISPRS J. Photogramm. Remote Sens. 2016, 114, 191–205. [Google Scholar] [CrossRef]
- Khanal, S.; Kc, K.; Fulton, J.; Shearer, S.; Ozkan, E. Remote Sensing in Agriculture—Accomplishments, Limitations, and Opportunities. Remote Sens. 2020, 12, 3783. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.; Huang, H.L.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Huang, Y.; Ryu, Y.; Jiang, C.; Kimm, H.; Kim, S.; Kang, M.; Shim, K. BESS-Rice: A remote sensing derived and biophysical process-based rice productivity simulation model. Agric. For. Meteorol. 2018, 256–257, 253–269. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Shin, T.; Ko, J.; Jeong, S.; Shawon, A.R.; Lee, K.D.; Shim, S.I. Simulation of wheat productivity using a model integrated with proximal and remotely controlled aerial sensing information. Front. Plant Sci. 2021, 12, 649660. [Google Scholar] [CrossRef]
- Shawon, A.R.; Ko, J.; Ha, B.; Jeong, S.; Kim, D.K.; Kim, H.-Y. Assessment of a proximal sensing-integrated crop model for simulation of soybean growth and yield. Remote Sens. 2020, 12, 410. [Google Scholar] [CrossRef] [Green Version]
- Yeom, J.-M.; Jeong, S.; Jeong, G.; Ng, C.T.; Deo, R.C.; Ko, J. Monitoring paddy productivity in North Korea employing geostationary satellite images integrated with GRAMI-rice model. Sci. Rep. 2018, 8, 16121. [Google Scholar] [CrossRef] [Green Version]
- Ko, J.; Maas, S.J.; Lascano, R.J.; Wanjura, D. Modification of the GRAMI Model for Cotton. Agron. J. 2005, 97, 1374–1379. [Google Scholar] [CrossRef] [Green Version]
- Maas, S.J. Parameterized model of gramineous crop growth: I. leaf area and dry mass simulation. Agron. J. 1993, 85, 348–353. [Google Scholar] [CrossRef]
- Maas, S.J. Parameterized model of gramineous crop growth: II. within-season simulation calibration. Agron. J. 1993, 85, 354–358. [Google Scholar] [CrossRef]
- Ko, J.; Maas, S.J.; Mauget, S.; Piccinni, G.; Wanjura, D. Modeling water-stressed cotton growth using within-season remote sensing data. Agron. J. 2006, 98, 1600–1609. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.; Maas, S.; Lascano, R.; Brightbill, J. Mapping spatial and temporal variability of cotton yield in West Texas. In Proceedings of the Beltwide Cotton Conferences, New Orleans, LA, USA, 4–7 January 2005; pp. 2067–2073. [Google Scholar]
- Guo, W. Spatial and Temporal Variability in Cotton Yield in Relation to Soil Apparent Electrical Conductivity, Topography, and Remote Sensing Imagery; Texas Tech University: Lubbock, TX, USA, 2005. [Google Scholar]
- Rajapakse, S. Automated Radiometric Normalization Technique for Multitemporal Landsat-TM and ETM+ Imagery; Texas Tech University: Lubbock, TX, USA, 2005. [Google Scholar]
- Monteith, J.L. Solar radiation and productivity in tropical ecosystems. J. Appl. Ecol. 1972, 9, 747–766. [Google Scholar] [CrossRef] [Green Version]
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere, 4th ed.; Academic Press: San Diego, CA, USA, 2013. [Google Scholar]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing; Cambridge University Press: New York, NY, USA, 1992. [Google Scholar]
- Nash, J.C. Compact Numerical Methods for Computers: Linear Algebra and Function Minimisation; CRC Press: New York, NY, USA, 1990. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Johnson, D.M. An assessment of pre- and within-season remotely sensed variables for forecasting corn and soybean yields in the United States. Remote Sens. Environ. 2014, 141, 116–128. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Ko, J.; Jeong, S.; Yeom, J.; Kim, H.; Ban, J.-O.; Kim, H.-Y. Simulation and mapping of rice growth and yield based on remote sensing. J. Appl. Remote Sens. 2015, 9, 096067. [Google Scholar] [CrossRef]
- Lövenstein, H.; Rabbinge, R.; van Keulen, H. World Food Production, Textbook 2: Biophysical Factors in Agricultural Production; Wageningen University & Research: Wageningen, The Netherlands, 1992. [Google Scholar]
- Ahuja, L.R.; Rojas, K.W.; Hanson, J.D.; Shaffer, M.J.; Ma, L. Root Zone Water Quality Model: Modeling Management Effects on Water Quality and Crop Production; Water Resources Publications, LLC: Highland Ranch, CO, USA, 2000. [Google Scholar]
- Verburg, P.H.; Neumann, K.; Nol, L. Challenges in using land use and land cover data for global change studies. Glob. Change Biol. 2011, 17, 974–989. [Google Scholar] [CrossRef] [Green Version]
- Ozdogan, M.; Woodcock, C.E. Resolution dependent errors in remote sensing of cultivated areas. Remote Sens. Environ. 2006, 103, 203–217. [Google Scholar] [CrossRef]
- Som-Ard, J.; Atzberger, C.; Izquierdo-Verdiguier, E.; Vuolo, F.; Immitzer, M. Remote sensing applications in sugarcane cultivation: A review. Remote Sens. 2021, 13, 4040. [Google Scholar] [CrossRef]
- Dong, J.; Xiao, X.; Menarguez, M.A.; Zhang, G.; Qin, Y.; Thau, D.; Biradar, C.; Moore, B., III. Mapping paddy rice planting area in northeastern Asia with Landsat 8 images, phenology-based algorithm and Google Earth Engine. Remote Sens. Environ. 2016, 185, 142–154. [Google Scholar] [CrossRef] [Green Version]


| Field Division | Location | Size (ha) | Field Shape | Soil Type | Irrigation Method |
|---|---|---|---|---|---|
| #26 | Halfway | 50 | Circle | Brownfield fine sand | LEPA |
| #28 | Halfway | 50 | Circle | Brownfield fine sand | LEPA |
| #30 | Halfway | 50 | Circle | Brownfield fine sand | LEPA |
| TAMUAR | Lamesa | 45 | Circle | Amarillo fine sandy loam | LEPA |
| PSWCL | Lubbock | 5 | Rectangle | Amarillo fine sandy loam | Subsurface drip |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, S.; Shin, T.; Ban, J.-O.; Ko, J. Simulation of Spatiotemporal Variations in Cotton Lint Yield in the Texas High Plains. Remote Sens. 2022, 14, 1421. https://doi.org/10.3390/rs14061421
Jeong S, Shin T, Ban J-O, Ko J. Simulation of Spatiotemporal Variations in Cotton Lint Yield in the Texas High Plains. Remote Sensing. 2022; 14(6):1421. https://doi.org/10.3390/rs14061421
Chicago/Turabian StyleJeong, Seungtaek, Taehwan Shin, Jong-Oh Ban, and Jonghan Ko. 2022. "Simulation of Spatiotemporal Variations in Cotton Lint Yield in the Texas High Plains" Remote Sensing 14, no. 6: 1421. https://doi.org/10.3390/rs14061421
APA StyleJeong, S., Shin, T., Ban, J.-O., & Ko, J. (2022). Simulation of Spatiotemporal Variations in Cotton Lint Yield in the Texas High Plains. Remote Sensing, 14(6), 1421. https://doi.org/10.3390/rs14061421







