Land Use Quantile Regression Modeling of Fine Particulate Matter in Australia
Abstract
:1. Introduction
2. Literature Review
3. Study Area and Data
3.1. Study Area and Air Pollution Data
3.2. Explanatory Variables
3.2.1. Land Use
3.2.2. Population
3.2.3. Road Network
3.2.4. Elevation
3.2.5. Vegetation
4. Land Use Quantile Regression (LUQR) for Air Pollution Prediction
5. Results
5.1. Optimal Spatial Buffers and Variable Selection
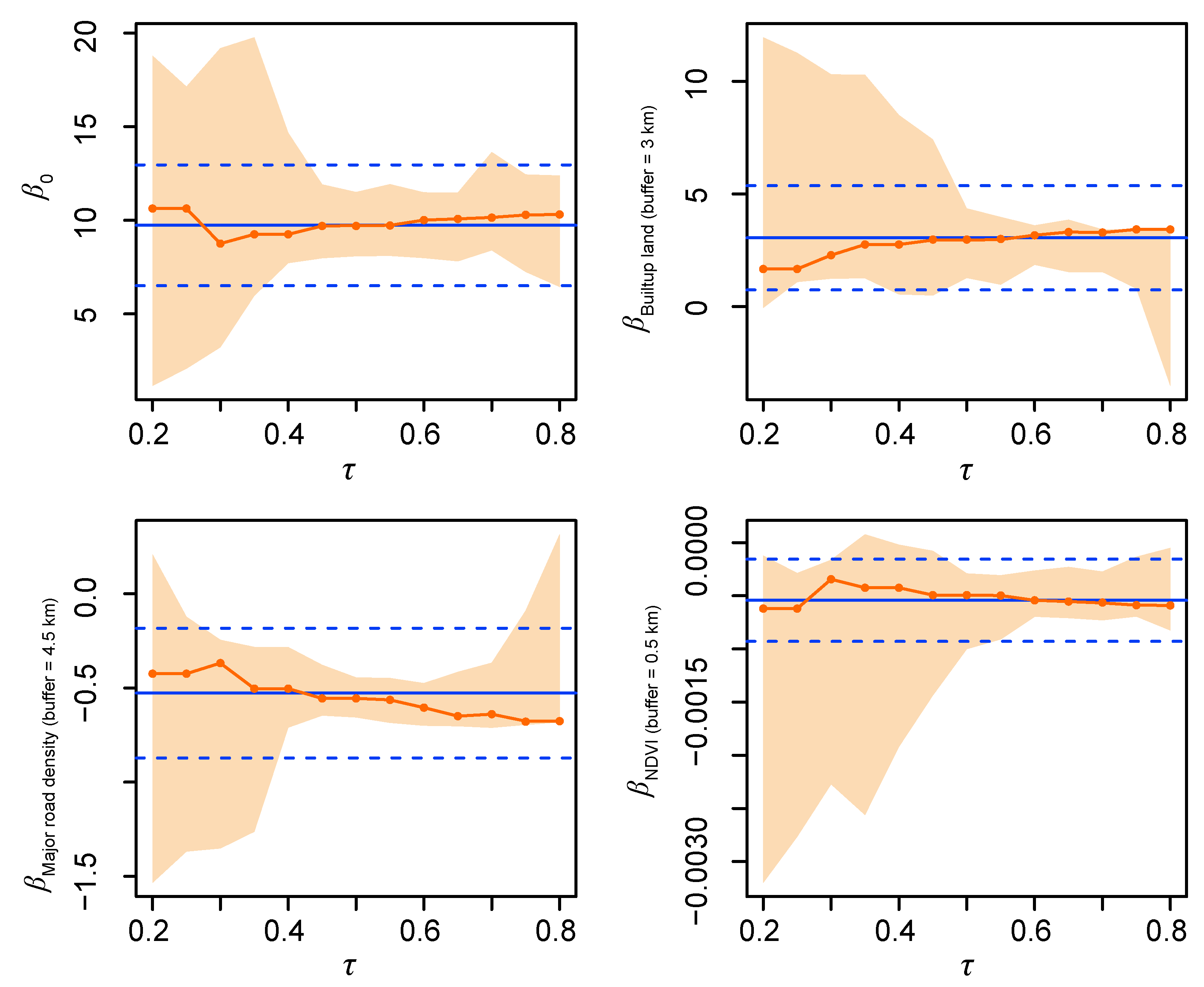
5.2. LUQR Model
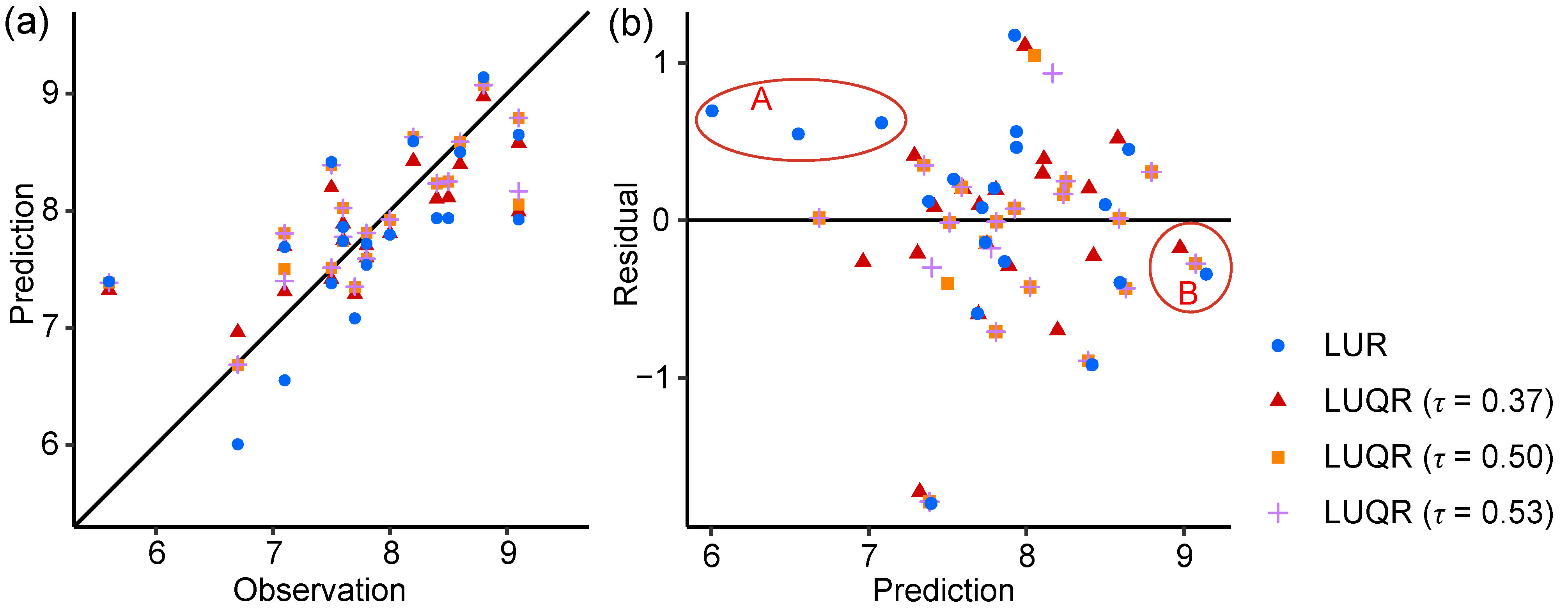
5.3. Model Validation
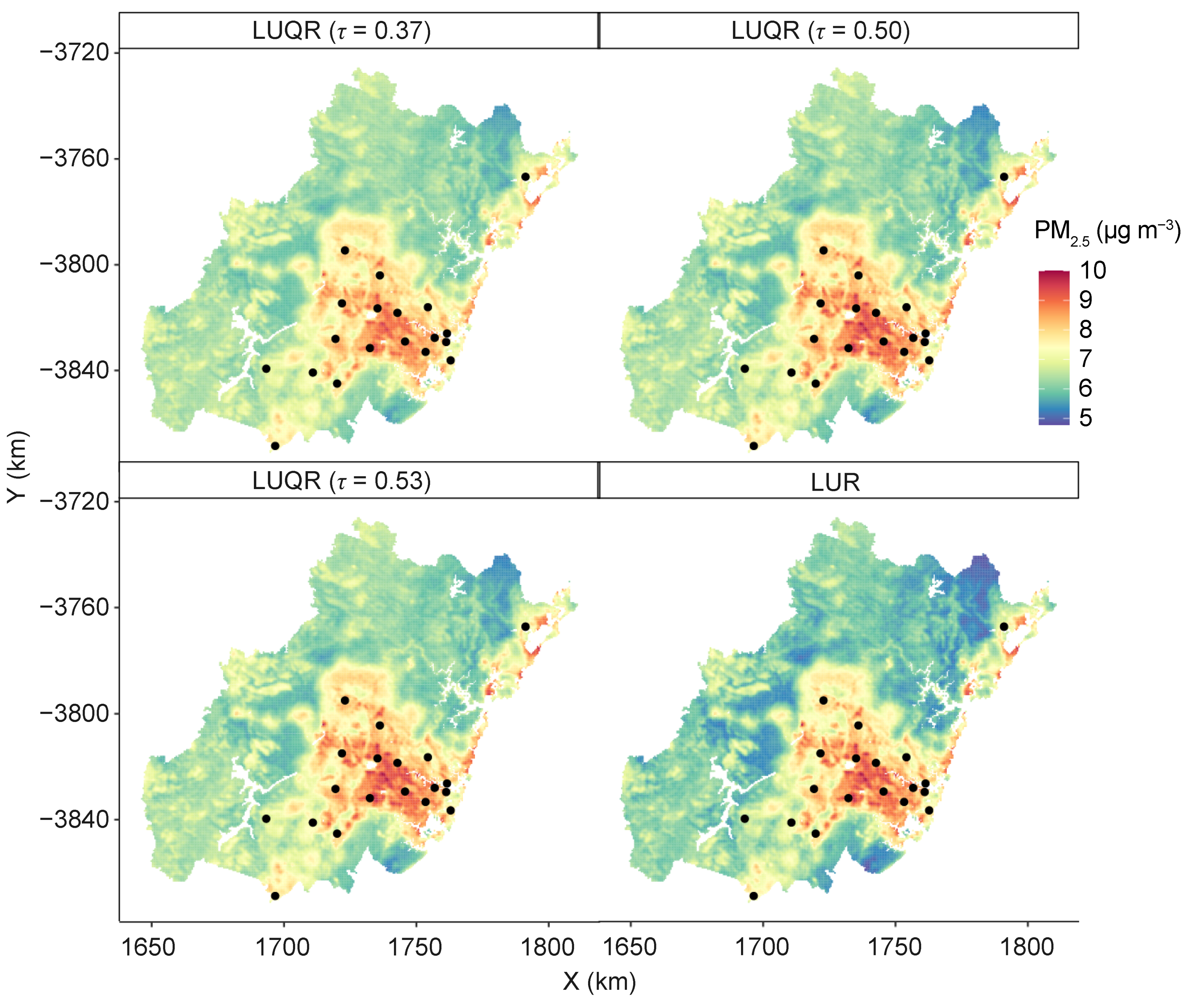
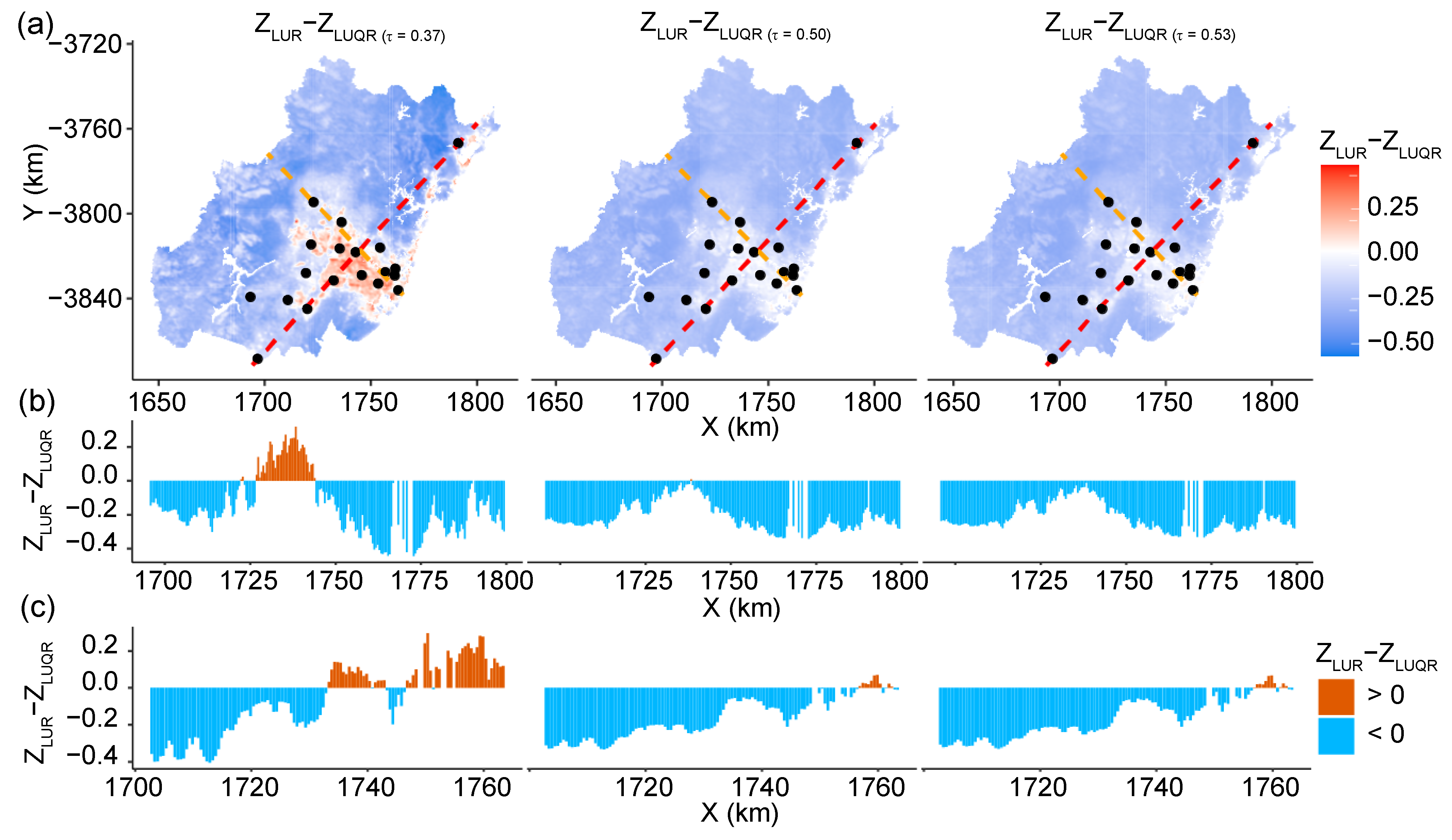
5.4. Spatial Prediction
6. Discussion
6.1. Methodological Contributions
6.2. Findings from the LUQR-Based Predictions
6.3. Limitations and Future Recommendations
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kitchin, R.; Lauriault, T.P. Small data in the era of big data. GeoJournal 2015, 80, 463–475. [Google Scholar] [CrossRef]
- Phillips, S.J.; Dudík, M.; Elith, J.; Graham, C.H.; Lehmann, A.; Leathwick, J.; Ferrier, S. Sample selection bias and presence-only distribution models: Implications for background and pseudo-absence data. Ecol. Appl. 2009, 19, 181–197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hernandez, P.A.; Graham, C.H.; Master, L.L.; Albert, D.L. The effect of sample size and species characteristics on performance of different species distribution modeling methods. Ecography 2006, 29, 773–785. [Google Scholar] [CrossRef]
- Grinand, C.; Arrouays, D.; Laroche, B.; Martin, M.P. Extrapolating regional soil landscapes from an existing soil map: Sampling intensity, validation procedures, and integration of spatial context. Geoderma 2008, 143, 180–190. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. The Variogram and Modelling. In Basic Steps in Geostatistics: The Variogram and Kriging; Springer International Publishing: Cham, Switzerland, 2015; pp. 15–42. [Google Scholar]
- Wang, J.; Xu, C.; Hu, M.; Li, Q.; Yan, Z.; Zhao, P.; Jones, P. A new estimate of the China temperature anomaly series and uncertainty assessment in 1900–2006. J. Geophys. Res. Atmos. 2014, 119, 1–9. [Google Scholar] [CrossRef]
- Deng, Y.; Wang, S.; Bai, X.; Wu, L.; Cao, Y.; Li, H.; Wang, M.; Li, C.; Yang, Y.; Hu, Z.; et al. Comparison of soil moisture products from microwave remote sensing, land model, and reanalysis using global ground observations. Hydrol. Process. 2020, 34, 836–851. [Google Scholar] [CrossRef]
- Luo, P.; Song, Y.; Huang, X.; Ma, H.; Liu, J.; Yao, Y.; Meng, L. Identifying determinants of spatio-temporal disparities in soil moisture of the Northern Hemisphere using a geographically optimal zones-based heterogeneity model. ISPRS J. Photogramm. Remote Sens. 2022, 185, 111–128. [Google Scholar] [CrossRef]
- Liu, J.; Chai, L.; Lu, Z.; Liu, S.; Qu, Y.; Geng, D.; Song, Y.; Guan, Y.; Guo, Z.; Wang, J.; et al. Evaluation of SMAP, SMOS-IC, FY3B, JAXA, and LPRM soil moisture products over the Qinghai-Tibet plateau and its surrounding areas. Remote Sens. 2019, 11, 792. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Chai, L.; Dong, J.; Zheng, D.; Wigneron, J.P.; Liu, S.; Zhou, J.; Xu, T.; Yang, S.; Song, Y.; et al. Uncertainty analysis of eleven multisource soil moisture products in the third pole environment based on the three-corned hat method. Remote Sens. Environ. 2021, 255, 112225. [Google Scholar] [CrossRef]
- Ross, Z.; Jerrett, M.; Ito, K.; Tempalski, B.; Thurston, G.D. A land use regression for predicting fine particulate matter concentrations in the New York City region. Atmos. Environ. 2007, 41, 2255–2269. [Google Scholar] [CrossRef]
- Beelen, R.; Voogt, M.; Duyzer, J.; Zandveld, P.; Hoek, G. Comparison of the performances of land use regression modelling and dispersion modelling in estimating small-scale variations in long-term air pollution concentrations in a Dutch urban area. Atmos. Environ. 2010, 44, 4614–4621. [Google Scholar] [CrossRef]
- Olvera, H.A.; Garcia, M.; Li, W.W.; Yang, H.; Amaya, M.A.; Myers, O.; Burchiel, S.W.; Berwick, M.; Pingitore, N.E., Jr. Principal component analysis optimization of a PM2.5 land use regression model with small monitoring network. Sci. Total Environ. 2012, 425, 27–34. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Xu, H. A novel hybrid spatiotemporal land use regression model system at the megacity scale. Atmos. Environ. 2021, 244, 117971. [Google Scholar] [CrossRef]
- Li, Z.; Tong, X.; Ho, J.M.W.; Kwok, T.C.; Dong, G.; Ho, K.F.; Yim, S.H.L. A practical framework for predicting residential indoor PM2.5 concentration using land-use regression and machine learning methods. Chemosphere 2021, 265, 129140. [Google Scholar] [CrossRef]
- Wong, P.Y.; Lee, H.Y.; Chen, Y.C.; Zeng, Y.T.; Chern, Y.R.; Chen, N.T.; Lung, S.C.C.; Su, H.J.; Wu, C.D. Using a land use regression model with machine learning to estimate ground level PM2.5. Environ. Pollut. 2021, 277, 116846. [Google Scholar] [CrossRef]
- Song, Y.; Shen, Z.; Wu, P.; Viscarra Rossel, R. Wavelet geographically weighted regression for spectroscopic modelling of soil properties. Sci. Rep. 2021, 11, 17503. [Google Scholar] [CrossRef]
- Halliru, A.M.; Loganathan, N.; Hassan, A.A.G.; Mardani, A.; Kamyab, H. Re-examining the environmental Kuznets curve hypothesis in the Economic Community of West African States: A panel quantile regression approach. J. Clean. Prod. 2020, 276, 124247. [Google Scholar] [CrossRef]
- Tang, J.; Gao, F.; Liu, F.; Han, C.; Lee, J. Spatial heterogeneity analysis of macro-level crashes using geographically weighted Poisson quantile regression. Accid. Anal. Prev. 2020, 148, 105833. [Google Scholar] [CrossRef]
- Xu, B.; Lin, B. Investigating drivers of CO2 emission in China’s heavy industry: A quantile regression analysis. Energy 2020, 206, 118159. [Google Scholar] [CrossRef]
- Cade, B.S.; Noon, B.R. A gentle introduction to quantile regression for ecologists. Front. Ecol. Environ. 2003, 1, 412–420. [Google Scholar] [CrossRef]
- Koenker, R. Quantile Regression: Economic Society Monograph Series; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Song, Y.Z.; Yang, H.L.; Peng, J.H.; Song, Y.R.; Sun, Q.; Li, Y. Estimating PM2.5 concentrations in Xi’an City using a generalized additive model with multi-source monitoring data. PLoS ONE 2015, 10, e0142149. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zou, B.; Luo, Y.; Wan, N.; Zheng, Z.; Sternberg, T.; Liao, Y. Performance comparison of LUR and OK in PM2.5 concentration mapping: A multidimensional perspective. Sci. Rep. 2015, 5, 8698. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, L.; Zhao, J.; Gao, Y.; Gu, Z.; Xin, K.; Zhang, J. Spatial distribution characteristics of PM2.5 and PM10 in Xi’an City predicted by land use regression models. Sustain. Cities Soc. 2020, 61, 102329. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Bilal, M.; Ho, H.C.; Omar, A. Urbanization and regional air pollution across South Asian developing countries–A nationwide land use regression for ambient PM2.5 assessment in Pakistan. Environ. Pollut. 2020, 266, 115145. [Google Scholar] [CrossRef]
- Harper, A.; Baker, P.N.; Xia, Y.; Kuang, T.; Zhang, H.; Chen, Y.; Han, T.L.; Gulliver, J. Development of spatiotemporal land use regression models for PM2.5 and NO2 in Chongqing, China, and exposure assessment for the CLIMB study. Atmos. Pollut. Res. 2021, 12, 101096. [Google Scholar] [CrossRef]
- Hoek, G.; Beelen, R.; De Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Shi, Y.; Ren, C.; Cai, M.; Lau, K.K.L.; Lee, T.C.; Wong, W.K. Assessing spatial variability of extreme hot weather conditions in Hong Kong: A land use regression approach. Environ. Res. 2019, 171, 403–415. [Google Scholar] [CrossRef]
- Tsin, P.K.; Knudby, A.; Krayenhoff, E.S.; Brauer, M.; Henderson, S.B. Land use regression modeling of microscale urban air temperatures in greater Vancouver, Canada. Urban Clim. 2020, 32, 100636. [Google Scholar] [CrossRef]
- Shi, Y.; Katzschner, L.; Ng, E. Modelling the fine-scale spatiotemporal pattern of urban heat island effect using land use regression approach in a megacity. Sci. Total Environ. 2018, 618, 891–904. [Google Scholar] [CrossRef]
- Guo, Y.; Su, J.G.; Dong, Y.; Wolch, J. Application of land use regression techniques for urban greening: An analysis of Tianjin, China. Urban For. Urban Green. 2019, 38, 11–21. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Chen, H.; Zhao, J.; Xu, Z.; Li, W.; Xu, M. Improving spatial prediction of health risk assessment for Hg, As, Cu, and Pb in soil based on land-use regression. Environ. Geochem. Health 2020, 42, 1415–1428. [Google Scholar] [CrossRef]
- Henderson, S.B.; Beckerman, B.; Jerrett, M.; Brauer, M. Application of land use regression to estimate long-term concentrations of traffic-related nitrogen oxides and fine particulate matter. Environ. Sci. Technol. 2007, 41, 2422–2428. [Google Scholar] [CrossRef]
- Jones, R.R.; Hoek, G.; Fisher, J.A.; Hasheminassab, S.; Wang, D.; Ward, M.H.; Sioutas, C.; Vermeulen, R.; Silverman, D.T. Land use regression models for ultrafine particles, fine particles, and black carbon in Southern California. Sci. Total Environ. 2020, 699, 134234. [Google Scholar] [CrossRef]
- Tularam, H.; Ramsay, L.F.; Muttoo, S.; Brunekreef, B.; Meliefste, K.; de Hoogh, K.; Naidoo, R.N. A hybrid air pollution/land use regression model for predicting air pollution concentrations in Durban, South Africa. Environ. Pollut. 2021, 274, 116513. [Google Scholar] [CrossRef]
- Eeftens, M.; Beelen, R.; De Hoogh, K.; Bellander, T.; Cesaroni, G.; Cirach, M.; Declercq, C.; Dedele, A.; Dons, E.; De Nazelle, A.; et al. Development of land use regression models for PM2.5, PM2.5 absorbance, PM10 and PMcoarse in 20 European study areas; results of the ESCAPE project. Environ. Sci. Technol. 2012, 46, 11195–11205. [Google Scholar] [CrossRef]
- Lee, H.J.; Chatfield, R.B.; Strawa, A.W. Enhancing the applicability of satellite remote sensing for PM2.5 estimation using MODIS deep blue AOD and land use regression in California, United States. Environ. Sci. Technol. 2016, 50, 6546–6555. [Google Scholar] [CrossRef]
- Derdouri, A.; Murayama, Y. A comparative study of land price estimation and mapping using regression kriging and machine learning algorithms across Fukushima prefecture, Japan. J. Geogr. Sci. 2020, 30, 794–822. [Google Scholar] [CrossRef]
- Munyati, C.; Sinthumule, N. Comparative suitability of ordinary kriging and Inverse Distance Weighted interpolation for indicating intactness gradients on threatened savannah woodland and forest stands. Environ. Sustain. Indic. 2021, 12, 100151. [Google Scholar] [CrossRef]
- Wang, J.; Cohan, D.S.; Xu, H. Spatiotemporal ozone pollution LUR models: Suitable statistical algorithms and time scales for a megacity scale. Atmos. Environ. 2020, 237, 117671. [Google Scholar] [CrossRef]
- Rahman, M.M.; Karunasinghe, J.; Clifford, S.; Knibbs, L.D.; Morawska, L. New insights into the spatial distribution of particle number concentrations by applying non-parametric land use regression modelling. Sci. Total Environ. 2020, 702, 134708. [Google Scholar] [CrossRef]
- Fritsch, M.; Behm, S. Agglomeration and infrastructure effects in land use regression models for air pollution—Specification, estimation, and interpretations. Atmos. Environ. 2021, 253, 118337. [Google Scholar] [CrossRef]
- Australian Bureau of Statistics. National, State and Territory Population; Australian Bureau of Statistics: Canberra, Australia, 2020.
- Department of Planning, Industry and Environment, New South Wales. New South Wales Air Quality Data Services; Department of Planning, Industry and Environment: New South Wales, Parramatta, Australia, 2021. [Google Scholar]
- Tucker, W.G. An overview of PM2.5 sources and control strategies. Fuel Process. Technol. 2000, 65, 379–392. [Google Scholar] [CrossRef]
- Chen, R.; Yin, P.; Meng, X.; Wang, L.; Liu, C.; Niu, Y.; Liu, Y.; Liu, J.; Qi, J.; You, J.; et al. Associations between coarse particulate matter air pollution and cause-specific mortality: A nationwide analysis in 272 Chinese cities. Environ. Health Perspect. 2019, 127, 017008. [Google Scholar] [CrossRef] [Green Version]
- Giugliano, M.; Lonati, G.; Butelli, P.; Romele, L.; Tardivo, R.; Grosso, M. Fine particulate (PM2.5–PM1) at urban sites with different traffic exposure. Atmos. Environ. 2005, 39, 2421–2431. [Google Scholar] [CrossRef]
- Kinney, P.L.; Gichuru, M.G.; Volavka-Close, N.; Ngo, N.; Ndiba, P.K.; Law, A.; Gachanja, A.; Gaita, S.M.; Chillrud, S.N.; Sclar, E. Traffic impacts on PM2.5 air quality in Nairobi, Kenya. Environ. Sci. Policy 2011, 14, 369–378. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Chen, Q.; Qian, Q.; Lin, C.; Chen, Y.; Tian, W. Impacts of traffic and street characteristics on the exposure of cycling commuters to PM2.5 and PM10 in urban street environments. Build. Environ. 2021, 188, 107476. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, J.; Zhong, C.; Li, X.; Wei, J. Spatiotemporal PM2.5 variations and its response to the industrial structure from 2000 to 2018 in the Beijing-Tianjin-Hebei region. J. Clean. Prod. 2021, 279, 123742. [Google Scholar] [CrossRef]
- Fang, D.; Yu, B. Driving mechanism and decoupling effect of PM2.5 emissions: Empirical evidence from China’s industrial sector. Energy Policy 2021, 149, 112017. [Google Scholar] [CrossRef]
- Aguilera, R.; Corringham, T.; Gershunov, A.; Benmarhnia, T. Wildfire smoke impacts respiratory health more than fine particles from other sources: Observational evidence from Southern California. Nat. Commun. 2021, 12, 1493. [Google Scholar] [CrossRef]
- Hua, J.; Zhang, Y.; de Foy, B.; Mei, X.; Shang, J.; Feng, C. Competing PM2.5 and NO2 holiday effects in the Beijing area vary locally due to differences in residential coal burning and traffic patterns. Sci. Total Environ. 2021, 750, 141575. [Google Scholar] [CrossRef]
- Zhang, Y.; Shen, Z.; Sun, J.; Zhang, L.; Zhang, B.; Zou, H.; Zhang, T.; Ho, S.S.H.; Chang, X.; Xu, H.; et al. Parent, alkylated, oxygenated and nitrated polycyclic aromatic hydrocarbons in PM2.5 emitted from residential biomass burning and coal combustion: A novel database of 14 heating scenarios. Environ. Pollut. 2021, 268, 115881. [Google Scholar] [CrossRef] [PubMed]
- Ikemori, F.; Uranishi, K.; Asakawa, D.; Nakatsubo, R.; Makino, M.; Kido, M.; Mitamura, N.; Asano, K.; Nonaka, S.; Nishimura, R.; et al. Source apportionment in PM2.5 in central Japan using positive matrix factorization focusing on small-scale local biomass burning. Atmos. Pollut. Res. 2021, 12, 162–172. [Google Scholar] [CrossRef]
- Xu, W.; Jin, X.; Liu, M.; Ma, Z.; Wang, Q.; Zhou, Y. Analysis of spatiotemporal variation of PM2.5 and its relationship to land use in China. Atmos. Pollut. Res. 2021, 12, 101151. [Google Scholar] [CrossRef]
- Song, J.; Zhou, S.; Peng, Y.; Xu, J.; Lin, R. Relationship between neighborhood land use structure and the spatiotemporal pattern of PM2.5 at the microscale: Evidence from the central area of Guangzhou, China. Environ. Plan. B Urban Anal. City Sci. 2021, 49, 485–500. [Google Scholar] [CrossRef]
- Lu, D.; Mao, W.; Xiao, W.; Zhang, L. Non-Linear Response of PM2.5 Pollution to Land Use Change in China. Remote Sens. 2021, 13, 1612. [Google Scholar] [CrossRef]
- Mhawish, A.; Banerjee, T.; Sorek-Hamer, M.; Bilal, M.; Lyapustin, A.I.; Chatfield, R.; Broday, D.M. Estimation of high-resolution PM2.5 over the indo-gangetic plain by fusion of satellite data, meteorology, and land use variables. Environ. Sci. Technol. 2020, 54, 7891–7900. [Google Scholar] [CrossRef] [PubMed]
- Australian Bureau of Agricultural and Resource Economics and Sciences. ABARES 2021, Catchment Scale Land Use of Australia—Update December 2020; Australian Bureau of Agricultural and Resource Economics and Sciences: Canberra, Australia, 2021. [CrossRef]
- Australian Bureau of Statistics. 1270.0.55.001—Australian Statistical Geography Standard (ASGS): Volume 1—Main Structure and Greater Capital City Statistical Areas, July 2016; Australian Bureau of Statistics: Canberra, Australia, 2017.
- Australia, G. Digital Elevation Model (DEM) of Australia Derived from LiDAR 5 Metre Grid; Commonwealth of Australia and Geoscience Australia: Canberra, Australia, 2015. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Sheng, Q.; Zhang, Y.; Zhu, Z.; Li, W.; Xu, J.; Tang, R. An experimental study to quantify road greenbelts and their association with PM2.5 concentration along city main roads in Nanjing, China. Sci. Total Environ. 2019, 667, 710–717. [Google Scholar] [CrossRef]
- Witkowska, A.; Lewandowska, A.U.; Saniewska, D.; Falkowska, L.M. Effect of agriculture and vegetation on carbonaceous aerosol concentrations (PM2.5 and PM10) in Puszcza Borecka National Nature Reserve (Poland). Air Qual. Atmos. Health 2016, 9, 761–773. [Google Scholar] [CrossRef] [Green Version]
- Song, Z.; Li, R.; Qiu, R.; Liu, S.; Tan, C.; Li, Q.; Ge, W.; Han, X.; Tang, X.; Shi, W.; et al. Global land surface temperature influenced by vegetation cover and PM2.5 from 2001 to 2016. Remote Sens. 2018, 10, 2034. [Google Scholar] [CrossRef] [Green Version]
- Didan, K. MOD13A1 MODIS/Terra Vegetation Indices 16-Day L3 Global 500m SIN Grid V006, NASA EOSDIS Land Processes DAAC. 2015. Available online: https://lpdaac.usgs.gov/products/mod13a1v006/ (accessed on 30 October 2021).
- Hair, J.; Anderson, R.; Babin, B.; Black, W. Multivariate Data Analysis: A Global Perspective (Vol. 7); Pearson Upper Saddle River: Hoboken, NJ, USA, 2010. [Google Scholar]
- Song, Y.; Ge, Y.; Wang, J.; Ren, Z.; Liao, Y.; Peng, J. Spatial distribution estimation of malaria in northern China and its scenarios in 2020, 2030, 2040 and 2050. Malar. J. 2016, 15, 345. [Google Scholar] [CrossRef] [Green Version]
- Ge, Y.; Song, Y.; Wang, J.; Liu, W.; Ren, Z.; Peng, J.; Lu, B. Geographically weighted regression-based determinants of malaria incidences in northern China. Trans. GIS 2017, 21, 934–953. [Google Scholar] [CrossRef]
- Buchinsky, M. Estimating the asymptotic covariance matrix for quantile regression models a Monte Carlo study. J. Econom. 1995, 68, 303–338. [Google Scholar] [CrossRef]
- Koenker, R.; Machado, J.A. Goodness of fit and related inference processes for quantile regression. J. Am. Stat. Assoc. 1999, 94, 1296–1310. [Google Scholar] [CrossRef]
- Bernales, A.; Antolihao, J.; Samonte, C.; Campomanes, F.; Rojas, R.; Silapan, J. Modelling the relationship between land surface temperature and landscape patterns of land use land cover classification using multi linear regression models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 851–856. [Google Scholar] [CrossRef] [Green Version]
- Ross, Z.; English, P.B.; Scalf, R.; Gunier, R.; Smorodinsky, S.; Wall, S.; Jerrett, M. Nitrogen dioxide prediction in Southern California using land use regression modeling: Potential for environmental health analyses. J. Expo. Sci. Environ. Epidemiol. 2006, 16, 106–114. [Google Scholar] [CrossRef]
- John, O.O. Robustness of quantile regression to outliers. Am. J. Appl. Math. Stat. 2015, 3, 86–88. [Google Scholar]
- Furno, M.; Vistocco, D. Quantile Regression: Estimation and Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2018; Volume 216. [Google Scholar]




| Variable | Code | Optimal Buffer (km) | Min | Mean | Median | Max | Std | |
|---|---|---|---|---|---|---|---|---|
| PM (g/m) | / | / | 5.60 | 7.83 | 7.80 | 9.10 | 0.86 | |
| Land use: ratio (%) | Natural environments | NE | 3 | 0.38 | 12.22 | 6.51 | 63.19 | 15.38 |
| Production from natural environments | PNE | 3.5 | 0.00 | 3.87 | 0.56 | 30.04 | 7.51 | |
| Dryland agriculture | DA | 0.5 | 0.00 | 7.86 | 0.00 | 45.00 | 13.18 | |
| Built-up region | BUR | 3 | 16.08 | 61.81 | 62.75 | 78.44 | 15.62 | |
| Industrial region | IR | 3 | 0.85 | 14.93 | 13.37 | 27.04 | 8.07 | |
| Population density (persons/km) | PPDS | 5 | 110 | 3077 | 2328 | 9292 | 2767 | |
| Highway density (km/km) | HWDS | 2.5 | 0.000 | 0.821 | 0.688 | 2.600 | 0.790 | |
| Major road density (km/km) | MRDS | 4.5 | 0.169 | 1.710 | 1.828 | 3.925 | 1.093 | |
| Elevation (m) | ELV | 5 | 14.04 | 81.54 | 45.28 | 416.71 | 108.23 | |
| NDVI | NDVI | 0.5 | 0.368 | 0.534 | 0.533 | 0.732 | 0.107 | |
| Variable | Code | Optimal Buffer (km) | R | RMSE | MAE | |
|---|---|---|---|---|---|---|
| Land use: ratio (%) | Natural environments | NE | 3 | 0.187 | 0.835 | 0.706 |
| Production from natural environments | PNE | 3.5 | 0.001 | 1.129 | 0.813 | |
| Dryland agriculture | DA | 0.5 | 0.057 | 0.894 | 0.684 | |
| Built-up regions | BUR | 3 | 0.234 | 0.754 | 0.638 | |
| Industrial regions | IR | 3 | 0.033 | 0.902 | 0.741 | |
| Population density (persons/km) | PPDS | 5 | 0.002 | 0.898 | 0.735 | |
| Highway density (km/km) | HWDS | 2.5 | 0.053 | 0.847 | 0.693 | |
| Major road density (km/km) | MRDS | 4.5 | 0.037 | 0.910 | 0.746 | |
| Elevation (m) | ELV | 5 | 0.189 | 0.765 | 0.620 | |
| NDVI | NDVI | 0.5 | 0.034 | 0.905 | 0.708 | |
| Model | R | RMSE | MAE |
|---|---|---|---|
| LUQR ( = 0.37) | 0.568 | 0.569 | 0.412 |
| LUQR ( = 0.50) | 0.540 | 0.587 | 0.395 |
| LUQR ( = 0.53) | 0.564 | 0.574 | 0.385 |
| LUR | 0.430 | 0.657 | 0.511 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, P.; Song, Y. Land Use Quantile Regression Modeling of Fine Particulate Matter in Australia. Remote Sens. 2022, 14, 1370. https://doi.org/10.3390/rs14061370
Wu P, Song Y. Land Use Quantile Regression Modeling of Fine Particulate Matter in Australia. Remote Sensing. 2022; 14(6):1370. https://doi.org/10.3390/rs14061370
Chicago/Turabian StyleWu, Peng, and Yongze Song. 2022. "Land Use Quantile Regression Modeling of Fine Particulate Matter in Australia" Remote Sensing 14, no. 6: 1370. https://doi.org/10.3390/rs14061370
APA StyleWu, P., & Song, Y. (2022). Land Use Quantile Regression Modeling of Fine Particulate Matter in Australia. Remote Sensing, 14(6), 1370. https://doi.org/10.3390/rs14061370







