Assessing Desert Dust Indirect Effects on Cloud Microphysics through a Cloud Nucleation Scheme: A Case Study over the Western Mediterranean
Abstract
1. Introduction
2. Materials and Methods
2.1. The Embedded Cloud Nucleation Scheme
2.2. Methodology
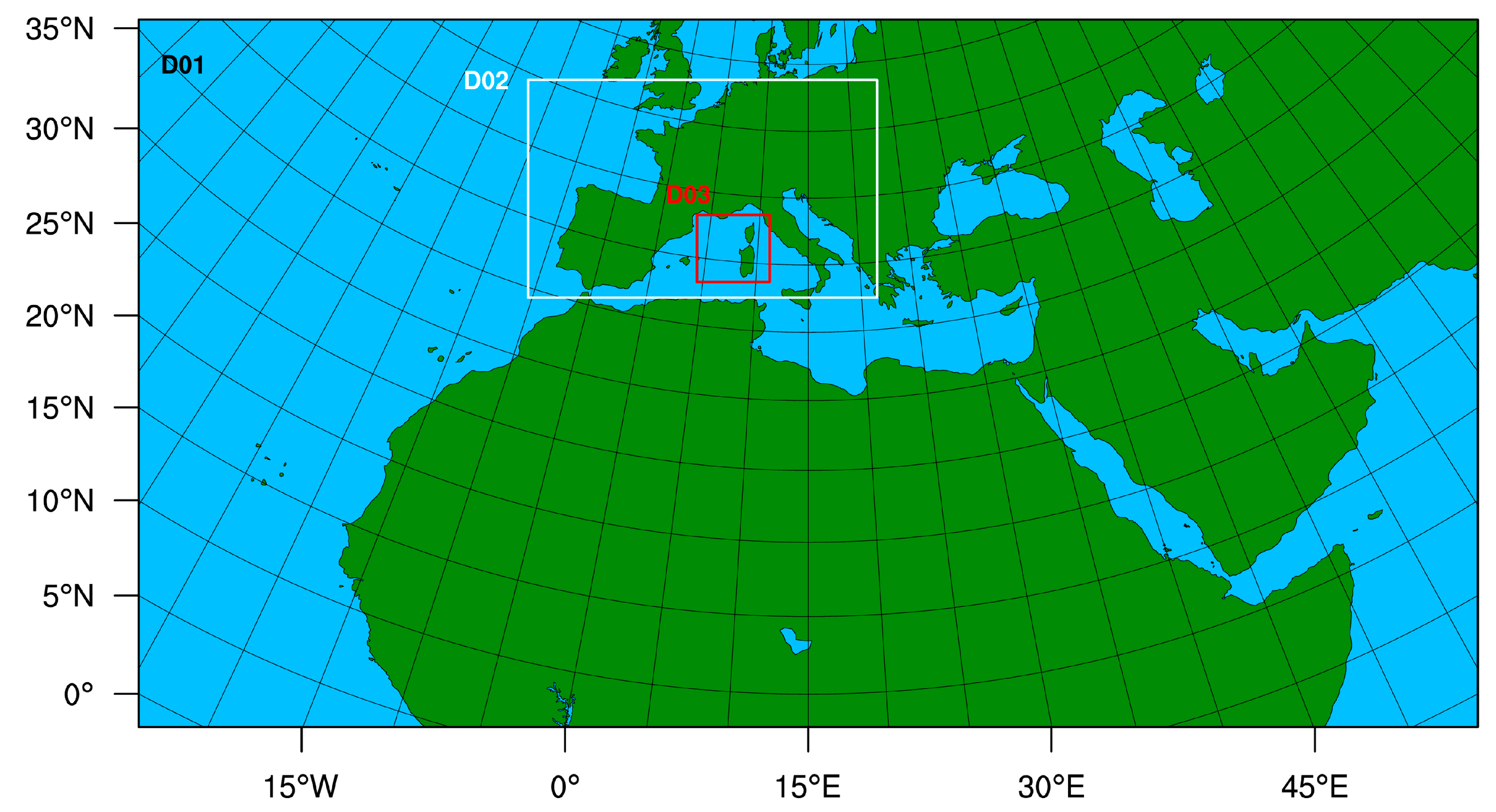
Configuration of the Modeling Experiments
3. Results
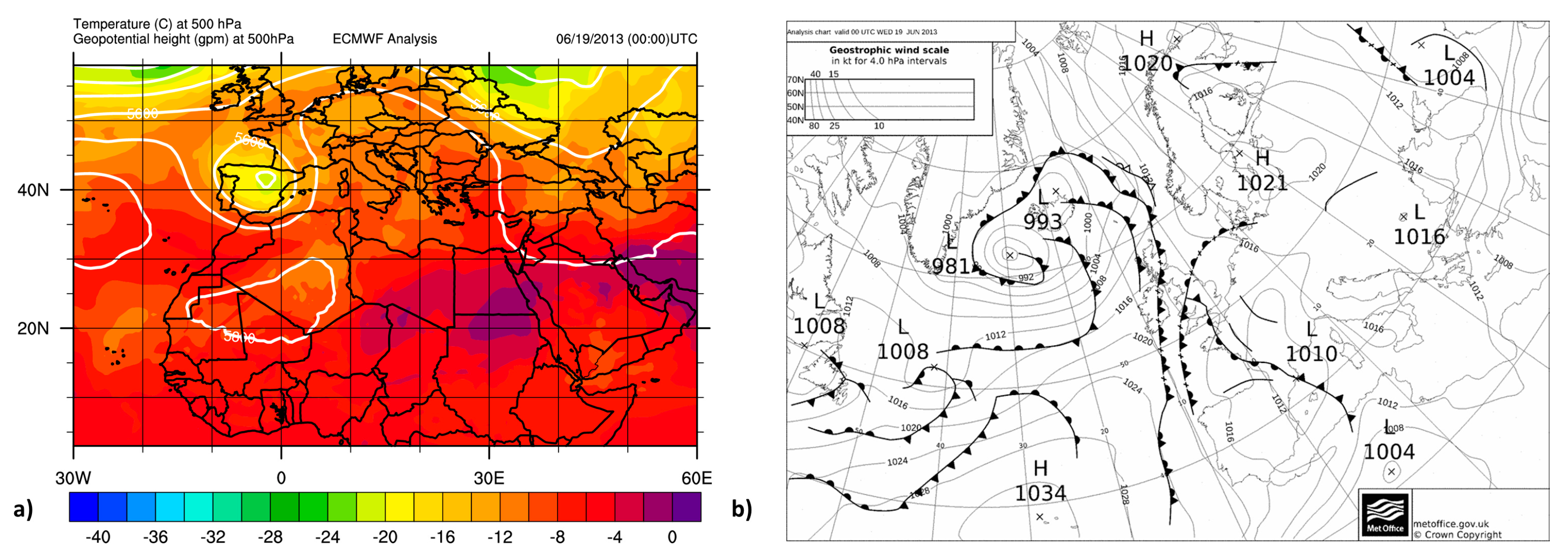
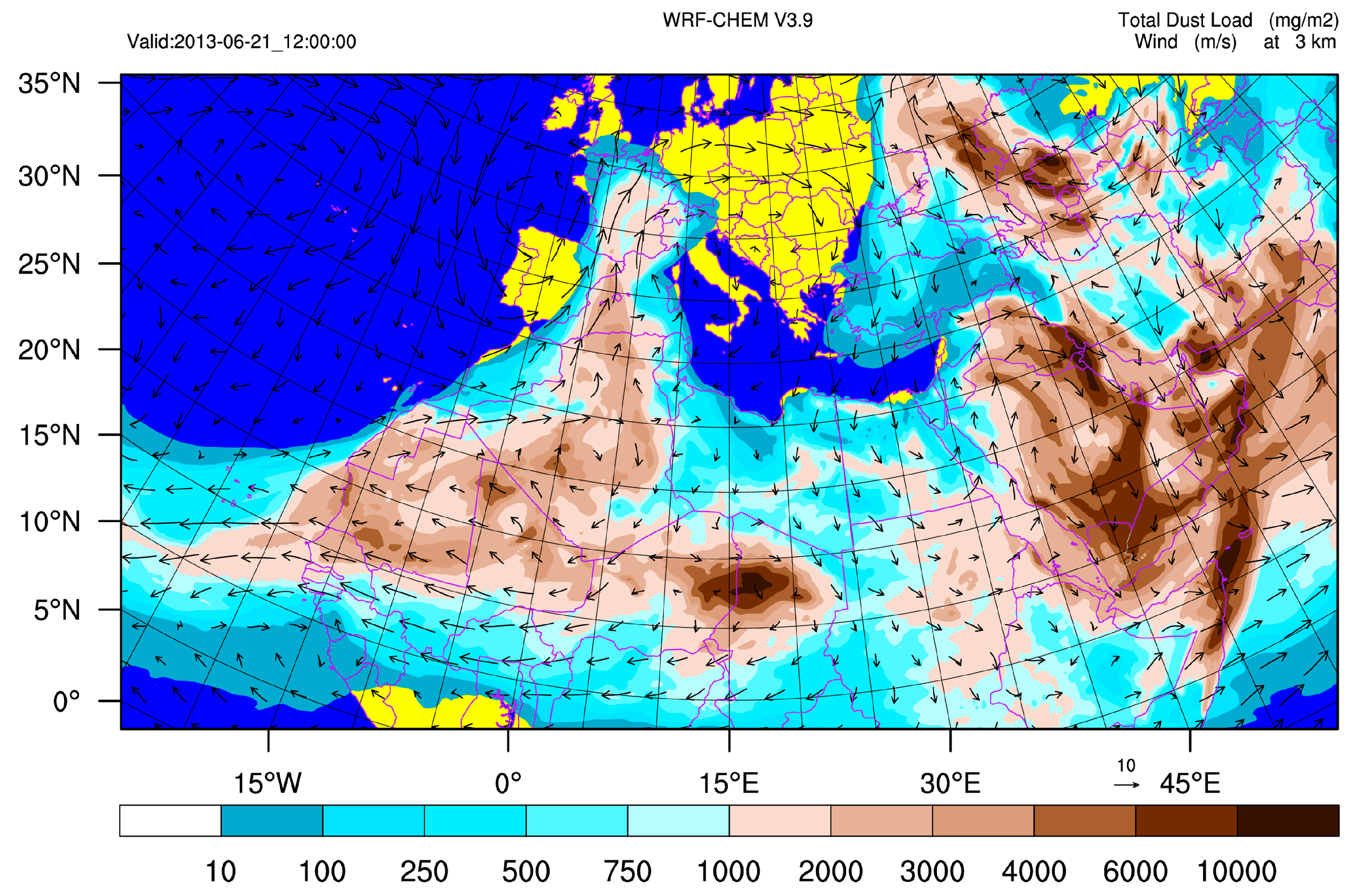
3.1. Description of the 20–25 June 2013 Synoptic Conditions
3.2. Comparison of NCCN, Nc and RH
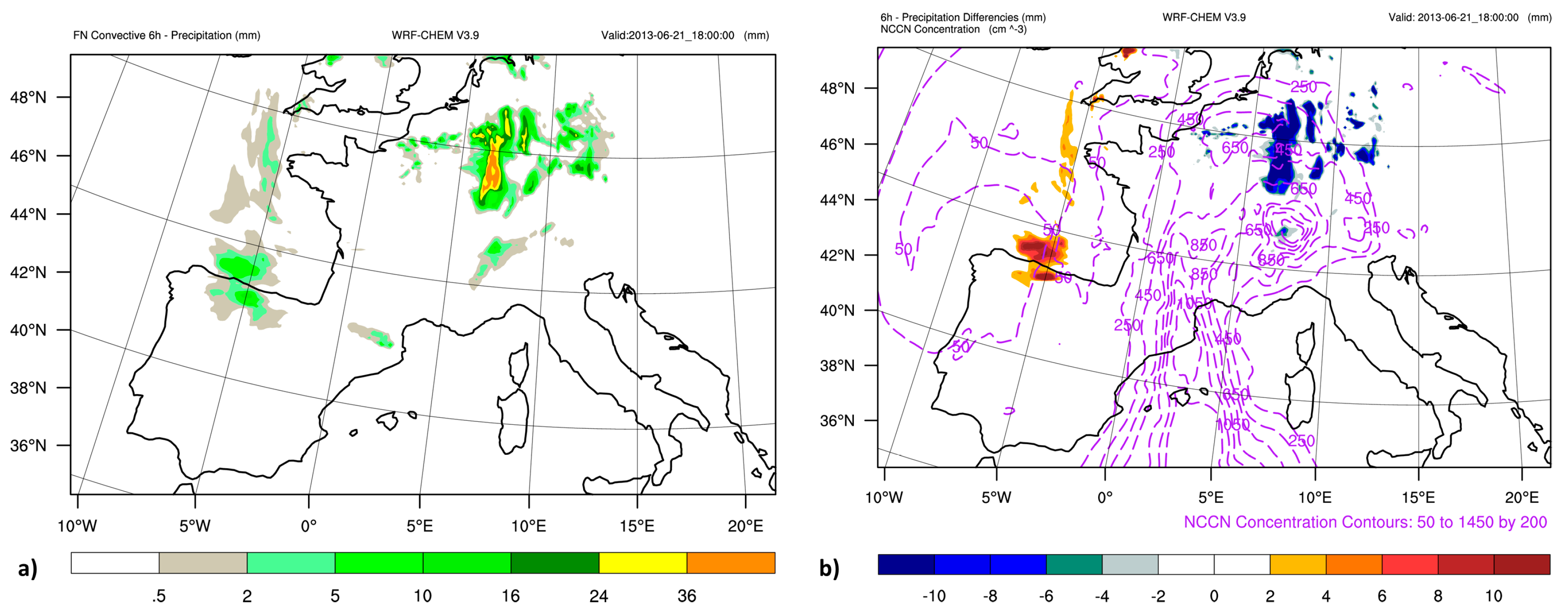
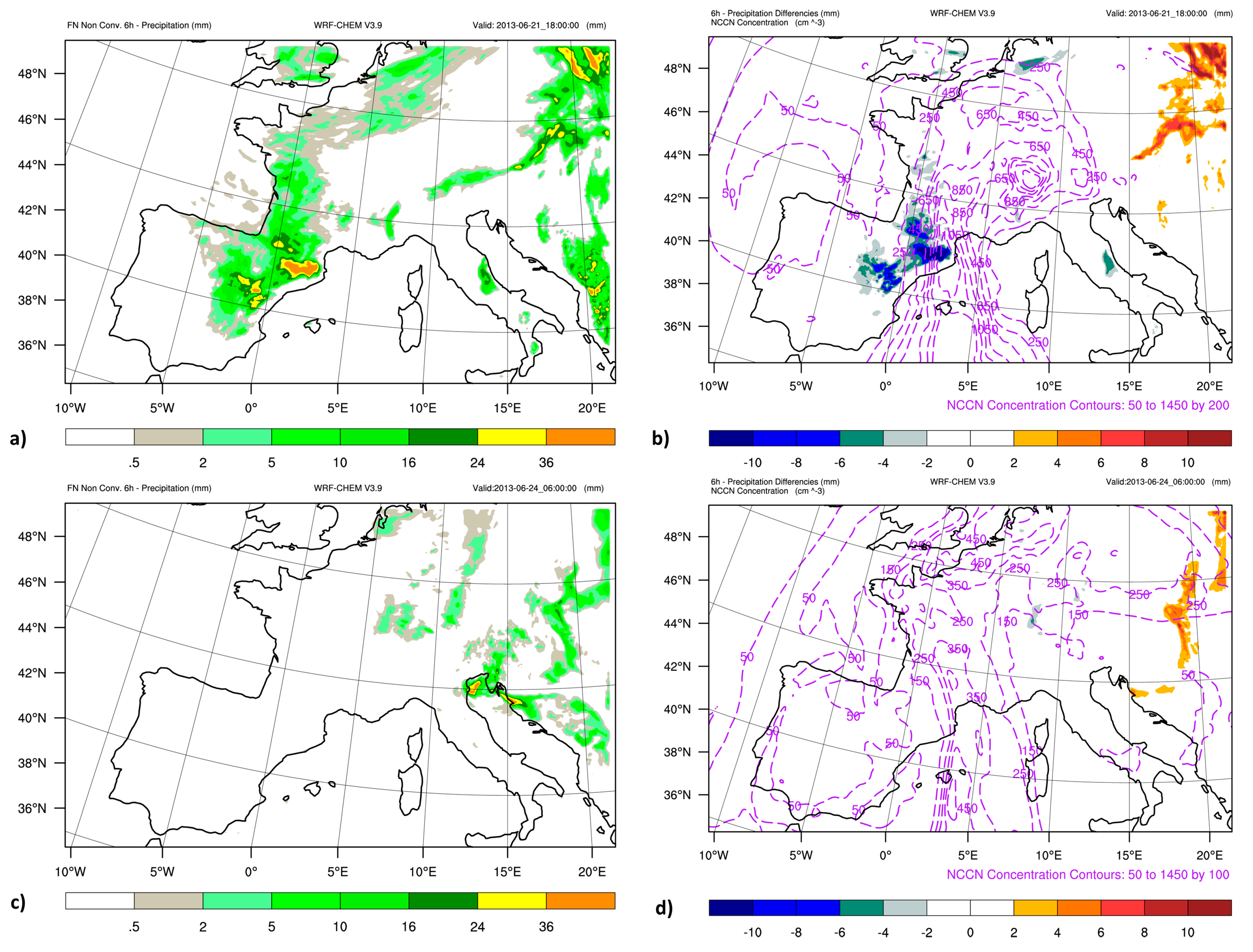
3.3. Impact on the Precipitation Pattern
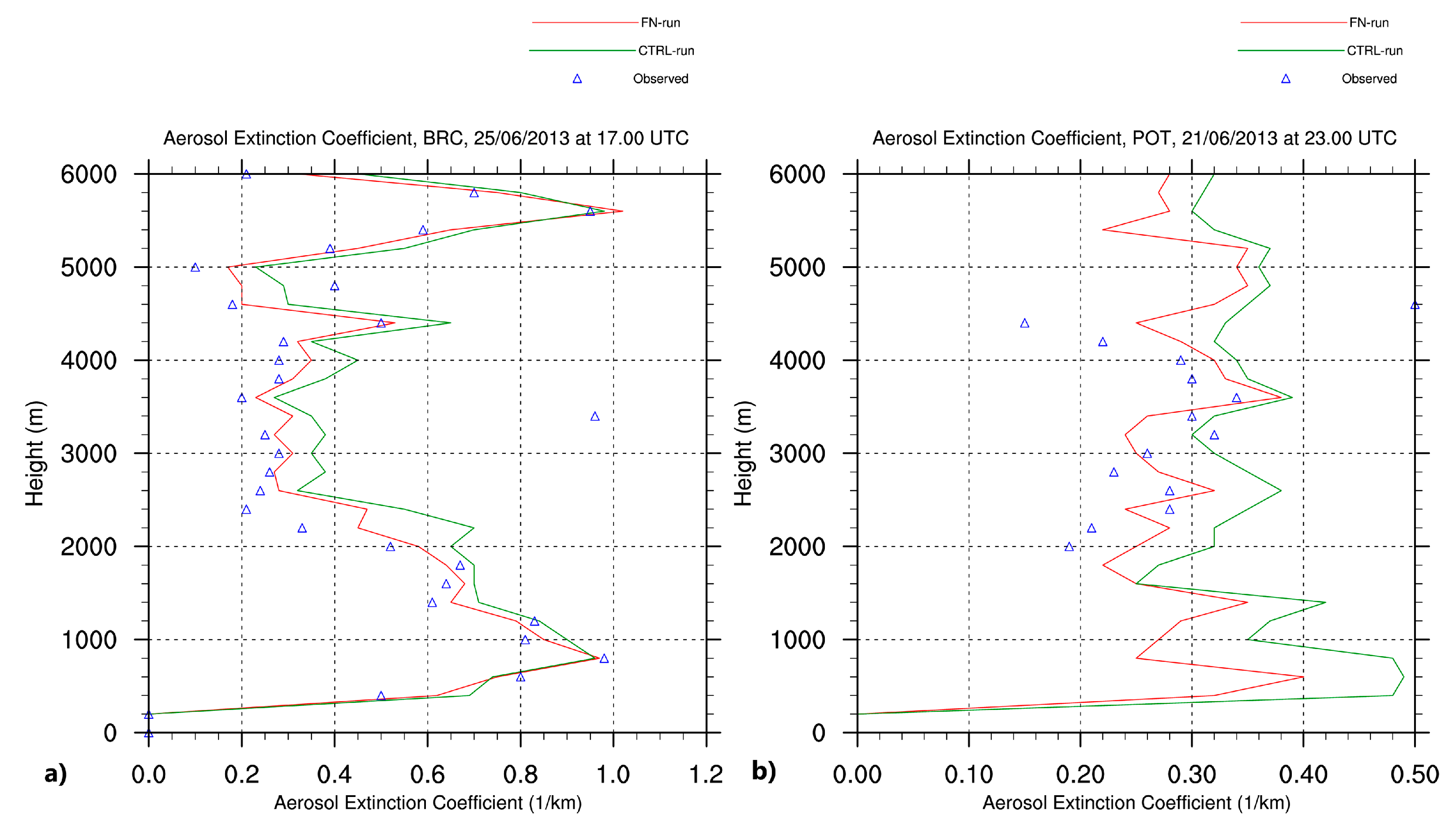
3.4. Evaluation of the FN Scheme Through the Optical Properties.
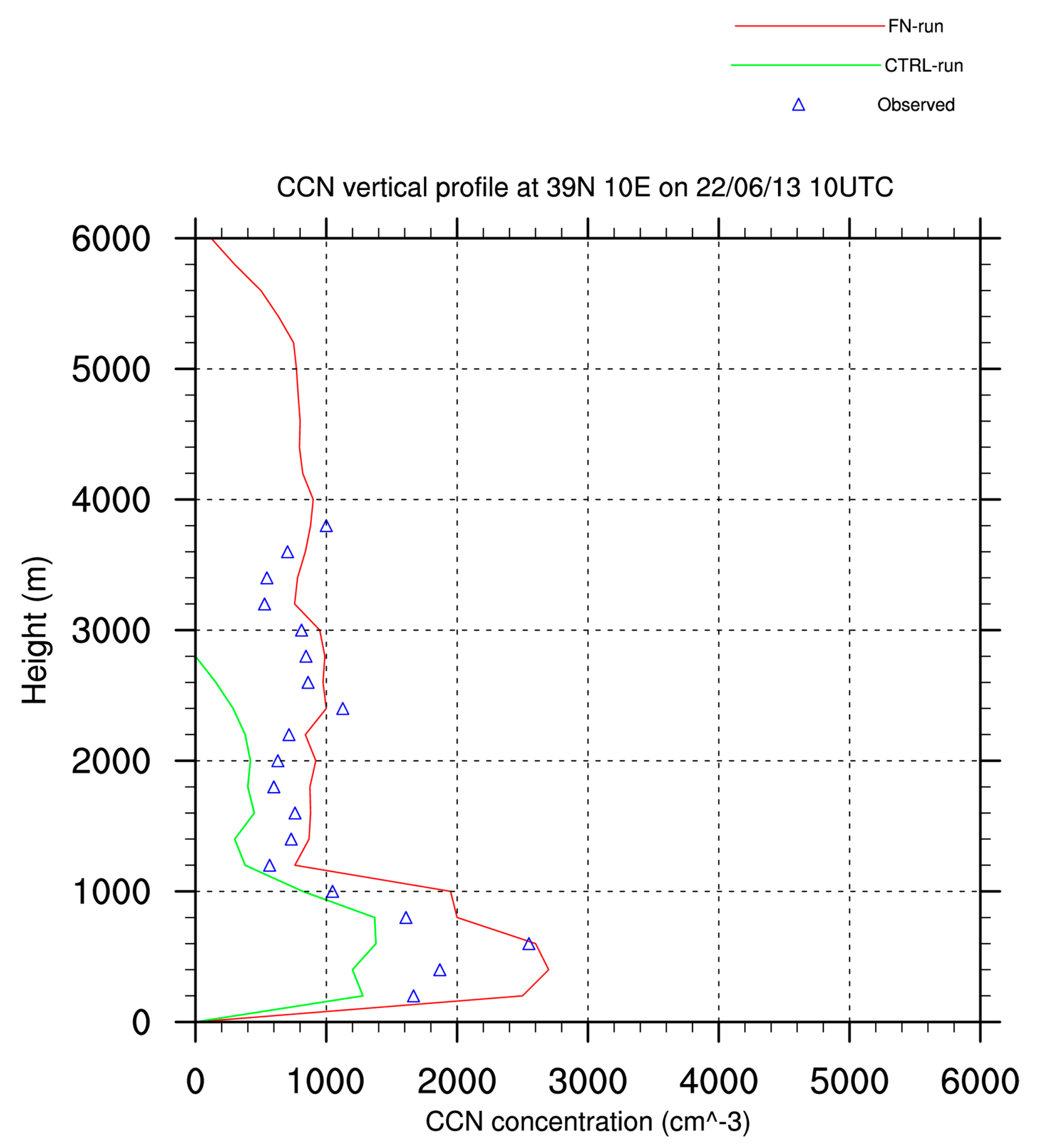
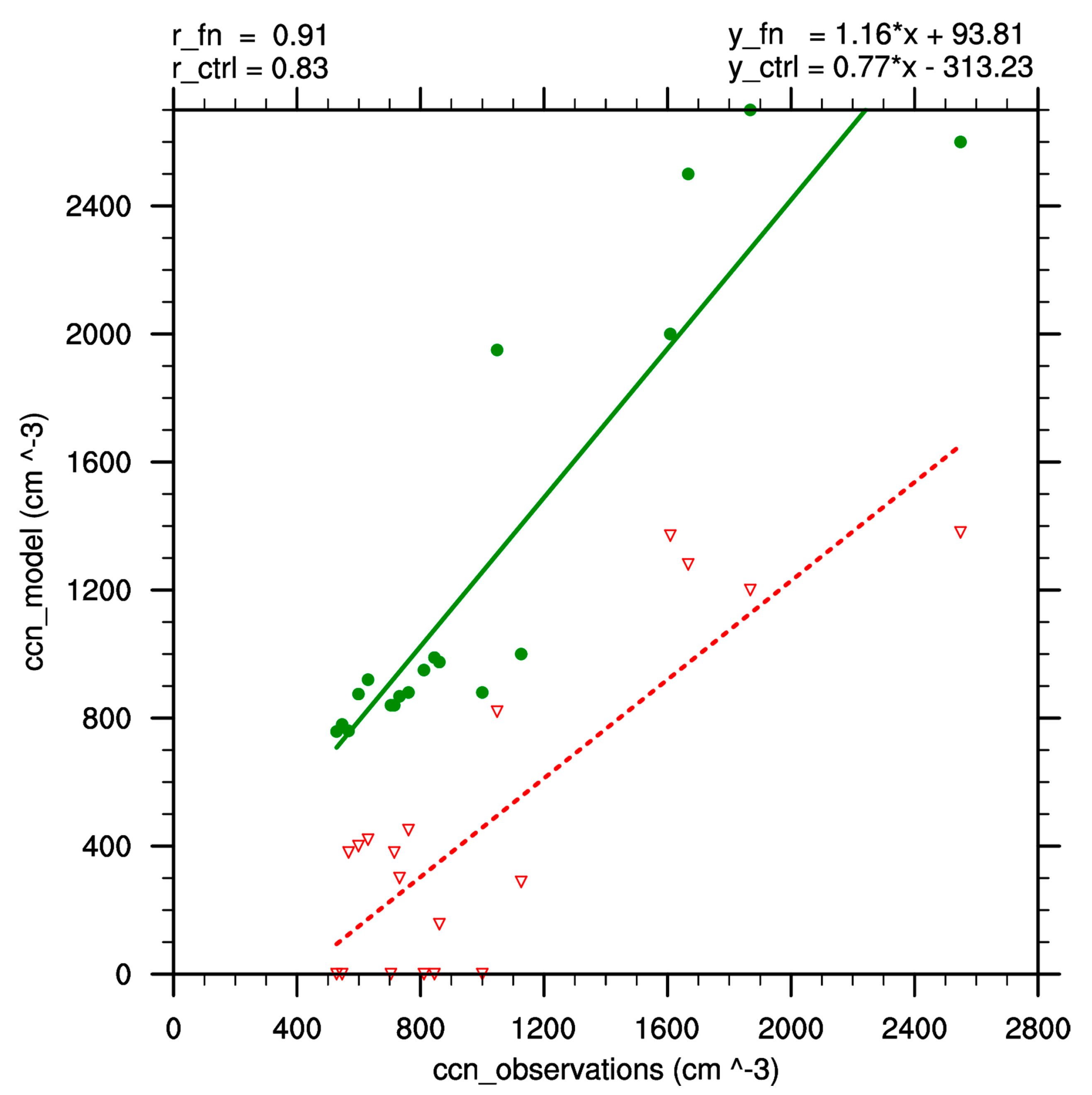
3.5. Estimation of CCN vVertical Profiles and Comparison with Observational Data
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andreae, M.O.; Charlson, R.J.; Bruynseels, F.; Storms, H.; VAN Grieken, R.; Maenhaut, W. Internal Mixture of Sea Salt, Silicates, and Excess Sulfate in Marine Aerosols. Science 1986, 232, 1620–1623. [Google Scholar] [CrossRef] [PubMed]
- Zender, C.S.; Miller, R.L.; Tegen, I. Quantifying Mineral Dust Mass Budgets: Terminology, Constraints, and Current Estimates. Eos 2004, 85, 509–512. [Google Scholar] [CrossRef]
- Ben-Ami, Y.; Koren, I.; Altaratz, O. Patterns of North African Dust Transport over the Atlantic: Winter vs. Summer, Based on CALIPSO First Year Data. Atmos. Chem. Phys. 2009, 9, 7867–7875. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Tanré, D.; Boucher, O. A Satellite View of Aerosols in the Climate System. Nature 2002, 419, 215–223. [Google Scholar] [CrossRef] [PubMed]
- Nenes, A.; Charlson, R.J.; Facchini, M.C.; Kulmala, M.; Laaksonen, A.; Seinfeld, J.H. Can Chemical Effects on Cloud Droplet Number Rival the First Indirect Effect? Geophys. Res. Lett. 2002, 29, 29-1–29-4. [Google Scholar] [CrossRef]
- Perlwitz, J.; Tegen, I.; Miller, R.L. Interactive Soil Dust Aerosol Model in the GISS GCM 1. Sensitivity of the Soil Dust Cycle to Radiative Properties of Soil Dust Aerosols. J. Geophys. Res. Atmos. 2001, 106, 18167–18192. [Google Scholar] [CrossRef]
- Myhre, G.; Grini, A.; Haywood, J.M.; Stordal, F.; Chatenet, B.; Tanré, D.; Sundet, J.K.; Isaksen, I.S.A. Modeling the Radiative Impact of Mineral Dust during the Saharan Dust Experiment (SHADE) Campaign. J. Geophys. Res. D Atmos. 2003, 108, 1–13. [Google Scholar] [CrossRef]
- Ramanathan, V.; Ramana, M.V.; Roberts, G.; Kim, D.; Corrigan, C.; Chung, C.; Winker, D. Warming Trends in Asia Amplified by Brown Cloud Solar Absorption. Nature 2007, 448, 575–578. [Google Scholar] [CrossRef]
- Pérez, C.; Nickovic, S.; Baldasano, J.M.; Sicard, M.; Rocadenbosch, F.; Cachorro, V.E. A Long Saharan Dust Event over the Western Mediterranean: Lidar, Sun Photometer Observations, and Regional Dust Modeling. J. Geophys. Res. Atmos. 2006, 111, D15214. [Google Scholar] [CrossRef]
- Heinold, B.; Tegen, I.; Schepanski, K.; Hellmuth, O. Dust Radiative Feedback on Saharan Boundary Layer Dynamics and Dust Mobilization. Geophys. Res. Lett. 2008, 35, L20817. [Google Scholar] [CrossRef]
- Lau, K.M.; Kim, M.K.; Kim, K.M. Asian Summer Monsoon Anomalies Induced by Aerosol Direct Forcing: The Role of the Tibetan Plateau. Clim. Dyn. 2006, 26, 855–864. [Google Scholar] [CrossRef]
- Lau, K.M.; Kim, K.M.; Sud, Y.C.; Walker, G.K. A GCM Study of the Response of the Atmospheric Water Cycle of West Africa and the Atlantic to Saharan Dust Radiative Forcing. Ann. Geophys. 2009, 27, 4023–4037. [Google Scholar] [CrossRef]
- Lim, K.S.S.; Hong, S.Y. Development of an Effective Double-Moment Cloud Microphysics Scheme with Prognostic Cloud Condensation Nuclei (CCN) for Weather and Climate Models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Herut, B.; Collier, R.; Krom, M.D. The Role of Dust in Supplying Nitrogen and Phosphorus to the Southeast Mediterranean. Limnol. Oceanogr. 2002, 47, 870–878. [Google Scholar] [CrossRef]
- Spyrou, C.; Mitsakou, C.; Kallos, G.; Louka, P.; Vlastou, G. An Improved Limited Area Model for Describing the Dust Cycle in the Atmosphere. J. Geophys. Res. Atmos. 2010, 115, D17211. [Google Scholar] [CrossRef]
- Meskhidze, N.; Chameides, W.L.; Nenes, A. Dust and Pollution: A Recipe for Enhanced Ocean Fertilization? J. Geophys. Res. D Atmos. 2005, 110, D03301. [Google Scholar] [CrossRef]
- Mahowald, N.; Jickells, T.D.; Baker, A.R.; Artaxo, P.; Benitez-Nelson, C.R.; Bergametti, G.; Bond, T.C.; Chen, Y.; Cohen, D.D.; Herut, B.; et al. Global Distribution of Atmospheric Phosphorus Sources, Concentrations and Deposition Rates, and Anthropogenic Impacts. Glob. Biogeochem. Cycles 2008, 22, GB4026. [Google Scholar] [CrossRef]
- Lelieveld, J.; Evans, J.S.; Fnais, M.; Giannadaki, D.; Pozzer, A. The Contribution of Outdoor Air Pollution Sources to Premature Mortality on a Global Scale. Nature 2015, 525, 367–371. [Google Scholar] [CrossRef]
- Prospero, J.M. Saharan Dust Transport Over the North Atlantic Ocean and Mediterranean: An Overview BT. In The Impact of Desert Dust Across the Mediterranean; Guerzoni, S., Chester, R., Eds.; Springer: Dordrecht, The Netherlands, 1996; pp. 133–151. [Google Scholar] [CrossRef]
- Twomey, S. The Nuclei of Natural Cloud Formation Part II: The Supersaturation in Natural Clouds and the Variation of Cloud Droplet Concentration. Geofis. Pura E Appl. 1959, 43, 243–249. [Google Scholar] [CrossRef]
- Albrecht, B.A. Aerosols, Cloud Microphysics, and Fractional Cloudiness. Science 1989, 245, 1227–1230. [Google Scholar] [CrossRef] [PubMed]
- DeMott, P.J.; Prenni, A.J.; Liu, X.; Kreidenweis, S.M.; Petters, M.D.; Twohy, C.H.; Richardson, M.S.; Eidhammer, T.; Rogers, D.C. Predicting Global Atmospheric Ice Nuclei Distributions and Their Impacts on Climate. Proc. Natl. Acad. Sci. USA 2010, 107, 11217–11222. [Google Scholar] [CrossRef] [PubMed]
- Sassen, K.; DeMott, P.J.; Prospero, J.M.; Poellot, M.R. Saharan Dust Storms and Indirect Aerosol Effects on Clouds: CRYSTAL-FACE Results. Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Andreae, M.O.; Rosenfeld, D. Aerosol-Cloud-Precipitation Interactions. Part 1. The Nature and Sources of Cloud-Active Aerosols. Earth-Sci. Rev. 2008, 89, 13–41. [Google Scholar] [CrossRef]
- Twomey, S. The Influence of Pollution on the Shortwave Albedo of Clouds. J. Atmos. Sci. 1977, 34, 1149–1152. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Koren, I.; Remer, L.A.; Rosenfeld, D.; Rudich, Y. The Effect of Smoke, Dust, and Pollution Aerosol on Shallow Cloud Development over the Atlantic Ocean. Proc. Natl. Acad. Sci. USA 2005, 102, 11207–11212. [Google Scholar] [CrossRef]
- Teller, A.; Levin, Z. The Effects of Aerosols on Precipitation and Dimensions of Subtropical Clouds: A Sensitivity Study Using a Numerical Cloud Model. Atmos. Chem. Phys. 2006, 6, 67–80. [Google Scholar] [CrossRef]
- Pincus, R.; Baker, M.B. Effect of Precipitation on the Albedo Susceptibility of Clouds in the Marine Boundary Layer. Nature 1994, 372, 250–252. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R. Radiative Forcing and Climate Response. J. Geophys. Res. 1997, 102, 6831–6864. [Google Scholar] [CrossRef]
- Fernández-González, S.; Wang, P.K.; Gascón, E.; Valero, F.; Sánchez, J.L. Latent Cooling and Microphysics Effects in Deep Convection. Atmos. Res. 2016, 180, 189–199. [Google Scholar] [CrossRef]
- Khain, A.; Pokrovsky, A.; Pinsky, M.; Seifert, A.; Phillips, V. Simulation of Effects of Atmospheric Aerosols on Deep Turbulent Convective Clouds Using a Spectral Microphysics Mixed-Phase Cumulus Cloud Model. Part I: Model Description and Possible Applications. J. Atmos. Sci. 2004, 61, 2963–2982. [Google Scholar] [CrossRef]
- Cotton, W.R.; Zhang, H.; McFarquhar, G.M.; Saleeby, S.M. Should We Consider Polluting Hurricanes to Reduce Their Intensity? J. Weather Modif. 2007, 39, 70–73. [Google Scholar]
- Rosenfeld, D.; Lohmann, U.; Raga, G.B.; O’Dowd, C.D.; Kulmala, M.; Fuzzi, S.; Reissell, A.; Andreae, M.O. Flood or Drought: How Do Aerosols Affect Precipitation? Science 2008, 321, 1309–1313. [Google Scholar] [CrossRef] [PubMed]
- Khain, A.; Rosenfeld, D.; Pokrovsky, A. Aerosol Impact on the Dynamics and Microphysics of Deep Convective Clouds. Q. J. R. Meteorol. Soc. 2005, 131, 2639–2663. [Google Scholar] [CrossRef]
- Lebo, Z.J.; Morrison, H.; Seinfeld, J.H. Are Simulated Aerosol-Induced Effects on Deep Convective Clouds Strongly Dependent on Saturation Adjustment? Atmos. Chem. Phys. 2012, 12, 9941–9964. [Google Scholar] [CrossRef]
- Andreae, M.O.; Rosenfeld, D.; Artaxo, P.; Costa, A.A.; Frank, G.P.; Longo, K.M.; Silva-Dias, M.A.F. Smoking Rain Clouds over the Amazon. Science 2004, 303, 1337–1342. [Google Scholar] [CrossRef]
- Koren, I.; Remer, L.A.; Altaratz, O.; Martins, J.V.; Davidi, A. Aerosol-Induced Changes of Convective Cloud Anvils Produce Strong Climate Warming. Atmos. Chem. Phys. 2010, 10, 5001–5010. [Google Scholar] [CrossRef]
- Niu, F.; Li, Z. Systematic Variations of Cloud Top Temperature and Precipitation Rate with Aerosols over the Global Tropics. Atmos. Chem. Phys. 2012, 12, 8491–8498. [Google Scholar] [CrossRef]
- Charlson, R.J.; Seinfeld, J.H.; Nenes, A.; Kulmala, M.; Laaksonen, A.; Facchini, M.C. Atmospheric Science. Reshaping the Theory of Cloud Formation. Science 2001, 292, 2025–2026. [Google Scholar] [CrossRef]
- Solomos, S.; Kallos, G.; Kushta, J.; Astitha, M.; Tremback, C.; Nenes, A.; Levin, Z. An Integrated Modeling Study on the Effects of Mineral Dust and Sea Salt Particles on Clouds and Precipitation. Atmos. Chem. Phys. 2011, 11, 873–892. [Google Scholar] [CrossRef]
- Yin, Y.; Chen, L. The Effects of Heating by Transported Dust Layers on Cloud and Precipitation: A Numerical Study. Atmos. Chem. Phys. 2007, 7, 3497–3505. [Google Scholar] [CrossRef]
- Wilcox, E.M. Direct and Semi-Direct Radiative Forcing of Smoke Aerosols over Clouds. Atmos. Chem. Phys. 2012, 12, 139–149. [Google Scholar] [CrossRef]
- Lynn, B.; Khain, A.; Rosenfeld, D.; Woodley, W.L. Effects of Aerosols on Precipitation from Orographic Clouds. J. Geophys. Res. Atmos. 2007, 112, D10225. [Google Scholar] [CrossRef]
- Zhang, H.; McFarquhar, G.M.; Saleeby, S.M.; Cotton, W.R. Impacts of Saharan Dust as CCN on the Evolution of an Idealized Tropical Cyclone. Geophys. Res. Lett. 2007, 34, L14812. [Google Scholar] [CrossRef]
- Menon, S.; Del Genio, A.D.; Koch, D.; Tselioudis, G. GCM Simulations of the Aerosol Indirect Effect: Sensitivity to Cloud Parameterization and Aerosol Burden. J. Atmos. Sci. 2002, 59, 692–713. [Google Scholar] [CrossRef]
- Ghan, S.J.; Easter, R.C.; Chapman, E.G.; Abdul-Razzak, H.; Zhang, Y.; Leung, L.R.; Laulainen, N.S.; Saylor, R.D.; Zaveri, R.A. A Physically Based Estimate of Radiative Forcing by Anthropogenic Sulfate Aerosol. J. Geophys. Res. Atmos. 2001, 106, 5279–5293. [Google Scholar] [CrossRef]
- Khain, A.P.; BenMoshe, N.; Pokrovsky, A. Factors Determining the Impact of Aerosols on Surface Precipitation from Clouds: An Attempt at Classification. J. Atmos. Sci. 2008, 65, 1721–1748. [Google Scholar] [CrossRef]
- Khain, A. Simulation of a Supercell Storm in Clean and Dirty Atmosphere Using Weather Research and Forecast Model with Spectral Bin Microphysics. J. Geophys. Res. Atmos. 2009, 114, 11419. [Google Scholar] [CrossRef]
- Han, J.-Y.; Baik, J.-J.; Lee, H. Urban Impacts on Precipitation. Asia-Pac. J. Atmos. Sci. 2014, 50, 17–30. [Google Scholar] [CrossRef]
- Lerach, D.G.; Gaudet, B.J.; Cotton, W.R. Idealized Simulations of Aerosol Influences on Tornadogenesis. Geophys. Res. Lett. 2008, 35, 1–6. [Google Scholar] [CrossRef]
- Wang, C.A. Modeling Study of the Response of Tropical Deep Convection to the Increase of Cloud Condensation Nuclei Concentration: 1. Dynamics and Microphysics. J. Geophys. Res. Atmos. 2005, 110, D21211. [Google Scholar] [CrossRef]
- Grell, G.A.; Freitas, S.R. A Scale and Aerosol Aware Stochastic Convective Parameterization for Weather and Air Quality Modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Berg, L.K.; Shrivastava, M.; Easter, R.C.; Fast, J.D.; Chapman, E.G.; Liu, Y.; Ferrare, R.A. A New WRF-Chem Treatment for Studying Regional-Scale Impacts of Cloud Processes on Aerosol and Trace Gases in Parameterized Cumuli. Geosci. Model Dev. 2015, 8, 409–429. [Google Scholar] [CrossRef]
- Kang, J.Y.; Bae, S.Y.; Park, R.S.; Han, J.Y. Aerosol Indirect Effects on the Predicted Precipitation in a Global Weather Forecasting Model. Atmosphere 2019, 10, 392. [Google Scholar] [CrossRef]
- Fountoukis, C.; Nenes, A. Continued Development of a Cloud Droplet Formation Parameterization for Global Climate Models. J. Geophys. Res. D Atmos. 2005, 110, D11212. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, B.J.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3, NCAR Tech. Note, NCAR/TN-468+STR; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar] [CrossRef]
- Grell, G.A.; Peckham, S.E.; Schmitz, R.; McKeen, S.A.; Frost, G.; Skamarock, W.C.; Eder, B. Fully Coupled “Online” Chemistry within the WRF Model. Atmos. Environ. 2005, 39, 6957–6975. [Google Scholar] [CrossRef]
- Kessler, E. On the Distribution and Continuity of Water Substance in Atmospheric Circulations; Kessler, E., Ed.; American Meteorological Society: Boston, MA, USA, 1969; pp. 1–84. [Google Scholar] [CrossRef]
- Lin, Y.-L.; Farley, R.; Orville, H. Bulk Parameterization of the Snow Field in a Cloud Model. J. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Ferrier, B.S.; Jin, Y.; Lin, Y.; Black, T.; Rogers, E.; Dimego, G. Implementation of a New Grid-Scale Cloud and Precipitation Scheme in the NCEP Eta Model. In Proceedings of the 15th Conference on Numerical Weather Prediction, State College, PA, USA, 11 August 2002; pp. 280–283. [Google Scholar]
- Hong, S.-Y.; Kim, J.-H.; Lim, J.; Dudhia, J. The WRF Single Moment Microphysics Scheme (WSM). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Thompson, G.; Field, P.R.; Rasmussen, R.M.; Hall, W.D. Explicit Forecasts of Winter Precipitation Using an Improved Bulk Microphysics Scheme. Part II: Implementation of a New Snow Parameterization. Mon. Weather Rev. 2008, 136, 5095–5115. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of Cloud Microphysics on the Development of Trailing Stratiform Precipitation in a Simulated Squall Line: Comparison of One- and Two-Moment Schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part I: Analysis of the Role of the Spectral Shape Parameter. J. Atmos. Sci. 2005, 62, 3051–3064. [Google Scholar] [CrossRef]
- Milbrandt, J.A.; Yau, M.K. A Multimoment Bulk Microphysics Parameterization. Part II: A Proposed Three-Moment Closure and Scheme Description. J. Atmos. Sci. 2005, 62, 3065–3081. [Google Scholar] [CrossRef]
- Shi, Z.; Tan, Y.; Liu, Y.; Liu, J.; Lin, X.; Wang, M.; Luan, J. Effects of Relative Humidity on Electrification and Lightning Discharges in Thunderstorms. Terr. Atmos. Ocean. Sci. 2018, 29, 695–708. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Lim, K.-S.S.; Lee, Y.-H.; Ha, J.-C.; Kim, H.-W.; Ham, S.-J.; Dudhia, J. Evaluation of the WRF Double-Moment 6-Class Microphysics Scheme for Precipitating Convection. Adv. Meteorol. 2010, 2010, 707253. [Google Scholar] [CrossRef]
- Reddy, M.V.; Prasad, S.B.S.; Krishna, U.V.M.; Reddy, K.K. Effect of Cumulus and Microphysical Parameterizations on the JAL Cyclone Prediction. Indian J. Radio Space Phys. 2014, 43, 103–123. [Google Scholar]
- Mayor, Y.G.; Mesquita, M.D.S. Numerical Simulations of the 1 May 2012 Deep Convection Event over Cuba: Sensitivity to Cumulus and Microphysical Schemes in a High-Resolution Model. Adv. Meteorol. 2015, 2015. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A Revised Approach to Ice Microphysical Processes for the Bulk Parameterization of Clouds and Precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Morrison, H.; Milbrandt, J.A. Parameterization of Cloud Microphysics Based on the Prediction of Bulk Ice Particle Properties. Part I: Scheme Description and Idealized Tests. J. Atmos. Sci. 2015, 72, 287–311. [Google Scholar] [CrossRef]
- Cohard, J.-M.; Pinty, J.-P. A Comprehensive Two-Moment Warm Microphysical Bulk Scheme. I: Description and Tests. Q. J. R. Meteorol. Soc. 2000, 126, 1815–1842. [Google Scholar] [CrossRef]
- Khairoutdinov, M.; Kogan, Y. A New Cloud Physics Parameterization in a Large-Eddy Simulation Model of Marine Stratocumulus. Mon. Weather Rev. 2000, 128, 229–243. [Google Scholar] [CrossRef]
- Nenes, A.; Seinfeld, J.H. Parameterization of Cloud Droplet Formation in Global Climate Models. J. Geophys. Res. Atmos. 2003, 108, 1–14. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N.; Noone, K. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change. Phys. Today 1998, 51, 88. [Google Scholar] [CrossRef]
- Krikken, F.; Steeneveld, G. Modelling the re-intensification of tropical storm Erin (2007) over Oklahoma: Understanding the key role of downdraft formulation. Tellus A Dyn. Meteorol. Oceanogr. 2012, 64, 61. [Google Scholar] [CrossRef]
- Freitas, S.R.; Grell, G.A.; Molod, A.; Thompson, M.A.; Putman, W.M.; Santos e Silva, C.M.; Souza, E.P. Assessing the Grell-Freitas Convection Parameterization in the NASA GEOS Modeling System. J. Adv. Model. Earth Syst. 2018, 10, 1266–1289. [Google Scholar] [CrossRef] [PubMed]
- Chin, M.; Rood, R.B.; Lin, S.J.; Müller, J.F.; Thompson, A.M. Atmospheric Sulfur Cycle Simulated in the Global Model GOCART: Model Description and Global Properties. J. Geophys. Res. Atmos. 2000, 105, 24671–24687. [Google Scholar] [CrossRef]
- Ginoux, P.; Chin, M.; Tegen, I.; Goddard, T.; Prospero, J.M.; Holben, B.; Dubovik, O.; Lin, S.-J. Sources and distributions of dust aerosols simulated with the GOCART model. J. Geophys. Res. 2001, 106, 20255–20273. [Google Scholar] [CrossRef]
- Jones, S.L.; Creighton, G.A.; Kuchera, E.L.; Rentschler, S.A. Adapting WRF-CHEM GOCART for Fine-Scale Dust Forecasting. In AGU Fall Meeting Abstracts; 2011; Volume 2011, p. U14A-06. Available online: https://ui.adsabs.harvard.edu/abs/2011AGUFM.U14A..06J/abstract (accessed on 7 September 2020).
- Jones, S.L.; Adams-Selin, R.; Hunt, E.D.; Creighton, G.A.; Cetola, J.D. Update on Modifications to WRF-CHEM GOCART for Fine-Scale Dust Forecasting at AFWA. In AGU Fall Meeting Abstracts; 2012; Volume 2012, p. A33D-0188. Available online: https://ui.adsabs.harvard.edu/abs/2012AGUFM.A33D0188J/abstract (accessed on 7 September 2020).
- Marticorena, B.; Bergametti, G. Modeling the Atmospheric Dust Cycle: 1. Design of a Soil-Derived Dust Emission Scheme. J. Geophys. Res. Atmos. 1995, 100, 16415–16430. [Google Scholar] [CrossRef]
- LeGrand, S.L.; Polashenski, C.; Letcher, T.W.; Creighton, G.A.; Peckham, S.E.; Cetola, J.D. The AFWA Dust Emission Scheme for the GOCART Aerosol Model in WRF-Chem v3.8.1. Geosci. Model Dev. 2019, 12, 131–166. [Google Scholar] [CrossRef]
- White, B.R. Soil Transport by Winds on Mars. J. Geophys. Res. Solid Earth 1979, 84, 4643–4651. [Google Scholar] [CrossRef]
- Rizza, U.; Barnaba, F.; Marcello Miglietta, M.; Mangia, C.; Di Liberto, L.; Dionisi, D.; Costabile, F.; Grasso, F.; Paolo Gobbi, G. WRF-Chem Model Simulations of a Dust Outbreak over the Central Mediterranean and Comparison with Multi-Sensor Desert Dust Observations. Atmos. Chem. Phys. 2017, 17, 93–115. [Google Scholar] [CrossRef]
- Fécan, F.; Marticorena, B.; Bergametti, G. Parametrization of the Increase of the Aeolian Erosion Threshold Wind Friction Velocity Due to Soil Moisture for Arid and Semi-Arid Areas. Ann. Geophys. 1998, 17, 149–157. [Google Scholar] [CrossRef]
- Kok, J.F. Does the Size Distribution of Mineral Dust Aerosols Depend on the Wind Speed at Emission? Atmos. Chem. Phys. 2011, 11, 10149–10156. [Google Scholar] [CrossRef]
- Wesely, M.L. Parameterization of Surface Resistances to Gaseous Dry Deposition in Regional-Scale Numerical Models. Atmos. Environ. 1989, 23, 1293–1304. [Google Scholar] [CrossRef]
- Tsarpalis, K.; Papadopoulos, A.; Mihalopoulos, N.; Spyrou, C.; Michaelides, S.; Katsafados, P. The Implementation of a Mineral Dust Wet Deposition Scheme in the GOCART-AFWA Module of the WRF Model. Remote Sens. 2018, 10, 1595. [Google Scholar] [CrossRef]
- Marshall, G. Statistical Methods in the Atmospheric Sciences, 2nd ed.; Wilks, D.S., Ed.; International Geophysics Series; Academic Press: New York, NY, USA, 1995; Volume 59, 464p, ISBN10: 0127519653, ISBN13: 978-0127519654. [Google Scholar]
- Shinozuka, Y.; Clarke, A.D.; Nenes, A.; Jefferson, A.; Wood, R.; McNaughton, C.S.; Ström, J.; Tunved, P.; Redemann, J.; Thornhill, K.L.; et al. The Relationship between Cloud Condensation Nuclei (CCN) Concentration and Light Extinction of Dried Particles: Indications of Underlying Aerosol Processes and Implications for Satellite-Based CCN Estimates. Atmos. Chem. Phys. 2015, 15, 7585–7604. [Google Scholar] [CrossRef]
- Denjean, C.; Cassola, F.; Mazzino, A.; Triquet, S.; Chevaillier, S.; Grand, N.; Bourrianne, T.; Momboisse, G.; Sellegri, K.; Schwarzenbock, A.; et al. Size Distribution and Optical Properties of Mineral Dust Aerosols Transported in the Western Mediterranean. Atmos. Chem. Phys. 2016, 16, 1081–1104. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative Forcing by Long-Lived Greenhouse Gases: Calculations with the AER Radiative Transfer Models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Monin, A.S.; Obukhov, A.M. Basic Laws of Turbulent Mixing in the Surface Layer of the Atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 1954, 151, e187. [Google Scholar]
- Chen, F.; Dudhia, J. Coupling and Advanced Land Surface-Hydrology Model with the Penn State-NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Janjić, Z.I. Nonsingular Implementation of the Mellor-Yamada Level 2.5 Scheme in the NCEP Meso Model; National Centers for Encironmental Prediction: Washington, DC, USA, 2001; pp. 1–61.
- Hermida, L.; Merino, A.; Sánchez, J.L.; Fernández-González, S.; García-Ortega, E.; López, L. Characterization of Synoptic Patterns Causing Dust Outbreaks That Affect the Arabian Peninsula. Atmos. Res. 2018, 199, 29–39. [Google Scholar] [CrossRef]
- Jung, C.H.; Yoon, Y.J.; Kang, H.J.; Gim, Y.; Lee, B.Y.; Ström, J.; Krejci, R.; Tunved, P. The Seasonal Characteristics of Cloud Condensation Nuclei (CCN) in the Arctic Lower Troposphere. Tellusser. B Chem. Phys. Meteorol. 2018, 70, 1–13. [Google Scholar] [CrossRef]
- Almeida, G.P.; Brito, J.; Morales, C.A.; Andrade, M.F.; Artaxo, P. Measured and Modelled Cloud Condensation Nuclei (CCN) Concentration in São Paulo, Brazil: The Importance of Aerosol Size-Resolved Chemical Composition on CCN Concentration Prediction. Atmos. Chem. Phys. 2014, 14, 7559–7572. [Google Scholar] [CrossRef]
- Burkart, J.; Steiner, G.; Reischl, G.; Hitzenberger, R. Long-Term Study of Cloud Condensation Nuclei (CCN) Activation of the Atmospheric Aerosol in Vienna. Atmos. Environ. 2011, 45, 5751–5759. [Google Scholar] [CrossRef]
- Fountoukis, C.; Nenes, A.; Meskhidze, N.; Bahreini, R.; Conant, W.C.; Jonsson, H.; Murphy, S.; Sorooshian, A.; Varutbangkul, V.; Brechtel, F.; et al. Aerosol-Cloud Drop Concentration Closure for Clouds Sampled during the International Consortium for Atmospheric Research on Transport and Transformation 2004 Campaign. J. Geophys. Res. Atmos. 2007, 112, 112. [Google Scholar] [CrossRef]
- Pringle, K.J.; Carslaw, K.S.; Spracklen, D.V.; Mann, G.M.; Chipperfield, M.P. The Relationship between Aerosol and Cloud Drop Number Concentrations in a Global Aerosol Microphysics Model. Atmos. Chem. Phys. 2009, 9, 4131–4144. [Google Scholar] [CrossRef]
- Ackerman, A.S.; Toon, O.B.; Stevens, D.E.; Coakley, J.A. Enhancement of Cloud Cover and Suppression of Nocturnal Drizzle in Stratocumulus Polluted by Haze. Geophys. Res. Lett. 2003, 30, 1381. [Google Scholar] [CrossRef]
- Beydoun, H.; Hoose, C. Aerosol-Cloud-Precipitation Interactions in the Context of Convective Self-Aggregation. J. Adv. Model. Earth Syst. 2019, 11, 1066–1087. [Google Scholar] [CrossRef]
- Barthlott, C.; Hoose, C. Aerosol Effects on Clouds and Precipitation over Central Europe in Different Weather Regimes. J. Atmos. Sci. 2018, 75, 4247–4264. [Google Scholar] [CrossRef]
- Jia, H.; Ma, X.; Yu, F.; Liu, Y.; Yin, Y. Distinct Impacts of Increased Aerosols on Cloud Droplet Number Concentration of Stratus/Stratocumulus and Cumulus. Geophys. Res. Lett. 2019, 46, 13517–13525. [Google Scholar] [CrossRef]
- Karydis, V.A.; Tsimpidi, A.P.; Bacer, S.; Pozzer, A.; Nenes, A.; Lelieveld, J. Global Impact of Mineral Dust on Cloud Droplet Number Concentration. Atmos. Chem. Phys. 2017, 17, 5601–5621. [Google Scholar] [CrossRef]
- Fountoukis, C.; Ackermann, L.; Ayoub, M.A.; Gladich, I.; Hoehn, R.D.; Skillern, A. Impact of Atmospheric Dust Emission Schemes on Dust Production and Concentration over the Arabian Peninsula. Model. Earth Syst. Environ. 2016, 2, 115. [Google Scholar] [CrossRef]
- Liu, J.; Li, Z. Estimation of Cloud Condensation Nuclei Concentration from Aerosol Optical Quantities: Influential Factors and Uncertainties. Atmos. Chem. Phys. 2014, 14, 471–483. [Google Scholar] [CrossRef]





| Observations | ||
|---|---|---|
| Model | Yes | No |
| Yes | a | B |
| No | c | D |
| Model Configuration | |
|---|---|
| Model | WRF/Chem 3.9 [55,56] |
| Initial and boundary conditions | ECMWF (0.5° × 0.5°) |
| Emissions scheme | GOCART/AFWA [83] |
| Microphysics scheme | WDM6 [13,67] |
| Cumulus scheme | GF [52] |
| Radiation scheme | RRTMG [93] |
| Surface layer scheme | Monin–Obukov Similarity Theory [94] |
| Land surface scheme | Noah Land surface model [95] |
| Boundary layer scheme | Melor-Yamanda-Janjic [96] |
| Time step | 60 s |
| Radiation time step | 18 min |
| Cumulus time step | 60 s |
| AB Area | |||||
|---|---|---|---|---|---|
| Precipitation Thresholds (mm) | 0.5 | 1 | 5 | 15 | 25 |
| FN-BIAS | 1.7 | 1.5 | 1.4 | 1.8 | 1.6 |
| CTRL-BIAS | 2.0 | 1.8 | 1.7 | 2.1 | 2.1 |
| FN-FAR | 0.38 | 0.32 | 0.31 | 0.39 | 0.37 |
| CTRL-FAR | 0.45 | 0.39 | 0.39 | 0.46 | 0.45 |
| FN-FOM | 0.28 | 0.25 | 0.26 | 0.27 | 0.27 |
| CTRL-FOM | 0.29 | 0.28 | 0.28 | 0.29 | 0.28 |
| CD Area | |||||
|---|---|---|---|---|---|
| Precipitation Thresholds (mm) | 0.5 | 1 | 5 | 15 | 25 |
| FN-BIAS | 1.1 | 1.4 | 1.3 | 1.3 | 1.2 |
| CTRL-BIAS | 0.8 | 0.6 | 0.6 | 0.5 | 0.3 |
| FN-FAR | 0.31 | 0.31 | 0.30 | 0.30 | 0.30 |
| CTRL-FAR | 0.28 | 0.27 | 0.28 | 0.27 | 0.25 |
| FN-FOM | 0.25 | 0.26 | 0.25 | 0.24 | 0.24 |
| CTRL-FOM | 0.32 | 0.38 | 0.37 | 0.35 | 0.39 |
| EF Area | |||||
|---|---|---|---|---|---|
| Precipitation Thresholds (mm) | 0.5 | 1 | 5 | 15 | 25 |
| FN-BIAS | 1.3 | 1.4 | 1.2 | 1.4 | 1.4 |
| CTRL-BIAS | 0.4 | 0.3 | 0.2 | 0.3 | 0.3 |
| FN-FAR | 0.31 | 0.31 | 0.29 | 0.30 | 0.30 |
| CTRL-FAR | 0.26 | 0.25 | 0.24 | 0.26 | 0.25 |
| FN-FOM | 0.25 | 0.26 | 0.24 | 0.26 | 0.25 |
| CTRL-FOM | 0.36 | 0.38 | 0.40 | 0.39 | 0.38 |
| BRC | FN (1/km) | CTRL (1/km) |
|---|---|---|
| BIAS | 0.013 | 0.070 |
| RMSE | 0.14 | 0.17 |
| POT | FN (1/km) | CTRL (1/km) |
|---|---|---|
| BIAS | 0.028 | 0.041 |
| RMSE | 0.048 | 0.066 |
| FN-Observed (cm−3) | CTRL-Observed (cm−3) | |
|---|---|---|
| BIAS | 38 | −280 |
| RMSE | 125 | 358 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsarpalis, K.; Katsafados, P.; Papadopoulos, A.; Mihalopoulos, N. Assessing Desert Dust Indirect Effects on Cloud Microphysics through a Cloud Nucleation Scheme: A Case Study over the Western Mediterranean. Remote Sens. 2020, 12, 3473. https://doi.org/10.3390/rs12213473
Tsarpalis K, Katsafados P, Papadopoulos A, Mihalopoulos N. Assessing Desert Dust Indirect Effects on Cloud Microphysics through a Cloud Nucleation Scheme: A Case Study over the Western Mediterranean. Remote Sensing. 2020; 12(21):3473. https://doi.org/10.3390/rs12213473
Chicago/Turabian StyleTsarpalis, Konstantinos, Petros Katsafados, Anastasios Papadopoulos, and Nikolaos Mihalopoulos. 2020. "Assessing Desert Dust Indirect Effects on Cloud Microphysics through a Cloud Nucleation Scheme: A Case Study over the Western Mediterranean" Remote Sensing 12, no. 21: 3473. https://doi.org/10.3390/rs12213473
APA StyleTsarpalis, K., Katsafados, P., Papadopoulos, A., & Mihalopoulos, N. (2020). Assessing Desert Dust Indirect Effects on Cloud Microphysics through a Cloud Nucleation Scheme: A Case Study over the Western Mediterranean. Remote Sensing, 12(21), 3473. https://doi.org/10.3390/rs12213473








