Effusion Rates on Mt. Etna and Their Influence on Lava Flow Hazard Assessment
Abstract
:1. Introduction
2. Materials and Methods
3. Results
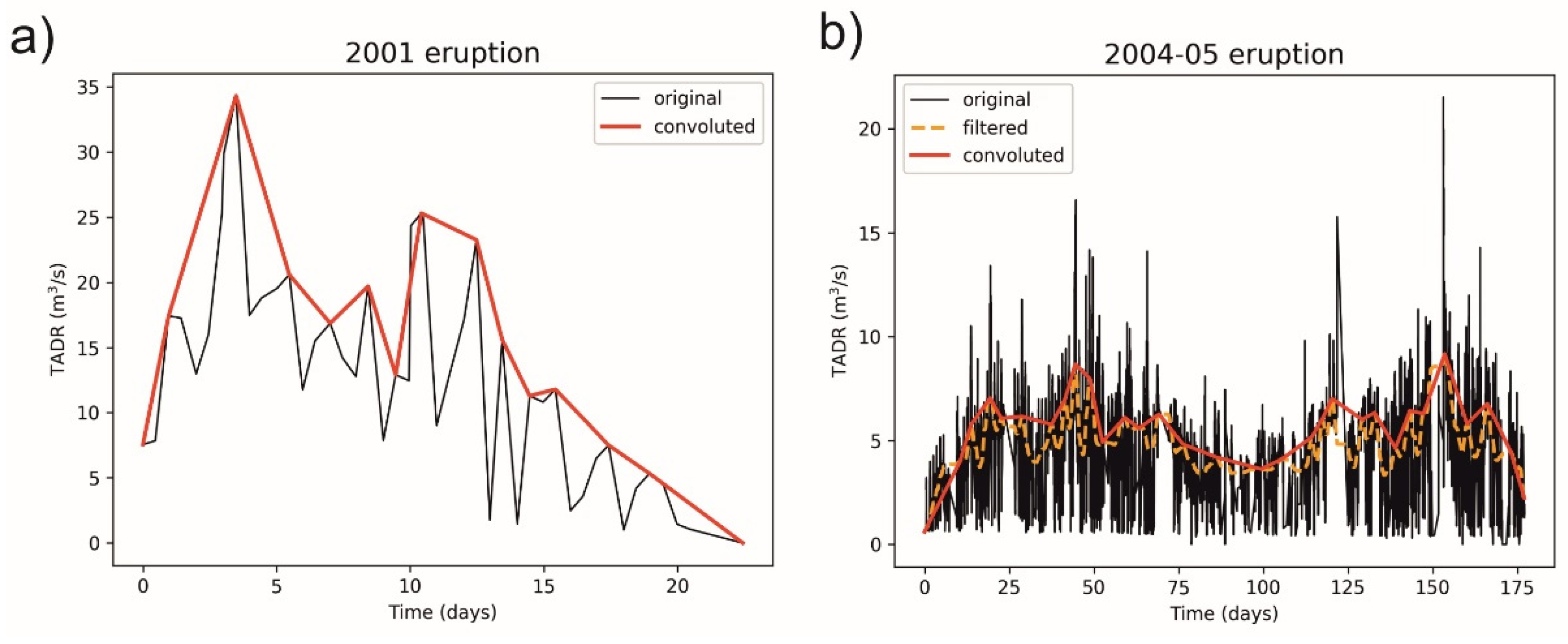
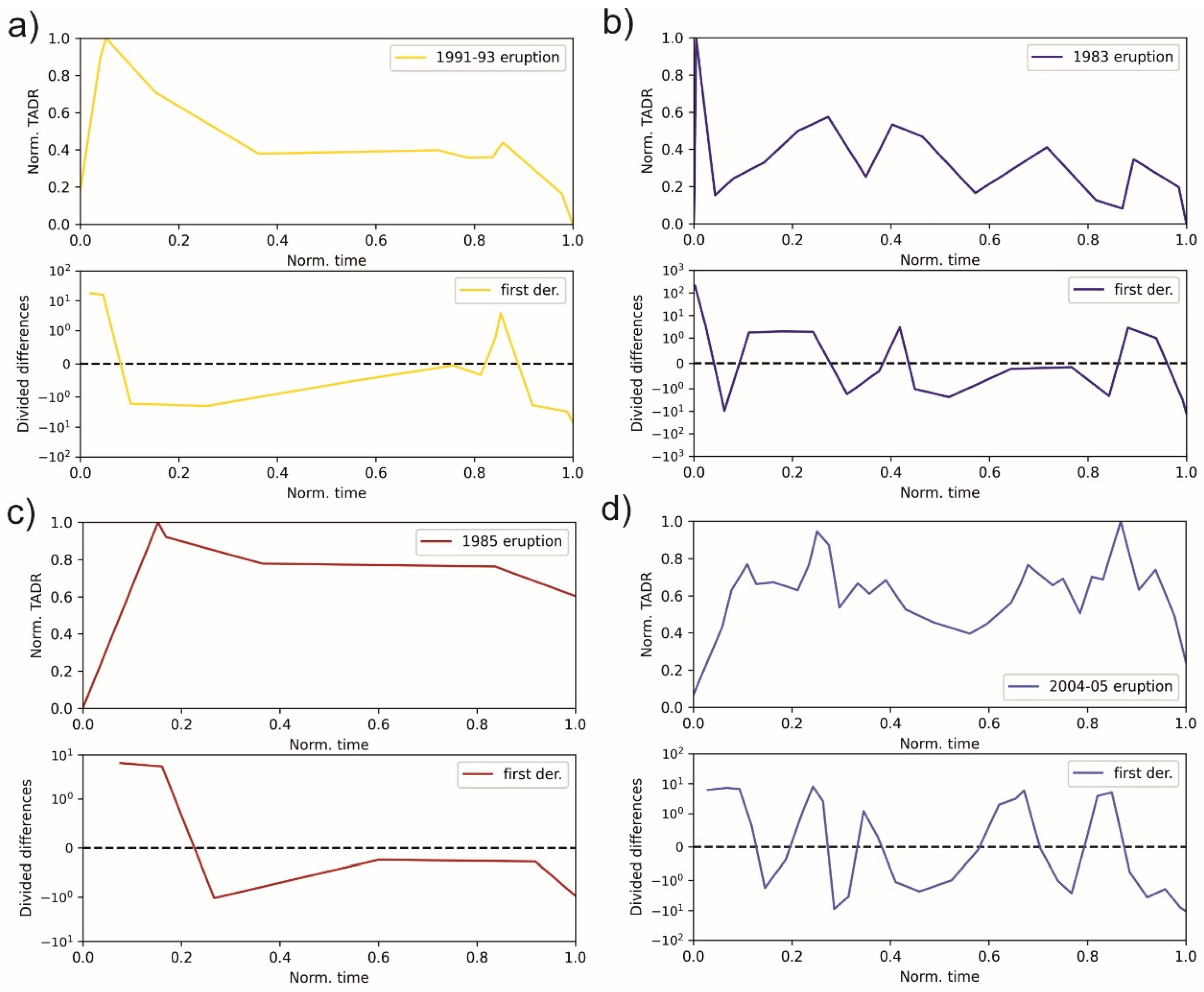
3.1. Analysis of the TADR Curves
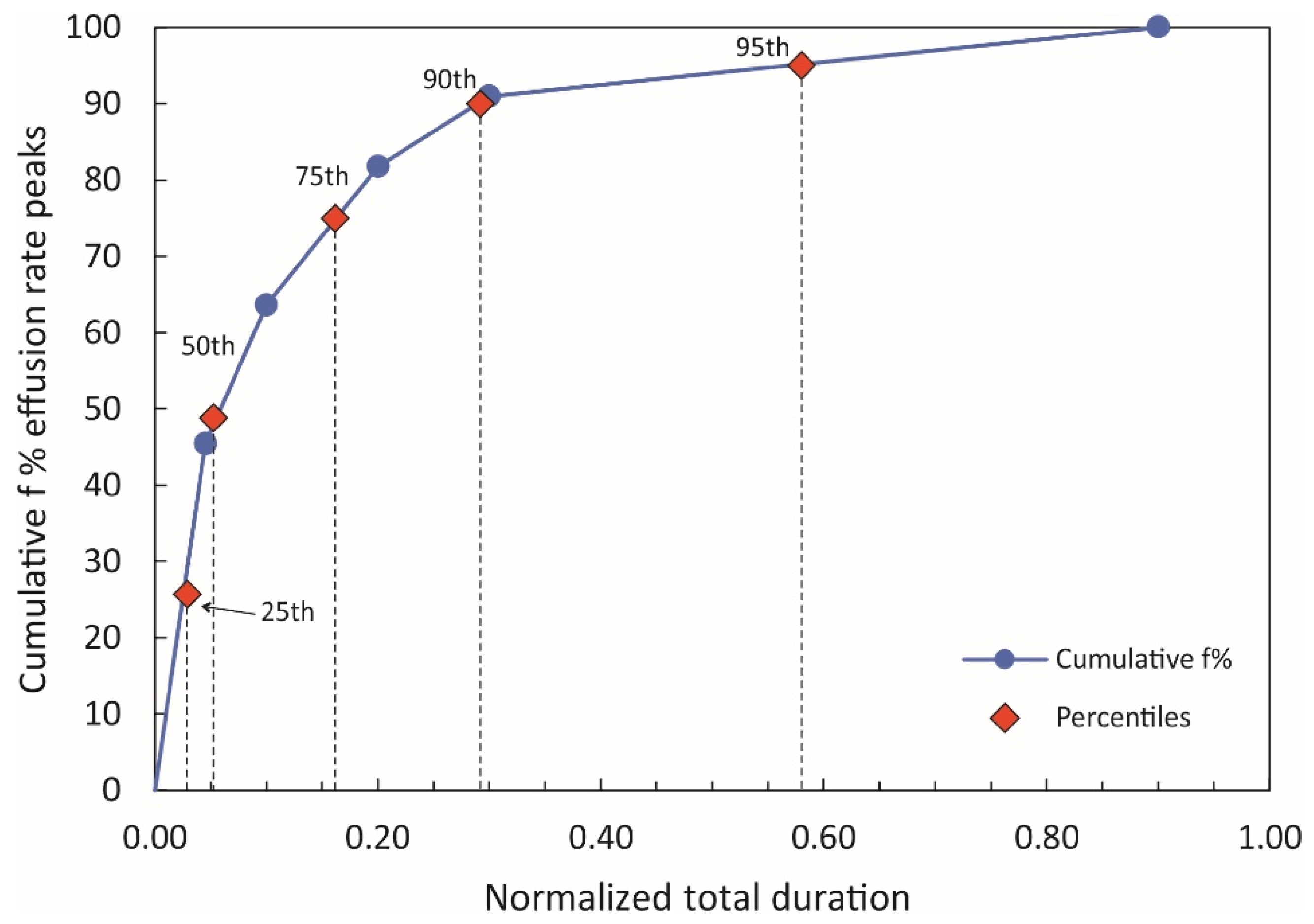
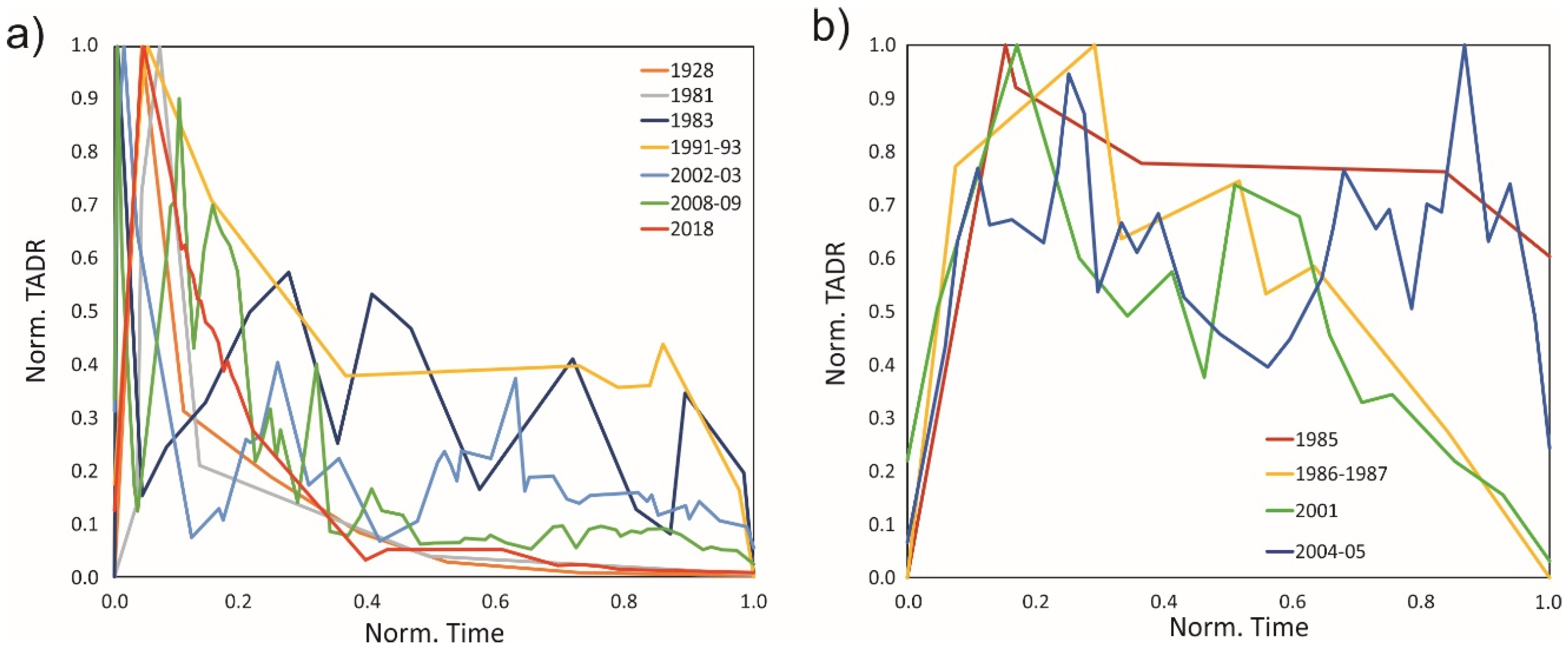
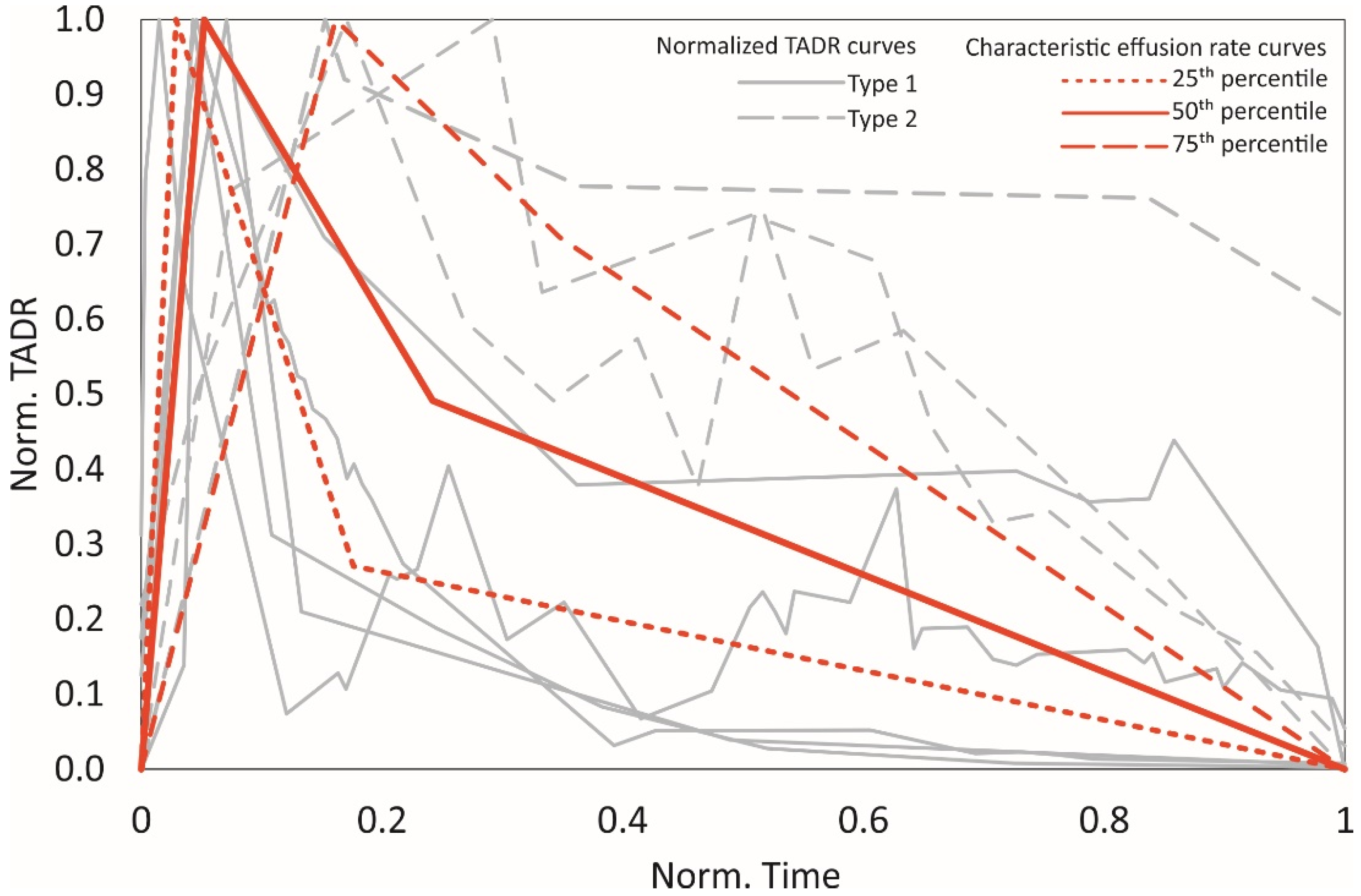
3.2. Definition of “Characteristic” Effusion Rate Curves
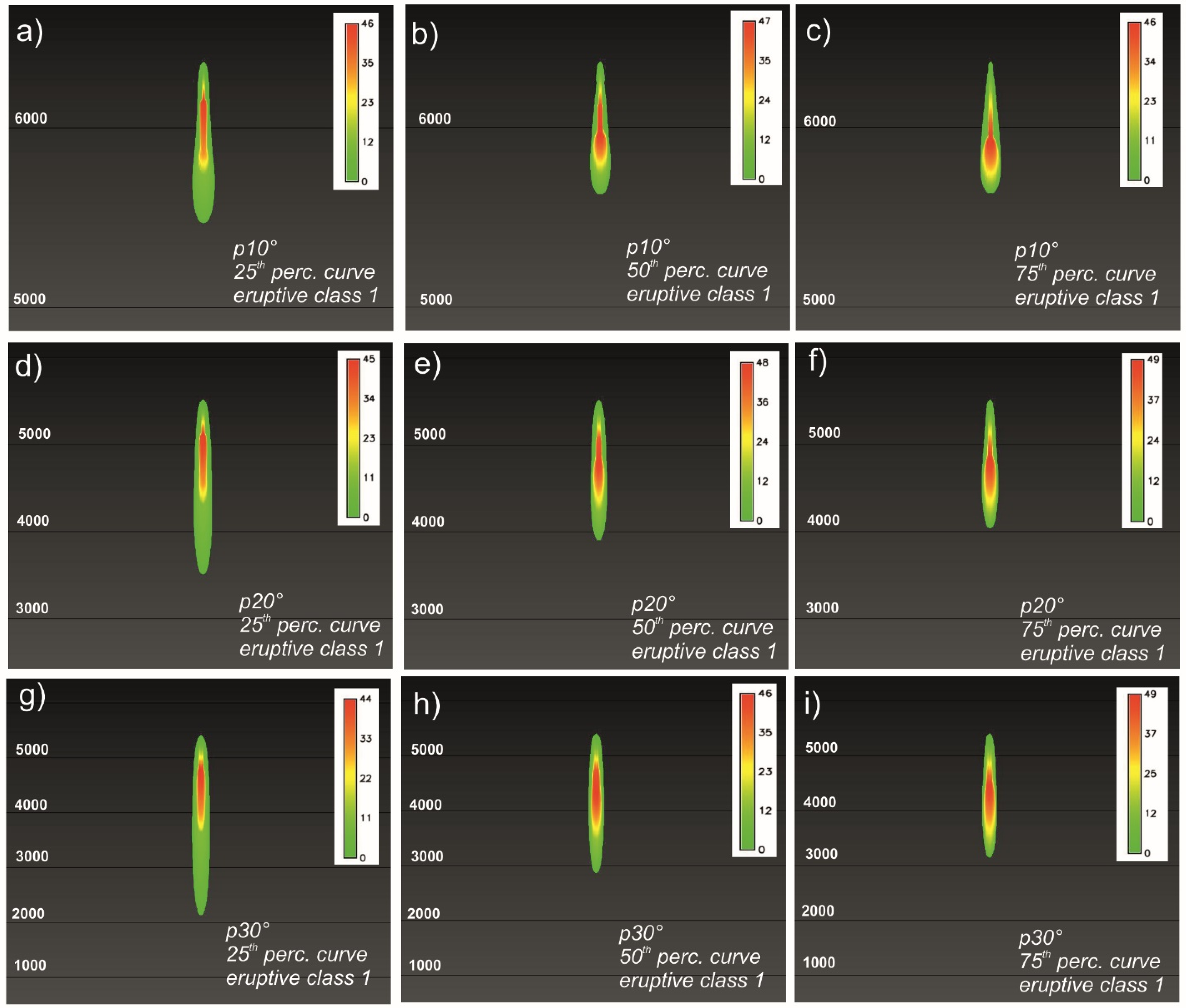
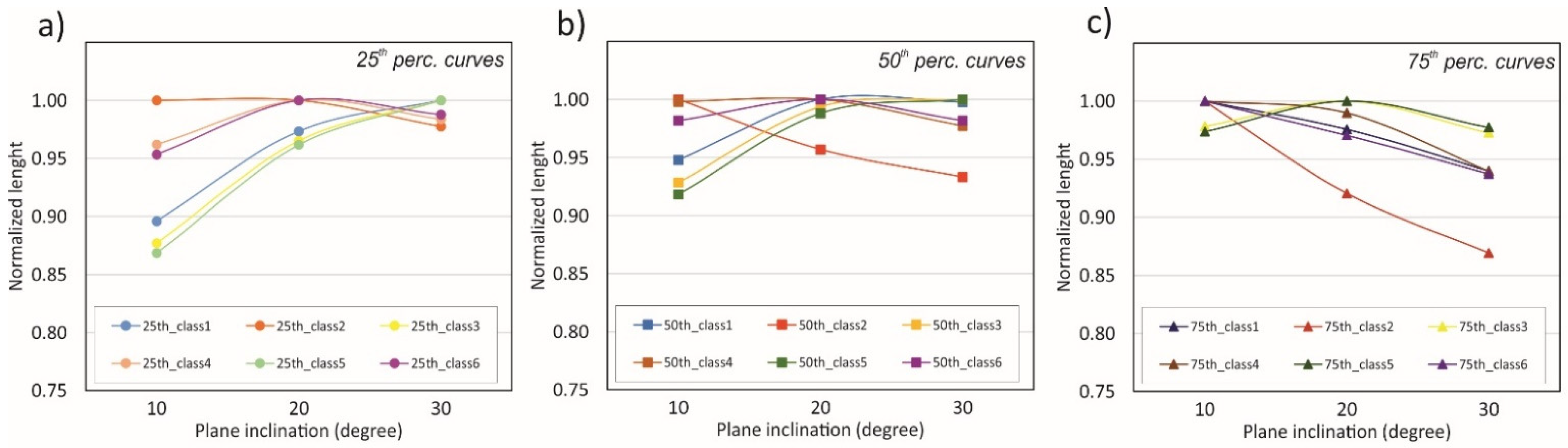
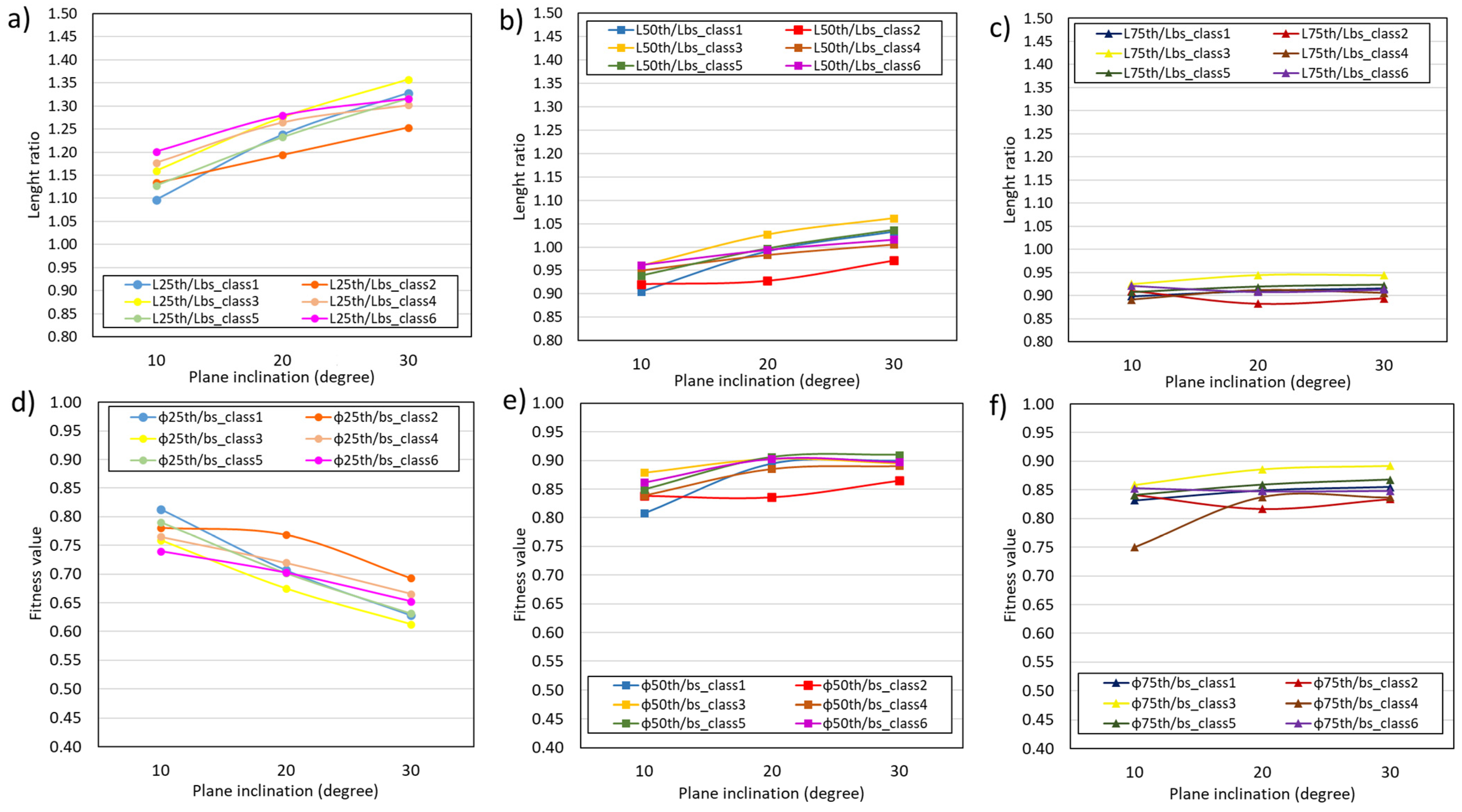
3.3. GPUFLOW Simulations
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Crisci, G.; Gregorio, D.; Pindaro, O.; Ranieri, G. Lava flow simulation by a discrete cellular model: First implementation. Int. J. Simul. Model. 1986, 6, 137–140. [Google Scholar] [CrossRef]
- Miyamoto, H.; Sasaki, S. Simulating lava flows by an improved cellular automata method. Comput. Geosci. 1997, 23, 283–292. [Google Scholar] [CrossRef]
- Avolio, M.V.; Crisci, G.M.; Gregorio, S.D.; Rongo, R.; Spataro, W.; Trunfio, G.A. SCIARA g2: An improved cellular automata model for lava flows and applications to the 2002 Etnean crisis. Comput. Geosci. 2006, 32, 876–889. [Google Scholar] [CrossRef]
- Cappello, A.; Hérault, A.; Bilotta, G.; Ganci, G.; Del Negro, C. MAGFLOW: A physics-based model for the dynamics of lava-flow emplacement. Geol. Soc. Lond. Spec. Publ. 2016, 426, 357–373. [Google Scholar] [CrossRef]
- Vicari, A.; Herault, A.; Del Negro, C.; Coltelli, M.; Marsella, M.; Proietti, C. Simulations of the 2001 lava flow at Etna volcano by the Magflow cellular automata model. Environ. Model. Softw. 2007, 22, 1465–1471. [Google Scholar] [CrossRef]
- Vicari, A.; Ganci, G.; Behncke, B.; Cappello, A.; Neri, M.; Del Negro, C. Near-real-time forecasting of lava flow hazards during the 12–13 January 2011 Etna eruption. Geophys. Res. Lett. 2011, 38, 13. [Google Scholar] [CrossRef] [Green Version]
- D’Ambrosio, D.; Filippone, G.; Rongo, R.; Spataro, W.; Trunfio, G.A. Cellular automata and GPGPU: An application to lava flow modeling. Int. J. Grid High Perform. Comput. 2012, 4, 18. [Google Scholar] [CrossRef] [Green Version]
- Cappello, A.; Ganci, G.; Bilotta, G.; Herault, A.; Zago, V.; Del Negro, C. Satellite-driven modeling approach for monitoring lava flow hazards during the 2017 Etna eruption. Ann. Geophys. 2019, 62, 2. [Google Scholar] [CrossRef]
- Favalli, M.; Mazzarini, F.; Pareschi, M.T.; Boschi, E. Topographic control on lava flow paths at Mount Etna, Italy: Implications for hazard assessment. J. Geophys. Res. Earth Surf. 2009, 114, F01019. [Google Scholar] [CrossRef]
- Del Negro, C.; Cappello, A.; Neri, M.; Bilotta, G.; Hérault, A.; Ganci, G. Lava flow hazards at Mount Etna: Constraints imposed by eruptive history and numerical simulations. Sci. Rep. 2013, 3, 3493. [Google Scholar] [CrossRef] [Green Version]
- Walker, G.P.L. Lengths of lava flows. Phil. Trans. R. Soc. Lond. 1973, 274, 107–118. [Google Scholar]
- Harris, A.J.L.; Rowland, S.K. Effusion rate controls on lava flow length and the role of heat loss: A review. Geol. Soc. Lond. Spec. Publ. 2009, 2, 33–51. [Google Scholar]
- Wadge, G. The variation of magma discharge during basaltic eruptions. J. Volcanol. Geotherm. Res. 1981, 11, 139–168. [Google Scholar] [CrossRef]
- Harris, A.; Steffke, A.; Calvari, S.; Spampinato, L. Thirty years of satellite-derived lava discharge rates at Etna: Implications for steady volumetric output. J. Geophys. Res. 2011, 116, B08204. [Google Scholar] [CrossRef] [Green Version]
- Bilotta, G.; Cappello, A.; Hérault, A.; Vicari, A.; Russo, G.; Del Negro, C. Sensitivity analysis of the MAGFLOW cellular automaton model for lava flow simulation. Environ. Model. Softw. 2012, 35, 122–131. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Dehn, J.; Calvari, S. Lava effusion rate definition and measurement: A review. Bull. Volcanol. 2007, 70, 1. [Google Scholar] [CrossRef]
- Coltelli, M.; Marsella, M.; Proietti, C.; Scifoni, S. The case of the 1981 eruption of Mount Etna: An example of very fast moving lava flows. Geochem. Geophys. Geosyst. 2012, 13, Q01004. [Google Scholar] [CrossRef]
- Branca, S.; De Beni, E.; Proietti, C. The large and destructive 1669 AD Etna eruption: Reconstruction of the lava flow field evolution and effusion rate trend. Bull. Volcanol. 2013, 75, 2–16. [Google Scholar] [CrossRef]
- Branca, S.; De Beni, E.; Chester, D.; Duncan, A.; Lotteri, A. The 1928 eruption of Mount Etna (Italy): Reconstructing lava flow evolution and the destruction and recovery of the town of Mascali. J. Volcanol. Geotherm. Res. 2017, 335, 54–70. [Google Scholar] [CrossRef]
- Harris, A.J.L.; Blake, S.; Rothery, D.A.; Stevens, N.F. A chronology of the 1991 to 1993 Mount Etna eruption using advanced very high resolution radiometer data: Implications for real-time thermal volcano monitoring. J. Geophys. Res. 1997, 102, 7985–8003. [Google Scholar] [CrossRef]
- Wright, R.; Blake, S.; Harris, A.J.; Rothery, D.A. A simple explanation for the space-based calculation of lava eruption rates. Earth Planet. Sci. Lett. 2001, 192, 223–233. [Google Scholar] [CrossRef]
- Ganci, G.; Bilotta, G.; Cappello, A.; Hérault, A.; Del Negro, C. HOTSAT: A multiplatform system for the satellite thermal monitoring of volcanic activity. Geol. Soc. Lond. Spec. Publ. 2016, 426, 207–221. [Google Scholar] [CrossRef]
- Ganci, G.; Cappello, A.; Bilotta, G.; Hérault, A.; Zago, V.; Del Negro, C. Mapping volcanic deposits of the 2011–2015 Etna eruptive events using satellite remote sensing. Front. Earth Sci. 2018, 6, 83. [Google Scholar] [CrossRef]
- Kaneko, T.; Yasuda, A.; Fujii, T. Simple empirical method for estimating lava-effusion rate using nighttime Himawari-8 1.6-µm infrared images. Earth Planets Space 2021, 73, 37. [Google Scholar] [CrossRef]
- Cappello, A.; Ganci, G.; Calvari, S.; Pérez, N.M.; Hernández, P.A.; Silva, S.V.; Cabral, J.; Del Negro, C. Lava flow-hazard modeling during the 2014–2015 Fogo eruption, Cape Verde. J. Geophys. Res. Solid Earth 2016, 121, 2290–2303. [Google Scholar] [CrossRef] [Green Version]
- Harris, A.J.L.; Villeneuve, N.; Di Muro, A.; Ferrazzini, V.; Peltier, A.; Coppola, D.; Favalli, M.; Bachèlery, P.; Froger, J.L.; Gu-rioli, L.; et al. Effusive crises at Piton de la Fournaise 2014–2015: A review of a multi-national response model. J. Appl. Volcanol. 2017, 6, 11. [Google Scholar] [CrossRef] [Green Version]
- Branca, S.; Del Carlo, P. Types of eruptions of Etna volcano AD 1670–2003: Implications for short-term eruptive behaviour. Bull. Volcanol. 2005, 67, 732–742. [Google Scholar] [CrossRef]
- Cappello, A.; Bilotta, G.; Neri, M.; Del Negro, C. Probabilistic modeling of future volcanic eruptions at Mount Etna. J. Geophys. Res. Earth Surf. 2013, 118, 1925–1935. [Google Scholar] [CrossRef] [Green Version]
- Ganci, G.; Vicari, A.; Fortuna, L.; Del Negro, C. The HOTSAT volcano monitoring system based on combined use of SEVIRI and MODIS multispectral data. Ann. Geophys. 2011, 54, 544–550. [Google Scholar] [CrossRef]
- Rogic, N.; Bilotta, G.; Ganci, G.; Thompson, J.O.; Cappello, A.; Rymer, H.; Ramsey, M.S.; Ferrucci, F. The impact of dynamic emissivity-temperature trends on spaceborne data of the 2001 Mount Etna eruption. Remote Sens. 2022; submitted. [Google Scholar]
- Del Negro, C.; Cappello, A.; Ganci, G. Quantifying lava flow hazards in response to effusive eruption. GSA Bull. 2016, 128, 752–763. [Google Scholar] [CrossRef]
- Ganci, G.; Vicari, A.; Cappello, A.; Del Negro, C. An emergent strategy for volcano hazard assessment: From thermal satellite monitoring to lava flow modeling. Remote Sens. Environ. 2012, 119, 197–207. [Google Scholar] [CrossRef]
- Calvari, S.; Bilotta, G.; Bonaccorso, A.; Caltabiano, T.; Cappello, A.; Corradino, C.; Del Negro, C.; Ganci, G.; Neri, M.; Pecora, E.; et al. The VEI 2 Christmas 2018 Etna eruption: A small but intense eruptive event or the starting phase of a larger one? Remote Sens. 2020, 12, 905. [Google Scholar] [CrossRef] [Green Version]
- PeakFit—The Automatic Choice For Spectroscopy, Chromatography and Electrophoresis, Trial Version. Available online: http://www.sigmaplot.co.uk/products/peakfit/peakfit.php (accessed on 24 September 2021).
- Bilotta, G.; Ganci, G.; Cappello, A. Modelling of geophysical flows through GPUFLOW. Appl. Sci. 2022; manuscript in preparation. [Google Scholar]
- Del Negro, C.; Fortuna, L.; Herault, A.; Vicari, A. Simulations of the 2004 lava flow at Etna volcano using the magflow cellular automata model. Bull. Volcanol. 2008, 70, 805–812. [Google Scholar] [CrossRef] [Green Version]
- Viccaro, M.; Ferlito, C.; Cortesogno, L.; Cristofolini, R.; Gaggero, L. Magma mixing during the 2001 event at Mt. Etna (Italy): Effects on the eruptive dynamics. J. Volcanol. Geotherm. Res. 2006, 149, 139–159. [Google Scholar] [CrossRef]
- Burton, M.; Neri, M.; Andronico, D.; Branca, S.; Caltabiano, T.; Calvari, S.; Corsaro, R.A.; Del Carlo, P.; Lanzafame, G.; Lodato, L.; et al. Etna 2004–2005: An archetype for geodynamically-controlled effusive eruptions. Geophys. Res. Lett. 2005, 32, 9. [Google Scholar] [CrossRef]
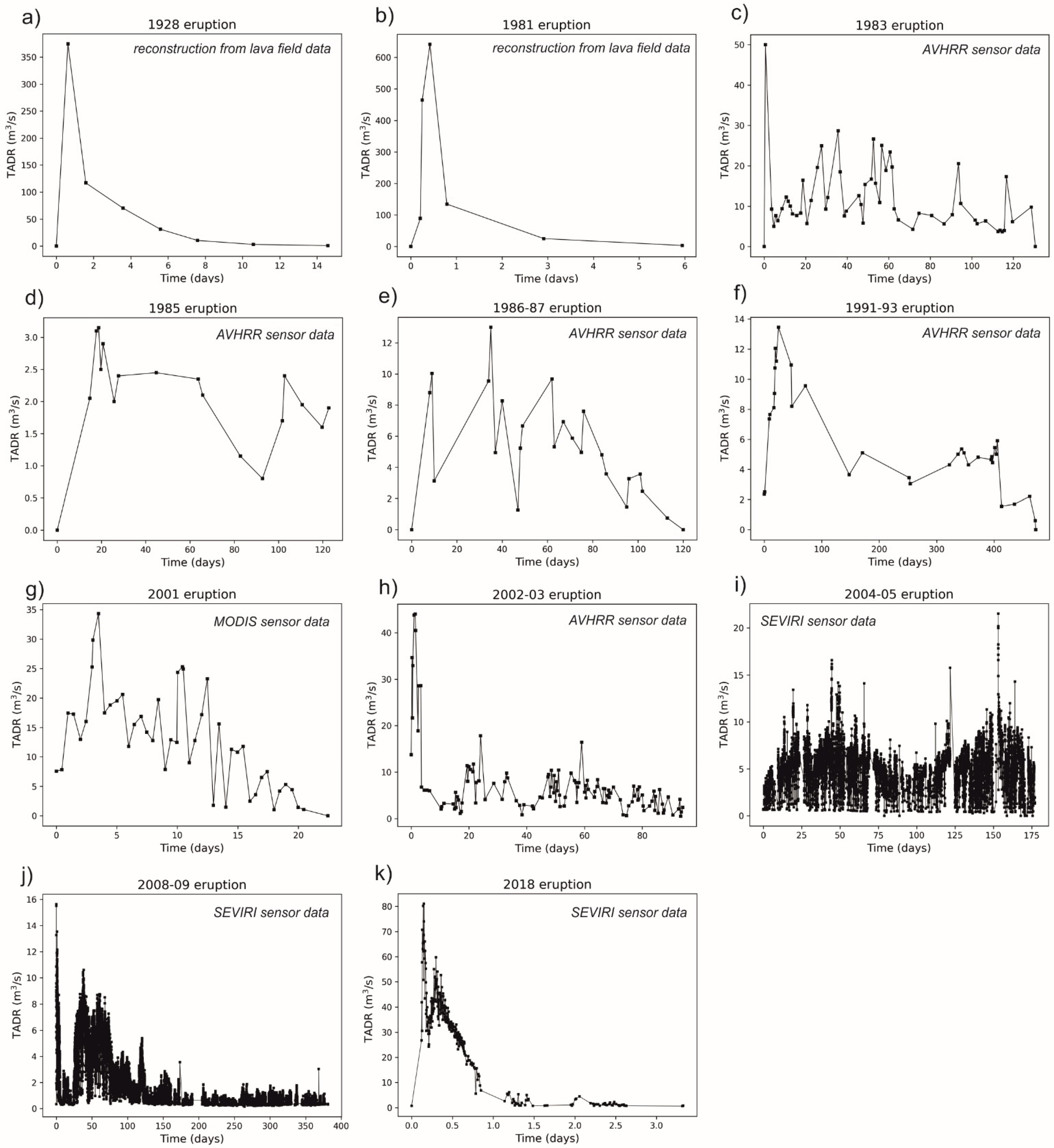


| Eruption | Start Date | End Date | Duration (Days) | Volume (×106 m3) | Effusion Rate Peak (m3s−1) | Reference |
|---|---|---|---|---|---|---|
| 1928 (Lower fissure) | 4 November 1928 | 19 November 1928 | 15 | 53 | 374.4 | [19] |
| 1981 | 17 March 1981 | 23 March 1981 | 6 | 23 | 641.4 | [17] |
| 1983 | 27 April 1983 | 16 October 1983 | 131 | 62 | 50.0 | [14] |
| 1985 | 12 March 1985 | 13 July 1985 | 124 | 15 | 3.2 | [14] |
| 1986–87 | 30 October 1986 | 27 February 1987 | 120 | 82 | 13.0 | [14] |
| 1991–93 | 14 December 1991 | 30 March 1993 | 471 | 183 | 13.5 | [14] |
| 2001 (Calcarazzi system) | 17 July 2001 | 9 August 2001 | 23 | 38 | 34.3 | [30] |
| 2002–03 (south flank) | 27 October 2002 | 29 January 2003 | 94 | 50 | 39.2 | [14] |
| 2004–05 | 7 September 2004 | 8 March 2005 | 182 | 64 | 21.5 | [31] |
| 2008–09 | 13 May 2008 | 7 July 2009 | 420 | 68 | 15.6 | [32] |
| 2018 | 24 December 2018 | 27 December 2018 | 4 | 2.5 | 80.2 | [33] |
| Eruptive Classes | Total Time (Days) | Volume (m3) |
|---|---|---|
| Class 1 | 30 | 30 × 106 |
| Class 2 | 90 | 30 × 106 |
| Class 3 | 30 | 100 × 106 |
| Class 4 | 90 | 100 × 106 |
| Class 5 | 30 | 200 × 106 |
| Class 6 | 90 | 200 × 106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuccarello, F.; Bilotta, G.; Cappello, A.; Ganci, G. Effusion Rates on Mt. Etna and Their Influence on Lava Flow Hazard Assessment. Remote Sens. 2022, 14, 1366. https://doi.org/10.3390/rs14061366
Zuccarello F, Bilotta G, Cappello A, Ganci G. Effusion Rates on Mt. Etna and Their Influence on Lava Flow Hazard Assessment. Remote Sensing. 2022; 14(6):1366. https://doi.org/10.3390/rs14061366
Chicago/Turabian StyleZuccarello, Francesco, Giuseppe Bilotta, Annalisa Cappello, and Gaetana Ganci. 2022. "Effusion Rates on Mt. Etna and Their Influence on Lava Flow Hazard Assessment" Remote Sensing 14, no. 6: 1366. https://doi.org/10.3390/rs14061366
APA StyleZuccarello, F., Bilotta, G., Cappello, A., & Ganci, G. (2022). Effusion Rates on Mt. Etna and Their Influence on Lava Flow Hazard Assessment. Remote Sensing, 14(6), 1366. https://doi.org/10.3390/rs14061366








