HybridGBN-SR: A Deep 3D/2D Genome Graph-Based Network for Hyperspectral Image Classification
Abstract
:1. Introduction
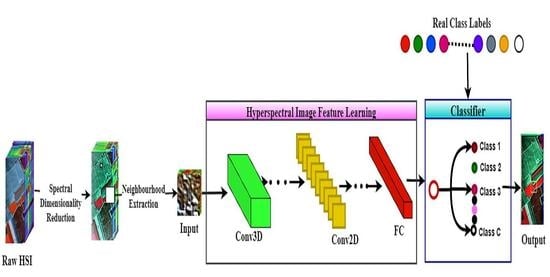
2. The Context of the Proposed Model
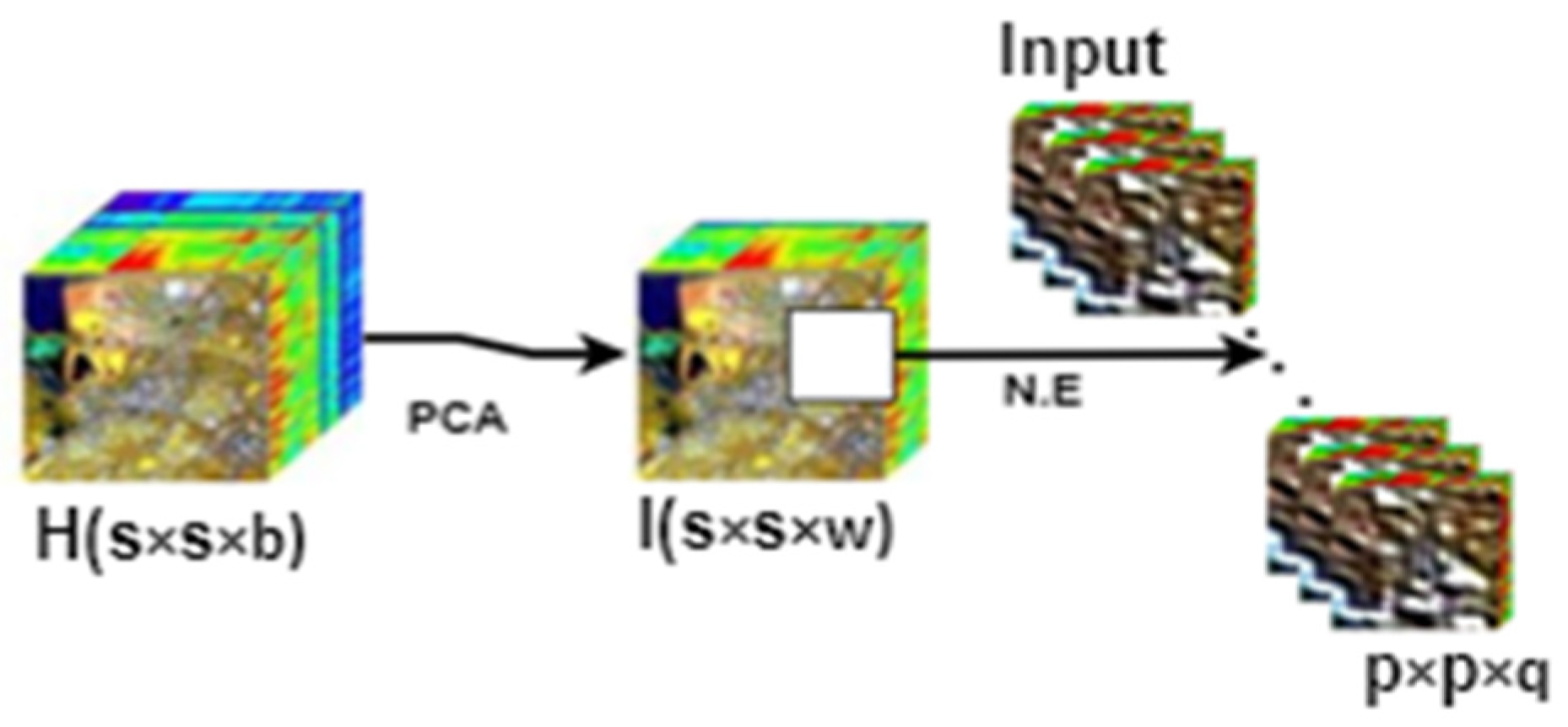
2.1. HSI Data Preprocessing Step
| Algorithm 1: Spectral Data Reduction and Neighborhood Extraction | |
| 1 | Input: HSI data matrix, pixels, number of bands. |
| 2 | Compute the covariance matrix H. |
| 3 | Compute the eigenvalues and eigenvector of Q. |
| 4 | Sort the eigenvectors to decrease eigenvalues: , and normalize the columns to unity. |
| 5 | Make the diagonal entries of and non-negative. |
| 6 | Choose the value such that . |
| 7 | Construct the transform matrix from the selected eigenvectors. |
| 8 | Transform to in eigenspace to express data in terms of eigenvectors reduced from to . This gives a new set of basis vectors and a reduced dimensional subspace of vectors where data resides. |
| 9 | Reduced HSI data cube will have dimensionality , where . |
| 10 | Perform neighborhood extraction on the new data cube . |
| 11 | Output: number of small overlapping 3D patches of spatial dimension and depth . |
2.2. Feature Extraction and Classification Step
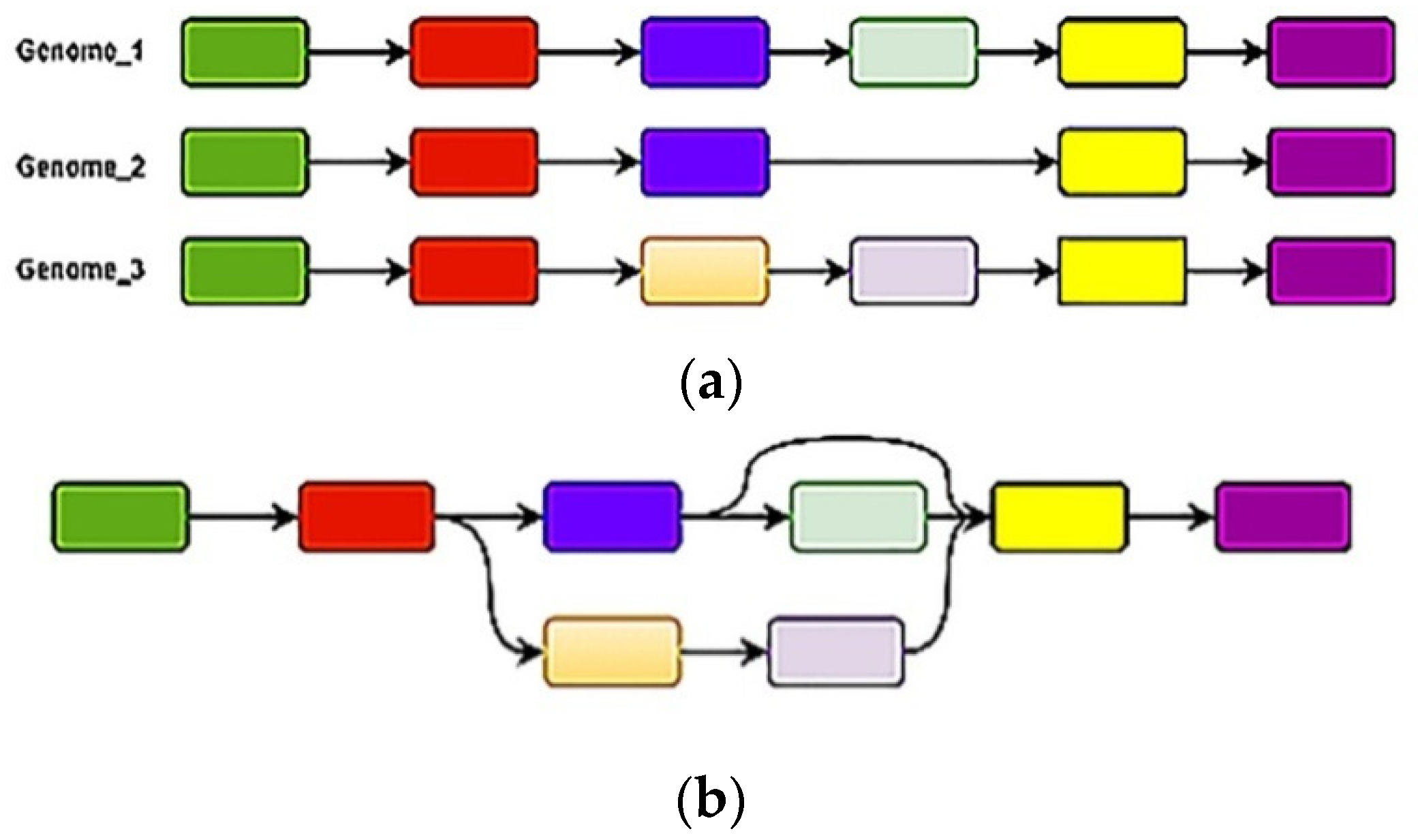
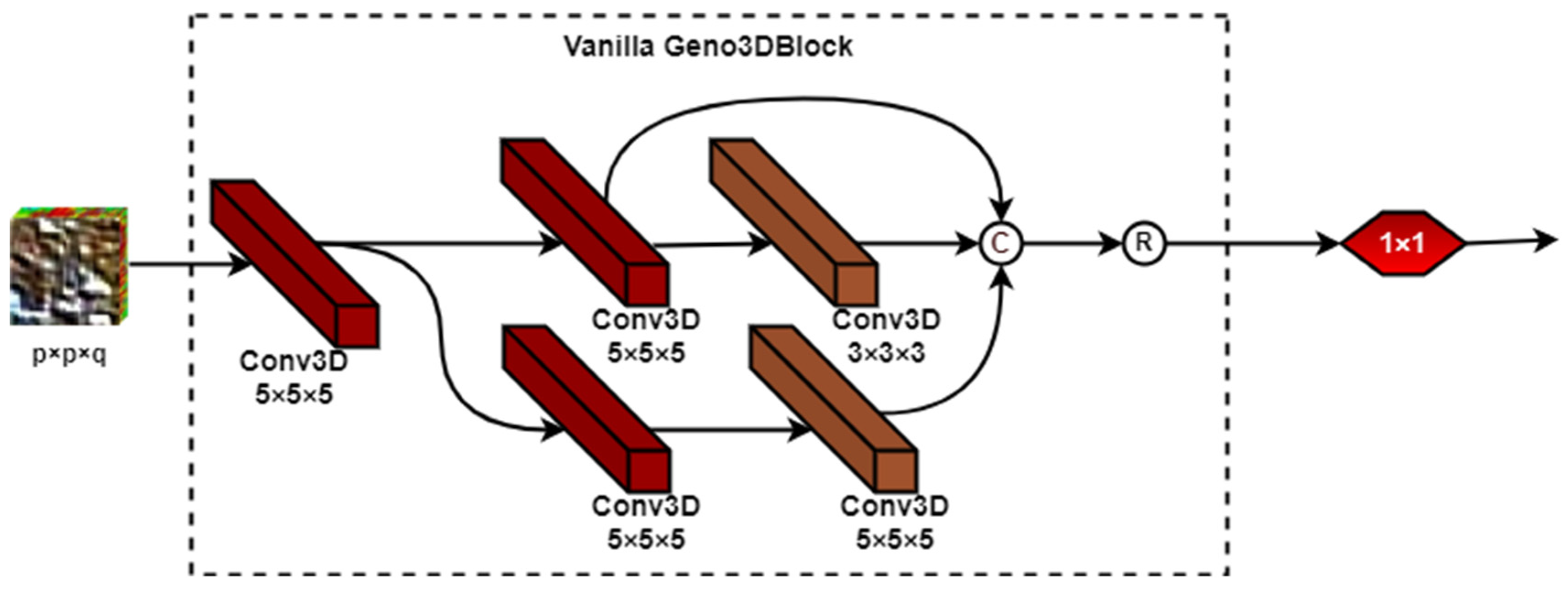
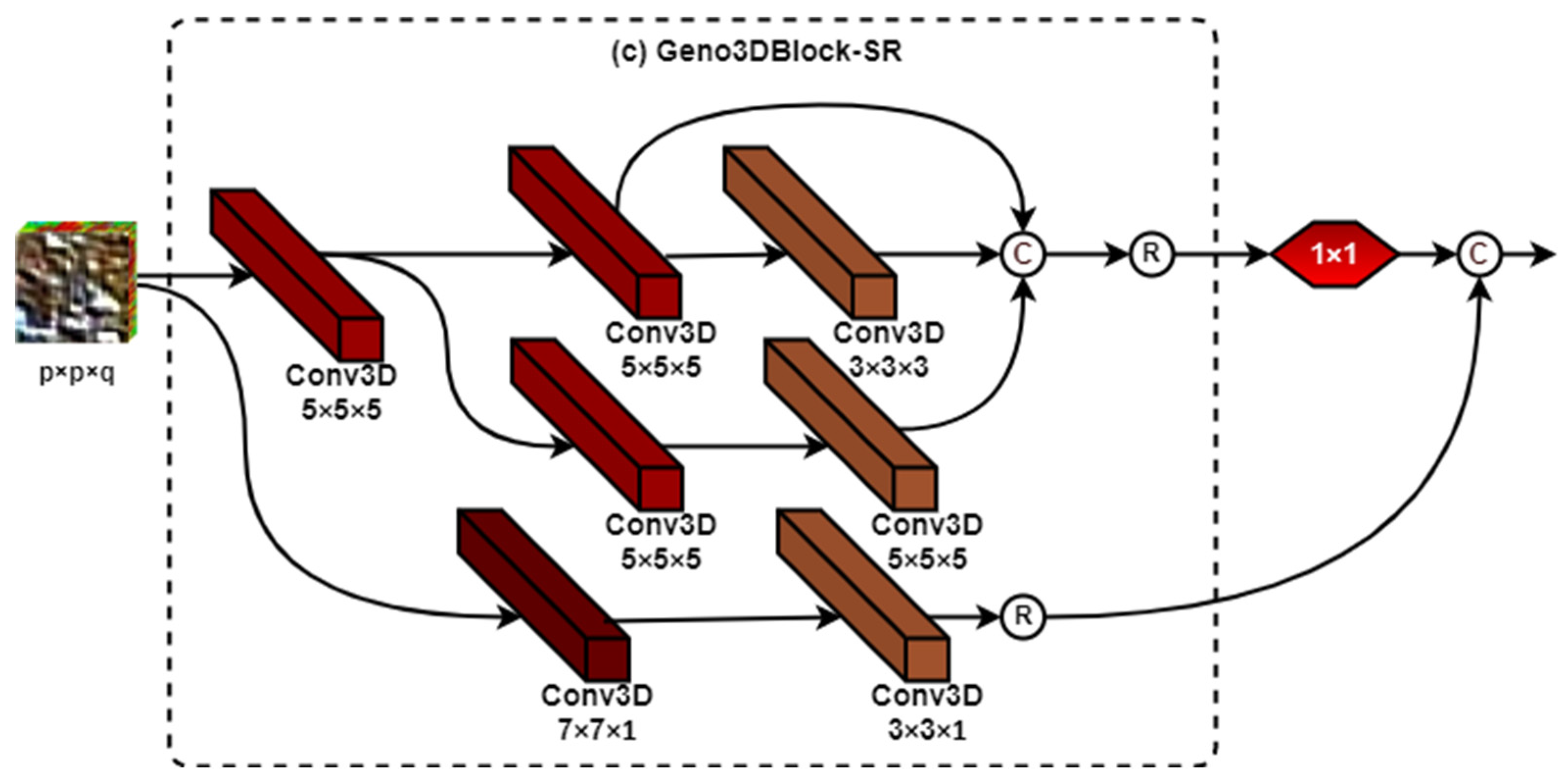
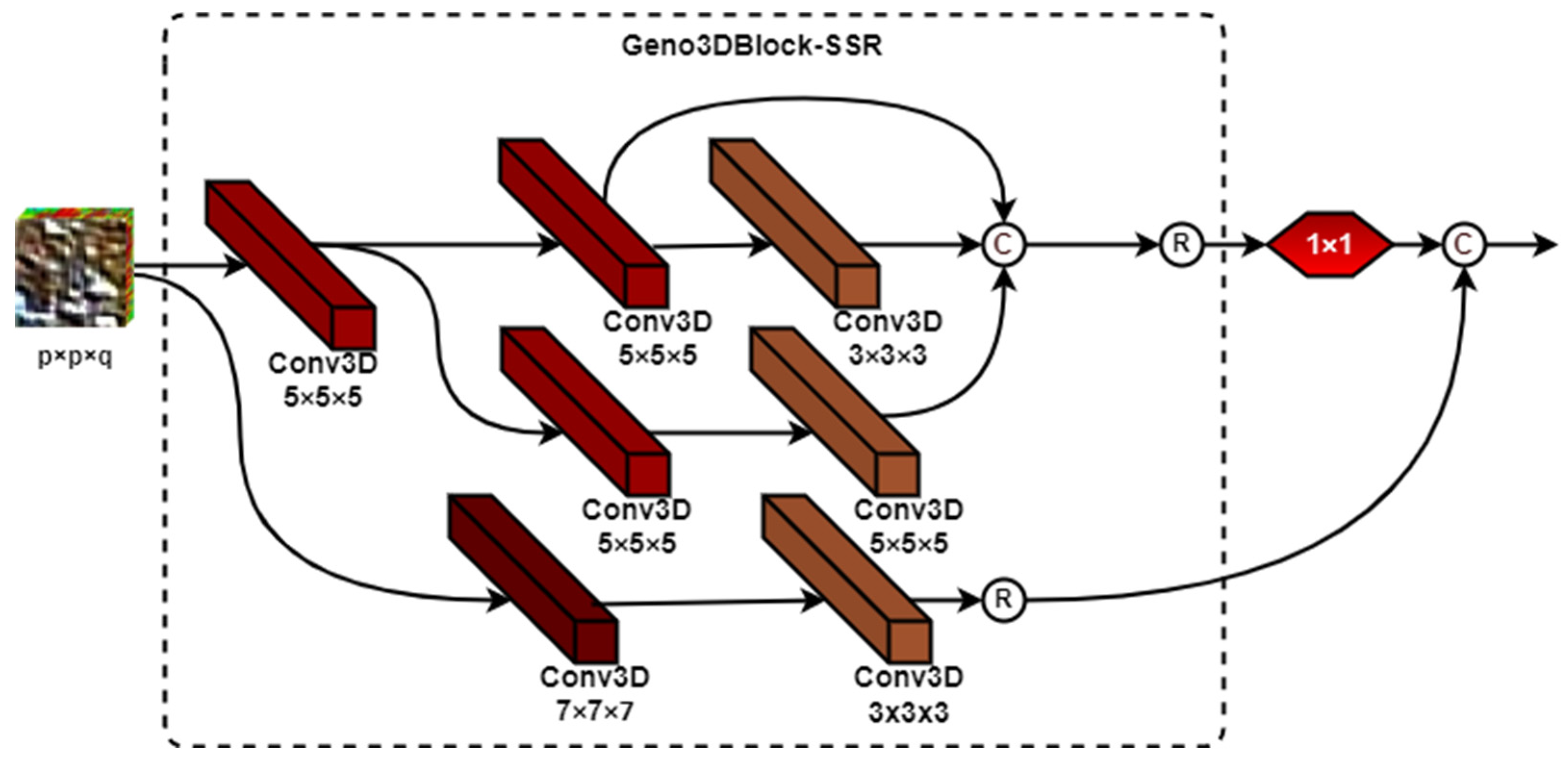
2.2.1. The Architecture of Genoblocks
2.2.2. The Genoblock Variants
3. Experimental Results and Discussion
3.1. Experimental Datasets
3.2. Experimental Setup
3.3. Evaluation Criteria
3.4. Experimental Results and Discussions on Very Small Training Sample Data
3.4.1. Distribution of the Training and Testing Sample Data over IP, UP, and SA Datasets on Very Little Sample Data
3.4.2. The Performance of Selected Models over IP, UP, and SA Datasets Using Very Limited Training Sample Data
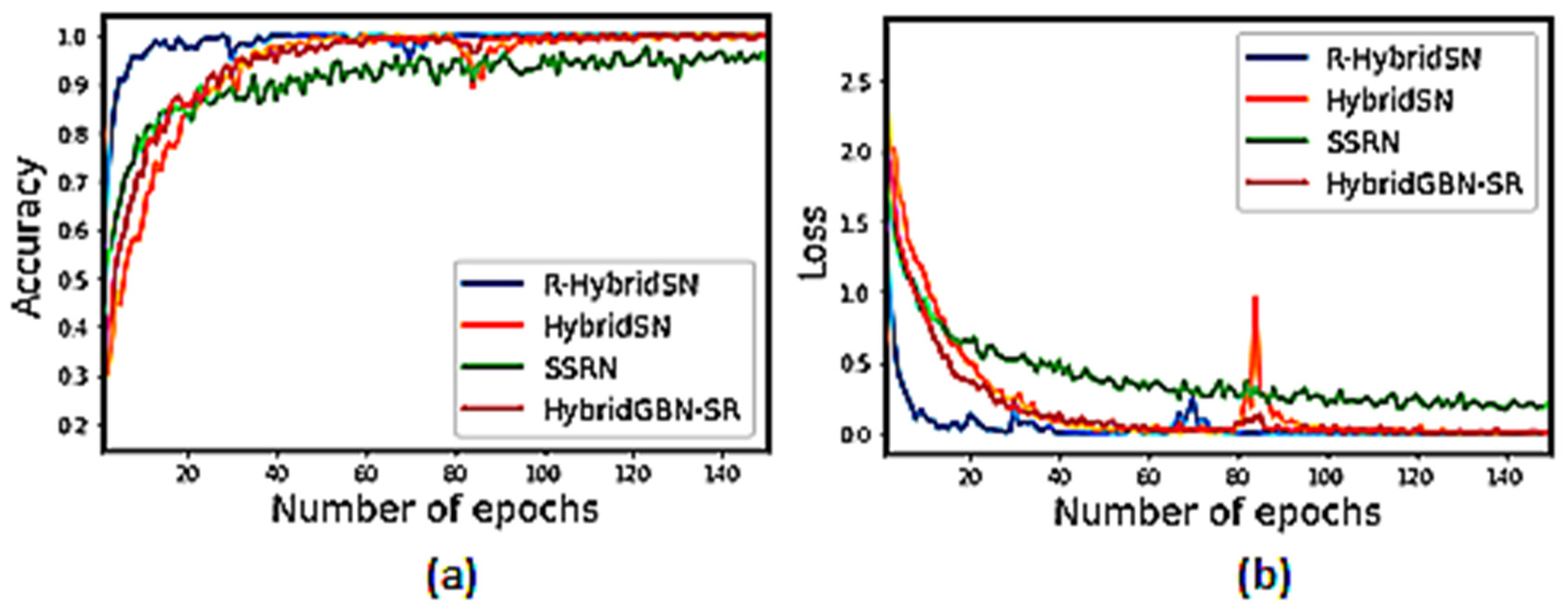
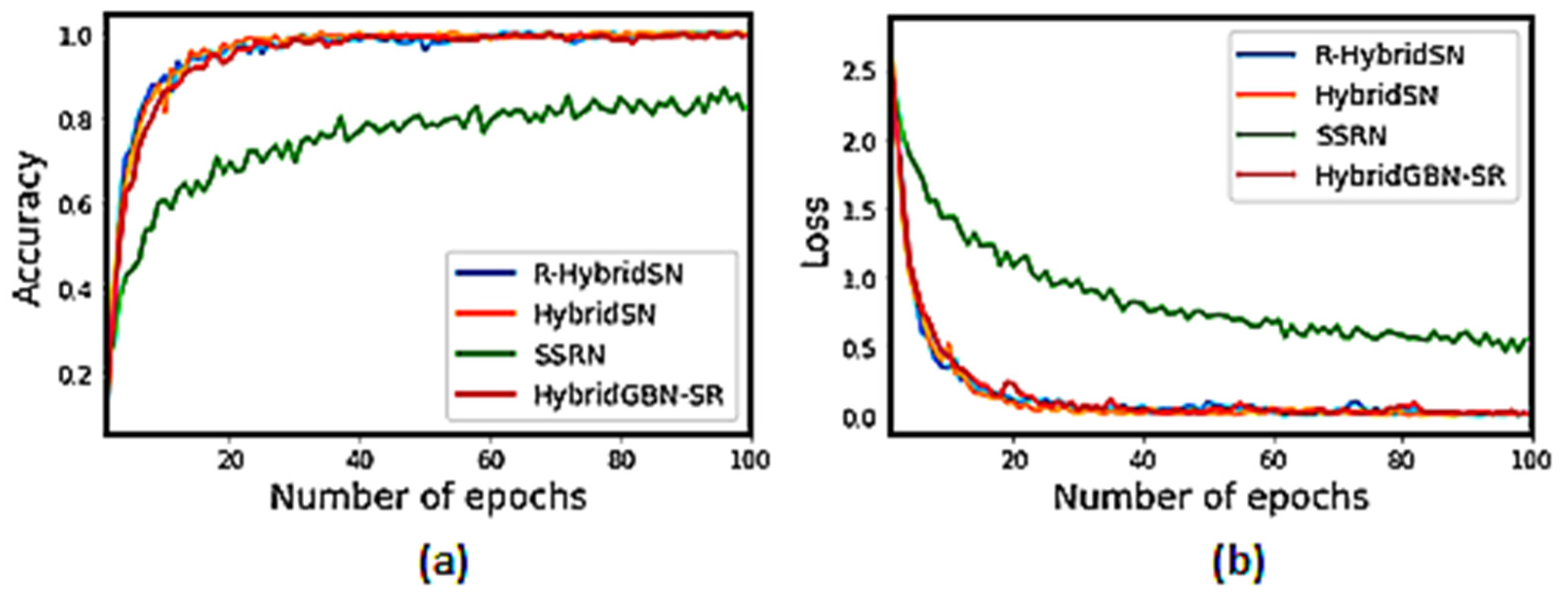
3.4.3. Training Accuracy and Loss Graph of the Selected Models on Very Limited Sample Data
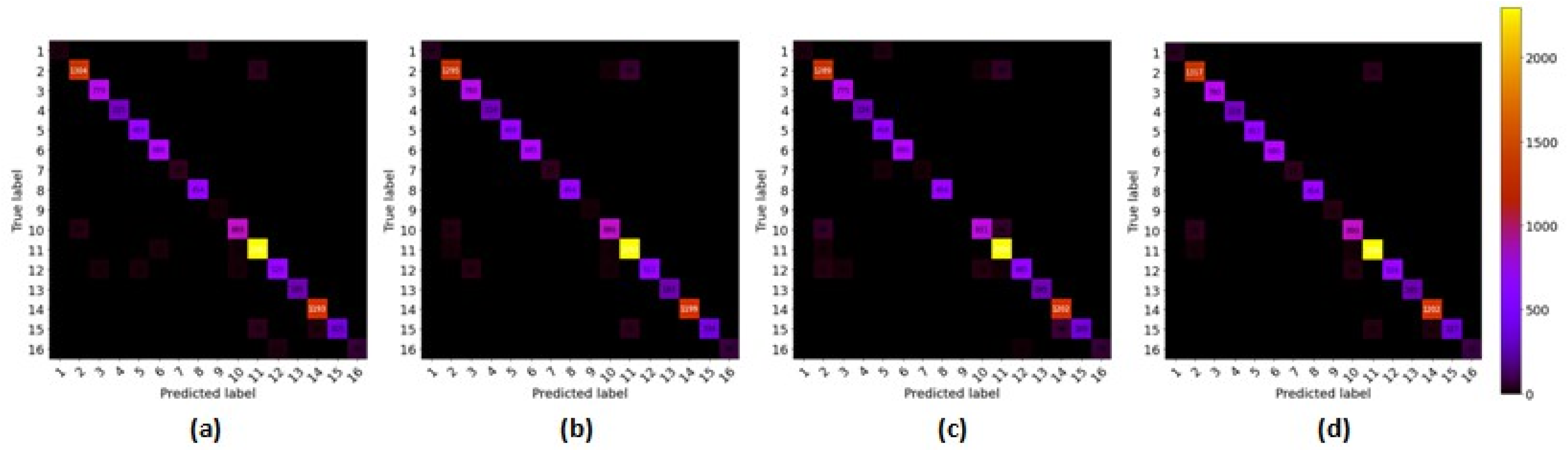
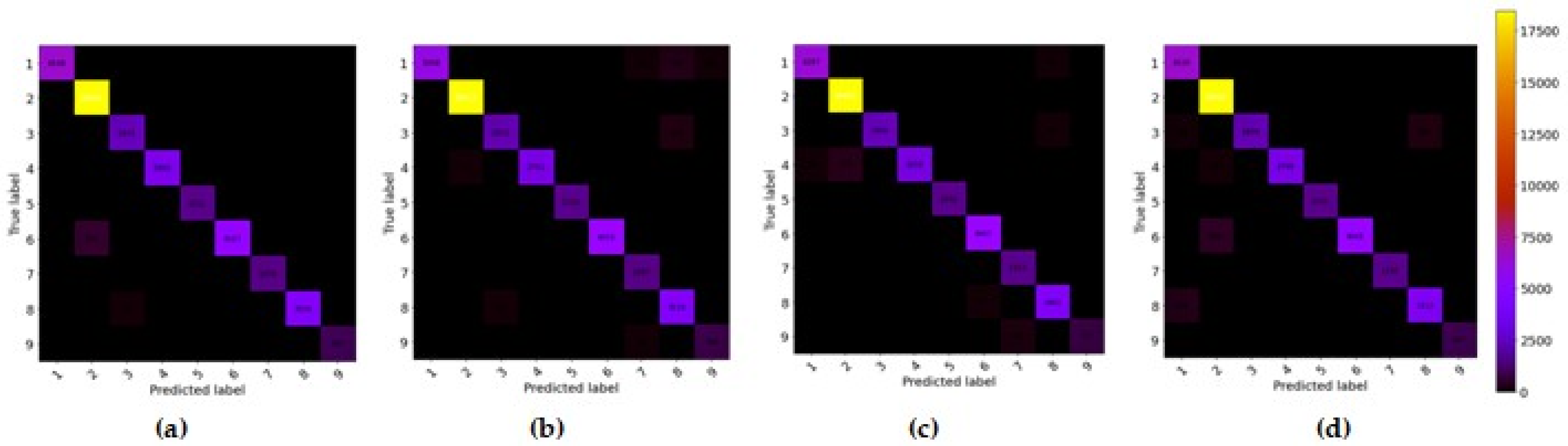
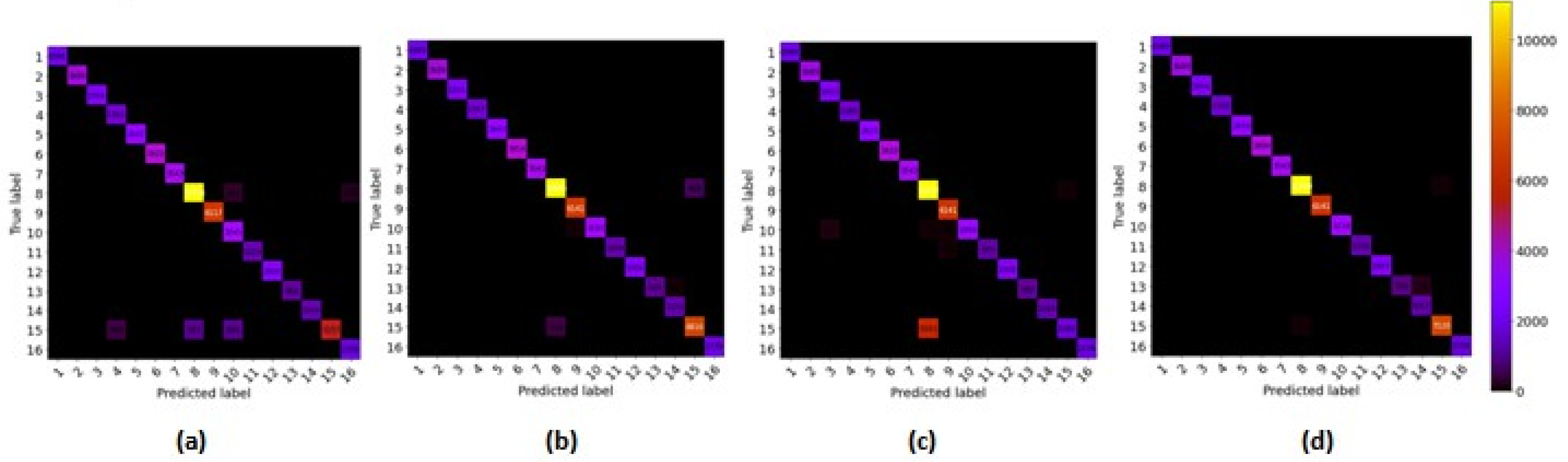
3.4.4. Confusion Matrix
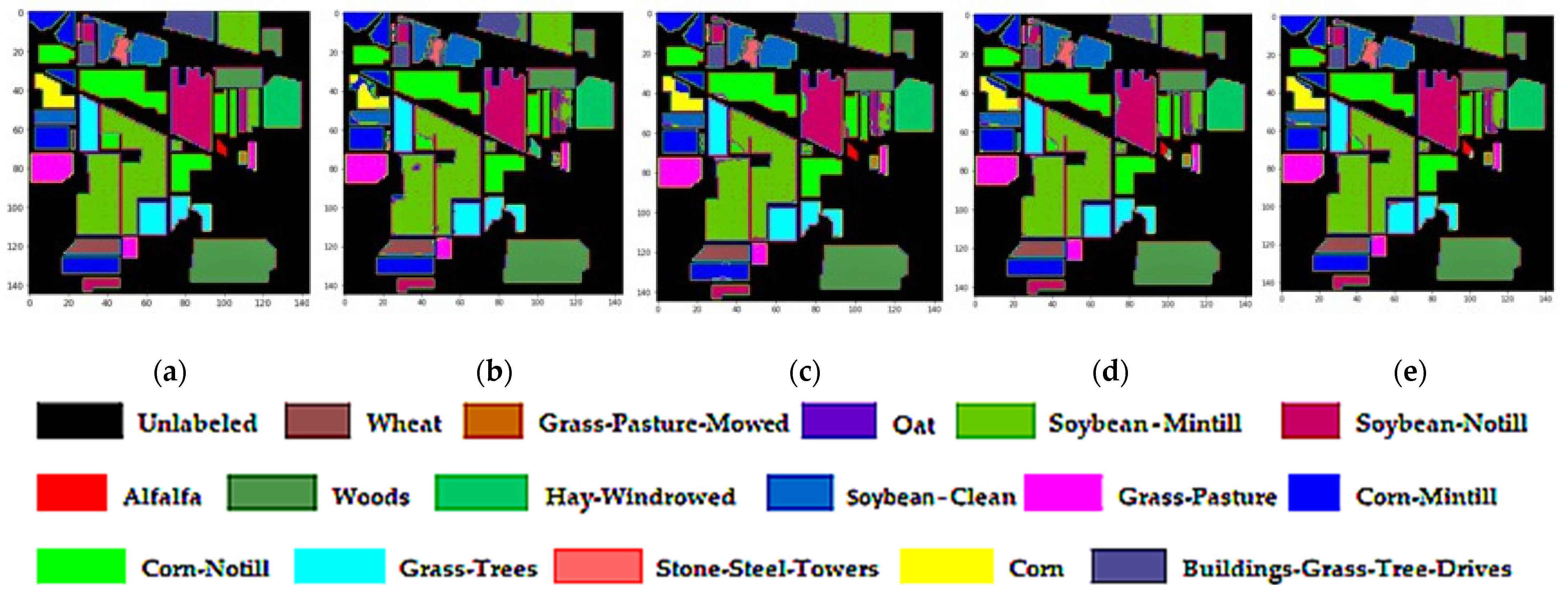
3.4.5. Classification Diagrams
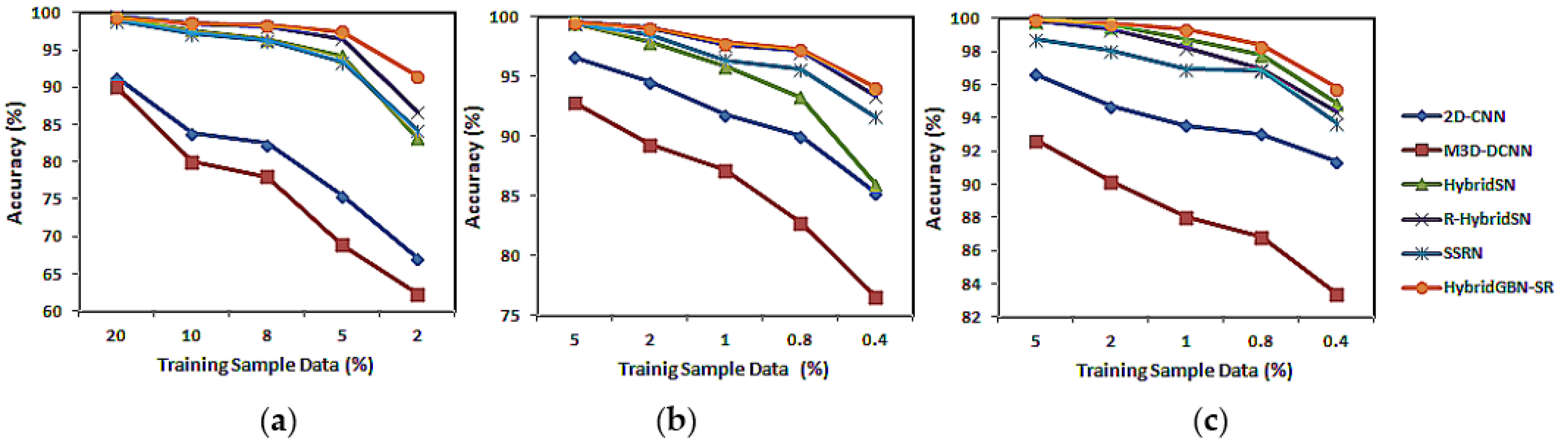
3.5. Varying Training Sample Data
3.6. The Time Complexity of the Selected Models over IP, UP, and SA Datasets
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern Trends in Hyperspectral Image Analysis: A Review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral Image Classification With Independent Component Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef] [Green Version]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of Hyperspectral Images With Regularized Linear Discriminant Analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Licciardi, G.; Marpu, P.R.; Chanussot, J.; Benediktsson, J.A. Linear Versus Nonlinear PCA for the Classification of Hyperspectral Data Based on the Extended Morphological Profiles. IEEE Geosci. Remote Sens. Lett. 2011, 9, 447–451. [Google Scholar] [CrossRef] [Green Version]
- Lin, Z.; Chen, Y.; Zhao, X.; Wang, G. Spectral-spatial classification of hyperspectral image using autoencoders. In Proceedings of the 2013 9th International Conference on Information, Communications & Signal Processing, Tainan, Taiwan, 10–13 December 2013; pp. 1–5. [Google Scholar] [CrossRef] [Green Version]
- Ben Hamida, A.; Benoit, A.; Lambert, P.; Ben Amar, C. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Nyabuga, D.O.; Song, J.; Liu, G.; Adjeisah, M. A 3D-2D Convolutional Neural Network and Transfer Learning for Hyperspectral Image Classification. Comput. Intell. Neurosci. 2021, 2021, 1759111. [Google Scholar] [CrossRef]
- Qiu, Z.; Yao, T.; Mei, T. Learning Spatio-Temporal Representation with Pseudo-3D Residual Networks. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 5534–5542. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef] [Green Version]
- Garifulla, M.; Shin, J.; Kim, C.; Kim, W.H.; Kim, H.J.; Kim, J.; Hong, S. A Case Study of Quantizing Convolutional Neural Networks for Fast Disease Diagnosis on Portable Medical Devices. Sensors 2021, 22, 219. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Li, S.; Bai, Q.; Yang, J.; Jiang, S.; Miao, Y. Review of Image Classification Algorithms Based on Convolutional Neural Networks. Remote Sens. 2021, 13, 4712. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. MixConv: Mixed depthwise convolutional kernels. arXiv 2019, arXiv:1907.09595. [Google Scholar]
- Tan, M.; Le, Q.V. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- Tinega, H.; Chen, E.; Ma, L.; Mariita, R.M.; Nyasaka, D. Hyperspectral Image Classification Using Deep Genome Graph-Based Approach. Sensors 2021, 21, 6467. [Google Scholar] [CrossRef] [PubMed]
- Manolov, A.; Konanov, D.; Fedorov, D.; Osmolovsky, I.; Vereshchagin, R.; Ilina, E. Genome Complexity Browser: Visualization and quantification of genome variability. PLoS Comput. Biol. 2020, 16, e1008222. [Google Scholar] [CrossRef]
- Yang, X.; Lee, W.-P.; Ye, K.; Lee, C. One reference genome is not enough. Genome Biol. 2019, 20, 104. [Google Scholar] [CrossRef] [Green Version]
- Schatz, M.C.; Witkowski, J.; McCombie, W.R. Current challenges in de novo plant genome sequencing and assembly. Genome Biol. 2012, 13, 243. [Google Scholar] [CrossRef]
- Rakocevic, G.; Semenyuk, V.; Lee, W.-P.; Spencer, J.; Browning, J.; Johnson, I.J.; Arsenijevic, V.; Nadj, J.; Ghose, K.; Suciu, M.C.; et al. Fast and accurate genomic analyses using genome graphs. Nat. Genet. 2019, 51, 354–362. [Google Scholar] [CrossRef]
- Cheng, G.; Xie, X.; Han, J.; Guo, L.; Xia, G.-S. Remote Sensing Image Scene Classification Meets Deep Learning: Challenges, Methods, Benchmarks, and Opportunities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3735–3756. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Unsupervised Spectral–Spatial Feature Learning via Deep Residual Conv–Deconv Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 56, 391–406. [Google Scholar] [CrossRef] [Green Version]
- He, M.; Li, B.; Chen, H. Multi-scale 3D deep convolutional neural network for hyperspectral image classification. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3904–3908. [Google Scholar]
- Chen, L.-C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, G.; Qi, L.; Tie, Y.; Ma, L. Hyperspectral Image Classification Using Kernel Fused Representation via a Spatial-Spectral Composite Kernel With Ideal Regularization. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1422–1426. [Google Scholar] [CrossRef]
- Feng, F.; Wang, S.; Wang, C.; Zhang, J. Learning Deep Hierarchical Spatial–Spectral Features for Hyperspectral Image Classification Based on Residual 3D-2D CNN. Sensors 2019, 19, 5276. [Google Scholar] [CrossRef] [PubMed] [Green Version]






| Class No | Class Label | Total Samples (Pixels) | Total Samples (%) | Training | Testing |
|---|---|---|---|---|---|
| 1 | Alfalfa | 46 | 0.45 | 2 | 44 |
| 2 | Corn-notill | 1428 | 13.93 | 71 | 1357 |
| 3 | Corn-mintill | 830 | 8.1 | 41 | 789 |
| 4 | Corn | 237 | 2.31 | 12 | 225 |
| 5 | Grass-pasture | 483 | 4.71 | 24 | 459 |
| 6 | Grass-trees | 730 | 7.12 | 37 | 693 |
| 7 | Grass-pasture-mowed | 28 | 0.27 | 1 | 27 |
| 8 | Hay-windrowed | 478 | 4.66 | 24 | 454 |
| 9 | Oats | 20 | 0.2 | 1 | 19 |
| 10 | Soybean-notill | 972 | 9.48 | 49 | 923 |
| 11 | Soybean-mintill | 2455 | 23.95 | 123 | 2332 |
| 12 | Soybean-clean | 593 | 5.79 | 30 | 563 |
| 13 | Wheat | 205 | 2 | 10 | 195 |
| 14 | Woods | 1265 | 12.34 | 63 | 1202 |
| 15 | Buildings-Grass-Trees-Drives | 386 | 3.77 | 19 | 367 |
| 16 | Stone-Steel-Towers | 93 | 0.91 | 5 | 88 |
| Class No | Class Label | Total Samples (Pixels) | Total Samples (%) | Training | Testing |
|---|---|---|---|---|---|
| 1 | Asphalt | 6631 | 15.5 | 66 | 6565 |
| 2 | Meadows | 18,649 | 43.6 | 186 | 18,463 |
| 3 | Gravel | 2099 | 4.91 | 21 | 2078 |
| 4 | Trees | 3064 | 7.16 | 31 | 3033 |
| 5 | Painted | 1345 | 3.14 | 13 | 1332 |
| 6 | Bare | 5029 | 11.76 | 50 | 4979 |
| 7 | Bitumen | 1330 | 3.11 | 13 | 1317 |
| 8 | Self-Blocking | 3682 | 8.61 | 37 | 3645 |
| 9 | Shadows | 947 | 2.21 | 10 | 937 |
| Class No | Class Label | Total Samples (Pixels) | Total Samples (%) | Training | Testing |
|---|---|---|---|---|---|
| 1 | Broccoli_green_weeds_1 | 2009 | 3.71 | 20 | 1989 |
| 2 | Broccoli_green_weeds_2 | 3726 | 6.88 | 37 | 3689 |
| 3 | Fallow | 1976 | 3.65 | 20 | 1956 |
| 4 | Fallow_rough_plow | 1394 | 2.58 | 14 | 1380 |
| 5 | Fallow_smooth | 2678 | 4.95 | 27 | 2651 |
| 6 | Stubble | 3959 | 7.31 | 39 | 3920 |
| 7 | Celery | 3579 | 6.61 | 36 | 3543 |
| 8 | Grapes_untrained | 11,271 | 20.82 | 113 | 11,158 |
| 9 | Soil_vineyard_develop | 6203 | 11.46 | 62 | 6141 |
| 10 | Corn_senesced_green_weeds | 3278 | 6.06 | 33 | 3245 |
| 11 | Lettuce_romaine_4wk | 1068 | 1.97 | 11 | 1057 |
| 12 | Lettuce_romaine_5wk | 1927 | 3.56 | 19 | 1908 |
| 13 | Lettuce_romaine_6wk | 916 | 1.69 | 9 | 907 |
| 14 | Lettuce_romaine_7wk | 1070 | 1.98 | 11 | 1059 |
| 15 | Vineyard_untrained | 7268 | 13.43 | 72 | 7196 |
| 16 | Vineyard_vertical_trellis | 1807 | 3.34 | 18 | 1789 |
| Class | 2D-CNN | M3D-DCNN | HybridSN | R-HybridSN | SSRN | HybridGBN -Vanilla | HybridGBN -SSR | HybridGBN -SR |
|---|---|---|---|---|---|---|---|---|
| 1 | 7.95 | 27.5 | 61.82 | 45 | 12.99 | 84.68 | 81.13 | 83.12 |
| 2 | 70.69 | 59.15 | 92.25 | 95.45 | 93.04 | 94.76 | 95.96 | 95.55 |
| 3 | 52.84 | 45.07 | 92.97 | 97.36 | 93.72 | 98.89 | 98.58 | 99.51 |
| 4 | 27.51 | 38.49 | 78.22 | 94.8 | 72.38 | 93.44 | 93.7 | 96.38 |
| 5 | 90.44 | 70.33 | 96.6 | 98.85 | 98.16 | 99.69 | 99.72 | 99.6 |
| 6 | 98.59 | 97.2 | 98.11 | 99.32 | 99.86 | 99.07 | 98.99 | 99.09 |
| 7 | 10.37 | 18.52 | 68.52 | 95.56 | 0 | 98.37 | 95.77 | 99.47 |
| 8 | 99.96 | 98.04 | 99.96 | 100 | 99.94 | 100 | 100 | 100 |
| 9 | 16.32 | 25.79 | 83.68 | 65.26 | 0 | 64.66 | 76.69 | 78.2 |
| 10 | 67.84 | 55.85 | 96.12 | 95.9 | 91.01 | 97.83 | 97.29 | 96.61 |
| 11 | 78.16 | 76.2 | 96.66 | 98.09 | 95.63 | 97.89 | 98.36 | 98.21 |
| 12 | 42.01 | 33.89 | 85.44 | 89.15 | 87.9 | 90.57 | 91.29 | 92.46 |
| 13 | 98.97 | 91.23 | 94.97 | 99.74 | 98.53 | 97.05 | 98.53 | 98.1 |
| 14 | 97.65 | 94.68 | 99.34 | 99.26 | 99.82 | 99.56 | 99.3 | 99.73 |
| 15 | 62.62 | 42.37 | 82.92 | 87.66 | 82.09 | 94.36 | 92.76 | 92.41 |
| 16 | 76.02 | 49.32 | 80 | 88.18 | 82.31 | 91.52 | 91.06 | 89.94 |
| Kappa | 0.718 ± 0.01 | 0.642 ± 0.045 | 0.934 ± 0.012 | 0.96 ± 0.004 | 0.923 ± 0.49 | 0.968 ± 0.43 | 0.97 ± 0.4 | 0.971 ± 0.25 |
| OA (%) | 75.47 ± 0.81 | 68.88 ± 3.77 | 94.24 ± 1.01 | 96.46 ± 0.33 | 93.39 ± 0.43 | 97.15 ± 0.38 | 97.32 ± 0.35 | 97.42 ± 0.22 |
| AA (%) | 62.37 ± 1.64 | 57.73 ± 6.52 | 87.97 ± 1.93 | 90.6 ± 1.53 | 75.28 ± 1.25 | 93.9 ± 1.11 | 94.32 ± 1.89 | 94.9 ± 2.4 |
| Class | 2D-CNN | M3D-DCNN | HybridSN | R-HybridSN | SSRN | HybridGBN -Vanilla | HybridGBN -SSR | HybridGBN -SR |
|---|---|---|---|---|---|---|---|---|
| 1 | 96.88 | 90.56 | 95.72 | 96.94 | 98.76 | 97.54 | 98.02 | 98.13 |
| 2 | 99.01 | 89.47 | 99.68 | 99.69 | 99.91 | 99.65 | 99.81 | 99.55 |
| 3 | 75.08 | 59.11 | 84.38 | 87.17 | 85.72 | 90.77 | 90.67 | 93.81 |
| 4 | 87.74 | 93.25 | 87.7 | 89.15 | 94.85 | 90.23 | 87.49 | 91.07 |
| 5 | 98.17 | 93.66 | 98.99 | 99.51 | 99.76 | 99.75 | 99.5 | 99.09 |
| 6 | 75.51 | 69.63 | 96.82 | 98.44 | 96.11 | 97.55 | 97.49 | 98.85 |
| 7 | 61.32 | 65.71 | 84.42 | 95.82 | 95.98 | 99.29 | 95.75 | 99.44 |
| 8 | 80.61 | 78.35 | 89.18 | 93.28 | 94.96 | 93.8 | 92.22 | 95.82 |
| 9 | 97.97 | 94.41 | 71.71 | 77.82 | 99.89 | 91.65 | 94.22 | 92.07 |
| Kappa | 0.881 ± 0.008 | 0.798 ± 0.016 | 0.935 ± 0.011 | 0.955 ± 0.007 | 0.97 ± 0.54 | 0.964 ± 0.56 | 0.960 ± 0.82 | 0.972 ± 0.53 |
| OA (%) | 91.13 ± 0.55 | 84.63 ± 1.21 | 95.09 ± 0.8 | 96.59 ± 0.5 | 97.67 ± 0.4 | 97.28 ± 0.42 | 97.02 ± 0.61 | 97.85 ± 0.4 |
| AA (%) | 85.81 ± 1.48 | 81.57 ± 1.79 | 89.84 ± 1.93 | 93.09 ± 1.2 | 96.22 ± 0.82 | 95.58 ± 0.79 | 95.02 ± 1.26 | 96.42 ± 0.54 |
| Class | 2D-CNN | M3D-DCNN | HybridSN | R-HybridSN | SSRN | HybridGBN -Vanilla | HybridGBN -SSR | HybridGBN -SR |
|---|---|---|---|---|---|---|---|---|
| 1 | 99.97 | 94.88 | 99.99 | 100 | 100 | 100 | 100 | 100 |
| 2 | 99.86 | 99.61 | 100 | 99.97 | 100 | 100 | 100 | 100 |
| 3 | 99.43 | 91.89 | 99.82 | 99.49 | 99.96 | 99.92 | 99.97 | 100 |
| 4 | 98.83 | 98.33 | 98.38 | 98.72 | 99.72 | 99.23 | 97.64 | 99.67 |
| 5 | 96.77 | 98.83 | 99.26 | 98.43 | 98.73 | 98.43 | 98.66 | 99 |
| 6 | 99.79 | 98.09 | 99.93 | 99.9 | 100 | 99.89 | 99.89 | 99.71 |
| 7 | 99.33 | 97.67 | 99.95 | 99.96 | 99.99 | 99.95 | 99.94 | 100 |
| 8 | 87.39 | 82.4 | 97.77 | 98.23 | 95.06 | 99.75 | 99.64 | 99.69 |
| 9 | 99.97 | 98.14 | 99.99 | 99.99 | 100 | 100 | 100 | 100 |
| 10 | 93.98 | 87.6 | 98.36 | 97.9 | 98.33 | 98.78 | 98.78 | 99 |
| 11 | 89.62 | 86.72 | 96.06 | 96.46 | 97.42 | 99.53 | 98.72 | 99.18 |
| 12 | 99.99 | 96.99 | 97.44 | 99.09 | 100 | 99.98 | 99.59 | 99.69 |
| 13 | 98.52 | 97.14 | 97.42 | 82.82 | 93.02 | 82.89 | 85.42 | 93.89 |
| 14 | 97.64 | 91.78 | 99.52 | 97.25 | 95.62 | 94.94 | 98.03 | 95.71 |
| 15 | 79.46 | 64.42 | 97.06 | 95.12 | 88.18 | 97.2 | 98.31 | 98.21 |
| 16 | 95.71 | 78.14 | 100 | 99.71 | 99.49 | 99.98 | 99.98 | 99.96 |
| Kappa | 0.928 ± 0.003 | 0.867 ± 0.002 | 0.985 ± 0.007 | 0.98 ± 0.004 | 0.966 ± 0.61 | 0.989 ± 0.61 | 0.991 ± 0.34 | 0.993 ± 0.16 |
| OA (%) | 93.55 ± 0.26 | 88.02 ± 1.35 | 98.72 ± 0.59 | 98.25 ± 0.4 | 96.94 ± 0.55 | 98.91 ± 0.55 | 99.16 ± 0.31 | 99.34 ± 0.14 |
| AA (%) | 96.02 ± 0.42 | 91.41 ± 0.81 | 98.81 ± 0.5 | 97.69 ± 0.69 | 97.84 ± 0.52 | 97.84 ± 1 | 98.41 ± 1.06 | 98.98 ± 0.32 |
| Training Sample Data in Percentage | |||||
|---|---|---|---|---|---|
| Model | 20% | 10% | 8% | 5% | 2% |
| 2D-CNN | 91.23 ± 0.21 | 83.86 ± 1 | 82.43 ± 0.62 | 75.47 ± 0.81 | 67.13 ± 1.12 |
| M3D-DCNN | 90.03 ± 2.18 | 80.1 ± 4.56 | 78.04 ± 2.13 | 68.88 ± 3.77 | 62.28 ± 3.18 |
| HybridSN | 99.3 ± 0.18 | 97.66 ± 0.23 | 96.37 ± 1.19 | 94.24 ± 1.01 | 83.14 ± 1.6 |
| R-HybridSN | 99.52 ± 0.16 | 98.44 ± 0.44 | 98.12 ± 0.35 | 96.46 ± 0.33 | 86.67 ± 1.02 |
| SSRN | 98.91 ± 0.12 | 97.25 ± 0.35 | 96.33 ± 0.41 | 93.39 ± 0.43 | 84.3 ± 1.61 |
| HybridGBN-SR | 99.3 ± 0.2 | 98.62 ± 0.22 | 98.31 ± 0.26 | 97.42 ± 0.22 | 91.44 ± 0.39 |
| Model | Training Sample Data | ||||
|---|---|---|---|---|---|
| 5% | 2% | 1% | 0.80% | 0.40% | |
| 2D-CNN | 96.59 ± 0.21 | 94.5 ± 0.4 | 91.82 ± 0.56 | 89.98 ± 0.38 | 85.27 ± 0.90 |
| M3D-DCNN | 92.8 ± 0.95 | 89.27 ± 1.35 | 87.19 ± 1.71 | 82.75 ± 2.84 | 76.53 ± 3.94 |
| HybridSN | 99.45 ± 0.09 | 97.86 ± 0.56 | 95.86 ± 0.93 | 93.3 ± 1.41 | 85.95 ± 1.58 |
| SSRN | 99.57 ± 0.13 | 99.07 ± 0.17 | 97.67 ± 0.4 | 97.12 ± 0.28 | 93.41 ± 0.77 |
| R-HybridSN | 99.47 ± 0.14 | 98.47 ± 0.27 | 96.4 ± 1.66 | 95.64 ± 0.52 | 91.60 ± 1.12 |
| HybridGBN-SR | 99.54 ± 0.07 | 99.13 ± 0.17 | 97.85 ± 0.4 | 97.33 ± 0.45 | 94.14 ± 0.61 |
| Model | Training Sample Data | ||||
|---|---|---|---|---|---|
| 5% | 2% | 1.00% | 0.80% | 0.40% | |
| 2D-CNN | 96.63 ± 0.24 | 94.67 ± 0.15 | 93.55 ± 0.26 | 93.03 ± 0.26 | 91.38 ± 0.44 |
| M3D-DCNN | 92.65 ± 0.49 | 90.17 ± 0.56 | 88.02 ± 1.35 | 86.82 ± 1.18 | 83.42 ± 1.6 |
| HybridSN | 99.83 ± 0.1 | 99.57 ± 0.25 | 98.72 ± 0.59 | 97.78 ± 0.78 | 94.88 ± 0.9 |
| R-HybridSN | 99.82 ± 0.04 | 99.36 ± 0.14 | 98.25 ± 0.4 | 96.97 ± 0.57 | 94.33 ± 0.48 |
| SSRN | 98.7 ± 0.51 | 98.02 ± 0.16 | 96.94 ± 0.55 | 96.87 ± 0.29 | 93.64 ± 0.22 |
| HybridGBN-SR | 99.94 ± 0.02 | 99.72 ± 0.11 | 99.34 ± 0.14 | 98.37 ± 0.43 | 95.8 ± 1.19 |
| Dataset | SSRN | HybridSN | R-HybridSN | HybridGBN-SR | ||||
|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | |
| IP | 91.1 | 2.6 | 31.9 | 3.2 | 23.1 | 2.6 | 43.6 | 3.4 |
| UP | 108.9 | 7.3 | 12.4 | 6.9 | 30.1 | 9.4 | 21.3 | 6.2 |
| SA | 122.6 | 12.3 | 13.2 | 8.9 | 16.4 | 12.3 | 30.2 | 12.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tinega, H.C.; Chen, E.; Ma, L.; Nyasaka, D.O.; Mariita, R.M. HybridGBN-SR: A Deep 3D/2D Genome Graph-Based Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 1332. https://doi.org/10.3390/rs14061332
Tinega HC, Chen E, Ma L, Nyasaka DO, Mariita RM. HybridGBN-SR: A Deep 3D/2D Genome Graph-Based Network for Hyperspectral Image Classification. Remote Sensing. 2022; 14(6):1332. https://doi.org/10.3390/rs14061332
Chicago/Turabian StyleTinega, Haron C., Enqing Chen, Long Ma, Divinah O. Nyasaka, and Richard M. Mariita. 2022. "HybridGBN-SR: A Deep 3D/2D Genome Graph-Based Network for Hyperspectral Image Classification" Remote Sensing 14, no. 6: 1332. https://doi.org/10.3390/rs14061332
APA StyleTinega, H. C., Chen, E., Ma, L., Nyasaka, D. O., & Mariita, R. M. (2022). HybridGBN-SR: A Deep 3D/2D Genome Graph-Based Network for Hyperspectral Image Classification. Remote Sensing, 14(6), 1332. https://doi.org/10.3390/rs14061332