Granularity of Digital Elevation Model and Optimal Level of Detail in Small-Scale Cartographic Relief Presentation
Abstract
:1. Introduction
2. Related Research
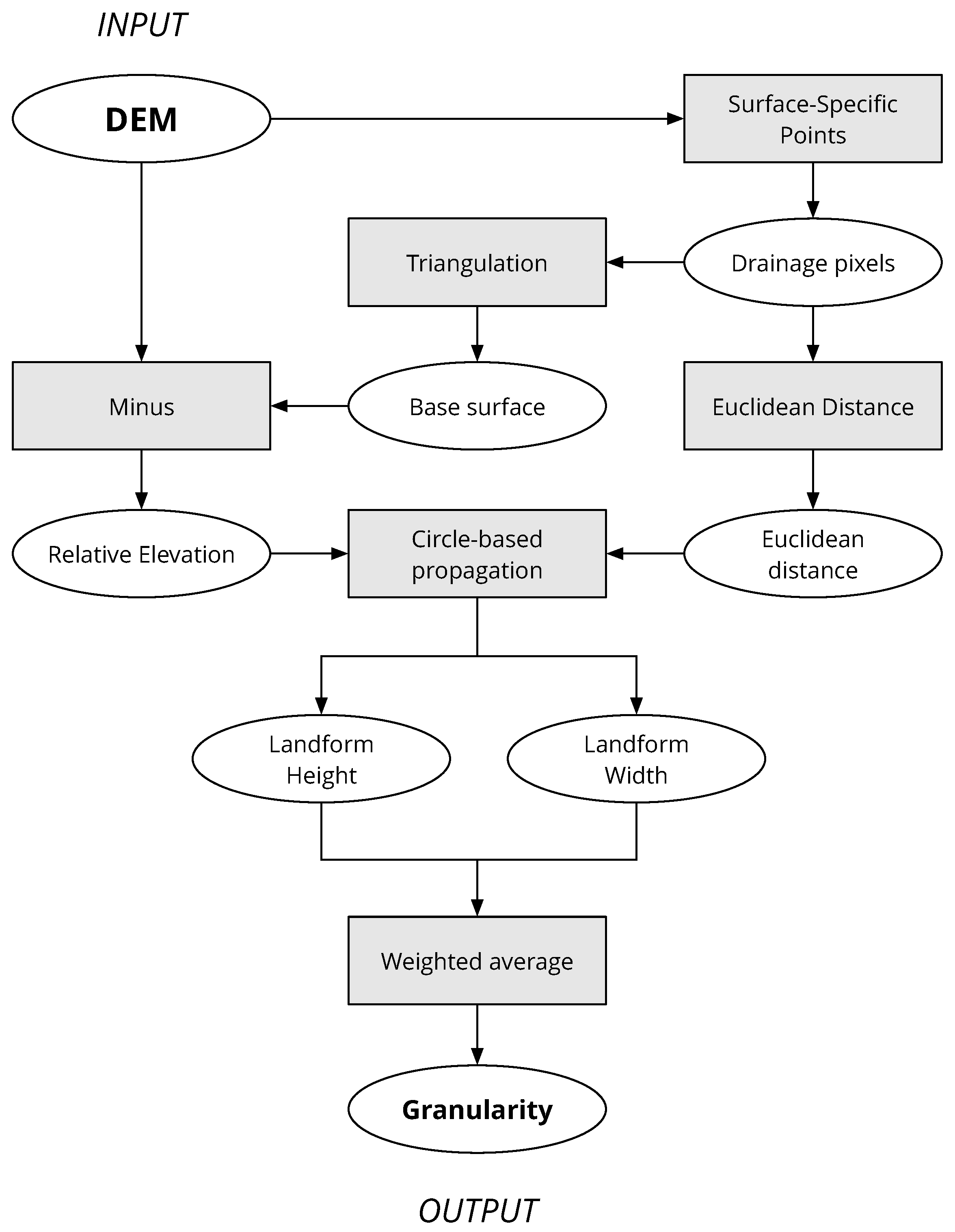
3. Methodology
3.1. Rationale
- Parameter free: The method must be able to estimate DEM granularity without any parameters;
- Height responsive: The computation of DEM granularity must account not only for the horizontal dimensions of landforms, but also for their heights. Higher landforms must have a higher impact on the granularity value;
- Upsampling resistant: Granularity changes should be insignificant when the DEM is upsampled (pixel size is made smaller).
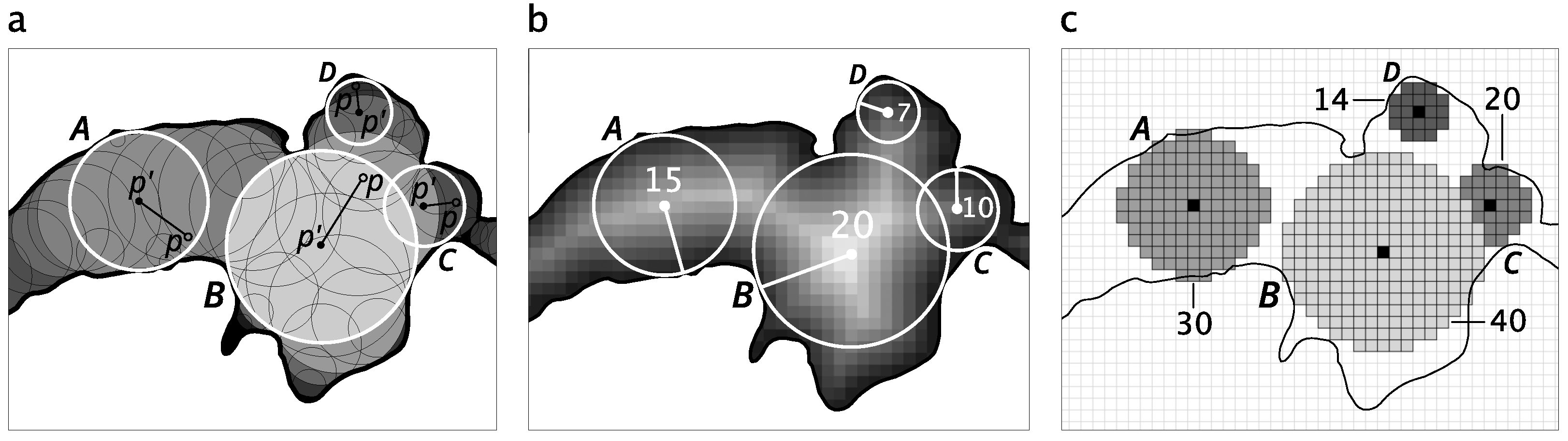
3.2. Landform width Measure
The landform width at each location is the diameter of the largest circle that covers the location and is inscribed in a landform boundary.
3.3. Granularity Calculation
3.4. Resistance to Upsampling
4. Implementation and Data Processing
4.1. Implementation
4.2. Data Processing
4.2.1. Generation of Reference DEMs
4.2.2. Experiments
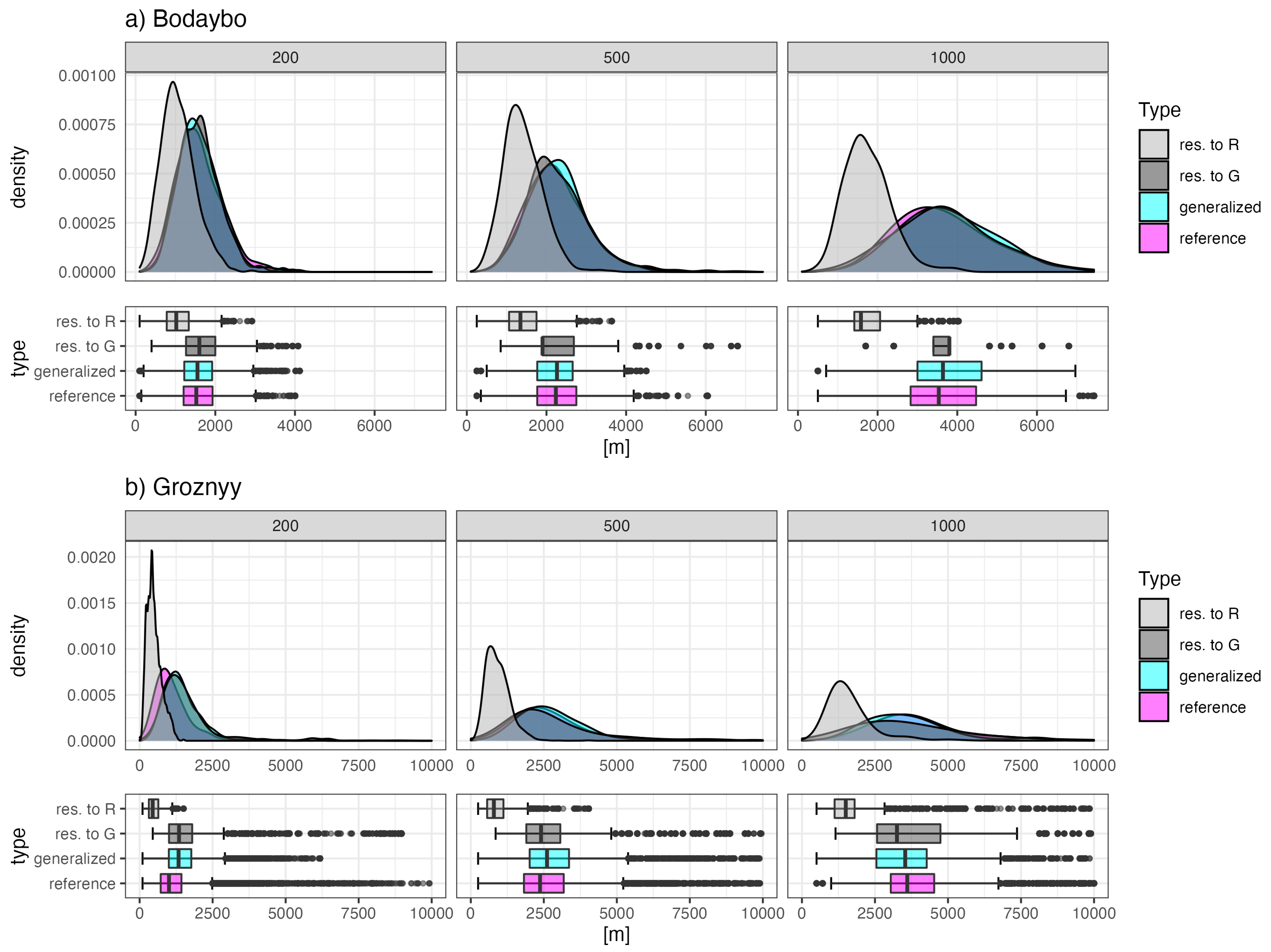
5. Results
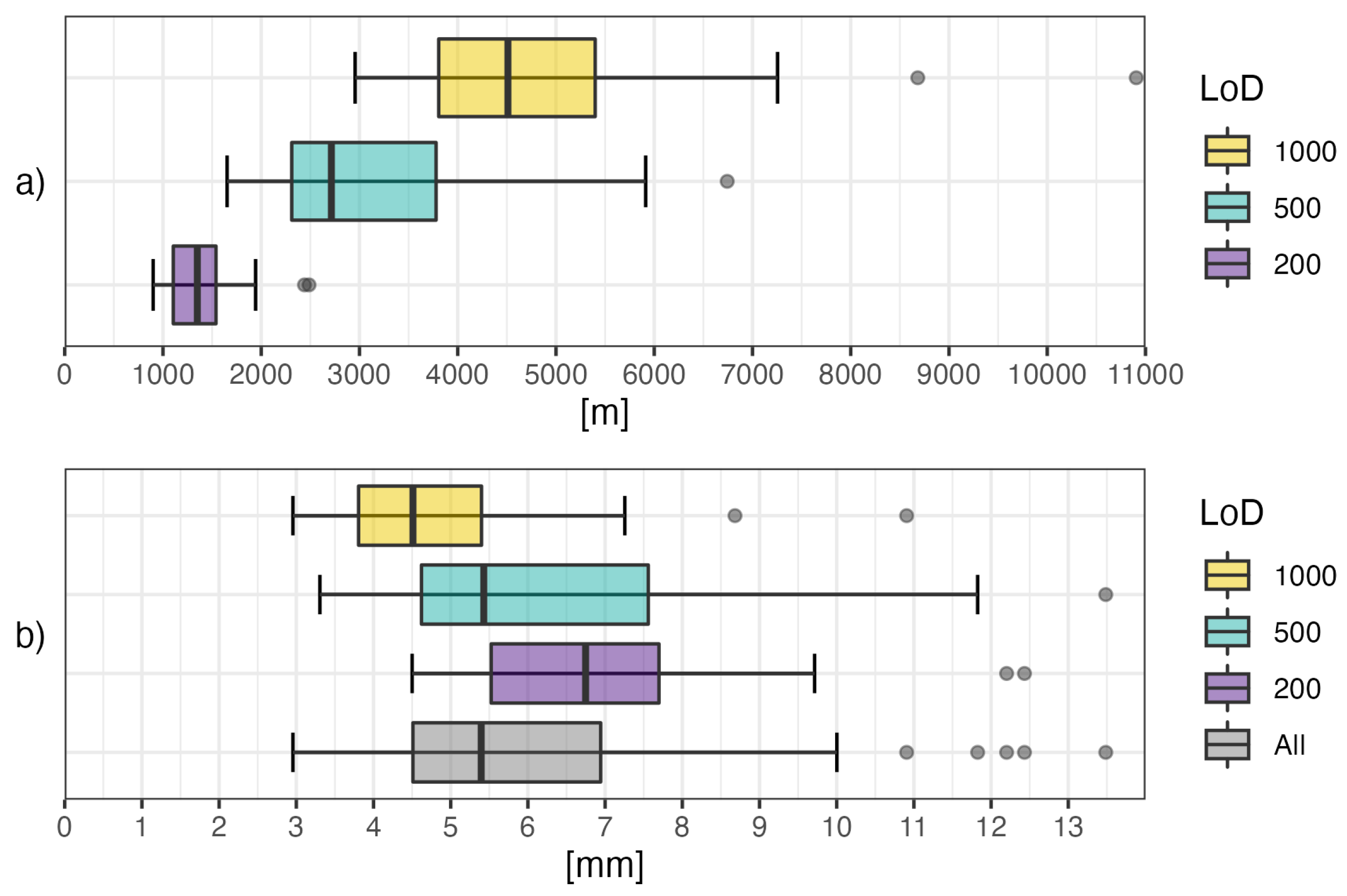
5.1. Optimal Granularity
The optimal relative granularity of the digital elevation model for small-scale mapping is 5–6 mm.
Landform selection intensity during relief generalization on topographic maps follows Töpfer’s radical law.
5.2. DEM Generalization and Optimal Level of Detail
The optimal level of detail in small-scale cartographic relief presentation requires a combination of DEM generalization constrained by granularity and a fine resolution of the generalized DEM which facilitates the high quality of visualization. DEM resampling alone is not effective for this purpose.
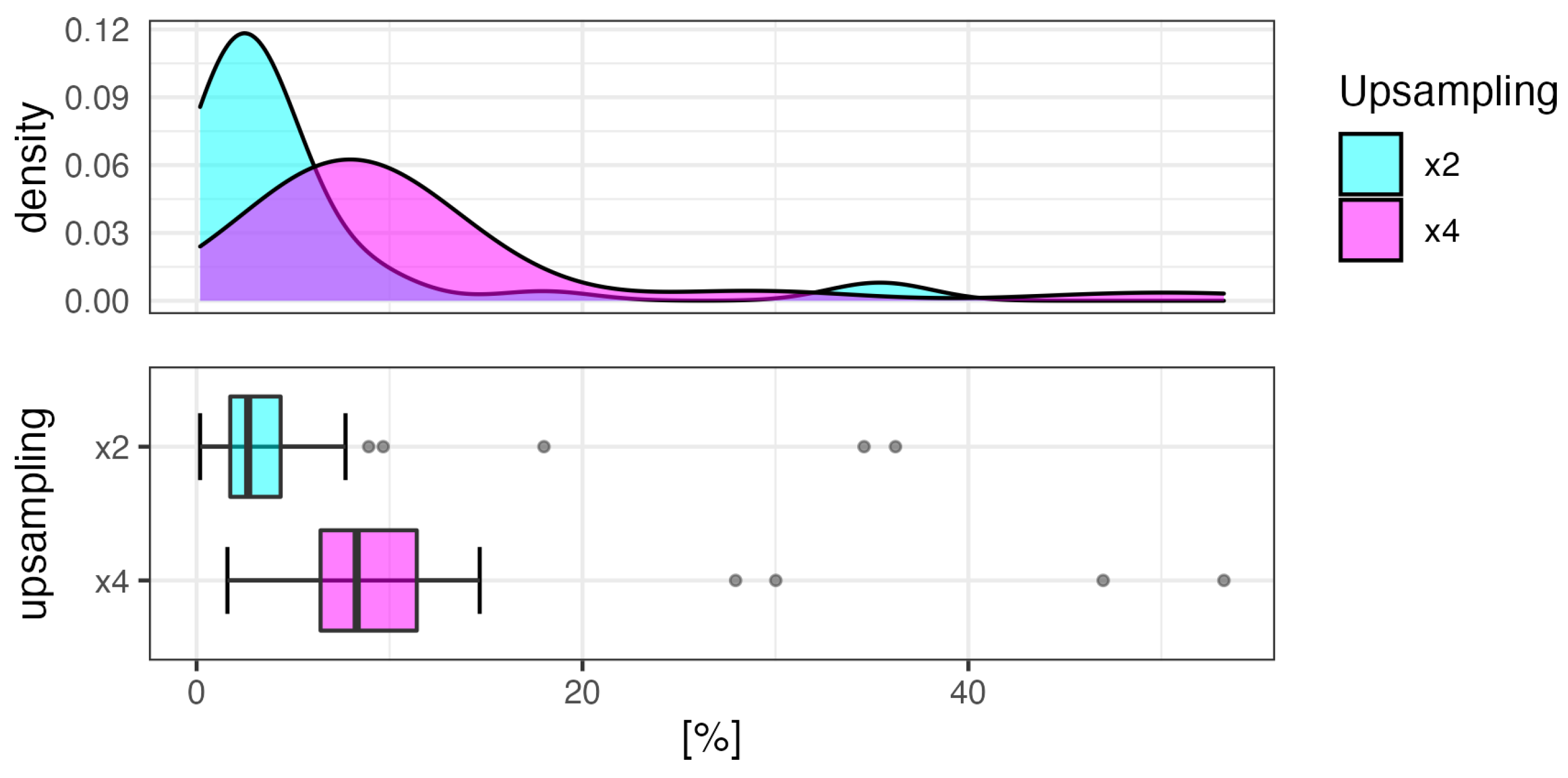
5.3. DEM Upsampling and Resistance of Granularity
6. Discussion
- Granularity was developed and evaluated as a property of the DEM for mapping purposes. Hence, it helps to ensure that cartographic relief presentation has the desired level of detail. While granularity can be potentially valuable for DEM analysis, such an application is out of the scope of the current paper and requires a separate investigation;
- Granularity is not equivalent to the level of detail and must be used in conjunction with other LoD properties to characterize the DEM comprehensively. The precision, accuracy, and vertical resolution of the elevation data also affect the LoD of the DEM. However, it is the horizontal DEM resolution that is the crucially important granularity counterpart in LoD estimation for small-scale mapping purposes. In particular, if the horizontal resolution is too coarse, the resulting image will not be sharp enough to achieve the desired image quality. The influence of other enlisted properties on the overall LoD of the DEM is more important for analytical and large-/middle-scale mapping purposes and should be investigated in a specially dedicated research work;
- Granularity characterizes the typical size of landforms represented on the DEM surface, but says nothing about their morphology. At the same time, different DEM generalization methods result in surfaces that tend to be smooth or crude, which may distort the initial character of the landforms. Gaussian filtering and structural-TIN-based simplification are examples of such contrasting approaches. To evaluate how realistic the landform representation is after generalization, advanced morphological techniques must be applied in addition to the estimation of granularity;
- The proposed approach to calculate the DEM granularity is based on the landform width measure, which is defined in terms of the distance between surface-specific points. Currently, only drainage pixels are used for this purpose. However, any type of surface-specific point can be incorporated in the calculation of the landform width. In particular, if some objective algorithm for delineating landform boundaries will be developed, the resulting lines or polygons can be used instead of the surface-specific points in the granularity assessment without any need to change the methodology;
- Drainage pixels that are extracted from the surface can be quite sporadic and accidental at places. In this case, some additional filtering (e.g., removing of the single outlier pixels) can improve the quality of landform width assessment and reduce its susceptibility to noise. Currently, no such processing has been applied to demonstrate the effectiveness of the developed method in the wild. We also revealed that for DEMs representing the flat relief, the simple morphometric approach to drainage pixel extraction can be sensible for DEM upsampling. Therefore, its robustness must be improved in future investigations;
- Evaluations of typical DEM granularity are based in this paper on reference DEMs reconstructed from manually drawn topographic maps with a horizontal resolution of mm at the mapping scale. It is possible to achieve the same granularity with a much coarser resolution. However, our experiments showed convincingly that the optimal level of detail for high-quality small-scale cartographic relief presentation requires a fine resolution of the DEM in addition to a reasonable DEM granularity.
7. Conclusions
Funding
Conflicts of Interest
Abbreviations
| DEM | Digital elevation model |
| GIS | Geographical Information System |
| LoD | Level of detail |
| TIN | Triangular irregular network |
Appendix A





References
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.; Sampson, C.; Kanae, S.; Bates, P. A high-accuracy map of global terrain elevations: Accurate Global Terrain Elevation map. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef] [Green Version]
- NASADEM Merged DEM Global 1 Arc Second V001. 2020. Available online: https://cmr.earthdata.nasa.gov/search/concepts/C1546314043-LPDAACECS.html (accessed on 13 February 2022).
- Guillaume, A.; Leempoel, K.; Rochat, E.; Rogivue, A.; Kasser, M.; Gugerli, F.; Parisod, C.; Joost, S. Multiscale Very High Resolution Topographic Models in Alpine Ecology: Pros and Cons of Airborne LiDAR and Drone-Based Stereo-Photogrammetry Technologies. Remote Sens. 2021, 13, 1588. [Google Scholar] [CrossRef]
- Imhof, E. Cartographic Relief Presentation; Walter der Gruyter: Berlin, Germany, 1982. [Google Scholar]
- Ruas, A.; Bianchin, A. Echelle et Niveau de Detail; Generalisation et Representation Miltiple, Hermes Lavoisier: Paris, France, 2002; pp. 25–44. [Google Scholar]
- Zarutskaya, I. Methods of Representing Relief on Hypsometric Maps; Publishing House of Geodesic Literature: Moscow, Russia, 1958. [Google Scholar]
- Military Topographic Service. Guide to Cartographic and Cartographic Works. Part 2. Drafting and Preparation for Publication of 1:200,000 and 1:500,000 Topographic Maps; Editorial and Publishing Department of Military Topographic Service: Moscow, Russia, 1980. [Google Scholar]
- Swiss Society of Cartography. Cartographic Generalization: Topographic Maps, 2nd ed.; Swiss Society of Cartography: Zürich, Switzerland, 1987. [Google Scholar]
- Polidori, L.; El Hage, M. Digital Elevation Model Quality Assessment Methods: A Critical Review. Remote Sens. 2020, 12, 3522. [Google Scholar] [CrossRef]
- Wechsler, S. Perceptions by Digital Elevation Model Users of DEM Uncertainty. URISA J. 2003, 15, 1–10. [Google Scholar]
- Florinsky, I. Accuracy of local topographic variables derived from digital elevation models. Int. J. Geogr. Inf. Sci. 1998, 12, 47–62. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. Remote Sens. 2009, 64, 398–406. [Google Scholar] [CrossRef] [Green Version]
- Mesa-Mingorance, J.; Ariza-López, F. Accuracy Assessment of Digital Elevation Models (DEMs): A Critical Review of Practices of the Past Three Decades. Remote Sens. 2020, 12, 2630. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X.; Sun, Y. Terrain complexity and uncertainties in grid-based digital terrain analysis. Int. J. Geogr. Inf. Sci. 2006, 20, 1137–1147. [Google Scholar] [CrossRef]
- Erdogan, S. Modelling the spatial distribution of DEM error with geographically weighted regression: An experimental study. Comput. Geosci. 2010, 36, 34–43. [Google Scholar] [CrossRef]
- Guth, P.L.; Van Niekerk, A.; Grohmann, C.H.; Muller, J.P.; Hawker, L.; Florinsky, I.V.; Gesch, D.; Reuter, H.I.; Herrera-Cruz, V.; Riazanoff, S.; et al. Digital Elevation Models: Terminology and Definitions. Remote Sens. 2021, 13, 3581. [Google Scholar] [CrossRef]
- Podobnikar, T. Methods for visual quality assessment of a digital terrain model. Surv. Perspect. Integr. Environ. Soc. 2008, 1, 1–11. [Google Scholar]
- Peucker, T.; Douglas, D. Detection of Surface-Specific Points by Local Parallel Processing of Discrete Terrain Elevation Data. Comput. Graph. Image Process. 1975, 4, 375–387. [Google Scholar] [CrossRef]
- Band, L. Topographic Partition of Watersheds with Digital Elevation Models. Water Resour. Res. 1986, 20, 15–24. [Google Scholar] [CrossRef]
- O’Callaghan, J.; Mark, D. The extraction of drainage networks from digital elevation data. Comput. Vis. Graph. Image Process. 1984, 28, 323–344. [Google Scholar] [CrossRef]
- Jenson, S.; Domingue, J. Extracting Topographic Structure from Digital Elevation Data for Geographic Information System Analysis. Photogramm. Eng. Remote Sens. 1988, 54, 1593–1600. [Google Scholar]
- Iwahashi, J.; Pike, R. Automated classifications of topography from DEMs by an unsupervised nested-means algorithm and a three-part geometric signature. Geomorphology 2007, 86, 409–440. [Google Scholar] [CrossRef]
- Schmidt, J.; Hewitt, A. Fuzzy land element classification from DTMs based on geometry and terrain position. Geoderma 2004, 121, 243–256. [Google Scholar] [CrossRef]
- Wood, J. Scale-based Characterization of Digital Elevation Models. In Innovations in GIS; CRC Press: Boca Raton, FL, USA, 1996; Volume 3, pp. 163–175. [Google Scholar]
- Drăguţ, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- Romstad, B.; Etzelmüller, B. Mean-curvature watersheds: A simple method for segmentation of a digital elevation model into terrain units. Geomorphology 2012, 139–140, 293–302. [Google Scholar] [CrossRef] [Green Version]
- Jasiewicz, J.; Stepinski, T. Geomorphons—A pattern recognition approach to classification and mapping of landforms. Geomorphology 2013, 182, 147–156. [Google Scholar] [CrossRef]
- Guilbert, E.; Gaffuri, J.; Jenny, B. Terrain Generalisation; Abstracting Geographic Information in a Data Rich World; Springer International Publishing: Cham, Switzerland, 2014; pp. 227–258. [Google Scholar] [CrossRef]
- Loon, J. Cartographic Generalization of Digital Terrain Models. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 1977. [Google Scholar]
- Weibel, R. An Adaptive Methodology for Automated Relief Generalization. In Proceedings of the AutoCarto 8, Baltimore, MD, USA, 29 March–3 April 1987; pp. 42–49. [Google Scholar]
- Zakšek, K.; Podobnikar, T. An effective DEM generalization with basic GIS operations. In Proceedings of the 8th ICA Workshop on Generalisation and Multiple Representation, La Coruńa, Spain, 9–16 July 2005. [Google Scholar]
- Pedrini, H. Multiresolution terrain modeling based on triangulated irregular networks. Revista Brasileira de Geociencias 2001, 31, 117–122. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Yang, B. Multi-Resolution Representation of Digital Elevation Models With Topographical Features Preservation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1–7. [Google Scholar]
- Chen, Y.; Wilson, J.; Zhu, Q.; Zhou, Q. Comparison of drainage-constrained methods for DEM generalization. Comput. Geosci. 2012, 48, 41–49. [Google Scholar] [CrossRef]
- Zhou, Q.; Chen, Y. Generalization of DEM for terrain analysis using a compound method. ISPRS J. Photogramm. Remote Sens. 2011, 66, 38–45. [Google Scholar] [CrossRef]
- Jordan, G. Adaptive smoothing of valleys in DEMs using TIN interpolation from ridgeline elevations: An application to morphotectonic aspect analysis. Comput. Geosci. 2007, 33, 573–585. [Google Scholar] [CrossRef]
- Ai, T.; Li, J. A DEM generalization by minor valley branch detection and grid filling. ISPRS J. Photogramm. Remote Sens. 2010, 65, 198–207. [Google Scholar] [CrossRef]
- Weibel, R. Models and Experiments for Adaptive Computer-Assisted Terrain Generalization. Cartogr. Geogr. Inf. Sci. 1992, 19, 133–153. [Google Scholar] [CrossRef]
- Leonowicz, A.; Jenny, B.; Hurni, L. Automatic generation of hypsometric layers for small-scale maps. Comput. Geosci. 2009, 35, 2074–2083. [Google Scholar] [CrossRef] [Green Version]
- Samsonov, T. Multiscale Hypsometric Mapping. In Lecture Notes in Geoinformation and Cartography; Springer: Berlin/Heidelberg, Germany, 2011; Volume 1, pp. 497–520. [Google Scholar]
- Raposo, P. Variable DEM generalization using local entropy for terrain representation through scale. Int. J. Cartogr. 2020, 6, 99–120. [Google Scholar] [CrossRef]
- Zhang, C.; Pan, M.; Wu, H.; Xu, H. Study on simplification of contour lines preserving topological coherence. Acta Sci. Nat. Univ. Pekin. 2007, 43, 216–222. [Google Scholar]
- Ai, T. The drainage network extraction from contour lines for contour line generalization. ISPRS J. Photogramm. Remote Sens. 2007, 62, 93–103. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, T.; Chen, X.; Chen, Z.; Yang, C.; Lin, C.; Shan, L. A New DEM Generalization Method Based on Watershed and Tree Structure. PLoS ONE 2016, 11, e0159798. [Google Scholar] [CrossRef] [PubMed]
- Samsonov, T.; Koshel, S.; Walther, D.; Jenny, B. Automated placement of supplementary contour lines. Int. J. Geogr. Inf. Sci. 2019, 33, 2072–2093. [Google Scholar] [CrossRef]
- Mark, D. Automated Detection Of Drainage Networks From Digital Elevation Models. Cartogr. Int. J. Geogr. Inf. Geovis. 1984, 21, 168–178. [Google Scholar] [CrossRef]
- Koshel, S. Algorithm for Topologically Correct Gridding of Contour Data. In Proceedings of the Seventh International Conference on Geographic Information Science (GIScience 2012), Columbus, OH, USA, 18–21 September 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Kennelly, P.; Patterson, T.; Jenny, B.; Huffman, D.; Marston, B.; Bell, S.; Tait, A. Elevation models for reproducible evaluation of terrain representation. Cartogr. Geogr. Inf. Sci. 2021, 48, 63–77. [Google Scholar] [CrossRef]
- Töpfer, F.; Pillewizer, W. The Principles of Selection. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Sun, X.; Rosin, P.; Martin, R.; Langbein, F. Fast and Effective Feature-Preserving Mesh Denoising. IEEE Trans. Vis. Comput. Graph. 2007, 13, 925–938. [Google Scholar] [CrossRef]








| Scale | Plains | Mountains |
|---|---|---|
| 1:200,000 | 20 | 40 |
| 1:500,000 | 50 | 100 |
| 1:1,000,000 | 50, 100 | 100, 200 |
| Granularity, m | ||||||
|---|---|---|---|---|---|---|
| Fragment | LoD | Resolution | Reference | Generalization | Resampling to G | Resampling to R |
| Bodaybo | 200 | 50 | 1595 | 1611 | 1606 | 1073 |
| 500 | 125 | 2282 | 2275 | 2278 | 1407 | |
| 1000 | 250 | 3678 | 3780 | 3864 | 1750 | |
| Groznyy | 200 | 50 | 1392 | 1436 | 1339 | 501 |
| 500 | 125 | 2992 | 2966 | 3109 | 927 | |
| 1000 | 250 | 4510 | 4448 | 4689 | 1662 | |
| D | ||||
|---|---|---|---|---|
| Fragment | LoD | Resampling to R | Resampling to G | Generalization |
| Bodaybo | 200 | 0.3493 | 0.0430 | 0.0000 |
| 500 | 0.4650 | 0.1377 | 0.0000 | |
| 1000 | 0.7090 | 0.1654 | 0.0141 | |
| Groznyy | 200 | 0.5263 | 0.3015 | 0.1820 |
| 500 | 0.7730 | 0.1638 | 0.0278 | |
| 1000 | 0.7455 | 0.1976 | 0.0565 | |
| Bodaybo | Groznyy | |||||
|---|---|---|---|---|---|---|
| LoD | Upsampling | Resolution, m | Granularity, m | Change, % | Granularity, m | Change, % |
| 200 | ×4 | 12.50 | 1588 | 1.45 | 1390 | 3.31 |
| 200 | ×2 | 25.00 | 1597 | 0.88 | 1408 | 1.99 |
| 200 | ×1 | 50.00 | 1611 | 0.00 | 1436 | 0.00 |
| 500 | ×4 | 31.25 | 2147 | 5.96 | 2693 | 10.14 |
| 500 | ×2 | 62.50 | 2208 | 3.03 | 2750 | 7.85 |
| 500 | ×1 | 125.00 | 2275 | 0.00 | 2966 | 0.00 |
| 1000 | ×4 | 62.50 | 3611 | 4.68 | 3887 | 14.43 |
| 1000 | ×2 | 125.00 | 3681 | 2.69 | 4144 | 7.34 |
| 1000 | ×1 | 250.00 | 3780 | 0.00 | 4448 | 0.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samsonov, T. Granularity of Digital Elevation Model and Optimal Level of Detail in Small-Scale Cartographic Relief Presentation. Remote Sens. 2022, 14, 1270. https://doi.org/10.3390/rs14051270
Samsonov T. Granularity of Digital Elevation Model and Optimal Level of Detail in Small-Scale Cartographic Relief Presentation. Remote Sensing. 2022; 14(5):1270. https://doi.org/10.3390/rs14051270
Chicago/Turabian StyleSamsonov, Timofey. 2022. "Granularity of Digital Elevation Model and Optimal Level of Detail in Small-Scale Cartographic Relief Presentation" Remote Sensing 14, no. 5: 1270. https://doi.org/10.3390/rs14051270
APA StyleSamsonov, T. (2022). Granularity of Digital Elevation Model and Optimal Level of Detail in Small-Scale Cartographic Relief Presentation. Remote Sensing, 14(5), 1270. https://doi.org/10.3390/rs14051270






