Coastal Bathymetry Estimation from Sentinel-2 Satellite Imagery: Comparing Deep Learning and Physics-Based Approaches
Abstract
:1. Introduction
2. Data and Methods
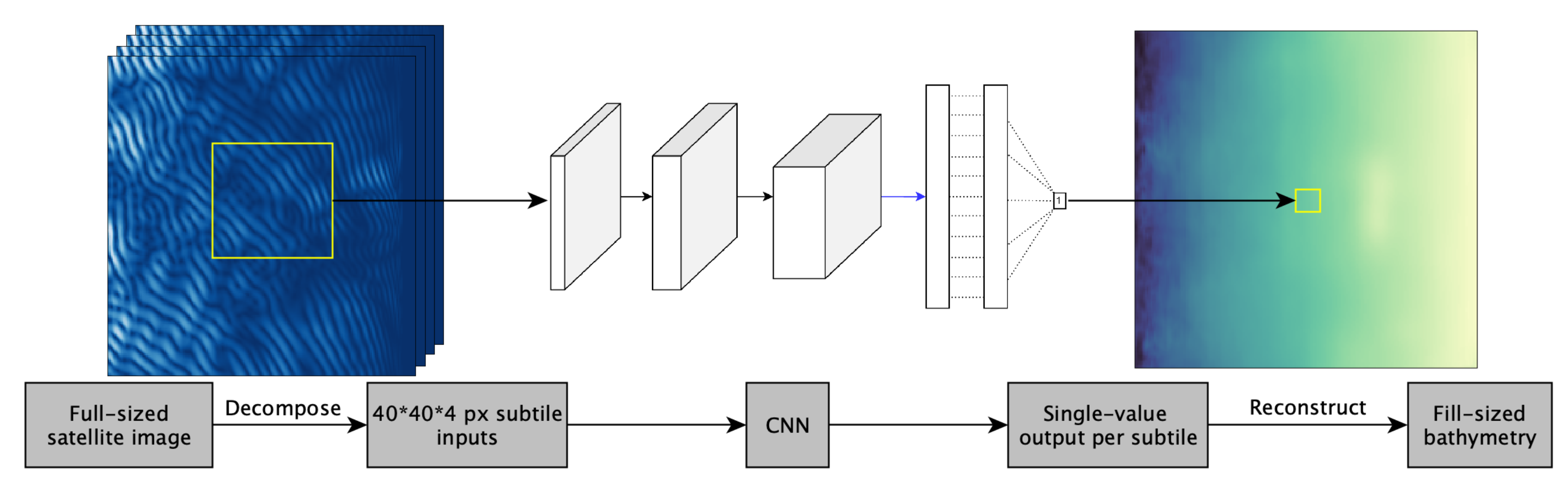
2.1. Deep Single-Point Estimation of Bathymetry
2.2. Satellite to Shores
2.3. Sentinel-2 Data Pre-Processing
2.4. Study Sites
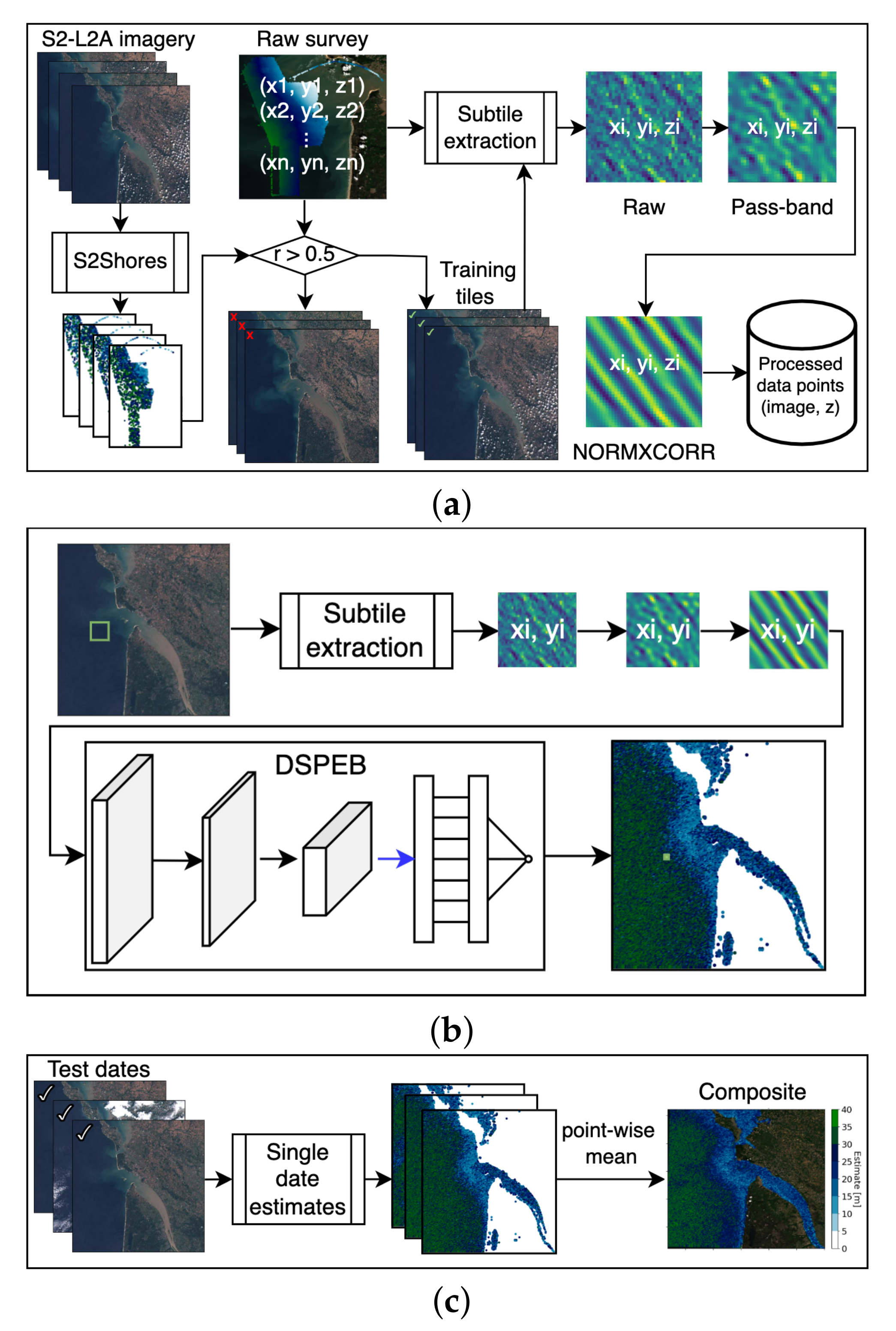
2.5. Application Workflow
3. Research and Results
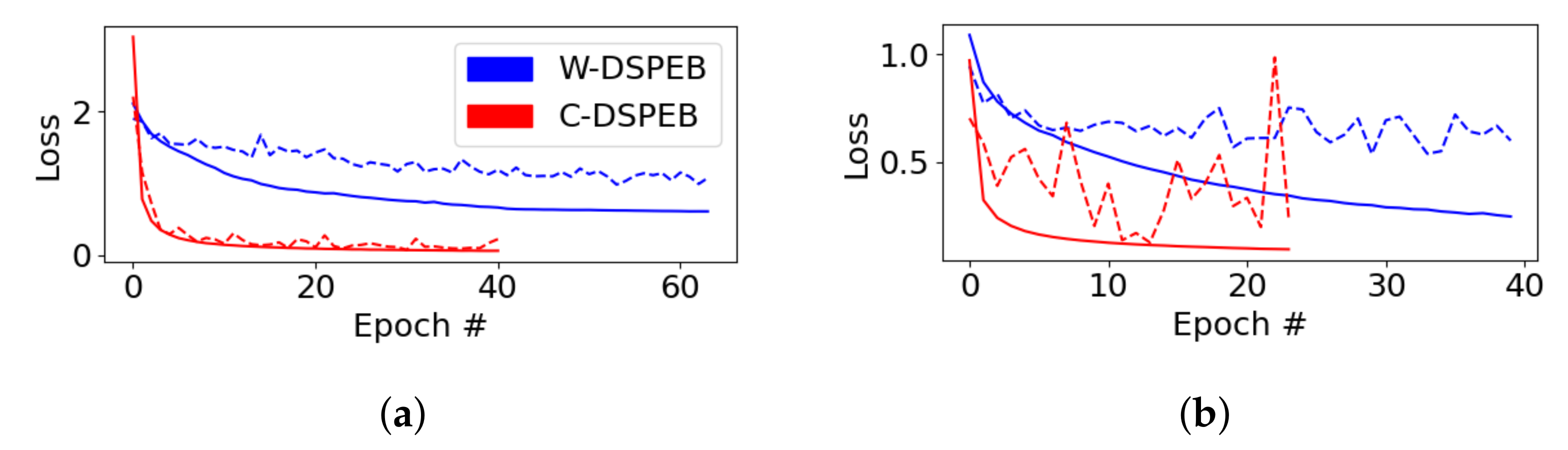
3.1. Model Training
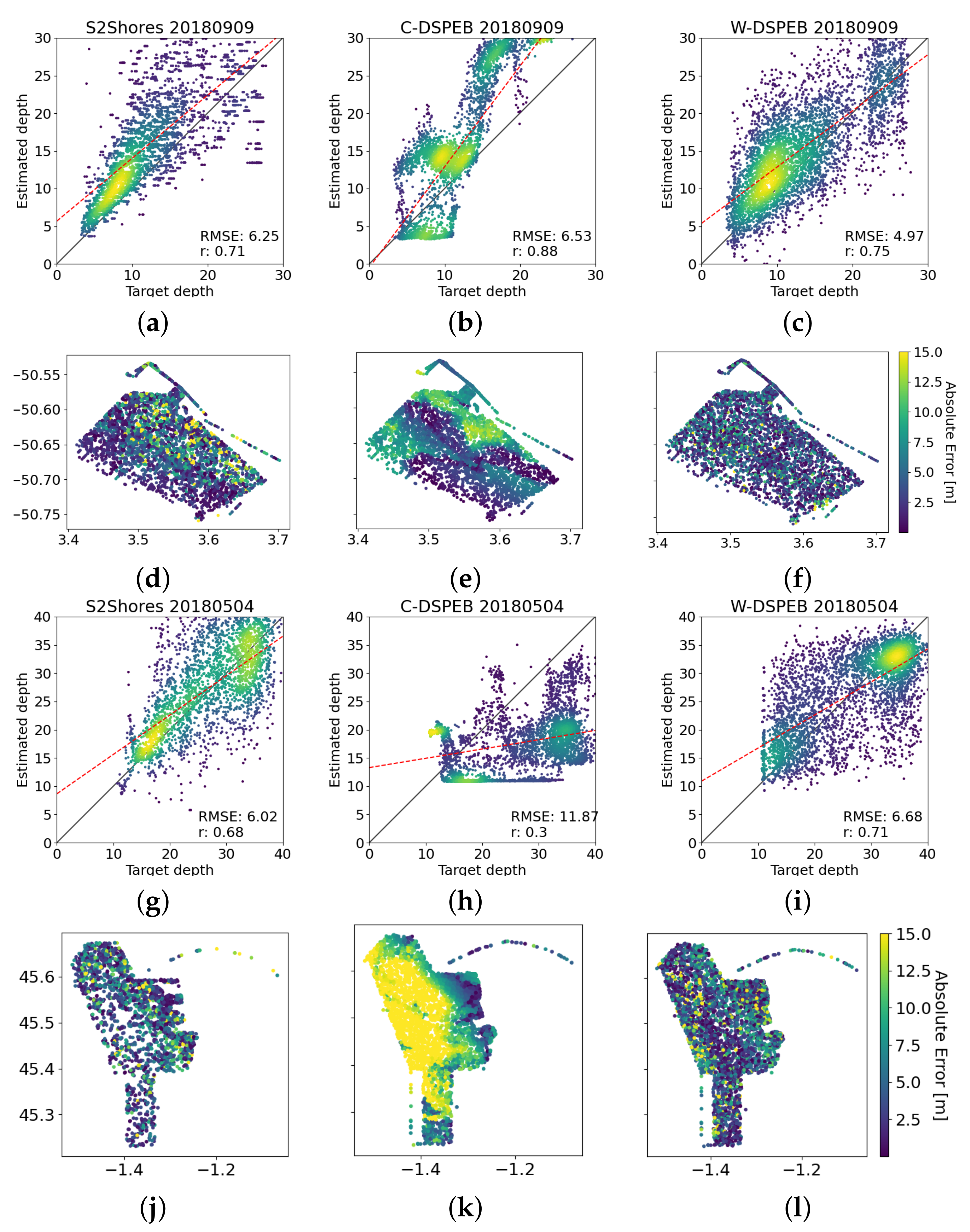
3.2. Single Date Estimation Comparison
3.3. Composite Estimation Comparison
4. Discussion
4.1. Research Implications
4.2. Limitations
4.3. Future Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Data Used in This Work
| Site | Sentinel-2 Image ID |
|---|---|
| Guyane | SENTINEL2B_20180417-140050-461_L2A_T22NCL_D_V1-7 |
| SENTINEL2A_20180711-140053-463_L2A_T22NCL_D_V1-8 | |
| SENTINEL2A_20180731-140053-455_L2A_T22NCL_D_V1-8 | |
| SENTINEL2A_20180909-140049-464_L2A_T22NCL_D_V1-9 | |
| SENTINEL2B_20181024-140049-459_L2A_T22NCL_D_V1-9 | |
| SENTINEL2A_20181228-140102-278_L2A_T22NCL_D_V1-9 | |
| SENTINEL2B_20190919-140108-144_L2A_T22NCL_D_V2-2 | |
| SENTINEL2A_20200809-140115-000_L2A_T22NCL_D_V2-2 | |
| SENTINEL2B_20200814-140112-512_L2A_T22NCL_D_V2-2 | |
| SENTINEL2B_20200824-140112-496_L2A_T22NCL_D_V2-2 | |
| SENTINEL2A_20200918-140113-715_L2A_T22NCL_D_V2-2 | |
| SENTINEL2B_20201023-140112-483_L2A_T22NCL_D_V2-2 | |
| SENTINEL2A_20201107-140113-483_L2A_T22NCL_D_V2-2 | |
| Gironde | SENTINEL2A_20160504-105917-634_L2A_T30TXR_D_V1-1 |
| SENTINEL2A_20170618-110415-683_L2A_T30TXR_D_V1-4 | |
| SENTINEL2B_20180419-110127-730_L2A_T30TXR_C_V2-2 | |
| SENTINEL2A_20180504-110230-455_L2A_T30TXR_C_V2-2 | |
| SENTINEL2A_20180802-105938-888_L2A_T30TXR_C_V2-2 | |
| SENTINEL2B_20180817-110514-624_L2A_T30TXR_C_V2-2 | |
| SENTINEL2B_20190325-110833-768_L2A_T30TXR_C_V2-0 | |
| SENTINEL2B_20190424-110839-893_L2A_T30TXR_C_V2-0 | |
| SENTINEL2B_20190524-110841-657_L2A_T30TXR_C_V2-1 | |
| SENTINEL2B_20190703-110841-774_L2A_T30TXR_C_V2-2 | |
| SENTINEL2A_20190906-110832-459_L2A_T30TXR_C_V2-2 | |
| SENTINEL2A_20200622-110838-839_L2A_T30TXR_C_V2-2 | |
| SENTINEL2A_20210717-110836-344_L2A_T30TXR_C_V2-2 |
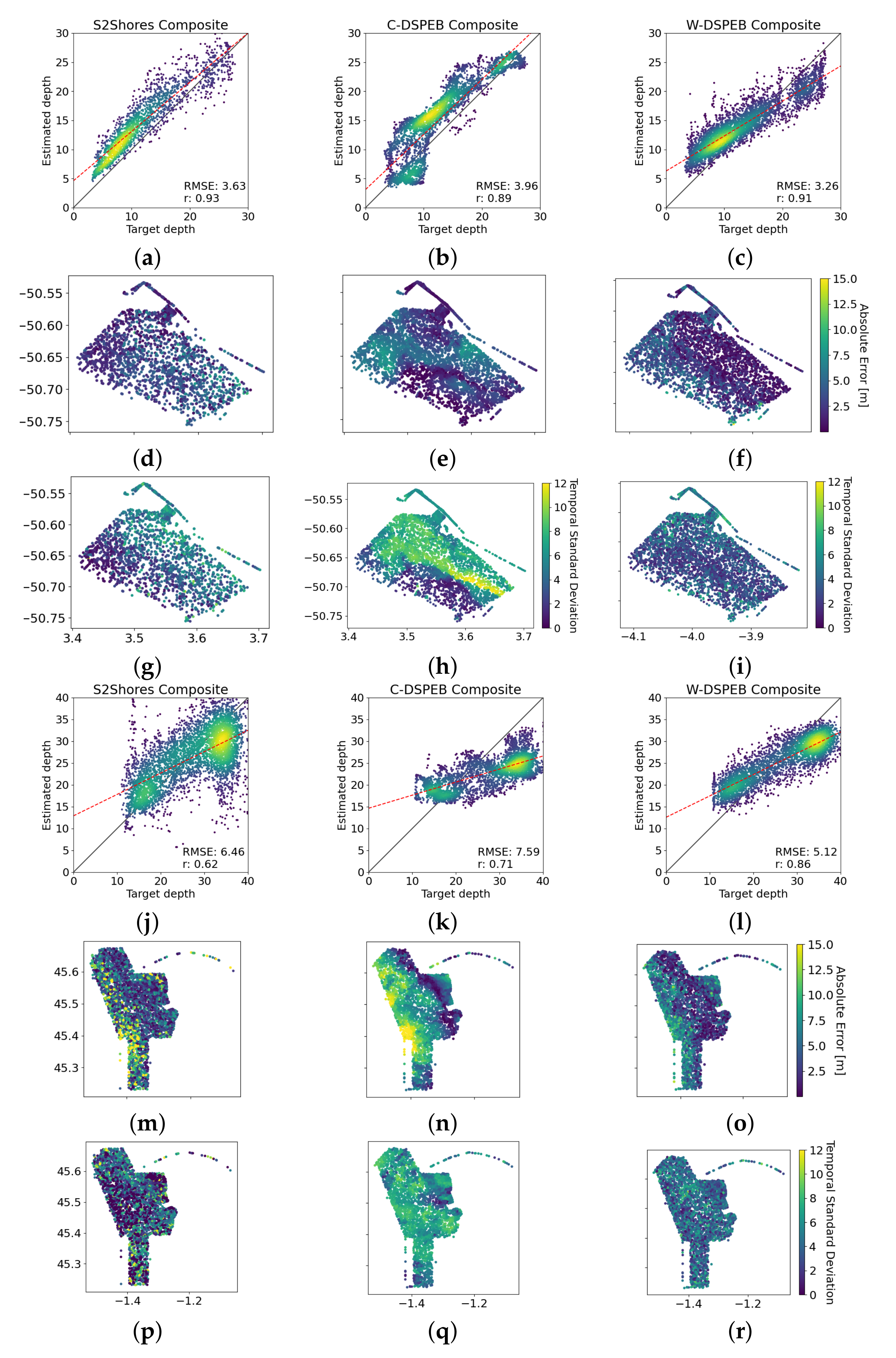
Appendix B. Detailed Composite Results
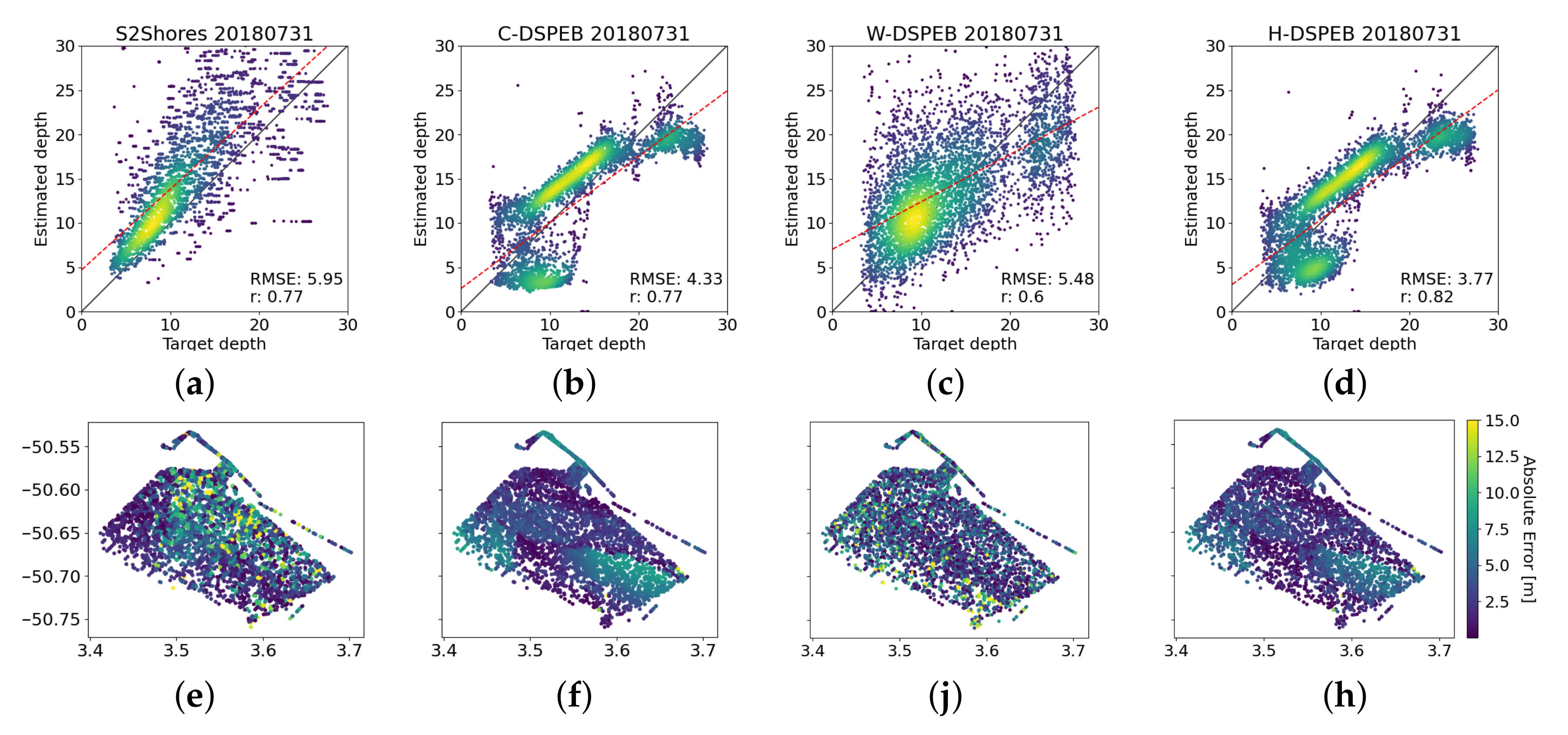
Appendix C. Single Date Results
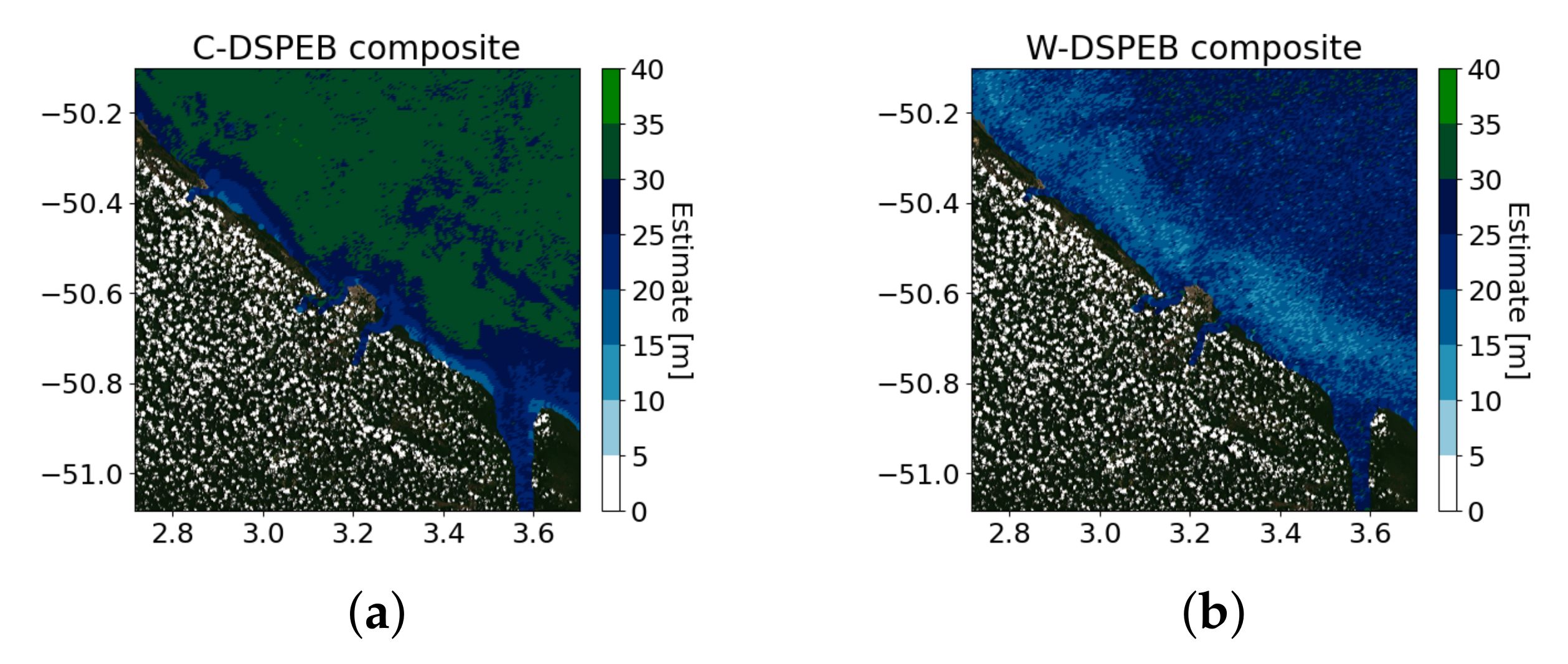
Appendix D. French Guiana Composite over the Full Water Body
Appendix E. Hybrid-DSPEB Model

Hybrid H-DSPEB Preliminary Results

References
- Cesbron, G.; Melet, A.; Almar, R.; Lifermann, A.; Tullot, D.; Crosnier, L. Pan-European Satellite-Derived Coastal Bathymetry—Review, User Needs and Future Services. Front. Mar. Sci. 2021, 8, 1591. [Google Scholar] [CrossRef]
- Gonçalves, G.; Santos, S.; Duarte, D.; Santos, J. Monitoring Local Shoreline Changes by Integrating UASs, Airborne LiDAR, Historical Images and Orthophotos. In Proceedings of the 5th International Conference on Geographical Information Systems Theory, Applications and Management GISTAM, Crete, Greece, 3–5 May 2019. [Google Scholar] [CrossRef]
- Jagalingam, P.; Akshaya, B.; Hegde, A.V. Bathymetry Mapping Using Landsat 8 Satellite Imagery. Procedia Eng. 2015, 116, 560–566. [Google Scholar] [CrossRef] [Green Version]
- Gao, J. Bathymetric mapping by means of remote sensing: Methods, accuracy and limitations. Prog. Phys. Geogr. 2009, 33, 103–116. [Google Scholar] [CrossRef]
- Salameh, E.; Frappart, F.; Almar, R.; Baptista, P.; Heygster, G.; Lubac, B.; Raucoules, D.; Almeida, L.P.; Bergsma, E.W.J.; Capo, S.; et al. Monitoring Beach Topography and Nearshore Bathymetry Using Spaceborne Remote Sensing: A Review. Remote Sens. 2019, 11, 2212. [Google Scholar] [CrossRef] [Green Version]
- Ashphaq, M.; Srivastava, P.K.; Mitra, D. Review of near-shore satellite derived bathymetry: Classification and account of five decades of coastal bathymetry research. J. Ocean. Eng. Sci. 2021, 6, 340–359. [Google Scholar] [CrossRef]
- Benveniste, J.; Cazenave, A.; Vignudelli, S.; Fenoglio-Marc, L.; Shah, R.; Almar, R.; Andersen, O.; Birol, F.; Bonnefond, P.; Bouffard, J.; et al. Requirements for a Coastal Hazards Observing System. Front. Mar. Sci. 2019, 6, 348. [Google Scholar] [CrossRef] [Green Version]
- Melet, A.; Teatini, P.; Le Cozannet, G.; Jamet, C.; Conversi, A.; Benveniste, J.; Almar, R. Earth observations for monitoring marine coastal hazards and their drivers. Surv. Geophys. 2020, 41, 1489–1534. [Google Scholar] [CrossRef]
- Almar, R.; Bonneton, P.; Senechal, N.; Roelvink, D. Wave celerity from video imaging: A new method. In Coastal Engineering 2008: (In 5 Volumes); World Scientific: Hackensack, NJ, USA, 2009; pp. 661–673. [Google Scholar]
- Holman, R.A.; Plant, N.; Holland, T. cBathy: A Robust Algorithm For Estimating Nearshore Bathymetry. J. Geophys. Res. Oceans 2013, 118, 2595–2609. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R.; de Almeida, L.P.M.; Sall, M. On the operational use of UAVs for video-derived bathymetry. Coast. Eng. 2019, 152, 103527. [Google Scholar] [CrossRef]
- Drusch, M.; Bello, U.D.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Bergsma, E.W.J.; Almar, R. Coastal coverage of ESA’ Sentinel 2 mission. Adv. Space Res. 2020, 65, 2636–2644. [Google Scholar] [CrossRef]
- Erena, M.; Domínguez, J.A.; Aguado-Giménez, F.; Soria, J.; García-Galiano, S. Monitoring coastal lagoon water quality through remote sensing: The Mar Menor as a case study. Water 2019, 11, 1468. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Islam, M.A.; Gao, J. Quantification of shallow water quality parameters by means of remote sensing. Prog. Phys. Geogr. 2003, 27, 24–43. [Google Scholar] [CrossRef]
- Brando, V.; Dekker, A. Satellite hyperspectral remote sensing for estimating estuarine and coastal water quality. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1378–1387. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Passive remote sensing techniques for mapping water depth and bottom features. Appl. Opt. 1978, 17, 379–383. [Google Scholar] [CrossRef] [PubMed]
- Giardino, C.; Candiani, G.; Bresciani, M.; Lee, Z.; Gagliano, S.; Pepe, M. BOMBER: A tool for estimating water quality and bottom properties from remote sensing images. Comput. Geosci. 2012, 45, 313–318. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Roberts, D.A.; Lawrence, R.L. Spectrally based remote sensing of river bathymetry. Earth Surf. Process. Landforms 2009, 34, 1039–1059. Available online: https://onlinelibrary.wiley.com/doi/pdf/10.1002/esp.1787 (accessed on 13 December 2021). [CrossRef]
- Caballero, I.; Stumpf, R. Retrieval of nearshore bathymetry from Sentinel-2A and 2B satellites in South Florida coastal waters. Estuar. Coast. Shelf Sci. 2019, 226, 106277. [Google Scholar] [CrossRef]
- Evagorou, E.; Mettas, C.; Agapiou, A.; Themistocleous, K.; Hadjimitsis, D. Bathymetric maps from multi-temporal analysis of Sentinel-2 data: The case study of Limassol, Cyprus. Adv. Geosci. 2019, 45, 397–407. [Google Scholar] [CrossRef] [Green Version]
- Sagawa, T.; Yamashita, Y.; Okumura, T.; Yamanokuchi, T. Satellite Derived Bathymetry Using Machine Learning and Multi-Temporal Satellite Images. Remote Sens. 2019, 11, 1155. [Google Scholar] [CrossRef] [Green Version]
- Almar, R.; Bergsma, E.W.J.; Thoumyre, G.; Baba, M.W.; Cesbron, G.; Daly, C.; Garlan, T.; Lifermann, A. Global Satellite-Based Coastal Bathymetry from Waves. Remote Sens. 2021, 13, 4628. [Google Scholar] [CrossRef]
- Bergsma, E.W.; Almar, R.; Rolland, A.; Binet, R.; Brodie, K.L.; Bak, A.S. Coastal morphology from space: A showcase of monitoring the topography-bathymetry continuum. Remote Sens. Environ. 2021, 261, 112469. [Google Scholar] [CrossRef]
- Pacheco, A.; Horta, J.; Loureiro, C.; Ferreira, O. Retrieval of nearshore bathymetry from Landsat 8 images: A tool for coastal monitoring in shallow waters. Remote Sens. Environ. 2015, 159, 102–116. [Google Scholar] [CrossRef] [Green Version]
- Chénier, R.; Faucher, M.A.; Ahola, R. Satellite-Derived Bathymetry for Improving Canadian Hydrographic Service Charts. Int. J. Geo-Inf. 2018, 7, 306. [Google Scholar] [CrossRef] [Green Version]
- Traganos, D.; Poursanidis, D.; Aggarwal, B.; Chrysoulakis, N.; Reinartz, P. Estimating Satellite-Derived Bathymetry (SDB) with the Google Earth Engine and Sentinel-2. Remote Sens. 2018, 10, 859. [Google Scholar] [CrossRef] [Green Version]
- Sandidge, J.C.; Holyer, R.J. Coastal Bathymetry from Hyperspectral Observations of Water Radiance. Remote Sens. Environ. 1998, 65, 341–352. [Google Scholar] [CrossRef]
- Vojinovic, Z.; Abebe, Y.; Ranasinghe, R.; Vacher, A.; Martens, P.; Mandl, D.; Frye, S.; Van Ettinger, E.; De Zeeuw, R. A Machine Learning Approach for Estimation of Shallow Water Depths from Optical Satellite Images and Sonar Measurements. J. Hydroinform. 2013, 15, 1408–1424. [Google Scholar] [CrossRef] [Green Version]
- Iglovikov, V.; Mushinskiy, S.; Osin, V. Satellite imagery feature detection using deep convolutional neural network: A kaggle competition. arXiv 2017, arXiv:1706.06169. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef] [Green Version]
- Hoeser, T.; Kuenzer, C. Object Detection and Image Segmentation with Deep Learning on Earth Observation Data: A Review-Part I: Evolution and Recent Trends. Remote Sens. 2020, 12, 1667. [Google Scholar] [CrossRef]
- Ma, L.; Liu, Y.; Zhang, X.; Ye, Y.; Yin, G.; Johnson, B.A. Deep learning in remote sensing applications: A meta-analysis and review. ISPRS J. Photogramm. Remote Sens. 2019, 152, 166–177. [Google Scholar] [CrossRef]
- Ghorbanidehno, H.; Lee, J.; Farthing, M.; Hesser, T.; Darve, E.F.; Kitanidis, P.K. Deep learning technique for fast inference of large-scale riverine bathymetry. Adv. Water Resour. 2021, 147, 103715. [Google Scholar] [CrossRef]
- Collins, A.M.; Geheran, M.P.; Hesser, T.J.; Bak, A.S.; Brodie, K.L.; Farthing, M.W. Development of a Fully Convolutional Neural Network to Derive Surf-Zone Bathymetry from Close-Range Imagery of Waves in Duck, NC. Remote Sens. 2021, 13, 4907. [Google Scholar] [CrossRef]
- Mandlburger, G.; Kölle, M.; Nübel, H.; Soergel, U. BathyNet: A Deep Neural Network for Water Depth Mapping from Multispectral Aerial Images. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2021, 89, 1–19. [Google Scholar] [CrossRef]
- Dickens, K.; Armstrong, A. Application of Machine Learning in Satellite Derived Bathymetry and Coastline Detection. SMU Data Sci. Rev. 2019, 2, 4. [Google Scholar]
- Wilson, B.; Kurian, N.C.; Singh, A.; Sethi, A. Satellite-Derived Bathymetry Using Deep Convolutional Neural Network. In Proceedings of the IGARSS 2020–2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2280–2283. [Google Scholar]
- Lumban-Gaol, Y.; Ohori, K.; Peters, R. Satellite-derived bathymetry using convolutional neural networks and multispectral sentinel-2 images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2021, 43, 201–207. [Google Scholar] [CrossRef]
- Danilo, C.; Melgani, F. Wave period and coastal bathymetry using wave propagation on optical images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6307–6319. [Google Scholar] [CrossRef]
- Benshila, R.; Thoumyre, G.; Al Najar, M.; Abessolo, G.; Almar, R.; Bergsma, E.; Hugonnard, G.; Labracherie, L.; Lavie, B.; Ragonneau, T.; et al. A deep learning approach for estimation of the nearshore bathymetry. J. Coast. Res. 2020, 95, 1011–1015. [Google Scholar] [CrossRef]
- Al Najar, M.; Thoumyre, G.; Bergsma, E.W.J.; Almar, R.; Benshila, R.; Wilson, D.G. Satellite derived bathymetry using deep learning. Mach. Learn. 2021. [Google Scholar] [CrossRef]
- Baba, W.M.; Bergsma, E.W.J.; Almar, R.; Daly, C.J. Deriving large-scale coastal bathymetry from Sentinel-2 images using an High-Performance Cluster: A case study covering North Africa’s coastal zone. Sensors 2021, 21, 7006. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef] [Green Version]
- Wightman, R.; Touvron, H.; Jégou, H. Resnet strikes back: An improved training procedure in timm. arXiv 2021, arXiv:2110.00476. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Bergsma, E.W.J.; Almar, R.; Maisongrande, P. Radon-Augmented Sentinel-2 Satellite Imagery to Derive Wave-Patterns and Regional Bathymetry. Remote Sens. 2019, 11, 1918. [Google Scholar] [CrossRef] [Green Version]
- Lin, L.I.K. A Concordance Correlation Coefficient to Evaluate Reproducibility. Biometrics 1989, 45, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Lathuilière, S.; Mesejo, P.; Alameda-Pineda, X.; Horaud, R. A comprehensive analysis of deep regression. IEEE Trans. Pattern Anal. Mach. Intell. 2019, 42, 2065–2081. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xian, Y.; Schiele, B.; Akata, Z. Zero-shot learning-the good, the bad and the ugly. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4582–4591. [Google Scholar]
- Arcucci, R.; Zhu, J.; Hu, S.; Guo, Y.K. Deep data assimilation: Integrating deep learning with data assimilation. Appl. Sci. 2021, 11, 1114. [Google Scholar] [CrossRef]
- Dua, N.; Singh, S.N.; Semwal, V.B. Multi-input CNN-GRU based human activity recognition using wearable sensors. Computing 2021, 103, 1461–1478. [Google Scholar] [CrossRef]
- Oktay, O.; Bai, W.; Lee, M.; Guerrero, R.; Kamnitsas, K.; Caballero, J.; de Marvao, A.; Cook, S.; O’Regan, D.; Rueckert, D. Multi-input Cardiac Image Super-Resolution Using Convolutional Neural Networks. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2016, Athens, Greece, 17–21 October 2016; Ourselin, S., Joskowicz, L., Sabuncu, M.R., Unal, G., Wells, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 246–254. [Google Scholar]
- Cheng, D.; Gong, Y.; Zhou, S.; Wang, J.; Zheng, N. Person Re-Identification by Multi-Channel Parts-Based CNN With Improved Triplet Loss Function. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
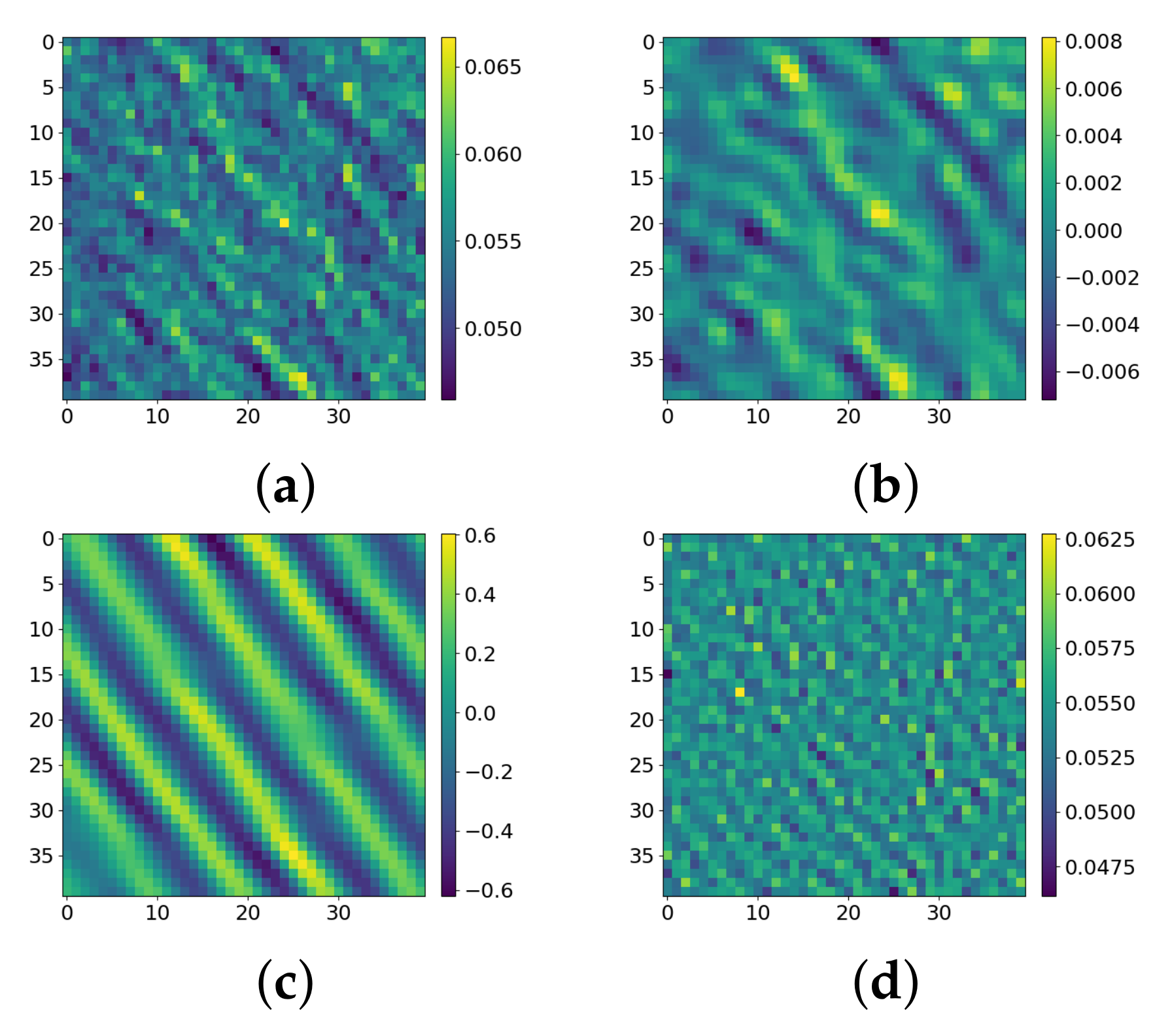
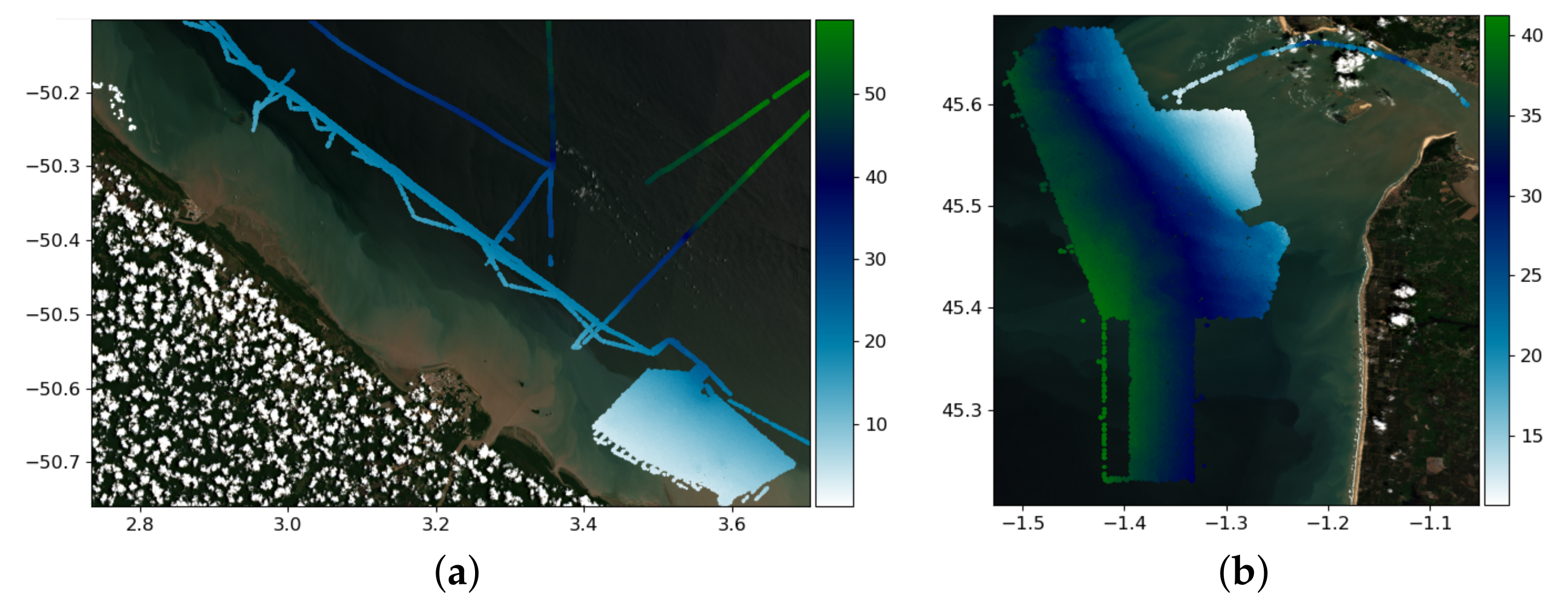
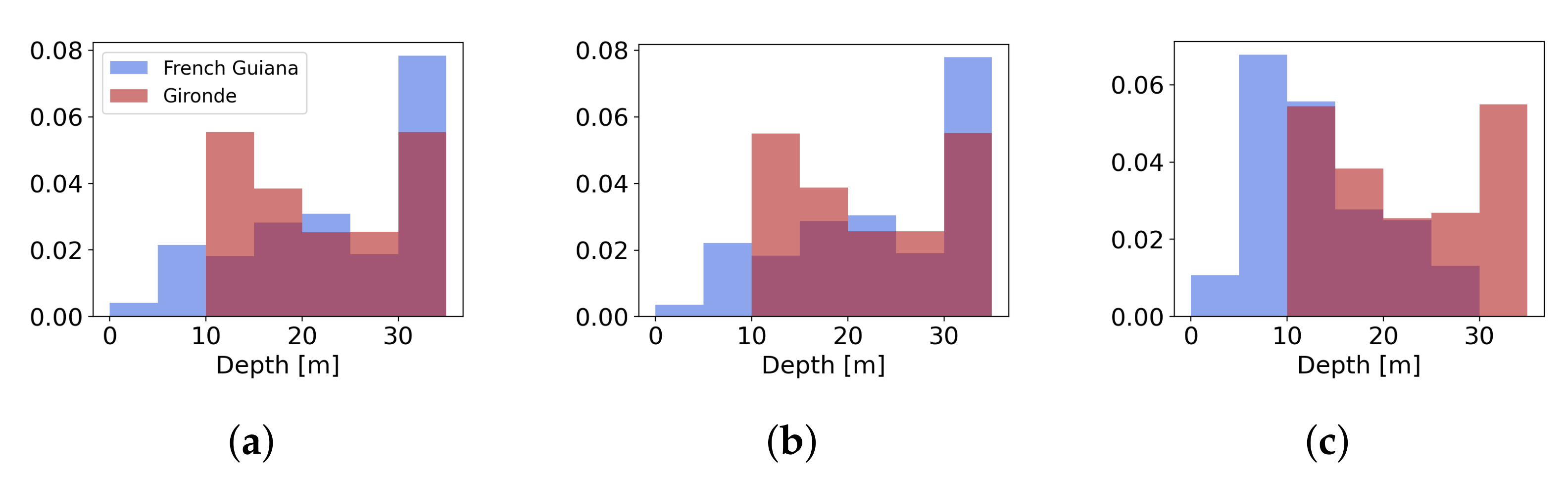
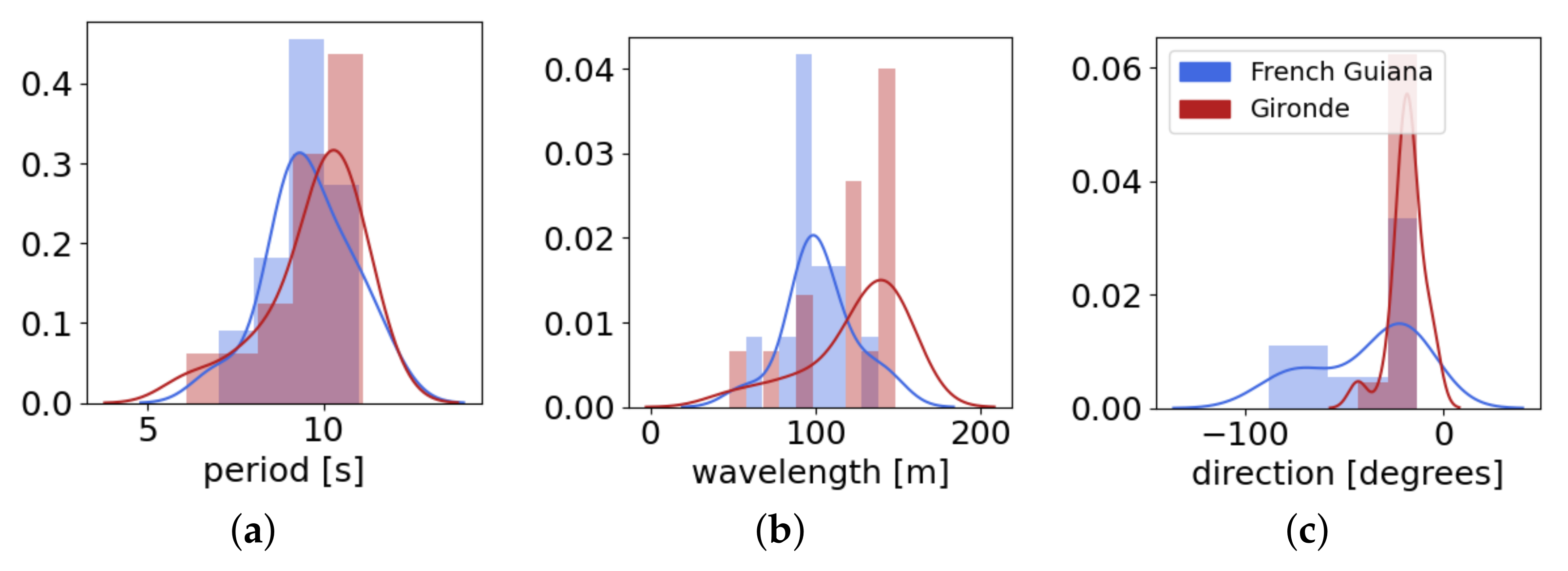
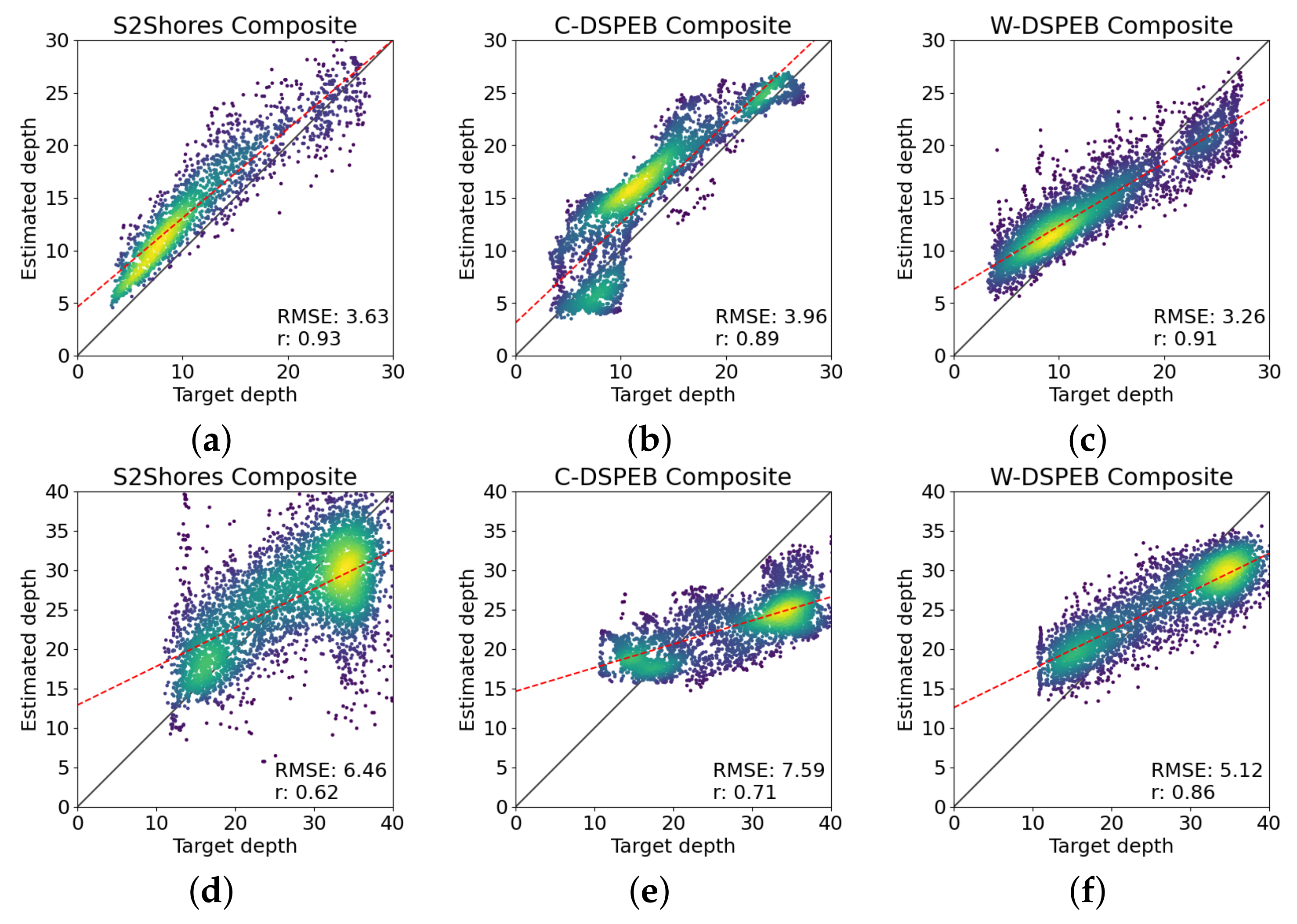


| Site | Metric | S2Shores | C-DSPEB | W-DSPEB |
|---|---|---|---|---|
| French Guiana | r | 0.93 | 0.89 | 0.91 |
| RMSE (m) | 3.63 | 3.96 | 3.26 | |
| Temporal STD (m) | 3.99 | 6.23 | 3.49 | |
| Gironde | r | 0.62 | 0.71 | 0.86 |
| RMSE (m) | 6.46 | 7.59 | 5.12 | |
| Temporal STD (m) | 3.89 | 6.13 | 4.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najar, M.A.; Benshila, R.; Bennioui, Y.E.; Thoumyre, G.; Almar, R.; Bergsma, E.W.J.; Delvit, J.-M.; Wilson, D.G. Coastal Bathymetry Estimation from Sentinel-2 Satellite Imagery: Comparing Deep Learning and Physics-Based Approaches. Remote Sens. 2022, 14, 1196. https://doi.org/10.3390/rs14051196
Najar MA, Benshila R, Bennioui YE, Thoumyre G, Almar R, Bergsma EWJ, Delvit J-M, Wilson DG. Coastal Bathymetry Estimation from Sentinel-2 Satellite Imagery: Comparing Deep Learning and Physics-Based Approaches. Remote Sensing. 2022; 14(5):1196. https://doi.org/10.3390/rs14051196
Chicago/Turabian StyleNajar, Mahmoud Al, Rachid Benshila, Youssra El Bennioui, Grégoire Thoumyre, Rafael Almar, Erwin W. J. Bergsma, Jean-Marc Delvit, and Dennis G. Wilson. 2022. "Coastal Bathymetry Estimation from Sentinel-2 Satellite Imagery: Comparing Deep Learning and Physics-Based Approaches" Remote Sensing 14, no. 5: 1196. https://doi.org/10.3390/rs14051196
APA StyleNajar, M. A., Benshila, R., Bennioui, Y. E., Thoumyre, G., Almar, R., Bergsma, E. W. J., Delvit, J.-M., & Wilson, D. G. (2022). Coastal Bathymetry Estimation from Sentinel-2 Satellite Imagery: Comparing Deep Learning and Physics-Based Approaches. Remote Sensing, 14(5), 1196. https://doi.org/10.3390/rs14051196






