Affinity Propagation Based on Structural Similarity Index and Local Outlier Factor for Hyperspectral Image Clustering
Abstract
:1. Introduction
- 1.
- New spatial-spectral similarity metrics for the hyperspectral dataset were defined and applied to AP clustering.
- 2.
- The CW-SSIM was used to measure the similarity of the HSI samples and a new computational strategy was defined to reduce the computational effort.
- 3.
- The LOF was used to define the degree of the uniformity and smoothness of the local neighborhood density of a sample and applied to revise the exemplar preference of AP.
2. Method
2.1. Affinity Propagation
2.2. Complex Wavelet Structural Similarity
2.3. Local Outlier Factor
- 1.
- For at least samples , it holds that , and
- 2.
- For at most objects , it holds that .
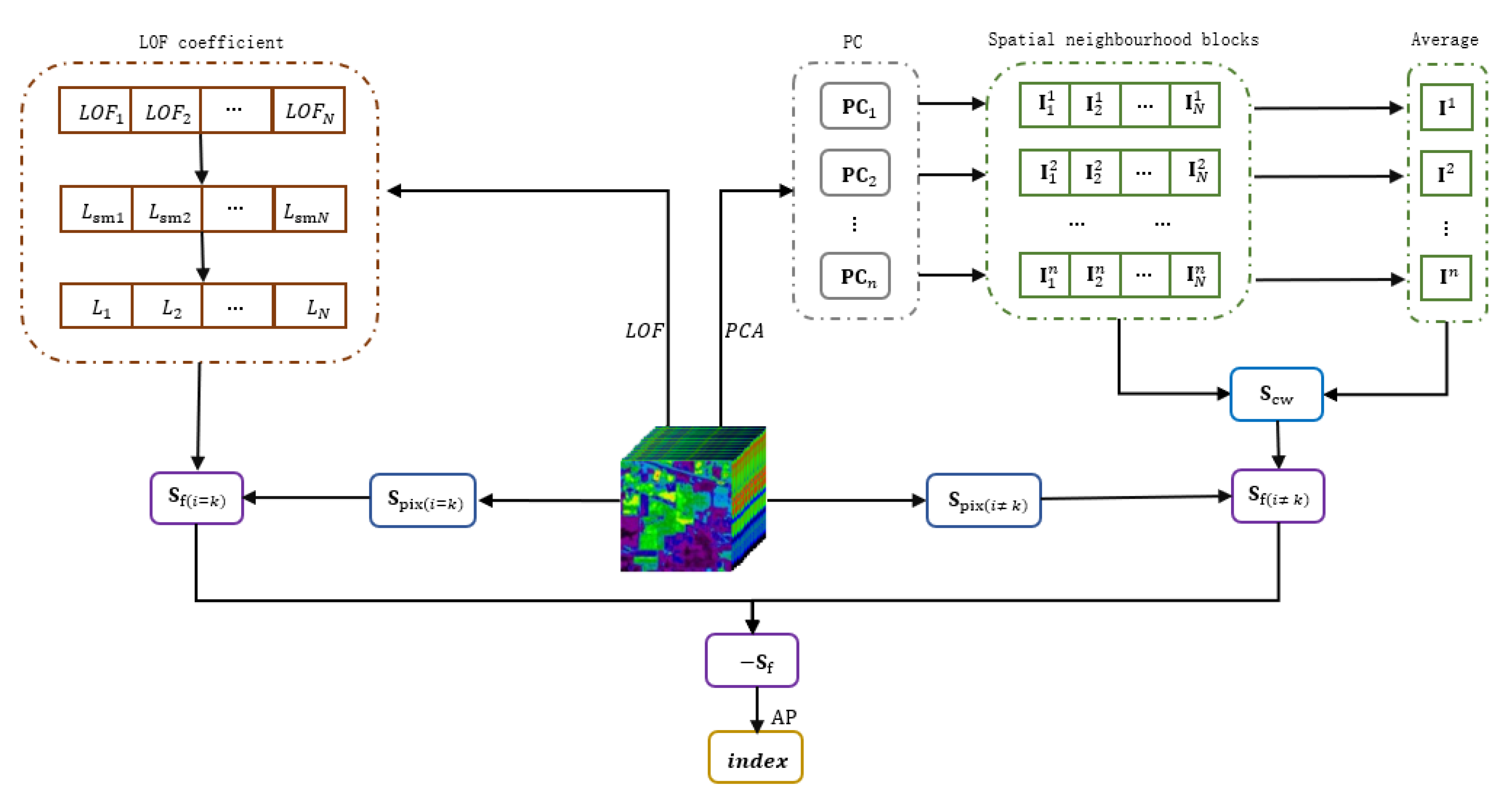
2.4. Affinity Propagation Based on Structural Similarity Index and Local Outlier Factor
3. Experiments
3.1. Hyperspectral Dataset
3.2. Experimental Setup
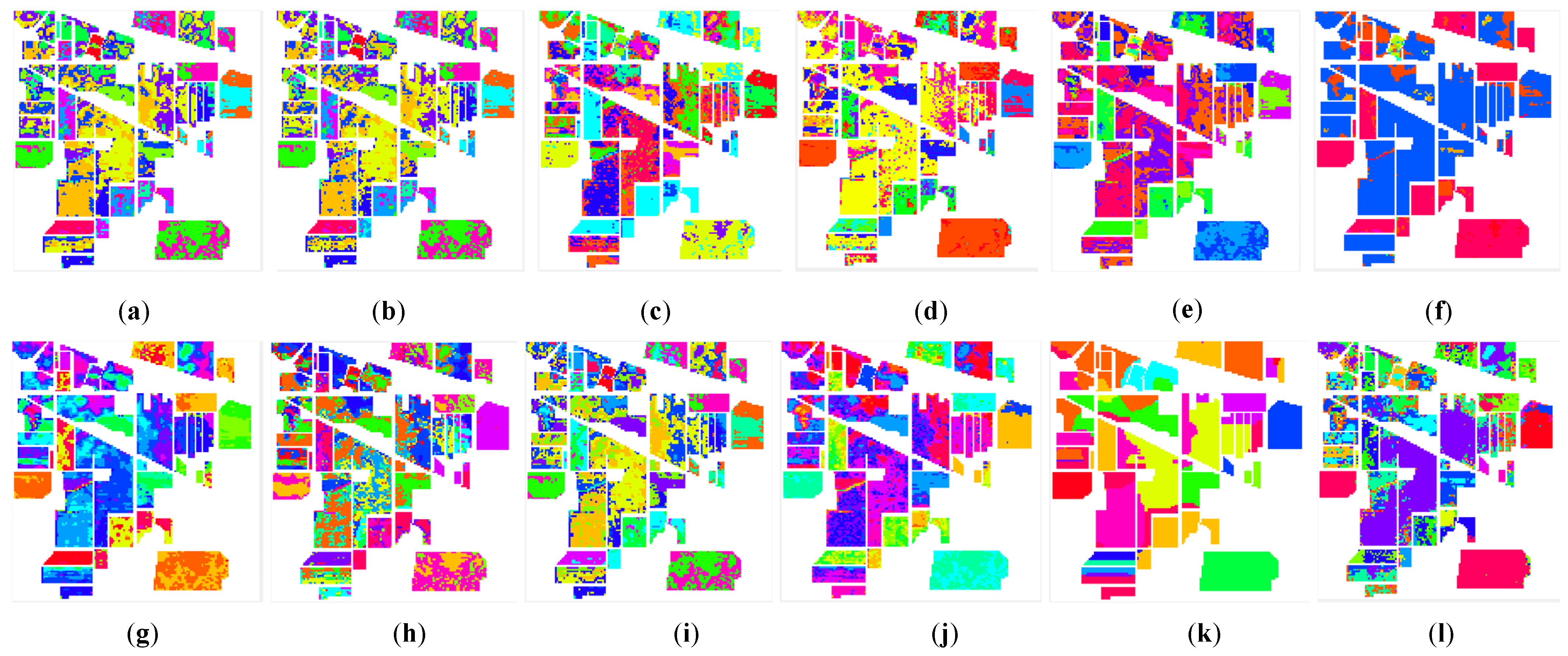
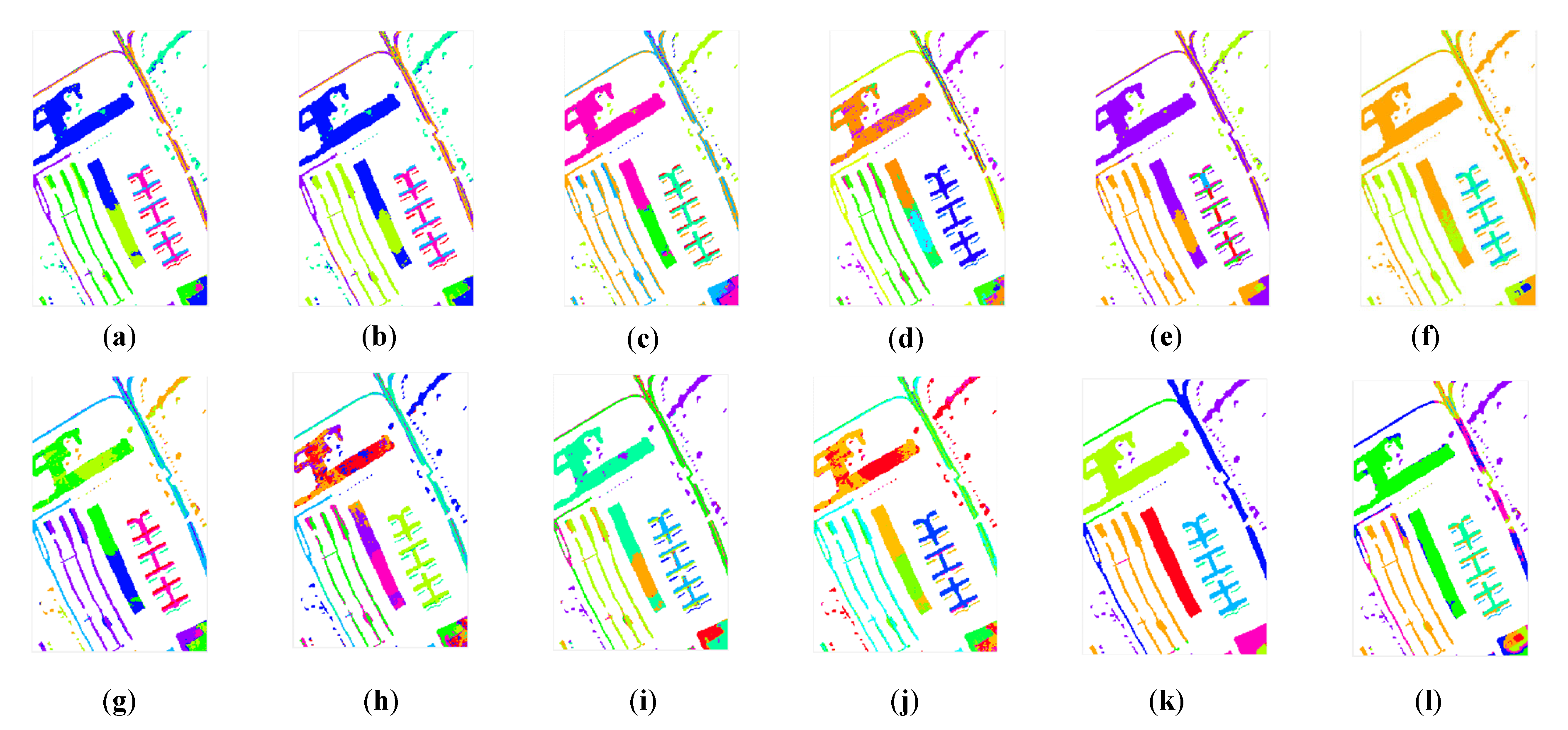
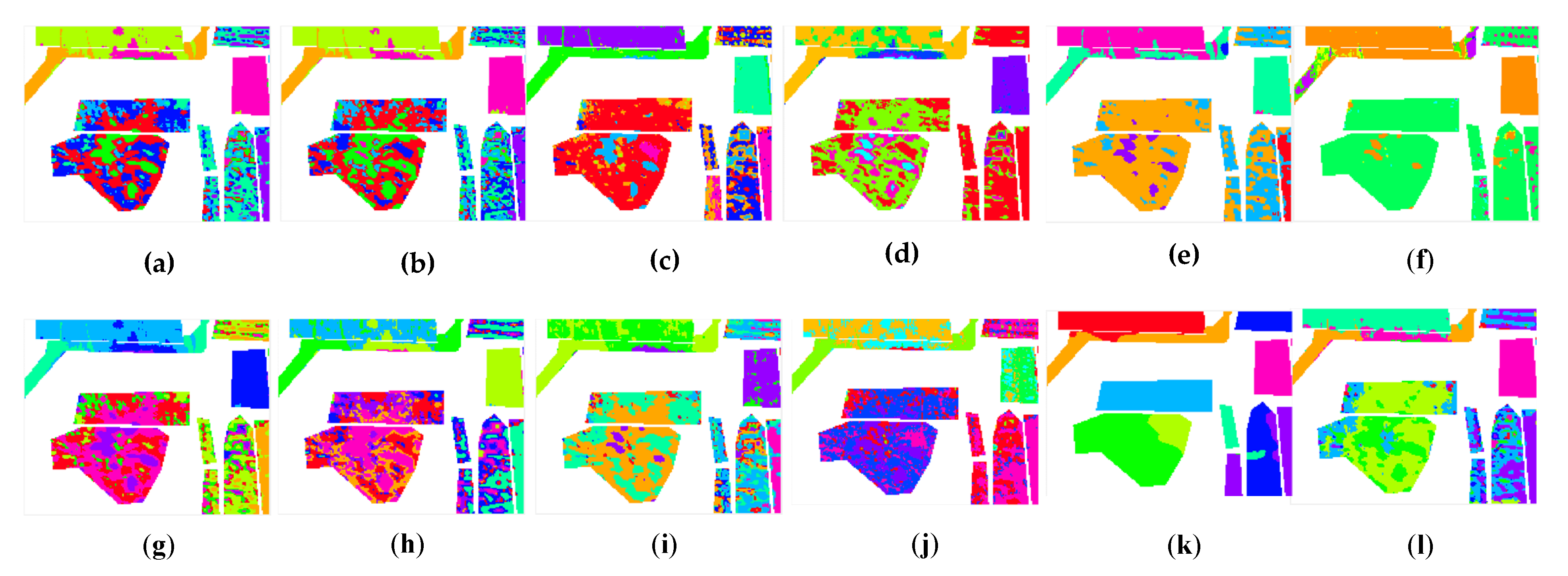
3.3. Experimental Results in Different HSIs
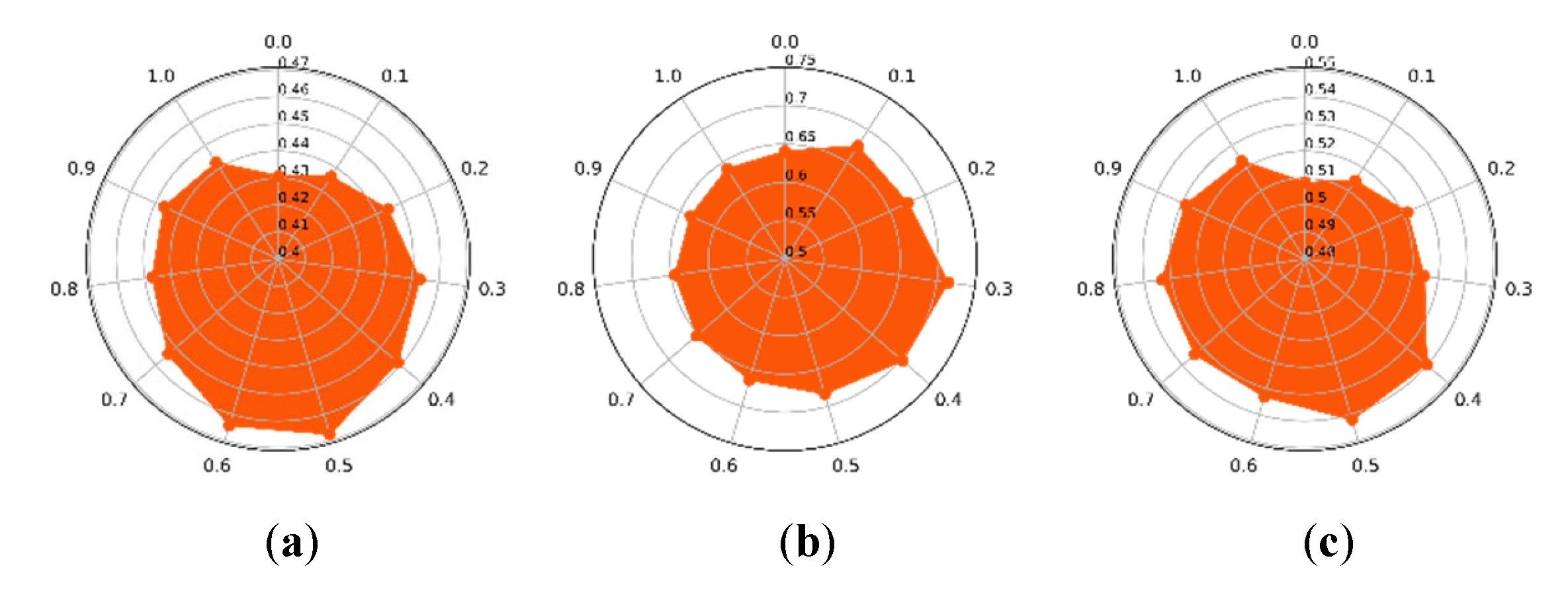
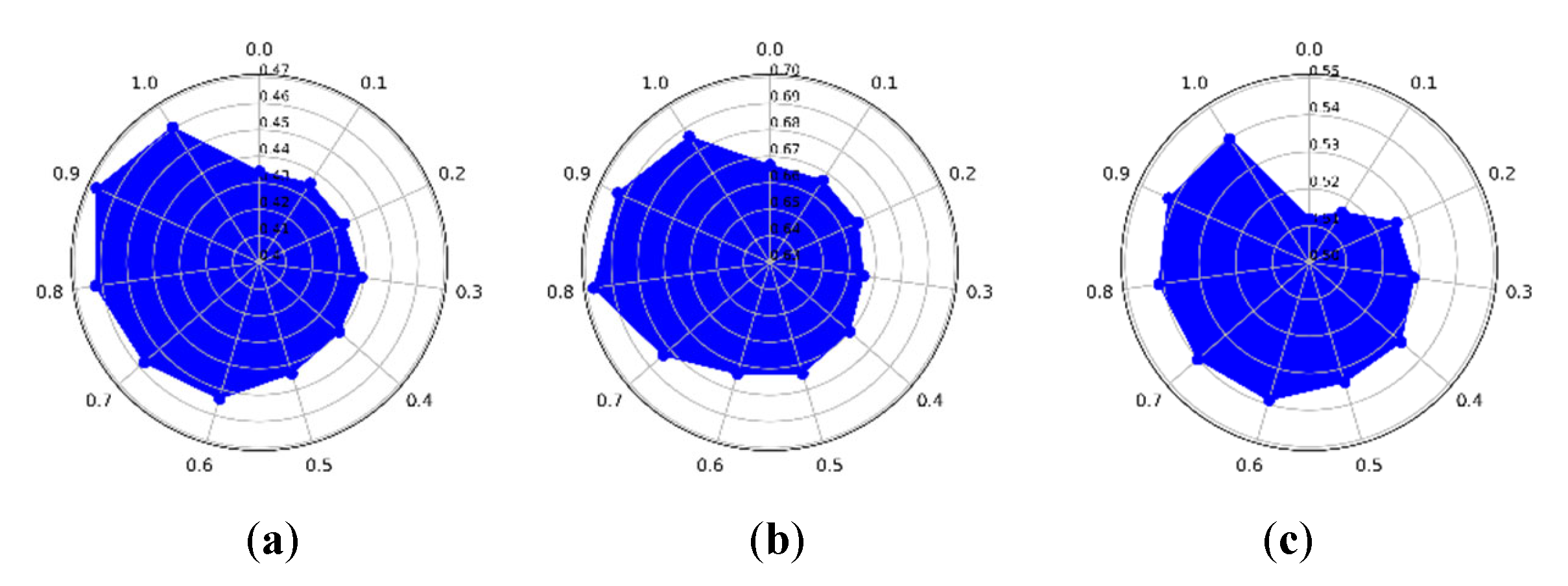
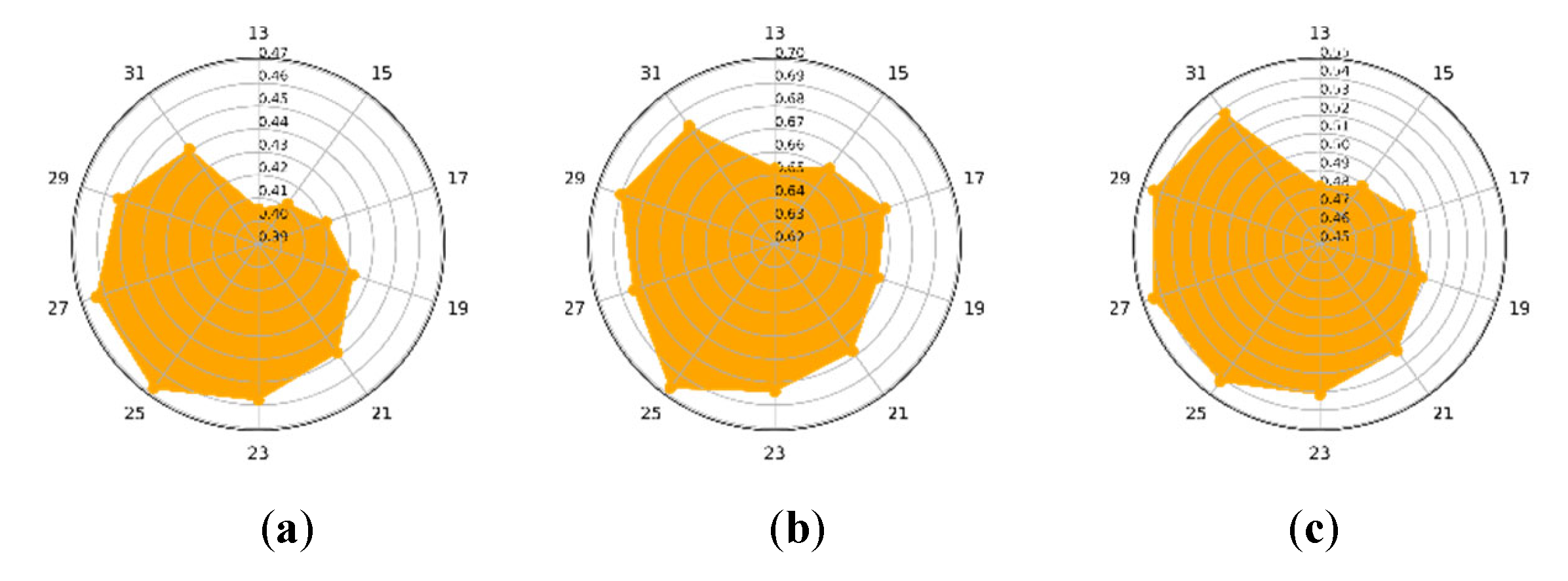
3.4. The Optimization Strategy of , , and
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HIS | Hyperspectral image |
| AP | Affinity propagation |
| SSIM | Structural similarity |
| CW-SSIM | Complex wavelet structural similarity |
| LOF | Local outlier factor |
| CLAP | Improved AP with CW-SSIM and LOF |
| PCA | Principal component analysis |
| PC | Principal component |
| IP | Indian Pines dataset |
| PU | Pavia University dataset |
| HH | WHU-Hi-HongHu dataset |
| ED | Euclidean distance |
| SC | Spectral clustering |
| GMM | Gaussian mixture models |
| DPC | Density peaks clustering |
| Self-org | Self-organizing maps |
| CL | Competitive layers |
| HESSC | Hierarchical sparse subspace clustering |
| GR-RSCNet | Graph regularized residual subspace clustering network |
| NMI | Normalized mutual information |
| ACC | Accuracy |
| ARI | Adjusted rand index |
References
- Ou, D.P.; Tan, K.; Du, Q.; Zhu, J.S.; Wang, X.; Chen, Y. A Novel Tri-Training Technique for the Semi-Supervised Classification of Hyperspectral Images Based on Regularized Local Discriminant Embedding Feature Extraction. Remote Sens. 2019, 11, 654. [Google Scholar] [CrossRef] [Green Version]
- Chung, B.; Yu, J.; Wang, L.; Kim, N.H.; Lee, B.H.; Koh, S.; Lee, S. Detection of Magnesite and Associated Gangue Minerals using Hyperspectral Remote Sensing-A Laboratory Approach. Remote Sens. 2020, 12, 1325. [Google Scholar] [CrossRef] [Green Version]
- Shimoni, M.; Haelterman, R.; Perneel, C. Hyperspectral Imaging for Military and Security Applications Combining myriad processing and sensing techniques. IEEE Geosci. Remote Sens. Mag. 2019, 7, 101–117. [Google Scholar] [CrossRef]
- Chehdi, K.; Soltani, M.; Cariou, C. Pixel classification of large-size hyperspectral images by affinity propagation. J. Appl. Remote Sens. 2014, 8, 083567. [Google Scholar] [CrossRef] [Green Version]
- Zhai, H.; Zhang, H.Y.; Li, P.X.; Zhang, L.P. Hyperspectral Image Clustering: Current Achievements and Future Lines. IEEE Geosci. Remote Sens. Mag. 2021, 9, 35–67. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. Ieee Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Wong, J.A.H.A. Algorithm AS 136: A K-Means Clustering Algorithm. J. R. Stat. Soc. 1979, 28, 100–108. [Google Scholar]
- Ros, F.; Guillaume, S. DENDIS: A new density-based sampling for clustering algorithm. Expert Syst. Appl. 2016, 56, 349–359. [Google Scholar] [CrossRef] [Green Version]
- Tao, X.M.; Guo, W.J.; Ren, C.; Li, Q.; He, Q.; Liu, R.; Zou, J.R. Density peak clustering using global and local consistency adjustable manifold distance. Inf. Sci. 2021, 577, 769–804. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [Green Version]
- Fraley, C.; Raftery, A.E. Model-based clustering, discriminant analysis, and density estimation. J. Am. Stat. Assoc. 2002, 97, 611–631. [Google Scholar] [CrossRef]
- Reynolds, D.A.; Quatieri, T.F.; Dunn, R.B. Speaker verification using adapted Gaussian mixture models. Digit. Signal. Processing 2000, 10, 19–41. [Google Scholar] [CrossRef] [Green Version]
- Fakoor, D.; Maihami, V.; Maihami, R. A machine learning recommender system based on collaborative filtering using Gaussian mixture model clustering. In Mathematucal Methods in the Applied Science; Wiley Online Library: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Fuchs, R.; Pommeret, D.; Viroli, C. Mixed Deep Gaussian Mixture Model: A clustering model for mixed datasets. Adv. Data Anal. Classif. 2021, 1–23. [Google Scholar] [CrossRef]
- Jiao, H.; Zhong, Y.; Zhang, L. An unsupervised spectral matching classifier based on artificial DNA computing for hyperspectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 4524–4538. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, L.; Huang, B.; Li, P. An unsupervised artificial immune classifier for multi/hyperspectral remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 420–431. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, S.; Zhang, L. Automatic fuzzy clustering based on adaptive multi-objective differential evolution for remote sensing imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 2290–2301. [Google Scholar] [CrossRef]
- Ma, A.; Zhong, Y.; Zhang, L. Adaptive multiobjective memetic fuzzy clustering algorithm for remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4202–4217. [Google Scholar] [CrossRef]
- Zhu, W.; Chayes, V.; Tiard, A.; Sanchez, S.; Dahlberg, D.; Bertozzi, A.L.; Osher, S.; Zosso, D.; Kuang, D. Unsupervised classification in hyperspectral imagery with nonlocal total variation and primal-dual hybrid gradient algorithm. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2786–2798. [Google Scholar] [CrossRef]
- Liu, W.; Li, S.; Lin, X.; Wu, Y.; Ji, R. Spectral–spatial co-clustering of hyperspectral image data based on bipartite graph. Multimed. Syst. 2016, 22, 355–366. [Google Scholar] [CrossRef]
- Zhai, H.; Zhang, H.; Xu, X.; Zhang, L.; Li, P. Kernel sparse subspace clustering with a spatial max pooling operation for hyperspectral remote sensing data interpretation. Remote Sens. 2017, 9, 335. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Zhai, H.; Zhang, L.; Li, P. Spectral–spatial sparse subspace clustering for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3672–3684. [Google Scholar] [CrossRef]
- Tian, L.; Du, Q.; Kopriva, I.; Younan, N. Spatial-spectral Based Multi-view Low-rank Sparse Sbuspace Clustering for Hyperspectral Imagery. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8488–8491. [Google Scholar]
- Shahi, K.R.; Khodadadzadeh, M.; Tusa, L.; Ghamisi, P.; Tolosana-Delgado, R.; Gloaguen, R. Hierarchical Sparse Subspace Clustering (HESSC): An Automatic Approach for Hyperspectral Image Analysis. Remote Sens. 2020, 12, 2421. [Google Scholar] [CrossRef]
- Hsu, C.-C.; Lin, C.-W. Cnn-based joint clustering and representation learning with feature drift compensation for large-scale image data. IEEE Trans. Multimed. 2017, 20, 421–429. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Fu, X.; Sidiropoulos, N.D.; Hong, M. Towards k-means-friendly spaces: Simultaneous deep learning and clustering. In Proceedings of the 34th International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR: New York City, NY, USA, 2017; Volume 70, pp. 3861–3870. [Google Scholar]
- Cai, Y.M.; Zeng, M.; Cai, Z.H.; Liu, X.B.; Zhang, Z.J. Graph Regularized Residual Subspace Clustering Network for hyperspectral image clustering. Inf. Sci. 2021, 578, 85–101. [Google Scholar] [CrossRef]
- Xie, H.; Zhao, A.; Huang, S.; Han, J.; Liu, S.; Xu, X.; Luo, X.; Pan, H.; Du, Q.; Tong, X. Unsupervised hyperspectral remote sensing image clustering based on adaptive density. IEEE Geosci. Remote Sens. Lett. 2018, 15, 632–636. [Google Scholar] [CrossRef]
- Neagoe, V.-E.; Chirila-Berbentea, V. Improved Gaussian mixture model with expectation-maximization for clustering of remote sensing imagery. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 3063–3065. [Google Scholar]
- Frey, B.J.; Dueck, D. Clustering by passing messages between data points. Science 2007, 315, 972–976. [Google Scholar] [CrossRef] [Green Version]
- Dagher, I.; Mikhael, S.; Al-Khalil, O. Gabor face clustering using affinity propagation and structural similarity index. Multimed. Tools Appl. 2021, 80, 4719–4727. [Google Scholar] [CrossRef]
- Ge, H.; Pan, H.; Wang, L.; Li, C.; Liu, Y.; Zhu, W.; Teng, Y. A semi-supervised learning method for hyperspectral imagery based on self-training and local-based affinity propagation. Int. J. Remote Sens. 2021, 42, 6391–6416. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.X.; Chen, Z.G.; Zhao, J. Intelligent fault diagnosis for rotating machinery based on potential energy feature and adaptive transfer affinity propagation clustering. Meas. Sci. Technol. 2021, 32, 094012. [Google Scholar] [CrossRef]
- Liu, J.J.; Kan, J.Q. Recognition of genetically modified product based on affinity propagation clustering and terahertz spectroscopy. Spectrochim. Acta Part A-Mol. Biomol. Spectrosc. 2018, 194, 14–20. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.X.; Yu, D.; Tang, Z. Video summary generation by visual shielding compressed sensing coding and double-layer affinity propagation. J. Vis. Commun. Image Represent. 2021, 81, 103321. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Deng, J.; Zhu, K.K.; Tao, Y.Q.; Liu, X.L.; Cui, L.G. Location and Expansion of Electric Bus Charging Stations Based on Gridded Affinity Propagation Clustering and a Sequential Expansion Rule. Sustainability 2021, 13, 8957. [Google Scholar] [CrossRef]
- Wan, X.J.; Li, H.L.; Zhang, L.P.; Wu, Y.J. Multivariate Time Series Data Clustering Method Based on Dynamic Time Warping and Affinity Propagation. Wirel. Commun. Mob. Comput. 2021, 2021, 9915315. [Google Scholar] [CrossRef]
- Wang, L.M.; Ji, Q.; Han, X.M. Aaptive semi-supervised affinity propagation clustering algorithm based on structural similarity. Teh. Vjesn.-Tech. Gaz. 2016, 23, 425–435. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wu, X.F.; Zhu, W.P.; Yu, L. Unsupervized Image Clustering With SIFT-Based Soft-Matching Affinity Propagation. Ieee Signal. Processing Lett. 2017, 24, 461–464. [Google Scholar] [CrossRef]
- Qin, Y.; Li, B.; Ni, W.; Quan, S.; Bian, H. Affinity Matrix Learning Via Nonnegative Matrix Factorization for Hyperspectral Imagery Clustering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 402–415. [Google Scholar] [CrossRef]
- Fan, L.; Messinger, D.W. Joint spatial-spectral hyperspectral image clustering using block-diagonal amplified affinity matrix. Opt. Eng. 2018, 57. [Google Scholar] [CrossRef]
- Chen, D.W.; Sheng, J.Q.; Chen, J.J.; Wang, C.D. Stability-based preference selection in affinity propagation. Neural Comput. Appl. 2014, 25, 1809–1822. [Google Scholar] [CrossRef]
- Gan, G.J.; Ng, M.K.P. Subspace clustering using affinity propagation. Pattern Recognit. 2015, 48, 1455–1464. [Google Scholar] [CrossRef]
- Li, P.; Ji, H.F.; Wang, B.L.; Huang, Z.Y.; Li, H.Q. Adjustable preference affinity propagation clustering. Pattern Recognit. Lett. 2017, 85, 72–78. [Google Scholar] [CrossRef]
- Hu, J.S.; Liu, H.L.; Yan, Z. Adaptive Affinity Propagation Algorithm Based on New Strategy of Dynamic Damping Factor and Preference. Ieej Trans. Electr. Electron. Eng. 2019, 14, 97–104. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. Ieee Trans. Image Processing 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sampat, M.P.; Wang, Z.; Gupta, S.; Bovik, A.C.; Markey, M.K. Complex wavelet structural similarity: A new image similarity index. IEEE Trans. Image Process. 2009, 18, 2385–2401. [Google Scholar] [CrossRef] [PubMed]
- Rehman, A.; Gao, Y.; Wang, J.H.; Wang, Z. Image classification based on complex wavelet structural similarity. Signal. Processing-Image Commun. 2013, 28, 984–992. [Google Scholar] [CrossRef]
- Rodriguez-Pulecio, C.G.; Benitez-Restrepo, H.D.; Bovik, A.C. Making long-wave infrared face recognition robust against image quality degradations. Quant. Infrared Thermogr. J. 2019, 16, 218–242. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, Z.; Shen, L.; Li, Q. A Two-Stage Feature Selection Framework for Hyperspectral Image Classification Using Few Labeled Samples. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1023–1035. [Google Scholar] [CrossRef]
- Casti, P.; Mencattini, A.; Salmeri, M.; Rangayyan, R.M. Analysis of Structural Similarity in Mammograms for Detection of Bilateral Asymmetry. IEEE Trans. Med. Imaging 2015, 34, 662–671. [Google Scholar] [CrossRef] [PubMed]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. Sigmod Rec. 2000, 29, 93–104. [Google Scholar] [CrossRef]
- Tu, B.; Zhou, C.L.; Kuang, W.L.; Guo, L.Y.; Ou, X.F. Hyperspectral Imagery Noisy Label Detection by Spectral Angle Local Outlier Factor. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1417–1421. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Lan, H.M.; Zhao, T.J. Detection and mitigation of radiometers radio-frequency interference by using the local outlier factor. Remote Sens. Lett. 2017, 8, 311–319. [Google Scholar] [CrossRef]
- Yu, S.Q.; Li, X.R.; Zhao, L.Y.; Wang, J. Hyperspectral Anomaly Detection Based on Low-Rank Representation Using Local Outlier Factor. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1279–1283. [Google Scholar] [CrossRef]
- Ge, H.M.; Pan, H.Z.; Wang, L.G.; Liu, M.Q.; Li, C. Self-training algorithm for hyperspectral imagery classification based on mixed measurement k-nearest neighbor and support vector machine. J. Appl. Remote Sens. 2021, 15, 042604. [Google Scholar] [CrossRef]
- Guo, Z.H.; Zhang, D.; Zhang, L.; Liu, W.H. Feature Band Selection for Online Multispectral Palmprint Recognition. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1094–1099. [Google Scholar] [CrossRef]
- Portilla, J.; Simoncelli, E.P. A parametric texture model based on joint statistics of complex wavelet coefficients. Int. J. Comput. Vis. 2000, 40, 49–71. [Google Scholar] [CrossRef]
- Simoncelli, E.P.; Freeman, W.T.; Adelson, E.H.; Heeger, D.J. Shiftable multiscale transforms. IEEE Trans. Inf. Theory 1992, 38, 587–607. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.F.; Hu, X.; Luo, C.; Wang, X.Y.; Zhao, J.; Zhang, L.P. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H-2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Reynolds, D.A. Gaussian mixture models. Encycl. Biom. 2009, 741, 659–663. [Google Scholar]
- Birant, D.; Kut, A. ST-DBSCAN: An algorithm for clustering spatial–temporal data. Data Knowl. Eng. 2007, 60, 208–221. [Google Scholar] [CrossRef]
- Du, M.; Ding, S.; Jia, H. Study on density peaks clustering based on k-nearest neighbors and principal component analysis. Knowl.-Based Syst. 2016, 99, 135–145. [Google Scholar] [CrossRef]
- Kohonen, T. Exploration of very large databases by self-organizing maps. In Proceedings of the International Conference on Neural Networks (icnn’97), Houston, TX, USA, 12 June 1997; Volume 1, pp. PL1–PL6. [Google Scholar]
- Steffen, J.; Pardowitz, M.; Steil, J.J.; Ritter, H. Integrating feature maps and competitive layer architectures for motion segmentation. Neurocomputing 2011, 74, 1372–1381. [Google Scholar] [CrossRef]
- Studholme, C.; Hill, D.L.G.; Hawkes, D.J. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognit. 1999, 32, 71–86. [Google Scholar] [CrossRef]
- Huang, X.H.; Ye, Y.M.; Zhang, H.J. Extensions of Kmeans-Type Algorithms: A New Clustering Framework by Integrating Intracluster Compactness and Intercluster Separation. IEEE Trans. Neural. Netw. Learn. Syst. 2014, 25, 1433–1446. [Google Scholar] [CrossRef] [PubMed]



| Classes | Land Cover Type | Number of Samples |
|---|---|---|
| Class 1 | Alfalfa | 46 |
| Class 2 | Corn-Notill | 1428 |
| Class 3 | Corn-Mintill | 830 |
| Class 4 | Corn | 237 |
| Class 5 | Grass-Pasture | 483 |
| Class 6 | Grass-Trees | 730 |
| Class 7 | Grass-Pasture-Mowed | 28 |
| Class 8 | Hay-Windrowed | 478 |
| Class 9 | Oats | 20 |
| Class 10 | Soybean-Notill | 972 |
| Class 11 | Soybean-Mintill | 2455 |
| Class 12 | Soybean-Clean | 593 |
| Class 13 | Wheat | 205 |
| Class 14 | Woods | 1265 |
| Class 15 | Buildings-Grass-Trees-Drives | 386 |
| Class 16 | Stone-Steel-Towers | 93 |
| Classes | Land Cover Type | Number of Samples |
|---|---|---|
| Class 1 | Asphalt | 2578 |
| Class 2 | Meadows | 5216 |
| Class 3 | Gravel | 47 |
| Class 4 | Trees | 1054 |
| Class 5 | Painted metal sheets | 1345 |
| Class 6 | Bare Soil | 868 |
| Class 7 | Bitumen | 21 |
| Class 8 | Self-Blocking Bricks | 1693 |
| Class 9 | Shadows | 215 |
| Classes | Land Cover Type | Number of Samples |
|---|---|---|
| Class 1 | Red roof | 1981 |
| Class 2 | Road | 1633 |
| Class 3 | Chinese cabbage | 4902 |
| Class 4 | Cabbage | 446 |
| Class 5 | Brassica parachinensis | 6 |
| Class 6 | Brassica chinensis | 367 |
| Class 7 | White radish | 632 |
| Class 8 | Broad bean | 1322 |
| Class 9 | Tree | 4040 |
| Dataset | Method | NMI | FM | ACC | ARI | Time(s) |
|---|---|---|---|---|---|---|
| IP | K-means | 0.4402 | 0.4083 | 0.3637 | 0.2218 | 2.24 |
| K-methods | 0.4369 | 0.4064 | 0.3843 | 0.2186 | 11.9 | |
| GMM | 0.4338 | 0.4184 | 0.4417 | 0.2333 | 1.08 | |
| DBSCAN | 0.4202 | 0.4587 | 0.5274 | 0.2771 | 21.07 | |
| SC | 0.4431 | 0.4407 | 0.4410 | 0.2275 | 242.01 | |
| DPC | 0.4053 | 0.4988 | 0.8808 | 0.1976 | 43.99 | |
| Self-org | 0.4319 | 0.3879 | 0.3606 | 0.2077 | 42.61 | |
| CL | 0.4023 | 0.3757 | 0.3886 | 0.1848 | 564.22 | |
| AP | 0.4395 | 0.4418 | 0.4848 | 0.2638 | 356.8 | |
| HESSC | 0.4004 | 0.3609 | 0.3522 | 0.1917 | 286.74 | |
| GR-RSCNet | 0.5848 | 0.5368 | 0.5772 | 0.3378 | 3883.31 | |
| CLAP | 0.4525 | 0.4674 | 0.5334 | 0.3237 | 661.51 | |
| PU | K-means | 0.6901 | 0.7219 | 0.7012 | 0.6060 | 0.41 |
| K-methods | 0.7078 | 0.7770 | 0.7463 | 0.6394 | 5.12 | |
| GMM | 0.6305 | 0.6466 | 0.6923 | 0.5596 | 0.78 | |
| DBSCAN | 0.6523 | 0.7034 | 0.7388 | 0.5490 | 16.3 | |
| SC | 0.4815 | 0.6779 | 0.7519 | 0.3646 | 490.49 | |
| DPC | 0.4373 | 0.6770 | 0.8131 | 0.2973 | 43.66 | |
| Self-org | 0.6469 | 0.6530 | 0.6695 | 0.5081 | 42.68 | |
| CL | 0.5898 | 0.5691 | 0.5146 | 0.3597 | 593.55 | |
| AP | 0.7066 | 0.7600 | 0.7592 | 0.6639 | 634.7 | |
| HESSC | 0.5228 | 0.5648 | 0.6087 | 0.3871 | 430.07 | |
| GR-RSCNet | 0.8623 | 0.8183 | 0.8030 | 0.7041 | 2430.22 | |
| CLAP | 0.6832 | 0.7807 | 0.7608 | 0.7540 | 936.55 | |
| HH | K-means | 0.5033 | 0.5533 | 0.5165 | 0.3038 | 2.77 |
| K-methods | 0.5097 | 0.5602 | 0.5308 | 0.3148 | 18.96 | |
| GMM | 0.5930 | 0.6486 | 0.6588 | 0.4043 | 2.22 | |
| DBSCAN | 0.4959 | 0.5478 | 0.6279 | 0.3003 | 54.36 | |
| SC | 0.4815 | 0.6779 | 0.7519 | 0.3646 | 490.49 | |
| DPC | 0.4823 | 0.5894 | 0.8980 | 0.3258 | 89.65 | |
| Self-org | 0.5030 | 0.5532 | 0.5167 | 0.3035 | 42.272 | |
| CL | 0.4843 | 0.5222 | 0.4795 | 0.2743 | 625.25 | |
| AP | 0.4811 | 0.5698 | 0.5689 | 0.3073 | 623.79 | |
| HESSC | 0.4651 | 0.4962 | 0.4940 | 0.2692 | 334.21 | |
| GR-RSCNet | 0.8424 | 0.7920 | 0.7693 | 0.6970 | 3759.08 | |
| CLAP | 0.5460 | 0.5898 | 0.5715 | 0.3488 | 947.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ge, H.; Wang, L.; Pan, H.; Zhu, Y.; Zhao, X.; Liu, M. Affinity Propagation Based on Structural Similarity Index and Local Outlier Factor for Hyperspectral Image Clustering. Remote Sens. 2022, 14, 1195. https://doi.org/10.3390/rs14051195
Ge H, Wang L, Pan H, Zhu Y, Zhao X, Liu M. Affinity Propagation Based on Structural Similarity Index and Local Outlier Factor for Hyperspectral Image Clustering. Remote Sensing. 2022; 14(5):1195. https://doi.org/10.3390/rs14051195
Chicago/Turabian StyleGe, Haimiao, Liguo Wang, Haizhu Pan, Yuexia Zhu, Xiaoyu Zhao, and Moqi Liu. 2022. "Affinity Propagation Based on Structural Similarity Index and Local Outlier Factor for Hyperspectral Image Clustering" Remote Sensing 14, no. 5: 1195. https://doi.org/10.3390/rs14051195
APA StyleGe, H., Wang, L., Pan, H., Zhu, Y., Zhao, X., & Liu, M. (2022). Affinity Propagation Based on Structural Similarity Index and Local Outlier Factor for Hyperspectral Image Clustering. Remote Sensing, 14(5), 1195. https://doi.org/10.3390/rs14051195







