Multiscale Feature Aggregation Capsule Neural Network for Hyperspectral Remote Sensing Image Classification
Abstract
:1. Introduction
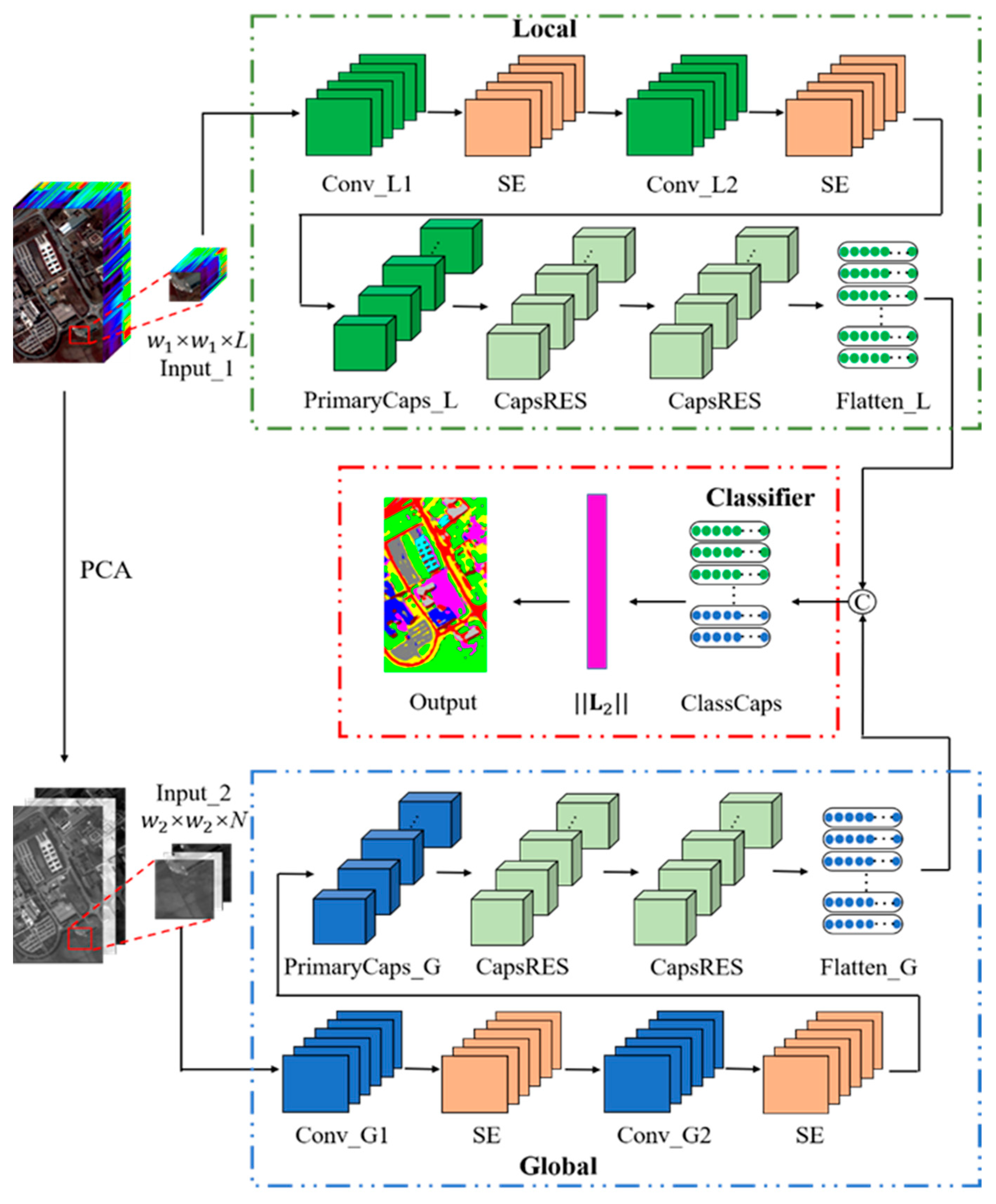
2. Multiscale Feature Aggregation Capsule Neural Network for HSI Classification
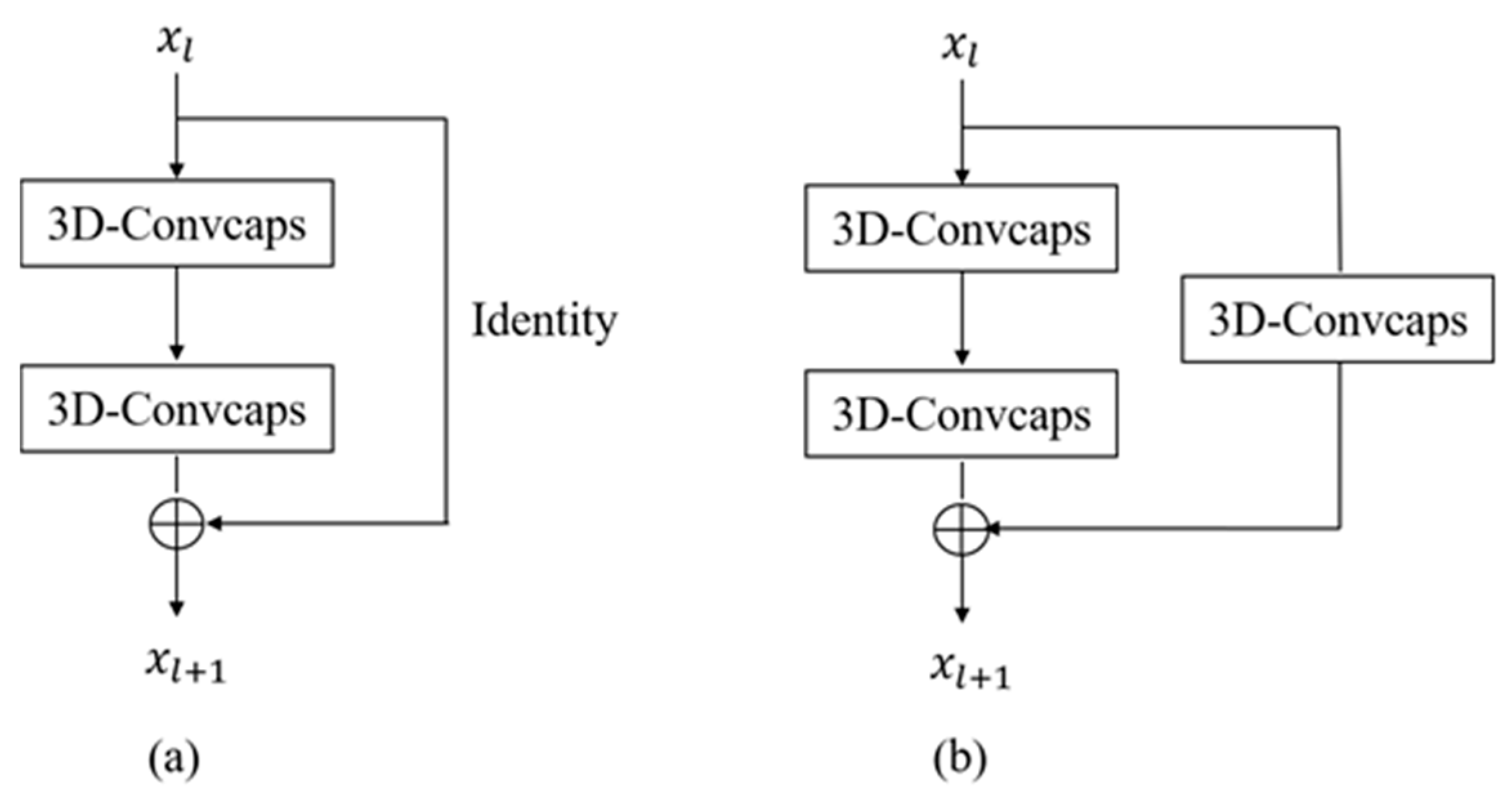
2.1. The Capsule Residual Block
2.2. Local Feature Extraction Module
2.3. Global Feature Extraction Module
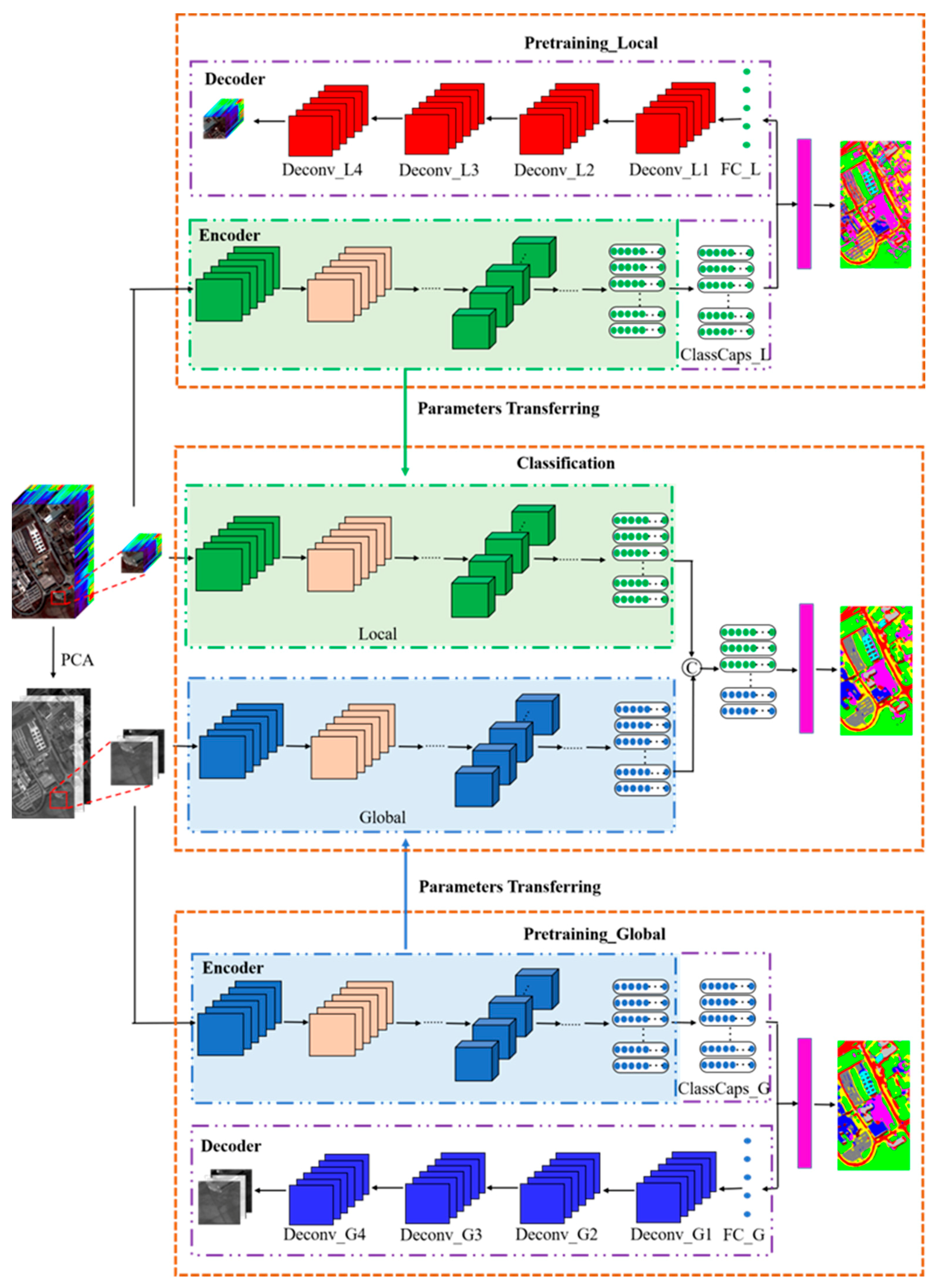
2.4. Framework of the Proposed Model
2.5. Initialization Strategy
3. Experimental Results and Analysis
3.1. Experimental Datasets
3.2. Influence of Parameters
3.2.1. Neighboring Pixel Block Size
3.2.2. Number of Principal Components
3.2.3. Number of Capsule Residual Blocks
3.2.4. Squeeze-and-Excitation Block
3.2.5. Feature Aggregation
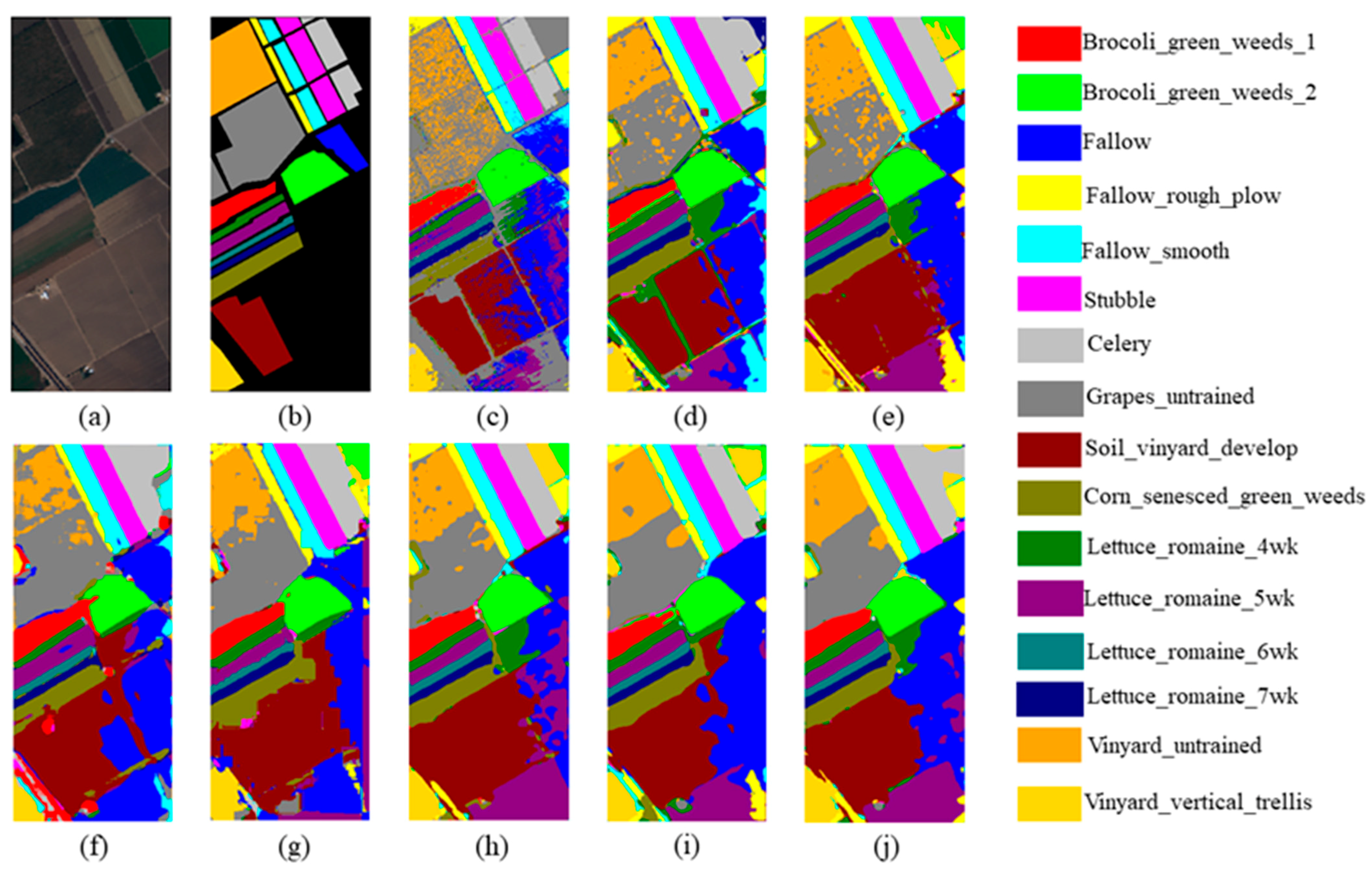
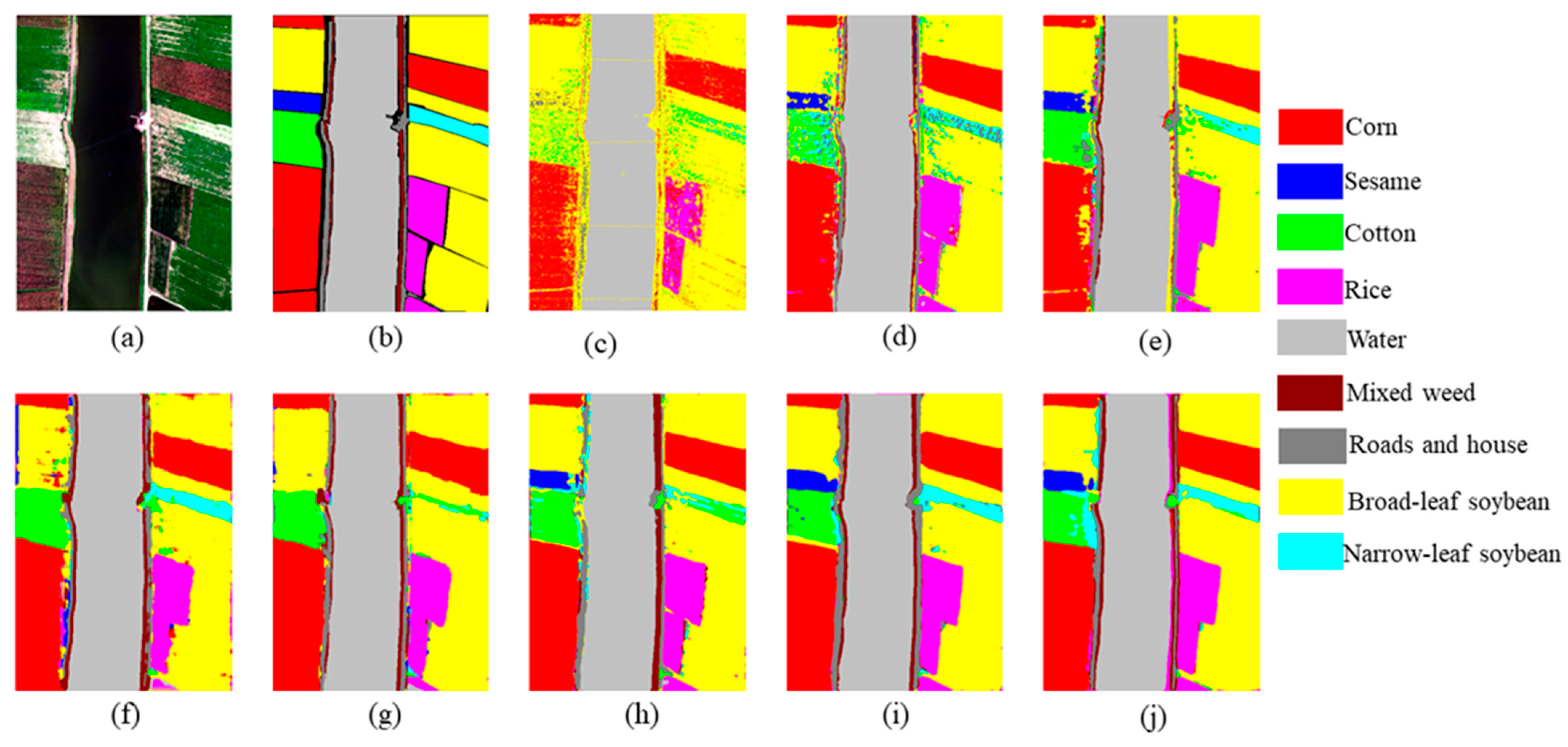
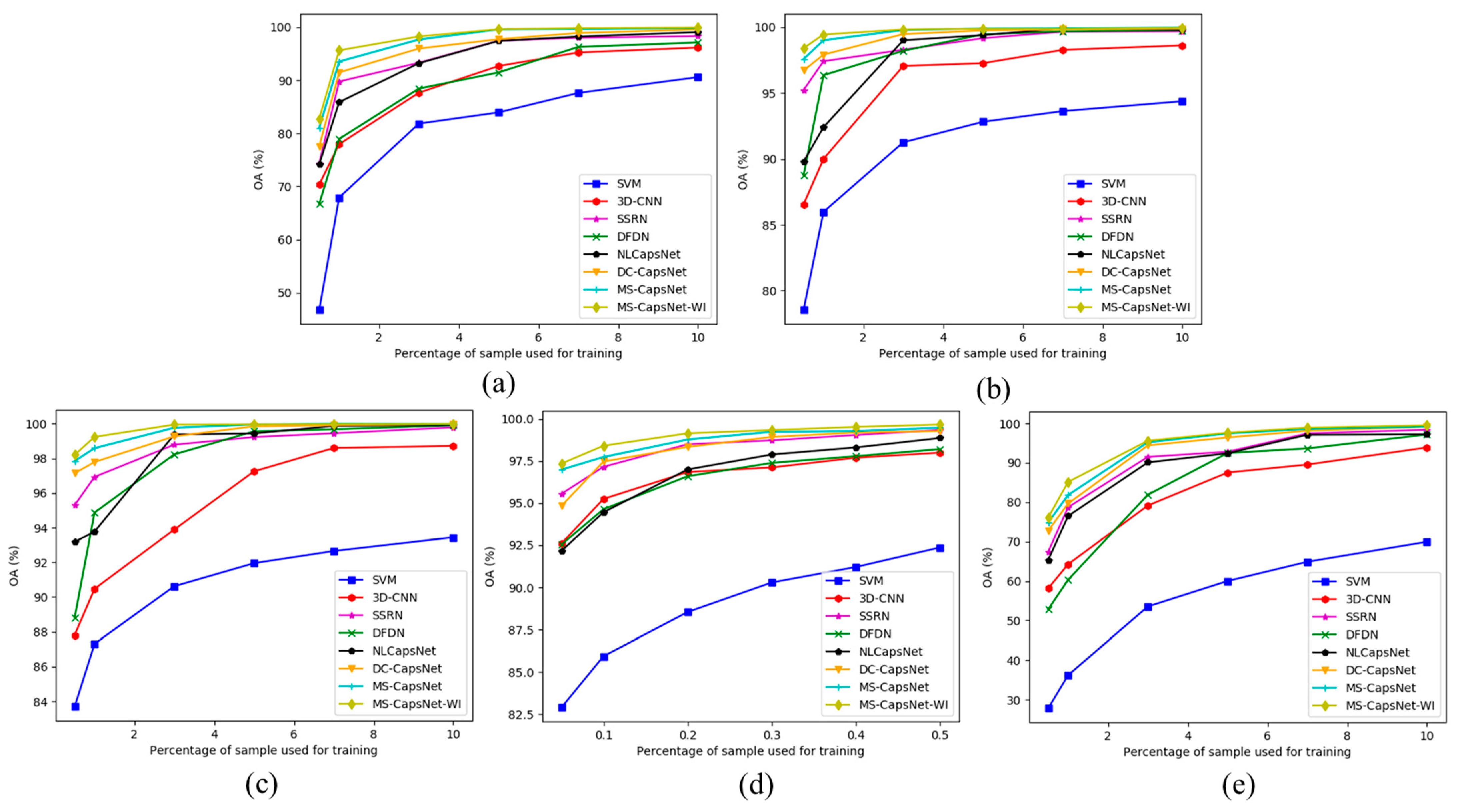
3.3. Experimental Results and Discusion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gevaert, C.M.; Suomalainen, J.; Tang, J.; Kooistra, L. Generation of Spectral–Temporal Response Surfaces by Combining Multispectral Satellite and Hyperspectral UAV Imagery for Precision Agriculture Applications. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 3140–3146. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, D.; Zhang, L.; Jiao, Q.; Li, Q. Application of hyperspectral remote sensing for environment monitoring in mining areas. Environ. Earth Sci. 2012, 65, 649–658. [Google Scholar] [CrossRef]
- Eslami, M.; Mohammadzadeh, A. Developing a Spectral-Based Strategy for Urban Object Detection from Airborne Hyperspectral TIR and Visible Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 1808–1816. [Google Scholar] [CrossRef]
- Naoto, Y.; Jonathan, C.; Karl, S. Potential of Resolution-Enhanced Hyperspectral Data for Mineral Mapping Using Simulated EnMAP and Sentinel-2 Images. Remote Sens. 2016, 8, 172. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Yu, Y.; Du, Q.; Du, P. Ensemble Learning for Hyperspectral Image Classification Using Tangent Collaborative Representation. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3778–3790. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef] [Green Version]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Qian, Y.; Li, C. Improved KNN text classification algorithm with MapReduce implementation. In Proceedings of the 2017 4th International Conference on Systems and Informatics (ICSAI), Hangzhou, China, 11–13 November 2017; pp. 1417–1422. [Google Scholar]
- Shen, L.; Jia, S. Three-Dimensional Gabor Wavelets for Pixel-Based Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 5039–5046. [Google Scholar] [CrossRef]
- Su, H.; Zhao, B.; Du, Q.; Du, P.; Xue, Z. Multifeature dictionary learning for collaborative representation classification of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2467–2484. [Google Scholar] [CrossRef]
- Su, H.; Zhao, B.; Du, Q.; Du, P. Kernel collaborative representation with local correlation features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1230–1241. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Kong, S.G. Band-Subset-Based Clustering and Fusion for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 747–756. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.; Chanussot, J.; Jia, X.; Benediktsson, J.A. Multiple Kernel Learning for Hyperspectral Image Classification: A Review. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6547–6565. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–Spatial Classification of Hyperspectral Data Based on Deep Belief Network. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification with Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, K.; Zhu, L.; He, X.; Ghamisi, P.; Benediktsson, J.A. Automatic Design of Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7048–7066. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Tan, X.; Yu, A.; Xue, Z. A semi-supervised convolutional neural network for hyperspectral image classification. Remote Sens. Lett. 2017, 8, 839–848. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Santara, A.; Mani, K.; Hatwar, P.; Singh, A.; Garg, A.; Padia, K.; Mitra, P. BASS Net: Band-Adaptive Spectral-Spatial Feature Learning Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5293–5301. [Google Scholar] [CrossRef] [Green Version]
- Pan, B.; Shi, Z.; Xu, X. R-VCANet: A New Deep-Learning-Based Hyperspectral Image Classification Method. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 1975–1986. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training Very Deep Networks. arXiv 2015, arXiv:1507.06228. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Beltran, R.F.; Plazza, A.J.; Pla, F. Deep pyramidal residual networks for spectral-spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 740–754. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Zhang, C.; Li, G.; Du, S.; Zhang, X. 3D densely connected convolutional network for hyperspectral remote sensing image classification. Appl. Remote Sens. 2019, 13, 016519. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Deep&Dense Convolutional Neural Network for Hyperspectral Image Classification. Remote Sens. 2018, 10, 1454. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Li, G.; Lei, R.; Du, S.; Zhang, X.; Zheng, H.; Wu, Z. Deep Feature Aggregation Network for Hyperspectral Remote Sensing Image Classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 5314–5325. [Google Scholar] [CrossRef]
- Li, X.; Ding, M.; Pižurica, A. Deep Feature Fusion via Two-Stream Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2615–2629. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Gao, L.; Xiao, C.; Qu, Y.; Zheng, K.; Marinoni, A. Hyperspectral Image Classification Based on a Shuffled Group Convolutional Neural Network with Transfer Learning. Remote Sens. 2020, 12, 1780. [Google Scholar] [CrossRef]
- Liang, H.; Li, Q. Hyperspectral Imagery Classification Using Sparse Representations of Convolutional Neural Network Features. Remote Sens. 2016, 8, 99. [Google Scholar] [CrossRef] [Green Version]
- Gong, Z.; Zhong, P.; Yu, Y.; Hu, W.; Li, S. A CNN With Multiscale Convolution and Diversified Metric for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3599–3618. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, B.; Sun, L.; Zhan, T.; Tang, S. 3-D Channel and Spatial Attention Based Multiscale Spatial–Spectral Residual Network for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 4311–4324. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, L.; Ghamisi, P.; Jia, X.; Li, G.; Tang, L. Hyperspectral images classification with Gabor filtering and convolutional neural network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2355–2359. [Google Scholar] [CrossRef]
- Zhu, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Generative Adversarial Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5046–5063. [Google Scholar] [CrossRef]
- Zhong, Z.; Li, J.; Clausi, D.A.; Wong, A. Generative Adversarial Networks and Conditional Random Fields for Hyperspectral Image Classification. IEEE Trans. Cybern. 2020, 50, 3318–3329. [Google Scholar] [CrossRef] [Green Version]
- Sabour, S.; Frosst, N.; Hinton, G. Dynamic routing between capsules. arXiv 2014, arXiv:1710.09829. [Google Scholar]
- Ma, Y.; Zheng, Z.; Guo, Z.; Mou, F.; Zhou, F.; Kong, R.; Hou, A. Classification Based on Capsule Network with Hyperspectral Image. In Proceedings of the International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 2750–2753. [Google Scholar]
- Deng, F.; Pu, S.; Chen, X.; Shi, Y.; Yuan, T.; Pu, S. Hyperspectral Image Classification with Capsule Network Using Limited Training Samples. Sensors 2018, 18, 3153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, W.; Li, H.; Pan, L.; Yang, G.; Du, Q. Hyperspectral Image Classification Based on Capsule Network. In Proceedings of the International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3571–3574. [Google Scholar]
- Jia, S.; Zhao, B.; Tang, L.; Feng, F.; Wang, W. Spectral–spatial classification of hyperspectral remote sensing image based on capsule network. J. Eng. 2019, 2019, 7352–7355. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Beltran, R.F.; Plaza, J.; Plaza, A.; Li, J. Capsule Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2145–2160. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, W.; Zhang, Y.; Liu, J.; Li, S.; Lin, J. Spectral–Spatial Hyperspectral Image Classification Using Dual-Channel Capsule Networks. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1094–1098. [Google Scholar] [CrossRef]
- Yin, J.; Li, S.; Zhu, H.; Luo, X. Hyperspectral Image Classification Using CapsNet With Well-Initialized Shallow Layers. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1095–1099. [Google Scholar] [CrossRef]
- Lei, R.; Zhang, C.; Du, S.; Wang, C.; Zhang, X.; Zheng, H.; Huang, J.; Yu, M. A non-local capsule neural network for hyperspectral remote sensing image classification. Remote Sens. Lett. 2020, 12, 40–49. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.; Pan, L.; Li, W.; Du, Q.; Tao, R. Robust Capsule Network Based on Maximum Correntropy Criterion for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2020, 13, 738–751. [Google Scholar] [CrossRef]
- Wang, W.-Y.; Li, H.-C.; Deng, Y.-J.; Shao, L.-Y.; Lu, X.-Q.; Du, Q. Generative Adversarial Capsule Network with ConvLSTM for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 523–527. [Google Scholar] [CrossRef]
- Zhang, H.; Meng, L.; Wei, X.; Tang, X.; Tang, X.; Wang, X.; Jin, B.; Yao, W. 1D-Convolutional Capsule Network for Hyperspectral Image Classification. arXiv 2019, arXiv:1903.09834. [Google Scholar]
- Zhu, K.; Chen, Y.; Ghamisi, P.; Jia, X.; Benediktsson, J.A. Deep Convolutional Capsule Network for Hyperspectral Image Spectral and Spectral-Spatial Classification. Remote Sens. 2019, 11, 582. [Google Scholar] [CrossRef] [Green Version]
- Lei, R.; Zhang, C.; Liu, W.; Zhang, L.; Zhang, X.; Yang, Y.; Huang, J.; Li, Z.; Zhou, Z. Hyperspectral Remote Sensing Image Classification Using Deep Convolutional Capsule Network. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021, 14, 8297–8315. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Misra, D. Mish: A Self Regularized Non-Monotonic Neural Activation Function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Zhong, Y.; Hu, X.; Luo, C.; Wang, X.; Zhao, J.; Zhang, L. WHU-Hi: UAV-borne hyperspectral with high spatial resolution (H2) benchmark datasets and classifier for precise crop identification based on deep convolutional neural network with CRF. Remote Sens. Environ. 2020, 250, 112012. [Google Scholar] [CrossRef]


| Layer | Kernel Size | Stride | Batch Normalization | Padding | Activation Function | SE |
|---|---|---|---|---|---|---|
| Local Feature Extraction Module | ||||||
| L1 | (1 × 1) × 128 | (1, 1) | YES | YES | Mish [57] | YES |
| L2 | (3 × 3) × 64 | (1, 1) | YES | YES | Mish | YES |
| L3 | (3 × 3) × 4 × 8 | (2, 2) | YES | YES | Mish, Squash | NO |
| L4-L5 | (3 × 3 × 4) × 4 × 8 | (1, 1, 4) | NO | YES | Squash | NO |
| L6-L8 | (3 × 3 × 4) × 8 × 8 (3 × 3 × 8) × 8 × 8 | (2, 2, 4) (1, 1, 8) | NO | YES | Squash | NO |
| Global Feature Extraction Module | ||||||
| L1 | (5 × 5) × 128 | (1, 1) | YES | NO | Mish | YES |
| L2 | (5 × 5) × 64 | (1, 1) | YES | NO | Mish | YES |
| L3 | (9 × 9) × 4 × 8 | (2, 2) | YES | NO | Mish, Squash | NO |
| L4-L5 | (3 × 3 × 4) × 4 × 8 | (1, 1, 4) | NO | YES | Squash | NO |
| L6-L8 | (3 × 3 × 4) × 8 × 8 (3 × 3 × 8) × 8 × 8 | (2, 2, 4) (1, 1, 8) | NO | YES | Squash | NO |
| Feature Fusion Module | ||||||
| Layer | Output size | Activation function | ||||
| L1 | × 16 | Squash | ||||
| Local Feature Extraction Module | ||||
|---|---|---|---|---|
| Fully connected layer | ||||
| Layer | Number of Neurons | Batch Normalization | Activation Function | |
| L1 | 3 × 3 × 16 | YES | ReLU | |
| Deconvolutional layers | ||||
| Layer | Kernel Size | Stride | Batch Normalization | Activation Function |
| L2 | (3 × 3) × 64 | (1, 1) | NO | ReLU |
| L3 | (3 × 3) × 32 | (1, 1) | NO | ReLU |
| L4 | (3 × 3) × 16 | (1, 1) | NO | ReLU |
| L5 | (1 × 1) × L | (1, 1) | NO | ReLU |
| Global feature extraction module | ||||
| Fully connected layer | ||||
| Layer | Number of Neurons | Batch Normalization | Activation Function | |
| L1 | 7 × 7 × 16 | YES | ReLU | |
| Deconvolutional Layers | ||||
| Layer | Kernel Size | Stride | Batch Normalization | Activation Function |
| L2 | (3 × 3) × 64 | (1, 1) | NO | ReLU |
| L3 | (5 × 5) × 32 | (1, 1) | NO | ReLU |
| L4 | (5 × 5) × 16 | (2, 2) | NO | ReLU |
| L5 | (3 × 3) × N | (1, 1) | NO | ReLU |
| Dataset | Local | Global | ||||||
|---|---|---|---|---|---|---|---|---|
| 3 × 3 | 5 × 5 | 7 × 7 | 9 × 9 | 23 × 23 | 25 × 25 | 27 × 27 | 29 × 29 | |
| KSC | 98.63 | 98.61 | 99.27 | 98.72 | 98.33 | 98.10 | 99.27 | 97.86 |
| UP | 97.83 | 97.97 | 98.94 | 98.83 | 98.35 | 98.55 | 98.94 | 98.42 |
| SA | 96.74 | 97.31 | 98.58 | 98.65 | 98.05 | 97.92 | 98.58 | 98.61 |
| LK | 98.26 | 98.35 | 98.47 | 98.14 | 98.36 | 98.43 | 98.47 | 97.58 |
| Dataset | 1 | 3 | 5 | 7 | 10 |
|---|---|---|---|---|---|
| KSC | 98.31 | 99.27 | 99.02 | 99.44 | 99.11 |
| UP | 97.85 | 98.94 | 99.04 | 99.19 | 99.00 |
| SA | 97.55 | 98.58 | 98.97 | 98.82 | 99.04 |
| LK | 98.23 | 98.47 | 98.54 | 98.78 | 98.53 |
| Dataset | L1 + G1 | L1 + G2 | L2 + G1 | L2 + G2 | L2 + G3 | L3 + G3 |
|---|---|---|---|---|---|---|
| KSC | 99.35 | 99.48 | 99.05 | 99.44 | 99.34 | 98.76 |
| UP | 99.05 | 99.17 | 99.07 | 99.19 | 99.30 | 99.08 |
| SA | 98.89 | 98.40 | 98.95 | 98.82 | 98.44 | 98.56 |
| LK | 98.75 | 98.67 | 98.38 | 98.78 | 97.86 | 98.10 |
| Dataset | NO | YES |
|---|---|---|
| KSC | 98.87 | 99.27 |
| UP | 98.77 | 98.94 |
| SA | 98.32 | 98.58 |
| LK | 98.33 | 98.47 |
| Dataset | Local | Global | Local + Global |
|---|---|---|---|
| KSC | 97.56 | 99.14 | 99.44 |
| UP | 97.19 | 98.48 | 99.19 |
| SA | 96.38 | 98.57 | 98.82 |
| LK | 97.96 | 98.31 | 98.78 |
| Dataset | Models | SVM | 3D-CNN | SSRN | DFDN | NLCapsNet | DC-CapsNet | MS-CapsNet | MS-CapsNet-WI |
|---|---|---|---|---|---|---|---|---|---|
| KSC | OA (%) | 81.83 ± 0.04 | 87.65 ± 1.89 | 93.28 ± 1.25 | 88.43 ± 0.88 | 93.21 ± 0.79 | 95.97 ± 1.16 | 97.67 ± 0.63 | 98.25 ± 0.66 |
| AA (%) | 73.86 ± 2.33 | 85.69 ± 2.40 | 91.62 ± 1.02 | 87.58 ± 1.44 | 92.00 ± 0.95 | 93.43 ± 1.84 | 96.60 ± 0.71 | 96.87 ± 1.49 | |
| K × 100 | 79.73 ± 0.05 | 86.24 ± 2.11 | 92.51 ± 1.41 | 87.11 ± 0.96 | 92.43 ± 0.88 | 95.51 ± 1.29 | 97.41 ± 0.69 | 98.05 ± 0.73 | |
| UP | OA (%) | 78.53 ± 0.74 | 86.55 ± 0.97 | 95.23 ± 0.57 | 88.77 ± 1.47 | 89.79 ± 1.96 | 96.71 ± 0.38 | 97.58 ± 0.54 | 98.41 ± 0.58 |
| AA (%) | 69.94 ± 0.91 | 82.76 ± 2.07 | 93.74 ± 0.52 | 86.06 ± 1.36 | 87.87 ± 2.05 | 95.51 ± 0.41 | 96.71 ± 1.01 | 97.59 ± 0.81 | |
| K × 100 | 70.68 ± 0.92 | 81.96 ± 1.29 | 93.75 ± 0.77 | 84.96 ± 2.01 | 86.42 ± 2.64 | 95.63 ± 0.50 | 96.79 ± 0.72 | 97.89 ± 0.77 | |
| SA | OA (%) | 83.69 ± 1.39 | 87.81 ± 1.72 | 95.29 ± 0.26 | 88.80 ± 1.78 | 93.17 ± 1.61 | 97.14 ± 0.32 | 97.84 ± 0.74 | 98.20 ± 0.01 |
| AA (%) | 86.34 ± 2.05 | 92.18 ± 1.81 | 97.40 ± 0.13 | 90.53 ± 2.24 | 94.69 ± 0.71 | 98.06 ± 0.43 | 98.67 ± 0.35 | 98.60 ± 0.16 | |
| K × 100 | 81.75 ± 1.57 | 86.36 ± 1.96 | 94.76 ± 0.28 | 87.51 ± 1.99 | 92.39 ± 1.79 | 96.82 ± 0.35 | 97.60 ± 0.82 | 98.00 ± 0.01 | |
| LK | OA (%) | 82.89 ± 0.35 | 92.60 ± 0.88 | 95.54 ± 0.48 | 92.54 ± 0.55 | 92.16 ± 0.91 | 94.83 ± 0.66 | 96.99 ± 0.47 | 97.35 ± 0.45 |
| AA (%) | 45.62 ± 0.52 | 83.13 ± 1.96 | 93.75 ± 0.22 | 80.99 ± 2.17 | 78.88 ± 1.58 | 86.56 ± 1.47 | 93.61 ± 0.44 | 93.03 ± 1.52 | |
| K × 100 | 76.45 ± 0.48 | 90.23 ± 1.12 | 94.10 ± 0.64 | 90.15 ± 0.74 | 89.61 ± 1.20 | 93.19 ± 0.86 | 96.03 ± 0.63 | 96.52 ± 0.60 |
| Dataset | Methods | 3D-CNN | SSRN | DFDN | NLCapsNet | DC-CapsNet | MS-CapsNet | MS-CapsNet-WI |
|---|---|---|---|---|---|---|---|---|
| KSC | Train (s) | 36.41 | 60.08 | 798.56 | 1492.91 | 98.40 | 143.97 | 269.66 |
| Test (s) | 1.54 | 5.29 | 35.49 | 55.50 | 2.96 | 10.01 | 10.09 | |
| Parameters | 2,087,553 | 309,845 | 1,244,410 | 6,068,096 | 409,728 | 716,864 | - | |
| UP | Train (s) | 46.24 | 67.65 | 659.64 | 1441.15 | 47.42 | 132.58 | 307.78 |
| Test (s) | 8.67 | 11.39 | 151.76 | 323.62 | 20.01 | 61.77 | 66.23 | |
| Parameters | 832,349 | 199,153 | 1,239,922 | 4,429,696 | 309,248 | 654,272 | - | |
| SA | Train (s) | 61.44 | 125.94 | 1562.30 | 3040.28 | 129.61 | 283.18 | 420.32 |
| Test (s) | 18.86 | 26.63 | 373.50 | 778.01 | 32.65 | 87.96 | 92.87 | |
| Parameters | 2,401,756 | 352,928 | 1,247,776 | 7,296,896 | 454,272 | 760,384 | - | |
| LK | Train (s) | 35.29 | 80.62 | 2632.34 | 730.90 | 57.67 | 125.84 | 129.51 |
| Test (s) | 60.41 | 121.66 | 6011.48 | 1633.44 | 131.30 | 378.15 | 329.45 | |
| Parameters | 3,497,949 | 454,129 | 1,239,922 | 4,429,696 | 501,632 | 675,648 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, R.; Zhang, C.; Zhang, X.; Huang, J.; Li, Z.; Liu, W.; Cui, H. Multiscale Feature Aggregation Capsule Neural Network for Hyperspectral Remote Sensing Image Classification. Remote Sens. 2022, 14, 1652. https://doi.org/10.3390/rs14071652
Lei R, Zhang C, Zhang X, Huang J, Li Z, Liu W, Cui H. Multiscale Feature Aggregation Capsule Neural Network for Hyperspectral Remote Sensing Image Classification. Remote Sensing. 2022; 14(7):1652. https://doi.org/10.3390/rs14071652
Chicago/Turabian StyleLei, Runmin, Chunju Zhang, Xueying Zhang, Jianwei Huang, Zhenxuan Li, Wencong Liu, and Hao Cui. 2022. "Multiscale Feature Aggregation Capsule Neural Network for Hyperspectral Remote Sensing Image Classification" Remote Sensing 14, no. 7: 1652. https://doi.org/10.3390/rs14071652
APA StyleLei, R., Zhang, C., Zhang, X., Huang, J., Li, Z., Liu, W., & Cui, H. (2022). Multiscale Feature Aggregation Capsule Neural Network for Hyperspectral Remote Sensing Image Classification. Remote Sensing, 14(7), 1652. https://doi.org/10.3390/rs14071652








