Airborne Validation of ICESat-2 ATLAS Data over Crevassed Surfaces and Other Complex Glacial Environments: Results from Experiments of Laser Altimeter and Kinematic GPS Data Collection from a Helicopter over a Surging Arctic Glacier (Negribreen, Svalbard)
Abstract
:1. Introduction
2. ICESat-2 ATLAS Data
2.1. ATLAS Instrumentation, Data Collection Geometry, Basic Corrections and ATL03 Data Product
2.2. The Density-Dimension Algorithm for Ice-Surface-Height Determination (DDA-Ice) in Crevassed and Other Complex Terrain—Description in a Nutshell
3. Experiment Setup for the Negribreen ICESat-2 Airborne Geophysical Validation Campaign
3.1. Geographic Region and Ice-Surface Types during Surge
3.2. Experiment Setup
3.3. Instrumentation
- (1)
- Laser altimetry: Universal Laser System (ULS), LaserTech Inc. (Denver, Colorado, U.S.A.), mounted on helicopter (400 Hz data);
- (2)
- Global Positioning System (GPS) Receivers (Base and Rover):
- (2.1)
- Kinematic GPS
- (2.1.1)
- GPS Base Station placed on the side of Negribreen (Trimble NetR9)
- (2.1.2)
- GPS Rover, mounted on a skid of helicopter (Septentrio APS-3G in 2018, Trimble R10 in 2019) (10 Hz data)
- (2.2)
- “Button GPS”, a simple GPS system placed on the dashboard of the helicopter under the window (1 Hz data)
- (3)
- Attitude correction: Inertial Measurement Unit (IMU), LORD 3DM-GX5-15 Vertical Reference Unit (mounted inside the helicopter, taped to the floor) (1 Hz data)
- (4)
- Nadir-pointed time-lapse imagery: GoPro Hero5 Camera, mounted outside on the helicopter (2 Hz data)
- (5)
- Photographs: Several handheld cameras (NIKON D5100 and other Nikon cameras)
4. Comparison of Different Approaches to GPS-Data Collection and Processing: Real-Time Kinematic (RTK) Compared to Kinematic GPS Data Collection with Differential Correction Using Base and Rover Data
4.1. Scientific Motivation and Experiments
- (1)
- Kinematic GPS data collection with differential correction using base and rover data (summer 2018)
- (2)
- Real-time kinematic (RTK) GPS data collection using base and rover data (summer 2018)
- (3)
4.2. Results
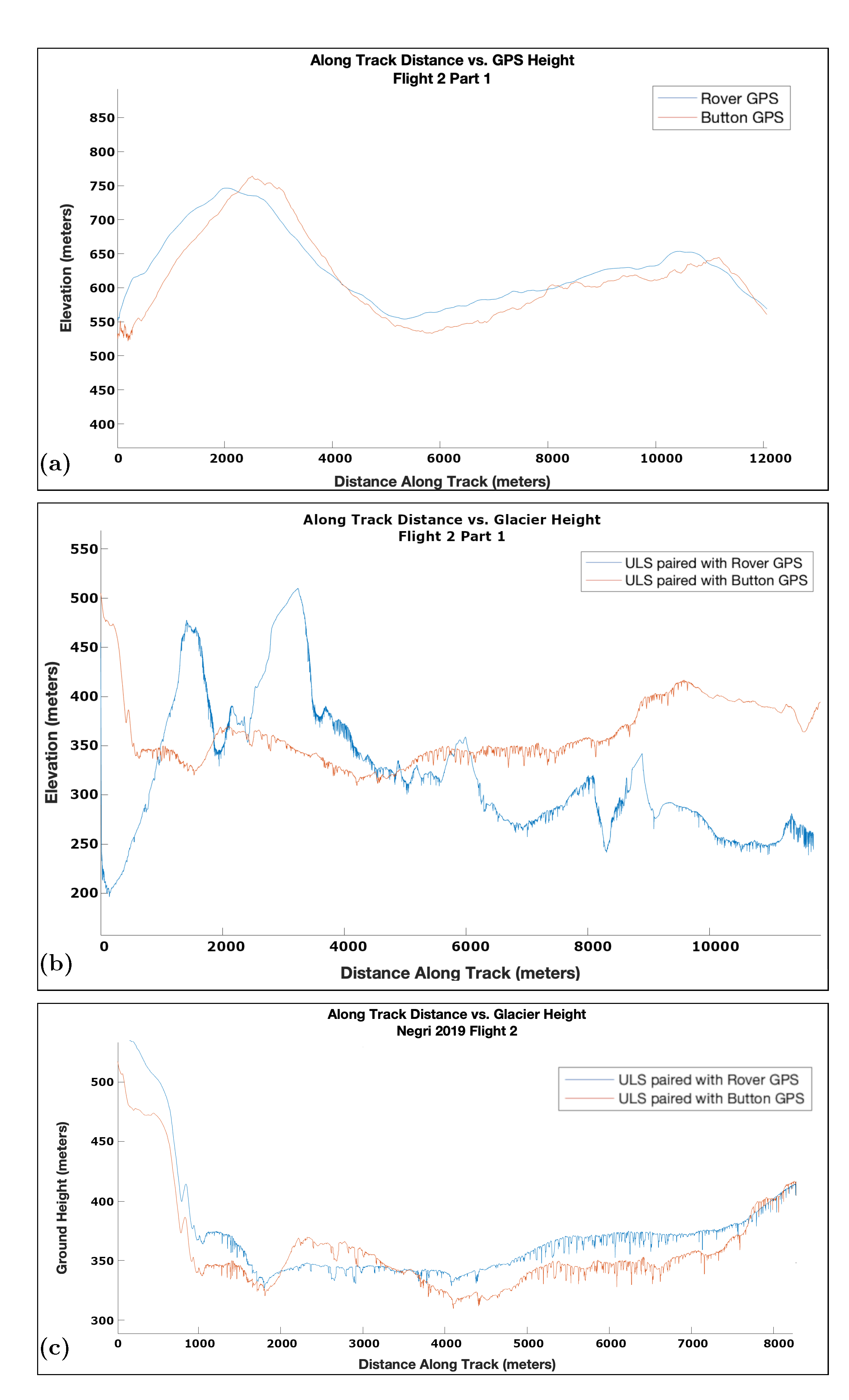
5. Surface-Height Determination from Synchronization of Laser and GPS and IMU Corrections
5.1. Processing of 2019 GPS Data
- (1)
- GPS data were downloaded from the rover and the base station. In the 2019, flight 2 GPS recordings, the base station recorded only 15s-data. The rover recorded at 10Hz. In the differential data analysis, using the rover/base data, we were not able to obtain a fixed solution in the Trimble Business Center (TBC), only a float solution. We attribute this to the likely possibility that the rover was not tracking a sufficient number of satellite vehicles (SVs) to get a fixed solution. Therefore, the following steps were undertaken to obtain a solution.
- (2)
- GPS data from the rover (Trimble R10) (rover_data_set_v1.T02) were converted from Trimble format (.T02) to RINEX (Receiver INdependent EXchange format) (rover_data_set_v2.RINEX). This is performed using Trimble’s Convert to RINEX utility (accessed on 3 October 2021).
- (3)
- The RINEX (rover_data_set_v2.RINEX) file is submitted to the Spatial Reference System Precise Point Positioning (CSRS-PPP), provided by Natural Resources of Canada. CSRS-PPP is an online application for global navigation satellite systems (GNSS) data post-processing. It uses precise satellite orbit, clock and bias corrections derived from a global network of receivers to determine accurate user positions anywhere on the globe, regardless of proximity to reference stations (from: https://www.nrcan.gc.ca/maps-tools-and-publications/tools/geodetic-reference-systems/data/10923 (accessed on 3 October 2021)). Upon submission of RINEX files, enhanced positioning precisions in the North American Datum of 1983 of the Canadian Spatial Reference System (NAD83(CSRS)) or the International Terrestrial Reference System (ITRS) in realization ITRF14 are returned.
5.2. Comparison of Button GPS and Corrected Rover GPS Data
5.3. Derivation of Surface Height Using ULS and Differential GPS or Button GPS
5.4. Synchronization of Laser and Differential GPS and Button GPS
5.5. IMU Correction
6. Analysis of Airborne Geophysical Data and Results: Ice-Surface Heights, Technical Information and Crossover Analysis
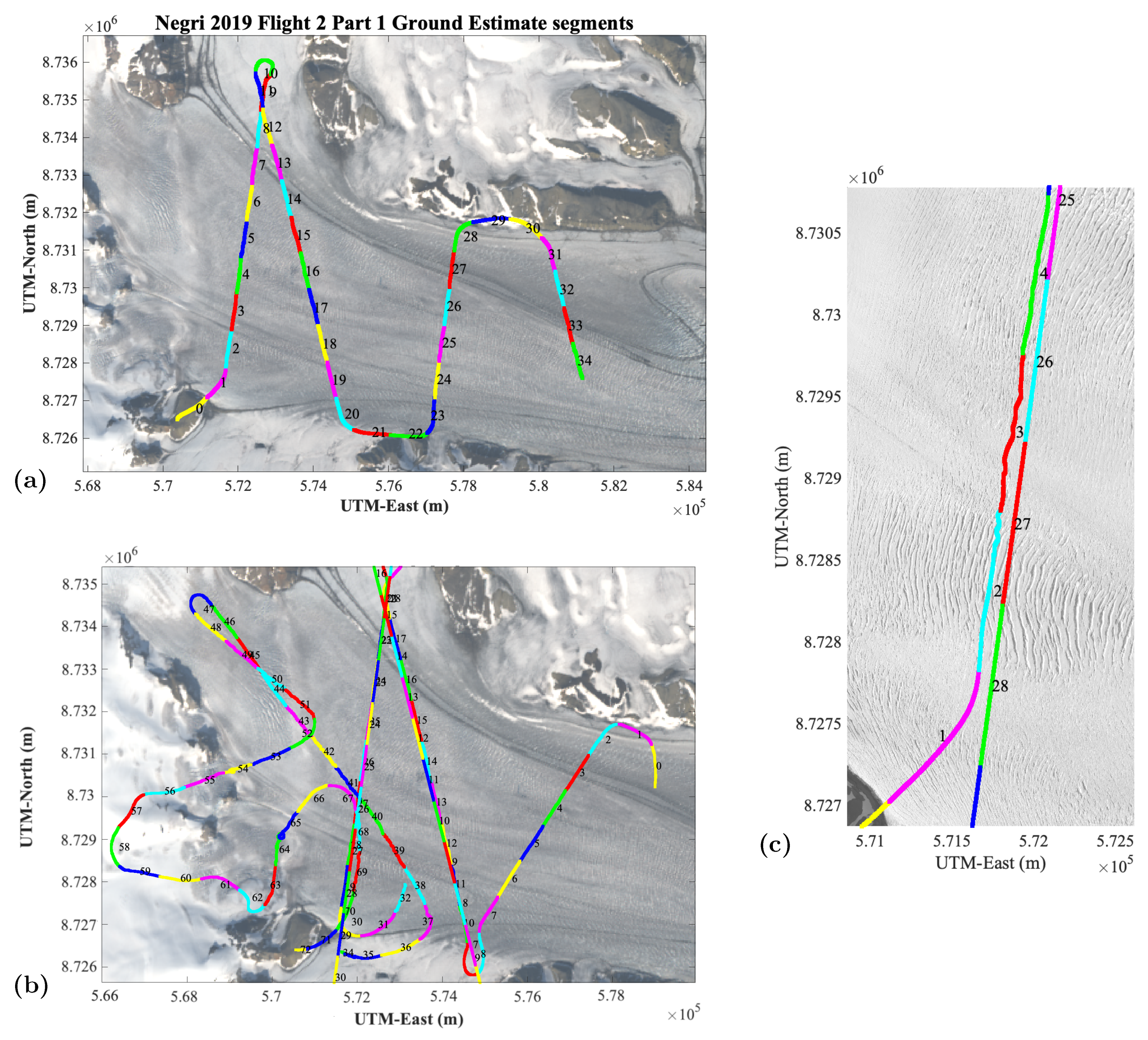
6.1. Results Part 1: ULS Range and Ice-Surface Heights Based on GPS and IMU-Corrected Data
6.2. Results Part 2: Technical Information: Helicopter Velocity, ULS Range, Data Frequency and On-Ice-Spacing
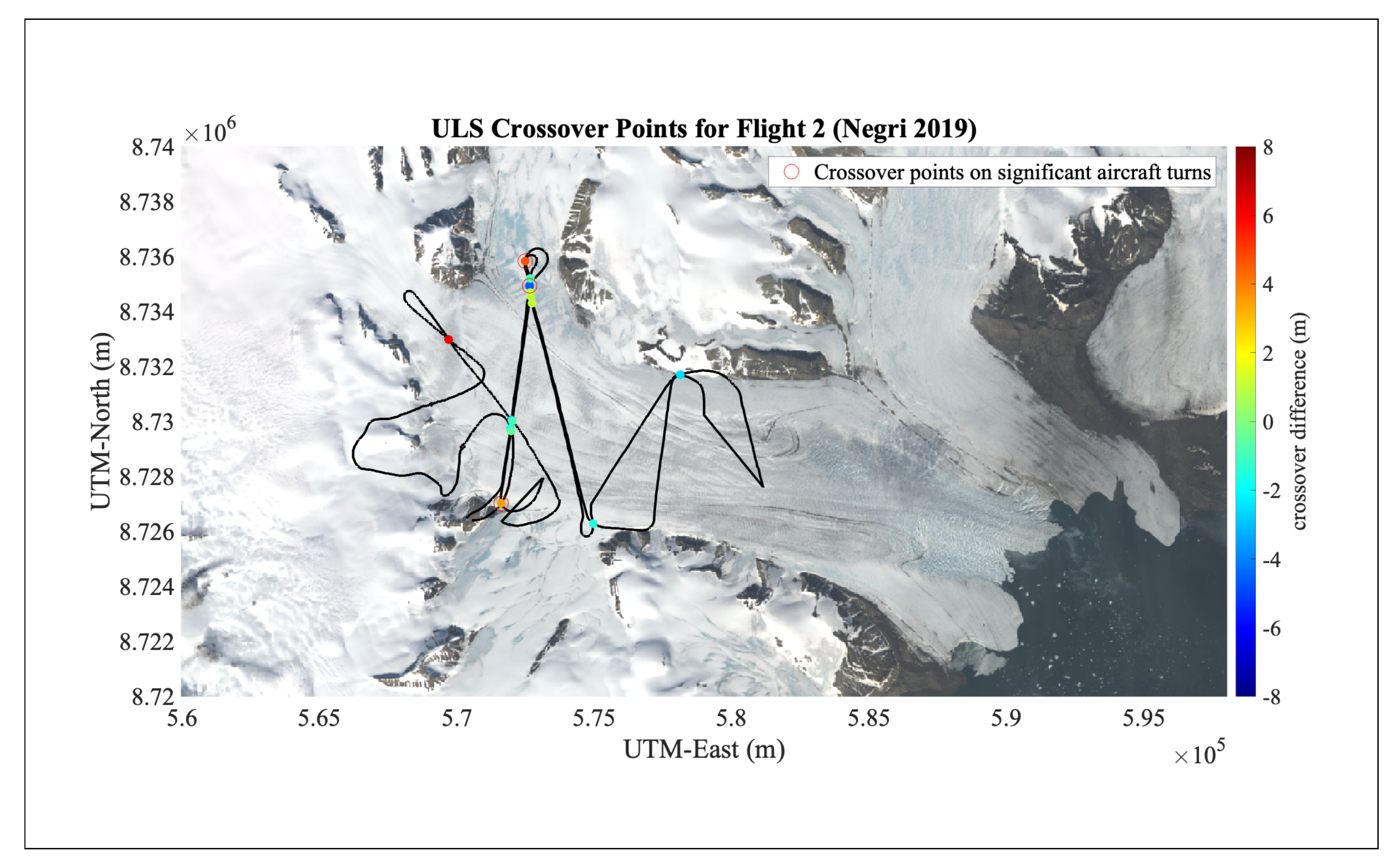
6.3. Results Part 3: Crossover Analysis of ULS Heights
7. Analysis of Geolocated ULS and ICESat-2 ATLAS Data
7.1. Overview
7.2. Concepts of Crevasse Provinces and Surface Roughness
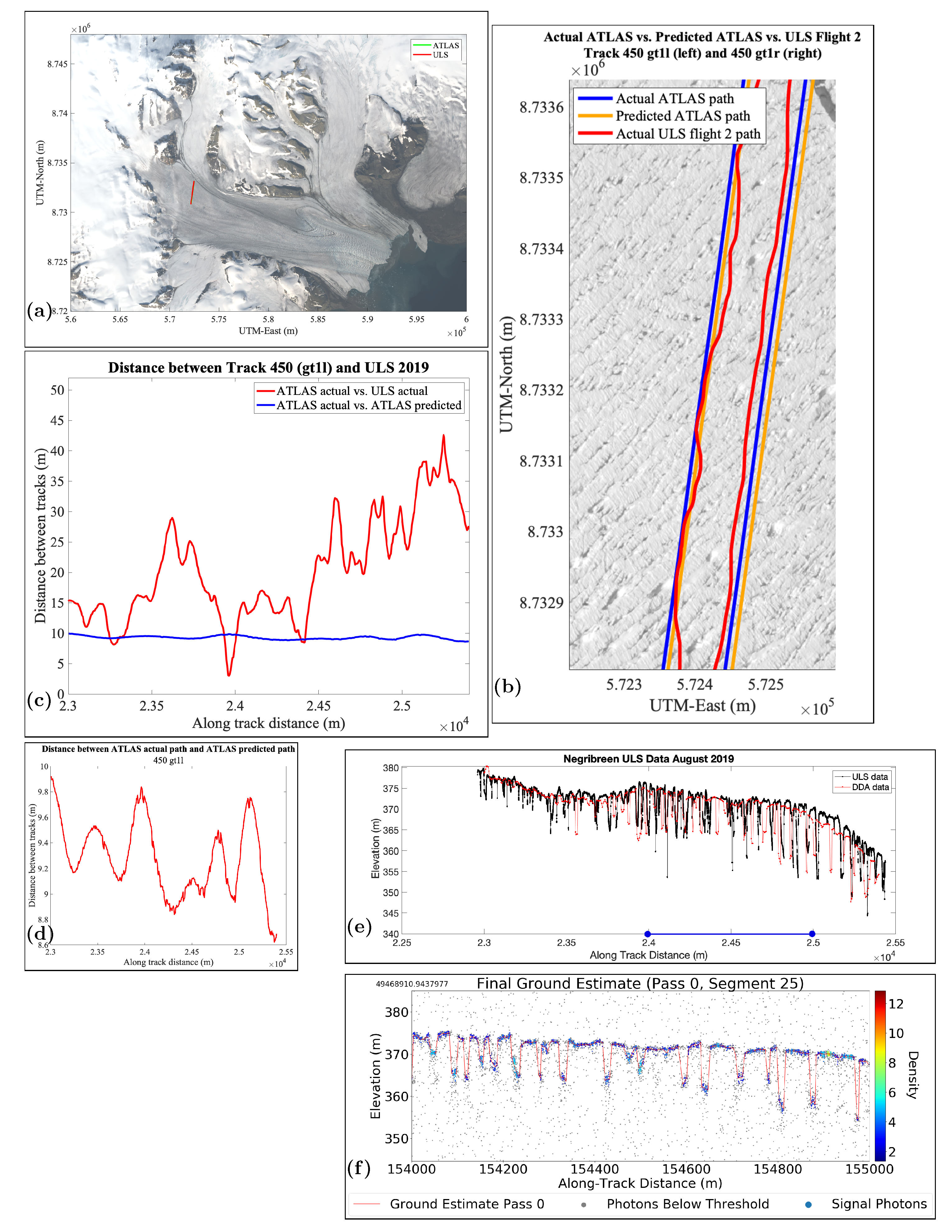
7.3. Analysis of Data for RGT 450, gt1l (Strong Beam)
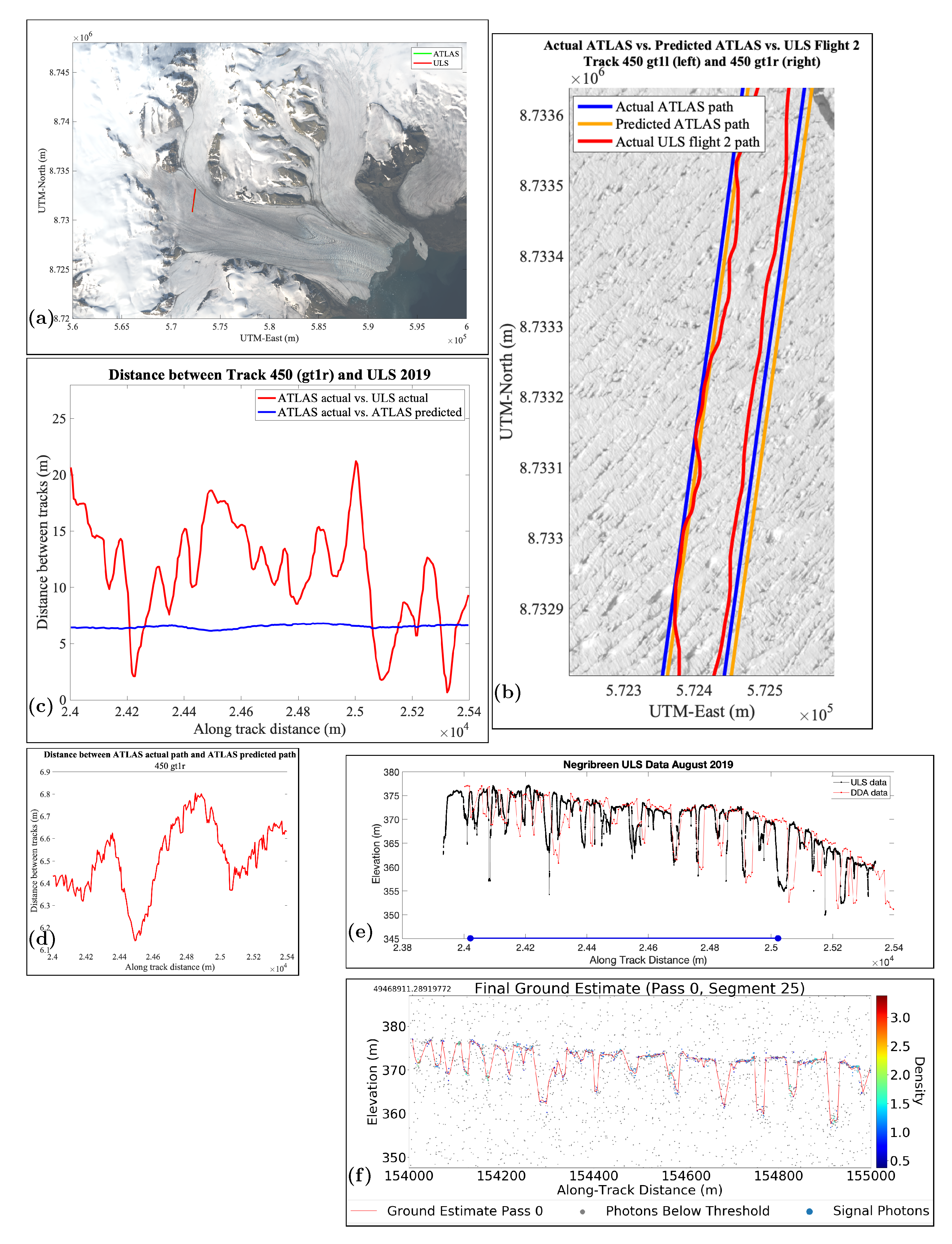
7.4. Analysis of Data for RGT 450, gt1r (Weak Beam)
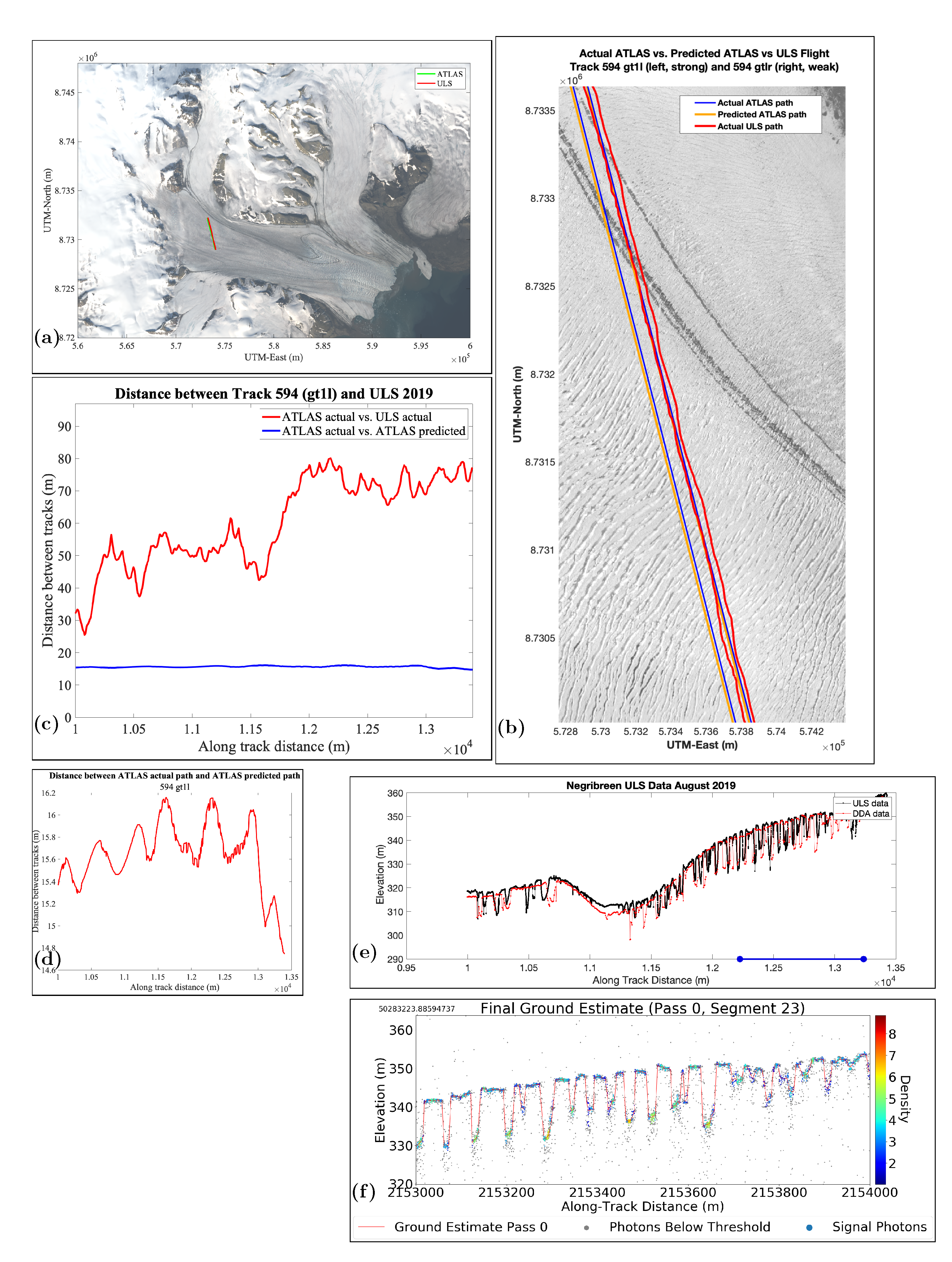
7.5. Analysis of Data for RGT 594, gt1l (Strong Beam)
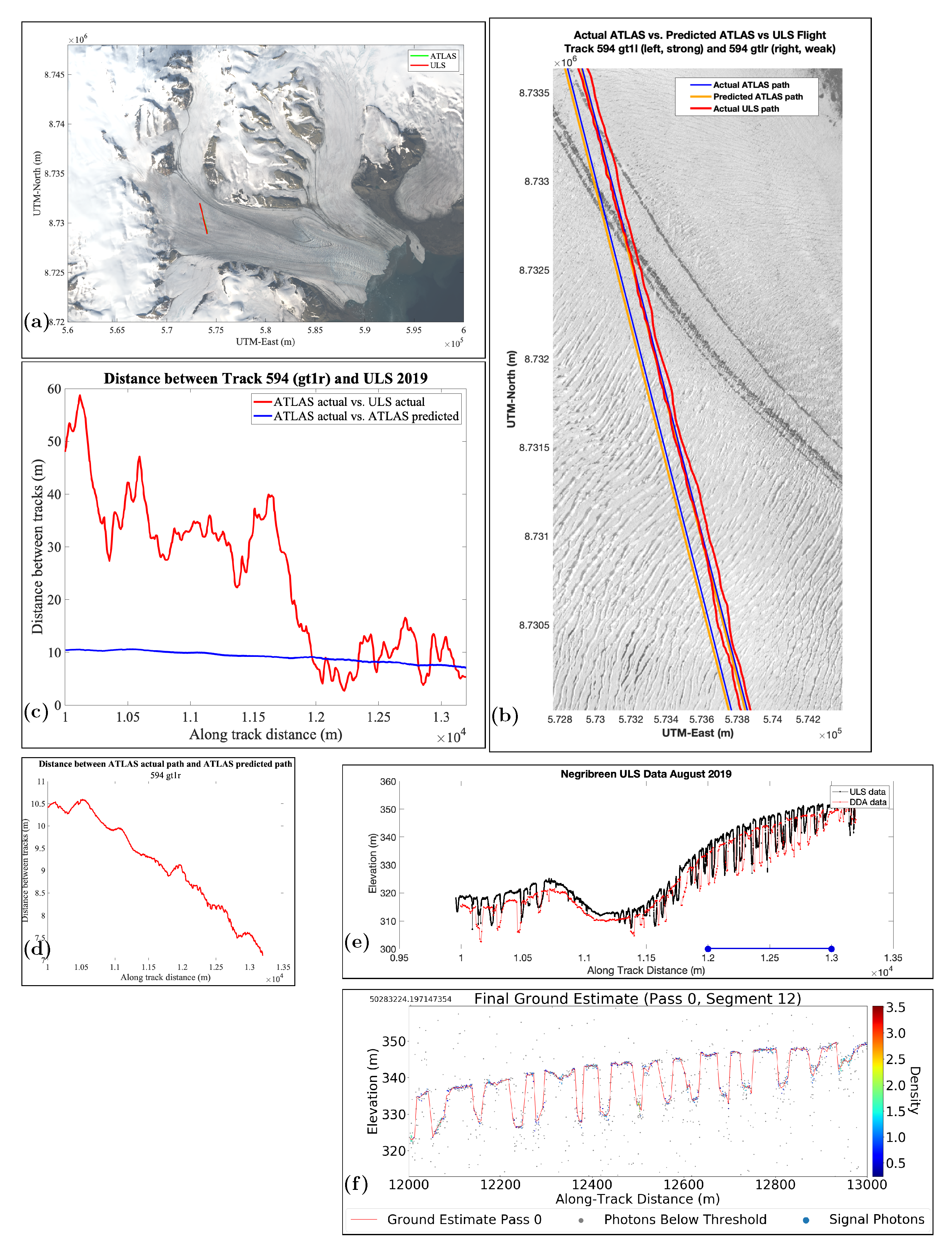
7.6. Analysis of Data for RGT 594, gt1r (Weak Beam), Overpass 1
7.7. Analysis of Data for RGT 594, gt1r (Weak Beam), Overpass 2
8. Results Part 4: Track-Repeat Accuracies (ULS versus ICESat-2 ATLAS-Predicted and ATLAS-Actual)
9. Results Part 5: Comparison of Surface Heights and Crevasse Characteristics from ULS and ICESat-2 ATLAS Data. Surface Roughness
9.1. Surface Heights and Crevasse Morphologies
9.2. Crevasse Spacing, Crevasse Depth and Surface Roughness
10. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote. Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neumann, T.A.; Martino, A.J.; Markus, T.; Bae, S.; Bock, M.R.; Brenner, A.C.; Brunt, K.M.; Cavanaugh, J.; Fernandes, S.T.; Hancock, D.W.; et al. The Ice, Cloud, and Land Elevation Satellite–2 mission: A global geolocated photon product derived from the Advanced Topographic Laser Altimeter System. Remote. Sens. Environ. 2019, 233, 111325. [Google Scholar] [CrossRef] [PubMed]
- Herzfeld, U.; Trantow, T.; Lawson, M.; Hans, J.; Medley, G. Surface heights and crevasse types of surging and fast-moving glaciers from ICESat-2 laser altimeter data—Application of the density-dimension algorithm (DDA-ice) and validation using airborne altimeter and planet skysat data. Sci. Remote. Sens. 2021, 3, 100013. [Google Scholar] [CrossRef]
- Schutz, B.; Zwally, H.; Shuman, C.; Hancock, D.; DiMarzio, J. Overview of the ICESat Mission. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Zwally, H.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef] [Green Version]
- Stocker, T.F.; Qin, H.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M.E. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Herzfeld, U.C.; Mayer, H. Surge of Bering Glacier and Bagley Ice Field, Alaska: An update to August 1995 and an interpretation of brittle-deformation patterns. J. Glaciol. 1997, 43, 427–434. [Google Scholar] [CrossRef] [Green Version]
- Herzfeld, U.C.; McDonald, B.; Wallin, B.F.; Krabill, W.; Manizade, S.; Sonntag, J.; Mayer, H.; Yearsley, W.A.; Chen, P.A.; Weltman, A. Elevation changes and dynamic provinces of Jakobshavn Isbræ, Greenland, derived using generalized spatial surface roughness from ICESat GLAS and ATM data. J. Glaciol. 2014, 60, 834–848. [Google Scholar] [CrossRef] [Green Version]
- Mayer, H.; Herzfeld, U. Structural glaciology of the fast-moving Jakobshavn Isbræ, Greenland, compared to the surging Bering Glacier, Alaska, USA. Ann. Glaciol. 2000, 30, 243–249. [Google Scholar] [CrossRef] [Green Version]
- Mayer, H.; Herzfeld, U. A structural segmentation, kinematic analysis and dynamic interpretation of Jakobshavns Isbræ, West Greenland. Z. Gletsch. Glazialgeol. 2001, 37, 107–124. [Google Scholar]
- Trantow, T.; Herzfeld, U.C. Crevasses as indicators of surge dynamics in the Bering Bagley Glacier System, Alaska: Numerical experiments and comparison to image data analysis. J. Geophys. Res. Earth Surf. 2018, 123, 1615–1637. [Google Scholar] [CrossRef]
- Herzfeld, U.; Trantow, T.; Bennetts, S. Surge-forced structural disintegration, enhanced calving and resultant rapid mass loss of a large Arctic fjord glacier (Negribreen, Svalbard). GRL 2018. submitted. [Google Scholar]
- Murray, T.; Strozzi, T.; Luckman, A.; Jiskoot, H.; Christakos, P. Is there a single surge mechanism? Contrasts in dynamics between glacier surges in Svalbard and other regions. J. Geophys. Res. 2003, 108, 2237. [Google Scholar] [CrossRef]
- Smith, B.; Fricker, H.; Gardner, A.; Siegfried, M.; Adusumilli, S.; Csatho, B.; Holschuh, N.; Paolo, F. ICESat-2 L3a Land Ice Height, Version 3; NASA ICESat-2 Project; NASA: Boulder, CO, USA, 2020.
- Smith, B.; Hancock, D.; Harbeck, K.; Roberts, L.; Neumann, T.; Brunt, K.; Fricker, H.; Gardner, A.; Siegfried, M.; Adusumilli, S.; et al. ICESat-2 Algorithm Theoretical Basis Document for Land Ice Along-Track Height Product, February 20, 2020; NASA ICESat-2 Project; NASA: Greenbelt, MD, USA, 2020; 107p.
- Brunt, K.M.; Smith, B.E.; Sutterly, T.C.; Kurtz, N.T.; Neumann, T.A. Comparisons of Satellite and Airborne Altimetry With Ground-Based Data From the Interior of the Antarctic Ice Sheet. Geophys. Res. Lett. 2020, 48, e2020GL090572. [Google Scholar] [CrossRef]
- Cui, H.; Li, R.; Li, H.; Hao, T.; Qiao, G.; He, Y.; Hai, G.; Xie, H.; Cheng, Y.; Li, B. Field validation of ICESat-2 data along CHINARE Route in East Antarctica. In The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; XLIII-B3-2021 (XXIV ISPRS Congress); Copernicus: Göttingen, Germany, 2021; pp. 443–448. [Google Scholar]
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.; Rebold, T. ICESat-2 Algorithm Theoretical Basis Document for Global Geolocated Photons, 15 October 2019; NASA ICESat-2 Project; NASA: Greenbelt, MD, USA, 2019; 202p.
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.; Rebold, T. ATLAS/ICESat-2 L2A Global Geolocated Photon Data, Version 3; NASA ICESat-2 Project; NASA: Greenbelt, MD, USA, 2020.
- Magruder, L.; Neumann, T.; Kurtz, N. ICESat-2 early mission synopsis and observatory performance. Earth Space Sci. 2021, 8, e2020EA001555. [Google Scholar] [CrossRef]
- Herzfeld, U.; Trantow, T.; Harding, D.; Dabney, P. Surface-height determination of crevassed glaciers—Mathematical principles of an Auto-Adaptive Density-Dimension Algorithm and validation using ICESat-2 Simulator (SIMPL) data. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 1874–1896. [Google Scholar] [CrossRef]
- Luthcke, S.B.; Pennington, T.; Rebold, T.; Thomas, T. Algorithm Theoretical Basis Document (ATBD) for ATL03g ICESat-2 Receive Photon Geolocation, 28 October 2019; NASA ICESat-2 Project; NASA: Greenbelt, MD, USA, 2019; 63p.
- Luthcke, S.; Zelensky, N.; Rowlands, D.; Lemoine, F.; Williams, T. The 1-centimeter orbit: Jason-1 precision orbit determination using gps, slr, doris, and altimeter data special issue: Jason-1 calibration/validation. Mar. Geod. 2003, 26, 399–421. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions (2010) IERS; Technical Note No. 36; International Earth Rotation and Reference Systems Service: Frankfurt, Germany, 2010. [Google Scholar]
- Dabney, P.W.; Harding, D.J.; Abshire, J.; Huss, T.; Jodor, G.; Machan, R.; Marzouk, J.; Rush, K.; Seas, A.; Shuman, C.; et al. The Slope Imaging Multi-polarization Photon-counting Lidar: Development and performance results. In Geoscience and Remote Sensing Symposium (IGARSS), 2010 IEEE International; IEEE: Piscataway, NJ, USA, 2010; pp. 653–656. Available online: http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5650862 (accessed on 3 October 2021).
- Harding, D.; Dabney, P.; Valett, S.; Yu, A.; Vasilyev, A.; Kelly, A. Airborne polarimetric, two-color laser altimeter measurements of lake ice cover: A pathfinder for nasa’s icesat-2 spaceflight mission. In Geoscience and Remote Sensing Symposium (IGARSS), 2011 IEEE international; IEEE: Piscataway, NJ, USA, 2011; pp. 3598–3601. [Google Scholar]
- Palm, S.; Yang, Y.; Herzfeld, U. ICESat-2 Algorithm Theoretical Basis Document for the Atmosphere, Part I: Level 2 and 3 Data Products, February 14, 2020; NASA ICESat-2 Project; NASA: Greenbelt, MD, USA, 2020; 104p.
- Palm, S.; Yang, Y.; Herzfeld, U.; Hancock, D.; Barbieri, K.; Wimert, J. ATLAS/ICESat-2 L2A Normalized Relative Backscatter Profiles, Version 3; NASA ICESat-2 Project; NASA: Greenbelt, MD, USA, 2020.
- Neumann, T.; Brenner, A.; Hancock, D.; Robbins, J.; Saba, J.; Harbeck, K.; Gibbons, A.; Lee, J.; Luthcke, S.; Rebold, T. ICESat-2 Algorithm Theoretical Basis Document for Global Geolocated Photons, April 2020; NASA ICESat-2 Project; NASA: Greenbelt, MD, USA, 2020; 207p.
- Crocker, R.I.; Maslanik, J.A.; Palo, S.E.; Adler, J.J.; Herzfeld, U.C.; Emery, W.J. A sensor package for ice surface characterization using small unmanned aircraft systems. IEEE Trans. Geosc. Remote Sens. 2011, 49, 1033–1047. [Google Scholar]
- Herzfeld, U.; Hunke, E.; McDonald, B.; Wallin, B. Sea Ice Deformation in Fram Strait—Comparison of CICE simulations with analysis and classification of airborne remote-sensing data. Cold Reg. Sci. Technol. 2015, 117, 19–33. [Google Scholar] [CrossRef] [Green Version]
- Brodin, G.; Cooper, J.; Stevens, J. Measuring the effect of helicopter rotors on GPS reception. Aeronaut. J. New Ser. 2007, 111, 561–570. [Google Scholar] [CrossRef]
- Banville, S.; Hassen, E.; Lamothe, P.; Farinaccio, J.; Donahue, B.; Mireault, Y.; Goudarzi, M.A.; Collins, P.; Ghoddousi-Fard, R.; Kamali, O. Enabling ambiguity resolution in CSRS-PPP. Navigation 2021, 68, 433–451. [Google Scholar] [CrossRef]
- Tétreault, P.; Kouba, J.; Héroux, P.; Legree, P. CSRS-PPP: An internet service for GPS user access to the Canadian Spatial Reference Frame. Geomatica 2005, 59, 17–28. [Google Scholar]
- Langley, R.B. Rtk gps. Gps World 1998, 9, 70–76. [Google Scholar]
- Parent, R. Computer Animation, Algorithms and Techniques; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Herzfeld, U.C.; Clarke, G.K.C.; Mayer, H.; Greve, R. Derivation of deformation characteristics in fast-moving glaciers. Comput. Geosci. 2004, 30, 291–302. [Google Scholar] [CrossRef] [Green Version]
- Herzfeld, U.C.; McDonald, B.; Stachura, M.; Hale, R.G.; Chen, P.; Trantow, T. Bering Glacier surge 2011: Analysis of laser altimeter data. Ann. Glaciol. 2013, 54, 158–170. [Google Scholar] [CrossRef]
- Herzfeld, U.C. Vario functions of higher order–definition and application to characterization of snow surface roughness. Comput. Geosci. 2002, 28, 641–660. [Google Scholar] [CrossRef]
- Herzfeld, U.C. Master of the obscure—Automated geostatistical classification in presence of complex geophysical processes. Math. Geosci. 2008, 40, 587–618. [Google Scholar] [CrossRef]
- Matheron, G. Principles of geostatistics. Econ. Geol. 1963, 58, 1246. [Google Scholar] [CrossRef]
- Matheron, G. The intrinsic random functions and their applications. Adv. Appl. Probab. 1973, 5, 439–468. [Google Scholar] [CrossRef] [Green Version]

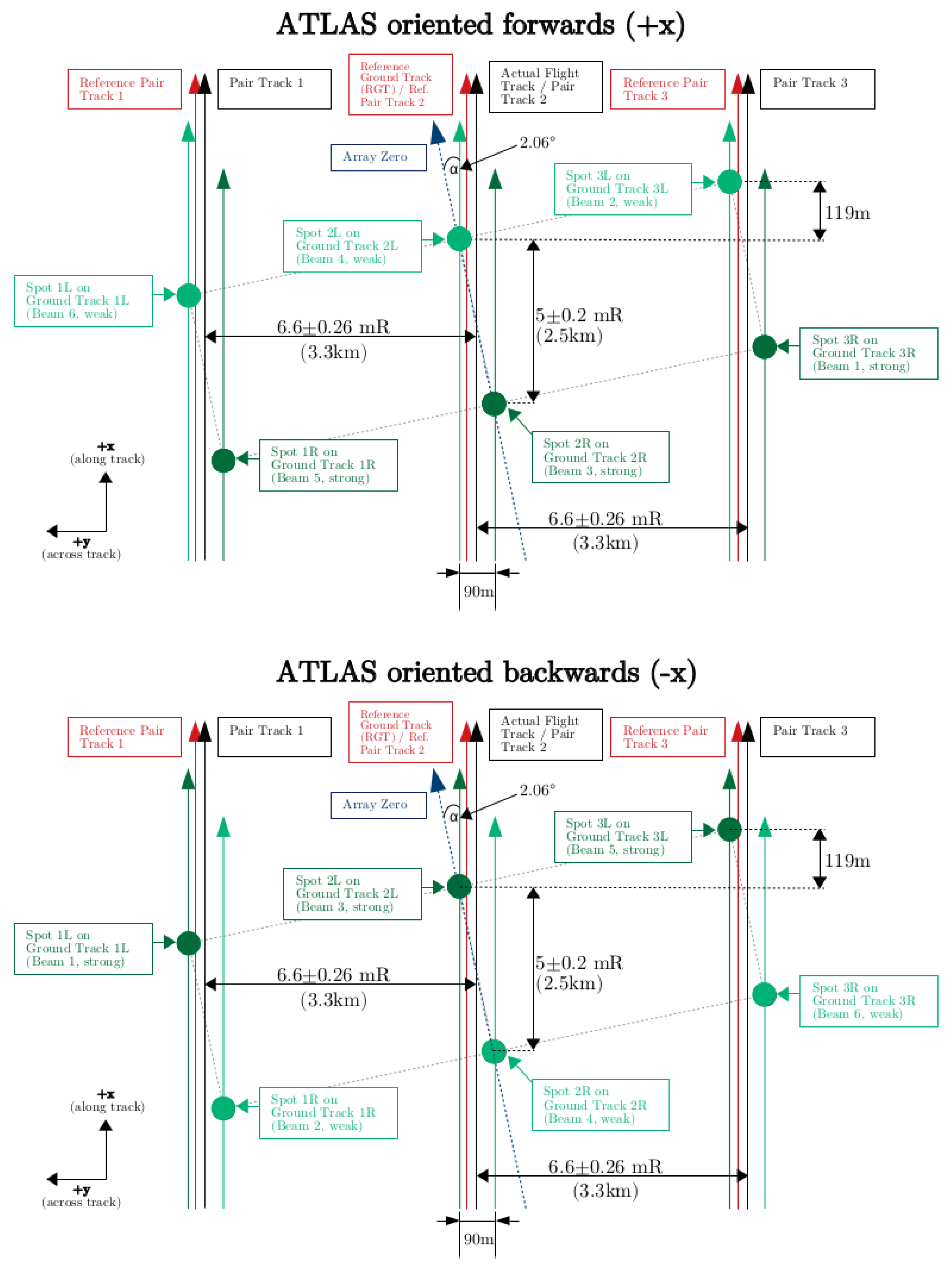




| ATLAS Flying Forwards | |||||||
|---|---|---|---|---|---|---|---|
| PCE | Strength | ATLAS Spot | Pair | GT | ATL03 Beam | ATL04/09 Atmosphere | Orientation |
| 1 | Strong | 1 | Right | gt3r | 5 | profile_3 | 1 |
| 1 | Weak | 2 | Left | gt3l | 6 | profile_3 | 1 |
| 2 | Strong | 3 | Right | gt2r | 3 | profile_2 | 1 |
| 2 | Weak | 4 | Left | gt2l | 4 | profile_2 | 1 |
| 3 | Strong | 5 | Right | gt1r | 1 | profile_1 | 1 |
| 3 | Weak | 6 | Left | gt1l | 2 | profile_1 | 1 |
| ATLAS Flying Backwards | |||||||
| PCE | Strength | ATLAS Spot | Pair | GT | ATL03Beam | ATL04/09Atmosphere | Orientation |
| 1 | Strong | 1 | Right | gt1l | 5 | profile_1 | 0 |
| 1 | Weak | 2 | Left | gt1r | 6 | profile_1 | 0 |
| 2 | Strong | 3 | Right | gt2l | 3 | profile_2 | 0 |
| 2 | Weak | 4 | Left | gt2r | 4 | profile_2 | 0 |
| 3 | Strong | 5 | Right | gt3l | 1 | profile_3 | 0 |
| 3 | Weak | 6 | Left | gt3r | 2 | profile_3 | 0 |
| Symbol | Meaning | Strong Beam ATLAS (Actual) | Weak Beam ATLAS (Actual) |
|---|---|---|---|
| s | standard deviation (m) | 3 | 4 |
| u | cutoff (number of standard deviations) | 1 | 1 |
| a | anisotropy | 1 | 1 |
| q | threshold quantile | 0.5 | 0.6 |
| k | threshold bias offset | 1 | 0.2 |
| l | slab thickness (m) | 200 | 200 |
| R | resolution of ground follower (m) | 5 | 5 |
| r | factor to reduce the R parameter | 2 | 1 |
| - | resolution of ground follower for rough surfaces (m) | 2.5 | 5 |
| Q | crevasse depth quantile | 0.5 | 0.5 |
| S | standard deviation threshold | 1.75 | 1.75 |
| of thresholded signal to trigger | |||
| small step size in ground follower (m) |
| Manufacturer | Laser Technology, Inc. |
| Model | Universal Laser System (ULS) |
| Wavelength | 905 nm (IR) |
| Beam Divergence | 3 mrad (∼30 cm diameter footprint at 100 m range) |
| Exit Aperture | 42 mm |
| Pulse Repetition Frequency (PRF) | 10–4500 Hz, configurable, 4000 Hz for Negribreen campaign |
| Averaging | 10 points for Negribreen campaign (400 Hz effective PRF) |
| Maximum Range Over Ice Targets | 500 m |
| Eye Safety | Class 1, 7mm eye safe (FDA, CFR21) |
| Accuracy | ±2 cm |
| Resolution | 1 mm |
| Dimensions | 5.3 in L × 4.75 in W × 2.5 in H |
| Weight | 1.75 lbs (0.8 kg) |
| Mean Elevation Difference (m) | Standard Deviation of Elevation Difference (m) | Number of Points | Crossover Radius (m) | |
|---|---|---|---|---|
| All Crossover Locations | 0.111 | 3.056 | 14 | 10 |
| Crossover Locations Excluding Turns | −0.172 | 2.564 | 11 | 10 |
| RGT_Beam | ATLAS Predicted vs. ATLAS Actual (m) | ATLAS Actual vs. ULS Actual (m) | Figure |
|---|---|---|---|
| 450_gt1l (strong) | 9.28 | 20.40 | Figure 10 |
| 450_gt1r (weak) | 6.51 | 11.32 | Figure 11 |
| 594_gt1l (strong) | 15.65 | 60.38 | Figure 12 |
| 594_gt1r (weak) (part 1) | 9.16 | 24.87 | Figure 13 |
| 594_gt1r (weak) (part 2) | 9.16 | 24.35 | Figure 14 |
| Mean Crevasse | Maximum Crevasse | Mean Crevasse | |
|---|---|---|---|
| Spacing (m) | Depth (m) | Depth (m) (>5 m) | |
| DDA-ice | 52.12 | 16.01 | 10.95 |
| ULS | 58.82 | 13.96 | 10.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herzfeld, U.C.; Lawson, M.; Trantow, T.; Nylen, T. Airborne Validation of ICESat-2 ATLAS Data over Crevassed Surfaces and Other Complex Glacial Environments: Results from Experiments of Laser Altimeter and Kinematic GPS Data Collection from a Helicopter over a Surging Arctic Glacier (Negribreen, Svalbard). Remote Sens. 2022, 14, 1185. https://doi.org/10.3390/rs14051185
Herzfeld UC, Lawson M, Trantow T, Nylen T. Airborne Validation of ICESat-2 ATLAS Data over Crevassed Surfaces and Other Complex Glacial Environments: Results from Experiments of Laser Altimeter and Kinematic GPS Data Collection from a Helicopter over a Surging Arctic Glacier (Negribreen, Svalbard). Remote Sensing. 2022; 14(5):1185. https://doi.org/10.3390/rs14051185
Chicago/Turabian StyleHerzfeld, Ute C., Matthew Lawson, Thomas Trantow, and Thomas Nylen. 2022. "Airborne Validation of ICESat-2 ATLAS Data over Crevassed Surfaces and Other Complex Glacial Environments: Results from Experiments of Laser Altimeter and Kinematic GPS Data Collection from a Helicopter over a Surging Arctic Glacier (Negribreen, Svalbard)" Remote Sensing 14, no. 5: 1185. https://doi.org/10.3390/rs14051185
APA StyleHerzfeld, U. C., Lawson, M., Trantow, T., & Nylen, T. (2022). Airborne Validation of ICESat-2 ATLAS Data over Crevassed Surfaces and Other Complex Glacial Environments: Results from Experiments of Laser Altimeter and Kinematic GPS Data Collection from a Helicopter over a Surging Arctic Glacier (Negribreen, Svalbard). Remote Sensing, 14(5), 1185. https://doi.org/10.3390/rs14051185






