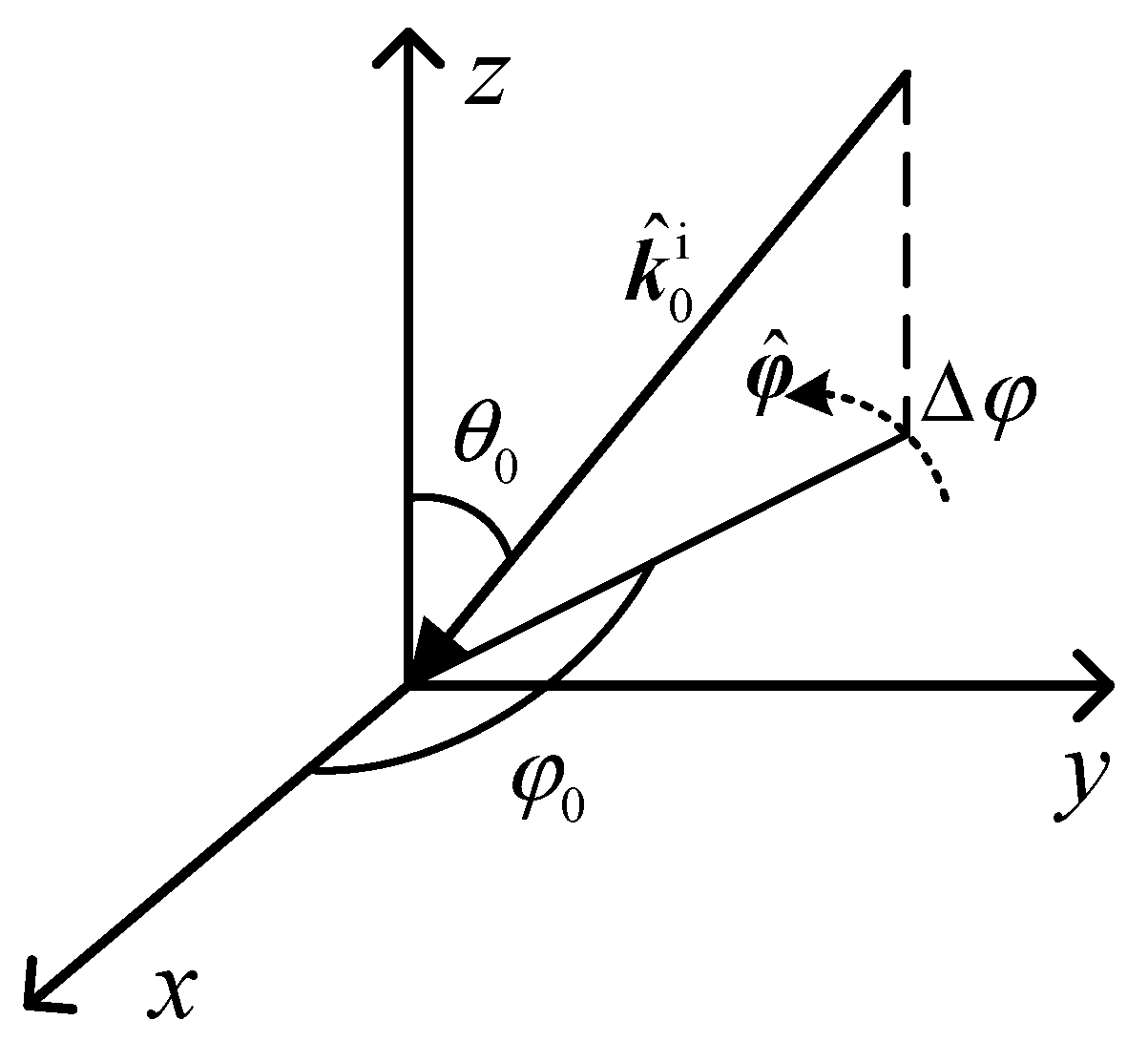1. Introduction
As active microwave imaging radar systems, synthetic aperture radar (SAR) and inverse synthetic aperture radar (ISAR) have been widely used in military and civil applications because they can be used continuously [
1,
2]. At the present, researchers pay more attention to the imaging algorithms, and few research works exist on the acquisition of the radar echo. It is undeniable, however, that the accurate and efficient acquisition of the radar echo data plays an essential role in designing radar imaging systems and the analytics of imaging algorithms. The echo data is needed for the system design to determine several parameters and evaluate its performance. During development, echo data is also required to verify the performance of each part of the system. Many researchers have studied imaging algorithms based on measured data [
3,
4,
5,
6,
7,
8,
9,
10]. Although the measured data is accurate, this approach is often very costly. For instance, the imaging of large targets requires a large anechoic chamber and a sizeable measured target model, which are both expensive to build and take a long time to construct. For the space-borne SARs, it is impossible to collect actual data before the system is developed successfully. Benefiting from the rapid development of computer technology, computational electromagnetic simulations are often used instead of experimental measurements to obtain the scattering characteristics of the targets. The electromagnetic simulation incorporates the scattering mechanism between the electromagnetic wave and the target. Such accurate simulation solutions address the issues attributed to the experimental measurement.
The research on microwave imaging based on computational electromagnetics has been developed over a long period of time. In terms of target imaging, R. Bhalla and H. Ling [
11] presented an ISAR imaging technique using bistatic scattering field data based on the physical optics (PO) method. They also used a shooting and bouncing rays (SBR) method to calculate multiple scattering data. They showed that in cases where multiple scattering is the dominant scattering mechanism, ghost artifacts might appear in both the monostatic and bistatic images. In 2010, Miao Sui [
12] developed a near-field electromagnetic scattering method to predict the high-frequency wideband EM scattering from the targets in the near-field region. They then proposed an approach for a two-dimensional high-resolution ISAR image sequence generation and synthesis. For composite scattering imaging, Chen [
13] proposed an efficient hybrid algorithm to simulate the scattering from a ship-like target on the sea surface. The scattering model is well suited to deal with the SAR imagery simulation of a large ship on the sea surface. Ye Zhao [
14] developed a bistatic SAR imaging method for metallic targets in the ocean. The image intensity distribution for the ocean surface is analyzed, and the facet scattering model is used to give the individual returns from separate facets. In 2017, Feng Xu [
15] presented a simplified small perturbation method (SPM) to evaluate the scattering of finite-length conducting rough surfaces. The simplified SPM greatly facilitated the derivation of the analytical expression of the SAR image. Currently, the radar echo is often obtained using the frequency-domain electromagnetic scattering method. High range resolution is then achieved by employing frequency sweep. However, the actual electromagnetic waves emitted by radar are mostly pulse signals with a definite frequency bandwidth and a higher carrier frequency. Compared with frequency-domain (FD) electromagnetic scattering methods, TD methods can avoid the time-consuming frequency-scanning process. The total wideband scattering results can be obtained by a single Fourier transform of TD scattering echoes, which can significantly improve the computational efficiency; thus, TD electromagnetic scattering methods are more suitable for simulating radar echoes.
There is extensive research on the TD electromagnetic scattering methods. There are many classical TD numerical methods, such as the finite-difference time-domain (FDTD) [
16,
17] and the TD integral equation [
18,
19]. These methods can be used to obtain the accurate scattering echo of the target. However, with the increase of the electrical size of a target, the computational resources and simulation time required by these numerical methods are sharply increased. Hence, they are not suitable for the scattering calculation of larger targets. In order to obtain the TD scattering echoes of large targets, researchers developed a series of TD high-frequency scattering methods based on FD high-frequency scattering methods. Among them, the TDSBR method effectively combines the advantages of TD geometrical optics (TDGO) and TD physical optics (TDPO) [
20,
21], and fully considers the existing reflection fields on the target. This method is widely used in the electromagnetic scattering of electrically large and complex targets. In 1993, Ling and Bhalla [
22] proposed a TDSBR method based on the classical FDSBR algorithm. In [
22], they then derived a closed-form TD ray tube integral expression to calculate the TD response of complex targets quickly. In 2015, Zhou [
23] presented a TDSBR method based on the beam-tracing (BT) technique to analyze the transient scattering responses from large PEC objects illuminated by a pulsed plane wave. In 2019, Guo [
24] extended the application scope of the TDSBR method from far-field scattering to near-field scattering and proposed a near-field TDSBR method for large and complex targets. In radar imaging, Guo [
25,
26] proposed ISAR imaging technology based on the TDPO and TDSBR methods, respectively. However, the previously mentioned TD methods focus on a single target. There are few studies on transient scattering echo simulations of composite scenes. In particular, to the best of our knowledge, there is no research on the radar imaging of composite scenes by using TD simulated scattering echoes.
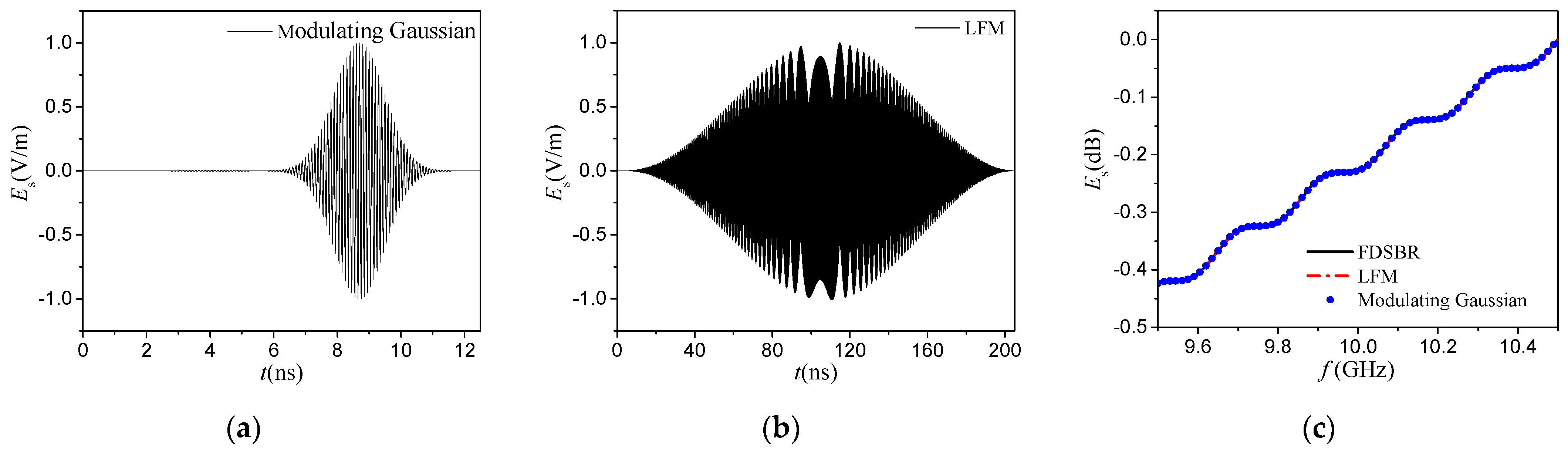
Because of the high cost of experimental measurements and the difficulty in obtaining non-cooperative target image data, we propose an ISAR imaging method for a composite target-ocean scene by using simulated scattering echoes. As the electromagnetic wave emitted by radar is a TD pulse signal with a frequency bandwidth, we use the TD electromagnetic scattering method to simulate the scattering echo. The difficulty of a composite scene scattering echo simulation is that the coupling scattering between the target and the sea surface is very complex. In this paper, based on a ray-tracing model, we propose a TDSBR method for calculating the transient scattering echo from a composite target-ocean scene. In the TDSBR method, the coupling scattering field comes from the radiation field of the equivalent electromagnetic current generated by the electromagnetic wave repeatedly bouncing between the target and the sea surface. The scattering field expressions of the conducting target and the dielectric sea surface are derived. Then, we derive the ISAR imaging formulas based on the electromagnetic scattering echo expressions used in TDSBR. In addition, to improve the simulation efficiency, we replace the LFM pulse with a modulating Gaussian pulse. We then modify the matched filter to achieve pulse compression under a modulating Gaussian pulse excitation.
2. Description of TDSBR Method
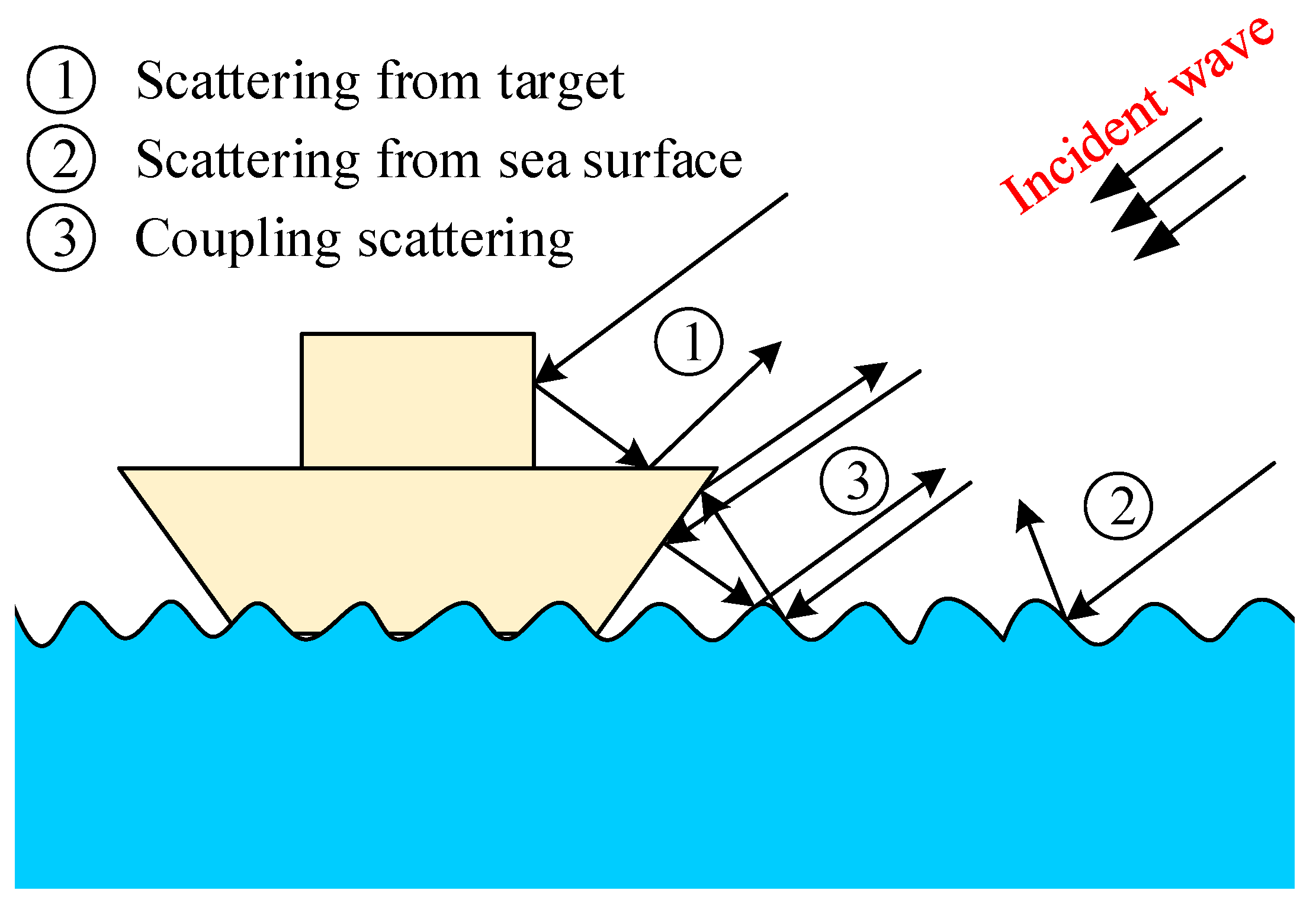
In
Figure 1, we consider the composite target-ocean scene illuminated by an incident plane wave. The scattering echo consists of three parts: target scattering, sea surface scattering, and coupled scattering. The scattering echoes from these three parts can be easily obtained using the TDSBR method. The TDSBR method consists of both TDGO and TDPO. The main goal of the TDSBR method is to imitate the propagation behavior of electromagnetic waves by using rays. As shown in
Figure 1, the initial rays hit the surface of the target and the sea, respectively. When a ray intersects with the surface of an object, it reflects. The reflected rays continue to travel forward, intersecting objects until no more reflections occur. The TDGO method is used to calculate the intensity and phase value of the reflected rays. The object’s surface that intersects with the rays is thought to be illuminated by electromagnetic waves. The scattering field of the illuminated surface is calculated using the TDPO method.
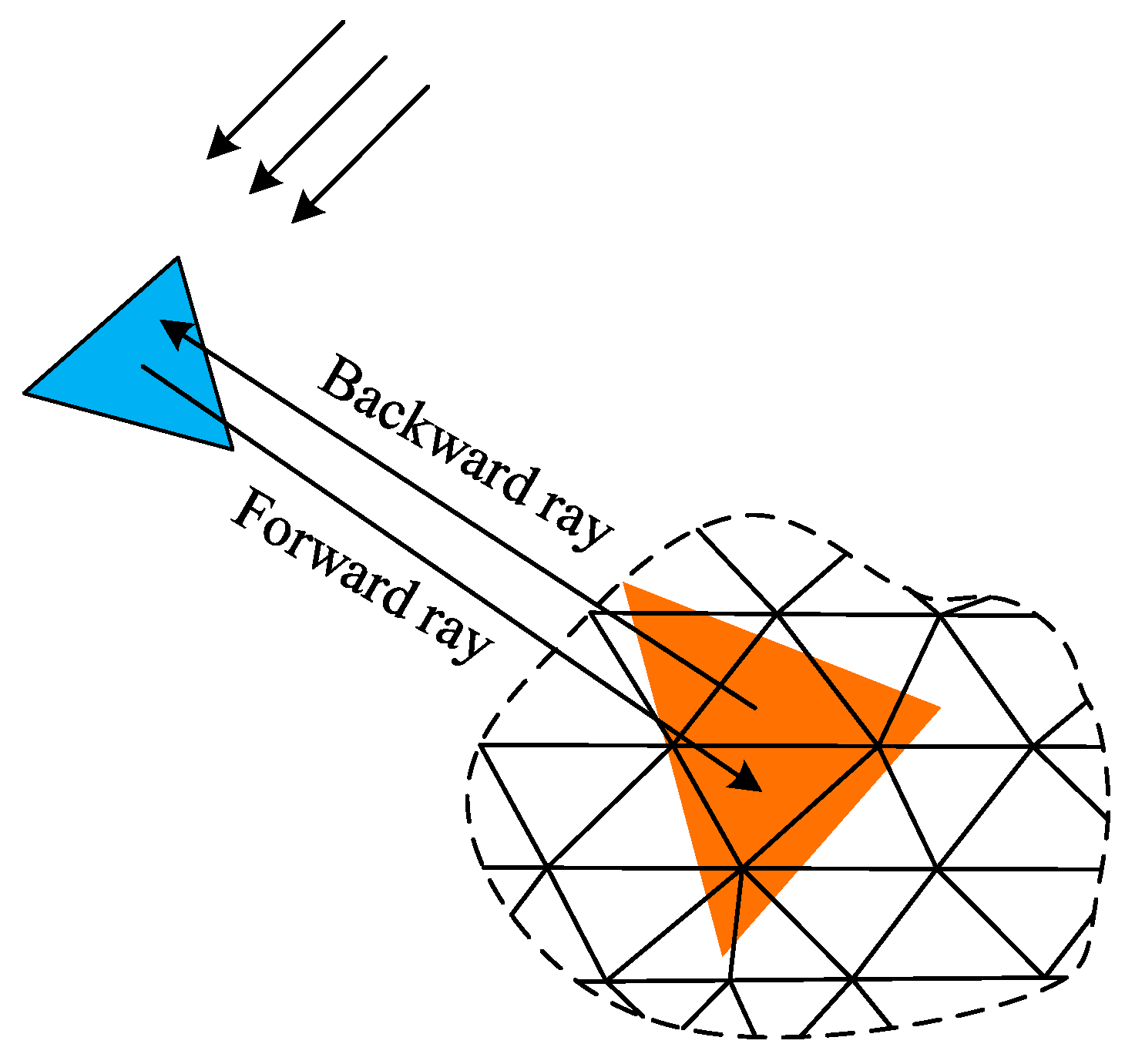
Several efficient ray-tracing techniques have been developed to find the illuminated surface of an object. In this paper, the surface of the target and sea is subdivided into triangular patches. As shown in
Figure 2, we introduce the forward and backward ray tracing technology, as was previously done in [
27], into the TDSBR. Forward ray tracing is used to obtain the illuminated triangle; then, backward ray tracing is used to judge whether the triangle adjacent to the illuminated triangle is illuminated.
Next, we calculate the scattering fields of the illuminated triangles. Before calculating the scattering fields, the TDGO method is used to obtain the incident fields of the triangles. The electric and magnetic fields of the initial incident plane wave with the excitation pulse
are as follows:
where
and
are amplitude vectors.
denotes the normalized incidence direction.
is the impulse function.
is the speed of light in free space. The symbol “
” represents the convolution operation.
For the
mth reflection, the incident fields
and
show the following relationship:
and
where
RTM and
denote the reflection coefficients and normalized direction of the TM wave.
and
indicate the reflection coefficients and normalized direction of the TE wave.
The transient scattering fields is calculated by the TDPO integrals as follows:
where
r is the distance between the observation point and the coordinate origin.
denotes normalized scattering direction. The integral region S is the region where the target surface is illuminated.
and
are the equivalent current and equivalent magnetic current distributed on the surface, respectively. Based on Fresnel’s reflection law,
and
are derived as:
By substituting (3), (4), and (10) into(9), the scattering field
can be written as:
where
For the triangular patch,
can be reduced to a closed-form representation:
In the above equation, is the center of triangular patch. and . . is the position vector of the vertices of in the global coordinate system, and . is a step function.
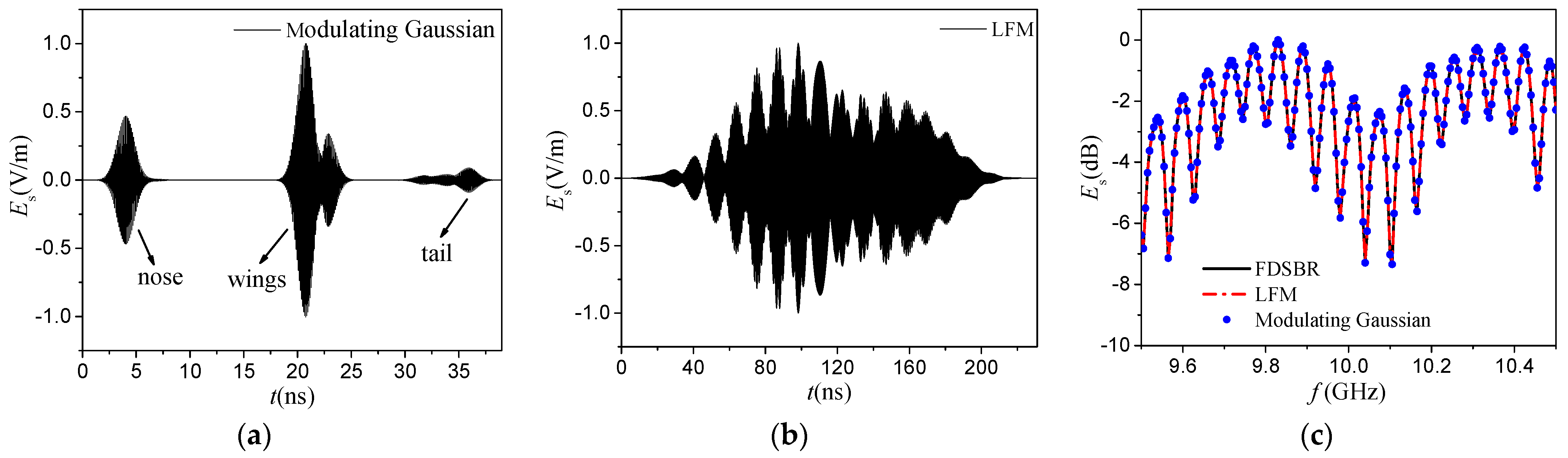
To verify the accuracy and efficiency of the TDSBR method, results from TDSBR are shown and compared with the full-wave solutions that were simulated using the multilevel fast multipole algorithm (MLFMA) obtained using FEKO commercial software. In addition, the results of the frequency domain SBR (FDSBR) are given as a reference. In the TDSBR method, the excitation pulse is the modulating Gaussian pulse:
where
is the carrier frequency.
.
.
fb denotes the bandwidth.
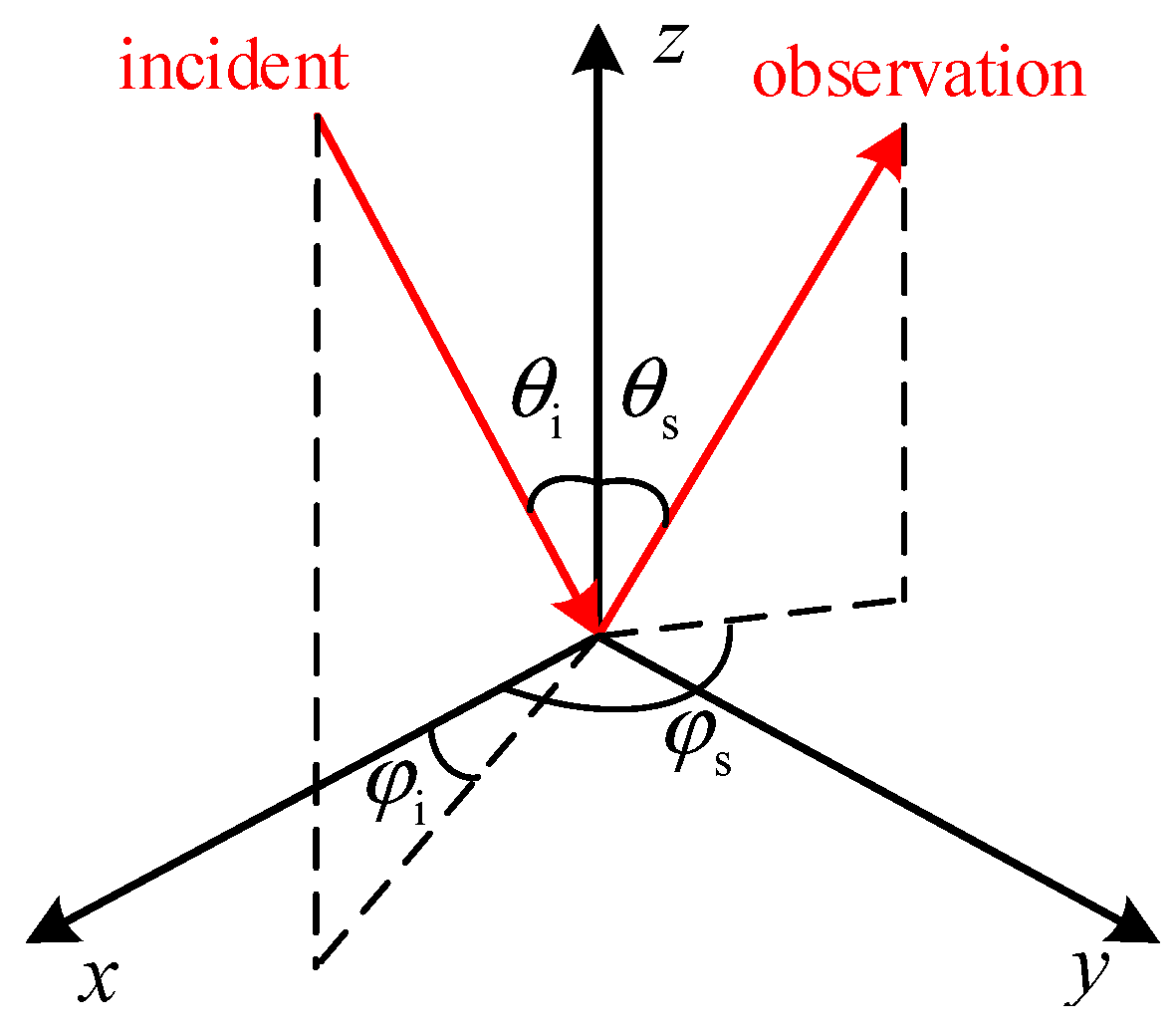
Figure 3 shows the definition of the incident and the observation direction in the global coordinate system.
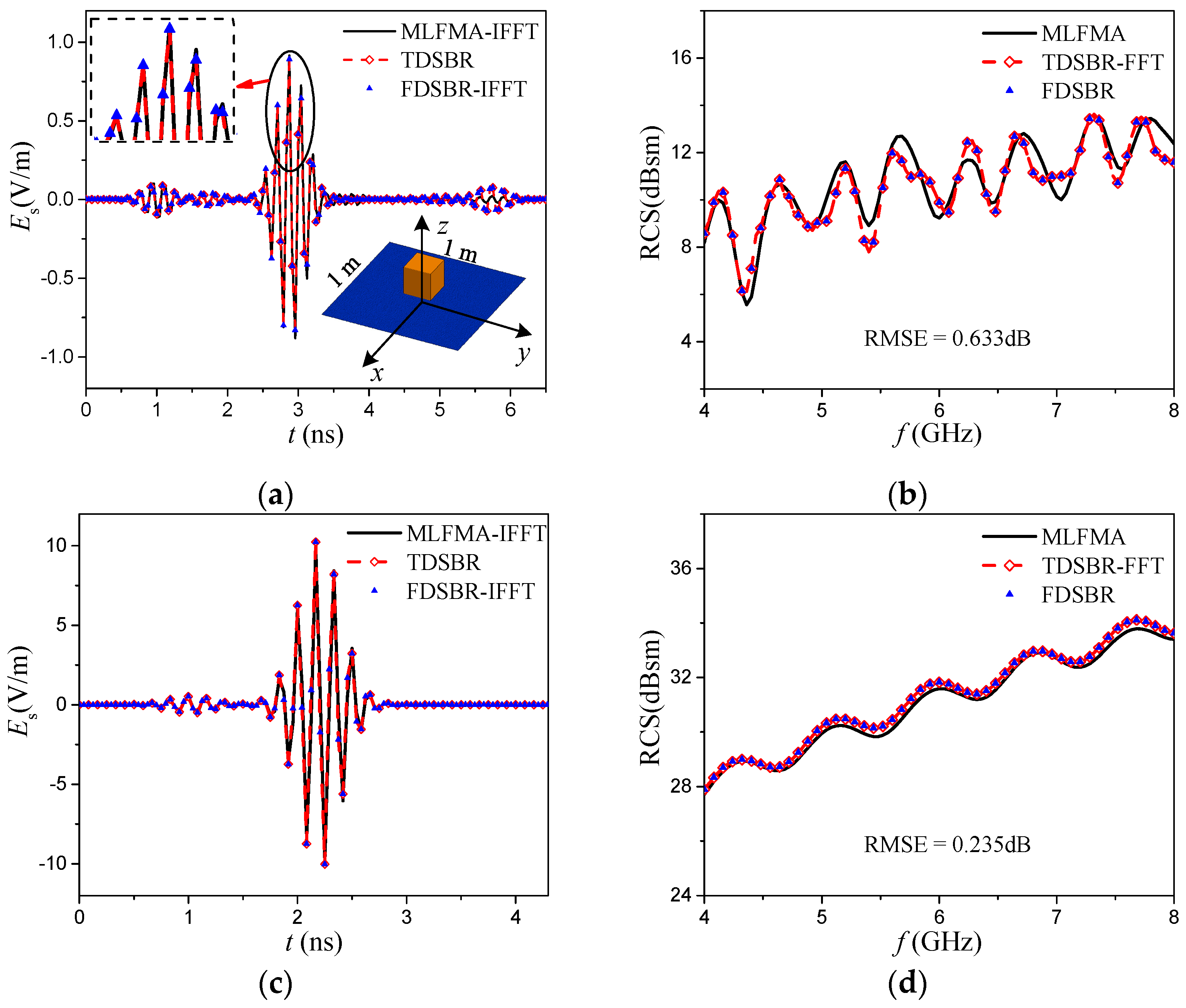
Figure 4 shows the monostatic (
θi = 45°,
= 0°) and bistatic (
= 45°,
= 0°,
= 45°,
= 180°) scattering results of a composite cube-ocean scene (see
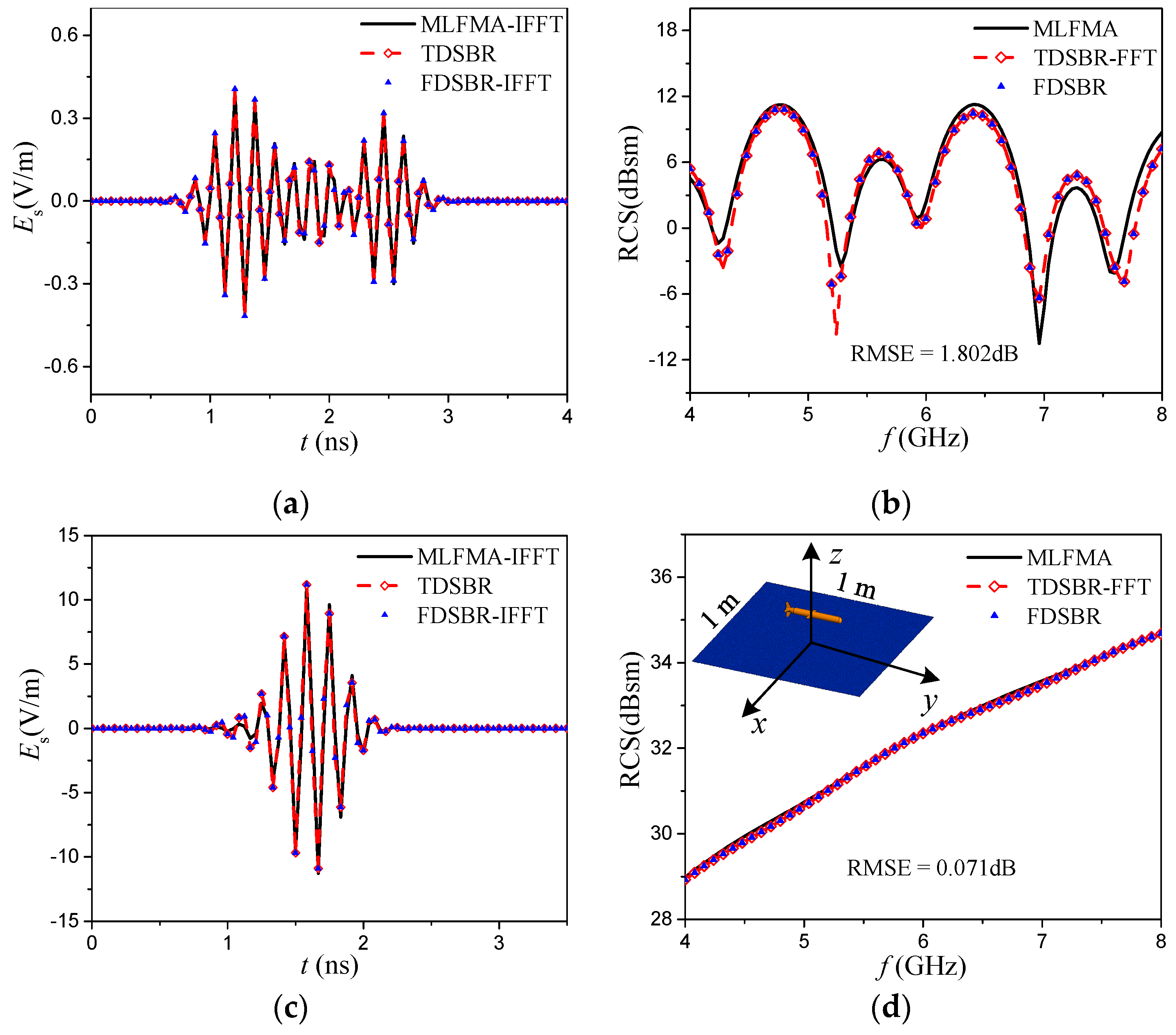
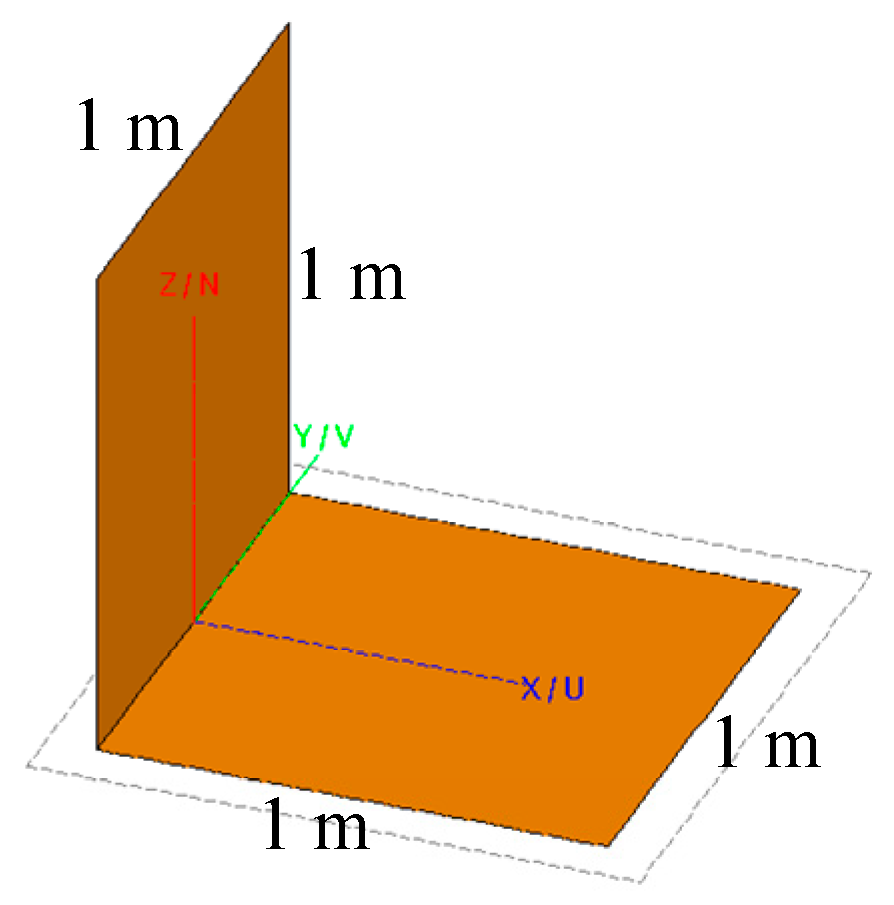
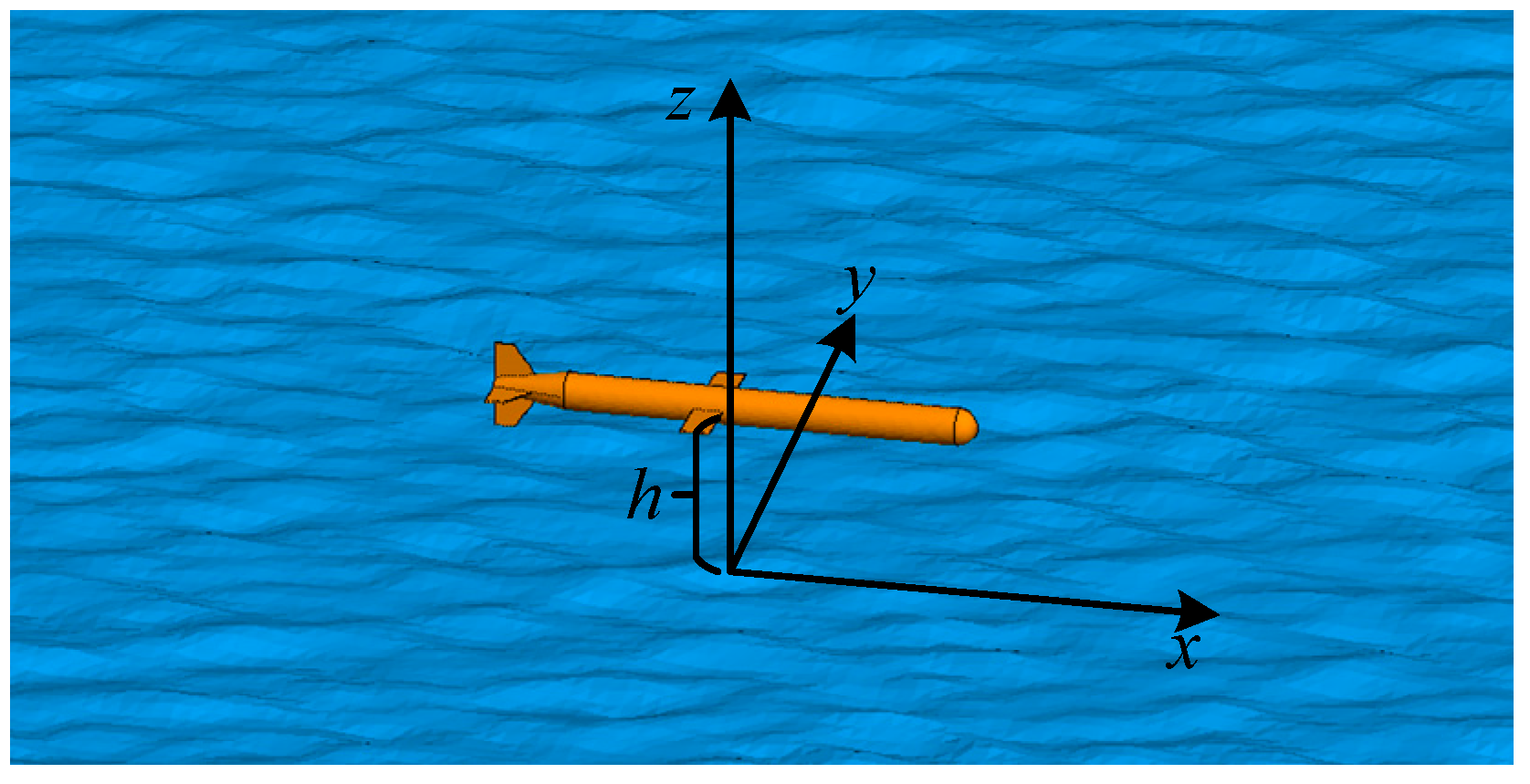
Figure 4a). The side length of the cube is 0.2 m. The height of the cube’s center is 0.15 m. The size of the rough sea surface is 1 m × 1 m.
Figure 5 shows the monostatic (
= 10°,
= 90°) and bistatic (
= 45°,
= 0°,
= 45°,
= 180°) scattering results of a composite missile-ocean scene (see
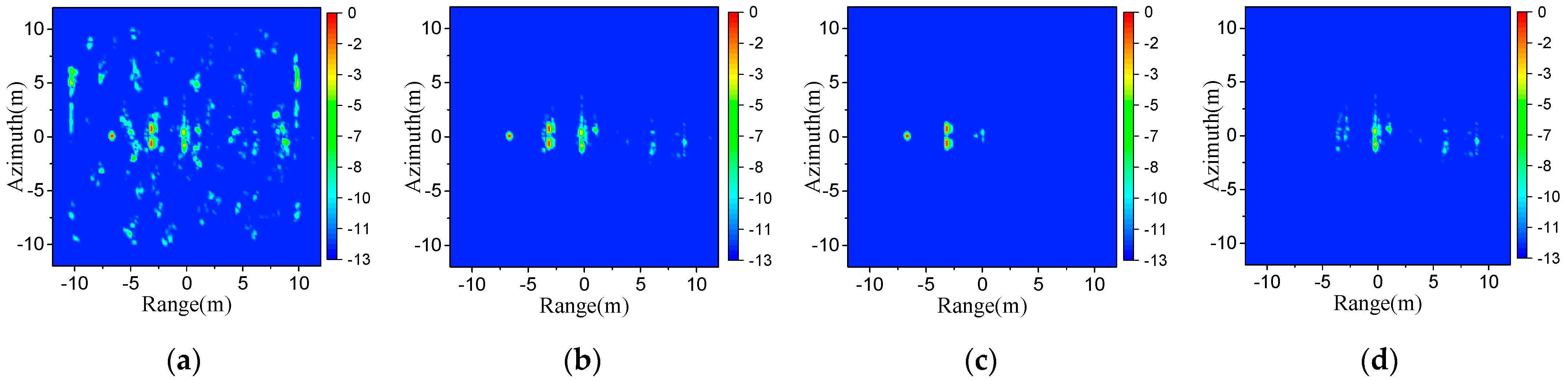
Figure 5d). The size of the missile is about 0.33 m × 0.1 m × 0.026 m. The height of the missile’s center is 0.1 m. The size of the rough sea surface is 1 m × 1 m. The power spectrum of the sea surface is PM spectrum. The wind speed is 3 m/s. The relative dielectric constant of the sea is
. The rough sea surface is generated by the Monte Carlo method. The carrier frequency
is 6 GHz and the bandwidth is 4 GHz.
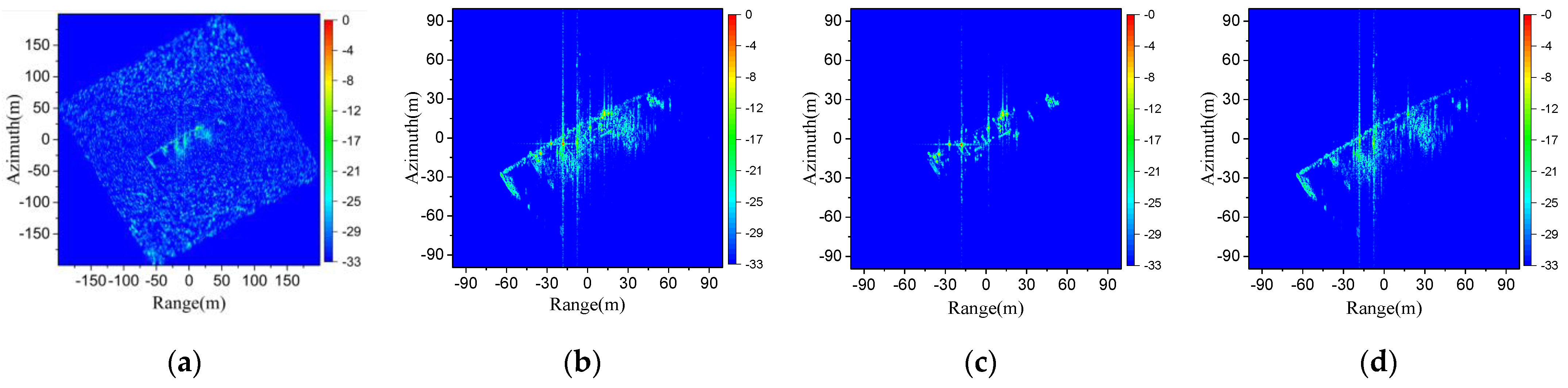
In
Figure 4 and
Figure 5, the wideband scattering fields obtained by MLFAM and FDSBR are converted into TD by the inverse fast Fourier transform (IFFT) and compared with those obtained from TDSBR. The transient results by TDSBR are transformed to the FD using the fast Fourier transform (FFT). It can be seen from the figures that the results from TDSBR and FDSBR agree well, but are slightly different from those using MLFMA; TDSBR and FDSBR belong to high frequency algorithms and the error between these results and those from MLFMA is due to the use of high frequency approximation. For wideband radar cross section (RCS), we give the root mean square error (RMSE) between TDSBR-FFT and MLFMA. The RMSE is expressed as:
where
and
represent the two sets of data to be compared. The “
n” is the number of elements in the data.
Table 1 compares the computational costs between the three methods. The experiment platform is a desktop computer with Quad 3.2 GHz CPU and 16 GB memory. The simulation time is estimated based on the single thread using Windows 10. As we can see, the ratio of computation time of TDSBR and FDSBR is about 1:5, and MLFMA takes 10
6 times longer than TDSBR.
3. ISAR Imaging Algorithm
Section 2 shows that the total echo of the composite scene is the sum of the echoes from all of the illuminated triangular patches. In this section, the ISAR imaging algorithm is derived based on the scattering field expression (12) of
Section 2.
As it is shown in
Figure 6, we consider a plane wave scanning a small angle
along
near
. In this example, the angular velocity is
. Thus, the azimuth angle
is
and
where
and
. For backscattering, we have
.
in
and
.
Assuming the polarization direction of the receiving antenna is
, the received echo is
where
is a window function.
In general,
and
in Equation (16) are not equal to zero for most observation directions. Thus,
can be written as the superposition of the step function:
where
.
In general, the transmitted signal
with carrier frequency
can be expressed as:
where
is the baseband signal and
is the pulse width.
In order to avoid the integral operation in the convolution operation, we use the first derivative of
as the excitation impulse. The echo expression can then be rewritten as:
We then derive the imaging formula under small-bandwidth small-angle approximation based on (25). First, the echo needs to be demodulated to the baseband domain. This procedure can be completed by multiplying the echo signal by the phase factor
. The echo after demodulation can be written as:
Then, by taking the range Fourier transform of
, we can get
The next step is matched filtering. For the LFM pulse, the matched filter is usually set to:
The spectrum
of LFM is a window function of complex-type. However, since the spectrum of the modulating Gaussian pulse is a Gaussian-type function, the matching filter is unable to achieve the pulse compression effect. Therefore, we redesign the matched filter as follows:
where
is a window function. It can be seen from the filter’s expression that the filter is suitable for modulating the Gaussian pulse and for the LFM pulse.
The output of the matched filter is
For small values of
,
can be approximated by 1 and
can be approximated by
. Therefore,
is reduced to
and
can be approximated as
Therefore,
can be simplified as:
By further applying the small-bandwidth approximation:
we can get
where
.
Finally, we take the range and azimuth inverse Fourier transform (IFT) of
. We can obtain the final ISAR image expression:
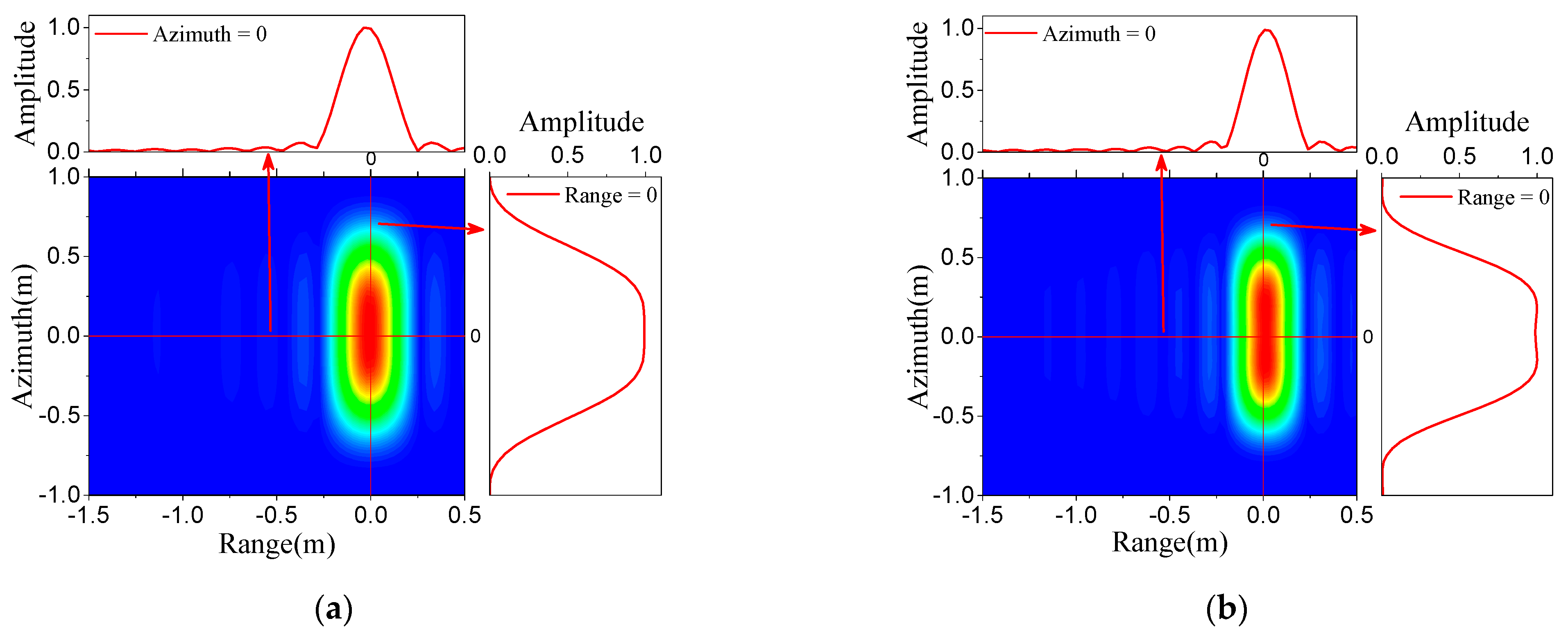
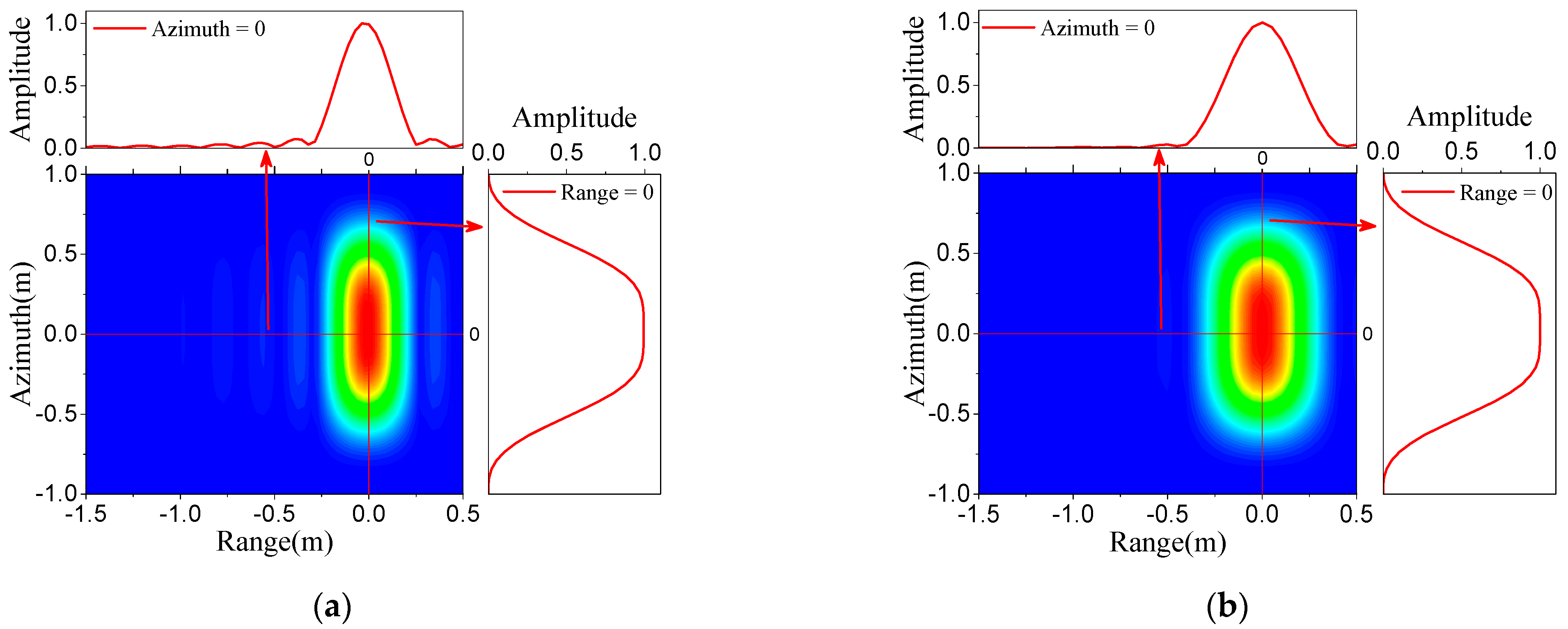
where
and
are
sinc-type functions. The image intensity of each triangular patch can be obtained by (38). The imaging process for one of the triangles is the same for all the triangles. The overall image is the sum of the image of all the illuminated triangles.