Next Article in Journal
A Simple Statistical Intra-Seasonal Prediction Model for Sea Surface Variables Utilizing Satellite Remote Sensing
Next Article in Special Issue
Characterizing Garden Greenspace in a Medieval European City: Added Values of Spatial Resolution and Multi-Temporal Stereo Imagery
Previous Article in Journal
Graph-Based Embedding Smoothing Network for Few-Shot Scene Classification of Remote Sensing Images
Previous Article in Special Issue
Assessing Storm Response of Multiple Intertidal Bars Using an Open-Source Automatic Processing Toolbox
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 14
Issue 5
10.3390/rs14051163
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Harmonization of Multi-Mission High-Resolution Time Series: Application to BELAIR

by
Else Swinnen
1,*,
Sindy Sterckx
1,
Charlotte Wirion
2,
Boud Verbeiren
2 and
Dieter Wens
1
1
Remote Sensing Unit, Flemish Institute for Technological Research (VITO), Boeretang 200, 2400 Mol, Belgium
2
Hydrology and Hydraulic Engineering Department, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussel, Belgium
*
Author to whom correspondence should be addressed.
Remote Sens. 2022, 14(5), 1163; https://doi.org/10.3390/rs14051163
Submission received: 14 January 2022 / Revised: 18 February 2022 / Accepted: 23 February 2022 / Published: 26 February 2022
(This article belongs to the Special Issue Innovative Belgian Earth Observation Research for the Environment)
Browse Figures
Versions Notes

Abstract

:
High-resolution data are increasingly used for various applications, yet the revisit time is still low for some applications, particularly in frequently cloud-covered areas. Therefore, sensors are often combined, which raises issues on data consistency. In this study, we start from L1 to L3 data, and investigate the impact of harmonization measures, correcting for difference in radiometric gain and spectral response function (SRF), and the use of a common processing chain with the same atmospheric correction for Sentinel-2A/B, Landsat-8, DEIMOS-1, and Proba-V center cameras. These harmonization measures are evaluated step-wise in two applications: (1) agricultural monitoring, and (2) hydrological modelling in an urban context, using biophysical parameters and NDVI. The evaluation includes validation with in situ data, relative consistency analysis between different sensors, and the evaluation of the time series noise. A higher accuracy was not obtained when validating against in situ data. Yet, the relative analysis and the time series noise analysis clearly demonstrated that the largest improvement in consistency between sensors was obtained when applying the same atmospheric correction to all sensors. The gain correction obtained and its impact on the results was small, indicating that the sensors were already well calibrated. We could not demonstrate an improved consistency after SRF correction. It is likely that other factors, such as anisotropy effects, play a larger role, requiring further research.

1. Introduction

There are clear tendencies in the use of higher spatial resolution satellite sensors, both for land [1,2,3] and water applications [4]. The revisit time of these sensors has greatly improved since the launch of the two Sentinel-2 satellites. Still, in areas with frequent cloud coverage, the update frequency of cloud-free data can be considerably lower. A solution is to combine data from different missions in order to obtain more frequent observations. A combination of different sensors is also necessary when data from a sufficiently long time series are required for analysis. This is, for example, the case for agricultural monitoring in which anomaly analysis is a frequently used method to assess the agricultural production of the current growing season [5,6]. Combining the recent and temporally more dense Sentinel-2 data with an archive of similar datasets is then important [5,7]. The availability of sufficiently fine spatial resolution data with an adequate temporal frequency and sufficient spectral information is still considered as a challenge, e.g., in agricultural monitoring [8,9] and vegetation monitoring [10,11]. The use of multi-mission time series should also contribute to decrease the uncertainty in derived products [12].
The joint use of data from different sensors raises some clear concerns about data consistency [13,14], and a seamless combination of EO products coming from different missions require corrections that account for the sensor differences. The Harmonized Landsat Sentinel-2 (HLS) dataset [15] and Sen2Like tool [16] include co-registration, the same atmospheric correction method for both sensors, bi-directional distribution function (BRDF) normalization, and correction for the differences in spectral response functions (SRF) to generate top-of-Canopy (TOC) reflectances and NDVI. Many publications exist that focus on one aspect of harmonizing data from similar sensors: radiometric gain assessment (e.g., [17,18,19,20,21]), atmospheric correction (e.g., [22,23]), BRDF normalization (e.g., [24]) and SRF correction (e.g., [25,26,27,28,29]).
The relative importance in the consistency of the datasets for each of these corrections has not yet been explored. The evaluation of the improved consistency mainly focusses on the comparison of simultaneous acquisitions, simulations, or artificial data derived from e.g.hyperspectral images (e.g., [25]). General statistics such as RMSE and regression analysis are often used to evaluate the performance of the harmonization measure (e.g., [25,26,27]), whereas evaluation on a time series is not often performed (e.g., [15,23]). The evaluation is predominantly completed on TOC reflectance data or NDVI, but the impact of the harmonization measures on downstream products is not assessed.
For the Belharmony project, we considered the harmonization of a multi-sensor time series from the viewpoint of two applications: agricultural monitoring and vegetation monitoring for hydrological modelling in an urban context. The different harmonization measures were evaluated in their relative contribution to obtain more accurate and more consistent time series of NDVI and biophysical parameter fractions of absorbed photosynthetically active radiation (fAPAR), leaf area index (LAI), and fraction of vegetation cover (fCover) for these applications. We made use of the extensive set of EO data and in situ reference data which have been systematically collected over the BELAIR urban and agricultural sites. The BELAIR initiative [30], which started in 2013, aims to develop Belgian test sites, for which targeted EO data and other measurement results are collected on behalf of the Belgian and international research communities, and which may be used as calibration and validation sites for new EO missions, data and products.
In this paper, we present a bottom-up approach where we start from the L1 TOA level of four satellite sensors: Sentinel-2A&B (S2), Landsat-8, Deimos-1 (DMC) and the center camera of PROBA-V (PV). We analyzed different causes of differences and formulated corrections for them using well-established methods. Unlike HLS [15] and Sen2Like [16], we started the investigation with the L1 TOA reflectance data, as differences at L1 can strongly be amplified at L2 and should therefore already be corrected for at the L1 level. Next, the impact of SRF differences was analyzed and SRF adjustment functions were proposed. A common processing chain was used to generate L2 and L3 products such that the risk of biases introduced through different algorithms (e.g., atmospheric correction) or processors was significantly reduced. BRDF normalization was not included in the processing chain, because we focused on derived biophysical parameters that were retrieved from angular reflectances. Finally, we analyzed the added value of each of the corrections on the derived L3 datasets by means of two case studies. The scientific questions that are central to this research are: (i) What is the relative impact of the harmonization measures on the data per sensor? This question includes the analysis of the relative importance of radiometric gain correction, changing the atmospheric correction to a common method for all sensors, and SRF correction on the TOC reflectances, NDVI, and downstream products. (ii) What is the impact of the harmonization measures on the accuracy of the downstream products? (iii) What is the impact of these harmonization measures on the consistency of the multi-sensor L2/L3 time series? This includes the analysis of the data between sensors and over time.

2. Materials

2.1. Satellite Missions Considered in the Study

In this paper, we make use of data from 4 satellite sensors—Sentinel-2A&B (S2), Landsat-8, Deimos-1 (DMC) and the center camera of PROBA-V (PV)—in order to evaluate the impacts of the applied harmonization measures on data accuracy and time series consistency. Obviously, each sensor has specific spatial and spectral characteristics. Table 1 shows the spectral response curves for all sensors divided into three spectral ranges: visual blue, green and/or red bands (VIS), near-infrared bands (NIR) and short-wave infra-red bands (SWIR).

2.1.1. PROBA-V

The Project for on-board autonomy–VEGETATION (PROBA-V) is a small satellite designed to monitor global vegetation [31,32]. It was operational between November 2013 and June 2020. PROBA-V has a field of view of 102, resulting in a swath width of 2295 km. The optical design of PROBA-V consists of three cameras, of which the central camera (considered in this study) observes at a 100 m nominal resolution and covers a swath of approximately 517 km, which ensures global coverage every five days. PROBA-V observes in four spectral bands: blue (centered at 0.463 µm), red (0.655 µm), near infrared (NIR, 0.837 µm), and short-wave infrared (SWIR, 1.603 µm, see Table 1). Although the resolution of 100 m is not considered as high resolution, the sensors were included in the analysis because they were also used in the applications that we are targeting (e.g., LAI dynamics).
The standard products of PROBA-V were also compared to the Belharmony products: the PROBA-V 100 m C1 top-of-canopy reflectance data which are atmospherically corrected with SMAC A/C [33] by the PROBA-V processing facility. The available layers were TOC reflectance and NDVI [34]. BIOPARS were not distributed.

2.1.2. DEIMOS-1

The DEIMOS-1 (DMC) mission is fully owned and operated by Deimos Imaging (DMI, Spain) [35]. The payload is the Surrey linear imager−6 channel−22 m resolution optical imager (SLIM-6-22). The imager delivers observations in three spectral bands: red (centered at 0.549 μm), green (0.679 μm), and NIR (0.803 μm) with 22 m ground sample distance (GSD) at a nominal altitude of 663 km, with a 625 km swath.
Only L1 DMC data can be ordered. For the processing of the DMC data to L2 and L3 products, the in-house Morpho processing chain (which uses ATCOR [36] for atmospheric correction) has been used in the past. This dataset was used as the original data in the evaluation.

2.1.3. Sentinel-2

Sentinel-2 consists of a constellation of two operational satellites [37,38,39]. Sentinel-2A (S2A) and Sentinel-2B (S2B). Sentinel-2 carries the multi-spectral instrument (MSI) that samples in 13 spectral bands (Table 1): four bands at 10 m spatial resolution, six bands at 20 m, and three bands at 60 m. The orbital swath width is 290 km. An on-board calibration device (OBCD) is used for the radiometric calibration of Sentinel-2 MSI.
The standard products of Sentinel-2 used in the evaluation consist of Level 2A top-of-canopy (TOC) products, downloaded from the ESA hubs. These data are processed with Sen2Cor [40]. Terrascope [41] also provides the BIOPARS using the same neural network as used in Belharmony (see Section 3.1.4). This dataset was also used in the comparison.

2.1.4. Landsat-8

Landsat-8 (L8) has two imagers onboard: the operational land imager (OLI) and the thermal infrared sensor (TIRS) [42]. The OLI has nine spectral bands (Table 1) covering the blue to SWIR wavelengths with a spatial resolution of 30 m for bands 1–7 and 9. The spatial resolution for band 8 (panchromatic) is 15 m.
As original data, Landsat-8 land-surface reflectance products were ordered from USGS (e.g., produced with the Landsat-8 Surface Reflectance Code (LaSRC) [43]). The available layers were TOC reflectance.

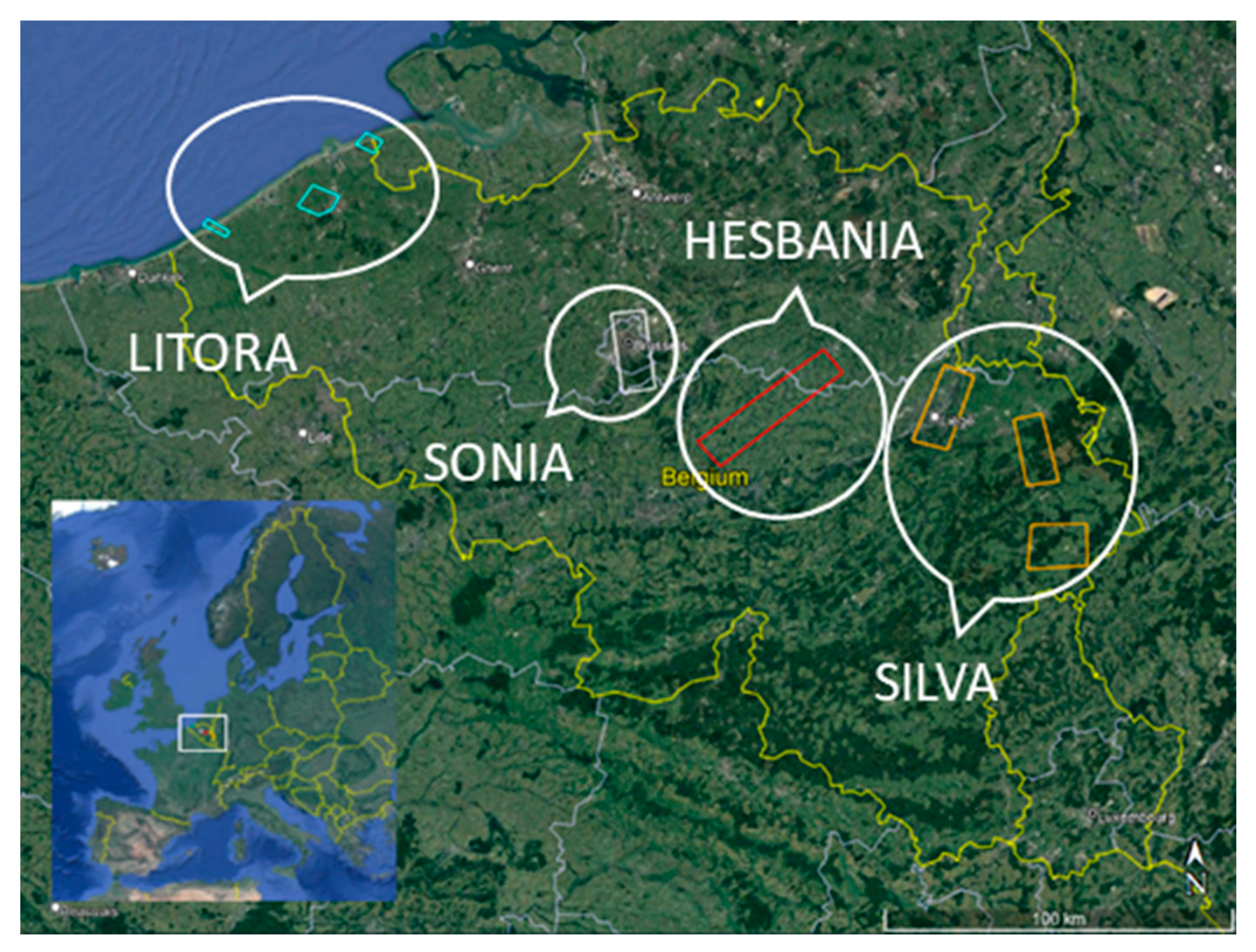
2.2. Case Sites

BELAIR is a Belgian STEREO initiative which was established to foster joint research and long-term data collection at 4 sites in Belgium, each with a different thematic focus. A variety of research projects use the data acquired on these sites. We focused on two case studies which required the combination of data from different sensors, one on HESBANIA, which covers the fruit and agricultural area between Sint-Truiden and Gembloux, and the other on the SONIA area, located in the urban area of Brussels (see Figure 1).

2.2.1. HESBANIA Agricultural Case Study

Time series of satellite-retrieved BIOPARs (fAPAR, LAI and fCover) are used for the monitoring of agricultural fields. The case study initial research focused on potato monitoring for the Belgian potato industry. Meanwhile, this research led to the WatchItGrow application [9], where farmers can obtain information on the state of the crop, its health status and development phase, predicted yield, and harvest date. This application requires sufficient cloud-free data over the entire growth season. Therefore, the L3 products from L8, S2 and DMC are combined to have a higher temporal frequency of the BIOPARs.
The BIOPARs are generated with the neural network (NN) approach of INRA-EMMAH. The neural network for S2 is publicly available [44], and is based on 8 input bands (8B_NN). Additional neural networks were trained by INRA-EMMAH for S2 (3B_NN), L8 (5B_NN, 3B_NN) and DMC (3B_NN) in the frame of WatchItGrow resulting in two sets of NN: (1) NN based on all relevant bands per sensor, and (2) NN based on green, red and NIR bands for each sensor (3B_NN). For S2, the 10 m bands are used for the 3B-NN, whereas the 8B_NN uses 8 spectral bands as input.
The available in situ data consists of FAPAR, LAI and fCover measures derived from hemispherical pictures since 2014, at several potato fields at regular intervals during the growth season. This reference dataset was used to assess and quantify the impact of the various harmonization measures on the accuracy of the final end products (i.e., the retrieved biophysical parameters).
The analysis was further extended at the parcel level for a large number of fields extracted from the parcel database of Flanders.

2.2.2. SONIA Urban Case Study

The SONIA site is located in the urban area of Brussels. Urban heat waves are predicted to occur more frequently with climate change. Urban vegetation and the linked evapotranspiration rate can play a mitigating role. However, a major challenge in urban hydrological modelling remains the mapping of vegetation dynamics and its role in hydrological processes, in particular interception storage and evapotranspiration. Conventional mapping of vegetation usually implies intensive labor and time-consuming field work.
Remote sensing data offers a great potential to characterize urban vegetation dynamics, but this requires long-term data with high spatial and spectral resolution to distinguish the urban landcover types, and frequent revisiting times to capture seasonal vegetation dynamics. Therefore, NDVI and LAI from a combination of sensors are used in this application.
At the SONIA site we collected in situ data for BELAIR campaigns in both 2015 and 2018. Spectral measurements of both homogeneous urban impervious and grass surfaces were taken. The LAI measurements of trees were taken with the Sunscan system (Type SS1-COM-R4). The Sunscan measures and compares incidents, transmits photosynthetically active radiation, and subsequently derives LAI [11]. The measurements were taken 1 m below the canopy in 8 compass directions of each studied tree. For each compass direction the Sunscan was positioned at a 1 m distance from the stem. We mostly restricted ourselves to the four most dominant species in Brussels: chestnut, linden, plane and maple, although some birch trees were also selected. During tree selection we made sure to have trees of different sizes, contexts (park vs street trees) and health. The in situ data for urban built-up, grass and trees were used as reference to evaluate the harmonization measures on the different satellite-derived biophysical parameters (NDVI and LAI).

3. Methods

Figure 2 shows the overall flowchart of the work performed and relates it to the different sections of the paper.

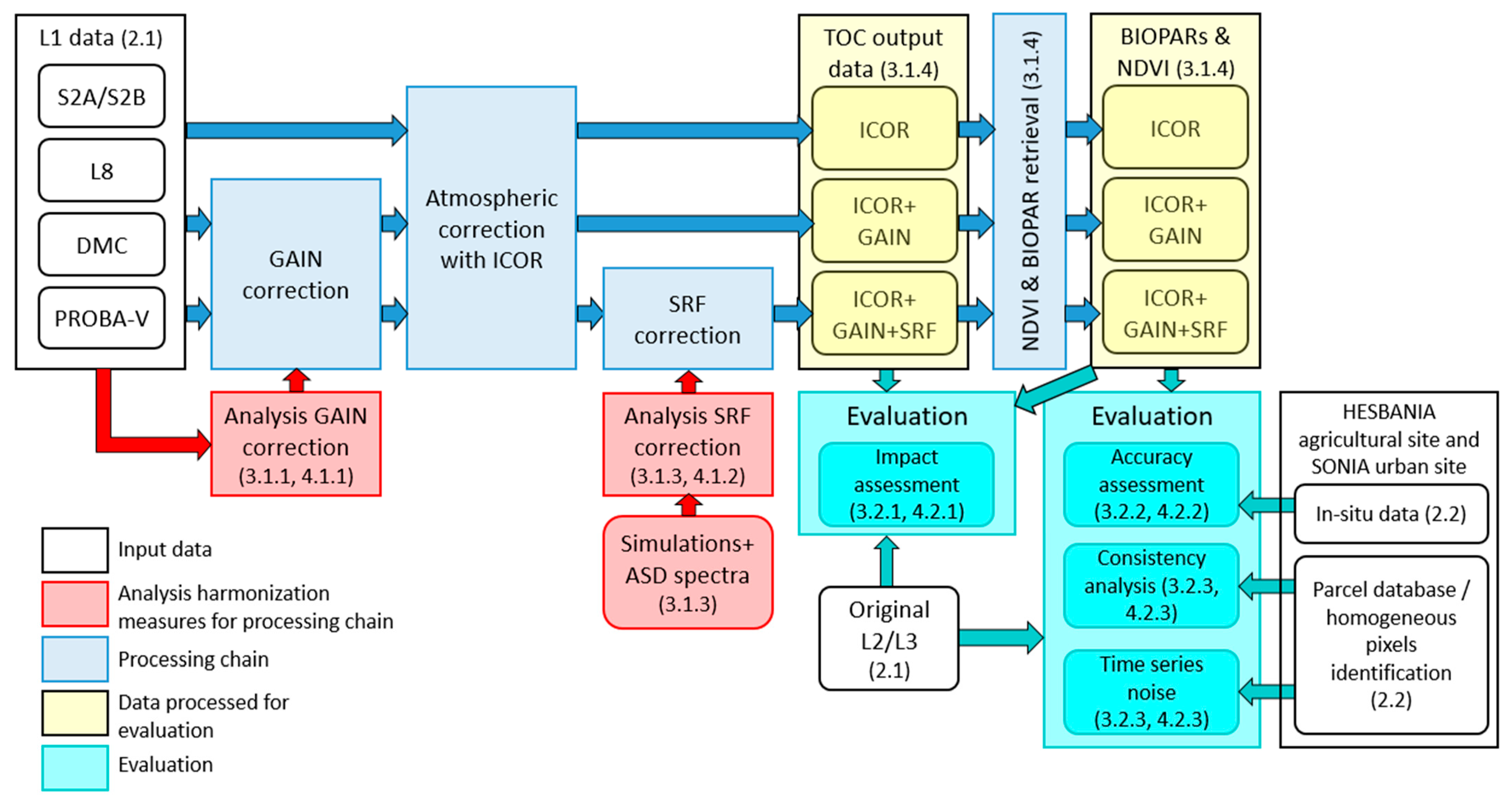
3.1. Harmonisation Approach

A bottom-up approach from L1 to L3 products, based on well-established methods, was used to identify the main sources of inconsistencies between data from S2, L8, DMC and PV, and to correct for them. First, the inter-satellite consistency was checked at L1 top-of-atmosphere (TOA) reflectances. Second, the same atmospheric correction method was used to process all datasets to top-of-Canopy (TOC) reflectances, and third, the difference in SRF was assessed between comparable bands of the four sensors. For the radiometric gain and SRF correction, S2A was used as reference because it has bands that overlap with the bands of the other sensors needed for NDVI and BIOPAR retrieval, and because it covers the longest period, and therefore overlaps with the period for which we had data from the other sensors.

3.1.1. L1 TOA Intercalibration

The aim was to verify the inter-satellite radiometric consistency of Landsat-8, Sentinel-2, DMC and PROBA-V (100 m) and to derive, if needed, temporally averaged gains to be applied to the L1 data for the improvement of the L1 inter-sensor consistency.
When assessing the consistency at L1, a distinction between low and high radiance levels is required (but often neglected) as, particularly at very low (and also extremely high) scene brightness, the radiometric response of the optical system might not be linear. To assess the L1 TOA consistency at medium to high radiance levels, the OSCAR Libya-4 approach [45] was used. Here, we only summarize the methodology as the methods and results have been described in detail in [46]. In the OSCAR Libya-4 approach [45], simulated TOA bidirectional reflectance factors (BRFs) define an absolute reference against which optical sensors can be cross-calibrated. The simulated TOA BRFs are calculated with 6SV with, as input, Rahman–Pinty–Verstraete (RPV) bi-directional reflectance distribution factor (BRDF) model parameters derived for the Libya-4 desert site, meteorological input data, and aerosol characterization data derived from Aerosol Robotic Network (AERONET) stations [47] in the Sahara region. The modeled TOA reflectance values were simulated for the actual illumination and observation geometry and by taking into account the actual spectral response curves of the sensors. The OSCAR Libya-4 calibration method was applied to S2A, S2B, LS8, DMC, and PROBA-V cloud-free TOA extractions over the Libya-4 region of interest.

3.1.2. Atmospheric Correction

For the atmospheric correction, the iCOR atmospheric correction method [48,49,50] was used. iCOR uses the Moderate-Resolution Atmospheric Radiance and Transmittance Model-5 “MODTRAN5” for radiative transfer calculations [51], and works with Look-Up Tables (LUT) to speed up the process. The validation of the method is part of ACIX I and II [50], and is not part of this study. The strength of iCOR is that (1) it is a surface adaptive correction method, i.e., the method identifies whether a pixel is water or land and applies a dedicated atmospheric correction, and (2) that implementations are available for all the different satellite missions used in this study.

3.1.3. Derivation of Spectral Adjustment Functions

Spectral response functions (SRFs) determine the position and width of a spectral band, and have been identified as one of the most important sources of uncertainty for the continuity and usability of multi-sensor datasets [52]. As no SRF corrections were available in the literature for all the sensors involved in this study with respect to S2A, the SRF corrections were estimated using well-established methods described below. The method included the estimation of a set of potential SRF correction functions, as well as the evaluation to select the best performing correction. In the analysis of the impact of difference in SRF, we deliberately neglected uncertainties caused by effects of the atmosphere, spatial sampling, or other sources of variability, and investigated the effect of the differences in SRF solely on the data.
The method to derive the SRF correction functions comprised 3 steps (see, e.g., [25,26]): (1) generate a large set of representative spectra, which were used to (2) calculate the sensor response using the SRFs of the concerned sensors. From these, (3) correction functions between the sensors relative to S2A were estimated.
The Coupled Soil-Leaf-Canopy (SLC) model of [53] was chosen as the radiative transfer model (RTM) to simulate the vegetation reflectances. The SLC model is a combination of the Hapke soil BRDF model, FLUSPECT and 4SAIL2 and is available on github (https://github.com/ajwdewit/pyslc, accessed on 20 November 2018). The definition of the input parameters was based on values found in the literature [25,26,54,55]. The illumination and observation geometry of the simulations varied between the minimum and the maximum values observed in the S2, L8, DMC and PROBA-V center camera images. The sampling scheme used Latin hypercube sampling. The simulations were completed with spectra of urban materials acquired with an ASD and/or from the hyperspectral sensor APEX. The representativeness of the total sample was iteratively evaluated by comparing the density of the entire set of spectra with the density of APEX measurements over the BELAIR sites and with global PROBA-V data over 1 year. A total set of 220,283 spectra were used to generate the sensor-specific responses for all the bands.
The different sets of correction functions found in the literature were used to correct for the difference in SRFs between sensors [25,26,27,28,56,57]. Appendix A lists all mathematical expressions of all functions that were used to model the differences in the SRF between a selected sensor and Sentinel-2A. This means that the bands of Landsat 8, DMC and PROBA-V center camera were adjusted to the spectral bands of Sentinel-2A. The corresponding bands are shown in Table 1. The naming of the S2 bands was used for all sensors when discussing the SRF correction functions.
The SRF correction functions were evaluated based on the following criteria:
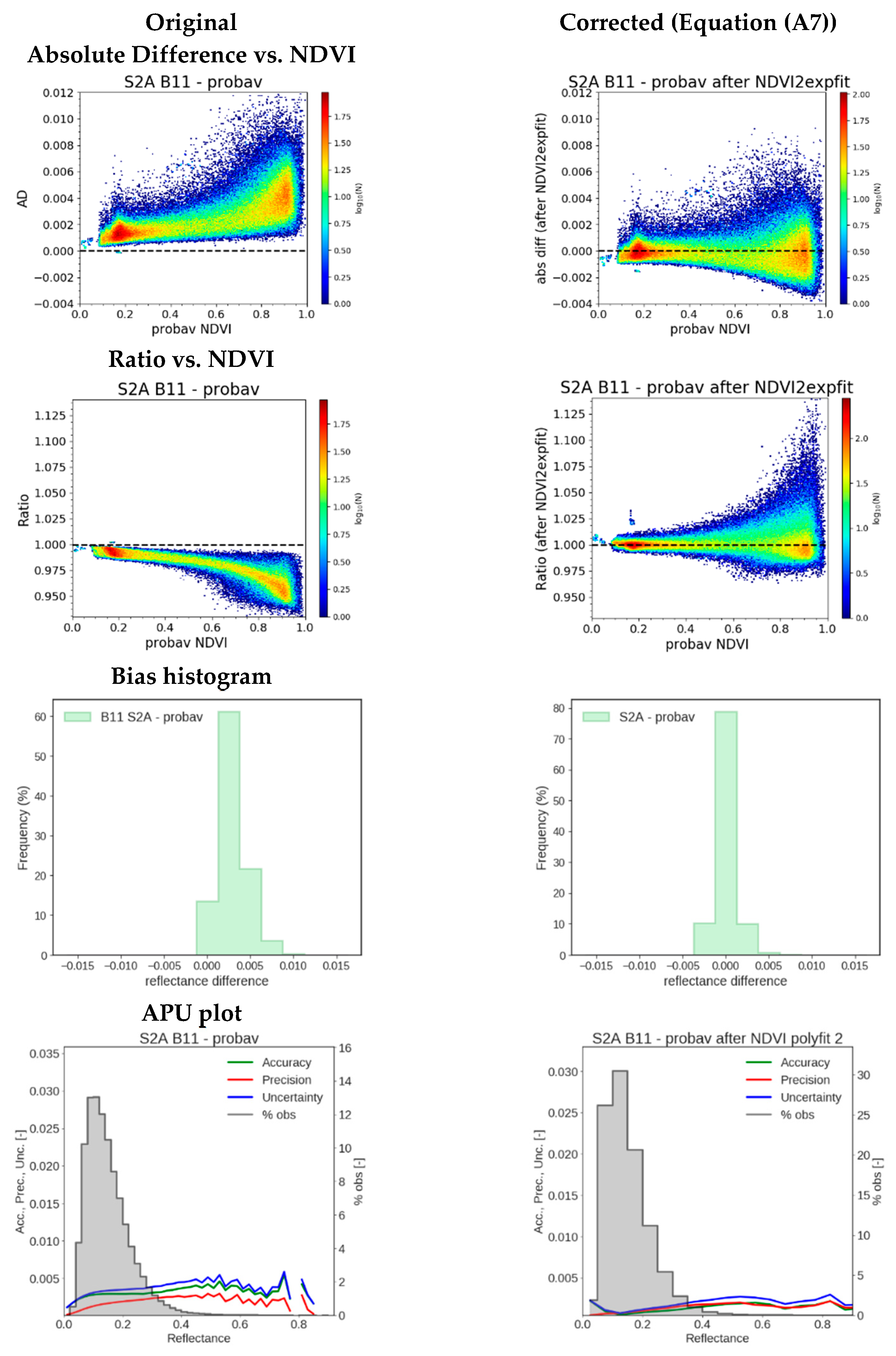
  • Shape of the correction function overlaid on a scatterplot of the data. This is only possible if the correction function is based on 1 input parameter, e.g., the NDVI;
  • Density scatterplots between the absolute difference (AD) of S1 and S2 (Y-axis) and the NDVI of S1 (X-axis). The majority of the simulations should be centered around an AD value of 0 and this should be stable for the entire NDVI range. Same plot for SBAF, which should be centered around an SBAF value of 1;
  • Bias histogram;
  • APU plot: the accuracy, precision and uncertainty should be smaller than compared to the comparison of the original data over the reflectance range.
All graphs, except the first one, were compared with the same plots generated with the original data.
The second step of the evaluation was performed on an independent dataset created from hyperspectral images from APEX. Two APEX images over the HESBANIA and SONIA site were selected and convoluted with the SRFs of the sensors under investigation to generate artificial images. The different correction functions were then applied to the artificial images of the respective sensors to create corrected artificial images. Then, we compared the bias histograms of the artificial images with and without spectral adjustment to the artificial S2A images. The result was the final selection of the SRF correction per band per sensor against S2A.

3.1.4. Generation of Enhanced L2 and L3 Products Using a Common Processing Chain

The generation of enhanced L2 and L3 PROBA-V, S2, L8 and DMC data consisted of (1) the applications of the cross-calibration gains to harmonize the TOA reflectance/radiance data against Sentinel-2A, (2) the use of the same atmospheric correction code for all sensors (iCOR), (3) the application of the spectral adjustment functions to correct for the difference in the SRFs between S2A and the other sensors, and (4) the derivation of the Normalized Difference Vegetation Index (NDVI) and biophysical indicators (BIOPARS) from the top-of-canopy (TOC) reflectance products using similar algorithms for the various missions. The biophysical indicators included: fAPAR, fCOVER and LAI. Note that the cloud mask delivered with the original data was used. The processing chain is visualized in Figure 3.
The generation of enhanced L2 and L3 time series was performed for the BELAIR study sites (see Section 2.2). In order to be able to assess the impact of the various “harmonization measures” separately, reprocessing of the datasets over the BELAIR sites was performed with and without the gain application (step 1) and with and without the application of the spectral adjustment functions (step 3) (see flowchart in Figure 3).
Next, the BIOPARs and NDVI were calculated. For S2 and L8, the BIOPARs were calculated with a 3B NN, but also 8B and 5B, respectively (see also Section 2.2.1). We combined the data into two groups:
  • 8B_BIOPAR: S2 8B_*, L8 5B_* and DMC 3B_*: all the available spectral information is used for the retrieval of the BIOPARs.
  • 3B_BIOPAR: S2 3B_*, L8 3B_* and DMC 3B_*: the same spectral information is used for the retrieval of the BIOPARs.
To compare the Belharmony-generated datasets to the nominal/original baseline level 2 products, these nominal baseline level 2 products over the BELAIR sites for the different missions were downloaded and/or processed (see Section 2.1 for description).
In the subsequent sections, we denote the different processing versions and levels as defined in Table 2.

3.2. Evaluation of the Enhanced L2 and L3 Time Series

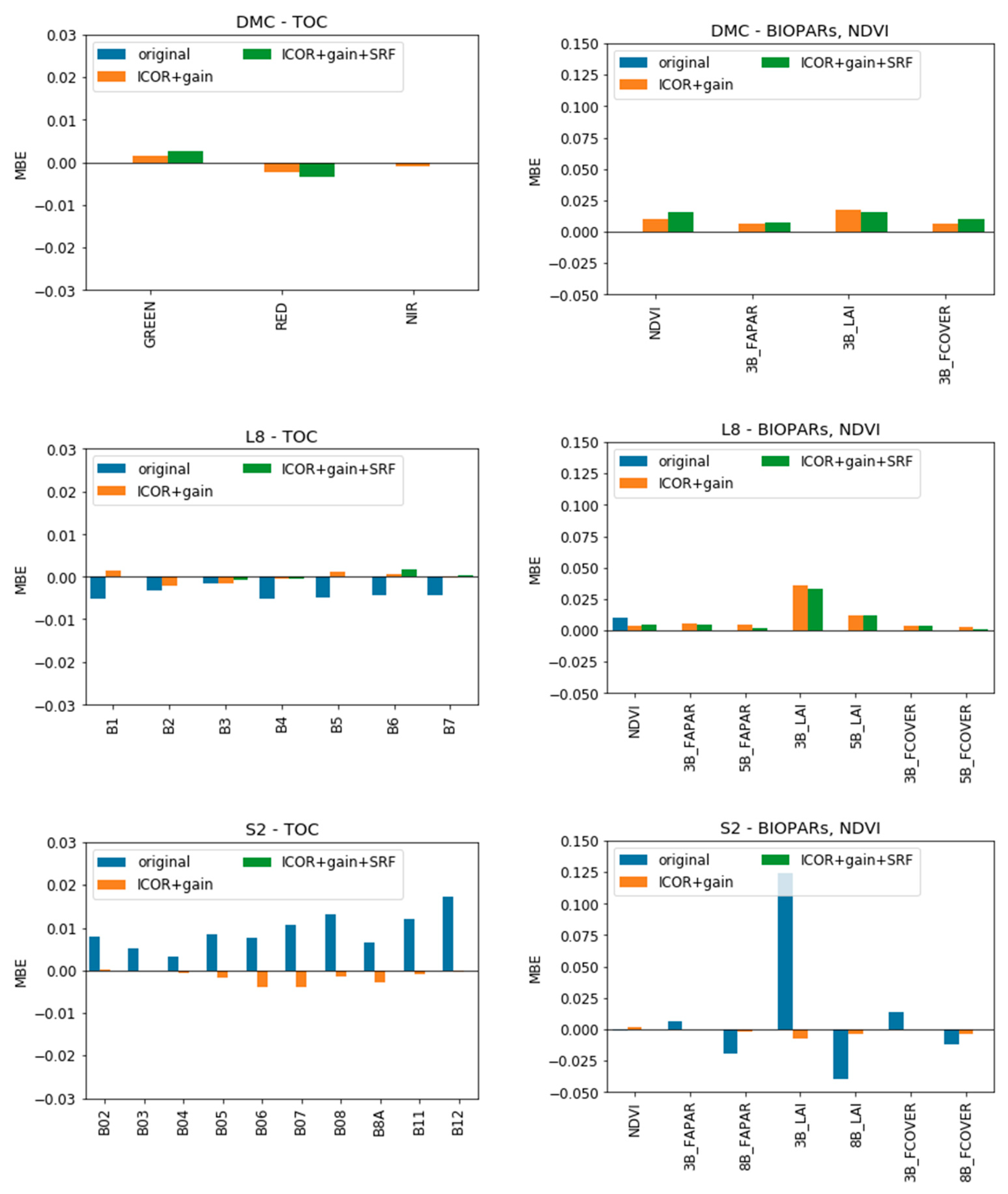
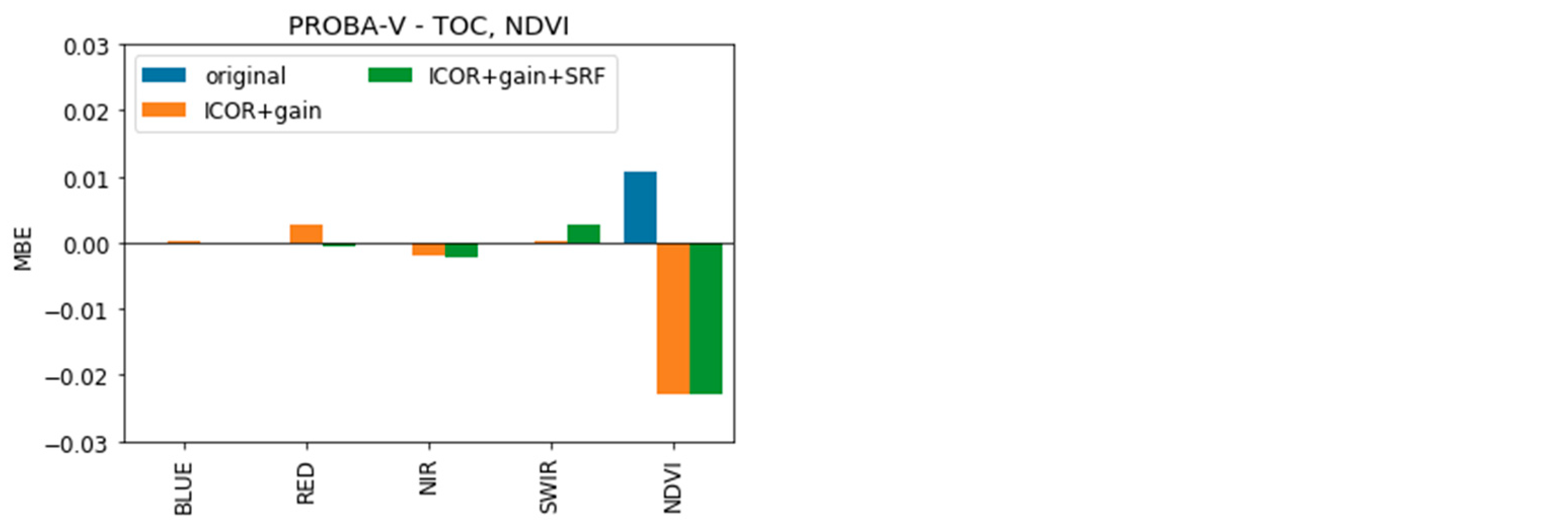
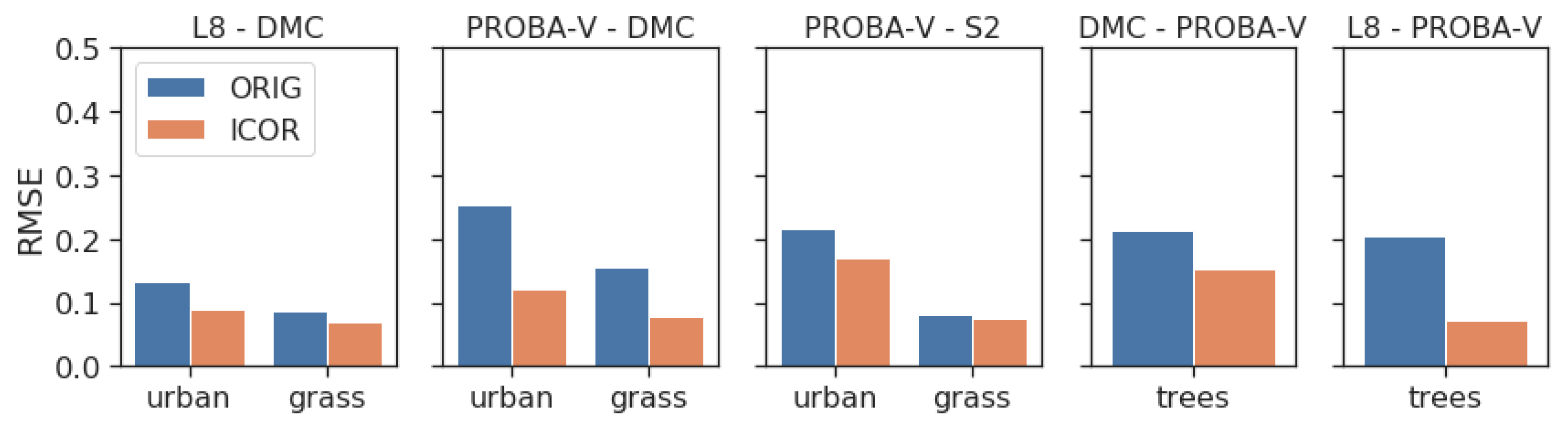
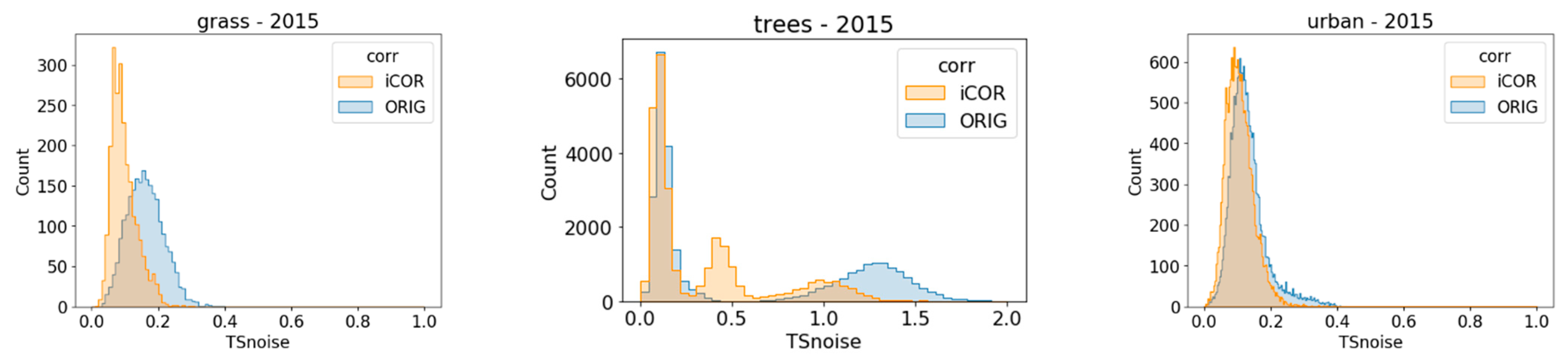
3.2.1. Impact Assessment of the Different Harmonization Measures per Sensor

In response to research question (i), the objective was to assess the magnitude of the impact of the different corrections applied on the data per sensor. The analysis was performed on the TOC reflectance bands, NDVI, and BIOPARs. ICOR was taken as the reference to compare to because standard TOC products are not available for all sensors (DMC). The following image pair sets per sensor were used:
  • ICOR—ICOR + gain
  • ICOR—ICOR + gain + SRF
  • ICOR—original
A large sample of paired images was taken from the time series of the different sensors. For S2 and L8, only 1 tile was processed. Every image was systematically subsampled taking every 10th pixel in a window size of 21 × 21 pixels to obtain a sufficiently large sample, while including the largest geographical extent and time period. For the S2 10 m layers, a subsample of the 21st pixel in a window size of 42 × 42 pixels was taken. Only cloud-free pixels were included in the overall sample. The mean bias between the samples with different corrections was calculated.

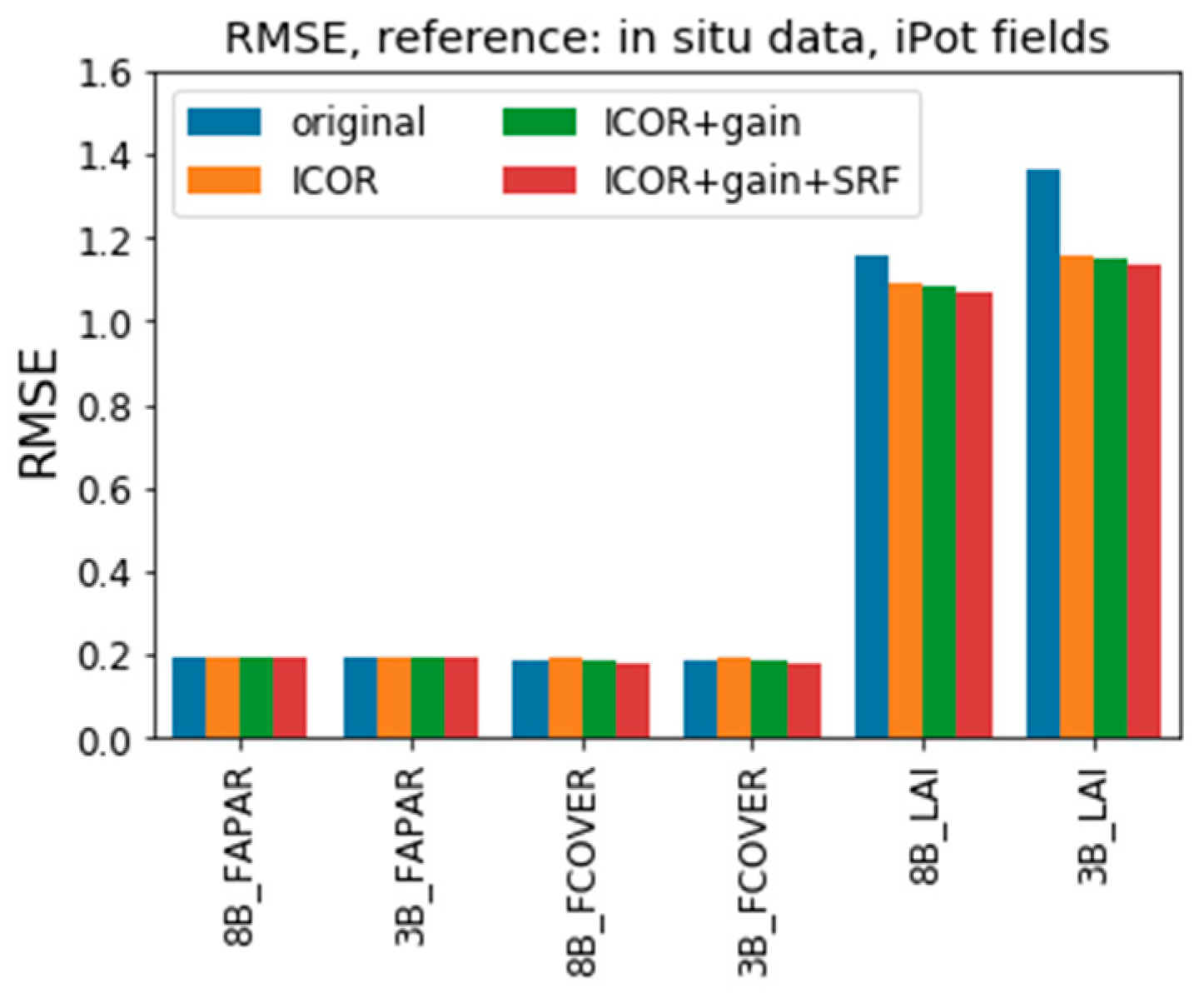
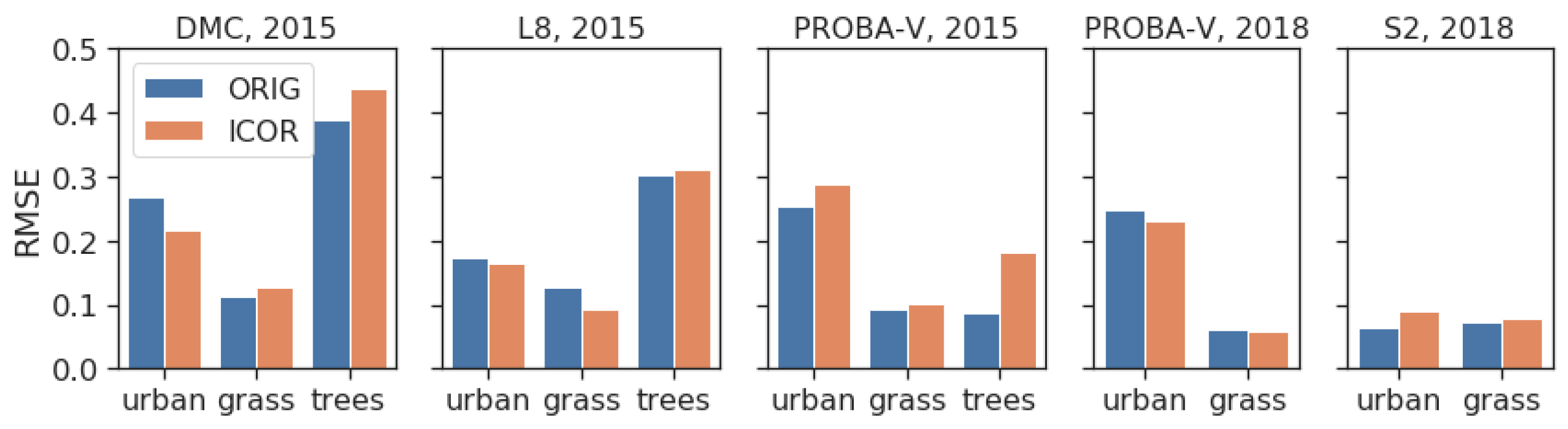
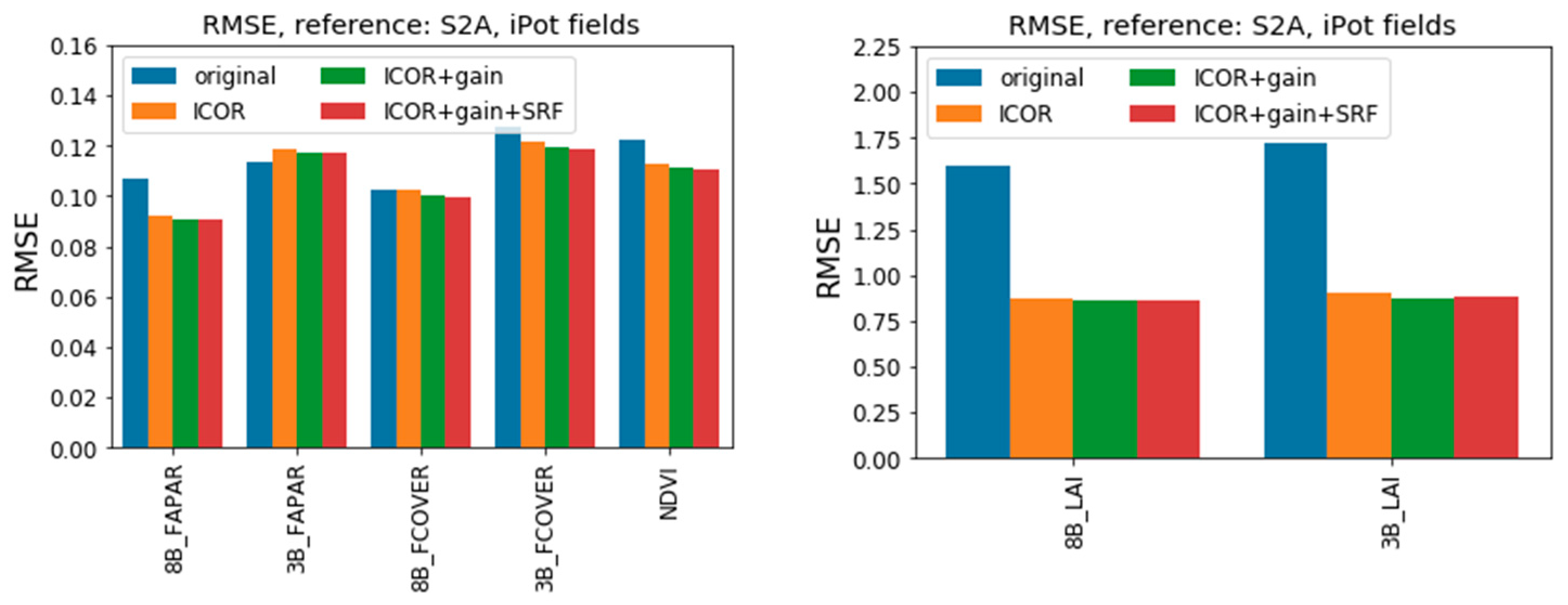
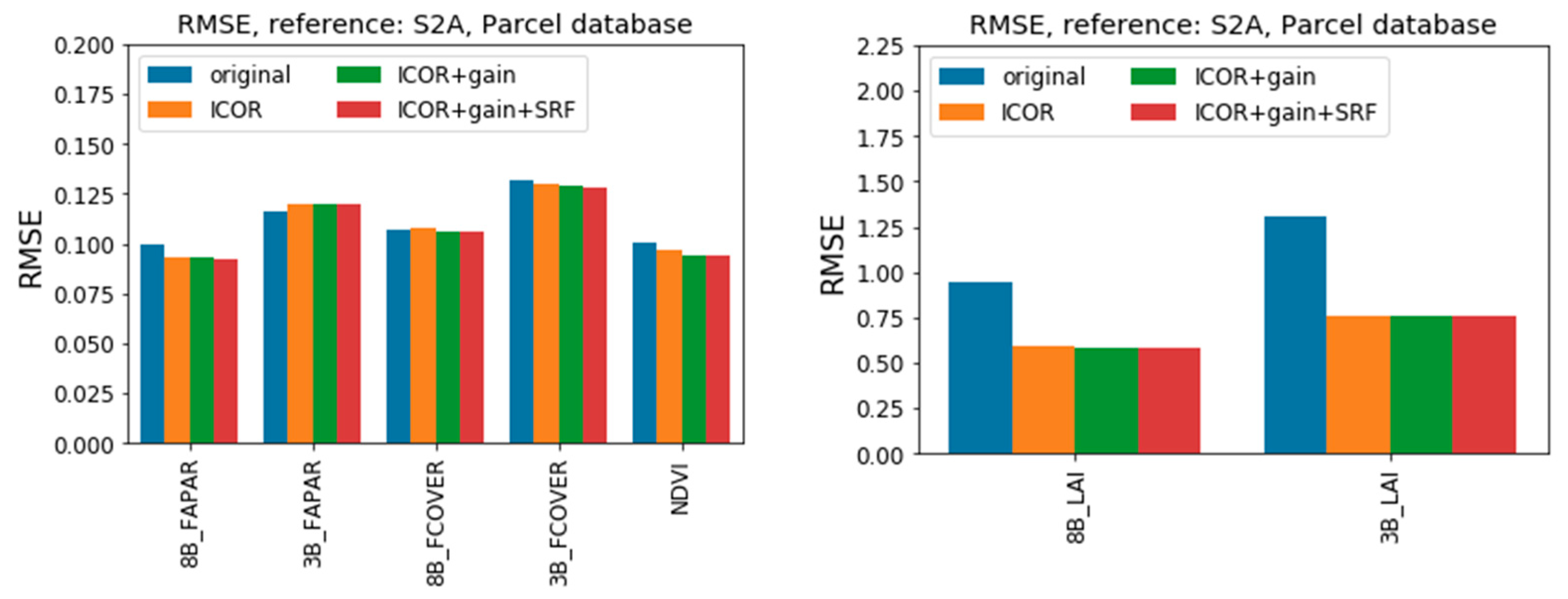
3.2.2. Accuracy Assessment of the Downstream Products against In Situ Data

To answer research question (ii), the processed data were validated against in situ data for the two case sites.
HESBANIA Case Study:
The objective was to assess the BIOPARs from a combination of sensors with in situ observations of FAPAR, FCOVER and LAI. The mean BIOPAR value of each image was calculated for each in situ field block.
This was performed per sensor, and for all corrections separately. For S2, the original data were also used. Then, the extracted time series were combined among sensors, resulting in 4 datasets per BIOPAR, as summarized in Table 3.
For all these combinations and corrections, a matchup dataset was created with the in situ data. A match between the in situ data and the BIOPAR data was found when the remote sensing data were not more than 3 days different than the in situ data, and when the area covered by the clear pixel within a block was at least 75% of the area defined by the shapefile. Scatterplots and statistics were calculated for all these datasets.
SONIA Case Study:
The objective was to evaluate the ICOR processing on satellite imagery in an urban context by analyzing the NDVI of urban built-up and grass areas, as well as LAI of trees from different sensors (S2, DMC, L8, and PV) compared to ground-truthing data available from the BELAIR 2015 and 2018 campaigns (see Table 4).

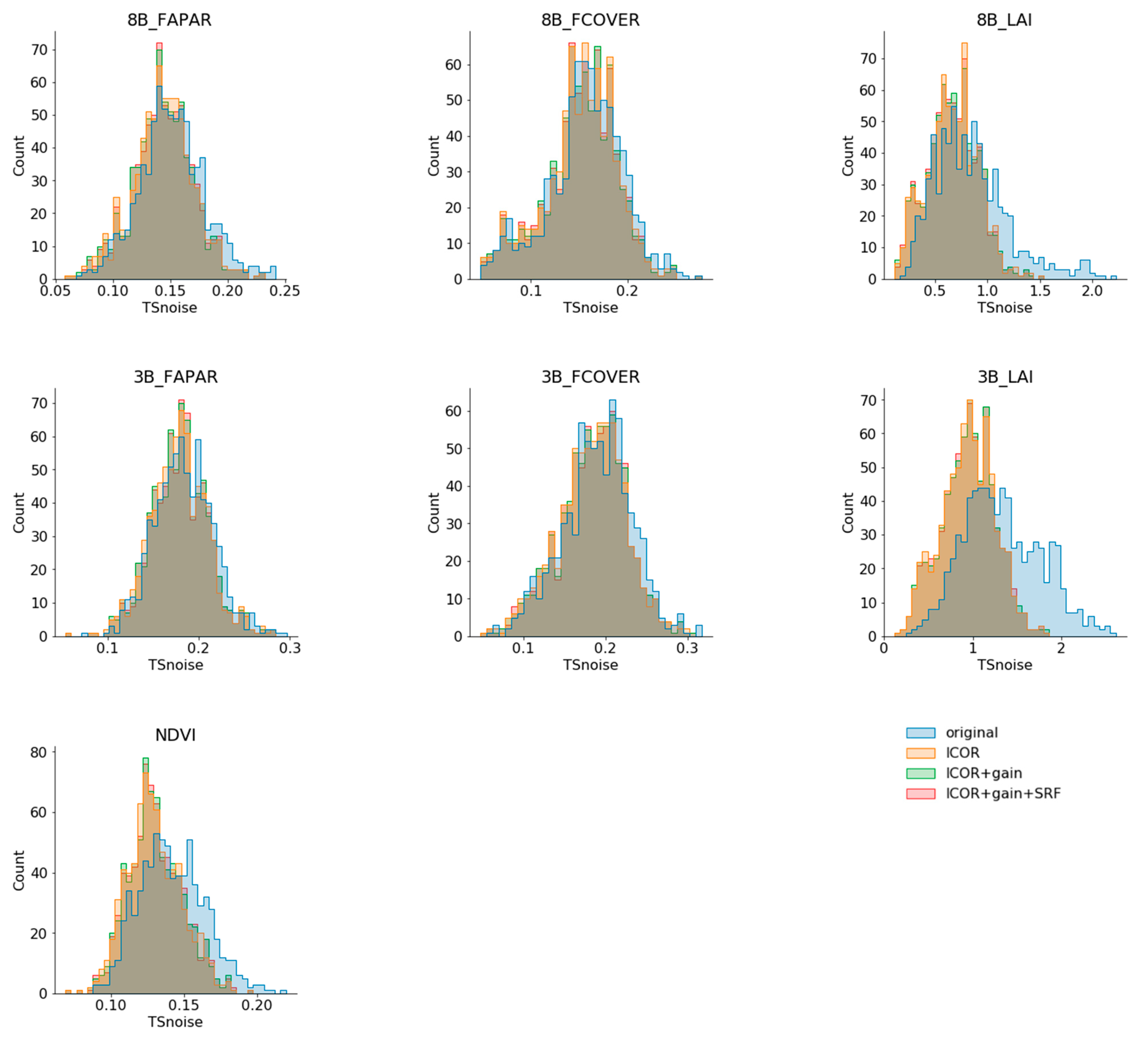
3.2.3. Consistency Analysis of the Downstream Products

Consistency Analysis with S2A as Reference

In this relative analysis, we compared S2A with data from other sensors that were corrected according to Table 3. This was performed for the in situ data, but also for a larger set of fields and sites. For HESBANIA, agricultural fields with a minimum size of 10 ha were selected from the parcel database of Flanders, resulting in a sample of 752 fields with various crop types. The mean value per field was calculated when min 75% of the field had cloud-free data. Again, match-ups were observations that had a maximum of 3 days difference. For SONIA, the consistency analysis was performed using homogeneous urban pixels (>90% of the pixel was covered by the specific landcover). Here, DMC was considered as a reference sensor in 2015 (because S2A was not yet operational) and S2A in 2018, to compare against the data from other sensors before and after ICOR processing.

Time Series Analyses

For all the sites in the parcel database over HESBANIA, the mean value per field was extracted for each BIOPAR and NDVI for each sensor and for each correction. These were then combined as specified in Table 3. The results were per-field time series composed of data from different sensors and with different corrections. For these time series, the temporal smoothness and the (relative) time series noise were calculated. The same is completed for the SONIA area, on time series of homogeneous pixels. Here, only ORIG and ICOR were compared.
The temporal smoothness δ [58] was evaluated by taking three consecutive observations and computing the absolute value of the difference between the center P(dn+1) and the corresponding linear interpolation between the two extremes P(dn) and P(dn+2), as follows:
δ ( d n ) = | P ( d n + 1 ) − P ( d n ) − P ( d n ) − P ( d n + 2 ) d n − d n + 2 ( d n − d n + 1 ) |
The output was a time series with smoothness values. The time series noise was then estimated by averaging δ over the time series [59]:
N o i s e = ∑ n = 1 N − 2 δ ( d n ) 2 N − 2
Output was a single value per field and per correction type. Histograms showing the distribution over all fields were plotted per correction type.

4. Results

4.1. Harmonization Approach Results

4.1.1. L1 TOA Intercalibration

The results are discussed relative to S2A. According to the Libya-4 OSCAR results, L8, PV, S2B, and DMC agree with S2A to within ±2% for comparable spectral bands, with the exception of the DMC green band, which was approximately 3.5% lower than S2A (Table 5). Deviations observed between S2A and S2B were of the same magnitude as those observed between S2A and the other missions. For most bands, S2A was slightly brighter than S2B, which is in line with results reported by [17,20,21,60]. These values were applied as gain correction in the processing.

4.1.2. Spectral Response Adjustment Functions

The SRF corrections were estimated based on the simulated dataset completed with hyperspectral ground measurements (see Section 3.1.2). The evaluation of the SRF correction functions was performed by applying the correction functions on the same dataset and on artificial images derived from APEX data (see Section 3.1.2 for full description).
Selection of the SRF correction function per band and per sensor was performed by interpreting all the plots that were generated in the evaluation process on the simulations. Examples of detailed plots were provided for the SWIR band of PV in Figure 3. The absolute difference between the original simulations of PV and S2A showed an almost linear trend with NDVI, which was removed after the SRF correction. The ratio between both bands in the function of NDVI showed a non-linear trend that was also removed after SRF correction. The bias histogram was also narrower and the APU plot showed lower values of accuracy, precision, and uncertainty over the reflectance range. This all indicates a higher agreement between B11 of S2A and the corresponding SWIR band of PROBA-V.
Figure 4 shows the bias histogram before and after the same SRF correction applied on the artificial data derived from APEX images. The bias histograms clearly demonstrate the improved correspondence between the data of the two SWIR bands.
The selected correction functions for all sensors compared to S2A are summarized in Table 6. For a number of sensor/band combinations, no correction was retained. This was either because both bands were already so similar that no improvement was obtained (see Table 1)—e.g., L8 B5 compared to S2 B8A, and DMC B3 compared to S2 B8—or because the correction could only correct for a very small part of the difference, and the remaining difference was still high. This was the case when comparing S2 B8 (broad) with L8 B5 (narrow), and S2 B8A (narrow) with DMC B3 (broad) (see also Table 1). Except for these band combinations, all other corrections functions were applied on the data for further analysis.

4.2. Evaluation of the Enhanced L2 and L3 Time Series

4.2.1. Impact Assessment of the Different Harmonization Measures per Sensor

In the impact assessment of the different corrections per sensor, we can see that the largest difference between the TOC reflectance datasets was obtained when applying the same atmospheric correction method compared to using different methods for L8 and S2 (Figure 5). The magnitude of the difference depends on the spectral band. L8 had a negative mean bias error (MBE) for all bands when comparing original data with ICOR processing, meaning that TOC reflectances after ICOR processing were higher. The opposite was true for S2. For DMC, this was not assessed, because only L1 are publicly available, and for PV it was only assessed for NDVI, and here the impact was not the largest. The gain corrections were correctly reflected at the TOC reflectance level. A positive (negative) % difference to S2A in the gain correction resulted in a negative (positive) MBE between the ICOR and ICOR+gain datasets. The magnitude of the % difference was also reflected in the MBE, although not linearly. The magnitude of the MBE when adding the SRF corrections was the smallest for all bands and sensors. Here, the ICOR data were compared with data having the gain and SRF corrections both combined. For DMC, this resulted in a larger difference with the ICOR dataset. For other sensors, the difference with the ICOR dataset was smaller, meaning that the gain and SRF corrections partially cancelled each other out.
The most interesting part of the analysis was how these corrections were translated into the derived parameters NDVI, LAI, FAPAR and FCOVER. For DMC, the MBE was positive for all parameters. The magnitude of the impact of the gain correction was largest for LAI (0.22), but this was because LAI was within the range of (0, 8) instead of (0, 1) for the other parameters. The impact of the gain correction on FAPAR and FCOVER was <0.01, and 0.015 for NDVI, which was overall very small. Adding the SRF correction resulted in a larger difference with the ICOR dataset for all parameters, except for LAI. For all derived parameters of L8, the MBE was positive after gain correction when compared to the ICOR dataset. Again, the magnitude was largest for LAI for the reason explained before. The MBE was higher for the parameters derived with the 3B NN than with the 5B NN. The 3B NN took only bands B3, B4 and B5 as input, which had the largest gain correction among the L8 bands. The 5B NN also included B6 and B7, for which the gain correction was almost negligible. Adding the SRF to the gain correction resulted for most parameters in a smaller difference with the ICOR dataset, except for NDVI and 5B_LAI. The largest difference for the NDVI was observed when comparing the original and the ICOR NDVI. The BIOPARs were not calculated based on the original L8 data. For S2, the largest difference in the derived parameters was again found when comparing the original with the ICOR data. There was an opposite impact for the parameters derived with the 3B_NN (MBE > 0) than with the 8B_NN (MBE < 0). The impact of the gain correction on S2-derived parameters resulted in a small difference >−0.01 for FAPAR and FCOVER. SRF corrections were not applied on S2, as S2A was used as reference and S2B was almost identical. For PROBA-V, the comparison with the original data was only assessed on the NDVI, which resulted in a positive MBE, meaning that the NDVI with iCOR processing was lower. The largest impact of the gain correction was observed for PROBA-V NDVI, with a difference >−0.02 after gain correction. For this sensor, the red and NIR bands had opposite gain correction, which was amplified in the NDVI. The impact of the SRF correction on the NDVI was negligible.

4.2.2. Accuracy Assessment of the Downstream Products against In Situ Data

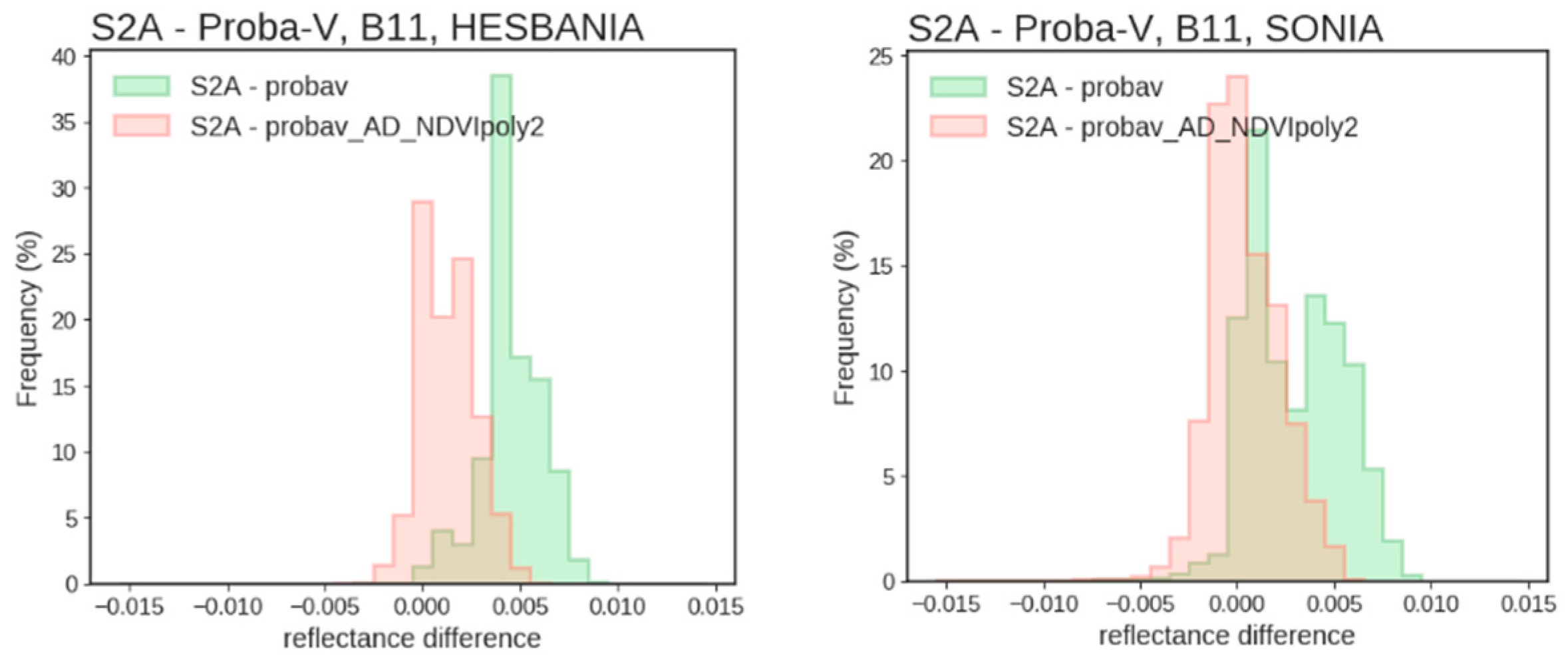
HESBANIA 

The BIOPARs derived with the different harmonization measures were validated against in situ data for a number of fields. Figure 6 shows that, for all BIOPARs, the various corrections resulted in small differences in uncertainty (RMSE) in comparison with in situ data. In general, there was a small increase in accuracy when going from ICOR, then added gain, and then added SRF corrections, except for LAI. The application of the ICOR atmospheric correction had the largest impact on increasing the accuracy of the LAI retrieval. The RMSE decreased very little when adding corrections. The harmonization measures only had a small influence on accuracy and uncertainty.

SONIA 

Figure 7 shows the results per sensor and per year for the SONIA area. Here, only the impact of using the same atmospheric correction compared to the original data was investigated, since it was demonstrated that the impact of the other harmonization measures was smaller (see Section 4.2.1), which was also confirmed for the HESBANIA case. The RMSE for the class Trees is always slightly higher when using ICOR for atmospheric correction. For the classes Urban and Grass, the results depend on the sensor, but also on the year. Overall, the difference in RMSE was small for most data analyzed. We can conclude that a higher absolute accuracy was not obtained when harmonizing the atmospheric correction.

4.2.3. Consistency Analysis of the Downstream Products

Consistency Analysis with S2A as Reference

Despite the limited impact on accuracy, the harmonization measures had, as primary goal, a better consistency between the datasets from different sensors. Therefore, the data extracted for the in situ fields from DMC, L8, S2B and Proba-V were also compared to S2A, here considered as reference sensor. Matchups between all available observations were selected in the same way as for the in situ data, i.e., observations with a maximum of 3 days difference. The RMSE is shown in Figure 8. For LAI, the impact of using the same atmospheric correction method results in a smaller RMSE compared to using the original data, indicating a higher consistency. The other harmonization measures showed little improvement. For the other BIOPARs and NDVI, the RMSE decreased slightly when adding harmonization measures. Using the same atmospheric correction resulted in a smaller RMSE for most of the BIOPARs, although the impact had a smaller magnitude compared to LAI. This was not only because the range of values was larger for LAI, as the RMSE was reduced by a factor 2.
This analysis was repeated on a large sample using the parcel database for the HESBANIA site, again taking S2A as reference in the comparison. The results are shown in Figure 9. The MBE had the largest magnitude when comparing the S2A with the original data of the other sensors, except for NDVI. The impact of the different harmonization measures was smaller and did not always result in a smaller RMSE, e.g., for FAPAR. For FCOVER, the RMSE was the smallest when applying all corrections. The impact of the harmonization measures was negligible for LAI, except for the application of the same atmospheric correction, which had a large impact on the RMSE.
Figure 10 shows the RMSE between match-ups of the SONIA data of two sensors for the in situ sites, for both the original data and the ICOR data. The graphs clearly demonstrate that the RMSE between the sensor data decreases when applying the same atmospheric correction method, resulting in a higher consistency between the data of the different sensors.

Time Series Analyses

The datasets extracted using the parcel database were also used to analyze the time series noise (TSnoise) of the time series resulting from combining the data from the different sensors, before and after the harmonization measures (see Table 3). It was expected that the TSnoise would decrease with higher consistency between the data of the sensors. Figure 11 shows the results for the HESBANIA site. All BIOPARs and NDVI showed a higher TSnoise for the original dataset. The difference was the largest for LAI and NDVI. The impact of using the same atmospheric correction and the other harmonization measures was hard to discern. The results suggest that the amount of noise in the time series decreased when applying the same atmospheric correction method on all datasets.
At the SONIA site, TSnoise decreased for the dataset after ICOR processing (Figure 12). The difference was the smallest for urban built-up areas and smaller for NDVI (grass and urban) than LAI (trees). The results showed that by using the same atmospheric correction, the amount of noise in a time series was reduced in urban areas.

5. Discussion

The Belharmony study was defined as a bottom-up approach from L1 to L3 products to improve consistency between S2A, S2B, L8, DMC and PV center camera, and also to analyze the relative importance of the various harmonization measures on downstream products for two applications (see Figure 3 for overall scheme). In the study, we took S2A bands as a reference to which the differences in radiometric calibration and differences in SRF of the comparable bands of other sensors were corrected. In addition, a common processing chain was developed for all sensors including the application of the same atmospheric correction for all sensors. The different steps of the harmonization process were then evaluated on two case studies in Belgium: on an agricultural site, HESBANIA, and an urban site, SONIA.
The results of the gain correction are shown and discussed in detail in [46]. In summary, we found inter-sensor deviations between comparable bands to be within the ±2% uncertainty range of the method applied, except for the DMC green band, where a difference of −3.5% was found. Similar results for S2 and L8 were obtained in [17,18,60]. The results indicate that, with the exception of the green DMC band, a high consistency already exists between the different sensors. Nevertheless, the small differences were applied on the datasets anyway and further assessed.
Next, correction functions for the differences in SRF were established. A large number of simulations with the addition of a set of urban spectra were used to model the differences in SRF with respect to the comparable band in S2A. Various correction functions were also estimated and evaluated on an independent dataset (APEX images). As in [28], the optimal correction differed per sensor combination and per band. Comparing the obtained results with correction functions published in the literature is difficult, because the reference was often different (e.g., MODIS/Aqua in [28]), or because not all sensors were part of the study, e.g., [25] only includes S2 and none of the other sensors discussed here. For a number of sensor/band combinations, no correction was retained. This was either because both bands were already so similar that no improvement was obtained, or because the correction did not yield a significant improvement. Except for these band combinations, all other corrections functions were applied on the data for further analysis.
After processing a large set of data, different analyses were performed to evaluate the performance of the harmonization measures. These included: (1) impact assessment of the various harmonization measures on the data per sensor; (2) accuracy assessment of the downstream products using in situ data; (3) comparison of match-ups between these products from different sensors; and (4) analyses of the noise in time series generated on the combination of the different sensors.
In the impact assessment of the different corrections at TOC reflectance level, we saw that the largest difference between comparable bands of the sensors was obtained when applying the same atmospheric correction instead of comparing the original data with each individual pre-processing choice. The same approach was followed in [22] in order to increase the consistency between NOAA-AVHRR sensors and SPOT-VEGETATION. In that study, all atmospheric input data were taken from external sources and the method for atmospheric correction was the same. In the current study, the AOT was derived from the images themselves; hence, these were not the same, but estimated in a similar way. The atmospheric correction, as such, was not evaluated in this study, but is part of ACIX I and II [50]. The impact of the gain and SRF correction on the TOC reflectances were, in general, much smaller. Next, we looked at how these differences at TOC reflectance level translated into the derived parameters, NDVI and BIOPARs. Again, the difference was the highest when comparing the original data with ICOR data. Adding the gain and SRF corrections resulted in smaller differences with respect to the ICOR dataset.
The added value of the different harmonization measures was further investigated for two distinct case study areas, in an agricultural (HESBANIA) and urban (SONIA) landscape. First, the obtained NDVI and BIOPARs generated with different corrections were validated against in situ data for these areas. The various harmonization measures did not necessarily lead to higher accuracy or precision. For LAI in HESBANIA, an agricultural site, accuracy was higher when applying the same atmospheric correction to all data sources compared to the original data. For FAPAR and FCOVER, there was only a very small difference in accuracy. For the SONIA urban site, the RMSE was higher after using the same atmospheric correction for most cases. Validation of the atmospheric correction was performed in ACIX I and II. The results of ACIX I are available in Doxani, which also includes the methods used for the original data (Sen2Cor for S2, LaSRC for L8). They demonstrate that iCOR performs almost equally as well as LaSRC for L8. On the other hand, Sen2Cor performs better than iCOR for S2. Meanwhile, some changes were made to iCOR, and these results were evaluated in ACIX II, but this study has not yet been published. The choice of iCOR was made because it can be applied to a suit of sensors.
Although using iCOR did not improve the accuracy with respect to in situ data, the consistency between the datasets improved. This was demonstrated first by creating match-ups between data from one sensor and from the other sensors for the case study sites and comparing these. For both case studies, a higher consistency was found after using the same atmospheric correction. The impact of the gain and SRF corrections lead, in most cases, to a slightly higher consistency, except for FAPAR. This analysis was repeated for a large number of agricultural fields (HESBANIA) and the same results were obtained. Second, the distribution of the time series noise for the same fields in HESBANIA and for homogeneous pixels in SONIA were assessed, which confirmed the previous results that using the same atmospheric correction had the largest contribution to a better consistency between the datasets. Applying the gain and SRF correction did not result in less noise in the time series. Although the two case sites covered different land cover types, similar results for the analysis were obtained.
Accurate calibrated instruments are a prerequisite for interoperability between sensors. The reason why the gain correction did not improve the consistency is because the sensors were already well calibrated [61,62,63,64] and the remaining difference estimated was small and within the uncertainty range of the method used [60]. The results obtained demonstrated the added value of correcting for SRF differences on a controlled dataset based on APEX images. Here, the only difference between the dataset was the SRF used to create artificial images. The added value of the SRF correction was not confirmed on the evaluation with the real sensor data. This could be because the impact was smaller than the differences that were induced by other sources such as BRDF effects in the images. The BIOPARs, however, were retrieved while considering the observation and illumination geometry, and the output should therefore already account for anisotropy effects. This was not the case for the NDVI. BRDF effects were not considered in the study and are a source of difference that have to be accounted for, as well for the generation of fully harmonized multi-mission time series [65]. Although satellites such as S2 or L8 acquire images close to nadir, they are not likely to observe the same target over a long period of time with a unique Sun-target-sensor geometry configuration. The latter changes according to day of the year, scanning strategy, and stage in the life of the mission. Thus, an inconsistent sampling of the BRDF in time and space will inevitably introduce directional effects that can hamper with the interpretation of observed temporal changes in surface reflectance time series. Thus, to properly disentangle changes due to vegetation from those simply introduced by directional effects, the BRDF of a target must be modeled. By approximating the anisotropy of a target with a BRDF model (e.g., [66,67]), we can normalize (adjust) all surface reflectance observations to a common Sun-sensor geometry in order to derive consistent and smooth surface reflectance time series.

6. Conclusions

To conclude, we recall the research questions that were formulated. What is the relative impact of the harmonization measures on the data per sensor? The relative impact of the harmonization measures differed from sensor to sensor and from band to band. In general, the impact of changing the atmospheric correction to ICOR was the largest. The gain and SRF corrections had smaller impacts, and sometimes had opposite signs. A similar impact was observed for the downstream BIOPAR products.
What is the impact of the harmonization measures on the accuracy of the downstream products? The harmonization measures did not necessarily lead to a higher accuracy of the products.
What is the impact of all these harmonization measures on the consistency of the multi-sensor L2/L3 time series? Using the same atmospheric correction method especially resulted in a better agreement between the NDVI and BIOPARs, and the noise in the time series was reduced. Accurate calibration of the sensors was, of course, also important, and the fact that we did not find an added value in applying a gain correction suggests that the sensors were already closely calibrated. The SRF correction impact could not be demonstrated, probably because other sources of differences were not taken into account, such as BRDF correction.

Author Contributions

E.S. wrote the paper and the revised paper, designed and performed the SRF corrections, the impact analysis and the HESBANIA case study evaluation. S.S. coordinated the project, performed the radiometric calibration activities and contributed to the paper. C.W. performed the SONIA case study analysis and contributed to the paper and the revised paper. B.V. supervised the SONIA case study analysis and contributed in the revision of the paper, and D.W. implemented the processing chain and processed all data. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Belgian Science Policy Office (Belspo) through the Stereo program (Belharmony project) (Contract number: NR SR/00/356).

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analysis, or interpretation of data; in the drafting of the manuscript, or in the decision to publish the results.

Appendix A. Mathematical Expressions of SRF Correction Functions

Linear model [56]:
ρ ¯ λ , r e f = a + b · ρ ¯ λ , t a r
Multi-linear regression models (e.g., [26]). The model uses two input bands, the target band (to be corrected band) and an additional band. When NIR is the target band, then red is the additional band, and when red or another band is the target band, then NIR is the additional band:
ρ ¯ λ , ( r e d , n i r ) , r e f = β 1 ρ ¯ r e d , t a r + β 2 ρ ¯ n i r , t a r + β 3 N D V I + β 3 N D V I 2 + ϵ
ρ ¯ λ , ( o t h e r   b a n d ) , r e f = β 1 ρ ¯ o t h e r   b a n d , t a r + β 2 ρ ¯ n i r , t a r + β 3 N D V I + β 3 N D V I 2 + ϵ
ρ ¯ λ , ( g , r e d , n i r ) , r e f = β 1 ρ ¯ ( g , r e d ) , t a r + β 2 ρ ¯ n i r , t a r + β 3 ( ρ ¯ ( g , r e d ) , t a r · ρ ¯ n i r , t a r ) + β 4 ( ρ ¯ ( g , r e d ) , t a r ) 2 + β 5 ( ρ ¯ ( n i r ) , t a r ) 2 + ϵ
ρ ¯ λ , ( g , o t h e r   b a n d , n i r ) , r e f = β 1 ρ ¯ ( g , o t h e r   b a n d ) , t a r + β 2 ρ ¯ n i r , t a r + β 3 ( ρ ¯ ( g , o t h e r   b a n d ) , t a r · ρ ¯ n i r , t a r ) + β 4 ( ρ ¯ ( g o t h e r   b a n d d ) , t a r ) 2 + β 5 ( ρ ¯ ( n i r ) , t a r ) 2 + ϵ
Quadratic model of the Spectral Band Adjustment Factor (SBAF) [28], the Absolute Difference (AD) or the Relative Difference (RD) [27]:
S B A F = ρ ¯ λ , r e f ρ ¯ λ , t a r = a + b · N D V I + c · N D V I 2
A D = ρ ¯ λ , t a r − ρ ¯ λ , r e f = a + b · N D V I + c · N D V I 2
R D = ρ ¯ λ , t a r − ρ ¯ λ , r e f ρ ¯ λ , t a r · 100 = a + b · N D V I + c · N D V I 2
Exponential function of the SBAF, AD or RD [28]:
S B A F = a · e b · N D V I + c · e d · N D V I
A D = a · e b · N D V I + c · e d · N D V I
R D = a · e b · N D V I + c · e d · N D V I

References

  1. Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest Monitoring Using Landsat Time Series Data: A Review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
  2. Gao, F.; Anderson, M.; Daughtry, C.; Johnson, D. Assessing the Variability of Corn and Soybean Yields in Central Iowa Using High Spatiotemporal Resolution Multi-Satellite Imagery. Remote Sens. 2018, 10, 1489. [Google Scholar] [CrossRef] [Green Version]
  3. Segarra, J.; Buchaillot, M.L.; Araus, J.L.; Kefauver, S.C. Remote Sensing for Precision Agriculture: Sentinel-2 Improved Features and Applications. Agronomy 2020, 10, 641. [Google Scholar] [CrossRef]
  4. Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-based remote sensing of lake water quality characteristics, including chlorophyll and colored dissolved organic matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
  5. Fritz, S.; See, L.; Bayas, J.C.L.; Waldner, F.; Jacques, D.; Becker-Reshef, I.; Whitcraft, A.; Baruth, B.; Bonifacio, R.; Crutchfield, J.; et al. A comparison of global agricultural monitoring systems and current gaps. Agric. Syst. 2019, 168, 258–272. [Google Scholar] [CrossRef]
  6. Rembold, F.; Meroni, M.; Urbano, F.; Csak, G.; Kerdiles, H.; Perez-Hoyos, A.; Lemoine, G.; Leo, O.; Negre, T. ASAP: A new global early warning system to detect anomaly hot spots of agricultural production for food security analysis. Agric. Syst. 2019, 168, 247–257. [Google Scholar] [CrossRef] [PubMed]
  7. Wulder, M.A.; Hermosilla, T.; White, J.C.; Hobart, G.; Masek, J.G. Augmenting Landsat time series with Harmonized Landsat Sentinel-2 data products: Assessment of spectral correspondence. Sci. Remote Sens. 2021, 4, 100031. [Google Scholar] [CrossRef]
  8. Weiss, M.; Jacob, F.; Duveiller, G. Remote sensing for agricultural applications: A meta-review. Remote Sens. Environ. 2020, 236, 111402. [Google Scholar] [CrossRef]
  9. WatchItGrow. Available online: https://vito.be/en/remote-sensing/watchitgrow (accessed on 24 November 2021).
  10. Beamish, A.; Raynolds, M.K.; Epstein, H.; Frost, G.V.; Macander, M.J.; Bergstedt, H.; Bartsch, A.; Kruse, S.; Miles, V.; Tanis, C.M.; et al. Recent trends and remaining challenges for optical remote sensing of Arctic tundra vegetation: A review and outlook. Remote Sens. Environ. 2020, 246, 111872. [Google Scholar] [CrossRef]
  11. Wirion, C.; Bauwens, W.; Verbeiren, B. Location- and Time-Specific Hydrological Simulations with Multi-Resolution Remote Sensing Data in Urban Areas. Remote Sens. 2017, 9, 645. [Google Scholar] [CrossRef] [Green Version]
  12. Bégué, A.; Arvor, D.; Bellon, B.; Betbeder, J.; de Abelleyra, D.; PD Ferraz, R.; Lebourgeois, V.; Lelong, C.; Simões, M.; R Verón, S. Remote Sensing and Cropping Practices: A Review. Remote Sens. 2018, 10, 99. [Google Scholar] [CrossRef] [Green Version]
  13. Mandanici, E.; Bitelli, G. Preliminary Comparison of Sentinel-2 and Landsat 8 Imagery for a Combined Use. Remote Sens. 2016, 8, 1014. [Google Scholar] [CrossRef] [Green Version]
  14. Van Leeuwen, W.J.D.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ. 2006, 100, 67–81. [Google Scholar] [CrossRef]
  15. Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
  16. Saunier, S.; Louis, J.; Debaecker, V.; Beaton, T.; Cadau, E.G.; Boccia, V.; Gascon, F. Sen2like, A Tool To Generate Sentinel-2 Harmonised Surface Reflectance Products—First Results with Landsat-8. In Proceedings of the IEEE IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; IEEE: Piscataway, NJ, USA,; pp. 5650–5653. [Google Scholar]
  17. Helder, D.; Markham, B.; Morfitt, R.; Storey, J.; Barsi, J.; Gascon, F.; Clerc, S.; LaFrance, B.; Masek, J.; Roy, D.; et al. Observations and Recommendations for the Calibration of Landsat 8 OLI and Sentinel 2 MSI for Improved Data Interoperability. Remote Sens. 2018, 10, 1340. [Google Scholar] [CrossRef] [Green Version]
  18. Barsi, J.A.; Alhammoud, B.; Czapla-Myers, J.; Gascon, F.; Haque, M.O.; Kaewmanee, M.; Leigh, L.; Markham, B.L. Sentinel-2A MSI and Landsat-8 OLI radiometric cross comparison over desert sites. Eur. J. Remote Sens. 2018, 51, 822–837. [Google Scholar] [CrossRef]
  19. Jing, X.; Leigh, L.; Teixeira Pinto, C.; Helder, D. Evaluation of RadCalNet Output Data Using Landsat 7, Landsat 8, Sentinel 2A, and Sentinel 2B Sensors. Remote Sens. 2019, 11, 541. [Google Scholar] [CrossRef] [Green Version]
  20. Alhammoud, B.; Jackson, J.; Clerc, S.; Arias, M.; Bouzinac, C.; Gascon, F.; Cadau, E.G.; Iannone, R.Q.; Boccia, V. Sentinel-2 Level-1 Radiometry Assessment Using Vicarious Methods from DIMITRI Toolbox and Field Measurements from RadCalNet Database. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3470–3479. [Google Scholar] [CrossRef]
  21. Lamquin, N.; Woolliams, E.; Bruniquel, V.; Gascon, F.; Gorroño, J.; Govaerts, Y.; Leroy, V.; Lonjou, V.; Alhammoud, B.; Barsi, J.A.; et al. An inter-comparison exercise of Sentinel-2 radiometric validations assessed by independent expert groups. Remote Sens. Environ. 2019, 233, 111369. [Google Scholar] [CrossRef]
  22. Swinnen, E.; Veroustraete, F. Extending the SPOT-VEGETATION NDVI time series (1998–2006) back in time with NOAA-AVHRR data (1985–1998) for Southern Africa. IEEE Trans. Geosci. Remote Sens. 2008, 46, 558–572. [Google Scholar] [CrossRef]
  23. Pahlevan, N.; Sarkar, S.; Franz, B.A.; Balasubramanian, S.V.; He, J. Sentinel-2 MultiSpectral Instrument (MSI) data processing for aquatic science applications: Demonstrations and validations. Remote Sens. Environ. 2017, 201, 47–56. [Google Scholar] [CrossRef]
  24. León-Tavares, J.; Roujean, J.-L.; Smets, B.; Wolters, E.; Toté, C.; Swinnen, E. Correction of Directional Effects in VEGETATION NDVI Time-Series. Remote Sens. 2021, 13, 1130. [Google Scholar] [CrossRef]
  25. D’Odorico, P.; Gonsamo, A.; Damm, A.; Schaepman, M.E. Experimental evaluation of sentinel-2 spectral response functions for NDVI time-series continuity. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1336–1348. [Google Scholar] [CrossRef]
  26. Gonsamo, A.; Chen, J.M. Spectral response function comparability among 21 satellite sensors for vegetation monitoring. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1319–1335. [Google Scholar] [CrossRef]
  27. Trishchenko, A.P.; Cihlar, J.; Li, Z. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors. Remote Sens. Environ. 2002, 81, 1–18. [Google Scholar] [CrossRef]
  28. Villaescusa-Nadal, J.L.; Franch, B.; Roger, J.-C.C.; Vermote, E.F.; Skakun, S.; Justice, C. Spectral Adjustment Model’s Analysis and Application to Remote Sensing Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 961–972. [Google Scholar] [CrossRef]
  29. Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.B.; Angal, A.; Choi, T.; Xiong, X.; Doelling, D.R. Applications of spectral band adjustment factors (SBAF) for cross-calibration. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1267–1281. [Google Scholar] [CrossRef]
  30. Belair. Available online: https://belair.vito.be/ (accessed on 23 November 2021).
  31. Dierckx, W.; Sterckx, S.; Benhadj, I.; Livens, S.; Duhoux, G.; Van Achteren, T.; Francois, M.; Mellab, K.; Saint, G. PROBA-V mission for global vegetation monitoring: Standard products and image quality. Int. J. Remote Sens. 2014, 35, 2589–2614. [Google Scholar] [CrossRef]
  32. PROBA-V. Available online: https://proba-v.vgt.vito.be (accessed on 24 November 2021).
  33. RAHMAN, H.; DEDIEU, G. SMAC: A simplified method for the atmospheric correction of satellite measurements in the solar spectrum. Int. J. Remote Sens. 1994, 15, 123–143. [Google Scholar] [CrossRef]
  34. Toté, C.; Swinnen, E.; Sterckx, S.; Adriaensen, S.; Benhadj, I.; Iordache, M.-D.; Bertels, L.; Kirches, G.; Stelzer, K.; Dierckx, W.; et al. Evaluation of PROBA-V Collection 1: Refined Radiometry, Geometry, and Cloud Screening. Remote Sens. 2018, 10, 1375. [Google Scholar] [CrossRef] [Green Version]
  35. Pisabarro, P.; Carballo, M.; Iturri, A.; Bueno, I.; Mazzoleni, A.; Luengo, M.; Bravo, F.A.; Santos, J.A.; Pirondini, F. Satellite Operations Strategies and Experience in DEIMOS-1 and DEIMOS-2 Missions. In Proceedings of the SpaceOps 2016 Conference, Daejeon, Korea, 16–20 May 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
  36. Richter, R. Atmospheric correction of DAIS hyperspectral image data. Comput. Geosci. 1996, 22, 785–793. [Google Scholar] [CrossRef]
  37. Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
  38. Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A.; et al. Copernicus Sentinel-2A Calibration and Products Validation Status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef] [Green Version]
  39. Sentinel-2. Available online: https://sentinel.esa.int/web/sentinel/missions/sentinel-2 (accessed on 24 November 2021).
  40. Main-Knorn, M.; Pflug, B.; Louis, J.; Debaecker, V.; Müller-Wilm, U.; Gascon, F. Sen2Cor for Sentinel-2. In Proceedings of the Image and Signal Processing for Remote Sensing XXIII, International Society for Optics and Photonics, Warsaw, Poland, 4 October 2017; Bruzzone, L., Bovolo, F., Benediktsson, J.A., Eds.; SPIE: Bellingham, WA, USA, 2017; p. 3. [Google Scholar]
  41. Terrascope. Available online: https://terrascope.be/ (accessed on 24 November 2021).
  42. USGS Landsat Collections. Available online: https://www.usgs.gov/core-science-systems/nli/landsat/landsat-collection-1?qt-science_support_page_related_con=1#qt-science_support_page_related_con (accessed on 24 November 2021).
  43. Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
  44. Weiss, M.; Baret, F. S2ToolBox Level 2 products: LAI, FAPAR, FCOVER—Version 1.1; INRAE: Paris, France, 2016. [Google Scholar]
  45. Govaerts, Y.; Sterckx, S.; Adriaensen, S. Use of simulated reflectances over bright desert target as an absolute calibration reference. Remote Sens. Lett. 2013, 4, 523–531. [Google Scholar] [CrossRef]
  46. Sterckx, S.; Wolters, E. Radiometric Top-of-Atmosphere Reflectance Consistency Assessment for Landsat 8/OLI, Sentinel-2/MSI, PROBA-V, and DEIMOS-1 over Libya-4 and RadCalNet Calibration Sites. Remote Sens. 2019, 11, 2253. [Google Scholar] [CrossRef] [Green Version]
  47. Holben, B.N.; Eck, T.F.; Slutsker, I.; Tanré, D.; Buis, J.P.; Setzer, A.; Vermote, E.; Reagan, J.A.; Kaufman, Y.J.; Nakajima, T.; et al. AERONET—A federated instrument network and data archive for aerosol characterization. Remote Sens. Environ. 1998, 66, 1–16. [Google Scholar] [CrossRef]
  48. De Keukelaere, L.; Sterckx, S.; Adriaensen, S.; Knaeps, E.; Reusen, I.; Giardino, C.; Bresciani, M.; Hunter, P.; Neil, C.; Van der Zande, D.; et al. Atmospheric correction of Landsat-8/OLI and Sentinel-2/MSI data using iCOR algorithm: Validation for coastal and inland waters. Eur. J. Remote Sens. 2018, 51, 525–542. [Google Scholar] [CrossRef] [Green Version]
  49. Wolters, E.; Tot, C.; Sterckx, S.; Adriaensen, S.; Henocq, C.; Scifoni, S.; Dransfeld, S. iCOR Atmospheric Correction on Sentinel-3/OLCI over Land: Intercomparison with AERONET, RadCalNet, and SYN Level-2. Remote Sens. 2021, 13, 654. [Google Scholar] [CrossRef]
  50. Doxani, G.; Vermote, E.; Roger, J.-C.; Gascon, F.; Adriaensen, S.; Frantz, D.; Hagolle, O.; Hollstein, A.; Kirches, G.; Li, F.; et al. Atmospheric Correction Inter-Comparison Exercise. Remote Sens. 2018, 10, 352. [Google Scholar] [CrossRef] [Green Version]
  51. Berk, A.; Anderson, G.P.; Acharya, P.K.; Bernstein, L.S.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.M.; Chetwynd, J.H., Jr.; Hoke, M.L.; et al. MODTRAN5: 2006 update. In SPIE 6233, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XII; Shen, S.S., Lewis, P.E., Eds.; SPIE: Bellingham, WA, USA, 2006; p. 62331F. [Google Scholar]
  52. Teillet, P.M.; Fedosejevs, G.; Thome, K.J.; Barker, J.L. Impacts of spectral band difference effects on radiometric cross-calibration between satellite sensors in the solar-reflective spectral domain. Remote Sens. Environ. 2007, 110, 393–409. [Google Scholar] [CrossRef]
  53. VERHOEF, W.; BACH, H. Coupled soil–leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
  54. Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C.; Corsi, F.; Cho, M. LAI and chlorophyll estimation for a heterogeneous grassland using hyperspectral measurements. ISPRS J. Photogramm. Remote Sens. 2008, 63, 409–426. [Google Scholar] [CrossRef]
  55. Mousivand, A.; Menenti, M.; Gorte, B.; Verhoef, W. Global sensitivity analysis of the spectral radiance of a soil-vegetation system. Remote Sens. Environ. 2014, 145, 131–144. [Google Scholar] [CrossRef]
  56. Steven, M.D.; Malthus, T.J.; Baret, F.; Xu, H.; Chopping, M.J. Intercalibration of vegetation indices from different sensor systems. Remote Sens. Environ. 2003, 88, 412–422. [Google Scholar] [CrossRef]
  57. TRISHCHENKO, A. Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors: Extension to AVHRR NOAA-17, 18 and METOP-A. Remote Sens. Environ. 2009, 113, 335–341. [Google Scholar] [CrossRef]
  58. WEISS, M.; BARET, F.; GARRIGUES, S.; LACAZE, R. LAI and fAPAR CYCLOPES global products derived from VEGETATION. Part 2: Validation and comparison with MODIS collection 4 products. Remote Sens. Environ. 2007, 110, 317–331. [Google Scholar] [CrossRef]
  59. Vermote, E.; Justice, C.O.; Bréon, F.M. Towards a generalized approach for correction of the BRDF effect in MODIS directional reflectances. IEEE Trans. Geosci. Remote Sens. 2009, 47, 898–908. [Google Scholar] [CrossRef]
  60. Revel, C.; Lonjou, V.; Marcq, S.; Desjardins, C.; Fougnie, B.; Coppolani-Delle Luche, C.; Guilleminot, N.; Lacamp, A.S.; Lourme, E.; Miquel, C.; et al. Sentinel-2A and 2B absolute calibration monitoring. Eur. J. Remote Sens. 2019, 52, 122–137. [Google Scholar] [CrossRef] [Green Version]
  61. Lozano, F.J.; Romo, A.; Moclan, C.; Gil, J.; Pirondini, F. The DEIMOS-1 mission: Absolute and relative calibration activities and radiometric optimisation. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 4754–4757. [Google Scholar]
  62. PROBA-V Radiometric Calibration. Available online: https://proba-v.vgt.vito.be/en/quality/radiometric/radiometric-calibration (accessed on 10 February 2022).
  63. Landsat 8 Calibration Updates. Available online: https://www.usgs.gov/landsat-missions/landsat-8-oli-and-tirs-calibration-notices (accessed on 10 February 2022).
  64. Sentinel-2 Quality Reports. Available online: https://sentinel.esa.int/web/sentinel/user-guides/sentinel-2-msi/document-library (accessed on 10 February 2022).
  65. Zhang, H.K.; Roy, D.P.; Yan, L.; Li, Z.; Huang, H.; Vermote, E.; Skakun, S.; Roger, J.C. Characterization of Sentinel-2A and Landsat-8 top of atmosphere, surface, and nadir BRDF adjusted reflectance and NDVI differences. Remote Sens. Environ. 2018, 215, 482–494. [Google Scholar] [CrossRef]
  66. Roy, D.; Li, Z.; Zhang, H. Adjustment of Sentinel-2 Multi-Spectral Instrument (MSI) Red-Edge Band Reflectance to Nadir BRDF Adjusted Reflectance (NBAR) and Quantification of Red-Edge Band BRDF Effects. Remote Sens. 2017, 9, 1325. [Google Scholar] [CrossRef] [Green Version]
  67. Franch, B.; Vermote, E.; Skakun, S.; Roger, J.-C.; Masek, J.; Ju, J.; Villaescusa-Nadal, J.; Santamaria-Artigas, A. A Method for Landsat and Sentinel 2 (HLS) BRDF Normalization. Remote Sens. 2019, 11, 632. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 14 01163 g001 550
Figure 1. BELAIR sites in Belgium. The HESBANIA (agriculture) and SONIA (urban) sites are used as case studies in this research.
Figure 1. BELAIR sites in Belgium. The HESBANIA (agriculture) and SONIA (urban) sites are used as case studies in this research.
Remotesensing 14 01163 g001
Remotesensing 14 01163 g002 550
Figure 2. Overall flowchart of the work performed. Numbers indicate the section numbers in the paper. Colours indicate the different parts of the work: white, input data; red, analysis of harmonization measures performed to set up the processing chain; blue, the processing chain; yellow, the processed data sets for evaluation; cyan, the evaluation performed to answer the research questions formulated in the Introduction (Section 1).
Figure 2. Overall flowchart of the work performed. Numbers indicate the section numbers in the paper. Colours indicate the different parts of the work: white, input data; red, analysis of harmonization measures performed to set up the processing chain; blue, the processing chain; yellow, the processed data sets for evaluation; cyan, the evaluation performed to answer the research questions formulated in the Introduction (Section 1).
Remotesensing 14 01163 g002
Remotesensing 14 01163 g003 550
Figure 3. Comparison between the SWIR band of PROBA-V and B11 of S2A, original data (left), and after applying the best correction functions AD_NDVIpoly2 (right). Top row: AD between PROBA-V SWIR and S2A B11 versus NDVI of PROBA-V, second row: ratio between PROBA-V SWIR and S2A B11 versus NDVI of PROBA-V, third row: bias histogram between PROBA-V SWIR and S2A B11, and bottom row: APU-plot between PROBA-V SWIR and S2A B11.
Figure 3. Comparison between the SWIR band of PROBA-V and B11 of S2A, original data (left), and after applying the best correction functions AD_NDVIpoly2 (right). Top row: AD between PROBA-V SWIR and S2A B11 versus NDVI of PROBA-V, second row: ratio between PROBA-V SWIR and S2A B11 versus NDVI of PROBA-V, third row: bias histogram between PROBA-V SWIR and S2A B11, and bottom row: APU-plot between PROBA-V SWIR and S2A B11.
Remotesensing 14 01163 g003
Remotesensing 14 01163 g004 550
Figure 4. Bias histogram between the SWIR band of PROBA-V and B11 of S2A, original data (green), and after applying the selected RSRF correction function AD_NDVIpoly2 (red), for the agricultural HESBANIA (left) and urban SONIA (right) images.
Figure 4. Bias histogram between the SWIR band of PROBA-V and B11 of S2A, original data (green), and after applying the selected RSRF correction function AD_NDVIpoly2 (red), for the agricultural HESBANIA (left) and urban SONIA (right) images.
Remotesensing 14 01163 g004
Remotesensing 14 01163 g005a 550Remotesensing 14 01163 g005b 550
Figure 5. MBE between ICOR and other datasets (colors) per sensor (row), and for TOC reflectances (left), and NDVI and BIOPARs (right).
Figure 5. MBE between ICOR and other datasets (colors) per sensor (row), and for TOC reflectances (left), and NDVI and BIOPARs (right).
Remotesensing 14 01163 g005aRemotesensing 14 01163 g005b
Remotesensing 14 01163 g006 550
Figure 6. Mean bias error (MBE) (left) and RMSE (right) for the different BIOPARs (X-axis) and for the different correction combinations (colors).
Figure 6. Mean bias error (MBE) (left) and RMSE (right) for the different BIOPARs (X-axis) and for the different correction combinations (colors).
Remotesensing 14 01163 g006
Remotesensing 14 01163 g007 550
Figure 7. RMSE between in situ data and sensor data for different classes (X-axis) and for ‘original’ and ‘ICOR’ data (colors).
Figure 7. RMSE between in situ data and sensor data for different classes (X-axis) and for ‘original’ and ‘ICOR’ data (colors).
Remotesensing 14 01163 g007
Remotesensing 14 01163 g008 550
Figure 8. RMSE between S2A and match-ups with other sensors for the different BIOPARs and NDVI (X) and for the original data and various harmonization measures (colors).
Figure 8. RMSE between S2A and match-ups with other sensors for the different BIOPARs and NDVI (X) and for the original data and various harmonization measures (colors).
Remotesensing 14 01163 g008
Remotesensing 14 01163 g009 550
Figure 9. Same as Figure 7 but for the parcel database.
Figure 9. Same as Figure 7 but for the parcel database.
Remotesensing 14 01163 g009
Remotesensing 14 01163 g010 550
Figure 10. RMSE between match-up data from two sensors for the in situ sites. Colors indicate the corrections applied to the images.
Figure 10. RMSE between match-up data from two sensors for the in situ sites. Colors indicate the corrections applied to the images.
Remotesensing 14 01163 g010
Remotesensing 14 01163 g011 550
Figure 11. Histograms of time series noise calculated for the different BIOPARs and NDVI for the original data and the different harmonization measured applied on the dataset (colors) for the HESBANIA site.
Figure 11. Histograms of time series noise calculated for the different BIOPARs and NDVI for the original data and the different harmonization measured applied on the dataset (colors) for the HESBANIA site.
Remotesensing 14 01163 g011
Remotesensing 14 01163 g012 550
Figure 12. Histograms of time series noise calculated for the classes Grass (NDVI), Trees (LAI) and Urban (NDVI) for the original and ICOR data (colors) for the SONIA site.
Figure 12. Histograms of time series noise calculated for the classes Grass (NDVI), Trees (LAI) and Urban (NDVI) for the original and ICOR data (colors) for the SONIA site.
Remotesensing 14 01163 g012
Table
Table 1. Band combinations relative to S2A and their spectral range (in nm).
Table 1. Band combinations relative to S2A and their spectral range (in nm).
Sentinel-2Landsat 8DMCPROBA-V
B3 543–578B3 533–590GREEN 520–600
B4 650–680B4 636–673RED 630–690B2 614–696
B5 698–713
B6 733–748
B7 773–793
B8 785–899B5 851–879NIR 770–900B3 772–902
B8A 855–875B5 851–879NIR 770–900B3 772–902
B11 1565–1655B6 1566–1651 SWIR 1570–1635
B12 2100–2280B7 2107–2294
Table
Table 2. Naming of datasets used in this study and description of the processing performed.
Table 2. Naming of datasets used in this study and description of the processing performed.
Dataset Name Processing Performed
Nominal/original baseline level2 products
ORIGOriginal data, processing performed with Sen2COR (for S2), LaSRC (for L8), SMAC (for PROBA-V)
Belharmony processing
ICORAtmospheric correction completed with ICOR
ICOR + GAINGain applied to TOA radiance data + atmospheric correction performed with ICOR
ICOR + GAIN + SRFGain applied to TOA radiance data + atmospheric correction performed with ICOR + SRF correction
Table
Table 3. Definition of the combined datasets extracted for the HESBANIA fields (in situ and from the parcel database).
Table 3. Definition of the combined datasets extracted for the HESBANIA fields (in situ and from the parcel database).
Name of Resulting Time SeriesS2AS2BL8DMC
ICORICORICORICORICOR
ICOR + gainICORICOR + gainICOR + gainICOR + gain
ICOR + gain + SRFICORICOR + gainICOR + gain + SRFICOR + gain + SRF
OriginalOriginalOriginalICORICOR
Table
Table 4. Datasets used in the SONIA evaluation.
Table 4. Datasets used in the SONIA evaluation.
ClassLabelDMCS2L8Proba-V
NDVI: urban imperviousUrban201520182015 and 20182015 and 2018
NDVI: urban grassGrass201520182015 and 20182015 and 2018
LAI: urban treesTrees201520182015 and 20182015 and 2018
Table
Table 5. Mean ratio (over all observations) of the satellite-measured TOA reflectances to the 6SV TOA reflectance reference simulations over Libya-4 (Table copied from [46]).
Table 5. Mean ratio (over all observations) of the satellite-measured TOA reflectances to the 6SV TOA reflectance reference simulations over Libya-4 (Table copied from [46]).
S2S2S2A%Diff S2BL8L8%Diff L8DMCDMC%Diff DMCPVPV%Diff PV
bandcwvratiovs. S2Abandcwvvs. S2Abandcwvvs. S2Abandcwvvs. S2A
14431.008−1.05%CA443−1.05% Blue460−1.30%
24900.985−0.03%Blue4920.94% 4600.97%
35600.999−0.16%Green 5610.82%Green549−3.5%
46651.005−0.76%Red6540.08%Red6790.2%Red658−1.55%
57051.016−1.32%
67401.023−1.49%
77831.034−1.35%
88420.999−0.40% NIR8030.8%NIR8340.78%
8A8651.027−0.84%NIR865−0.28%
9945NANA
101375NANACirrus1373NA
1116100.998−0.40%SWIR11610−0.30% SWIR1610−0.21%
1221900.973−0.12%SWIR222000.28%
Table
Table 6. Selected SRF correction functions.
Table 6. Selected SRF correction functions.
InputS2EquationCoefficients
bandBand abcdef
Landsat-8
B3B3A61.0074570.007411−0.0616800--
B4B4A60.983784−0.0541150.171154−0.030599--
B5B8No suitable correction found, SRFs too different.
B5B8AOriginal bands are already very similar
B6B11A100.0004494.081912−0.9541064.0818500.954195-
B7B12A50.0003690.000779−0.0206860.019961−0.0007081.000709
DMC
B1B3A61.0267470.023303−0.1653270-
B2B4A60.996053−0.0379690.0916270.063597
B3B8Original bands are already very similar
B3B8ANo suitable correction found, SRFs too different.
PROBA-V
B2B4A60.993998−0.1261060.3389880-
B3B8A90.9994683.211558−1.0005623.21078391.003200
B3B8ANo suitable correction found, SRFs too different.
SWIRB11A70.001377−0.0006690.0043920-
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Swinnen, E.; Sterckx, S.; Wirion, C.; Verbeiren, B.; Wens, D. Harmonization of Multi-Mission High-Resolution Time Series: Application to BELAIR. Remote Sens. 2022, 14, 1163. https://doi.org/10.3390/rs14051163

AMA Style

Swinnen E, Sterckx S, Wirion C, Verbeiren B, Wens D. Harmonization of Multi-Mission High-Resolution Time Series: Application to BELAIR. Remote Sensing. 2022; 14(5):1163. https://doi.org/10.3390/rs14051163

Chicago/Turabian Style

Swinnen, Else, Sindy Sterckx, Charlotte Wirion, Boud Verbeiren, and Dieter Wens. 2022. "Harmonization of Multi-Mission High-Resolution Time Series: Application to BELAIR" Remote Sensing 14, no. 5: 1163. https://doi.org/10.3390/rs14051163

APA Style

Swinnen, E., Sterckx, S., Wirion, C., Verbeiren, B., & Wens, D. (2022). Harmonization of Multi-Mission High-Resolution Time Series: Application to BELAIR. Remote Sensing, 14(5), 1163. https://doi.org/10.3390/rs14051163

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop