Long-Periodic Analysis of Boresight Misalignment of Ziyuan3-01 Three-Line Camera
Abstract
:1. Introduction
2. Methodology
2.1. Imaging Geometric Model of TLC
2.2. Geometric Calibration of the TLC Boresight Misalignment
2.3. Long-Periodic Analysis of Boresight Misalignment
3. Results
3.1. Experimental Datasets
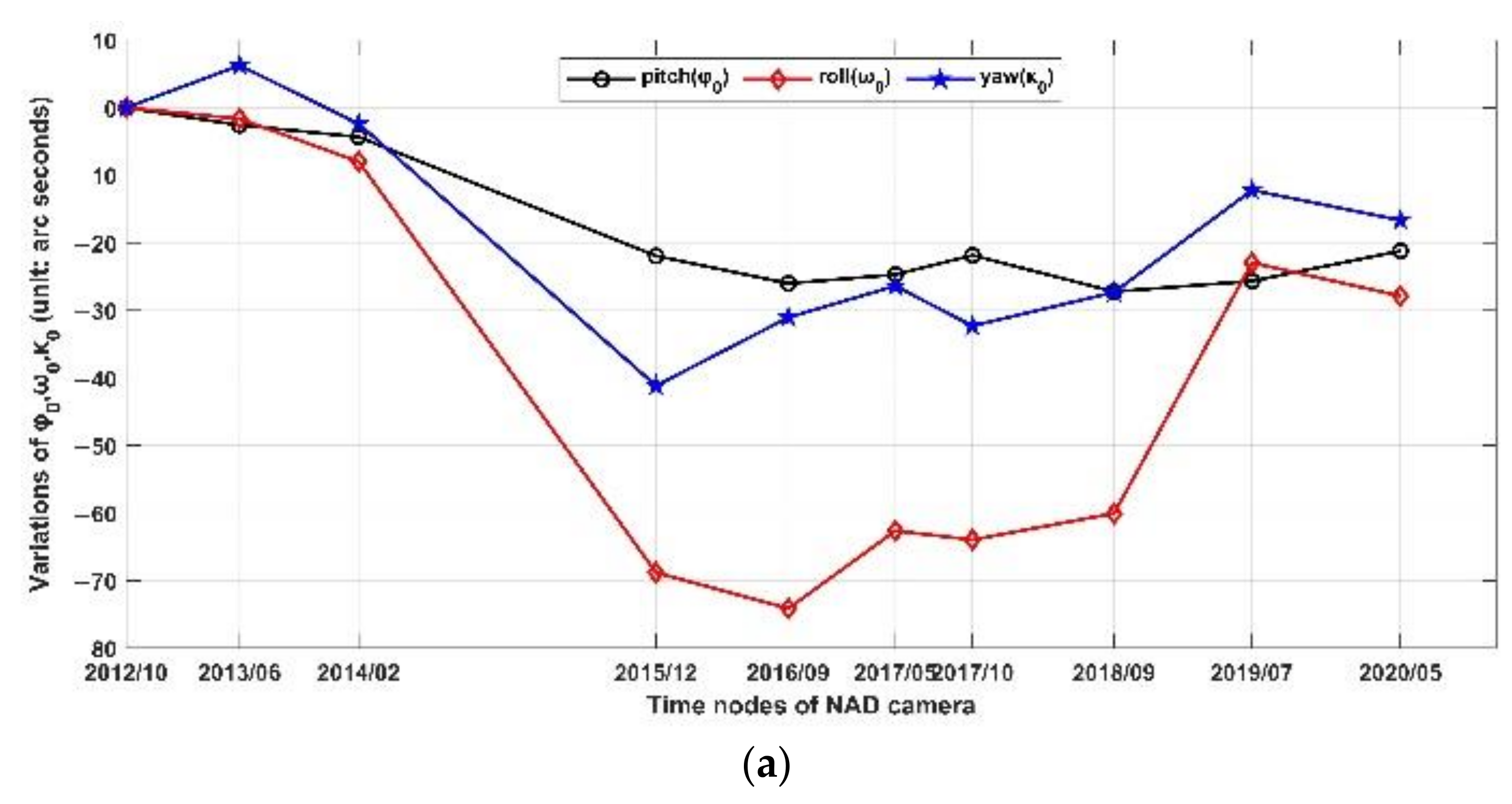
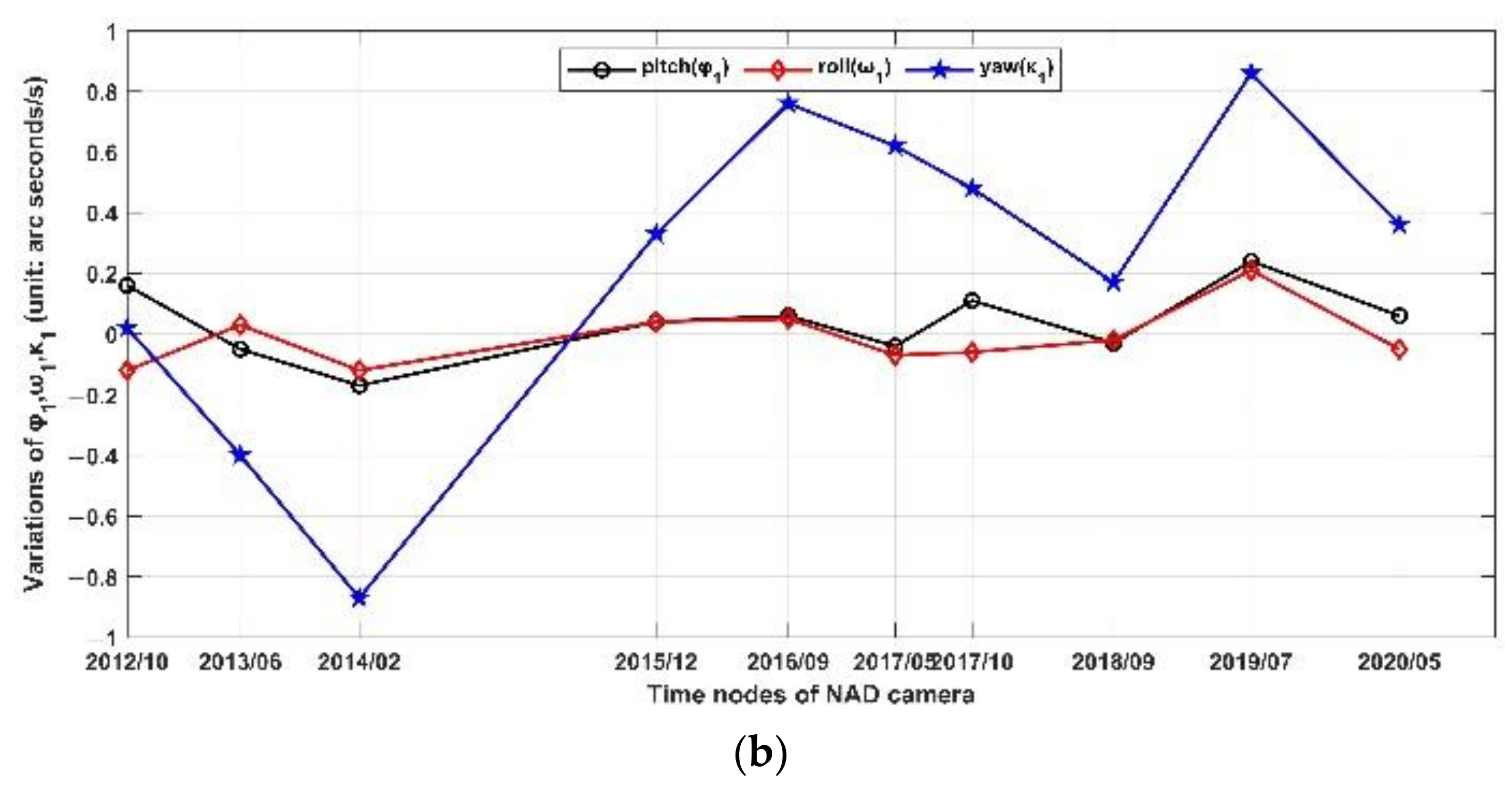
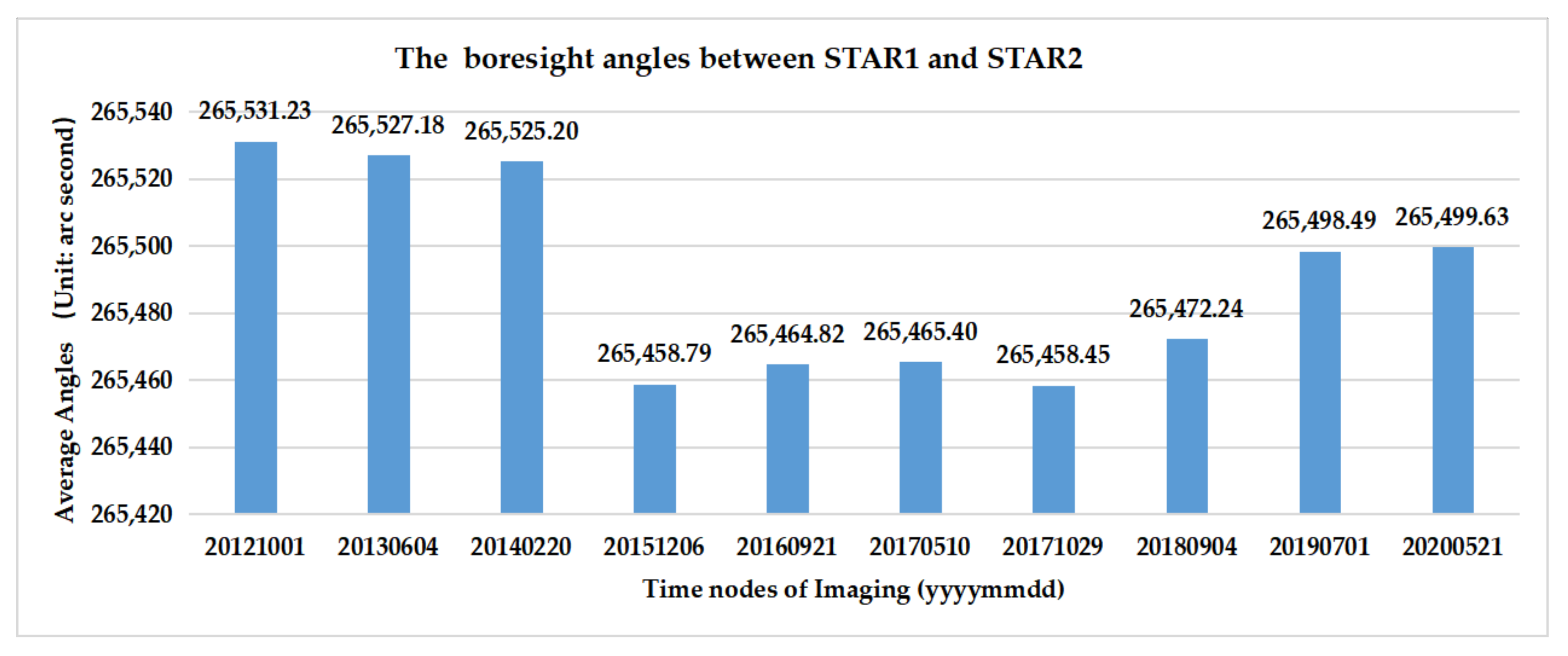
3.2. Calibration of NAD Camera
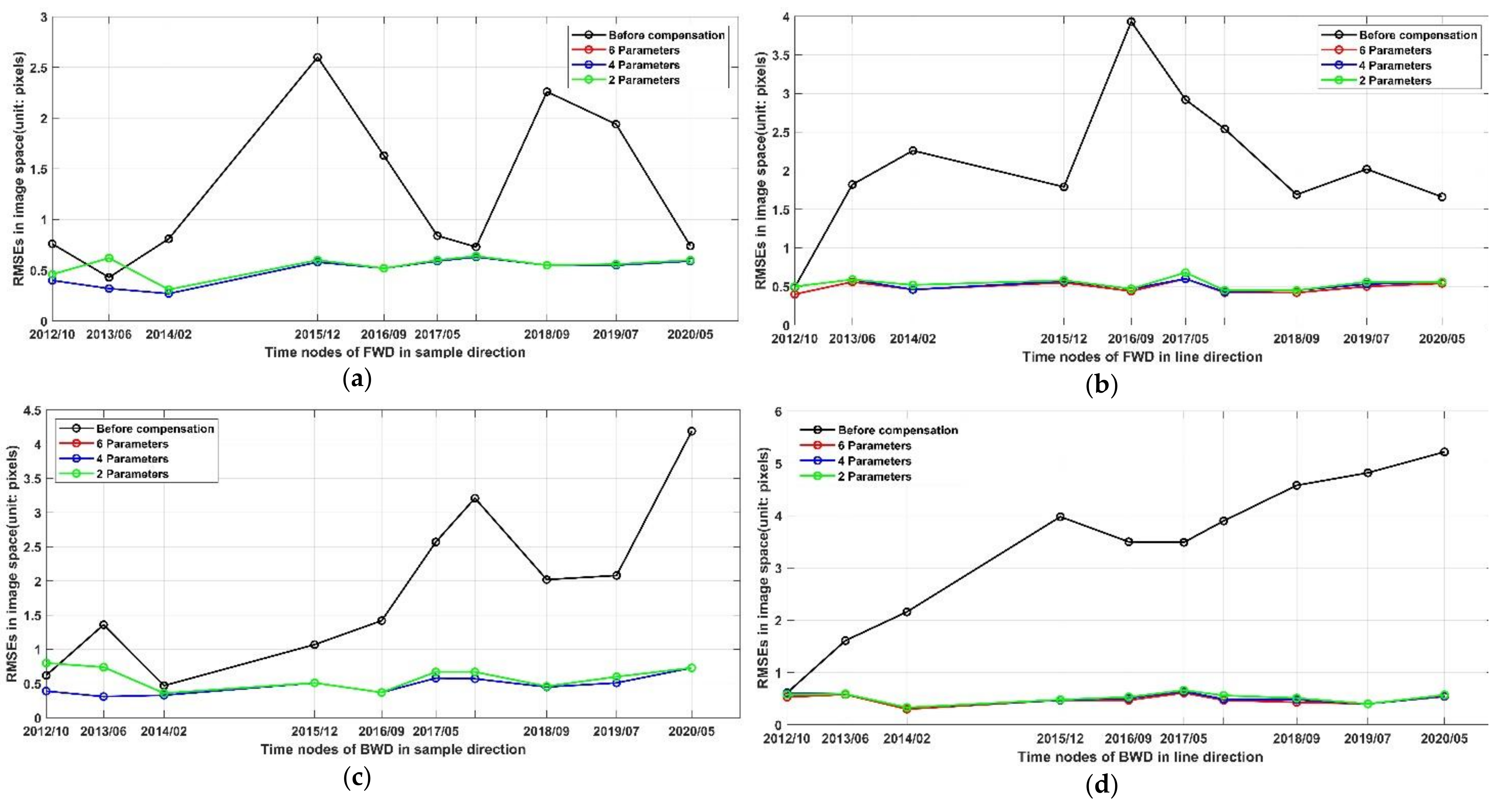
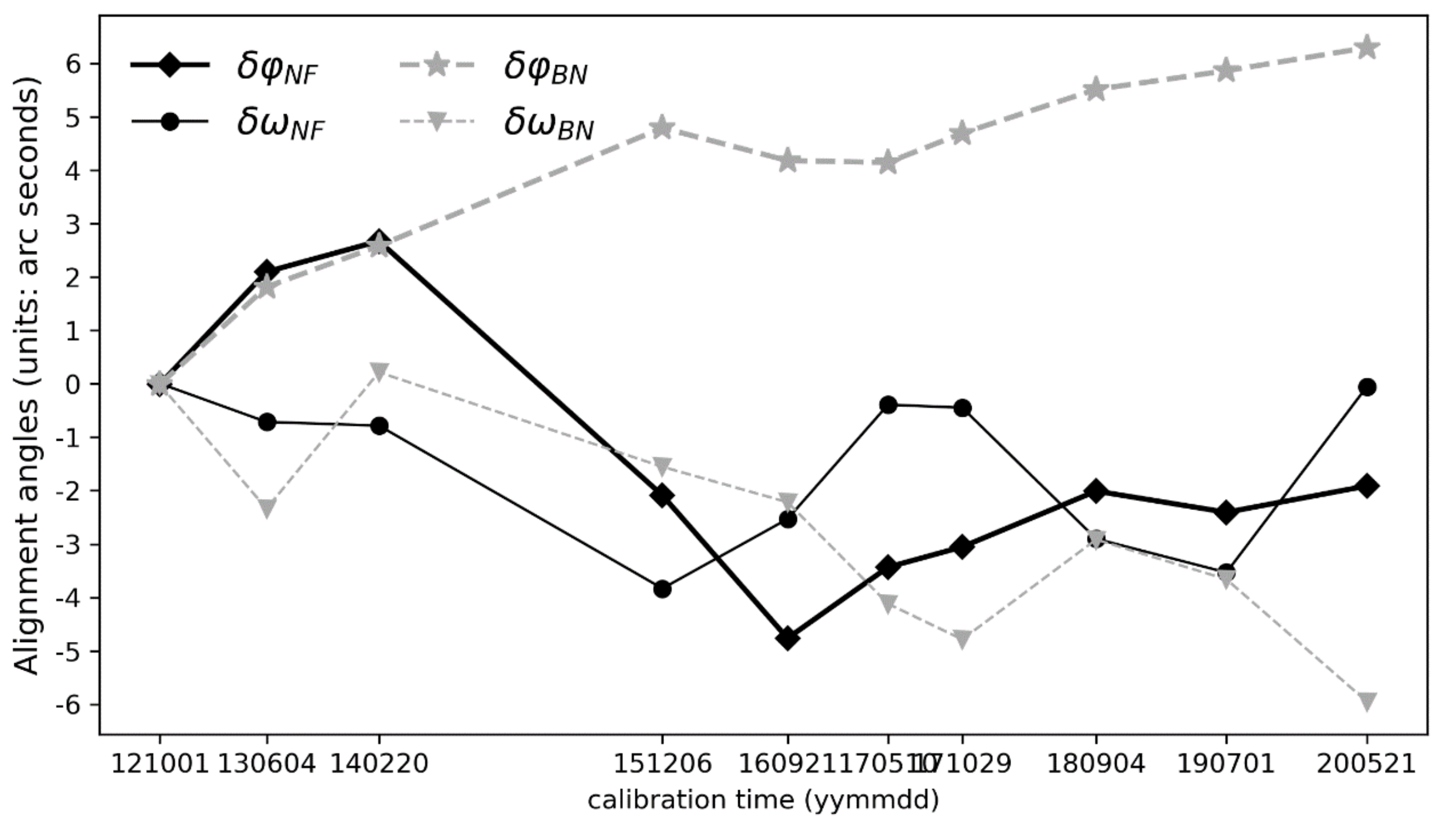
3.3. Boresight Misalignment Calibration and Characteristics of FWD and BWD Cameras
4. Discussion
4.1. Camera stability from Boresight Misalignment Calibration
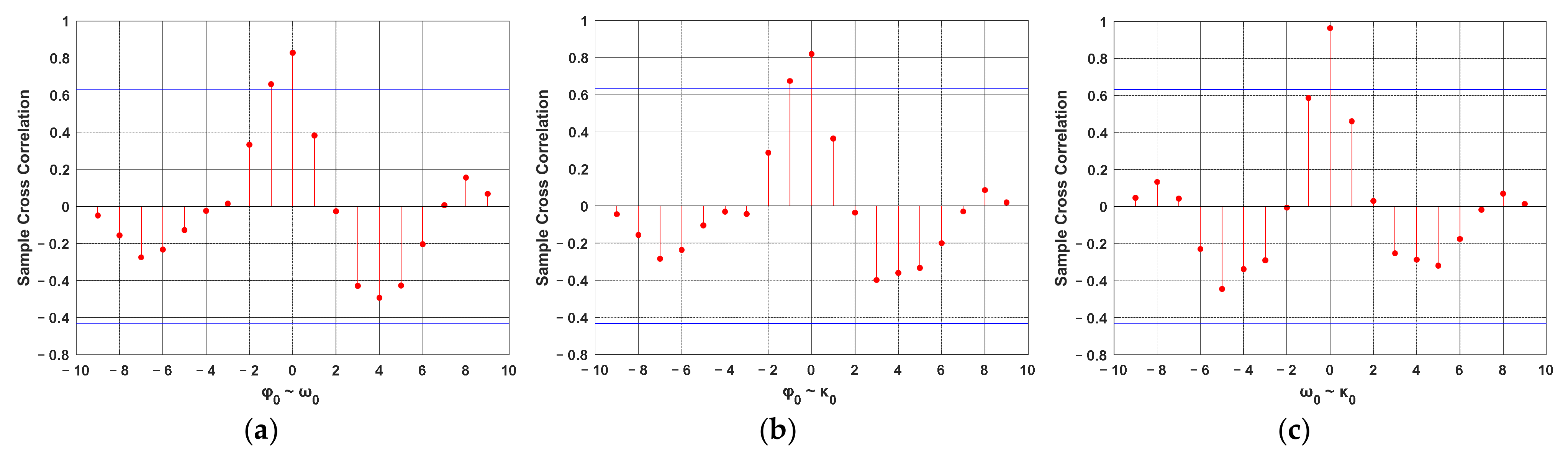
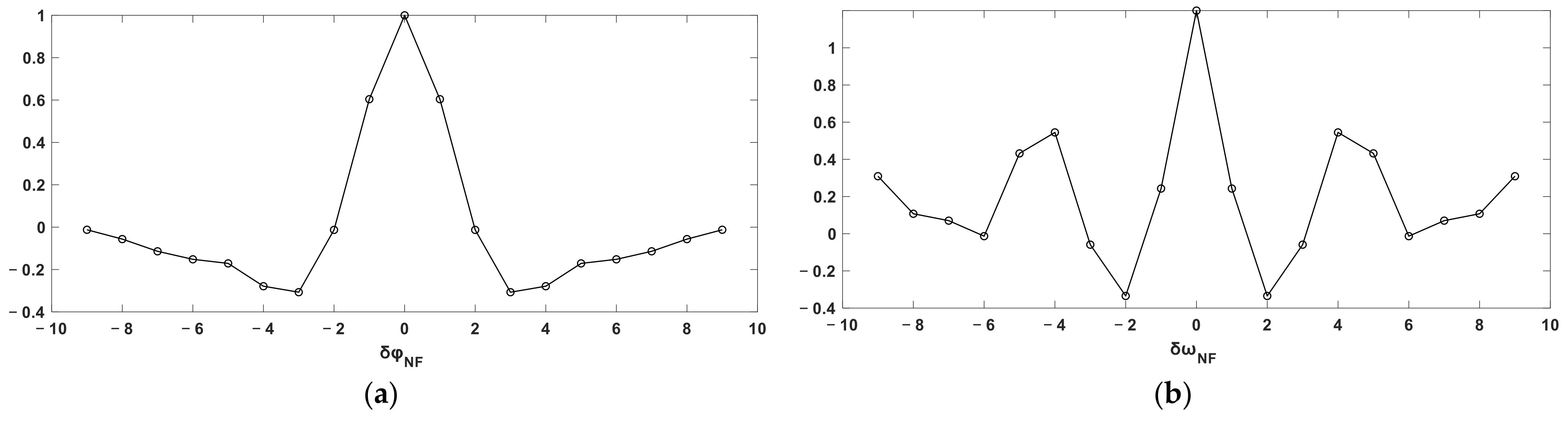
4.2. Error Sources for Boresight Misalignment Calibration
4.3. Effects of Long Time Series
5. Conclusions
- (1)
- The structure of ZY3-01 TLC was stable overall in the 10 years of operation, and the alignment angles of TLC were dynamic over time.
- (2)
- Compensation models of TLC are different for each camera. High-precision geo-positioning or mapping should consider the differences and relations of each camera rather than only a unified installation matrix.
- (3)
- Both the camera coordinates and the navigation coordinates change significantly with time. Therefore, regular geometric calibration is necessary for improving the positioning accuracy of high-resolution satellites.
- (4)
- Long-periodic analyses of TLC boresight misalignments indicate the changes in TLC angles, but the change patterns need further investigation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jovanovic, V.; Moroney, C.; Nelson, D. Multi-angle geometric processing for globally geo-located and co-registered MISR image data. Remote Sens. Environ. 2007, 107, 22–32. [Google Scholar] [CrossRef]
- Heipke, C.; Oberst, J.; Albertz, J.; Attwenger, M.; Dorninger, P.; Dorrer, E.; Ewe, M.; Gehrke, S.; Gwinner, K.; Hirschmueller, H.; et al. Evaluating planetary digital terrain models - The HRSC DTM test. Planet. Space Sci. 2007, 55, 2173–2191. [Google Scholar] [CrossRef]
- Tadono, T.; Shimada, M.; Takaku, J.; Kawamoto, S. Accuracy assessments of standard products of ALOS optical instruments and their high level products. In Proceedings of the Conference on Sensors, Systems, and Next-Generation Satellites XI, Florence, Italy, 17–20 September 2007. [Google Scholar]
- Grodecki, J.; Dial, G. Block adjustment of high-resolution satellite images described by rational polynomials. Photogramm. Eng. Remote Sens. 2003, 69, 59–68. [Google Scholar] [CrossRef]
- Hofmann, O.; Navé, P.; Ebner, H. DPS-A digital photogrammetric system for producing digital elevation models and orthophotos by means of linear array scanner imagery. Photogramm. Eng. Remote Sens. 1984, 50, 1135–1142. [Google Scholar]
- Bouillon, A.; Bernard, M.; Gigord, P.; Orsonia, A.; Rudowski, V. SPOT5 HRS geometric performances: Using block adjustment as a key issue to improve quality of DEM generation. ISPRS J. Photogramm. 2006, 60, 134–146. [Google Scholar] [CrossRef]
- Cao, J.; Yuan, X.; Gong, J. In-orbit geometric calibration and validation of ZY-3 three-line cameras based on CCD-detector look angles. Photogramm. Rec. 2015, 30, 211–226. [Google Scholar] [CrossRef]
- Cao, J.; Yuan, X.; Fang, Y.; Gong, J. Geometric calibration of Ziyuan-3 three-line cameras using ground control lines. Photogramm. Eng. Remote Sens. 2016, 82, 893–902. [Google Scholar] [CrossRef]
- Xing, L.; Dai, W.; Zhang, Y. Improving displacement measurement accuracy by compensating for camera motion and thermal effect on camera sensor. Mech. Syst. Signal Processing 2022, 167, 108525. [Google Scholar] [CrossRef]
- Zhang, X.; Zeinali, Y.; Story, B.A.; Rajan, D. Measurement of three-dimensional structural displacement using a hybrid inertial vision-based system. Sensors 2019, 19, 4083. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Qiu, Z.; Xie, Z.; Le, Y.; Fang, S.H. Detection of attitude constant error and in-orbit calibration for the three-line CCD sensor of the ZY-3 satellite. Int. J. Remote Sens. 2017, 38, 7333–7356. [Google Scholar] [CrossRef]
- Tang, X.; Zhu, X. The geometric calibration and validation for the ZY3-02 satellite optical image. In Proceedings of the ISPRS—International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Hannover, Germany, 6–9 June 2017. [Google Scholar]
- Zhang, G.; Jiang, Y.; Li, D.; Huang, W.; Pan, H.; Tang, X.; Zhu, X. In-orbit geometric calibration and validation of ZY-3 linear array sensors. Photogramm. Rec. 2014, 29, 68–88. [Google Scholar] [CrossRef]
- Zhang, Y.; Zheng, M.; Xiong, J.; Lu, Y.; Xiong, X. On-orbit geometric calibration of ZY-3 three-line array imagery with multistrip data sets. IEEE Trans. Geosci. Remote Sens. 2014, 52, 224–234. [Google Scholar] [CrossRef]
- Wang, M.; Yang, B.; Hu, F.; Zang, X. On-orbit geometric calibration model and its applications for high-resolution optical satellite imagery. Remote Sens. 2014, 6, 4391–4408. [Google Scholar] [CrossRef] [Green Version]
- Toutin, T. Geometric processing of remote sensing images: Models, algorithms and methods. Int. J. Remote Sens. 2010, 25, 1893–1924. [Google Scholar] [CrossRef]
- Grodecki, J.; Dial, G. IKONOS geometric accuracy validation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2002, 34, 50–55. [Google Scholar]
- Mulawa, D. On-orbit geometric calibration of the OrbView-3 high resolution imaging satellite. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 35, 1–6. [Google Scholar]
- Radhadevi, P.V.; Solanki, S.S. In-flight geometric calibration of different cameras of IRS-P6 using a physical sensor model. Photogramm. Rec. 2008, 23, 69–89. [Google Scholar] [CrossRef]
- Tadono, T.; Shimada, M.; Hashimoto, T.; Takaku, J.; Mukaida, A.; Kawamoto, S. Results of calibration and validation of ALOS optical sensors, and their accuracy assesments. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–27 July 2007. [Google Scholar]
- Kornus, W.; Lehner, M.; Schroeder, M. Geometric in-flight calibration of the stereoscopic line-CCD scanner MOMS-2P. ISPRS J. Photogramm. Remote Sens. 2000, 55, 59–71. [Google Scholar] [CrossRef]
- Gascon, F.; Bouzinac, C.; Thépaut, O.; Jung, M.; Francesconi, B.; Louis, J.; Lonjou, V.; Lafrance, B.; Massera, S.; Gaudel-Vacaresse, A. Copernicus Sentinel-2A calibration and products validation status. Remote Sens. 2017, 9, 584. [Google Scholar] [CrossRef] [Green Version]
- De Lussy, F.; Greslou, D.; Dechoz, C.; Amberg, V.; Delvit, J.M.; Lebegue, L.; Blanchet, G.; Fourest, S. Pleiades HR in flight geometrical calibration: Location and mapping of the focal plane. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 519–523. [Google Scholar] [CrossRef] [Green Version]
- Spiegel, M. Improvement of interior and exterior orientation of the three-line camera HRSC with a simultaneous adjustment. Int. Arch. Photogramm. Remote Sens. 2007, 36, 161–166. [Google Scholar]
- Wang, J.; Wang, R.; Hu, X.; Su, Z. The on-orbit calibration of geometric parameters of the Tian-Hui 1 (TH-1) satellite. ISPRS J. Photogramm. Remote Sens. 2017, 124, 144–151. [Google Scholar] [CrossRef]
- Wang, M.; Guo, B.; Zhu, Y.; Cheng, Y.; Nie, C. On-Orbit Calibration Approach Based on Partial Calibration-Field Coverage for the GF-1/WFV Camera. Photogramm. Eng. Remote Sens. 2019, 85, 815–827. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, Y.; Chang, X.; Jin, S.; Zhu, Y. On-orbit geometric calibration and geometric quality assessment for the high-resolution geostationary optical satellite GaoFen4. ISPRS J. Photogramm. Remote Sens. 2017, 125, 63–77. [Google Scholar] [CrossRef]
- Wang, M.; Cheng, Y.; Tian, Y.; He, L.; Wang, Y. A new on-orbit geometric self-calibration approach for the high-resolution geostationary optical satellite GaoFen4. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1670–1683. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, G.; Zhu, X.; Pan, H.; Jiang, Y.; Zhou, P.; Wang, X.; Guo, L. Triple linear-array image geometry model of ZiYuan-3 surveying satellite and its validation. Acta Geod. Et Cartogr. Sin. 2012, 41, 191–198. (In Chinese) [Google Scholar] [CrossRef]
- Kocaman, S.; Armin, G. Orientation and self-calibration of ALOS PRISM imagery. Photogramm. Rec. 2008, 23, 323–340. [Google Scholar]
- Li, D. China’s first civilian three-line-array stereo mapping satellite: ZY-3. Acta Geod. Et Cartogr. Sin. 2012, 41, 317–322. (In Chinese) [Google Scholar]
- Cao, J.; Fu, J.; Yuan, X.; Gong, J. Nonlinear bias compensation of ZiYuan-3 satellite imagery with cubic splines. ISPRS J. Photogramm. Remote Sens. 2017, 133, 174–185. [Google Scholar] [CrossRef]
- Pan, H.; Tao, C.; Zou, Z. Precise georeferencing using the rigorous sensor model and rational function model for ZiYuan-3 strip scenes with minimum control. ISPRS J. Photogramm. Remote Sens. 2016, 119, 259–266. [Google Scholar] [CrossRef]
- Yang, B.; Pi, Y.; Li, X.; Yang, Y. Integrated geometric self-calibration of stereo cameras onboard the ZiYuan-3 satellite. ISPRS J. Photogramm. Remote Sens. 2020, 162, 173–183. [Google Scholar] [CrossRef]
- Xu, K.; Jiang, Y.; Zhang, G.; Zhang, Q.; Wang, X. Geometric potential assessment for ZY3-02 triple linear array imagery. Remote Sens. 2017, 9, 658. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Zhang, G.; Tang, X.; Zhu, X.; Qin, Q.; Li, D.; Fu, X. High accuracy geometric calibration of ZY-3 three-line image. Acta Geod. Et Cartogr. Sin. 2013, 42, 523–529. (In Chinese) [Google Scholar]
- Lin, G.; Wolfe, R.E.; Zhang, P.; Tilton, J.C.; Dellomo, J.J.; Tan, B. Thirty-six combined years of MODIS geolocation trending. In Proceedings of the Conference on Earth Observing Systems XXIV, San Diego, CA, USA, 11–15 August 2019. [Google Scholar]
- Gao, H.; Luo, W.; Shi, H.; Mo, F.; Li, S.; Zhang, X.; Liu, X.; Cao, H. Structural stability design and implementation of ZY-3 satellite. Spacecr. Eng. 2016, 25, 18–24. (In Chinese) [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant key points. Int. J. Comput. Vision. 2004, 60, 91–110. [Google Scholar] [CrossRef]




| Datasets | FWD | NAD | BWD | |||
|---|---|---|---|---|---|---|
| 20121001 | 113.831° E | 33.852° N | 114.353° E | 35.838° N | 114.898° E | 37.807° N |
| 20130604 | 114.401° E | 34.110° N | 114.916° E | 36.061° N | 115.472° E | 38.069° N |
| 20140220 | 117.181° E | 33.480° N | 117.705° E | 35.462° N | 118.261° E | 37.435° N |
| 20151206 | 116.728° E | 37.268° N | 117.272° E | 39.224° N | 117.856° E | 41.214° N |
| 20160921 | 115.018° E | 34.101° N | 115.534° E | 36.061° N | 116.093° E | 38.059° N |
| 20170510 | 114.368° E | 34.101° N | 114.876° E | 36.060° N | 115.421° E | 38.059° N |
| 20171029 | 114.430° E | 34.102° N | 114.950° E | 36.061° N | 115.508° E | 38.060° N |
| 20180904 | 115.516° E | 34.102° N | 116.035° E | 36.061° N | 116.591° E | 38.059° N |
| 20190701 | 115.764° E | 34.102° N | 116.281° E | 36.061° N | 116.835° E | 38.059° N |
| 20200521 | 118.121° E | 32.913° N | 118.625° E | 34.874° N | 119.165° E | 36.873° N |
| Datasets | ||||||
|---|---|---|---|---|---|---|
| (Arc Seconds) | (Arc Seconds/s) | |||||
| 20121001 | 0.00 | 0.00 | 0.00 | 0.16 | −0.12 | 0.02 |
| 20130604 | −2.59 | −1.64 | 6.25 | −0.05 | 0.03 | −0.40 |
| 20140220 | −4.34 | −7.99 | −2.38 | −0.17 | −0.12 | −0.87 |
| 20151206 | −21.94 | −68.81 | −41.16 | 0.04 | 0.04 | 0.33 |
| 20160921 | −26.02 | −74.13 | −31.04 | 0.06 | 0.05 | 0.76 |
| 20170510 | −24.70 | −62.63 | −26.39 | −0.04 | −0.07 | 0.62 |
| 20171029 | −21.85 | −63.96 | −32.30 | 0.11 | −0.06 | 0.48 |
| 20180904 | −27.23 | −60.05 | −27.32 | −0.03 | −0.02 | 0.17 |
| 20190701 | −25.66 | −22.96 | −12.22 | 0.24 | 0.21 | 0.86 |
| 20200521 | −21.20 | −27.87 | −16.66 | 0.06 | −0.05 | 0.36 |
| Average | −17.55 | −39.00 | −18.32 | 0.04 | −0.01 | 0.23 |
| Absolute Maximum | 27.23 | 74.13 | 41.16 | 0.24 | 0.21 | 0.87 |
| Variance | 115.53 | 889.64 | 250.93 | 0.014 | 0.0098 | 0.29 |
| Dataset | NAD | FWD | BWD | |||
|---|---|---|---|---|---|---|
| Sample | Line | Sample | Line | Sample | Line | |
| 20121001 | 0.79 | 0.19 | 0.76 | 0.49 | 0.62 | 0.61 |
| 20130604 | 0.57 | 0.46 | 0.43 | 1.82 | 1.36 | 1.61 |
| 20140220 | 0.62 | 0.26 | 0.81 | 2.26 | 0.47 | 2.16 |
| 20151206 | 0.45 | 0.43 | 2.60 | 1.79 | 1.07 | 3.98 |
| 20160921 | 0.50 | 0.36 | 1.63 | 3.93 | 1.42 | 3.50 |
| 20170510 | 0.73 | 0.51 | 0.84 | 2.92 | 2.57 | 3.49 |
| 20171029 | 0.59 | 0.39 | 0.73 | 2.54 | 3.21 | 3.90 |
| 20180904 | 0.49 | 0.39 | 2.26 | 1.69 | 2.02 | 4.58 |
| 20190701 | 0.52 | 0.35 | 1.94 | 2.02 | 2.08 | 4.82 |
| 20200521 | 0.77 | 0.51 | 0.74 | 1.66 | 4.19 | 5.22 |
| Average | 0.60 | 0.39 | 1.27 | 2.11 | 1.90 | 3.39 |
| Variance | 0.015 | 0.01 | 0.58 | 0.82 | 1.37 | 2.21 |
| Datasets | Before | Sample Direction | Before | Line Direction | ||||
|---|---|---|---|---|---|---|---|---|
| After Compensation | After Compensation | |||||||
| 6 par. | 4 par. | 2 par. | 6 par. | 4 par. | 2 par. | |||
| 20121001 | 0.76 | 0.40 | 0.40 | 0.46 | 0.49 | 0.40 | 0.50 | 0.50 |
| 20130604 | 0.43 | 0.32 | 0.32 | 0.62 | 1.82 | 0.56 | 0.59 | 0.59 |
| 20140220 | 0.81 | 0.27 | 0.27 | 0.31 | 2.26 | 0.46 | 0.46 | 0.52 |
| 20151206 | 2.60 | 0.58 | 0.58 | 0.60 | 1.79 | 0.55 | 0.57 | 0.58 |
| 20160921 | 1.63 | 0.52 | 0.52 | 0.52 | 3.93 | 0.44 | 0.47 | 0.47 |
| 20170510 | 0.84 | 0.59 | 0.59 | 0.60 | 2.92 | 0.60 | 0.60 | 0.68 |
| 20171029 | 0.73 | 0.63 | 0.63 | 0.64 | 2.54 | 0.42 | 0.43 | 0.45 |
| 20180904 | 2.26 | 0.55 | 0.55 | 0.55 | 1.69 | 0.42 | 0.45 | 0.45 |
| 20190701 | 1.94 | 0.55 | 0.55 | 0.56 | 2.02 | 0.50 | 0.53 | 0.56 |
| 20200521 | 0.74 | 0.59 | 0.59 | 0.60 | 1.66 | 0.54 | 0.56 | 0.56 |
| Average | 1.27 | 0.5 | 0.5 | 0.55 | 2.11 | 0.49 | 0.52 | 0.54 |
| Datasets | Before | Sample Direction | Before | Line Direction | ||||
|---|---|---|---|---|---|---|---|---|
| After Compensation | After Compensation | |||||||
| 6 par. | 4 par. | 2 par. | 6 par. | 4 par. | 2 par. | |||
| 20121001 | 0.62 | 0.39 | 0.39 | 0.80 | 0.61 | 0.53 | 0.60 | 0.58 |
| 20130604 | 1.36 | 0.31 | 0.31 | 0.74 | 1.61 | 0.58 | 0.59 | 0.59 |
| 20140220 | 0.47 | 0.33 | 0.33 | 0.36 | 2.16 | 0.30 | 0.33 | 0.33 |
| 20151206 | 1.07 | 0.51 | 0.51 | 0.51 | 3.98 | 0.47 | 0.47 | 0.48 |
| 20160921 | 1.42 | 0.37 | 0.37 | 0.37 | 3.50 | 0.47 | 0.51 | 0.53 |
| 20170510 | 2.57 | 0.58 | 0.58 | 0.67 | 3.49 | 0.61 | 0.64 | 0.66 |
| 20171029 | 3.21 | 0.57 | 0.57 | 0.67 | 3.90 | 0.47 | 0.49 | 0.56 |
| 20180904 | 2.02 | 0.45 | 0.45 | 0.46 | 4.58 | 0.43 | 0.48 | 0.51 |
| 20190701 | 2.08 | 0.51 | 0.51 | 0.60 | 4.82 | 0.40 | 0.40 | 0.40 |
| 20200521 | 4.19 | 0.73 | 0.73 | 0.73 | 5.22 | 0.54 | 0.55 | 0.57 |
| Average | 1.90 | 0.48 | 0.48 | 0.59 | 3.39 | 0.48 | 0.51 | 0.52 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Tang, X.; Zhang, G.; Liu, B.; Hu, W.; Pan, H. Long-Periodic Analysis of Boresight Misalignment of Ziyuan3-01 Three-Line Camera. Remote Sens. 2022, 14, 1157. https://doi.org/10.3390/rs14051157
Zhu X, Tang X, Zhang G, Liu B, Hu W, Pan H. Long-Periodic Analysis of Boresight Misalignment of Ziyuan3-01 Three-Line Camera. Remote Sensing. 2022; 14(5):1157. https://doi.org/10.3390/rs14051157
Chicago/Turabian StyleZhu, Xiaoyong, Xinming Tang, Guo Zhang, Bin Liu, Wenmin Hu, and Hongbo Pan. 2022. "Long-Periodic Analysis of Boresight Misalignment of Ziyuan3-01 Three-Line Camera" Remote Sensing 14, no. 5: 1157. https://doi.org/10.3390/rs14051157
APA StyleZhu, X., Tang, X., Zhang, G., Liu, B., Hu, W., & Pan, H. (2022). Long-Periodic Analysis of Boresight Misalignment of Ziyuan3-01 Three-Line Camera. Remote Sensing, 14(5), 1157. https://doi.org/10.3390/rs14051157








