1. Introduction
The interaction of the atmosphere with the ocean is strongest in the tropics, where deep convection and rain-induced downbursts drive intense vertical exchanges of momentum, heat, and moisture. Under the right conditions, these moist convective processes organize upscale through aggregation of individual cloud systems (thunderstorms) into a mesoscale convective system (MCS)—a large contiguous area of convective and stratiform rain spanning about 100 km or more in at least one horizontal direction that can persist for several hours [
1]. Examples of MCSs over the tropical ocean include tropical cyclones and squall lines, and they are found embedded in tropical waves, superclusters, and the Madden–Julian oscillation. MCSs and other forms of organized convection are absent from contemporary global numerical weather prediction (NWP) and global climate models (GCMs) due to insufficient numerical resolution and inadequate parameterizations [
2,
3]. Furthermore, the global observing system does not allow the 4D tracking of these small-scale processes in NWP data assimilation [
4]. As a result, further theoretical and observational studies are necessary to support the appropriate representation of these processes in GCMs.
A conceptual model of a mature MCS and the relationship between its spatial structure and precipitation intensity are shown in
Figure 1 (see Refs. [
1,
5]). Precipitating clouds are organized horizontally into three regions: a stratiform region, a convective region, and a narrow transition zone linking the two. The convective region consists of young, active deep convection where moist surface air is drawn in and carried upwards in strong (5–10 m s
) convective-scale (∼10 km) updrafts to the top of the tropopause, where it diverges and spreads out. The moist updraft air rises, expands, cools, and then condenses into cloud and rain drops, which freeze when lifted above the 0
C level. Condensation and freezing releases heat into the air, increasing its buoyancy and uplift. As the convective updraft ages, vertical air motion weakens to the extent that aggregated precipitating particles fall out, melting and evaporating on the way down, cooling the surrounding air and forcing it to descend and diverge near the ocean surface in strong downdrafts. The collective outflow of cold air from the downdrafts of individual convective cells spreads out horizontally, displacing the warmer boundary layer air to form a
cold pool at the surface, and a
gust front at its periphery, which in turn promotes more deep convection. In the transition zone, convective cells age and decay such that vertical air motions weaken to the point that the level of peak convergence slopes upward until it sits atop the melting layer (appearing on radar as a “bright band”). Now the MCS has a stratiform structure consisting of two layers: an upper level dominated by weak updrafts (mesoscale updraft) and a lower level dominated by weak downdrafts (mesoscale downdraft). Hydrometeor trajectories are shown illustrating the process of fall speed sorting, differential hydrometeor source-region altitude, and nonuniform vertical air motions through the stratiform region. Clearly, the interaction of rain and wind is fundamental to the existence of MCSs.
The small-scale wind variability in and near MCSs can be resolved by C-band fixed fan-beam space-borne scatterometers, such as the advanced scatterometer (ASCAT) on-board the MetOp series of satellites [
6,
7,
8,
9,
10,
11,
12]. The potential of ASCAT to detect the horizontal wind divergence associated with individual MCS downdrafts was investigated by Kilpatrick and Xie [
9], who concluded that ASCAT could reliably detect mesoscale (100–300 km) downdrafts, but not convective-scale (5–20 km) gust fronts. However, that conclusion was based on an analysis that did not include wind vectors from areas with rain rates greater than 3 mmh
. The exclusion of such data was based on rain contamination problems experienced with Ku-band QuikSCAT winds. However, quality assessment studies showed that ASCAT winds are much less affected by rain than Ku-band scatterometer winds [
13].
Rain contamination (i.e., signal attenuation, volume scattering from drops, and rain splashing and capillary wave attenuation effects at the surface) of the radar signal was shown to be small for ASCAT [
6,
7] (see also [
14,
15]), while the presence of rain, downdrafts, and updrafts increases the variability of the wind within a wind vector cell (WVC, the area from which radar backscatter is received and processed to produce a wind vector (c.f., [
16])). This enhanced subcell wind variability increases the wind representativeness error in NWP model and buoy comparisons and leads to some uncertainty in the interpretation of ASCAT retrieved wind quality in triple collocation analyses [
8]. Furthermore, it degrades even more NWP wind quality, since NWP models are unable to resolve the rain-induced dynamics [
8]. Thus, the consistency between ASCAT, buoy, and NWP winds is not reduced by rain contamination, but mainly by the strong local wind gradients associated with heavy rain [
7]. As a result, Lin et al. [
8] concluded that in applications such as nowcasting and oceanography, flagged winds should be kept since they contain essential information on gustiness and air–sea interaction processes. That conclusion is supported by Priftis et al. [
10], who combined ASCAT with Next Generation Weather Radar (NEXRAD), soundings, and buoys to explore wind structures produced by oceanic MCSs near two coastal locations in the United States. Using all ASCAT winds, regions of convergence and divergence within the MCSs, as well as outflow boundaries associated with downdrafts, were successfully identified.
The above studies demonstrate that ASCAT-derived wind fields and their spatial derivatives contain useful information on the interaction between winds and rain. A next step is to quantify that information in ways that can help improve parameterizations of moist convection. If simultaneous and reliable measurements of wind and rain fields were possible, then it would be straightforward to calculate and analyze space–time correlations. At present that is not possible. (However, such simultaneous measurements will be acquired in the future (from 2024 approximately), as the Metop Second Generation (Metop-SG) satellite series will carry on board the C-band scatterometer SCA and the high-frequency microwave radiometer MWI.) On the other hand, correlations can be investigated in a more limited way using ASCAT winds from the ASCAT triple configuration (i.e., ASCAT-A, B, and C on-board MetOp-A, B, and C, respectively, separated in time by 50 min (max)) collocated with rain fields retrieved from Meteosat Second Generation (MSG) geostationary imagery (namely, the daytime MSG rain product produced by the Royal Netherlands Meteorological Institute (KNMI)). One such collocation is illustrated in
Figure 2. This figure shows wind vectors in the overlapped portion of two ASCAT swaths in the tandem configuration together with contours of a time-collocated MSG rain field. Note that the modification of the observed wind field (within 50 min) by the presence of heavy rain is remarkable and extends up to a few hundred kilometers from the rain cell location. Note also the areas of strongly converging and diverging wind vectors (pointed to in the figure by the letters C and D). These features occur near convective rain cells (>10 mm h
), implying the presence of updrafts, downdrafts, and gust fronts associated to moist convection and precipitation. Finally, note that MSG geostationary rain products are available every 15 min and are therefore particularly suitable to study fast moist convection processes.
The purpose of this paper is to present a statistical approach to identify and quantify correlations between MSG rain rates and ASCAT wind divergence. We focus our attention on MSCs in the Atlantic Intertropical Convergence Zone where MCSs are plentiful, rainfall is intense, and deep convection extends from the surface to the tropopause, strongly coupling the surface with the upper troposphere. Preliminary to the correlation analysis is the need to regrid MSG rain rates to the swath grid. One approach is to regrid with the WVC average rain rate (cf. [
17]). However, for our purposes, that choice is undesirable as averaging can mask the presence of convective-scale downbursts—even a single downburst in a WVC has the potential to produce significant wind gusts. Therefore, we elected to regrid with the WVC maximum rain rate.
As will be shown, the scattergram of wind divergence vs rain rate shows a strongly nonlinear correlation, and the probability distributions of each variable are found to be heavy-tailed with a non-extreme core (a Gaussian core in the case of wind divergence). This invites thinking in terms of extreme values and a data classification that highlights the extremes of convergence, divergence, and rain. The key result is that the extremes of rain are shown to correlate with the extremes of wind divergence.
An early version of the work presented here was reported in [
18]. Since then, we learned that a methodology similar to ours is used to correlate weather extremes with climate extremes. For example, Martius et al. [
19] and Zscheischler et al. [
20] correlated wind speed extremes with precipitation extremes. Key differences between their work and ours are (i) the motivation (assessing climate risks vs improving parameterizations of organized convection), and (ii) the data and scales of interest (ERA-40 100 km gridded daily data vs high resolution wind (12.5 km) and rain (3 km) acquired in minutes by satellite instruments). [Note that ERA essentially misses the substantial variability induced by fast moist convection processes [
3].]
The paper is organized as follows. The data and study area are described in
Section 2.
Section 3 describes the methods used to calculate and classify wind divergence and regrid and classify rain rates, while
Section 4 describes the methods used to correlate the two fields. The results of the correlation analysis are given in
Section 5, and a brief summary and ideas for future work are given in
Section 6.
6. Summary and Future Work
In this paper we introduce and apply a novel approach to quantify the correlation between wind convergence/divergence with rain in the Atlantic Inter-Tropical Convergence Zone (ITCZ) using ASCAT 12.5 km winds collocated with a short time series of Meteosat Second Generation 3 km rain fields. Our approach was motivated by the observed statistics; namely, that the probability distributions for each variable were heavy-tailed and that it was the extremes of each variable that were associated with moist convection processes. A summary of our results now follows.
The variability of ASCAT scatterometer winds near rain was verified and shown to be associated with the passage of MCSs (
Figure 2). Wind divergence
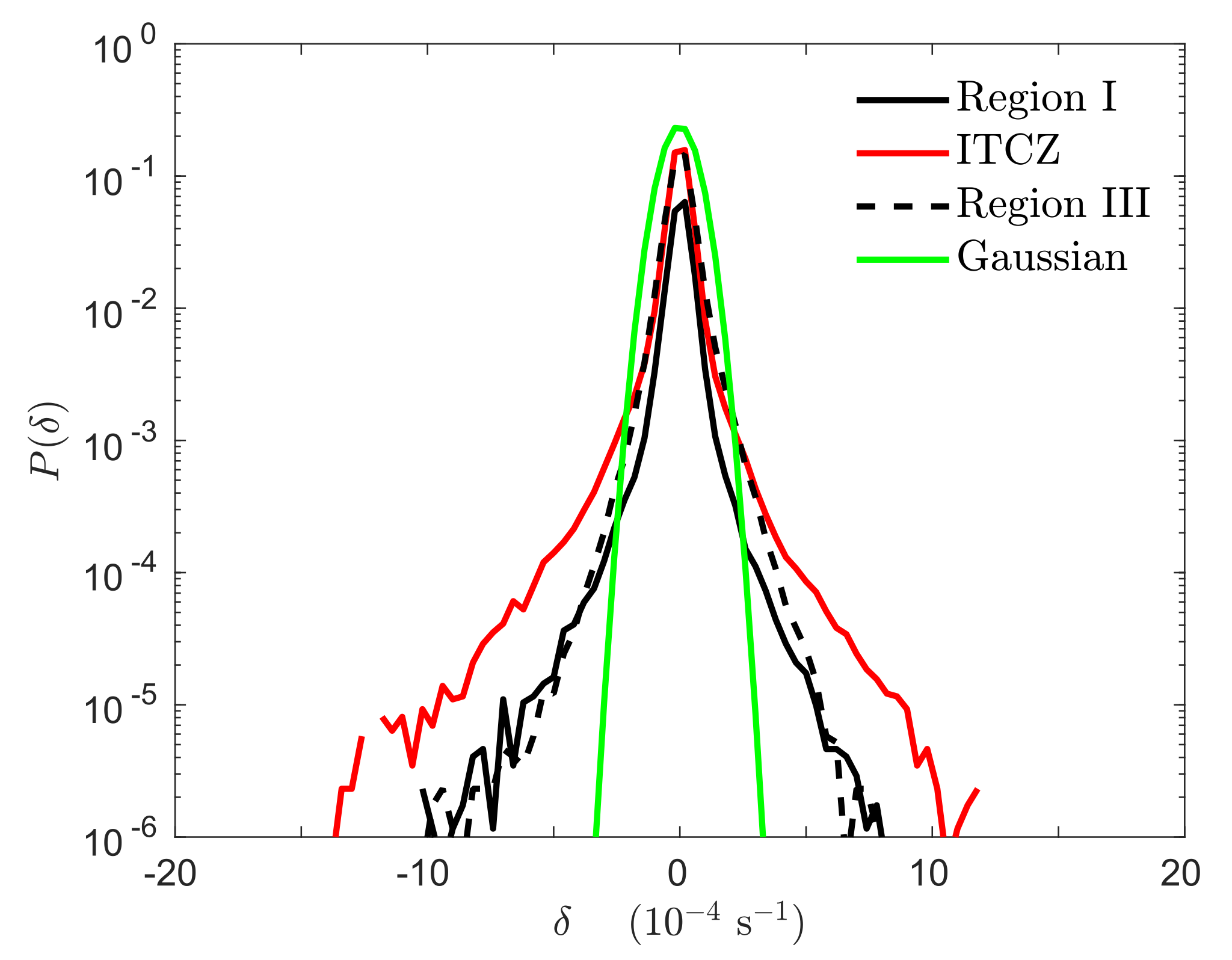
was calculated from the observed winds. Inspection of wind divergence PDFs and calculation of its moments showed that it was negatively skewed and had heavy tails (
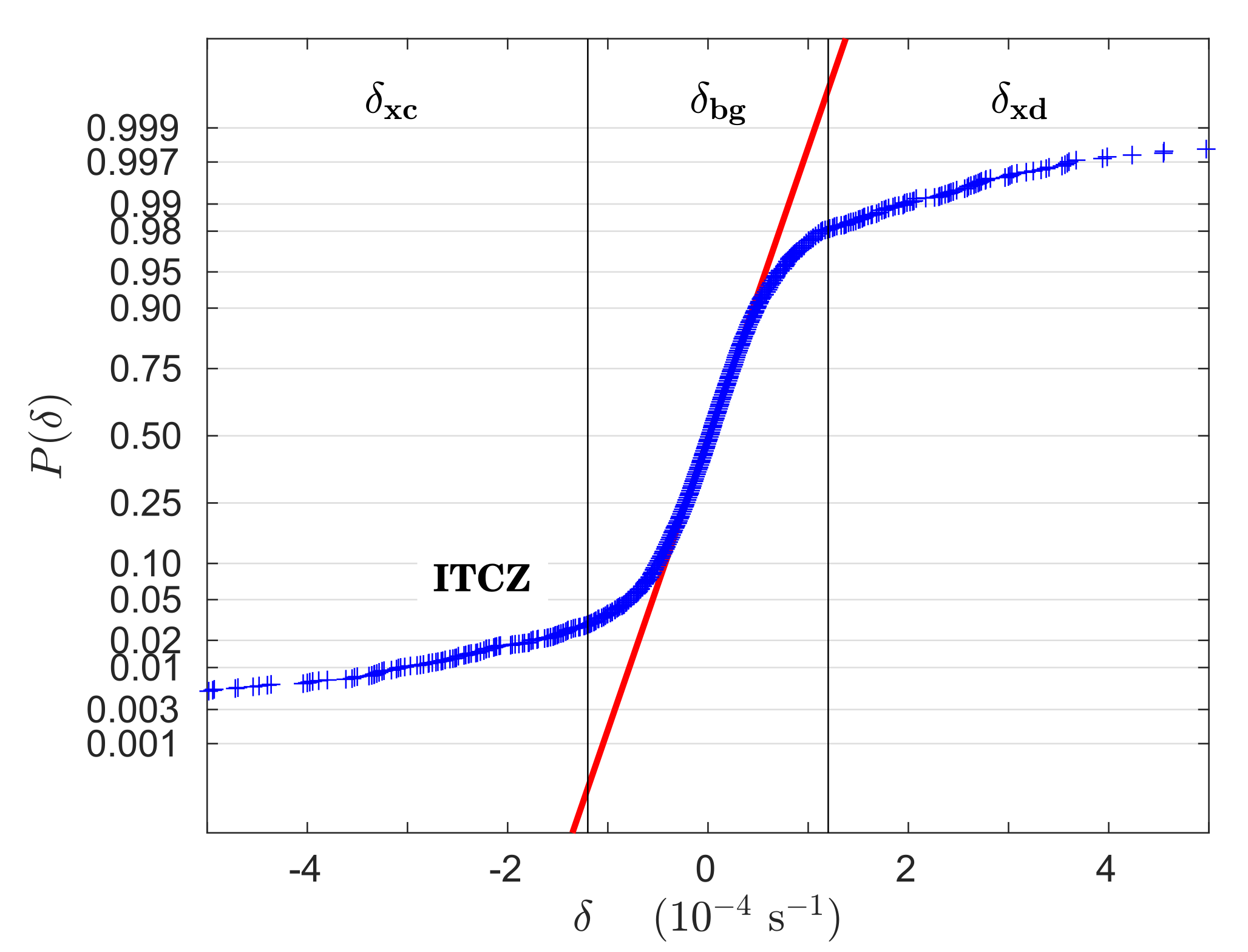
Figure 6). Physically, heavy tails are due to the processes associated with the generation of convective rain: accelerated updrafts (due to condensation and freezing of water particles) leading to reinforced convergence, and nearby cool and dry downdrafts (due to precipitation, melting and evaporation) leading to reinforced divergence. With the aid of a normal probability plot (
Figure 7), thresholds were defined to partition
into three classes: background
, convergence extremes
, and divergence extremes
.
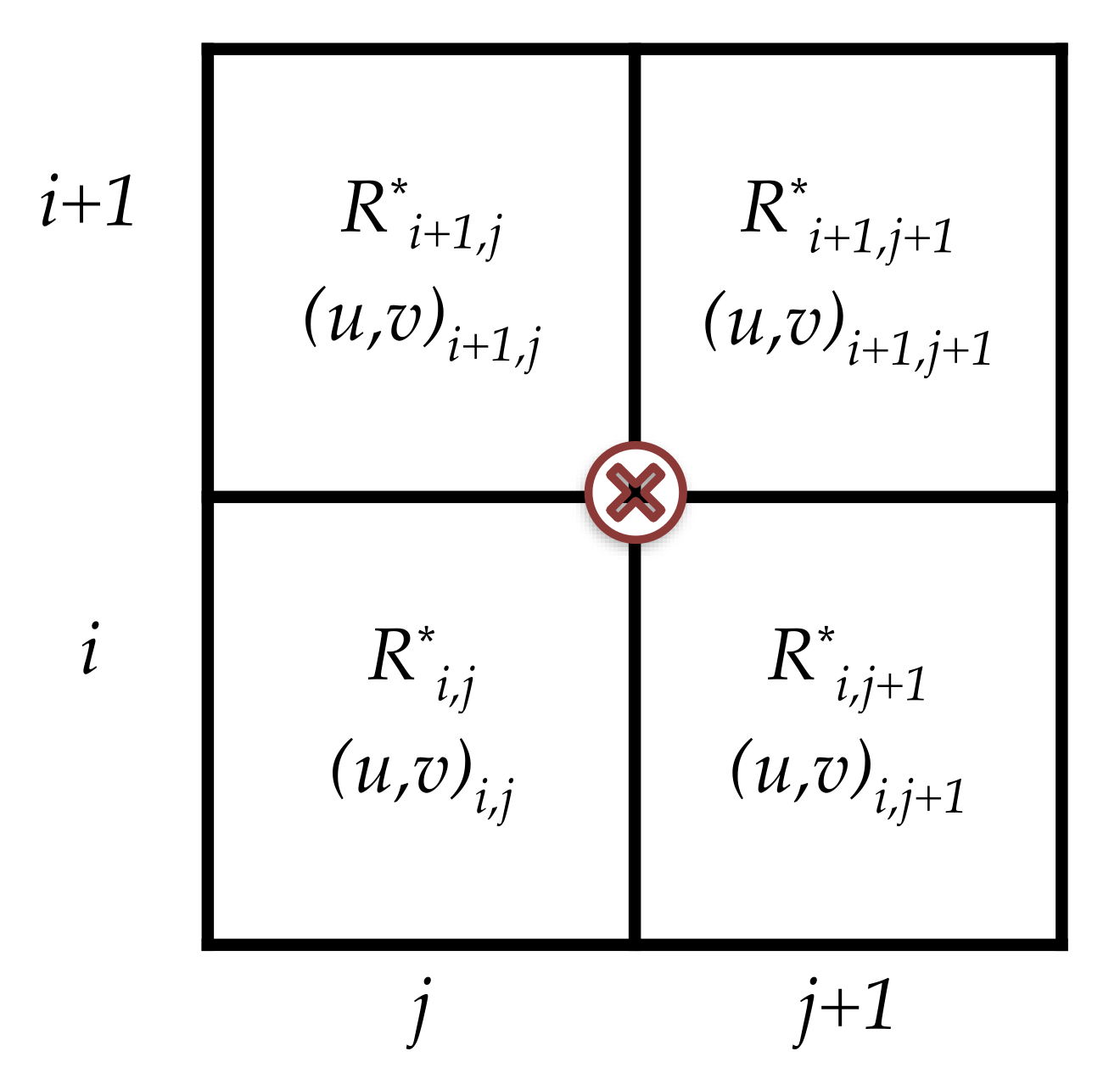
To avoid loss of information about convective-scale rain events, MSG rain was represented by the local maximum rain rate: the WVC maximum rain rate (
) on the wind grid, and the two-by-two block maximum rain rate (
) on the
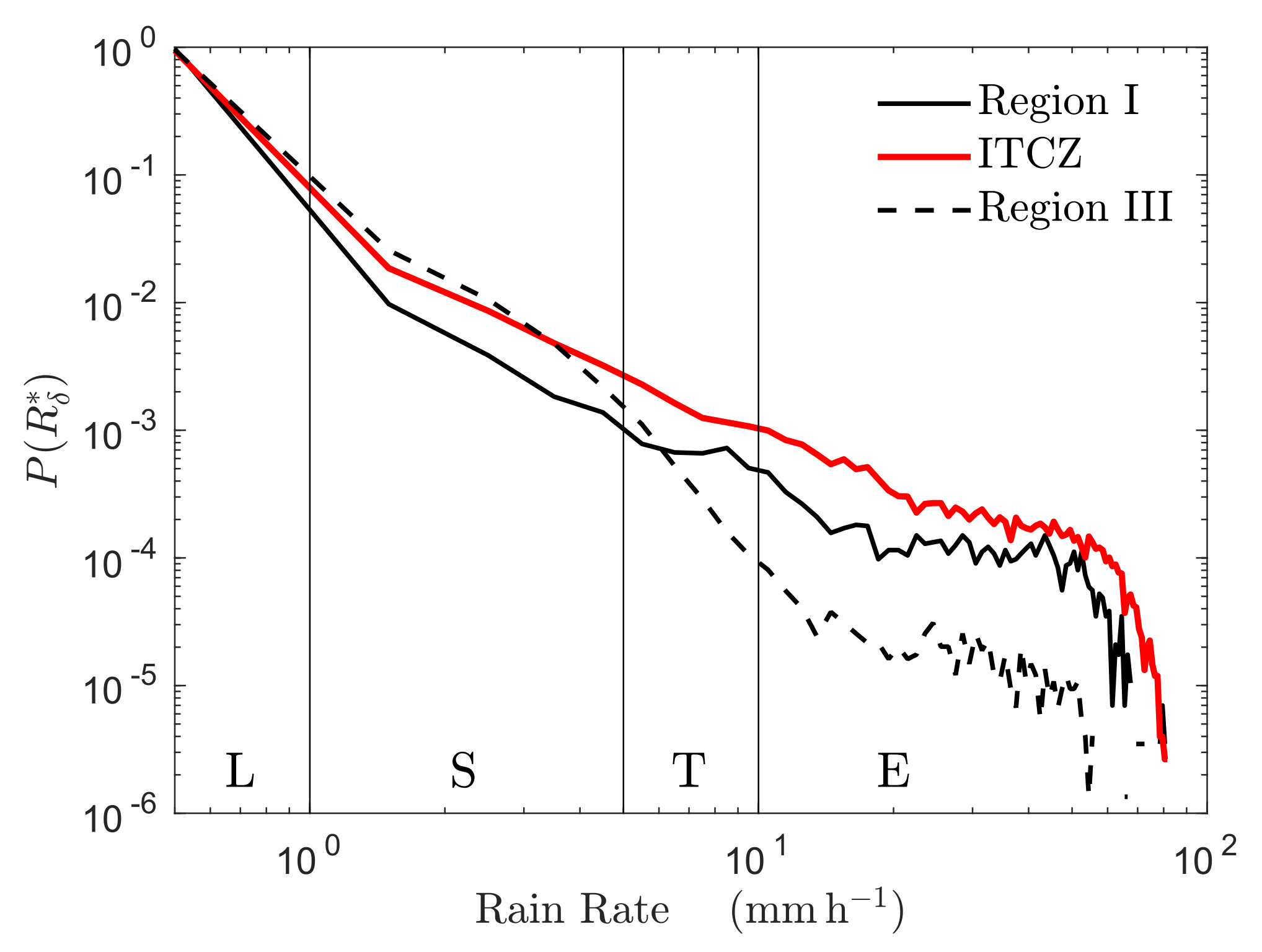
grid. Rain classes were defined based on results of observational studies of rain produced in MCS precipitating clouds (): no rain
, light rain
, stratiform rain
, transition rain
, and extreme rain
. Thresholds for these classes were based on results from many observational studies (
Table 3). PDFs of the rain rates ‘seen’ by ASCAT were presented in
Figure 8.
The correlation analysis proceeded in steps, starting with the scatter density plot (
Figure 10), which showed that the correlation between
and
is neither random nor simple. Using the class thresholds, two ways to correlate the data were identified. One was to use the rain and
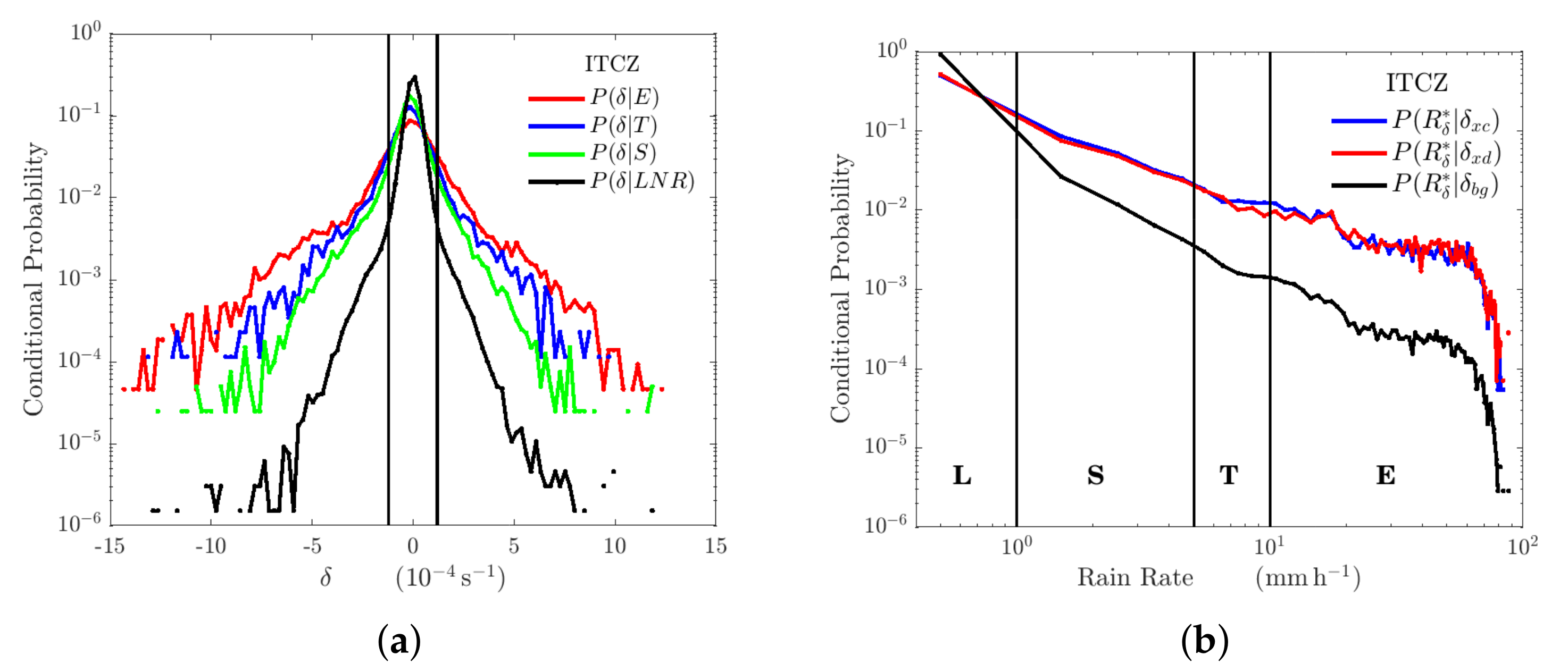
thresholds to partition the data into horizontal and vertical slices and calculate conditional distributions. In the case of horizontal slices, the conditional distributions
for each class
(
Figure 11a) show that the heavy left and right tails are approximately exponential:
, with slopes that flatten with increasing rain intensity. In the case of vertical slices, conditional distributions
for each class
(
Figure 11b) show that the heavy tails are described by a power-law:
, with a slower and approximately equal decay for the extremes of convergence and divergence.
Correlations were also quantified by the odds ratio between and extremes (i.e., and ). Many extreme rain events were found to co-occur with background divergence. A structural analysis was carried out showing that many of these points were close to extreme convergence or divergence. Reclassifying those points increased the odds ratios by a factor of three, therefore greatly strengthening the correlation.
We also found many points of extreme convergence/divergence in areas of light or no rain. These may be related to dry convection, early [
15] or late [
24] stages of moist convection, and/or small convection cells (<3 km) rather than MCSs.
An important takeaway from the structural analysis is that the nearest neighbor distributions are consistent with the moist convective processes summarized in
Figure 1, and hence reflect the known structure of MCSs. Further structural analysis of the data (e.g., using the radial distribution function) is possible and could be of interest.
Finally, the odds ratio was calculated as a function of time lag
, which showed broad but well-defined peaks at a time lag of
min for divergence and a lag of
min for convergence (
Figure 13), meaning that extreme rain lags extreme convergence by about 30 min, while extremes of rain closely precede divergence. This is consistent with descriptions of moist convection processes as described in the Introduction and conceptualized in
Figure 1. This consistency and coherence in the winds and divergence patterns, as well as its credible association with independent rain products, may be further exploited to obtain improved statistical descriptions of tropical MCS dynamics and implied fluxes.
Future Work
Here we list some ideas for future work using the ASCAT-MSG collocations. First, recall that the 2D velocity gradient tensor,
, can be decomposed as:
where
,
and
are, respectively, the divergence, rate-of-strain and rate-of-rotation tensors. Thus, the analysis carried out in this paper should be extended to investigate and correlate strain rate extremes and vorticity extremes. Exploiting this additional information should improve the fluid dynamical picture of the rain-induced dynamics near MCSs.
Second, there may be multiple deep convection cells in a WVC, or a squall line of deep convection passing through a WVC. Obviously, the spatial organization of the convection affects convergence, divergence, and shear patterns. This organization should be investigated, which could be made more efficient using databases consisting of divergence/vorticity/strain features, and of MSG cloud and precipitation features, as was performed by [
39] for observations from the Tropical Rainfall Measuring Mission (TRMM). Furthermore, applying additional statistical physics techniques to exploit the heterogeneous distribution of rain types in a WVC (e.g., using the radial distribution function), could reveal more structural information useful to modelers.
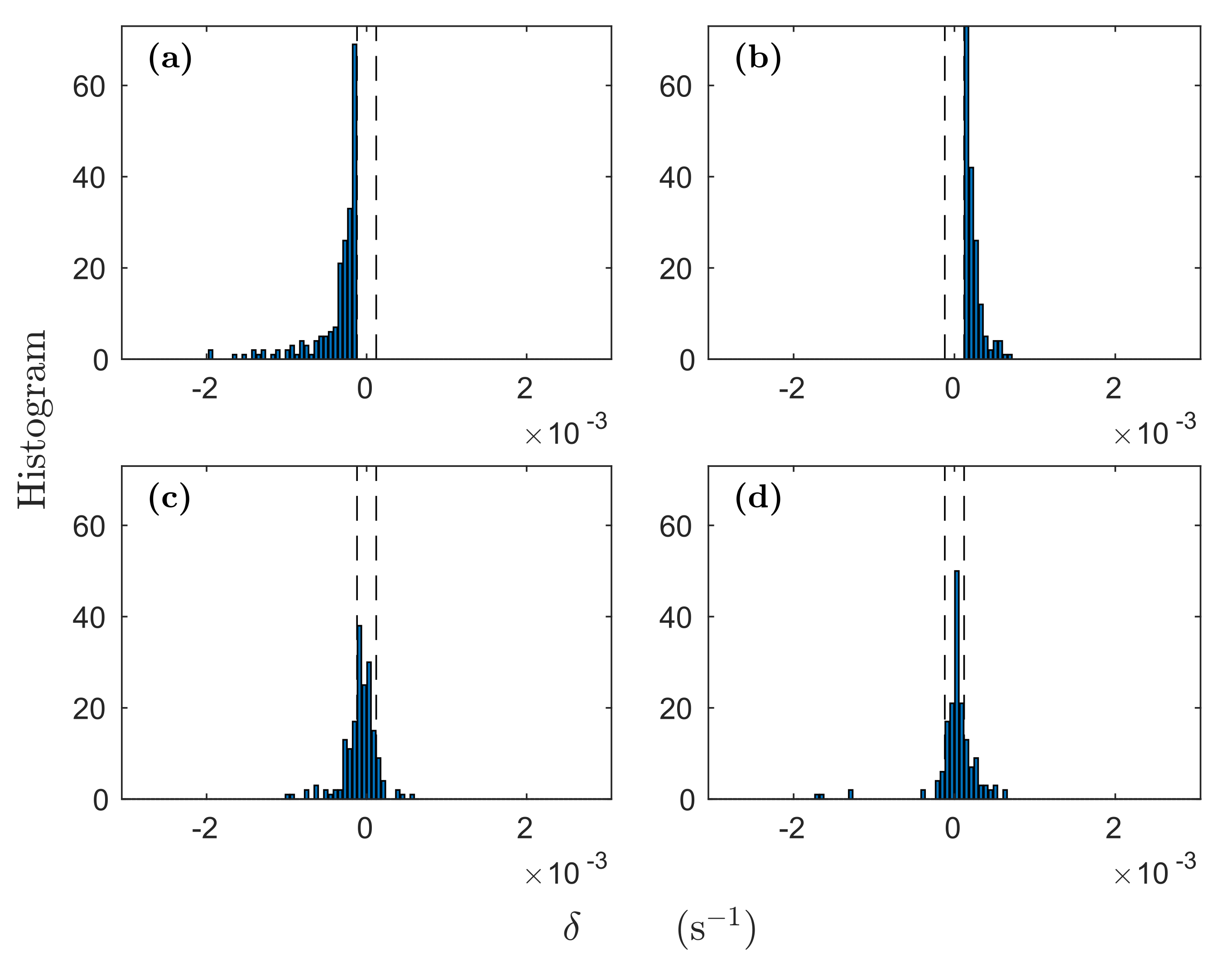
Third, there is information yet to be extracted about the time-dependent changes in the wind and rain fields from the overlapped SCAT-1 and SCAT-2 swaths. The scope of the present work did not permit us to do more than scratch the surface. A partial result that merely suggests a starting point for further work is shown in
Figure 14. The results in the figures were extracted after identifying clusters of contiguous grid points with extreme values of the convergence/divergence in the SCAT-1 swath. The top panels in the figure show the result of pooling the statistics of all
clusters (a) and
clusters (b) seen by SCAT-1. The locations of these clusters were identified in the SCAT-2 fields and the statistics were again pooled (bottom panels). The change going from the top to the bottom panel demonstrates the rapid change that occurs in the wind field by rain-induced dynamics after only 50 min.
The availability of more than 14 years of high-resolution, accurate ASCAT-derived wind fields (and about nine years of tandem ASCAT A/B and/or B/C observations) should definitely be exploited to better characterize rain-induced dynamics. Of further relevance, the same analysis should be carried out with pencil-beam Ku-band scatterometers. The latter are known to be more sensitive to rain (which was recently better depicted in [
40]). On the other hand, since they are rather noisy, spatial filters are applied, leading to rather smooth sea surface wind fields, as compared to that of fixed fan-beam C-band scatterometers (such as ASCAT). This will indeed impact their ability to capture extreme divergence/curl. However, a comprehensive analysis of the joint Ku-band and C-band scatterometer wind derivatives can help in improving the Ku-band wind derivatives near rain.
Finally, it is recommended that work be carried out in collaboration with modelers who can suggest further refinements in the analysis that can lead to improved parameterizations of moist convection.