Effect of Aerosol Vertical Distribution on the Modeling of Solar Radiation
Abstract
:1. Introduction
- How do changes in the vertical distribution of aerosol optical properties affect the solar radiation that reaches the Earth’s surface, and how do they affect the backscattered solar radiation?
- What is the magnitude of differences in the atmospheric heating rates due to changes in the vertical profile of the aerosols?
- How is the vertical distribution of actinic flux (AF), (i.e., the radiometric quantity that is of direct interest for photochemical reactions) affected by changes in the vertical profile of aerosols?
- What is the effect on spectral solar radiation from different aerosol loads and absorption properties of aerosols at different altitudes?
2. Data and Methodology
- As a first step, the sensitivity of the solar radiation profile to the altitude of a hypothetical aerosol layer was investigated using artificial aerosol extinction coefficient profiles.
- As a second step, radiative transfer (RT) simulations were performed using aerosol extinction coefficient profiles from the LIdar climatology of Vertical Aerosol Structure for space-based lidar simulation studies (LIVAS) [56], and the results were compared with the results of simulations with the default libRadtran profile [22] which assumed an exponential decrease in the aerosol extinction coefficient with altitude in the troposphere.
2.1. LIVAS
2.2. Radiative Transfer Simulations
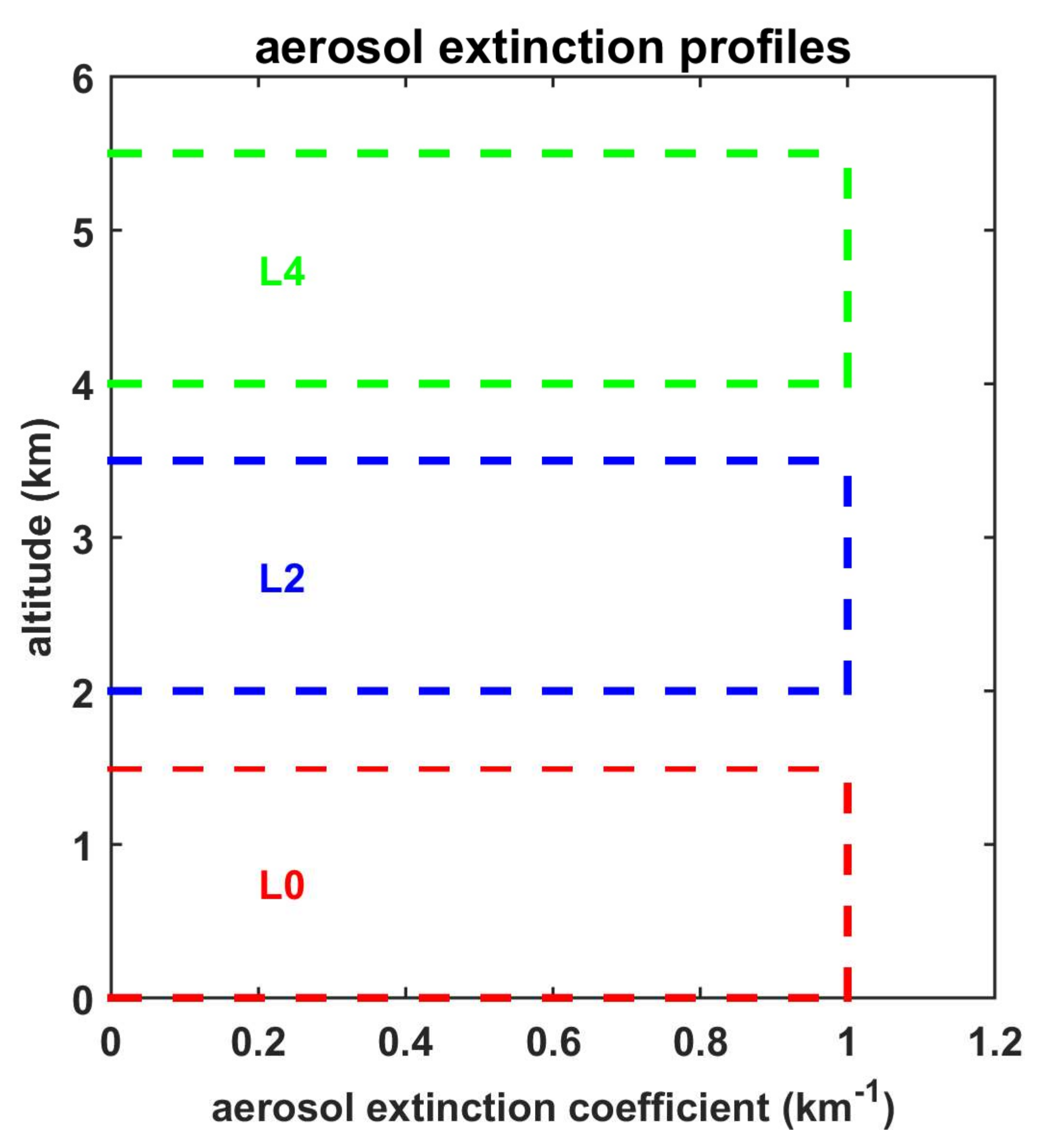
2.3. Sensitivity Study Using Artificial Extinction Profiles
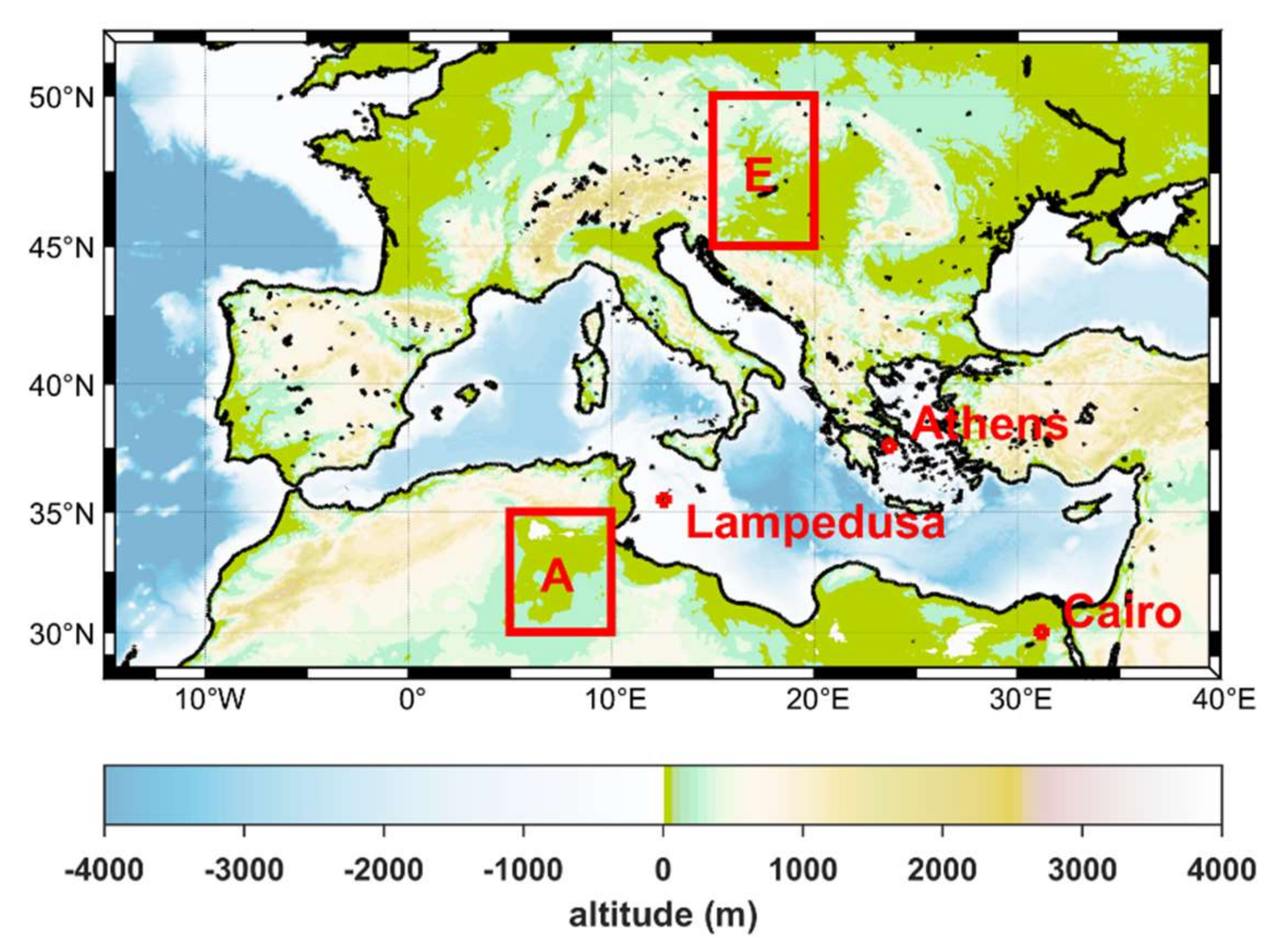
2.4. Simulations Using Theoretical and LIVAS Profiles for Typical Aerosol Conditions
2.5. Simulations Using Theoretical and LIVAS Profiles for High Aerosol Load
3. Results and Discussion
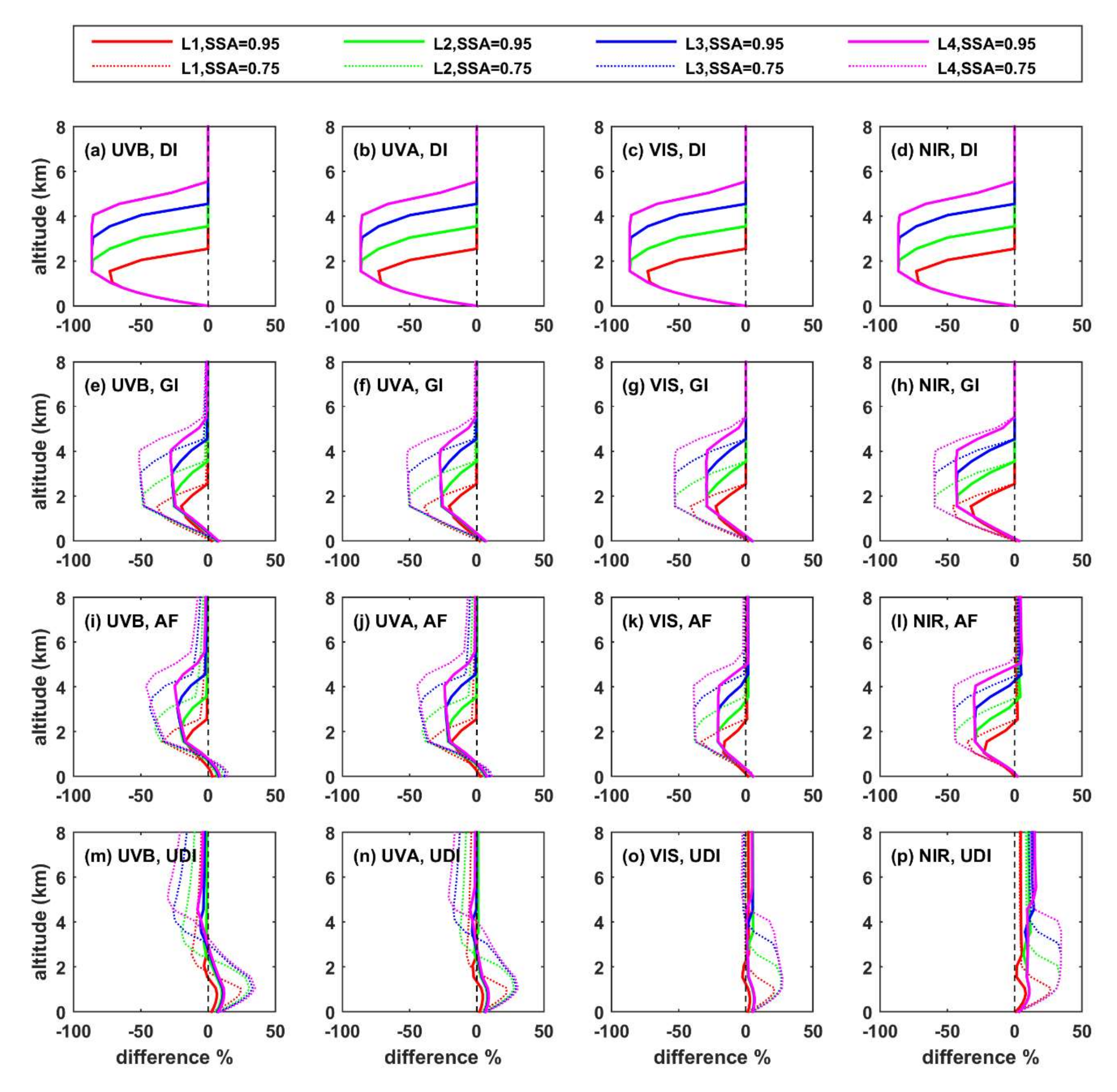
3.1. Altitude of the Aerosol Layer
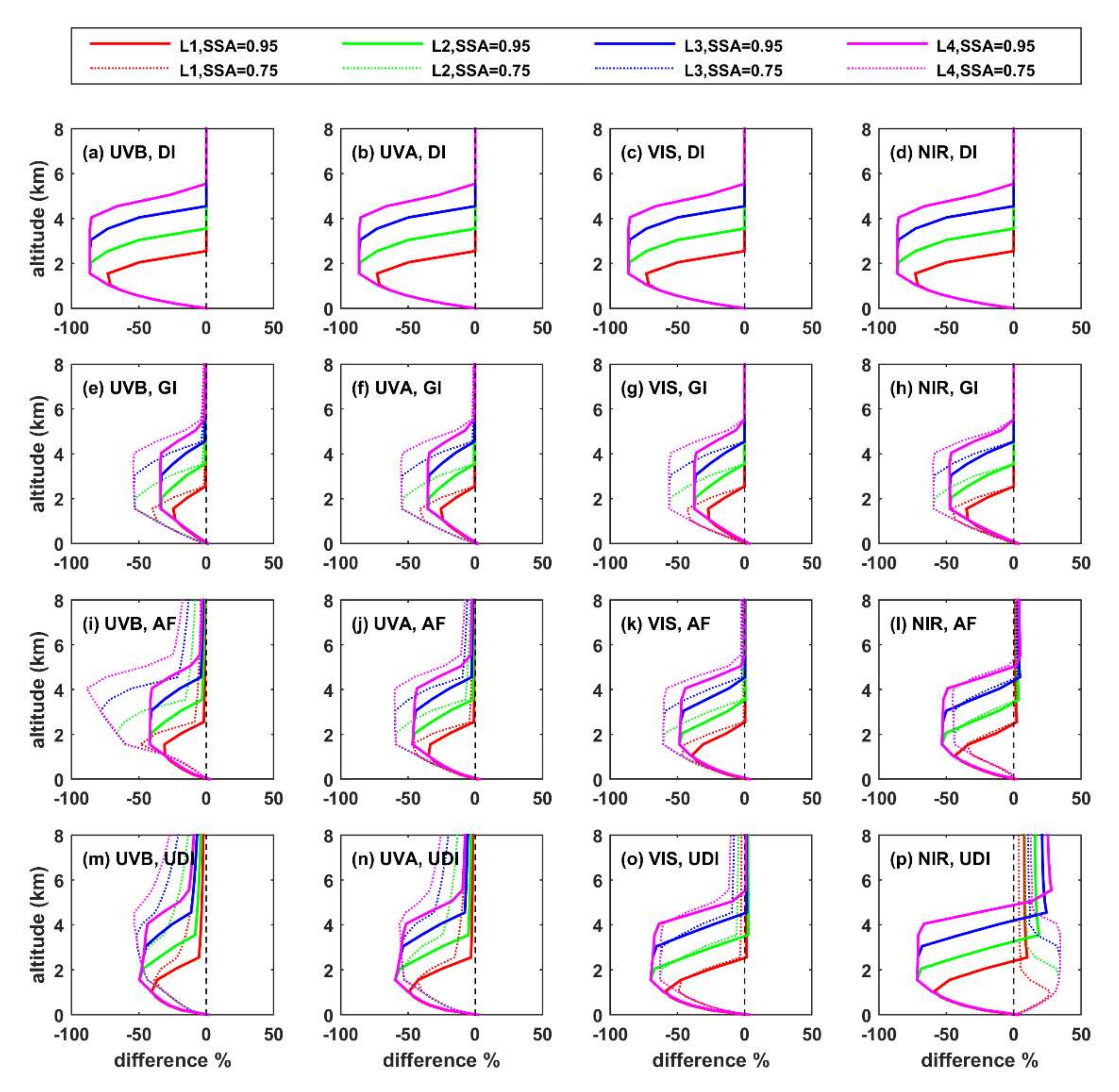
3.1.1. Direct Irradiance
3.1.2. Diffuse Downwelling and Upwelling Irradiances
Downwelling Diffuse Irradiance
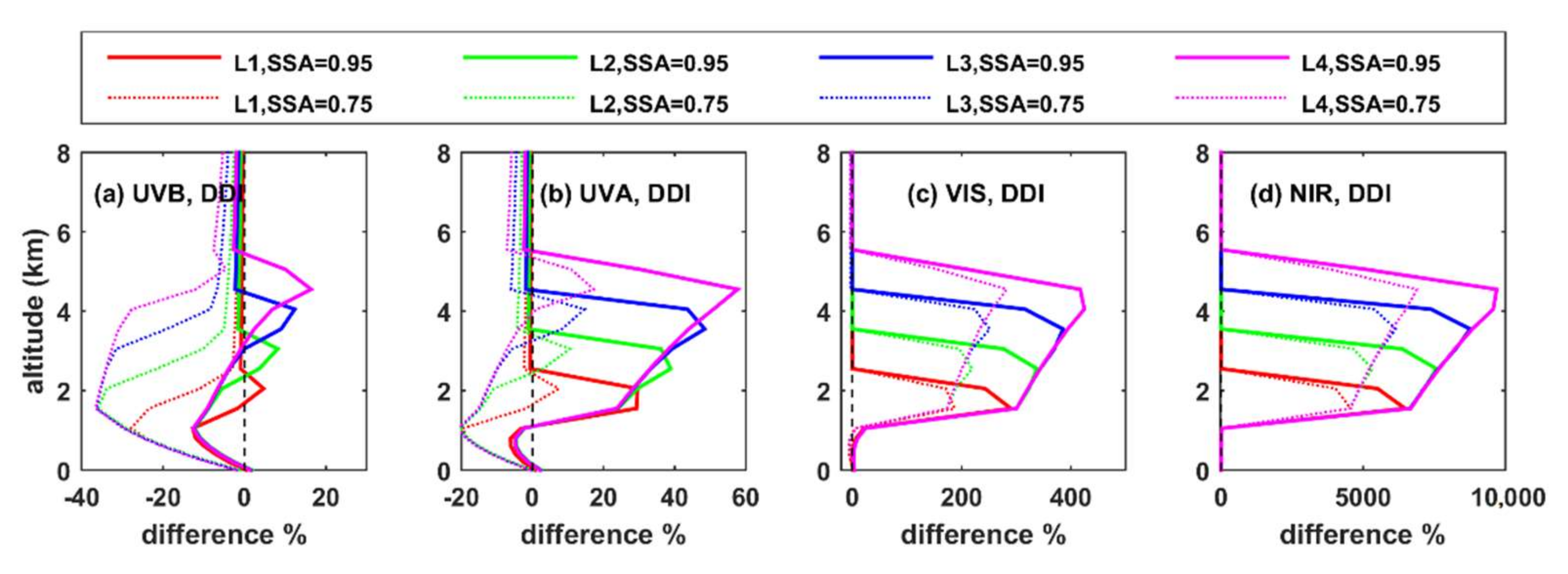
Upwelling Diffuse Irradiance
3.1.3. Global Irradiance
3.1.4. Actinic Flux
3.1.5. Heating Rates
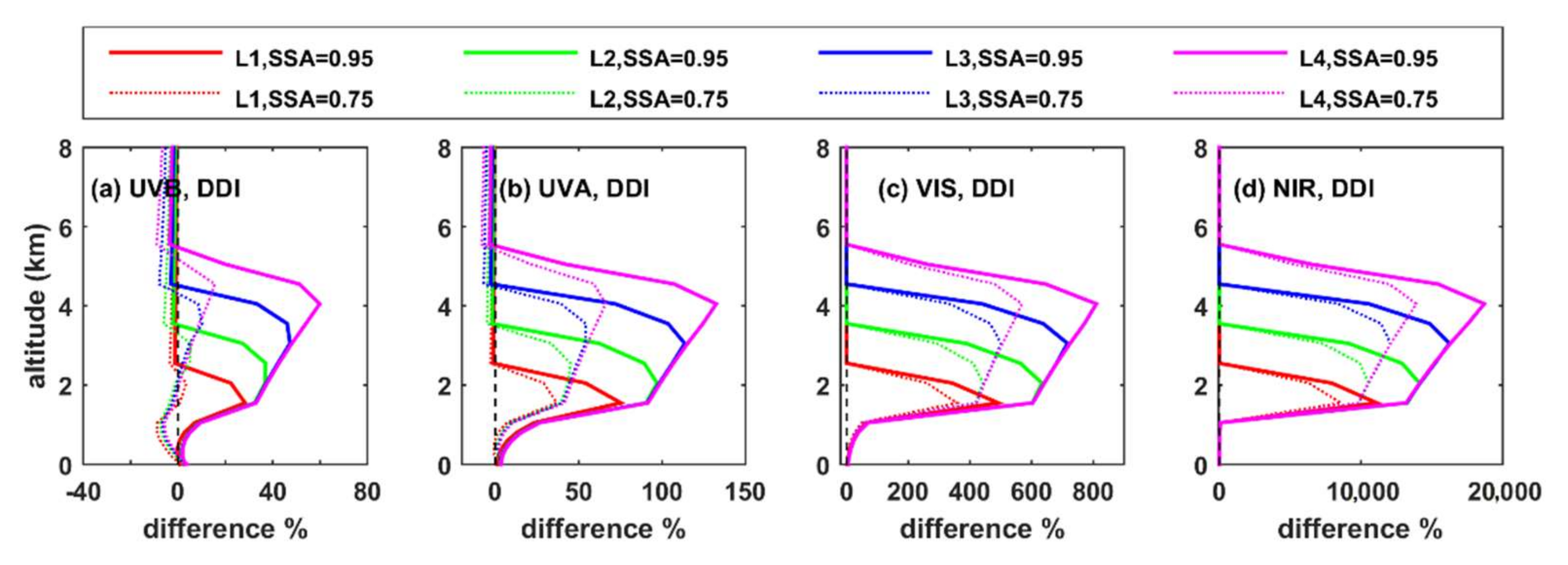
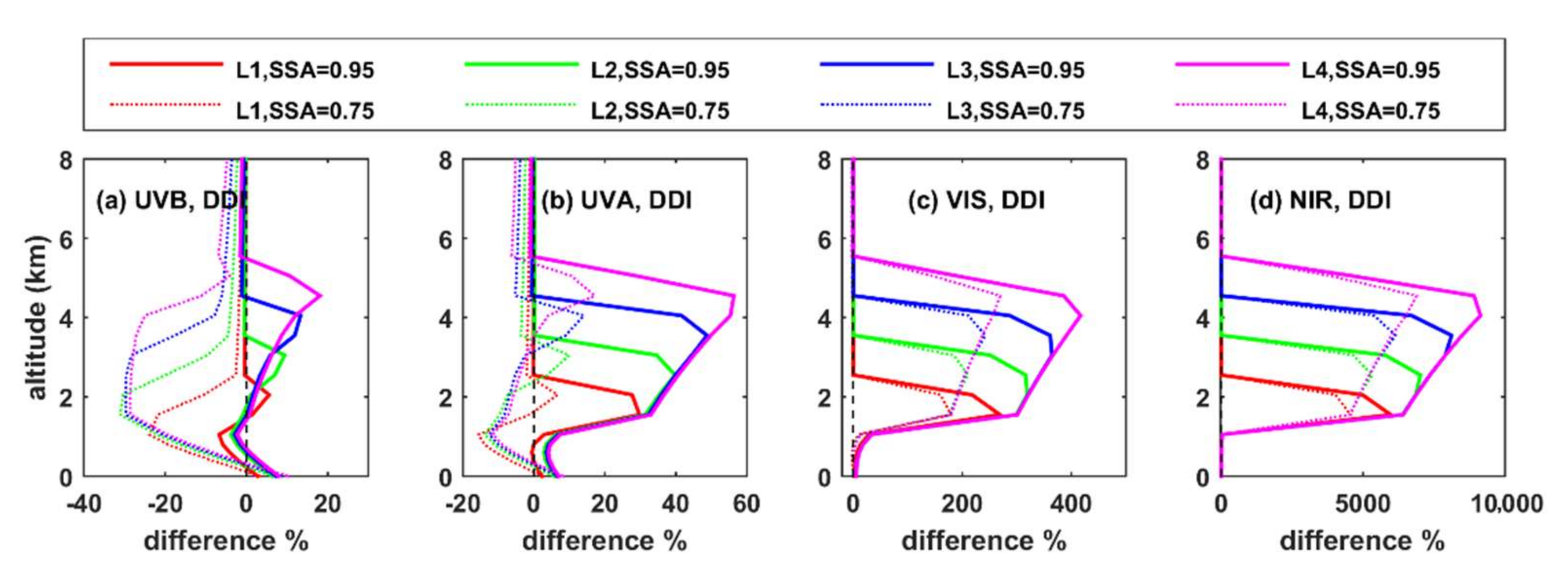
3.1.6. Top and Bottom of the Atmosphere
BOA
TOA
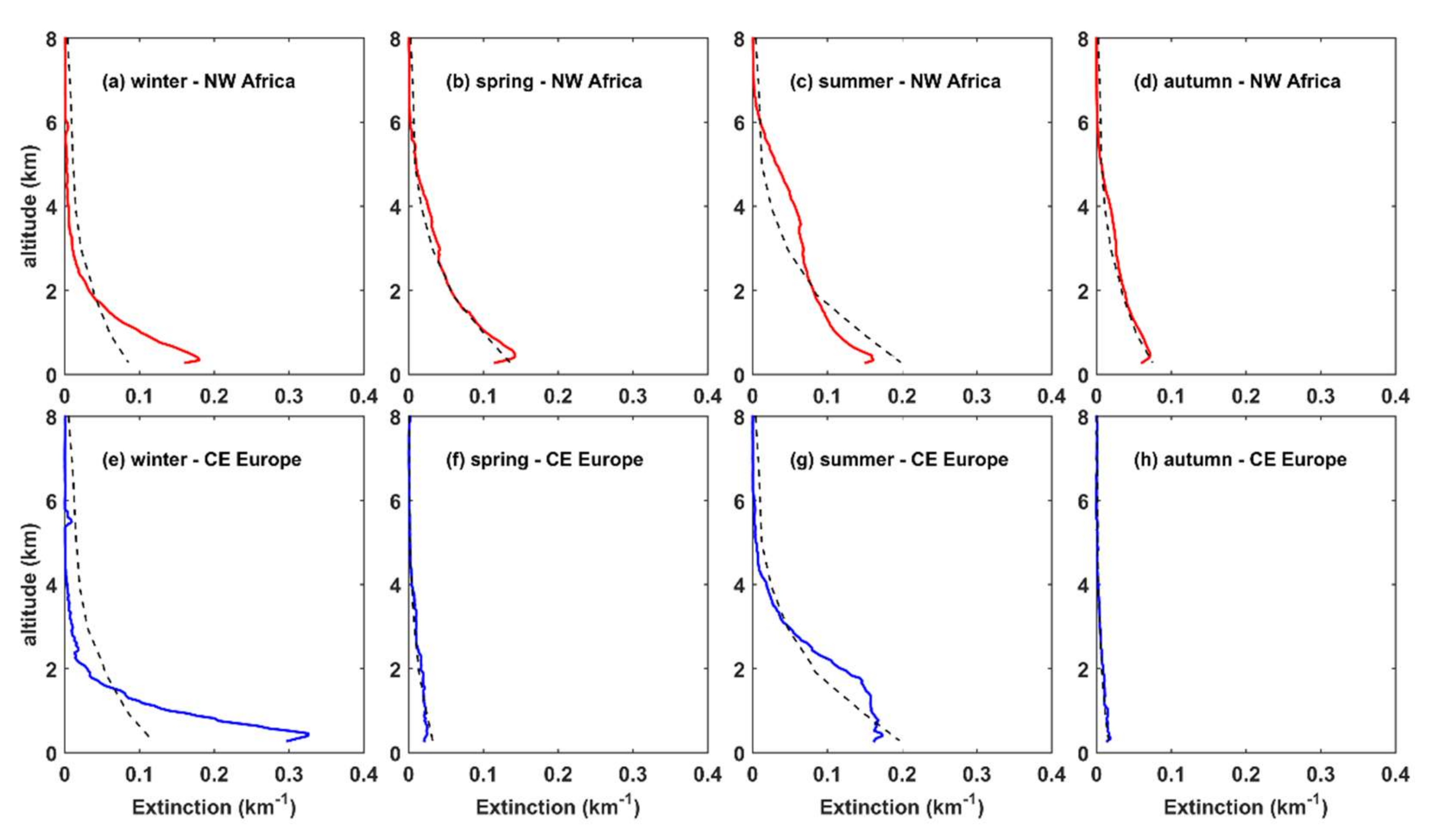
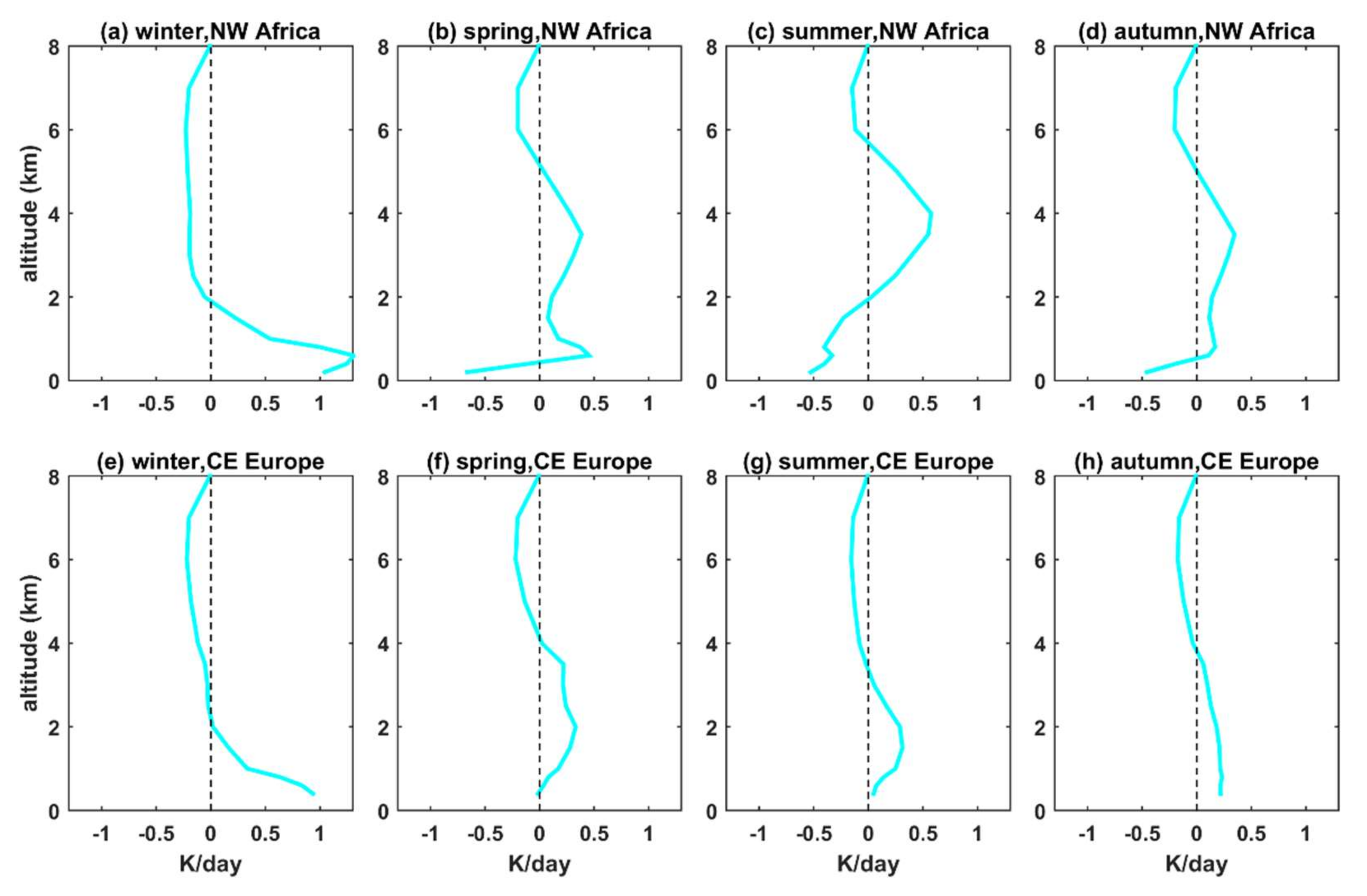
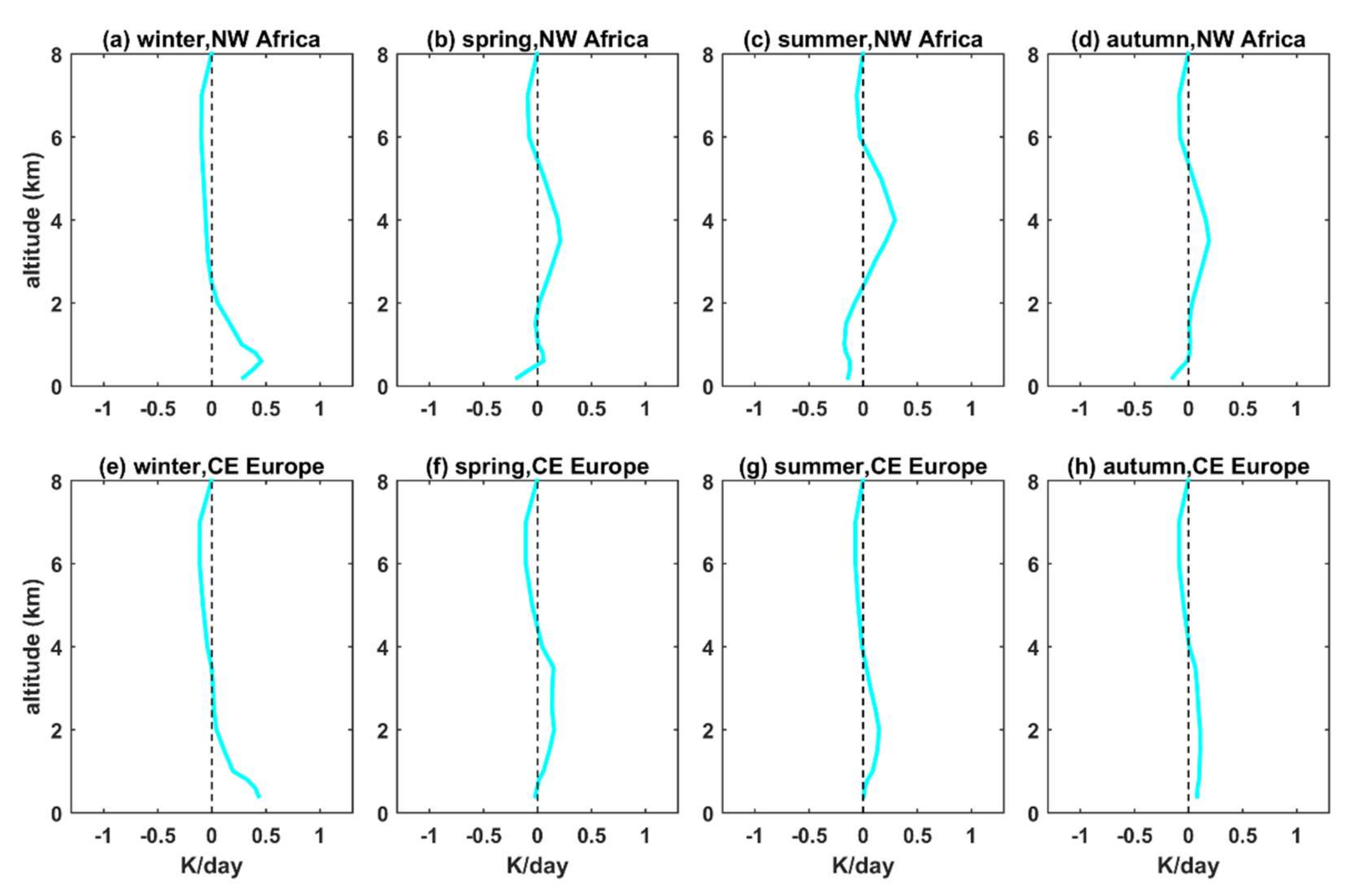
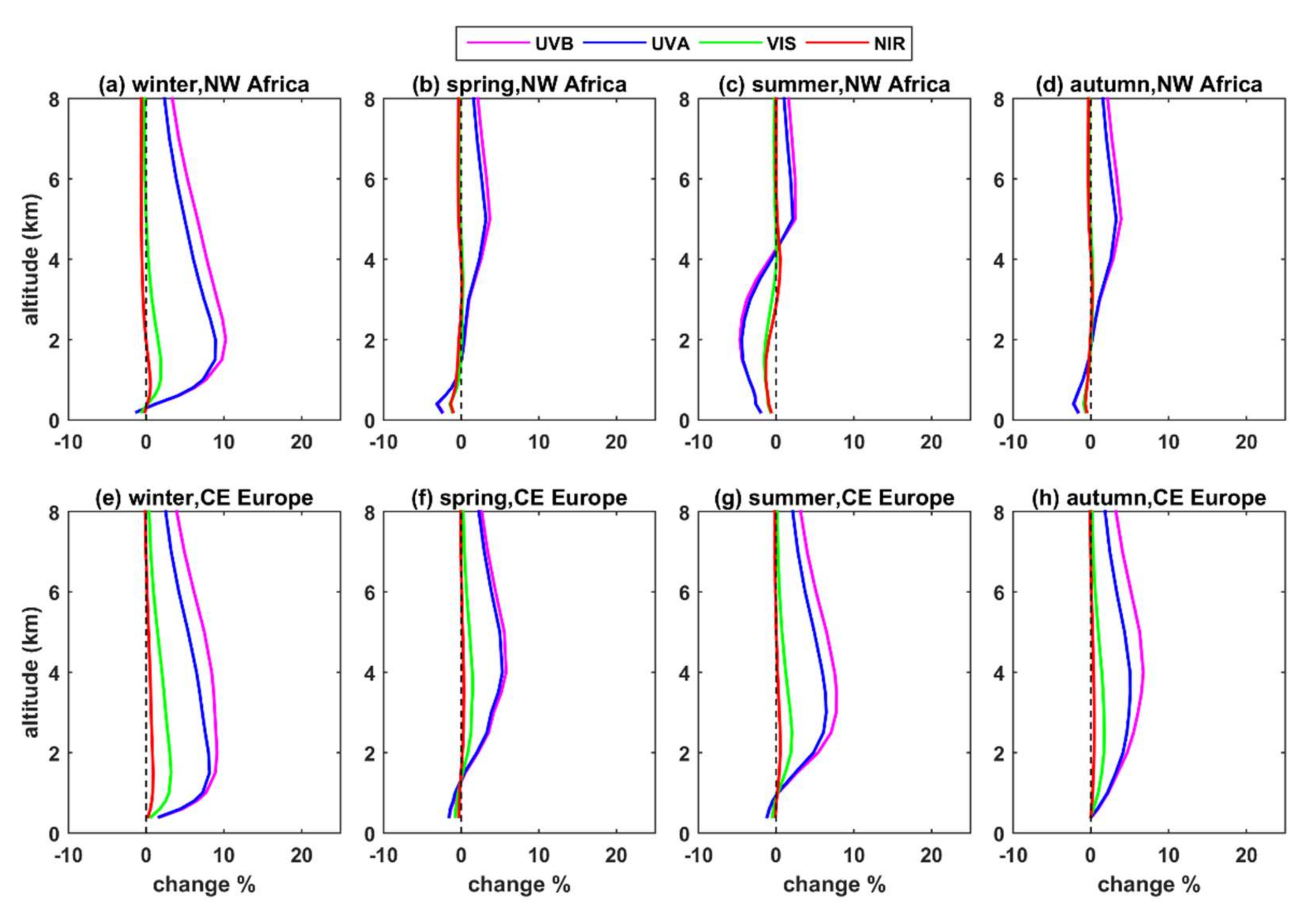
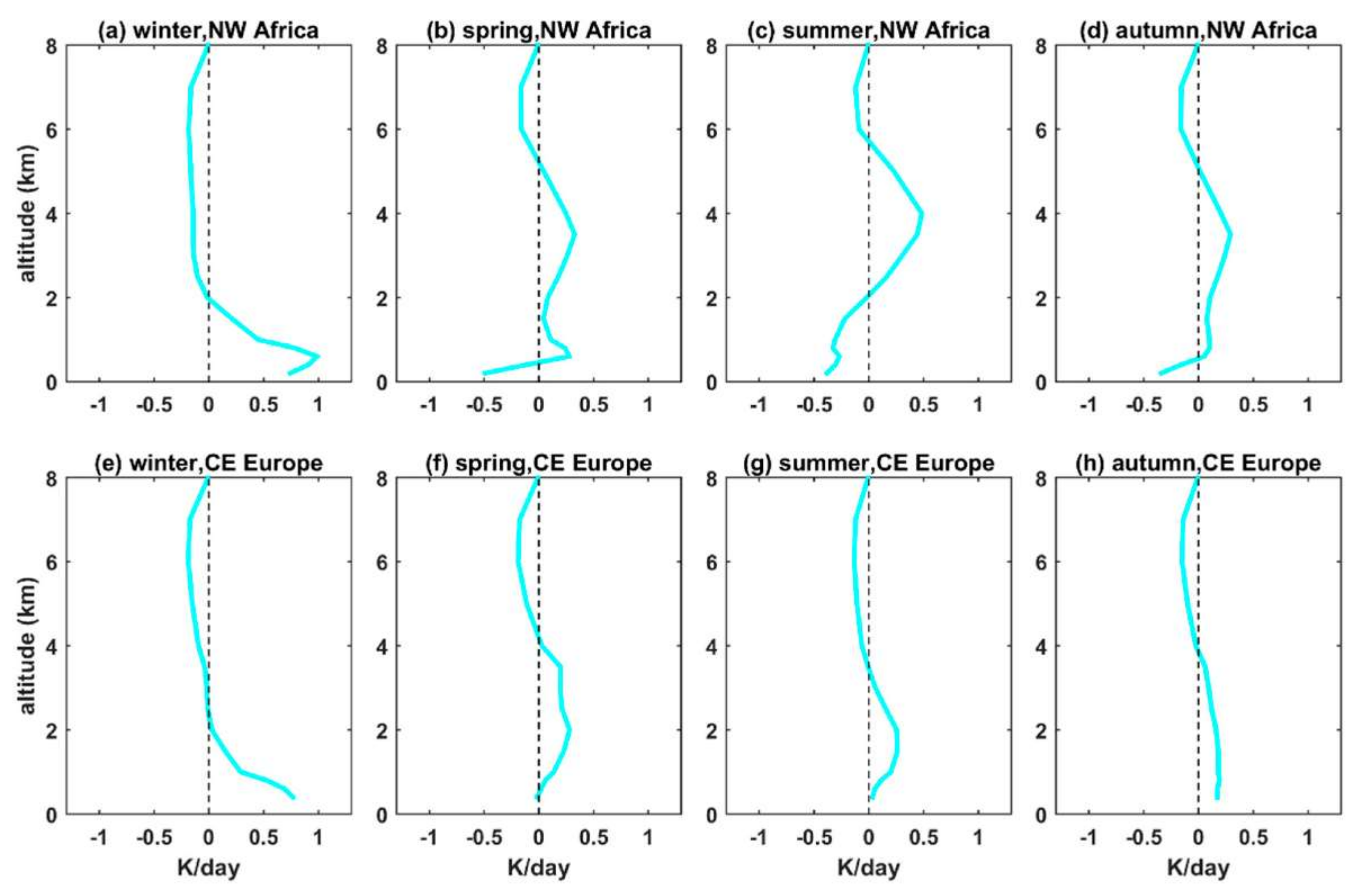
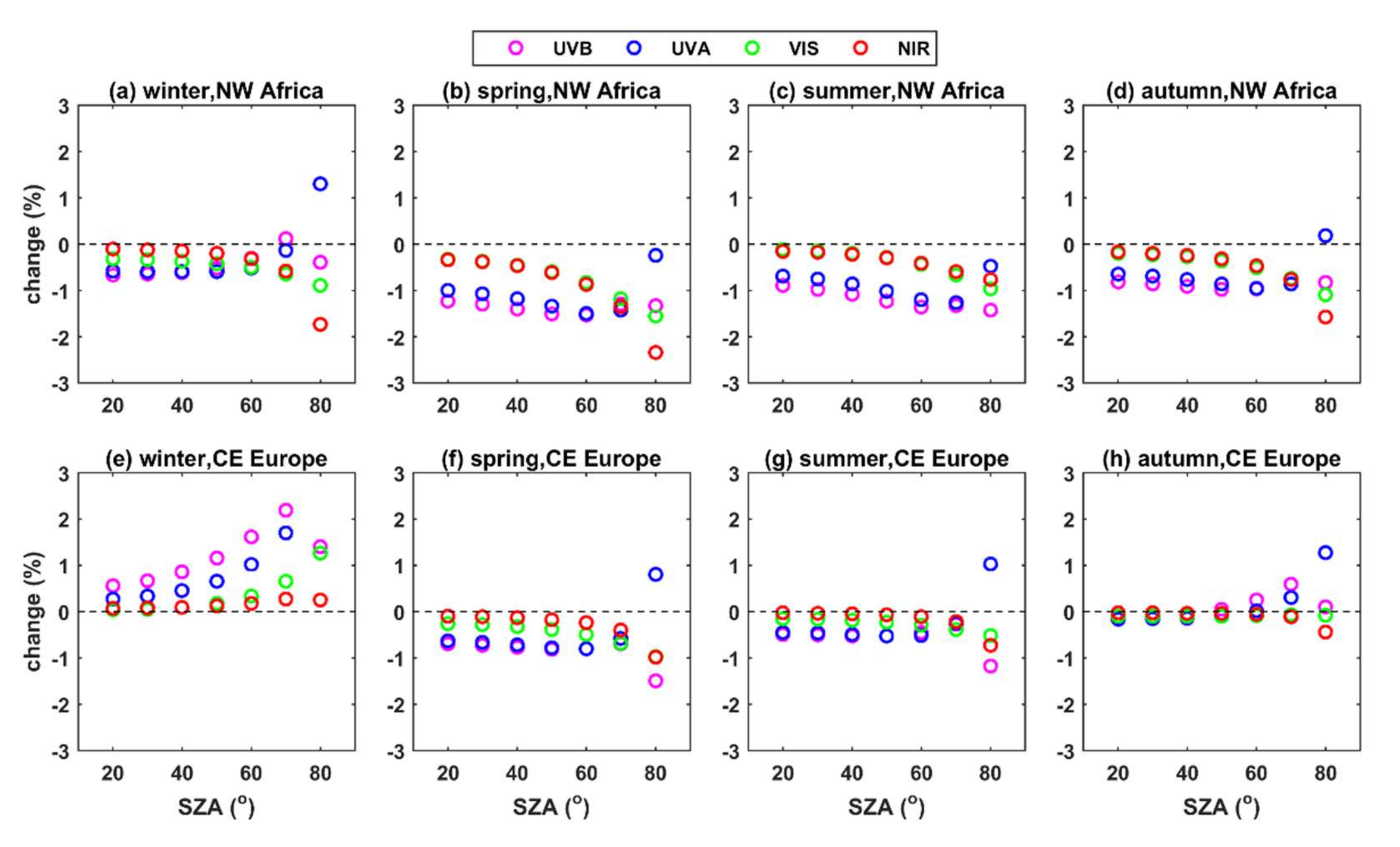
3.2. Effect of Extinction Coefficient Profile for Typical Aerosol Conditions
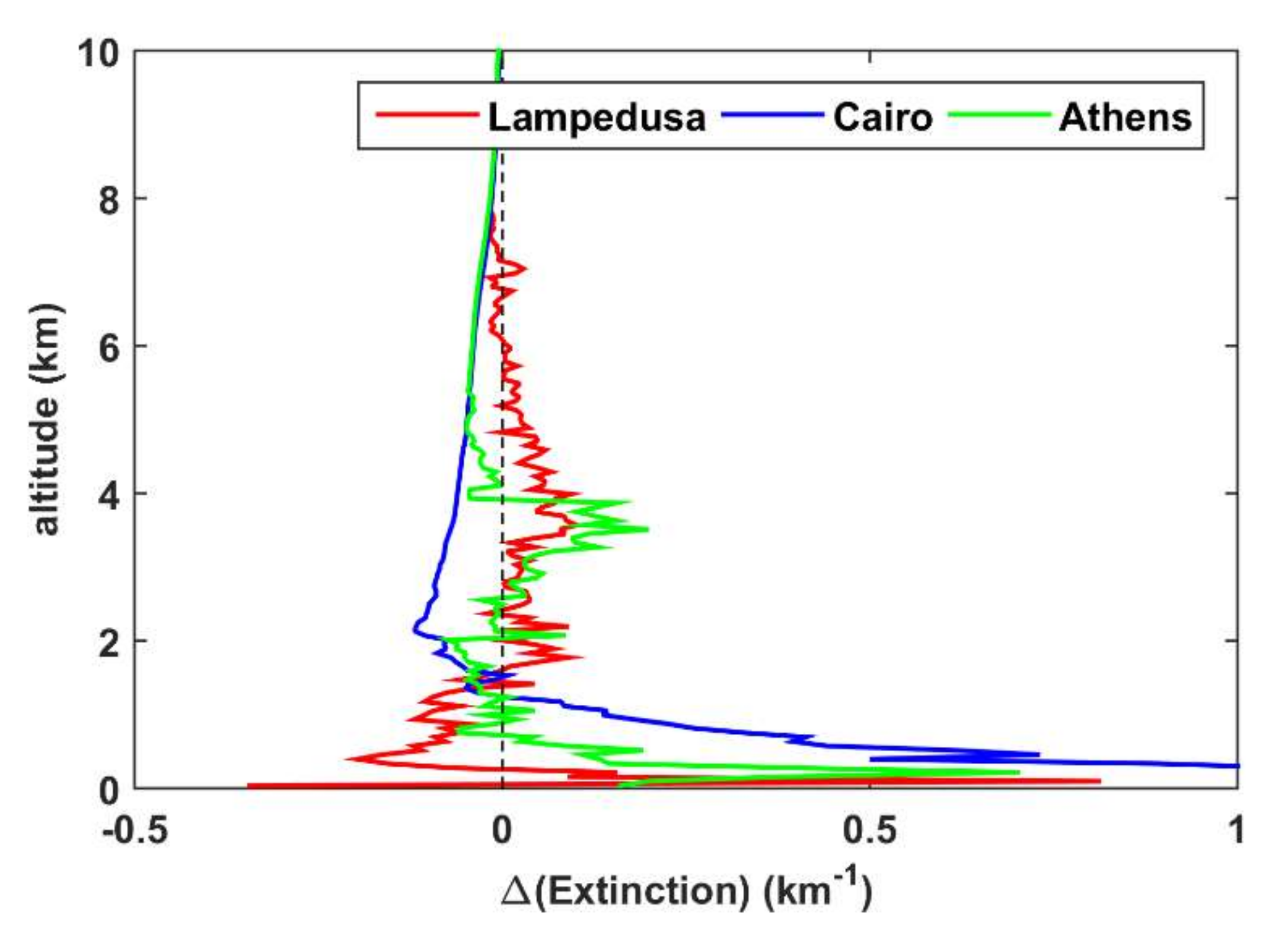
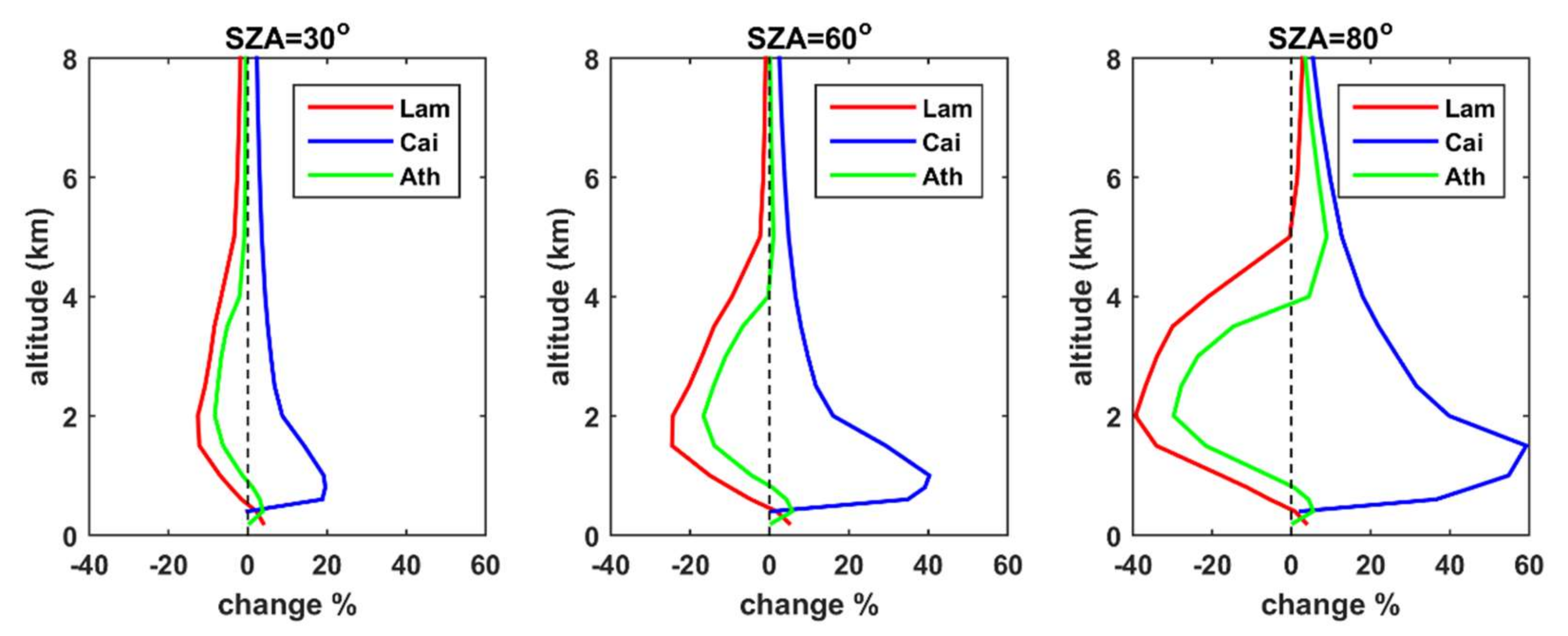
3.3. Effect of the Used Extinction Profile for Strong Dust Events
4. Summary and Conclusions
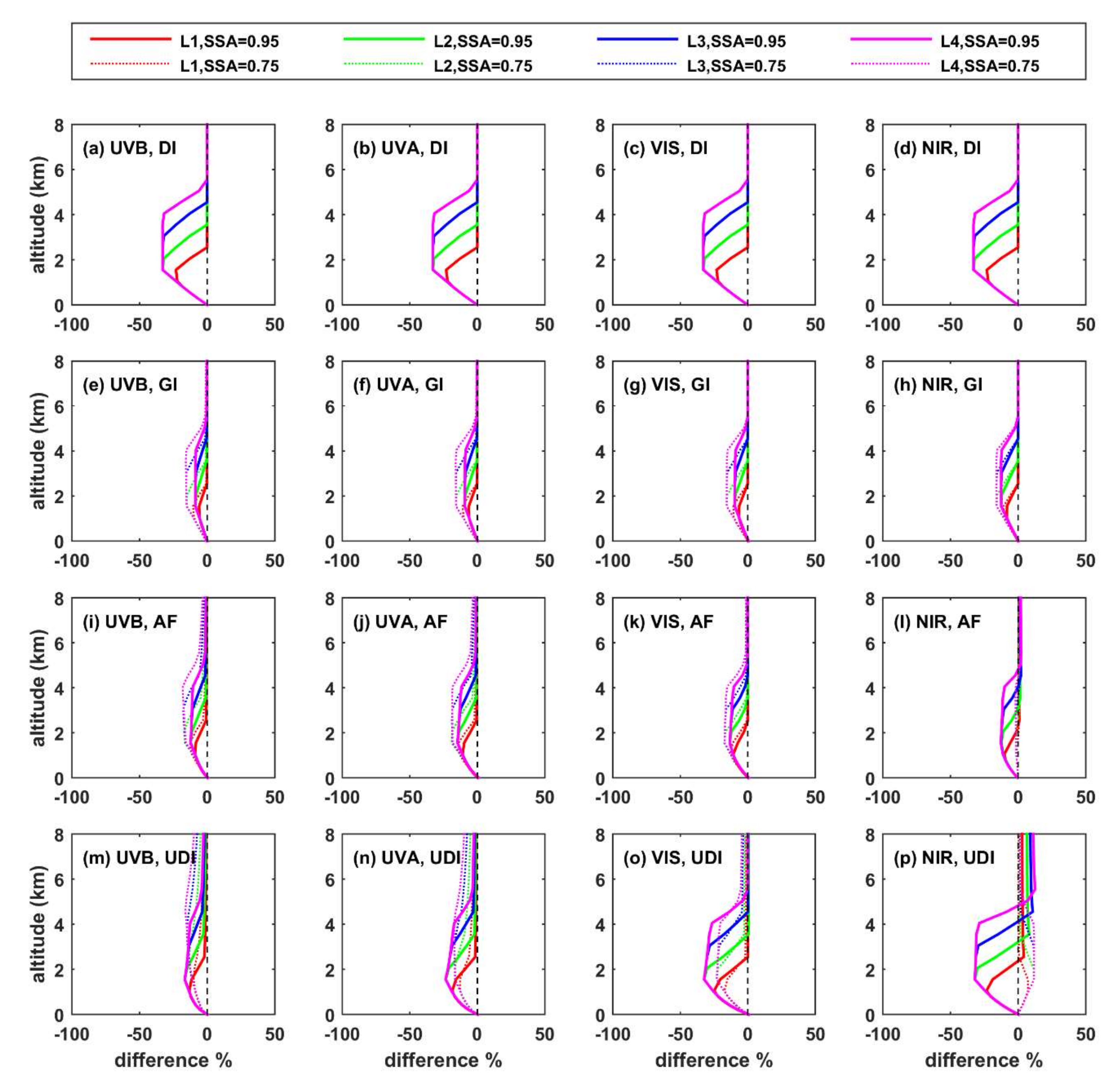
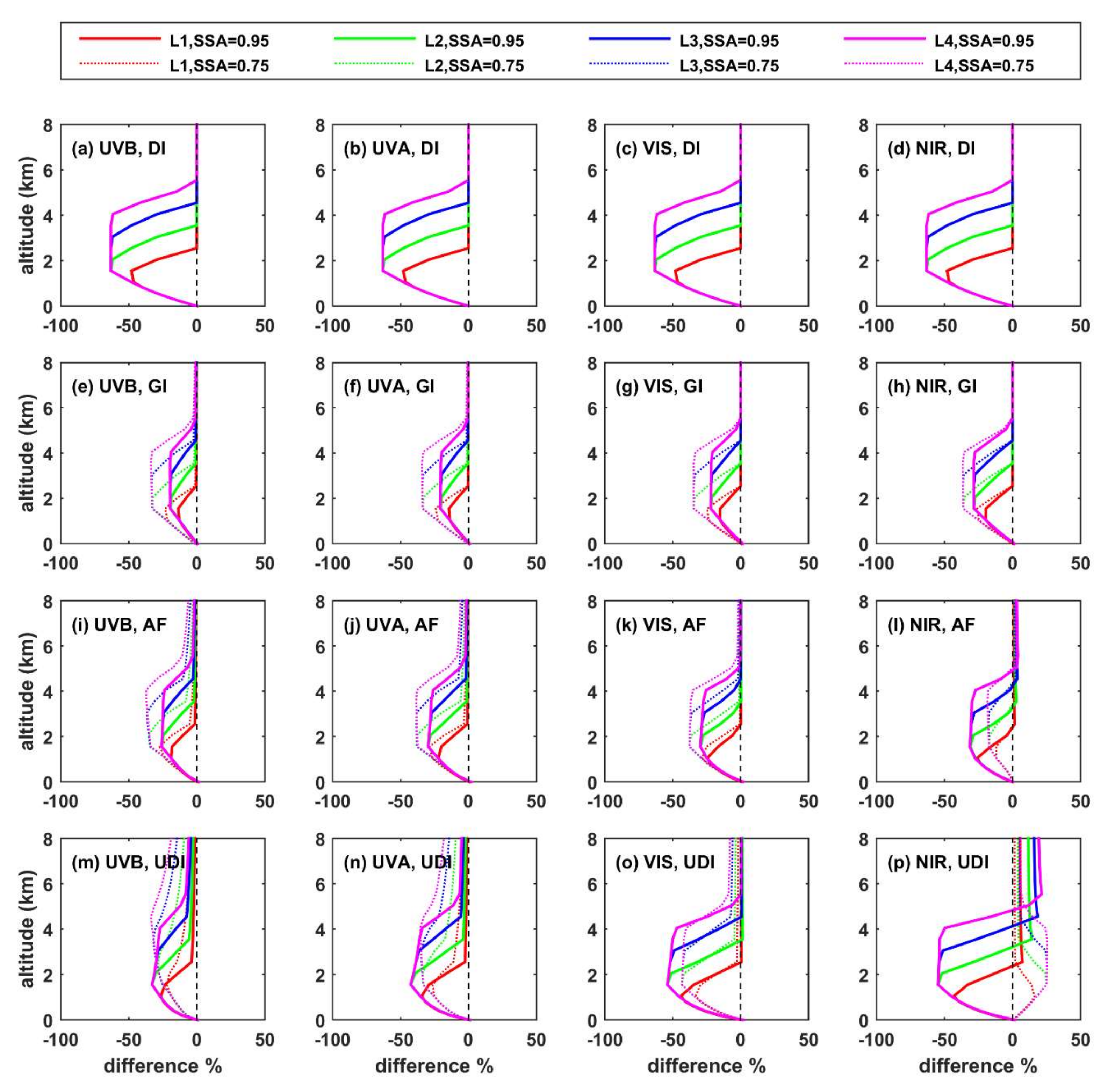
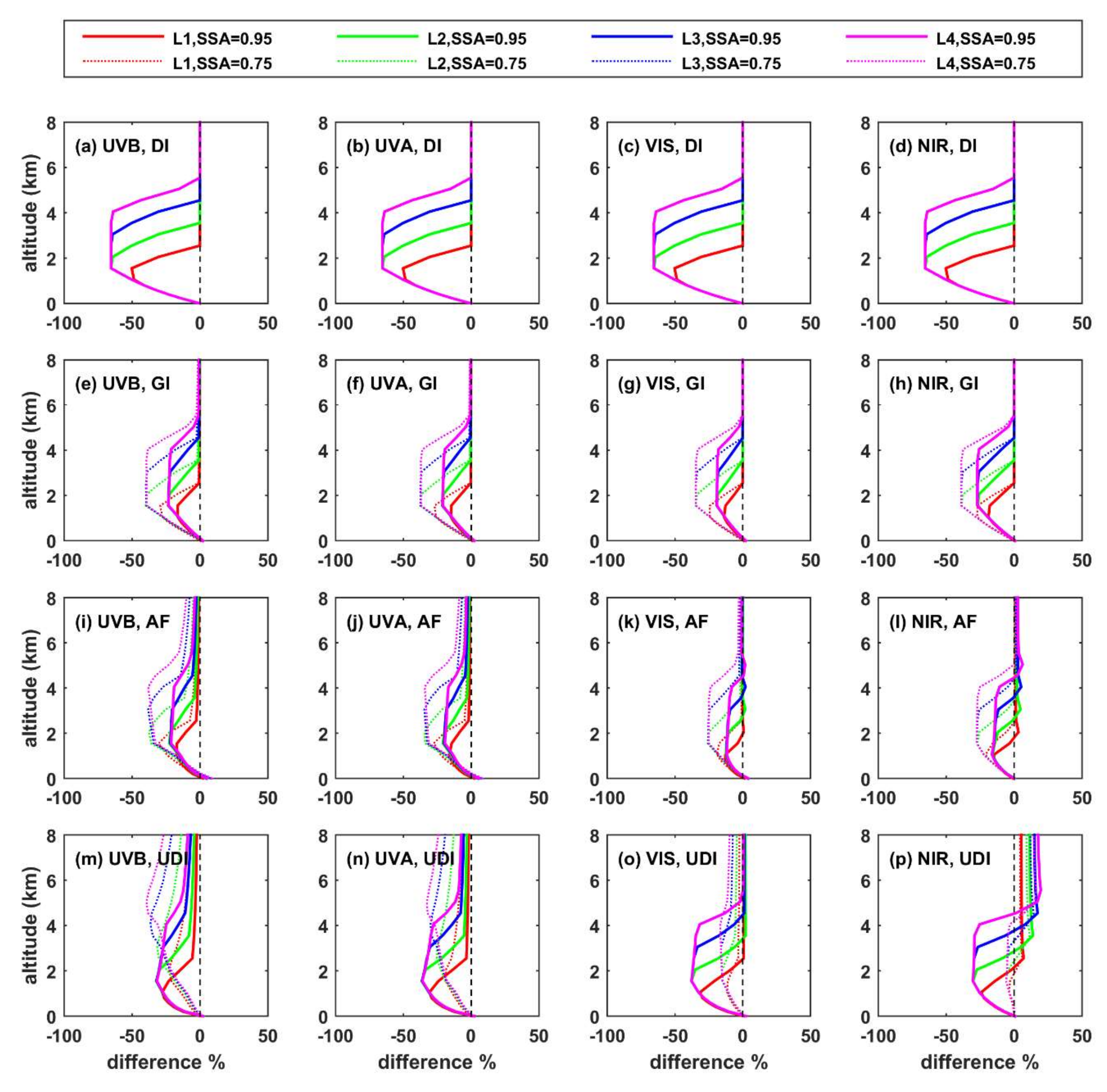
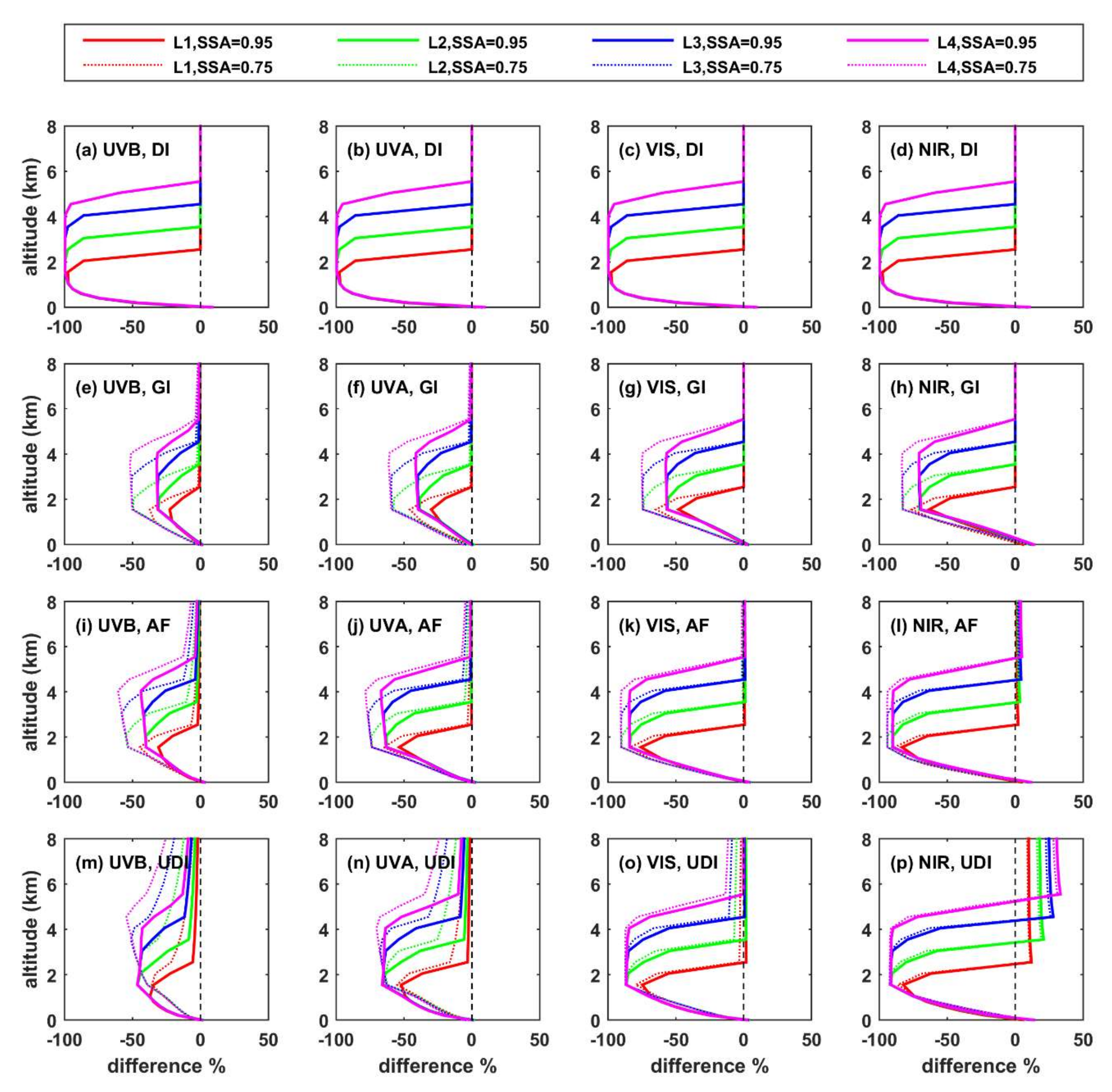
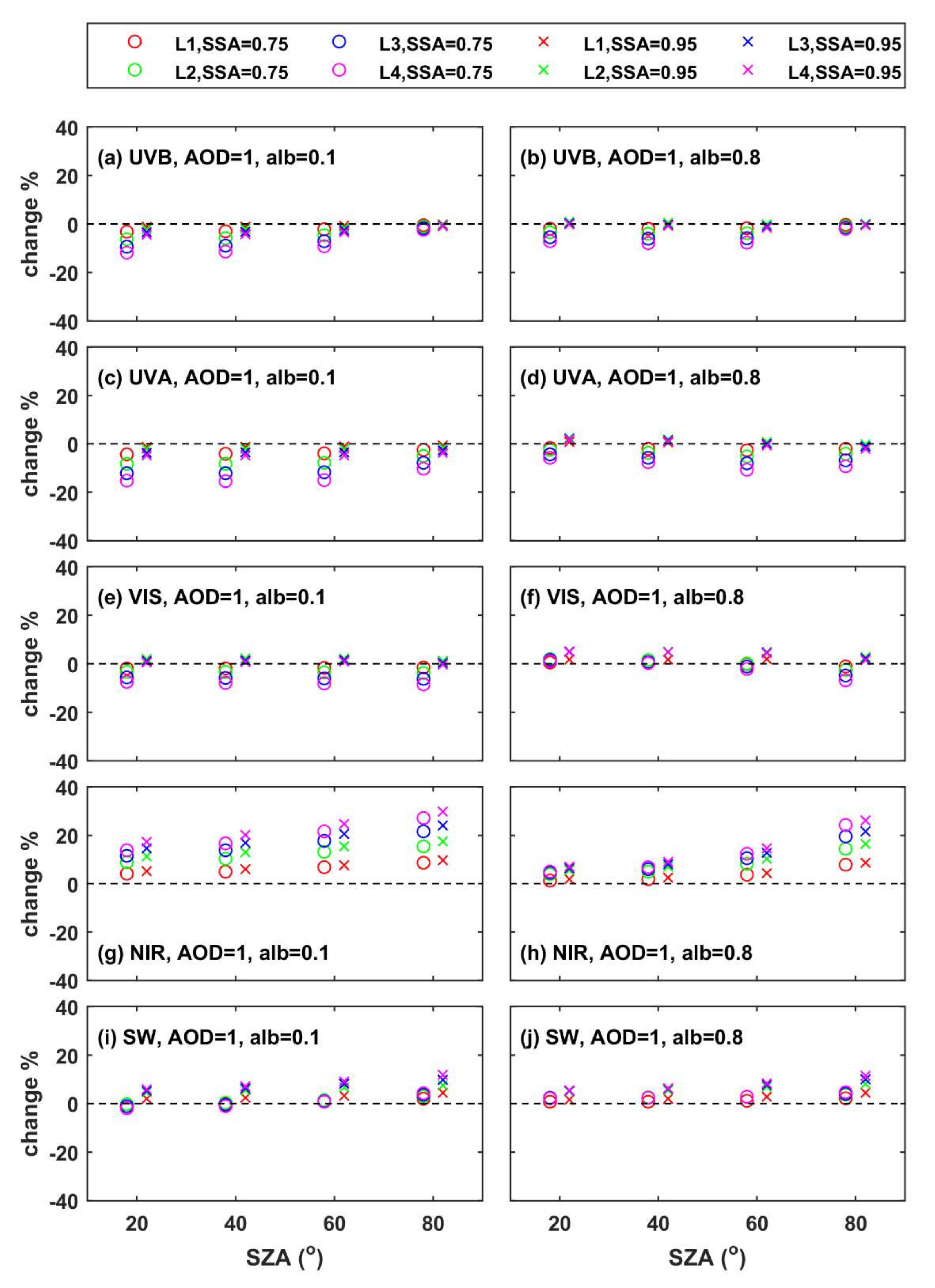
- The altitude of the aerosol layer has minor impact on the total shortwave GI at the BOA. Differences can be more significant for individual spectral regions, especially over high albedo surfaces, where increasing the altitude of the layer can lead to increases on the order of 10–15% in the UVB and UVA regions.
- For absorbing aerosols (SSA = 0.75), the SW UDI at the TOA practically does not change with changing altitude of the aerosol layer, while for more reflective aerosols (SSA = 0.95), the differences are larger, but again exceed 10% only at SZA = 80° and for large height differences in the altitude of the hypothetical aerosol layers.
- Increasing altitude of the aerosol layer corresponds to negative differences in the UDI in UVB, UVA, and VIS and positive differences in NIR at TOA. At BOA, the signs of differences in NIR are also opposite to the signs of changes in UVB, UVA, and VIS. This is because the changes in the fraction of photons that reach the BOA or the TOA are related with different processes in the different spectral regions. As also discussed in Mishra et al. [20], differences in the UV and VIS are mainly related with Rayleigh scattering, while differences in the NIR are mainly related with absorption in the atmosphere.
- Differences in the radiation profiles are larger in the atmosphere with respect to the TOA and the BOA. Increasing the altitude of the aerosol layer leads to a large increase in the SW HR at the level of the layer, and a large decrease at the level of L0, with respect to the case of having all aerosols at L0. Differences in AF are negative between the top of the elevated layer and the BOA when the AF profiles for elevated aerosol layers and aerosols at L0 are compared. For scattering aerosols (SSA = 0.95), differences in AF are more significant for longer (NIR) wavelengths, while for absorbing aerosols (SSA = 0.75), differences are more significant for shorter wavelengths (UVB). Increasing the SZA or the AOD increases the absolute differences, while increasing the surface albedo suppresses the differences.
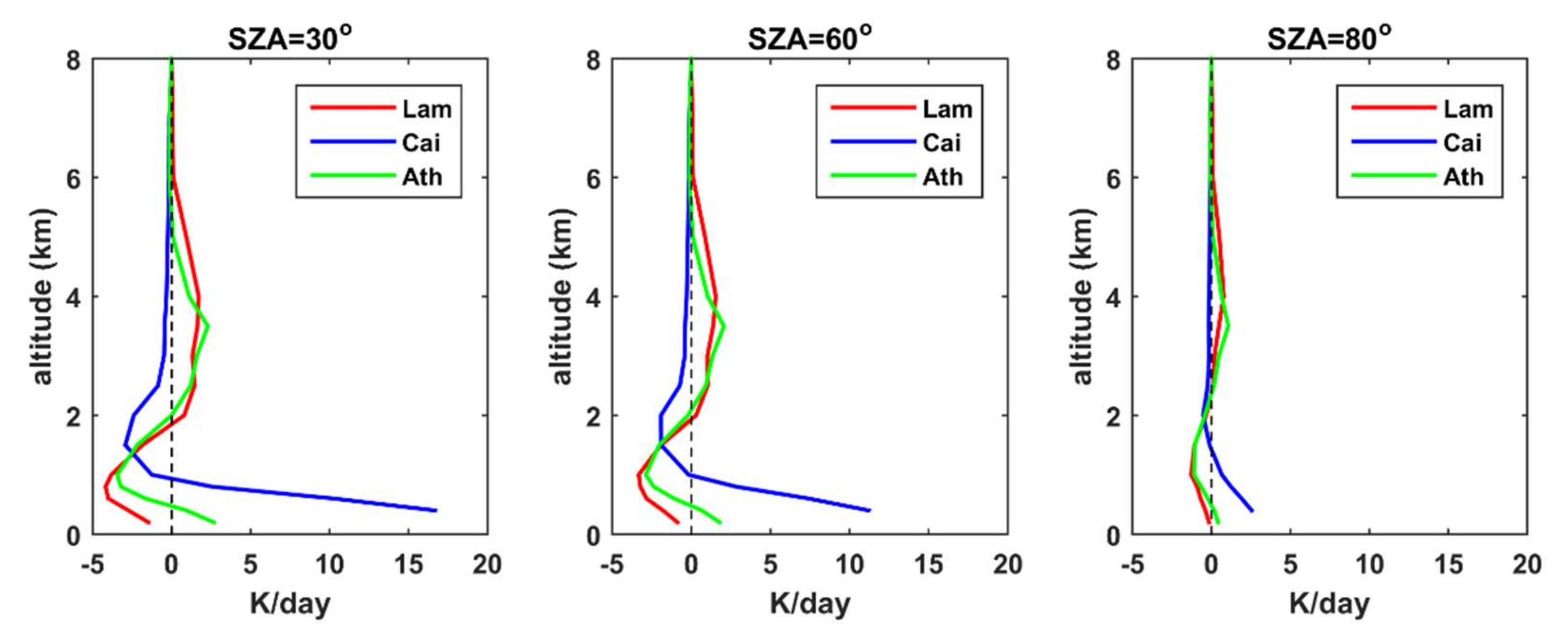
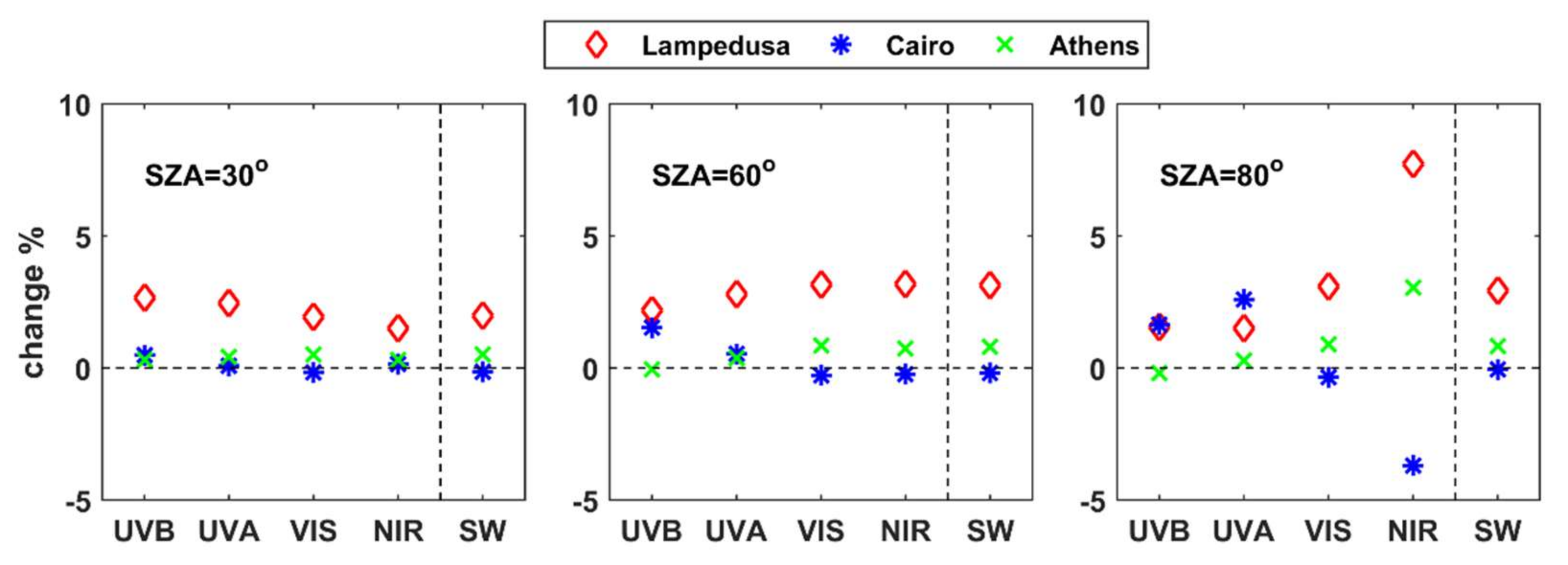
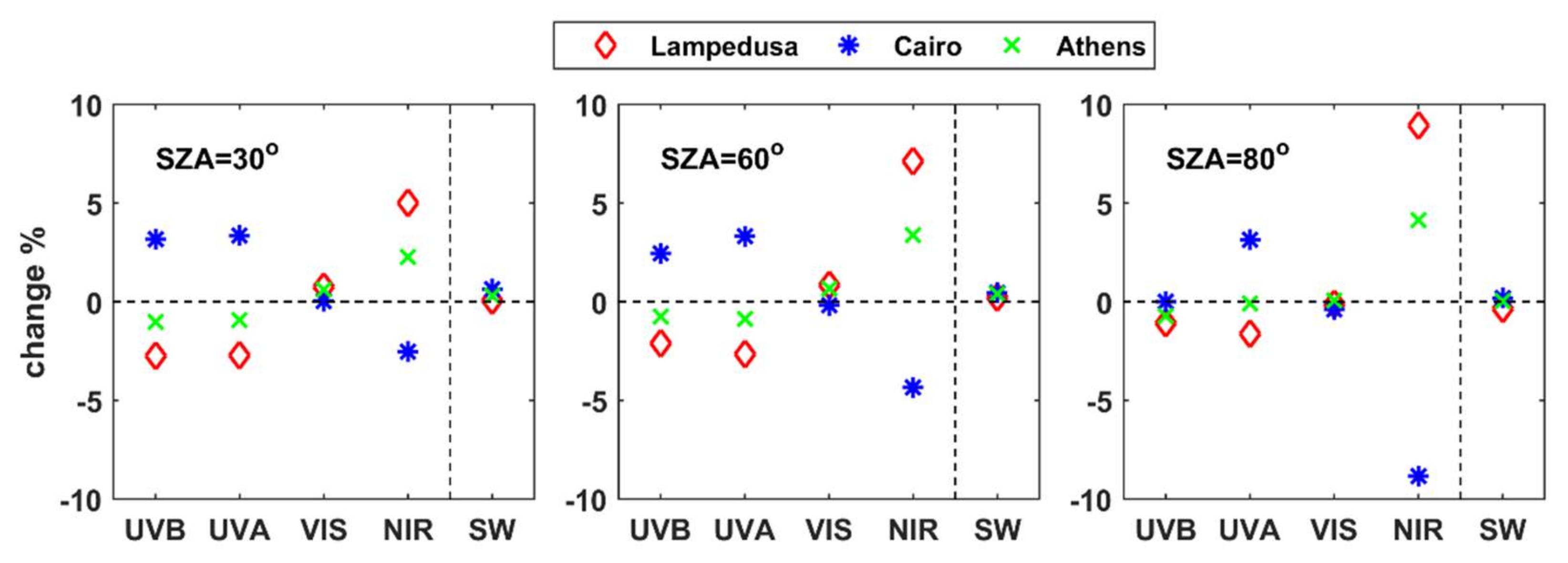
- For typical atmospheric and aerosol conditions in CE Europe and NW Africa, the differences in the UDI at the TOA and the GI at the BOA were, for all spectral bands (and obviously also for the SW radiation), below 5% when the seasonally averaged LIVAS profiles were used instead of the default profile. Differences in AF in the atmosphere were in most cases positive (i.e., more AF available for photochemical reactions when the LIVAS profiles were used), up to 10%, with the altitude of the maximum differences ranging between 1 km and 5 km depending on the region and the season. This was a consequence of the underestimation of the aerosol extinction by the default profile at low altitudes (near the surface). Differences in SW HR on the order of 0.5 to 1 K/day were found at the altitudes of maximum differences between the LIVAS and the default profile. Again, such differences cannot be considered negligible, since they can affect atmospheric stability, and subsequently the formation of clouds.
- At the three sites considered in the study, using average LIVAS instead of the theoretical extinction coefficient profiles for high AOD resulted in larger differences with respect to the comparison between the radiation profiles for average AOD conditions for the two regions. For Athens, the LIVAS extinction profile was closer to the theoretical, compared to the other two sites, resulting in the smallest differences in the radiation profile among the three sites. Differences in UV AF were negative at the lowest 4 km for Athens and Lampedusa, reaching −20% and −40% respectively at ~2 km when SZA = 80°. At the same SZA, differences in Cairo were positive, up to 60% at ~1.5 km. Differences in SW HR were also very large near the surface, reaching 17 K/day over Cairo for SZA = 30°. However, even for such a high aerosol load, differences at the BOA and the TOA were small, especially for the total SW radiation. Differences in SW UDI at the TOA were nearly zero for all sites, while differences in SW GI were smaller than 3% at BOA. Differences in individual spectral bands were more significant, mainly for NIR at high SZAs, where they could be on the order of 10% at TOA and 5–8% at the BOA.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A





References
- Wild, M. Global dimming and brightening: A review. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Wild, M. Decadal changes in radiative fluxes at land and ocean surfaces and their relevance for global warming. WIREs Clim. Change 2016, 7, 91–107. [Google Scholar] [CrossRef]
- Wild, M.; Folini, D.; Henschel, F.; Fischer, N.; Müller, B. Projections of long-term changes in solar radiation based on CMIP5 climate models and their influence on energy yields of photovoltaic systems. Sol. Energy 2015, 116, 12–24. [Google Scholar] [CrossRef] [Green Version]
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2013. [Google Scholar]
- Otto, S.; Bierwirth, E.; Weinzierl, B.; Kandler, K.; Esselborn, M.; Tesche, M.; Schladitz, A.; Wendisch, M.; Trautmann, T. Solar radiative effects of a Saharan dust plume observed during SAMUM assuming spheroidal model particles. Tellus B Chem. Phys. Meteorol. 2009, 61, 270–296. [Google Scholar] [CrossRef] [Green Version]
- Otto, S.; de Reus, M.; Trautmann, T.; Thomas, A.; Wendisch, M.; Borrmann, S. Atmospheric radiative effects of an in situ measured Saharan dust plume and the role of large particles. Atmos. Chem. Phys. 2007, 7, 4887–4903. [Google Scholar] [CrossRef] [Green Version]
- Zeng, L.; Zhang, A.; Wang, Y.; Wagner, N.L.; Katich, J.M.; Schwarz, J.P.; Schill, G.P.; Brock, C.; Froyd, K.D.; Murphy, D.M.; et al. Global measurements of brown carbon and estimated direct radiative effects. Geophys. Res. Lett. 2020, 47, e2020GL088747. [Google Scholar] [CrossRef]
- Hess, M.; Koepke, P.; Schult, I. Optical properties of aerosols and clouds: The software package OPAC. Bull. Am. Meteorol. Soc. 1998, 79, 831–844. [Google Scholar] [CrossRef]
- Tsekeri, A.; Lopatin, A.; Amiridis, V.; Marinou, E.; Igloffstein, J.; Siomos, N.; Solomos, S.; Kokkalis, P.; Engelmann, R.; Baars, H.; et al. GARRLiC and LIRIC: Strengths and limitations for the characterization of dust and marine particles along with their mixtures. Atmos. Meas. Tech. 2017, 10, 4995–5016. [Google Scholar] [CrossRef] [Green Version]
- Chen, L. Uncertainties in solar radiation assessment in the United States using climate models. Clim. Dyn. 2021, 56, 665–678. [Google Scholar] [CrossRef]
- Boé, J.; Somot, S.; Corre, L.; Nabat, P. Large discrepancies in summer climate change over Europe as projected by global and regional climate models: Causes and consequences. Clim. Dyn. 2020, 54, 2981–3002. [Google Scholar] [CrossRef]
- Bartók, B.; Wild, M.; Folini, D.; Lüthi, D.; Kotlarski, S.; Schär, C.; Vautard, R.; Jerez, S.; Imecs, Z. Projected changes in surface solar radiation in CMIP5 global climate models and in EURO-CORDEX regional climate models for Europe. Clim. Dyn. 2017, 49, 2665–2683. [Google Scholar] [CrossRef]
- Lakkala, K.; Kujanpää, J.; Brogniez, C.; Henriot, N.; Arola, A.; Aun, M.; Auriol, F.; Bais, A.F.; Bernhard, G.; de Bock, V.; et al. Validation of the TROPOspheric Monitoring Instrument (TROPOMI) surface UV radiation product. Atmos. Meas. Tech. 2020, 13, 6999–7024. [Google Scholar] [CrossRef]
- Zempila, M.M.; Fountoulakis, I.; Taylor, M.; Kazadzis, S.; Arola, A.; Koukouli, M.E.; Bais, A.; Meleti, C.; Balis, D. Validation of OMI erythemal doses with multi-sensor ground-based measurements in Thessaloniki, Greece. Atmos. Environ. 2018, 183, 106–121. [Google Scholar] [CrossRef] [Green Version]
- Merrouni, A.A.; Ghennioui, A.; Wolfertstetter, F.; Mezrhab, A. The uncertainty of the HelioClim-3 DNI data under Moroccan climate. AIP Conf. Proc. 2017, 1850, 140002. [Google Scholar] [CrossRef] [Green Version]
- Witthuhn, J.; Hünerbein, A.; Filipitsch, F.; Wacker, S.; Meilinger, S.; Deneke, H. Aerosol properties and aerosol–radiation interactions in clear-sky conditions over Germany. Atmos. Chem. Phys. 2021, 21, 14591–14630. [Google Scholar] [CrossRef]
- Raptis, I.-P.; Kazadzis, S.; Eleftheratos, K.; Amiridis, V.; Fountoulakis, I. Single scattering albedo’s spectral dependence effect on UV irradiance. Atmosphere 2018, 9, 364. [Google Scholar] [CrossRef] [Green Version]
- Bergstrom, R.W.; Pilewskie, P.; Russell, P.B.; Redemann, J.; Bond, T.C.; Quinn, P.K.; Sierau, B. Spectral absorption properties of atmospheric aerosols. Atmos. Chem. Phys. 2007, 7, 5937–5943. [Google Scholar] [CrossRef] [Green Version]
- Fountoulakis, I.; Natsis, A.; Siomos, N.; Drosoglou, T.; Bais, A.F. Deriving aerosol absorption properties from solar ultraviolet radiation spectral measurements at Thessaloniki, Greece. Remote Sens. 2019, 11, 2179. [Google Scholar] [CrossRef] [Green Version]
- Mishra, A.K.; Koren, I.; Rudich, Y. Effect of aerosol vertical distribution on aerosol-radiation interaction: A theoretical prospect. Heliyon 2015, 1, e00036. [Google Scholar] [CrossRef] [Green Version]
- Stevens, B.; Fiedler, S.; Kinne, S.; Peters, K.; Rast, S.; Müsse, J.; Smith, S.J.; Mauritsen, T. MACv2-SP: A parameterization of anthropogenic aerosol optical properties and an associated Twomey effect for use in CMIP6. Geosci. Model Dev. 2017, 10, 433–452. [Google Scholar] [CrossRef] [Green Version]
- Shettle, E. Models of aerosols, clouds, and precipitation for atmospheric propagation studies. AGARD Conf. Proc. 1989. Available online: https://www.researchgate.net/publication/234312286_Models_of_aerosols_clouds_and_precipitation_for_atmospheric_propagation_studies (accessed on 15 January 2021).
- Petrzala, J. Assessment of influence of urban aerosol vertical profile on clear-sky diffuse radiance pattern. J. Sol. Energy Eng. 2021, 144, 1–7. [Google Scholar] [CrossRef]
- Marinou, E.; Amiridis, V.; Binietoglou, I.; Tsikerdekis, A.; Solomos, S.; Proestakis, E.; Konsta, D.; Papagiannopoulos, N.; Tsekeri, A.; Vlastou, G.; et al. Three-dimensional evolution of Saharan dust transport towards Europe based on a 9-year EARLINET-optimized CALIPSO dataset. Atmos. Chem. Phys. 2017, 17, 5893–5919. [Google Scholar] [CrossRef] [Green Version]
- Langmann, B.; Folch, A.; Hensch, M.; Matthias, V. Volcanic ash over Europe during the eruption of Eyjafjallajökull on Iceland, April–May 2010. Atmos. Environ. 2012, 48, 1–8. [Google Scholar] [CrossRef]
- Bernard, A.; Rose, W.I. The injection of sulfuric acid aerosols in the stratosphere by the El Chichón volcano and its related hazards to the international air traffic. Nat. Hazards 1990, 3, 59–67. [Google Scholar] [CrossRef]
- Osborne, M.; Malavelle, F.F.; Adam, M.; Buxmann, J.; Sugier, J.; Marenco, F.; Haywood, J. Saharan dust and biomass burning aerosols during ex-hurricane Ophelia: Observations from the new UK lidar and sun-photometer network. Atmos. Chem. Phys. 2019, 19, 3557–3578. [Google Scholar] [CrossRef] [Green Version]
- Vaughan, G.; Wareing, D.; Ricketts, H. Measurement report: Lidar measurements of stratospheric aerosol following the 2019 Raikoke and Ulawun volcanic eruptions. Atmos. Chem. Phys. 2021, 21, 5597–5604. [Google Scholar] [CrossRef]
- Labonne, M.; Bréon, F.-M.; Chevallier, F. Injection height of biomass burning aerosols as seen from a spaceborne lidar. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Garratt, J.R. Review: The atmospheric boundary layer. Earth-Sci. Rev. 1994, 37, 89–134. [Google Scholar] [CrossRef]
- Soupiona, O.; Papayannis, A.; Kokkalis, P.; Foskinis, R.; Sánchez Hernández, G.; Ortiz-Amezcua, P.; Mylonaki, M.; Papanikolaou, C.-A.; Papagiannopoulos, N.; Samaras, S.; et al. EARLINET observations of Saharan dust intrusions over the northern Mediterranean region (2014–2017): Properties and impact on radiative forcing. Atmos. Chem. Phys. 2020, 20, 15147–15166. [Google Scholar] [CrossRef]
- Herut, B.; Rahav, E.; Tsagaraki, T.M.; Giannakourou, A.; Tsiola, A.; Psarra, S.; Lagaria, A.; Papageorgiou, N.; Mihalopoulos, N.; Theodosi, C.N.; et al. The potential impact of saharan dust and polluted aerosols on microbial populations in the east Mediterranean Sea, an overview of a mesocosm experimental approach. Front. Mar. Sci. 2016, 3, 226. [Google Scholar] [CrossRef] [Green Version]
- Fountoulakis, I.; Kosmopoulos, P.; Papachristopoulou, K.; Raptis, I.-P.; Mamouri, R.-E.; Nisantzi, A.; Gkikas, A.; Witthuhn, J.; Bley, S.; Moustaka, A.; et al. Effects of aerosols and clouds on the levels of surface solar radiation and solar energy in Cyprus. Remote Sens. 2021, 13, 2319. [Google Scholar] [CrossRef]
- Kosmopoulos, P.G.; Kazadzis, S.; El-Askary, H.; Taylor, M.; Gkikas, A.; Proestakis, E.; Kontoes, C.; El-Khayat, M.M. Earth-observation-based estimation and forecasting of particulate matter impact on solar energy in Egypt. Remote Sens. 2018, 10, 1870. [Google Scholar] [CrossRef] [Green Version]
- Rizza, U.; Canepa, E.; Ricchi, A.; Bonaldo, D.; Carniel, S.; Morichetti, M.; Passerini, G.; Santiloni, L.; Scremin Puhales, F.; Miglietta, M.M. Influence of wave state and sea spray on the roughness length: Feedback on medicanes. Atmosphere 2018, 9, 301. [Google Scholar] [CrossRef] [Green Version]
- Varlas, G.; Marinou, E.; Gialitaki, A.; Siomos, N.; Tsarpalis, K.; Kalivitis, N.; Solomos, S.; Tsekeri, A.; Spyrou, C.; Tsichla, M.; et al. Assessing sea-state effects on sea-salt aerosol modeling in the lower atmosphere using lidar and in-situ measurements. Remote Sens. 2021, 13, 614. [Google Scholar] [CrossRef]
- Revell, L.E.; Kuma, P.; le Ru, E.C.; Somerville, W.R.C.; Gaw, S. Direct radiative effects of airborne microplastics. Nature 2021, 598, 462–467. [Google Scholar] [CrossRef] [PubMed]
- Trainic, M.; Flores, J.M.; Pinkas, I.; Pedrotti, M.L.; Lombard, F.; Bourdin, G.; Gorsky, G.; Boss, E.; Rudich, Y.; Vardi, A.; et al. Airborne microplastic particles detected in the remote marine atmosphere. Commun. Earth Environ. 2020, 1, 64. [Google Scholar] [CrossRef]
- Allen, S.; Allen, D.; Baladima, F.; Phoenix, V.R.; Thomas, J.L.; le Roux, G.; Sonke, J.E. Evidence of free tropospheric and long-range transport of microplastic at Pic du Midi Observatory. Nat. Commun. 2021, 12, 7242. [Google Scholar] [CrossRef]
- Fasano, G.; Diémoz, H.; Fountoulakis, I.; Cassardo, C.; Kudo, R.; Siani, A.M.; Ferrero, L. Vertical profile of the clear-sky aerosol direct radiative effect in an Alpine valley, by the synergy of ground-based measurements and radiative transfer simulations. Bull. Atmos. Sci. Technol. 2021, 2, 11. [Google Scholar] [CrossRef]
- Thornton, J.M.; Palazzi, E.; Pepin, N.C.; Cristofanelli, P.; Essery, R.; Kotlarski, S.; Giuliani, G.; Guigoz, Y.; Kulonen, A.; Pritchard, D.; et al. Toward a definition of Essential Mountain Climate Variables. One Earth 2021, 4, 805–827. [Google Scholar] [CrossRef]
- Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraer, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Change 2015, 5, 424–430. [Google Scholar] [CrossRef] [Green Version]
- Lau, K.M.; Kim, M.K.; Kim, K.M. Asian summer monsoon anomalies induced by aerosol direct forcing: The role of the Tibetan Plateau. Clim. Dyn. 2006, 26, 855–864. [Google Scholar] [CrossRef] [Green Version]
- Surabi, M.; James, H.; Larissa, N.; Yunfeng, L. Climate effects of black carbon aerosols in China and India. Science 2002, 297, 2250–2253. [Google Scholar] [CrossRef] [Green Version]
- Lau, K.-M.; Kim, K.-M. Observational relationships between aerosol and Asian monsoon rainfall, and circulation. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Crutzen, P.J.; Zimmermann, P.H. The changing photochemistry of the troposphere. Tellus B Chem. Phys. Meteorol. 1991, 43, 136–151. [Google Scholar] [CrossRef]
- Carroll, M.A.; Ridley, B.A.; Montzka, D.D.; Hubler, G.; Walega, J.G.; Norton, R.B.; Huebert, B.J.; Grahek, F.E. Measurements of nitric oxide and nitrogen dioxide during the Mauna Loa Observatory Photochemistry Experiment. J. Geophys. Res. Atmos. 1992, 97, 10361–10374. [Google Scholar] [CrossRef]
- Topaloglou, C.; Kazadzis, S.; Bais, A.F.; Blumthaler, M.; Schallhart, B.; Balis, D. NO2 and HCHO photolysis frequencies from irradiance measurements in Thessaloniki, Greece. Atmos. Chem. Phys. 2005, 5, 1645–1653. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Xue, L.; Dong, C.; Wang, T.; Mellouki, A.; Zhang, Q.; Wang, W. Gaseous carbonyls in China’s atmosphere: Tempo-spatial distributions, sources, photochemical formation, and impact on air quality. Atmos. Environ. 2019, 214, 116863. [Google Scholar] [CrossRef]
- Edinger, J.G. Vertical distribution of photochemical smog in Los Angeles basin. Environ. Sci. Technol. 1973, 7, 247–252. [Google Scholar] [CrossRef]
- Velasco, E.; Márquez, C.; Bueno, E.; Bernabé, R.M.; Sánchez, A.; Fentanes, O.; Wöhrnschimmel, H.; Cárdenas, B.; Kamilla, A.; Wakamatsu, S.; et al. Vertical distribution of ozone and VOCs in the low boundary layer of Mexico City. Atmos. Chem. Phys. 2008, 8, 3061–3079. [Google Scholar] [CrossRef] [Green Version]
- Diémoz, H.; Barnaba, F.; Magri, T.; Pession, G.; Dionisi, D.; Pittavino, S.; Tombolato, I.K.F.; Campanelli, M.; Della Ceca, L.S.; Hervo, M.; et al. Transport of Po Valley aerosol pollution to the northwestern Alps—Part 1: Phenomenology. Atmos. Chem. Phys. 2019, 19, 3065–3095. [Google Scholar] [CrossRef] [Green Version]
- Liao, H.; Yung, Y.L.; Seinfeld, J.H. Effects of aerosols on tropospheric photolysis rates in clear and cloudy atmospheres. J. Geophys. Res. Atmos. 1999, 104, 23697–23707. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Li, X.; Shao, M.; Hu, M.; Zeng, L.; Wu, Y.; Tan, T. The impact of aerosols on photolysis frequencies and ozone production in Beijing during the 4-year period 2012–2015. Atmos. Chem. Phys. 2019, 19, 9413–9429. [Google Scholar] [CrossRef] [Green Version]
- Kylling, A.; Webb, A.R.; Kift, R.; Gobbi, G.P.; Ammannato, L.; Barnaba, F.; Bais, A.; Kazadzis, S.; Wendisch, M.; Jäkel, E.; et al. Spectral actinic flux in the lower troposphere: Measurement and 1-D simulations for cloudless, broken cloud and overcast situations. Atmos. Chem. Phys. 2005, 5, 1975–1997. [Google Scholar] [CrossRef] [Green Version]
- Amiridis, V.; Marinou, E.; Tsekeri, A.; Wandinger, U.; Schwarz, A.; Giannakaki, E.; Mamouri, R.; Kokkalis, P.; Binietoglou, I.; Solomos, S.; et al. LIVAS: A 3-D multi-wavelength aerosol/cloud database based on CALIPSO and EARLINET. Atmos. Chem. Phys. 2015, 15, 7127–7153. [Google Scholar] [CrossRef] [Green Version]
- Winker, D.M.; Pelon, J.; Coakley, J.A.; Ackerman, S.A.; Charlson, R.J.; Colarco, P.R.; Flamant, P.; Fu, Q.; Hoff, R.M.; Kittaka, C.; et al. The CALIPSO mission: A global 3D view of aerosols and clouds. Bull. Am. Meteorol. Soc. 2010, 91, 1211–1230. [Google Scholar] [CrossRef]
- Gkikas, A.; Proestakis, E.; Amiridis, V.; Kazadzis, S.; di Tomaso, E.; Tsekeri, A.; Marinou, E.; Hatzianastassiou, N.; Pérez García-Pando, C. ModIs Dust AeroSol (MIDAS): A global fine-resolution dust optical depth data set. Atmos. Meas. Tech. 2021, 14, 309–334. [Google Scholar] [CrossRef]
- Proestakis, E.; Amiridis, V.; Marinou, E.; Georgoulias, A.K.; Solomos, S.; Kazadzis, S.; Chimot, J.; Che, H.; Alexandri, G.; Binietoglou, I.; et al. Nine-year spatial and temporal evolution of desert dust aerosols over South and East Asia as revealed by CALIOP. Atmos. Chem. Phys. 2018, 18, 1337–1362. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.-H.; Omar, A.H.; Tackett, J.L.; Vaughan, M.A.; Winker, D.M.; Trepte, C.R.; Hu, Y.; Liu, Z.; Poole, L.R.; Pitts, M.C.; et al. The CALIPSO version 4 automated aerosol classification and lidar ratio selection algorithm. Atmos. Meas. Tech. 2018, 11, 6107–6135. [Google Scholar] [CrossRef] [Green Version]
- Tackett, J.L.; Winker, D.M.; Getzewich, B.J.; Vaughan, M.A.; Young, S.A.; Kar, J. CALIPSO lidar level 3 aerosol profile product: Version 3 algorithm design. Atmos. Meas. Tech. 2018, 11, 4129–4152. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef] [Green Version]
- Anderson, G.; Clough, S.; Kneizys, F.; Chetwynd, J.; Shettle, E. AFGL Atmospheric Constituent Profiles (0.120 km); Air Force Geophysics Lab.: Bedford, MA, USA, 1986; p. 46. [Google Scholar]
- Kurucz, R.L. Synthetic infrared spectra. Symp.-Int. Astron. Union 1994, 154, 523–531. [Google Scholar] [CrossRef] [Green Version]
- Buras, R.; Dowling, T.; Emde, C. New secondary-scattering correction in DISORT with increased efficiency for forward scattering. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 2028–2034. [Google Scholar] [CrossRef]
- Wandji Nyamsi, W.; Arola, A.; Blanc, P.; Lindfors, A.V.; Cesnulyte, V.; Pitkänen, M.R.A.; Wald, L. Technical note: A novel parameterization of the transmissivity due to ozone absorption in the k-distribution method and correlated-k approximation of Kato et al. (1999) over the UV band. Atmos. Chem. Phys. 2015, 15, 7449–7456. [Google Scholar] [CrossRef] [Green Version]
- Kato, S.; Ackerman, T.P.; Mather, J.H.; Clothiaux, E.E. The k-distribution method and correlated-k approximation for a shortwave radiative transfer model. J. Quant. Spectrosc. Radiat. Transf. 1999, 62, 109–121. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations—Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef] [Green Version]
- Inness, A.; Ades, M.; Agustí-Panareda, A.; Barré, J.; Benedictow, A.; Blechschmidt, A.-M.; Dominguez, J.J.; Engelen, R.; Eskes, H.; Flemming, J.; et al. The CAMS reanalysis of atmospheric composition. Atmos. Chem. Phys. 2019, 19, 3515–3556. [Google Scholar] [CrossRef] [Green Version]
- Bhartia, P.K. OMI/Aura TOMS-Like Ozone, Aerosol Index, Cloud Radiance Fraction L3 1 Day 1 Degree x 1 Degree V3 (OMTO3d). NASA Goddard Sp. Flight Center, Goddard Earth Sci. Data Inf. Serv. Cent. (GES DISC), 2012. Available online: https://disc.gsfc.nasa.gov/datasets/OMTO3d_003/summary (accessed on 13 January 2022). [CrossRef]
- Wei, J.; Li, Z.; Peng, Y.; Sun, L. MODIS Collection 6.1 aerosol optical depth products over land and ocean: Validation and comparison. Atmos. Environ. 2019, 201, 428–440. [Google Scholar] [CrossRef]
- Global Modeling and Assimilation Office (GMAO) MERRA-2 tavgM_2d_rad_Nx: 2d, Monthly Mean, Time-Averaged, Single-Level, Assimilation, Radiation Diagnostics V5.12.4, Greenbelt, MD, USA, Goddard Earth Sciences Data and Information Services Center (GES DISC). Available online: 10.5067/OU3HJDS973O0 (accessed on 21 December 2021).
- Varotsos, C.A.; Melnikova, I.N.; Cracknell, A.P.; Tzanis, C.; Vasilyev, A. V New spectral functions of the near-ground albedo derived from aircraft diffraction spectrometer observations. Atmos. Chem. Phys. 2014, 14, 6953–6965. [Google Scholar] [CrossRef] [Green Version]
- Feister, U.; Grewe, R. Spectral albedo measurements in the uv and visible region over different types of surfaces. Photochem. Photobiol. 1995, 62, 736–744. [Google Scholar] [CrossRef]
- Kinne, S. The MACv2 aerosol climatology. Tellus B Chem. Phys. Meteorol. 2019, 71, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Tanré, D.; Haywood, J.; Pelon, J.; Léon, J.F.; Chatenet, B.; Formenti, P.; Francis, P.; Goloub, P.; Highwood, E.J.; Myhre, G. Measurement and modeling of the Saharan dust radiative impact: Overview of the Saharan Dust Experiment (SHADE). J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Rizza, U.; Kandler, K.; Eknayan, M.; Passerini, G.; Mancinelli, E.; Virgili, S.; Morichetti, M.; Nolle, M.; Eleftheriadis, K.; Vasilatou, V.; et al. Investigation of an intense dust outbreak in the mediterranean using XMed-Dry network, multiplatform observations, and numerical modeling. Appl. Sci. 2021, 11, 1566. [Google Scholar] [CrossRef]
- Choi, J.-O.; Chung, C.E. Sensitivity of aerosol direct radiative forcing to aerosol vertical profile. Tellus B Chem. Phys. Meteorol. 2014, 66, 24376. [Google Scholar] [CrossRef]
- Illingworth, A.J.; Barker, H.W.; Beljaars, A.; Ceccaldi, M.; Chepfer, H.; Clerbaux, N.; Cole, J.; Delanoë, J.; Domenech, C.; Donovan, D.P.; et al. The EarthCARE satellite: The next step forward in global measurements of clouds, aerosols, precipitation, and radiation. Bull. Am. Meteorol. Soc. 2015, 96, 1311–1332. [Google Scholar] [CrossRef] [Green Version]
- Brasseur, A.-L.; Ramaroson, R.; Delannoy, A.; Skamarock, W.; Barth, M. Three-dimensional calculation of photolysis frequencies in the presence of clouds and impact on photochemistry. J. Atmos. Chem. 2002, 41, 211–237. [Google Scholar] [CrossRef]
- Dickerson, R.R.; Kondragunta, S.; Stenchikov, G.; Civerolo, K.L.; Doddridge, B.G.; Holben, B.N. The impact of aerosols on solar ultraviolet radiation and photochemical smog. Science 1997, 278, 827–830. [Google Scholar] [CrossRef] [Green Version]
- Ding, K.; Huang, X.; Ding, A.; Wang, M.; Su, H.; Kerminen, V.-M.; Petäjä, T.; Tan, Z.; Wang, Z.; Zhou, D.; et al. Aerosol-boundary-layer-monsoon interactions amplify semi-direct effect of biomass smoke on low cloud formation in Southeast Asia. Nat. Commun. 2021, 12, 6416. [Google Scholar] [CrossRef]
- Barbaro, E.; Vilà-Guerau de Arellano, J.; Krol, M.C.; Holtslag, A.A.M. Impacts of aerosol shortwave radiation absorption on the dynamics of an idealized convective atmospheric boundary layer. Bound.-Layer Meteorol. 2013, 148, 31–49. [Google Scholar] [CrossRef]




| Property | Values |
|---|---|
| SZA | 20°, 40°, 60°, 80° |
| AOD (all wavelengths) | 0.2, 0.5, 1.0 |
| SSA (all wavelengths) | 0.75, 0.95 |
| Asymmetry factor | 0.7 |
| AE | 0 |
| TCO | 350 DU |
| TCWV | 1.3 g/cm2 |
| Surface albedo | 0.1, 0.4, 0.8 |
| Winter | Spring | Summer | Autumn | |
|---|---|---|---|---|
| 550 nm AOD | ||||
| NW Africa | 0.19 | 0.35 | 0.35 | 0.26 |
| CE Europe | 0.07 | 0.18 | 0.22 | 0.13 |
| TCWV (g/cm2) | ||||
| NW Africa | 11.4 | 14.6 | 22.3 | 20.4 |
| CE Europe | 9.6 | 14.4 | 25.7 | 17.4 |
| Total ozone (DU) | ||||
| NW Africa | 299.4 | 318.3 | 298.4 | 282.2 |
| CE Europe | 333.3 | 358.6 | 320.2 | 287.8 |
| Surface albedo | ||||
| NW Africa VIS/IR | 0.42 | 0.40 | 0.41 | 0.41 |
| NW Africa UVB/UVA | 0.10 | 0.10 | 0.10 | 0.10 |
| CE Europe VIS/IR | 0.15 | 0.15 | 0.15 | 0.15 |
| CE Europe UVB/UVA | 0.05 | 0.05 | 0.05 | 0.05 |
| Winter | Spring | Summer | Autumn | ||
|---|---|---|---|---|---|
| NW Africa | UVB | 0.84 | 0.77 | 0.81 | 0.80 |
| UVA | 0.85 | 0.78 | 0.82 | 0.81 | |
| VIS | 0.93 | 0.93 | 0.94 | 0.93 | |
| IR | 0.94 | 0.96 | 0.96 | 0.96 | |
| CE Europe | UVB | 0.80 | 0.86 | 0.87 | 0.83 |
| UVA | 0.81 | 0.87 | 0.88 | 0.85 | |
| VIS | 0.87 | 0.91 | 0.92 | 0.90 | |
| IR | 0.86 | 0.91 | 0.91 | 0.89 |
| Winter | Spring | Summer | Autumn | ||
|---|---|---|---|---|---|
| NW Africa | UVB | 1.32 | 0.74 | 1.04 | 0.89 |
| UVA | 1.32 | 0.74 | 1.04 | 0.89 | |
| VIS | 1.32 | 0.74 | 1.04 | 0.89 | |
| IR | 0.65 | 0.20 | 0.31 | 0.30 | |
| CE Europe | UVB | 1.32 | 1.52 | 1.66 | 1.41 |
| UVA | 1.32 | 1.52 | 1.66 | 1.41 | |
| VIS | 1.32 | 1.52 | 1.66 | 1.41 | |
| IR | 1.32 | 1.30 | 1.40 | 1.27 |
| 550 nm AOD | SSA | AE | TCWV (g/cm2) | TCO (DU) | Surface Albedo | |
|---|---|---|---|---|---|---|
| Cairo | ||||||
| UVB | 1 | 0.80 | 0.3 | 1.66 | 295 | 0.05 |
| UVA | 1 | 0.85 | 0.3 | 0.05 | ||
| VIS | 1 | 0.95 | 0.3 | 0.11 | ||
| IR | 1 | 0.98 | 0.3 | 0.11 | ||
| Lampedusa | ||||||
| UVB | 1 | 0.80 | 0.3 | 2.03 | 312 | 0.05 |
| UVA | 1 | 0.85 | 0.3 | 0.05 | ||
| VIS | 1 | 0.95 | 0.3 | 0.08 | ||
| IR | 1 | 0.98 | 0.3 | 0.08 | ||
| Athens | ||||||
| UVB | 1 | 0.80 | 0.3 | 1.85 | 317 | 0.05 |
| UVA | 1 | 0.85 | 0.3 | 0.05 | ||
| VIS | 1 | 0.95 | 0.3 | 0.11 | ||
| IR | 1 | 0.98 | 0.3 | 0.11 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fountoulakis, I.; Papachristopoulou, K.; Proestakis, E.; Amiridis, V.; Kontoes, C.; Kazadzis, S. Effect of Aerosol Vertical Distribution on the Modeling of Solar Radiation. Remote Sens. 2022, 14, 1143. https://doi.org/10.3390/rs14051143
Fountoulakis I, Papachristopoulou K, Proestakis E, Amiridis V, Kontoes C, Kazadzis S. Effect of Aerosol Vertical Distribution on the Modeling of Solar Radiation. Remote Sensing. 2022; 14(5):1143. https://doi.org/10.3390/rs14051143
Chicago/Turabian StyleFountoulakis, Ilias, Kyriakoula Papachristopoulou, Emmanouil Proestakis, Vassilis Amiridis, Charalampos Kontoes, and Stelios Kazadzis. 2022. "Effect of Aerosol Vertical Distribution on the Modeling of Solar Radiation" Remote Sensing 14, no. 5: 1143. https://doi.org/10.3390/rs14051143
APA StyleFountoulakis, I., Papachristopoulou, K., Proestakis, E., Amiridis, V., Kontoes, C., & Kazadzis, S. (2022). Effect of Aerosol Vertical Distribution on the Modeling of Solar Radiation. Remote Sensing, 14(5), 1143. https://doi.org/10.3390/rs14051143









