Three-Dimensional Geometry Reconstruction Method for Slowly Rotating Space Targets Utilizing ISAR Image Sequence

Abstract

For a slowly rotating space target (SRST) with a fixed axis, traditional 3D geometry reconstruction methods become invalid as the projection vectors cannot be formed without accurate target rotational parameters. To tackle this problem, we present a new technique for 3D geometry reconstruction by using inverse synthetic aperture radar (ISAR) image sequence energy accumulation (ISEA). Firstly, by constituting the motion model of SRST, an explicit expression is derived to describe the relative geometric relationship between the 3D geometry and ISAR image sequence. Then accurate rotational parameters and the 3D geometry of SRST can be estimated by combining the idea of the ISEA method and quantum-behaved particle swarm optimization (QPSO). Compared with the ISEA method, which can be only applied to triaxial stabilized space targets, the proposed method can achieve 3D geometry reconstruction of SRST. Experimental results based on the simulated point model and simulated electromagnetic computer aided design (CAD) model validate the effectiveness and robustness of the proposed method.

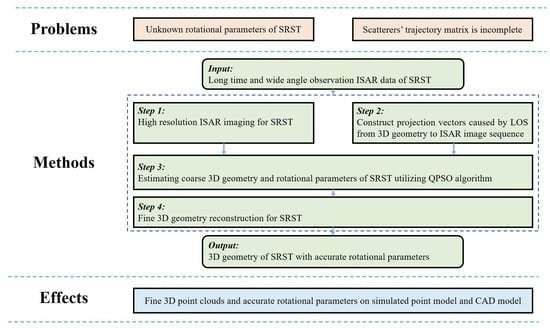
1. Introduction

Inverse synthetic aperture radar (ISAR) has found wide applications in space target surveillance and situation perception due to its all-day and all-weather observation and imaging capacity [1,2,3,4,5]. By utilizing the pulse compression and echo coherent accumulation technique, high resolution two-dimensional (2D) ISAR images of space targets can be acquired [6,7,8,9,10,11]. Since ISAR images are only the projection of three-dimensional (3D) geometry of space targets on different imaging planes, it is limited when applied in target geometry analysis and classification problems. Hence, precise 3D geometry reconstruction of space targets will facilitate space surveillance and situation perception. Many excellent algorithms have been presented to reconstruct the 3D geometry of targets and have shown extremely high performance [12,13,14]. However, they cannot be used on ISAR data directly owing to the great differences between ISAR data and others. Combined with the unique 2D imaging ability of ISAR systems, ISAR image sequence-based 3D geometry reconstruction has become a critical research topic.

According to the number of sensors in the imaging system, the existing 3D geometry reconstruction methods can be categorized into two classes: (a) 3D ISAR imaging methods based on multi-static radar system [15,16,17,18], and (b) structure-from-motion (SFM)-based 3D geometry reconstruction methods utilizing monostatic radar [19,20,21,22]. In the first class of methods, the 3D interferometric ISAR (InISAR) imaging technique has been widely developed. In 3D InISAR imaging, the instantaneous range difference between the target and each receiver is the basis for the phase difference of the same scatterer in different ISAR images. Therefore, through the phase interference processing, the coordinate information of the scatterers can be calculated after ISAR images registration. Then the 3D point cloud of the target can be obtained. Such methods require that different receivers must form a certain geometric distribution and keep precise time synchronization. As a result, high complexity in the hardware and algorithm generally limits the practical application of the InISAR system. To this end, 3D scattering image sparse reconstruction methods based on a radar network have been proposed [23,24]. Under the compress sensing framework, the 3D scattering distribution and coefficients can be simultaneously reconstructed by utilizing the non-binary ISAR images generated by different radars. These methods can reduce the restriction on the radar system and can be more effective in practical applications.

Unlike interferometric ISAR, 3D reconstruction using an ISAR image sequence should estimate the 3D distribution of scatterers from the 2D ISAR image sequence, according to the geometry of space targets. The factorization method [25] is one of the most classic solutions for SFM problems and has been widely used in 3D scene reconstruction of an optical image sequence. Generally, in the factorization method, we first form the measurement matrix, which is composed of the coordinates of each feature point in the image sequence. According to the rank deficient theorem, the measurement matrix can be decomposed into the multiplication of the 3D coordinates matrix of feature points and the motion matrix of the camera. Unfortunately, however, the observed scatterers may be anisotropic, sliding, or even obscured owing to the scattering characteristics of the microwave in real observation. Therefore, they cannot be tracked steadily in the ISAR image sequence, leading to the failure of the factorization methods. To solve this problem, many feature points extracting and tracking algorithms have been proposed [26,27,28,29]. In [27], speeded-up robust features (SURF) method is used to associate the scatterers in the ISAR image sequence. Firstly, the initial measurement matrix is obtained by feature points extraction of each ISAR image. Then, based on the SURF algorithm and on the minimum of the Euclid norm after back projection, the measurement matrix is further optimized to reconstruct the 3D geometry of the target. However, the initial measurement matrix is always incomplete, making it impossible to optimize and factorize the measurement matrix in real observation scenarios. To this end, several trajectory completion algorithms are proposed to retrieve the missing data in the measurement matrix [25,30], making that the factorization method can be used in the ISAR image sequence. Nevertheless, the huge difference between ISAR images and optical images is still the main obstacle to achieve great performance of the factorization method in practical applications. In other words, the 3D geometry reconstruction process can be hardly executed automatically. Therefore, a new 3D geometry reconstruction method based on ISAR image sequence energy accumulation (ISEA) is presented in [31]. The proposed method completely abandons the process of the factorization method, and makes full use of the ISAR measurement information to construct the projection relationship from the 3D geometry of targets to the ISAR image sequence. By taking the projection energy accumulation value of real scatterers on the ISAR image sequence as the fitness function, the 3D point cloud of the space target can be reconstructed via the particle swarm optimization (PSO) algorithm. With no feature points extraction and tracking process needed, the ISEA method can be used in practical applications with high accuracy and high effectiveness.

In the context of space situational awareness, there are usually two categories of space targets, i.e., satellites and space debris, which differ in motion types. For the space debris, they usually have high velocity with micro-motion [32,33]. The rotational motion of satellites, however, is usually much simpler. Under normal operating conditions, the satellites generally keep triaxial stabilized, i.e., their attitudes in the orbital coordinate system (OCS) remain unchanged. However, after losing control with ground telecommand telemetry, the satellites always start to rotate slowly due to the gravity gradient torque. During the same ISAR observation process, we can consider that its rotational axis is fixed. These satellites can be called the slowly rotating space target (SRST). Moreover, accurate estimation of rotational parameters and 3D geometry of SRST can provide key support for the working state evaluation and space surveillance. Nevertheless, because of the unknown rotational motion, the cross-range scaling of each ISAR image of SRST is inaccurate. In other words, the projection relationship between the 3D positions of SRST and the ISAR image sequence depends not only on the variation of line of sight (LOS), but also on the unknown rotational motion. That is the reason why the traditional factorization methods and ISEA method fail when it comes to the 3D geometry reconstruction problem for SRST. To solve this problem, a new 3D reconstruction method for SRST is proposed in this paper. Firstly, the rotational motion model of the SRST is constructed. Then, the explicit expression is derived to describe the projection relationship between the 3D geometry of the SRST and ISAR image sequence. After that, the accurate rotational parameters and the coarse 3D point cloud of SRST can be obtained by the quantum-behaved particle swarm optimization (QPSO) algorithm. Finally, the projection matrix is formed with the parameters obtained, and an accurate 3D geometry of SRST can be reconstructed. By considering the extra rotation of SRST, the proposed method is more robust and feasible than the ISEA method in practical applications.

The rest of this paper is organized as follows. Section 2 constructs the ISAR observation and projection model for SRST. In the meantime, the proposed 3D reconstruction method for SRST and the performance analysis are presented, respectively. After that, the validity of the proposed method is verified by experiments based on the simulated point model and simulated electromagnetic CAD model in Section 3. Section 4 discusses the results of the experiments. Finally, the conclusion is drawn in Section 5.

2. Materials and Methods

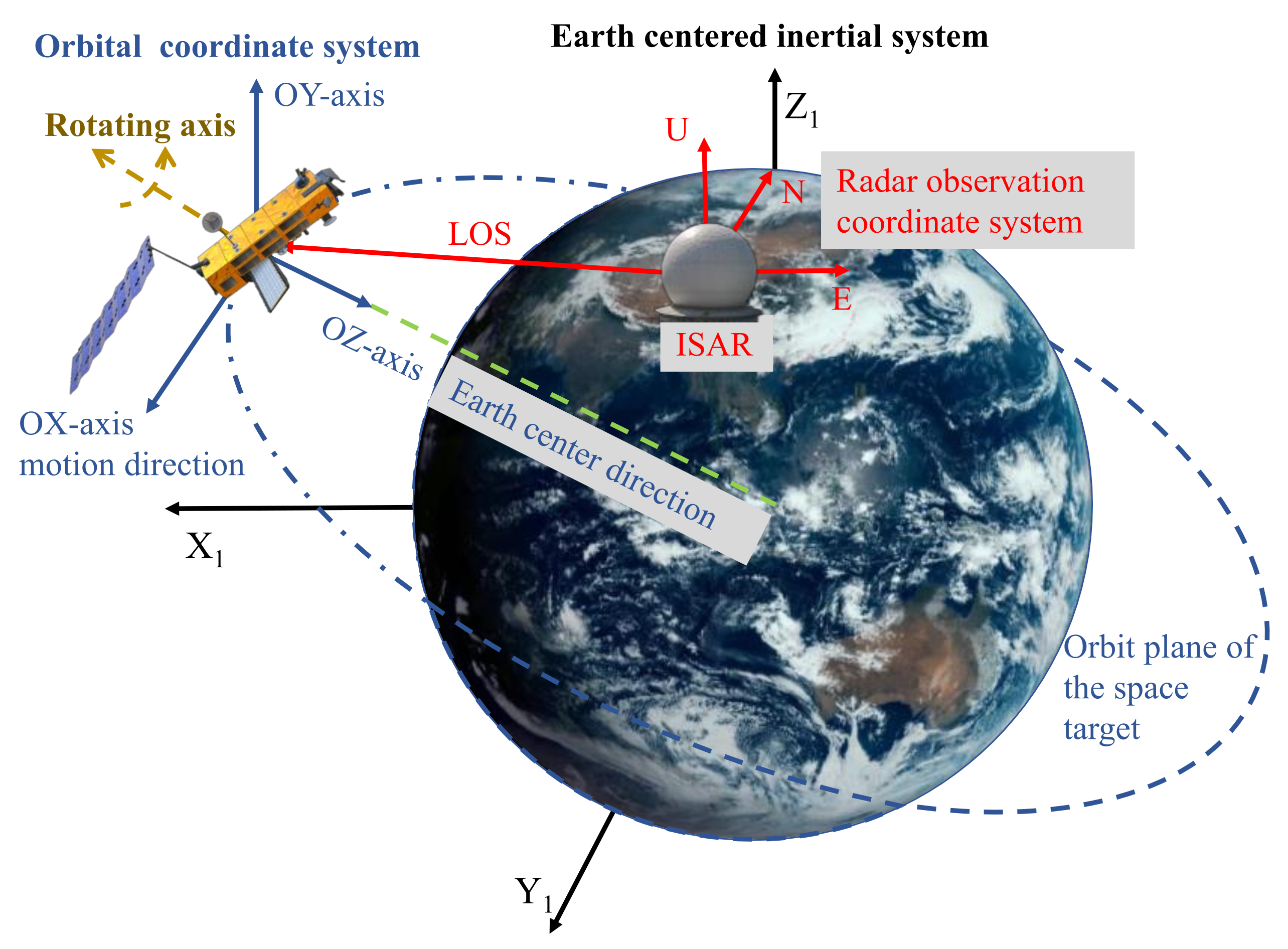
2.1. The ISAR Observation and Projection Model for Slowly Rotating Space Targets

As reported in [34,35], the environmental satellite (ENVISAT), an earth observation satellite operated by the European Space Agency (ESA), and Tiangong-1, China’s first space laboratory, were two typical SRSTs after losing contact with ground monitoring and the controlling system in 2012 and 2016, respectively. Unlike the triaxial stabilized satellites, the SRST rotates around a fixed axis with a constant rotational velocity rather than maintaining stillness in the orbital coordinate system. As shown in Figure 1, the OZ-axis points to the center of the earth, the OX-axis points to the motion direction of SRST, and the OY-axis can be obtained through the right-hand rule. Therefore, the ISAR observation and projection model for SRST can be defined in OCS. In Figure 1, the blue arrow represents the rotational axis of SRST and the green curve consists of the instantaneous radar observation lines of sight (LOS). $\theta \left(t\right)$ and $\varphi \left(t\right)$ are the instantaneous pitch and azimuth angles of LOS in the OCS, respectively. $t$ represents the slow time in cross-range direction. Therefore, the instantaneous LOS can be defined by:

$$l\left(t\right)={\left[\sin \theta \left(t\right)\cos \varphi \left(t\right),\sin \theta \left(t\right)\sin \varphi \left(t\right),\cos \theta \left(t\right)\right]}^T.$$

(1)

Define that the rotational angular velocity of SRST is $\omega$, with $\omega =\left|\omega \right|$ and the sign of $\omega$ can be determined by the Ampere’s Law. Similarly, the unit vector of the rotational axis can be represented as:

$$r={\left[\sin \alpha \cos \beta ,\sin \alpha \sin \beta ,\cos \alpha \right]}^T,$$

(2)

where $\alpha$ and $\beta$ are the pitch and azimuth angles of rotational axis in the OCS, respectively. Therefore, the instantaneous position of any arbitrary scatterer on the SRST can be obtained by:

$$p_n\left(t\right)=R_r\left(t\right)p_n,$$

(3)

where $p_n={\left[x_n,y_n,z_n\right]}^T$ is the initial position of the scatterer, and $R_r\left(t\right)$ is the Rodriguez formula [36] defined by:

$$R_r\left(t\right)=I+K\sin \omega t+K^2\left(1-\cos \omega t\right),$$

(4)

in which,

$$K=\left[\begin{array}{ccc}0& -\cos \alpha & \sin \alpha \sin \beta \\ \cos \alpha & 0& -\sin \alpha \cos \beta \\ -\sin \alpha \sin \beta & \sin \alpha \cos \beta & 0\end{array}\right].$$

(5)

Assume that the distance between the radar system $q\left(t\right)$ and the geometry center of SRST is $r_0\left(t\right)$. The projected distance on radar LOS from radar to any arbitrary scatterer $p\left(t\right)$ of SRST can be represented as:

$$r_n\left(t\right)=\left(p\left(t\right)-q\left(t\right)\right)\cdot l\left(t\right),$$

(6)

where ‘$\cdot$’ represents the inner product. By substituting Equation (3) into Equation (6), the instantaneous projection distance of $p\left(t\right)$ on the range dimension in an ISAR image is:

$$r_n\left(t\right)=\left(R_r\left(t\right)p_n\right)\cdot l\left(t\right)-r_0\left(t\right),$$

(7)

where $r_0\left(t\right)$ reflects the translational motion in the ISAR imaging process and can be compensated by high resolution ISAR imaging algorithms [6,7,8,9]. Suppose that the translational motion is well compensated, then Equation (7) can be rewritten as:

$$r_n\left(t\right)=l\left(t\right)\cdot \left(R_r\left(t\right)p_n\right)={\left(R_r\left(t\right)\right)}^{T}l\left(t\right)\cdot p_n.$$

(8)

Therefore, the Doppler of the scatterer $p\left(t\right)$ can be represented as:

$$\begin{array}{c}{f}_n\left(t\right)=-\frac{2}{\lambda }\frac{\partial r_n\left(t\right)}{\partial t}=-\frac{2}{\lambda }\frac{\partial \left({\left(R_r\left(t\right)\right)}^{T}l\left(t\right)\cdot p_n\right)}{\partial t}\\ =-\frac{2}{\lambda }\left[{\left(R_r\left(t\right)\right)}^T\frac{\partial l\left(t\right)}{\partial t}+{\left(\frac{\partial R_r\left(t\right)}{\partial t}\right)}^{T}l\left(t\right)\right]\cdot p_n.\end{array}$$

(9)

As a matter of fact, the positions in the ISAR image coordinate of any arbitrary scatterer can be expressed by the instantaneous range and Doppler. Therefore, the relationship between the 3-D coordinates of any arbitrary scatterer $p\left(t\right)$ and the projected positions in ISAR image sequence can be explicitly written as:

$$\left[\begin{array}{l}{f}_n^k\\ r_n^k\end{array}\right]=\left[\begin{array}{l}{\left({\rho }_d^k\right)}^T\\ {\left({\rho }_r^k\right)}^T\end{array}\right]p_n,$$

(10)

where $f_n^k$ and $r_n^k$ are the instantaneous Doppler and range position of the $n-th$ scatterer in the $k-th$ ISAR image, respectively. ${\rho }_r^k$ and ${\rho }_d^k$ are the range and Doppler projection vectors from the 3D coordinate of scatterers to the $k-th$ 2D ISAR image, respectively. The subindexes ‘r’ and ‘d’ represent “range” and “Doppler”, respectively.

Therefore,

$${\rho }_d^k=-\frac{2}{\lambda }\left[{\left(R_r\left(t_k\right)\right)}^T\frac{\partial l}{\partial t}\left(t_k\right)+{\left(\frac{\partial R_r}{\partial t}\left(t_k\right)\right)}^{T}l\left(t_k\right)\right],$$

(11)

$${\rho }_r^k={\left(R_r\left(t_k\right)\right)}^{T}l\left(t_k\right).$$

(12)

It is noted that the projection vectors above can be divided into two parts by substituting Equation (4) into Equations (11) and (12):

$$\begin{array}{l}{\mathsf{\rho }}_d^k=={\rho }_{ds}^k+{\rho }_{dl}^k,\\ {\rho }_r^k=={\rho }_{rs}^k+{\rho }_{rl}^k,\end{array}$$

(13)

where the subindexes “ds, dl, rs, and rl” present “Doppler by spin”, “Doppler by LOS”, “range by spin”, and “range by LOS”, respectively. Besides:

$${\rho }_{rs}^k={\left[K\sin \omega t_k+K^2\left(1-\cos \omega t_k\right)\right]}^{T}l\left(t_k\right),$$

(14)

and

$${\rho }_{ds}^k=-\frac{2}{\lambda }{\left[K\sin \omega t_k+K^2\left(1-\cos \omega t_k\right)\right]}^T\frac{\partial l}{\partial t}\left(t_k\right)-\frac{2}{\lambda }{\left[K\omega \cos \omega t_k+K^2\omega \sin \omega t_k\right]}^{T}l\left(t_k\right),$$

(15)

are the range and Doppler projection vectors caused by the rotational motion of SRST. Besides:

$${\rho }_{rl}^k=l\left(t_k\right),$$

(16)

and

$${\rho }_{dl}^k=-\frac{2}{\lambda }\frac{\partial l}{\partial t}\left(t_k\right),$$

(17)

are the range and cross-range projection vectors caused by the relative motion between the radar and SRST, respectively. A detailed expression can be found in [31].

Until now, the explicit projection relationship between the 3D geometry and ISAR image sequence of SRST is constructed. It is obvious to see from Equation (10) to Equation (12) that the unknown rotational parameters and coordinates of scatterers on the SRST are severely coupled, making it impossible to obtain the rotational parameters and 3D coordinates of SRST by solving the equations. In fact, the factorization method is one of the effective ways to solve this problem if enough scatterers can be tracked throughout the ISAR image sequence. However, because of the severe anisotropy of scatterers in the ISAR image sequence, few of them can be tracked steadily, making the reconstructed 3D point cloud too sparse to describe the 3D geometry of SRST. To also induce to the unexpected rotation motion of SRST, the observation and imaging model in [31] become invalid, making the ISEA method inapplicable.

To this end, by constructing a suitable observation and projection model for SRST in this section, a new 3D geometry reconstruction method is proposed on the basis of the ISEA method. The specific algorithm will be discussed in Section 2.2.

2.2. 3D Geometry Reconstruction Method for Slowly Rotating Space Targets

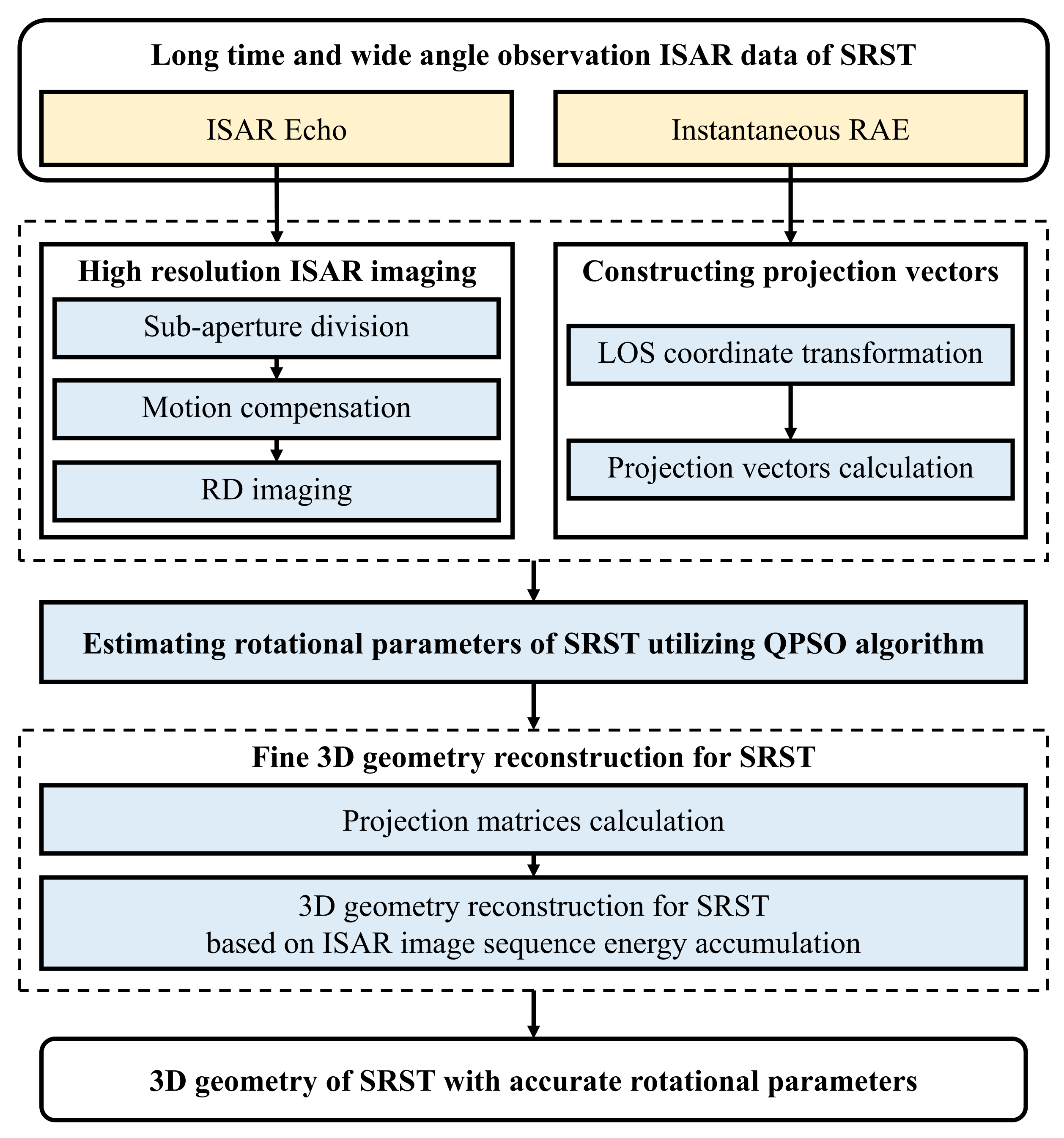
2.2.1. Algorithm Flowchart

Before a detailed discussion, the flowchart of the proposed method is shown below in Figure 2. It indicates that there are four key steps in the algorithm. It is necessary to note that the input of the algorithm is the long-time and wide-angle ISAR observation data of SRST, including ISAR echoes, as well as instantaneous range, azimuth, and elevation angles (RAE). Besides, the imaging process and the projection vectors constructing process can be executed simultaneously and independently for each sub-aperture. The imaging process takes the ISAR echo as the input and outputs high resolution ISAR image sequence of the SRST. The projection vectors constructing process takes the instantaneous RAE as the input and constructs the projection vectors caused by LOS. Then the QPSO algorithm is utilized to estimate the rotational parameters of SRST. Finally, with the estimated rotational parameters, the 3D geometry of SRST can be reconstructed. The detailed description of each key step will be presented in the following subsections.

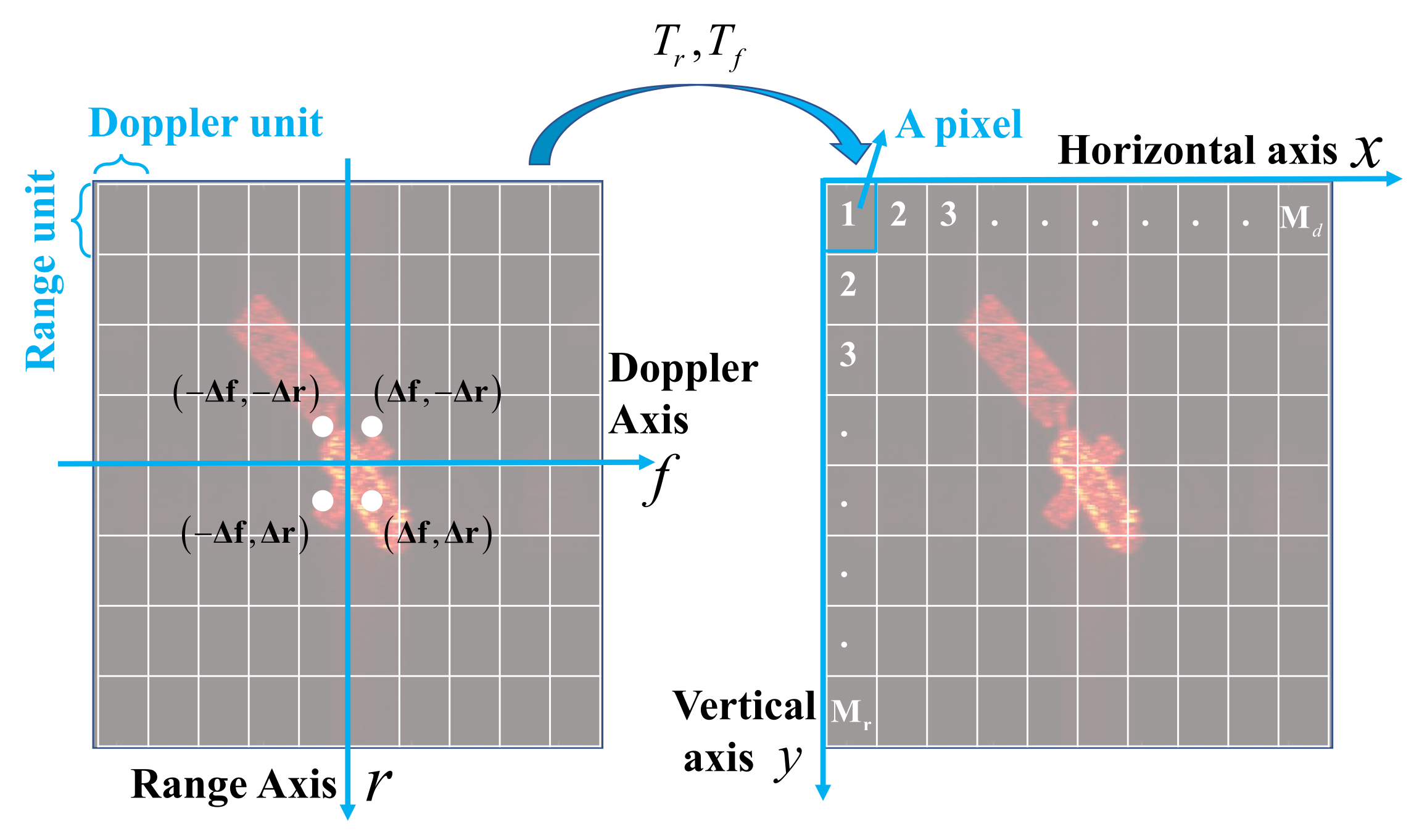
2.2.2. High Resolution ISAR Imaging for SRST

As a typical example of SRST, the only moment of the ENVISAT is the gravity of earth after losing control. It is reported that the ENVISAT is rotating around a fixed axis with a small speed of no more than 4°/s [35]. Therefore, the rotating velocity of SRST referenced in this paper is comparable to that of an equivalent turntable in ISAR imaging. The classic range-Doppler (RD) imaging method, after simple improving, can be used to obtain an ISAR image sequence of SRST. When generating an ISAR image sequence of SRST, the long time and wide angle ISAR observation echoes should be divided into several short sub-apertures. Then the RD algorithm is utilized to obtain the ISAR image of each sub-aperture. It is noted that when the rotational axis of SRST and that induced by the LOS variation points to the same direction, the migration through resolution cell (MTRC) will be much exacerbated. Fortunately, some effective methods have been proposed to solve this problem [6,7]. Therefore, with an improved RD imaging method, a high resolution ISAR image sequence can be obtained.

2.2.3. Constructing Projection Vectors

The projection relationship from the 3D geometry of SRST to the ISAR image sequence is defined in the OCS shown in Figure 3, which is the same coordinate system as that shown in Figure 1. However, the observation information can only be obtained in the radar observation coordinate system (ROCS). Therefore, coordinate transformation should be done before reconstructing the 3D geometry of SRST. As introduced in Section 2.1, the OZ-axis points to the center of the earth, the OX-axis coincides with the motion direction of the SRST, and the OY-axis can be obtained through the right-hand rule in the OCS. Therefore, the three axes of OCS can be defined in the earth centered inertial (ECI) system as follows:

$$x=\frac{u\times v\times u}{\left|u\times v\times u\right|},$$

(18)

$$y=\frac{u\times v}{\left|u\times v\right|},$$

(19)

$$z=\frac{u}{\left|u\right|},$$

(20)

where $u$ and $v$ are the position vector and velocity vector of the SRST in ECI system, respectively. Assuming that the instantaneous LOS in the radar observation coordinate system is $l_{ROCS}$, the LOS in the orbital coordinate system can be represented as:

$$l=H_{E2O}{H}_{R2E}{l}_{ROCS},$$

(21)

in which:

$$H_{R2E}={\left[\frac{u\times v\times u}{\left|u\times v\times u\right|},\frac{u\times v}{\left|u\times v\right|},\frac{u}{\left|u\right|}\right]}^T,$$

(22)

is the transformation matrix from ROCS to the ECI system and $H_{E2O}$ is the transformation matrix from the ECI system to OCS [37]. By transforming the LOS into an orbital coordinate system, the projection vectors caused by the relative motion between the radar and SRST can be obtained via Equation (16) and Equation (17). After that, in order to construct the exact projection vectors from 3D geometry to the ISAR image sequence, accurate rotational parameters should be estimated first and the detailed procedure will be introduced in Section 2.2.4.

2.2.4. Rotational Parameters Estimation Based on the QPSO Algorithm

It is obvious that the 3D geometry of the SRST can be determined via Equation (10) if the rotational parameters can be estimated accurately. Therefore, the projection images of the SRST can be obtained by re-projecting the 3D geometry on the ISAR imaging planes. Clearly, the projection images show an extremely high similarity with the practical ISAR images. In other words, if we put the practical ISAR image and projection image together, the energy covered by the projected geometry is much higher than that of the uncovered part in the ISAR image sequence under accurate rotational parameters. Based on the analysis, the problem of estimating the rotational parameters of the SRST can be transformed into an unconstrained optimization problem, of which the objective function is defined as:

$$\left[{\omega }_{opt},{\alpha }_{opt},{\beta }_{opt}\right]=\arg \underset{\omega ,\alpha ,\beta }{\max }\left({\displaystyle \sum _{k=1}^K{\displaystyle \sum _{n=1}^N{I}_k\left[T_r\left(r_n^k\right),T_f\left(f_n^k\right)\right]}}\right),$$

(23)

where $r_n^k$ and $f_n^k$ are the instantaneous range and Doppler values of the $n-th$ scatterer of the SRST in the $k-th$ ISAR image, respectively. $T_r$ and $T_f$ are the transformation function from the range-Doppler coordinate system to the image coordinate system, which is shown in Figure 4. The definitions are presented below:

$$\begin{array}{l}{T}_r\left(r_n^k\right)=r_n^k/\mathsf{\Delta }r+M_r/2,\\ T_f\left(f_n^k\right)=f_n^k/\mathsf{\Delta }f+M_d/2,\end{array}$$

(24)

where $\mathsf{\Delta }r$ and $\mathsf{\Delta }f$ are the range resolution unit and Doppler resolution unit, respectively. $M_r$ and $M_d$ are the numbers of the range and Doppler cells, respectively.

Until now, the rotational parameters and unknown 3D geometry of SRST can be estimated by solving Equation (23). Usually, the PSO algorithm is an effective way to solve the unconstrained optimization problem in Equation (23). However, the state of particles in PSO are only determined by their positions and velocities, lessening the randomicity of their trajectory. Therefore, the PSO algorithm cannot guarantee the global convergence, which has been proved in [38]. Fortunately, owing to the strong uncertainty of the quantum behaviors, it is brought into the PSO algorithm and the new algorithm is called the QPSO algorithm [39,40]. Compared to the classical PSO algorithm, the QPSO algorithm shows better performance on solving a non-convex problem. Meanwhile, QPSO has been proved to be convergent to the global optimization solution with probability 1 [41]. Besides, owing to fewer adjustable parameters in the QPSO algorithm, the searching process can be greatly simplified and with much less manual intervention. Therefore, a rotational parameters estimation method for SRST is proposed based on QPSO in this section. The detailed procedure is presented as follows.

• Step 1: Initialization. Randomly initialize a group of particles consisting of $D$ individuals, in which the initial position of the m-th individual is ${\chi }_m^l=\left[{\omega }_m^l,{\alpha }_m^l,{\beta }_m^l\right],l=1$. Set the individual best position of each particle ${\left({\chi }_{best}\right)}_m^l={\chi }_m^l$. Initialize the max number of iterations as $L$.

• Step 2: Average best position calculation. The average best position of the particle swarm can be calculated by:

$$C^l=\frac{1}{M}{\displaystyle \sum _{m=1}^M{\left({\chi }_{best}\right)}_m^l}.$$

(25)

• Step 3: Fitness value calculation. For each particle, construct the projection vectors via Equation (11)–(17). Then the coarse 3D geometry matrix $P$ of the SRST can be reconstructed through the ISEA method, which will be introduced in Section 2.2.5. The fitness value of each particle can be calculated by:

$$\varpi \left({\chi }_m^l\right)={\displaystyle \sum _{k=1}^K{I}_k\left[\frac{{\rho }_r^{k}P}{\mathsf{\Delta }r}+\frac{M_r}{2},\frac{{\rho }_d^{k}P}{\mathsf{\Delta }f}+\frac{M_d}{2}\right]}.$$

(26)

• Step 4: Individual best position updating. Compare the fitness value of each particle to its individual best position. If $\varpi \left({\chi }_m^l\right)>\varpi \left[{\left({\chi }_{best}\right)}_m^l\right]$, set ${\left({\chi }_{best}\right)}_m^l={\chi }_m^l$. Otherwise, ${\left({\chi }_{best}\right)}_m^l$ remains.

• Step 5: Global best position updating. Set the global best position $G^l$ to be equal to ${\left({\chi }_{best}\right)}_j^l,j\in \left[1,M\right]$ where ${\left({\chi }_{best}\right)}_j^l$ satisfies:

$$\varpi \left[{\left({\chi }_{best}\right)}_j^l\right]>\varpi \left[{\left({\chi }_{best}\right)}_m^l\right],\forall m\ne j.$$

(27)

• Step 6: Individual particle position updating. Find a random position for each particle via:

  $${\chi }_m^{l+1}={\xi }_m^l\pm \sigma \cdot \left|C^l-{\chi }_m^l\right|\cdot \ln \frac{1}{{\tau }_1^l},$$

  (28)

  in which the ‘$\pm$’ means that it can take a plus and a minus sign with equal probability. In addition,

  $${\xi }_m^l={\tau }_2^l\cdot {\left({\chi }_{best}\right)}_m^l+\left(1-{\tau }_2^l\right)\cdot G^l$$

  (29)

  shows how the local best position and the global best position influence the new position of the particles. ${\tau }_1^l$ and ${\tau }_2^l$ are two random values generated from uniform distribution, i.e., ${\tau }_1^l,{\tau }_2^l~U\left(0,1\right)$. $\sigma$ is called the shrink-expansion factor. If $\sigma$ decreases linearly from 1 to 0.5, the QPSO usually shows better performance in the searching process.

• Step 7: Iterative stop condition. If $l<L$, set $l=l+1$ and go back to step 2. Otherwise, stop the iterative process and output the global optimal position $G^l=\left[{\omega }_{opt},{\alpha }_{opt},{\beta }_{opt}\right]$ as the optimization solution.

2.2.5. 3D Geometry Reconstruction

In the ISEA-based 3D geometry reconstruction method [31], a 3D scatterer candidate is considered as a true scatterer of the space target if the ISEA value of this candidate is above a predetermined threshold. On the contrary, if this scatterer candidate is a fake one, most of the corresponding projection positions in the image sequence would be noise, resulting in the ISEA value being much lower than that of true scatterers. Therefore, based on this analysis, the 3D point cloud of space target can be reconstructed via the PSO algorithm.

Nonetheless, owing to the limitation of the projection geometry, the ISEA-based method can only be used to reconstruct the 3D geometry of triaxial stabilized space targets. However, in addition to the relative motion with the radar, SRST also has its own rotational motion, leading the projection relationship constructed in [31] to become invalid. In fact, through the estimation in a previous subsection, the rotational parameters can be obtained and the projection vectors can be constructed. Hence, the ISEA idea can be used to reconstruct the 3D geometry of the SRST. The detailed procedure is presented as follows.

• Step 1: Initialization. A sequence of ISAR images $I_k$ can be obtained via a high resolution ISAR imaging method. The projection vectors ${\left[{\rho }_d^k,{\rho }_r^k\right]}^T$ from the 3D geometry of SRST to the corresponding ISAR image sequence are constructed through Equations (11) to (17). Calculate the total energy $E_{total}$ and remaining energy $E_{remain}$ of all the ISAR images. Initialize the lower limit $\epsilon$ of $E_{remain}/E_{total}$ to 0.001, which is selected based on experiments and shows better performance. Initialize the reconstructed 3D point cloud of the SRST $\mathsf{\Theta }=\varnothing$.

• Step 2: 3D scatterer estimation. By taking the energy of the projection positions in the ISAR image sequence as the objective function value, the 3D scatterer $p_{opt}=\left[x_{opt},y_{opt},z_{opt}\right]$ can be estimated via the optimization algorithms [31]. Then let $\mathsf{\Theta }=\mathsf{\Theta }\cup p_{opt}$.

• Step 3: Residual images updating. By taking ${\chi }_{opt}$ into Equation (10), the projection positions of the 3D geometry of SRST ${\left[f_n^k,r_n^k\right]}^T$ in each ISAR image can be obtained. Also, set $I_k\left[\frac{{\rho }_r^{k}P}{\mathsf{\Delta }r}+\frac{M_r}{2},\frac{{\rho }_d^{k}P}{\mathsf{\Delta }f}+\frac{M_d}{2}\right]=0$.

• Step 4: Iterative stop condition. Update the remaining energy of the ISAR image sequence $E_{remain}$. If $E_{remain}/E_{total}<\epsilon$, stop the iterative process and output $\mathsf{\Theta }$ as the reconstructed 3D point cloud. Otherwise, go back to step 2.

2.3. Performance Analysis

To better evaluate the accuracy of estimated rotational parameters and reconstructed 3D geometry of SRST, we define the following three criterions.

2.3.1. Rotational Parameter Estimation Error

If the rotational axis of the SRST is defined in the opposite direction, the signs of rotational velocity will also be opposite. Actually, the rotation motion is exactly the same under these two cases. Based on the analysis, the estimation error for rotational velocity is:

$$E_{velocity}=\left|\omega -\widehat{\omega }\right|,$$

(30)

and the estimation error for rotational axis is:

$$E_{axis}=〈r,\widehat{r}〉=\mathrm{acos}\left(\frac{r\cdot \widehat{r}}{\left|r\right|\cdot \left|\widehat{r}\right|}\right),$$

(31)

where:

$$r=sign\left(\omega \right)\cdot \left[\sin \alpha \cos \beta ,\sin \alpha \sin \beta ,\cos \alpha \right]$$

(32)

$$\widehat{r}=sign\left(\omega \right)\cdot \left[\sin \widehat{\alpha }\cos \widehat{\beta },\sin \widehat{\alpha }\sin \widehat{\beta },\cos \widehat{\alpha }\right].$$

(33)

2.3.2. Root-Mean-Square Error

The root-mean-square error (RMSE) of the reconstructed 3D geometry can be defined as:

$$E_{RMSE}=\sqrt{\frac{1}{N}{\displaystyle \sum _{n=1}^N{\left(p_n^{opt}-p_n\right)}^2}},$$

(34)

where $N$ represents the number of the scatterers on the SRST, $p_n^{opt}$ denotes the reconstructed 3D coordinates of the n-th scatterer, and $p_n$ is the true position of the n-th scatterer. RMSE reflects the error between the reconstructed geometry and true geometry. However, the computation process may become much more complex for a complicated target because two geometries might not be matched correctly. Therefore, another criterion is proposed to better evaluate the accuracy of the reconstructed geometry.

2.3.3. Similarity of the Projection Image Sequence and ISAR Image Sequence

In order to evaluate the accuracy of the reconstructed point cloud in a more convenient way, we define the similarity of the projection image sequence and ISAR image sequence as follows:

$$Sim=\frac{1}{K}{\displaystyle \sum _k\left\{\frac{{\displaystyle \sum _{m_r}{\displaystyle \sum _{m_d}\left[\left(I_{proj}^k-{\overline{I}}_{proj}^k\right)\circ \left(I_{bin}^k-{\overline{I}}_{bin}^k\right)\right]}}}{\sqrt{\left[{\displaystyle \sum _{m_r}{\displaystyle \sum _{m_d}{\left(I_{proj}^k-{\overline{I}}_{proj}^k\right)}^2}}\right]\left[{\displaystyle \sum _m{\displaystyle \sum _n{\left(I_{bin}^k-{\overline{I}}_{bin}^k\right)}^2}}\right]}}\right\}},$$

(35)

In which “$\circ$” represents the Hadamard product. $I_{proj}^k$ and $I_{bin}^k$ are the k-th binarized projection image of the reconstructed result and the k-th binarized ISAR image, respectively. ${\overline{I}}_{proj}^k$ and ${\overline{I}}_{bin}^k$ are the energy averages of all pixels in $I_{proj}^k$ and $I_{bin}^k$, respectively. $m_r\in \left[1,M_r\right]$, $m_d\in \left[1,M_d\right]$, and $k\in \left[1,K\right]$ are the index of range cell, cross-range cell, and image sequence, respectively.

3. Results

To validate the effectiveness of the proposed method, three experiments based on the simulated point model and simulated electromagnetic CAD model are carried out in this section.

3.1. Experiment Based on a Simple Point Model of a Satellite

As is shown in Figure 5a, a simple point model of a satellite consisting of 24 scatterers is constructed to analyze the estimation accuracy of the rotational parameters and the 3D point cloud of the SRST. The simulated model is rotating clockwise around the rotational axis with the rotational velocity of 3°/s, i.e., about 0.0524 rad/s. The pitch and azimuth angles of its rotational axis are 10° and 5°, respectively. The observation and imaging parameters are list in

Table 1. Radar observation parameters.

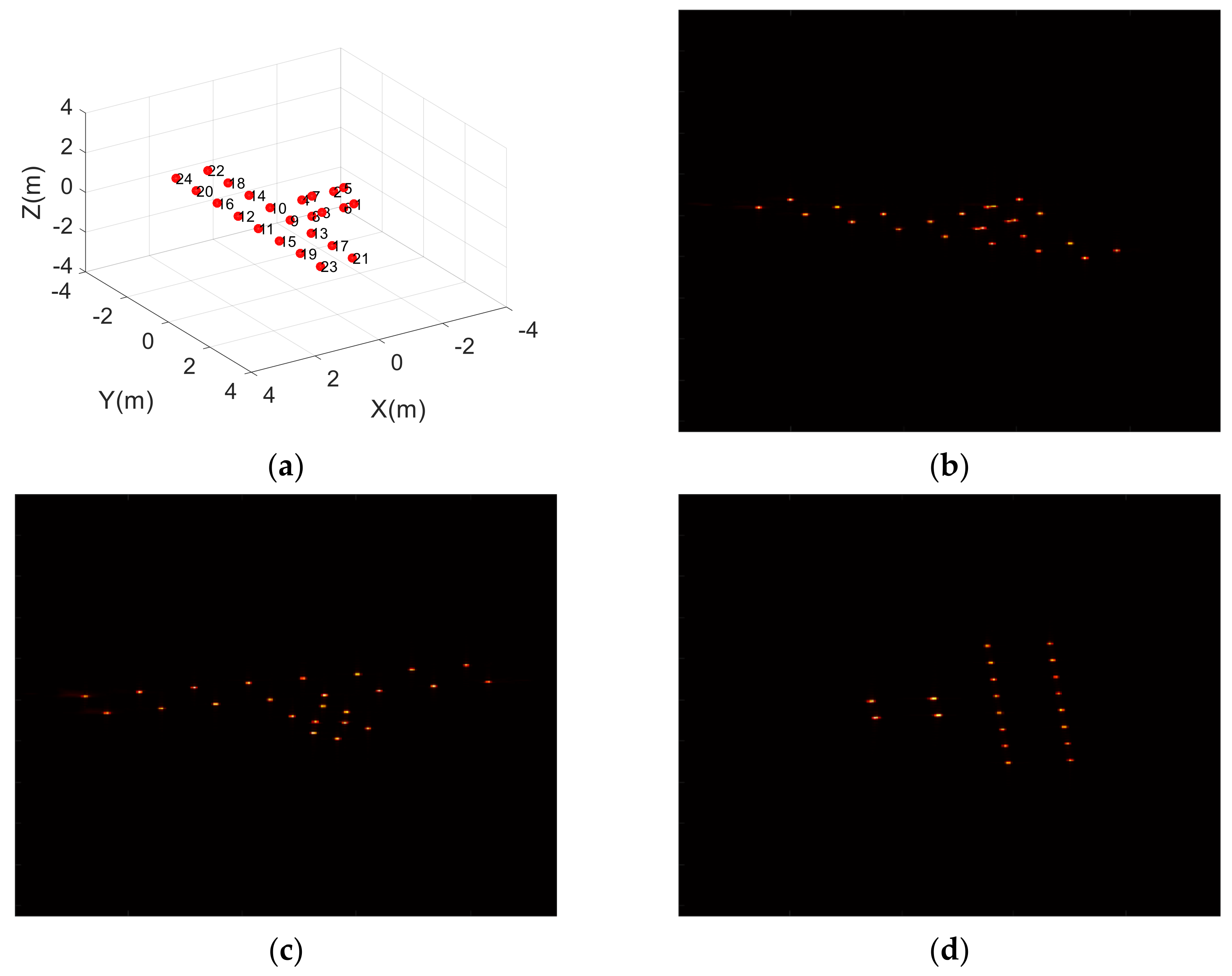
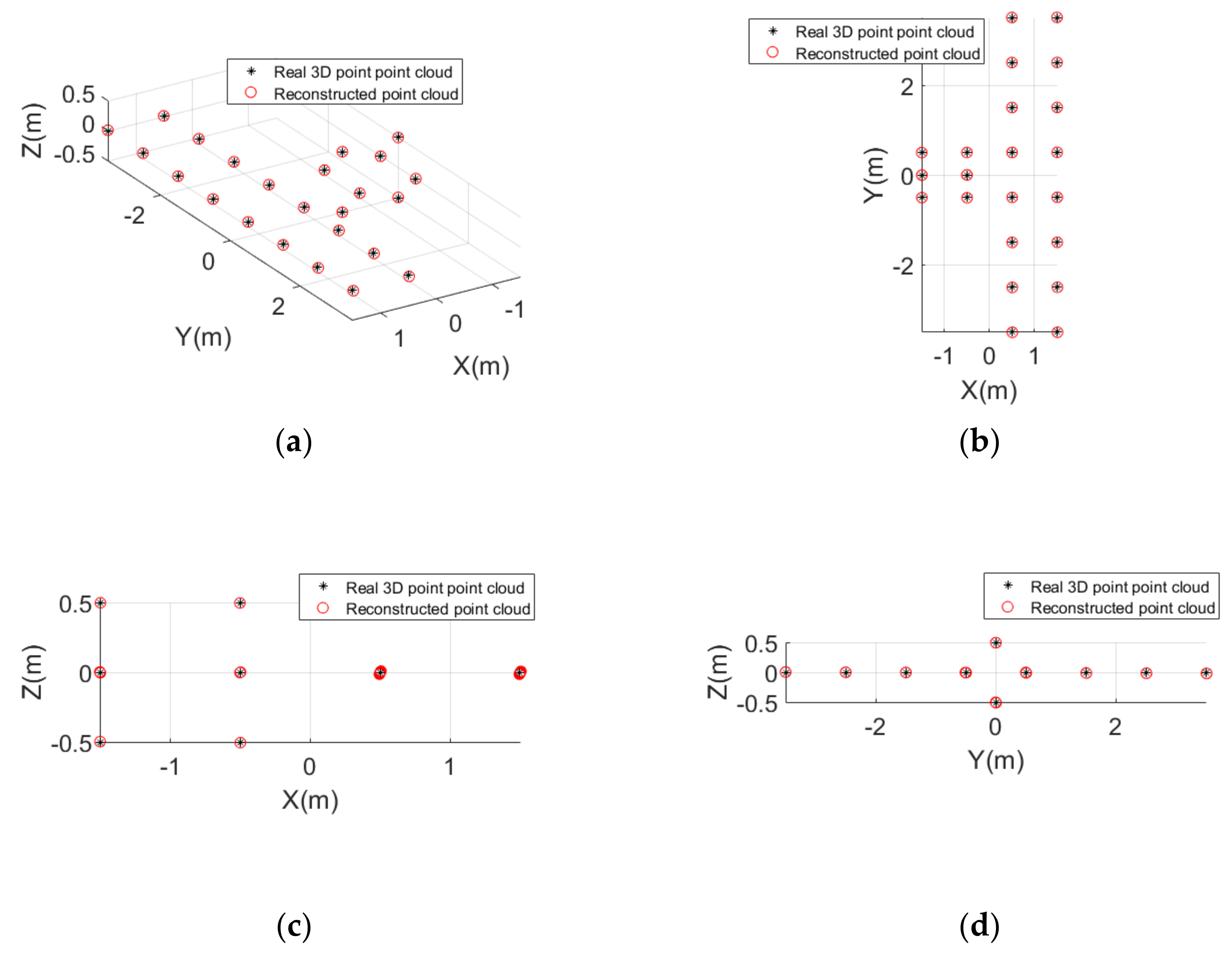
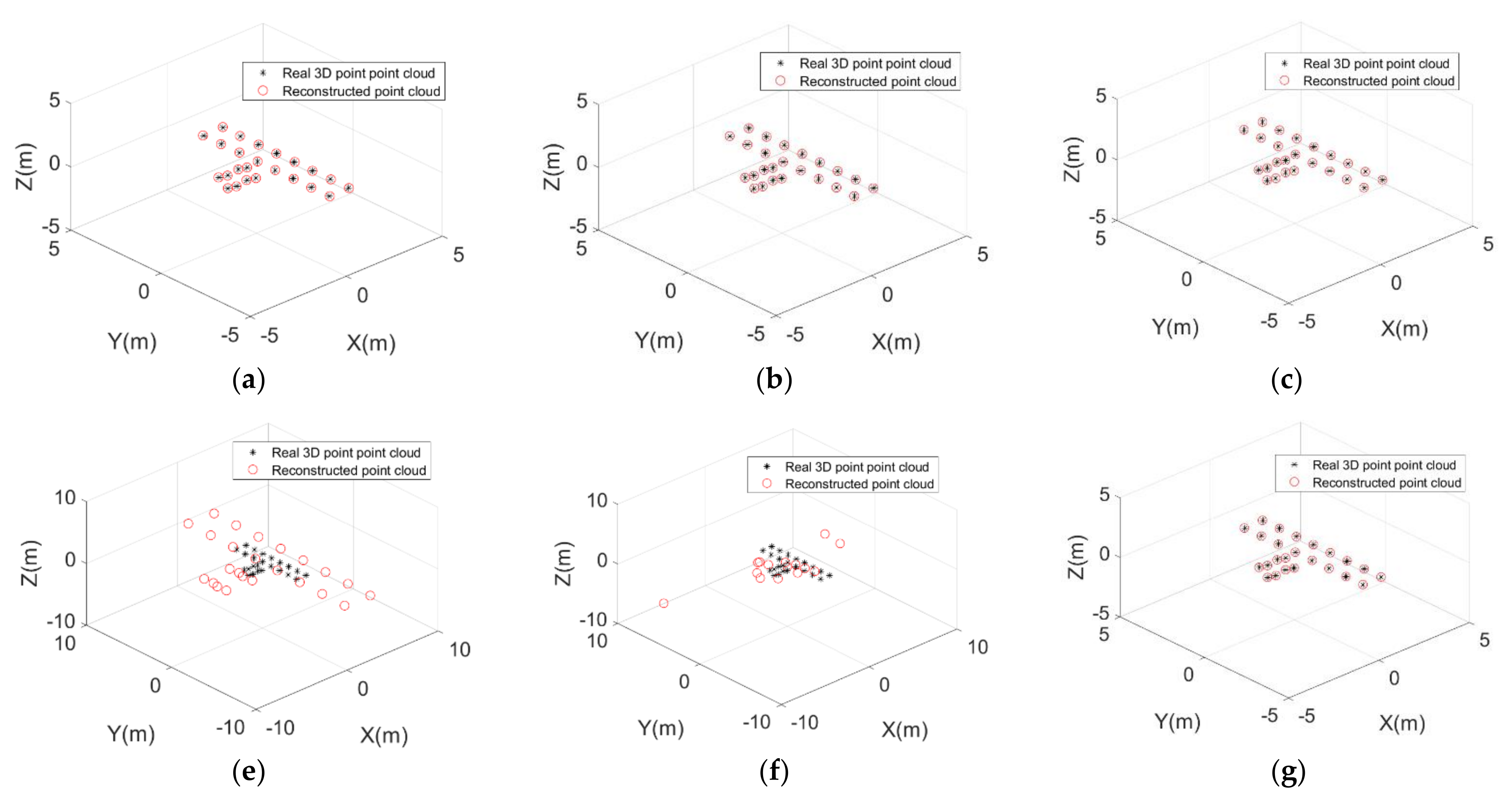
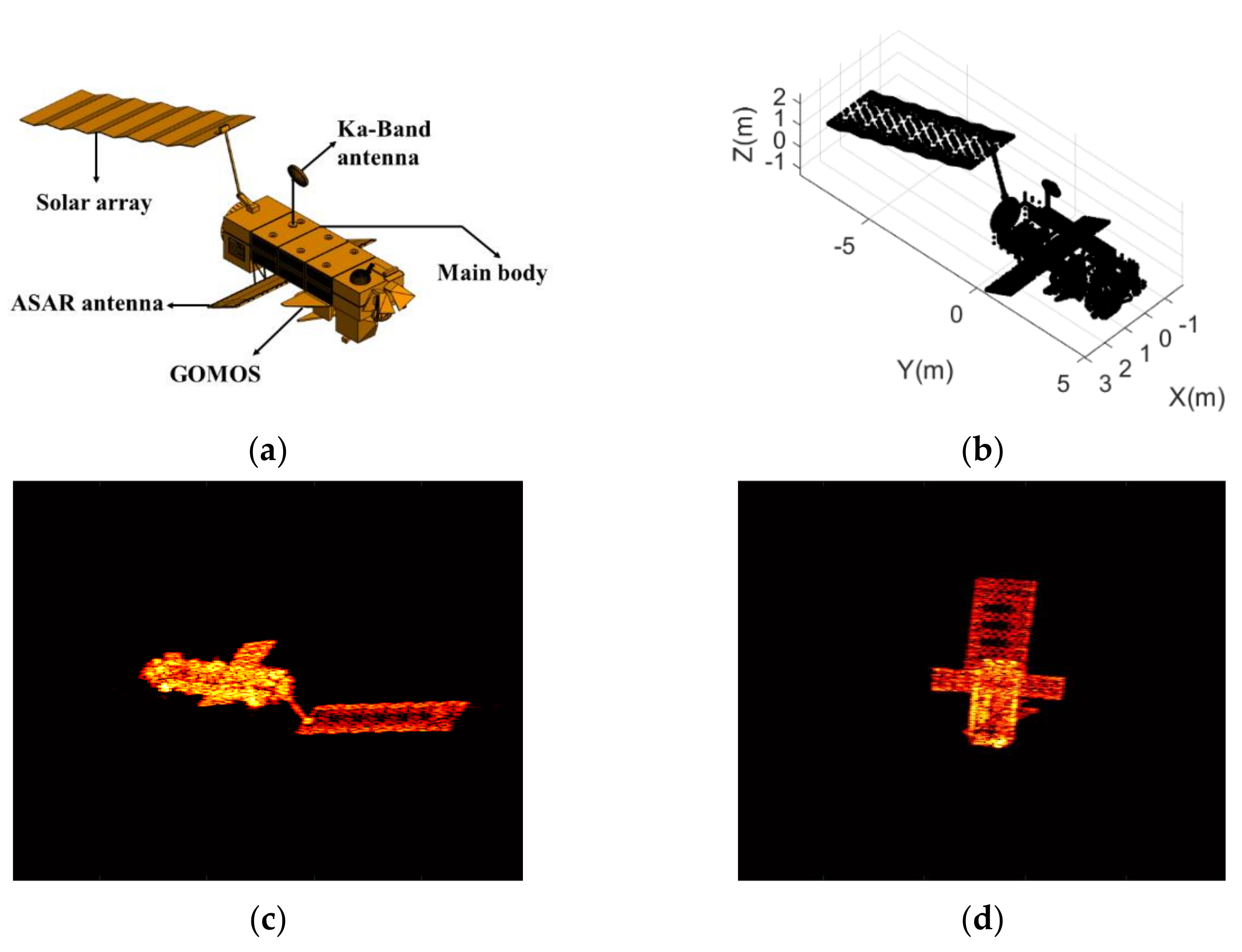
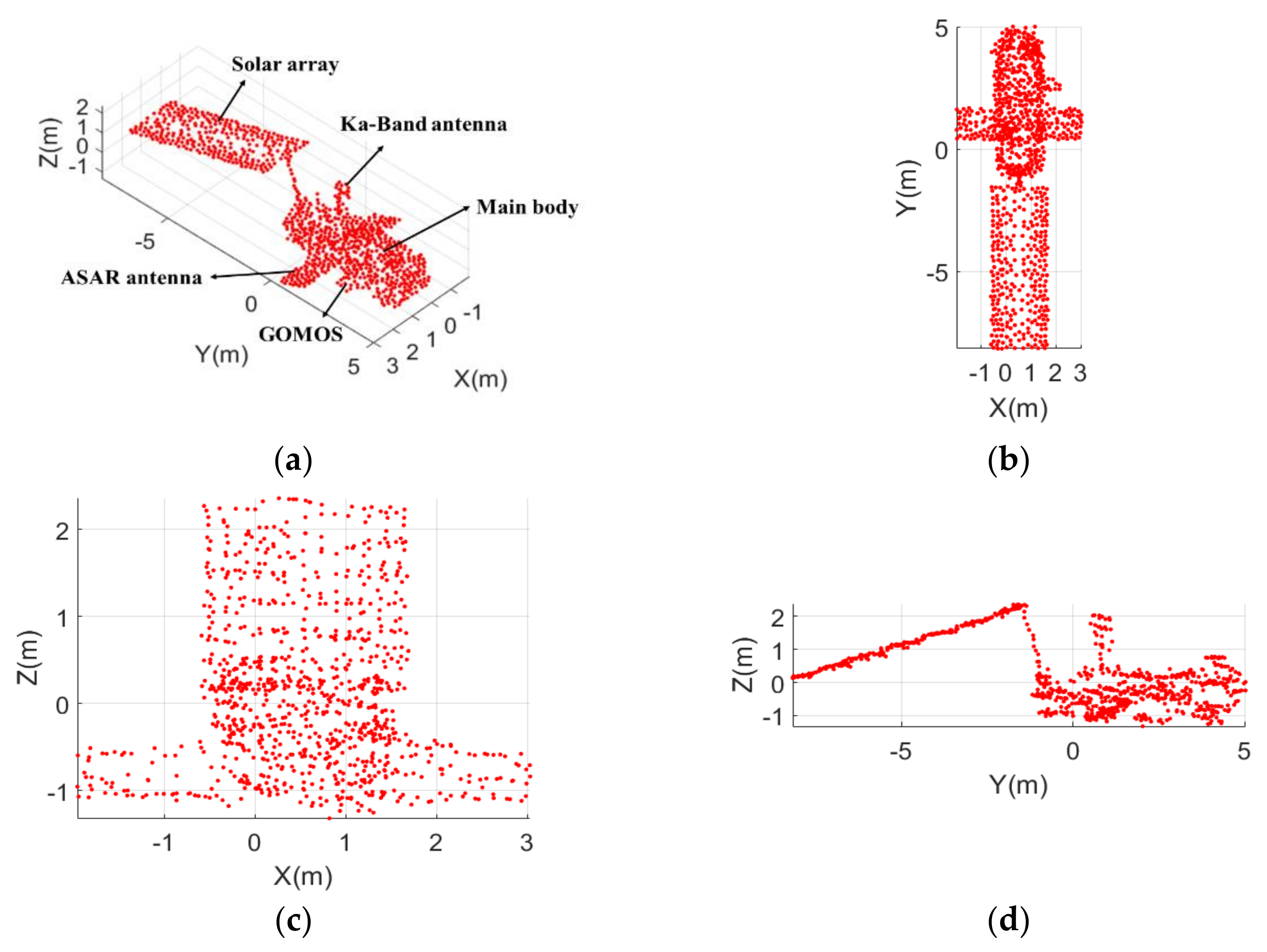
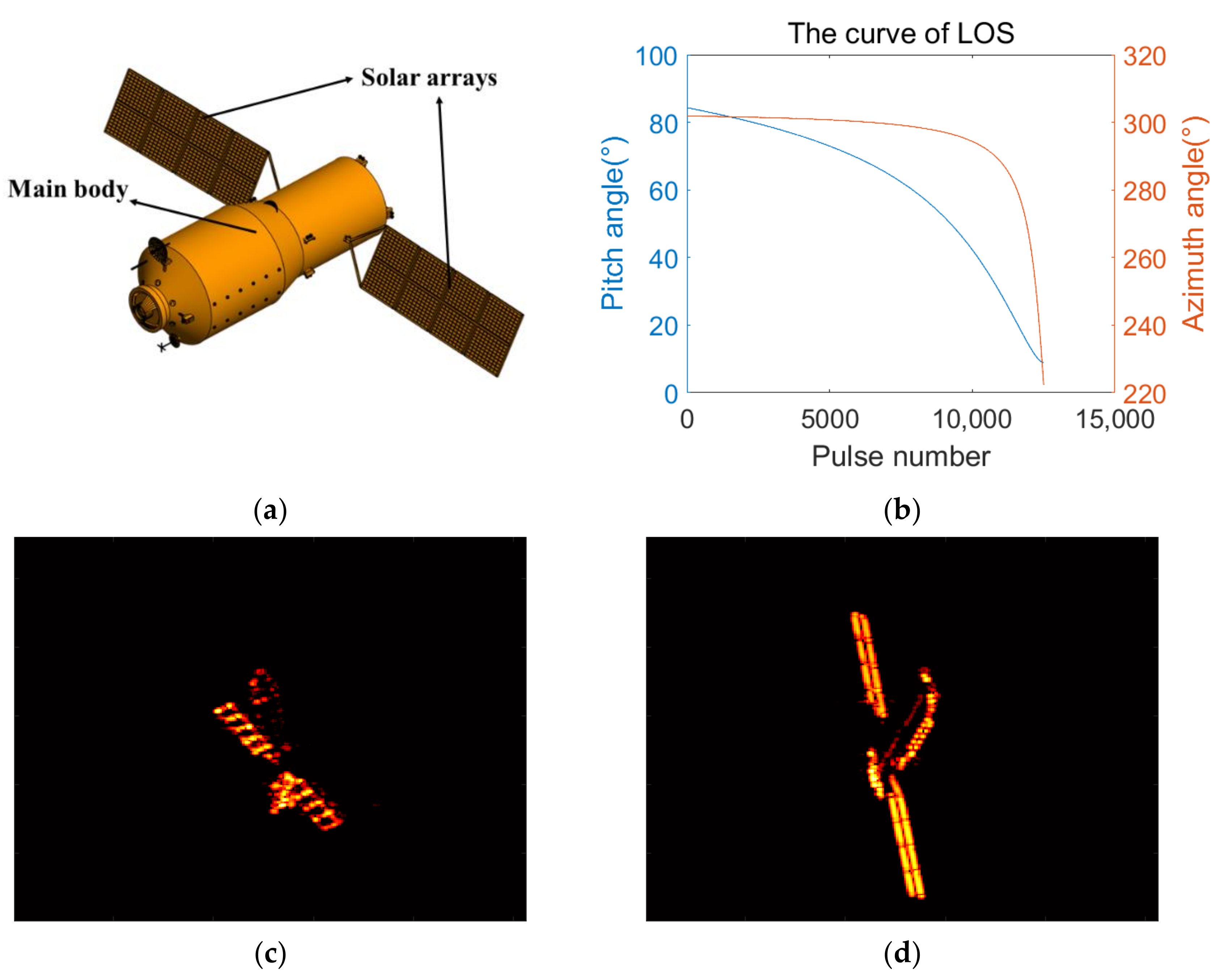
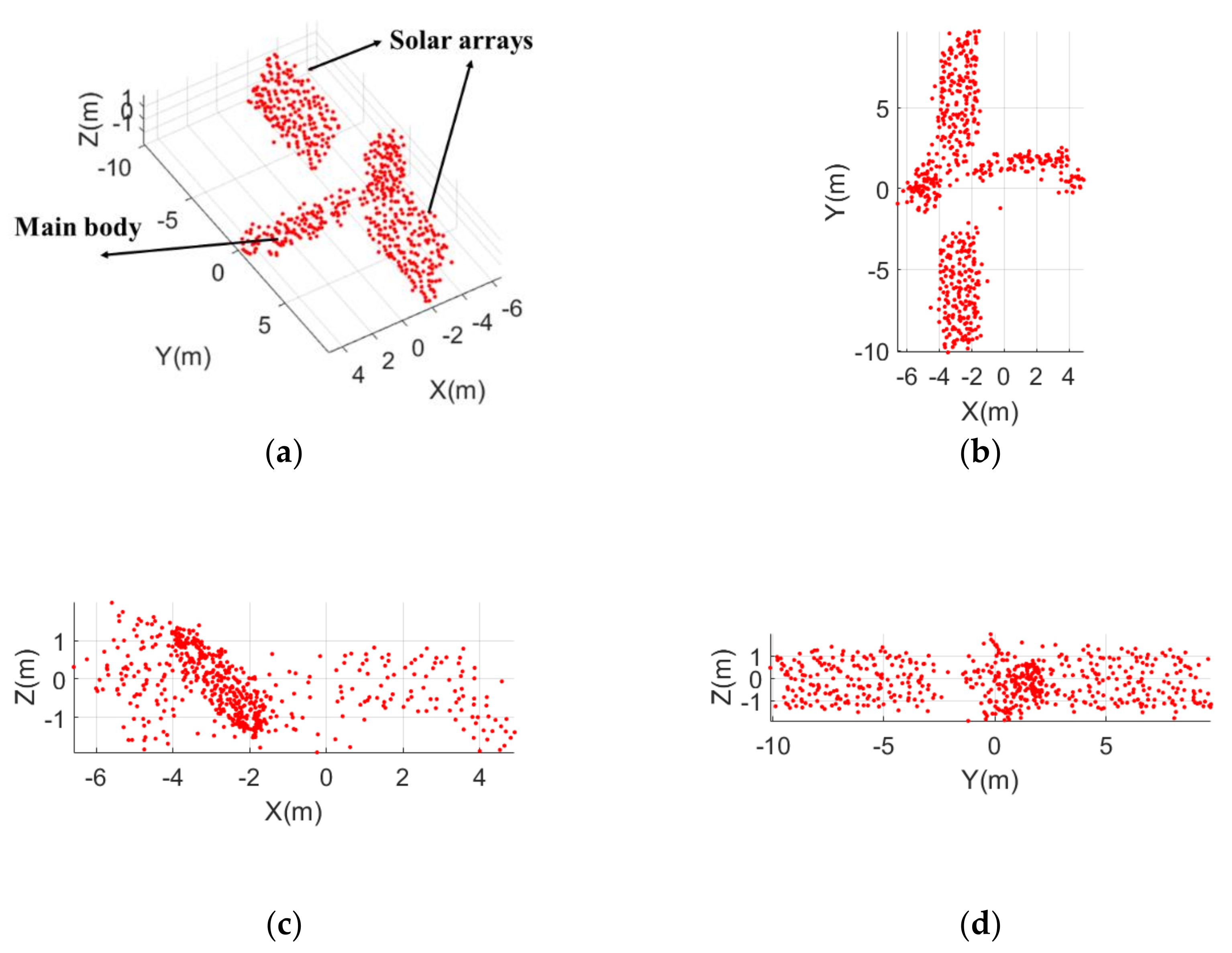
Parameters	Value
Duration of observation	100 s
Number of ISAR images	48
Observation azimuth angle	0°–180°
Observation pitch angle	45°

.

The 12,500 returns are divided into 48 sub-apertures and the RD algorithm is used to generate the ISAR image sequence. The 1st, 13th, and 24th frames are shown in Figure 5b–d.

By utilizing the proposed 3D geometry reconstruction method for SRST, the rotational parameters and the 3D point cloud of the point model can be estimated. The estimated rotational parameters are shown in

Table 2. Estimation result of rotational parameters of the point model.

Rotational Parameters	Rotational Velocity (rad/s)	Pitch Angle of the Rotational Axis (°)	Azimuth Angle of the Rotational Axis (°)
Real value	−0.05236	10	5
Estimated value	−0.05247	10.1702	6.2495
Error	1.1 × 10−4	0.2772

, while the reconstructed 3D point cloud of the point model is shown in Figure 6. According to the definition shown in Equation (30) to (34), the estimation error for rotational velocity and rotational axis are 1.1 × 10⁻⁴ rad/s and 0.2772° respectively. The root-mean-square error of the reconstructed point cloud is $E_{RMSE}=0.0082 m$. It is noted that the estimation error of the azimuth angle is about 1.2495° while the error of the estimated rotational axis is about 0.2772°. This is because the estimation error of the rotational axis defined in Equation (31) is highly relevant to the pitch angle. In other words, the estimation error of the rotational axis varies with the pitch angle when the error of the azimuth angle is fixed. The closer the pitch angle is to 0° and 180°, the smaller the estimation error of the rotational axis. In particular, when the pitch angle happens to be 0° or 180°, the estimated rotational axis and the real one will become the same under any arbitrary azimuth angles. Therefore, it is more intuitive to evaluate the estimation accuracy by the errors on the rotational axis rather than that on the specific observation angles. That is also the reason why the estimation errors of the rotational axis are calculated eventually.

Besides, with the estimated rotational parameters, accurate projection vectors can be constructed via Equation (13) to (17). By combining the reconstructed point cloud of the point model, the projection image sequence can be calculated. The partial ISAR image sequence and corresponding projection image sequence are shown in Figure 7. It can be noted that the reconstructed point cloud is highly similar to the ground truth. The similarity of the projection image sequence and ISAR image sequence can be calculated via Equation (35), whose value is $Sim=93.30\%$. Therefore, it is obvious that the proposed method can reconstruct the 3D geometry of SRST accurately and the rotational parameters can be estimated accurately as well.

For comparison, we also reconstruct the 3D geometry of space targets via the factorization method [25], the ISEA method [31], and the proposed method when the space target is (a) triaxial stabilized and (b) slowly rotating.

The same simple point model of a satellite is adopted in this experiment, and the radar observation parameters shown in Table 1. The rotational velocity of the point model is set to (a) 0, i.e., the space target keeps triaxial stabilized in the orbital coordinate system and (b) 0.0524 rad/s, i.e., the space target is slowly rotating around a fixed axis.

In the same way, the 12,500 returns are divided into 48 sub-apertures and the RD algorithm is used to generate the ISAR image sequences. The 1st, 13th, and 24th frames of the non-rotating space target and the slowly rotating space target are shown in Figure 8 and Figure 5b–d, respectively. It is noted that the point model on the ISAR image sequence shown in Figure 5b–d is larger than those shown in Figure 8 despite the imaging parameters being the same, owning to larger Doppler frequencies induced by larger rotational velocity. Consequently, the target shown in Figure 5b–d has a larger proportion in the cross-range direction (horizontal direction) on the image sequence.

The reconstruction results of the point model are shown in Figure 9, with the evaluation values shown in

Table 3. Comparisons on the evaluation values of the reconstructed results.

Targets Status	Evaluation Values	The Factorization Method	The ISEA Method	The Proposed Method
Non-rotating	RMSE (m)	0.0183	0.0068	0.0091
	Image similarity	0.9321	0.9458	0.9451
Slowly rotating	RMSE (m)	-	-	0.0082
	Image similarity	0.0410	0.2871	0.9330

. Note that the plot areas in Figure 9d,e are twice as large as that in the others in order to cover as many reconstructed points as possible. It is indicated that the 3D geometry of the non-rotating space target can be easily reconstructed via the factorization method, the ISEA method, and the proposed method. The estimation error of rotational velocity by the proposed method is 4.68e−5 rad/s, which leads to a bias on the projection vectors. That is the reason why there is nuance between the evaluation values of the ISEA method and the proposed method. However, such an error is perfectly acceptable. Besides, when the target begins to rotate, the cross-range scaling of each ISAR image is inaccurate. In other words, the projection relationship between the 3D positions of the space target and the ISAR image sequence not only depends on the variation of line of sight (LOS), but also depends on the unknown rotational motion. Therefore, there is severe stretching and distortion for the factorization method and the ISEA method, and it is no longer necessary to calculate the RMSEs. In general, the proposed method shows a better performance for both the triaxial stabilized and slowly rotating space targets, demonstrating its effectiveness and robustness.

3.2. Experiment Based on a Complex Point Model of ENVISAT

To better analyze the performance of the proposed method, another experiment based on a complex point model of ENVISAT is carried out in this part. The CAD model of ENVISAT is shown in Figure 10a and the main structures on the satellite are the main body, the solar array, the advanced synthetic aperture radar (ASAR), Ka-band antenna, and the global ozone monitoring by occultation of the stars (GOMOS) [42]. The complex point model, which is shown in Figure 10b, is generated from the CAD model of ENVISAT. This point cloud consists of 44,165 points, with which the 3D geometry of ENVISAT can be easily represented. In addition, the rotational parameters are the same as that in the first experiment. The radar observation and imaging parameters are shown in Table 1 as well.

In the same way, the 12,500 returns are used to form the ISAR image sequence. There are 48 images and the 13th and 24th frames are shown in Figure 10c,d.

The rotational parameters and the 3D point cloud of ENVISAT are estimated by applying the proposed 3D geometry reconstruction method. The estimated rotational parameters are shown in

Table 4. Estimation result of rotational parameters of ENVISAT.

Rotational Parameters	Rotational Velocity (rad/s)	Pitch Angle of the Rotational Axis (°)	Azimuth Angle of the Rotational Axis (°)
Real value	−0.05236	10	5
Estimated value	−0.05234	9.9430	6.0751
Error	2 × 10−5	0.1947

, which indicates that the estimation error for rotational velocity and rotational axis are 2 × 10⁻⁵ rad/s and 0.1947°, respectively. The reconstructed 3D point cloud of ENVISAT is shown in Figure 11, from which the five main structures can be clearly seen.

In addition, the accurate projection vectors can be constructed via Equation (13) to (17) by utilizing the estimated rotational parameters. Then the projection image sequence can be calculated by projecting the reconstructed point cloud into each imaging planes. The partial ISAR image sequence and the corresponding projection image sequence of ENVISAT are shown in Figure 12. It can be noted that the reconstructed point cloud is highly similar to the ground truth. The similarity of the projection image sequence and ISAR image sequence can be calculated via Equation (35), whose value is $Sim=93.68\%$.

3.3. Experiment Based on Simulated Electromagnetic Data of Tiangong-1

In order to validate the effectiveness of the proposed method in simulated electromagnetic data, another experiment based on Tiangong-1 is carried out in this part. The CAD model of Tiangong-1 is shown in Figure 13a.

The simulated radar is working in X-band and the bandwidth is 2 GHz. The number of frames of ISAR image sequence is 48. The LOS is calculated in STK 11 from the two-line element (TLE) file on https://www.space-track.org (accessed on 21 December 2021). The observation azimuth and pitch angles are shown in Figure 13b. In addition, suppose that Tiangong-1 is rotating clockwise around the rotational axis with the rotational velocity of 3°/s, i.e., about 0.0524 rad/s. The pitch and azimuth angles of its rotational axis are 130° and 120°, respectively.

After that, a total of 12,500 returns are divided into 48 sub-apertures and by utilizing the RD imaging algorithm on each of them, the ISAR image sequence is obtained. The 13th and 24th frames are shown in Figure 13c,d, respectively.

Similarly, by applying the proposed method on Tiangong-1, the rotational parameters and the 3D point cloud of Tiangong-1 are estimated. The estimated rotational parameters are shown in

Table 5. Estimated result of rotational parameters of Tiangong-1.

Rotational Parameters	Rotational Velocity (rad/s)	Pitch Angle of the Rotational Axis (°)	Azimuth Angle of the Rotational Axis (°)
Real value	−0.05236	130	120
Estimated value	−0.05269	130.3217	120.5304
Error	3.3 × 10−4	0.5175

, which indicates that the estimation error for rotational velocity and rotational axis are 3.3 × 10⁻⁴ rad/s and 0.5147°, respectively. The reconstructed 3D point cloud of Tiangong-1 is shown in Figure 14, from which the main body and solar array can be clearly seen. It can also be noted that a part of the main body and the solar array is missing in the reconstructed point cloud. Actually, this is because that parts of the main body and solar array cannot be illuminated by the electromagnetic wave during the most observation time, making little energy recorded in the ISAR image sequence. In the reconstruction process, the accumulated energy of this part is much smaller than the other part of Tiangong-1. Therefore, these parts can be barely reconstructed.

Besides, with the estimated rotational parameters of Tiangong-1, the accurate projection vectors can be constructed via Equation (13) to (17). By combining the reconstructed point cloud, the projection image sequence can be calculated. The partial ISAR image sequence and the corresponding projection image sequence of Tiangong-1 are shown in Figure 15. It can be noted that the reconstructed point cloud is highly similar to the ground truth. The similarity of the projection image sequence and ISAR image sequence can be calculated via Equation (35), whose value is $Sim=84.07\%$. Therefore, it is obvious that the proposed method can reconstruct the 3D geometry of SRST accurately and the rotational parameters can be estimated accurately as well.

4. Discussion

As is discussed in Section 3, the proposed method has shown its abilities on solving the 3D geometry reconstruction problem on SRST and triaxial stabilized space targets. On one hand, the non-rotating objects, i.e., the triaxial stabilized objects, are the specific cases of SRST with zero rotational velocity. Therefore, the proposed method can be readily applied to their 3D geometry reconstruction with fewer parameters to be estimated. As the attitude of non-rotating objects are unchanged in the orbital coordinate system, the changes on the effective imaging planes induced by the unknown rotational motion vanished. Therefore, the projection relationship can be easily obtained from the instantaneous LOS, and the 3D geometry can be reconstructed via the proposed method. On the other hand, as the projection relationship maps the 3D scatterers to the 2D ISAR image sequence, the cross-range direction of an ISAR image is the Doppler frequencies of scatterers. When the Doppler frequencies of them are larger than PRF of the transmitted signals, Doppler aliasing occurs. In this case, the mapping relationship becomes invalid and the proposed method cannot be used. Besides, the Doppler aliasing effect not only depends on the rotational velocity of targets, but also is highly correlated to the size of the targets, the observation angles, and the PRF of the radar. Therefore, the specific upper limit of the rotational velocity cannot be determined explicitly.

In general, the proposed method can be used when the target keeps still or rotates around a fixed axis without Doppler aliasing. In fact, there are indeed many satellites belonging to this category in the near-earth space as mentioned in Section 1. Therefore, the proposed method is highly valuable in practical applications.

5. Conclusions

Due to the unknown rotation of SRST, the projection relationship between the 3D geometry and the ISAR image sequence cannot be constructed only through the radar line of sight sequence. Hence, the 3D geometry of SRST can be hardly reconstructed without extracting features from the ISAR image sequence. To tackle this problem, a 3D geometry reconstruction method for SRST is proposed by utilizing the ISAR image sequence in this paper. By modeling the rotational motion of SRST, the explicit expression of the projection relationship between the 3D geometry and ISAR image sequence is derived first. Then, the accurate rotational parameters are estimated via the QPSO algorithm. Finally, with the estimated rotational parameters, the 3D point cloud of SRST is reconstructed by utilizing the ISAR image sequence. As the rotational motion is considered and with no scatterer exaction and association processes needed, the proposed method is much more robust and more effective in practical applications. Besides, the unexpected rotation is not always annoying, because the rotation of SRST can also provide extra information for the reconstruction task. As long as the rotational axis of SRST and that caused by the LOS variation are not coincident with each other, the radar observation angle required for 3D reconstruction will be smaller. However, the condition mentioned above can hardly be satisfied in the real observation scenario, making the reconstructed point cloud from a single observation ISAR data possibly not dense enough to represent the 3D geometry of targets either. Therefore, further study on dense 3D point cloud reconstruction and surface reconstruction methods for space targets combining multi observation ISAR data would be a research direction.