An Efficient UD Factorization Implementation of Kalman Filter for RTK Based on Equivalent Principle
Abstract
1. Introduction
2. Methods
2.1. RTK Mathematic Model
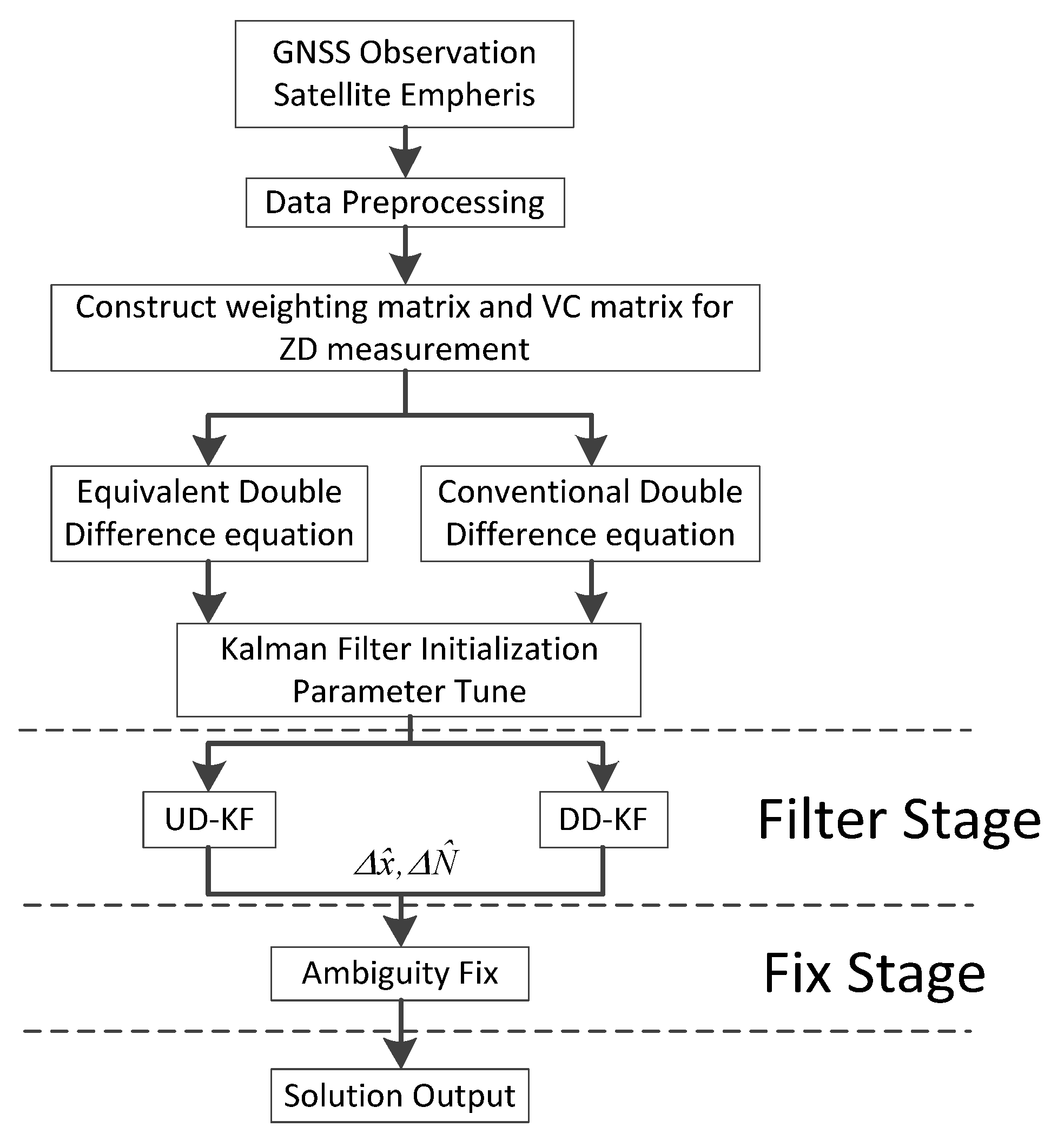
2.2. Proposed Methodology
2.2.1. Measurement Decorrelation
2.2.2. UD-KF Strategy
3. Results and Discussion
3.1. Zero-Baseline Test
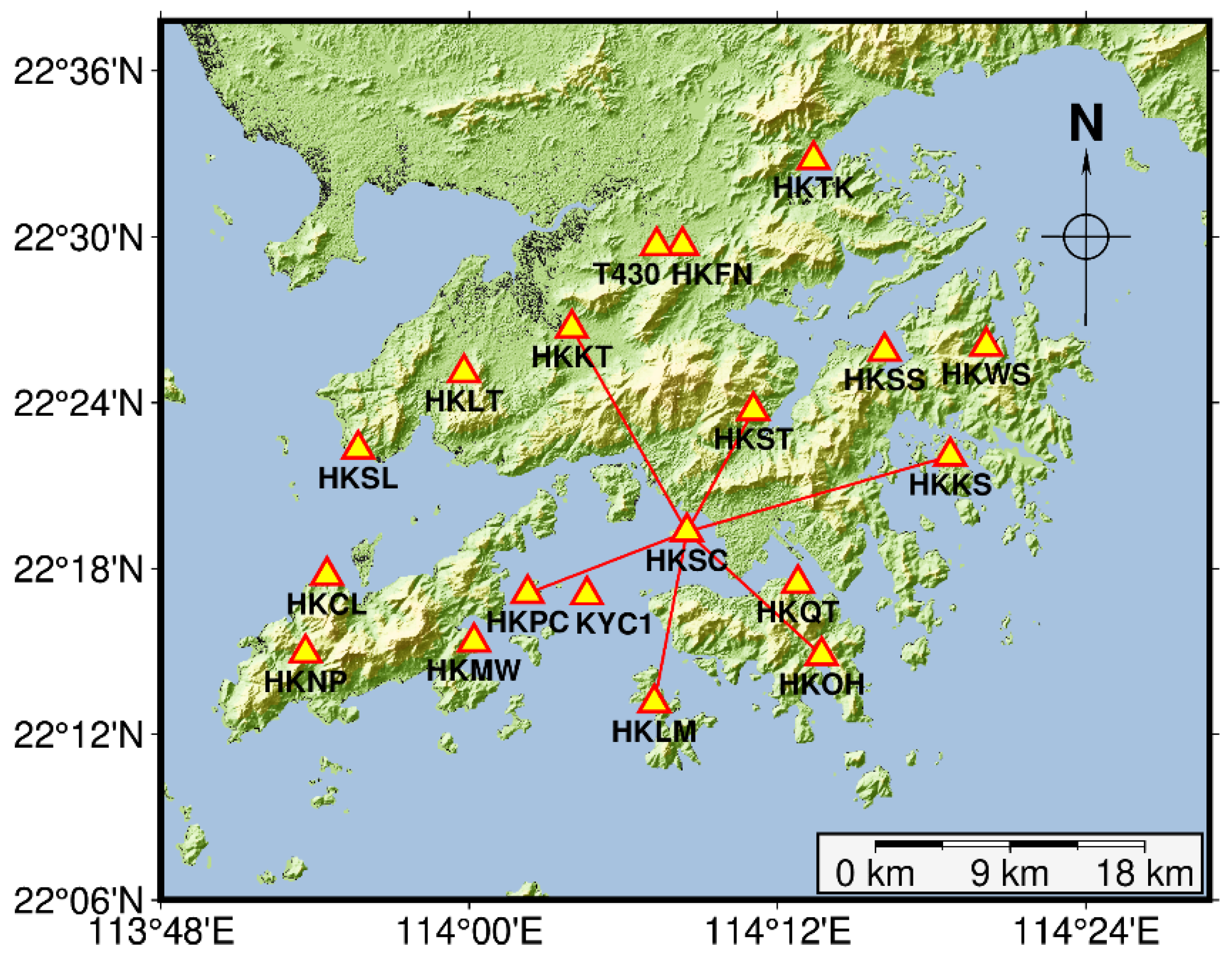
3.2. Static Test
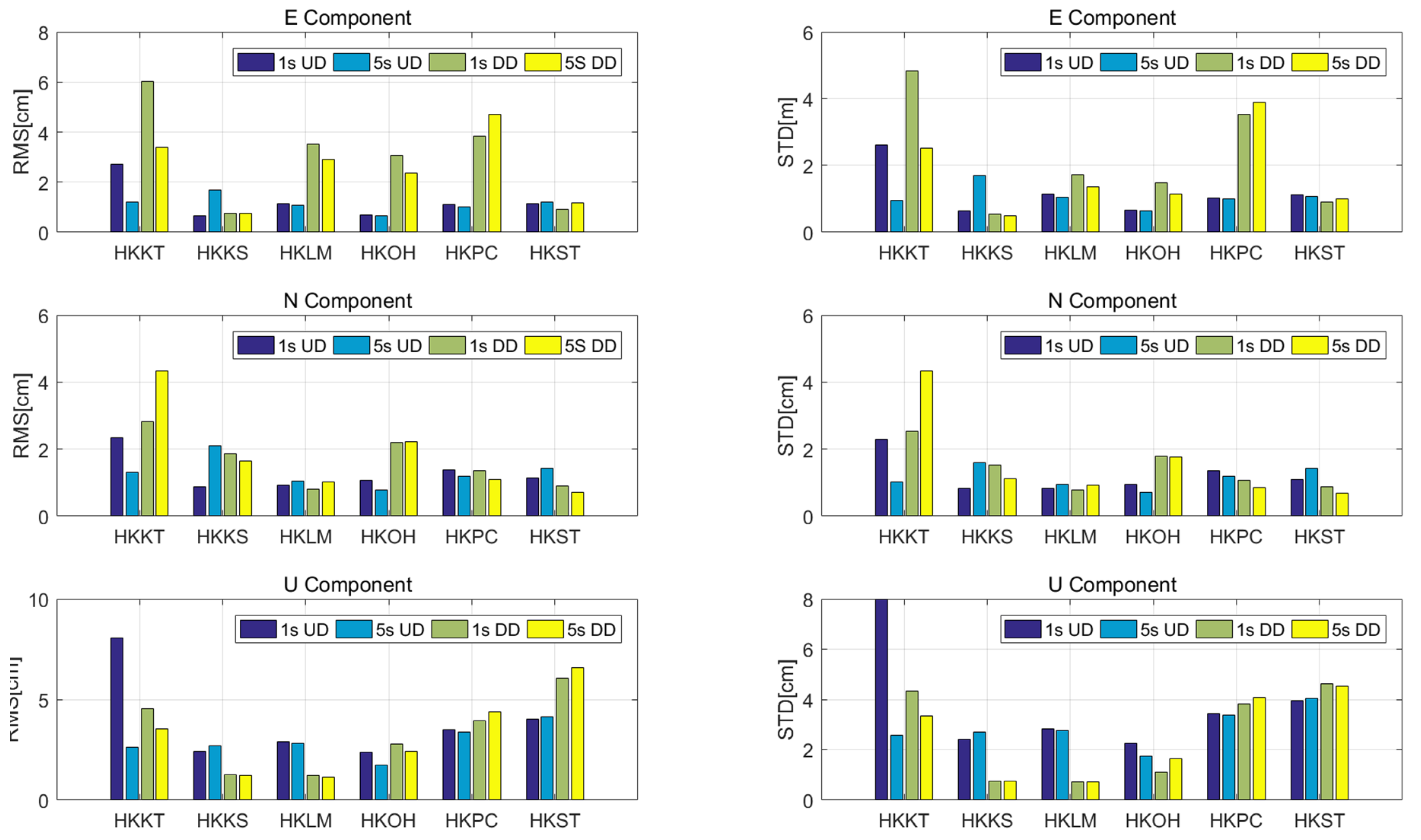
3.2.1. Position Accuracy Analysis
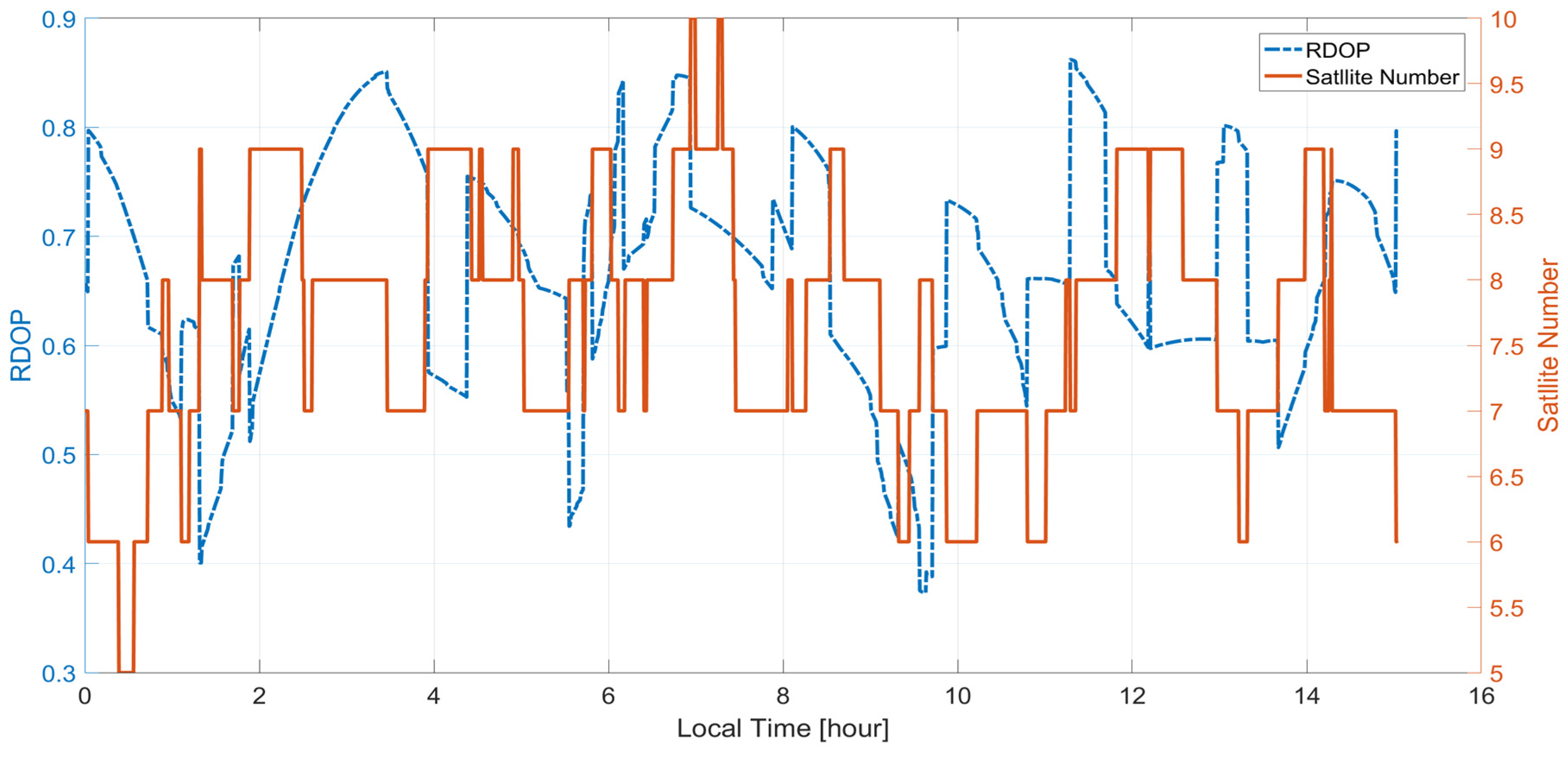
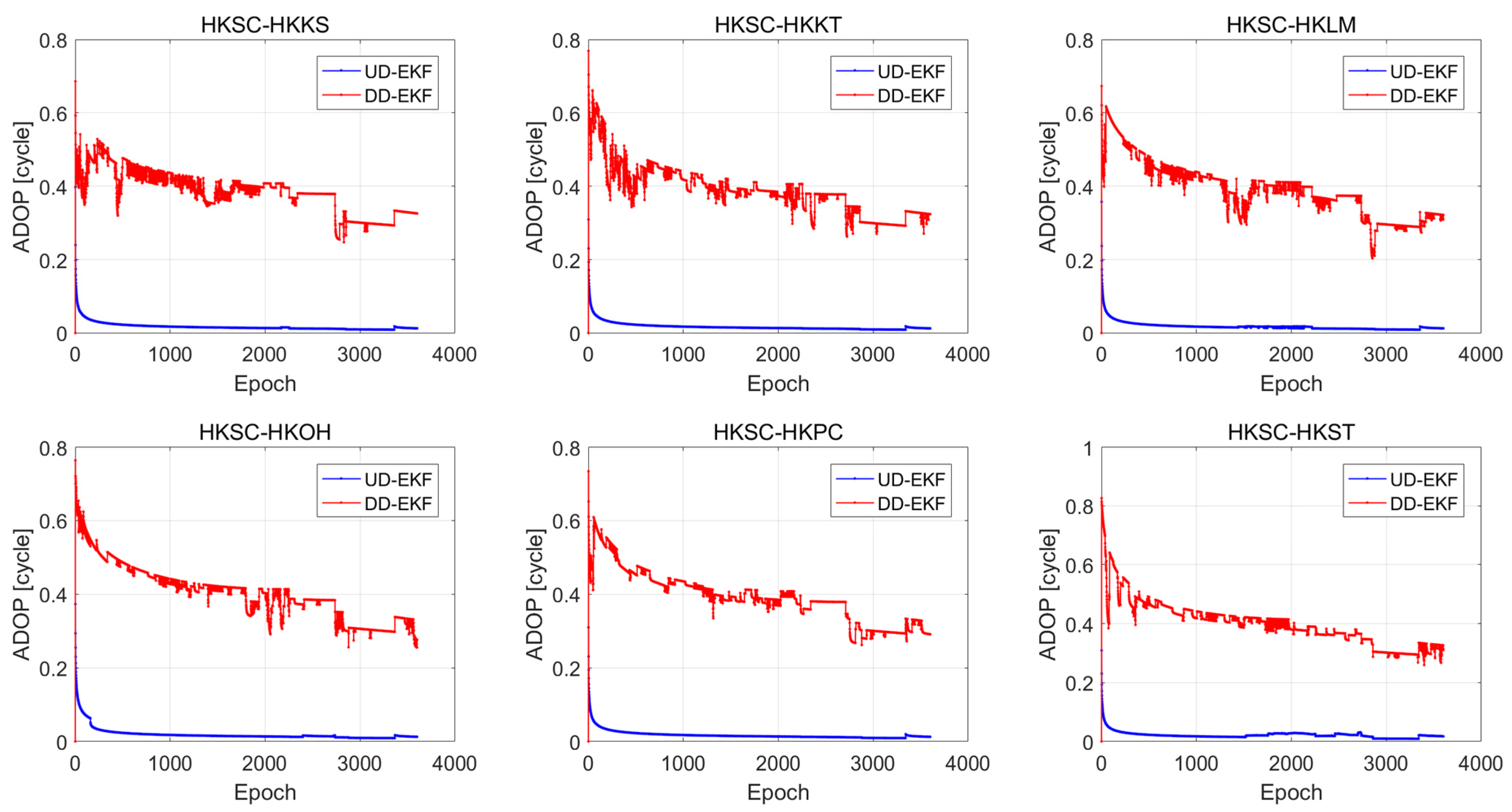
3.2.2. Redundancy and Ambiguity Dilution of Precision (ADOP) Analysis
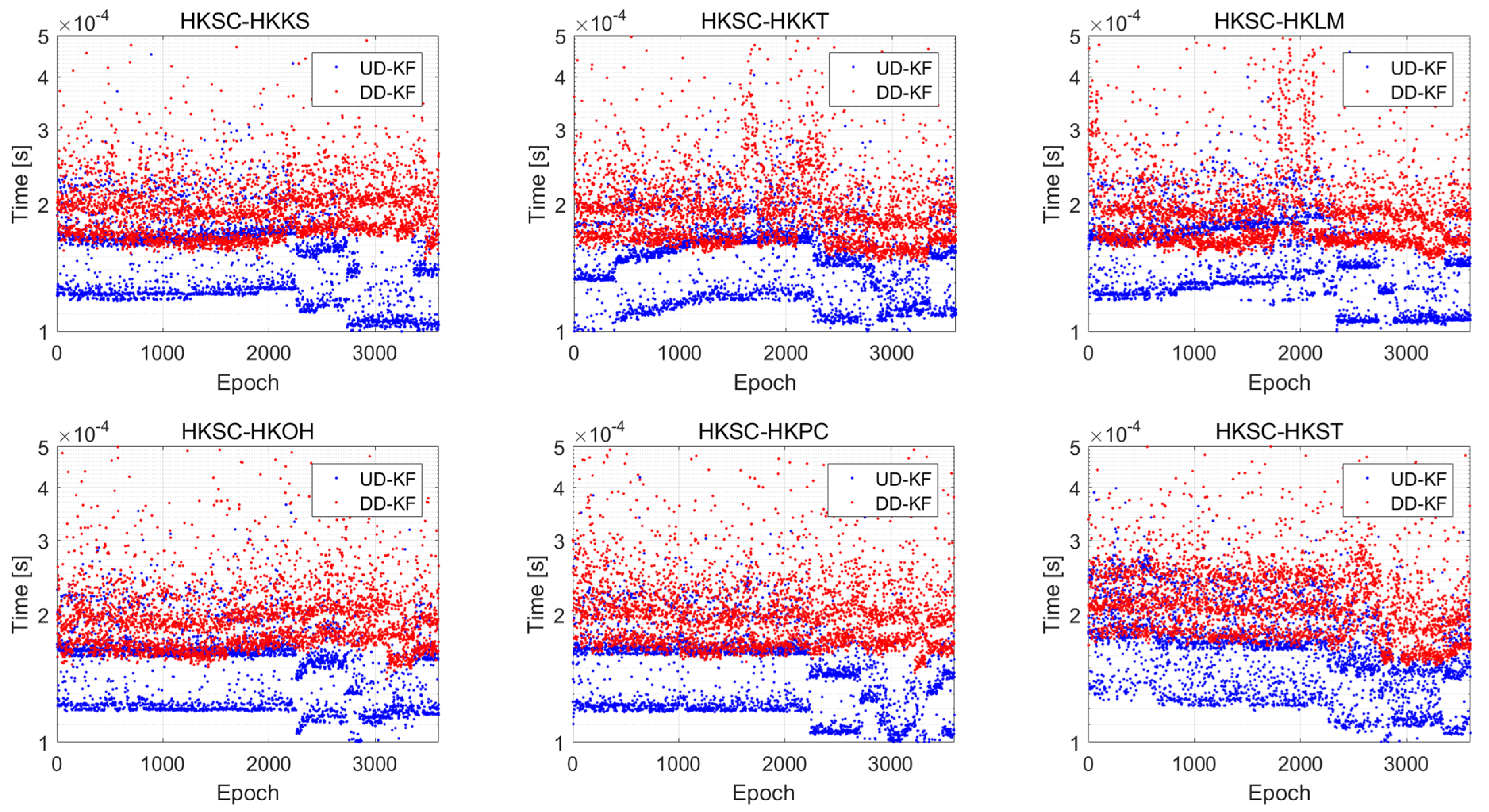
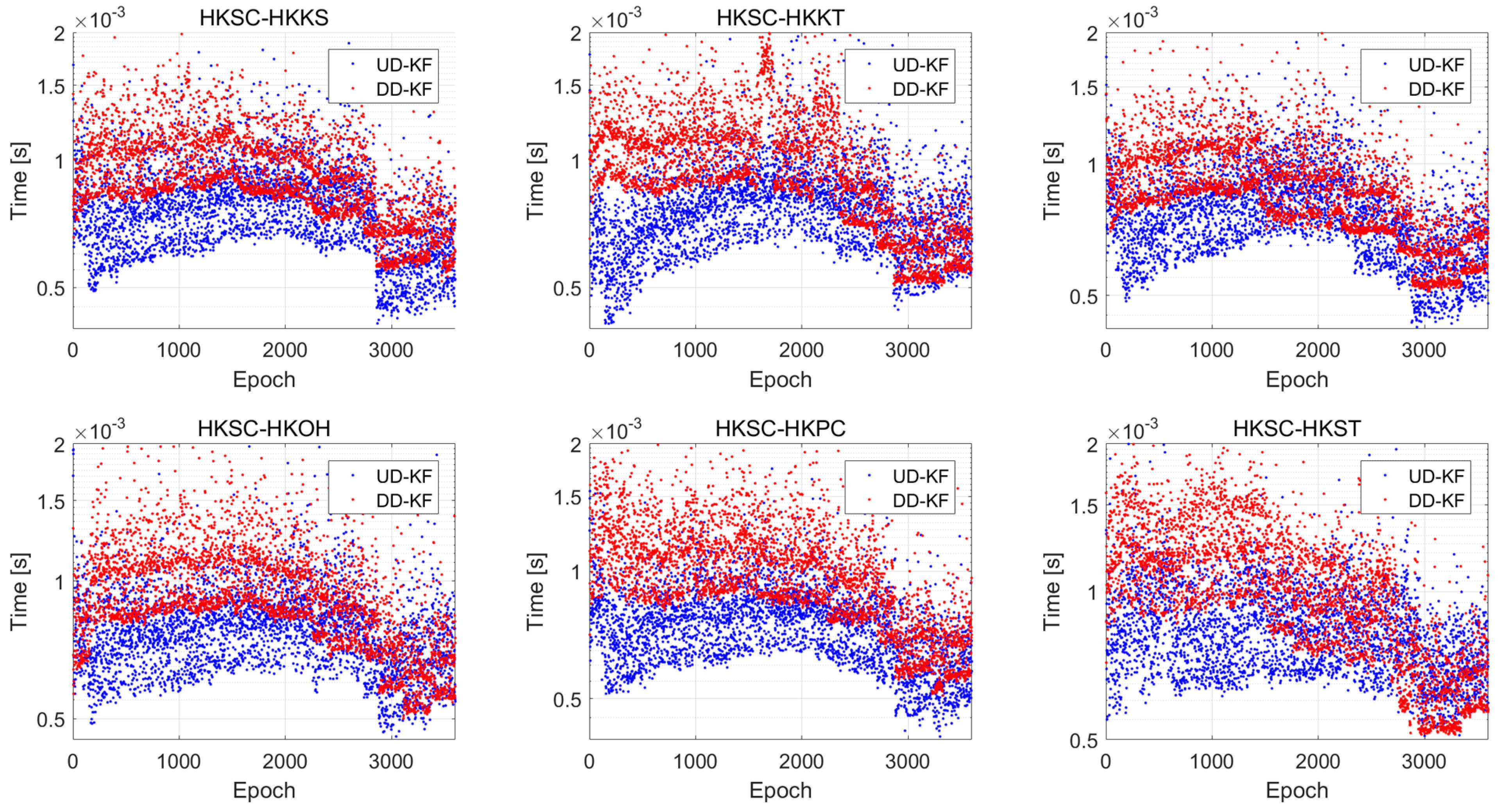
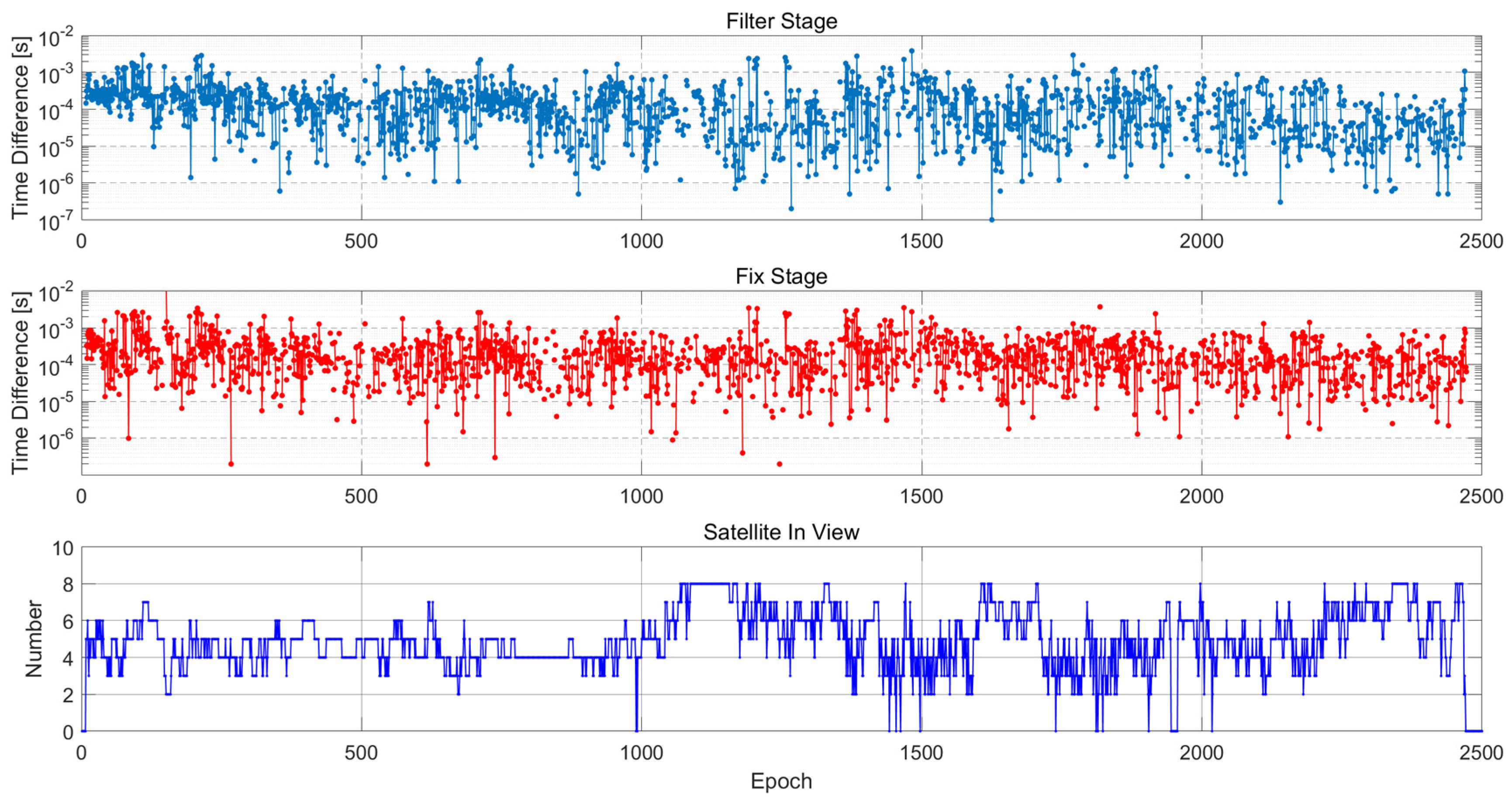
3.2.3. Computation Efficiency Analysis
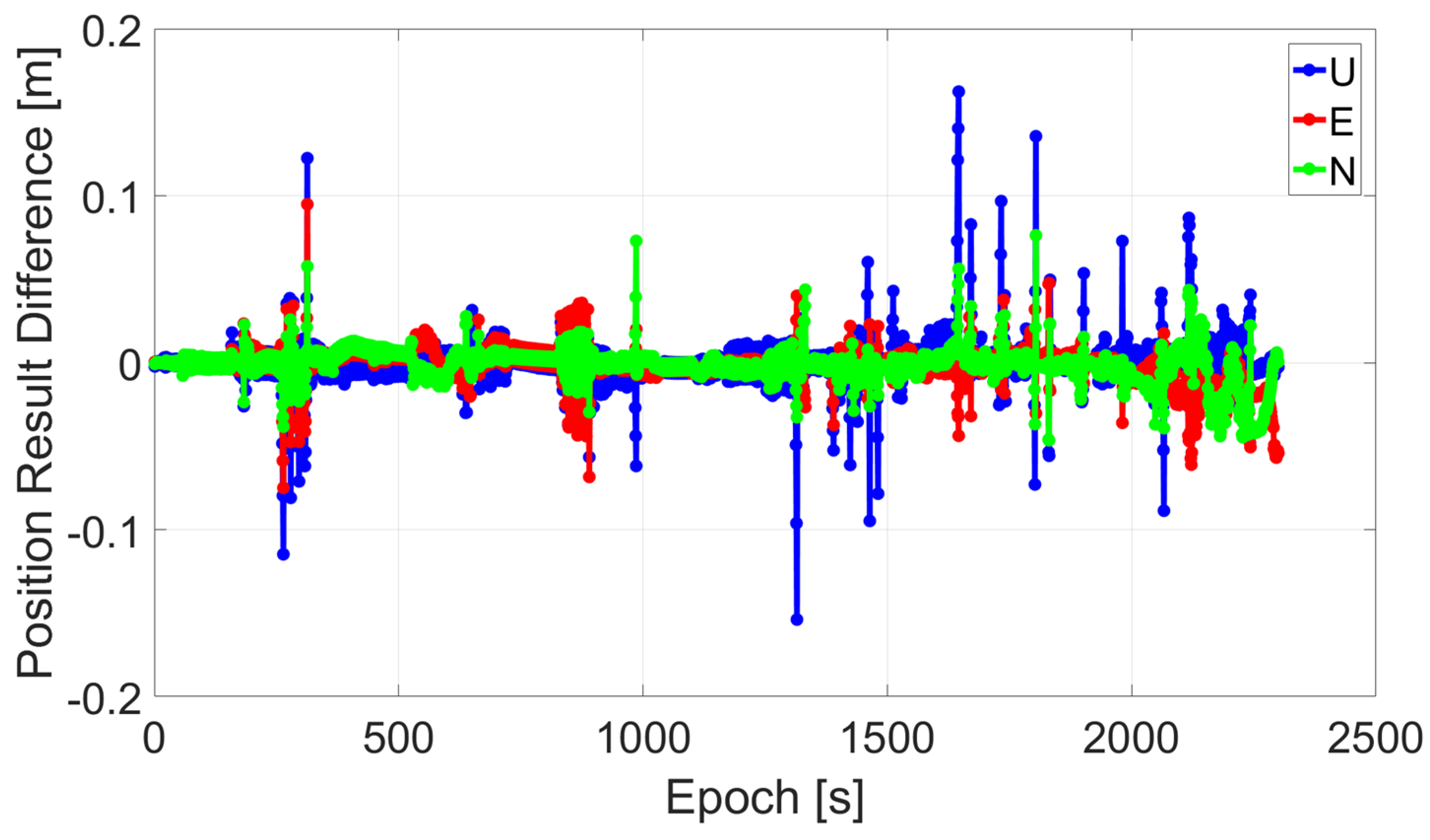
3.3. Kinematic Test
4. Conclusions
- (1)
- For the zero-baseline test, UD-KF achieved a better positioning accuracy than DD-KF, which validates the reliability and feasibility of the new proposed algorithm. If the same type of receivers is used at both ends of the baseline, UD-KF can reduce the RMS of the position error by 86% on E, 80% on N, and 83% on U, as compared to the conventional DD-KF.
- (2)
- For the static test, UD-KF achieved better position accuracy for short baselines. The increase in baseline distance does not affect the positioning performance of UD-KF. The average performance improvement of RMS for six baselines was 69% on E and 27% on N, and more errors occurred on the U component. The computational efficiency was improved by 25–50% at the filtering stage and 15–25% at the fixing stage.
- (3)
- For the dynamic test, the robustness of UD-KF was verified by the reduction in time consumption, which kept stable when satellites in view changed dramatically. The UD-KF achieved an accurate position in typical urban environments and accelerated the filtering and fixing process by (0.11 ms, 0.13 ms), respectively, for each epoch.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Xu, T.; Nie, W.; Xu, G. A Simplified Processing Algorithm for Multi-baseline RTK Positioning in Urban Environments. Measurement 2021, 179, 109446. [Google Scholar] [CrossRef]
- Liu, T.; Xu, T.; Nie, W.; Li, N. Optimal Independent Baseline Searching for Global GNSS Networks. J. Surv. Eng. 2020, 147, 05020010. [Google Scholar] [CrossRef]
- Krasuski, K.; Savchuk, S. Determination of the Precise Coordinates of the GPS Reference Station in of a GBAS System in the Air Transport. Komunikacie 2020, 22, 11–18. [Google Scholar] [CrossRef]
- Liu, T.; Yu, Z.; Ding, Z.; Nie, W.; Xu, G. Observation of Ionospheric Gravity Waves Introduced by Thunderstorms in Low Latitudes China by GNSS. Remote Sens. 2021, 13, 4131. [Google Scholar] [CrossRef]
- Cetin, S.; Aydin, C.; Dogan, U. Comparing GPS positioning errors derived from GAMIT/GLOBK and Bernese GNSS software packages: A case study in CORS-TR in Turkey. Surv. Rev. 2019, 51, 533–543. [Google Scholar] [CrossRef]
- Mao, X.; Arnold, D.; Girardin, V.; Villiger, A.; Jäggi, A. Dynamic GPS-based LEO orbit determination with 1 cm precision using the Bernese GNSS Software. Adv. Space Res. 2021, 67, 788–805. [Google Scholar] [CrossRef]
- Xu, P.; Du, F.; Shu, Y.; Zhang, H.; Shi, Y. Regularized reconstruction of peak ground velocity and acceleration from very high-rate GNSS precise point positioning with applications to the 2013 Lushan Mw6.6 earthquake. J. Geod. 2021, 95, 1–22. [Google Scholar] [CrossRef]
- Takasu, T.; Yasuda, A. Development of the Low-Cost RTK-GPS Receiver with an Open Source Program Package RTKLIB; International Symposium on Gps/gnss: Jeju, Korea, 2009; Volume 1, pp. 1–6. [Google Scholar]
- Jiang, X.; Gu, S.; Li, P.; Ge, M.; Schuh, H. A Decentralized Processing Schema for Efficient and Robust Real-time Multi-GNSS Satellite Clock Estimation. Remote Sens. 2019, 11, 2595. [Google Scholar] [CrossRef]
- Berkay, B.; Metin, N. PPPH: A MATLAB-based software for multi-GNSS precise point positioning analysis. GPS Solut. 2018, 22, 113. [Google Scholar]
- Tondaś, D.; Kapłon, J.; Rohm, W. Ultra-fast near real-time estimation of troposphere parameters and coordinates from GPS data. Measurement 2020, 162, 107849. [Google Scholar] [CrossRef]
- Aragon-Angel, A.; Garcia, A.R.; Arcediano-Garrido, E.; Ibáñez, D. Galileo Ionospheric correction algorithm integration into the open-source GNSS Laboratory Tool Suite (gLAB). Remote Sens. 2021, 13, 191. [Google Scholar] [CrossRef]
- Li, Y. Analysis of GAMIT/GLOBK in high-precision GNSS data processing for crustal deformation. Earthq. Res. Adv. 2021, 1, 100028. [Google Scholar] [CrossRef]
- Lyros, E.; Kostelecky, J.; Plicka, V.; Vratislav, F.; Sokos, E.; Nikolakopoulos, K. Detection of tectonic and crustal deformation using GNSS data processing: The case of ppgnet. Civ. Eng. J. 2021, 7, 14–23. [Google Scholar] [CrossRef]
- Jiang, C.; Xu, T.; Du, Y.; Sun, Z.; Xu, G. A parallel equivalence algorithm based on MPI for GNSS data processing. J. Spat. Sci. 2021, 66, 513–532. [Google Scholar] [CrossRef]
- Li, L.; Lu, Z.; Chen, Z.; Cui, Y.; Sun, D.; Wang, Y.; Kuang, Y.; Wang, F. GNSSer: Objected-oriented and design pattern-based software for GNSS data parallel processing. J. Spat. Sci. 2021, 66, 27–47. [Google Scholar] [CrossRef]
- Xu, G.; Xu, Y. Applications of GPS theory and algorithms. In GPS; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Szot, T.; Specht, C.; Specht, M.; Dabrowski, P.S. Comparative analysis of positioning accuracy of Samsung Galaxy smartphones in stationary measurements. PLoS ONE 2019, 14, e0215562. [Google Scholar] [CrossRef]
- Stateczny, A.; Kazimierski, W.; Burdziakowski, P.; Motyl, W.; Wisniewska, M. Shore Construction Detection by Automotive Radar for the Needs of Autonomous Surface Vehicle Navigation. ISPRS Int. J. Geo-Inf. 2019, 8, 80. [Google Scholar] [CrossRef]
- Lucas-Sabola, V.; Seco-Granados, G.; López-Salcedo, J.A.; García-Molina, J.A.; European Space Agency. GNSS IoT Positioning From Conventional Sensors to a Cloud-Based Solution. Inside GNSS 2018, 13, 53–62. [Google Scholar]
- Mayer, P.; Magno, M.; Berger, A.; Benini, L. RTK-LoRa: High-Precision, Long-Range, and Energy-Efficient Localization for Mobile IoT Devices. IEEE Trans. Instrum. Meas. 2020, 70, 1–11. [Google Scholar] [CrossRef]
- Duan, B.; Wang, J. Factorization Method for GNSS Parameter Estimation. In Proceedings of the International Symposium on Satellite Mapping Technology and Application (ISSMTA2013), Nanjing, China, 6–8 November 2013. [Google Scholar]
- Zarchan, P. Progress in Astronautics and Aeronautics: Fundamentals of Kalman Filtering: A Practical Approach; AIAA: Reston, VI, USA, 2005; Volume 208. [Google Scholar]
- Vaclavovic, P.; Dousa, J. Backward smoothing for precise GNSS applications. Adv. Space Res. 2015, 56, 1627–1634. [Google Scholar] [CrossRef]
- Evangelidis, A.; Parker, D. Quantitative verification of numerical stability for Kalman filters. In International Symposium on Formal Methods; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Wang, G.; Xue, R.; Zhao, J. Switching criterion for sub-and super-Gaussian additive noise in adaptive filtering. Signal Proc. 2018, 150, 166–170. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Y.; Wang, X. Maximum correntropy Rauch–Tung–Striebel smoother for nonlinear and non-Gaussian systems. IEEE Trans. Autom. Control 2020, 66, 1270–1277. [Google Scholar] [CrossRef]
- Kulikova, M.V. Factored-form Kalman-like implementations under maximum correntropy criterion. Signal Proc. 2019, 160, 328–338. [Google Scholar] [CrossRef]
- Cilden-Guler, D.; Hajiyev, C. SVD-aided EKF attitude estimation with UD factorized measurement noise covariance. Asian J. Control 2019, 21, 1423–1432. [Google Scholar] [CrossRef]
- Realini, E.; Reguzzoni, M. goGPS: Open source software for enhancing the accuracy of low-cost receivers by single-frequency relative kinematic positioning. Meas. Sci. Technol. 2013, 24, 115010. [Google Scholar] [CrossRef]
- Miao, W.; Li, B.; Zhang, Z.; Zhang, X. Combined BeiDou-2 and BeiDou-3 instantaneous RTK positioning: Stochastic modeling and positioning performance assessment. J. Spat. Sci. 2020, 65, 7–24. [Google Scholar] [CrossRef]
- Borko, A.; Even-Tzur, G. Stochastic model reliability in GNSS baseline solution. J. Geod. 2021, 95. [Google Scholar] [CrossRef]
- Jiang, Y.; Gao, Y.; Zhou, P.; Gao, Y.; Huang, G. Real-time cascading PPP-WAR based on Kalman filter considering time-correlation. J. Geod. 2021, 95, 1–15. [Google Scholar] [CrossRef]
- Liu, M.; Chang, G. Numerically and statistically stable Kalman filter for INS/GNSS integration. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 321–332. [Google Scholar] [CrossRef]
- Cao, X.; Li, J.; Zhang, S.; Pan, L.; Kuang, K. Performance assessment of uncombined precise point positioning using Multi-GNSS real-time streams: Computational efficiency and RTS interruption. Adv. Space Res. 2018, 62, 3133–3147. [Google Scholar] [CrossRef]
- Khamseh, H.B.; Ghorbani, S.; Janabi-Sharifi, F. Unscented Kalman filter state estimation for manipulating unmanned aerial vehicles. Aerosp. Sci. Technol. 2019, 92, 446–463. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, D.; Zhang, L.; Li, Q.; Wu, J. Tightly coupled GNSS/INS integration with robust sequential kalman filter for accurate vehicular navigation. Sensors 2020, 20, 561. [Google Scholar] [CrossRef] [PubMed]
- Tu, R.; Lu, C.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. The study of BDS RTK algorithm based on zero-combined observations and ionosphere constraints. Adv. Space Res. 2019, 63, 2687–2695. [Google Scholar] [CrossRef]
- Schaffrin, B.; Grafarend, E. Generating classes of equivalent linear models by nuisance parameter. Manuscr. Geod. 1986, 11, 262–271. [Google Scholar]
- Wang, J.; Xu, T.; Nie, W.; Xu, G. GPS/BDS RTK Positioning Based on Equivalence Principle Using Multiple Reference Stations. Remote Sens. 2020, 12, 3178. [Google Scholar] [CrossRef]
- Xu, Y. GNSS Precise Point Positioning with Application of the Equivalence Principle; Technische Universitaet Berlin (Germany): Berlin, Germany, 2016. [Google Scholar]
- Yongyuan, Q.; Hongyue, Z.; Shuhua, W. Kalman Filter and Principle of Integrated Navigation; The Publishing Company of Northwestern Polytechnical University: Xi’an, China, 2015; Volume 182, p. 187. [Google Scholar]
- Kulikova, M.V.; Tsyganova, J.V. The UD-based approach for designing pairwise Kalman filtering algorithms. IFAC-Pap. 2017, 50, 1619–1624. [Google Scholar] [CrossRef]
- Bierman, G.J. Measurement updating using the UD factorization. Automatica 1976, 12, 375–382. [Google Scholar] [CrossRef]
- Wang, G.; Chen, B.; Yang, X.; Peng, B.; Feng, Z. Numerically stable minimum error entropy Kalman filter. Signal Proc. 2021, 181, 107914. [Google Scholar] [CrossRef]
- Pang, C.; Long, F.; Liang, J.; Chen, H.; Yuan, M. Algorithm of rapid integer ambiguity resolution for single frequency GPS receivers based on improved UDVT decomposition. Acta Aeronaut. Astronaut. Sin. 2012, 33, 102–109. [Google Scholar]
- Xie, G. Principles of GPS and Receiver Design; Publishing House of Electronics Industry: Beijing, China, 2009; Volume 7, pp. 61–63. [Google Scholar]
- Li, B. Single-frequency GNSS cycle slip estimation with positional polynomial constraint. J. Geod. 2019, 93, 1781–1803. [Google Scholar] [CrossRef]
- Gelen, A.G.; Atasoy, A. A New Method for Kalman Filter Tuning. In Proceedings of the 2018 International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Zhao, S.; Cui, X.; Guan, F.; Lu, M. A Kalman filter-based short baseline RTK algorithm for single-frequency combination of GPS and BDS. Sensors 2014, 14, 15415–15433. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Xu, G. Simplified equivalent representation of GPS observation equations. GPS Solut. 2008, 12, 99–108. [Google Scholar] [CrossRef]
- Teunissen, P.J.; Odijk, D. Ambiguity dilution of precision: Definition, properties and application. In Proceedings of the 10th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1997), Kansas, MO, USA, 16–19 September 1997. [Google Scholar]
- Chang, G.; Chen, C.; Zhang, Q.; Zhang, S. Variational Bayesian adaptation of process noise covariance matrix in Kalman filtering. J. Frankl. Inst. 2021, 358, 3980–3993. [Google Scholar] [CrossRef]
- Furones, A.M.; Julián, A.B.A.; Dimas-Pages, A.; Cos-Gayón, F. Computational time reduction for sequential batch solutions in GNSS precise point positioning technique. Comput. Geosci. 2017, 105, 34–42. [Google Scholar] [CrossRef][Green Version]
- Kulikova, M.V. Sequential maximum correntropy Kalman filtering. Asian J. Control 2020, 22, 25–33. [Google Scholar] [CrossRef]
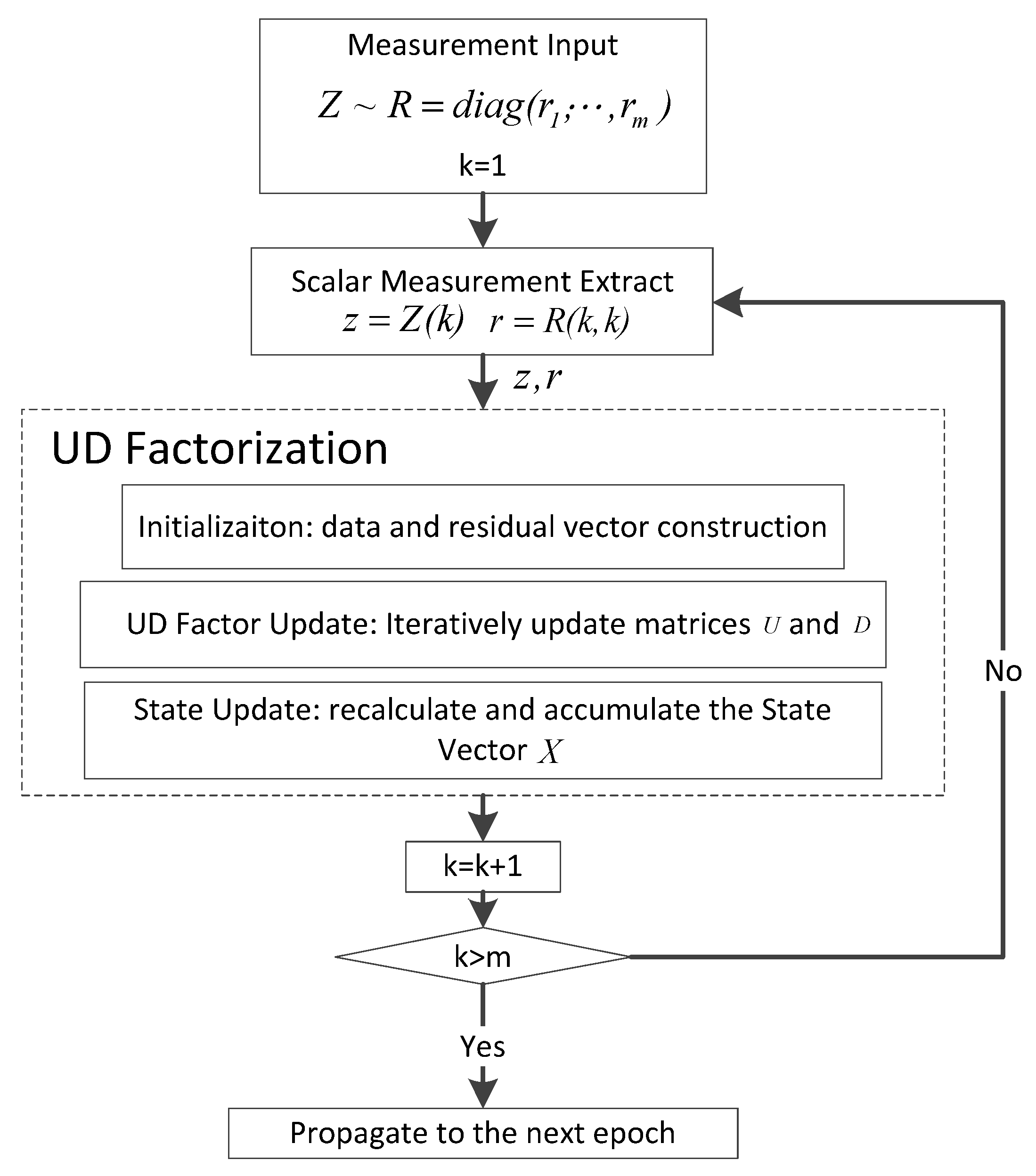




| Step | Stage | Implementation |
|---|---|---|
| 1 | Initialization | |
| 2 | U-D factor Update | for j = 2:n for i = 1: j − 1 , end end |
| 3 | State Update | for j = 1:g end |
| Processing Model | CUT0-CUT2 | CUT0-CUT3 | |||||
|---|---|---|---|---|---|---|---|
| E | N | U | E | N | U | ||
| RMS (mm) | UD-KF | 0.5 | 0.2 | 0.3 | 0.3 | 0.6 | 0.5 |
| DD-KF | 3.5 | 1.0 | 1.8 | 13.0 | 2.3 | 7.6 | |
| STD (mm) | UD-KF | 0.3 | 0.2 | 0.3 | 0.3 | 0.5 | 0.5 |
| DD-KF | 1.9 | 0.7 | 1.7 | 6.2 | 1.6 | 6.2 | |
| No. | Baseline | Distance (km) | Interval | Processing Model | |
|---|---|---|---|---|---|
| Base | Rover | ||||
| 1 | HKKT | HKSC | 15.613 | 1 s, 5 s | UD-KF, DD-KF |
| 2 | HKKS | HKSC | 18.303 | 1 s, 5 s | UD-KF, DD-KF |
| 3 | HKLM | HKSC | 11.634 | 1 s, 5 s | UD-KF, DD-KF |
| 4 | HKOH | HKSC | 12.211 | 1 s, 5 s | UD-KF, DD-KF |
| 5 | HKPC | HKSC | 11.418 | 1 s, 5 s | UD-KF, DD-KF |
| 6 | HKST | HKSC | 9.232 | 1 s, 5 s | UD-KF, DD-KF |
| Baseline | Interval | E | N | U | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| UD | DD | Improvement | UD | DD | Improvement | UD | DD | Improvement | |||
| RMSE (cm) | HKSC-HKKT | 1 s | 2.73 | 6.02 | 54.65% | 2.34 | 2.82 | 17.02% | 8.07 | 4.54 | −77.75% |
| 5 s | 1.19 | 3.39 | 64.90% | 1.314 | 4.34 | 69.72% | 2.61 | 3.54 | 26.27% | ||
| HKSC-HKKS | 1 s | 0.67 | 0.74 | 9.46% | 0.88 | 1.87 | 52.94% | 2.43 | 1.251 | −94.24% | |
| 5 s | 1.69 | 0.75 | −125.33% | 2.09 | 1.65 | −26.67% | 2.70 | 1.24 | −117.74% | ||
| HKSC-HKLM | 1 s | 1.14 | 3.50 | 67.43% | 0.93 | 0.81 | −14.81% | 2.89 | 1.24 | −133.06% | |
| 5 s | 1.07 | 2.92 | 63.36% | 1.06 | 1.01 | −4.95% | 2.80 | 1.12 | −150% | ||
| HKSC-HKOH | 1 s | 0.69 | 3.07 | 77.52% | 1.07 | 2.19 | 51.14% | 2.40 | 2.79 | 13.98% | |
| 5 s | 0.65 | 2.35 | 72.34% | 0.78 | 2.23 | 65.02% | 1.75 | 2.44 | 28.28% | ||
| HKSC-HKPC | 1 s | 1.12 | 3.83 | 70.76% | 1.37 | 1.36 | −0.73% | 3.51 | 3.95 | 11.14% | |
| 5 s | 1.01 | 4.72 | 78.60% | 1.19 | 1.09 | −9.17% | 3.36 | 4.39 | 23.46% | ||
| HKSC-HKST | 1 s | 1.15 | 0.91 | −26.37% | 1.14 | 0.89 | −28.09% | 4.012 | 6.08 | 34.01% | |
| 5 s | 1.21 | 1.18 | −2.54% | 1.43 | 0.71 | −101.41% | 4.16 | 6.58 | 36.78% | ||
| STD (cm) | HKSC-HKKT | 1 s | 2.61 | 4.83 | 45.96% | 2.28 | 2.52 | 9.52% | 7.97 | 4.35 | −83.22% |
| 5 s | 0.96 | 2.52 | 61.90% | 1.01 | 4.32 | 76.62% | 2.58 | 3.34 | 22.75% | ||
| HKSC-HKKS | 1 s | 0.64 | 0.54 | −18.52% | 0.82 | 1.51 | 45.70% | 2.43 | 0.74 | −228.38% | |
| 5 s | 1.69 | 0.49 | −244.90% | 1.60 | 1.12 | −42.86 | 2.70 | 0.77 | −250.65% | ||
| HKSC-HKLM | 1 s | 1.14 | 1.72 | 33.72% | 0.84 | 0.77 | −9.09% | 2.82 | 0.73 | −286.30% | |
| 5 s | 1.05 | 1.37 | 23.36% | 0.96 | 0.93 | −3.23% | 2.76 | 0.71 | −288.73% | ||
| HKSC-HKOH | 1 s | 0.65 | 1.48 | 56.08% | 0.94 | 1.79 | 47.49% | 2.25 | 1.12 | −100.89% | |
| 5 s | 0.65 | 1.15 | 43.48% | 0.72 | 1.77 | 59.32% | 1.75 | 1.66 | −5.42% | ||
| HKSC-HKPC | 1 s | 1.04 | 3.53 | 70.54% | 1.35 | 1.07 | −26.17% | 3.45 | 3.812 | 9.50% | |
| 5 s | 1.01 | 3.88 | 73.97% | 1.18 | 0.85 | −38.82% | 3.36 | 4.09 | 17.85% | ||
| HKSC-HKST | 1 s | 1.13 | 0.90 | −25.56% | 1.099 | 0.88 | −24.89% | 3.94 | 4.611 | 14.55% | |
| 5 s | 1.06 | 1.00 | −6.00% | 1.42 | 0.69 | −105.80% | 4.06 | 4.54 | 10.57% | ||
| Baseline | Total Filer Time (ms) | Improvement | Total Fix Time(ms) | Fix Rate | Improvement | |||
|---|---|---|---|---|---|---|---|---|
| UD-KF | DD-KF | UD-KF | DD-KF | UD-KF | DD-KF | |||
| HKSC-HKST | 599.37 | 844.83 | 29.05% | 3037.49 | 3715.58 | 98.47% | 100% | 18.25% |
| HKSC-HKKT | 525.31 | 1073.34 | 51.06% | 2801.20 | 3589.02 | 93.14% | 94.42% | 21.95% |
| HKSC-HKPC | 518.57 | 777.03 | 33.26% | 2729.49 | 3634.99 | 98.25% | 98.92% | 24.91% |
| HKSC-HKLM | 541.10 | 741.99 | 27.07% | 2803.85 | 3189.85 | 83.58% | 84.47% | 12.10% |
| HKSC-HKOH | 535.73 | 746.97 | 28.28% | 2858.32 | 3395.42 | 98.56% | 100% | 15.82% |
| HKSC-HKKS | 528.23 | 725.42 | 27.18% | 2798.22 | 3354.70 | 98.39% | 100% | 16.59% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, B.; Liu, T.; Xu, G.; Ji, Y.; Sun, M.; Nie, W.; He, Y. An Efficient UD Factorization Implementation of Kalman Filter for RTK Based on Equivalent Principle. Remote Sens. 2022, 14, 967. https://doi.org/10.3390/rs14040967
Liu J, Zhang B, Liu T, Xu G, Ji Y, Sun M, Nie W, He Y. An Efficient UD Factorization Implementation of Kalman Filter for RTK Based on Equivalent Principle. Remote Sensing. 2022; 14(4):967. https://doi.org/10.3390/rs14040967
Chicago/Turabian StyleLiu, Jian, Bing Zhang, Tong Liu, Guochang Xu, Yuanfa Ji, Mengfei Sun, Wenfeng Nie, and Yufang He. 2022. "An Efficient UD Factorization Implementation of Kalman Filter for RTK Based on Equivalent Principle" Remote Sensing 14, no. 4: 967. https://doi.org/10.3390/rs14040967
APA StyleLiu, J., Zhang, B., Liu, T., Xu, G., Ji, Y., Sun, M., Nie, W., & He, Y. (2022). An Efficient UD Factorization Implementation of Kalman Filter for RTK Based on Equivalent Principle. Remote Sensing, 14(4), 967. https://doi.org/10.3390/rs14040967






