Target Localization Based on High Resolution Mode of MIMO Radar with Widely Separated Antennas
Abstract
:1. Introduction
2. Materials and Methods
2.1. Signal Model
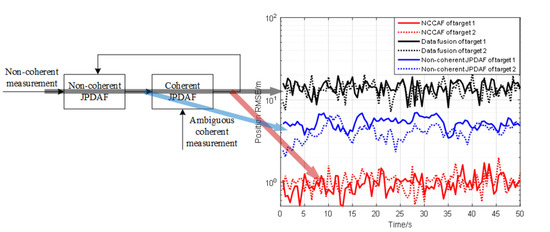
2.2. NCCAF Algorithm
2.2.1. Non-Coherent JPDAF
2.2.2. Coherent JPDAF
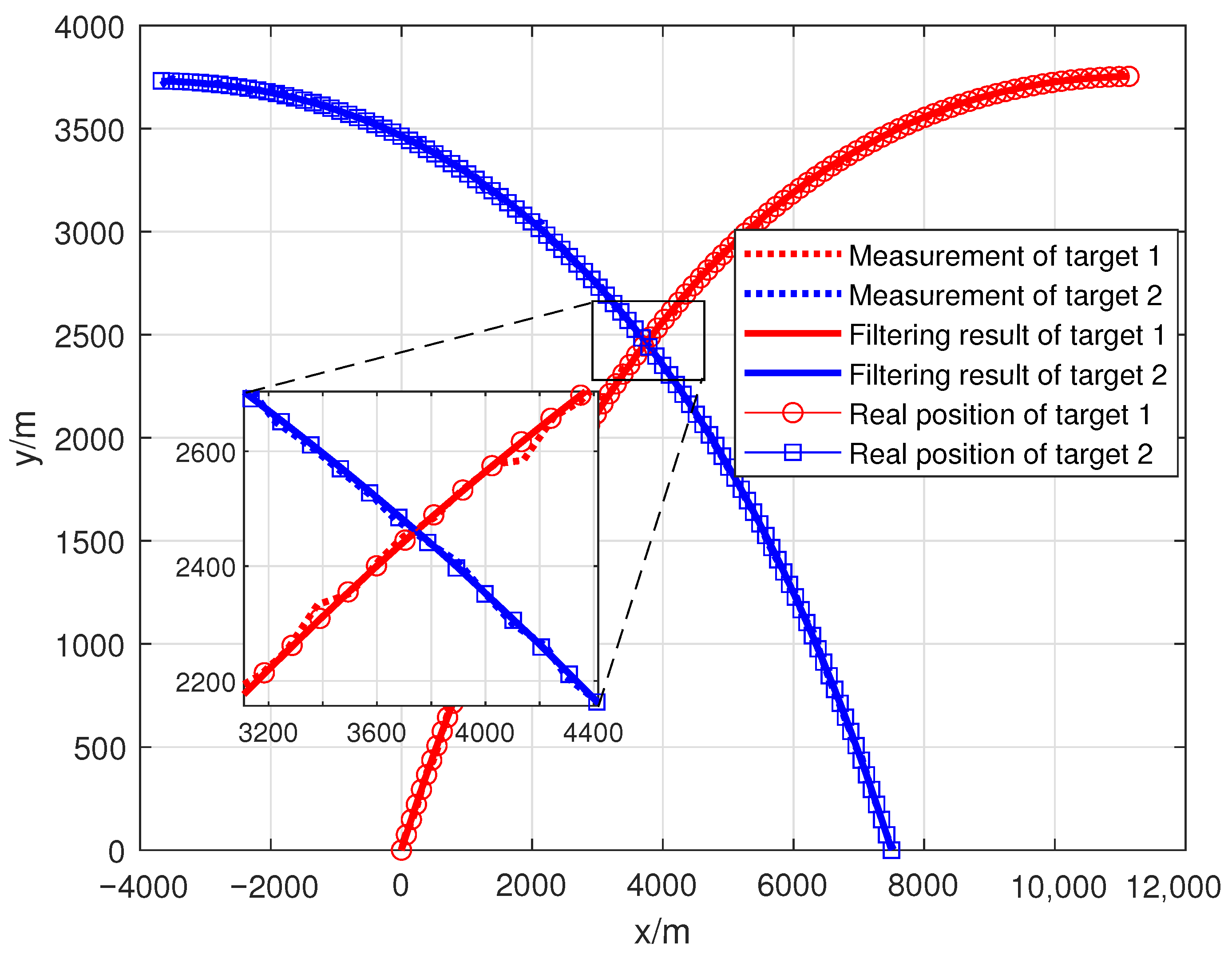
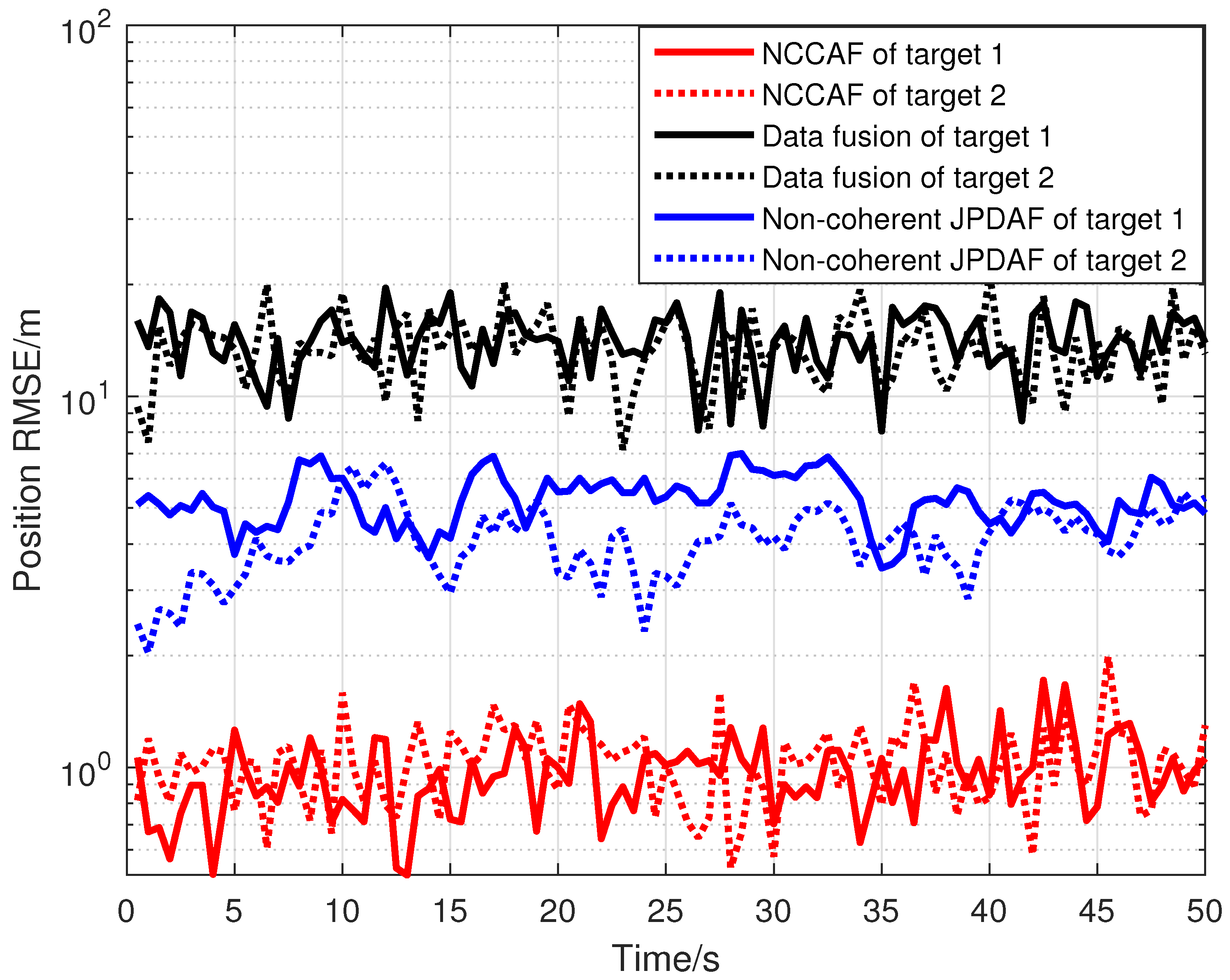
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haimovich, A.M.; Blum, R.S.; Cimini, L.J. MIMO Radar with Widely Separated Antennas. IEEE Signal Process. Mag. 2008, 25, 116–129. [Google Scholar] [CrossRef]
- Lehmann, N.H.; Haimovich, A.M.; Blum, R.S.; Cimini, L. High Resolution Capabilities of MIMO Radar. In Proceedings of the 2006 Fortieth Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 29 October–1 November 2006; pp. 25–30. [Google Scholar]
- Candes, E.; Romberg, J.; Tao, T. Stable Signal Recovery from Incomplete and Inaccurate Measurements. Commun. Pure Appl. Math. 2005, 59, 1207–1223. [Google Scholar] [CrossRef] [Green Version]
- Moffet, A. Minimum-redundancy linear arrays. IEEE Trans. Antennas Propag. 1968, 16, 172–175. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.; Feng, Q.; Liu, S.; Bignami, C.; Tolomei, C.; Zhao, D. Minimum Redundancy Array—A Baseline Optimization Strategy for Urban SAR Tomography. Remote Sens. 2020, 12, 3100. [Google Scholar] [CrossRef]
- Vertatschitsch, E.; Haykin, S. Nonredundant arrays. Proc. IEEE 1986, 74, 217. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef] [Green Version]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing With Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Zhang, Y.D.; Amin, M.G.; Himed, B. Sparsity-based DOA estimation using co-prime arrays. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2013; pp. 3967–3971. [Google Scholar]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized Coprime Array Configurations for Direction-of-Arrival Estimation. IEEE Trans. Signal Process. 2015, 63, 1377–1390. [Google Scholar] [CrossRef]
- Yang, X.; Li, Y.; Long, T. Antenna Position Optimization Based on Adaptive Genetic Algorithm with Self-supervised Differential Operator for Distributed Coherent Aperture Radar. IET Radar Sonar Navig. 2021, 15, 677–685. [Google Scholar] [CrossRef]
- Esch, C.; Köhler, J.; Gutjahr, K.; Schuh, W.D. On the Analysis of the Phase Unwrapping Process in a D-InSAR Stack with Special Focus on the Estimation of a Motion Model. Remote Sens. 2019, 11, 2295. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yang, Q.; Deng, B.; Qin, Y.; Wang, H. Estimation of Translational Motion Parameters in Terahertz Interferometric Inverse Synthetic Aperture Radar (InISAR) Imaging Based on a Strong Scattering Centers Fusion Technique. Remote Sens. 2019, 11, 1221. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.; Li, Z.; Bao, Z. Residues Cluster-Based Segmentation and Outlier-Detection Method for Large-Scale Phase Unwrapping. IEEE Trans. Image Process. 2011, 20, 2865–2875. [Google Scholar]
- Esch, C.; Köhler, J.; Gutjahr, K.; Schuh, W.D. One-Step Three-Dimensional Phase Unwrapping Approach Based on Small Baseline Subset Interferograms. Remote Sens. 2020, 12, 1473. [Google Scholar] [CrossRef]
- Spoorthi, G.E.; Gorthi, S.; Gorthi, R.K.S.S. PhaseNet: A Deep Convolutional Neural Network for Two-Dimensional Phase Unwrapping. IEEE Signal Process. Lett. 2019, 26, 54–58. [Google Scholar] [CrossRef]
- Pu, L.; Zhang, X.; Zhou, Z.; Li, L.; Zhou, L.; Shi, J.; Wei, S. A Robust InSAR Phase Unwrapping Method via Phase Gradient Estimation Network. Remote Sens. 2021, 13, 4564. [Google Scholar] [CrossRef]
- Mao, W.; Wang, S.; Xu, B.; Li, Z.; Zhu, Y. An Improved Phase Unwrapping Method Based on Hierarchical Networking and Constrained Adjustment. Remote Sens. 2021, 13, 4193. [Google Scholar] [CrossRef]
- Wang, W.; Liu, A.X.; Sun, K. Device-Free Gesture Tracking Using Acoustic Signals. In Proceedings of the International Conference on Mobile Computing and Networking, New York, NY, USA, 3–7 October 2016; ACM: New York, NY, USA, 2016; pp. 82–94. [Google Scholar]
- Sun, K.; Zhao, T.; Wang, W. VSkin: Sensing Touch Gestures on Surfaces of Mobile Devices Using Acoustic Signals. In Proceedings of the 24th Annual International Conference, New Delhi, India, 29 October–2 November 2018; pp. 1–15. [Google Scholar]
- Steudel, F. An Improved Process for Phase-Derived Range Measurements. World Intellectual Property. Organization Patent 1651978, 24 February 2005. [Google Scholar]
- Steudel, F. Process for Phase-Derived Range Measurements. U.S. Patent 7046190, 10 February 2005. [Google Scholar]
- Zhu, N.; Hu, J.; Xu, S.; Wu, W.; Zhang, Y.; Chen, Z. Micro-Motion Parameter Extraction for Ballistic Missile with Wideband Radar Using Improved Ensemble EMD Method. Remote Sens. 2021, 13, 3545. [Google Scholar] [CrossRef]
- Fan, H.; Ren, L.; Teng, L. A high-precision phase-derived range and velocity measurement method based on synthetic wideband pulse Doppler radar. Sci. China Inf. Sci. 2017, 60, 147–158. [Google Scholar] [CrossRef]
- Fan, H.; Ren, L.; Mao, E.; Liu, Q. A High-Precision Method of Phase-Derived Velocity Measurement and Its Application in Motion Compensation of ISAR Imaging. IEEE Trans. Geosci. Remote Sens. 2018, 56, 60–77. [Google Scholar] [CrossRef]
- Li, W.; Fan, H.; Ren, L.; Mao, E.; Liu, Q. A High-Accuracy Phase-Derived Velocity Measurement Method for High-Speed Spatial Targets Based on Stepped-Frequency Chirp Signals. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1999–2014. [Google Scholar] [CrossRef]
- Yang, X.; Shi, J.; Zhou, Y.; Wang, C.; Hu, Y.; Zhang, X.; Wei, S. Ground Moving Target Tracking and Refocusing Using Shadow in Video-SAR. Remote Sens. 2020, 12, 3083. [Google Scholar] [CrossRef]
- Seoane, L.; Ramillien, G.; Beirens, B.; Darrozes, J.; Rouxel, D.; Schmitt, T.; Salaün, C.; Frappart, F. Regional Seafloor Topography by Extended Kalman Filtering of Marine Gravity Data without Ship-Track Information. Remote Sens. 2022, 14, 169. [Google Scholar] [CrossRef]
- Chen, Y.; Xu, L.; Wang, G.; Yan, B.; Sun, J. An Improved Smooth Variable Structure Filter for Robust Target Tracking. Remote Sens. 2021, 13, 4612. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Fortmann, T.E. Tracking and Data Association; Academic Press: Cambridge, MA, USA, 1988. [Google Scholar]
- Stone, L.D.; Streit, R.L.; Corwin, T.L.; Kristine, L.B. Bayesian Multiple Target Tracking; Artech House: Norwood, MA, USA, 2014. [Google Scholar]
- Bar-Shalom, Y. Multitarget-Multisensor Tracking: Applications and Advances; Artech House: Norwood, MA, USA, 1990. [Google Scholar]
- Roecker, J.; Phillis, G. Suboptimal joint probabilistic data association. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 510–517. [Google Scholar] [CrossRef]
- Zhou, B.; Bose, N. Multitarget tracking in clutter: Fast algorithms for data association. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 352–363. [Google Scholar] [CrossRef]
- Godrich, H.; Haimovich, A.M.; Blum, R.S. Target localisation techniques and tools for multiple-input multiple-output radar. IET Radar Sonar Navig. 2009, 3, 314–327. [Google Scholar] [CrossRef]
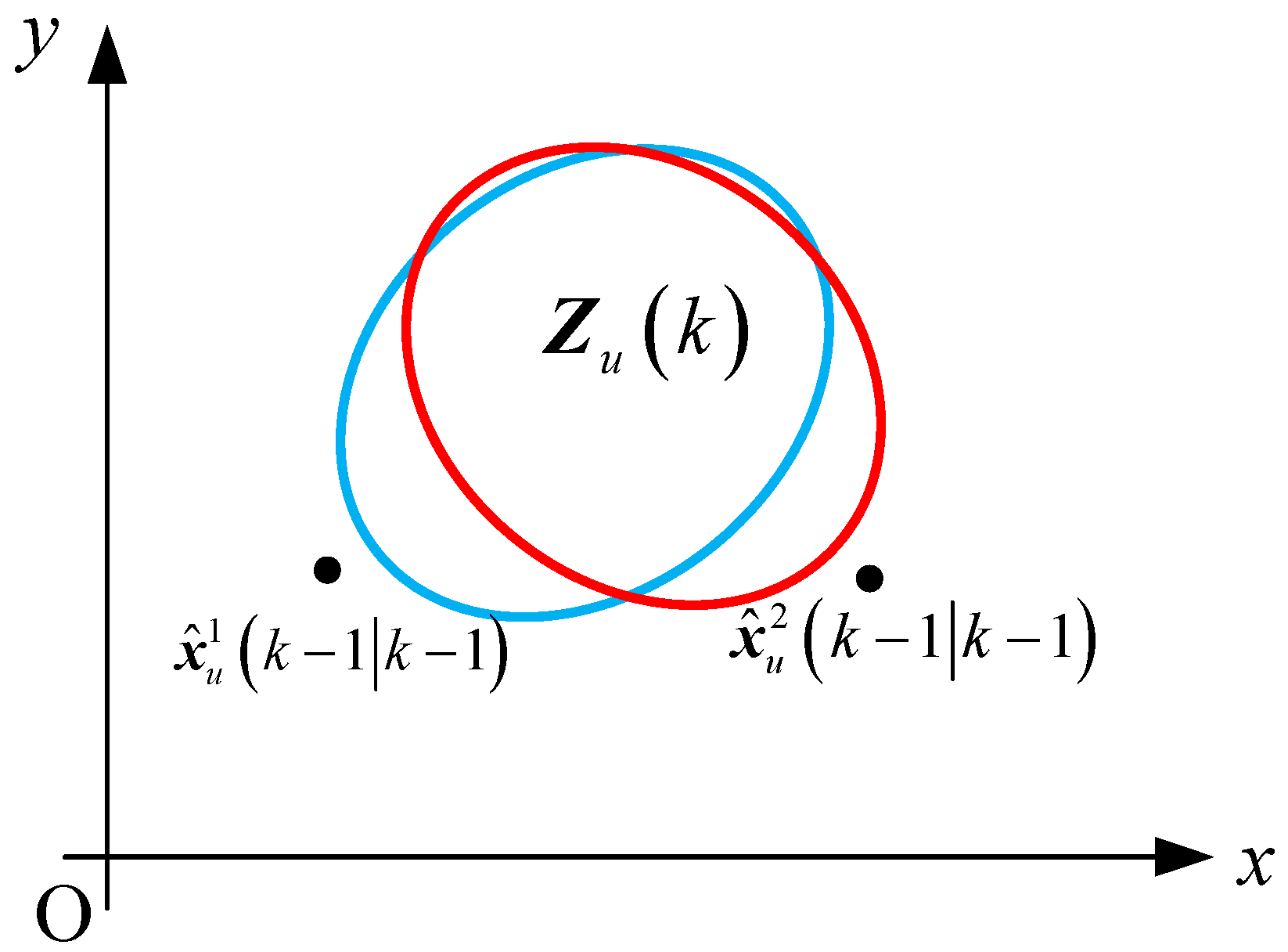
| Parameter Name | Parameter Value |
|---|---|
| Carrier frequency | 1 GHz |
| Bandwidth | 100 MHz |
| Number of targets | 2 |
| Initial target position | , (7500 m, 0) |
| Initial target velocity | (150 m/s, 150 m/s), (−150 m/s, 150 m/s) |
| Target acceleration | (3 m/s, −3 m/s), (−3 m/s, −3 m/s) |
| Time of tracking | 50 s |
| Interval of sampling time | 0.5 s |
| Standard deviation of non-coherent measurement | 10 m |
| Standard deviation of coherent measurement | 1 m |
| Number of Monte Carlo simulations | 100 |
| Signal-to-noise ratio | 20 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, J.; Liu, F.; Liu, H.; Liu, Q. Target Localization Based on High Resolution Mode of MIMO Radar with Widely Separated Antennas. Remote Sens. 2022, 14, 902. https://doi.org/10.3390/rs14040902
Lu J, Liu F, Liu H, Liu Q. Target Localization Based on High Resolution Mode of MIMO Radar with Widely Separated Antennas. Remote Sensing. 2022; 14(4):902. https://doi.org/10.3390/rs14040902
Chicago/Turabian StyleLu, Jiaxin, Feifeng Liu, Hongjie Liu, and Quanhua Liu. 2022. "Target Localization Based on High Resolution Mode of MIMO Radar with Widely Separated Antennas" Remote Sensing 14, no. 4: 902. https://doi.org/10.3390/rs14040902
APA StyleLu, J., Liu, F., Liu, H., & Liu, Q. (2022). Target Localization Based on High Resolution Mode of MIMO Radar with Widely Separated Antennas. Remote Sensing, 14(4), 902. https://doi.org/10.3390/rs14040902