Permafrost Ground Ice Melting and Deformation Time Series Revealed by Sentinel-1 InSAR in the Tanggula Mountain Region on the Tibetan Plateau
Abstract
:1. Introduction
2. Study Area and Datasets
2.1. Study Area
2.2. Datasets
3. Methods
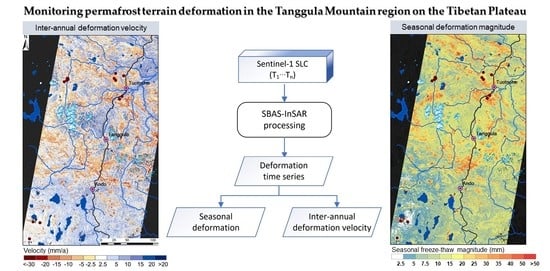
3.1. SBAS-InSAR Processing
- InSAR Processing
- Deformation Time Series Estimation
- Reference Point Refinement and Geocoding
3.2. Long-Term Deformation Velocity and Seasonal Deformation Calculation
4. Results
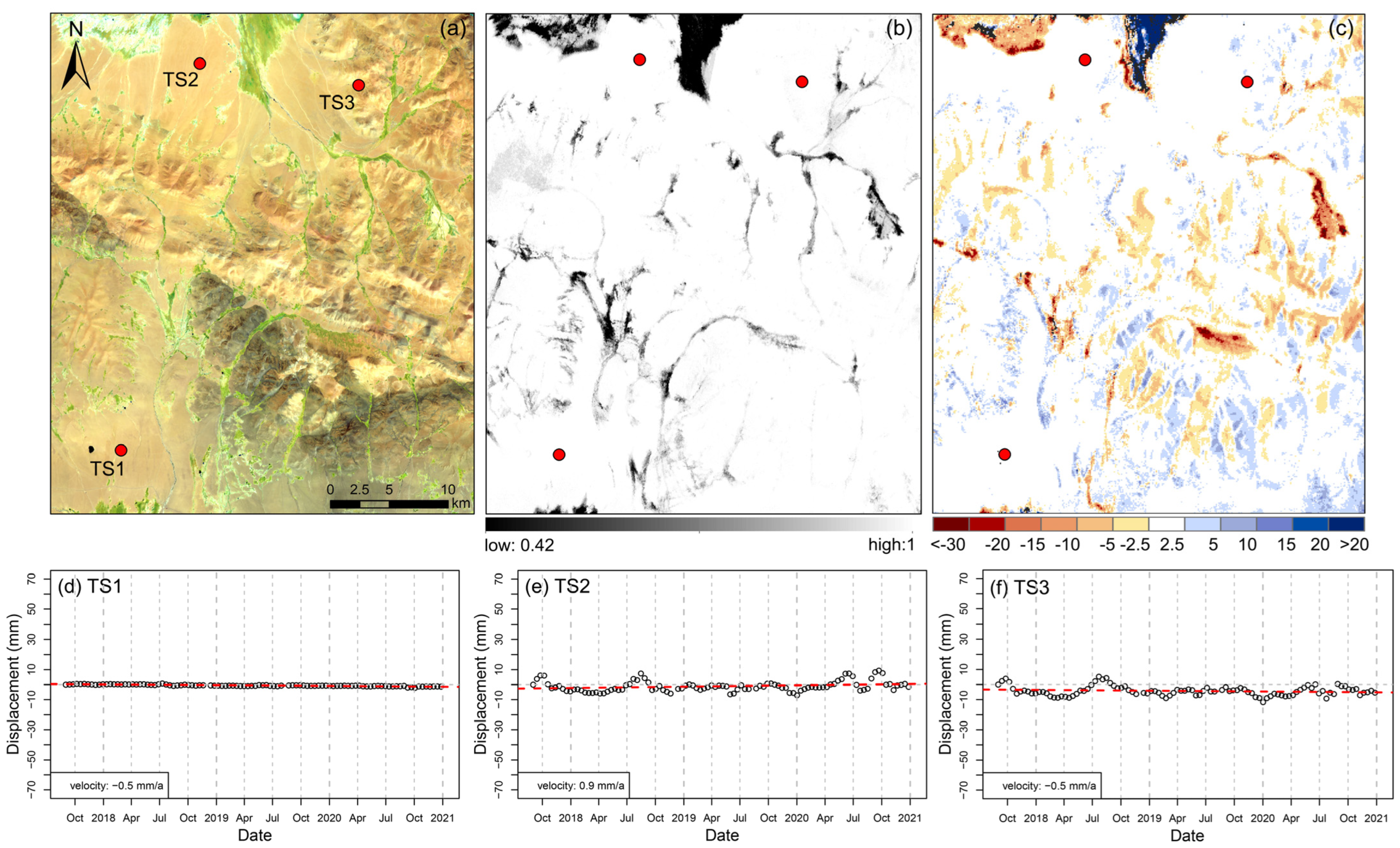
4.1. SBAS-InSAR Derived Deformation Time Series
4.2. Characteristics of Ground Surface Deformation in the Tanggula Mountain Region
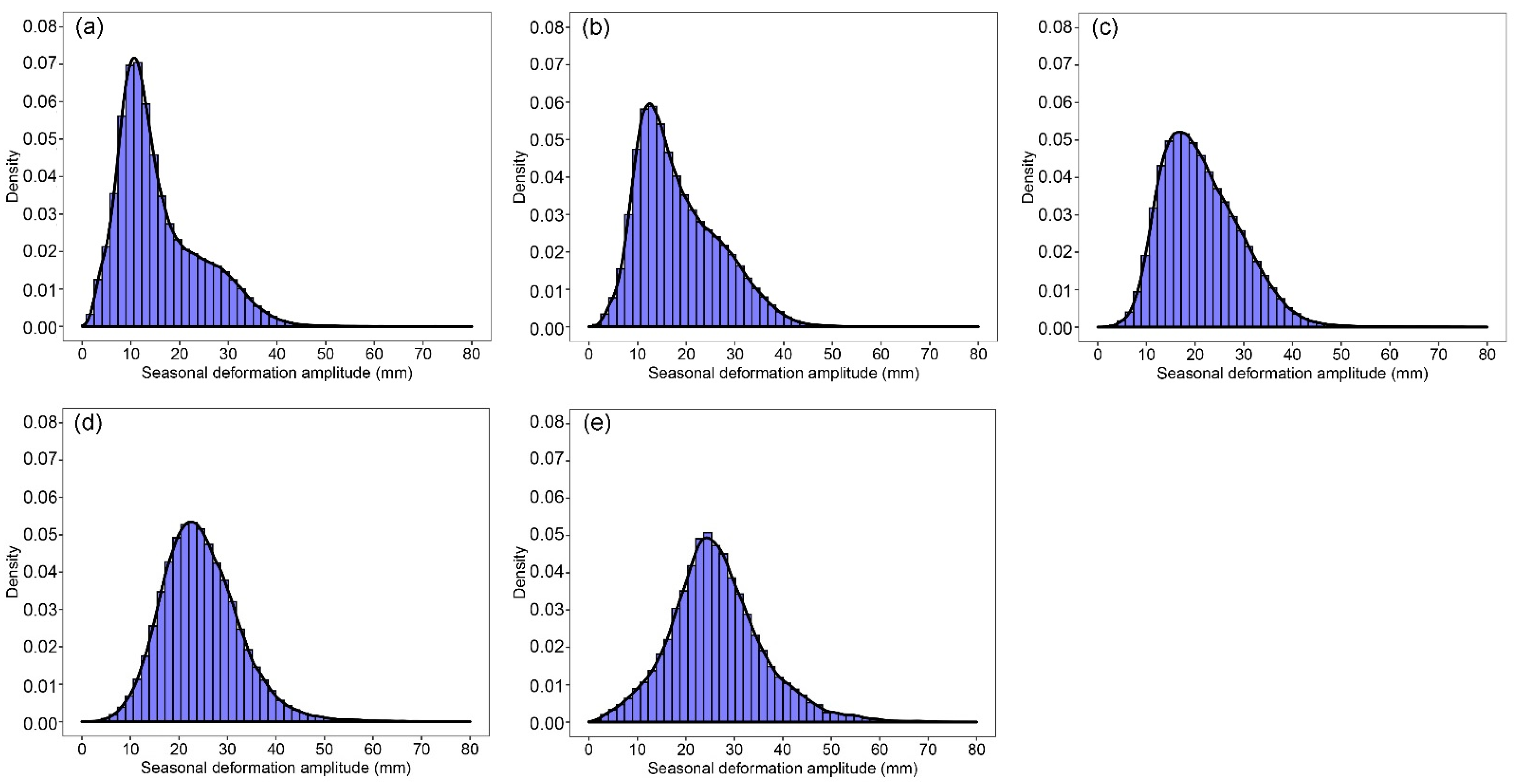
4.2.1. Spatial Distribution of Long-Term Deformation Velocity and Seasonal Deformation Magnitude
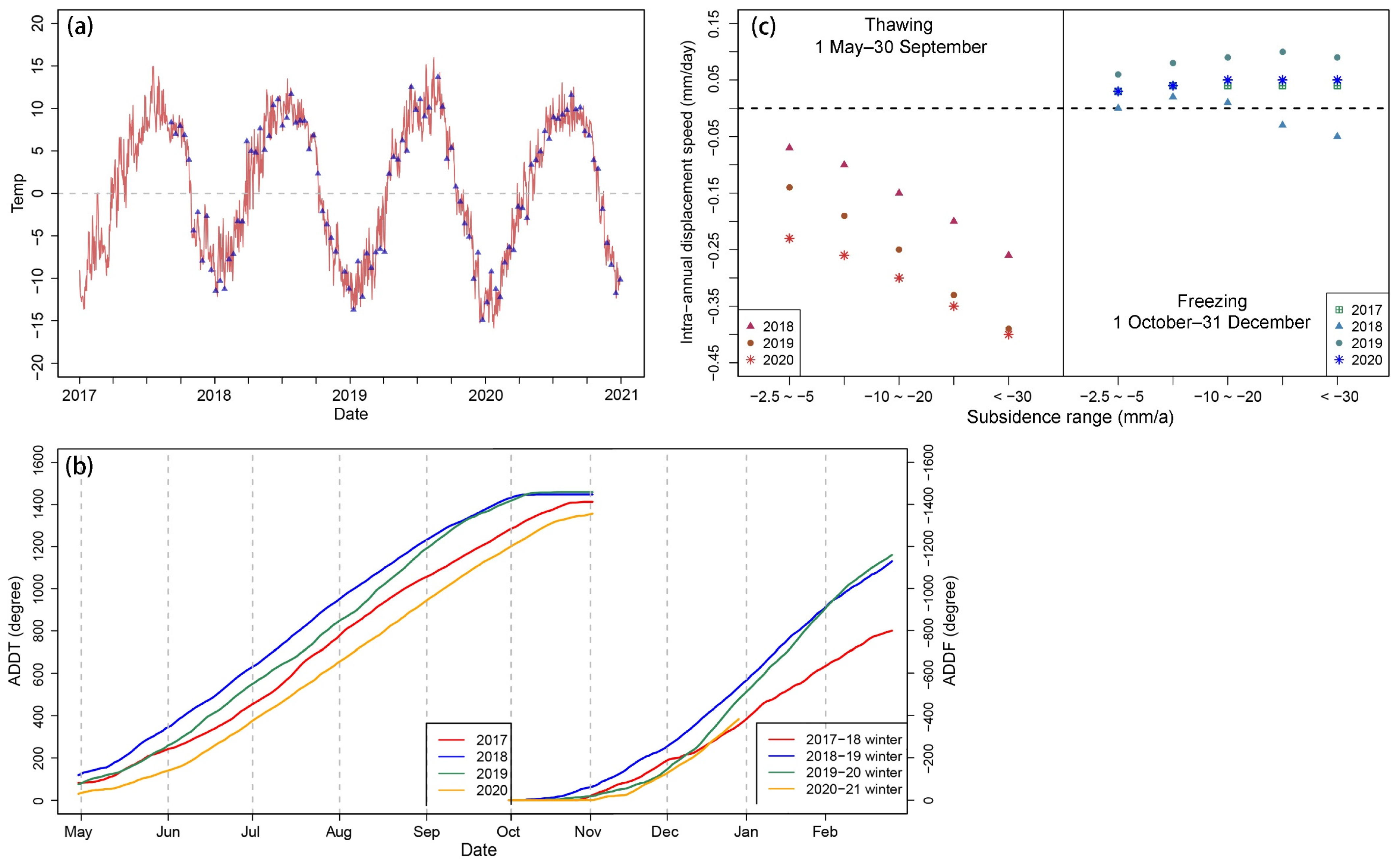
4.2.2. Relationship between Seasonal Amplitude and Deformation Velocity
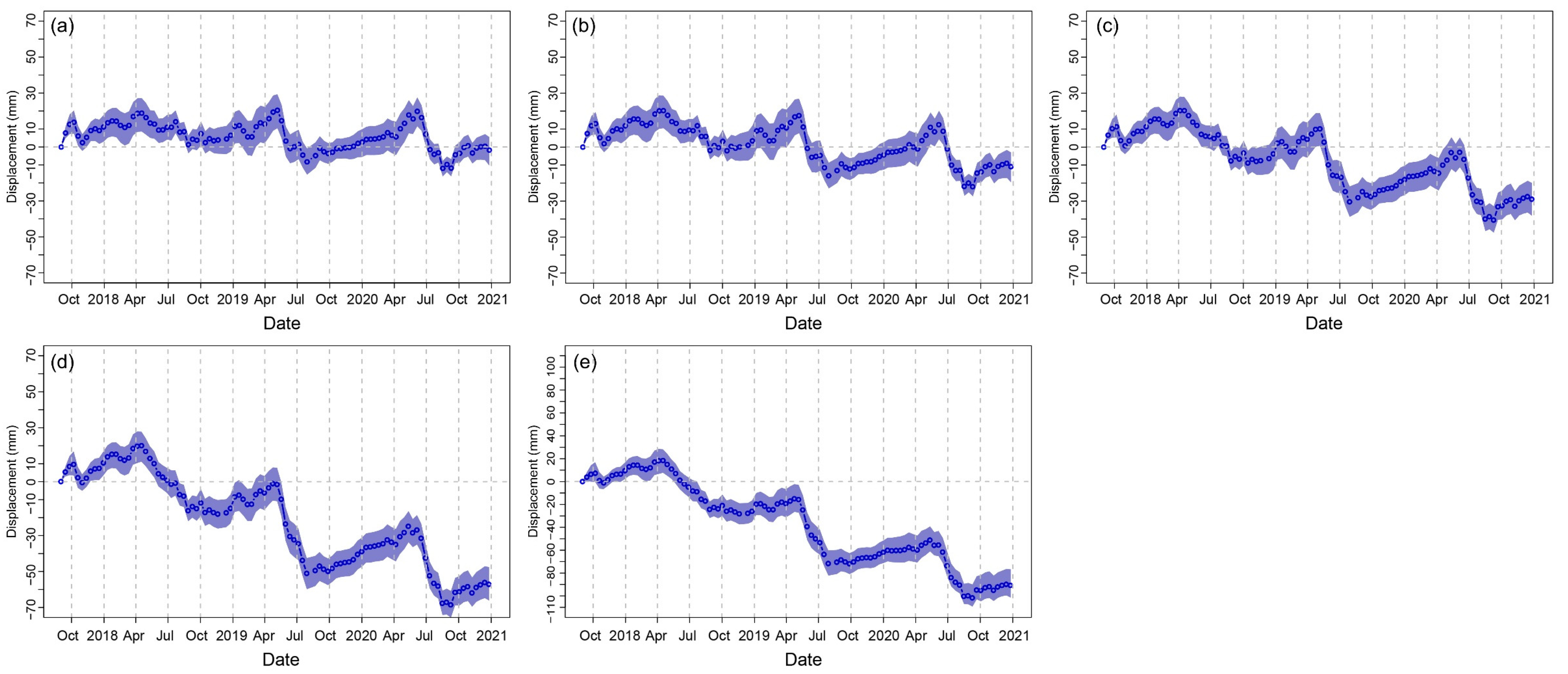
4.2.3. Deformation Curves of Degrading Permafrost with Different Subsidence Levels
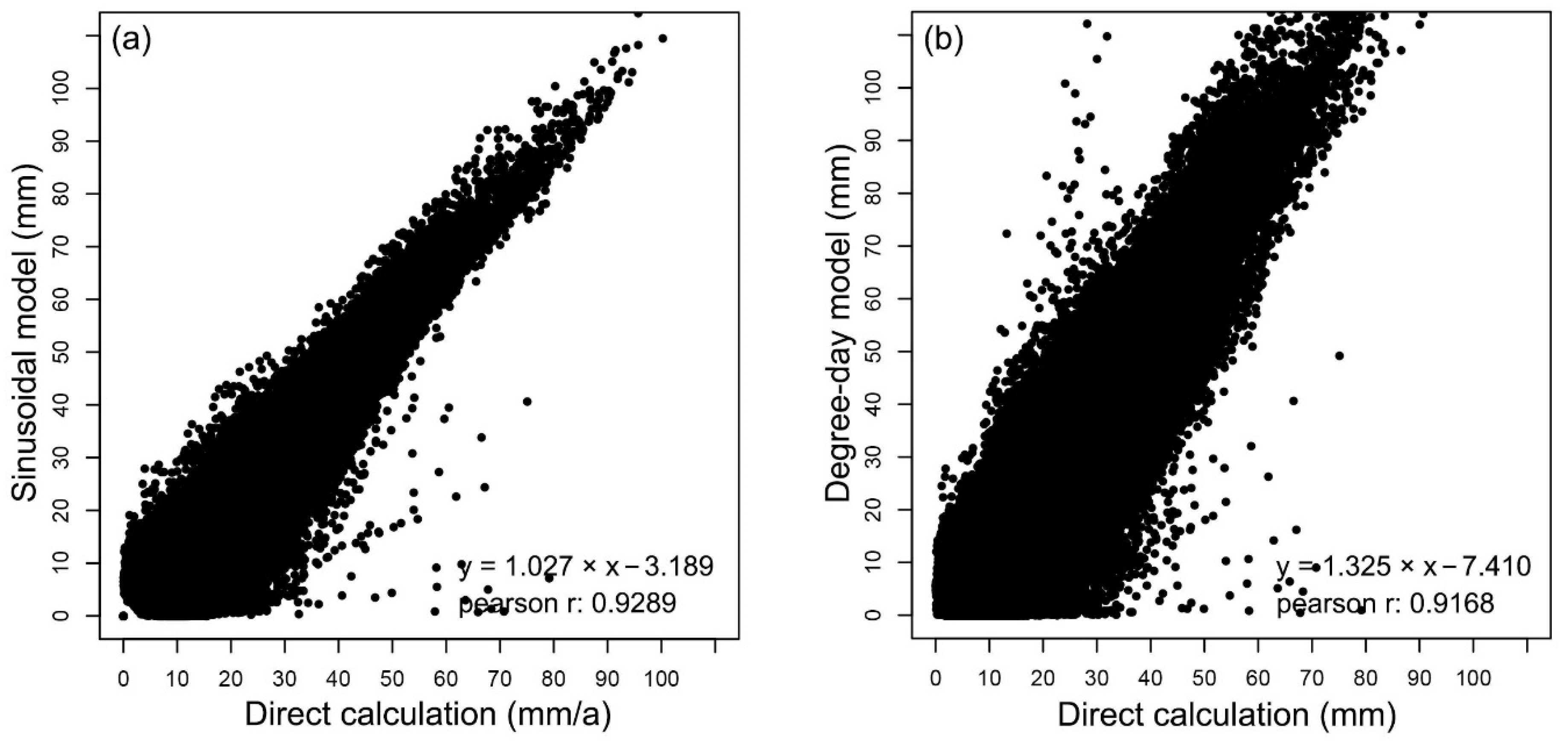
4.3. Differences in the Deformation Properties Derived by Different Calculation Methods
4.3.1. Differences between Long-Term Deformation Calculations
4.3.2. Differences between Seasonal Deformation Calculations
5. Discussion
5.1. InSAR Application in the Study Area
5.2. Seasonal Deformation Model Descriptions
6. Conclusions
- (1)
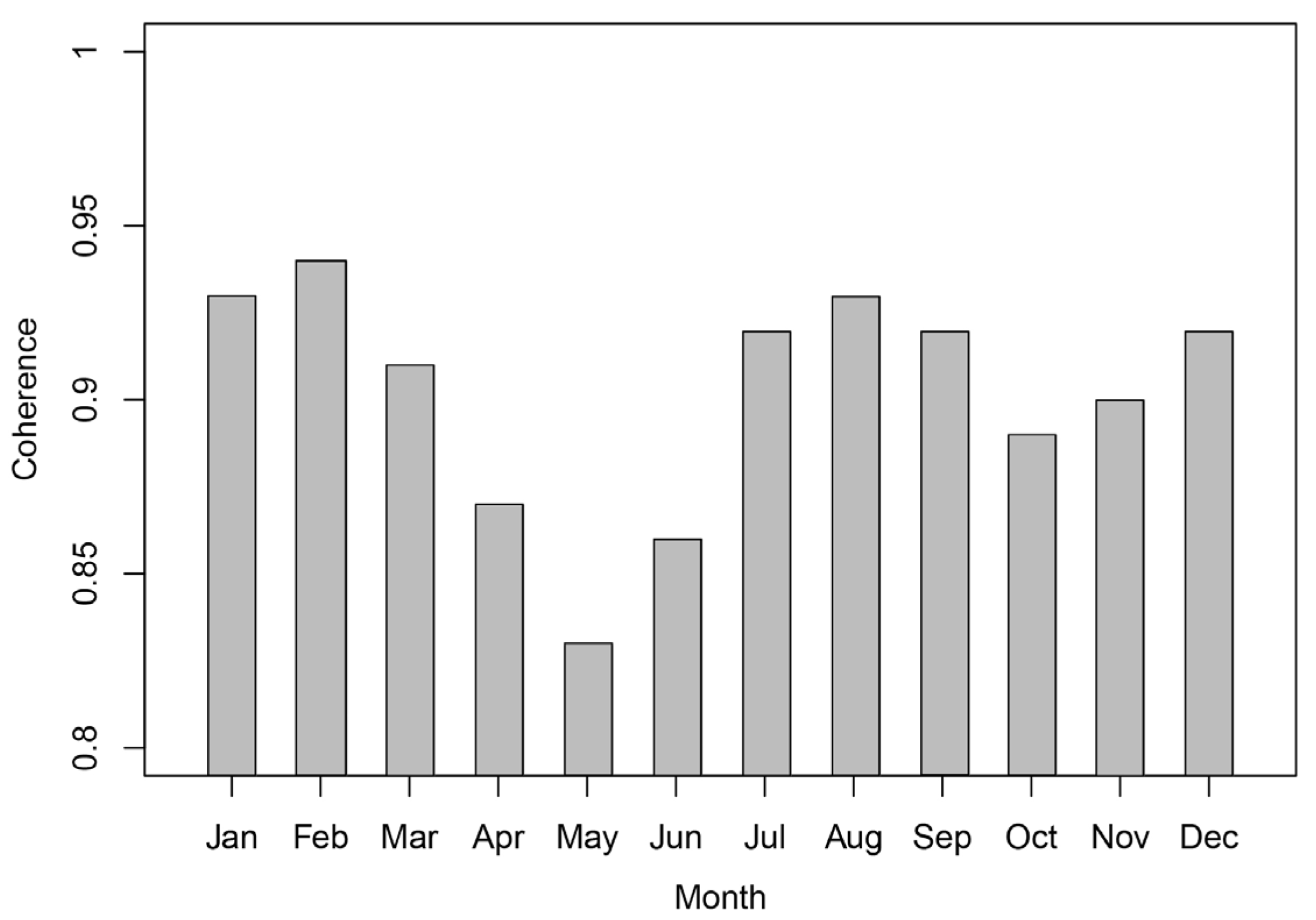
- The deformation curves of varied terrain surfaces, e.g., degrading permafrost, aggrading permafrost, stable permafrost, seasonally frozen ground, alluvial fan, in the permafrost environment in the Tanggula Mountain region were first revealed and analyzed in detail. Compared to non-permafrost areas, the permafrost-affected areas have lower coherence and large periodic seasonal deformation. Most permafrost deformation time series reveal that the displacement is very small from late January to the end of February (ground is stable), after a fast freeze-heaving speed from late October to the beginning of January. In the study area, due to low precipitation during November–February, the snowmelt or wet snowfall effect is limited, and interferometric coherence is high during this time. A lower coherence is noticed during April and June, which is most likely caused by the combined effects of snow and ground surface freeze/thaw state changes.
- (2)
- The average subsidence rate is 9.1 mm/a over subsiding terrain. The majority of the subsiding terrain (68.1%) has a subsidence rate between 5–20 mm/a. A very limited region (0.7%) has a subsidence rate larger than 30 mm/a, and the average seasonal deformation magnitude is 19.7 mm. Both the subsidence rate and the seasonal deformation are higher than those on the northwestern part of the Tibetan Plateau [18]. The subsidence values are similar to those on the ice-rich Eboling Mountain in the northeastern region of the Tibetan Plateau [28], and those in the Hohxil region from Wudaoliang to Tuotuohe [29]. In comparison to other permafrost areas in Arctic and subarctic regions [18,19,20,22,23,24,27,30,46,47,54,55,57,58,59,60,61,62,63,64,65,66,67,68,69], generally, the seasonal deformation value on the Tibetan Plateau is smaller, but the intra-annual subsidence rate is not a small value.
- (3)
- We compared two important deformation indices over permafrost terrain, i.e., long-term deformation trend and seasonal deformation magnitude, derived by direct calculation of deformation time series and model approximations using the sinusoidal and degree-day models. Regarding the long-term deformation trend rates, different calculations manifested very high agreement. Regarding the seasonal deformation magnitude, there is a deviation between the model-approximated values and the direct calculation of intra-annual highest-lowest elevation difference. We also detected a winter subsidence signal over heavily settled terrain in a warm year by examining the deformation time series. Thus, the piecewise separation of long-term deformation into the freezing and thawing season based on air or ground surface temperature may not describe this phenomenon well. When adequate SAR data acquisitions are available, the preset deformation model in MT-InSAR processing might introduce bias in deriving seasonal deformation properties.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- French, H.M. The Periglacial Environment; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Cheng, G. The mechanism of repeated-segregation for the formation of thick layered ground ice. Cold Reg. Sci. Technol. 1983, 8, 57–66. [Google Scholar]
- Shur, Y.; Hinkel, K.M.; Nelson, F.E. The transient layer: Implications for geocryology and climate-change science. Permafr. Periglac. Process. 2005, 16, 5–17. [Google Scholar] [CrossRef]
- Mackay, J.R. Some observations on the growth and deformation of epigenetic, syngenetic and anti-syngenetic ice wedges. Permafr. Periglac. Process. 1990, 1, 15–29. [Google Scholar] [CrossRef]
- Burn, C.R. The development of near-surface ground ice during the Holocene at sites near Mayo, Yukon Territory, Canada. J. Quat. Sci. 1988, 3, 31–38. [Google Scholar] [CrossRef]
- Streletskiy, D.; Shiklomanov, N.I.; Littlet, J.D.; Nelson, F.E.; Brown, J.; Nyland, K.E.; Klene, A.E. Thaw subsidence in undisturbed tundra landscapes, Barrow, Alaska, 1962–2015. Permafr. Periglac. Process. 2016, 28, 566–572. [Google Scholar] [CrossRef]
- Shiklomanov, N.I.; Streletskiy, D.A.; Little, J.D.; Nelson, F.E. Isotropic thaw subsidence in undisturbed permafrost landscapes. Geophys. Res. Lett. 2013, 40, 6356–6361. [Google Scholar] [CrossRef]
- Günther, F.; Overduin, P.P.; Yakshina, I.A.; Opel, T.; Baranskaya, A.V.; Grigoriev, M.N. Observing Muostakh disappear: Permafrost thaw subsidence and erosion of a ground-ice-rich island in response to arctic summer warming and sea ice reduction. Cryosphere 2015, 9, 151–178. [Google Scholar] [CrossRef] [Green Version]
- Lantuit, H.; Pollard, W. Fifty years of coastal erosion and retrogressive thaw slump activity on Herschel Island, southern Beaufort Sea, Yukon Territory, Canada. Geomorphology 2008, 95, 84–102. [Google Scholar] [CrossRef]
- Kokelj, S.V.; Jorgenson, M. Advances in thermokarst research. Permafr. Periglac. Process. 2013, 24, 108–119. [Google Scholar] [CrossRef]
- Lantuit, H.; Overduin, P.; Wetterich, S. Recent progress regarding permafrost coasts. Permafr. Periglac. Process. 2013, 24, 120–130. [Google Scholar] [CrossRef]
- Hjort, J.; Karjalainen, O.; Aalto, J.; Westermann, S.; Romanovsky, V.E.; Nelson, F.E.; Etzelmüller, B.; Luoto, M. Degrading permafrost puts Arctic infrastructure at risk by mid-century. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Zou, D.; Hu, G.; Du, E.; Pang, Q.; Xiao, Y.; Li, R.; Sheng, Y.; Wu, X.; Sun, Z.; et al. Changing climate and the permafrost environment on the Qinghai-Tibet (Xizang) Plateau. Permafr. Periglac. Process. 2020, 31, 396–405. [Google Scholar] [CrossRef]
- Zhao, L.; Sheng, Y. Permafrost and Environment Changes on the Qinghai-Tibetan Plateau; Science Press: Beijing, China, 2019. (In Chinese) [Google Scholar]
- Cheng, G.; Jin, H. Permafrost and groundwater on the Qinghai-Tibet Plateau and in northeast China. Hydrogeol. J. 2013, 21, 5–23. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Shum, C.K.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A.; et al. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Daout, S.; Doin, M.-P.; Peltzer, G.; Socquet, A.; Lasserre, C. Large-scale InSAR monitoring of permafrost freeze-thaw cycles on the Tibetan Plateau. Geophys. Res. Lett. 2017, 44, 901–909. [Google Scholar] [CrossRef]
- Zwieback, S.; Meyer, F.J. Top-of-permafrost ground ice indicated by remotely sensed late-season subsidence. Cryosphere 2021, 15, 2041–2055. [Google Scholar] [CrossRef]
- Antonova, S.; Sudhaus, H.; Strozzi, T.; Zwieback, S.; Kääb, A.; Heim, B.; Langer, M.; Bornemann, N.; Boike, J. Thaw Subsidence of a Yedoma Landscape in Northern Siberia, Measured In Situ and Estimated from TerraSAR-X Interferometry. Remote Sens. 2018, 10, 494. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.-W.; Zhao, R.; Hu, J.; Wetn, L.; Feng, G.; Zhalng, Z.; Wang, Q. InSAR analysis of surface deformation over permafrost to estimate active layer thickness based on one-dimensional heat transfer model of soils. Sci. Rep. 2015, 5, 1–9. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, T.; Wahr, J. InSAR measurements of surface deformation over permafrost on the North Slope of Alaska. J. Geophys. Res. Earth Surf. 2010, 115, F3. [Google Scholar] [CrossRef]
- Reinosch, E.; Bucketl, J.; Dong, J.; Gerke, M.; Baade, J.; Riedel, B. InSAR time series analysis of seasonal surface displacement dynamics on the Tibetan Plateau. Cryosphere 2020, 14, 1633–1650. [Google Scholar] [CrossRef]
- Daout, S.; Dini, B.; Haetberli, W.; Doin, M.-P.; Palrsons, B. Ice loss in the Northeastern Tibetan Plateau permafrost as seen by 16 yr of ESA SAR missions. Earth Planet. Sci. Lett. 2020, 545, 116404. [Google Scholar] [CrossRef]
- Lu, P.; Han, J.; Li, Z.; Xu, R.; Li, R.; Hao, T.; Qialo, G. Lake outburst accelerated permafrost degradation on Qinghai-Tibet Plateau. Remote Sens. Environ. 2020, 249, 112011. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, M.; Liu, X.; Wang, C.; Zhang, H.; Tang, Y.; Zhang, B. Deformation feature analysis of Qinghai–Tibet railway using TerraSAR-X and Sentinel-1A time-series interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5199–5212. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Wang, C.; Tang, Y.; Zhang, B.; Wu, F.; Wang, J.; Zhang, Z. Time-series InSAR monitoring of permafrost freeze-thaw seasonal displacement over Qinghai–Tibetan Plateau using Sentinel-1 data. Remote Sens. 2019, 11, 1000. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Liu, L.; Zhang, T.; Cao, B.; Lin, H. Using persistent scatterer interferometry to map and quantify permafrost thaw subsidence: A case study of Eboling Mountain on the Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surf. 2018, 123, 2663–2676. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Wang, C.; Tang, Y.; Zhang, B.; Wu, F.; Wang, J.; Zhang, Z. Active layer thickness retrieval over the Qinghai-Tibet Plateau using Sentinel-1 multitemporal InSAR monitored Permafrost subsidence and temporal-spatial multilayer soil moisture data. IEEE Access 2020, 8, 84336–84351. [Google Scholar] [CrossRef]
- Bartsch, A.; Leibman, M.; Strozzi, T.; Khomutov, A.; Widhalm, B.; Babkina, E.; Mullanurov, D.; Ermokhina, K.; Kroisleitner, C.; Bergstedt, H. Seasonal progression of ground displacement identified with satellite radar interferometry and the impact of unusually warm conditions on permafrost at the Yamal Peninsula in 2016. Remote Sens. 2019, 11, 1865. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Schaefer, K.; Zhang, T.; Walhr, J. Estimating 1992–2000 average active layer thickness on the Alaskan North Slope from remotely sensed surface subsidence. J. Geophys. Res. Earth Surf. 2012, 117. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.-L.; Li, Q.; Shen, Y.-P.; Zhou, N.; Wang, X.-S.; Li, J.; Jia, W.-R. Monitoring of aeolian desertification on the Qinghai-Tibet Plateau from the 1970s to 2015 using Landsat images. Sci. Total Environ. 2018, 619, 1648–1659. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhang, C.; Shen, Y.; Jia, W.; Li, J. Quantitative assessment of the relative roles of climate change and human activities in desertification processes on the Qinghai-Tibet Plateau based on net primary productivity. Catena 2016, 147, 789–796. [Google Scholar] [CrossRef]
- Wu, Q.; Yu, W.; Jin, H. No protection of permafrost due to desertification on the Qinghai–Tibet Plateau. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Liu, G. Preliminary results of permafrost investigation on northern and southern slopes of Mt. Geladandong, interior Qinghai-Tibet Plateau. J. Glaciol. Geocryol. 2022, 44, 1–13. (In Chinese) [Google Scholar]
- Zhang, X.; Zhang, X.; Zhou, J.; Tang, W.; Ding, L.; Ma, J.; Zhang, X. Daily 1-km All-Weather Land Surface Temperature Dataset for Western China; National Tibetan Plateau Data Center: Beijing, China, 2019. [Google Scholar]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote. Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Lanari, R.; Lundgren, P.; Manzo, M.; Casu, F. Satellite radar interferometry time series analysis of surface deformation for Los Angeles, California. Geophys. Res. Lett. 2004, 31, 23. [Google Scholar] [CrossRef]
- Usai, S. A least squares database approach for SAR interferometric data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 753–760. [Google Scholar] [CrossRef] [Green Version]
- Guarnieri, A.M.; Tebaldini, S. On the exploitation of target statistics for SAR interferometry applications. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3436–3443. [Google Scholar] [CrossRef]
- Tough, J.; Blacknell, D.; Quegan, S. A statistical description of polarimetric and interferometric synthetic aperture radar data. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1995, 449, 567–589. [Google Scholar]
- Jolivet, R.; Agram, P.S.; Lin, N.Y.; Simons, M.; Doin, M.; Peltzer, G.; Li, Z. Improving InSAR geodesy using global atmospheric models. J. Geophys. Res. Solid Earth 2014, 119, 2324–2341. [Google Scholar] [CrossRef]
- Fattahi, H.; Amelung, F. DEM error correction in InSAR time series. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4249–4259. [Google Scholar] [CrossRef]
- Zhang, Y.; Fattahi, H.; Amelung, F. Small baseline InSAR time series analysis: Unwrapping error correction and noise reduction. Comput. Geosci. 2019, 133, 104331. [Google Scholar]
- Chen, J.; Wu, T.; Zou, D.; Liu, L.; Wu, X.; Gong, W.; Zhu, X.; Li, R.; Hao, J.; Hu, G.; et al. Magnitudes and patterns of large-scale permafrost ground deformation revealed by Sentinel-1 InSAR on the central Qinghai-Tibet Plateau. Remote Sens. Environ. 2022, 268, 112778. [Google Scholar] [CrossRef]
- Chen, F.; Lin, H.; Zhou, W.; Hong, T.; Wang, G. Surface deformation detected by ALOS PALSAR small baseline SAR interferometry over permafrost environment of Beiluhe section, Tibet Plateau, China. Remote Sens. Environ. 2013, 138, 10–18. [Google Scholar] [CrossRef]
- Buckel, J.; Reinosch, E.; Hördt, A.; Zhang, F.; Riedel, B.; Gerke, M.; Schwalb, A.; Mäusbacher, R. Insights into a remote cryosphere: A multi-method approach to assess permafrost occurrence at the Qugaqie basin, western Nyainqêntanglha Range, Tibetan Plateau. Cryosphere 2021, 15, 149–168. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y.; O′Connor, M.; Cardenas, M.B.; Schaefer, K.; Michaelides, R.; Kling, G. Active layer freeze-thaw and water storage dynamics in permafrost environments inferred from InSAR. Remote Sens. Environ. 2020, 248, 112007. [Google Scholar] [CrossRef]
- Pepe, A.; Lanari, R. On the extension of the minimum cost flow algorithm for phase unwrapping of multitemporal differential SAR interferograms. IEEE Trans. Geosci. Remote. Sens. 2006, 44, 2374–2383. [Google Scholar] [CrossRef]
- Mackay, J.R.; Burn, C.R. The first 20 years (1978–1979 to 1998–1999) of active-layer development, Illisarvik experimental drained lake site, western Arctic coast, Canada. Can. J. Earth Sci. 2002, 39, 1657–1674. [Google Scholar] [CrossRef]
- Mackay, J.R. Downward water movement into frozen ground, western arctic coast, Canada. Can. J. Earth Sci. 1983, 20, 120–134. [Google Scholar] [CrossRef]
- French, H.; Harbor, J. The development and history of glacial and periglacial geomorphology. In Treatise on Geomorphology; Shroder, J.F., Ed.; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Short, N.; LeBlanc, A.-M.; Sladen, W.; Oldenborger, G.; Mathon-Dufour, V.; Brisco, B. RADARSAT-2 D-InSAR for ground displacement in permafrost terrain, validation from Iqaluit Airport, Baffin Island, Canada. Remote Sens. Environ. 2014, 141, 40–51. [Google Scholar] [CrossRef]
- Wang, L.; Marzahn, P.; Bernier, M.; Ludwig, R. Sentinel-1 InSAR measurements of deformation over discontinuous permafrost terrain, Northern Quebec, Canada. Remote Sens. Environ. 2020, 248, 111965. [Google Scholar] [CrossRef]
- Riseborough, D.; Shiklomanov, N.; Etzelmüller, B.; Gruber, S.; Marchenko, S. Recent advances in permafrost modelling. Permafr. Periglac. Process. 2008, 19, 137–156. [Google Scholar] [CrossRef]
- Liu, L.; Jafarov, E.E.; Schaefer, K.M.; Jones, B.M.; Zebker, H.A.; Williams, C.A.; Rogan, J.; Zhang, T. InSAR detects increase in surface subsidence caused by an Arctic tundra fire. Geophys. Res. Lett. 2014, 41, 3906–3913. [Google Scholar] [CrossRef]
- Liu, L.; Schaefer, K.; Gusmeroli, A.; Grosse, G.; Jones, B.M.; Zhang, T.; Parsekian, A.D.; Zebker, H.A. Seasonal thaw settlement at drained thermokarst lake basins, Arctic Alaska. Cryosphere 2014, 8, 815–826. [Google Scholar] [CrossRef] [Green Version]
- Strozzi, T.; Antonova, S.; Günther, F.; Mätzler, E.; Vieira, G.; Wegmüller, U.; Westermann, S.; Bartsch, A. Sentinel-1 SAR interferometry for surface deformation monitoring in low-land permafrost areas. Remote Sens. 2018, 10, 1360. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Günther, F.; Grosse, G.; Liu, L.; Lin, H. Sentinel-1 InSAR measurements of elevation changes over Yedoma uplands on Sobo-Sise Island, Lena Delta. Remote Sens. 2018, 10, 1152. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Zhao, L.; Liu, L.; Zhu, R.; Gao, Z.; Qiao, Y.; Tian, L.; Zhou, H.; Xie, M. Surface-deformation monitoring in the permafrost regions over the Tibetan Plateau, using Sentinel-1 data. Sci. Cold Arid. Reg. 2018, 10, 114–125. [Google Scholar]
- Li, Z.; Tang, P.; Zhou, J.; Tian, B.; Chen, Q.; Fu, S. Permafrost environment monitoring on the Qinghai-Tibet Plateau using time series ASAR images. Int. J. Digit. Earth 2015, 8, 840–860. [Google Scholar] [CrossRef]
- Chimitdorzhiev, T.N.; Dagurov, P.N.; Bykov, M.E.; Dmitriev, A.V.; Kirbizhekova, I.I. Comparison of ALOS PALSAR interferometry and field geodetic leveling for marshy soil thaw/freeze monitoring, case study from the Baikal lake region, Russia. J. Appl. Remote Sens. 2016, 10, 016006. [Google Scholar] [CrossRef]
- Rouyet, L.; Lauknes, T.R.; Christiansen, H.H.; Strand, S.M.; Larsen, Y. Seasonal dynamics of a permafrost landscape, Adventdalen, Svalbard, investigated by InSAR. Remote Sens. Environ. 2019, 231, 111236. [Google Scholar] [CrossRef]
- Rouyet, L.; Liu, L.; Strand, S.; Christiansen, H.; Lauknes, T.; Larsen, Y. Seasonal InSAR displacements documenting the active layer freeze and thaw progression in central-western Spitsbergen, Svalbard. Remote Sens. 2021, 13, 2977. [Google Scholar] [CrossRef]
- Rudy, A.C.; Lamoureux, S.F.; Treitz, P.; Short, N.; Brisco, B. Seasonal and multi-year surface displacements measured by DInSAR in a High Arctic permafrost environment. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 51–61. [Google Scholar] [CrossRef]
- Wang, L.; Marzahn, P.; Bernier, M.; Jacome, A.; Poulin, J.; Ludwig, R. Comparison of TerraSAR-X and ALOS PALSAR differential interferometry with multisource DEMs for monitoring ground displacement in a discontinuous permafrost region. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2017, 10, 4074–4093. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, M.; Wu, Z.; Liu, X. Permafrost deformation monitoring along the Qinghai-Tibet Plateau engineering corridor using InSAR observations with multi-sensor SAR datasets from 1997–2018. Sensors 2019, 19, 5306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, R.; Li, Z.; Feng, G.; Wang, Q.; Hu, J. Monitoring surface deformation over permafrost with an improved SBAS-InSAR algorithm: With emphasis on climatic factors modeling. Remote Sens. Environ. 2016, 184, 276–287. [Google Scholar] [CrossRef]




| Calculation | Description | Equation |
| Direct calculation |
| (1) (2) (3) where is the deformation time series, t is the temporal span of image acquisition dates away from the first acquisition date, is the long-term trend velocity, is the deformation time series minus the long-term linear trend and and represent the highest terrain elevation January–February and the lowest terrain elevation that occurred August–October in each year, respectively. |
| Model approximation | Sinusoidal model [18,21]
| (4) (5) where is periodic seasonal oscillation amplitude, T is the period of seasonal undulations (assumed to be one year), is the initial phase, and is the residual term. , , , and are the coefficients to be determined pixel by pixel in the spatial grid. The periodic peak-to-peak seasonal deformation magnitude is twice the absolute value of the periodic amplitude of . |
Degree-day model [29,46]
| (6) (7) (8) where and in Equation (6) represents the linear and seasonal deformation respectively, is the seasonal deformation magnitude, is the long-term displacement rate (mm/yr), the coefficient of linear deformation and seasonal deformation are expressed in Equations (7) and (8). In Equation (7), is the number of consecutive permafrost years (in units of years), and are the onsets of thawing and freezing, respectively. In Equation (8), is the composite index to account for the seasonal thaw subsidence and freeze uplift, is the coefficient for adjusting the soil thermal conductivities in the thaw and freeze seasons, ADDT (°C days) and ADDF (°C days) are the accumulated degree days of thaw and freeze, respectively. The ADDT is calculated as the sum of the daily air temperature above 0 °C, and the ADDF is calculated as the sum of the daily air temperature below 0 °C. The two indices are effective for indicating accumulated energy. |
| Long-Term Velocity Level (mm/Year) | Area (km2) | Coverage Perc. (%) | Deformation Characteristics (mm) | |
|---|---|---|---|---|
| Ave. Velocity (mm/Year) | Ave. Intra-Annual Seasonal Deformation Magnitude (mm) | |||
| −2.5–−5 | 5866.4 | 26.6 | −3.7 | 16.7 |
| −5–−10 | 8613.7 | 39.1 | −7.3 | 19.2 |
| −10–−20 | 6381.9 | 29.0 | −13.6 | 22.1 |
| −20–−30 | 1012.0 | 4.6 | −23.4 | 25.7 |
| <−30 | 143.2 | 0.7 | −34.9 | 28.6 |
| Overall | 22,017.3 | 100% | −9.1 | 19.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Zhao, L.; Zhou, H.; Liu, S.; Du, E.; Zou, D.; Liu, G.; Wang, C.; Li, Y. Permafrost Ground Ice Melting and Deformation Time Series Revealed by Sentinel-1 InSAR in the Tanggula Mountain Region on the Tibetan Plateau. Remote Sens. 2022, 14, 811. https://doi.org/10.3390/rs14040811
Wang L, Zhao L, Zhou H, Liu S, Du E, Zou D, Liu G, Wang C, Li Y. Permafrost Ground Ice Melting and Deformation Time Series Revealed by Sentinel-1 InSAR in the Tanggula Mountain Region on the Tibetan Plateau. Remote Sensing. 2022; 14(4):811. https://doi.org/10.3390/rs14040811
Chicago/Turabian StyleWang, Lingxiao, Lin Zhao, Huayun Zhou, Shibo Liu, Erji Du, Defu Zou, Guangyue Liu, Chong Wang, and Yan Li. 2022. "Permafrost Ground Ice Melting and Deformation Time Series Revealed by Sentinel-1 InSAR in the Tanggula Mountain Region on the Tibetan Plateau" Remote Sensing 14, no. 4: 811. https://doi.org/10.3390/rs14040811
APA StyleWang, L., Zhao, L., Zhou, H., Liu, S., Du, E., Zou, D., Liu, G., Wang, C., & Li, Y. (2022). Permafrost Ground Ice Melting and Deformation Time Series Revealed by Sentinel-1 InSAR in the Tanggula Mountain Region on the Tibetan Plateau. Remote Sensing, 14(4), 811. https://doi.org/10.3390/rs14040811