Retrieving Freeze/Thaw Cycles Using Sentinel-1 Data in Eastern Nunavik (Québec, Canada)
Abstract
:1. Introduction
2. Materials and Methods
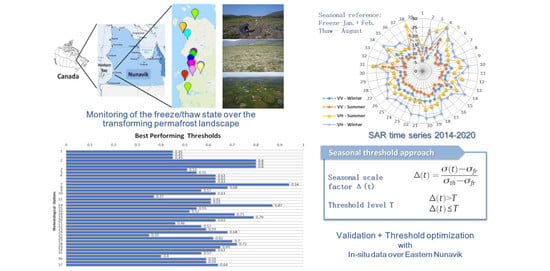
2.1. Study Area: Nunavik
2.2. SAR Sentinel-1
2.3. In Situ Measurements
2.4. Seasonal Threshold Approach
2.5. Validation and Threshold Optimization
3. Results
3.1. Backscatter Signal VH versus VV
3.2. Seasonal Reference Winter versus Summer
3.3. Threshold Distribution through All Selected Stations
3.4. Accuracy and Analysis
4. Discussion
4.1. Accuracy Aspect
4.2. Threshold Aspect
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Site No. | Site Name | Coordinate | Temperature Depth (cm) | Start | End |
|---|---|---|---|---|---|
| 1 | Salluit SILA (SALTSIL) | −75.6359, 62.1921 | 2 | 12 June 2017 | 23 September 2018 |
| 5 | 12 June 2017 | 23 September 2018 | |||
| 10 | 12 June 2017 | 23 September 2018 | |||
| 2 | Salluit SILA 2 (SALSIL2) | −75.6379, 62.1918 | 2 | 03 April 2014 | 08 June 2017 |
| 5 | 01 January 2014 | 08 June 2017 | |||
| 10 | 03 April 2014 | 08 June 2017 | |||
| 3 | Akulivik HT-162 (AKUL162) | −78.1550, 60.8174 | 10 | 03 April 2014 | 23 September 2019 |
| 4 | Akulivik HT-232 (AKUL232) | −78.2, 60.7833 | 0 | 28 October 2014 only | 28 October 2015 only |
| 5 | PuvirnituqRéference (PUVIREF) | −77.287, 60.0567 | 5 | 03 April 2014 | 21 October 2019 |
| 6 | Lac Bush (LACBUSH) | −75.9106, 57.9557 | 0 | 01 April 2014 | 29 August 2019 |
| 5 | 01 April 2014 | 29 August 2019 | |||
| 10 | 01 April 2014 | 29 August 2019 | |||
| 7 | Rivière Boniface Toundra—Station SILA (BONTSIL) | −76.0786, 57.7313 | 5 | 01 April 2014 | 20 August 2019 |
| 8 | Rivière Boniface Forêt-Station SILA (BONFSIL) | −76.087, 57.7269 | 5 | 01 April 2014 | 19 August 2019 |
| 10 | 01 April 2014 | 03 July 2014 | |||
| 9 | Hudsonie Biscarat (BISCARA) | −76.5825, 57.1702 | 0 | 18 August 2016 | 17 August 2017 |
| 10 | Sheldrake-1 | −76.4546, 56.6207 | 5 | 18 August 2016 | 17 August 2017 |
| 10 | 30 August 2015 | 06 July 2018 | |||
| 11 | Sheldrake-4 | −76.2572, 56.6215 | 5 | 30 August 2015 | 06 July 2018 |
| 10 | 30 August 2015 | 06 July 2018 | |||
| 12 | BGRA | −76.2138, 56.6116 | 5 | 04 September 2014 | 10 August 2015 |
| 13 | Rivière Sheldrake, Site B (SHELDRB) | −76.0909, 56.6141 | 10 | 06 July 2005 | 10 August 2007 |
| 14 | Hum1 | −76.5426, 56.5608 | 5 | 31 August 2014 | 22 August 2017 |
| 15 | Hum2 | −76.5447, 56.5558 | 5 | 07 September 2014 | 18 August 2018 |
| 16 | Hum10 | −76.5316, 56.5566 | 5 | 26 August 2015 | 18 August 2018 |
| 17 | Hum4 | −76.5326, 56.5486 | 5 | 29 August 2015 | 17 August 2018 |
| 18 | Hum5 | −76.5367, 56.5453 | 5 | 26 August 2015 | 17 August 2018 |
| 19 | Hum6 | −76.482, 56.5644 | 5 | 31 August 2014 | 02 May 2017 |
| 20 | Immatsiak_1 (IMMATS1) | −76.479, 56.563 | 10 | 01 January 2015 | 01 July 2019 |
| 21 | Hum3 | −76.482, 56.559 | 5 | 31 August 2014 | 19 August 2018 |
| 22 | Emplacement à dominance pessières (T/DP) | −76.482, 56.559 | 10 | 01 January 2015 | 03 July 2019 |
| 23 | Piézomètre à dominance arbustes moyen (MS/DA) | −76.48, 56.559 | 10 | 01 January 2015 | 07 July 2019 |
| 24 | Emplacment à dominance de lichens et arbustes (LLS/DL) | −76.479, 56.559 | 10 | 01 January 2015 | 03 July 2019 |
| 25 | Emplacement à dominance herbacée (LH/DH) | −76.479, 56.559 | 10 | 01 January 2015 | 07 July 2019 |
| 26 | Immatsiak_2 (IMMATS2) | −76.481, 56.559 | 10 | 01 January 2015 | 01 July 2019 |
| 27 | Immatsiak_3 (IMMATS3) | −76.464, 56.547 | 10 | 01 January 2015 | 03 July 2019 |
| 28 | Hum8 | −76.448, 56.543 | 5 | 01 September 2014 | 01 May 2018 |
| 29 | Hum7 | −76.438, 56.54 | 5 | 25 August 2015 | 29 June 2018 |
| 30 | Hum9 | −76.437, 56.537 | 5 | 07 September 2014 | 11 Mar 2016 |
| 31 | Station SILA-LEC Eloigne (LECESIL) | −74.511, 56.359 | 10 | 01 January 2015 | 13 August 2017 |
| 32 | Station SILA-LEC Proximite (LECPSIL) | −74.468, 56.339 | 5 | 19 August 2017 | 12 August 2019 |
| 10 | 01 January 2015 | 14 August 2017 | |||
| 33 | LacEauClairA (LECA) | −74.44, 56.351 | 5 | 01 January 2015 | 10 June 2015 |
| 34 | île tourbeuse (LECTOUR) | −74.491, 56.206 | 0 | 18 August 2017 | 15 August 2019 |
| 35 | Petite rivière de la baleine—Forêt (PBAFORE) | −76.161, 55.871 | 5 | 01 January 2015 | 01 September 2019 |
| 10 | 01 January 2015 | 01 September 2019 | |||
| 36 | Petite rivière de la baleine—Toundra (PBATOUN) | −76.161, 55.871 | 0 | 01 January 2015 | 01 September 2019 |
| 10 | 01 January 2015 | 01 September 2019 | |||
| 37 | Kuujjuarapik (KJRAPIK) | −77.746, 55.276 | 2 | 01 January 2015 | 31 May 2019 |
| 38 | Île Centrale (CENTRAL) | −77.13, 53.681 | 20 | 28 March 2015 | 29 August 2016 |
| 39 | Aupaluk HT-298 (AUPA298) | −69.583, 59.283 | >20 cm | - | - |
References
- Burgess, M.M.; Smith, S.L.; Brown, J.; Romanovsky, V.; Hinkel, K. Global Terrestrial Network for Permafrost (GTNet-P): Permafrost Monitoring Contributing to Global Climate Observations: Current Research Report 2000-E14; Geological Survey of Canada: Ottawa, ON, Canada, 2000. Available online: http://dsp-psd.pwgsc.gc.ca (accessed on 10 December 2021).
- Brown, J.; Hinkel, K.M.; Nelson, F.E. The circumpolar active layer monitoring (CALM) program: Research designs and initial results. Polar Geogr. 2000, 24, 166–258. [Google Scholar] [CrossRef]
- Nelson, F.E.; Shiklomanov, N.I.; Hinkel, K.M.; Christiansen, H.H. The circumpolar active layer monitoring (CALM) workshop and the CALM II program. Polar Geogr. 2004, 28, 253–266. [Google Scholar] [CrossRef]
- Ding, Y.; Ye, B.; Liu, S. Large-scale hydrological monitoring of frozen soil on the Qinghai-Tibet Plateau. Chin. Sci. Bull. 2000, 45, 208–214. [Google Scholar] [CrossRef]
- Wang, L.; Derksen, C.; Brown, R. Recent changes in pan-Arctic melt onset from satellite passive microwave measurements. Geophys. Res. Lett. 2013, 40, 522–528. [Google Scholar] [CrossRef]
- Mortin, J.; Schrøder, T.; Walløe Hansen, A.; Holt, B.; McDonald, K.C. Mapping of seasonal freeze-thaw transitions across the pan-Arctic land and sea ice domains with satellite radar. J. Geophys. Res. 2012, 117, C08004. [Google Scholar] [CrossRef] [Green Version]
- Bartsch, A.; Kidd, R.; Wagner, W.; Bartalis, Z. Temporal and spatial variability of the beginning and end of daily spring freeze/thaw cycles derived from scatterometer data. Remote Sens. Environ. 2007, 106, 360–374. [Google Scholar] [CrossRef]
- Bateni, S.M.; Huang, C.; Margulis, S.; Podest, E.; McDonald, K. Feasibility of characterizing snowpack and the freeze–thaw state of underlying soil using multifrequency active/passive microwave data. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4085–4102. [Google Scholar] [CrossRef]
- Jin, R.; Zhang, T.J.; Li, X.; Yang, X.G.; Ran, Y.H. Mapping surface soil freeze-thaw cycles in China based on SMMR and SSM/I brightness temperatures from 1978 to 2008. Arct. Antarct. Alp. Res. 2015, 47, 213–229. [Google Scholar] [CrossRef] [Green Version]
- Judge, J.; Galantowicz, J.F.; England, A.W.; Dahl, P. Freeze/thaw classification for prairie soils using SSM/I radiobrightnesses. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Singapore, 3–8 August 1997; pp. 827–832. [Google Scholar] [CrossRef]
- Zhang, T.J.; Armstrong, R.L. Soil freeze/thaw cycles over snow-free land detected by passive microwave remote sensing. Geophys. Res. Lett. 2001, 28, 763–766. [Google Scholar] [CrossRef]
- Zuerndorfer, B.; England, A.W. Radiobrightness decision criteria for freeze/thaw boundaries. IEEE Trans. Geosci. Remote Sens. 1992, 30, 89–102. [Google Scholar] [CrossRef]
- Zuerndorfer, B.W.; England, A.W.; Dobson, M.C.; Ulaby, F.T. Mapping freeze/thaw boundaries with SMMR data. Agric. For. Meteorol. 1990, 52, 199–225. [Google Scholar] [CrossRef] [Green Version]
- Jin, R.; Li, X.; Che, T. A decision tree algorithm for surface soil freeze/thaw classification over China using SSM/I brightness temperature. Remote Sens. Environ. 2009, 113, 2651–2660. [Google Scholar] [CrossRef]
- Han, M.L.; Yang, K.; Qin, J.; Jin, R.; Ma, Y.M.; Wen, J.; Chen, Y.Y.; Zhao, L.; Lazhu Tang, W.J. An algorithm based on the standard deviation of passive microwave brightness temperatures for monitoring soil surface freeze/thaw state on the Tibetan Plateau. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2775–2783. [Google Scholar] [CrossRef]
- Derksen, C.; Xu, X.L.; Dunbar, R.S.; Colliander, A.; Kim, Y.; Kimball, J.S.; Black, T.A.; Euskirchen, E.; Langlois, A.; Loranty, M.M. Retrieving landscape freeze/thaw state from Soil Moisture Active Passive (SMAP) radar and radiometer measurements. Remote Sens. Environ. 2017, 194, 48–62. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Mcdonald, K.C.; Glassy, J. Developing a global data record of daily landscape freeze/thaw status using satellite passive microwave remote sensing. IEEE Trans. Geosci. Remote Sens. 2011, 49, 949–960. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Aalto, T.; Tsuruta, A.; Kangasaho, V.; Ikonen, J.; Cohen, J.; Kontu, A.; Vehvildäinen, J.; Pulliainen, J. Smos retrievals of soil freezing and thawing and its applications. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 1463–1465. [Google Scholar] [CrossRef]
- Roy, A.; Royer, A.; Derksen, C.; Brucker, L.; Langlois, A.; Mialon, A.; Kerr, Y.H. Evaluation of spaceborne L-band radiometer measurements for terrestrial freeze/ thaw retrievals in Canada. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4442–4459. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Berg, A.A.; Lemmetyinen, J.; Arnold, L. Response of L-band brightness temperatures to freeze/thaw and snow dynamics in a prairie environment from ground-based radiometer measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Glassy, J.; Du, J.Y. An extended global earth system data record on daily landscape freeze-thaw status determined from satellite passive microwave remote sensing. Earth Syst. Sci. Data 2017, 9, 133–147. [Google Scholar] [CrossRef] [Green Version]
- Kou, X.K.; Jiang, L.M.; Yan, S.; Wang, J.; Gao, L.Y. Research on the improvement of passive microwave freezing and thawing discriminant algorithms for complicated surface conditions. In Proceedings of the IEEE International Symposium on Geoscience and Remote Sensing, Valencia, Spain, 22–27 July 2018; pp. 7161–7164. [Google Scholar] [CrossRef]
- Wang, P.K.; Zhao, T.J.; Shi, J.C.; Hu, T.X.; Roy, A.; Qiu, Y.B.; Lu, H. Parameterization of the freeze/thaw discriminant function algorithm using dense insitu observation network data. Int. J. Digit. Earth 2018, 12, 980–994. [Google Scholar] [CrossRef]
- Zhao, T.J.; Zhang, L.X.; Jiang, L.M.; Zhao, S.J.; Chai, L.N.; Jin, R. A new soil freeze/thaw discriminant algorithm using AMSR-E passive microwave imagery. Hydrol. Process. 2011, 25, 1704–1716. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Schwank, M.; Kontu, A.; Ménard, C.B.; Mätzler, C.; Drusch, M.; Wiesmann, A.; Ikonen, J.; Pulliainen, J. Detection of soil freezing from L-band passive microwave observations. Remote Sens. Environ. 2014, 147, 206–218. [Google Scholar] [CrossRef]
- Rautiainen, K.; Parkkinen, T.; Lemmetyinen, J.; Schwank, M.; Wiesmann, A.; Ikonen, J.; Derksen, C.; Davydov, S.; Davydova, A.; Boike, J. SMOS prototype algorithm for detecting autumn soil freezing. Remote Sens. Environ. 2016, 180, 346–360. [Google Scholar] [CrossRef]
- Kim, Y.; Kimball, J.S.; Xu, X.; Dunbar, R.S.; Colliander, A.; Derksen, C. Global assessment of the SMAP freeze/thaw data record and regional applications for detecting spring onset and frost events. Remote Sens. 2019, 11, 1317. [Google Scholar] [CrossRef] [Green Version]
- Colliander, A.; Mcdonald, K.; Zimmermann, R.; Schroeder, R.; Kimball, J.S.; Njoku, E.G. Application of QuikSCAT backscatter to SMAP validation planning: Freeze/thaw state over ALECTRA sites in Alaska from 2000 to 2007. IEEE Trans. Geosci. Remote Sens. 2012, 50, 461–468. [Google Scholar] [CrossRef]
- Davitt, A.; Schumann, G.; Forgotson, C.; McDonald, K.C. The utility of SMAP soil moisture and freeze-thaw datasets as precursors to spring-melt flood conditions: A case study in the Red River of the North Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2848–2861. [Google Scholar] [CrossRef]
- Lyu, H.B.; McColl, K.A.; Li, X.L.; Derksen, C.; Berg, A.; Black, T.A.; Euskirchen, E.; Loranty, M.; Pulliainen, J.; Rautiainen, K.; et al. Validation of the SMAP freeze/thaw product using categorical triple collocation. Remote Sens. Environ. 2018, 205, 329–337. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Derksen, C.; Rowlandson, T.; Sonnentag, O. Spatial variability of L-band brightness temperature during freeze/thaw events over a prairie environment. Remote Sens. 2017, 9, 894. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Jiang, L.; Cui, H.; Wang, G.; Yang, J.; Liu, X.; Su, X. Evaluation and analysis of SMAP, AMSR2 and MEaSUREs freeze/thaw products in China. Remote Sens. Environ. 2020, 242, 111734. [Google Scholar] [CrossRef]
- Kativik Regional Government (KRG). Parc national des Monts-Pyramides Project. statues report. In Productive Safety Management; Kativik Regional Government: Kativik, QC, Canada, 2011. [Google Scholar]
- Allard, M.; Fortier, R.; Sarrazin, D.; Calmels, F.; Fortier, D.; Chaumont, D.; Savard, J.P.; Tarussov, A. L’impact du Rechauffement Climatique Sur Les Aeroports du Nunavik: Caracteristiques du Pergelisol et Caracterisation des Processus de Degradation Des Pistes; Ouranos: Quebec City, QC, Canada, 2007. [Google Scholar]
- Romanovsky, V.E.; Smith, S.L.; Christiansen, H.H. Permafrost thermal state in the polar Northern Hemisphere during the international polar year 2007–2009: A synthesis. Permafr. Periglac. Processes 2010, 21, 106–116. [Google Scholar] [CrossRef] [Green Version]
- Allard, M.; Lemay, M.; Barrette, C.; L’Hérault, E.; Sarrazin, D.; Bell, T.; Doré, G. Permafrost and climate change in Nunavik and Nunatsiavut: Importance for municipal and transportation infrastructures. In Nunavik and Nunatsiavut: From Science to Policy. An Integrated Regional Impact Study (IRIS) of Climate Change and Modernization; ArcticNet Inc.: Quebec City, QC, Canada, 2012; pp. 171–197. [Google Scholar]
- Obu, J.; Westermann, S.; Bartsch, A.; Berdnikov, N.; Christiansen, H.H.; Dashtseren, A.; Delaloye, R.; Elberling, B.; Etzelmüller, B.; Kholodov, A.; et al. Northern Hemisphere permafrost map based on TTOP modelling for 2000–2016 at 1 km2 scale. Earth-Sci. Rev. 2019, 193, 299–316. [Google Scholar] [CrossRef]
- Beck, I.; Ludwig, R.; Bernier, M.; Lévesque, E.; Boike, J. Assessing permafrost degradation and land cover changes (1986–2009) using remote sensing data over Umiujaq, sub-arctic Québec. Permafr. Periglac. Processes 2015, 26, 129–141. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Marzahn, P.; Bernier, M.; Ludwig, R. Mapping permafrost landscape features using object-based image classification of multi-temporal SAR images. ISPRS J. Photogramm. Remote Sens. 2008, 141, 10–29. [Google Scholar] [CrossRef]
- Wang, L.; Marzahn, P.; Bernier, M.; Ludwig, R. Sentinel-1 InSAR measurements of deformation over discontinuous permafrost terrain, Northern Quebec, Canada. Remote Sens. Environ. 2020, 248, 111965. [Google Scholar] [CrossRef]
- Pelletier, M.; Allard, M.; Levesque, E. Ecosystem changes across a gradient of permafrost degradation in subarctic Québec (Tasiapik Valley, Nunavik, Canada). Arct. Sci. 2018, 5, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Ropars, P.; Lévesque, E.; Boudreau, S. How do climate and topography influence the greening of the forest-tundra ecotone in northern Québec? A dendrochronological analysis of Betula glandulosa. J. Ecol. 2015, 103, 679–690. [Google Scholar] [CrossRef]
- Calmels, F.; Allard, M.; Delisle, G. Development and decay of a lithalsa in Northern Quebec: A geomorphological history. Geomorphology 2008, 97, 287–299. [Google Scholar] [CrossRef]
- Allard, M.; Seguin, M.K. The Holocene evolution of permafrost near the tree line, on the eastern coast of Hudson Bay (northern Quebec). Can. J. Earth Sci. 1987, 24, 2206–2222. [Google Scholar] [CrossRef]
- Hachem, S.; Allard, M.; Duguay, C. Using the MODIS land surface temperature product for mapping permafrost: An application to Northern Quebec and Labrador, Canada. Permafr. Periglac. Processes 2009, 20, 407–416. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Google Earth Engine applications since inception: Usage, trends, and potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef] [Green Version]
- Mutanga, O.; Kumar, L. Google earth engine applications. Remote Sens. 2019, 11, 591. [Google Scholar] [CrossRef] [Green Version]











| Gamma3-Scale3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Without < −30 | With < −30 | ||||||||
| Station-Depth | Amount < −30 | VV | VH | Diff. VV-VH | VH | Diff. VHwo-VHw | |||
| Threshold | Accuracy | Threshold | Accuracy | Threshold | Accuracy | ||||
| 5–5 | 11 | 0.66 | 0.71 | 0.41 | 0.57 | 0.14 | 0.74 | 0.58 | −0.01 |
| 6–0 | 5 | 0.62 | 0.76 | 0.64 | 0.84 | −0.08 | 0.72 | 0.84 | 0.00 |
| 6–5 | 5 | 0.62 | 0.76 | 0.58 | 0.83 | −0.07 | 0.72 | 0.84 | −0.01 |
| 6–10 | 5 | 0.62 | 0.76 | 0.58 | 0.83 | −0.07 | 0.72 | 0.84 | −0.01 |
| 20–10 | 12 | 0.63 | 0.79 | 0.57 | 0.79 | 0.00 | 0.82 | 0.78 | 0.01 |
| 34–0 | 25 | 0.6 | 0.80 | 0.4 | 0.77 | 0.03 | 0.79 | 0.81 | −0.05 |
| Landcover | Infra | N-Vege | N-Mix | N-nVege | ||||
|---|---|---|---|---|---|---|---|---|
| Filter | W 3*3 | W 5*5 | W 3*3 | W 5*5 | W 3*3 | W 5*5 | W 3*3 | W 5*5 |
| Mean | 0.46 | 0.47 | 0.63 | 0.63 | 0.59 | 0.59 | 0.53 | 0.61 |
| StD. | 0.06 | 0.08 | 0.11 | 0.11 | 0.10 | 0.08 | 0.03 | 0.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Wang, L.; Bernier, M.; Ludwig, R. Retrieving Freeze/Thaw Cycles Using Sentinel-1 Data in Eastern Nunavik (Québec, Canada). Remote Sens. 2022, 14, 802. https://doi.org/10.3390/rs14030802
Chen Y, Wang L, Bernier M, Ludwig R. Retrieving Freeze/Thaw Cycles Using Sentinel-1 Data in Eastern Nunavik (Québec, Canada). Remote Sensing. 2022; 14(3):802. https://doi.org/10.3390/rs14030802
Chicago/Turabian StyleChen, Yueli, Lingxiao Wang, Monique Bernier, and Ralf Ludwig. 2022. "Retrieving Freeze/Thaw Cycles Using Sentinel-1 Data in Eastern Nunavik (Québec, Canada)" Remote Sensing 14, no. 3: 802. https://doi.org/10.3390/rs14030802
APA StyleChen, Y., Wang, L., Bernier, M., & Ludwig, R. (2022). Retrieving Freeze/Thaw Cycles Using Sentinel-1 Data in Eastern Nunavik (Québec, Canada). Remote Sensing, 14(3), 802. https://doi.org/10.3390/rs14030802