Remote Sensing Monitoring of Winter Wheat Stripe Rust Based on mRMR-XGBoost Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. Field Experimental Data Acquirement
2.2. Extraction of Canopy SIF Parameters
2.3. Calculation of Hyperspectral Vegetation Indices
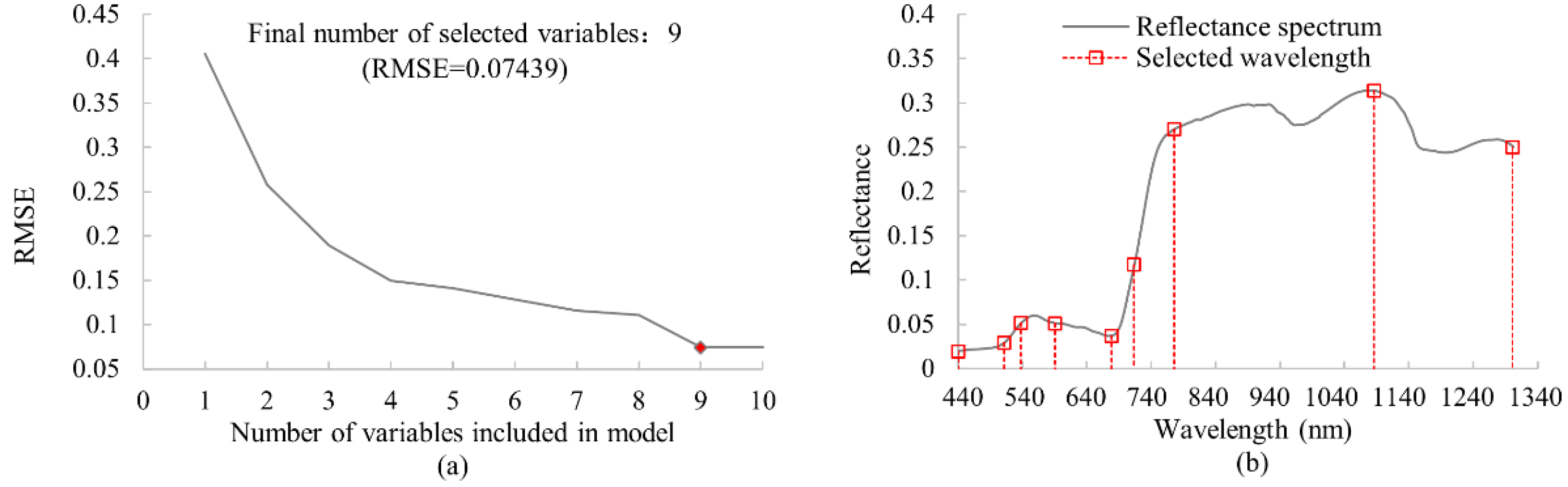
2.4. Extraction of Characteristic Band
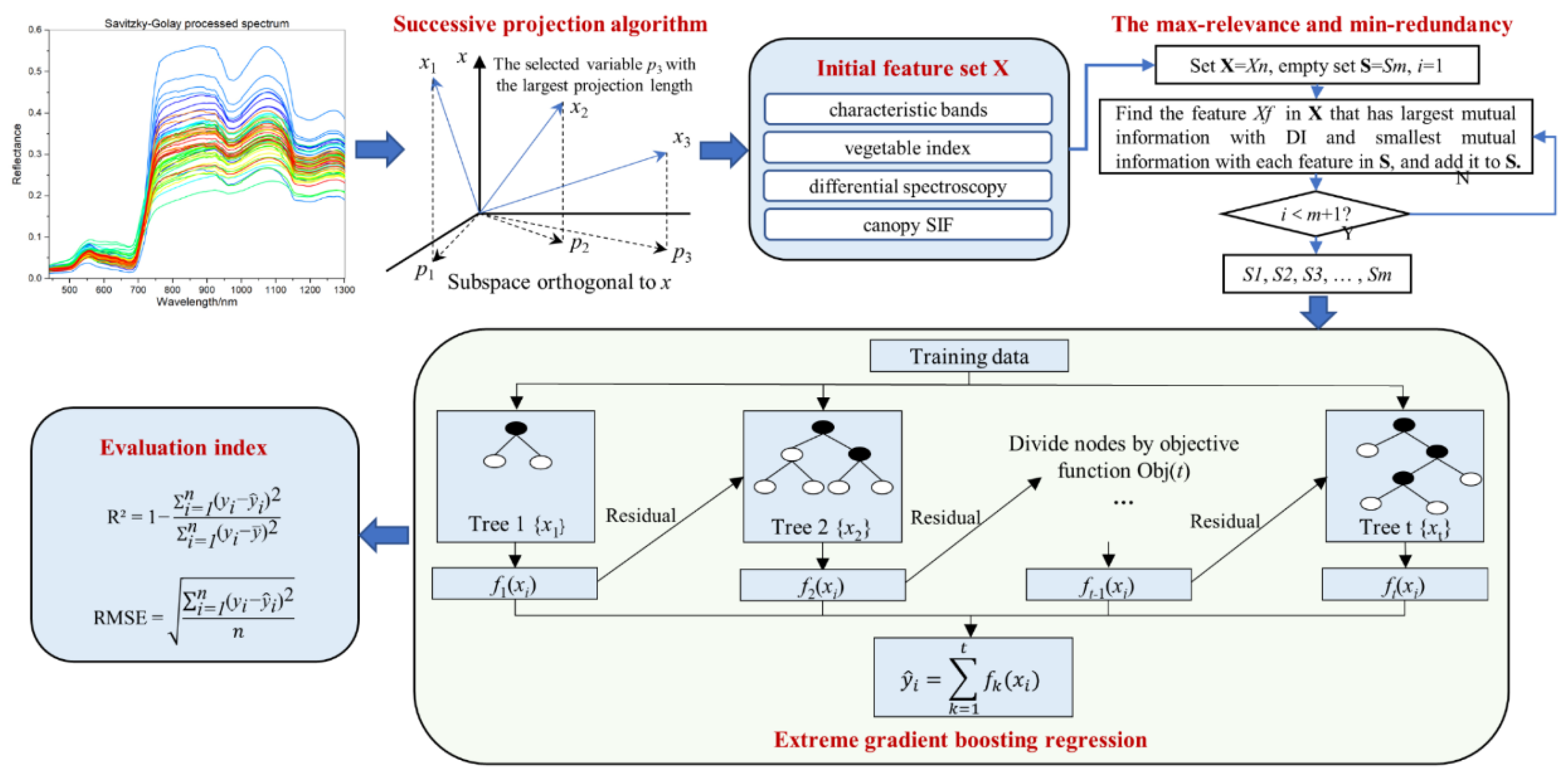
2.5. Methods
2.5.1. The Max-Relevance and Min-Redundancy Feature Selection
2.5.2. Extreme Gradient Boosting Regression
3. Results and Analysis
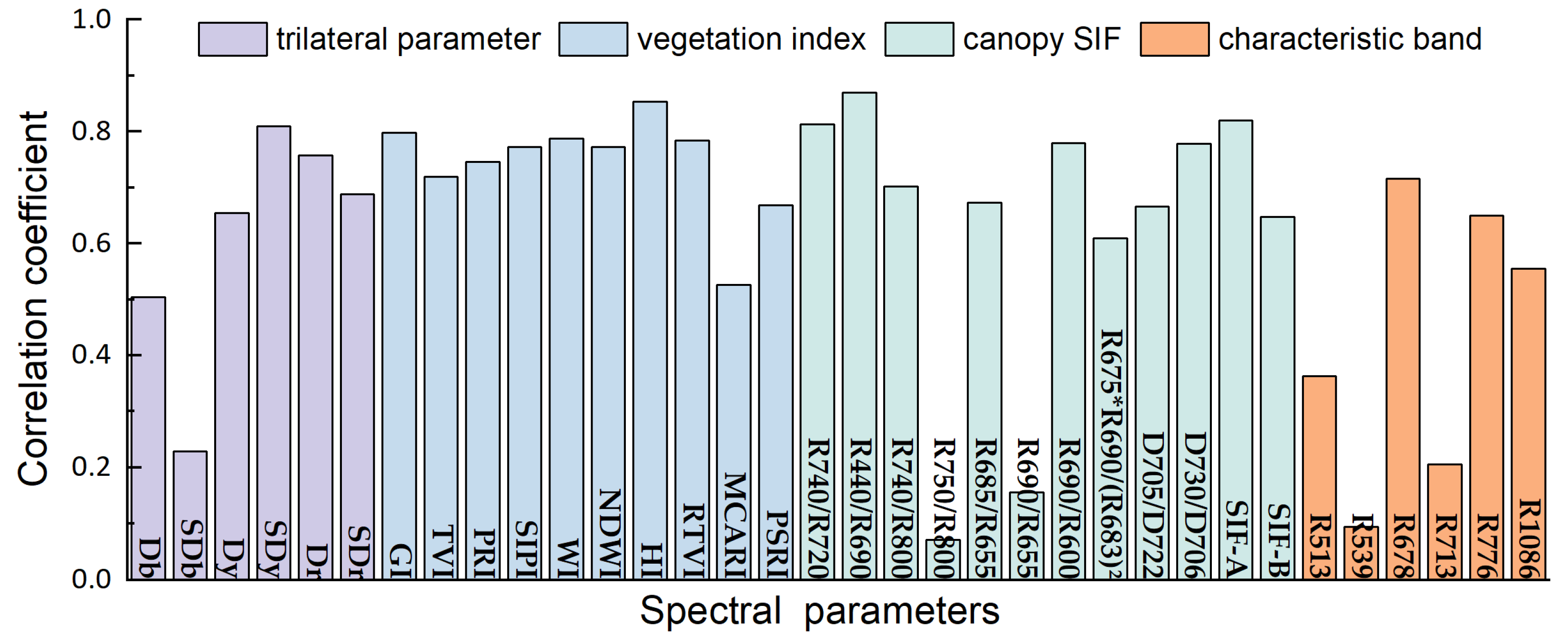
3.1. Features Selected by CC
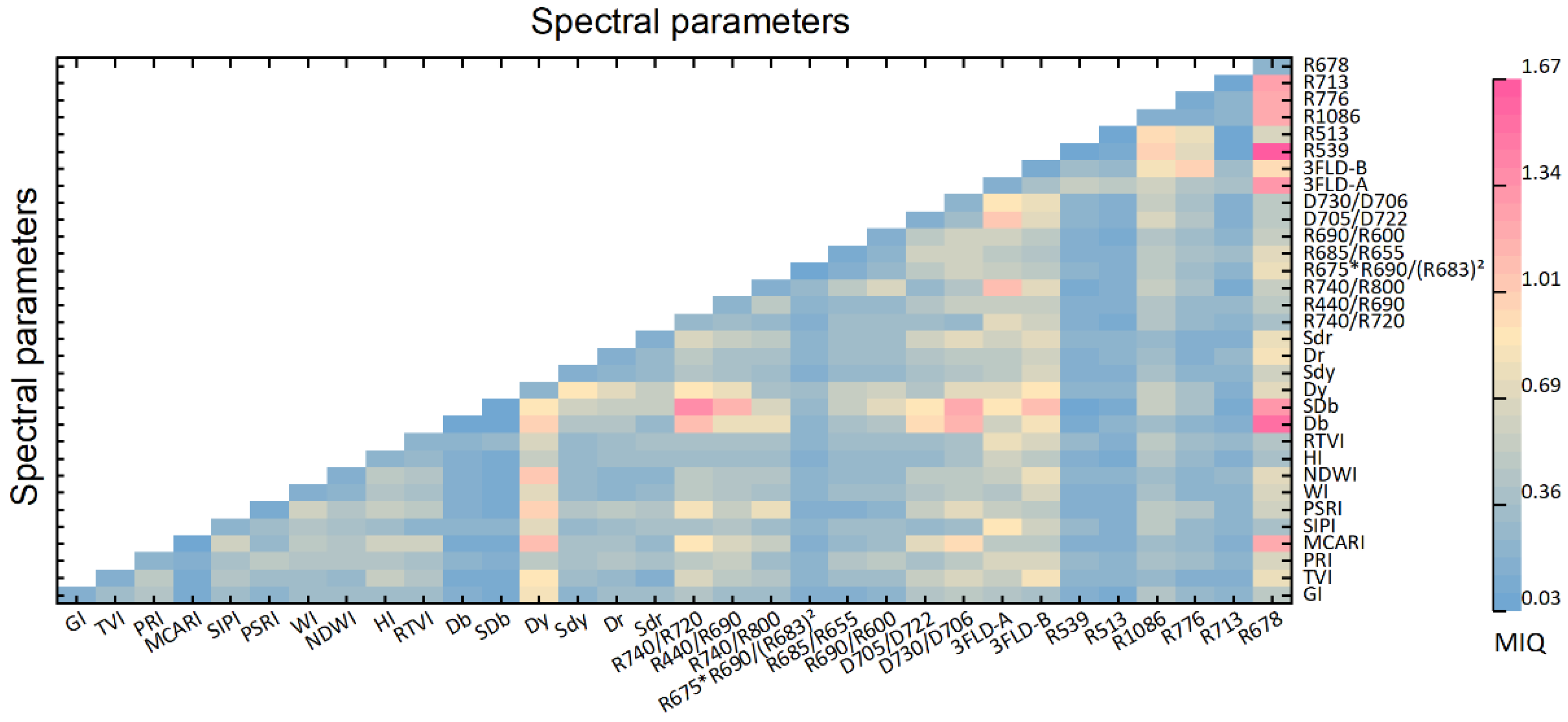
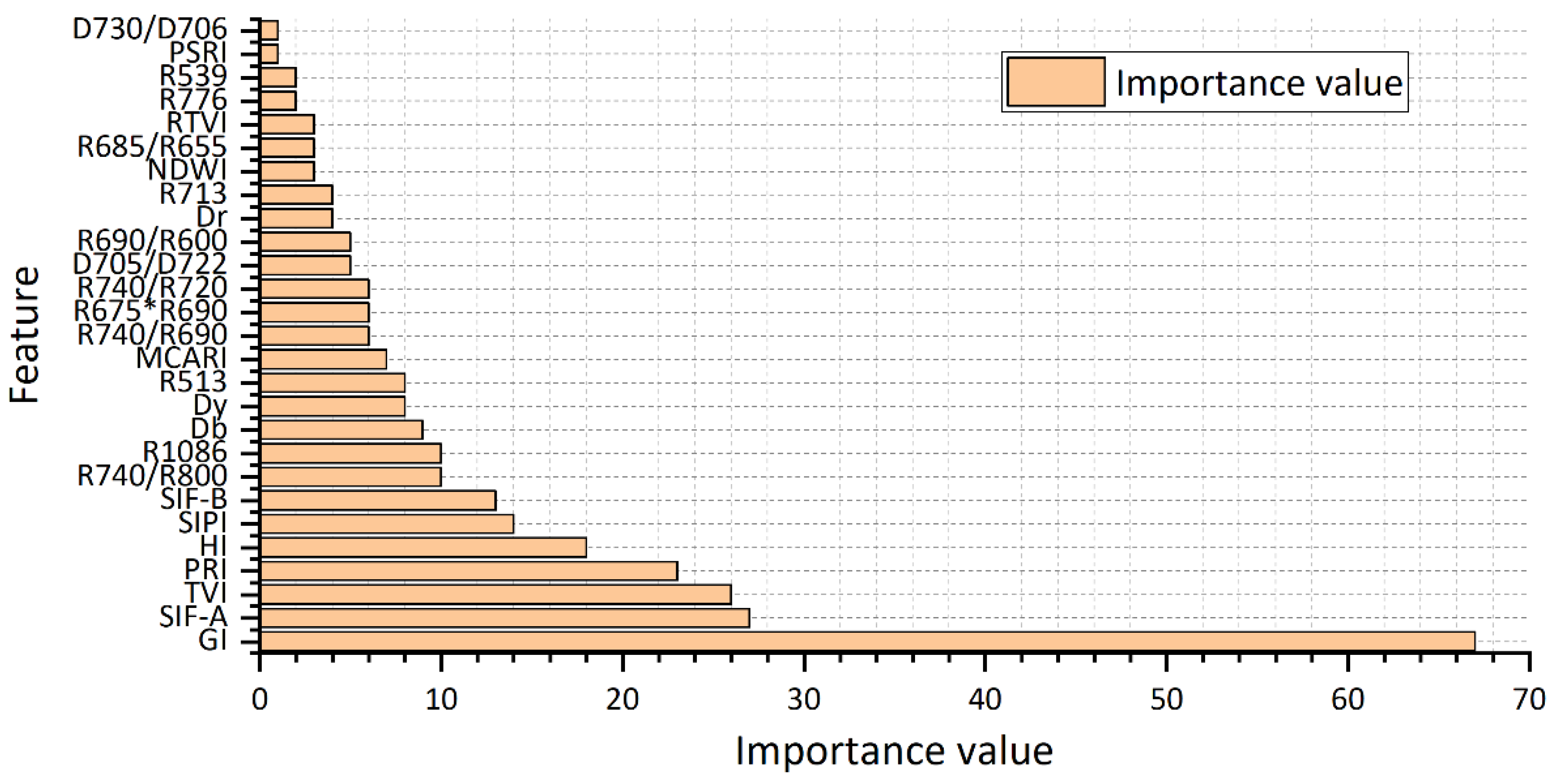
3.2. Features Selected by mRMR
3.3. Remote Sensing Monitoring Model of Wheat Stripe Rust
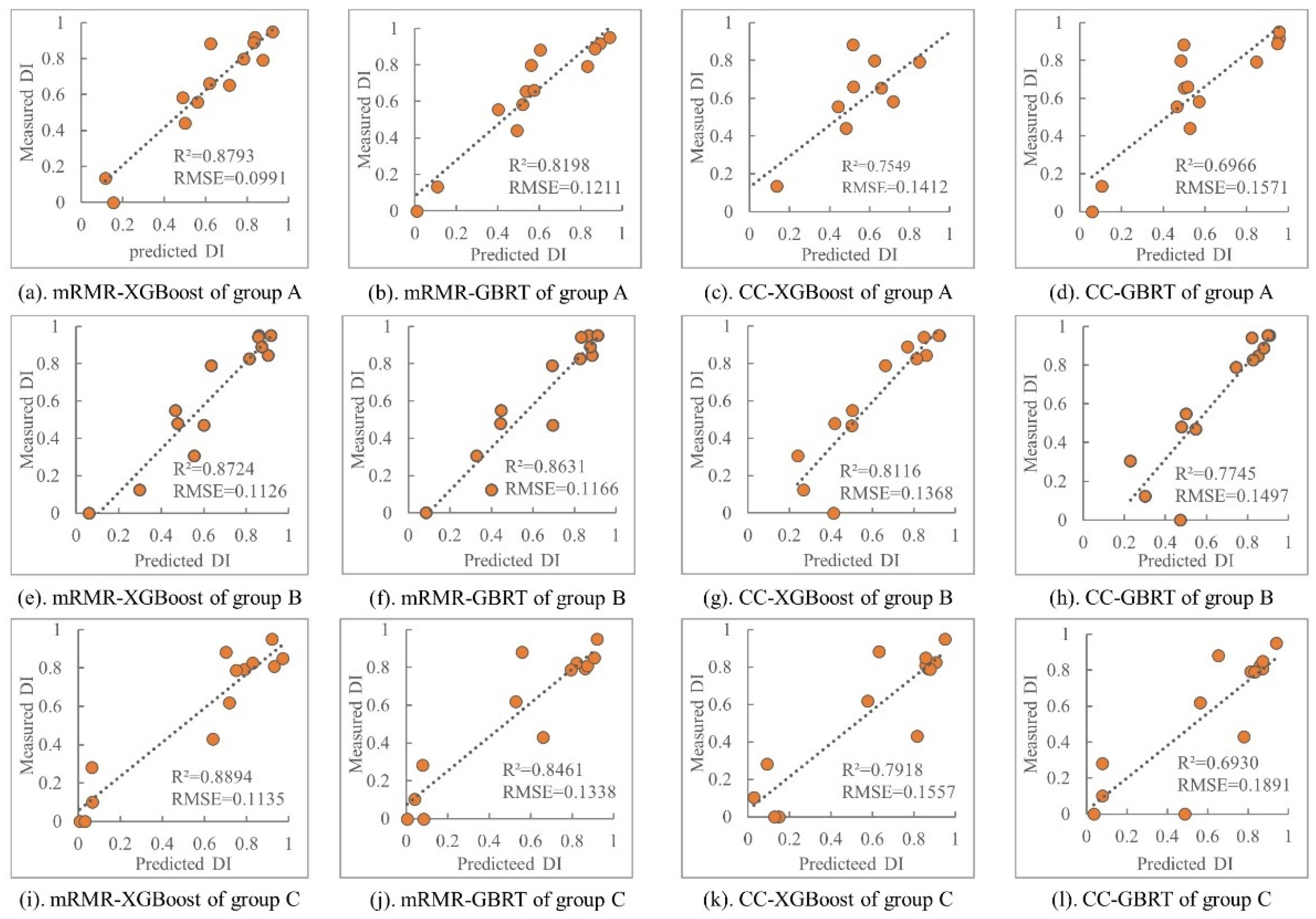
3.4. Model Evaluation
3.5. Field Survey Data Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lihua, C.; Shichang, X.; Ruiming, L.; Taiguo, L.; Wanquan, C. Early molecular diagnosis and detection of puccinia striiformis f. sp. tritici in China. Lett. Appl. Microbiol. 2008, 46, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, Y.; Pu, R.; Gonzalez-Moreno, P.; Yuan, L.; Wu, K.; Huang, W. Monitoring plant diseases and pests through remote sensing technology: A review. Comput. Electron. Agric. 2019, 165, 104943. [Google Scholar] [CrossRef]
- Mahlein, A.K.; Rumpf, T.; Welke, P.; Dehne, H.W.; Plümer, L.; Steiner, U.; Oerke, E.C. Development of spectral indices for detecting and identifying plant diseases. Remote Sens. Environ. 2013, 128, 21–30. [Google Scholar] [CrossRef]
- Graeff, S.; Link, J.; Claupein, W. Identification of powdery mildew (Erysiphe graminis sp. tritici) and take-all disease (Gaeumannomyces graminis sp. tritici) in wheat (Triticum aestivum L.) by means of leaf reflectance measurements. Cent. Eur. J. Biol. 2006, 1, 275–288. [Google Scholar] [CrossRef]
- Liu, Z.Y.; Wu, H.F.; Huang, J.F. Application of neural networks to discriminate fungal infection levels in rice panicles using hyperspectral reflectance and principal components analysis. Comput. Electron. Agric. 2010, 72, 99–106. [Google Scholar] [CrossRef]
- Li, X.; Yang, C.; Huang, W.; Tang, J.; Tian, Y.; Zhang, Q. Identification of cotton root rot by multifeature selection from Sentinel-2 images using Random Forest. Remote Sens. 2020, 21, 3054. [Google Scholar] [CrossRef]
- Huang, L.; Wu, Z.; Huang, W.; Ma, H.; Zhao, J. Identification of Fusarium Head Blight in winter wheat ears based on Fisher’s Linear Discriminant Analysis and a Support Vector Machine. Appl. Sci. 2019, 18, 3894. [Google Scholar] [CrossRef] [Green Version]
- Yuan, D.; Jiang, J.; Qi, X.; Xie, Z.; Zhang, G. Selecting key wavelengths of hyperspectral imagine for nondestructive classification of moldy peanuts using ensemble classifier. Infrared Phys. Technol. 2020, 111, 103518. [Google Scholar] [CrossRef]
- Davoud, A.; Mohammad, M.; Alfredo, H. Developing two spectral disease indices for detection of wheat leaf rust (pucciniatriticina). Remote Sens. 2014, 6, 4723–4740. [Google Scholar]
- Poblete, T.; Navas-Cortes, J.A.; Camino, C.; Calderon, R.; Hornero, A.; Gonzalez-Dugo, V.; Landa, B.B.; Zarco-Tejada, P.J. Discriminating xylella fastidiosa from verticillium dahliae infections in olive trees using thermal- and hyperspectral-based plant traits. ISPRS J. Photogramm. 2021, 179, 133–144. [Google Scholar] [CrossRef]
- Sankaran, S.; Mishra, A.; Ehsani, R.; Davis, C. A review of advanced techniques for detecting plant diseases. Comput. Electron. Agric. 2010, 72, 1–13. [Google Scholar] [CrossRef]
- Jing, X.; Zhang, T.; Bai, Z.; Huang, W. Feature Selection and Model Construction of Wheat Stripe Rust Based on GA and SVR Algorithm. Trans. Chin. Soc. Agric. Mach. 2020, 51, 253–263. [Google Scholar]
- Samat, A.; Li, E.; Wang, W.; Liu, S.; Lin, C.; Abuduwaili, J. Meta-XGBoost for hyperspectral image classification using extended MSER-guided morphological profiles. Remote Sens. 2020, 12, 1973. [Google Scholar] [CrossRef]
- Wenjiang, H.; David, W.L.; Zheng, N.; Yongjiang, Z.; Liangyun, L.; Jihua, W. Identification of yellow rust in wheat using in-situ spectral reflectance measurements and airborne hyperspectral imaging. Precis. Agric. 2007, 8, 187–197. [Google Scholar]
- Plascyk, J.A.; Gabriel, F.C. Fraunhofer line discriminator MK II—airborne instrument for precise and standardized ecological luminescence measurement. IEEE Trans. Instrum. Meas. 1975, 24, 306–313. [Google Scholar] [CrossRef]
- Maier, S.W.; Günther, K.P.; Stellmes, M. Sun-induced fluorescence: A new tool for precision farming. In Digital Imaging and Spectral Techniques: Applications to Precision Agriculture and Crop Physiology; Mcdonald, M., Schepers, J., Tartly, L., Eds.; American Society of Agronomy Special Publication: Madison, WI, USA, 2003; pp. 209–222. [Google Scholar]
- Damm, A.; Erler, A.; Hillen, W.; Meroni, M.; Schaepman, M.E.; Verhoef, W.; Rascher, U. Modeling the impact of spectral sensor configurations on the FLD retrieval accuracy of sun-induced chlorophyll fluorescence. Remote Sen. Environ. 2011, 115, 1882–1892. [Google Scholar] [CrossRef]
- Liu, L.; Cheng, Z. Detection of vegetation light-use efficiency based on solar-induced chlorophyll fluorescence separated from canopy radiance spectrum. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 306–312. [Google Scholar] [CrossRef]
- Dobrowski, S.Z.; Pushnik, J.C.; Zarco-Tejada, P.J.; Ustin, S.L. Simple reflectance indices track heat and water stress-induced changes in steady-state chlorophyll fluorescence at the canopy scale. Remote Sens. Environ. 2005, 97, 403–414. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Steady-state chlorophyll a fluorescence detection from canopy derivative reflectance and double-peak red-edge effects. Remote Sens. Environ. 2003, 84, 283–294. [Google Scholar] [CrossRef]
- Zhang, J.; Yuan, L.; Wang, J.; Luo, J.; Du, S.; Huang, W. Research progress of crop diseases and pests monitoring based on remote sensing. Trans. Chin. Soc. Agric. Eng. 2012, 28, 1–11. [Google Scholar]
- Zarco-Tejada, P.J.; Berjón, A.; López-Lozano, R.; Miller, J.R.; Martín, P.; Cachorro, V.; González, M.R.; de Frutos, A. Assessing vineyard condition with hyperspectral indices: Leaf and canopy reflectance simulation in a row-structured discontinuous canopy. Remote Sens. Environ. 2005, 99, 271–287. [Google Scholar] [CrossRef]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Peñuelas, J.; Baret, F.; Filella, I. Semi-empirical indices to assess carotenoids/chlorophyll a ratio from leaf spectral reflectance. Photosynthetica 1995, 31, 221–230. [Google Scholar]
- Merzlyak, M.N.; Gitelson, A.A.; Chivkunova, O.B.; Rakitin, V.Y. Non-destructive optical detection of pigment changes during leaf senescence and fruit ripening. Physiol. Plant. 1999, 106, 135–141. [Google Scholar] [CrossRef] [Green Version]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; Brown de Colstoun, E.; McMurtrey, J.E., III. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Peñuelas, J.; Pinol, J.; Ogaya, R.; Filella, I. Estimation of plant water concentration by the reflectance water index wi (r900/r970). Int. J. Remote Sens. 1997, 18, 2869–2875. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Verstraete, M.M.; Pinty, B.; Myneni, R.B. Potential and limitations of information extraction on the terrestrial biosphere from satellite remote sensing. Remote Sens. Environ. 1996, 58, 201–214. [Google Scholar] [CrossRef]
- Smith, K.L.; Steven, M.D.; Colls, J.J. Use of hyperspectral derivative ratios in the red-edge region to identify plant stress responses to gas leaks. Remote Sens. Environ. 2004, 92, 207–217. [Google Scholar] [CrossRef]
- Jiang, J.B.; Chen, Y.H.; Huang, W.J. Using hyperspectral derivative indices to diagnose severity of winter wheat stripe rust. Opt. Tech. 2007, 4, 620–623. [Google Scholar]
- Wu, D.; Nie, P.; He, Y.; Bao, Y. Determination of calcium content in powdered milk using near and mid-infrared spectroscopy with variable selection and chemometrics. Food Bioprocess Technol. 2012, 5, 1402–1410. [Google Scholar] [CrossRef]
- Peng, H.C.; Long, F.H.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 31507–31518. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Bhagat, S.K.; Tiyasha, T.; Awadh, S.M.; Tung, T.M.; Jawad, A.H.; Yaseen, Z.M. Prediction of sediment heavy metal at the Australian Bays using newly developed hybrid artificial intelligence models. Environ. Pollut. 2021, 268, 115663. [Google Scholar] [CrossRef]
- Knyazikhin, Y.; Schull, M.A.; Stenberg, P.; Moettus, M.; Rautiainen, M.; Yang, Y.; Marshak, A.; Carmona, P.L.; Kaufmann, R.K.; Lewis, P. Hyperspectral remote sensing of foliar nitrogen content. Proc. Natl. Acad. Sci. USA 2012, 110, E185–E192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verrelst, J.; Rivera, J.P.; Van der Tol, C.; Magnani, F.; Mohammed, G.; Moreno, J. Global sensitivity analysis of the SCOPE model: What drives simulated canopy-leaving sun-induced fluorescence? Remote Sens. Environ. 2015, 166, 8–21. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Jiao, Q.; Peng, D. Assessing photosynthetic light-use efficiency using a solar-induced chlorophyll fluorescence and photochemical reflectance index. Int. J. Remote Sens. 2013, 34, 4264–4280. [Google Scholar] [CrossRef]
- Atta, B.M.; Saleem, M.; Ali, H.; Bilal, M.; Fayyaz, M. Application of fluorescence spectroscopy in wheat crop: Early disease detection and associated molecular changes. J. Fluoresc. 2020, 30, 801–810. [Google Scholar] [CrossRef]
- Jing, X.; Bai, Z.F.; Gao, Y.; Liu, L.Y. Wheat stripe rust monitoring by random forest algorithm combined with SIF and reflectance spectrum. Trans. Chin. Soc. Agric. Mach. 2019, 35, 154–161. [Google Scholar]

| Type | Definition | Type | Definition | Type | Definition |
|---|---|---|---|---|---|
| Frelative of O2-A band | SIF-A | Reflectance ratio index | R740/R720 | Reflectance ratio index | R685/R655 |
| Frelative of O2-B band | SIF-B | R440/R690 | R690/R655 | ||
| Reflectance first derivative index | D705/D722 | R740/R800 | R690/R600 | ||
| D730/D706 | R750/R800 | R675*R690/(R683)2 |
| Type | Index | Definition | Reference |
|---|---|---|---|
| Vegetation index | Greenness index (GI) | R554/R677 | [22] |
| Photochemical reflectance index (PRI) | (R570 − R531)/(R570 + R531) | [23] | |
| Structural independent pigment index (SIPI) | (R800 − R445)/(R800 + R680) | [24] | |
| Plant senescence reflectance index (PSRI) | (R678 − R550)/R750 | [25] | |
| Modified chlorophyll absorbtion reflectance index (MCARI) | [(R700 − R670) − 0.2*(R700 − R550)]*(R700/R670) | [26] | |
| Water index (WI) | R900/R970 | [27] | |
| Normalized difference water index (NDWI) | (R860 − R1240)/(R860 + R1240) | [28] | |
| Triangular vegetation index (TVI) | 0.5*[120*(R750 − R550) − 200*(R670 − R550)] | [29] | |
| Ration triangular vegetation index (RTVI) | [55*(R750 − R550) − 90(R680 − R550)]/[90(R750 + R550)] | [30] | |
| Healthy index (HI) | (R534 − R698)/(R534 + R698) − 0.5 R704 | [3] | |
| Trilateral Parameters | Db | The maximum value of the 1st order differential in 490–539 nm | [32] |
| SDb | The sum of 1st order differential in 490–539 nm | [32] | |
| Dy | The maximum value of the 1st order differential in 550–582 nm | [32] | |
| SDy | The sum of 1st order differential in 550–582 nm | [32] | |
| Dr | The maximum value of the 1st order differential in 670–737nm | [32] | |
| SDr | The sum of 1st order differential in 670–737 nm | [32] |
| Parameter Type | Parameter | Adjustment Range | Step | Optimal Value |
|---|---|---|---|---|
| learning_rate | [0, 1] | 0.01 | 0.21 | |
| Booster | max_depth | [3, 10] | 1 | 3 |
| parameters | min_split_weight | [1, 6] | 1 | 5 |
| subsample | [0, 1] | 0.1 | 0.5 | |
| reg_alpha | [0, 0.5] | 0.01 | 0.02 | |
| Learning task parameters | n_estimators | [0, 800] | 1 | 11 |
| Sample Group | mRMR-XGBoost | mRMR-GBRT | CC-XGBoost | CC-GBRT | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| A | 0.915 | 0.181 | 0.721 | 0.157 | 0.890 | 0.161 | 0.769 | 0.166 |
| B | 0.830 | 0.201 | 0.346 | 0.125 | 0.695 | 0.165 | 0.359 | 0.127 |
| C | 0.676 | 0.131 | 0.608 | 0.119 | 0.245 | 0.137 | 0.200 | 0.162 |
| Numbers | Feature Combination | R2 of XGBoost | R2 of GBRT |
|---|---|---|---|
| 1 | GI | 0.12 | 0.16 |
| 2 | GI, SIF-A | 0.17 | 0.28 |
| 3 | GI, SIF-A, TVI | 0.25 | 0.18 |
| 4 | GI, SIF-A, TVI, PRI | 0.23 | 0.27 |
| 5 | GI, SIF-A, TVI, PRI, HI | 0.23 | 0.29 |
| 6 | GI, SIF-A, TVI, PRI, HI, SIPI | 0.64 | 0.62 |
| 7 | GI, SIF-A, TVI, PRI, HI, SIPI, SIF-B | 0.78 | 0.74 |
| 8 | GI, SIF-A, TVI, PRI, HI, SIPI, SIF-B, R740/R800 | 0.83 | 0.87 |
| 9 | GI, SIF-A, TVI, PRI, HI, SIPI, SIF-B, R740/R800, R1086 | 0.83 | 0.84 |
| 10 | GI, SIF-A, TVI, PRI, HI, SIPI, SIF-B, R740/R800, R1086, Db | 0.84 | 0.88 |
| 11 | GI, SIF-A, TVI, PRI, HI, SIPI, SIF-B, R740/R800, R1086, Db, Dy | 0.81 | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, X.; Zou, Q.; Yan, J.; Dong, Y.; Li, B. Remote Sensing Monitoring of Winter Wheat Stripe Rust Based on mRMR-XGBoost Algorithm. Remote Sens. 2022, 14, 756. https://doi.org/10.3390/rs14030756
Jing X, Zou Q, Yan J, Dong Y, Li B. Remote Sensing Monitoring of Winter Wheat Stripe Rust Based on mRMR-XGBoost Algorithm. Remote Sensing. 2022; 14(3):756. https://doi.org/10.3390/rs14030756
Chicago/Turabian StyleJing, Xia, Qin Zou, Jumei Yan, Yingying Dong, and Bingyu Li. 2022. "Remote Sensing Monitoring of Winter Wheat Stripe Rust Based on mRMR-XGBoost Algorithm" Remote Sensing 14, no. 3: 756. https://doi.org/10.3390/rs14030756
APA StyleJing, X., Zou, Q., Yan, J., Dong, Y., & Li, B. (2022). Remote Sensing Monitoring of Winter Wheat Stripe Rust Based on mRMR-XGBoost Algorithm. Remote Sensing, 14(3), 756. https://doi.org/10.3390/rs14030756






