Figure 1.
(a) Raw GPR image, (b) sample GPR image with pixel-wise missing entries, (c) sample GPR image with column-wise missing entries.
Figure 1.
(a) Raw GPR image, (b) sample GPR image with pixel-wise missing entries, (c) sample GPR image with column-wise missing entries.
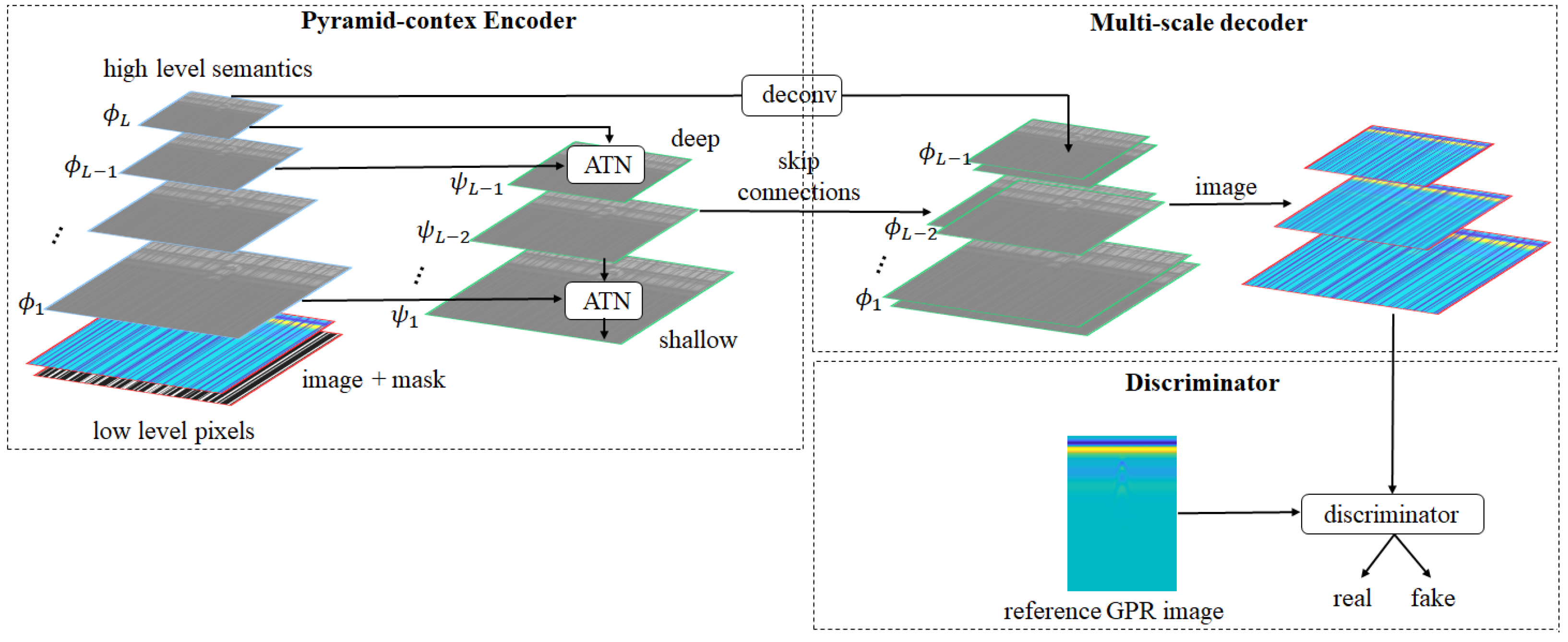
Figure 2.
Block diagram of the PEN-Net architecture.
Figure 2.
Block diagram of the PEN-Net architecture.
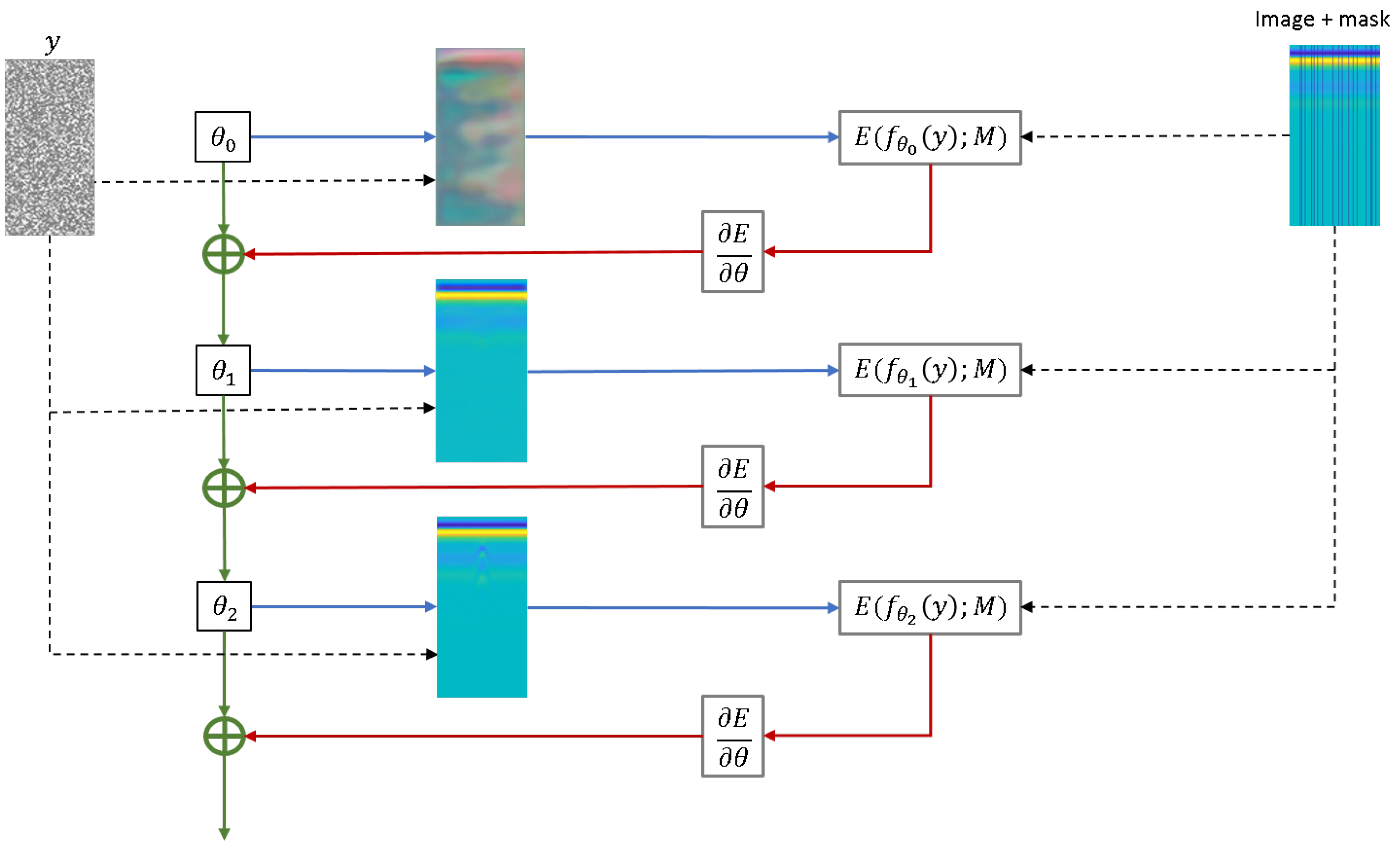
Figure 3.
Block diagram of DIP Model.
Figure 3.
Block diagram of DIP Model.
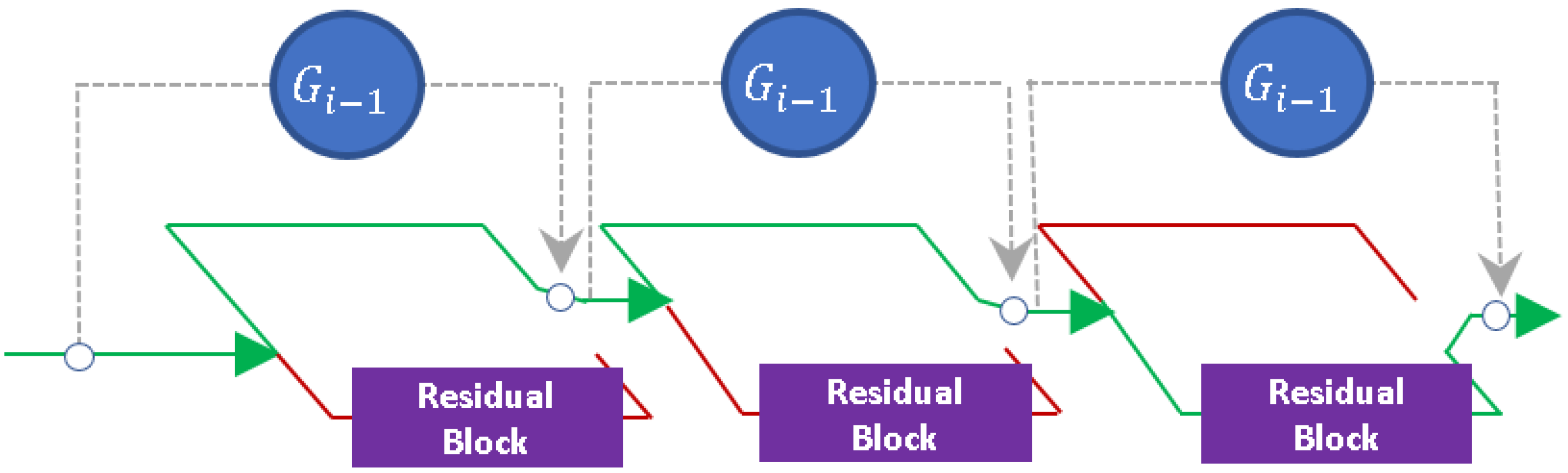
Figure 4.
SkipNet Architecture that is embedded into DIP model.
Figure 4.
SkipNet Architecture that is embedded into DIP model.
Figure 5.
Deep Image Prior Model Graph.
Figure 5.
Deep Image Prior Model Graph.
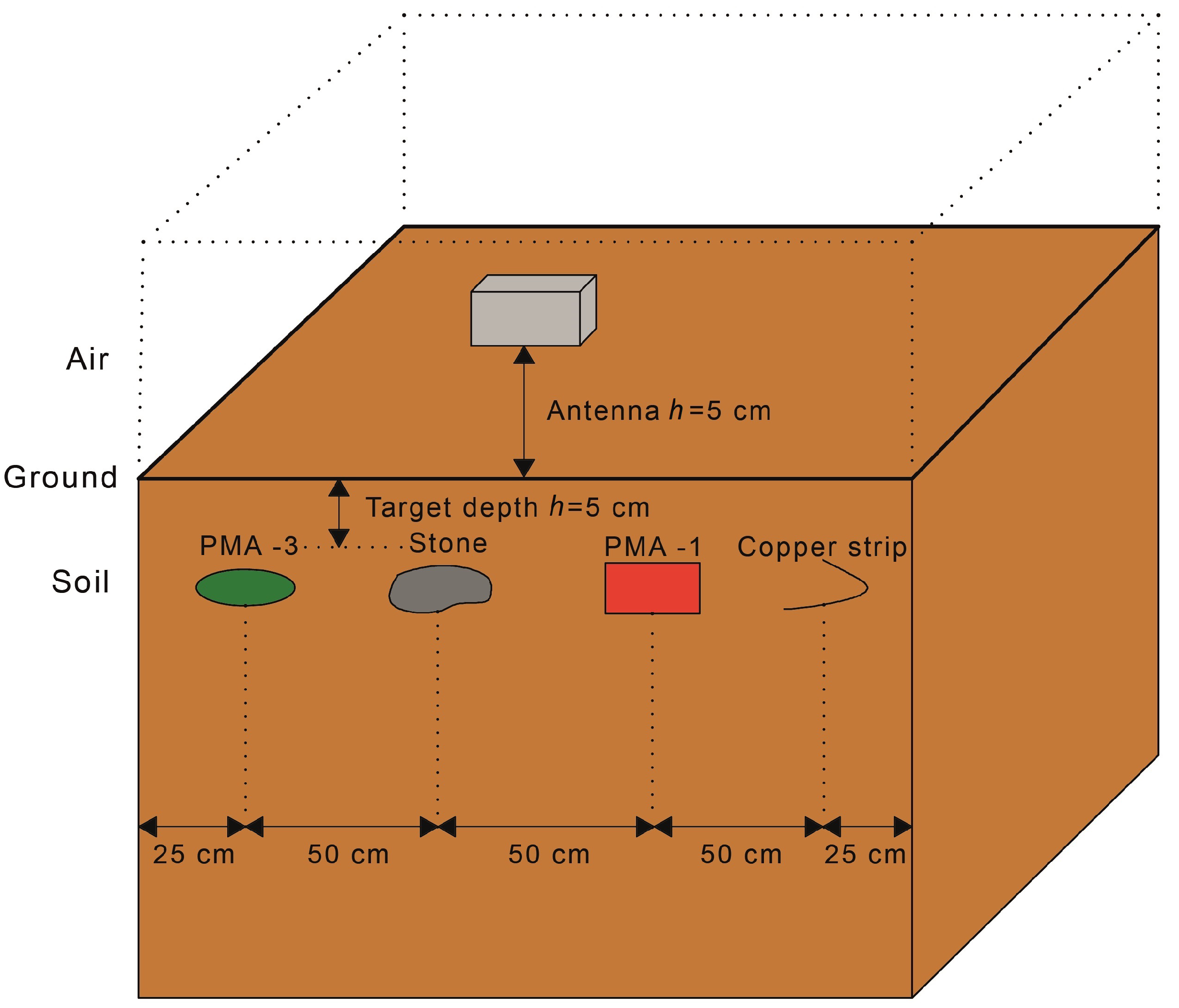
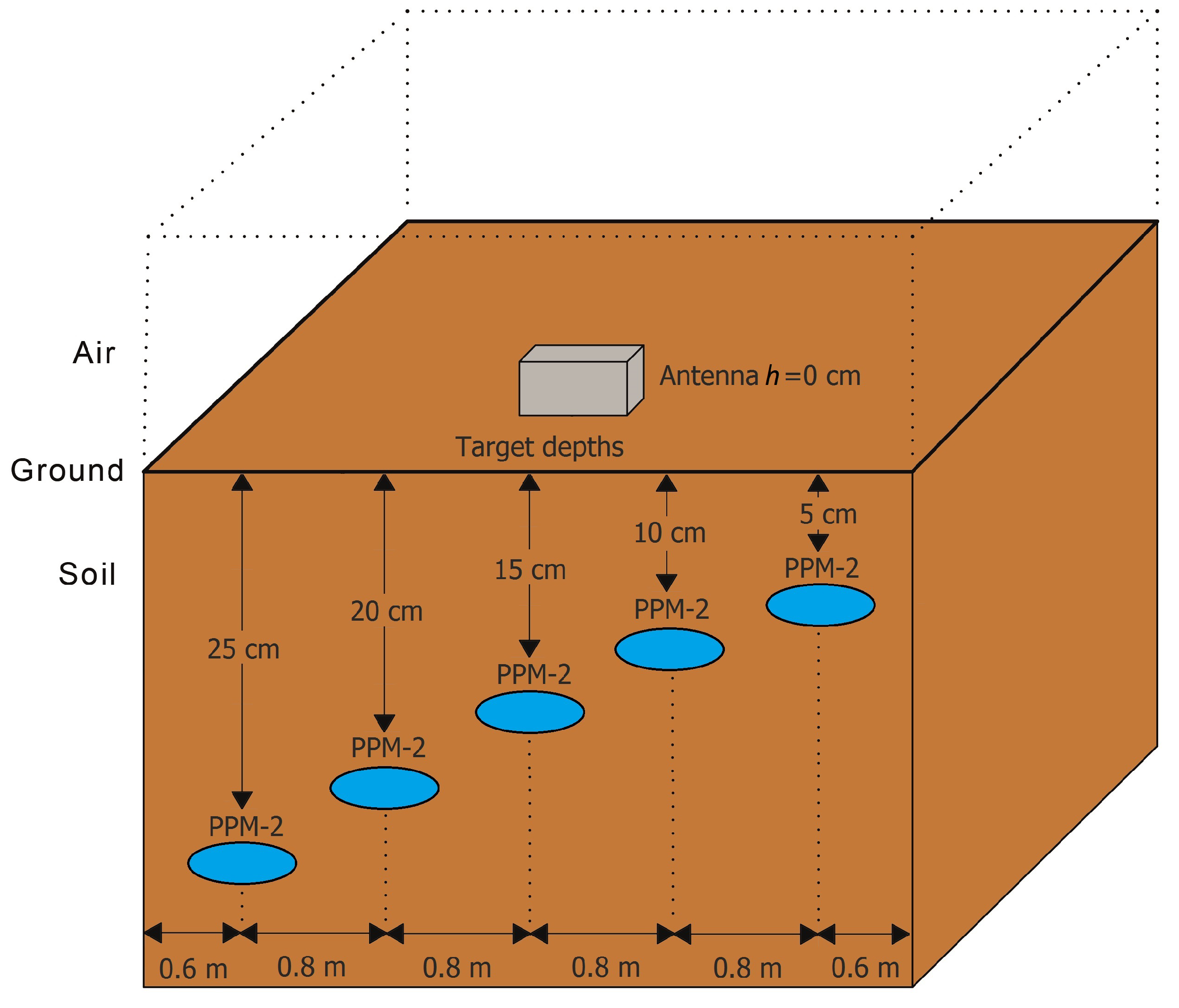
Figure 6.
Experimental setup of the simulated data.
Figure 6.
Experimental setup of the simulated data.
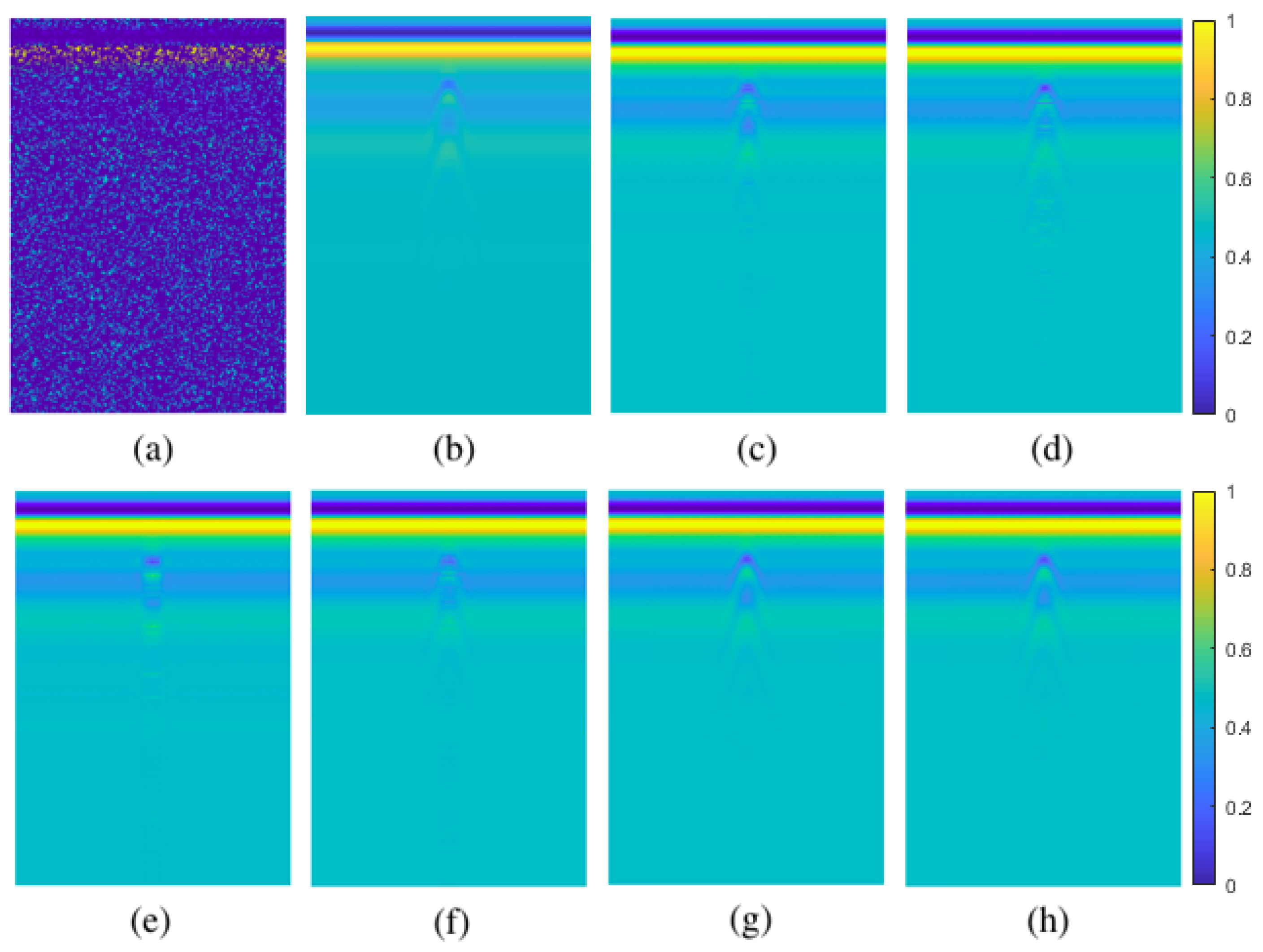
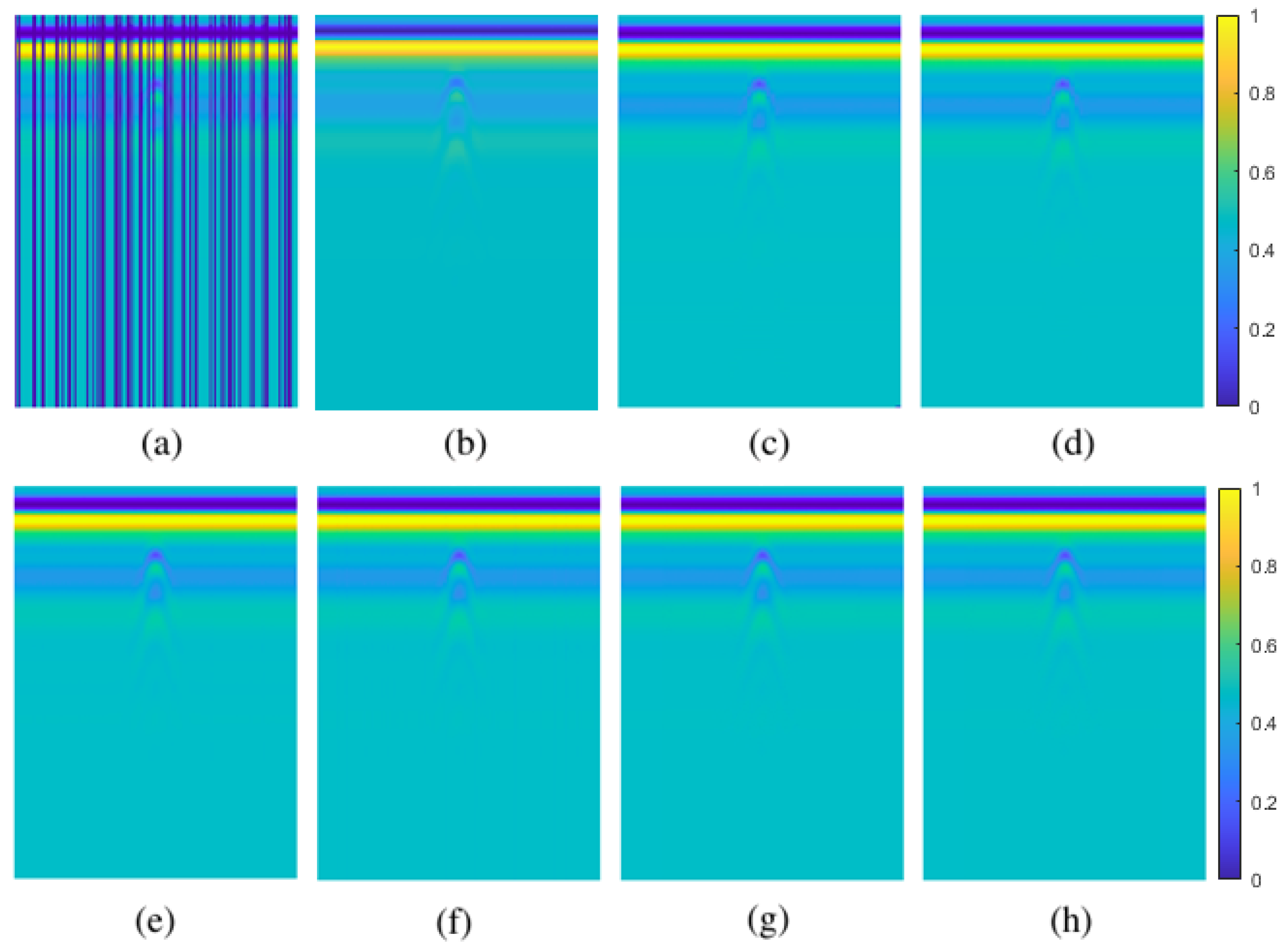
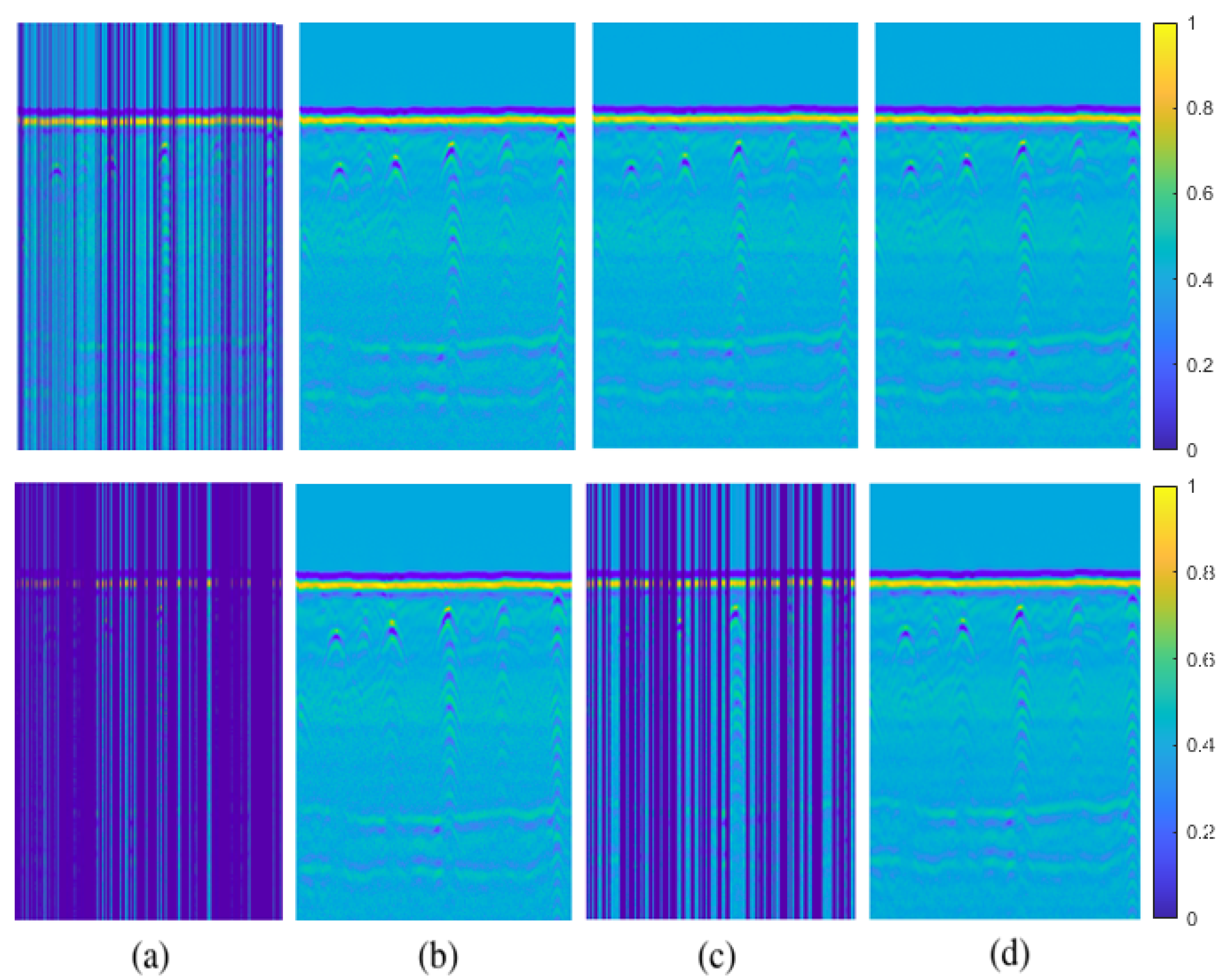
Figure 7.
30% pixel-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 7.
30% pixel-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
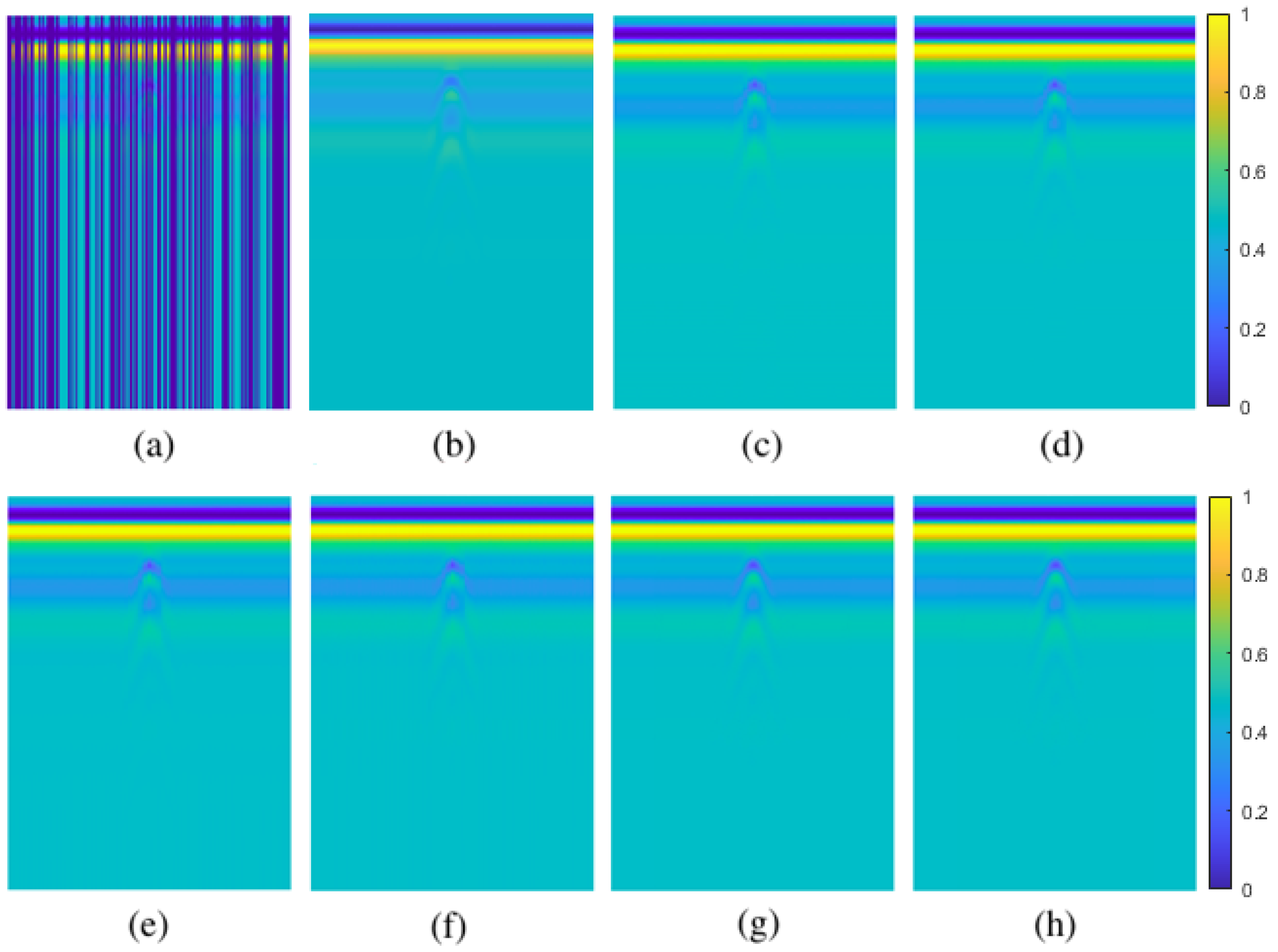
Figure 8.
50% pixel-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 8.
50% pixel-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
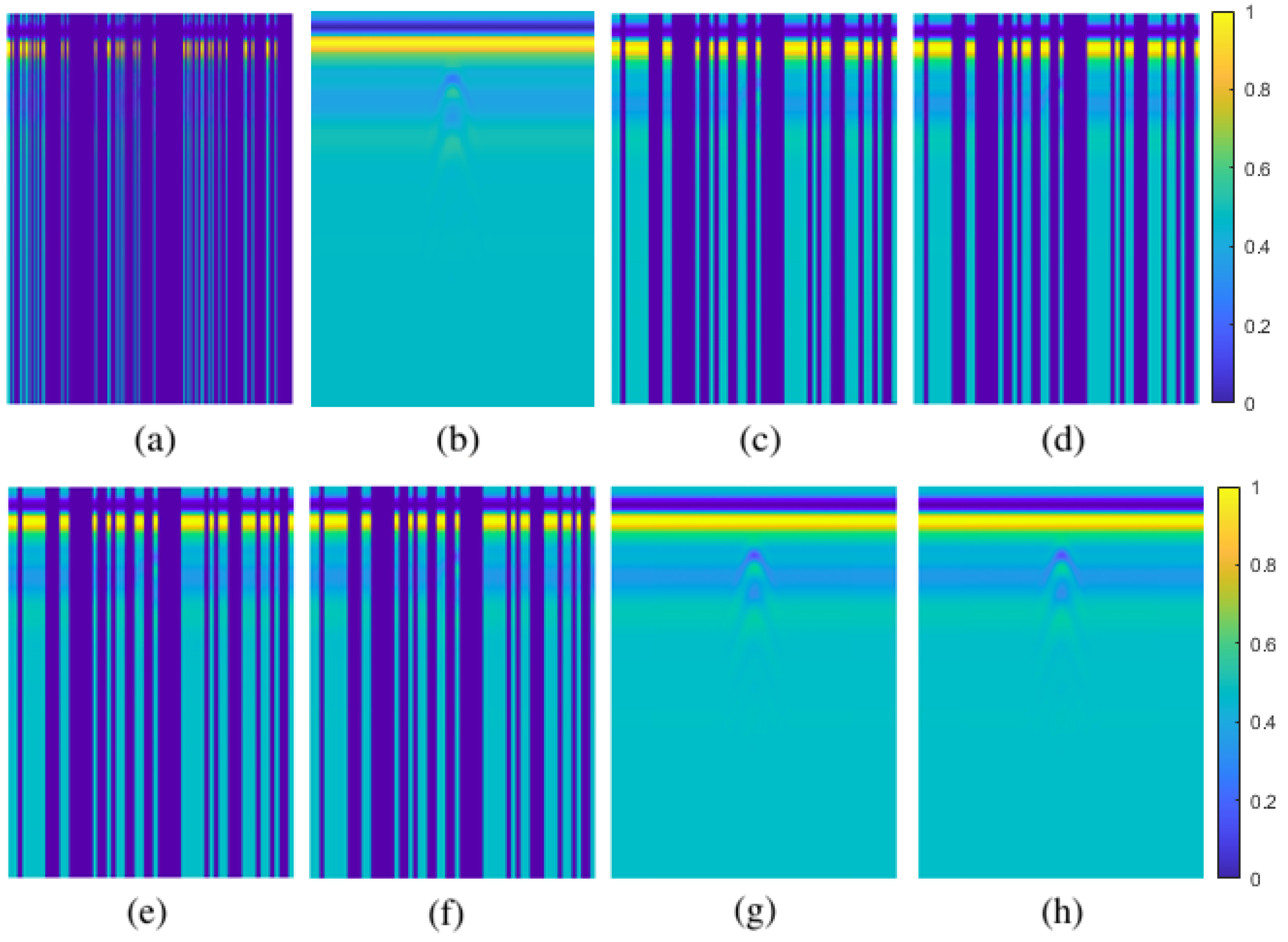
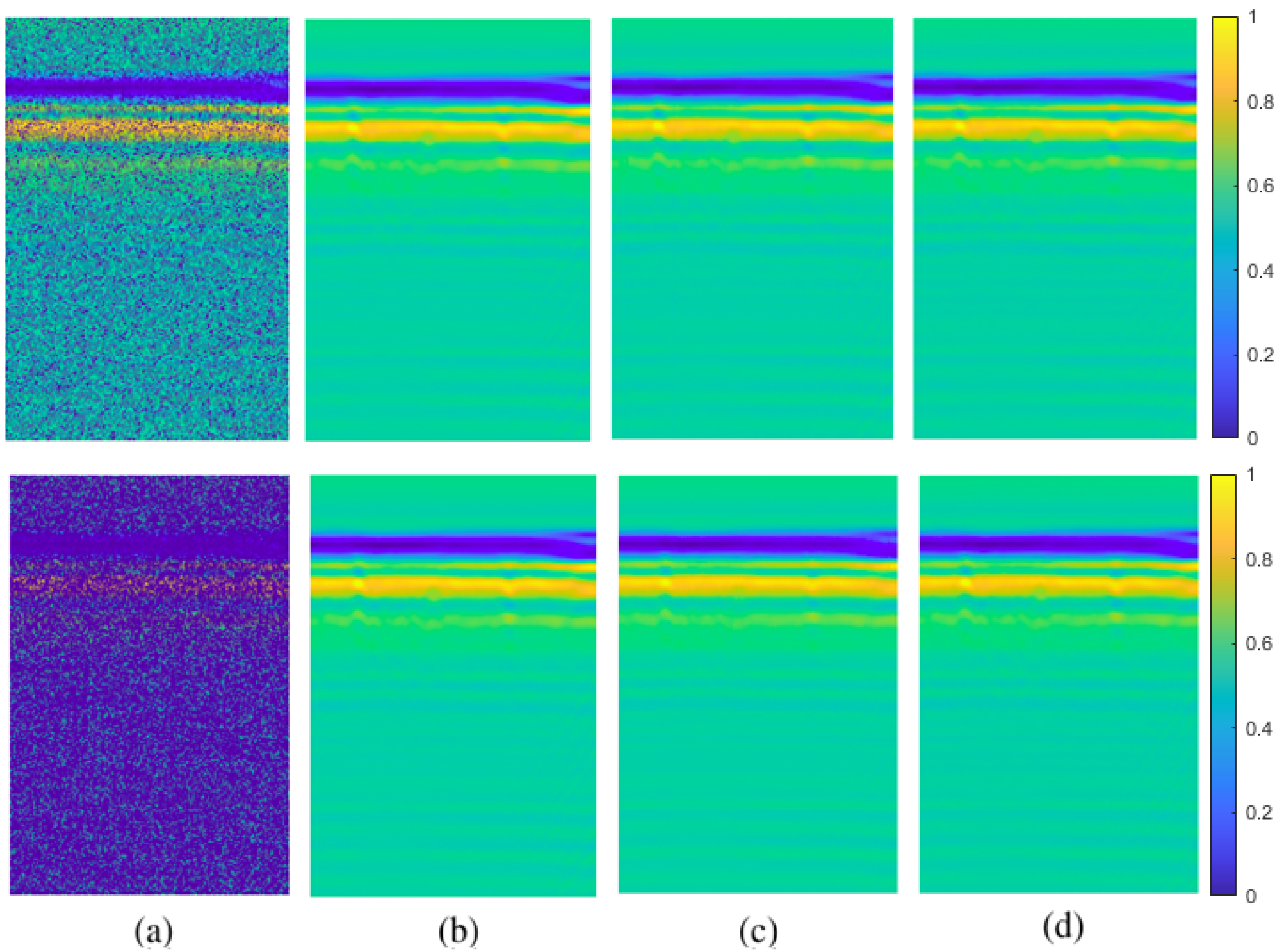
Figure 9.
80% pixel-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 9.
80% pixel-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
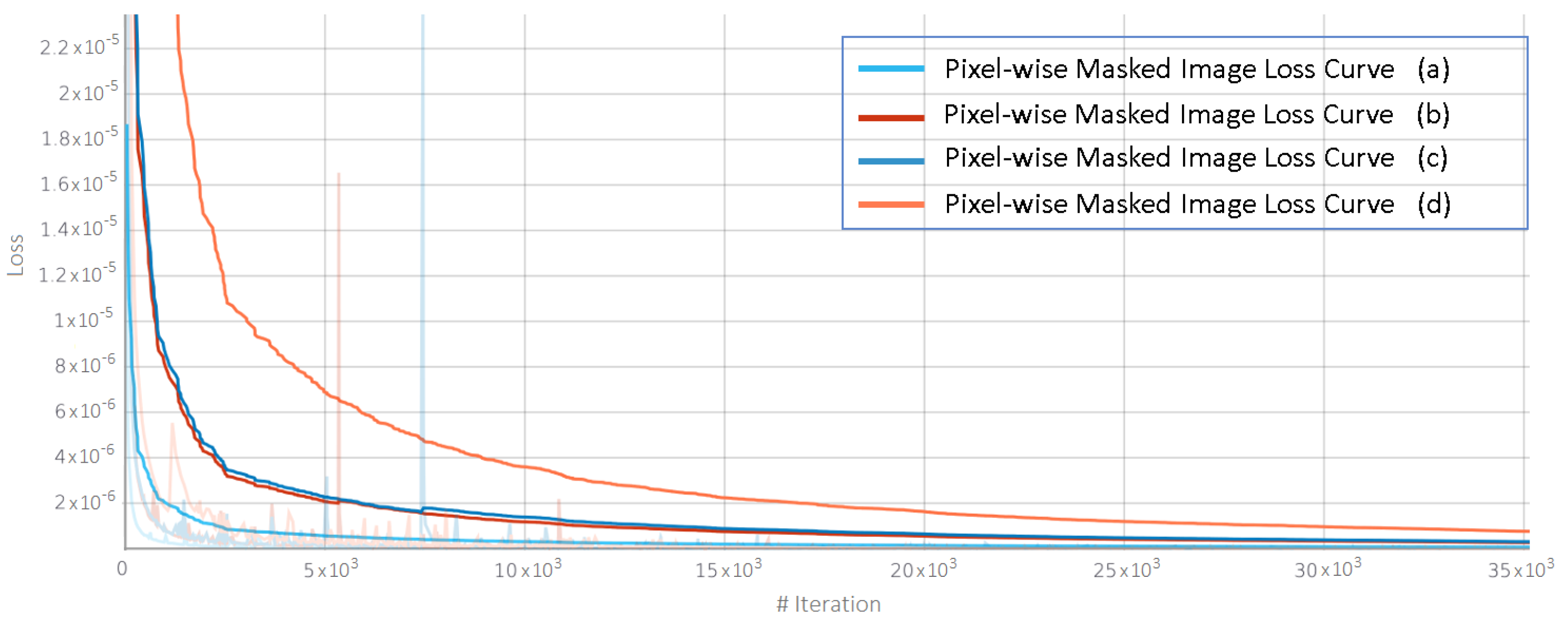
Figure 10.
Loss curves for pixel-wise missing data recovery.
Figure 10.
Loss curves for pixel-wise missing data recovery.
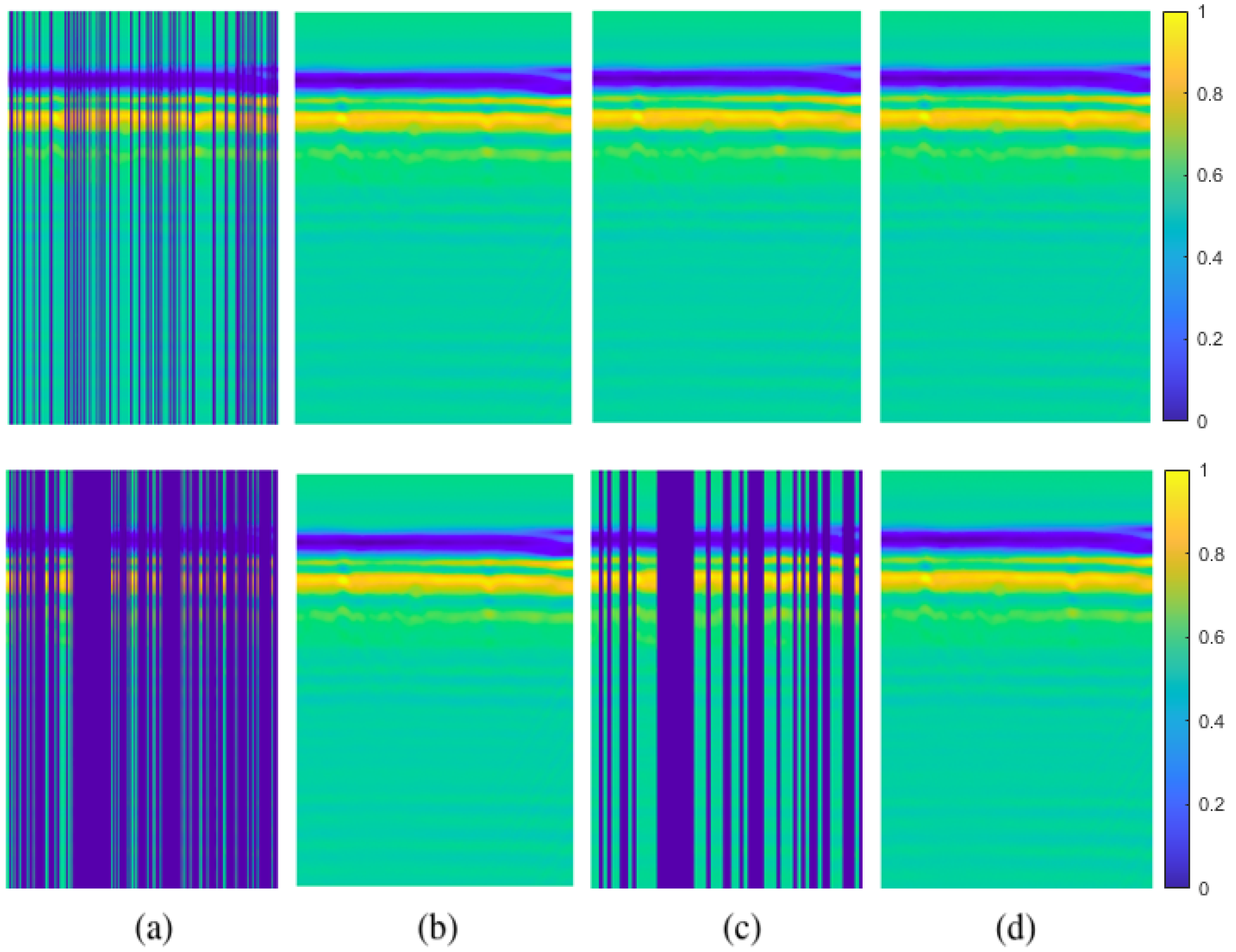
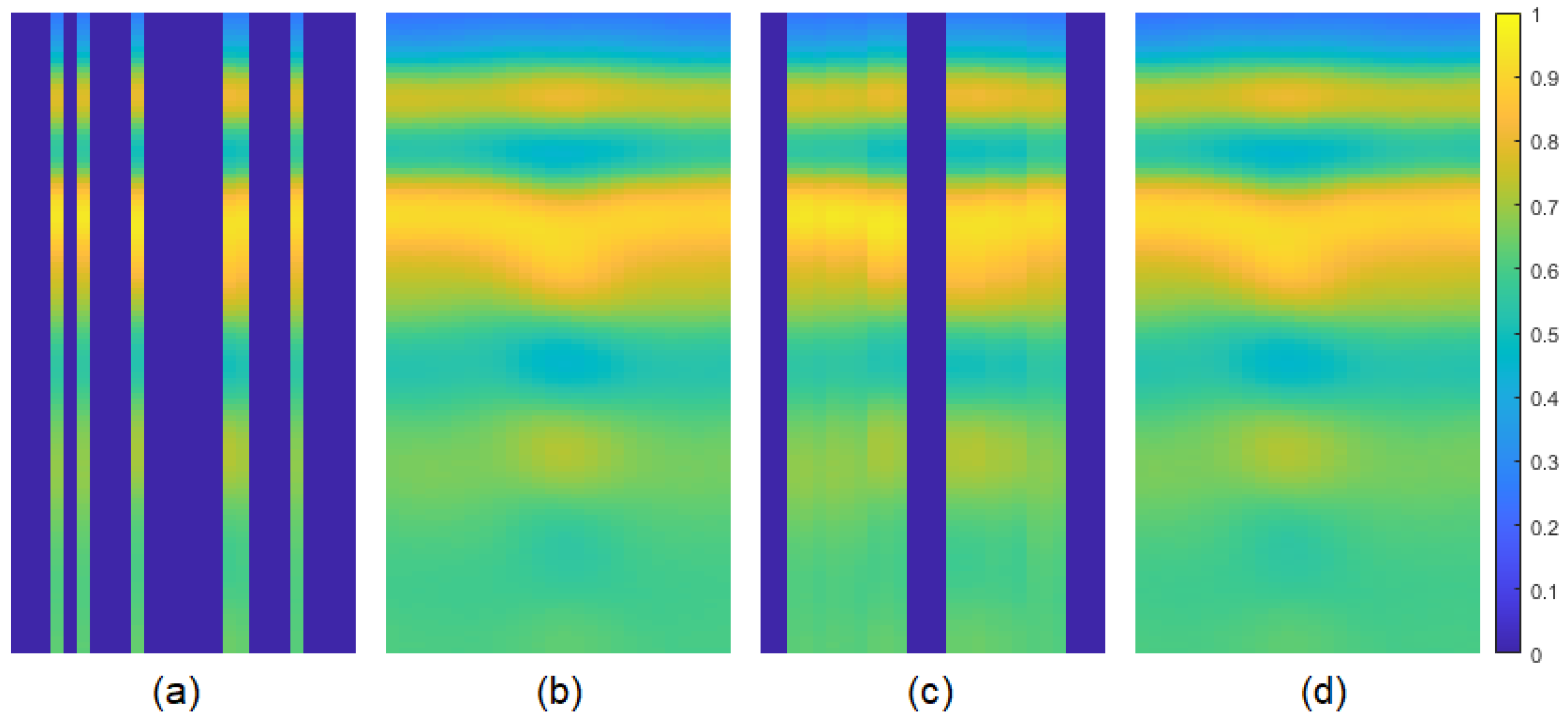
Figure 11.
30% column-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 11.
30% column-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 12.
50% column-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 12.
50% column-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 13.
80% column-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 13.
80% column-wise missing data case for simulated data: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) GoDec, (d) NMC, (e) Lmafit, (f) NNM, (g) PEN-Net, (h) DIP.
Figure 14.
Loss curves for column-wise missing data recovery.
Figure 14.
Loss curves for column-wise missing data recovery.
Figure 15.
Experimental setup of the real data-I.
Figure 15.
Experimental setup of the real data-I.
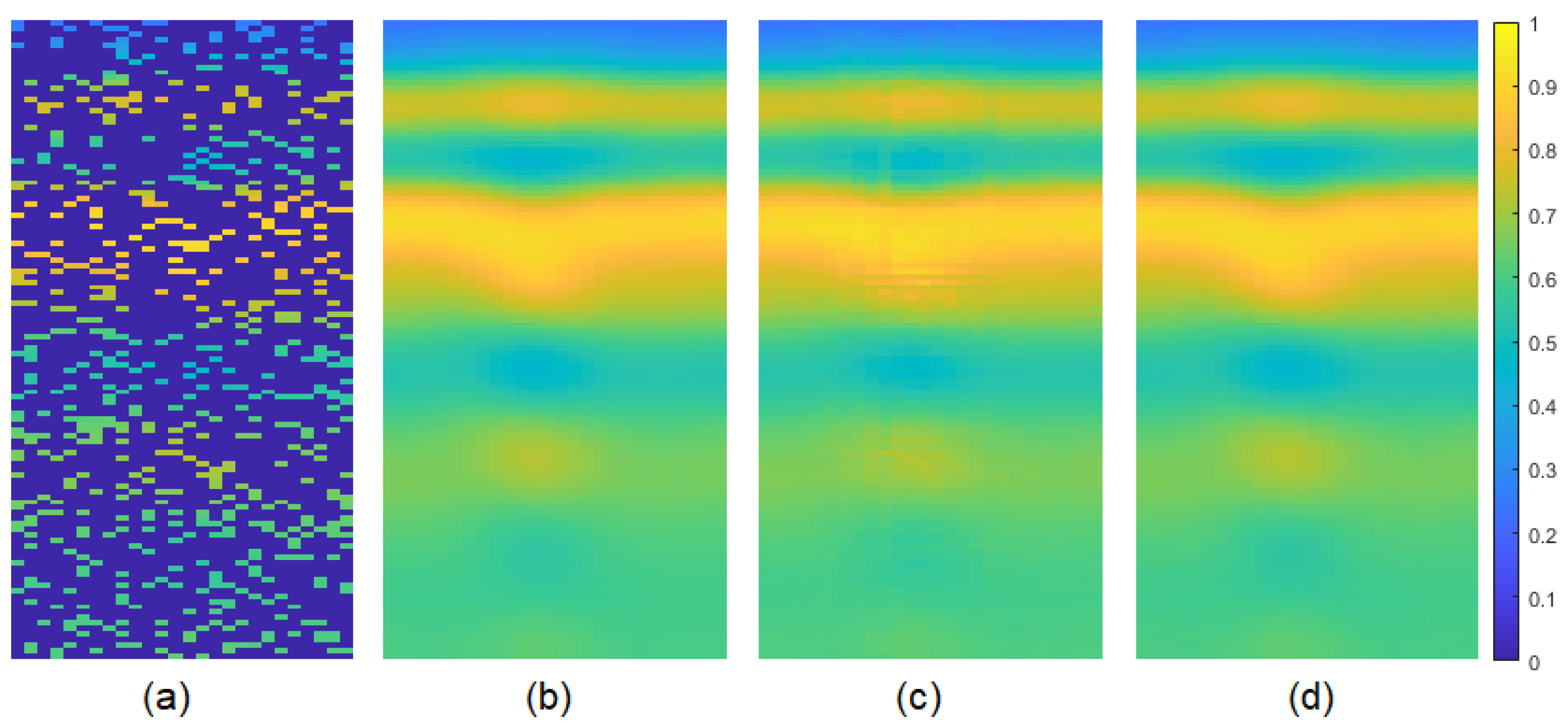
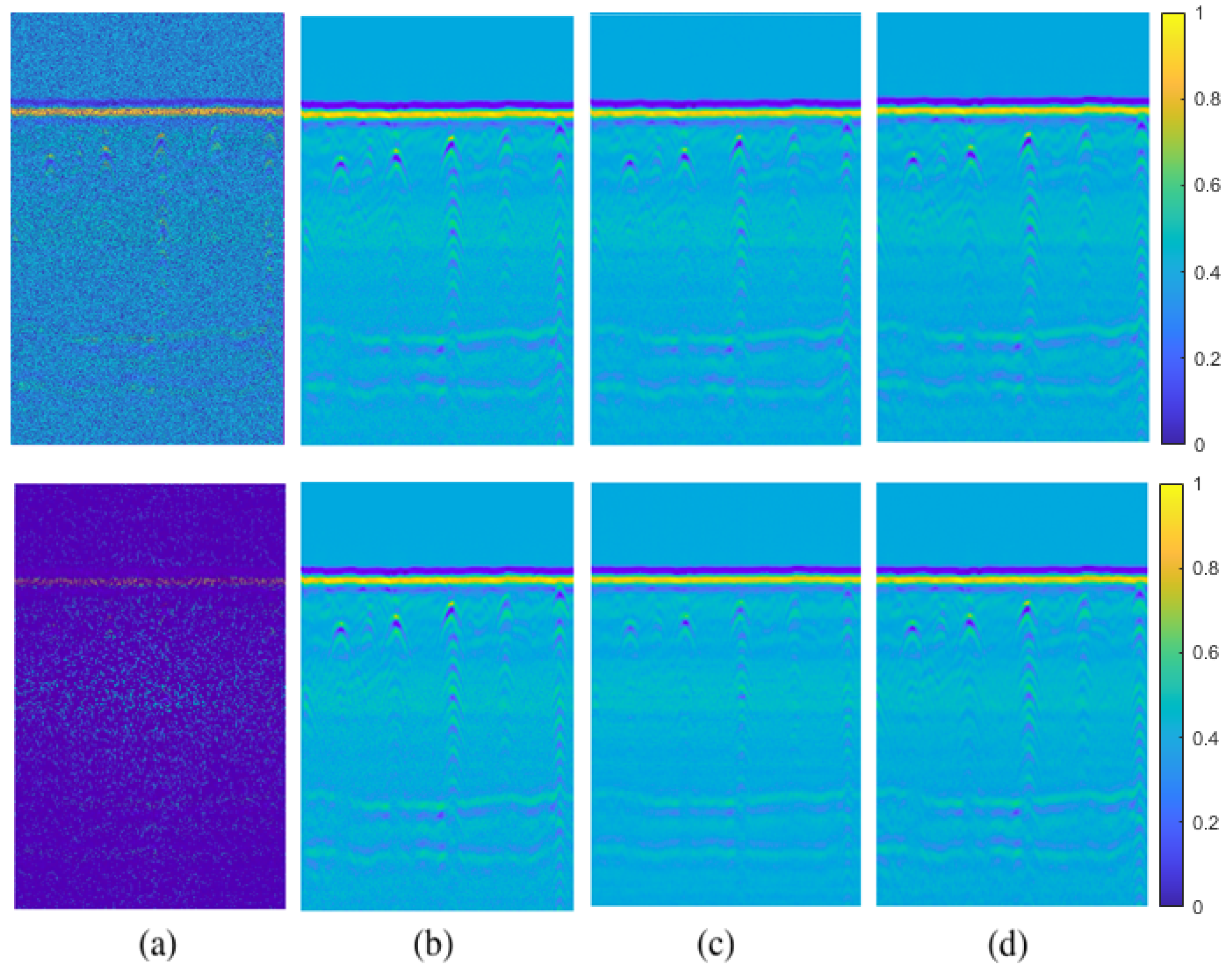
Figure 16.
First row 30% and second row 80% pixel-wise missing data case for real data-I: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 16.
First row 30% and second row 80% pixel-wise missing data case for real data-I: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
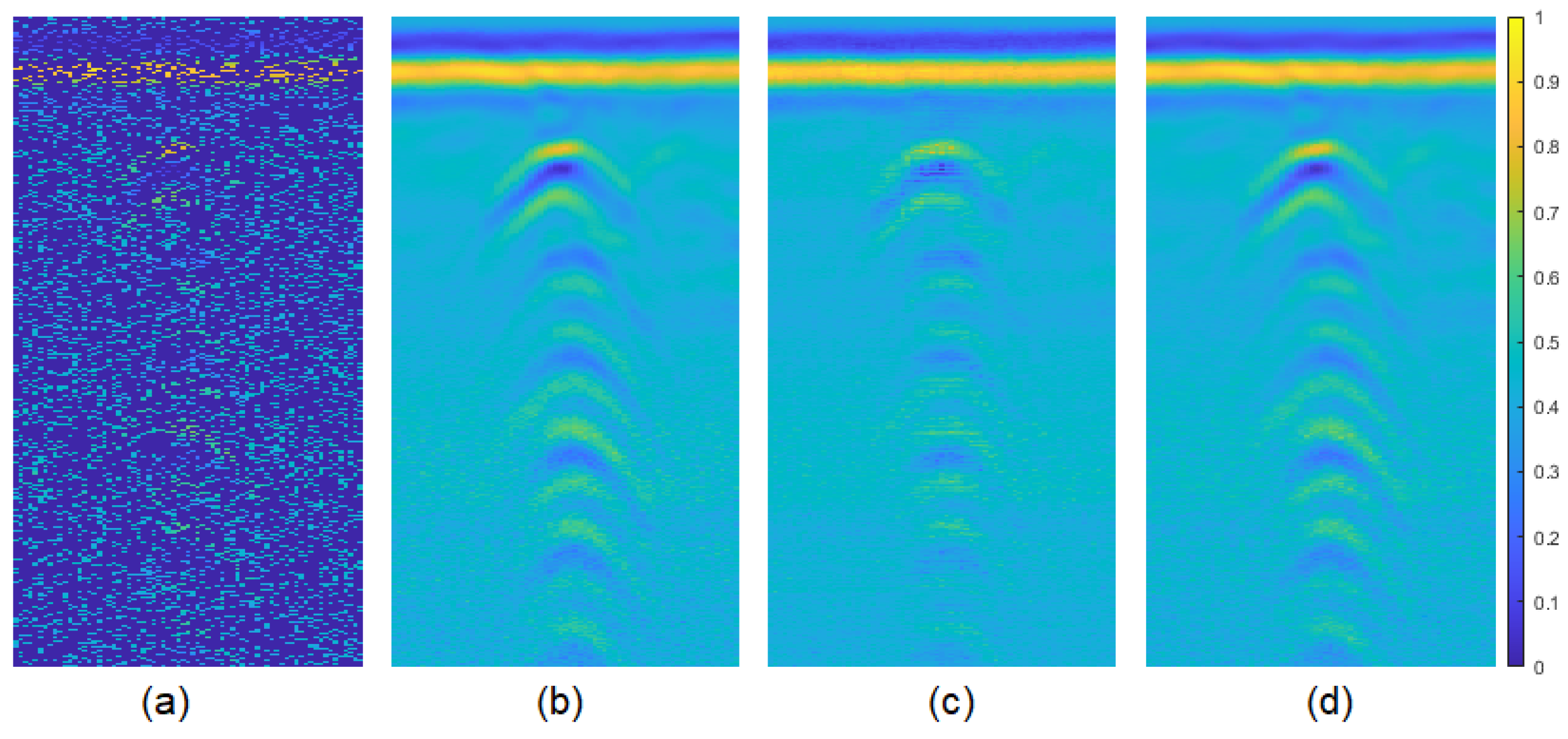
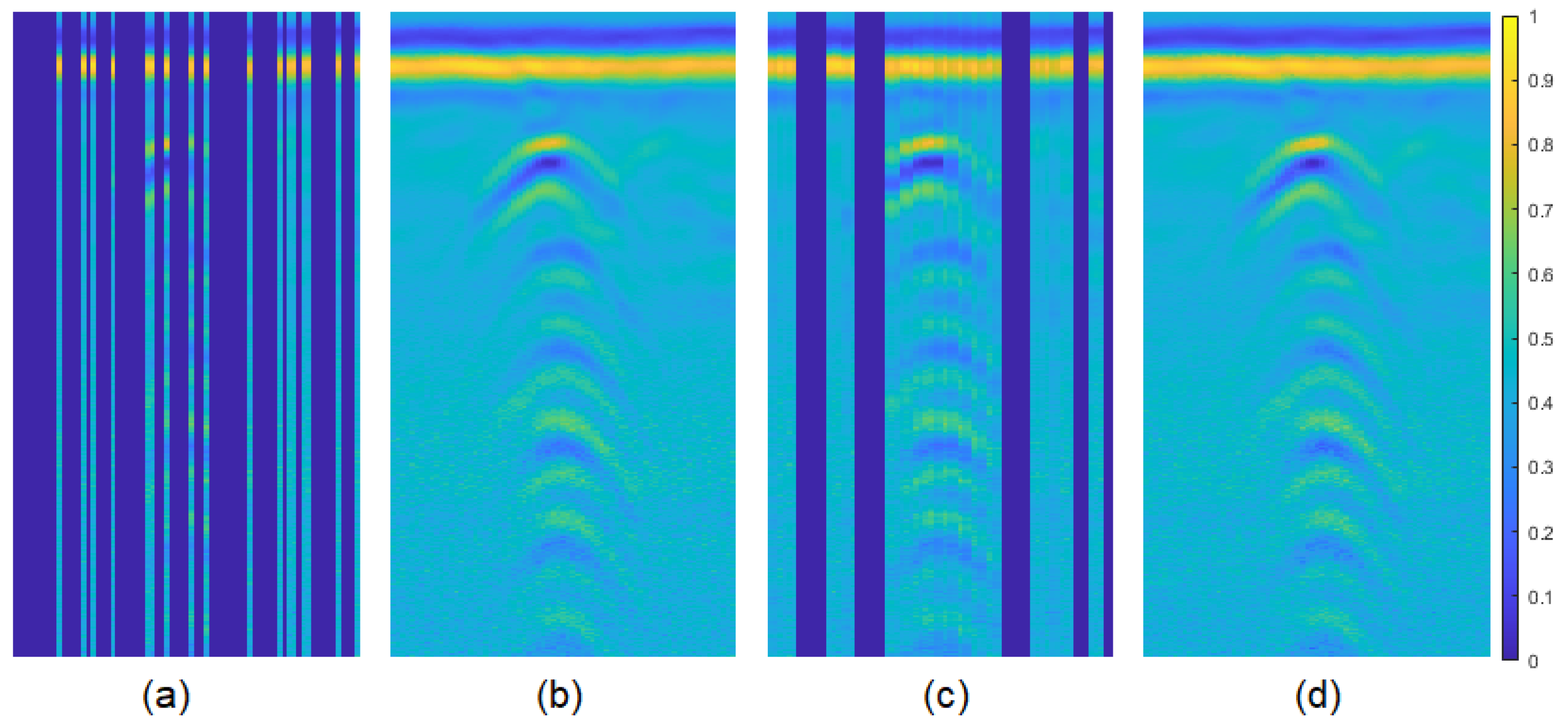
Figure 17.
80% pixel-wise missing data case for the zoomed target (third one) of real data-I: (a) GPR image with missing entries, recovered images by (b) original GPR image, (c) NNM, (d) DIP.
Figure 17.
80% pixel-wise missing data case for the zoomed target (third one) of real data-I: (a) GPR image with missing entries, recovered images by (b) original GPR image, (c) NNM, (d) DIP.
Figure 18.
First row 30% and second row 80% column-wise missing data case for real data-I: (a) GPR image with missing entree, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 18.
First row 30% and second row 80% column-wise missing data case for real data-I: (a) GPR image with missing entree, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 19.
80% column-wise missing data case for the zoomed target (third one) of real data-I: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 19.
80% column-wise missing data case for the zoomed target (third one) of real data-I: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 20.
Experimental setup of real data-II.
Figure 20.
Experimental setup of real data-II.
Figure 21.
First row 30% pixel-wise and second row 80% missing data case for real data-II: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 21.
First row 30% pixel-wise and second row 80% missing data case for real data-II: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 22.
80% pixel-wise missing data case for the zoomed target (third one) of real data-II: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 22.
80% pixel-wise missing data case for the zoomed target (third one) of real data-II: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 23.
First row 30% and second row 50% column-wise missing data case for real data-II: (a) GPR image with missing entries, recovered images by (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 23.
First row 30% and second row 50% column-wise missing data case for real data-II: (a) GPR image with missing entries, recovered images by (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 24.
80% column-wise missing data case for the zoomed third target of real data-II: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Figure 24.
80% column-wise missing data case for the zoomed third target of real data-II: (a) GPR image with missing entries, (b) original GPR image, recovered images by (c) NNM, (d) DIP.
Table 1.
Specifications of conventional matrix completion algorithms evaluated in this paper.
Table 1.
Specifications of conventional matrix completion algorithms evaluated in this paper.
| Category | Method | Main Techniques | Reference |
|---|
| Rank minimization | GoDec | Bilateral random projections | [17] |
| Matrix factorization | NMC | Alternating | [18] |
| Matrix factorization | LmaFit | Alternating | [11] |
| Rank minimization | NNM | Singular value decomposition | [12] |
Table 2.
PNSR comparison of data recovery methods for pixel-wise missing data.
Table 2.
PNSR comparison of data recovery methods for pixel-wise missing data.
| | Missing Rate (%) | GoDec | NMC | LmaFit | NNM | PEN-Net | DIP |
|---|
| | 30 | 63.21 | 67.67 | 90.82 | 92.21 | 104.31 | 117.82 |
| | 50 | 61.98 | 62.13 | 72.93 | 69.47 | 73.26 | 93.22 |
| | 80 | 47.25 | 42.02 | 43.60 | 48.34 | 45.79 | 57.77 |
Table 3.
PNSR comparison of data recovery methods for column-wise missing data.
Table 3.
PNSR comparison of data recovery methods for column-wise missing data.
| | Missing Rate (%) | GoDec | NMC | LmaFit | NNM | PEN-Net | DIP |
|---|
| | 30 | 46.83 | 59.61 | 50.38 | 54.43 | 53.50 | 63.43 |
| | 50 | 49.51 | 50.43 | 49.53 | 49.30 | 54.68 | 57.63 |
| | 80 | – | – | – | – | 30.55 | 31.19 |
Table 4.
PNSR comparison of data recovery methods for pixel-wise missing case for real data-I.
Table 4.
PNSR comparison of data recovery methods for pixel-wise missing case for real data-I.
| Missing Rate (%) | NNM | DIP | NNM | DIP |
|---|
| 30 | 59.51 | 60.89 | – | – |
| 80 | 45.80 | 51.12 | 34.24 | 47.36 |
Table 5.
PNSR comparison of data recovery methods for column-wise missing case for real data-I.
Table 5.
PNSR comparison of data recovery methods for column-wise missing case for real data-I.
| Missing Rate (%) | NNM | DIP | NNM | DIP |
|---|
| 30 | 52.79 | 58.99 | – | – |
| 80 | 8.06 | 33.64 | 12.05 | 32.28 |
Table 6.
PNSR comparison of data recovery methods for pixel-wise missing case for real data-II.
Table 6.
PNSR comparison of data recovery methods for pixel-wise missing case for real data-II.
| Missing Rate (%) | NNM | DIP | NNM | DIP |
|---|
| 30 | 35.99 | 39.57 | – | – |
| 80 | 30.41 | 33.04 | 27.61 | 37.24 |
Table 7.
PNSR comparison of data recovery methods for column-wise missing case for real data-II.
Table 7.
PNSR comparison of data recovery methods for column-wise missing case for real data-II.
| Missing Rate (%) | NNM | DIP | NNM | DIP |
|---|
| 30 | 33.33 | 36.37 | – | – |
| 80 | 10.06 | 39.60 | 13.83 | 25.77 |