Modelling of Greek Lakes Water Quality Using Earth Observation in the Framework of the Water Framework Directive (WFD)
Abstract
:1. Introduction
2. Study Area
3. Materials and Methods
3.1. Data Acquisition
3.1.1. In Situ Data
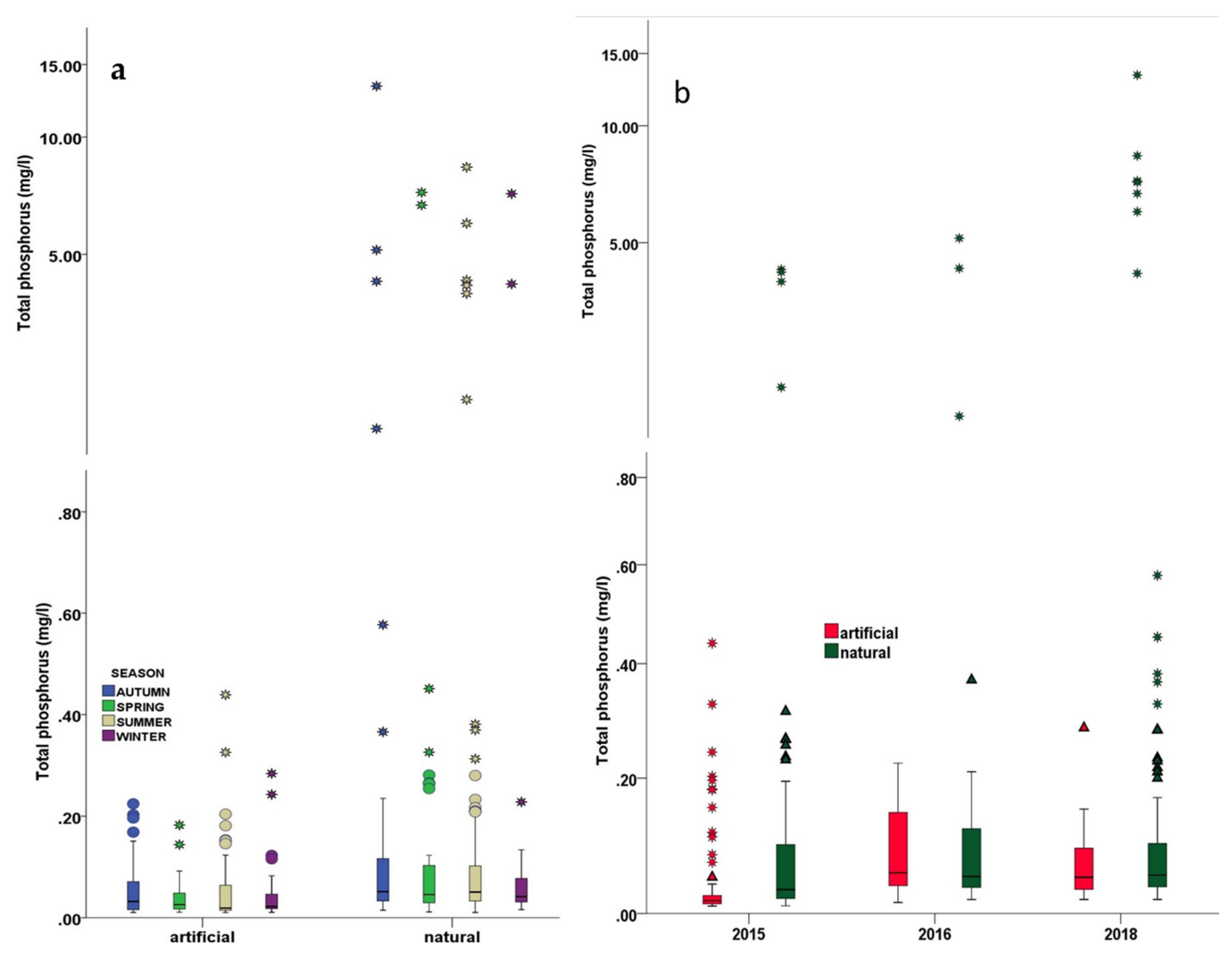
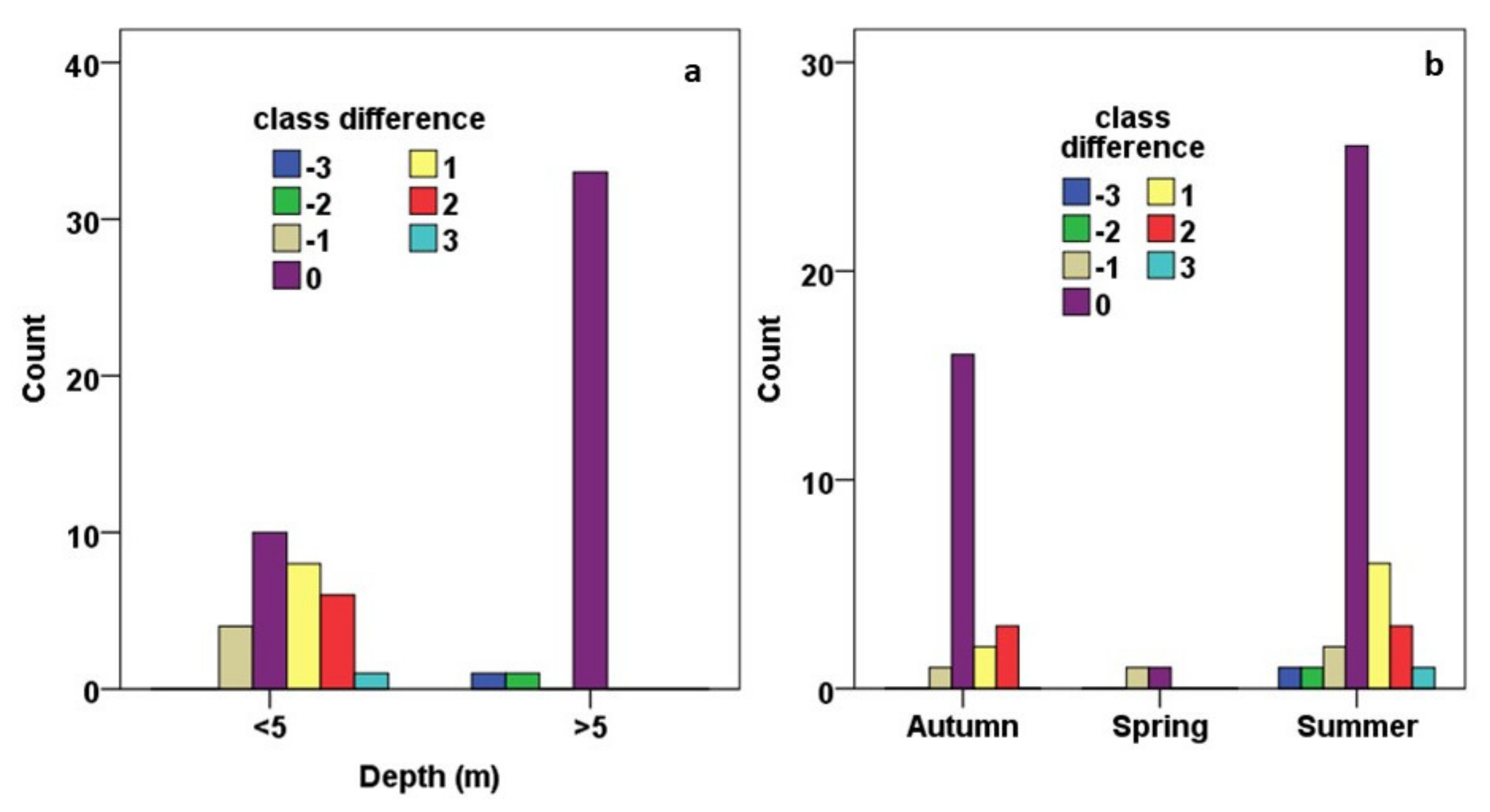
Exploratory Statistical Analyses
3.1.2. EO Data Acquisition and Pre-Processing
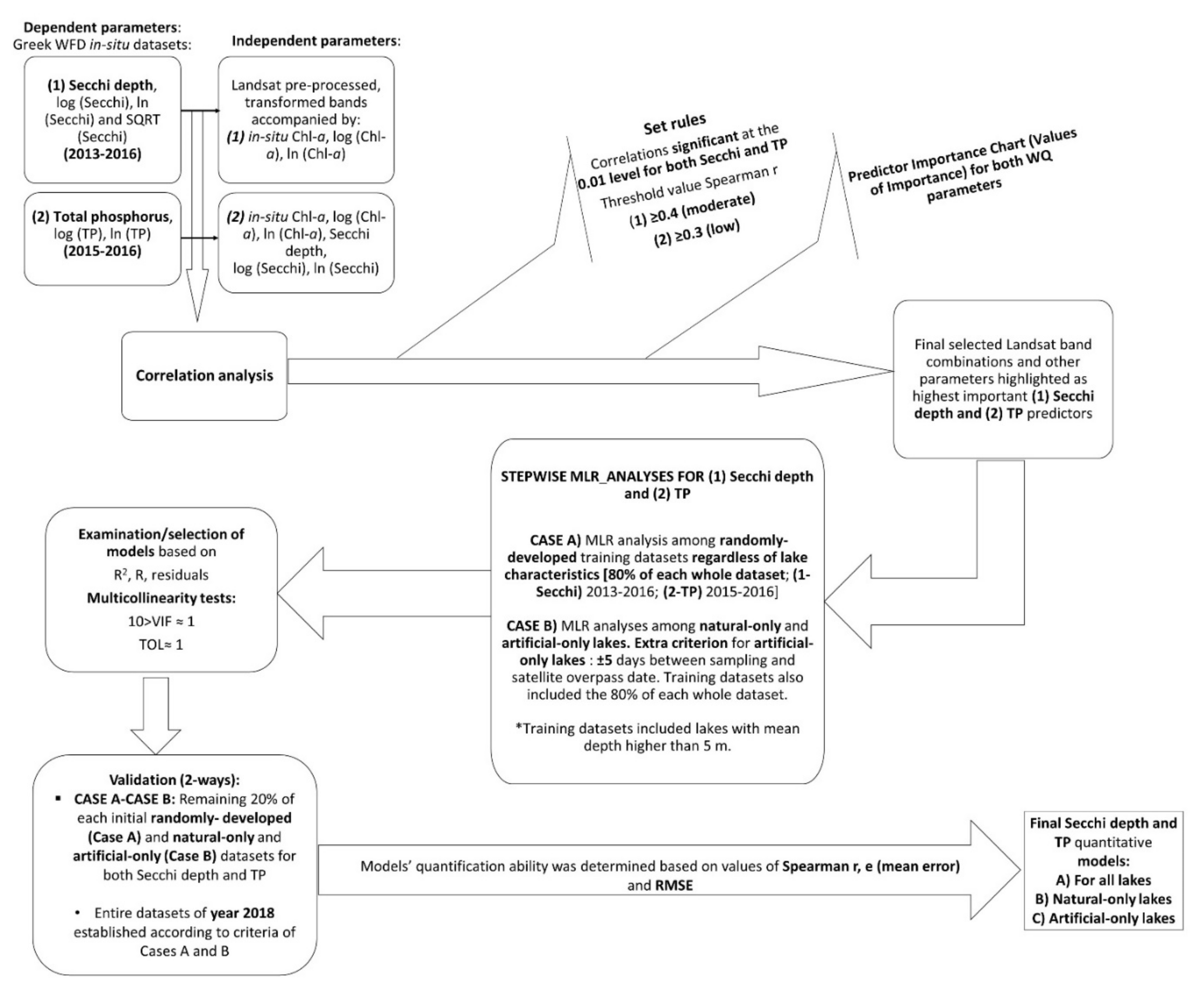
3.2. Statistical Approach
3.2.1. Establishment of Relationships between Landsat Data, Secchi Depths, and TP
| Reference | Parameters | Band Combinations and Sensors |
|---|---|---|
| [68] | TP | Blue, Green, Red, NIR, NIR/Green (L8) |
| [42,44] | TP | Blue, Green, Red, and NIR (L5) |
| [36] | Ln (TP) | Blue, Red/Green, Blue/Red (L5) |
| [4] | TP | Blue, Green, Red, NIR, SWIR1, and SWIR2 (L5) |
| [48] | (1) TP(2) Secchi depth | (1) Red, Green, Red/Blue, (Green + Red)/2, Green2, (Blue + Green)/2 (L5) (2) Red/Blue, Red2, Blue, (Blue+Green)/2, (Blue + Red)/2 (L5) |
| [69] | (1) SQRT (TP) (2) Secchi depth | (1) Red, SWIR2 (L7 ETM+) (2) LOGRed, LOGSWIR2 (L7 ETM+) |
| [70] | Phosphorus | Blue, Green, Red, NIR (L5) |
| [71] | LOG (P) | NIR/Visible light (GOCI) |
| [72] | (1) Phosphates (2) TP | (1) Red, MIR (2) Red IRS P6 (LISS III) |
| [5] | TP | LOG (Green/Red to NIR), (CASI) |
| [27] | (1) Secchi depth (m) (2) LN Secchi depth | (1) Blue/Red, (Blue-Red)/Green, LN [(Blue-Red)/Green] (L7 ETM+) (2) NIR, (Blue-Red)/Green, LN Red |
| [73] | LN Secchi depth | Blue, Blue/Red (L5) |
| [74] | Secchi depth | Blue, Green, Red (IRS-1A) |
| [75] | Secchi Depth | Green, Red, Blue, Vegetation red edge (B5), Water Vapour (Sentinel 2) |
| [76] | Secchi depth | Green, Blue (MODIS-Aqua) |
| [77] | Secchi depth | Blue, Red (MERIS) |
3.2.2. Validation Approach
3.3. Carlson’s Trophic State Index (TSI) and Validation
4. Results
4.1. Secchi Depth and Total Phosphorus Quantitative Models for Greek Lakes
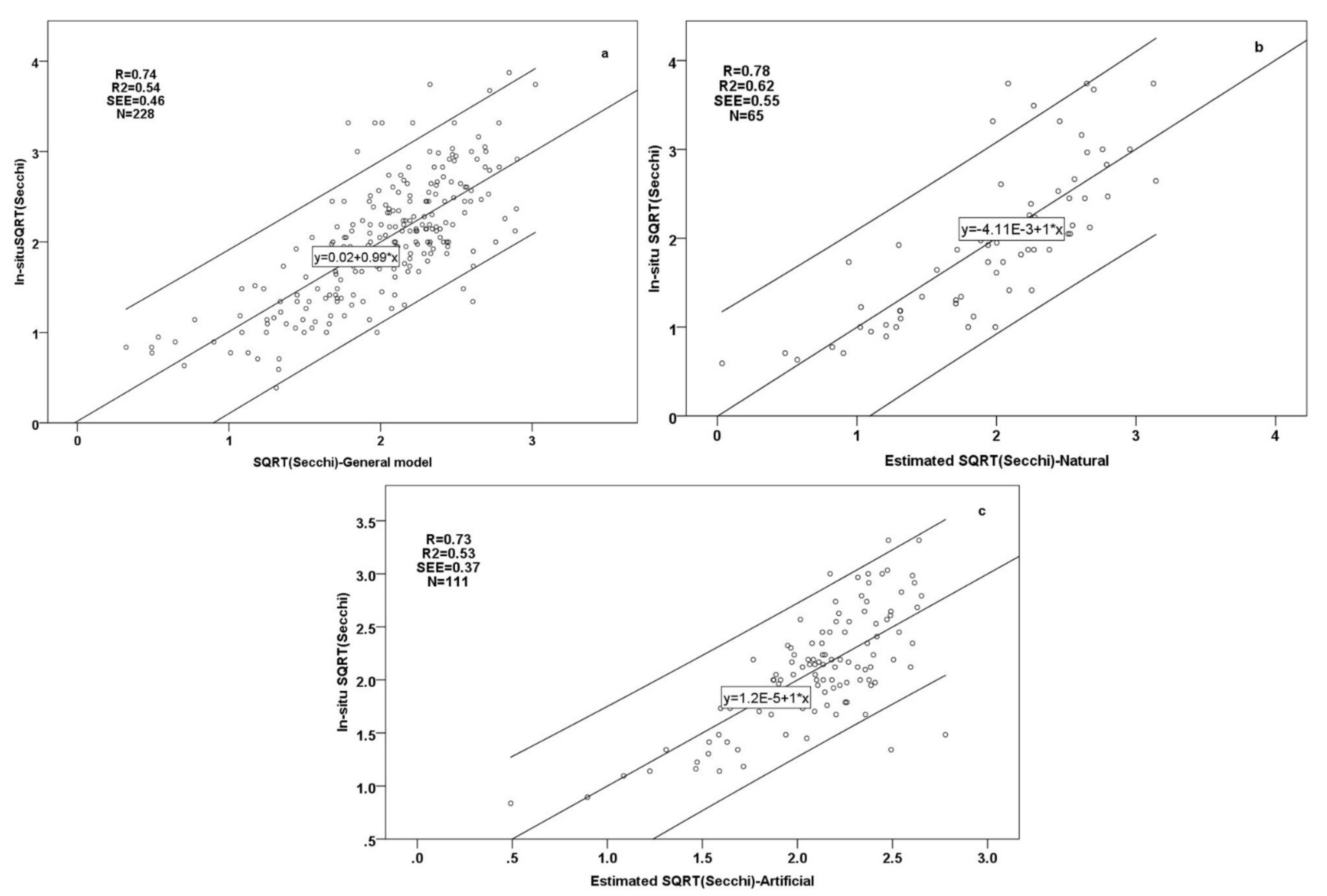
4.1.1. Secchi Depth Models
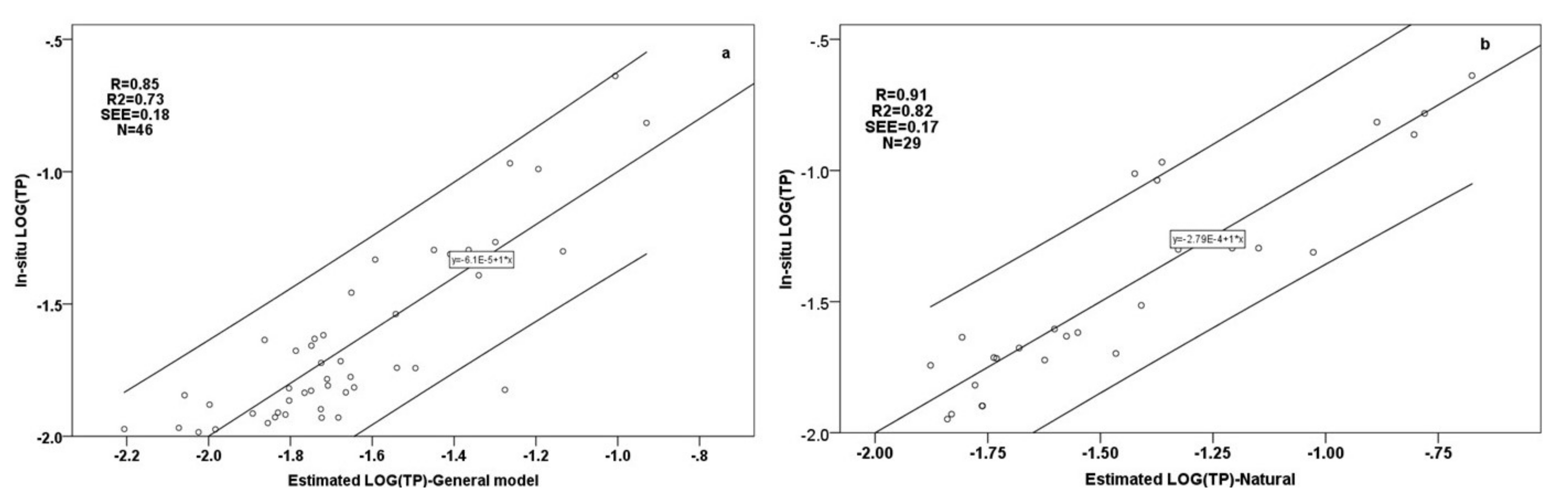
4.1.2. Total Phosphorus Models
4.2. Models’ Validation
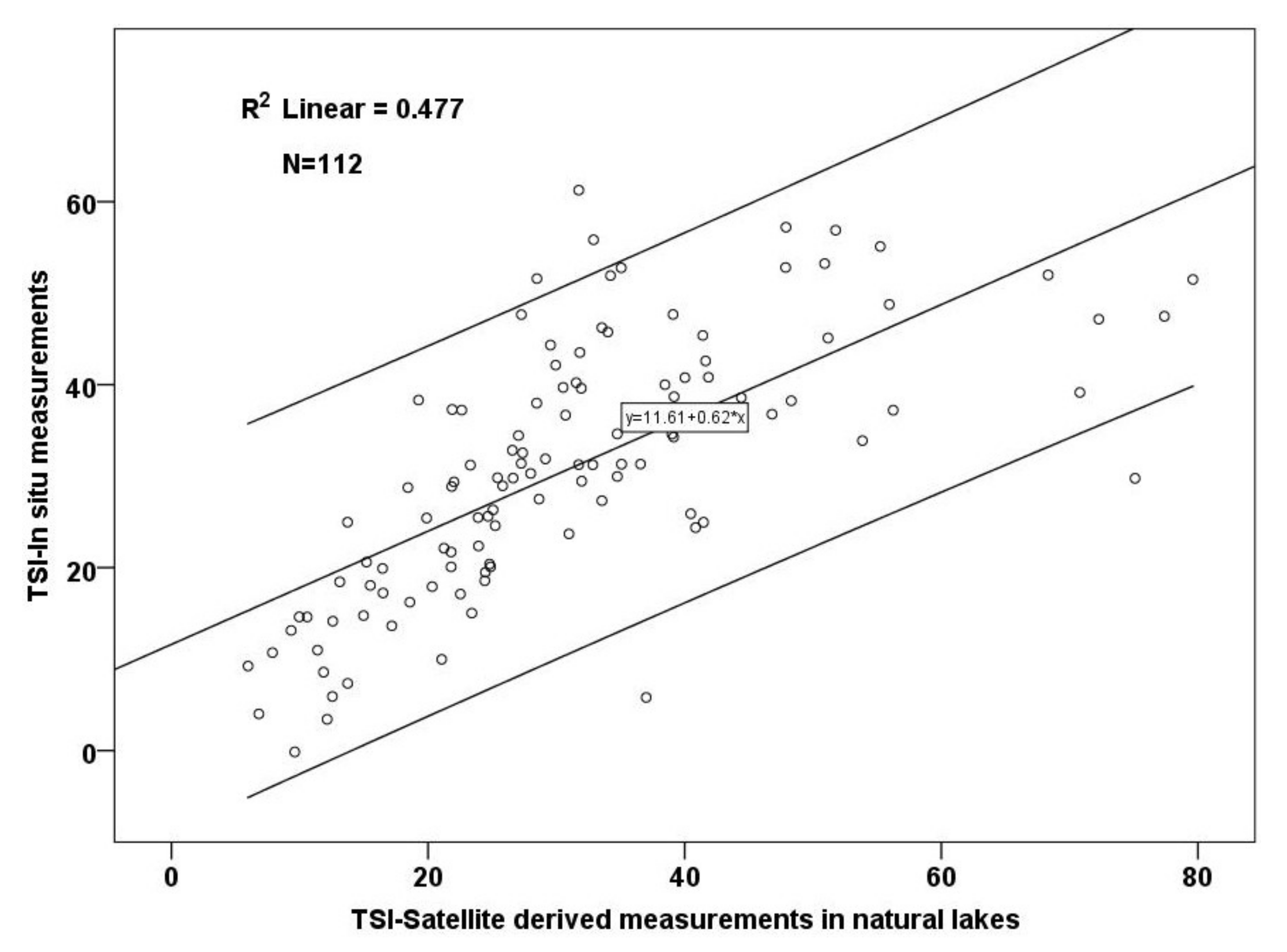
4.2.1. Secchi Depth Models
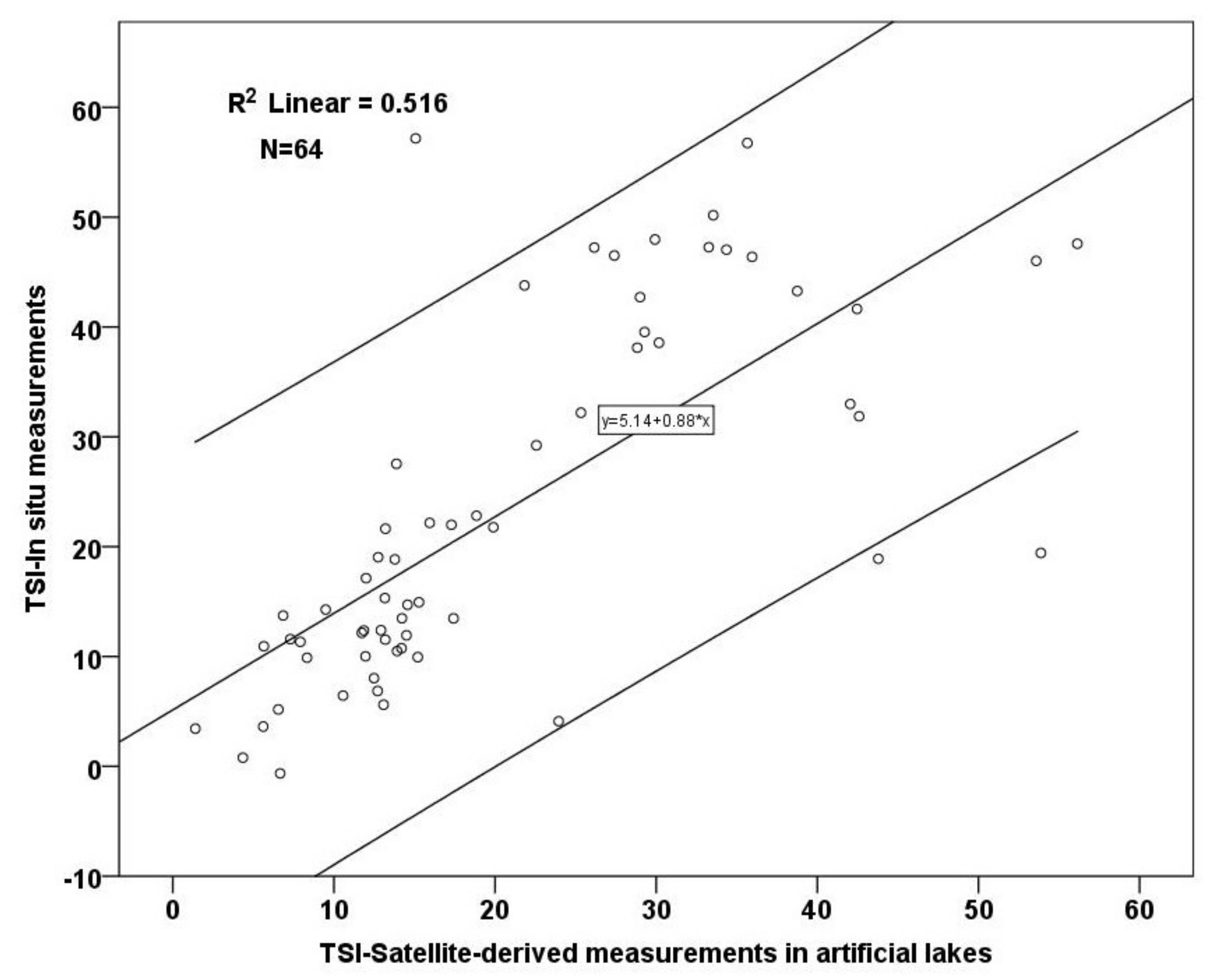
4.2.2. Total Phosphorus Models
4.3. Satellite Derived Assessment of Trophic Status of Greek Lakes Based on Carlson’s Trophic State Index
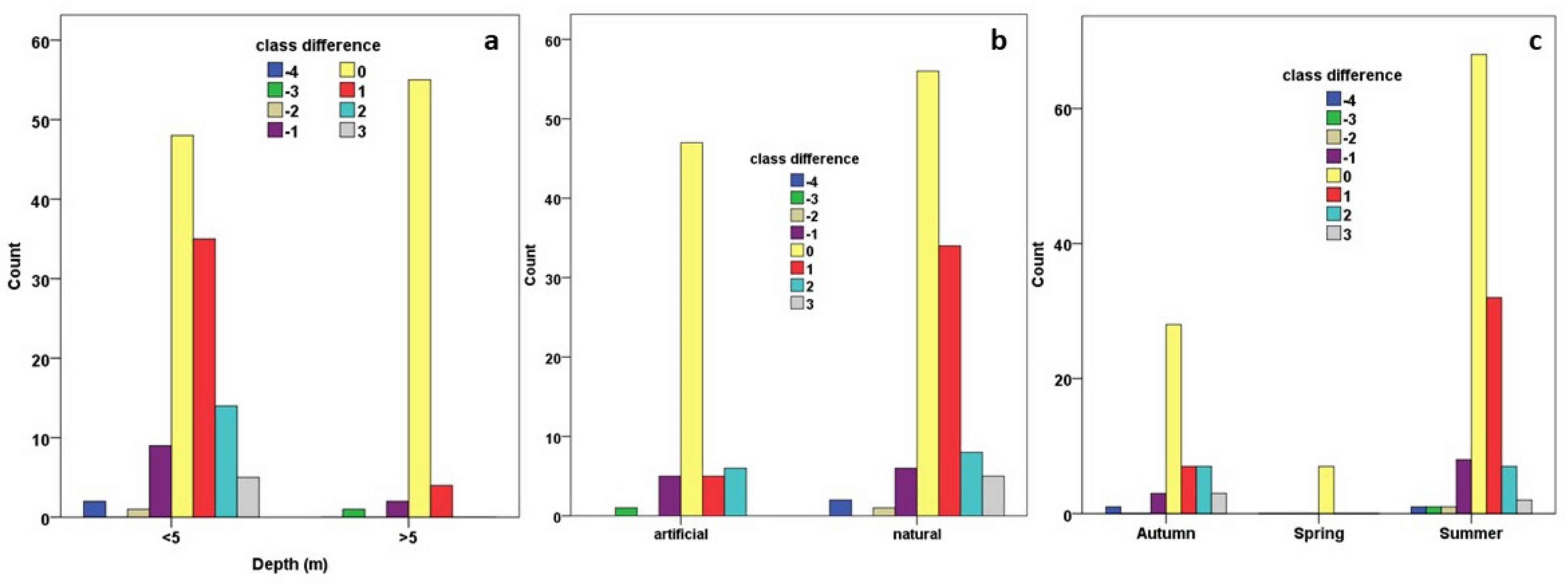
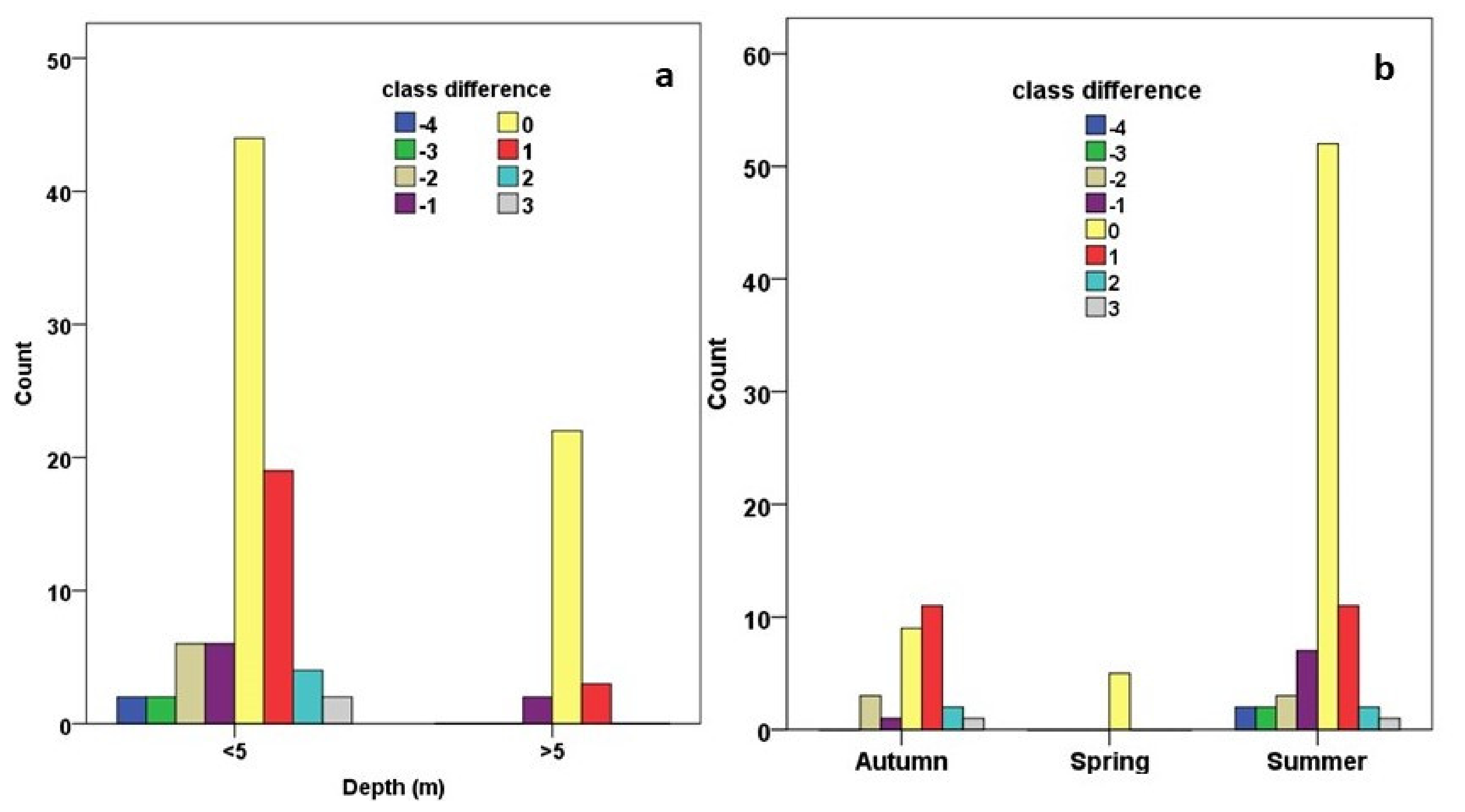
4.3.1. Evaluation of the Lake Trophic Status’s Assessment Based on the Whole Dataset
4.3.2. Evaluation of the Lake Trophic Status Assessment concerning Natural and Artificial Lakes
5. Discussion
5.1. The Significance of Lakes’ Nature concerning the Constituents’ Variance
5.2. MLR Analysis and Resulted Proxies of Studied WQ Parameters
5.3. Contribution of SWIR Bands in WQ Monitoring of Case 2 Waters
5.4. Lakes’ TSI Classification and Exploration of the Factors Affecting Its Accuracy
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Whyte, A.; Feredinos, K.; Petropoulos, G.P. A new synergistic approach for monitoring wetlands using Sentinels -1 and 2 data with object-based Machine Learning algorithms. Environ. Model Softw. 2018, 104, 40–57. [Google Scholar] [CrossRef] [Green Version]
- Michalak, A. Study role of climate change in extreme threats to water quality. Nature 2016, 535, 349–350. [Google Scholar] [CrossRef] [PubMed]
- El-Alem, A.; Chokmani, K.; Laurion, I.; El-Adlouni, S.E. Comparative analysis of four models to estimate chlorophyll—A concentration in case-2 waters using MODerate resolution imaging spectroradiometer (MODIS) imagery. Remote Sens. 2012, 4, 2373–2400. [Google Scholar] [CrossRef] [Green Version]
- Alparslan, E.; Coskun, H.G.; Alganci, U. Water quality determination of Küçükçekmece Lake, Turkey by using multispectral satellite data. Sci. World J. 2009, 9, 1215–1229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shafique, N.A.; Fulk, F.A.; Autrey, B.C.; Flotemersch, J.E. Hyperspectral remote sensing of water quality parameters for large rivers in the Ohio river basin. In Proceedings of the Ohio River Basin Consortium for Research and Education, Marietta, OH, USA, 5–7 November 2003. [Google Scholar]
- Bonansea, M.; Rodriguez, C.; Pinotti, L. Assessing the potential of integrating Landsat sensors for estimating chlorophyll-a concentration in a reservoir. Hydrol. Res. 2018, 49, 1608–1617. [Google Scholar] [CrossRef]
- Moore, T.S.; Dowell, M.D.; Bradt, S.; Verdu, A.R. An optical water type framework for selecting and blending retrievals from bio-optical algorithms in lakes and coastal waters. Remote Sens. Environ. 2014, 143, 97–111. [Google Scholar] [CrossRef] [Green Version]
- Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting chlorophyll, Secchi disk depth and surface temperature in a sub-alpine lake using Landsat imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef]
- He, W.; Chen, S.; Liu, X.; Chen, J. Water quality monitoring inland water body through remote sensing—A case study of Guanting Reservoir in Beijing, China. Front. Environ. Sci. Engin. China 2008, 2, 163–171. [Google Scholar] [CrossRef]
- Dekker, A.G.; Malthus, T.J.; Seyhan, E. Quantitative modeling of inland water quality for high resolution MSS system. IEEE Trans. Geosci. Remote Sens. 1991, 29, 89–95. [Google Scholar] [CrossRef]
- Poor, N.D. Effect of lake management efforts on the trophic state of a subtropical shallow lake in Lakeland, Florida, USA. Water Air Soil Pollut. 2010, 207, 333–347. [Google Scholar] [CrossRef]
- Brivio, P.A.; Giardino, C.; Zilioli, E. Determination of chlorophyll concentration changes in Lake Garda using an image-based radiative transfer code for Landsat TM images. Int. J. Remote Sens. 2001, 22, 487–502. [Google Scholar] [CrossRef]
- Pozdnyakov, D.; Shuchman, R.; Korosov, A.; Hatt, C. Operational algorithm for the retrieval of water quality in the Great Lakes. Remote Sens. Environ. 2005, 97, 352–370. [Google Scholar] [CrossRef]
- Tyler, A.N.; Svab, E.; Preston, T.; Presing, M.; Kovacs, W.A. Remote sensing of the water quality of shallow lakes: A mixture modeling approach to quantifying phytoplankton in water characterized by high suspended sediment. Int. J. Remote Sens. 2006, 27, 1521–1537. [Google Scholar] [CrossRef]
- Chatziantoniou, A.; Petropoulos, G.P.; Psomiadis, E. Co-Orbital Sentinel 1 and 2 for LULC mapping with emphasis on wetlands in a Mediterranean setting based on Machine Learning. Remote Sens. 2017, 9, 1259. [Google Scholar] [CrossRef] [Green Version]
- Haddad, K.D.; Harris, B.A. Use of remote sensing to assess estuarine habitats. In Proceedings of the 4th Symposium on Coastal and Ocean Management; Magoom, O.T., Converse, H., Miner, D., Clark, D., Tobin, L.T., Eds.; American Society of Civil Engineers: New York, NY, USA, 1985; pp. 662–675. [Google Scholar]
- Morel, A.; Gordon, H.R. Report of the working group on water colour. Bound. -Layer Meteorol. 1980, 18, 343–355. [Google Scholar] [CrossRef]
- Austin, R.W.; Petzold, T.J. Water Colour Measurements. In Oceanography from Space; Gower, J., Ed.; Plenum: New York, NY, USA, 1981; pp. 239–256. [Google Scholar]
- Sagan, V.; Peterson, T.K.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, A.B.; Samar, M.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth-Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Topp, S.; Pavelsky, T.; Jensen, D.; Simard, M.; Ross, M. Research trends in the use of remote sensing for inland water quality science: Moving towards multidisciplinary applications. Water 2020, 12, 169. [Google Scholar] [CrossRef] [Green Version]
- Gholizadeh, M.; Melesse, A.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [Green Version]
- Odermatt, D.; Gitelson, A.; Vittorio, E.V.; Schaepman, M. Review of constituent retrieval in optically deep and complex waters from satellite imagery. Remote Sens. Environ. 2012, 118, 116–126. [Google Scholar] [CrossRef] [Green Version]
- Gordon, H.R.; Morel, A. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery. A Review, Lecture Notes on Coastal and Estuarine Studies; Barber, R.T., Mooers, N.K., Bowman, M.J., Zeitzschel, B., Eds.; Springer: New York, NY, USA, 1983; p. 114. [Google Scholar]
- IOCCG. Remote Sensing of Ocean Colour in Coastal, and Other Optically-Complex, Waters; Reports of the International Ocean-Colour Coordinating Group, No. 3; Sathyendranath, S., Ed.; IOCCG: Dartmouth, NH, Canada, 2000. [Google Scholar]
- Spyrakos, E.; O’donnell, R.; Hunter, P.D.; Miller, C.; Scott, M.; Simis, S.G.; Neil, C.; Barbosa, C.C.; Binding, C.E.; Bradt, S.; et al. Optical types of inland and coastal waters. Limnol. Oceanogr. 2018, 63, 846–870. [Google Scholar] [CrossRef] [Green Version]
- Giardino, C.; Bresciani, M.; Cazzaniga, I.; Schenk, K.; Rieger, P.; Braga, F.; Matta, E.; Brando, V.E. Evaluation of multi-resolution satellite sensors for assessing water quality and bottom depth of lake garda. Sensors 2014, 14, 24116–24131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allan, M.G.; Hamilton, D.P.; Hicks, B.J.; Brabyn, L. Landsat remote sensing of chlorophyll a concentrations in central north island lakes of New Zealand. Int. J. Remote Sens. 2011, 32, 2037–2055. [Google Scholar] [CrossRef]
- Kim, S.I.; Kim, H.C.; Hyun, C.U. High resolution ocean color products estimation in Fjord of Svalbard, arctic sea using Landsat-8 oli. Korean J. Remote Sens. 2014, 30, 809–816. [Google Scholar] [CrossRef] [Green Version]
- Markogianni, V.; Dimitriou, E.; Karaouzas, I. Water quality monitoring and assessment of an urban Mediterranean lake facilitated by remote sensing applications. Environ. Monit. Assess. 2014, 186, 5009–5026. [Google Scholar] [CrossRef] [PubMed]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.; Dimitriou, E. An appraisal of the potential of Landsat 8 in estimating chlorophyll-a, ammonium concentrations and other water quality indicators. Remote Sens. 2018, 10, 1018. [Google Scholar] [CrossRef] [Green Version]
- Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Estimating Chlorophyll-a of Inland Water Bodies in Greece Based on Landsat Data. Remote Sens. 2020, 12, 2087. [Google Scholar] [CrossRef]
- Hans, H.; Haan, J.; Jordans, R.; Vos, R.; Peters, S.; Rijkeboer, M. Towards airborne remote sensing of water quality in The Netherlands—Validation and error analysis. ISPRS J. Photogramm. Remote Sens. 2002, 57, 171–183. [Google Scholar]
- Correll, D.L. Phosphorus: A rate limiting nutrient in surface waters. Poult. Sci. 1999, 78, 674–682. [Google Scholar] [CrossRef]
- Kutser, T.; Arst, H.; Miller, T.; Käärmann, L.; Milius, A. Telespectrometrical estimation of water transparency, chlorophyll-a and total phosphorus concentration of Lake Peipsi. Int. J. Remote Sens. 1995, 16, 3069–3085. [Google Scholar] [CrossRef]
- Wang, Y.P.; Xia, H.; Fu, J.; Sheng, G.Y. Water quality change in reservoirs of Shenzhen, China: Detection using LANDSAT/TM data. Sci. Total Environ. 2004, 328, 195–206. [Google Scholar] [CrossRef]
- Wu, C.F.; Wu, J.P.; Qi, J.G.; Zhang, L.S.; Huang, H.Q.; Lou, L.P.; Chen, Y. Empirical estimation of total phosphorus concentration in the mainstream of the Qiantang River in China using Landsat TM data. Int. J. Remote Sens. 2010, 31, 2309–2324. [Google Scholar] [CrossRef]
- Smith, V.H. The nitrogen and phosphorus dependence of algal biomass in lakes: An empirical and theoretical analysis. Limnol. Oceanogr. 1982, 27, 1101–1112. [Google Scholar] [CrossRef]
- Malve, O.; Qian, S.S. Estimating nutrients and chlorophyll a relationships in Finnish lakes. Environ. Sci. Technol. 2006, 40, 7848–7853. [Google Scholar] [CrossRef] [PubMed]
- Healey, F.P.; Hendzel, L.L. Indicators of phosphorus and nitrogen deficiency in five algae in culture. Can. J. Fish Aquat. Res. 1979, 36, 1364–1369. [Google Scholar] [CrossRef]
- Busse, L.B.; Simpson, J.C.; Cooper, S.D. Relationships among nutrients, algae, and land use in urbanized southern California streams. Can. J. Fish. Aquat. Sci. 2006, 63, 2621–2638. [Google Scholar] [CrossRef]
- Akbar, T.A.; Hassan, Q.K.; Achari, G. A remote sensing based frame work for predicting water quality of different source waters. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2010, 34, 1–4. [Google Scholar]
- Song, K.; Zhang, B.; Wang, Z.; Li, F.; Duan, H.; Guo, Y. Water TOC and TP concentration estimation using Landsat TM data with empirical algorithms in Chagan lake, China. In Proceedings of the 2006 IEEE International Symposium on Geoscience and Remote Sensing, Denver, CO, USA, 31 July–4 August 2006; pp. 3438–3442. [Google Scholar]
- Carlson, R.E. A trophic state index for lakes. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Song, K.; Li, L.; Li, S.; Tedesco, L.; Hall, B.; Li, L. Hyperspectral Remote Sensing of Total Phosphorus (TP) in Three Central Indiana Water Supply Reservoirs. Water Air Soil Pollut. 2012, 223, 1481–1502. [Google Scholar] [CrossRef]
- Fuller, L.M.; Aichele, S.S.; Minnerick, R.J. Predicting Water Quality by Relating Secchi-Disk Transparency and Chlorophyll a Measurements to Satellite Imagery for Michigan Inland Lakes, August 2002; US Geological Survey Scientific Investigations Report; US Geological Survey: Denver, CO, USA, 2004.
- Jiang, D.; Matsushita, B.; Setiawan, F.; Vundo, A. An improved algorithm for estimating the Secchi disk depth from remote sensing data based on the new underwater visibility theory. ISPRS J. Photogramm. Remote Sens. 2019, 152, 13–23. [Google Scholar] [CrossRef]
- McCullough, I.M.; Loftin, C.S.; Sader, S.A. Combining lake and watershed characteristics with Landsat TM data for remote estimation of regional lake clarity. Remote Sens. Environ. 2012, 123, 109–115. [Google Scholar] [CrossRef]
- Baban, S.M.J. Detecting water quality parameters in the norfolk broads, U.K., using landsat imagery. Int. J. Remote Sens. 1993, 14, 1247–1267. [Google Scholar] [CrossRef]
- Nelson, S.A.C.; Soranno, P.A.; Cheruvelil, K.S.; Batzli, S.A.; Skole, D.L. Regional Assessment of lake water clarity using satellite remote sensing. J. Limnol. 2003, 62, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Hicks, B.J.; Stichbury, G.A.; Brabyn, L.K.; Allan, M.G.; Ashraf, S. Hindcasting water clarity from Landsat satellite images of unmonitored shallow lakes in the Waikato region, New Zealand. Environ. Monit. Assess. 2013, 185, 7245–7261. [Google Scholar] [CrossRef]
- Wu, G.; de Leeuw, J.; Skidmore, A.K.; Prins, H.H.T.; Liu, Y. Comparison of MODIS and Landsat TM5 images for mapping tempo-spatial dynamics of Secchi disk depths in Poyang Lake National Nature Reserve, China. Int. J. Remote Sens. 2008, 29, 2183–2198. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in Inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Kloiber, S.M.; Bauer, M.E.; Brezonik, P.L. Image Processing Protocol for Regional Assessments of Lake Water Quality; University of Minnesota: St. Paul, MN, USA, 2001. [Google Scholar]
- Megard, R.O.; Settles, J.C.; Boyer, H.A.; Combs, W.S. Light, Secchi Disks, and Trophic States. Limnol. Oceanogr. 1980, 25, 373–377. [Google Scholar] [CrossRef]
- Olmanson, L.G.; Bauer, M.E.; Brezonik, P.L. A 20-year Landsat water clarity census of Minnesota’s 10,000 lakes. Remote Sens. Environ. 2008, 112, 4086–4097. [Google Scholar] [CrossRef]
- Peckham, S.D.; Chipman, J.W.; Lillesand, T.M.; Dodson, S.I. Alternate stable states and the shape of the lake trophic distribution. Hydrobiologia 2006, 571, 401–407. [Google Scholar] [CrossRef]
- Nauman, E. The Scope of chief problems of regional limnology. Int. Rev. Ges. Hydrobiol. 1929, 21, 423. [Google Scholar] [CrossRef]
- Mavromati, E.; Kagalou, I.; Kemitzoglou, D.; Apostolakis, A.; Seferlis, M.; Tsiaoussi, V. Relationships among land use patterns, hydromorphological features and physicochemical parameters of surface waters: WFD lake monitoring in Greece. Environ. Process. 2018, 5, 139–151. [Google Scholar] [CrossRef]
- American Public Health Association (APHA). Standard Methods for the Examination of Water and Wastewater, 17th ed.; American Public Health Association: Washington, DC, USA, 1989. [Google Scholar]
- Kloiber, S.M.; Brezonik, P.L.; Olmanson, L.G.; Bauer, M.E. A procedure for regional lake water clarity assessment using Landsat multispectral data. Remote Sens. Environ. 2002, 82, 38–47. [Google Scholar] [CrossRef]
- Hellweger, F.L.; Schlosser, P.; Lall, U.; Weissel, J.K. Use of satellite imagery for water quality studies in New York Harbor. Estuar. Coast. Shelf Sci. 2004, 61, 437–448. [Google Scholar] [CrossRef]
- Chu, H.-J.; Kong, S.-J.; Chang, C.-H. Spatio-temporal water quality mapping from satellite images using geographically and temporally weighted regression. Int. J. Appl. Earth Obs. Geoinf. 2018, 65, 1–11. [Google Scholar] [CrossRef]
- Barrett, D.C.; Frazier, A.E. Automated Method for Monitoring Water Quality Using Landsat Imagery. Water 2016, 8, 257. [Google Scholar] [CrossRef] [Green Version]
- Japitana, M.; Burce, M. A Satellite-based Remote Sensing Technique for Surface Water Quality Estimation. Eng. Technol. Appl. Sci. Res. 2019, 9, 3965–3970. [Google Scholar] [CrossRef]
- Doña, C.; Sánchez, M.J.; Caselles, V.; Domínguez, J.A.; Camacho, A. Empirical Relationships for Monitoring Water Quality of Lakes and Reservoirs Through Multispectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2014, 7, 1632–1641. [Google Scholar] [CrossRef]
- Dancey, C.P.; Reidy, J. Statistics without Maths for Psychology, 4th ed.; Pearson Education: Harlow, UK, 2007. [Google Scholar]
- McKinna, L.; Werdell, P. Approach for identifying optically shallow pixels when processing ocean-color imagery. Opt. Express 2018, 26, A915–A928. [Google Scholar] [CrossRef]
- Lim, J.; Choi, M. Assessment of water quality based on Landsat 8 operational land imager associated with human activities in Korea. Environ. Monit. Assess. 2015, 187, 384. [Google Scholar] [CrossRef]
- Isenstein, E.M.; Park, M.-H. Assessment of nutrient distribution in Lake Champlain using satellite remote sensing. J. Environ. Sci. 2014, 26, 1831–1836. [Google Scholar] [CrossRef]
- Chen, J.; Quan, W. Using Landsat/TM imagery to estimate nitrogen and phosphorus concentration in Taihu Lake, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 273–280. [Google Scholar] [CrossRef]
- Huang, C.; Guo, Y.; Yang, H.; Li, Y.; Zou, J.; Zhang, M.; Lyu, H.; Zhu, A.; Huang, T. Using remote sensing to track variation in phosphorus and its interaction with chlorophyll-a and suspended sediment. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4171–4180. [Google Scholar] [CrossRef]
- Moses, A.S.; Janaki, L.; Joseph, S.; Kizhur, K.R. Determining the spatial variation of phosphorus in a lake system using remote sensing techniques. Lakes Reserv. Res. Manag. 2014, 19, 24–36. [Google Scholar] [CrossRef]
- Brezonik, P.L.; Menken, K.; Bauer, M.E. Landsat-based remote sensing of lake water quality characteristics, including chlorophyll and colored dissolved organic matter (CDOM). Lake Reserv. Manag. 2005, 2, 373–382. [Google Scholar] [CrossRef]
- Choubey, V.K. Laboratory experiment, field and remotely sensed data analysis for the assessment of suspended solids concentration and secchi depth of the reservoir surface water. Int. J. Remote Sens. 1998, 19, 3349–3360. [Google Scholar] [CrossRef]
- Zhou, Y.; Liu, H.; He, B.; Yang, X.; Feng, Q.; Kutser, T.; Chen, F.; Zhou, X.; Xiao, F.; Kou, J. Secchi Depth estimation for optically-complex waters based on spectral angle mapping—Derived water classification using Sentinel-2 data. Int. J. Remote Sens. 2021, 42, 3123–3145. [Google Scholar] [CrossRef]
- Ohammad, M.M.; Alsahli, M.N. Spatiotemporal variability of Secchi depths of the North Arabian Gulf over the last two decades. Estuar. Coast. Shelf Sci. 2021, 260, 107487. [Google Scholar]
- Kratzer, S.; Kyryliuk, D.; Edman, M.; Philipson, P.; Lyon, S.W. Synergy of Satellite, In Situ and Modelled Data for Addressing the Scarcity of Water Quality Information for Eutrophication Assessment and Monitoring of Swedish Coastal Waters. Remote Sens. 2019, 11, 2051. [Google Scholar] [CrossRef] [Green Version]
- Prasad, A.D.; Siddaraju, P. Carlson’s Trophic State Index for the assessment of trophic status of two lakes in Mandya district. Adv. Appl. Sci. Res. 2012, 3. [Google Scholar]
- Zheng, L.; An, Z.; Chen, X.; Liu, H. Changes in Water Environment in Erhai Lake and Its Influencing Factors. Water 2021, 13, 1362. [Google Scholar] [CrossRef]
- Søballe, D.M.; Kimmel, B.L.; Kennedy, R.H.; Gaugush, R.F. Reservoirs. In Biodiversity of the Southeastern United States: Aquatic communities; Hackney, C.T., Adams, S.M., Martin, W.H., Eds.; John Wiley and Sons: New York, NY, USA, 1992; pp. 421–474. [Google Scholar]
- Canfield, D., Jr.; Bachmann, R. Prediction of total phosphorus concentrations, chlorophyll a, and secchi depths in natural and artificial lakes. Can. J. Fish. Aquat. Sci. 1981, 38, 414–423. [Google Scholar] [CrossRef]
- Virginia Water Resources Research Institute; State University Blacksburg. Nutrients in Lakes and Reservoirs-Aliterature Review for Use in Nutrient Criteria Development. VWRRC Special Report SR34–2007. Virginia. 2007. Available online: http://www.vwrrc.vt.edu (accessed on 10 October 2020).
- Canfield, D.E.; Hodgson, L.M. Prediction of Secchi disc depths in Florida lakes: Impact of algal biomass and organic color. Hydrobiologia 1983, 99, 51–60. [Google Scholar] [CrossRef]
- Heiskary, S.; Wilson, B. Minnesota Lake Water Quality: Developing Nutrient Criteria, 3rd ed.; Minnesota Pollution Control Agency: St. Paul, MN, USA, 2005. [Google Scholar]
- Lind, O.T. The effect of non-algal turbidity on the relationship of Secchi depth to chlorophyll a. Hydrobiologia 1986, 140, 27–35. [Google Scholar] [CrossRef]
- Lorenzen, M.W. The use of chlorophyll-secchi disk relationships. Limnol. Oceanogr. 1980, 25, 371–372. [Google Scholar] [CrossRef]
- Allee, R.; Johnson, J. Use of satellite imagery to estimate surface chlorophyll a and Secchi disc depth of Bull Shoals Reservoir, Arkansas, USA. Int. J. Remote Sens. 1999, 20, 1057–1072. [Google Scholar] [CrossRef]
- Page, B.P.; Olmanson, L.G.; Mishra, D.R. A harmonized image processing work-flow using Sentinel-2/MSI and Landsat-8/OLI for mapping water clarity in opti-cally variable lake systems. Remote Sens. Environ. 2019, 231, 111284. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Shi, K.; Zhou, Y.; Li, N. Remote sensing estimation of water clarity for various lakes in China. Water Res. 2021, 192, 116844. [Google Scholar] [CrossRef] [PubMed]
- Dekker, A.; Zamurović-Nenad, Ž.; Hoogenboom, H.; Peters, S. Remote sensing, ecological water quality modelling and in situ measurements: A case study in shallow lakes. Hydrolog. Sci. J. 1996, 41, 531–547. [Google Scholar] [CrossRef]
- Uusitalo, R.; Yli-Halla, M.; Turtola, E. Suspended soil as a source of potentially bioavailable phosphorus in surface runoff waters from clay soils. Water Res. 2000, 34, 2477–2482. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Cooper, C.M.; Schiebe, F.R. The relationship of MSS and TM digital data with suspended sediments, chlorophyll, and temperature in Moon Lake, Mississippi. Remote Sens. Environ. 1990, 33, 137–148. [Google Scholar] [CrossRef]
- Lathrop, R. Landsat Thematic Mapper monitoring of turbid inland water quality. Photogramm. Eng. Remote Sens. 1992, 58, 465–470. [Google Scholar]
- Lillesand, T.M.; Kiefer, R.W. Remote Sensing and Image Interpretation, 4th ed.; John Wiley and Sons: New York, NY, USA, 2000; p. 724. [Google Scholar]
- Buiteveld, H.; Hakvoort, J.H.M.; Donze, M. The optical properties of pure water. SPIE Ocean. Opt. XII 1994, 2258, 174–183. [Google Scholar]
- Ouma, O.Y.; Noor, K.; Herbert, K. Modelling Reservoir Chlorophyll-a, TSS, and Turbidity Using Sentinel-2A MSI and Landsat-8 OLI Satellite Sensors with Empirical Multivariate Regression. J. Sens. 2020, 2020, 8858408. [Google Scholar] [CrossRef]
- Kontopoulou, E.; Kolokoussis, P.; Karantzalos, K. Water quality estimation in Greek lakes from Landsat 8 multispectral satellite data. In Proceedings of the 10th World Congress of the European Water Resources Association (EWRA) on Water Resources and Environment (EWRA2017), European Water 2017 No.58, Athens, Greece, 5–9 July 2017; pp. 191–196. [Google Scholar]
- Tripathi, N.K.; Patil, A.A. Spectral characterization of aquatic nutrients and water quality parameters in marine environment. Bibliogr. Inform. 2004, 15, 25–31. [Google Scholar] [CrossRef] [Green Version]
- Membrillo-Abad, A.S.; Torres-Vera, M.A.; Alcocer, J.; Prol-Ledesma, R.M.; Oseguera, L.A.; Ruiz-Armenta, J.R. Trophic State Index estimation from remote sensing of lake Chapala, México. Rev. Mex. Cienc. Geol. 2016, 33. [Google Scholar]
- Papoutsa, C.; Akylas, E.; Hadjimitsis, D. Trophic State Index derivation through the remote sensing of Case-2 water bodies in the Mediterranean region. Cent. Eur. J. Geosci. 2014, 6, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Rivani, A.; Wicaksono, P. Water trophic status mapping of tecto-volcanic maninjau lake during algae bloom using landsat 8 OLI satellite imagery. In Proceedings of the 2018 IEEE International Conference on Aerospace Electronics and Remote Sensing Technology (ICARES), Bali, Indonesia, 20–21 September 2018. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, Y.; Hallikainen, M. Water quality monitoring using remote sensing in support of the EU water framework directive (WFD): A case study in the Gulf of Finland. Environ. Monit. Assess. 2007, 124, 157–166. [Google Scholar] [CrossRef]
- Kimmel, B.L.; Lind, O.T.; Paulson, L.J. Reservoir primary production. In Reservoir Limnology: Ecological Perspectives; Thorton, K.W., Kimmel, B.L., Payne, F.E., Eds.; John Wiley and Sons: New York, NY, USA, 1990; pp. 133–193. [Google Scholar]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a strong future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Brewin, R.J.; Sathyendranath, S.; Müller, D.; Brockmann, C.; Deschamps, P.Y.; Devred, E.; Doerffer, R.; Fomferra, N.; Franz, B.; Grant, S.M. Groom the Ocean Colour Climate Change Initiative: III. A round-robin comparison on in-water bio-optical algorithms. Remote Sens. Environ. 2015, 162, 271–294. [Google Scholar] [CrossRef] [Green Version]


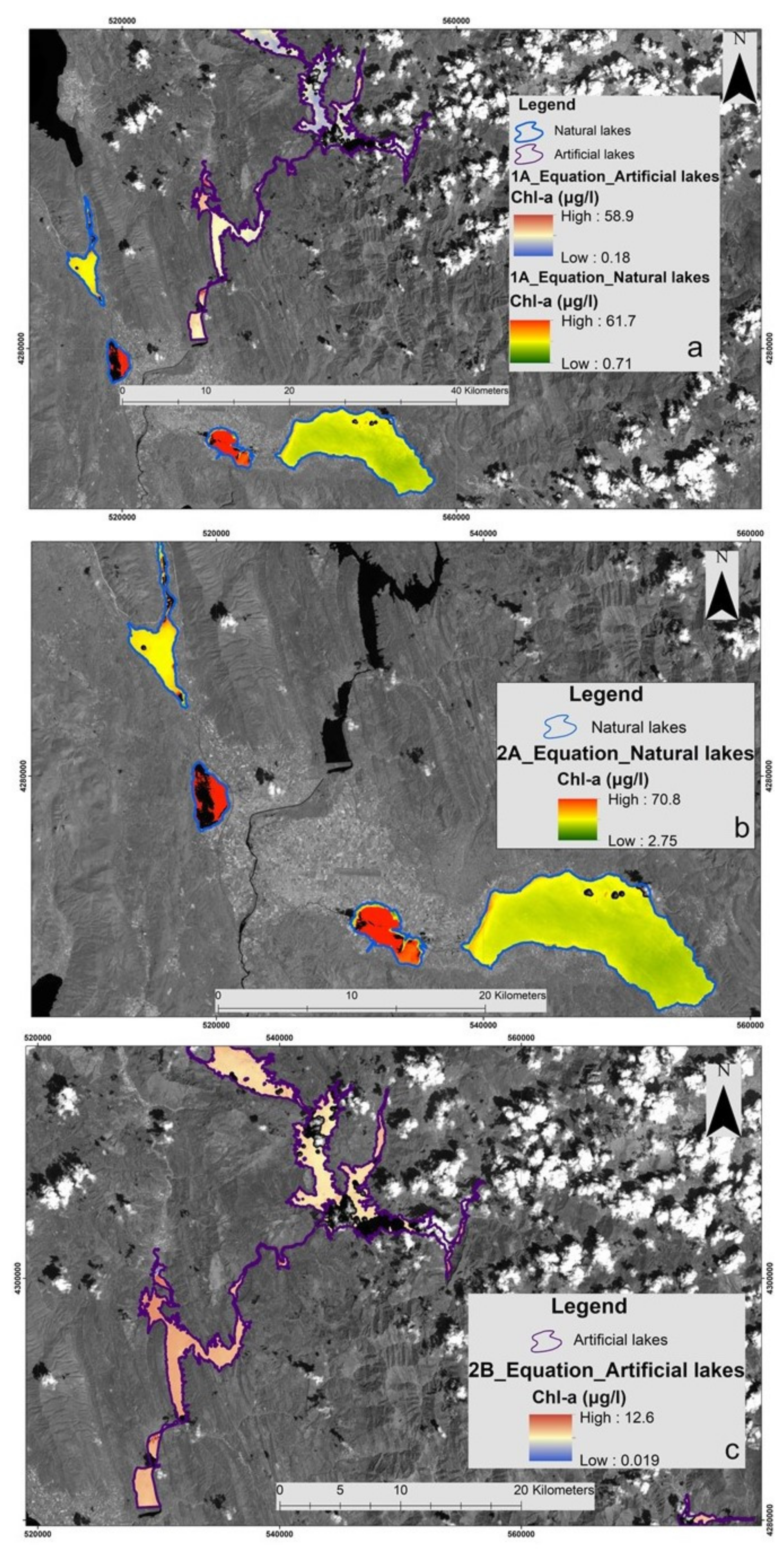
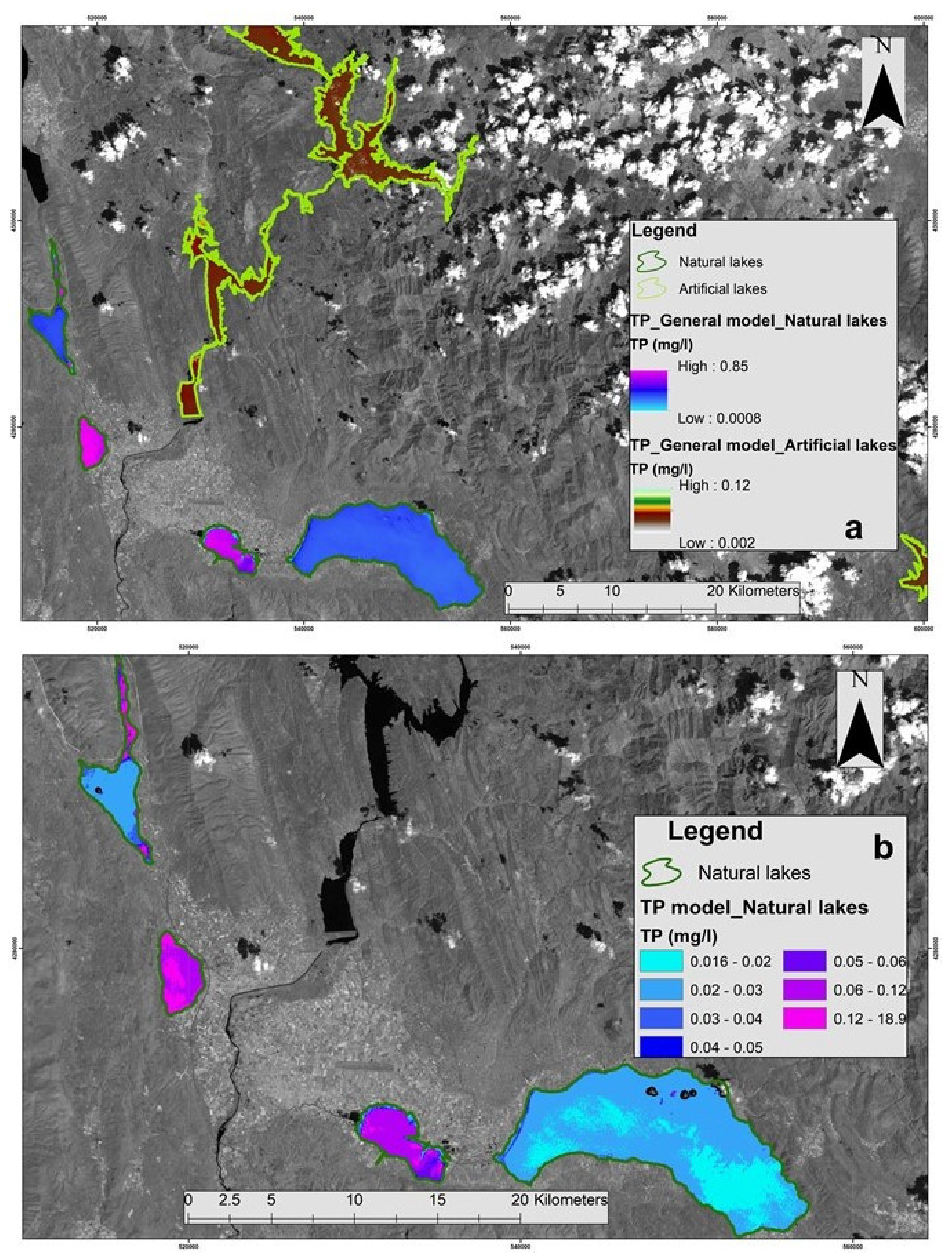
| No | National Name Station | Surface (km2) | (N)atural/ (A)rtificial | Mean Depth (m) | No | National Name Station | Surface (km2) | (N)atural/ (A)rtificial | Mean Depth (m) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Lake Ladona | - | A | - | 28 | Lake Petron | 11.91 | N | 3.1 |
| 2 | Lake Pineiou | 19.64 | A | 15.1 | 29 | Lake Zazari | 2.98 | N | 3.95 |
| 3 | Lake Stymfalia | - | N | 1.31 | 30 | Lake Cheimaditida | 9.82 | N | 1.01 |
| 4 | Lake Feneou | 0.47 | A | 10.5 | 31 | Lake Kastorias | 30.87 | N | 3.7 |
| 5 | Lake Kremaston | 68.43 | A | 47.2 | 32 | Lake Sfikias | 3.96 | A | 23.2 |
| 6 | Lake Kastrakiou | 25.58 | A | 33.2 | 33 | Lake Asomaton | 2.46 | A | 20.8 |
| 7 | Lake Stratou | 7.02 | A | 9.6 | 34 | Lake Polyfytou | 63.49 | A | 22.4 |
| 8 | Lake Tavropou | 21.46 | A | 15.0 | 35 | Lake Mikri Prespa A | - | N | 3.95 |
| 9 | Lake Lysimacheia | 10.87 | N | 3.5 | 36 | Lake Mikri Prespa B | N | - | |
| 10 | Lake Ozeros | 10.57 | N | 3.8 | 37 | Lake Megali Prespa A | - | N | 17 |
| 11 | Lake Trichonida | 93.53 | N | 29.6 | 38 | Lake Megali Prespa B | N | - | |
| 12 | Lake Amvrakia | 13.14 | N | 23.4 | 39 | Lake Doirani 1 | 33.25 | N | 4.6 |
| 13 | Lake Voulkaria | 7.38 | N | 0.96 | 40 | Lake Doirani 2 | N | - | |
| 14 | Lake Saltini | - | N | - | 41 | Lake Pikrolimni | 6.30 | N | 1.2 |
| 15 | Lake Mornou | 17.50 | A | 38.5 | 42 | Lake Koroneia | - | N | 3.8 |
| 16 | Lake Evinou | 2.68 | A | 31.5 | 43 | Lake Volvi | 70.36 | N | 12.3 |
| 17 | Lake Pigon Aoou | 11.44 | A | 20.8 | 44 | Lake Kerkini | - | A | 2.19 |
| 18 | Lake Pournariou | 19.28 | A | 29.8 | 45 | Lake Leukogeion | 0.83 | A | 4.05 |
| 19 | Lake Pamvotida | 21.82 | N | 5.3 | 46 | Lake Ismarida | - | N | 0.9 |
| 20 | Lake Pournariou II | 0.56 | A | 11.7 | 47 | Lake Platanovrysis | 2.99 | A | 26.4 |
| 21 | Lake Marathona | 2.17 | A | 15.8 | 48 | Lake Thisavrou | 13.43 | A | 38.4 |
| 22 | Lake Dystos | - | N | - | 49 | Lake Gratinis | 0.80 | A | 14.2 |
| 23 | Lake Yliki | 19.96 | N | 20.1 | 50 | Lake N. Adrianis | - | A | - |
| 24 | Lake Paralimni | 9.96 | N | 2.99 | 51 | Lake Kourna | - | N | 15 |
| 25 | Lake Karlas | - | A | 0.9 | 52 | Lake Bramianou | - | A | 10.1 |
| 26 | Lake Smokovou | - | A | - | 53 | Lake Faneromenis | 0.33 | A | 9.98 |
| 27 | Lake Vegoritida | 47.67 | N | 26.52 | |||||
| Secchi Depth (m) in Year: | N | Min | Max | Mean | Std. Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| 2013 | 134 | 0.20 | 14.0 | 3.1 | 2.8 | 1.5 | 3.3 |
| 2014 | 125 | 0.030 | 14.0 | 3.8 | 3.1 | 0.9 | 0.2 |
| 2015 | 140 | 0.030 | 11.0 | 3.2 | 2.6 | 0.8 | −0.2 |
| 2016 | 64 | 0.050 | 15.0 | 3.03 | 3.2 | 1.7 | 3.1 |
| 2018 | 314 | 0.100 | 15.5 | 3.04 | 2.7 | 1.4 | 2.4 |
| all years | 777 | 0.03 | 15.5 | 3.2 | 2.8 | 1.3 | 1.7 |
| Total Phosphorus (mg/L) in Year | N | Min | Max | Mean | Std. Deviation | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| 2015 | 169 | 0.01 | 4.2 | 0.14 | 0.56 | 6.7 | 45.4 |
| 2016 | 69 | 0.02 | 5.1 | 0.23 | 0.8 | 5.5 | 29.9 |
| 2018 | 132 | 0.02 | 13.3 | 0.48 | 1.8 | 4.9 | 25.98 |
| all years | 370 | 0.01 | 13.3 | 0.28 | 1.2 | 6.9 | 54.2 |
| TSI Values | Trophic Status | Attributes | |
|---|---|---|---|
| <40 | <30 | Oligotrophic | Transparent water |
| 30–40 | Oligotrophic-Mesotrophic | ||
| 41–50 | 41–48 | Mesotrophic | Higher turbidity, higher algae abundance and macrophytes |
| 49–50 | Mesotrophic-Eutrophic | ||
| 51–70 | 51–60 | Mesotrophic-Eutrophic | |
| 61–70 | Eutrophic | Usually blue-green algae blooms | |
| >70 | Hypereutrophic | Extreme blue-green algae blooms | |
| Value of Importance | |||
|---|---|---|---|
| Variable | Secchi | SQRT(Secchi) | LOG-LN(Secchi) |
| Green/SWIR1 | 0.014 | 0.008 | 0.011 |
| LOG(Blue/Red) | 0.033 | 0.044 | 0.041 |
| (Blue − Red)/(Blue + Red) | 0.034 | 0.045 | 0.042 |
| LN Green/LN Blue | 0.035 | 0.041 | 0.045 |
| Red/Blue | 0.035 | 0.045 | 0.046 |
| LOG Blue/LOG Green | 0.037 | 0.043 | 0.047 |
| LN((Blue − SWIR2)/(Green − SWIR1)) | 0.039 | 0.032 | 0.038 |
| (Blue − Red)/Green | 0.046 | 0.054 | 0.050 |
| Blue + Red + Red/Blue | 0.046 | 0.050 | 0.047 |
| Green/Blue | 0.052 | 0.052 | 0.058 |
| (Blue − Green)/(Blue + Green) | 0.056 | 0.055 | 0.059 |
| LOG (Blue/Green) | 0.056 | 0.055 | 0.059 |
| Model | R | R2 | Adjusted R2 | Std. Error of the Estimate | Change Statistics | Durbin-Watson | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 Change | F Change | df1 | df2 | Sig. F Change | ||||||
| Secchigeneral | 0.74 | 0.54 | 0.54 | 0.46 | 0.24 | 115.8 | 1 | 222 | 0.0 | 2.24 |
| Scenario/Model | R | R2 | Adjusted R2 | Std. Error of the Estimate | Change Statistics | Durbin-Watson | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 Change | F Change | df1 | df2 | Sig. F Change | ||||||
| Secchinatural | 0.78 | 0.6 | 0.59 | 0.55 | 0.06 | 8.6 | 1 | 59 | 0.005 | 2.14 |
| Secchiartificial | 0.73 | 0.53 | 0.51 | 0.37 | 0.07 | 16 | 1 | 105 | 0.0 | 2.12 |
| Value of Importance | ||
|---|---|---|
| Variable | TP | LOG-LN (TP) |
| Red/SWIR1 | 0.2672 | 0.3283 |
| Green/SWIR1 | 0.2296 | 0.2973 |
| LN Green/LNSWIR1 | 0.1308 | |
| Green/Red | 0.1249 | 0.1525 |
| LOG Chl-a | 0.0953 | 0.1848 |
| LOG (Red/Green) | 0.0776 | |
| LN Red/LN Green | 0.0344 | |
| LN Secchi | 0.1315 | |
| Model | R | R2 | Adjusted R2 | Std. Error of the Estimate | Change Statistics | Durbin-Watson | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 Change | F Change | df1 | df2 | Sig. F Change | ||||||
| LogTPgeneral | 0.85 | 0.73 | 0.71 | 0.18 | 0.05 | 7.6 | 1 | 43 | 0.008 | 2.34 |
| Model | R | R2 | Adjusted R2 | Std. Error of the Estimate | Change Statistics | Durbin-Watson | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 Change | F Change | df1 | df2 | Sig. F Change | ||||||
| LogTPnatural | 0.91 | 0.82 | 0.81 | 0.17 | 0.06 | 8.1 | 1 | 26 | 0.009 | 1.9 |
| 1st Validation (20%) | 2nd Validation (2018 Data) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Models | Spearman r | Average in situ * | Average Satellite * | Average Residuals (m) | RMSE (Secchi; m/% of Max Secchi/% of Average Secchi) | Spearman r | Average In Situ * | Average Satellite * | Average Residuals (m) | RMSE (Secchi; m/% of Max Secchi/% of Average Secchi) |
| Secchigeneral Training dataset N = 228 | 0.78 ** N = 57 | 2.1 | 2.1 | 0.00001 | 0.24/1.7%/5.1% | 0.58 ** N = 115 | 2.02 | 1.86 | 0.03 | 0.37/2.39%/8.2% |
| Secchigeneral applied on natural | 0.65 ** N=44 | 1.93 | 1.86 | 0.005 | 0.3 | |||||
| Secchigeneral applied on artificial | 0.51 ** N = 57 | 2.1 | 1.82 | 0.06 | 0.44 | |||||
| Secchinatural Training dataset N = 65 | 0.95 ** N = 27 | 1.76 | 1.74 | 0.0002 | 0.14/0.93%/3.6% | 0.73 ** N = 28 | 1.9 | 1.8 | 0.008 | 0.3/1.92%/7.1% |
| Secchiartificial Training dataset N = 111 | 0.62 ** N = 28 | 2.01 | 2.04 | 0.001 | 0.1/1.18%/2.3% | 0.56 ** N = 40 | 2.13 | 2.17 | 0.002 | 0.14/1.43%/3.3% |
| 1st Validation (20%) | 2nd Validation (2018 Data) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Models | Spearman r | Average In Situ * | Average Satellite * | Average Residuals (mg/L) | RMSE (TP; mg/L) | Spearman r | Average In Situ * | Average Satellite * | Average Residuals (mg/L) | RMSE (TP; mg/L) |
| LogTPgeneral Training dataset N = 46 | 0.71 ** N = 12 | −1.79 | −1.78 | 0.95 | 1.41 | 0.81 ** N = 33 | −1.22 | −1.18 | 0.91 | 1.46 |
| LogTPgeneral applied on natural | 0.55 ** N = 40 | −1.1 | −1.2 | 1.21 | 3.2 | |||||
| LogTPgeneral applied on artificial | 0.86 ** N = 11 | −1.33 | −1.21 | 0.76 | 1.51 | |||||
| LogTPnatural Training dataset N = 29 | 0.93 ** N = 7 | −1.61 | −1.54 | 0.86 | 1.43 | 0.68 ** N = 49 | −1.26 | −1.22 | 0.93 | 1.63 |
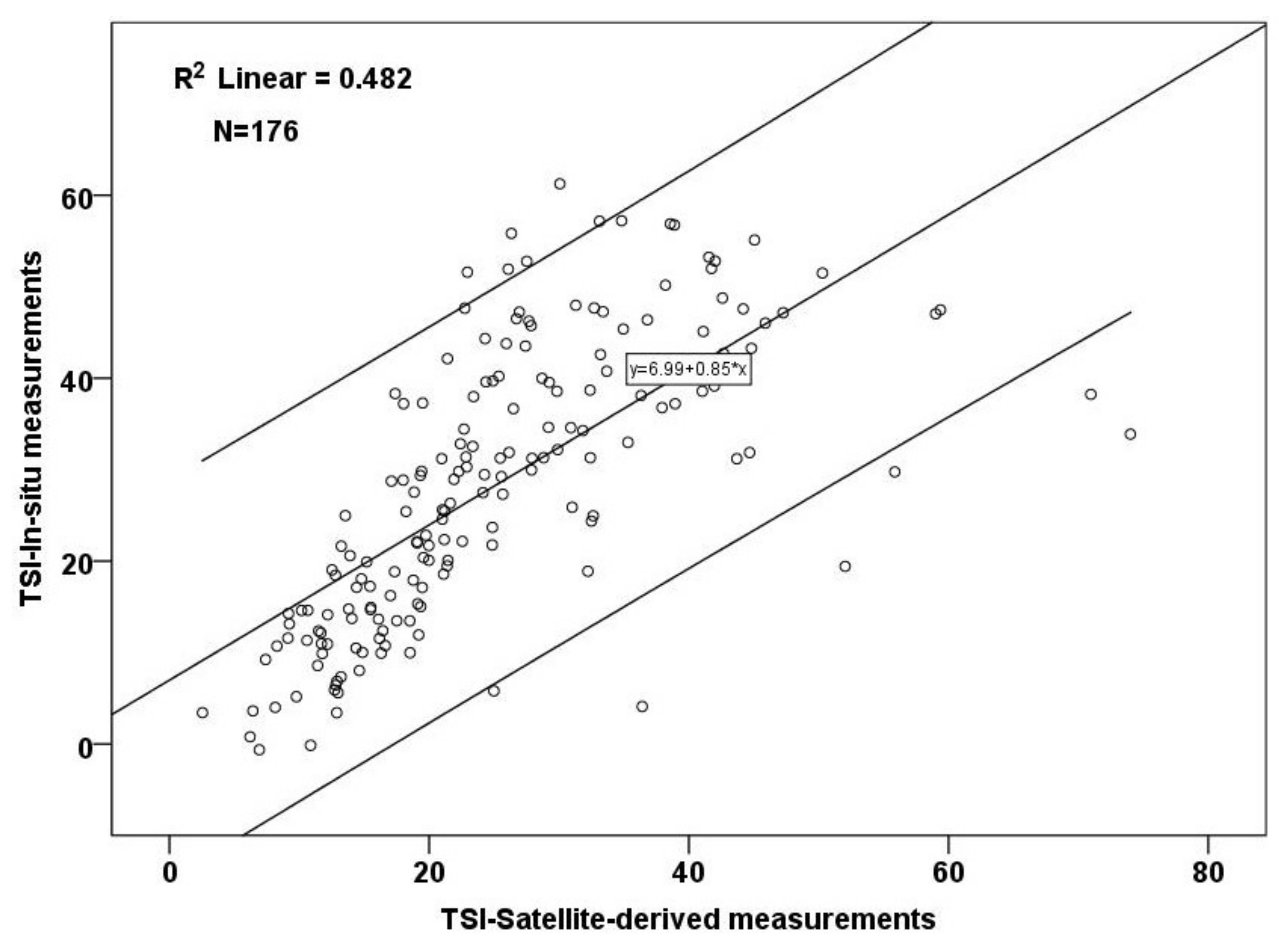
| Whole Dataset | TSI (In Situ) | TSI (Satellite) | TSI (In Situ) | TSI (Satellite) |
|---|---|---|---|---|
| Frequency | Valid Percent | |||
| 1 (Oligotrophic) | 92 | 124 | 52.3 | 70.5 |
| 2 (Oligotrophic-Mesotrophic) | 42 | 30 | 23.9 | 17 |
| 3 (Mesotrophic) | 26 | 15 | 14.8 | 8.5 |
| 4 (Mesotrophic-Eutrophic) | 15 | 5 | 8.5 | 2.8 |
| 5 (Eutrophic) | 1 | - | 0.6 | - |
| 6 (Hypereutrophic) | - | 2 | 1.1 | |
| Total | 176 | 176 | 100.0 | 100.0 |
| Natural Lakes | TSI (In Situ) | TSI (Satellite) | TSI (In Situ) | TSI (Satellite) |
|---|---|---|---|---|
| Frequency | Valid Percent | |||
| 1 (Oligotrophic) | 50 | 59 | 44.6 | 52.7 |
| 2 (Oligotrophic-Mesotrophic) | 35 | 29 | 31.3 | 25.9 |
| 3 (Mesotrophic) | 14 | 11 | 12.5 | 9.8 |
| 4 (Mesotrophic-Eutrophic) | 12 | 7 | 10.7 | 6.3 |
| 5 (Eutrophic) | 1 | 1 | 0.9 | 0.9 |
| 6 (Hypereutrophic) | - | 5 | - | 4.5 |
| Total | 112 | 112 | 100.0 | 100.0 |
| Artificial Lakes | TSI (In Situ) | TSI (Satellite) | TSI (In Situ) | TSI (Satellite) |
|---|---|---|---|---|
| Frequency | Valid Percent | |||
| 1 (Oligotrophic) | 42 | 48 | 65.6 | 75 |
| 2 (Oligotrophic-Mesotrophic) | 7 | 9 | 10.9 | 14.1 |
| 3 (Mesotrophic) | 12 | 4 | 18.8 | 6.3 |
| 4 (Mesotrophic-Eutrophic) | 3 | 3 | 4.7 | 4.7 |
| Total | 64 | 64 | 100.0 | 100.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markogianni, V.; Kalivas, D.; Petropoulos, G.P.; Dimitriou, E. Modelling of Greek Lakes Water Quality Using Earth Observation in the Framework of the Water Framework Directive (WFD). Remote Sens. 2022, 14, 739. https://doi.org/10.3390/rs14030739
Markogianni V, Kalivas D, Petropoulos GP, Dimitriou E. Modelling of Greek Lakes Water Quality Using Earth Observation in the Framework of the Water Framework Directive (WFD). Remote Sensing. 2022; 14(3):739. https://doi.org/10.3390/rs14030739
Chicago/Turabian StyleMarkogianni, Vassiliki, Dionissios Kalivas, George P. Petropoulos, and Elias Dimitriou. 2022. "Modelling of Greek Lakes Water Quality Using Earth Observation in the Framework of the Water Framework Directive (WFD)" Remote Sensing 14, no. 3: 739. https://doi.org/10.3390/rs14030739
APA StyleMarkogianni, V., Kalivas, D., Petropoulos, G. P., & Dimitriou, E. (2022). Modelling of Greek Lakes Water Quality Using Earth Observation in the Framework of the Water Framework Directive (WFD). Remote Sensing, 14(3), 739. https://doi.org/10.3390/rs14030739









