Spatiotemporal and Multiscale Analysis of the Coupling Coordination Degree between Economic Development Equality and Eco-Environmental Quality in China from 2001 to 2020
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sources
2.3. Data Methods
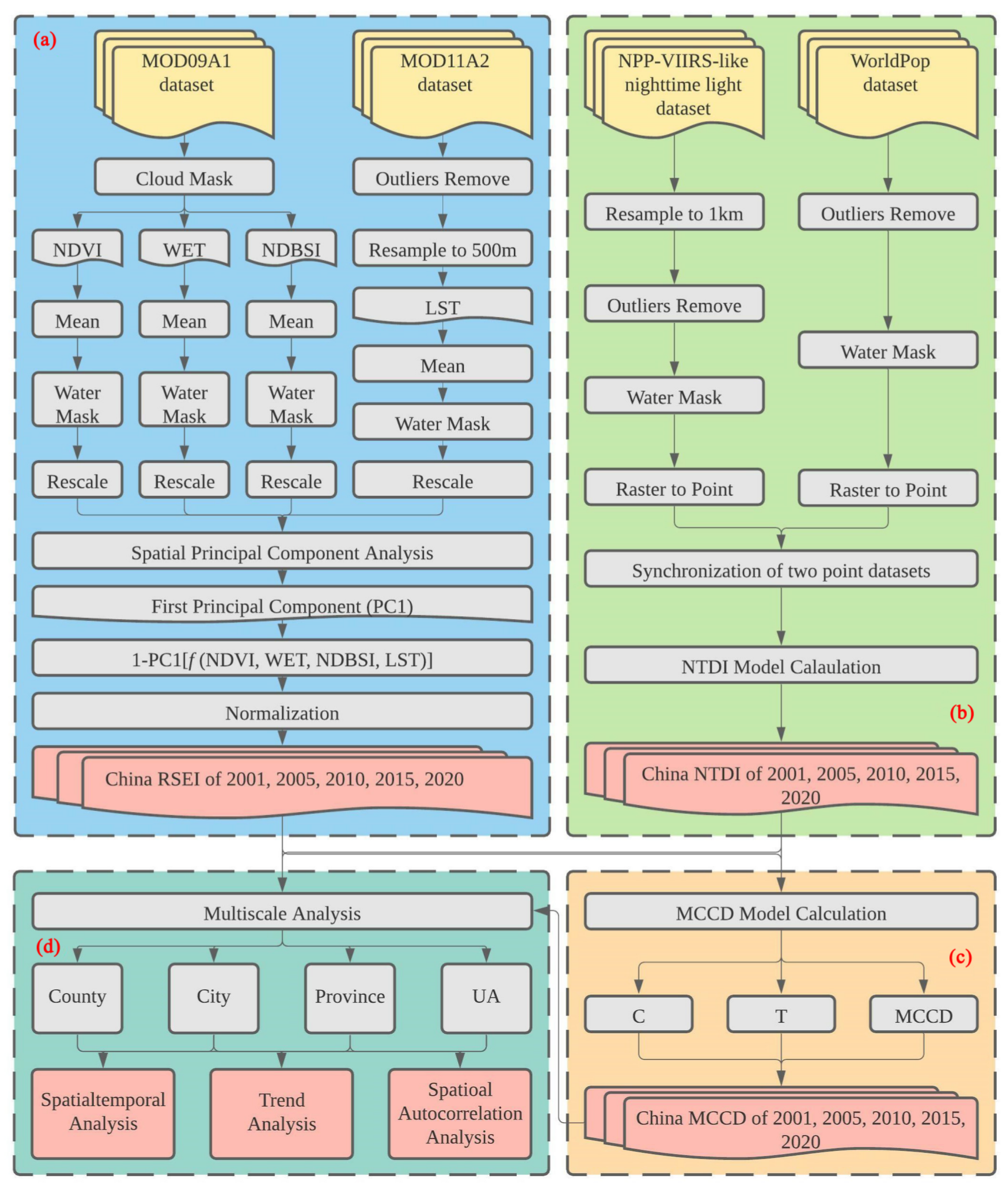
2.3.1. Calculation of the RSEI
2.3.2. Calculation of the NTDI
2.3.3. Calculation of the MCCD
2.3.4. Calculation of Spatial Autocorrelation
2.3.5. Trend Analysis Method
3. Results
3.1. Spatiotemporal and Change Trends of the RSEI at Different Scales
3.2. Spatiotemporal and Change Trends of the NTDI at Different Scales
3.3. Spatiotemporal and Change Trends of the MCCD at Different Scales
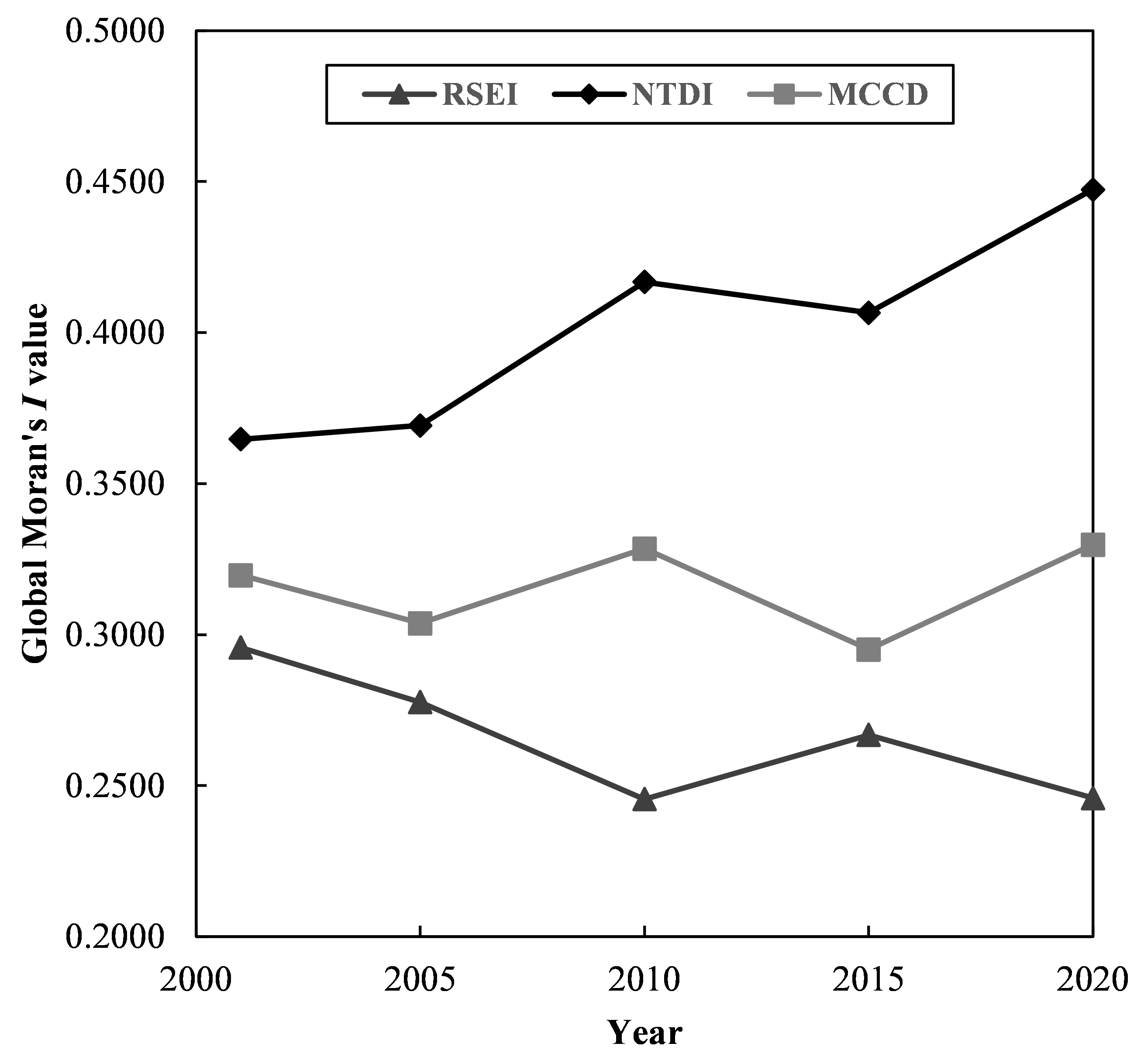
3.4. Spatial Autocorrelation Analysis of the RSEI, NTDI and MCCD at Different Scales
4. Discussion
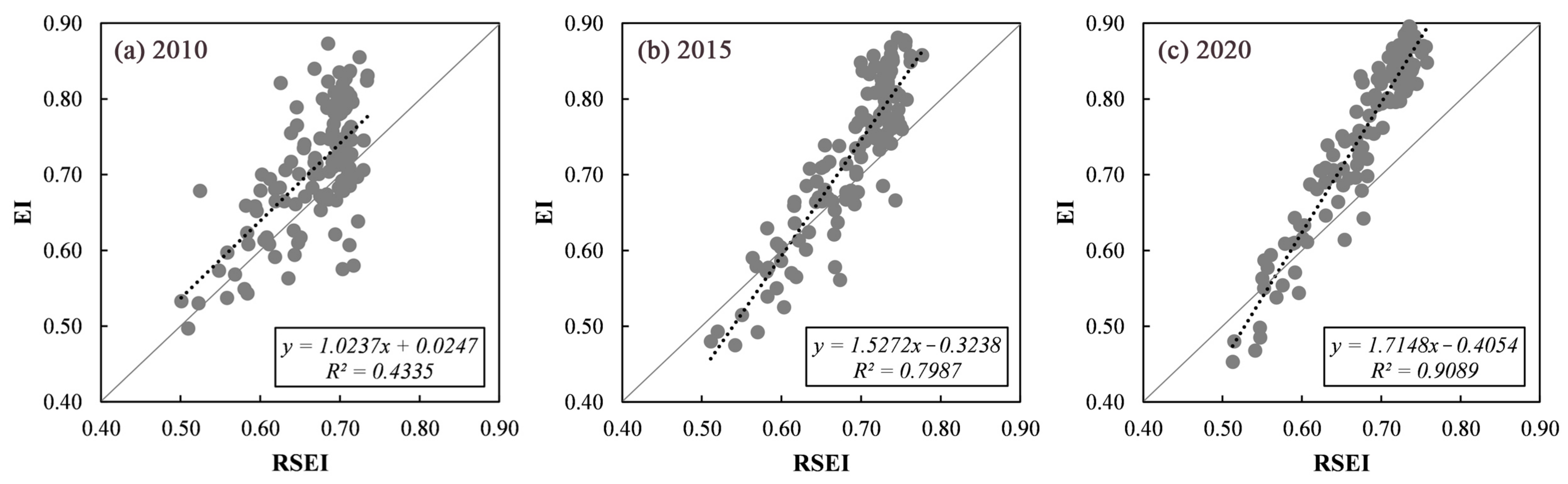
4.1. Spatial Principal Component Analysis of the RSEI and Its Validation
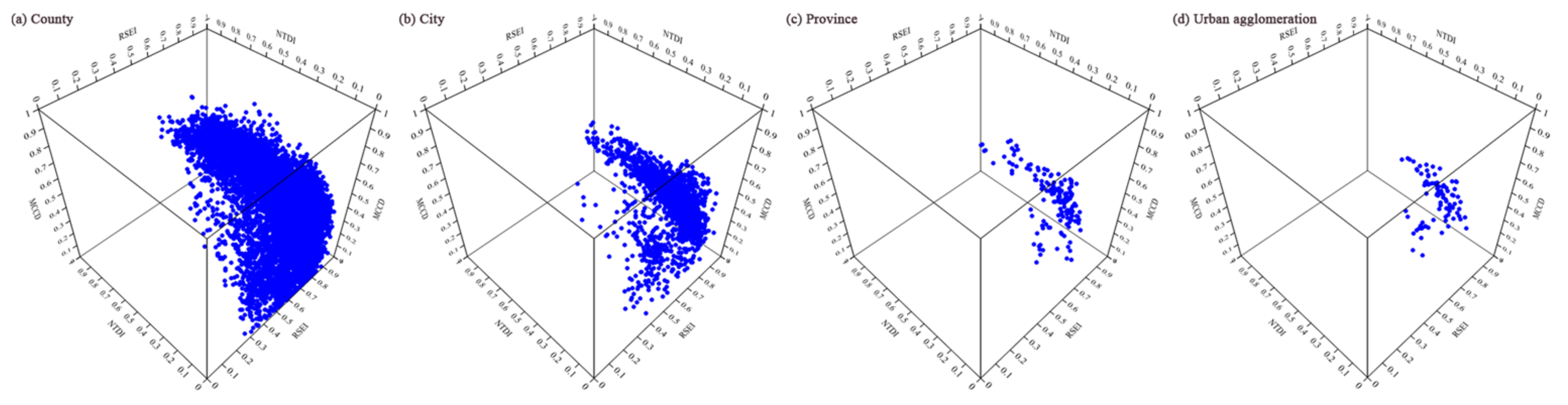
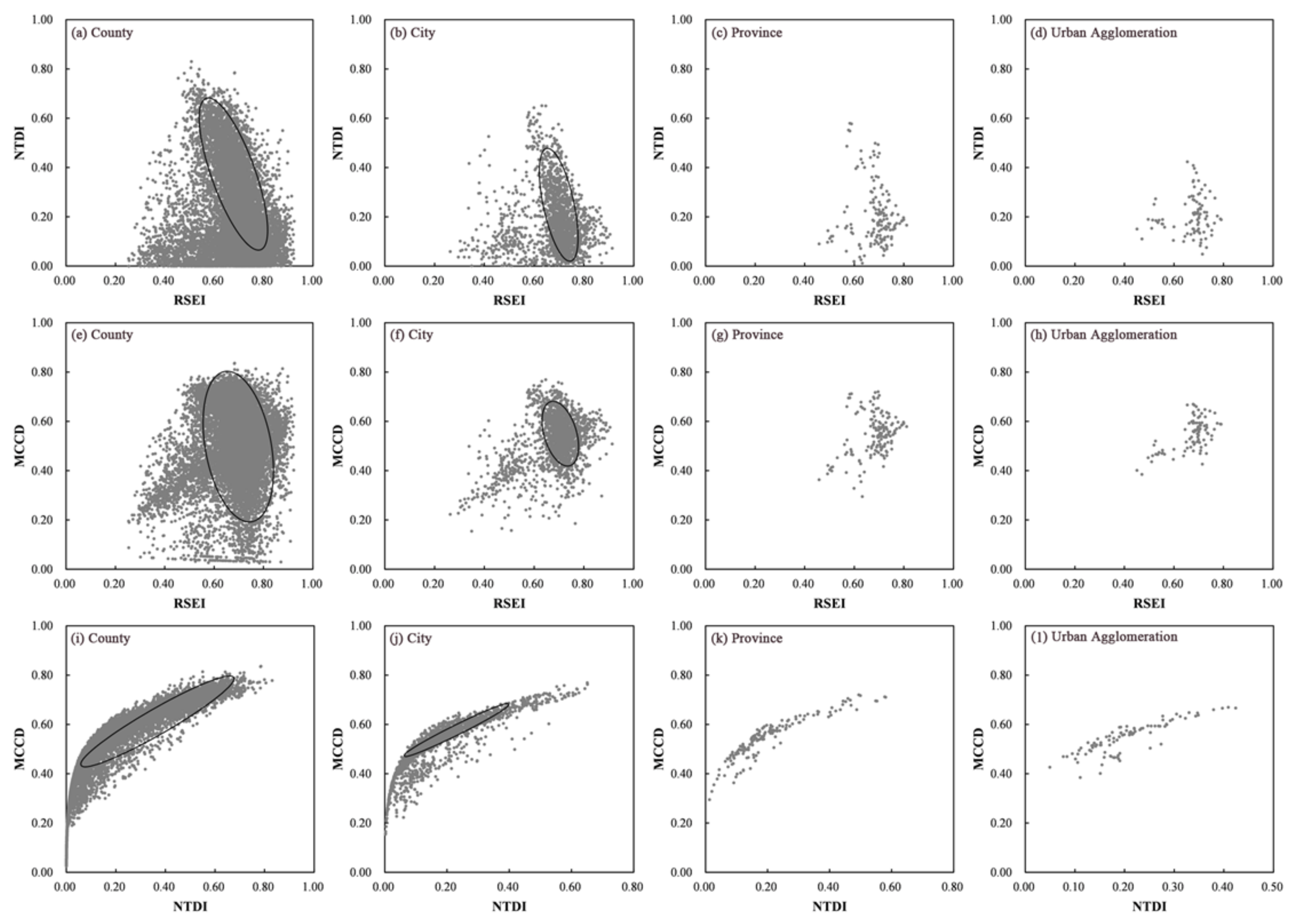
4.2. Relationship among the RSEI, NTDI and MCCD
4.3. Implications, Limitations and Further Research
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CCD | coupling coordination degree | A measure of coupling coordination level between systems |
| CCDM | coupling coordination degree model | A model for calculating the coupling coordination degree |
| EDE | economic development equality | A measure of regional economic development equality |
| EEQ | eco-environmental quality | A measure of regional eco-environmental quality |
| EI | ecological index | An index for describing ecological quality |
| EKC | environmental Kuznets curve | A hypothesis between environment and per capita income |
| GDP | gross domestic product | A measure of regional economic level |
| MCCD | modified coupling coordination degree | A modified index for describing the coupling coordination level |
| NDBSI | normalized difference build-up and soil index | An index for describing regional eco-environmental dryness |
| NDVI | normalized difference vegetation index | An index for describing regional eco-environmental greenness |
| NTDI | nighttime difference index | An index for describing economic development equality |
| RSEI | remote sensing ecological index | An index for describing eco-environmental quality |
| SPCA | spatial principal component analysis | A multivariate statistical analysis method |
| LST | land-surface temperature | An index for describing regional eco-environmental heat |
| WET | wetness | An index for describing regional eco-environmental wetness |
References
- Ji, J.; Wang, S.; Zhou, Y.; Liu, W.; Wang, L. Spatiotemporal Change and Coordinated Development Analysis of “Population-Society-Economy-Resource-Ecology-Environment” in the Jing-Jin-Ji Urban Agglomeration from 2000 to 2015. Sustainability 2021, 13, 4075. [Google Scholar] [CrossRef]
- National Bureau of Statistics of the People’s Republic of China. China Statistical Yearbook; China Statistics Press: Bejing, China, 2021.
- United Nations. World Urbanization Prospects; The 2013 Revision; United Nations: New York, NY, USA, 2014. [Google Scholar]
- Wu, H.; Guo, B.; Fan, J.; Yang, F.; Han, B.; Wei, C.; Lu, Y.; Zang, W.; Zhen, X.; Meng, C. A novel remote sensing ecological vulnerability index on large scale: A case study of the China-Pakistan Economic Corridor region. Ecol. Indic. 2021, 129, 107955. [Google Scholar] [CrossRef]
- Chen, S.; Guo, B.; Zhang, R.; Zang, W.; Wei, C.; Wu, H.; Yang, X.; Zhen, X.; Li, X.; Zhang, D.; et al. Quantitatively determine the dominant driving factors of the spatial-temporal changes of vegetation NPP in the Hengduan Mountain area during 2000–2015. J. Mt. Sci. 2021, 18, 427–445. [Google Scholar] [CrossRef]
- Zhao, G.; Mu, X.; Wen, Z.; Wang, F.; Gao, P. Soil erosion, conservation, and eco-environment changes in the Loess plateau of China. Land Degrad. Develop. 2013, 24, 499–510. [Google Scholar] [CrossRef]
- Ji, J.; Wang, S.; Zhou, Y.; Liu, W.; Wang, L. Studying the coupling coordination degree between socio-economic and eco-environment of Jing-Jin-Ji urban agglomeration during 2001–2015. IOP Conf. Ser. Earth Environ. Sci. 2021, 675, 012043. [Google Scholar] [CrossRef]
- Xu, H.; Yang, H.; Li, X.; Jin, H.; Li, D. Multi-Scale Measurement of Regional Inequality in Mainland China during 2005–2010 Using DMSP/OLS Night Light Imagery and Population Density Grid Data. Sustainability 2015, 7, 13469–13499. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Yang, R.; Wong, C.; Ji, J.; Miao, X. Efficiency and productivity of air pollution control in Chinese cities. Sustain. Cities Soc. 2022, 76, 103423. [Google Scholar] [CrossRef]
- Xu, D.; Yang, F.; Yu, L.; Zhou, Y.; Li, H.; Ma, J.; Huang, J.; Wei, J.; Xu, Y.; Zhang, C.; et al. Quantization of the coupling mechanism between eco-environmental quality and urbanization from multisource remote sensing data. J. Clean Prod. 2021, 321, 128948. [Google Scholar] [CrossRef]
- Ji, J.; Wang, S.; Zhou, Y.; Liu, W.; Wang, L. Spatiotemporal Change and Landscape Pattern Variation of Eco-Environmental Quality in Jing-Jin-Ji Urban Agglomeration From 2001 to 2015. IEEE Access 2020, 8, 125534–125548. [Google Scholar] [CrossRef]
- Ji, J.; Wang, S.; Zhou, Y.; Liu, W.; Wang, L. Studying the Eco-Environmental Quality Variations of Jing-Jin-Ji Urban Agglomeration and Its Driving Factors in Different Ecosystem Service Regions From 2001 To 2015. IEEE Access 2020, 8, 154940–154952. [Google Scholar] [CrossRef]
- Fu, B. The evaluation of eco-environmental qualities in China. China Popul. Resour. Environ. 1992, 2, 48–54. (In Chinese) [Google Scholar]
- He, C.; Gao, B.; Huang, Q.; Ma, Q.; Dou, Y. Environmental degradation in the urban areas of China: Evidence from multi-source remote sensing data. Remote Sens. Environ. 2017, 193, 65–75. [Google Scholar] [CrossRef]
- Chen, M.; Lu, D.; Zhang, H. Comprehensive Evaluation and the Driving Factors of China’s Urbanization. Acta Geogr. Sinica 2009, 64, 387–398. (In Chinese) [Google Scholar]
- Zang, R.; Zhang, P.; Yang, Q.; Li, L.; Zhang, X. Comprehensive Measure and Spatial-temporal Evolution of Urbanization Level in Jilin Province. Sci. Geogr. Sinica 2013, 33, 1231–1237. [Google Scholar]
- Sun, G.; Zhang, M.; Fan, J.; Jiang, Q.; Chen, J.; Zhang, P. A Comparative Study on the Characteristics of the Urbanization Processes Between China and India from 1992 to 2013 Using DMSP-OLS NTL Images. J. Indian Soc. Remote. Sens. 2021, 49, 3059–3070. [Google Scholar] [CrossRef]
- Sarkodie, S.; Strezov, V. Empirical study of the environmental Kuznets curve and environmental sustainability curve hypothesis for Australia, China, Ghana and USA. J. Clean Prod. 2018, 201, 98–110. [Google Scholar] [CrossRef]
- Li, W.; Yi, P.; Zhang, D.; Zhou, Y. Assessment of coordinated development between social economy and ecological environment: Case study of resource-based cities in Northeastern China. Sustain. Cities Soc. 2020, 59, 102208. [Google Scholar] [CrossRef]
- Fang, C.; Wang, S.; Li, G. Changing urban forms and carbon dioxide emissions in China: A case study of 30 provincial capital cities. Appl. Energy 2015, 158, 519–531. [Google Scholar] [CrossRef]
- Beloin-Saint-Pierre, D.; Rugani, B.; Lasvaux, S.; Mailhac, A.; Popovici, E.; Sibiude, G.; Benetto, E.; Schiopu, N. A review of urban metabolism studies to identify key methodological choices for future harmonization and implementation. J. Clean Prod. 2017, 163, 223–240. [Google Scholar] [CrossRef]
- Yang, Y.; Meng, G. A bibliometric analysis of comparative research on the evolution of international and Chinese ecological footprint research hotspots and frontiers since 2000. Ecol. Indic. 2019, 102, 650–665. [Google Scholar] [CrossRef]
- Fang, C.; Ren, Y. Analysis of emergy-based metabolic efficiency and environmental pressure on the local coupling and telecoupling between urbanization and the eco-environment in the Beijing-Tianjin-Hebei urban agglomeration. Sci. China Earth Sci. 2017, 60, 1083–1097. [Google Scholar] [CrossRef]
- Fanning, A.; O’Neill, D.; Büchs, M. Provisioning systems for a good life within planetary boundaries. Global Environ. Change 2020, 64, 102135. [Google Scholar] [CrossRef]
- Song, Q.; Zhou, N.; Liu, T.; Siehr, S.; Qi, Y. Investigation of a “coupling model” of coordination between low-carbon development and urbanization in China. Energy Pol. 2018, 121, 346–354. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Dong, C.; Lo, K. Analyzing and optimizing the impact of economic restructuring on Shanghai’s carbon emissions using STIRPAT and NSGA-II. Sustain. Cities Soc. 2018, 40, 44–53. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, G.; Casazza, M.; Hao, Y.; Zhang, Y.; Giannetti, B. Economy-pollution nexus model of cities at river basin scale based on multi-agent simulation: A conceptual framework. Ecol. Model. 2018, 379, 22–38. [Google Scholar] [CrossRef]
- Apergis, N.; Ozturk, I. Testing environmental Kuznets curve hypothesis in Asian countries. Ecol. Indic. 2015, 52, 16–22. [Google Scholar] [CrossRef]
- Shahbaz, M.; Mutascu, M.; Azim, P. Environmental Kuznets curve in Romania and the role of energy consumption. Renew. Sust. Energ. Rev. 2013, 18, 165–173. [Google Scholar] [CrossRef] [Green Version]
- Shahbaz, M.; Lean, H.; Shabbir, M. Environmental Kuznets curve hypothesis in Pakistan: Cointegration and granger causality. Renew. Sust. Energ. Rev. 2012, 16, 2947–2953. [Google Scholar] [CrossRef] [Green Version]
- Cui, D.; Chen, X.; Xue, Y.; Li, R.; Zeng, W. An integrated approach to investigate the relationship of coupling coordination between social economy and water environment on urban scale—A case study of Kunming. J. Environ. Manage. 2019, 234, 189–199. [Google Scholar] [CrossRef]
- Fu, S.; Zhuo, H.; Song, H.; Wang, J.; Ren, L. Examination of a coupling coordination relationship between urbanization and the eco-environment: A case study in Qingdao, China. Environ. Sci. Pollut. Res. 2020, 27, 23981–23993. [Google Scholar] [CrossRef]
- Liu, L.; Caloz, C.; Chang, C.; Itoh, T. Forward coupling phenomena between artificial left-handed transmission lines. J. Appl. Phys. 2002, 92, 5560–5565. [Google Scholar] [CrossRef] [Green Version]
- Fan, Y.; Fang, C.; Zhang, Q. Coupling coordinated development between social economy and ecological environment in Chinese provincial capital cities-assessment and policy implications. J. Clean Prod. 2019, 229, 289–298. [Google Scholar] [CrossRef]
- Li, W.; Yi, P. Assessment of city sustainability—Coupling coordinated development among economy, society and environment. J. Clean Prod. 2020, 256, 120453. [Google Scholar] [CrossRef]
- Xie, M.; Wang, J.; Chen, K. Coordinated development analysis of the “Resources-environment-ecology-economy-society” complex system in China. Sustainability 2016, 8, 582. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; Huang, Y.; Huang, Z.; Lou, Y.; Ye, G.; Wong, S. Improved coupling analysis on the coordination between socio-economy and carbon emission. Ecol. Indic. 2018, 94, 357–366. [Google Scholar] [CrossRef]
- Cong, X. Expression and Mathematical Property of Coupling Model, and Its Misuse in Geographical Science. Econ. Geogr. 2019, 39, 18–25. (In Chinese) [Google Scholar]
- He, Y.; You, N.; Cui, Y.; Xiao, T.; Hao, Y.; Dong, J. Spatio-temporal changes in remote sensing-based ecological index in China since 2000. J. Nat. Resour. 2021, 36, 1176–1185. (In Chinese) [Google Scholar] [CrossRef]
- Chi, Y.; Qian, T.; Sheng, C.; Xi, C.; Wang, J. Analysis of Differences in the Spatial Distribution among Terrestrial Mammals Using Geodetector—A Case Study of China. ISPRS Int. J. Geoinf. 2021, 10, 21. [Google Scholar] [CrossRef]
- Yue, H.; Liu, Y.; Li, Y.; Lu, Y. Eco-environmental quality assessment in China’s 35 major cities based on remote sensing ecological index. IEEE Access 2019, 7, 51295–51311. [Google Scholar] [CrossRef]
- Xu, H.; Wang, M.; Shi, T.; Guan, H.; Fang, C.; Lin, Z. Prediction of ecological effects of potential population and impervious surface increases using a remote sensing based ecological index (RSEI). Ecol. Indic. 2018, 93, 730–740. [Google Scholar] [CrossRef]
- Zhang, T.; Yang, R.; Yang, Y.; Li, L.; Chen, L. Assessing the Urban Eco-Environmental Quality by the Remote-Sensing Ecological Index: Application to Tianjin, North China. ISPRS Int. J. Geoinf. 2021, 10, 475. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, B.; Yang, C.; Zhou, Y.; Yao, S.; Qian, X.; Wang, C.; Wu, B.; Wu, J. An extended time series (2000-2018) of global NPP-VIIRS-like nighttime light data from a cross-sensor calibration. Earth Syst. Sci. Data 2021, 13, 889–906. [Google Scholar] [CrossRef]
- Xu, H. A remote sensing urban ecological index and its application. Acta Ecol. Sinica 2013, 33, 7853–7862. (In Chinese) [Google Scholar]
- Zhou, Y.; Ma, T.; Zhou, C.; Xu, T. Nighttime Light Derived Assessment of Regional Inequality of Socioeconomic Development in China. Remote Sens. 2015, 7, 1242–1262. [Google Scholar] [CrossRef] [Green Version]
- Xu, J. Mathematical Methods in Contemporary Geography, 2nd ed.; Higher Education Press: Beijing, China, 2002. (In Chinese) [Google Scholar]
- Zhao, H.; Chen, Y.; Zhou, Y.; Pei, T.; Xie, B.; Wang, X. Spatiotemporal variation of NDVI in vegetation growing season and its responses to climate factors in mid and eastern Gansu Province from 2008 to 2016. Arid Land Geogra. 2019, 42, 1427–1435. (In Chinese) [Google Scholar]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator ststistical tests in Serbia. Glob. Planet. Change 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Li, J. Heterogeneous effects of climate change and human activities on annual landscape change in coastal cities of mainland China. Ecol. Indic. 2021, 125, 107561. [Google Scholar] [CrossRef]
- Yuan, B.; Fu, L.; Zou, Y.; Zhang, S.; Chen, X.; Li, F.; Deng, Z.; Xie, Y. Spatiotemporal change detection of ecological quality and the associated affecting factors in Dongting Lake Basin, based on RSEI. J. Clean Prod. 2021, 302, 126995. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, S.; Rao, X.; Lin, X.; Li, R. Landsat TM/OLI-Based Ecological and Environmental Quality Survey of Yellow River Basin, Inner Mongolia Section. Remote Sens. 2021, 13, 4477. [Google Scholar] [CrossRef]
- Xiong, Y.; Xu, W.; Lu, N.; Huang, S.; Wu, C.; Wang, L.; Dai, F.; Kou, W. Assessment of spatial–temporal changes of ecological environment quality based on RSEI and GEE: A case study in Erhai Lake Basin, Yunnan province, China. Ecol. Indic. 2021, 125, 107518. [Google Scholar] [CrossRef]
- Hu, X.; Xu, H. A new remote sensing index based on the pressure-state-response framework to assess regional ecological change. Environ. Sci. Pollut. Res. 2019, 26, 5381–5393. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Wang, Y.; Guan, H.; Shi, T.; Hu, X. Detecting Ecological Changes with a Remote Sensing Based Ecological Index (RSEI) Produced Time Series and Change Vector Analysis. Remote Sens. 2019, 11, 2345. [Google Scholar] [CrossRef] [Green Version]
- Technical Criterion for Ecosystem Status Evaluation, Document, HJ 192–2015. 2015. Available online: https://www.mee.gov.cn/ywgz/fgbz/bz/bzwb/stzl/201503/t20150324_298011.shtml (accessed on 2 December 2021).
- Shan, W.; Jin, X.; Ren, J.; Wang, Y.; Xu, Z.; Fan, Y.; Gu, Z.; Hong, C.; Lin, J.; Zhou, Y. Ecological environment quality assessment based on remote sensing data for land consolidation. J. Clean Prod. 2019, 239, 118126. [Google Scholar] [CrossRef]
- Fang, C.; Liu, H.; Wang, S. The coupling curve between urbanization and the eco-environment: China’s urban agglomeration as a case study. Ecol. Indic. 2021, 130, 108107. [Google Scholar] [CrossRef]
- Han, Q.; Niu, Z. Construction of the Long-Term Global Surface Water Extent Dataset Based on Water-NDVI Spatio-Temporal Parameter Set. Remote Sens. 2020, 12, 2675. [Google Scholar] [CrossRef]




| Name | Spatial and Temporal Resolution | Data Availability | Brief Description |
|---|---|---|---|
| MOD09A1 | 500 m 8 days | https://lpdaac.usgs.gov/products/mod09a1v006/ accessed on 16 March 2021 | A product of surface spectral reflectance of MODIS bands 1–7 |
| MOD11A2 | 1000 m 8 days | https://lpdaac.usgs.gov/products/mod11a2v006/ accessed on 19 March 2021 | A product of land surface temperature |
| NPP-VIIRS-like nighttime light data | 500 m yearly | https://doi.org/10.7910/DVN/YGIVCD accessed on 19 March 2021 | A nighttime dataset for measuring regional economic development level |
| WorldPop | 1000 m yearly | https://www.worldpop.org accessed on 23 March 2021 | A dataset for measuring population spatial distribution |
| Administrative division data | \ | http://www.ngcc.cn/ngcc/html/1/index.html accessed on 5 March 2021 | A vector dataset for data clip and spatial analysis |
| Global Moran’s I Value | 2001 | 2005 | 2010 | 2015 | 2020 | Change Trend | |
|---|---|---|---|---|---|---|---|
| County Scale | RSEI | 0.2957 | 0.2777 | 0.2455 | 0.2668 | 0.2459 | 0.6189 |
| NTDI | 0.3647 | 0.3693 | 0.4168 | 0.4066 | 0.4474 | 0.2326 | |
| MCCD | 0.3197 | 0.3037 | 0.3285 | 0.2950 | 0.3298 | 0.1993 | |
| City Scale | RSEI | 0.3228 | 0.3092 | 0.2795 | 0.2763 | 0.2448 | 0.5559 |
| NTDI | 0.2776 | 0.3031 | 0.3129 | 0.3449 | 0.3863 | 0.3550 | |
| MCCD | 0.2889 | 0.3038 | 0.2977 | 0.3179 | 0.3446 | 0.2725 | |
| Province Scale | RSEI | 0.1392 | 0.0817 | 0.0675 | 0.0916 | 0.0522 | 0.2817 |
| NTDI | 0.2504 | 0.2797 | 0.2809 | 0.2462 | 0.3320 | 0.1049 | |
| MCCD | 0.2626 | 0.2953 | 0.2851 | 0.2161 | 0.2755 | 0.0709 | |
| Urban Agglomeration Scale | RSEI | 0.1460 | 0.0827 | 0.0575 | 0.0420 | 0.0020 | 0.1690 |
| NTDI | 0.0795 | 0.0821 | 0.0622 | 0.0483 | 0.0756 | 0.0831 | |
| MCCD | 0.1546 | 0.1461 | 0.1285 | 0.1215 | 0.1128 | 0.0627 | |
| Eigenvalue | PC1 | PC2 | PC3 | PC4 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NDVI | WET | NDBSI | LST | NDVI | WET | NDBSI | LST | NDVI | WET | NDBSI | LST | NDVI | WET | NDBSI | LST | |
| 2001 | 0.73 | 0.23 | −0.39 | −0.50 | 0.58 | −0.31 | −0.04 | 0.74 | −0.18 | 0.76 | −0.43 | 0.44 | 0.29 | 0.51 | 0.81 | 0.03 |
| 2005 | 0.73 | 0.24 | −0.40 | −0.49 | 0.58 | −0.33 | −0.03 | 0.73 | −0.17 | 0.76 | −0.41 | 0.45 | 0.30 | 0.49 | 0.81 | 0.02 |
| 2010 | 0.75 | 0.22 | −0.41 | −0.45 | 0.55 | −0.35 | −0.01 | 0.75 | −0.17 | 0.75 | −0.41 | 0.47 | 0.31 | 0.50 | 0.80 | 0.02 |
| 2015 | 0.71 | 0.21 | −0.40 | −0.52 | 0.59 | −0.29 | −0.07 | 0.74 | −0.18 | 0.77 | −0.44 | 0.41 | 0.31 | 0.51 | 0.79 | 0.03 |
| 2020 | 0.67 | 0.25 | −0.42 | −0.54 | 0.61 | −0.27 | −0.13 | 0.72 | −0.23 | 0.77 | −0.42 | 0.40 | 0.34 | 0.51 | 0.78 | 0.04 |
| Scale | Fitting Formula | Adjusted R2 |
|---|---|---|
| County | MCCD = 0.0473 + 0.4521 × RSEI + 0.7831 × NTDI | 0.8183 |
| City | MCCD = 0.0710 + 0.4574 × RSEI + 0.7576 × NTDI | 0.9156 |
| Province | MCCD = 0.0682 + 0.5053 × RSEI + 0.6441 × NTDI | 0.9732 |
| Urban agglomeration | MCCD = 0.1022 + 0.4595 × RSEI + 0.6561 × NTDI | 0.9915 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, J.; Tang, Z.; Zhang, W.; Liu, W.; Jin, B.; Xi, X.; Wang, F.; Zhang, R.; Guo, B.; Xu, Z.; et al. Spatiotemporal and Multiscale Analysis of the Coupling Coordination Degree between Economic Development Equality and Eco-Environmental Quality in China from 2001 to 2020. Remote Sens. 2022, 14, 737. https://doi.org/10.3390/rs14030737
Ji J, Tang Z, Zhang W, Liu W, Jin B, Xi X, Wang F, Zhang R, Guo B, Xu Z, et al. Spatiotemporal and Multiscale Analysis of the Coupling Coordination Degree between Economic Development Equality and Eco-Environmental Quality in China from 2001 to 2020. Remote Sensing. 2022; 14(3):737. https://doi.org/10.3390/rs14030737
Chicago/Turabian StyleJi, Jianwan, Zhanzhong Tang, Weiwei Zhang, Wenliang Liu, Biao Jin, Xu Xi, Futao Wang, Rui Zhang, Bing Guo, Zhiyu Xu, and et al. 2022. "Spatiotemporal and Multiscale Analysis of the Coupling Coordination Degree between Economic Development Equality and Eco-Environmental Quality in China from 2001 to 2020" Remote Sensing 14, no. 3: 737. https://doi.org/10.3390/rs14030737
APA StyleJi, J., Tang, Z., Zhang, W., Liu, W., Jin, B., Xi, X., Wang, F., Zhang, R., Guo, B., Xu, Z., Shifaw, E., Xiong, Y., Wang, J., Xu, S., & Wang, Z. (2022). Spatiotemporal and Multiscale Analysis of the Coupling Coordination Degree between Economic Development Equality and Eco-Environmental Quality in China from 2001 to 2020. Remote Sensing, 14(3), 737. https://doi.org/10.3390/rs14030737








