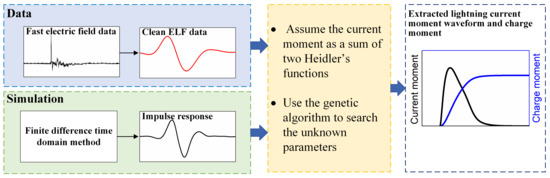
Remote Measurement of the Lightning Impulse Charge Moment Change Using the Fast Electric Field Antenna
Abstract
1. Introduction
2. Data and Methods
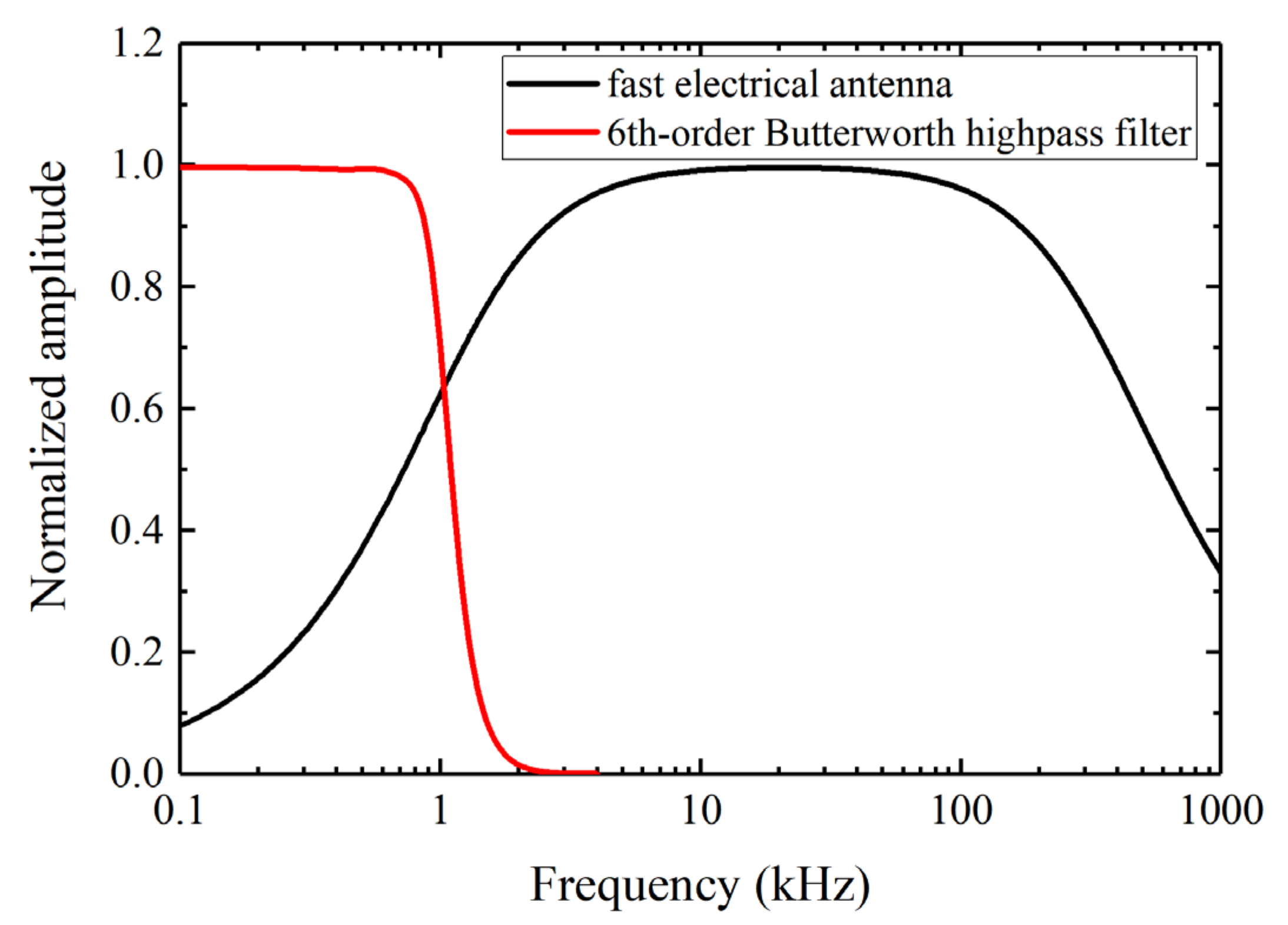
2.1. Instrument and Data
2.2. Simulation of the Impulse Response
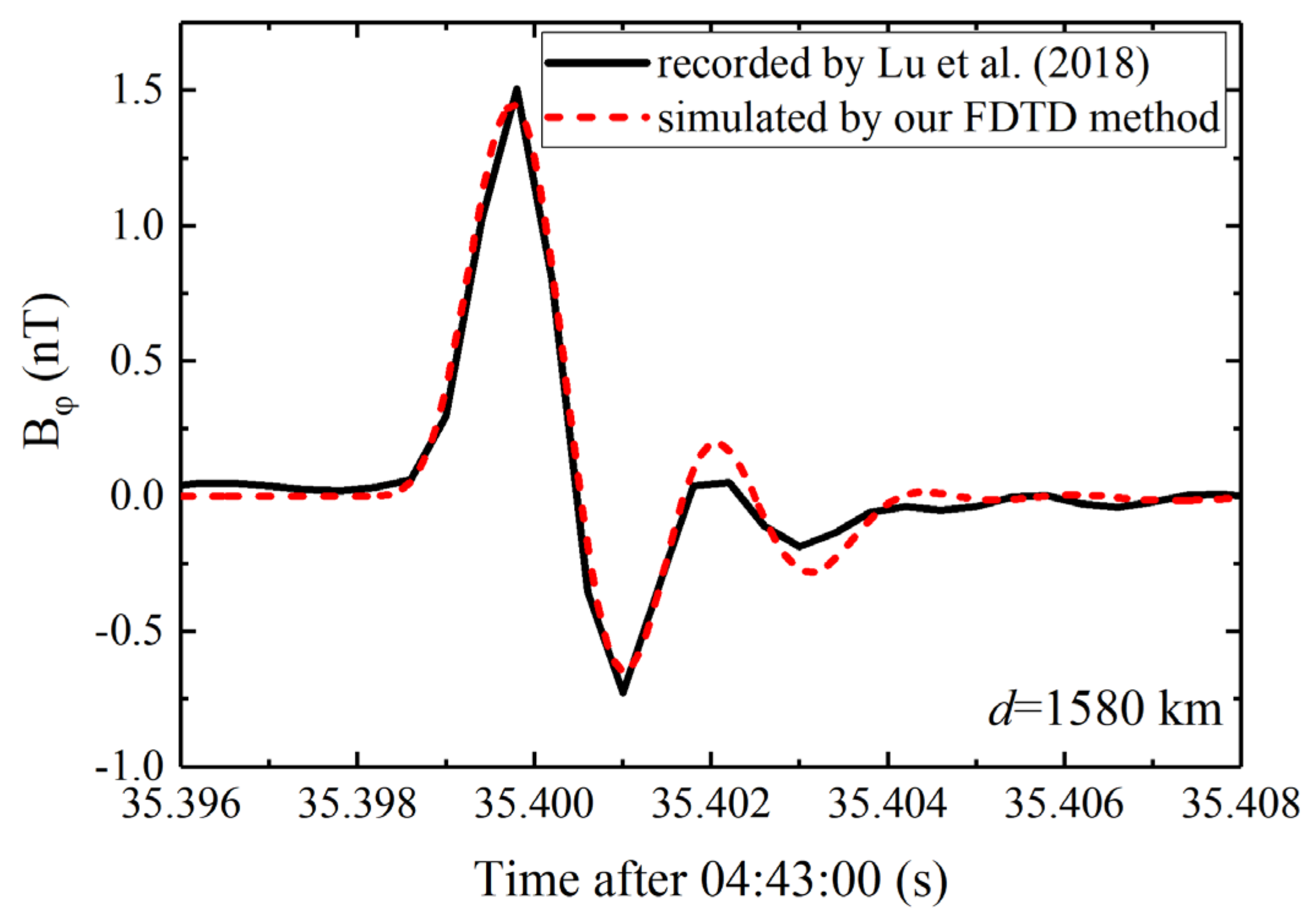
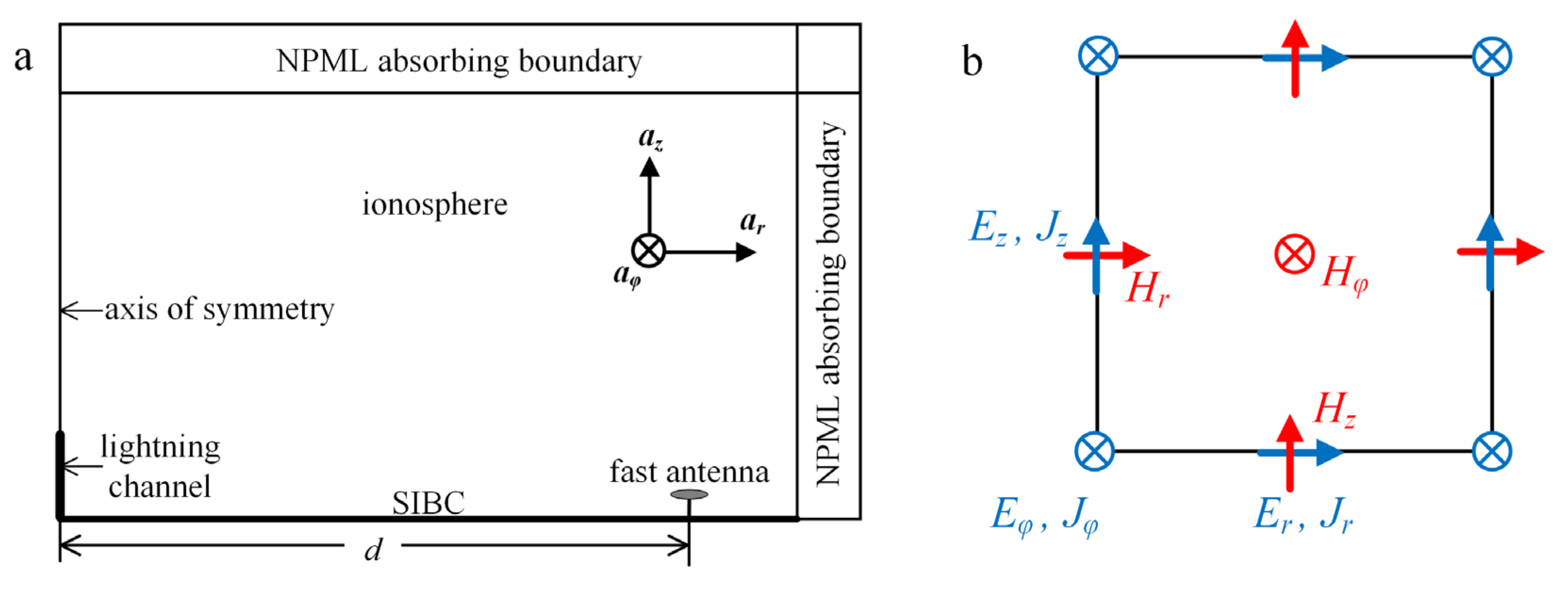
2.2.1. FDTD Model
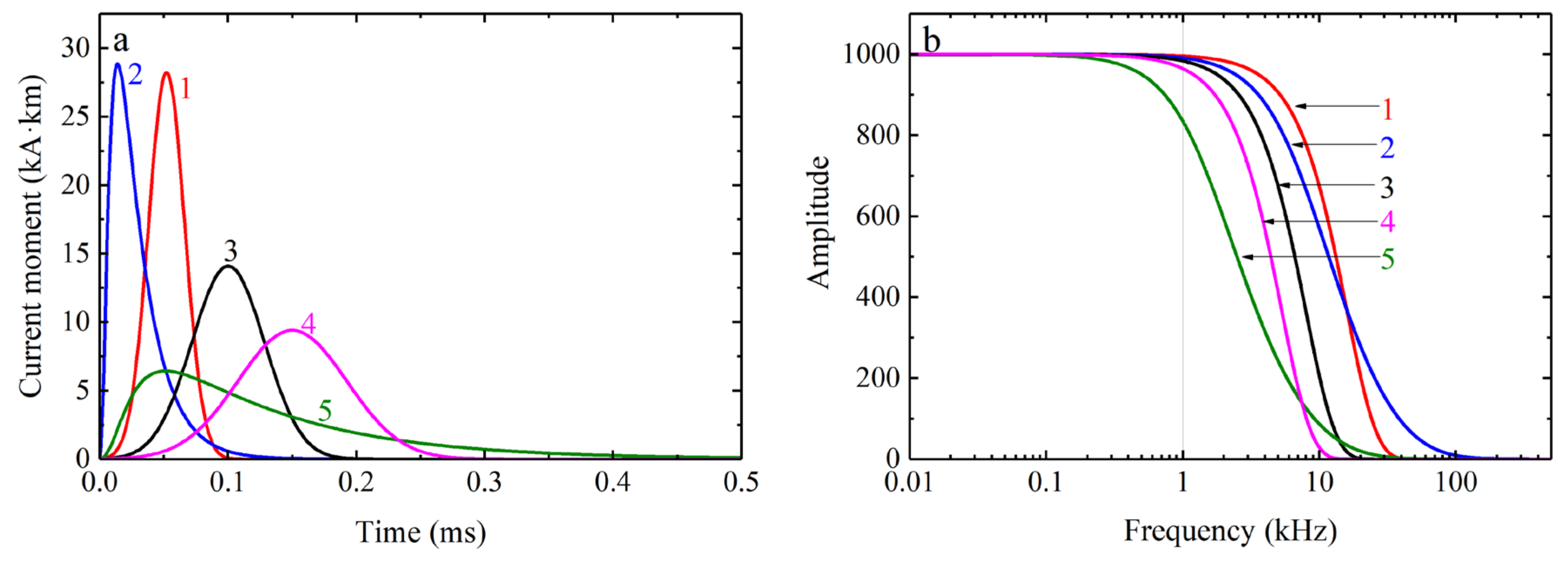
2.2.2. Modeled Impulse Response
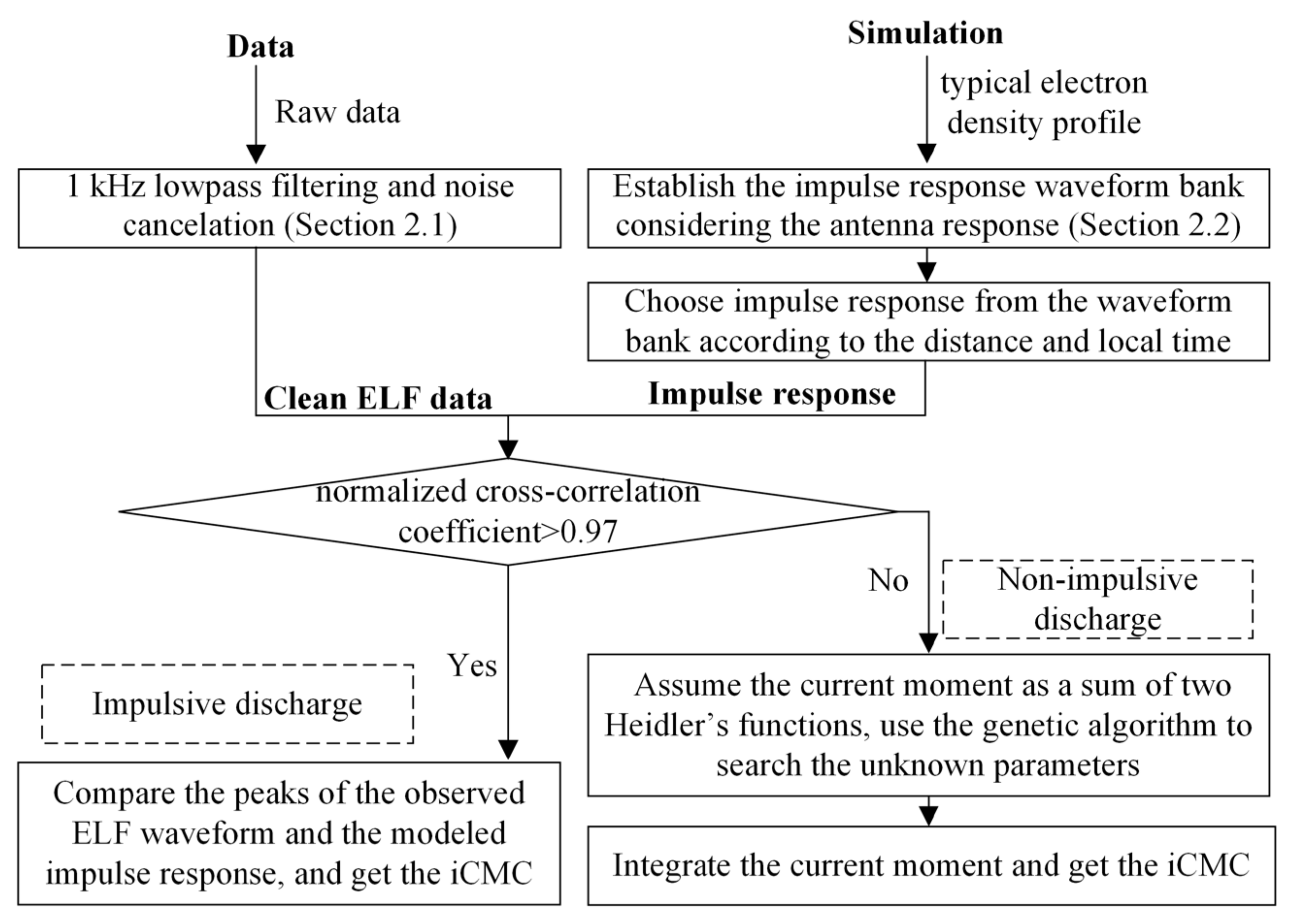
2.3. iCMC Measurement Method
2.3.1. Reconstructing the Current Moment Waveform Using Genetic Algorithm
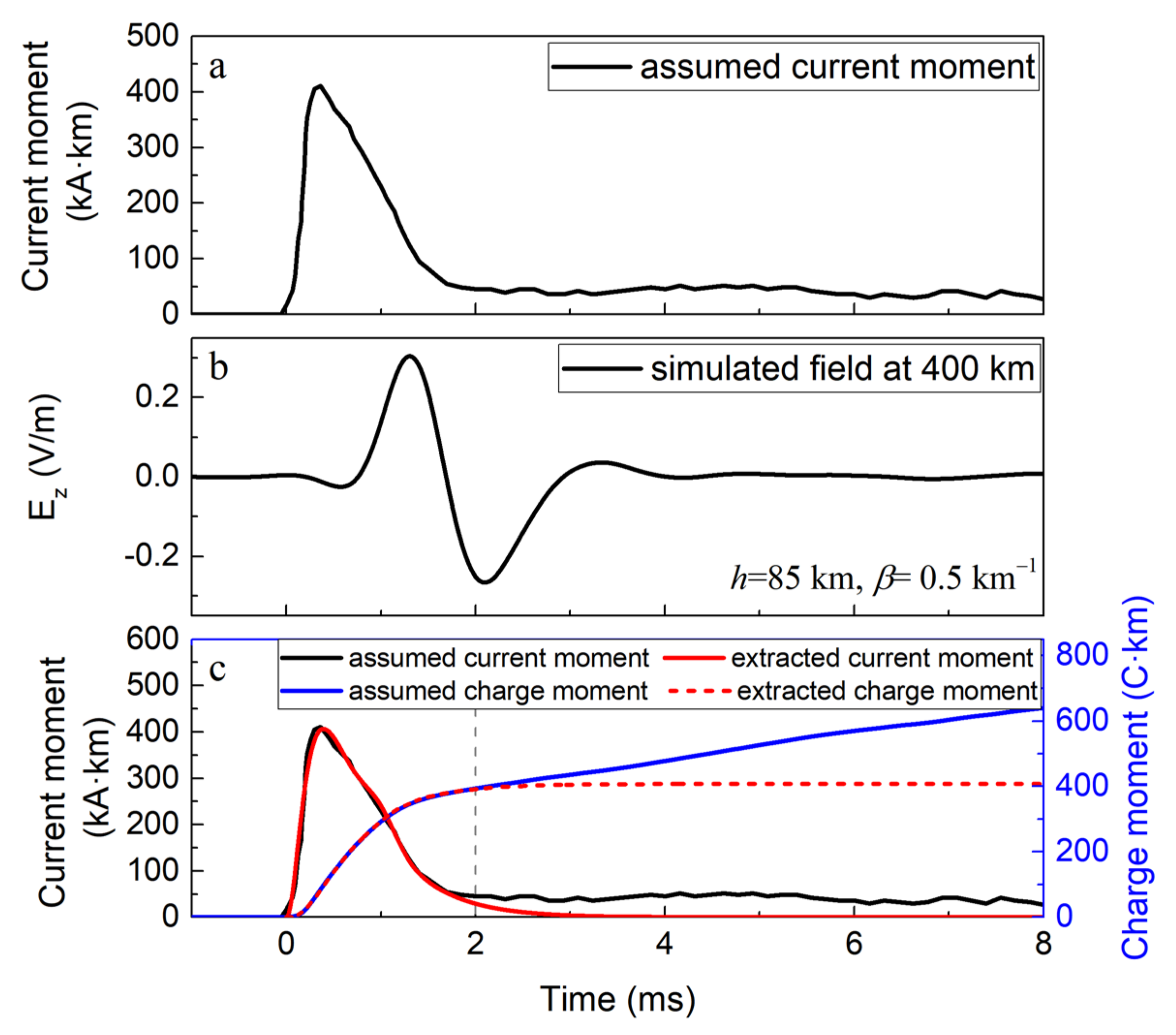
2.3.2. Method Validation
3. Results
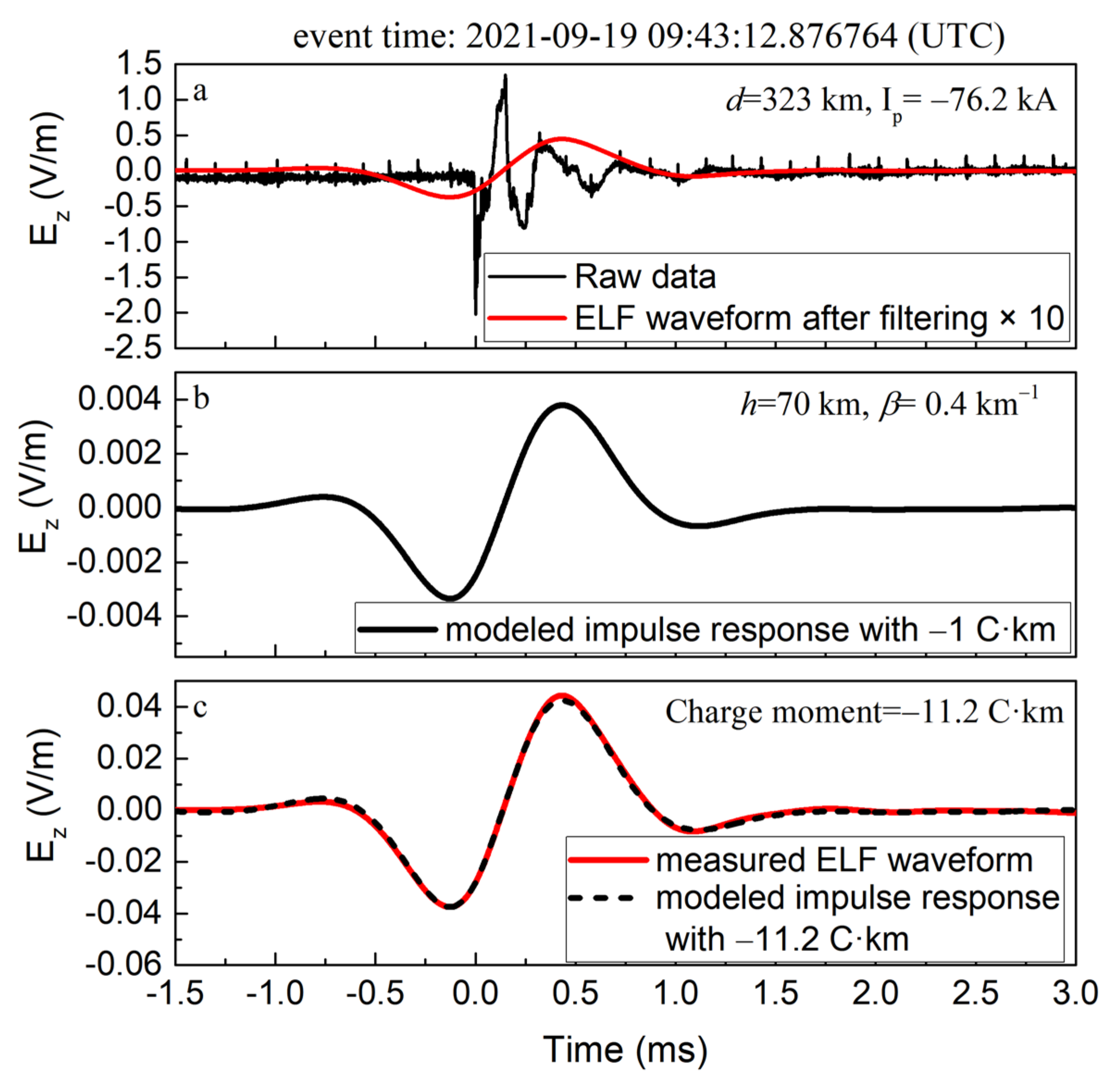
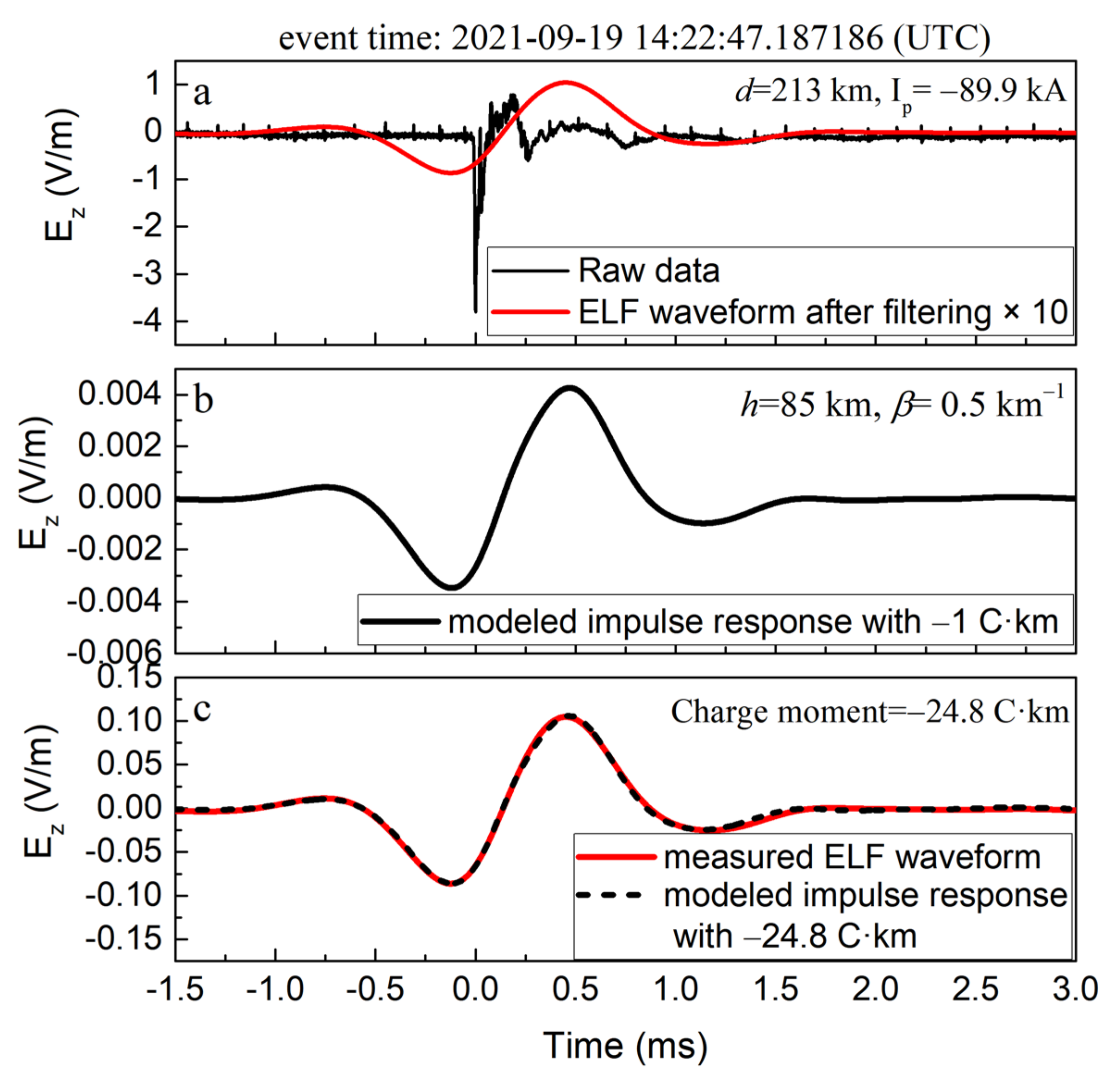
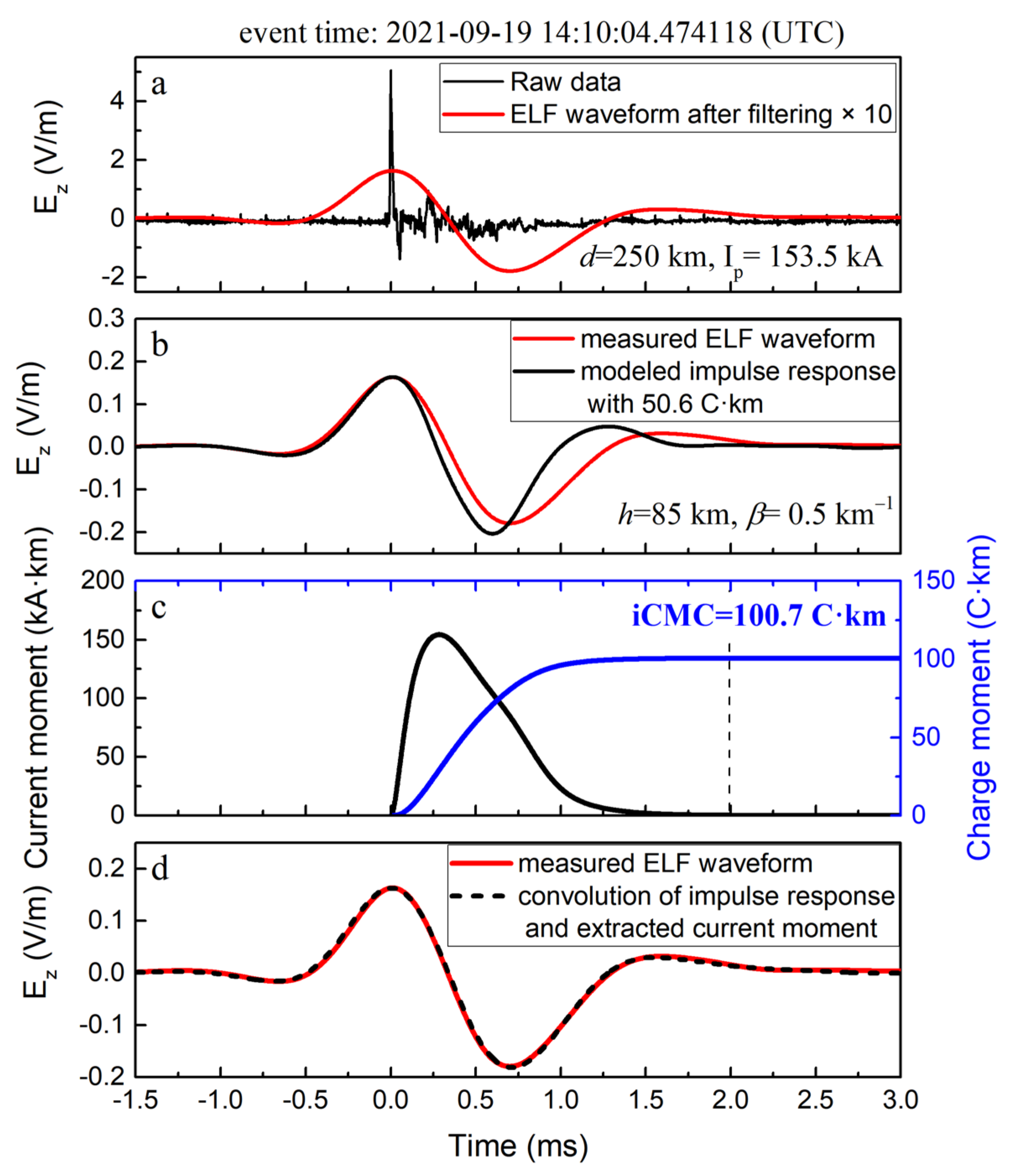
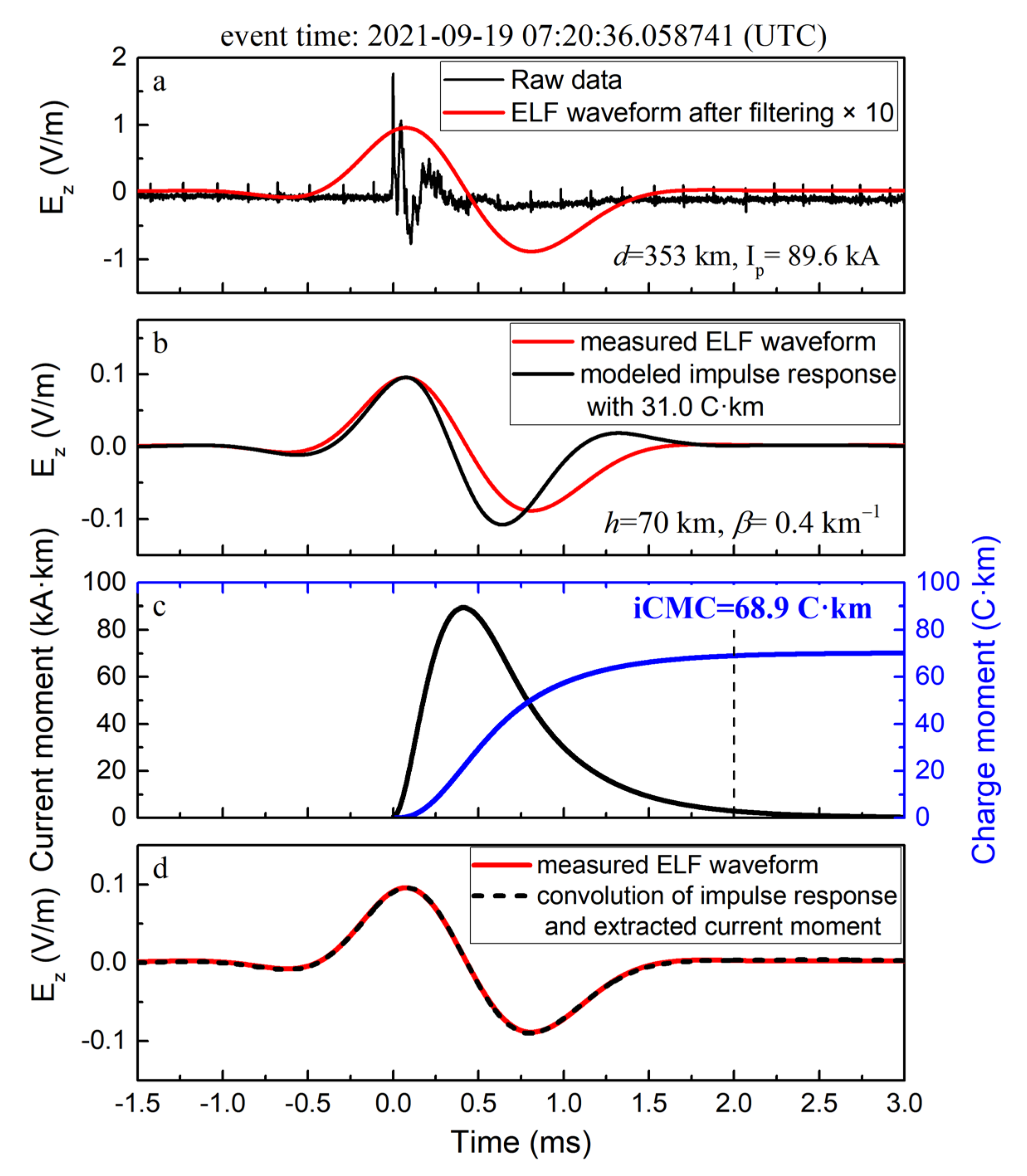
3.1. iCMC Measurement for the Impulsive Discharge
3.2. iCMC Measurement for the Non-Impulsive Discharge
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

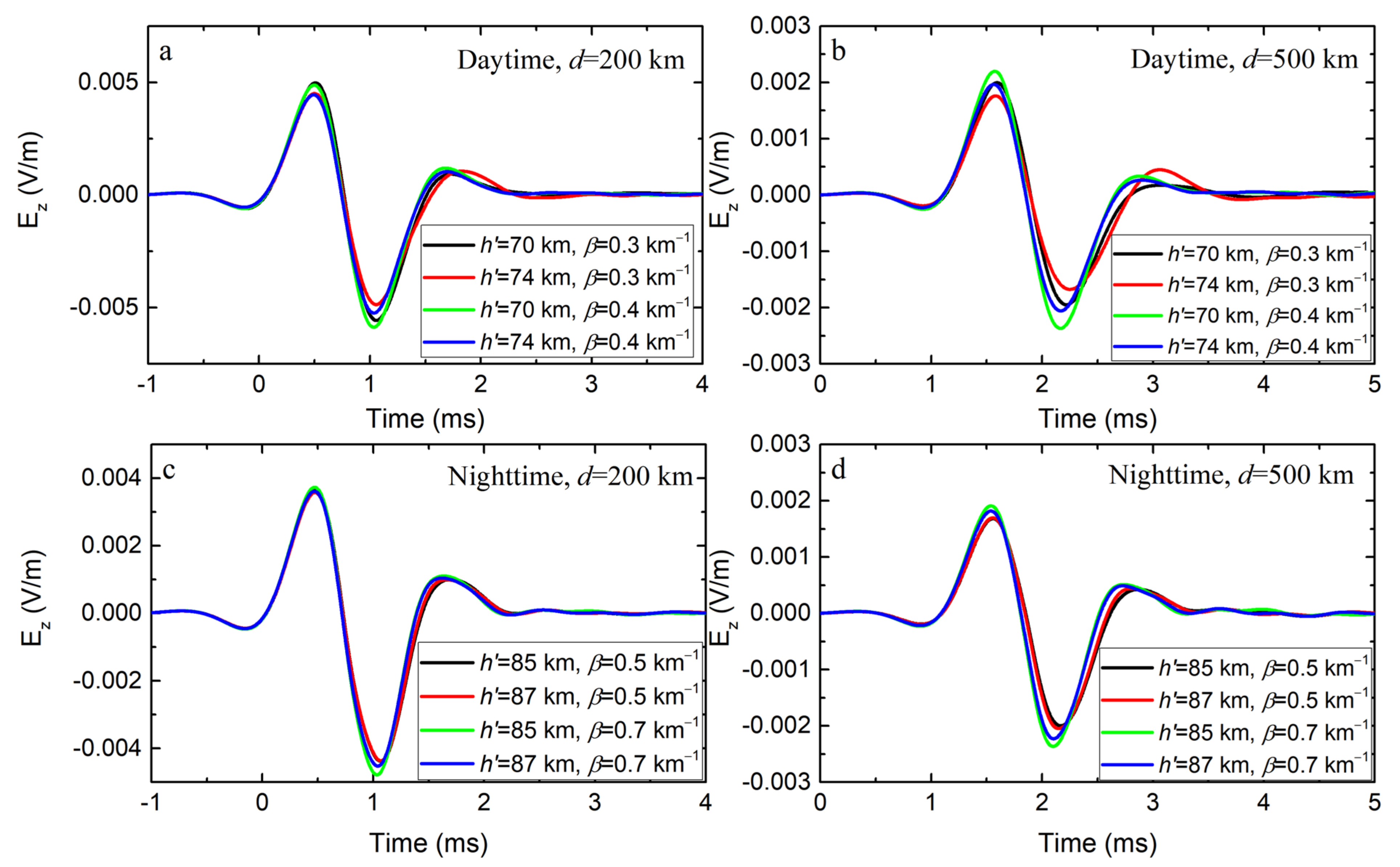
Appendix B

References
- Cummer, S.A.; Inan, U. Modeling ELF radio atmospheric propagation and extracting lightning currents from ELF observations. Radio Sci. 2000, 35, 385–394. [Google Scholar] [CrossRef]
- Cummer, S.A. Current moment in sprite-producing lightning. J. Atmos. Sol.-Terr. Phys. 2003, 65, 499–508. [Google Scholar] [CrossRef]
- Cummer, S.A.; Lyons, W.A.; Stanley, M.A. Three years of lightning impulse charge moment change measurements in the United States. J. Geophys. Res. Atmos. 2013, 118, 5176–5189. [Google Scholar] [CrossRef]
- Lu, G.; Cummer, S.A.; Blakeslee, R.J.; Weiss, S.; Beasley, W.H. Lightning morphology and impulse charge moment change of high peak current negative strokes. J. Geophys. Res. Space Phys. 2012, 117, D04212. [Google Scholar] [CrossRef]
- Lyu, F.; Cummer, S.A.; McTague, L. Insights into high peak current in-cloud lightning events during thunderstorms. Geophys. Res. Lett. 2015, 42, 6836–6843. [Google Scholar] [CrossRef]
- Cummer, S.A.; Inan, U.S. Measurement of charge transfer in sprite-producing lightning using ELF radio atmospherics. Geophys. Res. Lett. 1997, 24, 1731–1734. [Google Scholar] [CrossRef]
- Huang, E.; Williams, E.; Boldi, R.; Heckman, S.; Lyons, W.; Taylor, M.; Nelson, T.; Wong, C. Criteria for sprites and elves based on Schumann resonance observations. J. Geophys. Res. Earth Surf. 1999, 104, 16943–16964. [Google Scholar] [CrossRef]
- Hu, W.; Nelson, T.E.; Cummer, S.A.; Lyons, W.A. Lightning charge moment changes for the initiation of sprites. Geophys. Res. Lett. 2002, 29, 1279. [Google Scholar] [CrossRef]
- Li, J.; Cummer, S.A.; Lyons, W.A.; Nelson, T.E. Coordinated analysis of delayed sprites with high-speed images and remote electromagnetic fields. J. Geophys. Res. Earth Surf. 2008, 113, D20206. [Google Scholar] [CrossRef]
- Kułak, A.; Młynarczyk, J. A new technique for reconstruction of the current moment waveform related to a gigantic jet from the magnetic field component recorded by an ELF station. Radio Sci. 2011, 46, RS2016. [Google Scholar] [CrossRef]
- Lu, G.; Yu, B.; Cummer, S.A.; Peng, K.; Chen, A.B.; Lyu, F.; Xue, X.; Liu, F.; Hsu, R.; Su, H. On the Causative Strokes of Halos Observed by ISUAL in the Vicinity of North America. Geophys. Res. Lett. 2018, 45, 10781–10789. [Google Scholar] [CrossRef]
- Kulak, A.; Mlynarczyk, J.; Ostrowski, M.; Kubisz, J.; Michalec, A. Analysis of ELF electromagnetic field pulses recorded by the Hylaty station coinciding with terrestrial gamma-ray flashes. J. Geophys. Res. Earth Surf. 2012, 117, D18203. [Google Scholar] [CrossRef]
- Lu, G.; Zhang, H.; Cummer, S.A.; Wang, Y.; Lyu, F.; Briggs, M.; Xiong, S.; Chen, A. A comparative study on the lightning sferics associated with terrestrial gamma-ray flashes observed in Americas and Asia. J. Atmos. Sol.-Terr. Phys. 2019, 183, 67–75. [Google Scholar] [CrossRef]
- Jones, D.; Kemp, D. The nature and average magnitude of the sources of transient excitation of Schumann resonances. J. Atmos. Terr. Phys. 1971, 33, 557–566. [Google Scholar] [CrossRef]
- Wood, T.G.; Inan, U.S. Long-range tracking of thunderstorms using sferic measurements. J. Geophys. Res. Earth Surf. 2002, 107, ACL 1-1–ACL 1-9. [Google Scholar] [CrossRef]
- Krehbiel, P.R.; Brook, M.; McCrory, R.A. An analysis of the charge structure of lightning discharges to ground. J. Geophys. Res. Earth Surf. 1979, 84, 2432–2456. [Google Scholar] [CrossRef]
- Qie, X.; Yu, Y.; Liu, X.; Guo, C.; Wang, D.; Watanabe, T.; Ushio, T. Charge analysis on lightning discharges to the ground in Chinese inland plateau (close to Tibet). Ann. Geophys. 2000, 18, 1340–1348. [Google Scholar] [CrossRef][Green Version]
- Nieckarz, Z.; Baranski, P.; Mlynarczyk, J.; Kulak, A.; Wiszniowski, J. Comparison of the charge moment change calculated from electrostatic analysis and from ELF radio observations. J. Geophys. Res. Atmos. 2015, 120, 63–72. [Google Scholar] [CrossRef]
- Heidler, F.; Cvetic, J.; Stanic, B. Calculation of lightning current parameters. IEEE Trans. Power Deliv. 1999, 14, 399–404. [Google Scholar] [CrossRef]
- Hou, W.; Azadifar, M.; Rubinstein, M.; Rachidi, F.; Zhang, Q. The Polarity Reversal of Lightning-Generated Sky Wave. J. Geophys. Res. Atmos. 2020, 125, e2020JD032448. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, M.; Zhu, B.; Du, Y.-P. An improved ray theory and transfer matrix method-based model for lightning electromagnetic pulses propagating in Earth-ionosphere waveguide and its applications. J. Geophys. Res. Atmos. 2017, 122, 712–727. [Google Scholar] [CrossRef]
- Tran, T.H.; Baba, Y.; Somu, V.; Rakov, V.A. FDTD Modeling of LEMP Propagation in the Earth-Ionosphere Waveguide With Emphasis on Realistic Representation of Lightning Source. J. Geophys. Res. Atmos. 2017, 122, 12918–12937. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, J.; Ma, Q.; Huang, Q.; Xiao, F. A method for determining D region ionosphere reflection height from lightning skywaves. J. Atmos. Sol.-Terr. Phys. 2021, 221, 105692. [Google Scholar] [CrossRef]
- Hu, W.; Cummer, S. An FDTD Model for Low and High Altitude Lightning-Generated EM Fields. IEEE Trans. Antennas Propag. 2006, 54, 1513–1522. [Google Scholar] [CrossRef]
- Cummer, S.A. A simple, nearly perfectly matched layer for general electromagnetic media. IEEE Microw. Wirel. Compon. Lett. 2003, 13, 128–130. [Google Scholar] [CrossRef]
- Wait, J.R.; Spies, K.P. Characteristics of the Earth-Ionosphere Waveguide for VLF Radio Waves (NBS Tech. Note 300); National Bureau of Standards: Boulder, CO, USA, 1964. Available online: https://nvlpubs.nist.gov/nistpubs/Legacy/TN/nbstechnicalnote300.pdf (accessed on 2 February 2022).
- Thomson, N. Experimental daytime VLF ionospheric parameters. J. Atmos. Terr. Phys. 1993, 55, 173–184. [Google Scholar] [CrossRef]
- Han, F.; Cummer, S.A. Midlatitude daytime D region ionosphere variations measured from radio atmospherics. J. Geophys. Res. Earth Surf. 2010, 115, A10314. [Google Scholar] [CrossRef]
- Han, F.; Cummer, S.A. Midlatitude nighttime D region ionosphere variability on hourly to monthly time scales. J. Geophys. Res. Earth Surf. 2010, 115, A09323. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International Reference Ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Jones, D. Electromagnetic radiation from multiple return strokes of lightning. J. Atmos. Terr. Phys. 1970, 32, 1077–1093. [Google Scholar] [CrossRef]
- Li, J. Coordinated Analysis of Sprites with High Speed Images and Remote Electromagnetic Fields. Ph.D. Thesis, Duke University, Durham, UK, 2010. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Longman Publishing Co., Inc.: Reading, MA, USA, 1989. [Google Scholar]
- Bermudez, J.L.; Pena-Reyes, C.A.; Rachidi, F.; Heidler, F. Use of genetic algorithms to extract primary lightning current parameters. In Proceedings of the EMC Europe 2002 International Symposium on Electromagnetic Compatibility, Sorrento, Italy, 9–13 September 2002; pp. 241–246. [Google Scholar]
- Chandrasekaran, K.; Punekar, G.S. Use of Genetic Algorithm to Determine Lightning Channel-Base Current-Function Parameters. IEEE Trans. Electromagn. Compat. 2014, 56, 235–238. [Google Scholar] [CrossRef]
- Javor, V.; Lundengård, K.; Rančić, M.; Silvestrov, S. Application of Genetic Algorithm to Estimation of Function Parameters in Lightning Currents Approximations. Int. J. Antennas Propag. 2017, 2017, 4937943. [Google Scholar] [CrossRef]
- Shao, X.-M.; Lay, E.; Jacobson, A.R. Reduction of electron density in the night-time lower ionosphere in response to a thunderstorm. Nat. Geosci. 2013, 6, 29–33. [Google Scholar] [CrossRef]
- Karunarathne, S.; Marshall, T.C.; Stolzenburg, M.; Karunarathna, N. Modeling initial breakdown pulses of CG lightning flashes. J. Geophys. Res. Atmos. 2014, 119, 9003–9019. [Google Scholar] [CrossRef]



| Parameters | A1 (kA· km) | t1 (ms) | t2 (ms) | A2 (kA· km) | t3 (ms) | t4 (ms) | A3 (kA· km) | t5 (ms) | t6 (ms) |
|---|---|---|---|---|---|---|---|---|---|
| Lower limit | 0 | 0.2 | 0 | 0 | 0.2 | 0 | 0 | 0 | 0.2 |
| Upper limit | 500 | 0.5 | 1 | 500 | 3 | 3 | 100 | 5 | 5 |
| No. | Ionospheric Parameters | Geomagnetic Field Parameters * | EM Wave Propagation Direction | iCMC (C·km) | Relative Errors | Remark |
|---|---|---|---|---|---|---|
| 1 | h’ = 82 km, β = 0.5 km−1 | I = 45° | 0° | 97.9 | 2.2% | |
| 2 | h’ = 85 km, β = 0.5 km−1 | I = 45° | 0° | 100.6 | 5.0% | shown in Figure 11 |
| 3 | h’ = 87 km, β = 0.5 km−1 | I = 45° | 0° | 105.9 | 10.5% | |
| 4 | h’ = 82 km, β = 0.7 km−1 | I = 45° | 0° | 102.5 | 7.0% | |
| 5 | h’ = 85 km, β = 0.7 km−1 | I = 45° | 0° | 105.3 | 9.9% | |
| 6 | h’ = 87 km, β = 0.7 km−1 | I = 45° | 0° | 111.1 | 16.0% | |
| 7 | h’ = 85 km, β = 0.5 km−1 | I = 50°, D = −6° | 150° | 95.8 | — | set as reference |
| No. | Ionospheric Parameters | Geomagnetic Field Parameters * | EM Wave Propagation Direction | iCMC (C·km) | Relative Errors | Remark |
|---|---|---|---|---|---|---|
| 1 | h’ = 70 km, β = 0.3 km−1 | I = 45° | 0° | 61.1 | −11.4% | |
| 2 | h’ = 74 km, β = 0.3 km−1 | I = 45° | 0° | 69.7 | 1.0% | |
| 3 | h’ = 70 km, β = 0.4 km−1 | I = 45° | 0° | 68.9 | −0.1% | shown in Figure 12 |
| 4 | h’ = 74 km, β = 0.4 km−1 | I = 45° | 0° | 73.5 | 6.5% | |
| 5 | h’ = 70 km, β = 0.4 km−1 | I = 51°, D = −6° | 165° | 69.0 | — | set as reference |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, W.; Gu, J.; Wang, Y.; Dai, B.; Cui, X.; Wang, H.; Jiao, X.; Li, J.; Zhang, Q. Remote Measurement of the Lightning Impulse Charge Moment Change Using the Fast Electric Field Antenna. Remote Sens. 2022, 14, 724. https://doi.org/10.3390/rs14030724
Hou W, Gu J, Wang Y, Dai B, Cui X, Wang H, Jiao X, Li J, Zhang Q. Remote Measurement of the Lightning Impulse Charge Moment Change Using the Fast Electric Field Antenna. Remote Sensing. 2022; 14(3):724. https://doi.org/10.3390/rs14030724
Chicago/Turabian StyleHou, Wenhao, Jiaying Gu, Yaojun Wang, Bingzhe Dai, Xun Cui, Hongsheng Wang, Xue Jiao, Jie Li, and Qilin Zhang. 2022. "Remote Measurement of the Lightning Impulse Charge Moment Change Using the Fast Electric Field Antenna" Remote Sensing 14, no. 3: 724. https://doi.org/10.3390/rs14030724
APA StyleHou, W., Gu, J., Wang, Y., Dai, B., Cui, X., Wang, H., Jiao, X., Li, J., & Zhang, Q. (2022). Remote Measurement of the Lightning Impulse Charge Moment Change Using the Fast Electric Field Antenna. Remote Sensing, 14(3), 724. https://doi.org/10.3390/rs14030724