Abstract
The effects of the spatial resolution of remote sensing (RS) data on wildfire susceptibility prediction are not fully understood. In this study, we evaluate the effects of coarse (Landsat 8 and SRTM) and medium (Sentinel-2 and ALOS) spatial resolution data on wildfire susceptibility prediction using random forest (RF) and support vector machine (SVM) models. In addition, we investigate the fusion of the predictions from the different spatial resolutions using the Dempster–Shafer theory (DST) and 14 wildfire conditioning factors. Seven factors are derived separately from the coarse and medium spatial resolution datasets for the whole forest area of the Guilan Province, Iran. All conditional factors are used to train and test the SVM and RF models in the Google Earth Engine (GEE) software environment, along with an inventory dataset from comprehensive global positioning system (GPS)-based field survey points of wildfire locations. These locations are evaluated and combined with coarse resolution satellite data, namely the thermal anomalies product of the moderate resolution imaging spectroradiometer (MODIS) for the period 2009 to 2019. We assess the performance of the models using four-fold cross-validation by the receiver operating characteristic (ROC) curve method. The area under the curve (AUC) achieved from the ROC curve yields 92.15% and 91.98% accuracy for the respective SVM and RF models for the coarse RS data. In comparison, the AUC for the medium RS data is 92.5% and 93.37%, respectively. Remarkably, the highest AUC value of 94.71% is achieved for the RF model where coarse and medium resolution datasets are combined through DST.
1. Introduction
Forests are envisaged as a vital natural resource that conserves stability in the environment. The forest’s condition is the proper environment indicator, primarily the shape and health [1]. Forests are considered a crucial part of the economy of a few communities living in the periphery of forests with social significance and fostering weather conditions [2]. Forests enclosed around 5.9 billion hectares of the land surface before industrialization and currently cover approximately 4 billion hectares that account for 31% of the world’s land surface [3]. In recent times, wildfires are a grave problem that recurrently looms to extinguish a vast area of forests across the globe [4]. Wildfires have instigated severe destruction to ecosystems along with significant impairments to infrastructures and human lives. Major devastating wildfires in recent times occurred in Australia, the Amazon region, the United States [5], and different forest areas in Iran [1]. A wildfire is a disaster that can impact a community or ecosystem and can kill or severely injure wildlife, accounting for severe economic losses [6]. Wildfires have advanced into a very complex hazard, distressing habitats, people, and the economy. Forests are a valuable natural resource. Globally and in Iran, forests support the local communities’ economy. Wildfires can particularly affect young trees grown at the ground level, fostering deforestation. The frequency of forest fires has increased over the years. There is a need for far-reaching studies that support the monitoring and measures to mitigate the wildfires.
The modeling and mapping of wildfire susceptibility depend on a multifaceted and multi-scaled system of wildfire factors, including slope, elevation, aspect, landcover, normalized difference vegetation index (NDVI), temperature precipitation, distance to roads, distance to rivers, village density, power wind speed, and wind speed. Landcover and NDVI can be easily derived from Landsat and Sentinel-2 satellite images with different resolutions. Topological features such as slope and aspect can be obtained from a digital elevation model (DEM). Moreover, the modeling and mapping accuracy of wildfire susceptibility highly depends on the size of the existing burned areas. In addition, as we are using global positioning system (GPS) points for training and accuracy assessment processes, proper DEM resolution is a prerequisite in wildfire susceptibility modeling and mapping.
Similarly, the burned areas inventory points are important. The selection of appropriate spatial resolutions is increasingly addressed in literature [7,8,9]. However, the challenge of adequately representing hazard locations by a point feature as inventory together with image and raster data for training or testing the models needs to be investigated in greater detail.
Several studies have mapped wildfire susceptibility in forest areas across the globe. Different spatial modeling strategies have been developed to simulate and predict the spatial pattern of wildfire probability in different geographical regions. Some of these studies use multi-criteria decision analysis (MCDA) to combine remote sensing information and the geographic information system (GIS) for wildfire susceptibility prediction (WSP). Eskandari and Miesel [10] used a knowledge-based analytical hierarchical process (AHP) to determine the importance of each wildfire conditioning factor. The weighting is typically derived from prior knowledge of different stakeholder groups, local communities, and academic experts’ weighted individual factors regarding wildfire susceptibility. These authors used AHP and fuzzy sets (fuzzy AHP) to predict high-risk wildfire regions in the Mazandaran Province, Iran. The fuzzy AHP compares the wildfire conditioning factors in an unbounded space representing uncertainty in the resulting WSP. Moreover, other models such as the evidential belief function model are applied for the WSP [11]. This model was used based on fourteen predicting variables and 1162 wildfire points used for training and testing the model for WSPs in the Hyrcanian ecoregion, northern Iran. More recently, machine learning (ML) models have been extensively used to predict and analyze the spatial distribution of natural hazards like wildfires. ML models depend on the accessibility of the training data to train the model. Different ML techniques have particular advantages and drawbacks. The main advantage of integrating GIS models with ML models is usually a better performance of the resulting WSPs as well as a higher speed in data processing compared to conventional approaches like MCDA. ML models are state-of-the-art and have proven to be able to efficiently deal with non-linearity problems such as spatial simulation, modeling, and mapping, especially in natural hazard susceptibility mapping [12,13]. ML models have currently received more attention for WSPs. Kalantar et al. 2020 [14], in another instance, applied the three ML models of boosted regression tree, support vector machine (SVM), and multivariate adaptive regression splines for the WSP using fourteen key indicators contributing to wildfires. Naderpour et al. [15] proposed a deep neural network for the WSP in the Northern Beaches region of Sydney, and the resulting WSP was then used for risk assessment in that area. Kim et al. 2019 [16] applied two ML models of random forest (RF) and maximum entropy (Maxent) to predict the locations of forest fires in South Korea. Their study yielded the highest wildfire probabilities around settlement areas. The study revealed that this hazard has a strong correlation with human-related variables. A comprehensive WSP study [17] evaluated several statistical approaches and ML models of an artificial neural network, multi-layer perceptron, DM neural, radial basis function, dmine regression, least angle regression, RF, support vector machine (SVM), self-organizing maps, decision tree, and logistic regression. This study’s accuracy assessment revealed that RF represents the WSP with the highest accuracy of 88% area under the curve (AUC), followed by SVM with 79% AUC. As evident from the literature review, the resulting WSPs from the ML models were compared to each other to find the optimum model for this task. Although RF and SVM models have usually shown higher performance, there is no evidence that a particular method or approach is suitable for a specific hazard. Rather, the suitability of a method depends on the features of the study area, the availability of training data, and the spatial resolution of the data used [18]. Next to the choice of the WSP methodology, the spatial resolution of the remote sensing (RS) data in potential wildfire areas is essential, particularly in data-sparse conditions. The most used RS data for the WSP are optical data from satellite imageries along with DEM data. Some studies have evaluated RS data and resolutions for natural hazard assessments and susceptibility mapping, particularly the spatial resolution of DEMs. Mohammadi et al. 2020 [19] compared the impact of the spatial resolution of different DEMs derived from AIRSAR, ALOS-PALSAR, TanDEM-X, SRTM, and one generated from Sentinel-1 on the hydrological modeling in two different study areas in the Kurdistan Province, Iran, and in the Cameron Highlands, Malaysia. In addition, Chen et al. 2020 [20] evaluated the influence of the spatial resolution of seven DEMs ranging from 30 to 90 m for landslide susceptibility mapping. They applied statistical models, namely the entropy index, frequency ratio, and weight of evidence, and compared the performance of each model based on all applied DEMs. This study found that the highest accuracy was derived from 70 m spatial resolution and concluded that a coarser spatial resolution does not necessarily result in the lower landslide mapping performance of susceptible areas. Therefore, there is no general rule on which type of ML model to use and what the ideal RS spatial resolution is [21].
Consequently, each natural hazard susceptibility mapping, including the WSP, is associated with uncertainty regarding prediction performance. This uncertainty is reflected in the resulting WSPs [22]. However, there is a considerable gap in the literature. While some studies evaluated uncertainty caused by the model performance in different natural hazard susceptibility mapping, we do not know whether the uncertainty in the resulting WSPs is caused by the model limitations or the spatial resolution of the data. Ghorbanzadeh et al. 2018 [23], for instance, applied a Monte Carlo simulation to evaluate the uncertainty of the predicted areas as highly susceptible to land subsidence by an analytical network process (ANP). Other studies that used the Dempster–Shafer theory (DST) of evidence for spatial modeling, event occurrence, and susceptibility mapping of natural hazards, including wildfires, have shown the DST’s capability to generate consistent wildfire probability maps. Their results confirm those of [16] in South Korea, where human-related factors like distance to settlements and high road density played an important role in wildfire occurrence. Mezaal et al. 2018 [24] applied this theory for combining the resulting predictions from three ML models of K-nearest neighbor, SVM, and RF for landslide areas. They employed the DST for fusion predictions from different ML models to produce a more accurate landslide map. Other authors used the DST to assess and map the susceptibility of other natural hazards. Nachappa et al. 2020 [25] used it to optimize the flood susceptibility maps resulting from two different MCDA, namely the AHP and ANP, and two ML models, SVM and RF. DST could enhance the accuracy of MCDA and ML models. The best accuracy of 89.3% AUC was reached by combining the resulting susceptibility map from all four models. The result of flood susceptibility mapping using the DST technique was compared with frequency ratio and logistic regression models by Tehrany and Kumar, 2018 [26].
According to our literature review, although selecting the appropriate spatial resolution of the available Earth observation data is highly important in natural hazard studies, its application in WSP studies has received little attention. Specifically, the terrain characteristics derived from DEM significantly influence the WSP as the topography is correlated with fire size and duration, the direction of spread, fire line, and speed. Therefore, inspired by the literature mentioned above, this study evaluates the effects of coarse and medium spatial resolution RS data on the WSP. The main contributions include investigating the fusion of WSPs based on different spatial resolutions using the Dempster–Shafer theory and several wildfire conditioning factors. Figure 1 represents a summary of our proposed integration methodology and the working environment for each step. Except for the final steps of the methodology such as the fusion of WSP maps and accuracy assessment, the whole process was completed in Google Earth Engine (GEE). The proposed approach is applied to the actual situation of the whole forest area of the Guilan Province, Iran. Therefore, we aim to provide an in-depth assessment of the impact of the resolution of Earth observation data from different sources for wildfire susceptibility using GEE and machine learning approaches. Two ML models, SVM and RF, are trained and tested on these two datasets. We also compare which ML model and dataset is most suited for WSP. Additionally, we assess the application of the Dempster–Shafer theory to optimize the resulting WSPs by combining the results from different datasets and models.
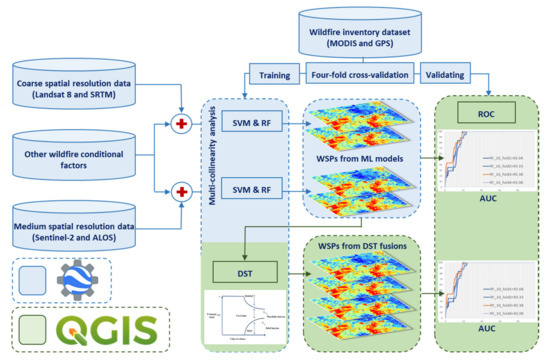
Figure 1.
The flowchart represents a summary of the integrated approach. The data preparation, preprocessing, multi-collinearity analysis, training of the applied machine learning models of the support vector machines and random forest, and the wildfire susceptibility prediction maps were performed in Google Earth Engine illustrated with the blue color. QGIS software was used to apply the Dempster–Shafer theory for data fusion, WSP optimization, and accuracy assessment.
2. Study Area
The study area is the whole forestry area of Guilan Province, located in northern Iran (see Figure 2). The province has an international border through Astara with the Republic of Azerbaijan. It is bordered by Mazandaran Province from the east, Zanjan and Qazvin Provinces from the south, and Ardabil Province from the west. According to the statistics of this province, it is the tenth province in terms of population density, which includes a population density of 177 people per square kilometer. The rainfall is between 1200 and 1800 mm in the coastal strip (Bandar Anzali and Astara) and reduces to less than 1000 mm in the Alborz mountainous areas in the south. The forests of Guilan cover a narrow area mainly in the northern slopes of this mountainous strip with a variety of species and animals. The potential of wood production and withstood activities of the local population have always been considered an important economic source for the local community and the government. The indigenous ranchers in the forest areas are rural people who are economically dependent on coal production. The activities of forest dwellers have altered the environment, and their activities are considered to be the major causes of wildfires in Guilan [27].
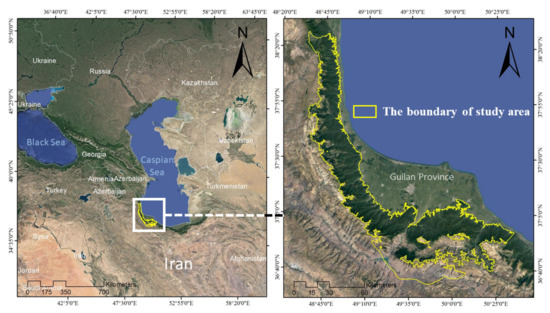
Figure 2.
The geographic location of the selected area under study, Guilan Province, is represented in the user interface of Google Earth Engine (GEE).
3. Inventory and Conditioning Factors
In this study, we identified wildfire locations using the moderate resolution imaging spectroradiometer (MODIS) thermal anomalies product and comprehensive field surveys using a GPS and detailed historical point records for a period of the recent ten years. All the fires that happened in our case study area in Guilan Province from 2009 to 2019 were acquired from MODIS hotspots available from https://modis.gsfc.nasa.gov/data/ (accessed on 10 December 2020).
Based on the data availability, MODIS product, GPS, and historical records, 97 wildfire locations were identified as a reliable and accurate inventory. These wildfire location points were then randomly classified into training and testing wildfire datasets using four-fold cross-validation. The training wildfire datasets were used for model preparation and training, whereas the testing wildfire datasets were used for model performance assessment. Wildfire locations were represented as point features and needed to be converted to rasters with pixel sizes of 30 m and 10 m. This conversion of the wildfire location points to raster cells with different resolutions may considerably affect the WSP results [28]. Thus, in this work, we investigated the effect of the raster resolution on susceptibility mapping in conjunction with the algorithm used to transform landslide polygons into a raster structure. The different pixel sizes of 30 m and 10 m are represented in Figure 3.
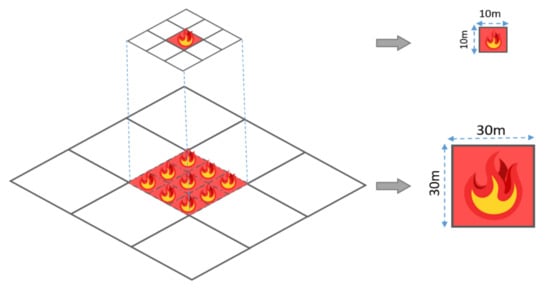
Figure 3.
Illustration of converting a wildfire location (point) into a raster with different pixel sizes of 10 m and 30 m spatial resolution.
Conditioning Factors with Different Spatial Resolutions
Any assessment must select the causative or influencing factors that significantly impact the hazard assessment [29]. A wildfire is one of the most complex natural hazards in terms of severity, spread speed, coverage, and degrees of destruction. It is essential to identify the major conditional factors [30]. In this study, we identified 14 conditional factors that significantly influence the wildfire ignition and spread speed while considering the characteristics of the forest area of the Guilan Province, Iran, based on recommendations from previous studies on similar areas in nearby provinces. These conditioning factors have been chosen according to their relevance to the hazard as well as the study area characteristics. These conditional factors consist of four groups: topographical, meteorological/hydrological, vegetation, and anthropological factors. Topographical factors include elevation, slope, aspect, and plan curvature. They dominate the climatic situation, particularly the spatial distribution of temperature and precipitation, which control the life cycle of flora and fauna. Meteorological/hydrological factors include distance to rivers, the topographic wetness index (TWI), temperature, precipitation, mean wind power density (MWPD), and mean wind speed (MWS). The NDVI is a vegetation conditioning factor. It is known that in the Guilan Province, human activities of the local population and tourists cause ignitions and are responsible for wildfires [27]. Therefore, the essential anthropological conditional factors of distance to roads, village density, and landcover were selected for further analyses. Landcover has a profound influence on fire incidence [31].
The baseline map for extracting the topographical factors and some others like TWI is the DEM. In this study, for investigating the effect of the spatial resolution of the DEM on the WSP, two DEMs with different spatial resolutions were prepared from different sources. Our coarse DEM is the advanced spaceborne thermal emission and reflection radiometer (ASTER) global digital elevation model (GDEM) with an approximate resolution of 30 m, which is available from (https://asterweb.jpl.nasa.gov/gdem.asp) (accessed on 20 December 2020) (see Figure 4). The advanced land observing satellite/phased array L-band synthetic aperture radar (ALOS/PALSAR) with 12.5 m spatial resolution can capture images under all-weather conditions and has day and night observation. It is extracted from https://vertex.daac.asf.alaska.edu/# (accessed on 20 December 2020).
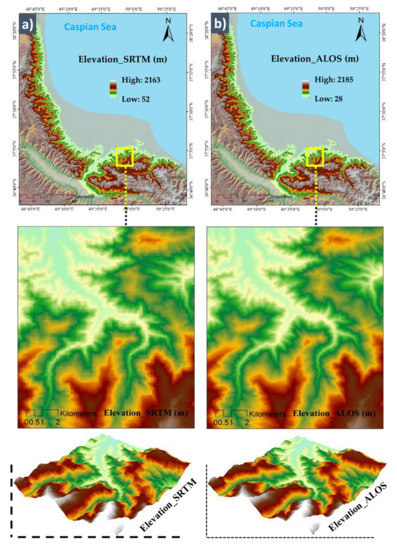
Figure 4.
Representation of the applied digital elevation models (DEMs) of (a) SRTM and (b) ALOS.
Similarly, the NDVI and landcover factors were generated using Landsat-8 and Sentinel-2 satellite imagery with 30 m and almost 10 m spatial resolution, respectively (see Figure 5). The Landsat-8 is available from the United States Geological Survey (USGS) archive (http://earthexplorer.usgs.gov) (accessed on 20 December 2020), and Sentinel-2 is available from (https://scihub.copernicus.eu) (accessed on 20 December 2020) (see Table 1). We resized the pixel size of ALOS DEM to the same as that of Sentinel-2 (10 m). All conditional factors were prepared to assess the WSP using ML models in the GEE platform. The wind-related factors of the MWPD and MWS are available from the wind global atlas archive (https://globalwindatlas.info/) (accessed on 20 December 2020). We obtained the distance to road and village density factors from Openstreetmap (https://www.openstreetmap.org/) (accessed on 20 December 2020). The conditional factors are represented in Figure 6, and Table 2 summarizes the literature review of the selected WSP factors and their significance.
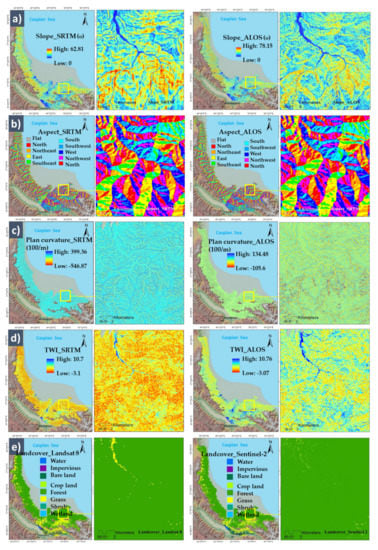
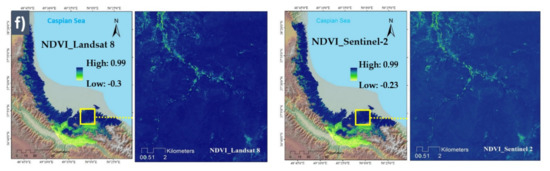
Figure 5.
Conditioning factors derived from different DEMs and Landsat 8 and Sentinel-2 satellite images: (a) slope, (b) aspect, (c) plan curvature, (d) topographic wetness index (TWI), (e) landcover, and (f) normalized difference vegetation index (NDVI).

Table 1.
Satellite data used for this study from the Earth engine data catalog.
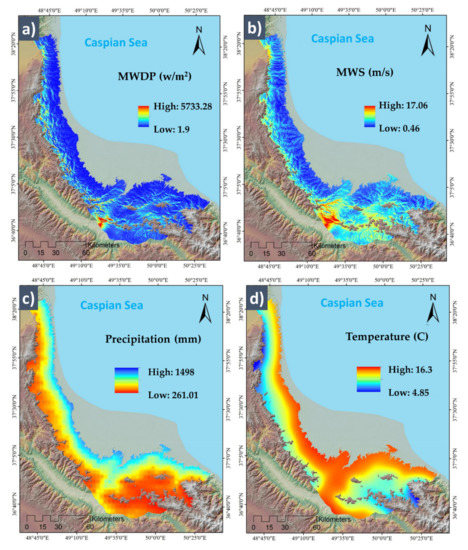
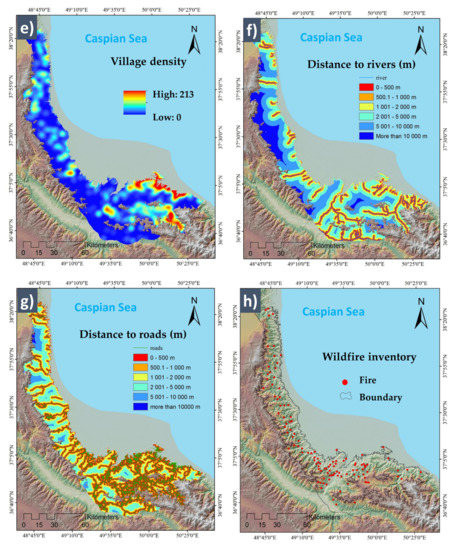
Figure 6.
The conditional factors considered in both datasets overlaid with the wildfire inventory points. The pixel size was resized based on the corresponding dataset. (a) Mean wind power density (MWPD), (b) mean wind speed (MWS), (c) precipitation, (d) temperature, (e) village density, (f) distance to rivers, (g) distance to roads, and (h) wildfire inventory.

Table 2.
A summary of the literature review: significance of the selected conditioning factors for wildfire susceptibility prediction (WSP).
4. Methodology
4.1. Training and Testing Dataset Organization
According to Ghorbanzadeh et al. (2018) [41], ML models result in a random output with little scientific value when the training and the test datasets are inappropriate. ML models often use a standard workflow that uses a training dataset to train the model and applies the trained model to predict phenomena like wildfire on unseen test data. One possible way to validate the results is based on a single hold-out dataset. This study used a four-fold cross-validation (CV) procedure for a more reliable model performance evaluation. The CV procedure removes dataset biases and prevents under/overfitting of the ML model in the optimization step [14]. This procedure was applied to appropriately prepare the dataset for training and testing the SVM and RF models. Therefore, the dataset d of wildfire inventory location/point was randomly partitioned into mutually exclusive four-folds of d1, d2, d3, and d4. Next, both ML models were run four times. For any time, one fold was not used for training and was reserved for validation. For example, when a model is run for the first time, the model is trained with d2, d3, and d4, while d1 is utilized to validate the model. Therefore, each time, 75% of the wildfire inventory points were used to train the model, and 25% of them were held out to validate the model performance (see Figure 7). Due to the amount of calculations in this study and the volume of our inventory dataset, the number of folds was selected as four. The CV procedure utilizes the training and test datasets and shall account for certain randomness associated with the resulting WSP. The whole procedure has been applied on both raster data sets with 30 m and 10 m pixel sizes.
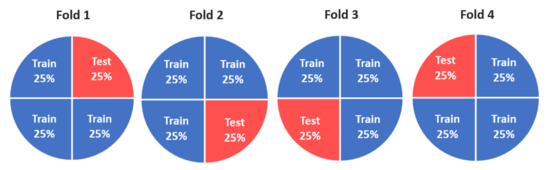
Figure 7.
We used four-fold cross-validation (CV) for our wildfire inventory dataset. Each section represents a randomly selected fold of the inventory wildfire points. The sections with red color were used for testing, and those with blue color were used for training the ML models.
4.2. Factor Analysis
Factors in an ML model can be correlated. This training significantly affects the model performance [14]. The variance inflation factor (VIF) and quantitative tolerance methods were used to measure the spatial autocorrelation among the conditional factors that we used to generate WSPs. The tolerance is a broad form of a multiple correlation coefficient, which ranges from zero to one, and lower values refer to higher multi-collinearity. A high multi-collinearity between a variable and other independent variables means that the variable can also be predicted using the other variables [42]. At the same time, VIF refers to a measurement of the disagreement in a multivariate model using model variance with an individual variable. The degree of disagreement is obtained using a regression coefficient amplified due to collinearity in an ordinary least square regression [14]. The VIF, tolerance, and coefficient values have been calculated for both models of SVM and RF, aiming for the highest CV procedure accuracy. The coefficients that show the importance of conditional factors were standardized by Equation (1) [43]:
where is the standardized weight at kth model, k = 1, 2, 3, and 4 refer to SVM10, RF10, SVM30, and RF30; is the derived weight by the kth model, and i is the index for the WSP conditioning factors.
4.3. Google Earth Engine (GEE) Platform
The Google Earth Engine (GEE) is a multi-petabyte public data catalog of commonly used geospatial and remote sensing data. The GEE particularly contains remote sensing images of the Earth’s surface captured by Landsat and Sentinel satellites. It also contains other datasets for landcover, as well as climate-related and environmental datasets. The collection is constantly updated at a rate of nearly 6000 satellite scenes per day from different sensors, typically provided within 24 h from the scene acquisition time. Users can add new datasets to the GEE from the public catalog or add their own dataset for further analysis using the REST interface. This way, high-performance computing has become possible for ordinary users, along with cloud-based computations for large petabyte data capacity [44]. Satellite data have been made freely available with global coverage, mainly geospatial and remotely sensed data through various agencies like NASA, the US Geological Survey, NOAA, European Space Agency, and others. This sharp increase in the availability of global-coverage remote sensing data is accompanied by the development of numerous precise tools for processing the geospatial and remote sensing data [45]. With all the easily accessible data from numerous sources, these resources’ captivating, complete benefit still entails effort and technical proficiency to derive significant and valuable results or outcomes. One of the most common hurdles faced is the management of information technology where the acquisition of data from multiple sources, storage of the enormous volumes of data derived from various sources, computational capabilities to deal with the vast data volumes, database management, and data processing frameworks restrict researchers or smaller organizations to make use of the freely available data to derive meaningful outcomes [46]. The GEE clearly lowers such barriers. Users can rapidly process vast amounts of remote sensing data without their own investments in computational capabilities, storage, and their own efforts to integrate data from multiple locations.
The GEE is a cloud-based platform that allows one to access and analyze satellite and other geospatial data, including 40 years of historic Earth observation imagery. This renders it possible to perform comparisons and time-series analyses, usually for the entire globe, but it depends on the coverage of the particular satellite [47]. The main advantage of the GEE is the easy access to the (satellite) data archives and high-performance computing resources to process massive geospatial and remote sensing datasets that are processed and periodically updated. Additionally, the dissemination of results in the GEE is easy as the GEE can deploy user-developed algorithms without requiring proficiency in web application or programming. The GEE offers diverse satellite data that consumers can retrieve and incorporate into their applications, particularly Landsat, Sentinel-2, and NEXRAD. Landsat datasets are multispectral satellite images of the Earth’s surface from the United States Geological Survey (USGS) and National Aeronautics and Space Administration (NASA) with resolutions between 15 m and 60 m since 1982. Landsat-8 satellite images are included for less populated areas but with lesser frequency. The Sentinel satellite images provided by the European Space Agency (ESA) have a resolution of 10–60 m. Sentinel-2 images with a resolution of 10 m are available with a frequency of 5 days. The NEXRAD is a weather radar dataset derived from 160 high-resolution Doppler weather radars from the National Oceanic and Atmospheric Administration National Weather Service (NOAA-NWS), the Federal Aviation Administration (FAA), and the US Air Force. Next to the described remote sensing and geospatial data, climate and weather data (surface temperature, climate, atmospheric, weather), and geophysical (terrain, landcover, cropland) data, the GEE provides computational infrastructure for processing the data. It also provides APIs for connecting and making requests to GEE servers (JavaScript and Python), and code editor, which is a web-based integrated development environment (IDE) for coding, prototyping, and visualizing the results [48].
4.4. Support Vector Machines (SVM)
The support vector machine (SVM) is a supervised model, which is built on the statistical learning theory, also known as the maximum-margin classifier proposed by Vladmir Vapnik in 1995 [49]. The SVM is a data mining approach that uses statistical learning theory and structural risk minimization theory to differentiate amongst two variants with a linear hyperplane [50]. The SVM can provide a good classification result when only a few training data samples are available. The main reason is that the closest samples can determine the position of a hyperparameter to the hyperplane [51]. Therefore, this model usually works better and shows higher performance than other ML models in the case of data scarcity [52]. The superlative hyperplane can be acquired when the splitting margins amongst the expressed classes of the problem are highest. The SVM, by nature, is a linear classifier. However, using the kernel trick, the SVM was generalized to nonlinear problems. This trick simply transforms the nonlinear data into a higher dimensional space where the data are linearly divisible. Thus, the SVM restructures the nonlinear domain into a linear one by creating a splitting hyperplane [53]. The sensitivity to the selection of the kernel function and setting the optimal parameters are considered the weaknesses of this model [54]. In our case, the radial basis function was selected following similar previous studies [17]. Therefore, a kernel width (γ) value of 0.95 was selected, and the regularization (C) parameter was set as 0.8 based on a test and trial process of previous studies.
4.5. Random Forest (RF)
The random decision forest algorithm was initially developed by applying the random subspace technique by Tin Kam Ho [55]. Later, the extension of this algorithm registered as ‘random forests (RF)’ was developed by Leo Breiman [56]. RF is an ML model where the input dataset is categorized to build an assortment of decision trees with a controlled variance or ideally an algorithm for classification and regression. The RF is a robust classifier in terms of accuracy in the case of lack of balance among the number and dimensionality of the training data sample at hand. RF has been widely used due to its ability to generate exceptional classification outcomes along with the increased processing speed [57]. It has also been widely applied in natural hazard spatial modeling since this ML model does not assume an underlying probability distribution for the data [51].
Furthermore, features are chosen arbitrarily while predicting at every phase. Each result is weighted based on the value derived from the votes. The majority of the votes are obtained based on the assessed decision trees’ outputs for the classification [58,59]. Uncertainty is a concern in each model. To overcome this issue in RF, it is recommended to use a single decision tree that yields greater prediction accuracy [60]. The critical practice in RF is to obtain a higher variance from diverse decision trees, which is essential in the classification technique. RF is considered as one of the top functioning non-parametric ensemble learning models in susceptibility mapping and modeling. We set the maximum number of trees as 1000, which was chosen from a test and trial using values of (500, 1000, 1500, and 2000). However, the default value of 25 was considered for the number of variables in each split of the RF model. The applied RF model showed the best performance using the cutoff fraction value of 0.01 and the resampling process with 500 repeats.
4.6. Dempster–Shafer Theory (DST)
The Dempster-Shafer Theory (DST) generalizes the Bayesian methodology known as a mathematical theory of evidence. It was introduced in the 1960s in the field of statistical inference by Arthur Dempster and developed later by Glenn Shafer into a general framework for reasoning on epistemic uncertainty [61]. The DST offers an alternative means to the traditional probabilistic theory for general uncertainty and explicitly considers the probable unknown cause of the observed data. It also provides a robust framework that makes it possible to allocate a probability mass to sets or intervals as divergent to mutually exclusive single events [62]. This theory has been employed as a fusion algorithm to extract probability-based evidence enclosed in a dataset. This probability can be considered as the susceptibility of a phenomenon or existing of a geographical feature [63,64]. Therefore, the primary motivation for selecting the DST is its flexibility to characterize and integrate diverse types of evidence gained from different sources. The DST is an operative technique for modeling accuracy assessment which has a comparatively high degree of theoretical progress between the non-traditional theories for illustrating associated uncertainty within outputs. It starts by assuming a frame of discernment (Θ), which is a basic set of hypotheses in the case of some problem domains. All possible subsets of Θ subset are U, which has been named as the power set of Θ. In this theory, information is assigned with three fundamental functions that are denoted by (1) mass function (m) also called basic belief assignment or basic probability assignment, (2) the degree of belief function (Bel) which can be calculated exactly from a mass function, and (3) the degree of plausibility function (Pl). Bel can be observed as a lower bound for an unknown probability function P. Under a lower and upper probability interpretation, the plausibility Pl can be observed as an upper bound. The uncertainty interval or the probability domain can be represented by the interval [Bel, Pl], which is the uncertainty validated with the distinction between Bel and Pl values. Figure 8 shows graphically the relationships between Bel, Pl, and uncertainty.
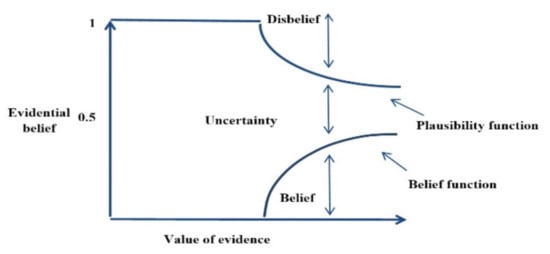
Figure 8.
The general DST scheme illustrates the applied functions [61]. Reproduced with permission from Feizizadeh, Geoscience and Remote Sensing Letters; published by IEEE, 2018.
The DST delivers an extension of the probability outline for measuring the associated uncertainty in any imprecise event of the probability P (Ml) in which the different methods Ml, l = 1, …, n is accurate. The lower bound shows the degree of knowledge or belief that supports Ml and is represented by Bel (Ml). The upper bound refers to the probability of Ml, and named plausibility Pl (Ml) are calculated by Equations (2) and (3).
The total amount of belief dedicated to a hypothesis A (A U) with all subsets B () is denoted by Bel (A). The summation in Equation (3) is taking over all B with B , which takes into account all the elements related to A, either supported by evidence or being unknown. The set of ɵ is mutually exclusive hypotheses and propositions, and the power set of ɵ is represented by . define the uncertainty interval for the subset of A, which has the following properties (Equations (4) and (5)):
where Ā is the negation of A and Bel (Ā) is named as the disbelief function. In contrast to the probabilistic theory that allocates a mass to each element of events, the theory of evidence or the bpa, makes m (A) on the set A of the P(U) power sets of the space U event, i.e., on a set of outputs rather than a single elementary event. This is a unique feature of the DST, which distinguishes it from other traditional probability theories. A mass function of the set of A or m (A) hypotheses measures the probability dedicated only to A and no subset of A [65]. Formally, a mass function is mapping the power set of U to [0, 1] and the mass of the empty set must be zero (Equation (6):
to solve implication problems, belief functions represent dissimilar pieces of evidence required to be combined in a meaningful way. The integration rules are a fundamental part of the DST. Generally, each part of the evidence is characterized by a separate belief function. The combined rules are then used sequentially to integrate these belief functions to obtain a belief function on behalf of all available evidence.
Bel(A) ≤ Pl(A)
Pl(A) = 1 − Bel(Ā)
m: P(U) → [0, 1], m(φ) = 0
The combination rule in the DST is for n sources of data. For each data with 1 ≤ i ≤ n, the probability masses mi (Bj) can be defined, where Bj , using the following equations:
where K is a grade of the amount of conflict among the mass sets given in Equation (9):
5. Results
5.1. Multi-Collinearity Analysis among Conditional Factors
We estimated the multi-collinearity among our WSP conditional factors in reducing repetitive spatial information in the training of the ML models. The results of the multi-collinearity among the WSP conditional factors are shown in Figure 9. A factor’s VIF values of less than five and tolerance values of more than 0.1 mean no multi-collinearity [14]. According to the represented results in this figure, all applied conditional factors have acceptable VIF and tolerance values. Therefore, all these factors were considered for training the SVM and RF models. The factor elevation in RF30 and the perception in RF10, received the lowest VIF values of 1.012 and 1.014, respectively.
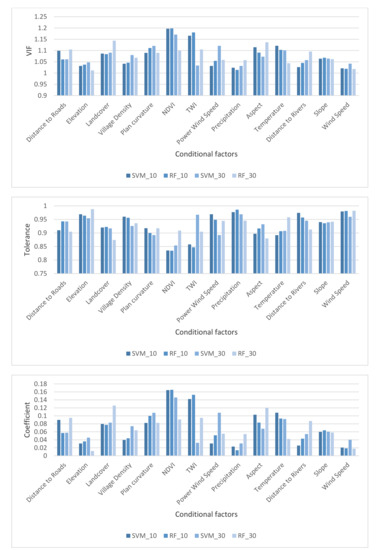
Figure 9.
The multi-collinearity assessment and coefficient values for the applied WSP conditional factors in this study.
In comparison, the factor NDVI yielded maximum SVM10 and RF10 VIF values of 1.196 and 1.198, respectively. As expected, NDVI received the lowest tolerance values: 0.834 for SVM10 and 0.835 for RF10. The highest tolerance value of 0.988 was attributed to the elevation factor, which is still acceptable. The resulting coefficient values are shown in Figure 9. This figure illustrates that the two ML models with two different training data were consistent in conditioning factors, especially NDVI, TWI, landcover, and temperature. NDVI was the most crucial factor contributing to the WSP in Guilan Province, followed by TWI. Other factors such as wind speed, elevation, and precipitation yielded relatively low importance for the WSP mapping in this study area. Although TWI ranked high, its impact was very low when using SVM30. For SVM30, the factors wind speed, and power wind speed yielded the highest importance values for training this model.
5.2. Wildfire Susceptibility Prediction (WSP) Maps Using Machine Learning (ML) Models
We investigated the performance of the four-fold CV on the two ML models. Overall, the map of the best performance of the models is represented in Figure 10. The WSP maps were generated using ML models of SVM and RF for two different spatial resolutions of 10 m and 30 m data. The natural break algorithm classified the resulting WSPs into very low, low, moderate, high, and very high classes. The results of the classification are shown in Figure 10. Several current studies prove the expansion of successful ML models in spatially explicit wildfire modeling and mapping, e.g., [7,14,15,39,40]. Here, the two ML models of SVM and RF were evaluated. The models’ predictive abilities were compared using conditional factors from different spatial resolutions to estimate the spatially explicit WSP across a forestry area. Although the same ML models (with the same parameters) and exactly the same wildfire inventory dataset were used for the WSP, the results of using conditional factors with different spatial resolutions turned out to be significantly different.
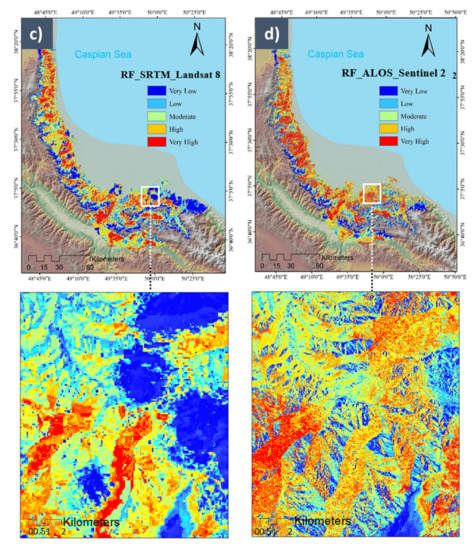
Figure 10.
The resulting wildfire susceptibility prediction (WSP) maps from (a) SVM30, (b) SVM10, (c) RF10, (d) RF30.
5.3. Dempster–Shafer Theory (DST) Optimization
This study used DST to fuse the ML models’ resulting WSP maps trained based on the coarse (Landsat 8 and SRTM) and medium (Sentinel-2 and ALOS) spatial resolutions for Guilan Province. Through DST, we integrated the results from RF10 and SVM10 based on the 10 m medium spatial resolution as well as the resulting WSP maps from the 30 m coarse spatial resolution dataset for RF30 and SVM30. Moreover, we also integrated the results of one ML model trained with two different resolutions while considering the medium resolution as the base pixel size for data fusion. The resulting WSP maps from each ML model and each dataset have been considered as the initial data evidence to create a modeling hypothesis of the integration technique. This was processed through the represented wildfire susceptibility prediction value in every single pixel of the WSP map, given the evidence of the probability and wildfire occurrence locations P(x) of only the training inventory dataset.
Consequently, we calculated the belief, plausibility, and confidence interval layers. The resulting pixel values ranging from 0 to 1 denote the susceptibility wildfire occurring probability for each pixel either 10 or 30 m. The belief value was calculated by ∀A∣A∈P(Θ): Bel (A) = ∑ X ⊆ Aμ(X), where Bel (A) is a probability ranging from 0 to 1. The resulting belief value accounted for the area of a given pixel. Each pixel’s value was the wildfire susceptibility probability derived from both WSP maps involved in DST integration. In addition, we calculated the plausibility using ∀A∣A ∈ P(Θ): PI (A) = ∑ X ∩ Aμ (X), where PI (A) is a probability value ranging from 0 to 1 [22,66]. Therefore, each pairwise WSP map was used for the DST integration process. The areas considered susceptible regions to wildfire using different spatial resolutions and ML methods were categorized into five susceptibility classes, from very low to very high. Class one refers to high and very high susceptibility. Thus, a DST-based WSP map can be considered the spatial distribution of the degree of support for the wildfire susceptibility [24]. The DST combined the majority of wildfire susceptible areas closer to the inventory dataset and then allocated them into the class of wildfire areas based on the DST (see Figure 11).
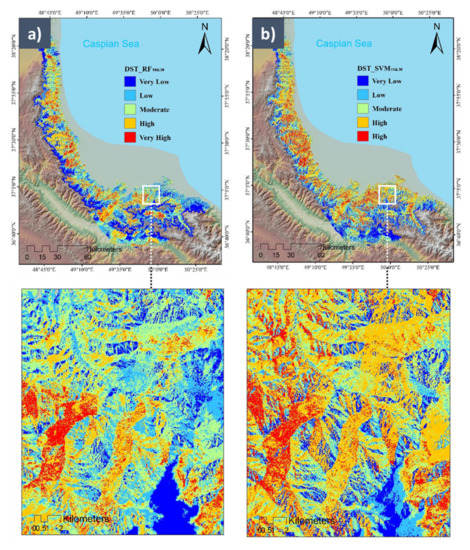
Figure 11.
The resulting wildfire susceptibility prediction (WSP) maps from the DST technique by integrating (a) RF10 & 30, (b) SVM10 & 30, (c) SVM10 & RF10, (d) SVM30 & RF30.
5.4. Cross-Validation (CV)
As mentioned, we used a four-fold CV procedure for a more consistent evaluation of the performance of the applied ML models. Stepwise, 25% of the wildfire inventory dataset was a hold-out for validating the model. We used the ROC curve method, a common accuracy assessment approach to assess the performance of the SVM and RF models and the results of DST by investigating the conformity among the validation folds of the inventory dataset and the results of the used methods. The ROC curve method is typically applied to investigate the quality of a map. The plotted ROC curves indicate the trade-off between the false positive rate on the X and Y axis and the true positive rate on the Y axis. The area under the curve (AUC) is a measurement calculated by Equation (10):
where, is the percentage of incorrectly predicted pixels for , is the percentage of correctly predicted pixels for , and the value of is referred on the number of whole pixels [67]. The resulting AUC values for a WSP map close to one indicate high accuracy of that map, whereas AUC values close to zero reveal that the prediction is random. Table 3 provides linguistic explanations of the resulting values. Figure 12 shows the ROC curves and the AUC values for all resulting WSP maps based on the applied four-fold CV.

Table 3.
The linguistic representation of the area under the curve (AUC).
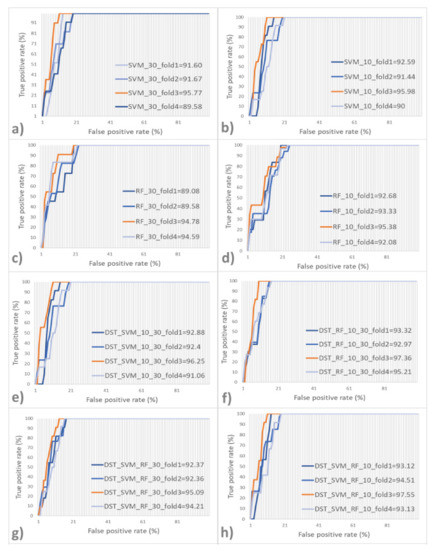
Figure 12.
The resulting ROC curves based on the four-fold CV for (a) SVM by coarse dataset 30 m, (b) SVM by medium dataset 10 m, (c) RF by coarse dataset 30 m, (d) RF by medium dataset 10 m, (e) DST using SVM results for coarse 30 m and medium 10 m datasets, (f) DST using RF results for coarse 30 m and medium 10 m datasets, (g) DST using results from SVM and RF-based on coarse dataset 30 m, (h) DST using results from SVM and RF-based on medium dataset 10 m. The corresponding ROC curve of the highest value of AUC measurement in each four-fold is specified by orange color.
The AUC measurements for all ML-based WSP maps of medium and coarse spatial resolution yielded more than 89% accuracy for all applied folds. The highest accuracy was based on the SVM model trained with 10 m spatial resolution, with an AUC value of almost 96% (see Figure 12b). However, for the same fold and dataset, RF also reached a very high value of 95.38 (see Figure 12d). The lowest resulting AUC values for the SVM and RF models for the 30 m resolution data were 89.58% and 89.08%, respectively. In comparison, those of the 10 m resolution data were 90% and 92.08%, respectively. Although the resulting AUC values are not far from each other, training and testing the ML models based on the coarse (30 m) resolution data showed the weakest performance.
We also performed an accuracy assessment for WSP maps based on the DST. This optimization could increase the accuracy of almost all of the resulting WSP maps (see Figure 12e–h). The highest AUC value was based on the application of the DST integrating the SVM and RF derived from the 10 m dataset, which yielded an accuracy of more than 97.5% (see Figure 12h). The lowest AUC value of 91.06% was obtained from the fusion of the SVM results from the coarse and medium datasets with AUC values of 89.58% and 90%, respectively (see Table 4).

Table 4.
The accuracy results for each fold of the applied cross-validation (CV) in percent. The obtained highest accuracy is bolded for each fold.
6. Discussion
Developing the best WSP methodology is a challenging task because of the associated spatial heterogeneity of the conditioning factors [14]. This challenge increases when the conditional factors stem from data with different spatial resolutions. Identifying potential wildfire zones is essential for a better understanding of the wildfire dynamics in wildfire-prone regions. Literature studies revealed that the common ML models of SVM and RF are appropriated for modeling WSPs [14,15,39]. However, the accuracy of a resulting WSP map is directly related to the applied ML model’s performance, which highly depends on the characteristics of the input data and the inventory data. Therefore, it is crucial to evaluate these characteristics, such as the spatial resolution of the input data regarding their application in ML models’ training and testing. Many conditional factors in wildfire modeling are typically derived from satellite imagery. In this study, two different input datasets with coarse (Landsat 8 and SRTM) and medium (Sentinel-2 and ALOS) spatial resolutions have been used for WSPs in Iran’s Guilan Province using the SVM and RF models. Studies show that ML models perform better for susceptibility predictions and mapping different natural hazards than knowledge-based multi-criteria decision-making and statistical approaches [25].
Moreover, ML models are valuable decision support tools to simulate and expand the knowledge of wildfire risk management [1,17]. However, these models show various performances as they deal with data of different spatial resolutions [20]. In addition, the structure and nature of each ML model vary noticeably, resulting in different WSP maps. This can be problematic as these WSP maps shall be used by decision-makers and natural resource managers and shall enable them to develop and implement corresponding environmental plans [25]. Furthermore, different ML models and datasets have been separately used for WSP map production in different wildfire-prone regions. For example, to produce a wildfire susceptibility prediction map, Eskandari et al. [14] compared the performance of the SVM model with some other ML models to produce WSP maps in the forests and rangelands of Golestan Province in northeastern Iran. The spatial resolution of the conditional factors was set to 30 m as they used ASTER DEM (30 m resolution), available from USGS (https://earthexplorer.usgs.gov) (accessed on 20 December 2020). Similar to this study, they used the DEM to determine their topographical factors, such as plan curvature and TWI, and the other conditional factors were resized based on that of the applied DEM.
Therefore, comparative assessments are necessary to evaluate the performance of ML models in different conditions and to be able to evaluate the resulting WSPs. In our work, we applied a DST for integrating the ML model results from different spatial resolutions to produce optimized WSP maps. In addition, we analyzed the WSP results from different ML models, trained and tested by the same spatial resolution dataset aiming to achieve optimized WSP maps with higher accuracy. The resulting WSPs showed some sort of variation when using a four-fold CV, but an apparent pattern that was similar for all CV scenarios. The difference in the accuracy of the applied ML models was slight, with a maximum of 5.8 percentage points (between RF10 in the third fold and SVM30 in the fourth fold). This minor difference illustrates that the performance of different ML models is generally high with no outliers, even by using data with different spatial resolutions. However, using a dataset with medium (30 m) spatial resolution generally performed slightly better and resulted in WSP maps with higher accuracy in both ML models. Therefore, we expected that the DST optimization would produce the best results from integrating RF10 and SVM10. This has happened for the third fold, with an overall result of 97.55%. However, the highest CV accuracy was obtained by integrating RF10 and RF30. This yielded about 0.15 percentage points more than the combination of RF10 and SVM10. The generated WSP maps were classified into five classes from very low to very high susceptibility of wildfire. The percentage of the area of each class is presented in Table 5. The RF10 model predicted the largest amount of areas falling into the class of very high susceptibility to wildfire with 11.22%. WSP maps from the integration of RF10 and SVM10 yielded an area of 9.74% for the class of very high susceptibility. The lowest percentage of this class was derived from SVM30, with the moderate class of 27.6%.

Table 5.
The percentage of the area of each wildfire susceptibility class.
7. Conclusions
The first goal of the presented study was to assess the use of wildfire susceptibility conditional factors with different spatial resolutions for WSP map production using two common ML models, namely the SVM and RF. The second goal was to evaluate if the DST can integrate the resulting WSP maps from different spatial resolution datasets while optimizing the accuracies of the derived WSP maps. This study showed that the RF model resulted in slightly higher accuracy than the SVM model. Moreover, the results for the study area of Iran’s Guilan Province demonstrate that the higher spatial resolution datasets yielded slightly more accurate wildfire susceptibility maps. Additionally, the fusion of these results with those derived from medium spatial resolution could even produce more accurate WSP maps. The study also shows that it was possible to integrate WSP maps with a different spatial resolution. This could slightly increase the accuracy and reliability of the resulting map. We demonstrated that integrating the two ML models using the DST technique could further increase the accuracy for predictive modeling and mapping wildfire susceptibility. This optimization technique was indeed able to enhance the performance of the separate use of RF and the SVM through their combination. Our future work may focus on a similar methodology framework but using spatially explicit polygons of burned areas as inventory data instead of commonly available points representing fire locations.
Author Contributions
Conceptualization, S.T.P., O.G. and T.B.; Data curation, K.G.; Investigation, S.T.P., G.E., O.G. and K.G.; Methodology, S.T.P., G.E., O.G. and K.G.; Supervision, T.B. and P.G.; Validation, S.T.P., G.E., O.G. and K.G.; Visualization, S.T.P., G.E., O.G. and K.G.; Writing—original draft, S.T.P., G.E., O.G. and T.G.N.; Writing—review and editing, O.G., T.B. and P.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Institute of Advanced Research in Artificial Intelligence (IARAI) GmbH.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available on request.
Acknowledgments
This research was funded by the Institute of Advanced Research in Artificial Intelligence (IARAI) GmbH. The authors are grateful to the anonymous referees for their helpful comments/suggestions that have helped us improve an earlier version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| advanced spaceborne thermal emission and reflection radiometer | (ASTER) |
| advanced land observing satellite/phased array L-band synthetic aperture radar | (ALOS/PALSAR) |
| analytical hierarchical process | (AHP) |
| analytical network process | (ANP) |
| area under the curve | (AUC) |
| climate hazards group infrared precipitation with station data | (CHIRPS) |
| cross-validation | (CV) |
| Dempster–Shafer theory | (DST) |
| digital elevation model | (DEM) |
| European Space Agency | (ESA) |
| federal aviation administration | (FAA) |
| Google Earth Engine | (GEE) |
| geographic information system | (GIS) |
| global positioning system | (GPS) |
| machine learning | (ML) |
| mean wind speed | (MWS) |
| mean wind power density | (MWPD) |
| moderate resolution imaging spectroradiometer | (MODIS) |
| multi-criteria decision analysis | (MCDA) |
| National Aeronautics and Space Administration | (NASA) |
| National Oceanic and Atmospheric Administration National Weather Service | (NOAA-NWS) |
| Next-Generation Radar | (NEXRAD) |
| normalized difference vegetation index | (NDVI) |
| random forest | (RF) |
| receiver operating characteristic | (ROC) |
| remote sensing | (RS) |
| shuttle radar topography mission | (SRTM) |
| support vector machines | (SVM) |
| topographic wetness index | (TWI) |
| United States Geological Survey | (USGS) |
| US Air Force | (USAF) |
| variance inflation factor | (VIF) |
| wildfire susceptibility prediction | (WSP) |
References
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Aryal, J. Forest fire susceptibility and risk mapping using social/infrastructural vulnerability and environmental variables. Fire 2019, 2, 50. [Google Scholar] [CrossRef] [Green Version]
- Moayedi, H.; Mehrabi, M.; Bui, D.T.; Pradhan, B.; Foong, L.K. Fuzzy-metaheuristic ensembles for spatial assessment of forest fire susceptibility. J. Environ. Manag. 2020, 260, 109867. [Google Scholar] [CrossRef] [PubMed]
- MacDicken, K.G. Global Forest Resources Assessment 2015: What, why and how? For. Ecol. Manag. 2015, 352, 3–8. [Google Scholar] [CrossRef] [Green Version]
- Sayad, Y.O.; Mousannif, H.; Al Moatassime, H. Predictive modeling of wildfires: A new dataset and machine learning approach. Fire Saf. J. 2019, 104, 130–146. [Google Scholar] [CrossRef]
- Hantson, S.; Pueyo, S.; Chuvieco, E. Global fire size distribution is driven by human impact and climate. Glob. Ecol. Biogeogr. 2015, 24, 77–86. [Google Scholar] [CrossRef]
- Tymstra, C.; Stocks, B.J.; Cai, X.; Flannigan, M.D. Wildfire management in Canada: Review, challenges and opportunities. Prog. Disaster Sci. 2020, 5, 100045. [Google Scholar] [CrossRef]
- Schlögel, R.; Marchesini, I.; Alvioli, M.; Reichenbach, P.; Rossi, M.; Malet, J.-P. Optimizing landslide susceptibility zonation: Effects of DEM spatial resolution and slope unit delineation on logistic regression models. Geomorphology 2018, 301, 10–20. [Google Scholar] [CrossRef]
- Tian, Y.; XiaO, C.; Liu, Y.; Wu, L. Effects of raster resolution on landslide susceptibility mapping: A case study of Shenzhen. Sci. China Ser. E Technol. Sci. 2008, 51, 188–198. [Google Scholar] [CrossRef]
- Avand, M.; Kuriqi, A.; Khazaei, M.; Ghorbanzadeh, O. DEM resolution effects on machine learning performance for flood probability mapping. J. Hydro-Environ. Res. 2022, 40, 1–16. [Google Scholar] [CrossRef]
- Eskandari, S.; Miesel, J.R. Comparison of the fuzzy AHP method, the spatial correlation method, and the Dong model to predict the fire high-risk areas in Hyrcanian forests of Iran. Geomat. Nat. Hazards Risk 2017, 8, 933–949. [Google Scholar] [CrossRef] [Green Version]
- Nami, M.; Jaafari, A.; Fallah, M.; Nabiuni, S. Spatial prediction of wildfire probability in the Hyrcanian ecoregion using evidential belief function model and GIS. Int. J. Environ. Sci. Technol. 2018, 15, 373–384. [Google Scholar] [CrossRef]
- Eskandari, S.; Pourghasemi, H.R.; Tiefenbacher, J.P. Fire-susceptibility mapping in the natural areas of Iran using new and ensemble data-mining models. Environ. Sci. Pollut. Res. 2021, 28, 47395–47406. [Google Scholar] [CrossRef] [PubMed]
- Jaafari, A.; Zenner, E.K.; Panahi, M.; Shahabi, H. Hybrid artificial intelligence models based on a neuro-fuzzy system and metaheuristic optimization algorithms for spatial prediction of wildfire probability. Agric. For. Meteorol. 2019, 266, 198–207. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Idrees, M.O.; Janizadeh, S.; Ahmadi, K.; Shabani, F. Forest fire susceptibility prediction based on machine learning models with resampling algorithms on remote sensing data. Remote Sens. 2020, 12, 3682. [Google Scholar] [CrossRef]
- Naderpour, M.; Rizeei, H.M.; Ramezani, F. Forest Fire Risk Prediction: A Spatial Deep Neural Network-Based Framework. Remote Sens. 2021, 13, 2513. [Google Scholar] [CrossRef]
- Kim, S.; Lim, C.-H.; Kim, G.; Lee, J.; Geiger, T.; Rahmati, O.; Son, Y.; Lee, W.-K. Multi-temporal analysis of forest fire probability using socio-economic and environmental variables. Remote Sens. 2019, 11, 86. [Google Scholar] [CrossRef] [Green Version]
- Gholamnia, K.; Gudiyangada Nachappa, T.; Ghorbanzadeh, O.; Blaschke, T. Comparisons of Diverse Machine Learning Approaches for Wildfire Susceptibility Mapping. Symmetry 2020, 12, 604. [Google Scholar] [CrossRef] [Green Version]
- Khosravi, K.; Panahi, M.; Bui, D.T. Spatial prediction of groundwater spring potential mapping based on an adaptive neuro-fuzzy inference system and metaheuristic optimization. Hydrol. Earth Syst. Sci. 2018, 22, 4771–4792. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, A.; Karimzadeh, S.; Jalal, S.J.; Kamran, K.V.; Shahabi, H.; Homayouni, S.; Al-Ansari, N. A Multi-Sensor Comparative Analysis on the Suitability of Generated DEM from Sentinel-1 SAR Interferometry Using Statistical and Hydrological Models. Sensors 2020, 20, 7214. [Google Scholar] [CrossRef]
- Chen, Z.; Ye, F.; Fu, W.; Ke, Y.; Hong, H. The influence of DEM spatial resolution on landslide susceptibility mapping in the Baxie River basin, NW China. Nat. Hazards 2020, 101, 853–877. [Google Scholar] [CrossRef]
- Meena, S.R.; Gudiyangada Nachappa, T. Impact of Spatial Resolution of Digital Elevation Model on Landslide Susceptibility Mapping: A case Study in Kullu Valley, Himalayas. Geosciences 2019, 9, 360. [Google Scholar] [CrossRef] [Green Version]
- González, C.; Castillo, M.; García-Chevesich, P.; Barrios, J. Dempster-Shafer theory of evidence: A new approach to spatially model wildfire risk potential in central Chile. Sci. Total Environ. 2018, 613, 1024–1030. [Google Scholar] [CrossRef] [PubMed]
- Ghorbanzadeh, O.; Feizizadeh, B.; Blaschke, T. Multi-criteria risk evaluation by integrating an analytical network process approach into GIS-based sensitivity and uncertainty analyses. Geomat. Nat. Hazards Risk 2018, 9, 127–151. [Google Scholar] [CrossRef] [Green Version]
- Mezaal, M.; Pradhan, B.; Rizeei, H. Improving Landslide Detection from Airborne Laser Scanning Data Using Optimized Dempster–Shafer. Remote Sens. 2018, 10, 1029. [Google Scholar] [CrossRef] [Green Version]
- Nachappa, T.G.; Piralilou, S.T.; Gholamnia, K.; Ghorbanzadeh, O.; Rahmati, O.; Blaschke, T. Flood susceptibility mapping with machine learning, multi-criteria decision analysis and ensemble using Dempster Shafer Theory. J. Hydrol. 2020, 590, 125275. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Kumar, L. The application of a Dempster–Shafer-based evidential belief function in flood susceptibility mapping and comparison with frequency ratio and logistic regression methods. Environ. Earth Sci. 2018, 77, 490. [Google Scholar] [CrossRef]
- Zarekar, A.; Zamani, B.K.; Ghorbani, S.; Moalla, M.A.; Jafari, H. Mapping spatial distribution of forest fire using MCDM and GIS (case study: Three forest zones in Guilan Province). Iran. J. For. Poplar Res. 2013, 21, 218–230. [Google Scholar]
- Arnone, E.; Francipane, A.; Scarbaci, A.; Puglisi, C.; Noto, L.V. Effect of raster resolution and polygon-conversion algorithm on landslide susceptibility mapping. Environ. Model. Softw. 2016, 84, 467–481. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Zeinivand, H. Flood susceptibility mapping using frequency ratio and weights-of-evidence models in the Golastan Province, Iran. Geocarto Int. 2015, 31, 42–70. [Google Scholar] [CrossRef]
- Eskandari, S.; Khoshnevis, M. Evaluating and mapping the fire risk in the forests and rangelands of Sirachal using fuzzy analytic hierarchy process and GIS. J. For. Res. Dev. 2020, 6, 219–245. [Google Scholar]
- Ljubomir, G.; Pamučar, D.; Drobnjak, S.; Pourghasemi, H.R. Modeling the Spatial Variability of Forest Fire Susceptibility Using Geographical Information Systems and the Analytical Hierarchy Process. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 337–369. [Google Scholar] [CrossRef]
- Jaafari, A.; Pourghasemi, H.R. Factors Influencing Regional-Scale Wildfire Probability in Iran. In Spatial Modeling in GIS and R for Earth and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2019; pp. 607–619. [Google Scholar] [CrossRef]
- Chen, H.X.; Zhang, S.; Peng, M.; Zhang, L.M. A physically-based multi-hazard risk assessment platform for regional rainfall-induced slope failures and debris flows. Eng. Geol. 2016, 203, 15–29. [Google Scholar] [CrossRef]
- Pourtaghi, Z.S.; Pourghasemi, H.R.; Rossi, M. Forest fire susceptibility mapping in the Minudasht forests, Golestan province, Iran. Environ. Earth Sci. 2015, 73, 1515–1533. [Google Scholar] [CrossRef]
- Molina, J.R.; Gonzalez-Caban, A.; Rodriguez, Y.S.F. Wildfires impact on the economic susceptibility of recreation activities: Application in a Mediterranean protected area. J. Environ. Manag. 2019, 245, 454–463. [Google Scholar] [CrossRef] [PubMed]
- Tien Bui, D.; Le, K.-T.; Nguyen, V.; Le, H.; Revhaug, I. Tropical Forest Fire Susceptibility Mapping at the Cat Ba National Park Area, Hai Phong City, Vietnam, Using GIS-Based Kernel Logistic Regression. Remote Sens. 2016, 8, 347. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Valizadeh Kamran, K.; Blaschke, T.; Aryal, J.; Naboureh, A.; Einali, J.; Bian, J. Spatial Prediction of Wildfire Susceptibility Using Field Survey GPS Data and Machine Learning Approaches. Fire 2019, 2, 43. [Google Scholar] [CrossRef] [Green Version]
- Gudiyangada Nachappa, T.; Tavakkoli Piralilou, S.; Ghorbanzadeh, O.; Shahabi, H.; Blaschke, T. Landslide Susceptibility Mapping for Austria Using Geons and Optimization with the Dempster-Shafer Theory. Appl. Sci. 2019, 9, 5393. [Google Scholar] [CrossRef] [Green Version]
- Verde, J.; Zêzere, J. Assessment and validation of wildfire susceptibility and hazard in Portugal. Nat. Hazards Earth Syst. Sci. 2010, 10, 485–497. [Google Scholar] [CrossRef]
- Shakesby, R.A. Post-wildfire soil erosion in the Mediterranean: Review and future research directions. Earth-Sci. Rev. 2011, 105, 71–100. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Rostamzadeh, H.; Blaschke, T.; Gholaminia, K.; Aryal, J. A new GIS-based data mining technique using an adaptive neuro-fuzzy inference system (ANFIS) and k-fold cross-validation approach for land subsidence susceptibility mapping. Nat. Hazards 2018, 94, 497–517. [Google Scholar] [CrossRef] [Green Version]
- Costache, R.; Arabameri, A.; Elkhrachy, I.; Ghorbanzadeh, O.; Pham, Q.B. Detection of areas prone to flood risk using state-of-the-art machine learning models. Geomat. Nat. Hazards Risk 2021, 12, 1488–1507. [Google Scholar] [CrossRef]
- Hong, H.; Pradhan, B.; Sameen, M.I.; Chen, W.; Xu, C. Spatial prediction of rotational landslide using geographically weighted regression, logistic regression, and support vector machine models in Xing Guo area (China). Geomat. Nat. Hazards Risk 2017, 8, 1997–2022. [Google Scholar] [CrossRef] [Green Version]
- Cossu, R.; Petitdidier, M.; Linford, J.; Badoux, V.; Fusco, L.; Gotab, B.; Hluchy, L.; Lecca, G.; Murgia, F.; Plevier, C.; et al. A roadmap for a dedicated Earth Science Grid platform. Earth Sci. Inform. 2010, 3, 135–148. [Google Scholar] [CrossRef] [Green Version]
- Loveland, T.R.; Dwyer, J.L. Landsat: Building a strong future. Remote Sens. Environ. 2012, 122, 22–29. [Google Scholar] [CrossRef]
- Sudmanns, M.; Tiede, D.; Lang, S.; Bergstedt, H.; Trost, G.; Augustin, H.; Baraldi, A.; Blaschke, T. Big Earth data: Disruptive changes in Earth observation data management and analysis? Int. J. Digit. Earth 2019, 13, 832–850. [Google Scholar] [CrossRef] [PubMed]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- GoogleEarthEngine. Available online: https://earthengine.google.com/#intro (accessed on 17 May 2020).
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2013, 11, 425–439. [Google Scholar] [CrossRef]
- Ghamisi, P.; Plaza, J.; Chen, Y.; Li, J.; Plaza, A.J. Advanced spectral classifiers for hyperspectral images: A review. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–32. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi, A.; Shahabi, H.; Bin Ahmad, B. Land-Cover Change Detection in a Part of Cameron Highlands, Malaysia Using ETM+ Satellite Imagery and Support Vector Machine (SVM) Algorithm. EnvironmentAsia 2019, 12, 145–154. [Google Scholar]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Ho, T.K. Random decision forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Pourghasemi, H.R.; Rahmati, O. Prediction of the landslide susceptibility: Which algorithm, which precision? Catena 2018, 162, 177–192. [Google Scholar] [CrossRef]
- Xu, R.; Lin, H.; Lü, Y.; Luo, Y.; Ren, Y.; Comber, A. A Modified Change Vector Approach for Quantifying Land Cover Change. Remote Sens. 2018, 10, 1578. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef] [Green Version]
- Valdez, M.C.; Chang, K.-T.; Chen, C.-F.; Chiang, S.-H.; Santos, J.L. Modelling the spatial variability of wildfire susceptibility in Honduras using remote sensing and geographical information systems. Geomat. Nat. Hazards Risk 2017, 8, 876–892. [Google Scholar] [CrossRef] [Green Version]
- Feizizadeh, B. A Novel Approach of Fuzzy Dempster–Shafer Theory for Spatial Uncertainty Analysis and Accuracy Assessment of Object-Based Image Classification. IEEE Geosci. Remote Sens. Lett. 2018, 15, 18–22. [Google Scholar] [CrossRef]
- Fei, L.; Xia, J.; Feng, Y.; Liu, L. A novel method to determine basic probability assignment in Dempster–Shafer theory and its application in multi-sensor information fusion. Int. J. Distrib. Sens. Netw. 2019, 15, 1550147719865876. [Google Scholar]
- Ghorbanzadeh, O.; Meena, S.R.; Abadi, H.S.S.; Piralilou, S.T.; Zhiyong, L.; Blaschke, T. Landslide Mapping Using Two Main Deep-Learning Convolution Neural Network (CNN) Streams Combined by the Dempster—Shafer (DS) model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 452–463. [Google Scholar] [CrossRef]
- Shahabi, H.; Jarihani, B.; Tavakkoli Piralilou, S.; Chittleborough, D.; Avand, M.; Ghorbanzadeh, O. A Semi-Automated Object-Based Gully Networks Detection Using Different Machine Learning Models: A Case Study of Bowen Catchment, Queensland, Australia. Sensors 2019, 19, 4893. [Google Scholar] [CrossRef] [Green Version]
- Shafer, G. A mathematical theory of evidence; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Rahmati, O.; Melesse, A.M. Application of Dempster–Shafer theory, spatial analysis and remote sensing for groundwater potentiality and nitrate pollution analysis in the semi-arid region of Khuzestan, Iran. Sci. Total Environ. 2016, 568, 1110–1123. [Google Scholar] [CrossRef]
- Schneider, L.C.; Pontius, R.G., Jr. Modeling land-use change in the Ipswich watershed, Massachusetts, USA. Agric. Ecosyst. Environ. 2001, 85, 83–94. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).