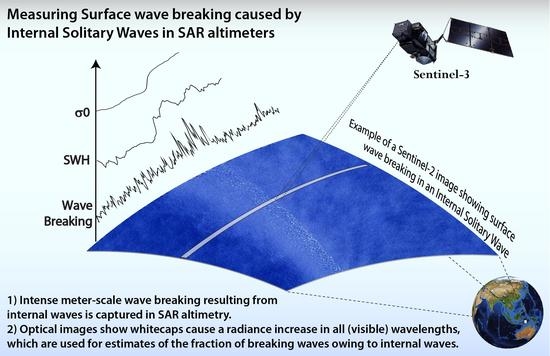
Effects of Surface Wave Breaking Caused by Internal Solitary Waves in SAR Altimeter: Sentinel-3 Copernicus Products and Advanced New Products
Abstract
1. Introduction
1.1. Oceanic Internal Waves, Their Surface Manifestations and Remote Sensing
1.2. Surface Wave Breaking Induced by Strong ISWs
2. Materials and Methods
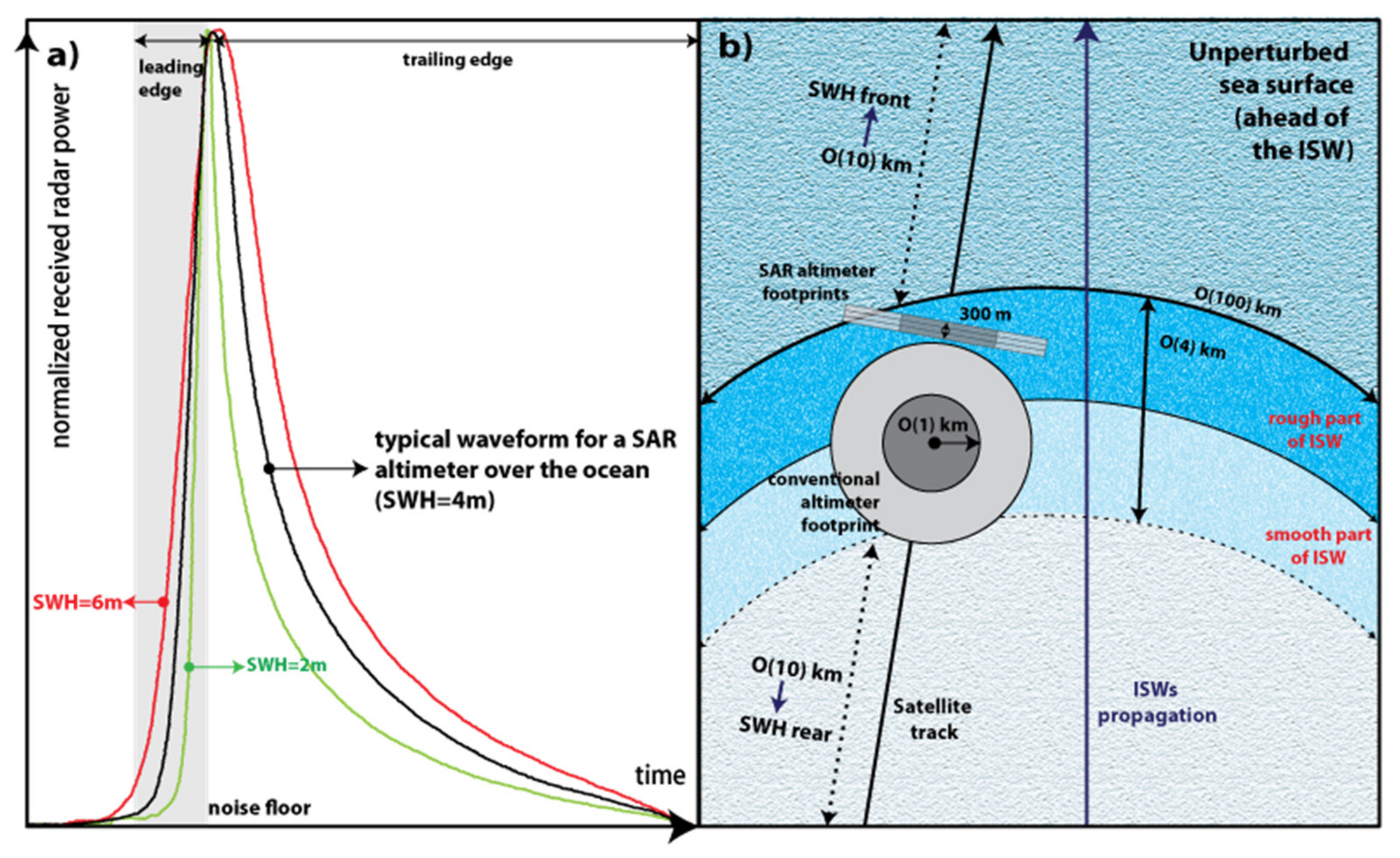
2.1. Fundamentals of Satellite Altimetry and Its Sea Surface Signatures of ISWs
2.2. Sentinel-3 SAR Altimeter and Detection of ISWs
2.2.1. Sentinel-3 Unfocused SAR (UFSAR)
2.2.2. Sentinel-3 Fully Focused SAR (FFSAR)
2.2.3. Retracking of SAR Altimeter Waveforms
2.2.4. Characterization of ISWs’ SWH Signatures
2.3. Ocean and Land Color Instrument (OLCI)
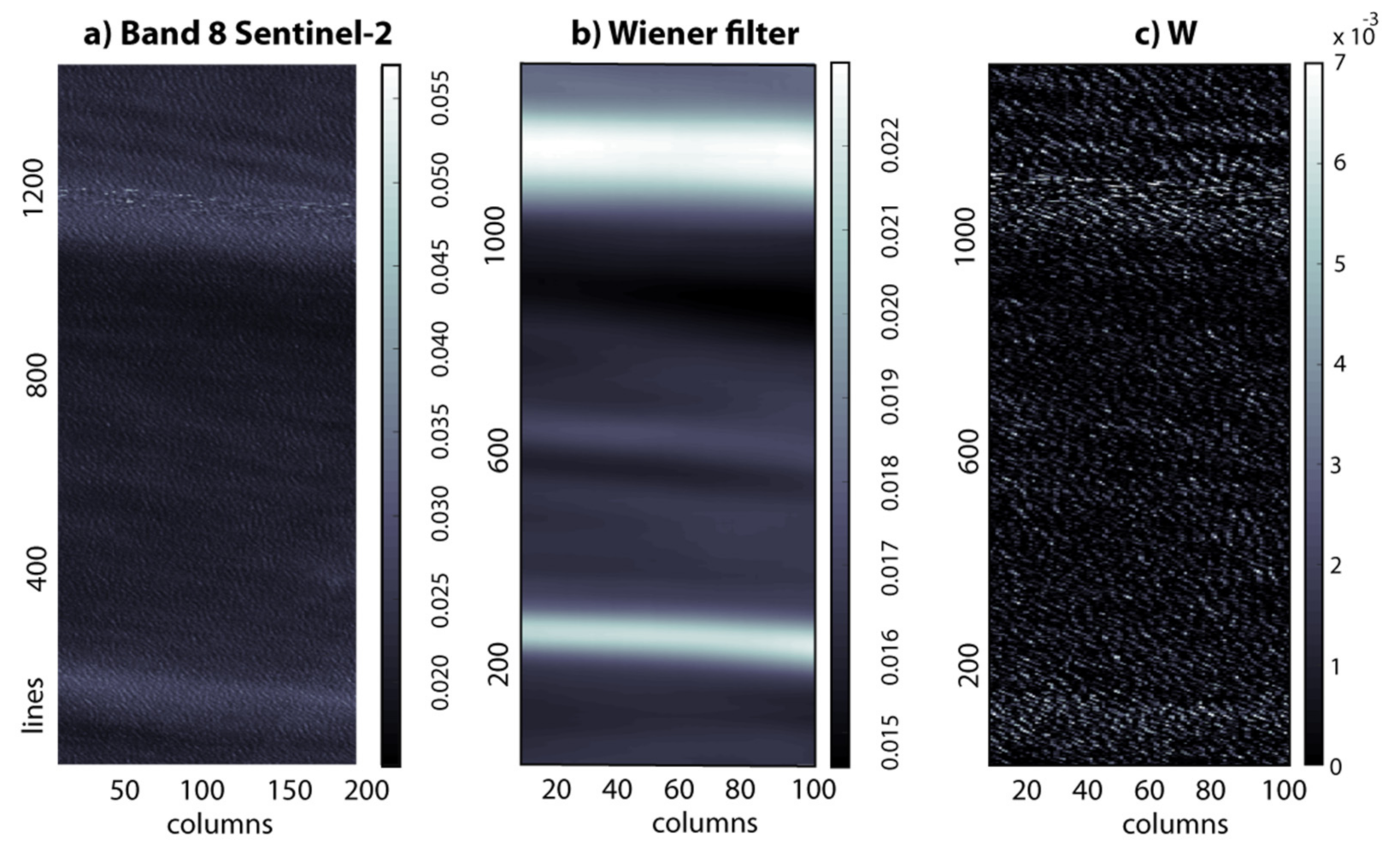
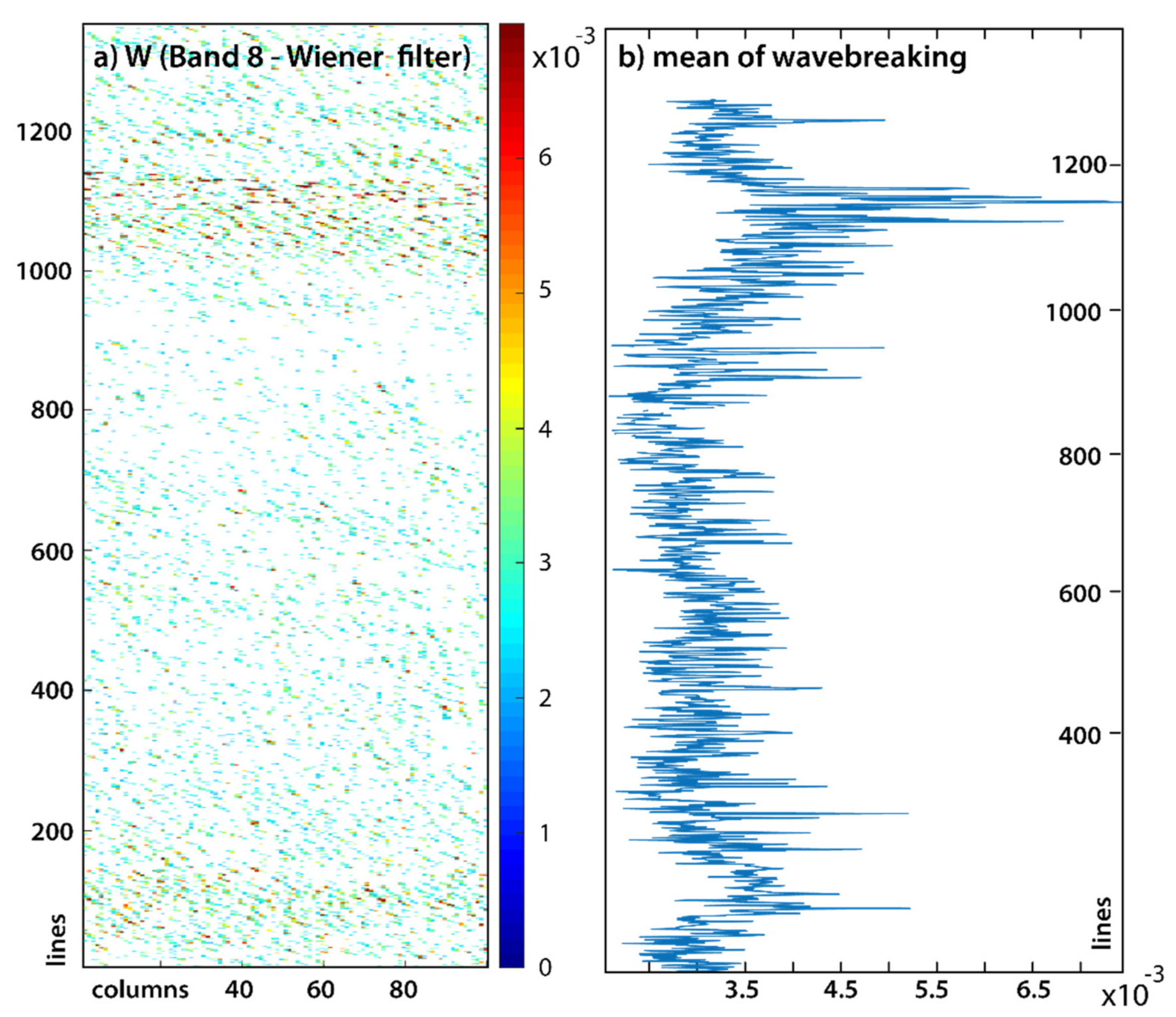
2.4. Characterization of Fraction of Wave Breaking in Sentinel-2 MultiSpetral Instrument (MSI)
3. Results
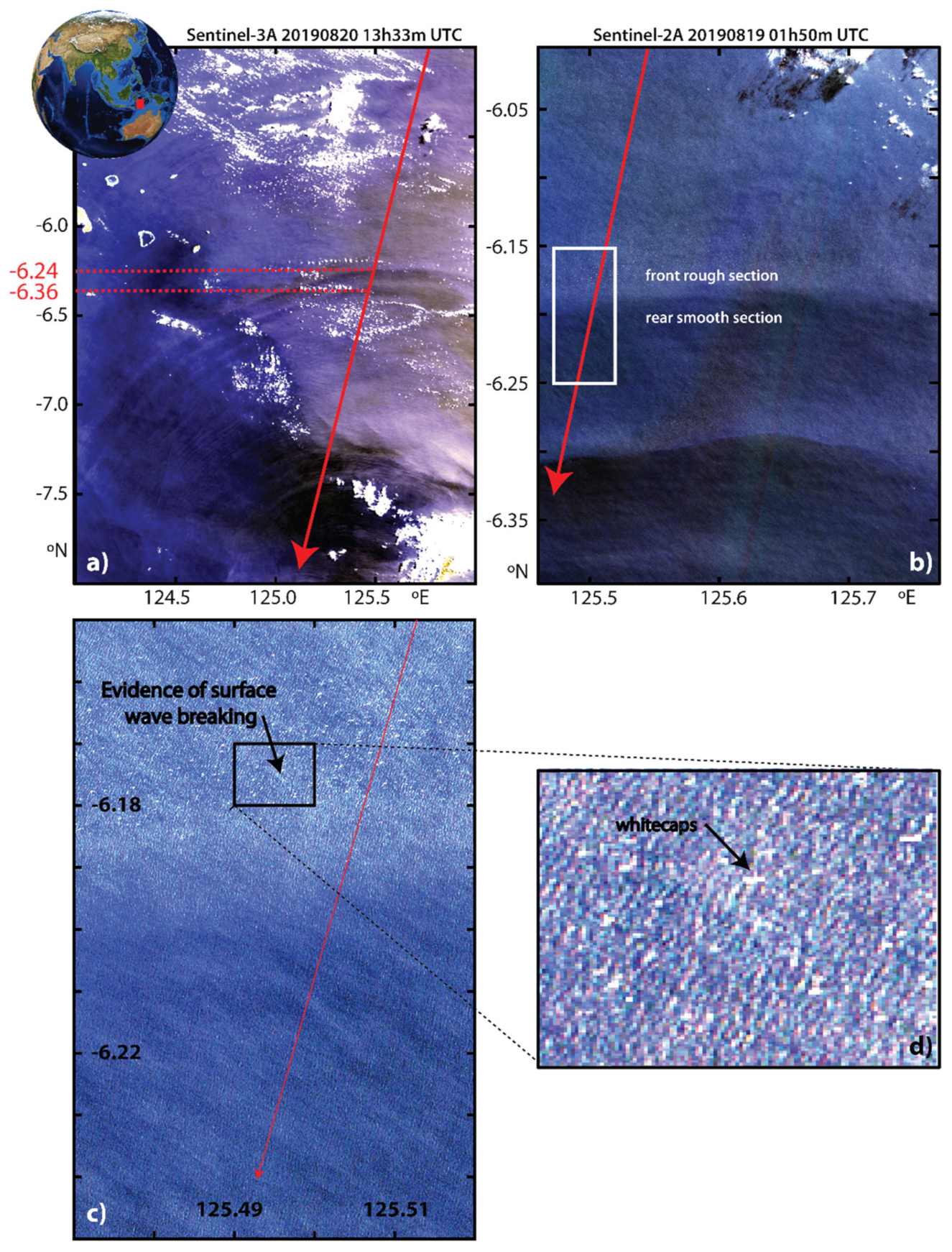
3.1. Sentinel-3 Case Study Using Optical Imagery and Standard Copernicus SAR Altimeter Data
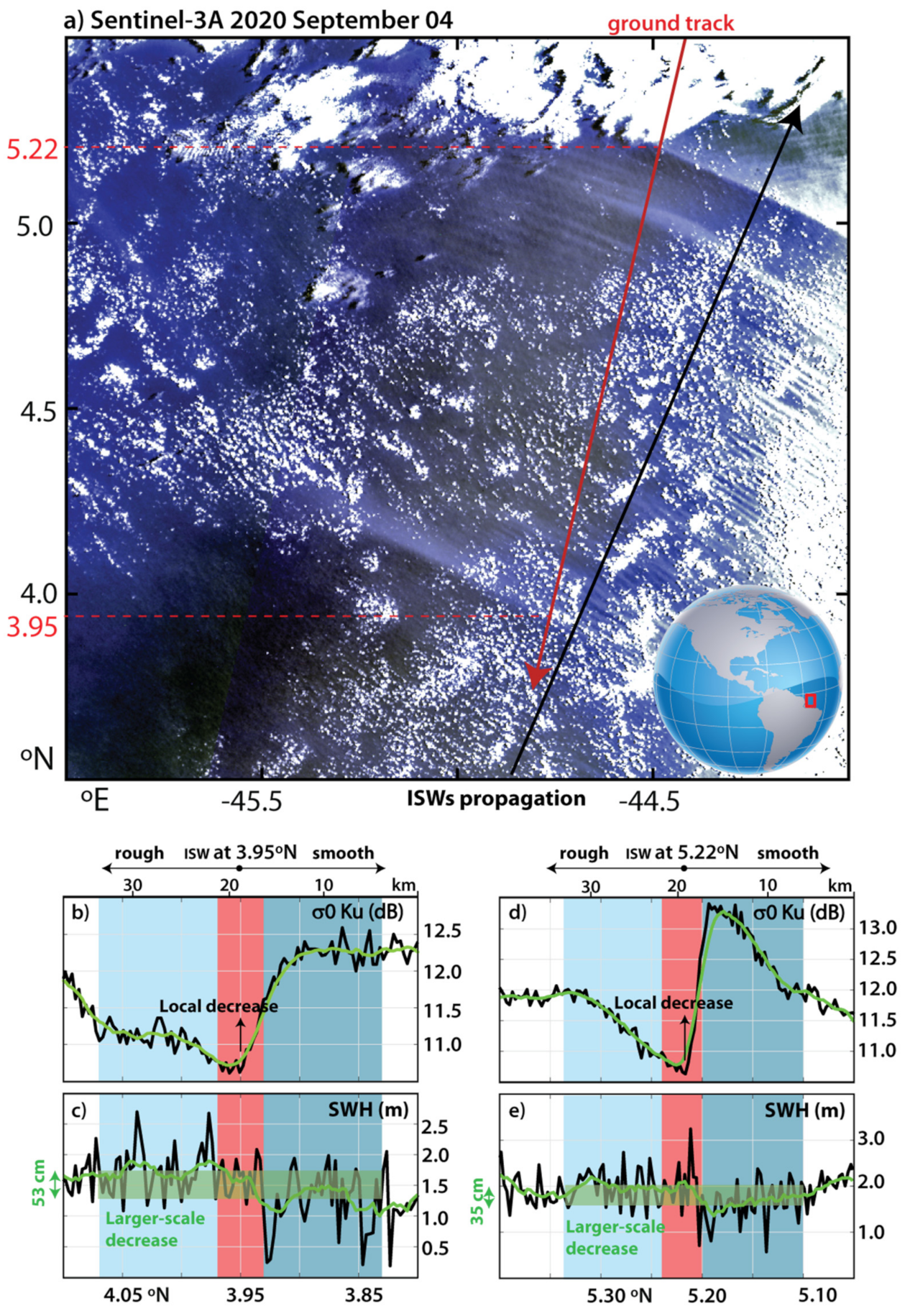
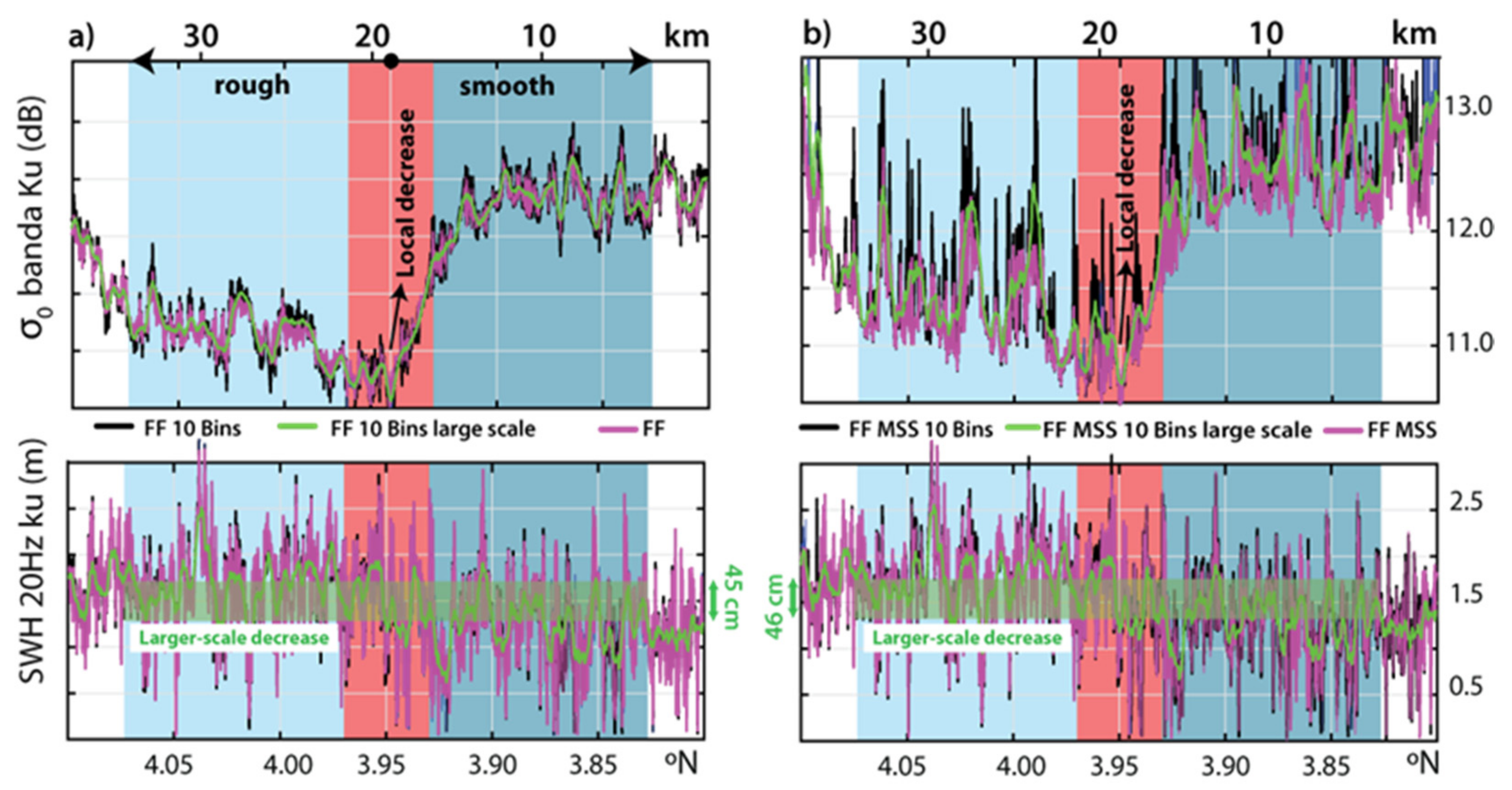
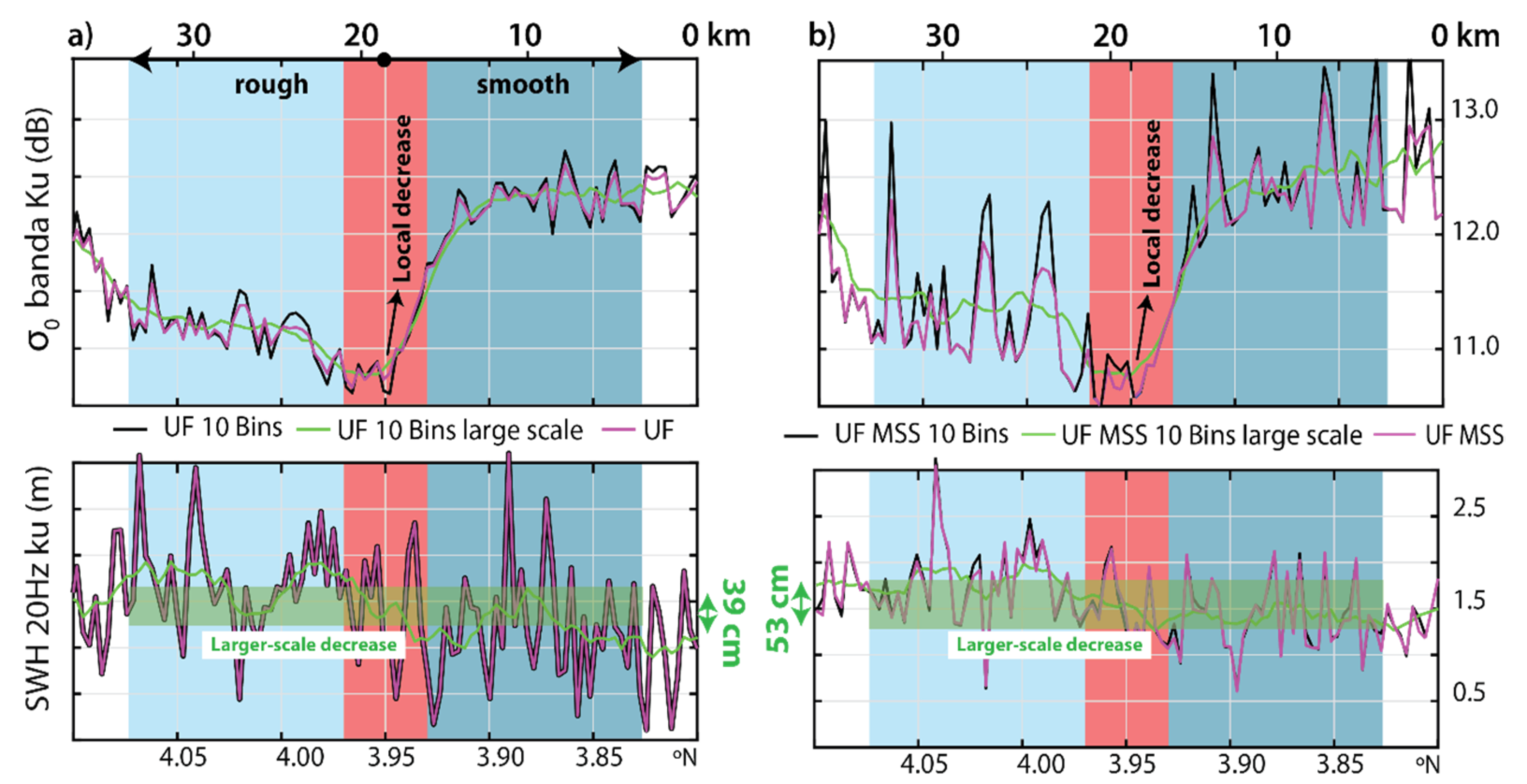
3.2. Results for Standard Copernicus SAR Data
3.3. A Case Study Using Optical Imagery and Advanced SAR Altimeter Products
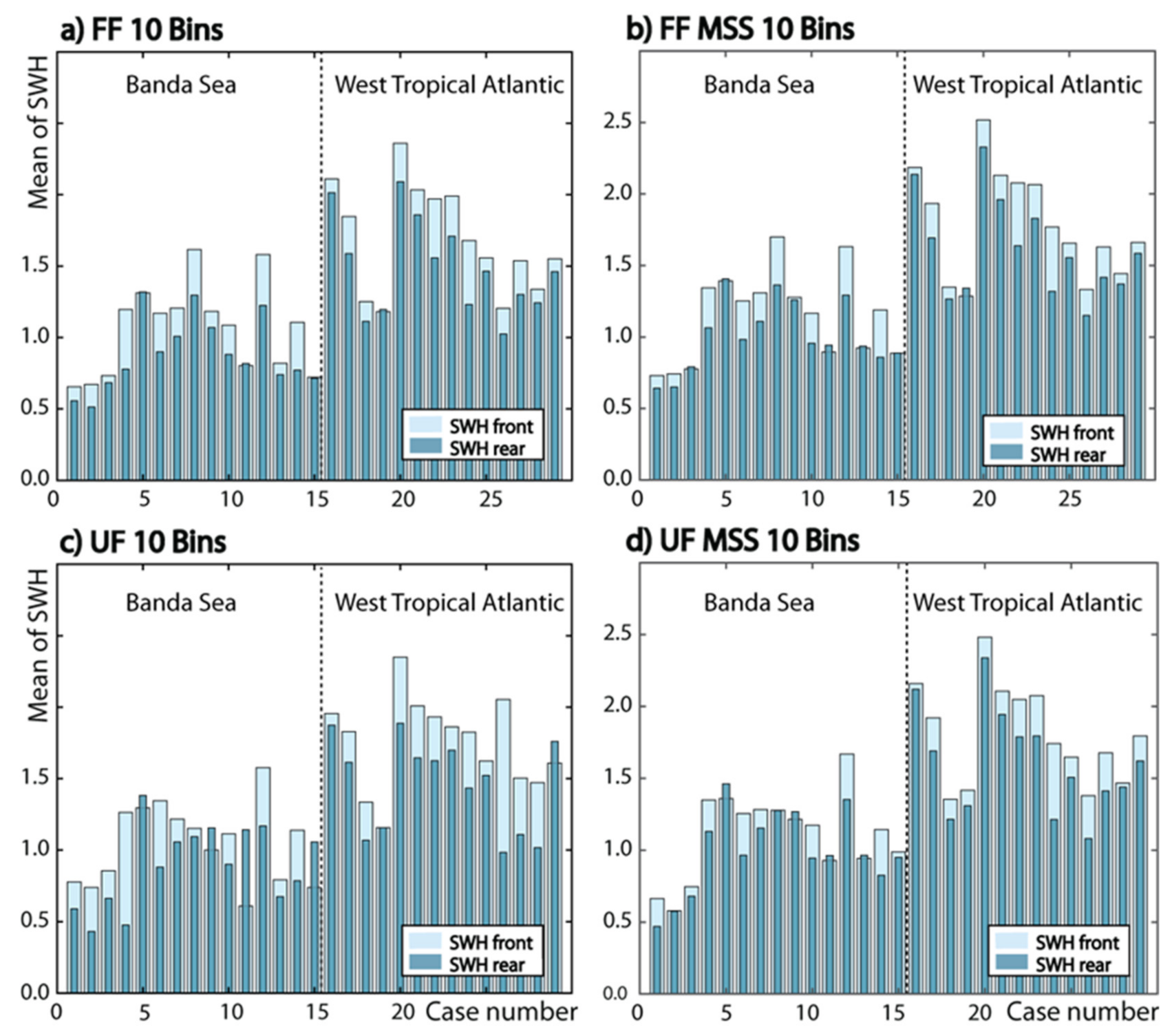
- Consistent results for all products: from Copernicus products, FF and UF full bins to FF and UF 10 bins processing schemes.
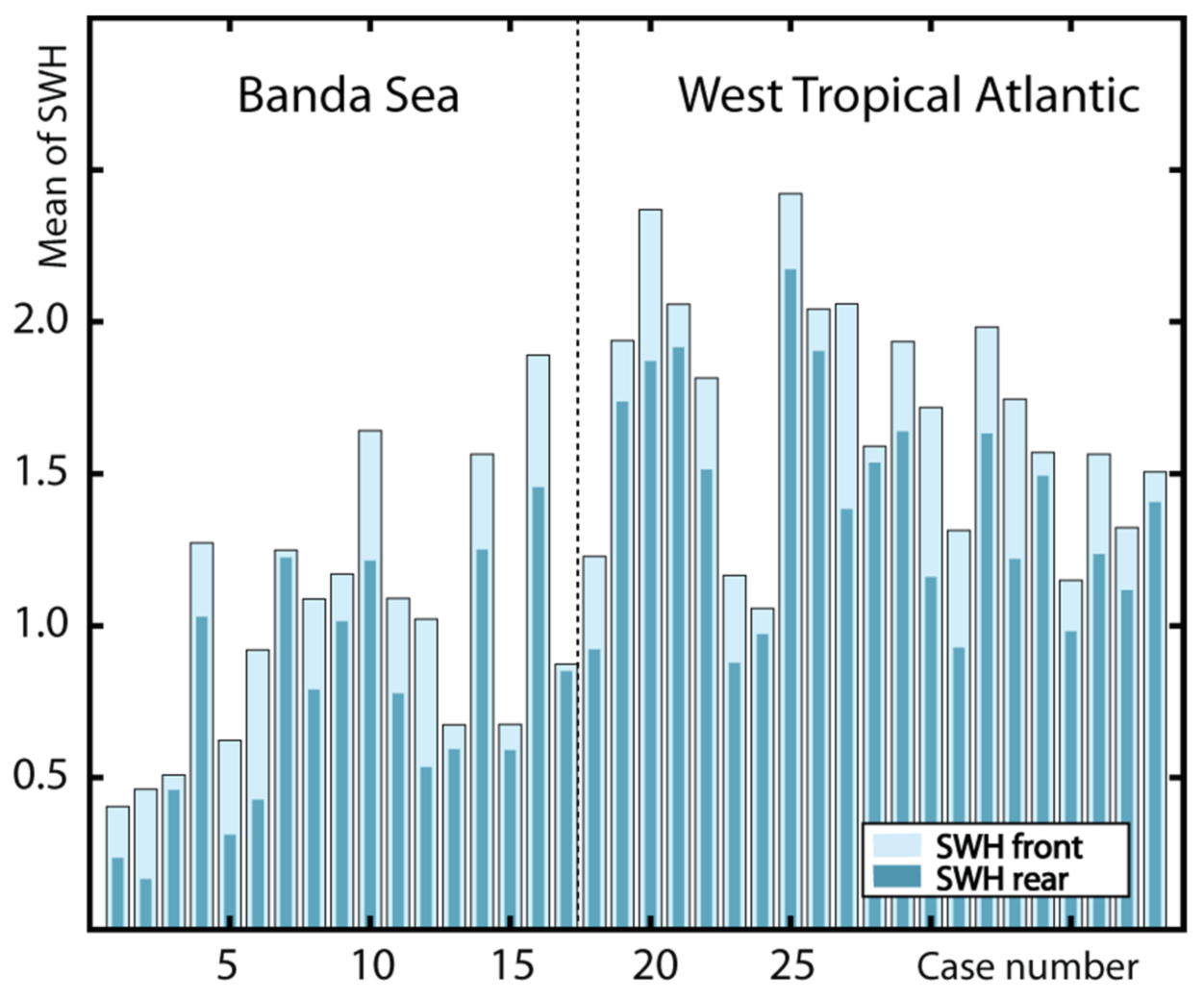
- SWHs from the Tropical Atlantic Ocean are higher than for the Banda Sea, which is understandable since in the Banda Sea, swell waves are practically absent; note that the average wave periods are 9.2 and 5.1 s, respectively.
- As expected, the adaptive MSS algorithms allow for better capturing of σ0 variations along the track, the 10 bin processing being a little more sensitive to heterogeneous sea surfaces.
- It is suggested however that the 10 bin processing has little impact on the SWH results for this applications and study regions.
- It is also suggested that the FFSAR processing (both schemes applied by CLS) has small impacts on SWH differences in this particular application (Internal Solitary Waves). It is as if by lowering the radar footprint, the processing is much less impacted by heterogeneities on the sea surface, making the MSS and 10 bin processing almost useless.
3.4. Results for Advanced FFSAR Products
3.5. Consistency of Results for Different SAR Products
3.6. Image Processsing for the Investigation of Wave Breaking in Sentinel-2 Images
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Apel, J.R.; Byrne, H.M.; Proni, J.R.; Charnell, R.L. Observations of oceanic internal and surface waves from the earth resources technology satellite. J. Geophys. Res. Oceans 1975, 80, 865–881. [Google Scholar] [CrossRef]
- Fu, L.-L.; Holt, B. Seasat Views Oceans and Sea Ice with Synthetic-Aperture Radar; California Institute of Technology, Jet Propulsion Laboratory: Pasadena, CA, USA, 1982; Volume 81, p. 200. [Google Scholar]
- Apel, J.R.; Gonzalez, F.I. Nonlinear features of internal waves off Baja California as observed from the SEASAT imaging radar. J. Geophys. Res. Oceans 1983, 88, 4459–4466. [Google Scholar] [CrossRef]
- Alpers, W.; Salusti, E. Scylla and Charybdis observed from space. J. Geophys. Res. Oceans 1983, 88, 1800. [Google Scholar] [CrossRef]
- Kim, H.; Son, Y.B.; Jo, Y.-H. Hourly Observed Internal Waves by Geostationary Ocean Color Imagery in the East/Japan Sea. J. Atmos. Ocean. Technol. 2018, 35, 609–617. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; Meng, J.; Fan, C.; Wang, J. Observation of internal waves with OLCI and SRAL on board Sentinel-3. Acta Oceanol. Sin. 2020, 39, 56–62. [Google Scholar] [CrossRef]
- Magalhaes, J.M.; Da Silva, J.C.B. Satellite Altimetry Observations of Large-Scale Internal Solitary Waves. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Santos-Ferreira, A.M.; Da Silva, J.C.B.; Magalhaes, J.M. SAR Mode Altimetry Observations of Internal Solitary Waves in the Tropical Ocean Part 1: Case Studies. Remote Sens. 2018, 10, 644. [Google Scholar] [CrossRef]
- Santos-Ferreira, A.M.; Da Silva, J.C.B.; Srokosz, M. SAR-Mode Altimetry Observations of Internal Solitary Waves in the Tropical Ocean Part 2: A Method of Detection. Remote Sens. 2019, 11, 1339. [Google Scholar] [CrossRef]
- Magalhães, J.; Alpers, W.; Santos-Ferreira, A.; da Silva, J. Surface Wave Breaking Caused by Internal Solitary Waves: Effects on Radar Backscattering Measured by SAR and Radar Altimeter. Oceanography 2021, 34, 166–176. [Google Scholar] [CrossRef]
- Babanin, A. Breaking and Dissipation of Ocean Surface Waves; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Maury, M.F. The Physical Geography of the Sea and Its Meteorology; Harper: New York, NY, USA, 1861. [Google Scholar]
- Osborne, A.R.; Burch, T.L. Internal Solitons in the Andaman Sea. Science 1980, 208, 451–460. [Google Scholar] [CrossRef]
- Perry, R.B.; Schimke, G.R. Large-amplitude internal waves observed off the northwest coast of Sumatra. J. Geophys. Res. Oceans 1965, 70, 2319–2324. [Google Scholar] [CrossRef]
- New, A.; Da Silva, J. Remote-sensing evidence for the local generation of internal soliton packets in the central Bay of Biscay. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2002, 49, 915–934. [Google Scholar] [CrossRef]
- Phillips, O.M. On the Interactions between Internal and Surface Waves. Izv. Atmos. Ocean. Phys. 1973, 9, 954–961. [Google Scholar]
- Lewis, J.E.; Lake, B.M.; Ko, D.R.S. On the interaction of internal waves and surface gravity waves. J. Fluid Mech. 1974, 63, 773–800. [Google Scholar] [CrossRef]
- Craig, W.; Guyenne, P.; Sulem, C. The surface signature of internal waves. J. Fluid Mech. 2012, 710, 277–303. [Google Scholar] [CrossRef]
- Kodaira, T.; Waseda, T.; Miyata, M.; Choi, W. Internal solitary waves in a two-fluid system with a free surface. J. Fluid Mech. 2016, 804, 201–223. [Google Scholar] [CrossRef]
- Taklo, T.M.A.; Choi, W. Group resonant interactions between surface and internal gravity waves in a two-layer system. J. Fluid Mech. 2020, 892, 14. [Google Scholar] [CrossRef]
- Lyzenga, D.R.; Bennett, J.R. Full-spectrum modeling of synthetic aperture radar internal wave signatures. J. Geophys. Res. Earth Surf. 1988, 93, 12345. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C.; Hayes, K.; Chatham, G. Normalized radar cross section of the sea for backscatter: 1. Mean levels. J. Geophys. Res. Oceans 2010, 115, 09032. [Google Scholar] [CrossRef]
- Ochi, M.K.; Tsai, C.-H. Prediction of Occurrence of Breaking Waves in Deep Water. J. Phys. Oceanogr. 1983, 13, 2008–2019. [Google Scholar] [CrossRef][Green Version]
- Stokes, G.G. Supplement to a paper on the Theory of Oscillatory Waves. Math. Phys. Pap. 2010, 1, 314–326. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Kozlov, I.; Chapron, B.; Johannessen, J.A. Quad-polarization SAR features of ocean currents. J. Geophys. Res. Oceans 2014, 119, 6046–6065. [Google Scholar] [CrossRef]
- Brown, G. The average impulse response of a rough surface and its applications. IRE Trans. Antennas Propag. 1977, 25, 67–74. [Google Scholar] [CrossRef]
- Dinardo, S.; Lucas, B.; Benveniste, J. Sentinel-3 STM SAR ocean retracking algorithm and SAMOSA model. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 5320–5323. [Google Scholar]
- Ray, R.D.; Mitchum, G.T. Surface manifestation of internal tides generated near Hawaii. Geophys. Lett. 1996, 23, 2101–2104. [Google Scholar] [CrossRef]
- Raney, R. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.-H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C.; et al. The Global Monitoring for Environment and Security (GMES) Sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Boy, F.; Desjonqueres, J.-D.; Picot, N.; Moreau, T.; Raynal, M. CryoSat-2 SAR-Mode Over Oceans: Processing Methods, Global Assessment, and Benefits. IEEE Trans. Geosci. Remote Sens. 2016, 55, 148–158. [Google Scholar] [CrossRef]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR Altimeter Backscattered Waveform Model. IEEE Trans. Geosci. Remote Sens. 2014, 53, 911–919. [Google Scholar] [CrossRef]
- Raynal, M.; Labroue, S.; Orsztynowicz, M.; Picot, N.; Guillot, A.; Boy, F. Sentinel-6A Delay Doppler Processing: Assessment over the Global Ocean. In Proceedings of the 2016 SAR Altimetry Workshop, La Rochelle, France, 31 October–1 November 2016. [Google Scholar]
- Egido, A.; Smith, W.H.F. Fully Focused SAR Altimetry: Theory and Applications. IEEE Trans. Geosci. Remote Sens. 2016, 55, 392–406. [Google Scholar] [CrossRef]
- Reale, F.; Carratelli, E.P.; Di Leo, A.; Dentale, F. Wave Orbital Velocity Effects on Radar Doppler Altimeter for Sea Monitoring. J. Mar. Sci. Eng. 2020, 8, 447. [Google Scholar] [CrossRef]
- Buchhaupt, C.; Fenoglio, L.; Becker, M.; Kusche, J. Impact of vertical water particle motions on focused SAR altimetry. Adv. Space Res. 2021, 68, 853–874. [Google Scholar] [CrossRef]
- Buchhaupt, C. Model Improvement for SAR Altimetry. Ph.D. Thesis, Schriftenreihe Fachriftenreihe Geodäsie der Technischen Universität Darmstadt, Darmstadt, Germany, 2019. [Google Scholar]
- Dinardo, S.; Fenoglio-Marc, L.; Becker, M.; Scharroo, R.; Fernandes, M.J.; Staneva, J.; Grayek, S.; Benveniste, J. A RIP-based SAR retracker and its application in North East Atlantic with Sentinel-3. Adv. Space Res. 2021, 68, 892–929. [Google Scholar] [CrossRef]
- Tourain, C.; Piras, F.; Ollivier, A.; Hauser, D.; Poisson, J.C.; Boy, F.; Thibaut, P.; Hermozo, L.; Tison, C. Benefits of the Adaptive Algorithm for Retracking Altimeter Nadir Echoes: Results From Simulations and CFOSAT/SWIM Observations. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9927–9940. [Google Scholar] [CrossRef]
- Magalhaes, J.M.; da Silva, J.C.B.; Buijsman, M.C.; Garcia, C.A.E. Effect of the North Equatorial Counter Current on the generation and propagation of internal solitary waves off the Amazon shelf (SAR observations). Ocean Sci. 2016, 12, 243–255. [Google Scholar] [CrossRef]
- Jackson, C. Internal wave detection using the Moderate Resolution Imaging Spectroradiometer (MODIS). J. Geophys. Res. Oceans 2007, 112, 11. [Google Scholar] [CrossRef]
- Kubryakov, A.; Kudryavtsev, V.; Stanichny, S. Application of Landsat imagery for the investigation of wave breaking. Remote Sens. Environ. 2021, 253, 112144. [Google Scholar] [CrossRef]
- Lim, J.S. Two-Dimensional Signal and Image Processing; Prentice Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Koepke, P. Effective reflectance of oceanic whitecaps. Appl. Opt. 1984, 23, 1816–1824. [Google Scholar] [CrossRef]
- Frouin, R.; Schwindling, M.; Deschamps, P.-Y. Spectral reflectance of sea foam in the visible and near-infrared: In Situ measurements and remote sensing implications. J. Geophys. Res. Earth Surf. 1996, 101, 14361–14371. [Google Scholar] [CrossRef]
- Liu, A.K.; Liu, C.-T.; Ming-Kuang, H.; Zheng, Q. Satellite Remote Sensing of South China Sea, 1st ed.; Liu, A.K., Ho, C.-R., Liu, C.-T., Eds.; Tingmao Publish Company: Taiwan, China, 2008; ISBN 978-986-122-948-5. [Google Scholar]
- Kudryavtsev, V.; Hauser, D.; Caudal, G.; Chapron, B. A semiempirical model of the normalized radar cross-section of the sea surface 1. Background model. J. Geophys. Res. Oceans 2003, 108, FET-2. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Akimov, D.; Johannessen, J.A.; Chapron, B. On radar imaging of current features: 1. Model and comparison with observations. J. Geophys. Res. Oceans 2005, 110, 07016. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Chapron, B.; Myasoedov, A.G.; Collard, F.; Johannessen, J.A. On Dual Co-Polarized SAR Measurements of the Ocean Surface. IEEE Geosci. Remote Sens. Lett. 2013, 10, 761–765. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Fan, S.; Zhang, B.; Mouche, A.A.; Chapron, B. On Quad-Polarized SAR Measurements of the Ocean Surface. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8362–8370. [Google Scholar] [CrossRef]
- Ermakov, S.; Dobrokhotov, V.; Sergievskaya, I.; Kapustin, I. Suppression of Wind Ripples and Microwave Backscattering Due to Turbulence Generated by Breaking Surface Waves. Remote Sens. 2020, 12, 3618. [Google Scholar] [CrossRef]
- Magalhaes, J.M.; da Silva, J.C.B.; Batista, M.; Gostiaux, L.; Gerkema, T.; New, A.L.; Jeans, D.R.G. On the detectability of internal waves by an imaging lidar. Geophys. Res. Lett. 2013, 40, 3429–3434. [Google Scholar] [CrossRef]
- Wang, D.W.; Wijesekera, H.W. Observations of Breaking Waves and Energy Dissipation in Modulated Wave Groups. J. Phys. Oceanogr. 2018, 48, 2937–2948. [Google Scholar] [CrossRef]
- Lyzenga, D.R. Effects of nonlinear energy transfer on short surface waves. J. Geophys. Res. Oceans 2010, 115, 10001. [Google Scholar] [CrossRef]
- Ardhuin, F.; Gille, S.T.; Menemenlis, D.; Rocha, C.B.; Rascle, N.; Chapron, B.; Gula, J.; Molemaker, J. Small-scale open ocean currents have large effects on wind wave heights. J. Geophys. Res. Oceans 2017, 122, 4500–4517. [Google Scholar] [CrossRef]
- Whalen, C.B.; De Lavergne, C.; Garabato, A.C.N.; Klymak, J.M.; MacKinnon, J.A.; Sheen, K.L. Internal wave-driven mixing: Governing processes and consequences for climate. Nat. Rev. Earth Environ. 2020, 1, 606–621. [Google Scholar] [CrossRef]


| Date | Rel. Orbit | Cycle | Pass | ISW (°E; °N) | SWH Front (m) | SWH Rear (m) | Delta SWH (m) | Peak Wave Direction | Permalink | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| °TN | Period (s) | ||||||||||
| Indian Ocean—Banda Sea | 27 October 2018 | 188A | 37 | 376 | 125,51; −6,12 | 0,40518 | 0,23571 | 0,16947 | 120 | 4,2 | https://odl.bzh/4EfSVZFC |
| 125,27; −7,23 | 0,46247 | 0,16659 | 0,29588 | 105 | 4,2 | https://odl.bzh/KrMExcZ1 | |||||
| 25 March 2019 | 245B | 23 | 490 | 125,93; −6,34 | 0,50846 | 0,45982 | 0,04864 | 340 | 4,6 | https://odl.bzh/WzP5Ezm1 | |
| 21 April 2019 | 245B | 24 | 490 | 125,97; −6,15 | 1,2725 | 1,0296 | 0,26201 | 115 | 5,1 | https://odl.bzh/b8LxyW55 | |
| 125,72; −7,28 | 0,62323 | 0,31226 | 0,31097 | 90 | 5,1 | https://odl.bzh/b8LxyW55 | |||||
| 10 June 2019 | 188B | 26 | 376 | 124,85; −6,53 | 0,92049 | 0,42788 | 0,49261 | 100 | 6,3 | https://odl.bzh/LF-Vxh__ | |
| 20 August 2019 | 188A | 48 | 376 | 125,68; −5,32 | 1,2486 | 1,2242 | 0,0244 | 120 | 6 | https://odl.bzh/HSaOiMnJ | |
| 125,49; −6,24 | 1,0881 | 0,78976 | 0,29834 | 110 | 6,1 | https://odl.bzh/HSaOiMnJ | |||||
| 3 September 2019 | 245B | 29 | 490 | 125,93; −6,37 | 1,1701 | 1,0148 | 0,1553 | 110 | 5,1 | https://odl.bzh/JQMuqIcm | |
| 16 September 2019 | 188A | 49 | 376 | 125,45; −6,28 | 1,6424 | 1,2135 | 0,4289 | 100 | 5,4 | https://odl.bzh/9_5wRYcZ | |
| 125,23; −7,34 | 1,0898 | 0,7775 | 0,3123 | 80 | 5,5 | https://odl.bzh/9_5wRYcZ | |||||
| 30 September 2019 | 245B | 30 | 490 | 125,95; −6,27 | 1,0215 | 0,53449 | 0,48701 | 115 | 5,1 | https://odl.bzh/MtaLtIvy | |
| 125,70; −7,33 | 0,67391 | 0,59438 | 0,07953 | 85 | 5 | https://odl.bzh/MtaLtIvy | |||||
| 2 May 2021 | 188A | 71 | 376 | 125,47; −6,21 | 1,5645 | 1,25 | 0,3145 | 120 | 4,8 | https://odl.bzh/bmzw6-sl | |
| 125,22; −7,38 | 0,67488 | 0,59038 | 0,0845 | 90 | 4,5 | https://odl.bzh/bmzw6-sl | |||||
| 29 May 2021 | 188A | 72 | 376 | 125,54; −6,00 | 1,8899 | 1,456 | 0,4339 | https://odl.bzh/UHooCZrC | |||
| 125,28; −7,17 | 0,87386 | 0,85046 | 0,0234 | https://odl.bzh/UHooCZrC | |||||||
| Tropical West Atlantic | 1 September 2016 | 152A | 8 | 304 | 43,01; 5,55 | 1,2279 | 0,92231 | 0,30559 | 120 | 8,4 | https://sentinelshare.page.link/uvbx |
| 7 October 2017 | 095A | 23 | 190 | 43,96; 5,52 | 1,9382 | 1,7371 | 0,2011 | 130 | 8,6 | https://odl.bzh/VdEggv5S | |
| 11 October 2017 | 152A | 23 | 304 | 43,30; 4,28 | 2,3694 | 1,8705 | 0,4989 | 110 | 9,6 | https://odl.bzh/Lpqi_JlT | |
| 27 September 2018 | 152A | 36 | 304 | 43,19; 4,75 | 2,0583 | 1,9157 | 0,1426 | 85 | 10,9 | https://odl.bzh/Na_TJmBh | |
| 24 October 2018 | 152A | 37 | 304 | 42,99; 5,71 | 1,815 | 1,5135 | 0,3015 | 340 | 11,2 | https://odl.bzh/JOAzPnPS | |
| 23 August 2019 | 095B | 29 | 190 | 44,56; 4,88 | 1,1651 | 0,87815 | 0,28695 | 110 | 9,1 | https://odl.bzh/6NeM1WHF | |
| 44,70; 4,3 | 1,0569 | 0,97263 | 0,08427 | 110 | 9,1 | https://odl.bzh/6NeM1WHF | |||||
| 20 November 2019 | 209B | 32 | 418 | 42,24; 6,94 | 2,4213 | 2,1723 | 0,249 | 45 | 9,2 | https://odl.bzh/KfnQ6nXW | |
| 42,50; 5,78 | 2,0414 | 1,9034 | 0,138 | 45 | 9,2 | https://odl.bzh/KfnQ6nXW | |||||
| 6 July 2020 | 152A | 60 | 304 | 43,02; 5,49 | 2,0593 | 1,3832 | 0,6761 | 100 | 8 | https://odl.bzh/Cjl1Y7Fp | |
| 43,31; 4,25 | 1,5908 | 1,5369 | 0,0539 | 100 | 8 | https://odl.bzh/Cjl1Y7Fp | |||||
| 12 August 2020 | 152B | 42 | 304 | 43,47; 5,56 | 1,9343 | 1,6387 | 0,2956 | 125 | 9,3 | https://odl.bzh/w_Bt-Fwr | |
| 21 August 2020 | 038A | 62 | 76 | 45,18; 4,2 | 1,7181 | 1,16 | 0,5581 | 105 | 9,2 | https://odl.bzh/ifCVN1l5 | |
| 45,46; 2,98 | 1,3141 | 0,92823 | 0,38587 | 105 | 9,1 | https://odl.bzh/ifCVN1l5 | |||||
| 4 September 2020 | 095B | 43 | 188 | 44,49; 5,22 | 1,9822 | 1,6322 | 0,35 | 115 | 9,1 | https://odl.bzh/zJX2Sql3 | |
| 44,77; 3,95 | 1,7456 | 1,2196 | 0,526 | 110 | 8,8 | https://odl.bzh/I10mN45U | |||||
| 45,05; 2,74 | 1,5703 | 1,4927 | 0,0776 | 105 | 8,7 | https://odl.bzh/I10mN45U | |||||
| 18 October 2020 | 095A | 64 | 190 | 44,05; 5,11 | 1,1499 | 0,98153 | 0,16837 | 100 | 8,1 | https://odl.bzh/U5tfVGM- | |
| 44,30; 3,98 | 1,5645 | 1,2352 | 0,3293 | 105 | 7,9 | https://odl.bzh/bSfaqEFH | |||||
| 44,62; 2,6 | 1,3232 | 1,1173 | 0,2059 | 95 | 7,6 | https://odl.bzh/bSfaqEFH | |||||
| 3 December 2020 | 366A | 65 | 732 | 45,37; 7,55 | 1,5067 | 1,4067 | 0,1 | 25 | 14,6 | https://odl.bzh/rLepYH4m | |
| Banda Sea | Tropical West Atlantic | |||||
|---|---|---|---|---|---|---|
| Products | <SWHf> (m) | <SWHr> (m) | <ΔSWH> (%) | <SWHf> (m) | <SWHr> (m) | <ΔSWH> (%) |
| FF 10 Bins | 1,06 | 0,88 | 16 | 1,67 | 1,49 | 12 |
| FF MSS 10 Bins | 1,15 | 1,01 | 12 | 1,79 | 1,61 | 10 |
| UF 10 Bins | 1,04 | 0,90 | 13 | 1,75 | 1,46 | 17 |
| UF MSS 10 Bins | 1,10 | 1,00 | 10 | 1,80 | 1,60 | 11 |
| UF Copernicus | 1,01 | 0,76 | 25 | 1,69 | 1,41 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos-Ferreira, A.M.; da Silva, J.C.B.; Magalhaes, J.M.; Amraoui, S.; Moreau, T.; Maraldi, C.; Boy, F.; Picot, N.; Borde, F. Effects of Surface Wave Breaking Caused by Internal Solitary Waves in SAR Altimeter: Sentinel-3 Copernicus Products and Advanced New Products. Remote Sens. 2022, 14, 587. https://doi.org/10.3390/rs14030587
Santos-Ferreira AM, da Silva JCB, Magalhaes JM, Amraoui S, Moreau T, Maraldi C, Boy F, Picot N, Borde F. Effects of Surface Wave Breaking Caused by Internal Solitary Waves in SAR Altimeter: Sentinel-3 Copernicus Products and Advanced New Products. Remote Sensing. 2022; 14(3):587. https://doi.org/10.3390/rs14030587
Chicago/Turabian StyleSantos-Ferreira, Adriana M., José C. B. da Silva, Jorge M. Magalhaes, Samira Amraoui, Thomas Moreau, Claire Maraldi, François Boy, Nicolas Picot, and Franck Borde. 2022. "Effects of Surface Wave Breaking Caused by Internal Solitary Waves in SAR Altimeter: Sentinel-3 Copernicus Products and Advanced New Products" Remote Sensing 14, no. 3: 587. https://doi.org/10.3390/rs14030587
APA StyleSantos-Ferreira, A. M., da Silva, J. C. B., Magalhaes, J. M., Amraoui, S., Moreau, T., Maraldi, C., Boy, F., Picot, N., & Borde, F. (2022). Effects of Surface Wave Breaking Caused by Internal Solitary Waves in SAR Altimeter: Sentinel-3 Copernicus Products and Advanced New Products. Remote Sensing, 14(3), 587. https://doi.org/10.3390/rs14030587