Abstract
Degradation of forest roads in Canada has strong negative effects on access to forestlands, together with economic (e.g., increased maintenance costs), environmental (e.g., erosion of materials and subsequent habitat contamination), and social (e.g., use risks) impacts. Maintaining sustainable and safe access to forestland requires a better understanding and knowledge of forest road degradation over time and space. Our study aimed to identify relevant spatiotemporal variables regarding the state of eastern Canadian forest road networks by (1) building predictive models of gravel forest road degradation and assessing effects of the slope, time, loss of the road surface, and road width (field approach), and (2) evaluating the potential of topography, roughness and vegetation indices obtained from Airborne Laser Scanning (ALS) data and Sentinel-2 optical images to estimate degradation rates (remote sensing approach). The field approach (n = 207 sample plots) confirmed that only four variables were efficient to estimate degradation rates (pseudo-R2 = 0.43 with ±8% error). Simulations that were conducted showed that after about five years without maintenance, the rate of degradation on a road, regardless of its width, increased exponentially, exacerbated by a high slope gradient and loss of road surface. The narrowest roads tended to degrade more rapidly over time. The remote sensing approach performed quite well (pseudo-R2 = 0.34 with ±9% error) in terms of predicting road degradation, giving us the valuable tools to spatialise the state of gravel forest road degradation in eastern Canadian forest. This study provided new knowledge and tools that are critical for maintaining and sustaining access to Canada’s boreal forest territory in both the short- and the long-term.
1. Introduction
Forest roads are anthropogenic disturbances that can considerably alter the connectivity and natural dynamics of the Canadian boreal forest. Indeed, the continued densification, usage and attendant damage sustained by these networks raise several questions about their economic, environmental, and social impacts. Significant impacts on ecosystem processes and structure arising from the effects of their geometry, traffic volume, proximity and connectivity on biodiversity, biophysical processes and ecosystem functioning are well documented and studied around the world [1,2,3,4,5]. Roads not only disturb forest ecosystems during their construction, but also in subsequent stages of degradation, rehabilitation, or decommissioning. Indeed, a lack of road maintenance leads to road degradation, with several consequences, including contamination of watercourses and neighbouring habitats, increased collision, and predation risks for certain animals (e.g., caribou) and accident risks for users, as well as decreases in their efficiency on wood logistic chain, and in providing forest ecosystem services [4,6,7]. The presence of degradation on a road also can limit access to the forest territory for all users (e.g., forest products industry, government agencies, recreationalists, and other members of the public), while significantly increasing maintenance costs. To minimize risks that are related to degradation of the forest road network, a better understanding and knowledge of the process and variables that allow identifying its current state is essential.
Many methods of data acquisition can be used to assess the current state of forest roads, including point data for road compaction (load-bearing capacity) that are taken with a penetrometer [8,9], ground-penetrating radar (GPR) [10,11], or a deflectometer [9,12,13]. Some approaches rely upon visual observations, such as the pavement conditions index (PCI) [14,15,16]. Deterioration can also be recorded as continuous data using a vehicle-mounted sensor that registers changes as the vehicle moves [17]. The resulting data can be used to generate roughness indices [17] that characterise the road surface quality [18,19,20,21,22]. It is also possible to use a vehicle that is equipped with mobile laser scanning [8,23].
All of these tools have proven their potential more than once in estimating road degradation. To date, their application has remained very rare in forest environments [9,23]. Moreover, their use requires that a systematic inventory be conducted in the field, which is costly in terms of time, money and resources [24]. These approaches are difficult to apply to Canadian forest road networks, which are in relatively remote areas, extending over more than one million kilometres. Remote acquisition tools, such as Airborne Laser Scanning (ALS) and multispectral satellite images, are methods that appear to be more promising, given that they offer the possibility of covering large areas [25].
The objective of this study is to provide a better understanding and new spatiotemporal knowledge regarding the state of Canadian forest road networks. To do so, two distinct approaches are used. First, we constructed a predictive model of gravel forest road degradation from an experimental set up in a field approach. Second, we evaluated the potential of topography and vegetation indices extracted from ALS and Sentinel-2 optical images for remotely estimating the degradation of the forest road network.
2. Materials and Methods
2.1. Study Area
The study area encompasses three portions of a boreal forest managed unit (FMU) of eastern Canada, each of which are approximately 100 km2 in size (Figure 1). These FMU are representative of Canadian forestry activity and were located (1) east of the municipality of Senneterre (48.42°N, −77.23°W), (2) southwest of La Tuque (47.51°N, −72.78°W, and (3) west of Dolbeau-Mistassini (48.89°N, −72.23°W). All three areas had relatively flat relief (Table 1), and a dominant surface deposit of glacial till. Their overall climate is cold continental, e.g., with temperate summers without a dry season. Each area has different characteristics since eastern Canada is characterised by longitudinal precipitation (generally less abundant in the west than in the east) and latitudinal temperature gradients (higher in the south than in the north) (Table 1).
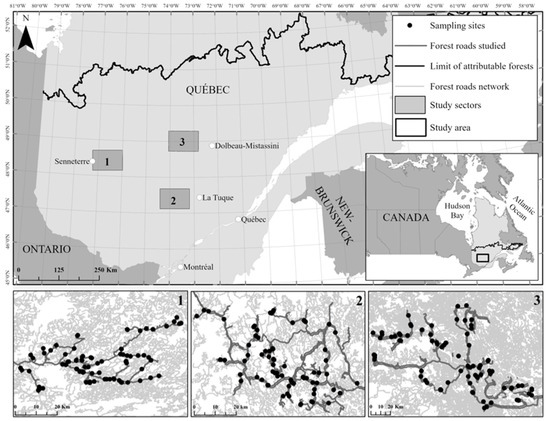
Figure 1.
Location of the three FMU areas in the boreal eastern Canadian forest. Overview (lower panels) of the sampling plots (black dots) and the network of forest roads that were studied (dark grey) within the three areas.

Table 1.
Characteristics of gravel forest roads within three FMU and their bioclimatic data [26,27,28].
2.2. Experimental Design
To quantify the degradation of forest roads, we established an experimental design of 207 sample plots in summer 2019. Road selection was based upon their variability in width, slope, and time since last maintenance that are considered crucial in explaining the observed degradation [6,29,30,31]. For the purposes of capturing a representative characterisation of roads across the region, we stratified road samples according to three width categories, e.g., narrow (4 to <7 m), medium (≥7 to <9.5 m) and wide (≥9.5 to 14 m) [range 4 to 14m], according to slope (≤4% vs. >4%) (range 0 to 16%), and according to two categories of time since last maintenance, e.g., recent (2015–2019) vs. old (1970–2014) (range 0 to 46 years). The width categories were chosen as a simplification of the provincial standards for gravelled forest roads with their expected maximum travel speeds of 30, 50 and 70 km/h, respectively. Speed is yet another variable that would influence forest road degradation [6]. The slope intervals that were selected took into consideration their respective effects on degradation through water accumulation [6,32] or through water runoff and vehicle acceleration [31,33]. Road maintenance data were obtained from historical records that were provided by the forest products company Resolute, which operate the three FMU.
Based upon the predefined categories of variables, five replications were carried out. We used 50-m-long sections, in which five perpendicular transects were arranged at intervals of 0, 10, 25, 40 and 50 m. Along each transect, we measured the width and depth (cm) of all forms of degradation that were present (potholes; ruts; erosion; furrows; subgrade emergence; washboard or ripples; see Section 2.3, Figure 2). Sample length section was based upon the feasibility of obtaining data that would provide a continuous view of degradation on a scale that could be easily detected with remote sensing tools. Widths of transects (m) corresponded to the current running surface width (CRSW) used by motorised traffic during sampling. We estimate percentage degradation per section by summing the lengths of the perpendicular transects, together with degradation observed on them.

Figure 2.
Examples of the observed forms of degradation, in decreasing importance: (A) ruts; (B) erosion (by water); (C) furrows; (D) subgrade emergence; (E) potholes; and (F) washboard.
Road width measurements were used to calculate the percentage road surface loss (PRSL) (Equation (1)). This calculation was the standardised difference between initial running surface width (IRSW) at the time of road construction (observable in terms of required dimensions during its construction) and CRSW, which can be identified by the absence of woody or herbaceous vegetation.
2.3. Observation of In Situ Degradation
The percentage of degradation varied between 0 and 82% for the 103.5 km of roads that were sampled. The observed total degradation was 42.4%, 35.1% and 22.5% of narrow, medium and wide-width roads, respectively. On average, 17% of observations with the last road maintenance dating back five years or less presented a form of degradation. This average increased to 33% for observations that had between 6 to 10 years without road maintenance, 41% for 11 to 15 years, 44% for 16 to 20 years, and 46% for those that were >20-years-old. Observations with lower PRSL < 25% showed an average 11% degradation. This proportion increased to 23%, 40%, and 55% of observed PRSL 25 to <50; 50 to <75; and 75 to 100 groups, respectively. Forest roads sampled with slopes >4% show higher degradation proportion (Figure 3).
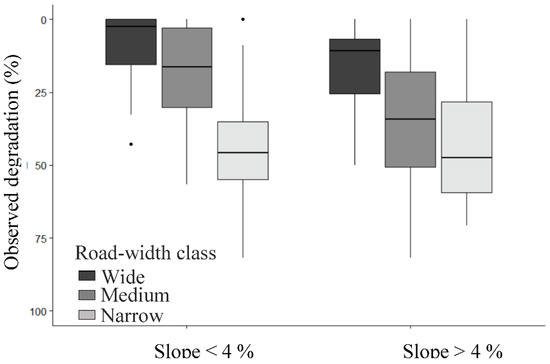
Figure 3.
Box-and-whisker plots of observed road degradation according to the road-width class (narrow 4 to <7 m, medium ≥7 to <9.5 m, and wide ≥9.5 to 14 m) and slopes. The horizon line within the box is the median (50th percentile). Box height defines the 25th and 75th percentiles (IQR, inter-quartile range). The whiskers are 10th and 90th percentiles. Dots are extreme values beyond 1.5 × IQR.
2.4. Observed Forms of Degradation
Dominant observed forms of degradation (Figure 2) within the sample plots were ruts (56%), erosion (24%), furrows (10%), subgrade emergence (6%), potholes (3%), and washboarding (1%). To distinguish them from furrows, ruts are defined here as deep parallel grooves that are worn into the road surface by the repeated passage of vehicle traffic on the left- or right-hand side of the section. Furrows are used to refer to multiple grooves across the width of the road surface and in the direction of travel. Washboard or road corrugation refers to parallel ripples or undulations that lay perpendicular to the direction of travel along the road section. The observed depth of these forms varied between 0 and 35 cm. Distributions of dominant forms of degradation changed according to the width of the road (Figure 4) and their slopes (Figure 5), where ruts and erosion were the most recurrent problems. Erosion occupied the largest surface areas on the widest roads, while ruts were more frequently observed on medium-width and narrow roads. Roads with a slope gradient >4% generally exhibited higher proportions of all forms of degradation, except for potholes (Figure 5).
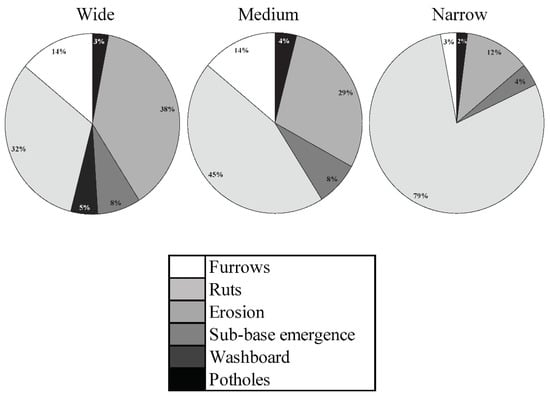
Figure 4.
Proportion (%) of the observed (cumulative sample sections) degradation forms showing furrows, ruts, erosion, sub-base emergence, washboard and, potholes following the three road-widths narrow (4 to <7 m), medium (≥7 to <9.5 m) and wide (≥9.5 to 14 m).
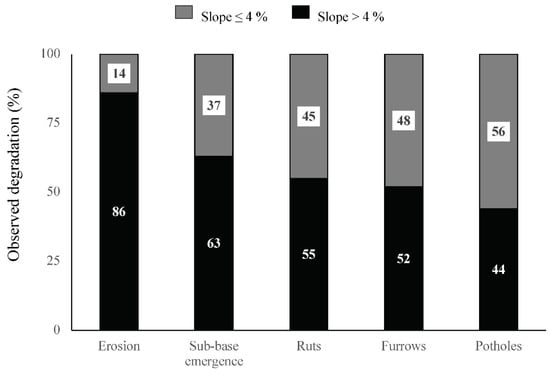
Figure 5.
Proportion (%) of the sample (cumulative of all sampled sections) exhibiting different forms of degradation for roads with slopes >4% (black boxes) and slopes ≤4% (hatched boxes). The numbers within the bars are their percentage values. The washboard is not presented because of its low percentage.
2.5. Remote Detection of Degradation
Degradation of a running surface tends to manifest itself as depressions (ruts, furrows, potholes, erosion, and washboard) of varying depths. According to Kiss et al. [34], variation in topography and fluctuations in the running surface are effective indicators for detecting road degradation. In forest environments, vegetation is often present on a road when maintenance is limited and is often associated with degradation [6]. Indices of topography, roughness (fluctuations) and vegetation have been used to detect degradation remotely (Table 2). In the current study, these spatial indices were generated using ALS DTMs and ALS CHMs (Source: MFFP, 1-m resolution, 2 to 4 points per m2, acquired summer 2017 and 2018) and Sentinel-2 multispectral images (Source: USGS Earth Explorer, 10-m resolution, acquired summer 2019, cloud cover <10%).

Table 2.
Descriptions of spatial indices that were used to estimate gravelled forest road degradation.
For each index that was extracted (Table 2), the mean, maximum, minimum value and standard deviation of the pixels corresponding to each sampled section were calculated. Additionally based upon the indices described in Table 2, we calculated: (1) the percentage of depressions from the Topographic Position Index (TPI), e.g., the number of pixels (values < 0) within the total pixel (value > 0) for each plot; (2) the percentage of concave forms of Surface Curvature Index (CSI), i.e., CSI that had values above zero expressing concave forms; and (3) the presence of vegetation in the percentage obtained from ALS Canopy Height Model (CHM) with a threshold above 1 m (because it becomes impassable for automotive vehicles when this limit is exceeded) within the plot.
2.6. Statistical Analyses
Beta regression models were constructed using the two respective approaches, e.g., field and remote sensing variables as variables with datasets divided into two groups (75%, model development; 25%, validation, randomly selected). These models determined the effect of the independent variables of degradation. Beta regression differed from linear regression, in that the dependent variable is expressed as continuous data that are restricted in their range [39] and where assumptions of normality and homoscedasticity of the residuals are not met [40]. Indeed, the dependent variable, i.e., percentage degradation, was converted to a bounded variable with a range of 0 to 1.
Beta regression assumes that the response follows a beta distribution and is logit-linked to its variables [41]. This distribution is more flexible when modelling intervals or proportions since it can take different forms, unlike linear regression, which does not deviate from its linear form [39]. Since the values 0 and 1 cannot be directly supported by the regression that is being used, the recommendations of Smithson and Verkuilen [40] were applied to transform the data to an interval between 0.005 and 0.995, according to the following equation:
where y″ = transformed degradation (0.005 to 0.995), y = observed degradation (0 to 1), and N = sample size.
y″ = [y (N − 1) + ½]/N
Selection of variables to be included in the beta regressions that were used in the two approaches was conducted with Spearman rank correlation (rs) tests between transformed degradation and each one of the variables. Selected field variables (rs: p < 0.05) included slope, time since last maintenance, PRSL and path width; all variables were continuous, except for the road-width class, which is an ordinal categorical variable. For each index of the remote sensing approach, the metrics with the highest rank correlation coefficients were selected, i.e., percentage depression from TPI, mean TRI, mean NDVI, percentage vegetation from CHM, standard deviation of TWI, and standard deviation of the cross-sectional CSI.
A total of 10,000 permutations were applied to both approaches, where no interaction was detected. The random effects of FMU (area) and road-width class were checked; none were found to be significant (p > 0.05). The intercept was forced through zero for models of the field approach, to obtain the observed (and not averaged) degradation rate as a function of the road-width class.
2.7. Candidate Model Selection
Selection of candidate models was conducted using an information-theoretic approach (Akaike Information Criterion, AIC) to determine what combination of variables would best permit estimation of gravelled forest road degradation. AICc was calculated using the dredge function of the package MuMln [42] within the R statistical environment [43]. We used AICc (AIC corrected for small sample size) for model selection in both approaches. Use of AICc was further indicated by the low n/k ratios (sample size/number of parameters), which were less than 40 [44]. Candidate models were selected up to an AICc weight (wi) = 1 and an ∆AICc < 2 [44]. The probability that a predictor is a component of the best model was calculated by summing the wi of the candidate models in which they appeared [44].
The resulting candidate regression models for each approach were validated with respect to the diagnostic residual graphs. Due to high heteroskedasticity and asymmetry of the beta distribution, the recommendations of Ferrari and Cribari-Neto [41] were applied using Pearson residuals rather than raw residuals.
2.8. Predictions and Validation of Candidate Models
Degradation was predicted using the model with the best performing wi for both approaches with the predict function of the betareg package [45]. To make predictions, the beta regression uses a logit-link for the coefficients that are estimated by maximum likelihood [40]. Simulations of the degradation were then conducted. By comparing the predicted degradation rate with actual data, it was possible to validate the performance of the models by calculating bias (e.g., scaled mean error [SME], overestimation and underestimation), precision (variance) and accuracy (scaled mean-square error [SMSE]) [46].
3. Results
3.1. Regression Models of Degradation
For the field approach, all four retained variables (e.g., width, slope, time since last maintenance and loss of road surfaces) were used to construct the regression model (Table 3). Percentage depression from TPI, the standard deviation of TWI, the standard deviation of cross-sectional CSI, the mean value of TRI, the mean value of NDVI, and the percentage presence of vegetation that is derived from the CHM are the indices that were selected to construct the regression model for the remote sensing approach.

Table 3.
Pearson product-moment correlations (r) between degradation and indices extracted from ALS or Sentinel-2 (e.g., NDVI), the field variables, and statistics such standard deviation (SD), minimum, maximum, mean and percent depression (% depress.).
3.2. Selection of Candidate Models
According to the AICc weights, three candidate models emerged from the field approach, whereas the remote sensing approach resulted in 25 candidates (Table 4). The best performing model includes the four variables that were selected beforehand (width, slope, time since last maintenance, and PRSL). According to the wi, this model has a 93% probability of being the most realistic and representative model explaining degradation. Accumulated AICc weights for the slope and PRSL have a 100% probability of being good variables of degradation given that were they employed in the three proposed models. Similar high probabilities are obtained when the time since last maintenance (93%) and road width (99.9%) are included, but these variables are excluded from the second and third field models, respectively. The high Δ (>2) for the latter two models indicate no support for their inclusion under the selection criterion for AICc.

Table 4.
Summary of candidate models for field and remote sensing approaches, including AICc, ΔAICc, and AICc weight (wi). Grey boxes represent variables that were selected in the candidate models.
For the remote sensing approach, the best candidate models that are selected incorporate the NDVI mean, the TRI mean, the percentage depression of TPI, the standard deviation of the cross-sectional CSI, or the standard deviation of TWI. Mean NDVI is present in all proposed models, having a 100% probability of being a good predictor of degradation. This same probability decreases to 96% for mean TRI, 67% for the percentage of depression from TPI, 26% for the percentage presence of HCM vegetation, 31% for the SD of cross-sectional CSI and 35% for the SD of TWI.
Predictions and Validation of Candidate Models
Equation (3) presents predicted degradation for a wide road using model estimates for the field approach that employed the logit-link required to perform beta regression (Table 5):
Degradation (%) = Invlogit (−3.10 + Slope × 0.09 + Time since last maintenance × 0.03 + PRSL × 0.02)

Table 5.
Estimated coefficients for the variables and the intercepts (different for the three road-width class) and p-values of these beta regression model variables for the field and remote sensing approaches.
Equation (4) predicts degradation using model estimates for the remote sensing approach (Table 5) by integrating the selected indices:
Degradation (%) = Invlogit (−4.09 + TRI × 3.43 + NDVI × 2.76 + TPI × 0.02)
4. Model Validation
Pseudo-R2 values of the prediction models for field and remote sensing approaches are 0.43 and 0.34, respectively. Furthermore, the mean errors that are associated with predicting degradation from each approach are 8% and 9%, respectively. When comparing predictions with actual data (e.g., minimum degradation = 0%, maximum = 82%), the minimum predicted values are similar for the two approaches (a 0.1% difference), although neither is equal to zero. The maximum predictions are, respectively, 5% and 15% lower for the models implementing the field and remote sensing approaches. Cross-validation analysis (Table 6) reveals that both models have a bias, precision and accuracy of less than 5%.

Table 6.
Validation of prediction models that were selected for the field and remote sensing approaches.
5. Degradation Prediction Curves
Figure 6 simulates predictions of degradation using Equation (3) (field approach) and shows that the forest road degradation rate increases as variables such as the slope, loss of road surfaces or time since last maintenance increase individually (Figure 6A). The predicted rate of degradation is lowest for the widest roads class, while medium-width and narrow road class respectively display 1.7 times and 2.5 times greater degradation, on average. When all variables are combined (Figure 6B), the disparity in degradation rates is maintained among road-width class, and degradation predictions are higher.
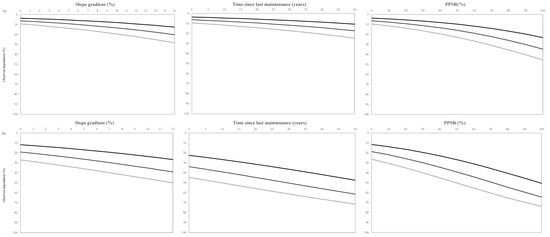
Figure 6.
Prediction curves for degradation (%) that were simulated from beta regression model estimates for the field approach based upon different slopes, time since last maintenance and PRSL values for the three road-width class. The simulations (A-top row) show predicted degradation rates when all variables, except the one that was selected in the respective graphs, have no effect (i.e., equal to zero). Simulations (B-bottom row) show predicted degradation rates when values of the variables increase.
Figure 7 shows degradation predictions for Equation (4) (remote sensing approach) and demonstrates that degradation increases as the mean values of NDVI, TRI and percentage of TPI depression individually increase (Figure 7, solid lines). When the three variables are combined, the predicted rate of degradation is then higher (Figure 7, dotted lines).

Figure 7.
Prediction curves for degradation (%) that were simulated from estimates of the beta regression model used for the remote sensing approach. For each of the variables (NDVI mean, TRI mean, percentage of TPI depression), the curves simulate their individual (solid lines) and combined effects (with the two other fixed-value variables; dotted lines). Fixed values that were used for the combined curves correspond to the averages of the variables, e.g., mean TRI = 0.22, mean NDVI = 0.5 and percentage of TPI depression = 50%.
6. Discussion
6.1. Model Performance in Predicting Degradation
The lack of studies proposing predictive models of forest road degradation prevent us from making comparisons with our regression model’s performance. Yet, studies on the degradation of roads and motorways in urban areas abound. For example, George et al. [47] used six variables, including road age, to predict degradation of the asphalt pavement and obtained an R2 = 0.75. For their part, Xu et al. [48] used 12 variables, including road age and daily transport flow, to create models that predicted pavement degradation with an R2 of 0.88. These similar results can be partly explained by the fact that asphalt road construction standards differ very little from one jurisdiction to the next, unlike forest roads [49], in part because of the environmental and structural requirements, and the construction material quality vary from one forest road to another. Our logistic regression model provides a McFadden pseudo-R2, a statistic that tends to be lower than the R2 of more standard linear models [50].
In terms of model accuracy, the results of the field approach were similar to those of Heidari et al. [51], who had developed a logistic regression model to predict forest road degradation in Iran. Of the 19 variables that were used to try to explain degradation, the slope, the age of the road, the material, the thickness of the road surface, and transport flow were significant variables (p < 0.05) that were retained in the authors’ prediction model, the prediction accuracy of which ranged from 82% to 89%. The model pseudo-R2 estimates for the remote sensing approach has also shown a good fit [50]. Again, very few studies had focused on detecting forest gravelled road degradation using indices that have been extracted from ALS data and optical images. Nevertheless, the prediction errors of our model are similar to those of Kiss et al. [52] who used ALS to extract a topography index (TPI) and fluctuation index (SE; normalized elevation index) to classify the quality (e.g., good and satisfactory) of forest roads at different resolutions.
6.2. Field Approach- Road Width
The three road-width classes that were used in this study could represent standards for road construction that are based on a predefined travel speed. To date, no studies establishing that road width would affect the rate of road degradation have been published in the scientific literature. Nevertheless, our results have shown that percentage degradation differs according to road width, which reflects shortcomings that results from the network’s construction standards.
In Canada, the widest roads are primary forest access roads and, therefore, are built for long-term functioning (e.g., Quebec, service life >25 years [53]; Alberta, service life >20 years [54]; Yukon, service life >10 years [55]; Manitoba, service life >20 years [56]). For example, their sub-grade consists of gravel and has a high compaction rate, which allows the structure to perform better while preventing degradation from occurring quickly. Narrower- to medium-width roads do not meet these standards; their construction is based upon a shorter-term vision and, therefore, their sub-grade consists of mineral soil, organic soil or woody debris. These materials do not facilitate an appropriate rate of compaction, so that the successive passage of vehicles more easily creates depressions on the road surface [8,34,57,58] through preferential formation of ruts and furrows [29]. Moreover, a higher recurrence of ruts was noted as the width of the road narrowed.
6.3. Field Approach- Slope
Integration of the slope into the Field approach model is corroborated by numerous works that attest to the importance of this variable on degradation rates of forest roads [6,30,32,33,51,59]. Degradation on a sloping road would mainly be caused by erosion due to runoff [33,59] and by vehicle acceleration [29,32]. Our results are consistent given that sampled roads with higher slope gradients showed a preponderance of runoff-induced erosion. Further, the notable emergence of the subgrade on steeply sloping road sections concurs with the findings of Ciobanu et al. [29], who noted significant effects of vehicle acceleration and deceleration on the road surface erosion when vehicles travel up or down sloping roads, since these processes expose the road subgrade.
Similar proportions of ruts and furrows in the two slope categories indicate that other factors, such as transport flow and lack of road compaction [29,30,32], may influence their presence on the road surface. Thus, we note that a low slope (≤4%) is not necessarily synonymous with the absence of degradation. Moreover, our results showed high pothole numbers on roads with slopes less than 4%. These observations are consistent with the guidelines of Ryan et al. [6], which state that a slope <3% would also be at risk of degradation, given that it leads to preferential pothole formation. Such recurrences on the road surface would indicate, in this case, an accumulation of runoff [32].
6.4. Field Approach- Time-Since-Last-Maintenance
The integration of time into the prediction of degradation corresponds with reports in the literature. To minimize the degradation of the road surface, many reports have stipulated that their systematic and regular maintenance is necessary [6,29,30,31,51,59]. However, we have noted that our projections included curves where degradation over time varies by less than 5% in the first five years. A priori, this increase seems relatively small, but it should not be neglected. In the first few years without maintenance, the forms of degradation appear gradually. The exponential effect in the temporal degradation curves would result precisely from this process of intensification and the addition of degradation over time.
6.5. PRSL
In the field approach model, the loss of the road surface indicates that vegetation is encroaching on a road. Applied studies in forest ecology [60,61] show that the presence of vegetation considerably reduces moisture loss and the rate of soil evaporation. This process is relevant to our study, given that the presence of vegetation would have the effect of containing moisture on the road surface and subgrade levels. Road stability would then be compromised [29], leading to an increase in its degradation.
6.6. Remote Sensing Approach
One basic hypothesis of the remote sensing approach that we had applied to the present study was that topography, roughness and vegetation played a significant role in estimating forest gravelled road degradation. ALS and Sentinel-2 remotely sensed data demonstrated that it is indeed possible to estimate this variable by combining a topography index (TPI), roughness index (TRI), and vegetation index (NDVI). These indices are very well documented in the literature and are easy to calculate and interpret. Generally, they are applied at the landscape scale, especially to detect hydrological processes (topographic indices) [62], geomorphological processes (roughness indices) [63], and to determine the characteristics and changes in vegetation and biomass (vegetation indices) [64]. However, our results show that these indices are not limited to the domains to which they are generally attached.
In fact, the presence of lower topography (TPI < 0) within the forest road would make it possible to characterize the most notable depressions, e.g., the most frequent forms of degradation. Our results showed that ruts, furrows and runoff are among the two most recurrent forms in the study. In our opinion, the percentage depression resulting from the TPI would be a good estimator of the presence of ruts, which are linear depressions that can attain more than one metre in width and length. Furrows and potholes, which also manifest themselves as large-area depressions on the running surface, would also be detectable using this index.
We are also aware that percentage TPI depression may not be the most efficient tool for finding small areas (<1 m) of degradation, including flows, undulations and subgrade emergence that have been observed with field surveys. These small forms of degradation are manifested by a more heterogeneous running surface. In our opinion, the addition of TRI to the model precisely filled this gap since it indicates whether there are strong variations in elevation within the running surface, without precisely positioning their location as TPI does. To increase the predictive capability of the model, the addition of NDVI appeared to capture the effect of time on road degradation.
6.7. Future Implications
The proposed degradation prediction models are innovative and easy to use. They provide new knowledge on both current and future states of the road network. For example, during the 2019 sampling, 21% of the 103.5 km of roads that had been inventoried were more than 40% degraded. Predictions from the field approach model assumed that 24% of roads would exhibit >40% degradation within five years if no maintenance was carried out. This proportion would rise to 31% after 10 years and 43% after 20 years without maintenance, e.g., double the current proportion. The relationships that were obtained from this study can now be integrated into the management of Canada’s forestlands. By combining spatiotemporal knowledge that is provided by the two approaches, it is especially possible to plan the frequency of forest road maintenance and the associated budget, together with the sectors that are most at risk for limited land access (e.g., unexpected road closures), for users (e.g., road accidents), and for surrounding ecosystems (e.g., increased erosion).
In addition, it is essential that the knowledge gained from this study be taken into consideration when implementing the construction of new roads. Annually, about 0.24% of Canada’s forest area is used for forest road construction. The constant growth of the network raises many questions regarding the alternatives that are available to maintain access to the forest territory, while reducing economic, environmental and social problems that arise due to road construction. Several possible solutions have emerged from this study, including the timely repair of roads, regular maintenance of road surfaces, ditches and the rights-of-way, a review of construction standards, and limitation of road construction in steep sections.
Until now, the remote sensing approach has made it possible to estimate degradation on previously positioned sections. Eventually, however, continuous mapping of forest road degradation would become an avenue that could offer more effective real-time management of forest disturbances. For example, it would then be possible to visualize and to determine the current state of all roads to be used when travelling through the forest to fight wildfires, to harvest timber, or to replant forest following disturbances.
7. Conclusions
The two approaches that were used, namely field observations and the use of remote sensing to detect forest gravelled road degradation, provided new temporal and spatial knowledge of the forest road. More specifically, the field approach provided greater understanding and predictive capability regarding the way a road degrades as a function of the slope, time since last maintenance, road-width class, and loss of the road surface. The remote sensing approach demonstrated that using a combination of topography, roughness, and vegetation, it was possible to predict the current state of degradation, thereby demonstrating the potential utility of remote tools such as airborne laser scanning and Sentinel-2. The versatility of these two approaches is an advantage of this study. Indeed, results that were obtained here can be exported to the entire eastern Canadian boreal forest domain, given that the required data are easily accessible and free of charge, and that several potential solutions for improving forest management emerge. Certainly, the integration of other factors would advance knowledge on road degradation in forest environments. This study takes a fresh look at the management of the road network, making it possible to maintain economic, environmental, and social benefits that are offered by forest roads, while minimising the issues that are related to these three spheres of sustainable development.
Author Contributions
P.G. did most of the work in French (field work, analysis, writing). As codirectors, O.V. and F.G. took the relay for editing and improving the English version. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Research Council of Canada (RGPIN04861-2016 and RDC 508853-17) and by the Canadian Foundation for Innovation (RFCI0388).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Authors are willing to give access upon demand.
Acknowledgments
Authors are grateful to Philippe Girardin and Lievin Kasanda NKuba for field work, to Philippe Marchand for assistance in statistical analysis, to William Parson for English editing and to many other lab colleagues for moral support. Field work of this project was supported by Resolute Forest Products Inc (Francis Perreault, Denis Dubé, François Lévesque and Martin Germain) and Barrette-Chapais (Denis Chiasson). Road data acquisition was supported by Rival Solutions (Claude Laflamme).
Conflicts of Interest
Authors state no conflict of interest. The sponsors (Resolute Forest Products, Barrette-Chapais and Rival Solutions) and had no role in the design, execution, interpretation, or writing of the study.
References
- Bourgeois, L.; Kneeshaw, D.; Boisseau, G. Les routes forestières au Québec: Les impacts environnementaux, sociaux et économiques. VertigO-La Rev. Électronique Sci. L’environnement 2005, 6, 1–12. [Google Scholar] [CrossRef]
- Caliskan, E. Environmental impacts of forest road construction on mountainous terrain. Iran. J. Environ. Health Sci. Eng. 2013, 10, 23. [Google Scholar] [CrossRef]
- Fahrig, L.; Rytwinski, T. Effects of roads on animal abundance: An empirical review and synthesis. Ecol. Soc. 2009, 14, 21. [Google Scholar] [CrossRef]
- Gucinski, H.; Furniss, M.J.; Ziemer, R.R.; Brookes, M.H. Forest Roads: A Synthesis of Scientific Information; USDA Forest Service; Pacific Northwest Research Station Portland: Portland, OR, USA, 2001; p. 103. [Google Scholar]
- Luce, C.H.; Wemple, B.C. Introduction to special issue on hydrologic and geomorphic effects of forest roads. Earth Surf. Process. Landf. 2001, 26, 111–113. [Google Scholar] [CrossRef]
- Ryan, T.; Phillips, H.; Ramsay, J.; Dempsey, J. Forest Road Manual: Guidelines for the Design, Construction and Management of Forest Roads; COFORD Dublin: Dublin, Ireland, 2004; p. 170. [Google Scholar]
- Robinson, C.; Duinker, P.; Beazley, K. A conceptual framework for understanding, assessing, and mitigating ecological effects of forest roads. Environ. Rev. 2010, 18, 61–86. [Google Scholar] [CrossRef]
- Akgul, M.; Akburak, S.; Yurtseven, H.; Akay, A.; Cigizoglu, H.; Demir, M.; Ozturk, T.; Eksi, M. Potential impacts of weather and traffic conditions on road surface performance in terms of forest operations continuity. Appl. Ecol. Environ. Res. 2019, 17, 2533–2550. [Google Scholar] [CrossRef]
- Kaakkurivaara, T.; Vuorimies, N.; Kolisoja, P.; Uusitalo, J. Applicability of portable tools in assessing the bearing capacity of forest roads. Silva Fenn. 2015, 49, 2–25. [Google Scholar] [CrossRef]
- Ciampoli, L.B.; Tosti, F.; Economou, N.; Benedetto, F. Signal processing of GPR data for road surveys. Geosciences 2019, 9, 96. [Google Scholar] [CrossRef]
- Salvi, R.; Ramdasi, A.; Kolekar, Y.A.; Bhandarkar, L.V. Use of Ground-Penetrating Radar (GPR) as an Effective Tool in Assessing Pavements—A Review. Geotech. Transp. Infrastruct. 2019, 29, 85–95. [Google Scholar]
- McFarlane, H.; Paterson, W.; Dohaney, W. Experience with the Benkelman Beam on Canadian Forest Roads; Transportation Research Board: Washington, DC, USA, 1975; Volume 16, p. 210. [Google Scholar]
- Thompson, M. Soil-Lime Mixtures for Construction of Fine-Grained Soil Pavements; 0360-859X; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1975. [Google Scholar]
- Karim, D.F.; Rubasi, D.K.A.H.; Saleh, D.A.A. The road pavement condition index (PCI) evaluation and maintenance: A case study of Yemen. Organ. Technol. Manag. Constr. Int. J. 2016, 8, 1446–1455. [Google Scholar] [CrossRef]
- Loprencipe, G.; Pantuso, A. A specified procedure for distress identification and assessment for urban road surfaces based on PCI. Coatings 2017, 7, 65. [Google Scholar] [CrossRef]
- Setyawan, A.; Nainggolan, J.; Budiarto, A. Predicting the remaining service life of road using pavement condition index. Procedia Eng. 2015, 125, 417–423. [Google Scholar] [CrossRef]
- Paterson, W. International Roughness Index: Relationship to Other Measures of Roughness and Riding Quality. In Proceedings of the Transportation Research Record, Washington, DC, USA; 1986; pp. 49–59. Available online: http://onlinepubs.trb.org/Onlinepubs/trr/1986/1084/1084-007.pdf (accessed on 5 October 2021).
- Abulizi, N.; Kawamura, A.; Tomiyama, K.; Fujita, S. Measuring and evaluating of road roughness conditions with a compact road profiler and ArcGIS. J. Traffic Transp. Eng. Engl. Ed. 2016, 3, 398–411. [Google Scholar] [CrossRef]
- Forslöf, L.; Jones, H. Roadroid: Continuous road condition monitoring with smart phones. J. Civ. Eng. Archit. 2015, 9, 485–496. [Google Scholar] [CrossRef]
- Múčka, P. Current approaches to quantify the longitudinal road roughness. Int. J. Pavement Eng. 2016, 17, 659–679. [Google Scholar] [CrossRef]
- Prasad, J.R.; Kanuganti, S.; Bhanegaonkar, P.N.; Sarkar, A.K.; Arkatkar, S. Development of relationship between roughness (IRI) and visible surface distresses: A study on PMGSY roads. Procedia-Soc. Behav. Sci. 2013, 104, 322–331. [Google Scholar] [CrossRef][Green Version]
- Sayers, M.W. On the Calculation of International Roughness Index from Longitudinal Road Profile; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1995; pp. 1–12. [Google Scholar]
- Akgul, M.; Yurtseven, H.; Akburak, S.; Demir, M.; Cigizoglu, H.K.; Ozturk, T.; Eksi, M.; Akay, A.O. Short term monitoring of forest road pavement degradation using terrestrial laser scanning. Measurement 2017, 103, 283–293. [Google Scholar] [CrossRef]
- Zhang, C. An UAV-based photogrammetric mapping system for road condition assessment. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci 2008, 37, 627–632. [Google Scholar]
- Hyyppä, J.; Pyysalo, U.; Hyyppä, H.; Samberg, A. Elevation accuracy of laser scanning-derived digital terrain and target models in forest environment. In Proceedings of the EARSeL-SIG-Workshop LIDAR, Dresden, Germany, 16–17 June 2000; pp. 16–17. Available online: http://eproceedings.uni-oldenburg.de/website/vol01%5F1/01%5F1%5Fhyyppae1%2Epdf (accessed on 12 August 2021).
- Blouin, J.; Berger, J. Guide de Reconnaissance des Types Écologiques de la Région Écologique 5b Coteaux du Réservoir Gouin; Ministère des Ressources Naturelles du Québec, Forêt Québec, Direction des Inventaires Forestiers, Division de la Classification écologique et Productivité des Stations: Québec, QC, Canada, 2001. [Google Scholar]
- Gosselin, J.; Berger, J.-P. Guide de Reconnaissance des Types Écologiques: Région Écologique 4b: Coteaux du Réservoir Cabonga: Région Écologique 4c: Collines du Moyen-Saint-Maurice; Ministère des Ressources Naturelles, Forêt Québec, Direction des Inventaires: Quebec, QC, Canada, 2002. [Google Scholar]
- Leboeuf, M. Arbres et Plantes Forestières du Québec et des Maritimes-Réédition; Éditions Michel Quintin: Montreal, QC, Canada, 2016. [Google Scholar]
- Ciobanu, V.; Alexandru, V.; Saceanu, S. Degradation Forms of Forest Gravel Road Roadways under Heavy Vehicles Used in Timber Transport. Agric. Food Eng. 2012, 5, 37. Available online: http://rs.unitbv.ro/BU2012/Series%20II/BULETIN%20II%20PDF/Ciobanu_V.pdf (accessed on 2 December 2021).
- Desautels, R.; Després, R.; Dufresne, F.; Gilbert, G.; Leblanc, S.; Méthot, L. Voirie forestière. In Manuel de Foresterie; Doucet, R., Côté, M., Eds.; Éditions Multimondes: Montréal, QC, Canada, 2009; pp. 1187–1244. [Google Scholar]
- Jetté, J.-P. Guide des Saines Pratiques Forestières Dans les Pentes du Québec; Gouvernement du Québec, Ministeère des Ressources Naturelles: Québec, QC, Canada, 1998. [Google Scholar]
- Fannin, R.J.; Lorbach, J. Guide to Forest Road Engineering in Moutainous Terrain; Food and Agricultural Organization: Rome, Italy, 2007; p. 38. [Google Scholar]
- Dittmer, M.; Johnson, A.A. Impacts of High-Intensity Rainstorms on Low-Volume Roads and Adjacent Land; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1975. [Google Scholar]
- Kiss, K.; Malinen, J.; Tokola, T. Forest road quality control using ALS data. Can. J. For. Res. 2015, 45, 1636–1642. [Google Scholar] [CrossRef]
- Weiss, A. Topographic position and landforms analysis. In Proceedings of the ESRI User Conference, San Diego, CA, USA, 9–13 July 2001. [Google Scholar]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Tarpley, J.D.; Schneider, S.R.; Money, R.L. Global Vegetation Indices from the NOAA-7 Meteorological Satellite. J. Clim. Appl. Meteorol. 1984, 23, 491–494. [Google Scholar] [CrossRef]
- Ferrari, S.; Cribari-Neto, F. Beta regression for modelling rates and proportions. J. Appl. Stat. 2004, 31, 799–815. [Google Scholar] [CrossRef]
- Smithson, M.; Verkuilen, J. A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. Psychol. Methods 2006, 11, 54. [Google Scholar] [CrossRef]
- Cribari-Neto, F.; Zeileis, A. Beta regression in R. J. Stat. Softw. 2010, 34, 1–24. [Google Scholar] [CrossRef]
- Barton, K.; Barton, M.K. Package ‘Mumin’; Version 1.43.17; 2015. Available online: https://cran.r-project.org/web/packages/MuMIn/MuMIn.pdf (accessed on 23 December 2021).
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Symonds, M.R.; Moussalli, A. A brief guide to model selection, multimodel inference and model averaging in behavioural ecology using Akaike’s information criterion. Behav. Ecol. Sociobiol. 2011, 65, 13–21. [Google Scholar] [CrossRef]
- Zeileis, A.; Cribari-Neto, F.; Gruen, B.; Kosmidis, I.; Simas, A.B.; Rocha, A.V.; Zeileis, M.A. Package ‘Betareg’; 2016. Available online: https://cran.r-project.org/web/packages/betareg/betareg.pdf (accessed on 23 December 2021).
- Walther, B.A.; Moore, J. The concepts of bias, precision and accuracy, and their use in testing the performance of species richness estimators, with a literature review of estimator performance. Ecography 2005, 28, 815–829. [Google Scholar] [CrossRef]
- George, K.; Rajagopal, A.; Lim, L. Models for Predicting Pavement Deterioration; The National Academies of Sciences, Engineering, and Medicine: Washington, DC, USA, 1989; pp. 1–7. [Google Scholar]
- Xu, G.; Bai, L.; Sun, Z. Pavement deterioration modeling and prediction for Kentucky interstate and highways. In Proceedings of the IIE Annual Conference, Montréal, QC, Canada, 31 May–3 June 2014; p. 993. [Google Scholar]
- Keramati, A.; Lu, P.; Sobhani, A.; Esmaeili, S.A.H. Impact of forest road maintenance policies on log transportation cost, routing, and carbon-emission trade-offs: Oregon case study. J. Transp. Eng. Part A Syst. 2020, 146, 4–28. [Google Scholar] [CrossRef]
- McFadden, D.; Talvitie, A.; Cosslett, S.; Hasan, I.; Johnson, M.; Reid, F.; Train, K. Demand Model Estimation and Validation; University of California: Berkeley, CA, USA, 1977. [Google Scholar]
- Heidari, M.J.; Najafi, A.; Alavi, S. Pavement deterioration modeling for forest roads based on logistic regression and artificial neural networks. Croat. J. For. Eng. J. Theory Appl. For. Eng. 2018, 39, 271–287. [Google Scholar]
- Kiss, K.; Malinen, J.; Tokola, T. Comparison of high and low density airborne lidar data for forest road quality assessment. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; pp. 167–172. Available online: https://www.researchgate.net/profile/Jukka-Malinen/publication/303845763_COMPARISON_OF_HIGH_AND_LOW_DENSITY_AIRBORNE_LIDAR_DATA_FOR_FOREST_ROAD_QUALITY_ASSESSMENT/links/57bd2ff508ae6c703bc530c2/COMPARISON-OF-HIGH-AND-LOW-DENSITY-AIRBORNE-LIDAR-DATA-FOR-FOREST-ROAD-QUALITY-ASSESSMENT.pdf (accessed on 28 December 2021).
- Government of Quebec. Guide D’application du Règlement sur L’aménagement Durable des Forêts du Domaine de L’état; Institution: Québec, QC, Canada, 2020; Available online: https://mffp.gouv.qc.ca/RADF/guide/ (accessed on 26 October 2021).
- Government of Alberta. Alberta Timber Harvest Planning and Operating Ground Rules Framework for Renewal; Institution: Calgary, AB, Canada, 2016; Available online: https://open.alberta.ca/dataset/9b063439-285b-4d38-b979-e3ae59c80d23/resource/28365bb7-9369-4f5a-8695-655a6ef0f6b3/download/2016-12-alberta-timber-harvest-planning-and-operating-groundrules-framework.pdf (accessed on 9 October 2021).
- Government of Yukon. Forest Resources Act: Standards and Guidelines—Forest Resources Roads; Institution: Whitehorse, YK, Canada, 2015. Available online: http://www.forestry.gov.yk.ca/ (accessed on 15 December 2021).
- Government of Manitoba. Forest Practices Guidebook: Forestry Road Management; Institution: Winnipeg, MB, Canada, 2012. Available online: https://www.gov.mb.ca/sd/forestry/pdf/practices/forestry_road_mgmt_2012.pdf (accessed on 23 December 2021).
- O’Mahony, M.; Ueberschaer, A.; Owende, P.; Ward, S. Bearing capacity of forest access roads built on peat soils. J. Terramech. 2000, 37, 127–138. [Google Scholar] [CrossRef]
- Adlinge, S.S.; Gupta, A. Pavement deterioration and its causes. Int. J. Innov. Res. Dev. 2013, 2, 437–450. [Google Scholar]
- Dobiaš, J. Forest road erosion. J. For. Sci. 2005, 51, 37–46. [Google Scholar] [CrossRef]
- Asbjornsen, H.; Goldsmith, G.R.; Alvarado-Barrientos, M.S.; Rebel, K.; Van Osch, F.P.; Rietkerk, M.; Chen, J.; Gotsch, S.; Tobon, C.; Geissert, D.R. Ecohydrological advances and applications in plant–water relations research: A review. J. Plant Ecol. 2011, 4, 3–22. [Google Scholar] [CrossRef]
- Aalto, J.; Le Roux, P.C.; Luoto, M. Vegetation mediates soil temperature and moisture in arctic-alpine environments. Arct. Antarct. Alp. Res. 2013, 45, 429–439. [Google Scholar] [CrossRef]
- Vaze, J.; Teng, J.; Spencer, G. Impact of DEM accuracy and resolution on topographic indices. Environ. Model. Softw. 2010, 25, 1086–1098. [Google Scholar] [CrossRef]
- Różycka, M.; Migoń, P.; Michniewicz, A. Topographic Wetness Index and Terrain Ruggedness Index in geomorphic characterisation of landslide terrains, on examples from the Sudetes, SW Poland. Z. Geomorphol. Suppl. Issues 2017, 61, 61–80. [Google Scholar] [CrossRef]
- Meneses-Tovar, C. NDVI as indicator of degradation. Unasylva 2011, 62, 39–46. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).