Exploring the Intrinsic Probability Distribution for Hyperspectral Anomaly Detection
Abstract
:1. Introduction
- (1)
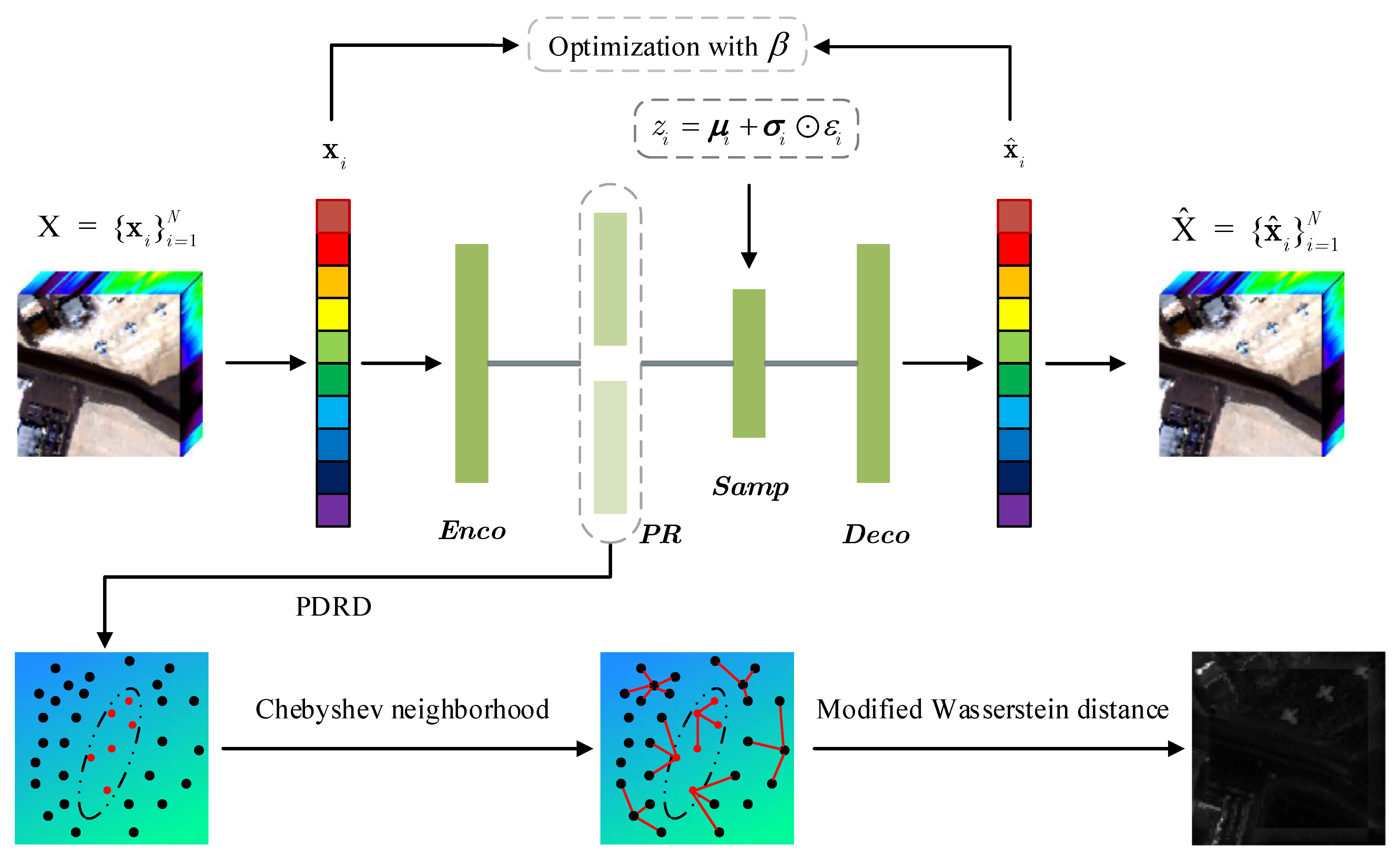
- We propose a framework to represent both the background and the anomalies in HSI by multivariate Gaussian distributions. The probabilistic characteristics of all objects can be discovered in the latent space.
- (2)
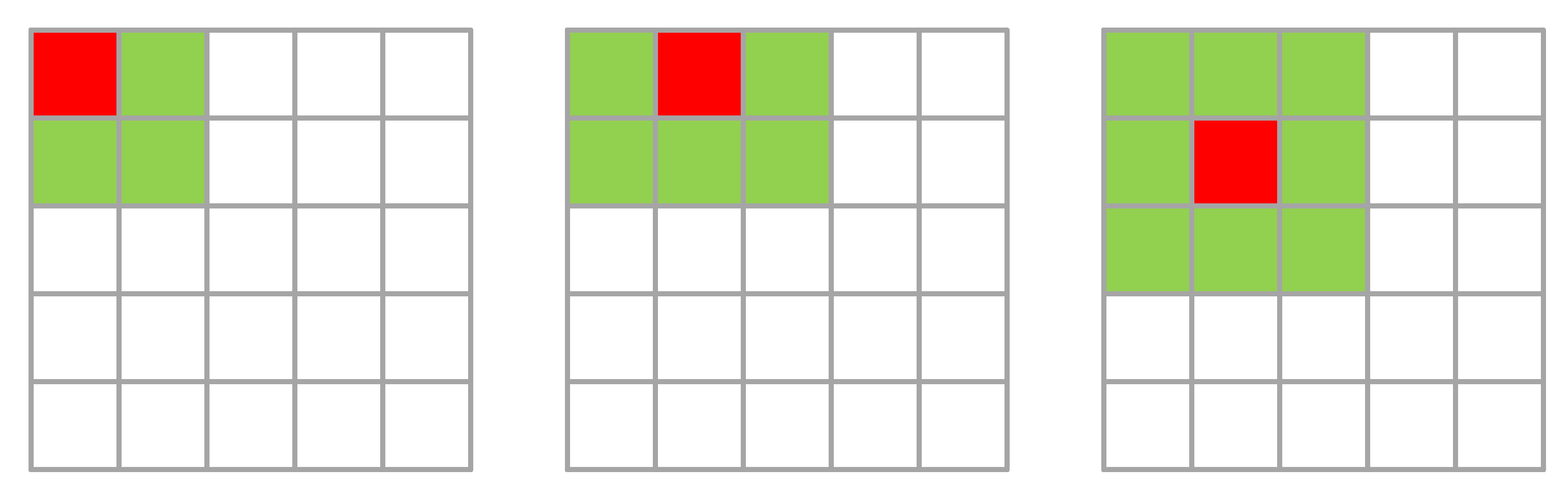
- Instead of exploiting reconstruction error, we integrate local statistics with probabilistic structural information by constructing the Chebyshev neighborhood for each pixel.
- (3)
- We build a valid criterion according to the actual property of HSI to evaluate the difference between two probability distributions, which highlights the anomalies and suppresses the background pixels.
2. Related Works
3. Methodology
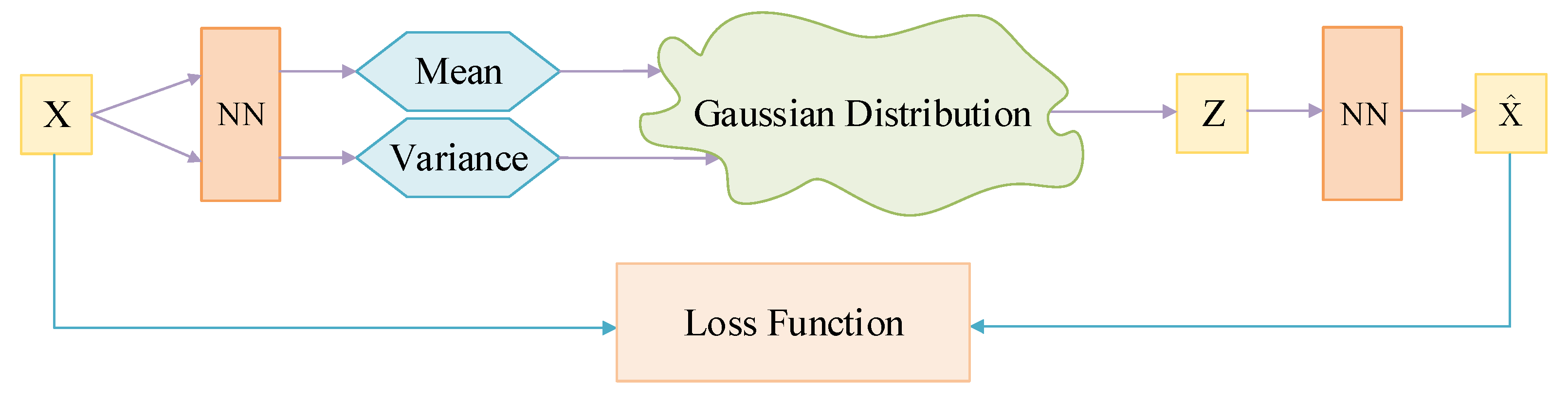
3.1. Probability Distribution Representation
3.1.1. The Framework
3.1.2. Implementation of Dimensional Independence
3.1.3. Selection of Chebyshev Neighborhood
3.2. Anomaly Detection with Modified Wasserstein Distance
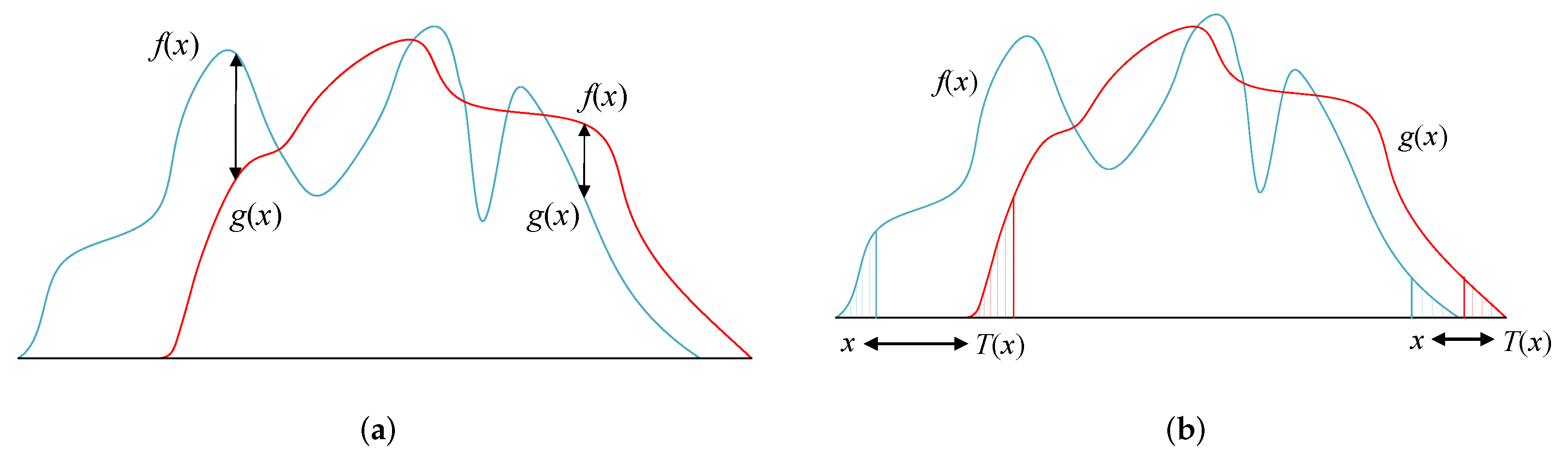
3.2.1. Measurement of Different Distributions
3.2.2. Modified Wasserstein Distance
| Algorithm 1 Anomaly detection for HSI based on PDRD |
| Input: Training samples and parameters: (1) trade-off parameter and weight parameter ; (2) Chebyshev neighborhood ; (3) dimensionality k of latent distribution. Output: Anomaly detection map.
|
4. Experimental Results
4.1. Hyperspectral Data Sets
4.1.1. Pavia City Data Set
4.1.2. Gulfport Data Set
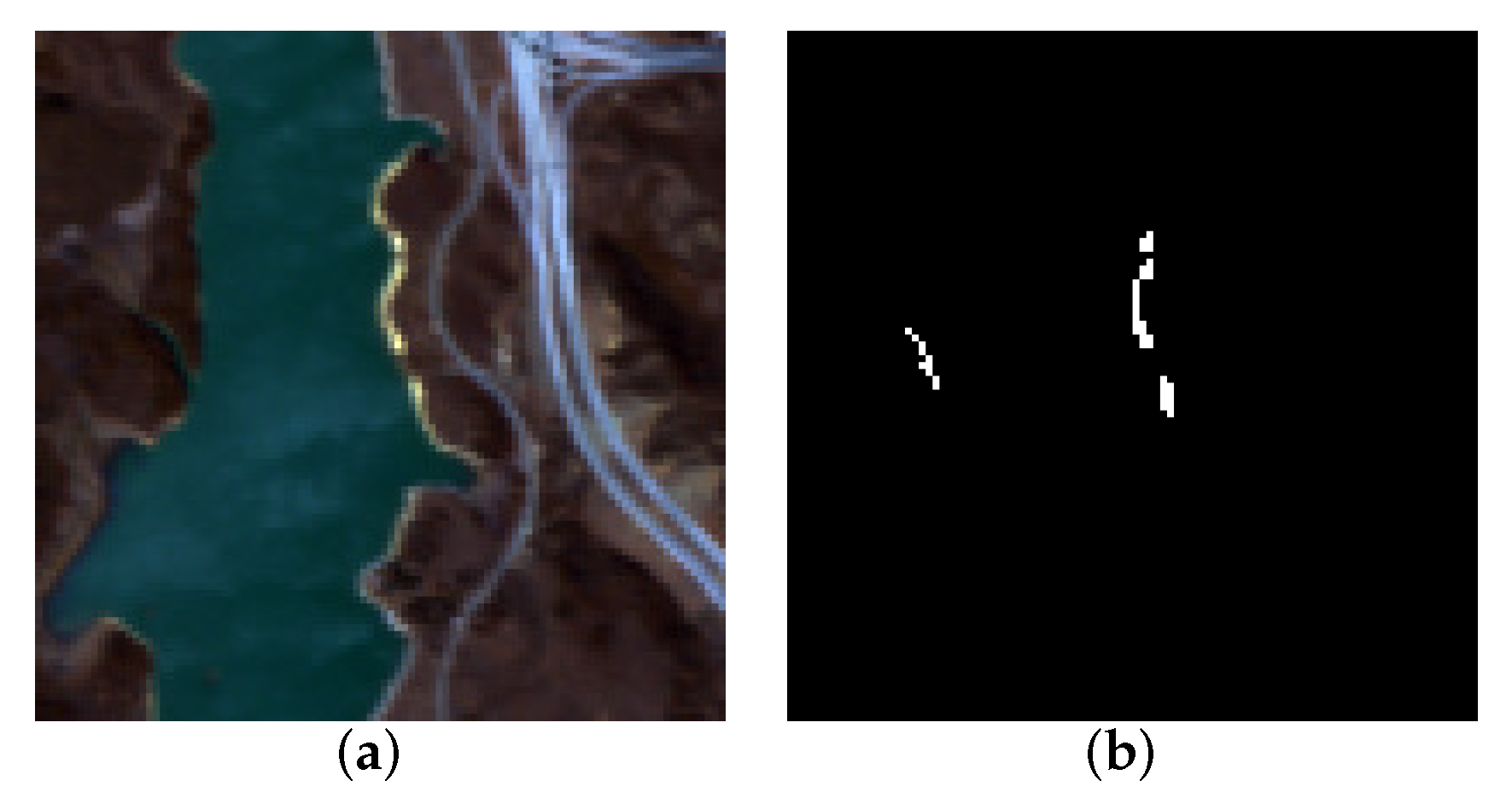
4.1.3. Jasper Ridge Data Set
4.2. Competitors
- (1)
- GRX [15] is a benchmark hyperspectral anomaly detector. It assumes that the background satisfies a multivariate Gaussian distribution. The background is estimated using the entire image.
- (2)
- CBAD [17] partitions the image into several clusters and compute the distance between each pixel and the centroid of the pixel belongs to.
- (3)
- LRASR [29] adopts a background dictionary that can fully discover the implicit background structure in the latent subspace by low rank and sparse representation. The separated anomaly part is exploited to detect anomalies.
- (4)
- LSMAD [32] decomposes the original data into a background part, an anomaly part, and a noise part. The Mahalanobis distance that reflected background signature is computed for the following detection process.
- (5)
- LSDM-MoG [33] models the noise component with a mixture of Gaussian distributions. The anomalies are separated from the noise components by variational Bayes.
- (6)
- AE [35] attempts to recover the background pixels by the structure of neural network. The anomalies hold larger reconstruction errors than the background pixels, which is the principle to distinguish the anomalies from the background.
- (7)
- RGAE [36] imposes the norm to the reconstruction error and embeds a superpixel segmentatio-based graph regularization term into AE.
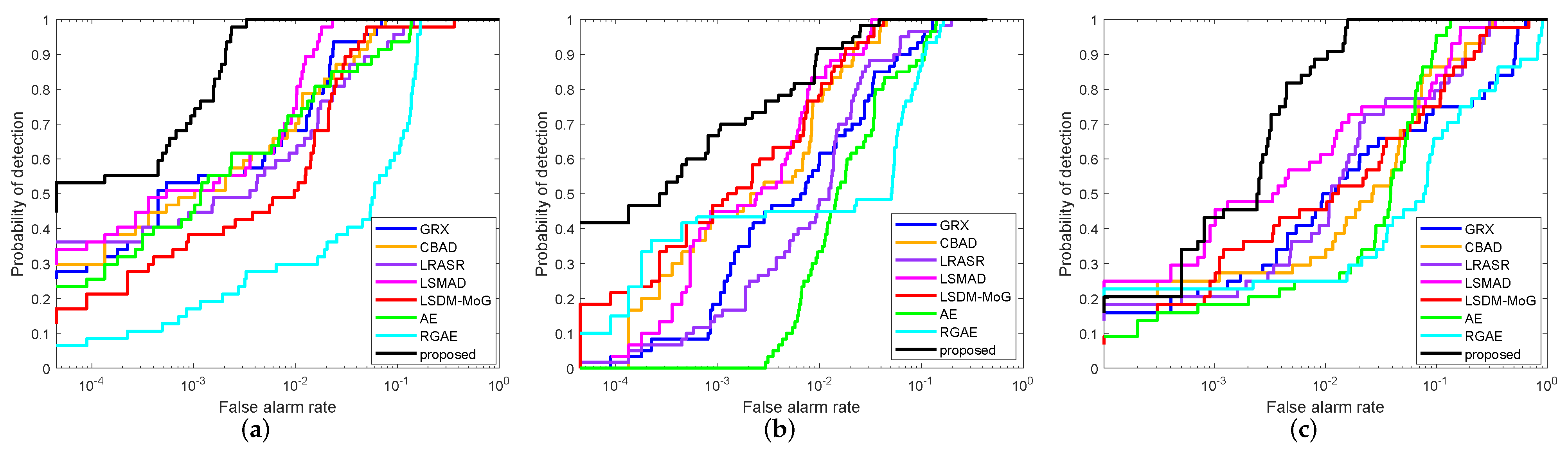
4.3. Detection Performance
4.3.1. Results of Paiva City Data Set
4.3.2. Results for Gulfport Data Set
4.3.3. Results for Jasper Ridge Data Set
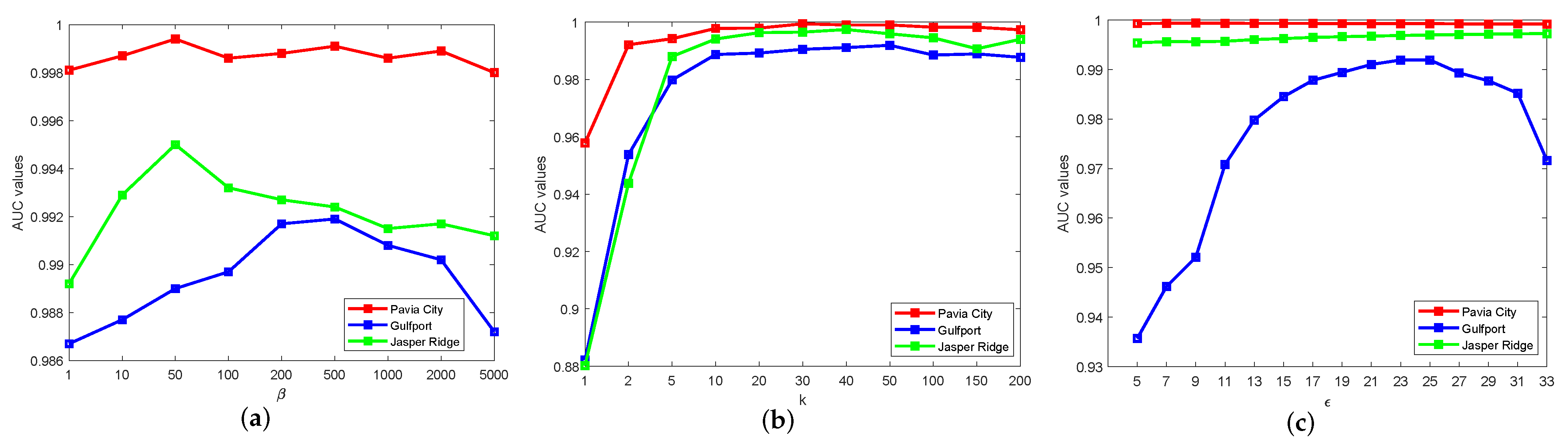
4.4. Parametric Analysis
4.4.1. Weight Parameter and Tradeoff Parameter
4.4.2. Dimensionality k of Latent Variable
4.4.3. Chebyshev Neighborhood
4.4.4. Parameters of Neural Network
4.5. Execution Time
4.6. Ablation Study
4.7. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cheng, T.; Wang, B. Graph and Total Variation Regularized Low-Rank Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 391–406. [Google Scholar] [CrossRef]
- Landgrebe, D. Hyperspectral image data analysis. IEEE Signal Process. Mag. 2002, 19, 17–28. [Google Scholar] [CrossRef]
- Huang, Z.; Kang, X.; Li, S.; Hao, Q. Game Theory-Based Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2965–2976. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral Remote Sensing Data Analysis and Future Challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Kruse, F.A.; Boardman, J.W.; Huntington, J.F. Comparison of airborne hyperspectral data and EO-1 Hyperion for mineral mapping. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1388–1400. [Google Scholar] [CrossRef] [Green Version]
- Grohnfeldt, C.; Zhu, X.X.; Bamler, R. Jointly sparse fusion of hyperspectral and multispectral imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium—IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 4090–4093. [Google Scholar]
- Yu, S.; Li, X.; Zhao, L.; Wang, J. Hyperspectral Anomaly Detection Based on Low-Rank Representation Using Local Outlier Factor. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1279–1283. [Google Scholar] [CrossRef]
- Nasrabadi, N.M. Hyperspectral Target Detection: An Overview of Current and Future Challenges. IEEE Signal Process. Mag. 2014, 31, 34–44. [Google Scholar] [CrossRef]
- Stein, D.W.J.; Beaven, S.G.; Hoff, L.E.; Winter, E.M.; Schaum, A.P.; Stocker, A.D. Anomaly detection from hyperspectral imagery. IEEE Signal Process. Mag. 2002, 19, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Li, S.; Zhang, K.; Hao, Q.; Duan, P.; Kang, X. Hyperspectral Anomaly Detection With Multiscale Attribute and Edge-Preserving Filters. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1605–1609. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Matteoli, S.; Diani, M.; Theiler, J. An Overview of Background Modeling for Detection of Targets and Anomalies in Hyperspectral Remotely Sensed Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2317–2336. [Google Scholar] [CrossRef]
- Ben Salem, M.; Ettabaa, K.S.; Hamdi, M.A. Anomaly detection in hyperspectral imagery: An overview. In Proceedings of the International Image Processing, Applications and Systems Conference, Hammamet, Tunisia, 5–7 November 2014; pp. 1–6. [Google Scholar]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral Anomaly Detection by the Use of Background Joint Sparse Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A nonlinear anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Carlotto, M.J. A cluster-based approach for detecting human-made objects and changes in imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 374–387. [Google Scholar] [CrossRef]
- Veracini, T.; Matteoli, S.; Diani, M.; Corsini, G. Fully Unsupervised Learning of Gaussian Mixtures for Anomaly Detection in Hyperspectral Imagery. In Proceedings of the 2009 Ninth International Conference on Intelligent Systems Design and Applications, Pisa, Italy, 30 November–2 December 2009; pp. 596–601. [Google Scholar]
- Matteoli, S.; Veracini, T.; Diani, M.; Corsini, G. Background Density Nonparametric Estimation With Data-Adaptive Bandwidths for the Detection of Anomalies in Multi-Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2014, 11, 163–167. [Google Scholar] [CrossRef]
- Tidhar, G.A.; Rotman, S.R. Anomaly and target detection by means of nonparametric density estimation. In Proceedings of the SPIE, Baltimore, MD, USA, 23–24 April 2012; pp. 625–636. [Google Scholar]
- Banerjee, A.; Burlina, P.; Meth, R. Fast Hyperspectral Anomaly Detection via SVDD. In Proceedings of the 2007 IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; Volume 4, pp. IV-101–IV-104. [Google Scholar]
- Theiler, J.; Foy, B.R. EC-GLRT: Detecting Weak Plumes in Non–Gaussian Hyperspectral Clutter Using an Elliptically-Contoured Generalized Likelihood Ratio Test. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 1, pp. I-221–I-224. [Google Scholar]
- Theiler, J.; Zimmer, B.; Ziemann, A. Closed-Form Detector for Solid Sub-Pixel Targets in Multivariate T-Distributed Background Clutter. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2773–2776. [Google Scholar]
- Bengio, Y.; Courville, A.; Vincent, P. Representation Learning: A Review and New Perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 45, 1798–1828. [Google Scholar] [CrossRef]
- Cai, J.; Candès, E.J.; Shen, Z. A Singular Value Thresholding Algorithm for Matrix Completion. SIAM J. Optim. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1463–1474. [Google Scholar] [CrossRef]
- Sun, W.; Liu, C.; Li, J.; Lai, Y.K.; Li, W. Low-rank and sparse matrix decomposition-based anomaly detection for hyperspectral imagery. J. Appl. Remote Sens. 2014, 8, 1–18. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Peng, Y.; Ma, Y. Robust Principal Component Analysis: Exact Recovery of Corrupted Low-Rank Matrices via Convex Optimization. In Proceedings of the 22th NIPS, Vancouver, BC, Canada, 7–10 December 2009; pp. 2080–2088. [Google Scholar]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly Detection in Hyperspectral Images Based on Low-Rank and Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust Recovery of Subspace Structures by Low-Rank Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Simultaneous Joint Sparsity Model for Target Detection in Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2011, 8, 676–680. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A Low-Rank and Sparse Matrix Decomposition-Based Mahalanobis Distance Method for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 11376–11389. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Du, Q. Low-rank and sparse decomposition with mixture of gaussian for hyperspectral anomaly detection. IEEE Trans. Cybern. 2021, 51, 4363–4372. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Du, Q. Transferred Deep Learning for Anomaly Detection in Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 597–601. [Google Scholar] [CrossRef]
- Bati, E.; Alper Koz, A.; Aydin Alatan, A. Hyperspectral anomaly detection method based on auto-encoder. In Proceedings of the SPIE, Toulouse, France, 21–24 September 2015; pp. 220–226. [Google Scholar]
- Fan, G.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Hyperspectral Anomaly Detection With Robust Graph Autoencoders. IEEE Trans. Geosci. Remote Sens. 2021; in press. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, W.; Huang, J. Exploiting Embedding Manifold of Autoencoders for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1527–1537. [Google Scholar] [CrossRef]
- An, J.; Sungzoon, C. Variational autoencoder based anomaly detection using reconstruction probability. Spec. Lect. IE 2015, 2, 1–18. [Google Scholar]
- Lei, J.; Fang, S.; Xie, W.; Li, Y.; Chang, C. Discriminative Reconstruction for Hyperspectral Anomaly Detection With Spectral Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7406–7417. [Google Scholar] [CrossRef]
- Kiran, B.R.; Thomas, D.M.; Parakkal, R. An overview of deep learning based methods for unsupervised and semi-supervised anomaly detection in videos. J. Imaging 2018, 4, 36. [Google Scholar] [CrossRef] [Green Version]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. β-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. In Proceedings of the 5th ICLR, Toulon, France, 24–26 April 2017. [Google Scholar]
- Chen, R.T.Q.; Li, X.; Grosse, R.B.; Duvenaud, D.K. Isolating Sources of Disentanglement in Variational Autoencoders. In Proceedings of the 32th NeurIPS, Montreal, QC, Canada, 3–8 December 2018; pp. 2615–2625. [Google Scholar]
- Martin Arjovsky, S.C.; Bottou, L. Wasserstein Generative Adversarial Networks. In Proceedings of the 34th ICML, Sydney, NSW, Australia, 6–11 August 2017. [Google Scholar]
- Olkin, I.; Pukelsheim, F. The distance between two random vectors with given dispersion matrices. Linear Algebra Appl. 1982, 48, 257–263. [Google Scholar] [CrossRef] [Green Version]





| Method Category | Method Characteristics | References |
|---|---|---|
| RX-based | Computing the Mahalanobis distance between the test pixel and background pixels | [15,17] |
| Density and representation-based | Discovering the spatial features and characterizing the distribution of anomalies and background pixels. | [18,23,26] |
| Matrix decompositon-based | Decomposing the original data into a low-rank background component and a sparse anomaly component. | [27,33] |
| Neural network-based | Using reconstruction error of the original data to discriminate the anomalies from the background pixels. | [34,39] |
| Data Set | GRX | CBAD | LRASR | LSMAD | LSDM-MoG | AE | RGAE | Proposed |
|---|---|---|---|---|---|---|---|---|
| Pavia City | 0.9906 | 0.9924 | 0.9824 | 0.9949 | 0.9807 | 0.9849 | 0.9292 | 0.9993 |
| Gulfport | 0.9525 | 0.9800 | 0.9534 | 0.9743 | 0.9860 | 0.9299 | 0.8959 | 0.9919 |
| Jasper Ridge | 0.8777 | 0.9634 | 0.9467 | 0.9741 | 0.9368 | 0.9579 | 0.8251 | 0.9968 |
| Average | 0.9403 | 0.9786 | 0.9608 | 0.9811 | 0.9678 | 0.9576 | 0.8834 | 0.9960 |
| Data Set | CBAD | LRASR | LSMAD | LSDM-MoG | RGAE | Proposed |
|---|---|---|---|---|---|---|
| Pavia City | ||||||
| Gulfport | ||||||
| Jasper Ridge |
| Data Set | GRX | CBAD | LRASR | LSMAD | LSDM-MoG | AE | RGAE | Proposed |
|---|---|---|---|---|---|---|---|---|
| Pavia City | 2.87 | 3.15 | 132.95 | 10.83 | 39.42 | 56.11 | 145.33 | 3.12 |
| Gulfport | 0.76 | 0.88 | 23.04 | 8.40 | 14.88 | 36.56 | 91.18 | 6.19 |
| Jasper Ridge | 0.77 | 1.26 | 27.24 | 11.54 | 14.38 | 30.93 | 95.17 | 3.6 |
| Average | 1.47 | 1.76 | 61.08 | 10.26 | 22.89 | 41.20 | 110.56 | 4.30 |
| Component | Pavia | Gulfport | Jasper Ridge | Average |
|---|---|---|---|---|
| PDRD without PR (using reconstruction error of VAE) | 0.9350 | 0.6432 | 0.6812 | 0.7531 |
| PDRD without PR (using AE) | 0.9130 | 0.9186 | 0.8855 | 0.9057 |
| PDRD without CN | 0.9753 | 0.9868 | 0.9764 | 0.9795 |
| PDRD without MLF | 0.9971 | 0.9906 | 0.9925 | 0.9934 |
| PDRD | 0.9993 | 0.9919 | 0.9968 | 0.9960 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Li, X.; Chen, S.; Zhao, L. Exploring the Intrinsic Probability Distribution for Hyperspectral Anomaly Detection. Remote Sens. 2022, 14, 441. https://doi.org/10.3390/rs14030441
Yu S, Li X, Chen S, Zhao L. Exploring the Intrinsic Probability Distribution for Hyperspectral Anomaly Detection. Remote Sensing. 2022; 14(3):441. https://doi.org/10.3390/rs14030441
Chicago/Turabian StyleYu, Shaoqi, Xiaorun Li, Shuhan Chen, and Liaoying Zhao. 2022. "Exploring the Intrinsic Probability Distribution for Hyperspectral Anomaly Detection" Remote Sensing 14, no. 3: 441. https://doi.org/10.3390/rs14030441
APA StyleYu, S., Li, X., Chen, S., & Zhao, L. (2022). Exploring the Intrinsic Probability Distribution for Hyperspectral Anomaly Detection. Remote Sensing, 14(3), 441. https://doi.org/10.3390/rs14030441







