Location and Extraction of Telegraph Poles from Image Matching-Based Point Clouds
Abstract
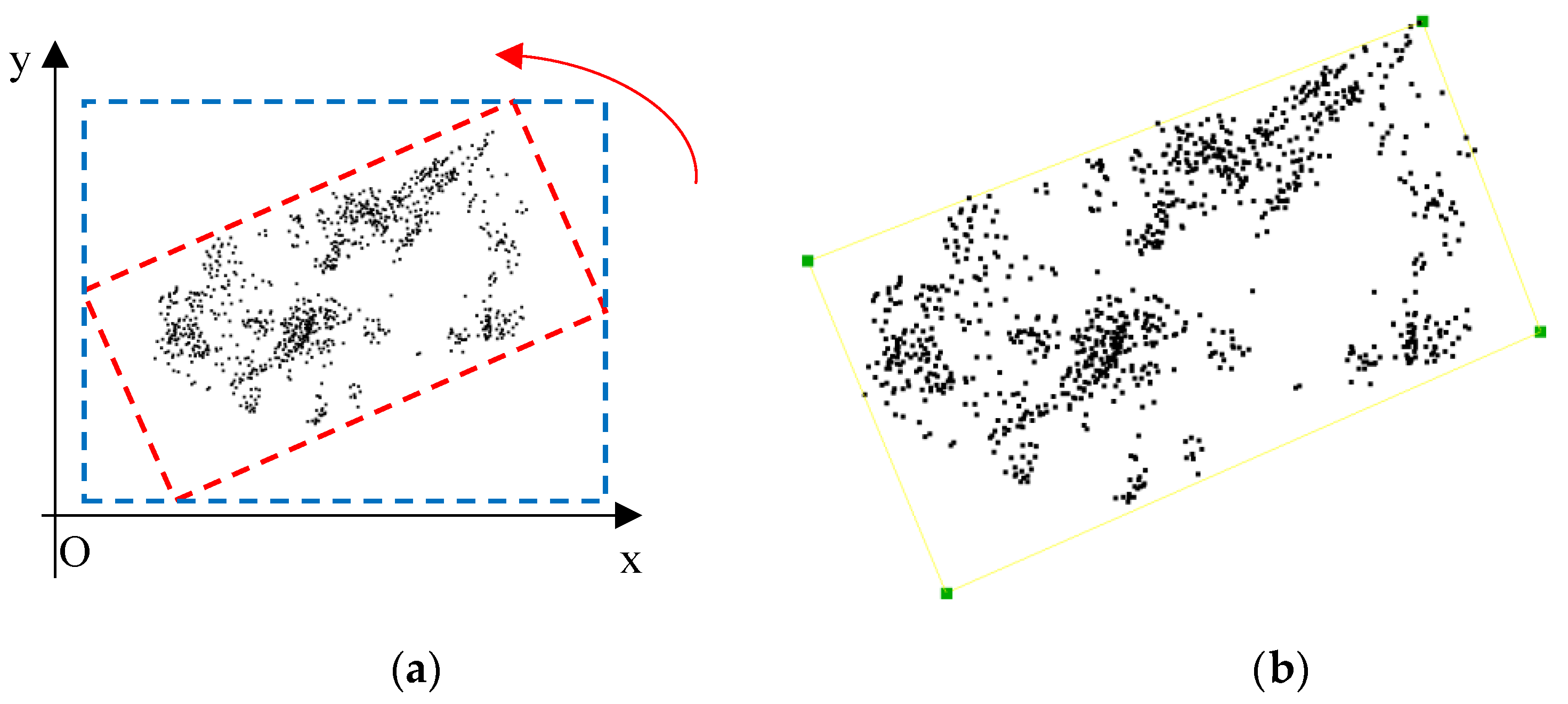
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Methodology
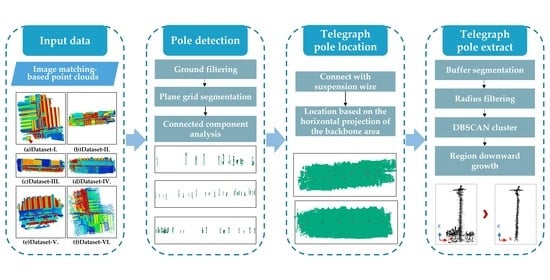
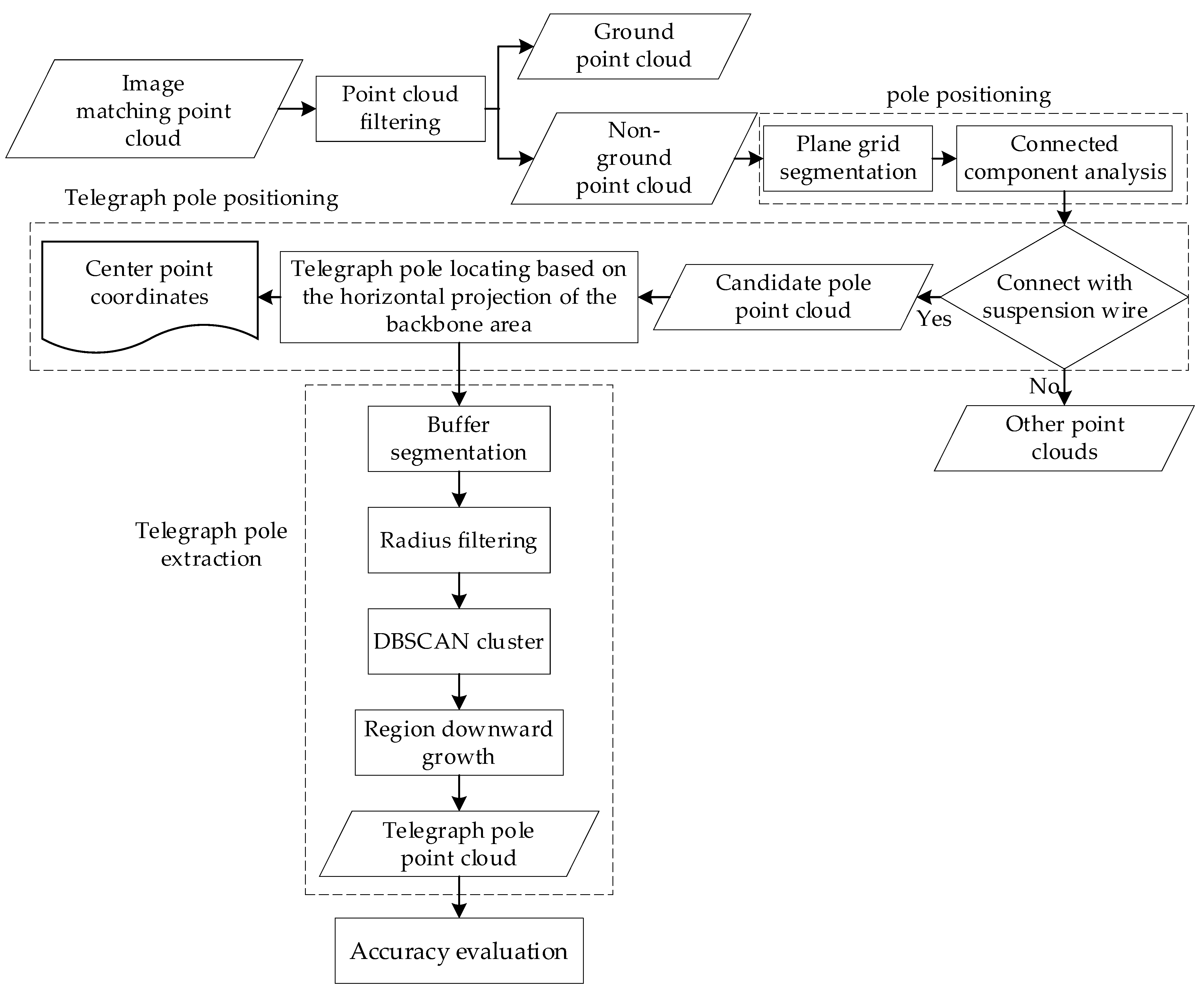
2.2.1. Pole Detection
- 1.
- Determining the seed grid: select the highest grid as the seed grid, and employ its number in the x, y, and z-axis directions as the grid coordinates ;
- 2.
- Take the seed grid as the center. If the five-neighbor (front, back, left, right, and bottom) grid contains the point cloud data, continue to compare the number of points in the grid with the threshold. If it is greater than the threshold, merge the points in the and grids, and push the grid coordinates . into the stack;
- 3.
- Select a grid from the stack and take it as the seed grid in the first step, and repeat the second step;
- 4.
- Repeat steps ②~③ until the stack becomes empty, and then complete the extraction of the point cloud-connected grid in a single plane grid.
2.2.2. Candidate Telegraph Pole Locating Based on Suspension Point in the Buffer Area
- The pole’s central point is taken as the center of the circle and the point cloud between a certain distance as the point cloud of the buffer.
- The buffer point cloud is divided into n layers at a specific interval Δz along the z-axis, while the number of points in each layer is counted.
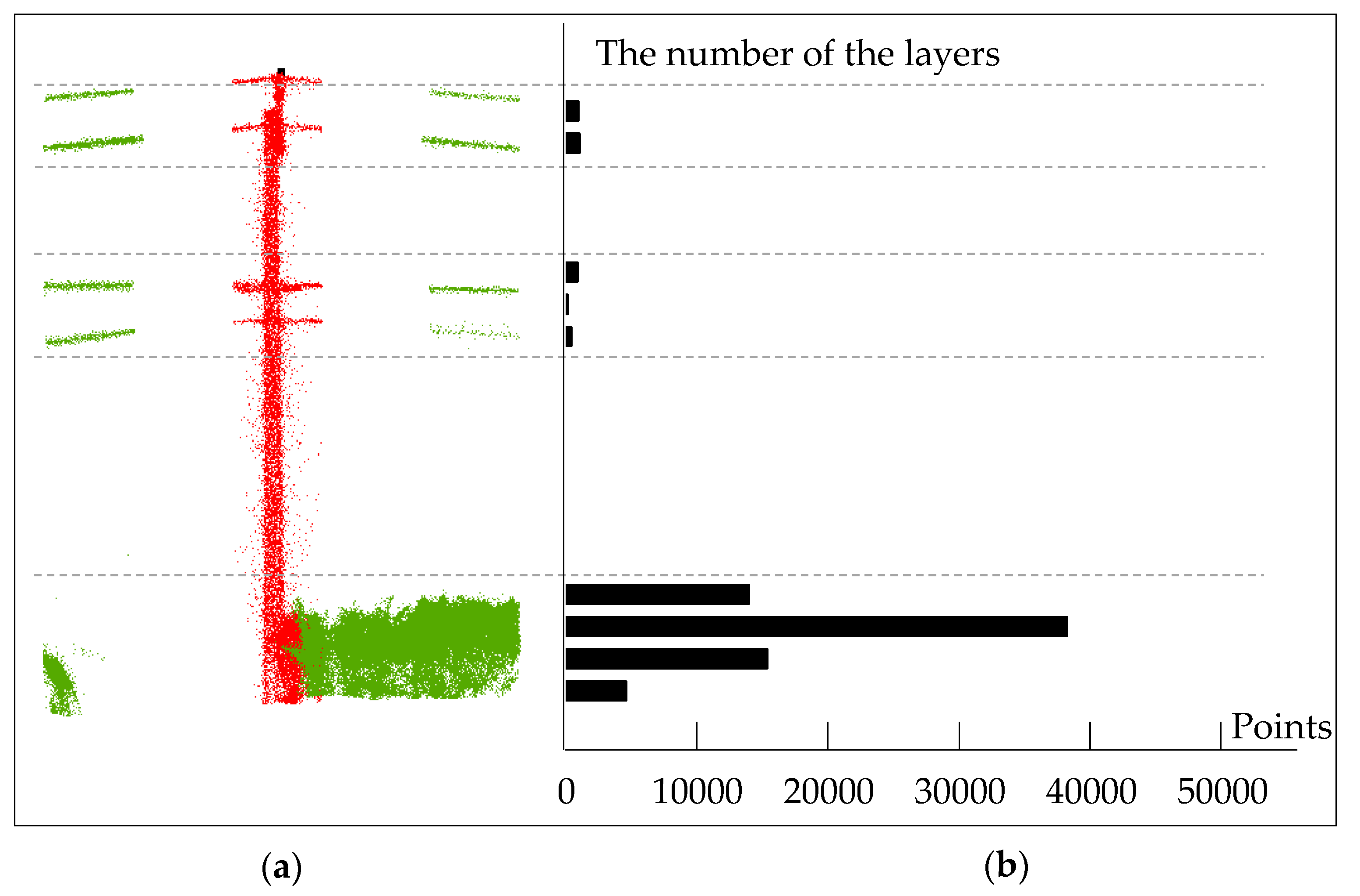
- Scan the points of each level from the top layer down. If the number of point clouds in the continuous local layer satisfies the rule of “greater than threshold-empty-greater than threshold-empty-greater than threshold”, the pole corresponding to the buffer zone is regarded as a candidate telegraph pole.
2.2.3. Telegraph Pole Locating Based on the Horizontal Projection of the Backbone Area
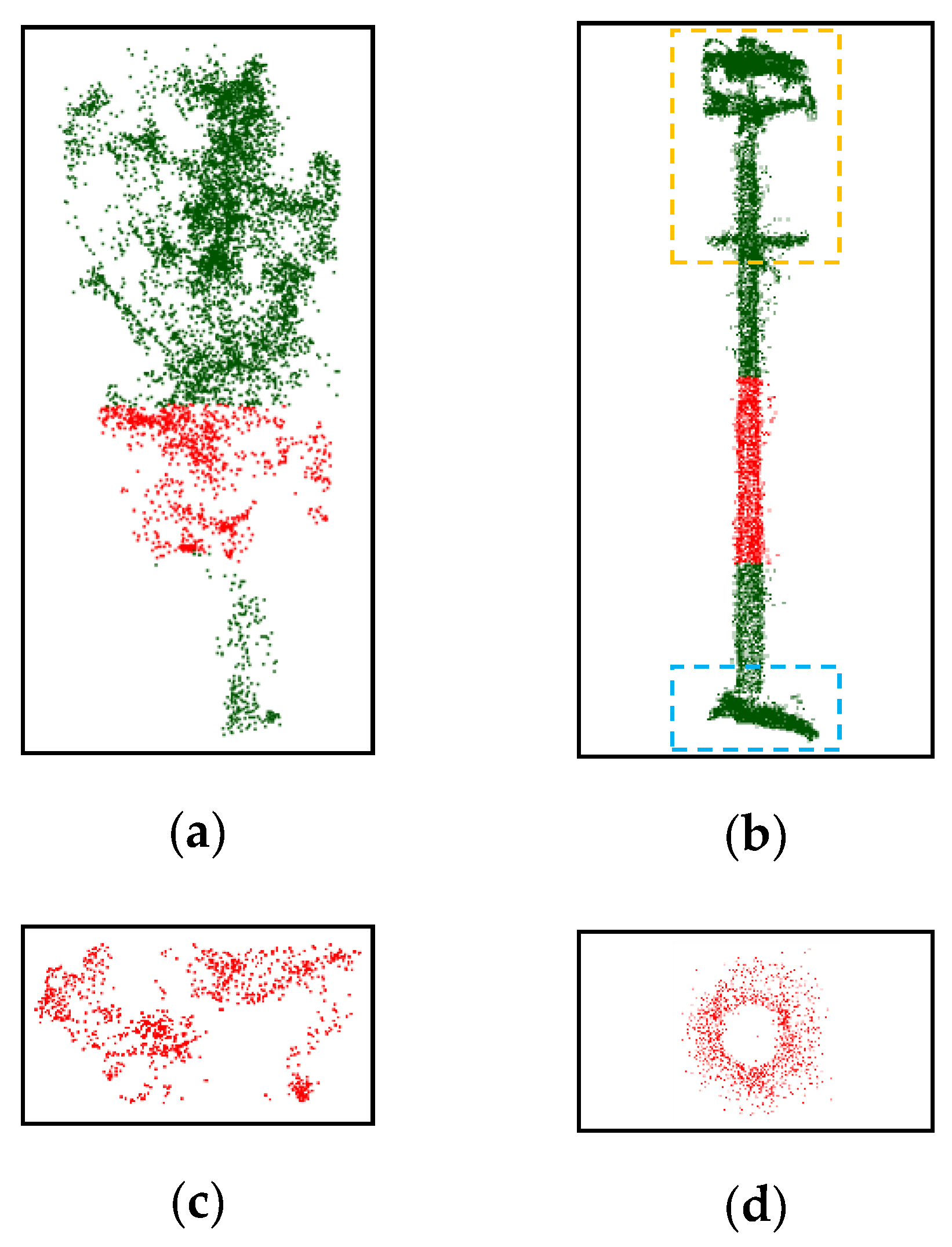
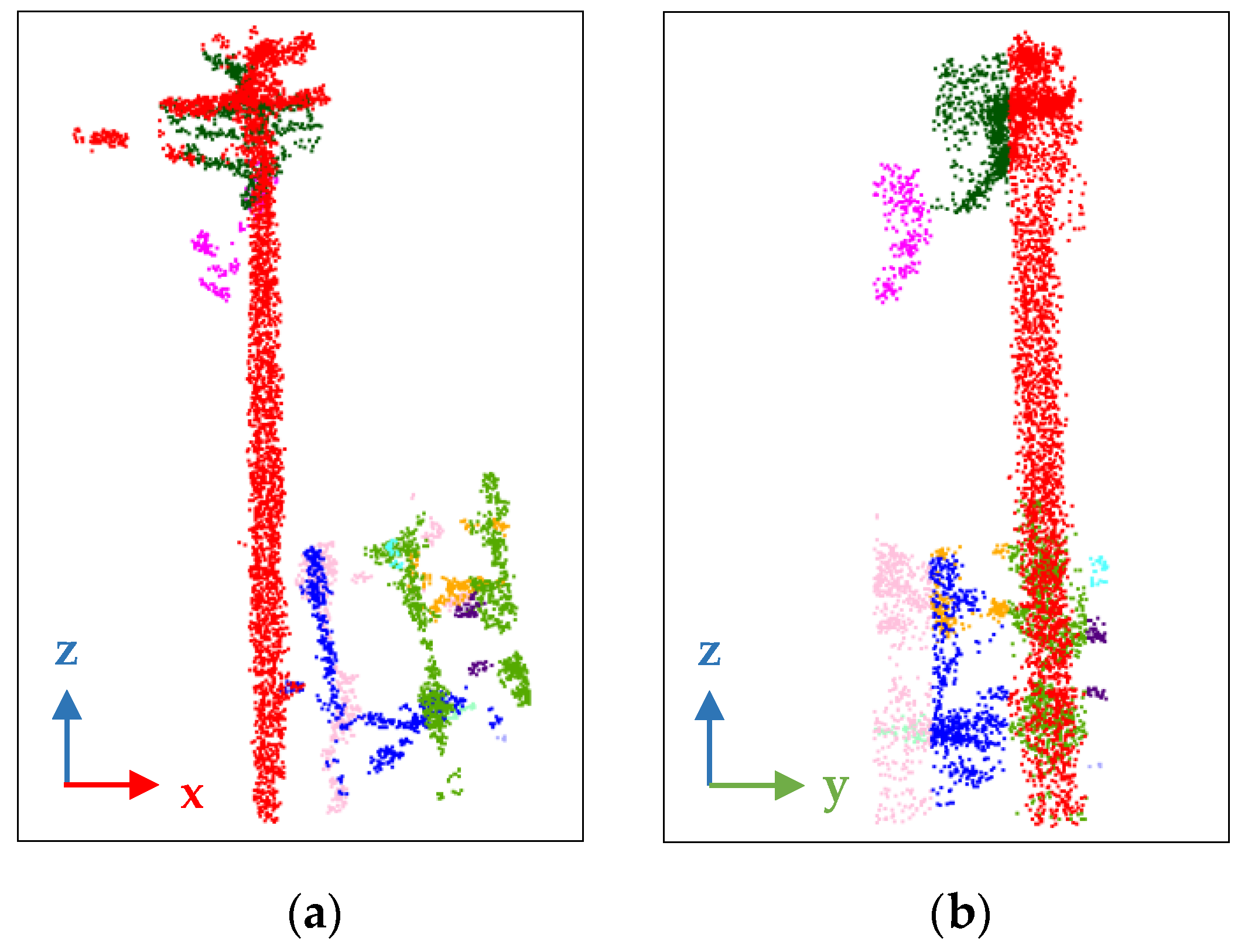
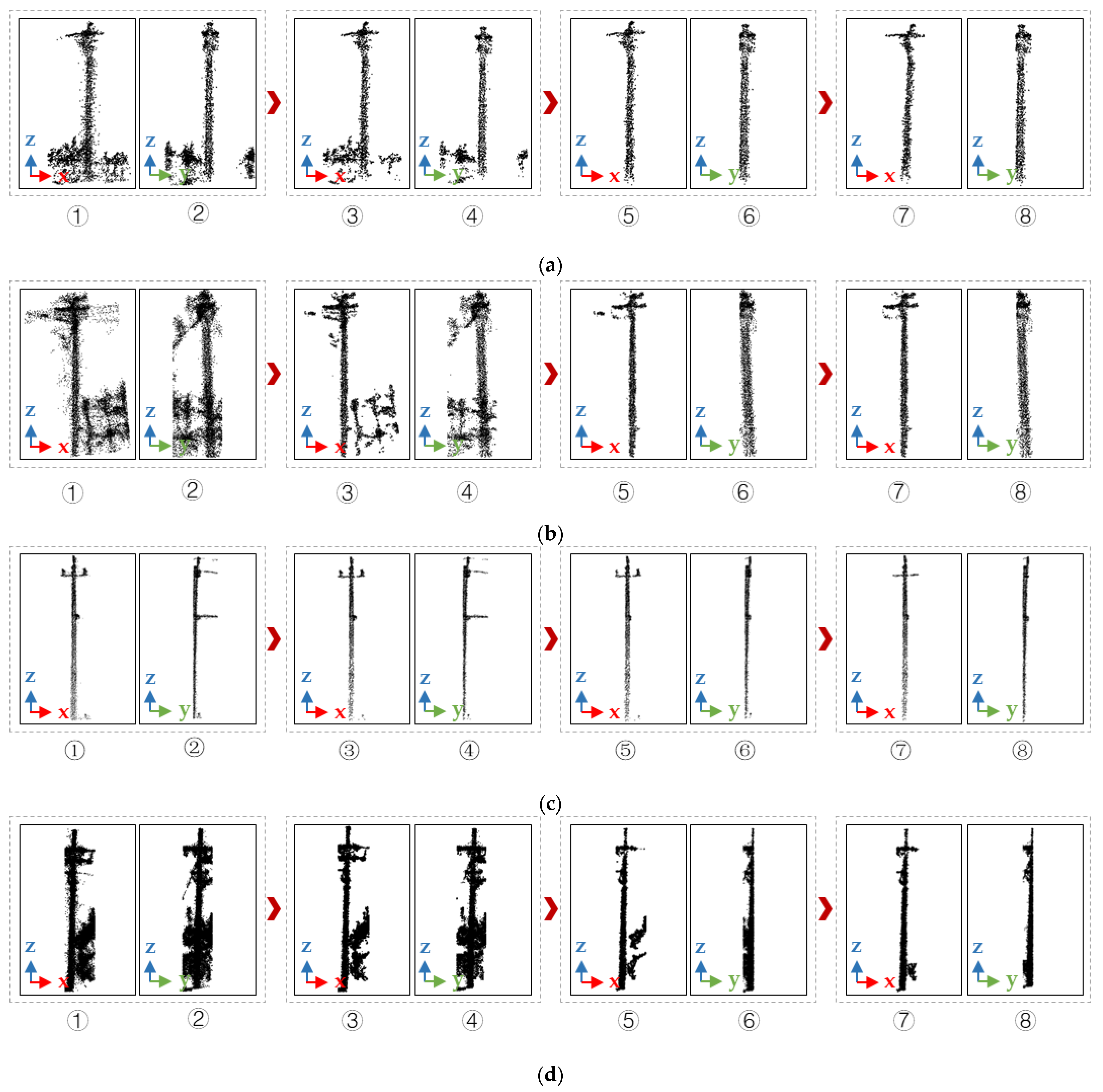
2.2.4. Telegraph Pole Extraction Based on DBSCAN Algorithm
- (1)
- The buffer segmentation:
- (2)
- Radius filtering:
- (3)
- DBSCAN clustering:
- (4)
- Region downward growth:
2.2.5. Accuracy Evaluation
- (1)
- Telegraph pole locating
- (2)
- Telegraph pole extraction
3. Results
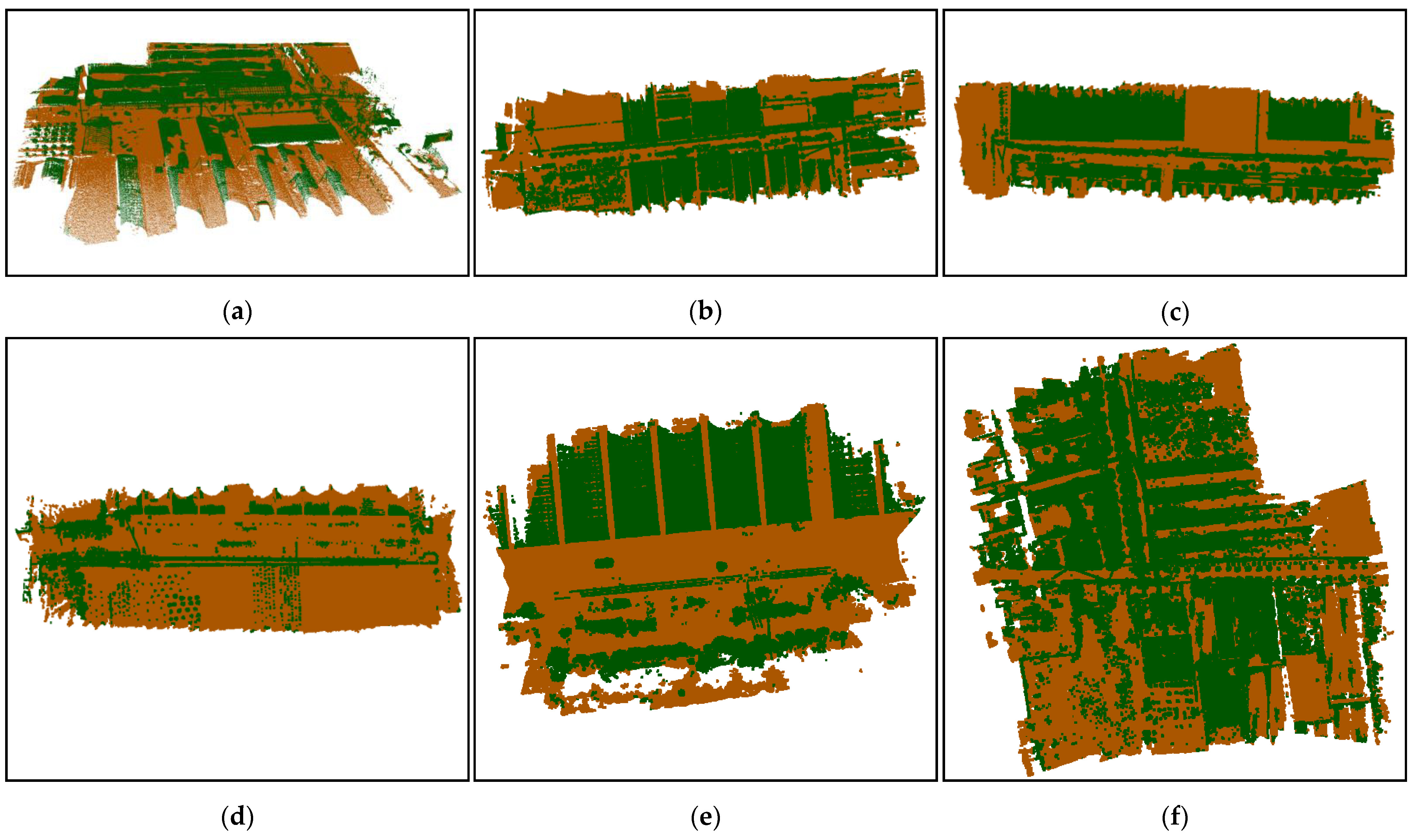
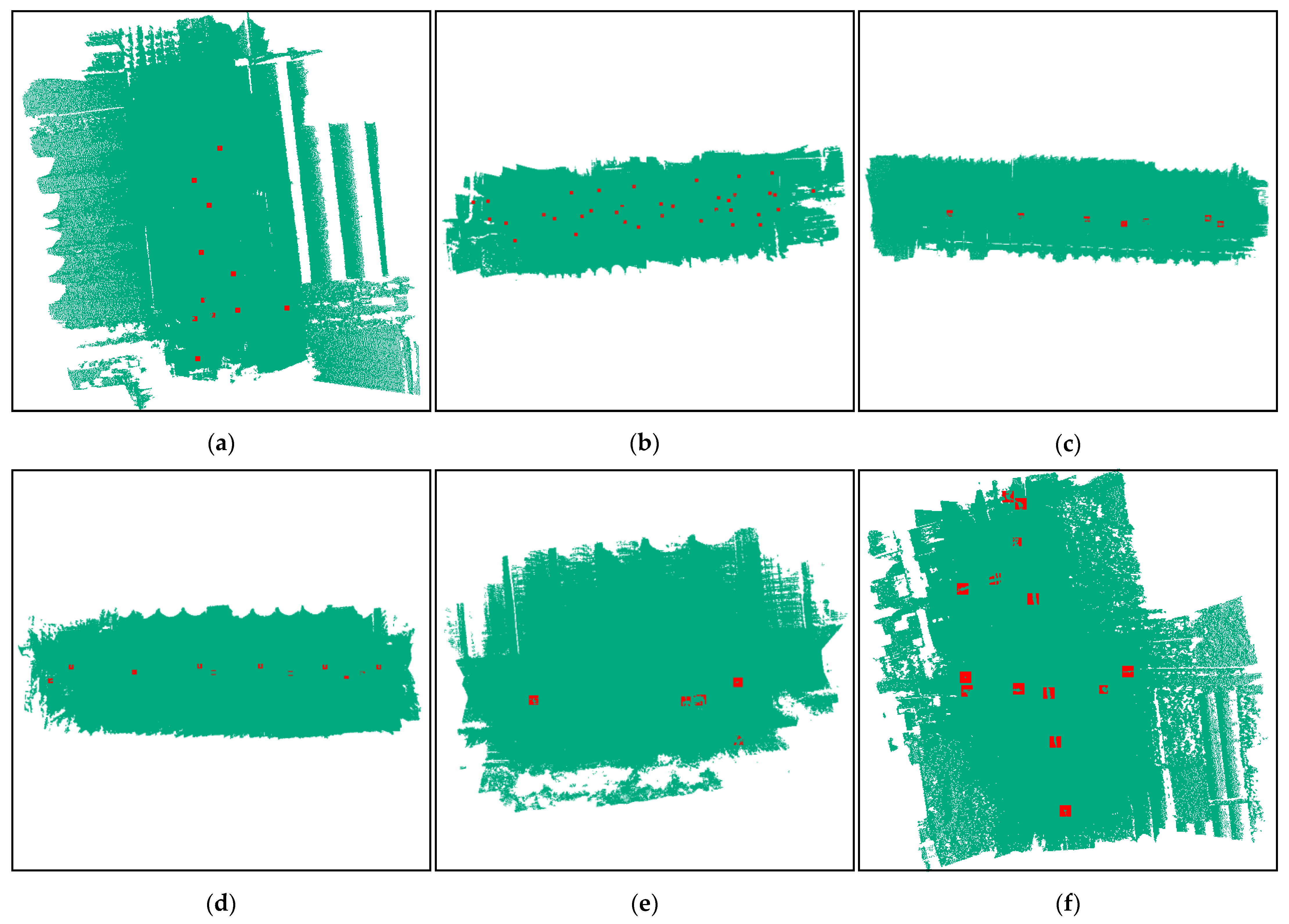
3.1. Telegraph Pole Location Result
- (1)
- Pole detection result
- (2)
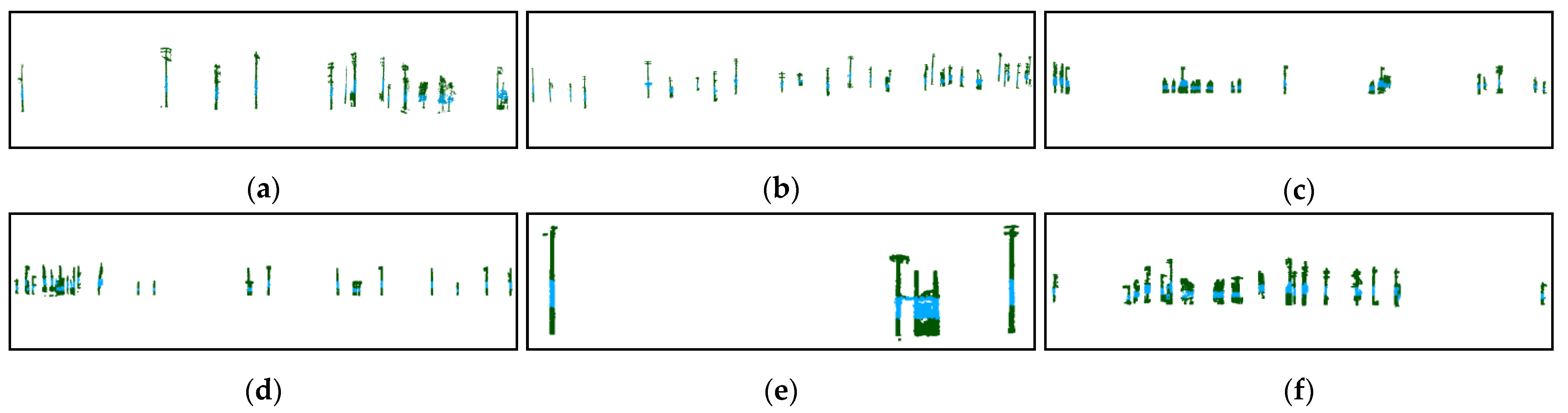
- Result of candidate telegraph pole location
- (3)
- Telegraph pole location result
- (4)
- Quantitative evaluation
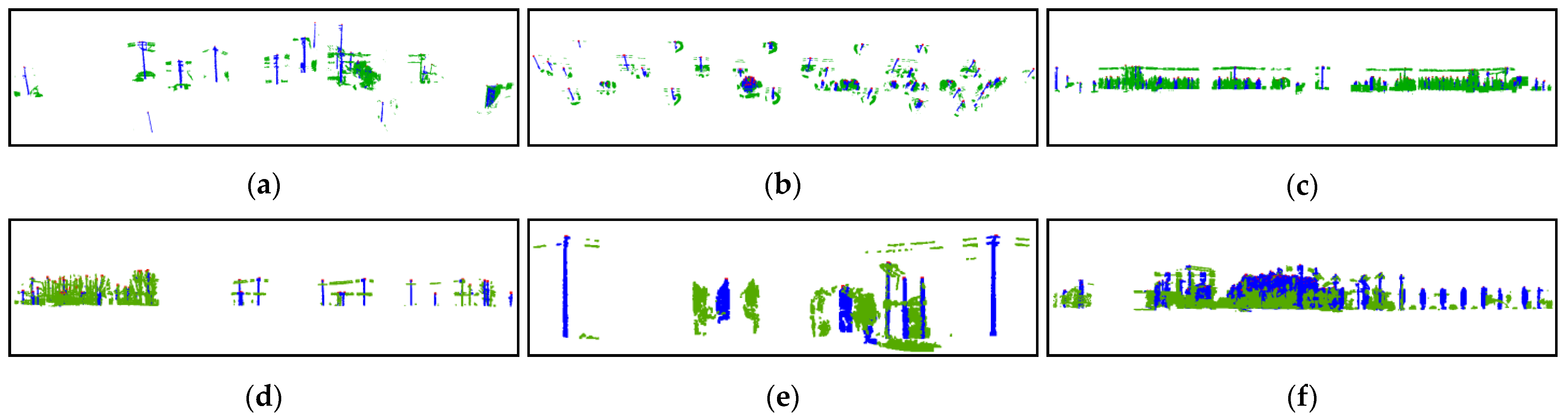
3.2. Telegraph Pole Extraction Results
4. Discussion
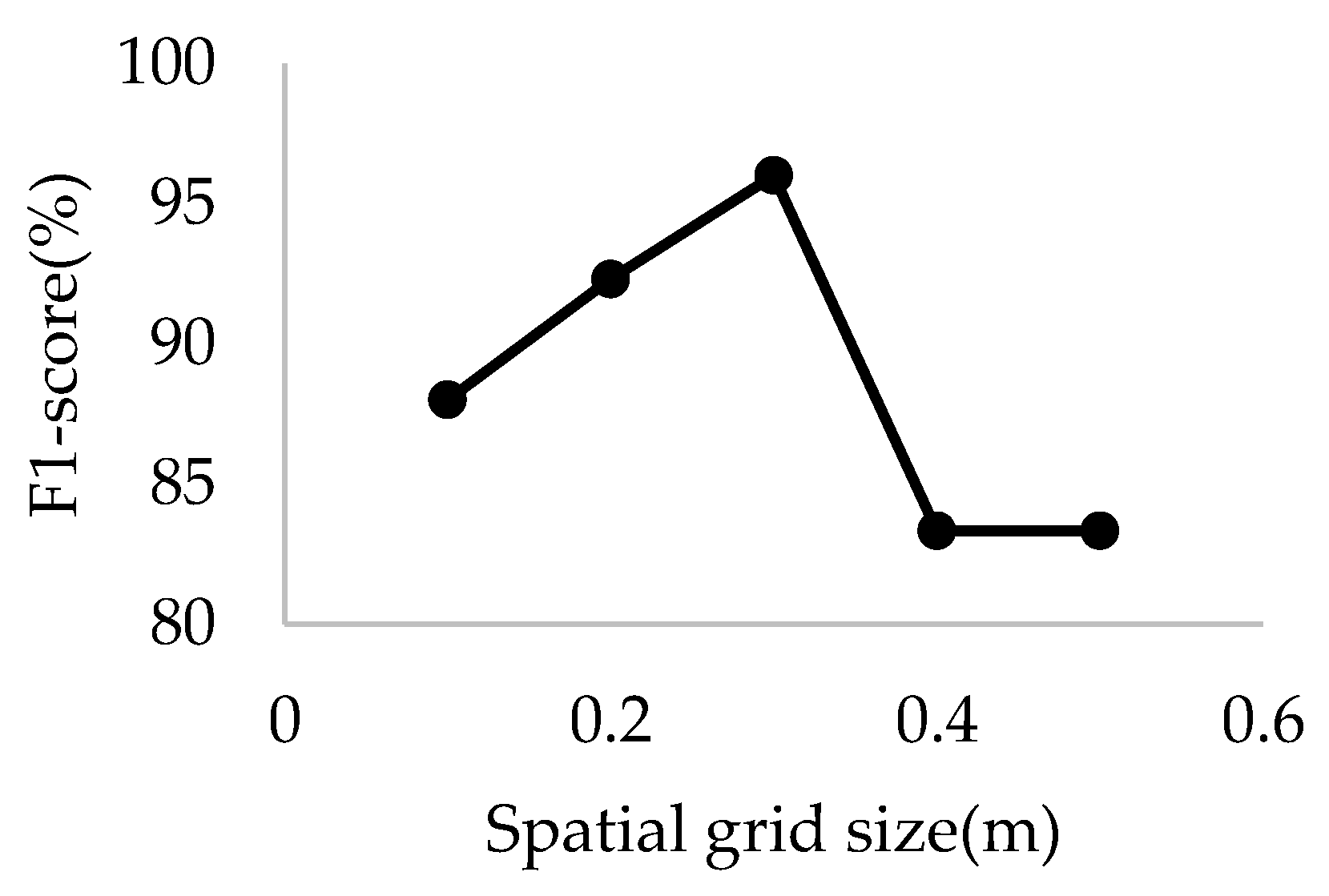
4.1. The Influence of the Length, Width, and Height of the Spatial Grid on Pole Detection
4.2. The Influence of Buffer Distance Threshold on the Telegraph Pole Locating
4.3. The Influence of Radius on the Telegraph Pole Extraction
5. Conclusions
- (1)
- Assuming that the top of the pole is connected to the power suspension line, the telegraph pole point cloud is clearly distinguished from that of other poles, which effectively removes interfering ground objects and guarantees the recall rate of the telegraph pole detection effectively.
- (2)
- Assuming that the horizontal projection area of the tree canopy is larger than the telegraph pole, the tree point cloud is further filtered out to improve the extraction accuracy.
- (3)
- Compared with the point cloud collected by LiDAR, point cloud generation based on dense image matching reduces the cost, and it is suitable for popularization and application in distribution network inspection.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guo, B.; Huang, X.; Li, Q.; Zhang, F.; Zhu, J.; Wang, C. A stochastic geometry method for pylon reconstruction from airborne lidar data. Remote Sens. 2016, 8, 243. [Google Scholar] [CrossRef] [Green Version]
- Conde, B.; Villarino, A.; Cabaleiro, M.; Gonzalez-Aguilera, D. Geometrical issues on the structural analysis of transmission electricity towers thanks to laser scanning technology and finite element method. Remote Sens. 2015, 7, 11551–11569. [Google Scholar] [CrossRef] [Green Version]
- You, A.; Wang, X.; Han, X.; Tang, D. Applications of LiDAR in patrolling electric-power lines. In Proceedings of the 2013 The International Conference on Technological Advances in Electrical, Electronics and Computer Engineering (TAEECE), Konya, Turkey, 9–11 May 2013; pp. 110–114. [Google Scholar]
- Qin, X.; Wu, G.; Lei, J.; Fan, F.; Ye, X. Detecting inspection objects of power line from cable inspection robot LiDAR data. Sensors 2018, 18, 1284. [Google Scholar] [CrossRef] [Green Version]
- Rhee, S.; Kim, T. Dense 3D point cloud generation from UAV images from image matching and global optimazation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 41, 1005. [Google Scholar] [CrossRef] [Green Version]
- Rosnell, T.; Honkavaara, E. Point cloud generation from aerial image data acquired by a quadrocopter type micro unmanned aerial vehicle and a digital still camera. Sensors 2012, 12, 453–480. [Google Scholar] [CrossRef] [Green Version]
- Rothermel, M.; Haala, N. Potential of dense matching for the generation of high quality digital elevation models. In Proceedings of the ISPRS Workshop High-Resoultion Earth Imaging for Geospatial Information; ISPRS: Hannover, Germany, 2011. [Google Scholar]
- Kang, Z.; Yang, J.; Zhong, R.; Wu, Y.; Shi, Z.; Lindenbergh, R. Voxel-based extraction and classification of 3-D pole-like objects from mobile LiDAR point cloud data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4287–4298. [Google Scholar] [CrossRef]
- Teo, T.-A.; Chiu, C.-M. Pole-like road object detection from mobile lidar system using a coarse-to-fine approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 4805–4818. [Google Scholar] [CrossRef]
- Yadav, M.; Lohani, B.; Singh, A.K.; Husain, A. Identification of pole-like structures from mobile lidar data of complex road environment. Int. J. Remote Sens. 2016, 37, 4748–4777. [Google Scholar] [CrossRef]
- Yan, W.Y.; Morsy, S.; Shaker, A.; Tulloch, M. Automatic extraction of highway light poles and towers from mobile LiDAR data. Opt. Laser Technol. 2016, 77, 162–168. [Google Scholar] [CrossRef]
- Yan, L.; Li, Z.; Liu, H.; Tan, J.; Zhao, S.; Chen, C. Detection and classification of pole-like road objects from mobile LiDAR data in motorway environment. Opt. Laser Technol. 2017, 97, 272–283. [Google Scholar] [CrossRef]
- McCulloch, J.; Green, R. Extraction of utility poles in LIDAR scans using cross-sectional slices. In Proceedings of the 2016 International Conference on Image and Vision Computing New Zealand (IVCNZ), Palmerston North, New Zealand, 21–22 November 2016; pp. 1–4. [Google Scholar]
- Yang, J.; Kang, Z.; Akwensi, P.H. A skeleton-based hierarchical method for detecting 3-D pole-like objects from mobile LiDAR point clouds. IEEE Geosci. Remote Sens. Lett. 2018, 16, 801–805. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Li, X.; Xie, L.; Wang, Y.; Guo, R.; Xiu, W.; Tang, S. Pole-like street furniture segmentation and classification in mobile LiDAR data by integrating multiple shape-descriptor constraints. Remote Sens. 2019, 11, 2920. [Google Scholar] [CrossRef] [Green Version]
- Yu, Y.; Guan, H.; Li, D.; Jin, S.; Chen, T.; Wang, C.; Li, J. 3-D feature matching for point cloud object extraction. IEEE Geosci. Remote Sens. Lett. 2019, 17, 322–326. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, H.; Li, Y.; Wu, Z.; Mao, J.; Liu, Y. Streetlamp extraction and identification from mobile LiDAR point cloud scenes. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1468–1471. [Google Scholar]
- Shi, Z.; Kang, Z.; Lin, Y.; Liu, Y.; Chen, W. Automatic recognition of pole-like objects from mobile laser scanning point clouds. Remote Sens. 2018, 10, 1891. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.; Yang, B.; Xiao, W.; Liang, F.; Liu, Y.; Wang, Z. Automatic extraction of high-voltage power transmission objects from UAV lidar point clouds. Remote Sens. 2019, 11, 2600. [Google Scholar] [CrossRef] [Green Version]
- Li, Q.; Chen, Z.; Hu, Q. A model-driven approach for 3D modeling of pylon from airborne LiDAR data. Remote Sens. 2015, 7, 11501–11524. [Google Scholar] [CrossRef] [Green Version]
- Guan, H.; Yu, Y.; Li, J.; Ji, Z.; Zhang, Q. Extraction of power-transmission lines from vehicle-borne lidar data. Int. J. Remote Sens. 2016, 37, 229–247. [Google Scholar] [CrossRef]
- Shen, X.; Qian, C.; Du, Y.; Yu, X.; Zhang, R. An automatic extraction algorithm of high voltage transmission lines from airborne LIDAR point cloud data. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 2043–2055. [Google Scholar] [CrossRef]
- Peng, X.; Song, S.; Qian, J.; Chen, C.; Wang, K.; Yang, Y.; Zheng, X. Research on Automatic Positioning Algorithm of Power Transmission Towers Based on UAV LiDAR. Power Syst. Technol. 2017, 41, 3670–3677. [Google Scholar]
- Ye, L.; Liu, Q.; Hu, Q. Research of power line fitting and extraction techniques based on LiDAR point cloud data. Geomat. Spat. Inf. Technol. 2010, 5, 30–34. [Google Scholar]
- Jwa, Y.; Sohn, G. A piecewise catenary curve model growing for 3D power line reconstruction. Photogramm. Eng. Remote Sens. 2012, 78, 1227–1240. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, C.; Xi, X.; Wang, P.; Tian, X.; Yang, X. Hierarchical threshold adaptive for point cloud filter algorithm of moving surface fitting. Acta Geod. Et Cartogr. Sin. 2018, 47, 153–160. [Google Scholar]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD’96), Portland, OR, USA, 2–4 August 1996. [Google Scholar]
- Chen, M.; Wu, J.; Liu, L.; Zhao, W.; Tian, F.; Shen, Q.; Zhao, B.; Du, R. DR-Net: An improved network for building extraction from high resolution remote sensing image. Remote Sens. 2021, 13, 294. [Google Scholar] [CrossRef]
- Zhu, L.; Zhang, Y.; Wang, J.; Tian, W.; Liu, Q.; Ma, G.; Kan, X.; Chu, Y. Downscaling Snow Depth Mapping by Fusion of Microwave and Optical Remote-Sensing Data Based on Deep Learning. Remote Sens. 2021, 13, 584. [Google Scholar] [CrossRef]



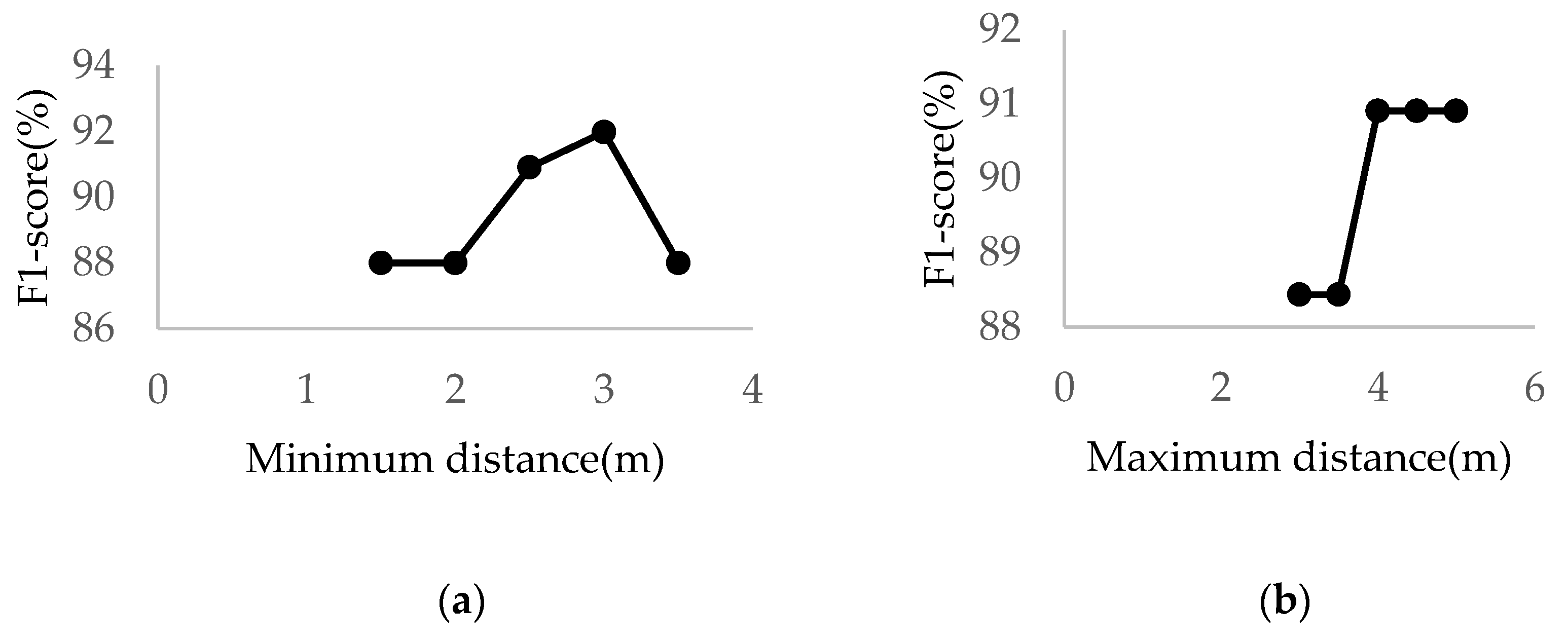
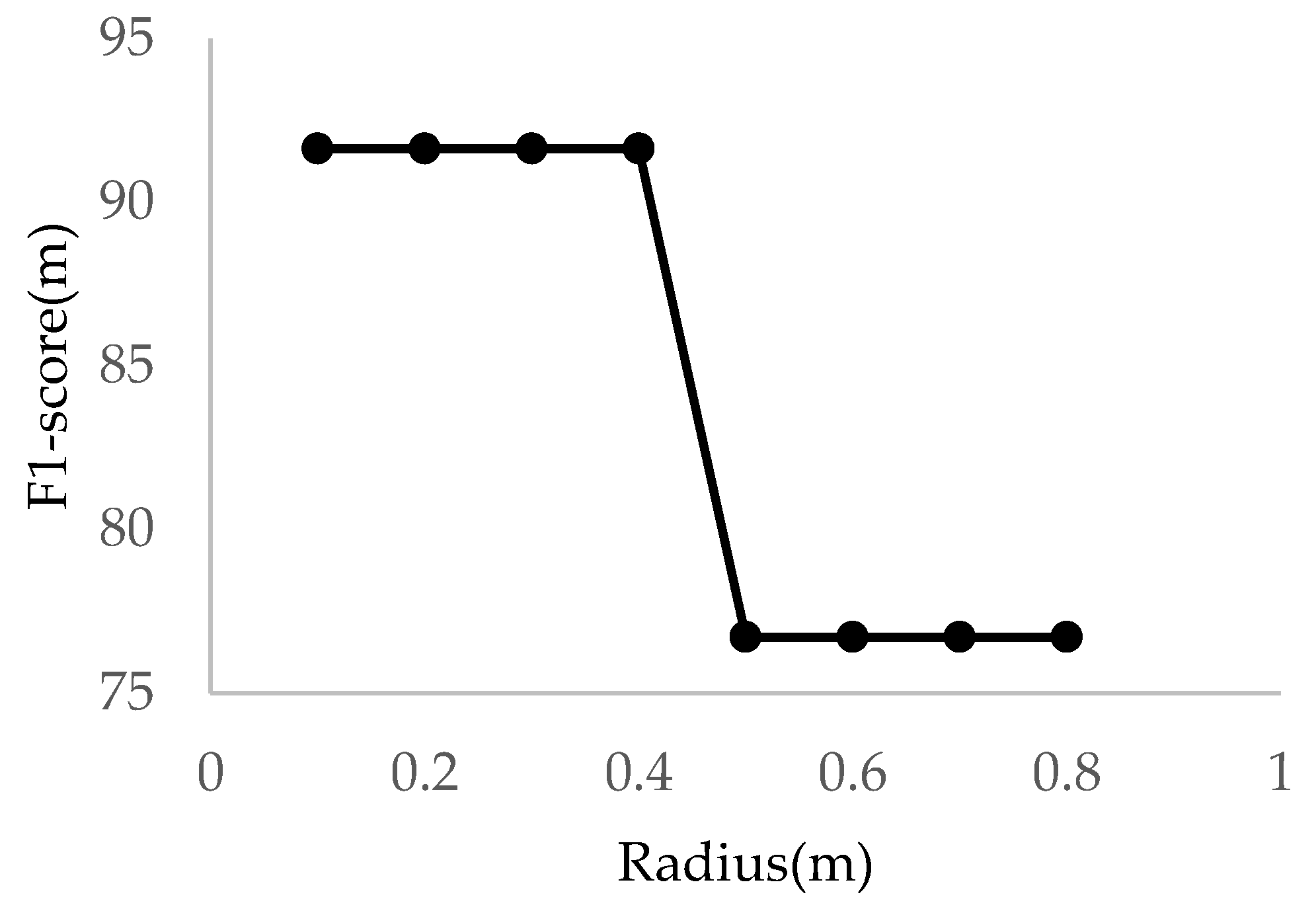
| Dataset Number | Area (m2) | Number of Points | Number of Telegraph Poles | Number of Telegraph Pole Points |
|---|---|---|---|---|
| Dataset-I | 171 × 171 | 2,015,500 | 11 | 26,370 |
| Dataset-II | 248 × 801 | 32,059,123 | 35 | 255,031 |
| Dataset-III | 310 × 87 | 3,213,093 | 7 | 20,614 |
| Dataset-IV | 252 × 84 | 1,238,186 | 12 | 13,225 |
| Dataset-V | 104 × 73 | 2,043,145 | 5 | 17,435 |
| Dataset-VI | 251 × 253 | 10,018,042 | 13 | 46,966 |
| Dataset Number | TP | FP | FN | Recall (%) | Precision (%) | F1-Score (%) |
|---|---|---|---|---|---|---|
| Dataset-I | 10 | 1 | 1 | 90.91 | 90.91 | 90.91 |
| Dataset-II | 33 | 3 | 2 | 94.29 | 91.67 | 92.96 |
| Dataset-III | 6 | 1 | 1 | 85.71 | 85.71 | 85.71 |
| Dataset-IV | 10 | 1 | 2 | 83.33 | 90.91 | 86.96 |
| Dataset-V | 5 | 0 | 0 | 100.00 | 100.00 | 100.00 |
| Dataset-VI | 12 | 2 | 1 | 92.31 | 85.71 | 88.89 |
| Dataset Number | Minimum (m) | Maximum (m) | Average (m) | RMSE (m) |
|---|---|---|---|---|
| Dataset-I | 0.078782 | 1.02 | 0.50 | 0.59 |
| Dataset-II | 0.038589 | 1.34 | 0.32 | 0.43 |
| Dataset-III | 0.225596 | 1.05 | 0.53 | 0.63 |
| Dataset-IV | 0.022969 | 0.50 | 0.20 | 0.23 |
| Dataset-V | 0.096417 | 0.41 | 0.25 | 0.50 |
| Dataset-VI | 0.066732 | 1.10 | 0.43 | 0.66 |
| Step | Parameters | |
|---|---|---|
| Name | Value | |
| Buffer segmentation | Radius(m) | 5 |
| Remove filtering | Radius (m) | 0.04 |
| Minimum points | 5 | |
| DBSCAN cluster | Radius(m) | 0.4 |
| Minimum points | 5 | |
| Region growing | Grid length(m) | 0.1 |
| Grid width(m) | 0.1 | |
| Grid height(m) | 0.1 | |
| Dataset Number | TP | FP | FN | Recall (%) | Precision (%) | F1-Score (%) | Total Times |
|---|---|---|---|---|---|---|---|
| Dataset-I | 23,603 | 1951 | 2767 | 89.51 | 92.37 | 90.91 | 0.90 |
| Dataset-II | 215,796 | 21,484 | 19,840 | 91.58 | 90.95 | 91.26 | 29.64 |
| Dataset-III | 18,417 | 1935 | 1371 | 93.07 | 90.49 | 91.76 | 0.53 |
| Dataset-IV | 9378 | 1016 | 1069 | 89.77 | 90.23 | 90.00 | 0.39 |
| Dataset-V | 16,194 | 427 | 1241 | 92.88 | 97.43 | 95.10 | 1.10 |
| Dataset-VI | 39,436 | 2950 | 3950 | 90.90 | 93.04 | 91.96 | 3.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, C.; Xi, X.; Wang, P.; Du, M.; Nie, S. Location and Extraction of Telegraph Poles from Image Matching-Based Point Clouds. Remote Sens. 2022, 14, 433. https://doi.org/10.3390/rs14030433
Wang J, Wang C, Xi X, Wang P, Du M, Nie S. Location and Extraction of Telegraph Poles from Image Matching-Based Point Clouds. Remote Sensing. 2022; 14(3):433. https://doi.org/10.3390/rs14030433
Chicago/Turabian StyleWang, Jingru, Cheng Wang, Xiaohuan Xi, Pu Wang, Meng Du, and Sheng Nie. 2022. "Location and Extraction of Telegraph Poles from Image Matching-Based Point Clouds" Remote Sensing 14, no. 3: 433. https://doi.org/10.3390/rs14030433
APA StyleWang, J., Wang, C., Xi, X., Wang, P., Du, M., & Nie, S. (2022). Location and Extraction of Telegraph Poles from Image Matching-Based Point Clouds. Remote Sensing, 14(3), 433. https://doi.org/10.3390/rs14030433