A Study on Pseudorange Biases in BDS B1I/B3I Signals and the Impacts on Beidou Wide Area Differential Services
Abstract
:1. Introduction
2. Pseudorange Bias in WADS
2.1. Calculation Method for Pseudorange Bias
2.2. Pseudorange Bias in WADS Parameters
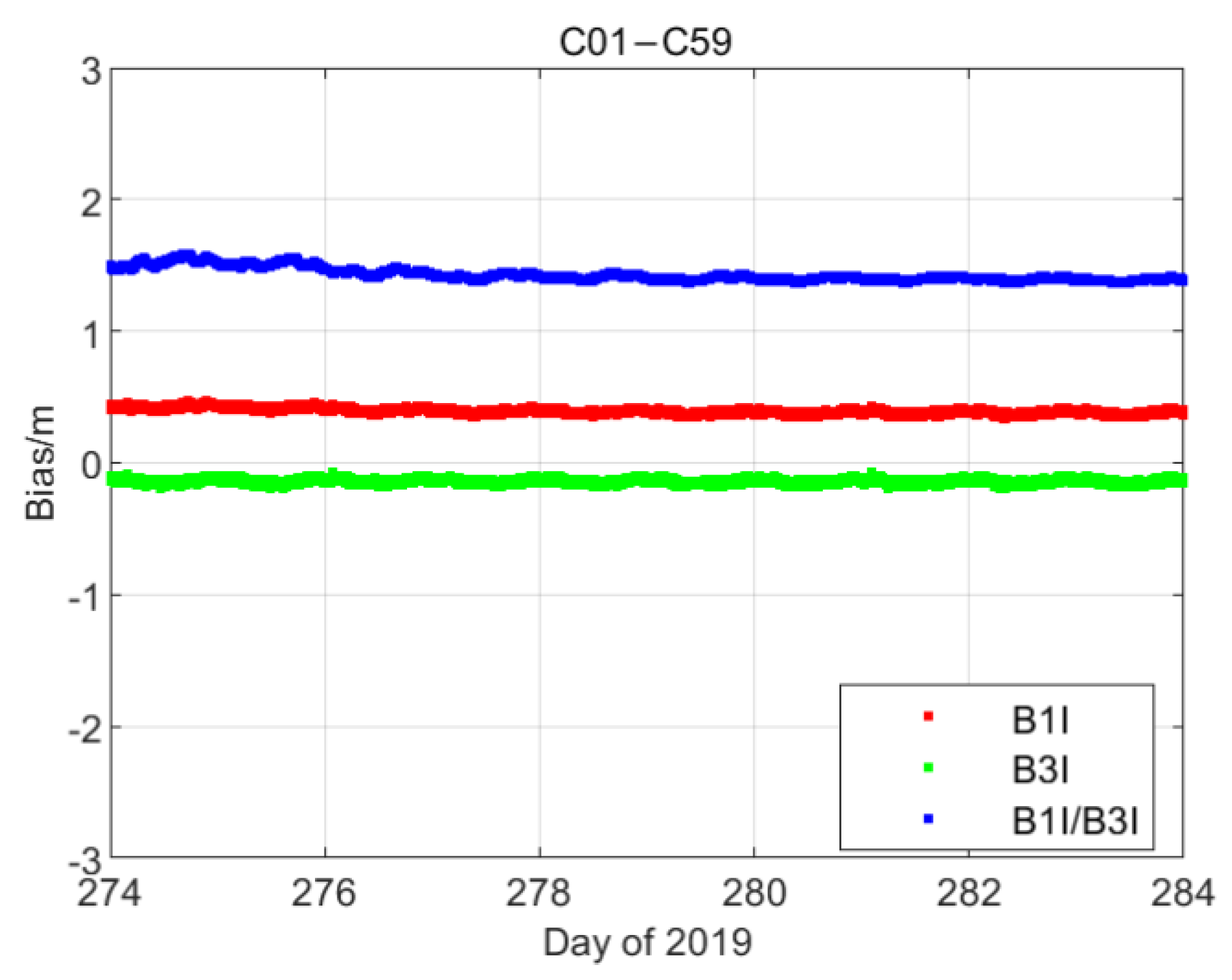
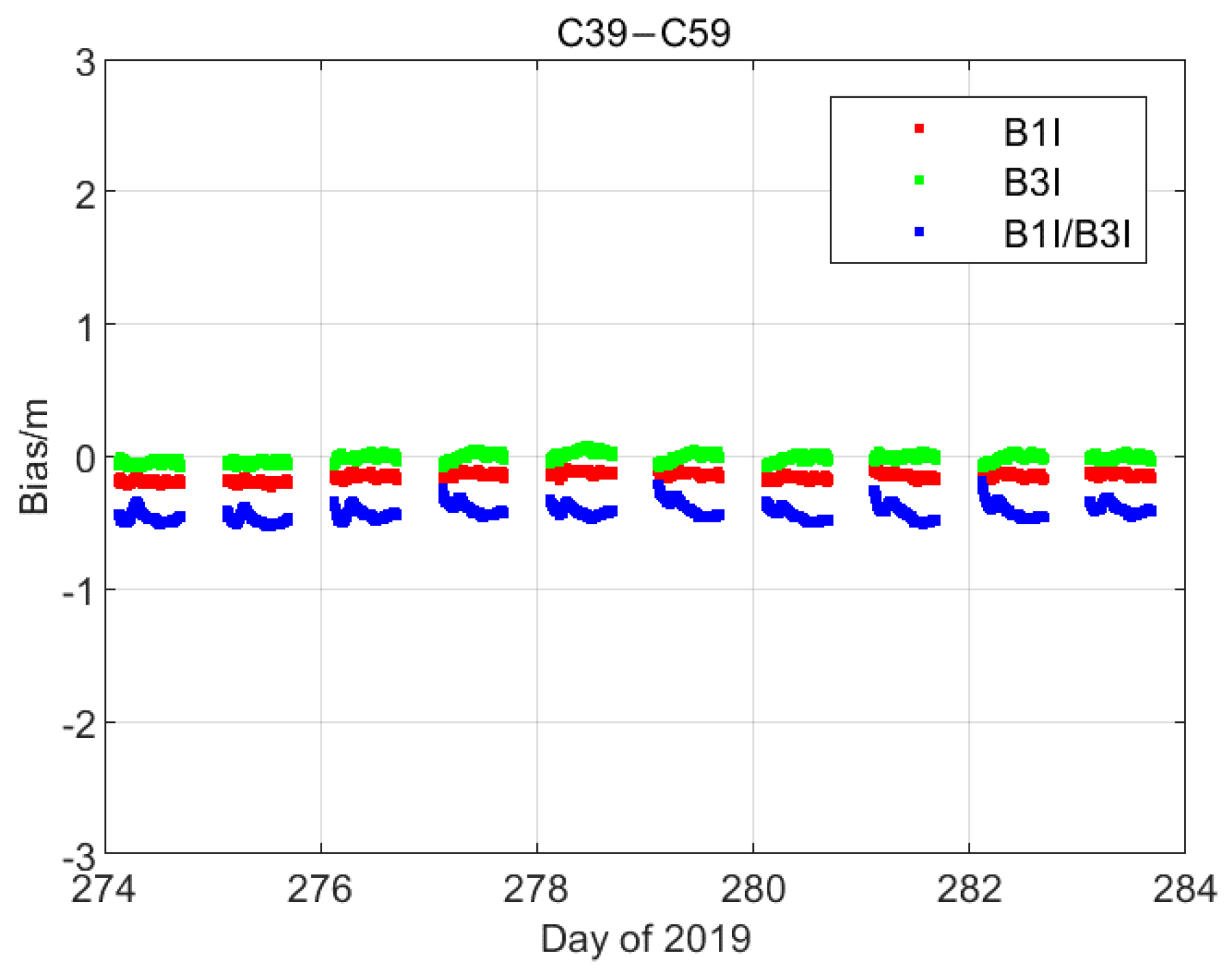
2.3. Pseudorange Bias in BDS Signal (B1/B3I)
3. Influence and Improvement for Pseudorange Bias
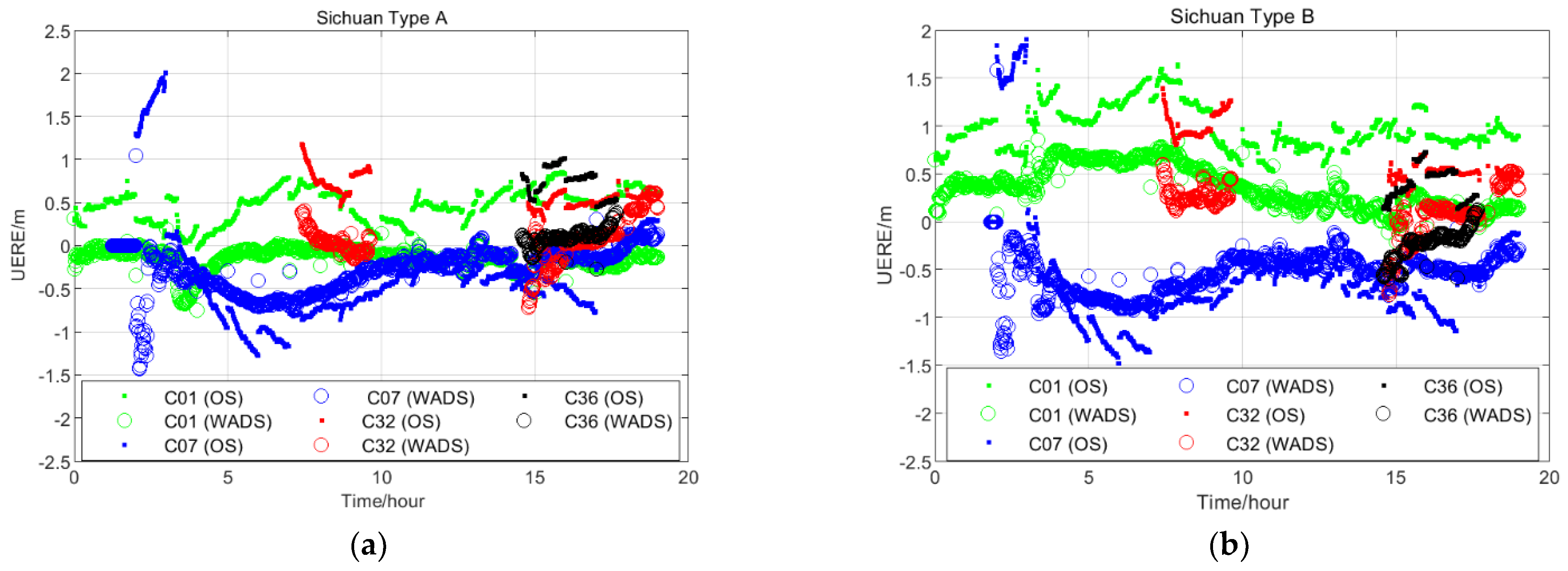
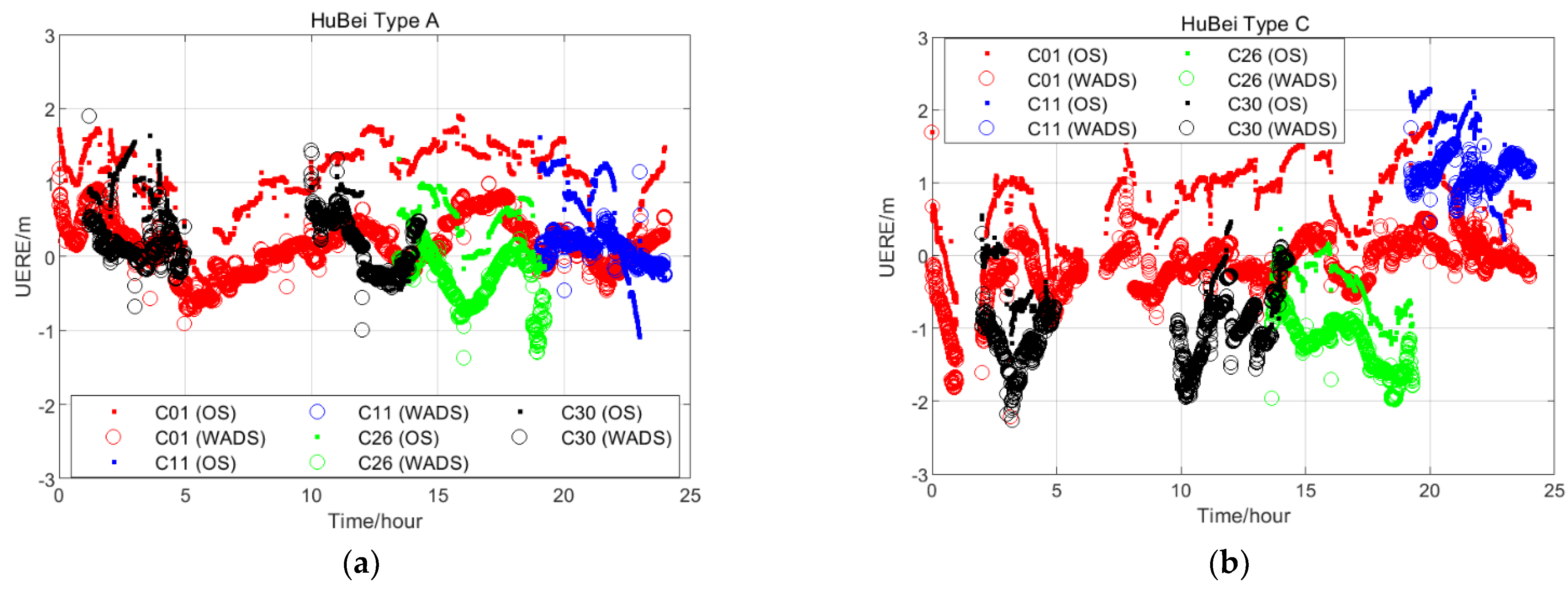
3.1. Influence on UERE and UDRE
3.2. Influence on Position Accuracy
3.3. Improvement after Deducting Pseudorange Bias
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Cheolsoon, L.; Byungwoon, P.; Changdon, K.; Youngsun, Y. Benefit of SFMC SBAS and its Performance Assessment for WAAS, EGNOS, and MSAS. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), 21–25 September 2020; pp. 1099–1131. [Google Scholar]
- Johnson, G.; Dhungana, G.; Delisle, J. An Evaluation of WAAS 2020+ to Meet Maritime Navigation Require-ments in Canadian Waters. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 855–875. [Google Scholar]
- Bauer, F.; Greze, G.; Haddad, F.; Tourtier, A.; Rols, B.; Urbanska, K. A Study on a New EGNOS V2 Release with Enhanced System Performances. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019; pp. 902–919. [Google Scholar]
- Sunda, S.; Sridharan, R.; Vyas, B.M.; Khekale, P.V.; Parikh, K.P.; Ganeshan, A.S.; Sudhir, C.S.; Satish, S.V.; Bagiya, M.S. Satellite-based augmentation systems: A novel and cost-effective tool for ionospheric and space weather studies. Space Weather Int. J. Res. Appl. 2015, 13, 6–15. [Google Scholar] [CrossRef]
- Luciano, T.; Andrea, D.C.C.W.; Pozzobon, O.; Serrano, G.F.; Calabrese, A.; Perring, A.; Mabilleau, M.; Vecchione, G. Broadcast Data Authentication Concepts for Future SBAS Ser-vices. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), 25–28 January 2020; pp. 1–26. [Google Scholar]
- Cheolsoon, L.; Donghyun, S.; Hwang, H.-Y.; Park, B.; Kim, E.; Kee, C.; Seo, S.; Park, J. Performance Analysis on Multi-Constellation SBAS of the Modified L1-only SBAS Message. In Proceedings of the 30th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 1089–1094. [Google Scholar]
- Grewal, M.S. Space-based augmentation for global navigation satellite systems. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2012, 59, 497–503. [Google Scholar] [CrossRef] [PubMed]
- Felski, A.; Nowak, A. On Egnos Monitoring in Local Conditions. Artif. Satell. 2013, 48, 85–92. [Google Scholar] [CrossRef] [Green Version]
- Felski, A.; Nowak, A.; Woźniak, T. Accuracy and Availability of Egnos-Results of Observations" Artificial Satellites. Artif. Satell. 2011, 46, 111–118. [Google Scholar] [CrossRef] [Green Version]
- Nandulal, S.; Rao, C.B.; Indi, C.L.; Irulappan, M.; Arulmozhi, S.; Soma, P. Evaluation of real-time position accuracy and LNAV/VNAV service availability of GAGAN SBAS (Wide Area Differential GPS) over Indian region. In Proceedings of the 2008 Tyrrhenian International Workshop on Digital Communications—Enhanced Surveillance of Aircraft and Vehicles, Capri, Italy, 3–5 September 2008; pp. 1–6. [Google Scholar] [CrossRef]
- CSNO. BeiDou Navigation Satellite System Signal B3I (Version 3.0) [EB/OL]. 2019. Available online: http://www.beidou.gov.cn.2020.02 (accessed on 30 December 2020).
- Liu, J.-L.; Cao, Y.-L.; Hu, X.-G.; Tang, C.-P. Beidou wide-area augmentation system clock error correction and performance verification. Adv. Space Res. 2020, 65, 2348–2359. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Hauschild, A. Broadcast versus precise ephemerides: A multi-GNSS perspective. GPS Solut. 2014, 19, 321–333. [Google Scholar] [CrossRef]
- Steigenberger, P.; Montenbruck, O. Galileo status: Orbits, clocks, and positioning. GPS Solut. 2017, 21, 319–331. [Google Scholar] [CrossRef]
- Chen, J.; Hu, X.; Tang, C.; Zhou, S.; Yang, Y.; Pan, J.; Ren, H.; Ma, Y.; Tian, Q.; Wu, B.; et al. SIS accuracy and service performance of the BDS-3 basic system. Sci. China Phys. Mech. Astron. 2020, 63, 269511. [Google Scholar] [CrossRef]
- Enge, P.; Walter, T.; Pullen, S.; Kee, C.; Chao, Y.C.; Tsai, Y.J. Wide area augmentation of the Global Positioning System. Proc. IEEE 1996, 84, 1063–1088. [Google Scholar] [CrossRef]
- Phelts, R.E.; Akos, D.M.; Enge, P. Robust Signal Quality Monitoring and Detection of Evil Waveforms. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Salt Lake City, UT, USA, 19–22 September 2000; pp. 1180–1190. [Google Scholar]
- Wong, G.; Chen, Y.H.; Phelts, R.E.; Walter, T.; Enge, P. Measuring code-phase differences due to inter-satellite hardware differences. In Proceedings of the 25th international technical meeting of the satellite division of the institute of navigation (ION GNSS 2012), ION GNSS, Nashville, TN, USA, 17–21 September 2012; pp. 2150–2158. [Google Scholar]
- Wong, G.; Phelts, R.E.; Walter, T.; Enge, P. Characterization of Signal Deformations for GPS and WAAS Satellites. In Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, Portlands, OR, USA, 21–24 September 2010; pp. 3143–3151. [Google Scholar]
- Wong, G.; Phelts, R.; Eric, W.T.; Enge, P. Bounding Errors Caused by Nominal GNSS Signal Deformations. In Proceedings of the 24th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2011), Portland, OR, USA, 21–24 September 2011; pp. 2657–2664. [Google Scholar]
- Hauschild, A.; Montenbruck, O. The Effect of Correlator and Front-End Design on GNSS Pseudorange Biases for Geodetic Receivers. Navigation 2016, 63, 443–453. [Google Scholar] [CrossRef]
- Hauschild, A.; Montenbruck, O. A study on the dependency of GNSS pseudorange biases on correlator spacing. GPS Solut. 2014, 20, 159–171. [Google Scholar] [CrossRef]
- Chen, L.; Li, M.; Zhao, Y.; Zheng, F.; Shi, C. Clustering Code Biases between BDS-2 and BDS-3 Satellites and Effects on Joint Solution. Remote Sens. 2021, 13, 15. [Google Scholar] [CrossRef]
- Tang, C.; Su, C.; Hu, X.; Gao, W.; Liu, L.; Lu, J.; Chen, Y.; Liu, C.; Wang, W.; Zhou, S. Characterization of pesudorange bias and its effect on positioning for BDS satellites. Acta Geodaet. Cartograph. Sin. 2020, 49, 1131–1138. [Google Scholar]
- Li, R.; Li, Z.; Wang, N.; Tang, C.; Ma, H.; Zhang, Y.; Wang, Z.; Wu, J. Considering inter-receiver pseudorange biases for BDS-2 precise orbit determination. Measurement 2021, 177, 109251. [Google Scholar] [CrossRef]
- Sun, G.; Shen, L.; Zhu, X.; Jia, X.; Liu, X.; Guo, M.; Zhai, W.; Hong, Y.; Zheng, J. Accuracy Analysis of GNSS Broadcast Ionospheric Model. In Proceedings of the China Satellite Navigation Conference (CSNC), CSNC 2019, Beijing, China, 22–25 May 2019; Sun, J., Yang, C., Yang, Y., Eds.; Springer: Cham, Switzerland; Volume 563. [Google Scholar]


| Information from BDS WADS | Update Period | Parameter Range |
|---|---|---|
| Equivalent Clock Correction (Δt) | 18 s | −4096~4096 |
| User Differential Range Error Index (UDREI) | 3 s | 0~15 |
| Vertical Delay at Ionospheric Grid Points (dτ) | 180 s | 0~63.625 m (the coverage area is 70–145 degrees East longitude and 7.5–55 degrees North latitude, divided according to 5 × 2.5 degrees) |
| Grid Ionospheric Vertical Error Index (GIVEI) | 180 s | 0~15 |
| BDS-2 | BDS-3 | |||||||
|---|---|---|---|---|---|---|---|---|
| PRN | System Type | Satellite Type | PRN | System Type | Satellite Type | PRN | System Type | Satellite Type |
| C01 | BDS-2 | GEO | C19 | BDS-3 | MEO | C36 | BDS-3 | MEO |
| C02 | BDS-2 | GEO | C20 | BDS-3 | MEO | C37 | BDS-3 | MEO |
| C03 | BDS-2 | GEO | C21 | BDS-3 | MEO | C38 | BDS-3 | IGSO |
| C04 | BDS-2 | GEO | C22 | BDS-3 | MEO | C39 | BDS-3 | IGSO |
| C05 | BDS-2 | GEO | C23 | BDS-3 | MEO | C40 | BDS-3 | IGSO |
| C06 | BDS-2 | IGSO | C24 | BDS-3 | MEO | C41 | BDS-3 | MEO |
| C07 | BDS-2 | IGSO | C25 | BDS-3 | MEO | C42 | BDS-3 | MEO |
| C08 | BDS-2 | IGSO | C26 | BDS-3 | MEO | C43 | BDS-3 | MEO |
| C09 | BDS-2 | IGSO | C27 | BDS-3 | MEO | C44 | BDS-3 | MEO |
| C10 | BDS-2 | IGSO | C28 | BDS-3 | MEO | C45 | BDS-3 | MEO |
| C11 | BDS-2 | MEO | C29 | BDS-3 | MEO | C46 | BDS-3 | MEO |
| C12 | BDS-2 | MEO | C30 | BDS-3 | MEO | C59 | BDS-3 | GEO |
| C13 | BDS-2 | IGSO | C32 | BDS-3 | MEO | C60 | BDS-3 | GEO |
| C14 | BDS-2 | MEO | C33 | BDS-3 | MEO | C61 | BDS-3 | GEO |
| C16 | BDS-2 | IGSO | C34 | BDS-3 | MEO | |||
| C18 | BDS-2 | GEO | C35 | BDS-3 | MEO | |||
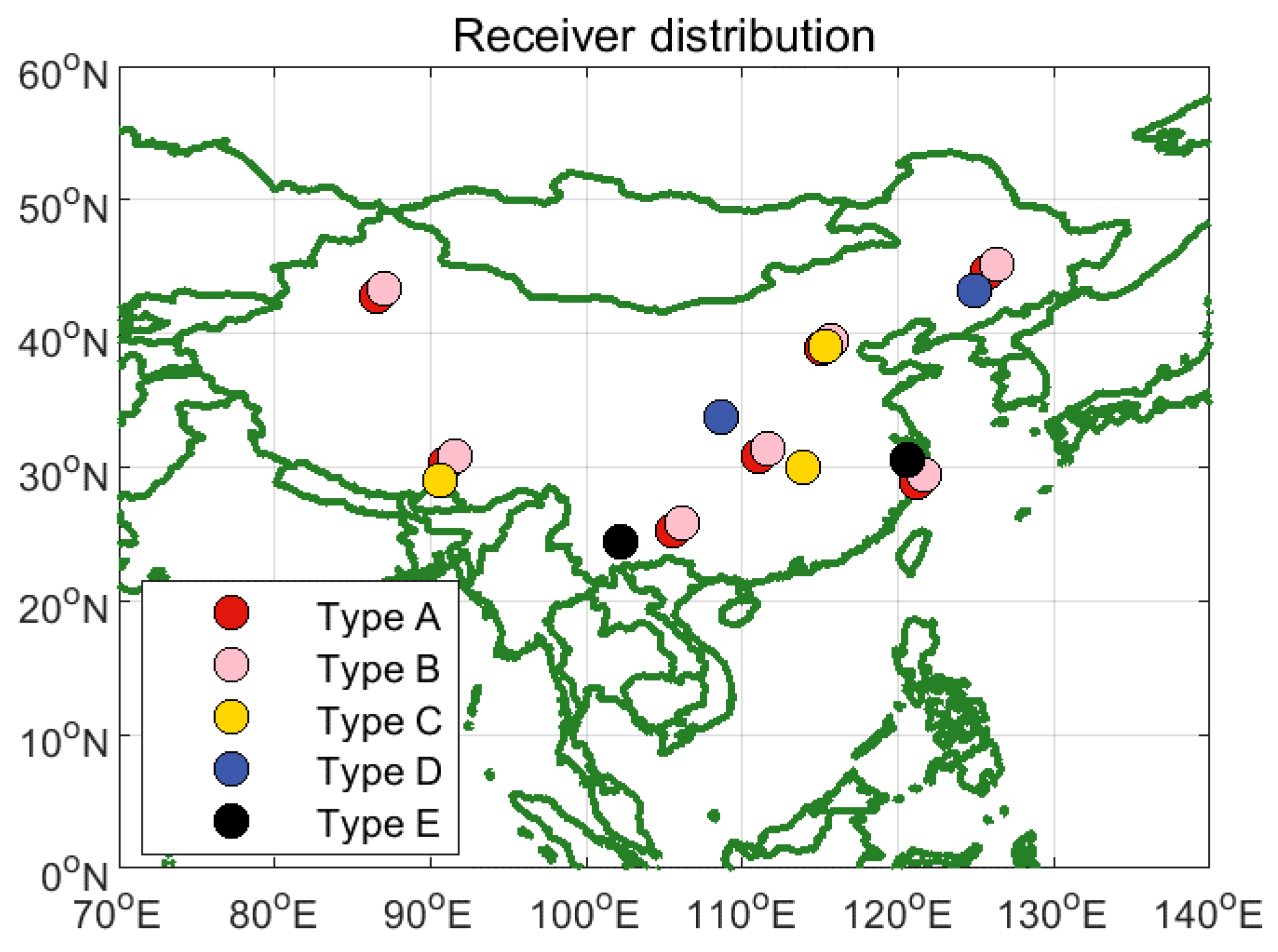
| Receiver Type | Information |
|---|---|
| A | WADS monitoring receiver |
| B | CETC-20-1 |
| C | CETC-54 |
| D | CETC-20-2 |
| E | UNICORE |
| Receiver Type | UERE (OS) | UERE (WADS) | ||
|---|---|---|---|---|
| Mean | Std | Mean | Std | |
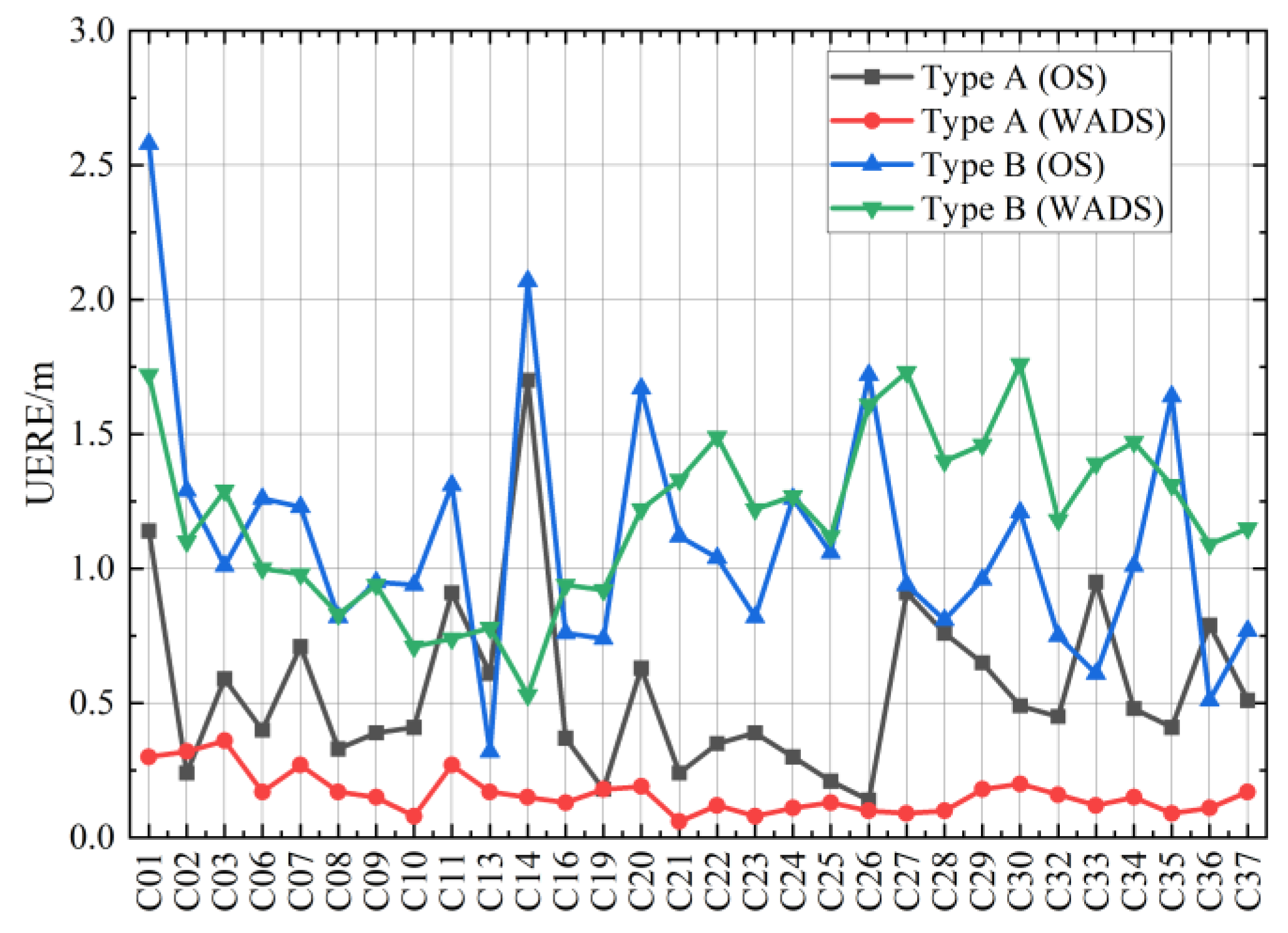
| Type A | 0.55 | 0.33 | 0.16 | 0.07 |
| Type B | 1.11 | 0.47 | 1.19 | 0.32 |
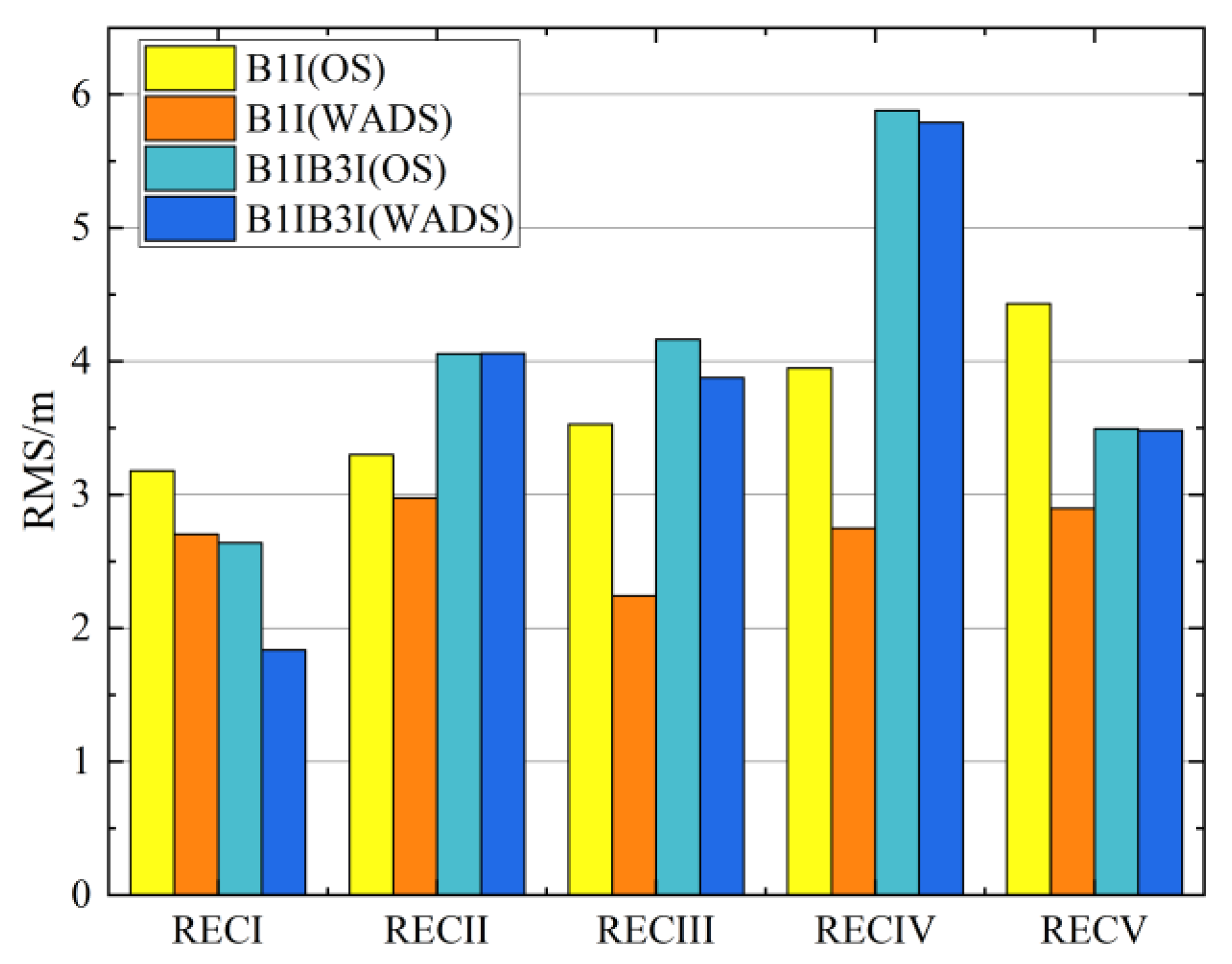
| Station | B1I | B1I/B3I | ||||||
|---|---|---|---|---|---|---|---|---|
| OS | WADS | OS | WADS | |||||
| Horizontal | Vertical | Horizontal | Vertical | Horizontal | Vertical | Horizontal | Vertical | |
| Type A 1 | 1.47 | 2.8 | 0.83 | 2.06 | 1.54 | 2.11 | 0.79 | 1.23 |
| Type A 2 | 1.54 | 2.97 | 0.8 | 1.77 | 0.94 | 2.16 | 0.5 | 1.97 |
| Type A 3 | 0.88 | 2.69 | 1.07 | 2.28 | 1.14 | 2.07 | 0.85 | 1.56 |
| Type A 4 | 1.84 | 2.64 | 1.38 | 2.18 | 1.48 | 2.92 | 1.14 | 2.07 |
| Type A 5 | 1.47 | 2.31 | 1.24 | 2.91 | 1.65 | 2.64 | 1.24 | 1.97 |
| Type A 6 | 1.13 | 3.14 | 0.98 | 2.52 | 1.09 | 2.45 | 0.65 | 1.49 |
| Type A 7 | 0.96 | 3.07 | 0.81 | 2.9 | 1.18 | 2.14 | 0.64 | 1.27 |
| Type B 1 | 1.63 | 2.89 | 1.09 | 2.05 | 1.96 | 2.84 | 1.8 | 2.84 |
| Type B 2 | 1.62 | 2.96 | 0.92 | 2.14 | 1.3 | 2.94 | 1.21 | 3.48 |
| Type B 3 | 1.03 | 2.8 | 1.14 | 2.62 | 1.54 | 3.19 | 1.37 | 3.32 |
| Type B 4 | 1.93 | 3.47 | 1.79 | 3.55 | 3.2 | 7.03 | 3.06 | 7.28 |
| Type B 5 | 1.75 | 2.34 | 1.5 | 2.76 | 1.99 | 4.88 | 1.94 | 4.33 |
| Type B 6 | 1.28 | 3.26 | 1.06 | 2.89 | 1.53 | 3.41 | 1.5 | 3.4 |
| Type B 7 | 0.96 | 2.7 | 0.71 | 2.54 | 1.33 | 2.32 | 0.95 | 2.35 |
| Type C 1 | 1.29 | 2.9 | 1.23 | 1.48 | 2.76 | 3.18 | 2.62 | 2.89 |
| Type C 2 | 1.07 | 3.88 | 1.52 | 2.57 | 2.43 | 3.27 | 2.4 | 2.57 |
| Type C 3 | 1.1 | 3.2 | 1.25 | 1.32 | 2.35 | 3.49 | 2.2 | 3.59 |
| Type D 1 | 1.66 | 3.48 | 1.65 | 2.31 | 2.86 | 4.97 | 2.69 | 4.44 |
| Type D 2 | 1.2 | 3.86 | 1.58 | 2.14 | 2.39 | 5.53 | 2.54 | 5.86 |
| Type E 1 | 1.82 | 5.3 | 1.62 | 2.61 | 2.08 | 2.4 | 1.86 | 2.48 |
| Type E 2 | 1.24 | 3.01 | 1.2 | 2.44 | 2.7 | 2.69 | 2.58 | 2.88 |
| Mean (type A) | 1.33 | 2.80 | 1.02 | 2.37 | 1.29 | 2.36 | 0.83 | 1.65 |
| Mean (type B) | 1.46 | 2.92 | 1.17 | 2.65 | 1.84 | 3.80 | 1.69 | 3.86 |
| Mean (type C) | 1.15 | 3.33 | 1.33 | 1.79 | 2.51 | 3.31 | 2.41 | 3.02 |
| Mean (type D) | 1.43 | 3.67 | 1.62 | 2.23 | 2.63 | 5.25 | 2.62 | 5.15 |
| Mean (type E) | 1.53 | 4.16 | 1.41 | 2.53 | 2.39 | 2.55 | 2.22 | 2.68 |
| Station | B1I | B1I/B3I | ||||||
|---|---|---|---|---|---|---|---|---|
| OS | WADS | OS | WADS | |||||
| Horizontal | Vertical | Horizontal | Vertical | Horizontal | Vertical | Horizontal | Vertical | |
| Type B 1 | 1.07 | 3.01 | 0.61 | 2.47 | 1.34 | 1.95 | 0.84 | 1.17 |
| Type B 2 | 2.47 | 2.70 | 2.20 | 2.77 | 0.69 | 2.31 | 0.52 | 2.54 |
| Type B 3 | 0.78 | 2.71 | 0.69 | 2.29 | 1.28 | 2.84 | 1.02 | 2.55 |
| Type B 4 | 1.38 | 3.00 | 1.30 | 2.52 | 1.93 | 3.99 | 1.61 | 3.44 |
| Type B 6 | 1.37 | 3.68 | 0.93 | 2.53 | 1.57 | 2.79 | 1.18 | 2.17 |
| Type B 7 | 1.08 | 2.44 | 1.08 | 2.11 | 1.85 | 4.87 | 1.59 | 3.98 |
| Type C 1 | 1.26 | 3.63 | 1.28 | 1.94 | 1.69 | 3.32 | 1.39 | 2.95 |
| Type C 2 | 1.24 | 4.62 | 1.43 | 2.92 | 1.33 | 2.90 | 1.53 | 2.35 |
| Type C 3 | 1.24 | 3.37 | 1.32 | 1.55 | 1.68 | 3.42 | 1.45 | 3.58 |
| Mean (type B) | 1.36 | 2.92 | 1.14 | 2.45 | 1.44 | 3.13 | 1.13 | 2.64 |
| Mean (type C) | 1.25 | 3.87 | 1.34 | 2.14 | 1.57 | 3.22 | 1.46 | 2.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Q.; Cao, Y.; Hu, X.; Tang, C.; Zhou, S.; Guo, R.; Li, X.; Tian, Y.; Yang, Y.; Yang, J. A Study on Pseudorange Biases in BDS B1I/B3I Signals and the Impacts on Beidou Wide Area Differential Services. Remote Sens. 2022, 14, 432. https://doi.org/10.3390/rs14030432
Tian Q, Cao Y, Hu X, Tang C, Zhou S, Guo R, Li X, Tian Y, Yang Y, Yang J. A Study on Pseudorange Biases in BDS B1I/B3I Signals and the Impacts on Beidou Wide Area Differential Services. Remote Sensing. 2022; 14(3):432. https://doi.org/10.3390/rs14030432
Chicago/Turabian StyleTian, Qiuning, Yueling Cao, Xiaogong Hu, Chengpan Tang, Shanshi Zhou, Rui Guo, Xiaojie Li, Yijun Tian, Yufei Yang, and Jianhua Yang. 2022. "A Study on Pseudorange Biases in BDS B1I/B3I Signals and the Impacts on Beidou Wide Area Differential Services" Remote Sensing 14, no. 3: 432. https://doi.org/10.3390/rs14030432
APA StyleTian, Q., Cao, Y., Hu, X., Tang, C., Zhou, S., Guo, R., Li, X., Tian, Y., Yang, Y., & Yang, J. (2022). A Study on Pseudorange Biases in BDS B1I/B3I Signals and the Impacts on Beidou Wide Area Differential Services. Remote Sensing, 14(3), 432. https://doi.org/10.3390/rs14030432







