Comprehensive Evaluation of Data-Related Factors on BDS-3 B1I + B2b Real-Time PPP/INS Tightly Coupled Integration
Abstract
1. Introduction
2. Methods
2.1. Observation Models
2.2. State Models
2.3. Robust Kalman Filter
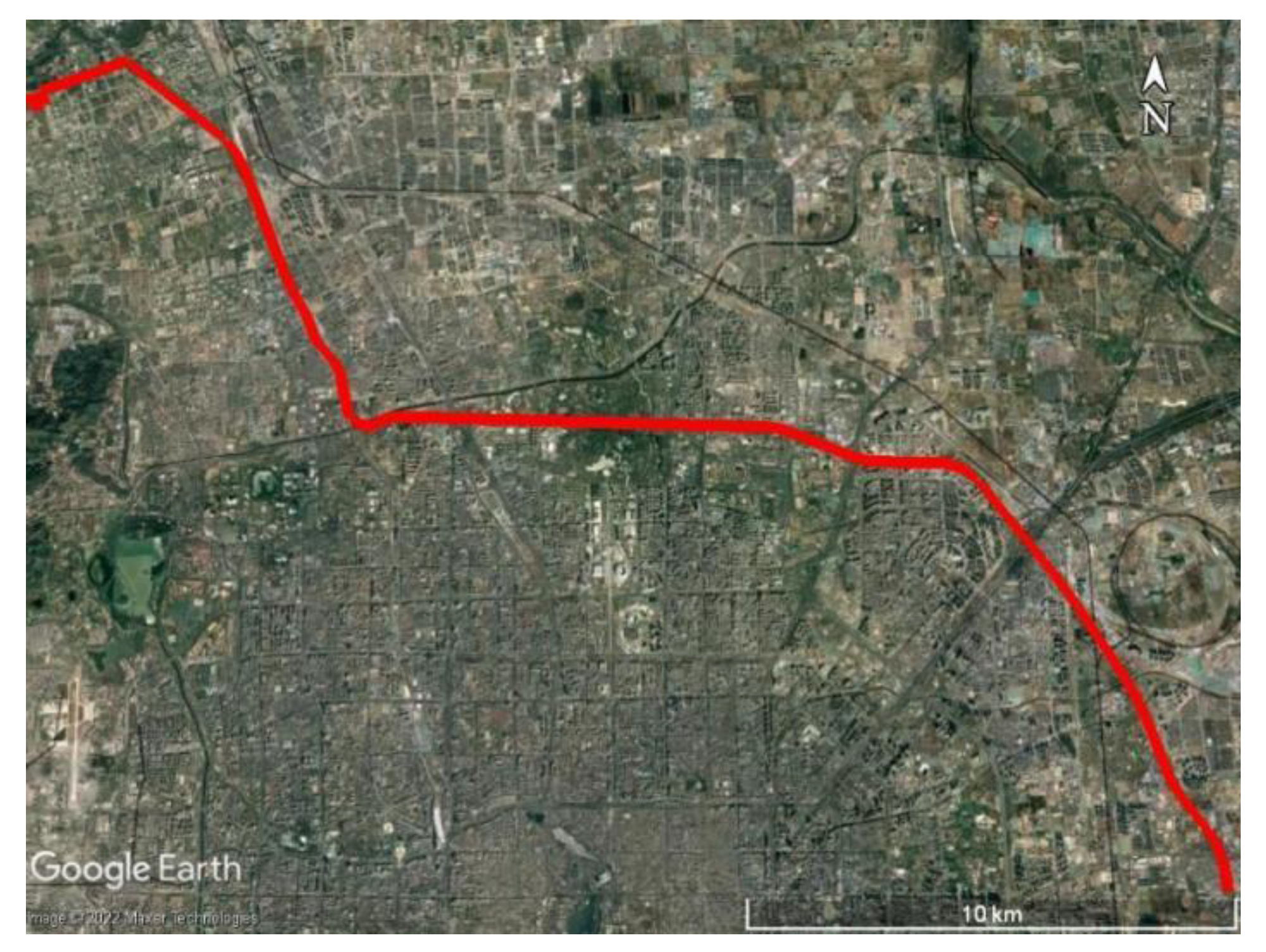
3. Experiments and Data Processing Schemes
4. Discussions
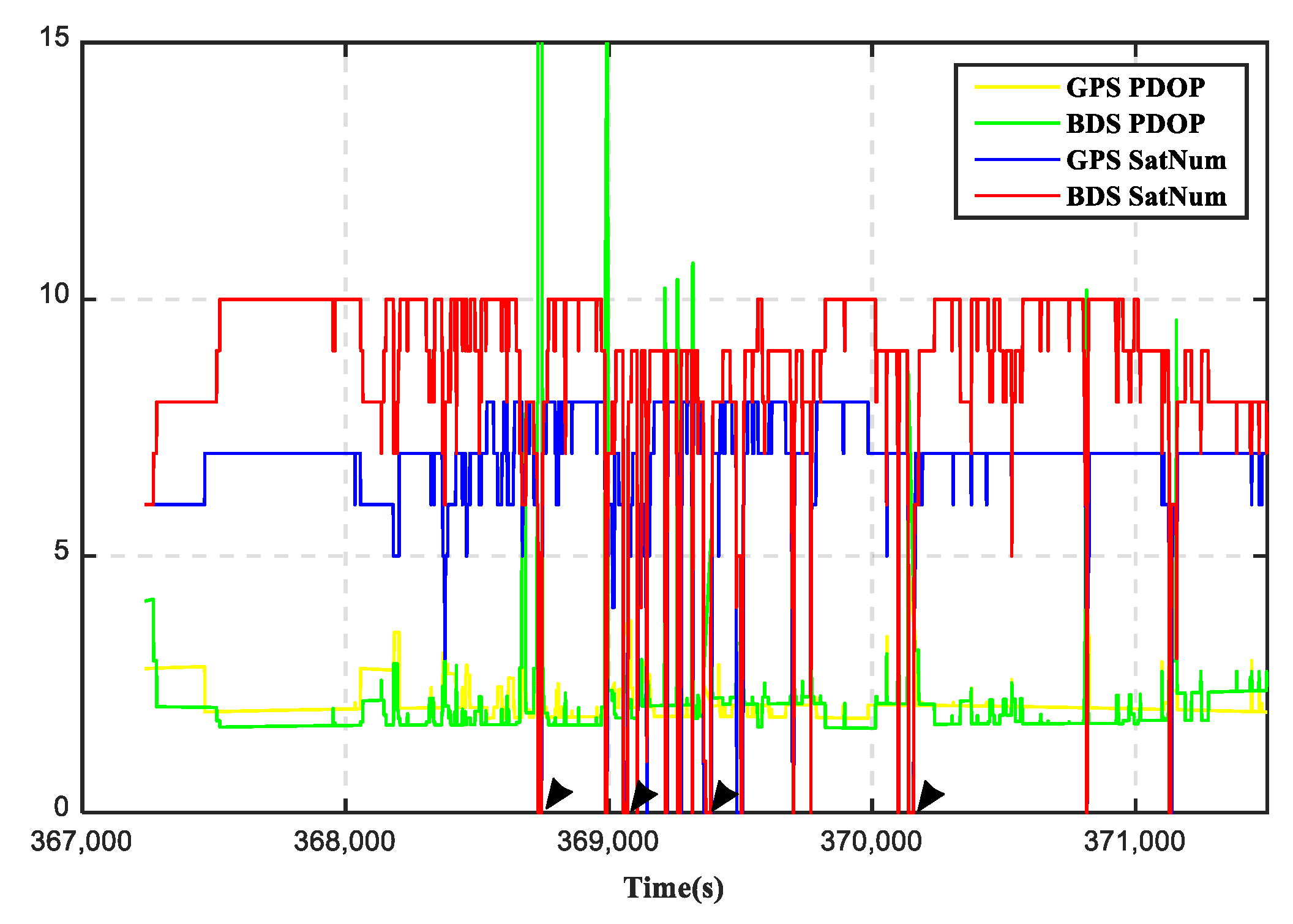
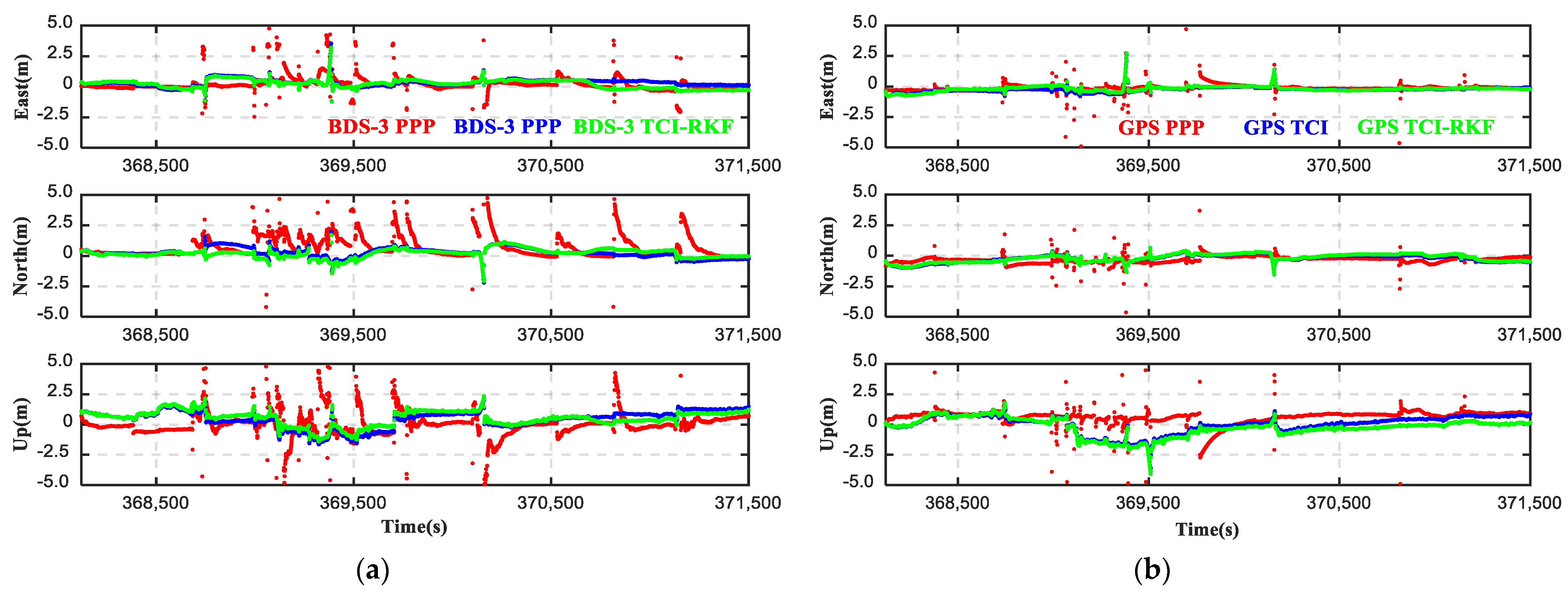
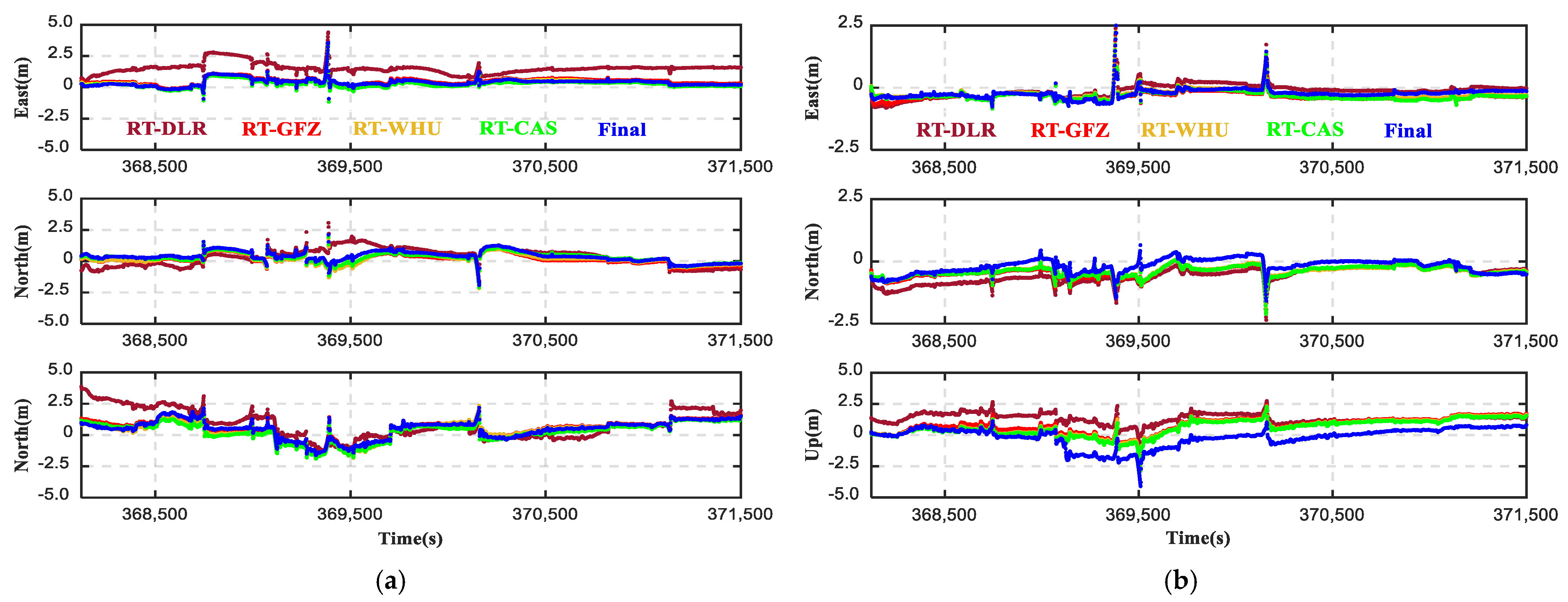
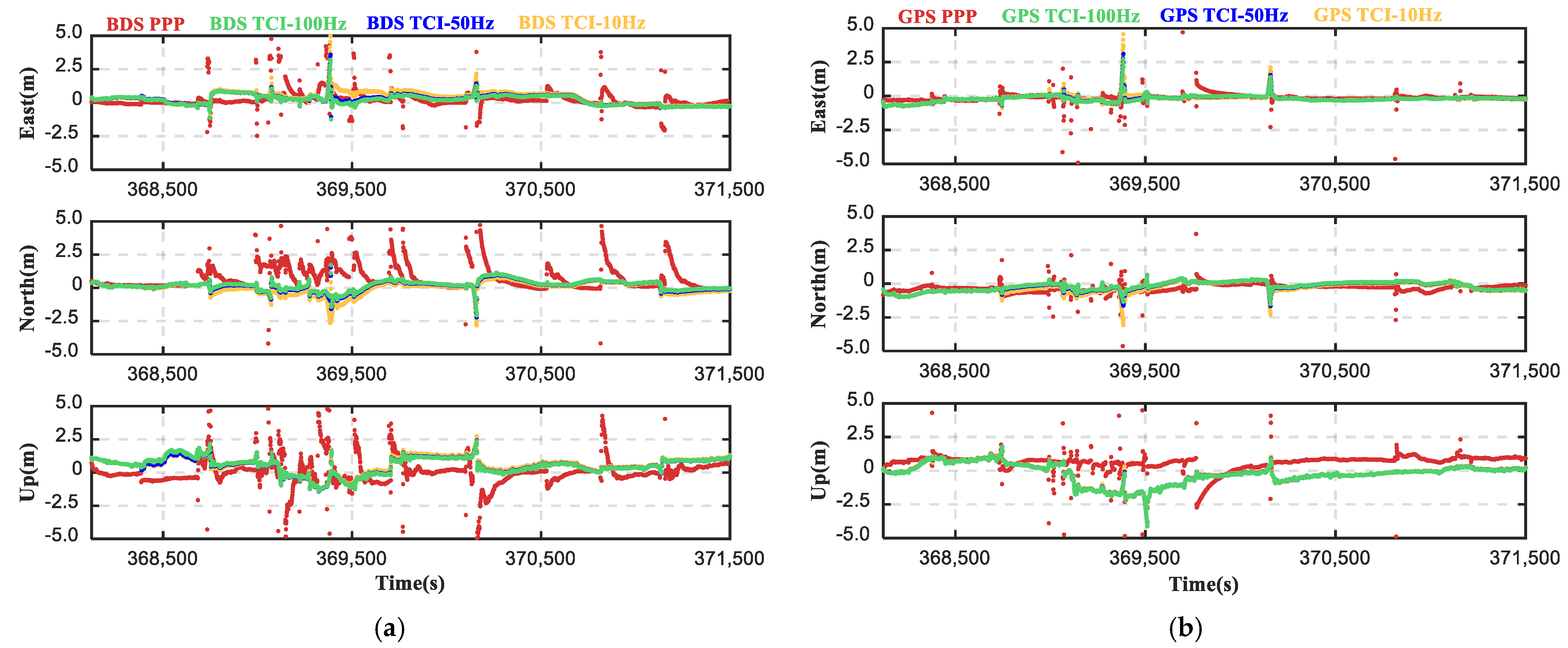
4.1. Impacts of SSR Products and Robust Algorithm on PPP/INS Integration
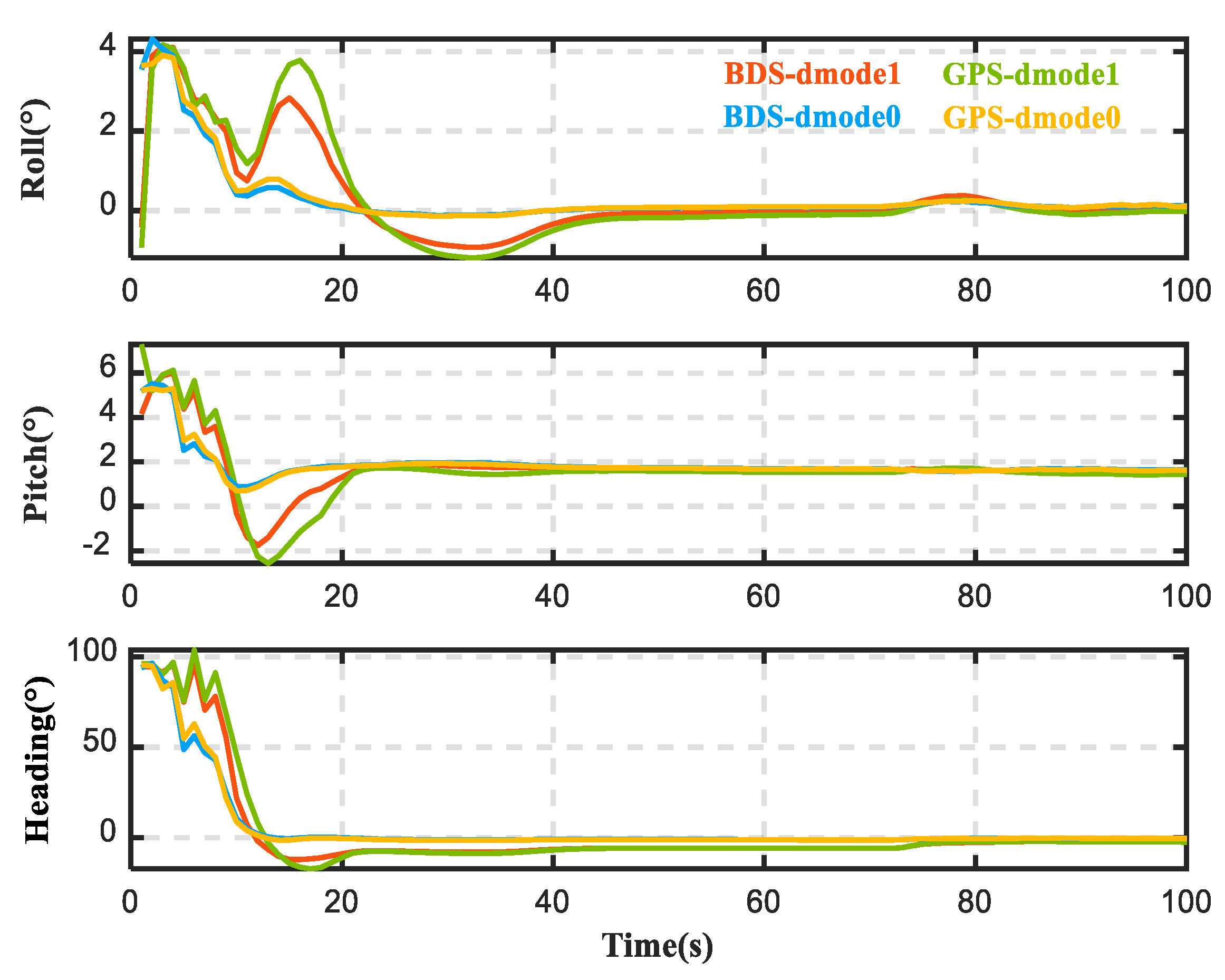
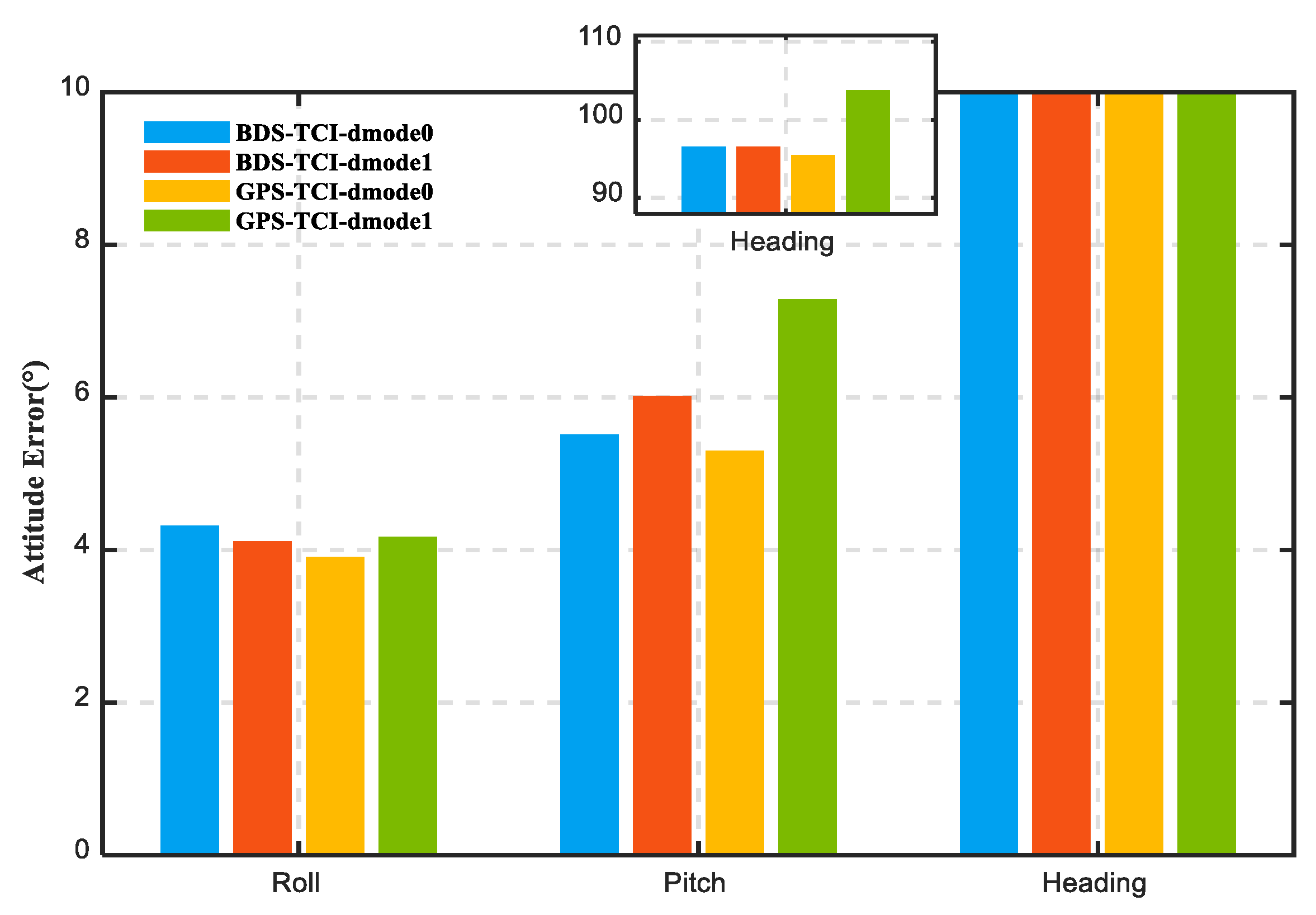
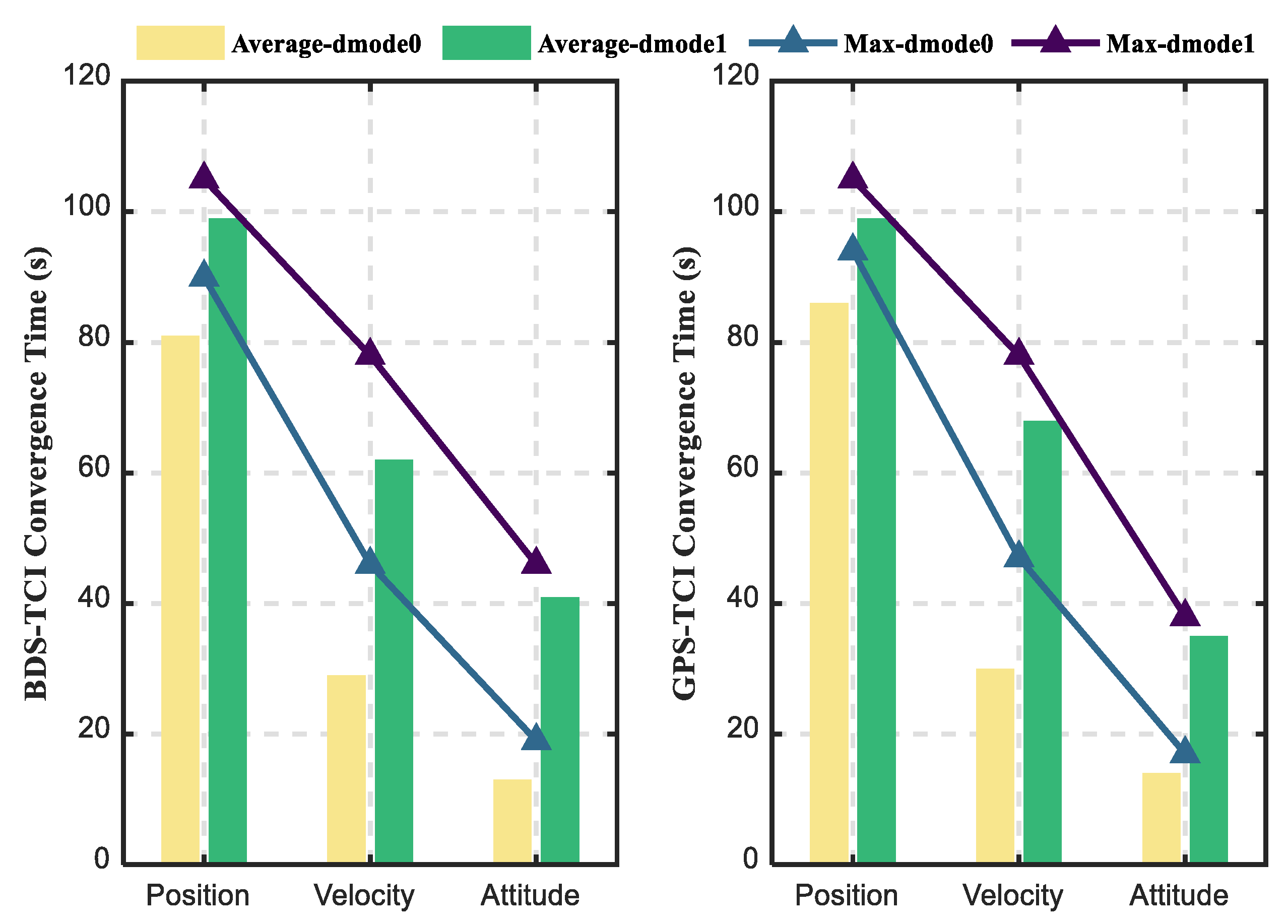
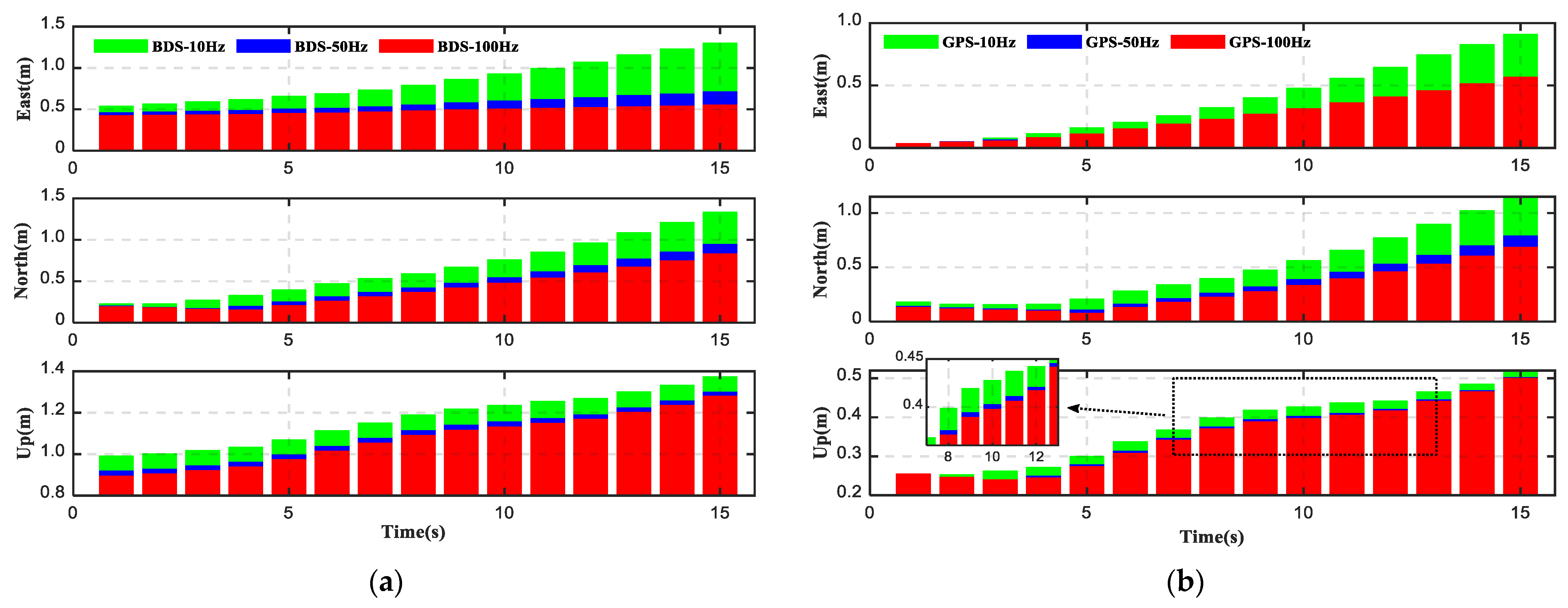
4.2. Impacts of Doppler Observation on PPP/INS Integration
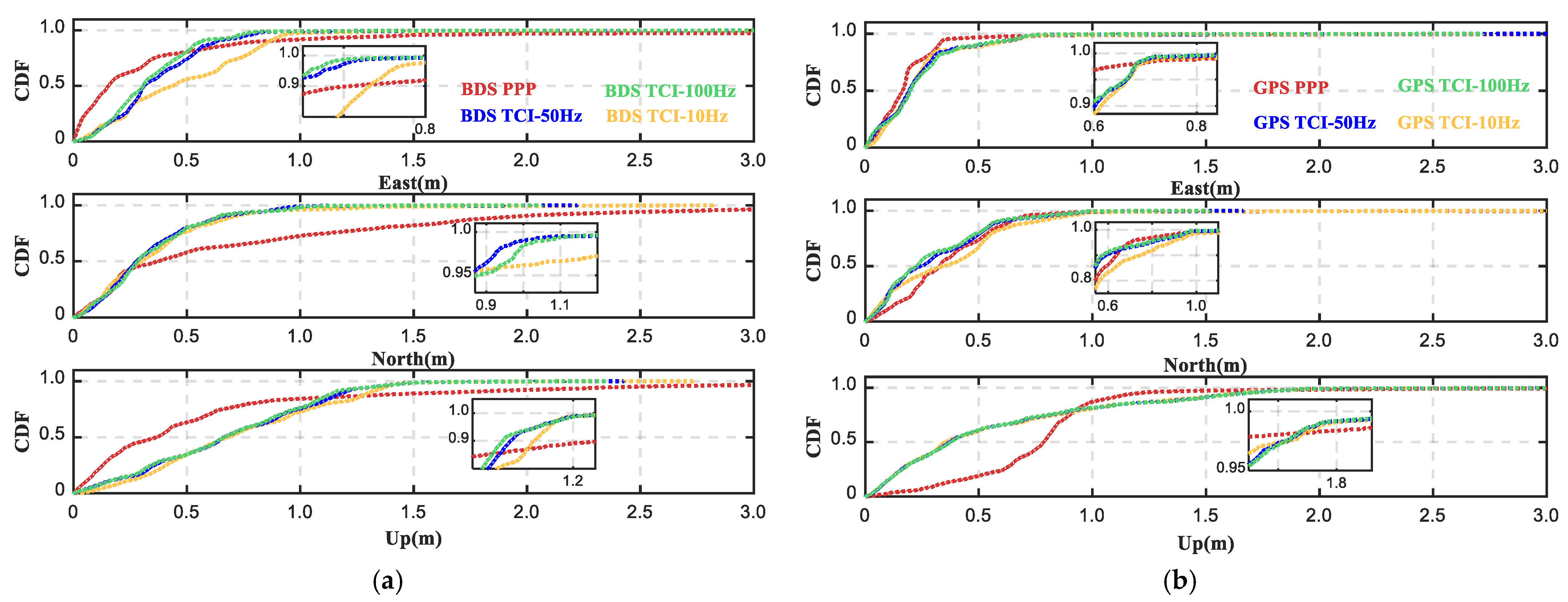
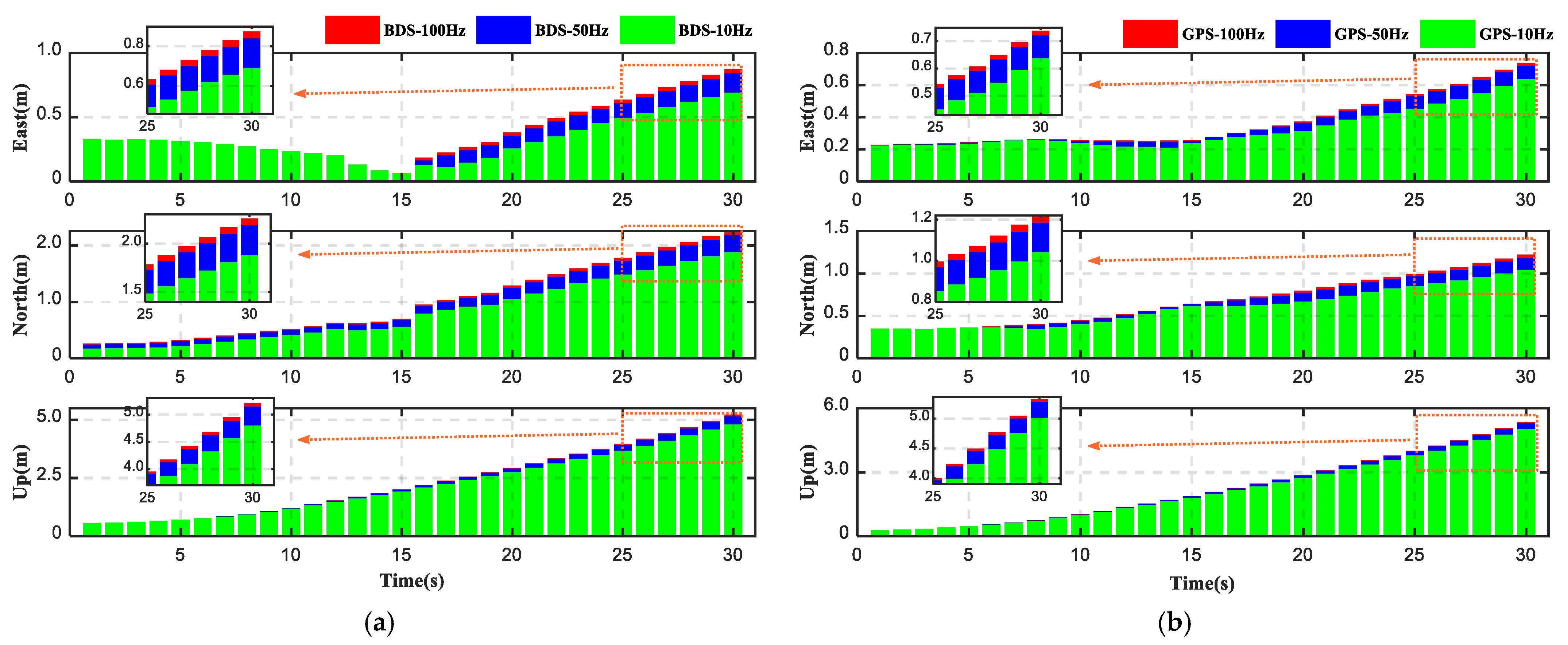
4.3. Impacts of IMU Data Interval on PPP/INS Integration
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Malys, S.; Jensen, P.A. Geodetic point positioning with GPS carrier beat phase data from the CASA UNO experiment. Geophys. Res. Lett. 1990, 17, 651–654. [Google Scholar] [CrossRef]
- Xun, S. GPS Measurement Principle and Application; Wuhan University Press: Wuhan, China, 2003. [Google Scholar]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Elsobeiey, M.; Al-Harbi, S. Performance of Real-Time Precise Point Positioning Using IGS Real-Time Service. GPS Solut. 2016, 20, 565–571. [Google Scholar] [CrossRef]
- Xia, F.; Ye, S.; Zhao, L.; Hu, G. Analysis of Real-time Precise Point Positioning Based on SSR Corrections. Navig. Position. Timing 2017, 4, 52–57. [Google Scholar]
- Weber, G.; Mervart, L.; Lukes, Z.; Rocken, C.; Dousa, J. Real-time clock and orbit corrections for improved point positioning via NTRIP. In Proceedings of the ION GNSS 20th International Technical Meeting of the Satellite Division (ION GNSS 2007), Fort Worth, TX, USA, 25–28 September 2007; pp. 1992–1998. [Google Scholar]
- Caissy, M.; Agrotis, L.; Weber, G.; Hernandez-Pajares, M.; Hugentobler, U. Coming soon: The international GNSS real-time service. GPS World 2012, 23, 52–58. [Google Scholar]
- Hadas, T.; Bosy, J. IGS RTS Precise Orbits and Clocks Verification and Quality Degradation over Time. GPS Solut. 2015, 19, 93–105. [Google Scholar] [CrossRef]
- Wang, L.; Li, Z.; Ge, M.; Neitzel, F.; Wang, X.; Yuan, H. Investigation of the performance of real-time BDS-only precise point positioning using the IGS real-time service. GPS Solut. 2019, 23, 66. [Google Scholar] [CrossRef]
- Wang, W.; Yu, W.; Zeng, Q.; Wu, R. Assessment of CNES real-time orbit and clock product. In Proceedings of the 10th China Satellite Navigation Conference, Beijing, China, 22–25 May 2019. [Google Scholar]
- Kazmierski, K.; Zajdel, R.; Sośnica, K. Evolution of Orbit and Clock Quality for Real-Time Multi-GNSS Solutions. GPS Solut. 2020, 24, 111. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Z.; Wang, L.; Wang, X.; Yuan, H. Assessment of Multiple GNSS Real-Time SSR Products from Different Analysis Centers. Int. J. Geo-Inf. 2018, 7, 85. [Google Scholar] [CrossRef]
- Li, W.; Kacmarik, M. Assessment of Multi-GNSS Precise Orbit and Clock Products from Different Analysis Centers Based on Precise Point Positioning. Acta Geodyn. Geomater. 2021, 18, 387–397. [Google Scholar] [CrossRef]
- Weiss, J.D.; Kee, D.S. A Direct Performance Comparison Between Loosely Coupled and Tightly Coupled GPS/INS Integration Techniques. In Proceedings of the 51st Annual Meeting of The Institute of Navigation 1995, Colorado Springs, CO, USA, 5–7 June 1995; pp. 537–544. [Google Scholar]
- Kjørsvik, N.S.; Gjevestad, J.G.; Brøste, E.; Gade, K.; Hagen, O.K. Tightly Coupled Precise Point Positioning and Inertial Navigation Systems. In Proceedings of the International Society for Photgrammetry and Remote Sensing European Calibration and Orientation Workshop, Casteldefels, Spain, 10–12 February 2010. [Google Scholar]
- Gao, Z.; Ge, M.; Shen, W.; Li, Y.; Chen, Q.; Zhang, H.; Niu, X. Evaluation on the Impact of IMU Grades on BDS + GPS PPP/INS Tightly Coupled Integration. Adv. Space Res. 2017, 60, 1283–1299. [Google Scholar] [CrossRef]
- Shin, E.; Scherzinger, B. Inertially Aided Precise Point Positioning. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009; pp. 1892–1897. [Google Scholar]
- Roesler, G.; Martell, H. Tightly coupled processing of precise point position (PPP) and INS data. In Proceedings of the 22nd International Meeting of the Satellite Division of the Institute of Navigation, Savannah, GA, USA, 22–25 September 2009. [Google Scholar]
- Falco, G.; Pini, M.; Marucco, G. Loose and tight GNSS/INS integrations: Comparison of performance assessed in real urban scenarios. Sensors 2017, 17, 255. [Google Scholar] [CrossRef]
- Du, S. Integration of Precise Point Positioning and Low-Cost MEMS IMU. Ph.D. Dissertation, University of Calgary, Calgary, AB, Canada, 2010. [Google Scholar]
- Abd Rabbou, M.; El-Rabbany, A. Tightly Coupled Integration of GPS Precise Point Positioning and MEMS-Based Inertial Systems. GPS Solut. 2015, 19, 601–609. [Google Scholar] [CrossRef]
- Gao, Z.; Zhang, H.; Ge, M.; Niu, X.; Shen, W.; Wickert, J.; Schuh, H. Tightly Coupled Integration of Multi-GNSS PPP and MEMS Inertial Measurement Unit Data. GPS Solut. 2017, 21, 377–391. [Google Scholar] [CrossRef]
- Elmezayen, A.; El-Rabbany, A. Ultra-Low-Cost Tightly Coupled Triple-Constellation GNSS PPP/MEMS-Based INS Integration for Land Vehicular Applications. Geomatics 2021, 1, 258–286. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Yang, Z.; Shao, K.; Chen, W. Motion Model-Assisted GNSS/MEMS-IMU Integrated Navigation System for Land Vehicle. GPS Solut. 2022, 26, 131. [Google Scholar] [CrossRef]
- Elmezayen, A.; El-Rabbany, A. Performance Evaluation of Real-Time Tightly-Coupled GNSS PPP/MEMS-Based Inertial Integration Using an Improved Robust Adaptive Kalman Filter. J. Appl. Geod. 2020, 14, 413–430. [Google Scholar] [CrossRef]
- Liu, X.; Li, D.; Shi, J.; Li, A.; Jiang, L. A Framework for Low-Cost Fusion Positioning with Single Frequency RTK/MEMS-IMU/VIO. J. Phys. Conf. Ser. 2021, 1738, 012007. [Google Scholar] [CrossRef]
- Gonzalez, R.; Dabove, P. Performance Assessment of an Ultra Low-Cost Inertial Measurement Unit for Ground Vehicle Navigation. Sensors 2019, 19, 3865. [Google Scholar] [CrossRef]
- Elsheikh, M.; Abdelfatah, W.; Noureldin, A.; Iqbal, U.; Korenberg, M. Low-Cost Real-Time PPP/INS Integration for Automated Land Vehicles. Sensors 2019, 19, 4896. [Google Scholar] [CrossRef] [PubMed]
- Shao, K.; Li, Z.; Yang, Z.; Liu, Z.; Sun, Y. A Doppler Enhanced TDCP Algorithm Based on Terrain Adaptive and Robust Kalman Filter Using a Stand-Alone Receiver. J. Navig. 2022, 75, 864–877. [Google Scholar] [CrossRef]
- He, K.; Xu, T.; Förste, C.; Wang, Z.; Zhao, Q.; Wei, Y. A Method to Correct the Raw Doppler Observations for GNSS Velocity Determination. In International Association of Geodesy Symposia; Springer: Berlin, Germany, 2022; pp. 1–6. [Google Scholar]
- Liu, S.; Sun, F.; Chen, P. Research on DGPS/INS Tightly Coupled Algorithms Based on Pseudo-range and Doppler Observations. Bull. Surv. Mapp. 2013, 6, 5–8. [Google Scholar]
- Liu, S.; Sun, F.; Zhang, L.; Li, W.; Zhu, X. Tight Integration of Ambiguity-Fixed PPP and INS: Model Description and Initial Results. GPS Solut. 2016, 20, 39–49. [Google Scholar] [CrossRef]
- Wen, Z.C.; Li, Y.; Guo, X.L.; Zhang, X.X. Design and Evaluation of GNSS/INS Tightly-Coupled Navigation Software for Land Vehicles. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, 46, 213–218. [Google Scholar] [CrossRef]
- Li, Z.; Yao, Y.; Wang, J.; Gao, J. Application of improved robust Kalman filter in data fusion for PPP/INS tightly coupled positioning system. Metrol. Meas. Syst. 2017, 24, 289–301. [Google Scholar] [CrossRef]
- Du, Z.; Chai, H.; Xiao, G.; Xiang, M.; Yin, X.; Shi, M. The Realization and Evaluation of PPP Ambiguity Resolution with INS Aiding in Marine Survey. Mar. Geod. 2021, 44, 136–156. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, W.; Rong, Y.; Hu, X.; Ma, J. Robust Adaptive Kalman Filtering Algorithm for Integrated Navigation Based on MEMS-INS/GNSS. Navig. Control 2018, 17, 14–20. [Google Scholar]
- He, X.; Liu, C.; Chen, Y.; Ba, X.; Chen, J. Analysis of B2b signal of BDS III satellite. Appl. Electron. Tech. 2020, 3, 1–4. [Google Scholar]
- Cheng, J.; Wang, W.; Ma, L.; Liu, W. Preliminary analysis of observation quality and positioning precision for BDS-3 satellites. Bull. Surv. Mapp. 2019, 8, 1–7. [Google Scholar]
- Gao, Z. Research on the methodology and application of the integration between the multi-constellation GNSS PPP and inertial navigation system. Ph.D. Dissertation, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Tu, R.; Ge, M.; Zhang, H.; Huang, G. The Realization and Convergence Analysis of Combined PPP Based on Raw Observation. Adv. Space Res. 2013, 53, 211–221. [Google Scholar] [CrossRef]
- Gendt, G.; Dick, G.; Reigber, C.; Tomassini, M.; Liu, Y. Demonstration of NRT GPS water vapor monitoring for weather prediction in Germany. J. Meteorol. Soc. Jpn. 2003, 82, 360–370. [Google Scholar]
- Shin, E.H. Estimation Techniques for Low-Cost Inertial Navigation; Library and Archives Canada: Ottawa, ON, Canada, 2006. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; Willey: New York, NY, USA, 1992. [Google Scholar]
- Yang, Y. Adaptive Navigation and Kinematic Positioning; Press of Surveying and Mapping: Beijing, China, 2006. [Google Scholar]
- Yang, Y.; Song, L.; Xu, T. Robust Estimator for Correlated Observations Based on Bifactor Equivalent Weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
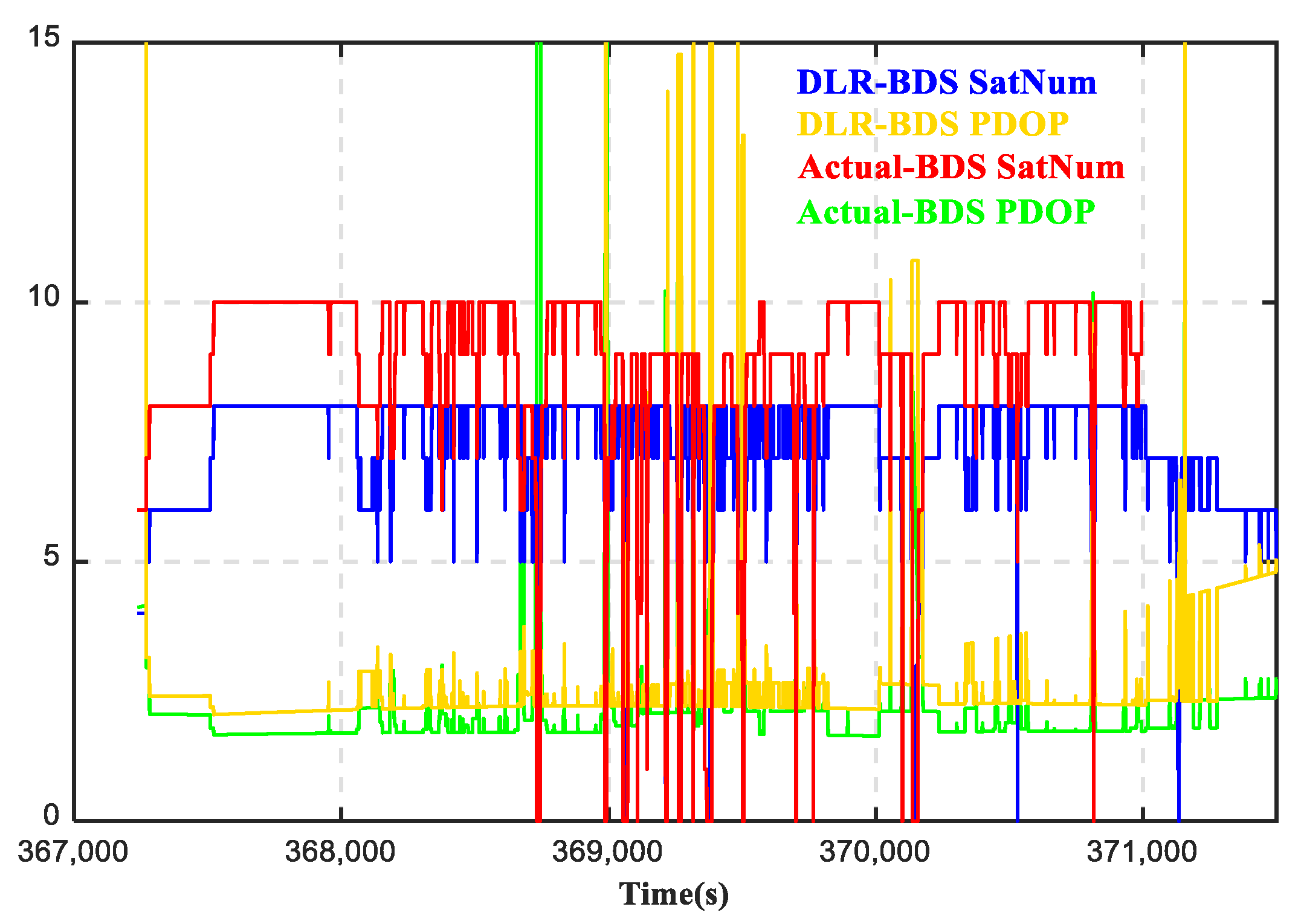
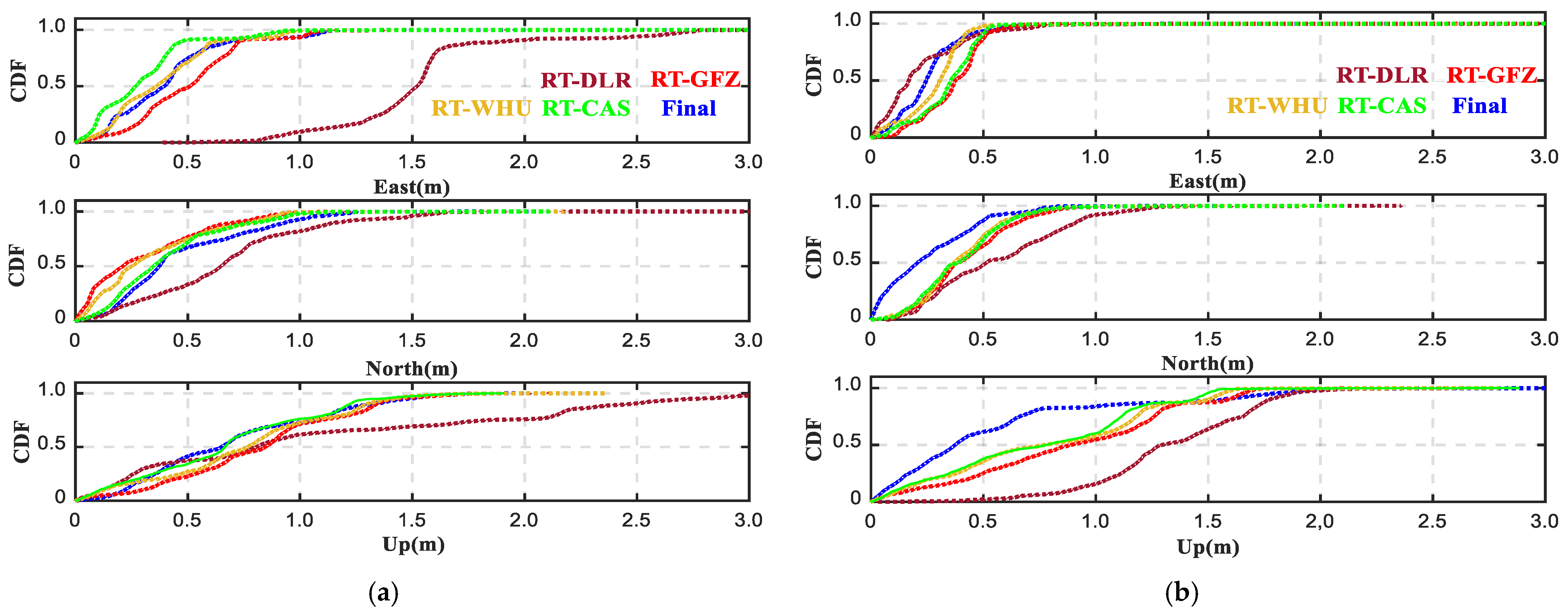

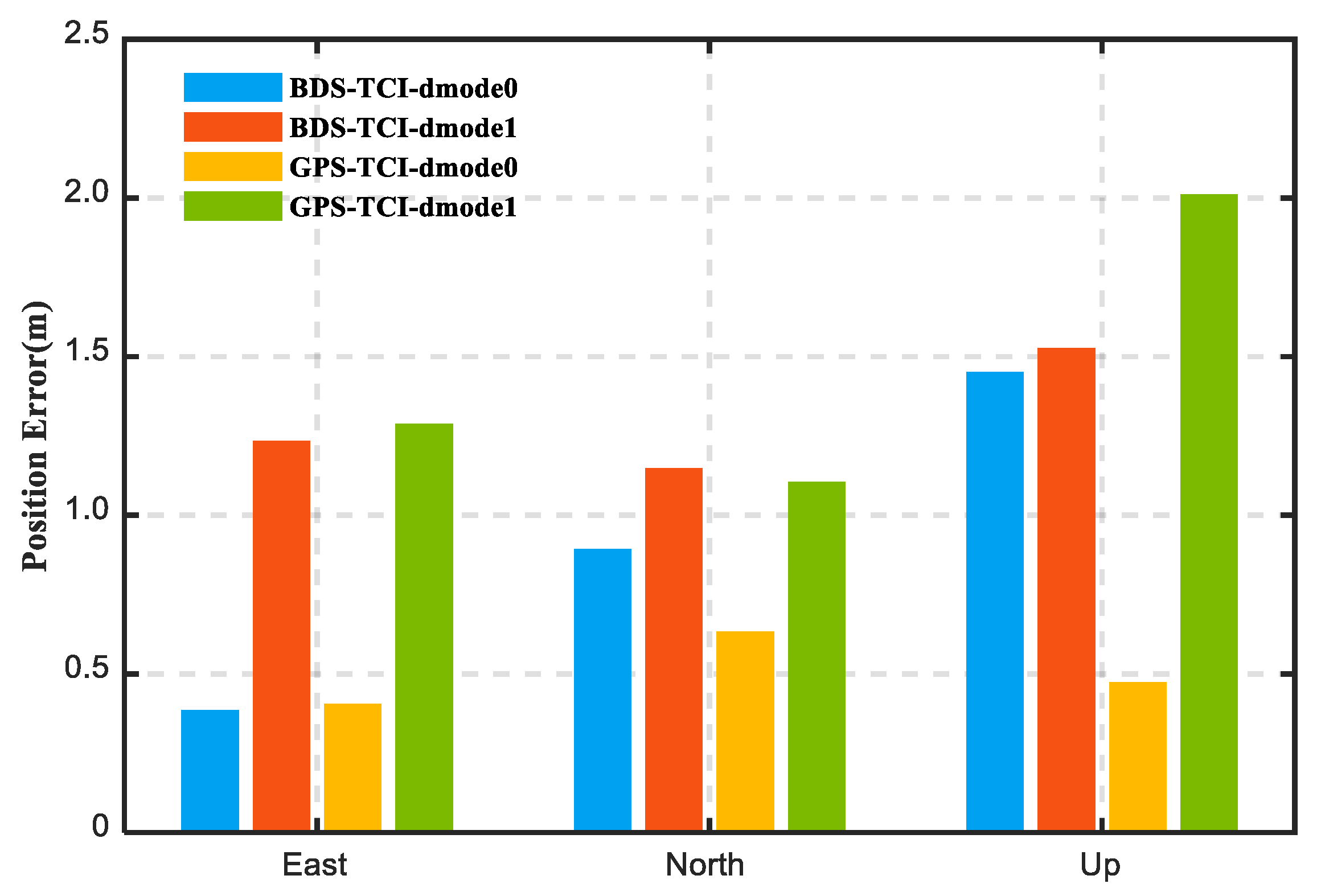

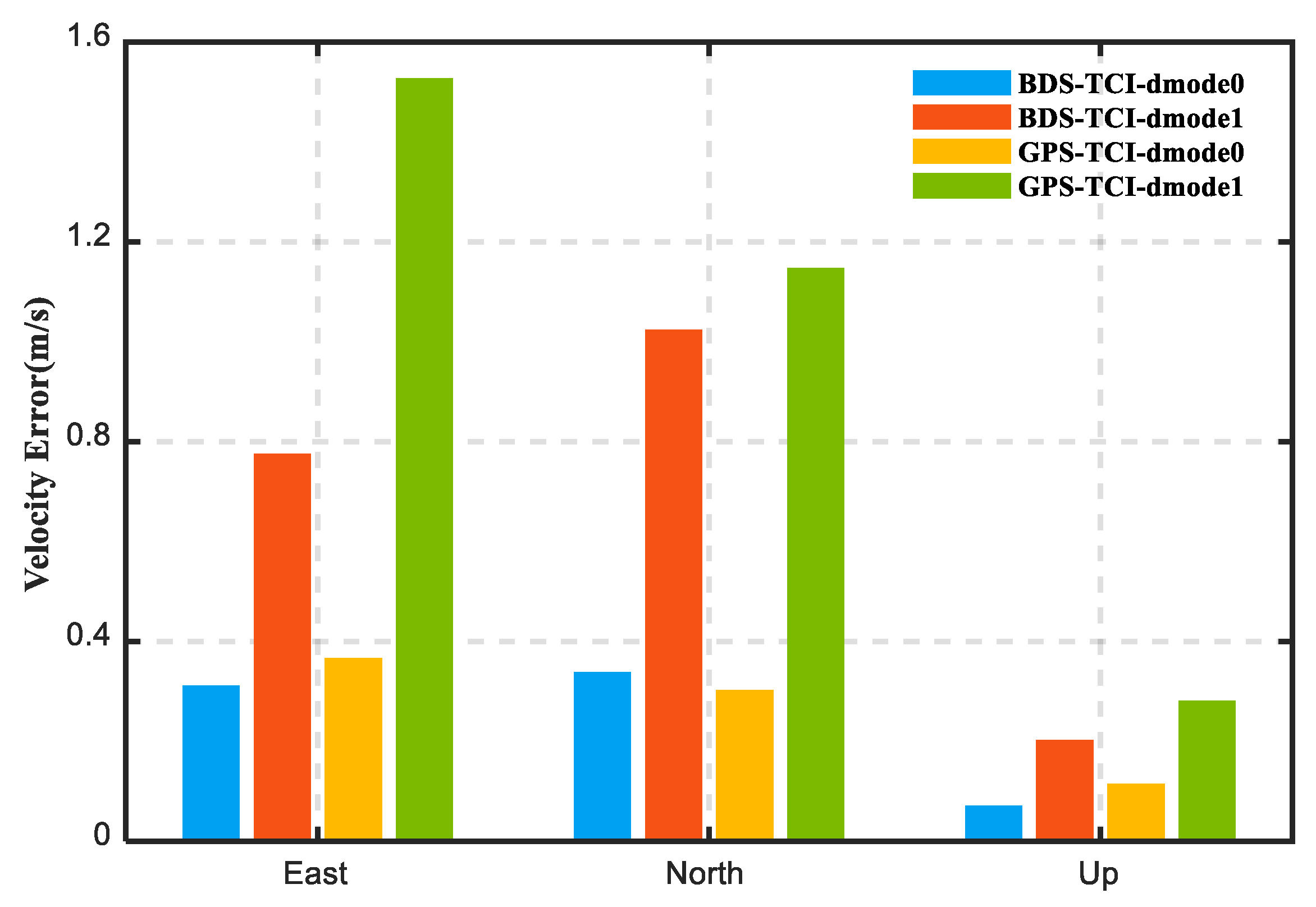





| Parameters | Values |
|---|---|
| Gyroscope bias (°) | 2 |
| Accelerometer bias (mGal) | 40 |
| Angular random walk (°) | 0.15 |
| Velocity random walk () | 0.05 |
| Schemes | EKF | RKF | Final Products | Real-Time Products | With Doppler | Without Doppler | IMU Data Rate |
|---|---|---|---|---|---|---|---|
| PPP | – | – | √ | – | – | – | – |
| TCI | √ | – | √ | – | √ | – | 100 Hz |
| TCI-RKF | – | √ | √ | – | √ | – | 100 Hz |
| RT-CAS | – | √ | – | CAS | √ | – | 100 Hz |
| RT-WHU | – | √ | – | WHU | √ | – | 100 Hz |
| RT-GFZ | – | √ | – | GFZ | √ | – | 100 Hz |
| RT-DLR | – | √ | – | DLR | √ | – | 100 Hz |
| TCI-dmode0 | – | √ | √ | – | √ | – | 100 Hz |
| TCI-dmode1 | – | √ | √ | – | – | √ | 100 Hz |
| TCI-100 Hz | – | √ | √ | – | √ | – | 100 Hz |
| TCI-50 Hz | – | √ | √ | – | √ | – | 50 Hz |
| TCI-10 Hz | – | √ | √ | – | √ | – | 10 Hz |
| Mode | BDS-3 | ||||||
|---|---|---|---|---|---|---|---|
| PPP | TCI | ||||||
| Final | Final | Final -Robust | RT-CAS | RT-WHU | RT-GFZ | RT-DLR | |
| East (m) | 0.882 | 0.432 | 0.406 | 0.383 | 0.464 | 0.572 | 1.576 |
| North (m) | 1.361 | 0.464 | 0.419 | 0.476 | 0.433 | 0.407 | 0.766 |
| Up (m) | 1.311 | 0.838 | 0.782 | 0.790 | 0.861 | 0.908 | 1.414 |
| Mode | GPS | ||||||
|---|---|---|---|---|---|---|---|
| PPP | TCI | ||||||
| Final | Final | Final -Robust | RT-CAS | RT-WHU | RT-GFZ | RT-DLR | |
| East (m) | 0.586 | 0.316 | 0.305 | 0.385 | 0.334 | 0.408 | 0.320 |
| North (m) | 0.539 | 0.396 | 0.372 | 0.450 | 0.443 | 0.477 | 0.646 |
| Up (m) | 0.984 | 0.769 | 0.758 | 0.889 | 0.938 | 1.01 | 1.387 |
| Mode | Position (m) | Velocity (cm/s) | Attitude (°) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| East | North | Up | East | North | Up | Roll | Pitch | Heading | |
| BDS-TCI-dmode0 1 | 0.406 | 0.419 | 0.782 | 1.88 | 2.04 | 3.16 | 0.276 | 1.319 | 0.502 |
| BDS-TCI-dmode1 2 | 0.408 | 0.419 | 0.788 | 1.90 | 2.17 | 3.16 | 0.276 | 1.321 | 0.503 |
| GPS-TCI-dmode0 1 | 0.305 | 0.372 | 0.758 | 1.69 | 2.04 | 3.06 | 0.275 | 1.314 | 0.506 |
| GPS-TCI-dmode1 2 | 0.301 | 0.387 | 0.759 | 1.72 | 2.46 | 3.06 | 0.276 | 1.318 | 0.505 |
| Mode | Position (m) | Velocity (cm/s) | Attitude (°) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| East | North | Up | East | North | Up | Roll | Pitch | Heading | |
| BDS-TCI-dmode0 1 | 0.286 | 0.650 | 0.966 | 4.15 | 6.11 | 1.09 | 0.364 | 1.869 | 6.626 |
| BDS-TCI-dmode1 2 | 0.744 | 0.777 | 0.904 | 18.01 | 11.04 | 2.65 | 0.619 | 1.835 | 12.667 |
| GPS-TCI-dmode0 1 | 0.192 | 0.499 | 0.275 | 4.45 | 5.96 | 1.46 | 0.384 | 1.851 | 6.837 |
| GPS-TCI-dmode1 2 | 0.419 | 0.496 | 0.748 | 27.49 | 11.60 | 4.44 | 0.761 | 1.834 | 13.861 |
| Mode | Position (m) | Velocity (cm/s) | Attitude (°) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| East | North | Up | East | North | Up | Roll | Pitch | Heading | |
| PPP | 0.882 | 1.361 | 1.311 | ||||||
| TCI-100 HZ | 0.406 | 0.419 | 0.782 | 1.88 | 2.04 | 3.16 | 0.276 | 1.319 | 0.502 |
| TCI-50 HZ | 0.438 | 0.415 | 0.791 | 2.17 | 2.28 | 3.29 | 0.275 | 1.324 | 0.504 |
| TCI-10 HZ | 0.598 | 0.481 | 0.834 | 3.38 | 3.38 | 4.27 | 0.278 | 1.443 | 0.528 |
| Mode | Position (m) | Velocity (cm/s) | Attitude (°) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| East | North | Up | East | North | Up | Roll | Pitch | Heading | |
| PPP | 0.586 | 0.539 | 0.984 | ||||||
| TCI-100 HZ | 0.305 | 0.372 | 0.758 | 1.69 | 2.04 | 3.06 | 0.275 | 1.314 | 0.506 |
| TCI-50 HZ | 0.309 | 0.388 | 0.773 | 2.01 | 2.31 | 3.21 | 0.275 | 1.319 | 0.508 |
| TCI-10 HZ | 0.349 | 0.476 | 0.774 | 3.33 | 3.45 | 4.22 | 0.277 | 1.436 | 0.529 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kan, J.; Gao, Z.; Xu, Q.; Lan, R.; Lv, J.; Yang, C. Comprehensive Evaluation of Data-Related Factors on BDS-3 B1I + B2b Real-Time PPP/INS Tightly Coupled Integration. Remote Sens. 2022, 14, 6395. https://doi.org/10.3390/rs14246395
Kan J, Gao Z, Xu Q, Lan R, Lv J, Yang C. Comprehensive Evaluation of Data-Related Factors on BDS-3 B1I + B2b Real-Time PPP/INS Tightly Coupled Integration. Remote Sensing. 2022; 14(24):6395. https://doi.org/10.3390/rs14246395
Chicago/Turabian StyleKan, Junyao, Zhouzheng Gao, Qiaozhuang Xu, Ruohua Lan, Jie Lv, and Cheng Yang. 2022. "Comprehensive Evaluation of Data-Related Factors on BDS-3 B1I + B2b Real-Time PPP/INS Tightly Coupled Integration" Remote Sensing 14, no. 24: 6395. https://doi.org/10.3390/rs14246395
APA StyleKan, J., Gao, Z., Xu, Q., Lan, R., Lv, J., & Yang, C. (2022). Comprehensive Evaluation of Data-Related Factors on BDS-3 B1I + B2b Real-Time PPP/INS Tightly Coupled Integration. Remote Sensing, 14(24), 6395. https://doi.org/10.3390/rs14246395






