Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Areas and Datasets
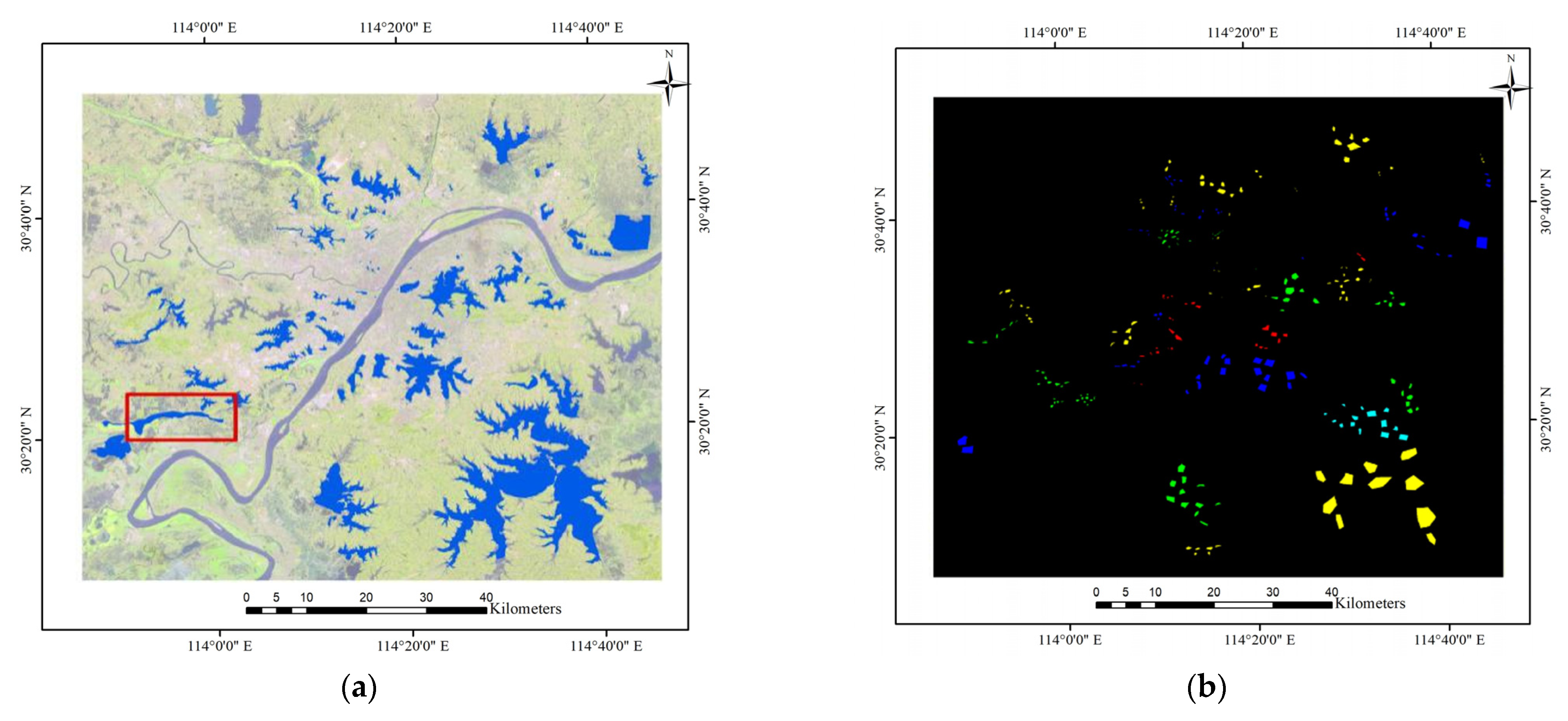
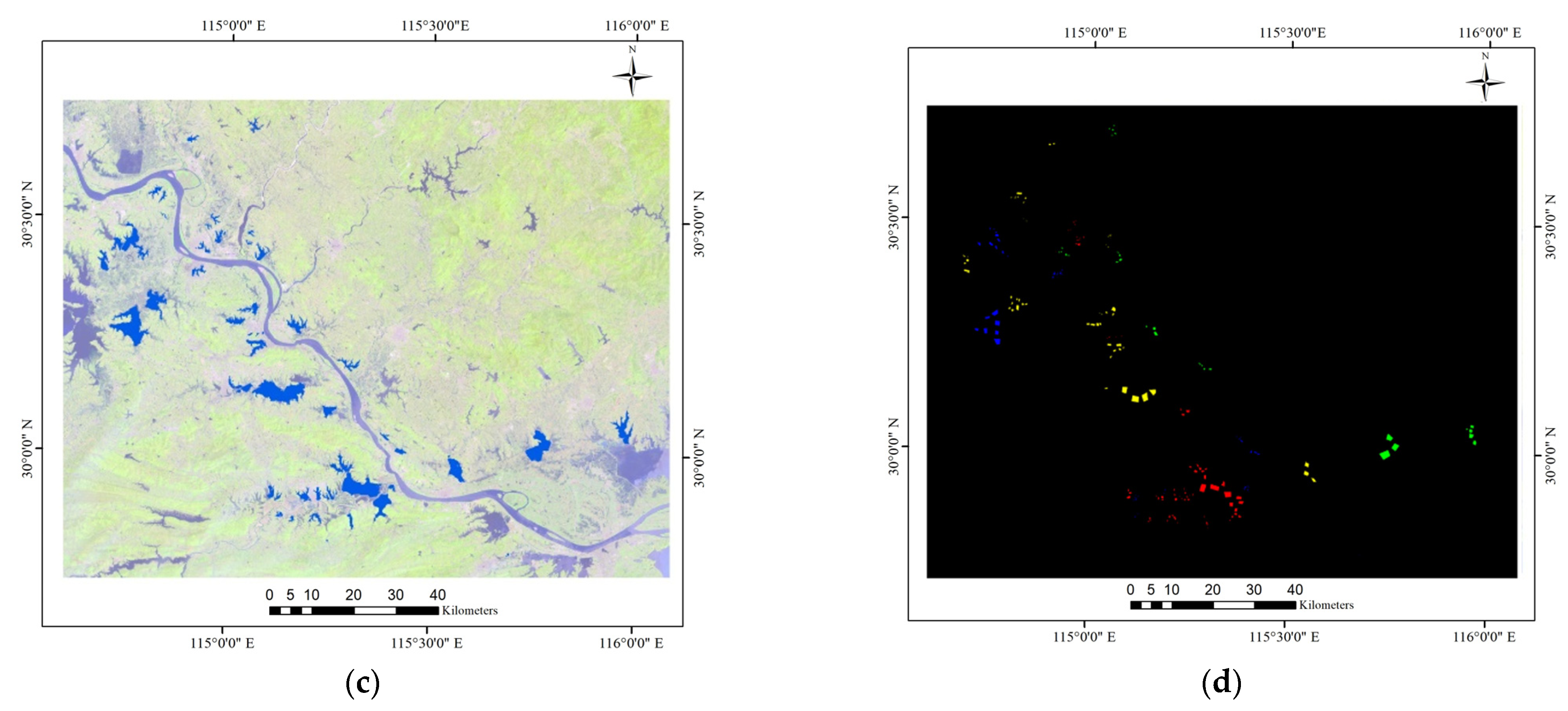
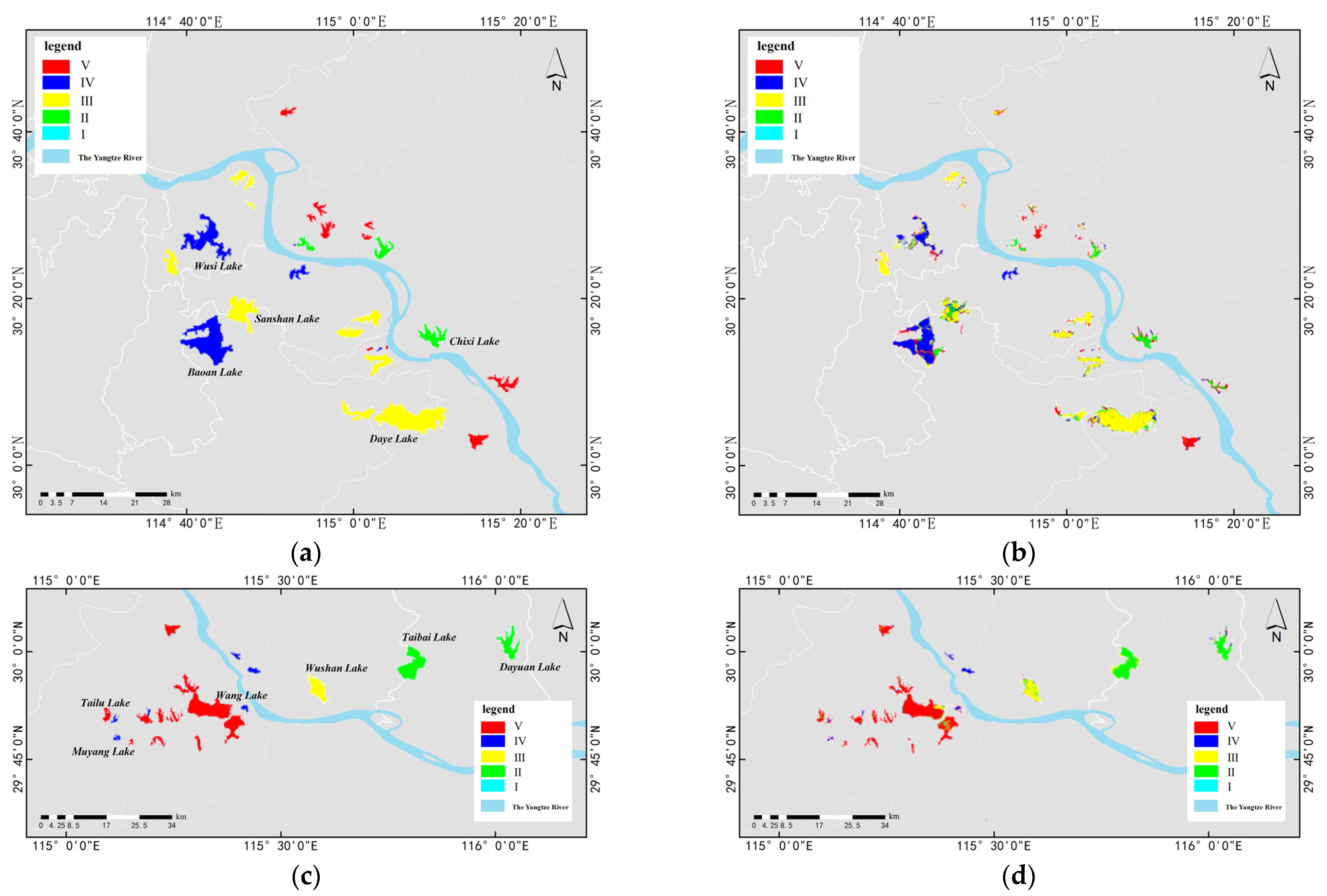
2.1.1. Study Areas
2.1.2. Image Data
2.1.3. Water Quality and Water Vector Data
2.2. Methods
2.2.1. Deep Neural Networks
2.2.2. Compared Models
Linear Support Vector Machine (L-SVM)
Decision Tree (DT)
Random Forest (RF)
Multi-Layer Perceptron (MLP)
2.2.3. Training Data Preparation
2.2.4. Accuracy Evaluation
3. Result
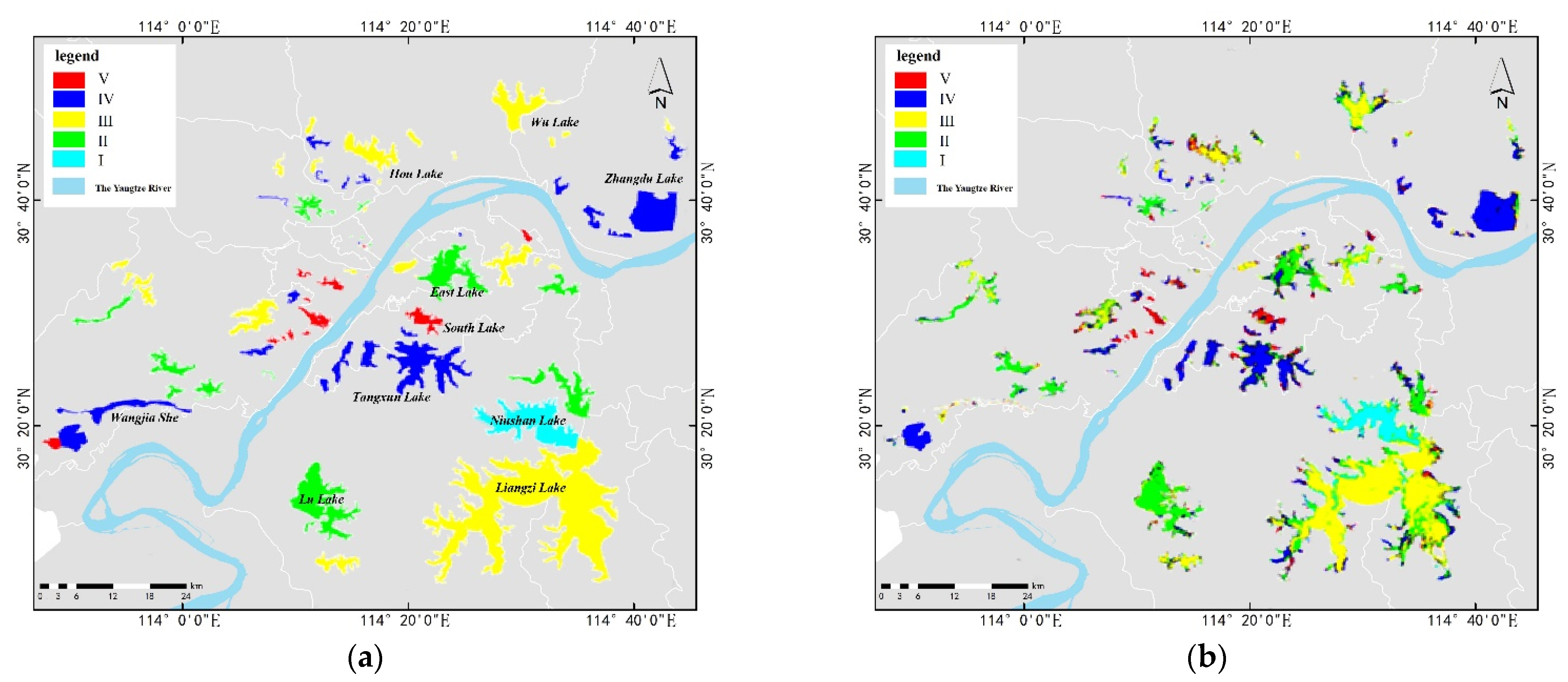
3.1. Experiment 1: The Wuhan Dataset
3.2. Experiment 2: The Huangshi Dataset
4. Discussion
4.1. Statistics-Pixel Assessment of Lake Water Quality Using a Deep Neural Network Model
4.2. Implications for Lake Ecosystem Management
4.3. Limitation and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ma, X.; Wang, L.; Yang, H.; Li, N.; Gong, C. Spatiotemporal Analysis of Water Quality Using Multivariate Statistical Techniques and the Water Quality Identification Index for the Qinhuai River Basin, East China. Water 2020, 12, 2764. [Google Scholar] [CrossRef]
- Yang, H.; Flower, R.J.; Thompson, J.R. Sustaining China’s Water Resources. Science 2013, 339, 141. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Xie, P.; Ni, L.; Flower, R.J. Pollution in the Yangtze. Science 2012, 337, 410. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Huang, X.; Thompson, J.R.; Flower, R.J. Enforcement Key to China’s Environment. Science 2015, 347, 834–835. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Guo, Y.; Yin, G.; Zhang, X.; Shi, Y.; Hao, F.; Fu, Y. UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China. Remote Sens. 2022, 14, 3272. [Google Scholar] [CrossRef]
- Salazar, K.; Staub, G. Remote Sensing Based Analysis of Changes in Water Quality—Case Study at Quintero Bay (Chile). In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7627–7630. [Google Scholar]
- Nasir, N.; Kansal, A.; Alshaltone, O.; Barneih, F.; Sameer, M.; Shanableh, A.; Al-Shamma’a, A. Water Quality Classification Using Machine Learning Algorithms. J. Water Process Eng. 2022, 48, 102920. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote Sensing Techniques to Assess Water Quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Son, S.; Wang, M. Water Quality Properties Derived from VIIRS Measurements in the Great Lakes. Remote Sens. 2020, 12, 1605. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Zhang, B.; Lee, Z.; Spyrakos, E.; Feng, L.; Liu, C.; Zhao, H.; Wu, Y.; Zhu, L.; et al. Changes of Water Clarity in Large Lakes and Reservoirs across China Observed from Long-Term MODIS. Remote Sens. Environ. 2020, 247, 111949. [Google Scholar] [CrossRef]
- Kupssinskü, L.S.; Guimarães, T.T.; de Souza, E.M. A Method for Chlorophyll-a and Suspended Solids Prediction through Remote Sensing and Machine Learning. Sensors 2020, 20, 2125. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Schalles, J.; Binding, C.; Cao, Z.; Ma, R.; Alikas, K.; Kangro, K.; Gurlin, D.; Ha, N.; et al. Seamless Retrievals of Chlorophyll-a from Sentinel-2 (MSI) and Sentinel-3 (OLCI) in Inland and Coastal Waters: A Machine-Learning Approach. Remote Sens. Environ. 2020, 240, 111604. [Google Scholar] [CrossRef]
- Guan, Q.; Feng, L.; Hou, X.; Schurgers, G.; Zheng, Y.; Tang, J. Eutrophication Changes in Fifty Large Lakes on the Yangtze Plain of China Derived from MERIS and OLCI Observations. Remote Sens. Environ. 2020, 246, 111890. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, D.; Cheng, W.; Gai, Y.; Yao, H.; Yang, L.; Pan, S. Monitoring Multi-Temporal and Spatial Variations of Water Transparency in the Jiaozhou Bay Using GOCI Data. Mar. Pollut. Bull. 2022, 180, 113815. [Google Scholar] [CrossRef]
- Nazirova, K.; Alferyeva, Y.; Lavrova, O.; Shur, Y.; Soloviev, D.; Bocharova, T.; Strochkov, A. Comparison of In Situ and Remote-Sensing Methods to Determine Turbidity and Concentration of Suspended Matter in the Estuary Zone of the Mzymta River, Black Sea. Remote Sens. 2021, 13, 143. [Google Scholar] [CrossRef]
- GB3838-2002; Surface Water Environmental Quality Standards. The State Environmental Protection Administration, The State Administration of Quality Supervision Inspection and Quarantine: Beijing, China, 2002; pp. 1–4. (In Chinese)
- Zou, Z.; Yun, Y.; Sun, J. Entropy Method for Determination of Weight of Evaluating Indicators in Fuzzy Synthetic Evaluation for Water Quality Assessment. J. Environ. Sci. 2006, 18, 1020–1023. [Google Scholar] [CrossRef]
- Wang, Y.; Ouyang, W.; Lin, C.; Zhu, W.; Critto, A.; Tysklind, M.; Wang, X.; He, M.; Wang, B.; Wu, H. Higher Fine Particle Fraction in Sediment Increased Phosphorus Flux to Estuary in Restored Yellow River Basin. Environ. Sci. Technol. 2021, 55, 6783–6790. [Google Scholar] [CrossRef]
- Zeng, S.; Du, C.; Li, Y.; Lyu, H.; Dong, X.; Lei, S.; Li, J.; Wang, H. Monitoring the Particulate Phosphorus Concentration of Inland Waters on the Yangtze Plain and Understanding Its Relationship with Driving Factors Based on OLCI Data. Sci. Total Environ. 2022, 809, 151992. [Google Scholar] [CrossRef]
- Du, N.; Ottens, H.; Sliuzas, R. Spatial Impact of Urban Expansion on Surface Water Bodies—A Case Study of Wuhan, China. Landsc. Urban Plan. 2010, 94, 175–185. [Google Scholar] [CrossRef]
- Wang, W.; Ndungu, A.W.; Li, Z.; Wang, J. Microplastics Pollution in Inland Freshwaters of China: A Case Study in Urban Surface Waters of Wuhan, China. Sci. Total Environ. 2017, 575, 1369–1374. [Google Scholar] [CrossRef]
- Fang, C.; Yang, X.; Ding, S.; Luan, X.; Xiao, R.; Du, Z.; Wang, P.; An, W.; Chu, W. Characterization of Dissolved Organic Matter and Its Derived Disinfection Byproduct Formation along the Yangtze River. Environ. Sci. Technol. 2021, 55, 12326–12336. [Google Scholar] [CrossRef]
- Geng, M.; Wang, K.; Yang, N.; Li, F.; Zou, Y.; Chen, X.; Deng, Z.; Xie, Y. Spatiotemporal Water Quality Variations and Their Relationship with Hydrological Conditions in Dongting Lake after the Operation of the Three Gorges Dam, China. J. Clean. Prod. 2021, 283, 124644. [Google Scholar] [CrossRef]
- Hinton, G.; Deng, L.; Yu, D.; Dahl, G.E. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Zhou, Z.-H.; Feng, J. Deep Forest: Towards An Alternative to Deep Neural Networks. In Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 19–25 August 2017; pp. 3553–3559. [Google Scholar]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. J. Mach. Learn. Res.—Proc. Track 2010, 9, 249–256. [Google Scholar]
- Zhang, Y.; Xia, G.; Wang, J.; Lha, D. A Multiple Feature Fully Convolutional Network for Road Extraction From High-Resolution Remote Sensing Image Over Mountainous Areas. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1600–1604. [Google Scholar] [CrossRef]
- Dewa, C.K. Afiahayati Suitable CNN Weight Initialization and Activation Function for Javanese Vowels Classification. Procedia Comput. Sci. 2018, 144, 124–132. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, Z.; Li, Y.; Guo, J. Making Deep Neural Networks Robust to Label Noise: Cross-Training with a Novel Loss Function. IEEE Access 2019, 7, 130893–130902. [Google Scholar] [CrossRef]
- Tang, M.; Huang, Z.; Yuan, Y.; Wang, C.; Peng, Y. A Bounded Scheduling Method for Adaptive Gradient Methods. Appl. Sci. 2019, 9, 3569. [Google Scholar] [CrossRef]
- Liang, D.; Ma, F.; Li, W. New Gradient-Weighted Adaptive Gradient Methods With Dynamic Constraints. IEEE Access 2020, 8, 110929–110942. [Google Scholar] [CrossRef]
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive Subgradient Methods for Online Learning and Stochastic Optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Yang, L.; Cai, D. AdaDB: An Adaptive Gradient Method with Data-Dependent Bound. Neurocomputing 2020, 419, 183–189. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Ghadimi, S.; Lan, G.; Zhang, H. Mini-Batch Stochastic Approximation Methods for Nonconvex Stochastic Composite Optimization. arXiv 2013, arXiv:1308.6594. [Google Scholar] [CrossRef]
- Santoro, A.; Bartunov, S.; Botvinick, M.; Wierstra, D.; Lillicrap, T. One-Shot Learning with Memory-Augmented Neural Networks. arXiv 2016, arXiv:1605.06065. [Google Scholar]
- Gilcher, M.; Ruf, T.; Emmerling, C.; Udelhoven, T. Remote Sensing Based Binary Classification of Maize. Dealing with Residual Autocorrelation in Sparse Sample Situations. Remote Sens. 2019, 11, 2172. [Google Scholar] [CrossRef]
- Mugiraneza, T.; Nascetti, A.; Ban, Y. WorldView-2 Data for Hierarchical Object-Based Urban Land Cover Classification in Kigali: Integrating Rule-Based Approach with Urban Density and Greenness Indices. Remote Sens. 2019, 11, 2128. [Google Scholar] [CrossRef]
- Phan, A.; Ha, D.N.; Man, C.D.; Nguyen, T.T.; Bui, H.Q.; Nguyen, T.T.N. Rapid Assessment of Flood Inundation and Damaged Rice Area in Red River Delta from Sentinel 1A Imagery. Remote Sens. 2019, 11, 2034. [Google Scholar] [CrossRef]
- Jiao, L.; Sun, W.; Yang, G.; Ren, G.; Liu, Y. A Hierarchical Classification Framework of Satellite Multispectral/Hyperspectral Images for Mapping Coastal Wetlands. Remote Sens. 2019, 11, 2238. [Google Scholar] [CrossRef]
- Xiong, Y.; Zhang, Q.; Chen, X. Large Scale Agricultural Plastic Mulch Detecting and Monitoring with Multi-Source Remote Sensing Data: A Case Study in Xinjiang, China. Remote Sens. 2019, 11, 2088. [Google Scholar] [CrossRef]
- Muñoz, D.F.; Cissell, J.R.; Moftakhari, H. Adjusting Emergent Herbaceous Wetland Elevation with Object-Based Image Analysis, Random Forest and the 2016 NLCD. Remote Sens. 2019, 11, 2346. [Google Scholar] [CrossRef]
- Shirvani, Z.; Abdi, O.; Buchroithner, M. A Synergetic Analysis of Sentinel-1 and -2 for Mapping Historical Landslides Using Object-Oriented Random Forest in the Hyrcanian Forests. Remote Sens. 2019, 11, 2300. [Google Scholar] [CrossRef]
- Yuan, H.; van der Wiele, C.F.; Khorram, S. An Automated Artificial Neural Network System for Land Use/Land Cover Classification from Landsat TM Imagery. Remote Sens. 2009, 1, 243–265. [Google Scholar] [CrossRef]
- Peña, J.M.; Gutiérrez, P.A.; Hervás-Martínez, C. Object-Based Image Classification of Summer Crops with Machine Learning Methods. Remote Sens. 2014, 6, 5019–5041. [Google Scholar] [CrossRef]
- Fu, G.; Liu, C.; Zhou, R.; Sun, T.; Zhang, Q. Classification for High Resolution Remote Sensing Imagery Using a Fully Convolutional Network. Remote Sens. 2017, 9, 498. [Google Scholar] [CrossRef]
- Zhu, K.; Chen, Y.; Ghamisi, P.; Jia, X.; Benediktsson, J.A. Deep Convolutional Capsule Network for Hyperspectral Image Spectral and Spectral-Spatial Classification. Remote Sens. 2019, 11, 223. [Google Scholar] [CrossRef]
- Miraki, S.; Zanganeh, S.H.; Chapi, K.; Singh, V.P.; Shirzadi, A.; Shahabi, H.; Pham, B.T. Mapping Groundwater Potential Using a Novel Hybrid Intelligence Approach. Water Resour. Manag. 2018, 33, 281–302. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, Y.; Huang, C.; Wang, Z.; Huang, Q.; Yin, F.; Guo, Y.; Cao, L. Inland Lakes Mapping for Monitoring Water Quality Using a Detail/Smoothing-Balanced Conditional Random Field Based on Landsat-8/Levels Data. Sensors 2020, 20, 1345. [Google Scholar] [CrossRef]
- Pu, F.; Ding, C.; Chao, Z.; Yu, Y.; Xu, X. Water-Quality Classification of Inland Lakes Using Landsat8 Images by Convolutional Neural Networks. Remote Sens. 2019, 11, 1674. [Google Scholar] [CrossRef]
- Hashemi, S.; Anthony, N.; Tann, H.; Bahar, R.I.; Reda, S. Understanding the Impact of Precision Quantization on the Accuracy and Energy of Neural Networks. In Proceedings of the Design, Automation Test in Europe Conference Exhibition (DATE), 2017, Lausanne, Switzerland, 27–31 March 2017; pp. 1474–1479. [Google Scholar]
- Yang, H. China Must Continue the Momentum of Green Law. Nature 2014, 509, 535. [Google Scholar] [CrossRef]
- Yang, H.; Flower, R.J.; Thompson, J.R. China’s New Leaders Offer Green Hope. Nature 2013, 493, 163. [Google Scholar] [CrossRef]
- Wei, L.; Guan, L.; Qu, L.; Guo, D. Prediction of Sea Surface Temperature in the China Seas Based on Long Short-Term Memory Neural Networks. Remote Sens. 2020, 12, 2697. [Google Scholar] [CrossRef]
- Wang, X.; Huang, J.; Feng, Q.; Yin, D. Winter Wheat Yield Prediction at County Level and Uncertainty Analysis in Main Wheat-Producing Regions of China with Deep Learning Approaches. Remote Sens. 2020, 12, 1744. [Google Scholar] [CrossRef]
- Chang, Y.; Luo, B. Bidirectional Convolutional LSTM Neural Network for Remote Sensing Image Super-Resolution. Remote Sens. 2019, 11, 2333. [Google Scholar] [CrossRef]
- Ji, J.; Jing, W.; Chen, G.; Lin, J.; Song, H. Multi-Label Remote Sensing Image Classification with Latent Semantic Dependencies. Remote Sens. 2020, 12, 1110. [Google Scholar] [CrossRef]
| Lakes | Grade | Parameters (mg/L) | |||
|---|---|---|---|---|---|
| TP | COD | BOD5 | CODMn | ||
| Niushan Lake | III | 0.084 (0.05) | 33.6 (20) | 4.28 (4) | 7.32 (6) |
| Chen Lake | IV | 0.16 (0.1) | 48 (30) | 8.28 (6) | 11.2 (10) |
| Longyang Lake | V | 0.76 (0.2) | 152 (40) | 16 (10) | 19.05 (15) |
| Chaibo Lake | VI | 0.72 (0.2) | 70 (40) | 17.5 (10) | 19.5 (15) |
| Study Areas | Grades | Sample Numbers | Percentages |
|---|---|---|---|
| Wuhan | II | 9311 | 7% |
| III | 24,006 | 18% | |
| IV | 63,717 | 47% | |
| V | 33,259 | 24% | |
| VI | 5745 | 4% | |
| Total | 136,038 | 100% | |
| Huangshi | III | 17,392 | 21% |
| IV | 26,008 | 32% | |
| V | 14,954 | 18% | |
| VI | 23,863 | 29% | |
| Total | 82,217 | 100% |
| Grade | L-SVM | DT | RF | MLP | DNN |
|---|---|---|---|---|---|
| II | 61.89 ± 1.52 | 90.34 ± 0.82 | 90.58 ± 0.90 | 71.18 ± 3.34 | 91.53 ± 0.87 |
| III | 47.08 ± 2.24 | 81.13 ± 0.53 | 85.20 ± 0.60 | 65.85 ± 7.18 | 90.11 ± 0.50 |
| IV | 79.09 ± 0.66 | 92.30 ± 0.39 | 95.18 ± 0.23 | 84.85 ± 2.41 | 95.30 ± 0.23 |
| V | 68.34 ± 0.57 | 88.14 ± 0.24 | 94.29 ± 0.29 | 88.44 ± 3.53 | 95.25 ± 0.36 |
| VI | 30.37 ± 2.58 | 70.37 ± 1.88 | 76.98 ± 1.50 | 54.30 ± 6.50 | 77.62 ± 1.54 |
| OA | 67.58 ± 0.35 | 88.26 ± 0.24 | 92.12 ± 0.21 | 80.15 ± 2.01 | 93.37 ± 0.09 |
| Kappa | 0.5229 ± 0.0059 | 0.8278 ± 0.0034 | 0.8842 ± 0.0031 | 0.7085 ± 0.0296 | 0.9028 ± 0.0015 |
| No. | Water Quality Grades | Lakes (Number) | Non-Water | OA | Prediction | ||||
|---|---|---|---|---|---|---|---|---|---|
| No. 1 | No. 2 | No. 3 | No. 4 | No. 5 | |||||
| 1 | Grade II | 1 | 0 | 100% | 1 | 0 | 0 | 0 | 0 |
| 2 | Grade III | 13 | 0 | 100% | 0 | 13 | 0 | 0 | 0 |
| 3 | Grade IV | 29 | 1 | 85.71% | 0 | 2 | 24 | 0 | 2 |
| 4 | Grade V | 20 | 1 | 100% | 0 | 0 | 0 | 19 | 0 |
| 5 | Grade VI | 13 | 1 | 83.33% | 0 | 1 | 0 | 1 | 10 |
| Grades | L-SVM | DT | RF | MLP | DNN |
|---|---|---|---|---|---|
| Grade III | 55.30 ± 0.52 | 91.05 ± 0.60 | 95.02 ± 0.54 | 88.16 ± 2.06 | 96.33 ± 0.59 |
| Grade IV | 76.32 ± 0.61 | 92.46 ± 0.26 | 95.68 ± 0.41 | 89.20 ± 2.06 | 96.36 ± 0.47 |
| Grade V | 42.21 ± 0.71 | 91.23 ± 0.56 | 93.98 ± 0.37 | 89.56 ± 2.68 | 94.58 ± 0.54 |
| Grade VI | 81.64 ± 0.43 | 92.06 ± 0.40 | 97.36 ± 0.23 | 94.92 ± 1.99 | 97.60 ± 0.36 |
| OA | 67.22 ± 0.27 | 91.82 ± 0.25 | 95.72 ± 0.17 | 90.71 ± 1.20 | 96.39 ± 0.17 |
| Kappa | 0.5460 ± 0.0039 | 0.8891 ± 0.0034 | 0.9419 ± 0.0023 | 0.8739 ± 0.0162 | 0.9510 ± 0.0023 |
| No. | Water Quality Grades | Lakes (Number) | Non-Water | OA | Prediction | |||
|---|---|---|---|---|---|---|---|---|
| No. 1 | No. 2 | No. 3 | No. 4 | |||||
| 1 | Grade III | 8 | 0 | 87.50% | 7 | 0 | 0 | 1 |
| 2 | Grade IV | 11 | 0 | 72.73% | 0 | 8 | 0 | 3 |
| 3 | Grade V | 11 | 1 | 70.00% | 0 | 0 | 7 | 3 |
| 4 | Grade VI | 19 | 0 | 89.47% | 0 | 0 | 2 | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, Z.; Wei, L.; Yang, H.; Wang, Z.; Xiao, Z.; Li, Z.; Yang, Y.; Xu, G. Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model. Remote Sens. 2022, 14, 6238. https://doi.org/10.3390/rs14246238
Wei Z, Wei L, Yang H, Wang Z, Xiao Z, Li Z, Yang Y, Xu G. Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model. Remote Sensing. 2022; 14(24):6238. https://doi.org/10.3390/rs14246238
Chicago/Turabian StyleWei, Zeyang, Lifei Wei, Hong Yang, Zhengxiang Wang, Zhiwei Xiao, Zhongqiang Li, Yujing Yang, and Guobin Xu. 2022. "Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model" Remote Sensing 14, no. 24: 6238. https://doi.org/10.3390/rs14246238
APA StyleWei, Z., Wei, L., Yang, H., Wang, Z., Xiao, Z., Li, Z., Yang, Y., & Xu, G. (2022). Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model. Remote Sensing, 14(24), 6238. https://doi.org/10.3390/rs14246238








