Comparison of Three Mixed-Effects Models for Mass Movement Susceptibility Mapping Based on Incomplete Inventory in China
Abstract
1. Introduction
2. Study Area and Materials
2.1. Characterization of the Study Area
2.2. Spatial Database
2.2.1. Inventory of Mass Movement
2.2.2. Mass Movement Influencing Factors
- (1)
- Fixed-Effect Factors
- (2)
- Random intercept factors
3. Methodology
3.1. Generalized Linear Mixed-Effects Model
3.2. Generalized Additive Mixed-Effects Model
3.3. Tree-Boosted Mixed-Effects Model
3.4. Model Evaluation
4. Results
4.1. Preliminary Data Analysis
4.1.1. Multicollinearity Test
4.1.2. Correlation Analysis between Mass Movements and Influencing Factors
4.2. Quantitative Performance Comparison
4.2.1. Cross-Validation Results
4.2.2. Predictions Based on Highly Biased Inventories
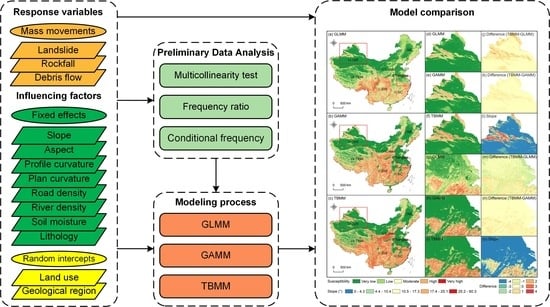
4.3. Spatial Pattern Comparison of the Susceptibility Map
4.4. Factor Contribution Analysis
5. Discussion
6. Conclusions
- (i)
- From a quantitative point of view, the tree-boosted mixed-effects model (TBMM) performs best in both spatial and non-spatial cross-validation for all mass movements. In addition, when further reducing the completeness of inventory data in different categories of land use or geological environment division, TBMM maintained the best AUROC scores with little variation among the different highly biased types.
- (ii)
- From a qualitative point of view, the derived TBMM yielded more plausible spatial susceptibility patterns than the other two mixed models and conventional methods discussed in the existing literature.
- (iii)
- Through the factor contribution analysis, it was found that the profile curvature and slope contribute significantly to the evaluation of debris flow. For rockfall, slope, soil moisture and road density had more significant contribution. Regarding the landslide, slope and road density were the most critical factors.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, Q.; Zhang, Q.-P.; Liu, Y.-Y.; Tong, L.-J.; Zhang, Y.-Z.; Li, X.-Y.; Li, J.-L. Characterizing the spatial distribution of typical natural disaster vulnerability in China from 2010 to 2017. Nat. Hazards 2020, 100, 3–15. [Google Scholar] [CrossRef]
- Xu, L.; Meng, X.; Xu, X. Natural hazard chain research in China: A review. Nat. Hazards 2014, 70, 1631–1659. [Google Scholar] [CrossRef]
- Wang, J.A.; Xiao, H.; Hartmann, R.; Yue, Y. Physical Geography of China and the US. In A Comparative Geography of China and the US; Springer: Berlin/Heidelberg, Germany, 2014; pp. 23–81. [Google Scholar]
- Lin, Q.; Wang, Y. Spatial and temporal analysis of a fatal landslide inventory in China from 1950 to 2016. Landslides 2018, 15, 2357–2372. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, Y.; Glade, T.; Zhang, J.; Zhang, Y. Assessing the spatiotemporal impact of climate change on event rainfall characteristics influencing landslide occurrences based on multiple GCM projections in China. Clim. Chang. 2020, 162, 761–779. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Teimoori Yansari, Z.; Panagos, P.; Pradhan, B. Analysis and evaluation of landslide susceptibility: A review on articles published during 2005–2016 (periods of 2005–2012 and 2013–2016). Arab. J. Geosci. 2018, 11, 193. [Google Scholar] [CrossRef]
- Wang, D.; Hao, M.; Chen, S.; Meng, Z.; Jiang, D.; Ding, F. Assessment of landslide susceptibility and risk factors in China. Nat. Hazards 2021, 108, 3045–3059. [Google Scholar] [CrossRef]
- Huang, H.; Wang, Y.; Li, Y.; Zhou, Y.; Zeng, Z. Debris-Flow Susceptibility Assessment in China: A Comparison between Traditional Statistical and Machine Learning Methods. Remote Sens. 2022, 14, 4475. [Google Scholar] [CrossRef]
- Gaprindashvili, G.; Van Westen, C.J. Generation of a national landslide hazard and risk map for the country of Georgia. Nat. Hazards 2016, 80, 69–101. [Google Scholar] [CrossRef]
- Ngo, P.T.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of deep learning algorithms for national scale landslide susceptibility mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Komac, M.; Ribičič, M. Landslide susceptibility map of Slovenia at scale 1: 250,000. Geologija 2006, 49, 295–309. [Google Scholar] [CrossRef]
- Saroglou, C. GIS-based rockfall susceptibility zoning in Greece. Geosciences 2019, 9, 163. [Google Scholar] [CrossRef]
- Titti, G.; Borgatti, L.; Zou, Q.; Cui, P.; Pasuto, A. Landslide susceptibility in the Belt and Road Countries: Continental step of a multi-scale approach. Environ. Earth Sci. 2021, 80, 630. [Google Scholar] [CrossRef]
- Broeckx, J.; Vanmaercke, M.; Duchateau, R.; Poesen, J. A data-based landslide susceptibility map of Africa. Earth-Sci. Rev. 2018, 185, 102–121. [Google Scholar] [CrossRef]
- Van Den Eeckhaut, M.; Hervás, J.; Jaedicke, C.; Malet, J.-P.; Montanarella, L.; Nadim, F. Statistical modelling of Europe-wide landslide susceptibility using limited landslide inventory data. Landslides 2012, 9, 357–369. [Google Scholar] [CrossRef]
- Günther, A.; Reichenbach, P.; Malet, J.-P.; Van Den Eeckhaut, M.; Hervás, J.; Dashwood, C.; Guzzetti, F. Tier-based approaches for landslide susceptibility assessment in Europe. Landslides 2013, 10, 529–546. [Google Scholar] [CrossRef]
- Lin, L.; Lin, Q.; Wang, Y. Landslide susceptibility mapping on a global scale using the method of logistic regression. Nat. Hazards Earth Syst. Sci. 2017, 17, 1411–1424. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.; Huffman, G. Use of satellite remote sensing data in the mapping of global landslide susceptibility. Nat. Hazards 2007, 43, 245–256. [Google Scholar] [CrossRef]
- Jia, G.; Alvioli, M.; Gariano, S.L.; Marchesini, I.; Guzzetti, F.; Tang, Q. A global landslide non-susceptibility map. Geomorphology 2021, 389, 107804. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.-P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Tien Bui, D.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar] [CrossRef]
- Ilia, I.; Tsangaratos, P. Applying weight of evidence method and sensitivity analysis to produce a landslide susceptibility map. Landslides 2016, 13, 379–397. [Google Scholar] [CrossRef]
- Li, L.; Lan, H.; Guo, C.; Zhang, Y.; Li, Q.; Wu, Y. A modified frequency ratio method for landslide susceptibility assessment. Landslides 2017, 14, 727–741. [Google Scholar] [CrossRef]
- Xiong, K.; Adhikari, B.R.; Stamatopoulos, C.A.; Zhan, Y.; Wu, S.; Dong, Z.; Di, B. Comparison of different machine learning methods for debris flow susceptibility mapping: A case study in the Sichuan Province, China. Remote Sens. 2020, 12, 295. [Google Scholar] [CrossRef]
- Melo, R.; Zêzere, J.L. Modeling debris flow initiation and run-out in recently burned areas using data-driven methods. Nat. Hazards 2017, 88, 1373–1407. [Google Scholar] [CrossRef]
- Goetz, J.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Lee, D.-H.; Kim, Y.-T.; Lee, S.-R. Shallow landslide susceptibility models based on artificial neural networks considering the factor selection method and various non-linear activation functions. Remote Sens. 2020, 12, 1194. [Google Scholar] [CrossRef]
- Di Napoli, M.; Marsiglia, P.; Di Martire, D.; Ramondini, M.; Ullo, S.L.; Calcaterra, D. Landslide susceptibility assessment of wildfire burnt areas through earth-observation techniques and a machine learning-based approach. Remote Sens. 2020, 12, 2505. [Google Scholar] [CrossRef]
- Lin, J.; He, P.; Yang, L.; He, X.; Lu, S.; Liu, D. Predicting future urban waterlogging-prone areas by coupling the maximum entropy and FLUS model. Sustain. Cities Soc. 2022, 80, 103812. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and Naïve Bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Park, S.-J.; Lee, C.-W.; Lee, S.; Lee, M.-J. Landslide susceptibility mapping and comparison using decision tree models: A Case Study of Jumunjin Area, Korea. Remote Sens. 2018, 10, 1545. [Google Scholar] [CrossRef]
- Shirvani, Z. A holistic analysis for landslide susceptibility mapping applying geographic object-based random forest: A comparison between protected and non-protected forests. Remote Sens. 2020, 12, 434. [Google Scholar] [CrossRef]
- Sahin, E.K. Comparative analysis of gradient boosting algorithms for landslide susceptibility mapping. Geocarto Int. 2020, 37, 2441–2465. [Google Scholar] [CrossRef]
- Cascini, L. Applicability of landslide susceptibility and hazard zoning at different scales. Eng. Geol. 2008, 102, 164–177. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Glade, T. The propagation of inventory-based positional errors into statistical landslide susceptibility models. Nat. Hazards Earth Syst. Sci. 2016, 16, 2729–2745. [Google Scholar] [CrossRef]
- Erener, A.; Düzgün, H. Landslide susceptibility assessment: What are the effects of mapping unit and mapping method? Environ. Earth Sci. 2012, 66, 859–877. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A.-X. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. Catena 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Sun, D.; Shi, S.; Wen, H.; Xu, J.; Zhou, X.; Wu, J. A hybrid optimization method of factor screening predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 2021, 379, 107623. [Google Scholar] [CrossRef]
- Cheng, J.; Dai, X.; Wang, Z.; Li, J.; Qu, G.; Li, W.; She, J.; Wang, Y. Landslide Susceptibility Assessment Model Construction Using Typical Machine Learning for the Three Gorges Reservoir Area in China. Remote Sens. 2022, 14, 2257. [Google Scholar] [CrossRef]
- Kang, L.; Chen, R.-S.; Xiong, N.; Chen, Y.-C.; Hu, Y.-X.; Chen, C.-M. Selecting hyper-parameters of Gaussian process regression based on non-inertial particle swarm optimization in Internet of Things. IEEE Access 2019, 7, 59504–59513. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2010, 111, 62–72. [Google Scholar] [CrossRef]
- Steger, S.; Mair, V.; Kofler, C.; Pittore, M.; Zebisch, M.; Schneiderbauer, S. Correlation does not imply geomorphic causation in data-driven landslide susceptibility modelling–Benefits of exploring landslide data collection effects. Sci. Total Environ. 2021, 776, 145935. [Google Scholar] [CrossRef]
- Zêzere, J.; Pereira, S.; Melo, R.; Oliveira, S.; Garcia, R.A. Mapping landslide susceptibility using data-driven methods. Sci. Total Environ. 2017, 589, 250–267. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Petschko, H.; Glade, T. Exploring discrepancies between quantitative validation results and the geomorphic plausibility of statistical landslide susceptibility maps. Geomorphology 2016, 262, 8–23. [Google Scholar] [CrossRef]
- Harp, E.L.; Keefer, D.K.; Sato, H.P.; Yagi, H. Landslide inventories: The essential part of seismic landslide hazard analyses. Eng. Geol. 2011, 122, 9–21. [Google Scholar] [CrossRef]
- Kirschbaum, D.; Stanley, T.; Zhou, Y. Spatial and temporal analysis of a global landslide catalog. Geomorphology 2015, 249, 4–15. [Google Scholar] [CrossRef]
- Steger, S.; Schmaltz, E.; Glade, T. The (f) utility to account for pre-failure topography in data-driven landslide susceptibility modelling. Geomorphology 2020, 354, 107041. [Google Scholar] [CrossRef]
- Yanar, T.; Kocaman, S.; Gokceoglu, C. Use of Mamdani fuzzy algorithm for multi-hazard susceptibility assessment in a developing urban settlement (Mamak, Ankara, Turkey). ISPRS Int. J. Geo-Inf. 2020, 9, 114. [Google Scholar] [CrossRef]
- Lima, P.; Steger, S.; Glade, T. Counteracting flawed landslide data in statistically based landslide susceptibility modelling for very large areas: A national-scale assessment for Austria. Landslides 2021, 18, 3531–3546. [Google Scholar] [CrossRef]
- Steger, S.; Brenning, A.; Bell, R.; Glade, T. The influence of systematically incomplete shallow landslide inventories on statistical susceptibility models and suggestions for improvements. Landslides 2017, 14, 1767–1781. [Google Scholar] [CrossRef]
- Dingemanse, N.J.; Dochtermann, N.A. Quantifying individual variation in behaviour: Mixed-effect modelling approaches. J. Anim. Ecol. 2013, 82, 39–54. [Google Scholar] [CrossRef] [PubMed]
- Ngufor, C.; Van Houten, H.; Caffo, B.S.; Shah, N.D.; McCoy, R.G. Mixed Effect Machine Learning: A framework for predicting longitudinal change in hemoglobin A1c. J. Biomed. Inform. 2019, 89, 56–67. [Google Scholar] [CrossRef]
- Lin, Q.; Lima, P.; Steger, S.; Glade, T.; Jiang, T.; Zhang, J.; Liu, T.; Wang, Y. National-scale data-driven rainfall induced landslide susceptibility mapping for China by accounting for incomplete landslide data. Geosci. Front. 2021, 12, 101248. [Google Scholar] [CrossRef]
- Steger, S.; Mair, V.; Kofler, C.; Schneiderbauer, S.; Zebisch, M. The necessity to consider the landslide data origin in statistically-based spatial predictive modelling-A landslide intervention index for South Tyrol (Italy). In EGU General Assembly Conference Abstracts; EGU: Munich, Germany, 2020; p. 3440. [Google Scholar]
- Sigrist, F. Gaussian process boosting. arXiv 2020, arXiv:2004.02653. [Google Scholar] [CrossRef]
- Domrös, M.; Peng, G. The Climate of China; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Chen, G.; Magistrale, H.; Rong, Y.; Cheng, J.; Binselam, S.A.; Xu, X. Seismic site condition of Mainland China from geology. Seismol. Res. Lett. 2021, 92, 998–1010. [Google Scholar] [CrossRef]
- Galli, M.; Ardizzone, F.; Cardinali, M.; Guzzetti, F.; Reichenbach, P. Comparing landslide inventory maps. Geomorphology 2008, 94, 268–289. [Google Scholar] [CrossRef]
- Pellicani, R.; Van Westen, C.J.; Spilotro, G. Assessing landslide exposure in areas with limited landslide information. Landslides 2014, 11, 463–480. [Google Scholar] [CrossRef]
- Luo, W.; Liu, C.-C. Innovative landslide susceptibility mapping supported by geomorphon and geographical detector methods. Landslides 2018, 15, 465–474. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Xu, C.; Xu, C.; Song, C. Local-scale landslide susceptibility mapping using the B-GeoSVC model. Landslides 2019, 16, 1301–1312. [Google Scholar] [CrossRef]
- Zhou, X.; Wen, H.; Zhang, Y.; Xu, J.; Zhang, W. Landslide susceptibility mapping using hybrid random forest with GeoDetector and RFE for factor optimization. Geosci. Front. 2021, 12, 101211. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Rossi, M. Landslide susceptibility modeling in a landslide prone area in Mazandarn Province, north of Iran: A comparison between GLM, GAM, MARS, and M-AHP methods. Theor. Appl. Climatol. 2017, 130, 609–633. [Google Scholar] [CrossRef]
- Burrough, P.A.; McDonnell, R.A.; Lloyd, C.D. Principles of Geographical Information Systems; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Farr, T.G.; Kobrick, M. Shuttle Radar Topography Mission produces a wealth of data. Eos Trans. Am. Geophys. Union 2000, 81, 583–585. [Google Scholar] [CrossRef]
- Huang, F.; Pan, L.; Fan, X.; Jiang, S.-H.; Huang, J.; Zhou, C. The uncertainty of landslide susceptibility prediction modeling: Suitability of linear conditioning factors. Bull. Eng. Geol. Environ. 2022, 81, 182. [Google Scholar] [CrossRef]
- Bui, D.T.; Lofman, O.; Revhaug, I.; Dick, O. Landslide susceptibility analysis in the Hoa Binh province of Vietnam using statistical index and logistic regression. Nat. Hazards 2011, 59, 1413–1444. [Google Scholar] [CrossRef]
- Hua, Y.; Wang, X.; Li, Y.; Xu, P.; Xia, W. Dynamic development of landslide susceptibility based on slope unit and deep neural networks. Landslides 2021, 18, 281–302. [Google Scholar] [CrossRef]
- Trabucco, A.; Zomer, R. Global High-Resolution Soil-Water Balance. Figshare. Fileset 2019, 10, m9. [Google Scholar] [CrossRef]
- Hartmann, J.; Moosdorf, N. The new global lithological map database GLiM: A representation of rock properties at the Earth surface. Geochem. Geophys. Geosyst. 2012, 13, 12. [Google Scholar] [CrossRef]
- Du, J.; Glade, T.; Woldai, T.; Chai, B.; Zeng, B. Landslide susceptibility assessment based on an incomplete landslide inventory in the Jilong Valley, Tibet, Chinese Himalayas. Eng. Geol. 2020, 270, 105572. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z. A comparative study of landslide susceptibility mapping using SVM and PSO-SVM models based on Grid and Slope Units. Math. Probl. Eng. 2021, 2021, 8854606. [Google Scholar] [CrossRef]
- Hussin, H.Y.; Zumpano, V.; Reichenbach, P.; Sterlacchini, S.; Micu, M.; van Westen, C.; Bălteanu, D. Different landslide sampling strategies in a grid-based bi-variate statistical susceptibility model. Geomorphology 2016, 253, 508–523. [Google Scholar] [CrossRef]
- Breslow, N.E.; Clayton, D.G. Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 1993, 88, 9–25. [Google Scholar] [CrossRef]
- Stroup, W.W. Generalized Linear Mixed Models: Modern Concepts, Methods and Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Rao, C.R.; Miller, J.P.; Rao, D.C. Essential statistical methods for medical statistics. In Handbook of Statistics: Epidemiology and Medical Statistics; Elsevier Inc.: Amsterdam, The Netherlands, 2011; pp. 1–351. [Google Scholar]
- Lin, X.; Zhang, D. Inference in generalized additive mixed modelsby using smoothing splines. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1999, 61, 381–400. [Google Scholar] [CrossRef]
- Wang, Y. Mixed effects smoothing spline analysis of variance. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 1998, 60, 159–174. [Google Scholar] [CrossRef]
- Mullah, M.A.S.; Hanley, J.A.; Benedetti, A. Modeling perinatal mortality in twins via generalized additive mixed models: A comparison of estimation approaches. BMC Med. Res. Methodol. 2019, 19, 209. [Google Scholar] [CrossRef]
- Iddrisu, W.A.; Nokoe, K.S.; Luguterah, A.; Antwi, E.O. Generalized Additive Mixed Modelling of River Discharge in the Black Volta River. Open J. Stat. 2017, 7, 621. [Google Scholar] [CrossRef]
- Sahin, E.K. Assessing the predictive capability of ensemble tree methods for landslide susceptibility mapping using XGBoost, gradient boosting machine, and random forest. SN Appl. Sci. 2020, 2, 1308. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. Adv. Neural Inf. Process. Syst. 2017, 30, 3146–3154. [Google Scholar]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef] [PubMed]
- Brenning, A. Spatial cross-validation and bootstrap for the assessment of prediction rules in remote sensing: The R package sperrorest. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5372–5375. [Google Scholar]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting linear mixed-effects models using lme4. arXiv 2014, arXiv:1406.5823. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017; pp. 1–496. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013, arXiv:1309.0238. [Google Scholar] [CrossRef]
- Mandal, K.; Saha, S.; Mandal, S. Applying deep learning and benchmark machine learning algorithms for landslide susceptibility modelling in Rorachu river basin of Sikkim Himalaya, India. Geosci. Front. 2021, 12, 101203. [Google Scholar] [CrossRef]
- Korup, O.; Stolle, A. Landslide prediction from machine learning. Geol. Today 2014, 30, 26–33. [Google Scholar] [CrossRef]
- Chen, W.; Chai, H.; Sun, X.; Wang, Q.; Ding, X.; Hong, H. A GIS-based comparative study of frequency ratio, statistical index and weights-of-evidence models in landslide susceptibility mapping. Arab. J. Geosci. 2016, 9, 204. [Google Scholar] [CrossRef]
- Petschko, H.; Bell, R.; Glade, T. Effectiveness of visually analyzing LiDAR DTM derivatives for earth and debris slide inventory mapping for statistical susceptibility modeling. Landslides 2016, 13, 857–872. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Liu, L.; Li, S.; Li, X.; Jiang, Y.; Wei, W.; Wang, Z.; Bai, Y. An integrated approach for landslide susceptibility mapping by considering spatial correlation and fractal distribution of clustered landslide data. Landslides 2019, 16, 715–728. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, R.; Wang, C. Evaluation and Prediction of Landslide Susceptibility in Yichang Section of Yangtze River Basin Based on Integrated Deep Learning Algorithm. Remote Sens. 2022, 14, 2717. [Google Scholar] [CrossRef]
- Liu, X.; Miao, C. Large-scale assessment of landslide hazard, vulnerability and risk in China. Geomat. Nat. Hazards Risk 2018, 9, 1037–1052. [Google Scholar] [CrossRef]
- Shirzadi, A.; Bui, D.T.; Pham, B.T.; Solaimani, K.; Chapi, K.; Kavian, A.; Shahabi, H.; Revhaug, I. Shallow landslide susceptibility assessment using a novel hybrid intelligence approach. Environ. Earth Sci. 2017, 76, 60. [Google Scholar] [CrossRef]
- Hajjem, A.; Bellavance, F.; Larocque, D. Mixed-effects random forest for clustered data. J. Stat. Comput. Simul. 2014, 84, 1313–1328. [Google Scholar] [CrossRef]
- Speiser, J.L.; Wolf, B.J.; Chung, D.; Karvellas, C.J.; Koch, D.G.; Durkalski, V.L. BiMM forest: A random forest method for modeling clustered and longitudinal binary outcomes. Chemom. Intell. Lab. Syst. 2019, 185, 122–134. [Google Scholar] [CrossRef]
- Hajjem, A.; Larocque, D.; Bellavance, F. Generalized mixed effects regression trees. Stat. Probab. Lett. 2017, 126, 114–118. [Google Scholar] [CrossRef]
- Fontana, L.; Masci, C.; Ieva, F.; Paganoni, A.M. Performing Learning Analytics via Generalised Mixed-Effects Trees. Data 2021, 6, 74. [Google Scholar] [CrossRef]
- Xiong, Y.; Kim, H.J.; Singh, V. Mixed effects neural networks (menets) with applications to gaze estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7743–7752. [Google Scholar]
- Simchoni, G.; Rosset, S. Integrating Random Effects in Deep Neural Networks. arXiv 2022, arXiv:2206.03314. [Google Scholar] [CrossRef]
- Robinson, T.R.; Rosser, N.J.; Densmore, A.L.; Williams, J.G.; Kincey, M.E.; Benjamin, J.; Bell, H.J. Rapid post-earthquake modelling of coseismic landslide intensity and distribution for emergency response decision support. Nat. Hazards Earth Syst. Sci. 2017, 17, 1521–1540. [Google Scholar] [CrossRef]
- Javidan, N.; Kavian, A.; Pourghasemi, H.R.; Conoscenti, C.; Jafarian, Z.; Rodrigo-Comino, J. Evaluation of multi-hazard map produced using MaxEnt machine learning technique. Sci. Rep. 2021, 11, 6496. [Google Scholar] [CrossRef] [PubMed]
- Rahmati, O.; Golkarian, A.; Biggs, T.; Keesstra, S.; Mohammadi, F.; Daliakopoulos, I.N. Land subsidence hazard modeling: Machine learning to identify predictors and the role of human activities. J. Environ. Manag. 2019, 236, 466–480. [Google Scholar] [CrossRef]
- Lombardo, L.; Opitz, T.; Huser, R. Point process-based modeling of multiple debris flow landslides using INLA: An application to the 2009 Messina disaster. Stoch. Environ. Res. Risk Assess. 2018, 32, 2179–2198. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of convolutional neural networks featuring Bayesian optimization for landslide susceptibility assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Samia, J.; Temme, A.; Bregt, A.; Wallinga, J.; Guzzetti, F.; Ardizzone, F.; Rossi, M. Do landslides follow landslides? Insights in path dependency from a multi-temporal landslide inventory. Landslides 2017, 14, 547–558. [Google Scholar] [CrossRef]













| Data | Original Data Type | Data Sources |
|---|---|---|
| Mass movements inventory | Point | China geological survey |
| Slope | Grid (90 m) | Derived from DEM https://srtm.csi.cgiar.org (accessed on 5 April 2022) |
| Aspect | Grid (90 m) | Derived from DEM |
| Profile curvature | Grid (90 m) | Derived from DEM |
| Plan curvature | Grid (90 m) | Derived from DEM |
| Road density | Line | https://www.tianditu.gov.cn (accessed on 9 April 2022) |
| River density | Line | https://www.tianditu.gov.cn (accessed on 9 April 2022) |
| Soil moisture | Grid (1 km) | https://csidotinfo.wordpress.com/data/global-high-resolution-soil-water-balance (accessed on 10 April 2022) |
| Lithology | Polygon | https://www.uni-hamburg.de (accessed on 6 April 2022) |
| Land use | Grid (1 km) | https://www.resdc.cn (accessed on 6 April 2022) |
| Geological environment division | Polygon | https://geocloud.cgs.gov.cn/#/home (accessed on 15 April 2022) |
| Parameter | Debris Flow | Rockfall | Landslide |
|---|---|---|---|
| learning_rate | 0.8 | 0.5 | 0.8 |
| max_depth | 10 | 6 | 5 |
| min_data_in_leaf | 80 | 30 | 30 |
| num_boost_round | 200 | 200 | 300 |
| Influencing Factors | VIF | TOL |
|---|---|---|
| Slope | 2.3926 | 0.4179 |
| Aspect | 3.1363 | 0.3188 |
| Profile curvature | 1.1988 | 0.8342 |
| Plan curvature | 1.1532 | 0.8672 |
| Road density | 1.2351 | 0.8087 |
| River density | 1.3272 | 0.7535 |
| Soil moisture | 4.3645 | 0.2291 |
| Lithology | 2.3306 | 0.4291 |
| Model | AUROC Median (1st–3rd Quantile) | Debris Flow | Rockfall | Landslide |
|---|---|---|---|---|
| GLMM | Non-spatial Cross Validation | 0.816 (0.813–0.819) | 0.773 (0.769–0.775) | 0.827 (0.825–0.830) |
| Spatial Cross Validation | 0.799 (0.760–0.832) | 0.805 (0.679–0.817) | 0.788 (0.654–0.845) | |
| GAMM | Non-spatial Cross Validation | 0.848 (0.844–0.852) | 0.801 (0.799–0.805) | 0.839 (0.836–0.842) |
| Spatial Cross Validation | 0.844 (0.781–0.855) | 0.805 (0.734–0.846) | 0.783 (0.751–0.806) | |
| TBMM | Non-spatial Cross Validation | 0.866 (0.863–0.868) | 0.830 (0.826–0.833) | 0.841 (0.837–0.844) |
| Spatial Cross Validation | 0.848 (0.800–0.858) | 0.817 (0.733–0.865) | 0.823 (0.678–0.867) |
| Movements | Original Data | SC and SW Regions | NW and Tibet Regions | Forest Land | Arable Land |
|---|---|---|---|---|---|
| Debris flow | 25,425 | 19,307 | 17,252 | 19,393 | 20,218 |
| Rockfall | 47,057 | 22,479 | 41,697 | 31,632 | 35,192 |
| Landslide | 90,558 | 28,187 | 85,622 | 58,112 | 66,092 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Zhang, Y. Comparison of Three Mixed-Effects Models for Mass Movement Susceptibility Mapping Based on Incomplete Inventory in China. Remote Sens. 2022, 14, 6068. https://doi.org/10.3390/rs14236068
He Y, Zhang Y. Comparison of Three Mixed-Effects Models for Mass Movement Susceptibility Mapping Based on Incomplete Inventory in China. Remote Sensing. 2022; 14(23):6068. https://doi.org/10.3390/rs14236068
Chicago/Turabian StyleHe, Yifei, and Yaonan Zhang. 2022. "Comparison of Three Mixed-Effects Models for Mass Movement Susceptibility Mapping Based on Incomplete Inventory in China" Remote Sensing 14, no. 23: 6068. https://doi.org/10.3390/rs14236068
APA StyleHe, Y., & Zhang, Y. (2022). Comparison of Three Mixed-Effects Models for Mass Movement Susceptibility Mapping Based on Incomplete Inventory in China. Remote Sensing, 14(23), 6068. https://doi.org/10.3390/rs14236068