Abstract
The Peninsular Malaysia Geodetic Vertical Datum 2000 (PMGVD2000) inherited several deficiencies due to offsets between local datums used, levelling error propagations, land subsidence, sea level rise, and sea level slopes along the southern half of the Malacca Strait on the west coast and the South China Sea in the east coast of the Peninsular relative to the Port Klang (PTK) datum point. To cater for a more reliable elevation-based assessment of both sea level rise and coastal flooding exposure, a new epoch-based height reference system PMGVD2022 has been developed. We have undertaken the processing of more than 30 years of sea level data from twelve tide gauge (TG) stations along the Peninsular Malaysia coast for the determination of the relative mean sea level (RMSL) at epoch 2022.0 with their respective trends and incorporates the quantification of the local vertical land motion (VLM) impact. PMGVD2022 is based on a new gravimetric geoid (PMGeoid2022) fitted to the RMSL at PTK. The orthometric height is realised through the GNSS levelling concept H = hGNSS–Nfit_PTK–NRMDT, where NRMDT is a constant offset due to the relative mean dynamic ocean topography (RMDT) between the fitted geoid at PTK and the local MSL datums along the Peninsular Malaysia coast. PMGVD2022 will become a single height reference system with absolute accuracies of better than ±3 cm and ±10 cm across most of the land/coastal area and the continental shelf of Peninsular Malaysia, respectively.
1. Introduction
Conventionally, spirit levelling has been used to establish and maintain the majority of national vertical datums or height reference systems, with local mean sea level (MSL) at one or multiple tide gauge (TG) stations serving as the zero levels. A vertical datum defines a reference for elevation comparisons and is required for a wide range of applications that rely on fluid flow, such as floodplain management, roadway and drainage design, agricultural management, and surveying in general [1]. The Land Survey Datum 1912 (LSD12) was the first official national vertical datum for Peninsular Malaysia. LSD12 was referred to as the MSL value derived from eight months (1 September 1911–31 May 1912) of tidal data observed by the British Admiralty hydrographic survey vessel HMS Waterwitch at Port Swettenham (currently known as Port Klang) [2]. The Department of Survey and Mapping Malaysia (DSMM) established the first precise levelling network, known as the first order levelling network 1967 (FOLN67), which is referred to as LSD12 [2,3]. FOLN67 was established to provide heights above MSL for Peninsular Malaysia, including Penang, Langkawi, and Tioman Islands. LSD12 has served surveying and mapping communities in Peninsular Malaysia for over 80 years.
Data on sea levels are collected, processed, archived, and disseminated by DSMM. Since 1984, twelve (12) TG stations have been operating along the coast of Peninsular Malaysia, forming the Tidal Observation Network (TON), which is shown in Figure 1 and Table 1, respectively. DSMM initiated and carried out this project from 1981 to 1986 with technical assistance from the Japan Maritime Safety Agency and funding from the Japan International Cooperation Agency (JICA) [4]. The stations were evenly distributed along the coast of Peninsular Malaysia, and their locations were selected to demonstrate the typical characteristics of the adjacent sea tides. The construction of the TG stations mostly took place on a rigid shore or a stable structure extending into the sea. However, in conjunction with establishing the new Precise Levelling Network (PLN) for Peninsular Malaysia, DSMM began determining new MSL values in 1983. Therefore, Port Klang (PTK) was selected to be adopted as the reference level for the new vertical datum based on 10 years of tidal observations (1984–1993) [3].
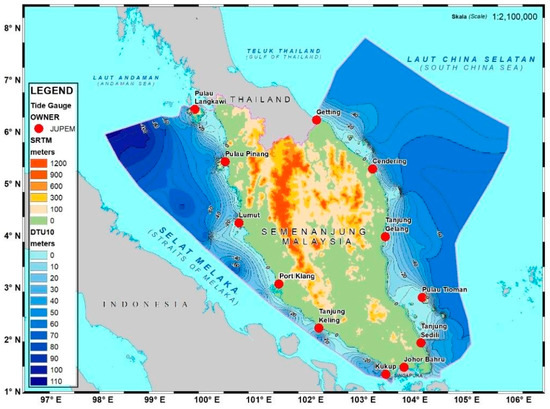
Figure 1.
Land and marine extent of Peninsular Malaysia. A solid pink line indicates the continental shelf limits. TG locations are indicated by red circles. Topographic heights and seabed depth are in metres.

Table 1.
Local vertical datums (LVD): LSD12, Tioman, and PMGVD2000 (Port Klang).
FOLN67, which was built sporadically over 50 years, became obsolete, and a new levelling network was needed to meet modern demands. The measurement of the second PLN by DSMM was completed in 2000 and was set to replace FOLN67. The new network has over 5000 benchmarks and 113 levelling lines covering a total distance of over 5000 km. The network was built using precise levelling techniques, with the allowable misclosure between the fore and back levelling being less than 3 mm per square root kilometre of line length. Its configuration was primarily determined by the pattern of land transportation routes. Based on a decade of tidal observations, the MSL value at PTK TG was adopted as the new Peninsular Malaysia geodetic vertical datum (PMGVD). The new MSL value at PTK is 3.624 m above the zero TG and lower than the LSD12 by 0.065 m [2,3]. However, the islands of Penang and Langkawi have continued to use LSD12 as their vertical datum to this day, as shown in Table 1.
The current PMGVD height system is accessible only in areas close to existing levelling lines. The network is not extended over the interior or unhabitable regions, and expansion to the such area is prohibitively expensive and technically challenging. The modernisation of the height reference system envisages the realization of a new vertical reference frame; instead of traditional geodetic levelling, gravimetric geoid modelling referenced to MSL is used (e.g., Japan [5]; Taiwan [6]; Canada [7,8]; New Zealand [9]; and USA [10]). By using GPS or Global Navigation Satellite System (GNSS) positioning techniques, elevation measurements relative to a uniform and seamless height reference frame anywhere in the country are feasible. However, spatial coverage and accuracy of gravity data are fundamental issues that need to be considered for a precise (<5 cm) geoid model determination. Data on surface gravity in Malaysia are scattered, mostly limited to coastal plains, and of varied accuracy. In 2002–2003, an airborne gravity survey was conducted over the land and coastal zones of the Peninsula by DSMM in collaboration with Kort & Matrikelstyrelsen (KMS), a Danish geodata agency. A total of about 38,200 km lines of airborne gravity data were acquired at 5 km flight line spacing [11]. The final fitted geoid of Peninsular Malaysia, known as PMGeoid2003, was established by tightly fitting it to 145 GPS-levelling points. However, it should be pointed out that the final hybrid gravimetric-geometric geoid model PMGeoid2003 may inherit possible systematic errors from the GPS-levelling and thus no longer constitute an equipotential surface [11,12]. Based on the studies carried out by DSMM, it was found that the achievable accuracy of GNSS levelling in Malaysia was at the second-order levelling standard [2,13].
Meanwhile, the effects of climate change on sea level change are becoming more and more worrying. Sea level rise is the term used to describe the rise in ocean levels caused by the consequences of global warming [14]. The amount of heat absorbed by the seas and the quantity of land ice melted by a warmer atmosphere and oceans cause a long-term shift in sea level [15]. Coastal sea level with respect to the land surface is the area of most practical interest for evaluating the societal implications of sea level change. TGs measure relative sea level, which is affected by global mean sea level and its regional fluctuations, vertical land motion, small-scale currents, waves, wind, shelf bathymetry, freshwater intake from river estuaries, as well as along-shore and cross-shore sediment transport [16]. Peninsular Malaysia is situated in the centre of the Sunda Shelf, bounded to the east by the South China Sea, the largest marginal sea in the Pacific Basin, and to the west by the Andaman Sea, which is part of the Indian Ocean, as seen in Figure 1. Nevertheless, the low-lying coastal areas of Peninsular Malaysia are threatened by the adverse effects of sea level rise due to increased frequency and severity of coastal flooding and inundation, coastal erosion and saltwater intrusion [17,18]. Sweet et al. [15], on the other hand, indicated that the relative sea level throughout the contiguous United States coastline is predicted to increase by as much as 0.25–0.30 m on average during the next 30 years (2020–2050), about the same value as recorded before over the last 100 years (1920–2020). Accurate elevation data linked to an updated localised height reference datum are thus crucial for assessing the risk of sea-level rise and coastal floods [19,20].
The Geocentric Datum for Malaysia 2020 (GDM2020) is the latest geodetic reference system, which is more accurate and robust, and it has been developed to be fully aligned and compatible with ITRF2014 [21]. The semi-kinematic GDM2020 incorporates a regional crustal motion model, allowing users to have accurate and continuous access to the national reference frame both on land and marine areas using GNSS positioning services. Nonetheless, a new geodetic height reference system is urgently needed for Peninsular Malaysia to address the following issues: (i) non-uniformity of the existing local vertical datums; (ii) impacts of the sea level rise; and (iii) other oceanographic phenomena acting on the Peninsular Malaysia’s east and west coasts. The methodology for the realisation of a new epoch-based height reference system is provided in Section 2.1. Section 2.2 describes TGs’ vertical stability analysis incorporating the VLM model. Section 2.3 examines the trend and variability of the mean sea level around the Peninsular from TG records data. Section 2.4 describes a newly established precise and seamless land-to-sea gravimetric geoid model (PMGeoid2022) derived from terrestrial and airborne gravity data over land and marine zones of Peninsular Malaysia. The referencing of the gravimetric geoid with reference to the new MSL2022 values at TON’s stations throughout Peninsular Malaysia, as well as the re-examination of the existing PLN, are provided in Section 3. Lastly, Section 4 describes the new vertical datum for Peninsular Malaysia, which is PMGVD2022. PMGVD2022 and GDM2020 will collaborate to implement an epoch-based height reference system to assess effective sea level rise impact.
2. Materials and Methods
2.1. Epoch-Based Height Reference System
The coordinate surface resulting from the elevation, otherwise known as the vertical coordinates of points, is referred to as the height reference system [22]. Geoid naturally defines Global Vertical Datum (GVD), and according to Gauss-Bessel-Listing’s definition, a geoid is a level surface of Earth’s gravitational field that is best fitted to the uninterrupted sea level [23]. Meanwhile, conventionally, the local relative-MSL measured by one or more TG typically estimates the local vertical datum (LVD). Therefore, there are two practical options for identifying the desired horizontal surface:
- A physical option of GVD, in which a constant value of the Earth’s gravity potential, W = W0 = constant, is specified, characterising the geoid as a single horizontal surface. The geopotential number at point P (in a geocentric reference frame) is given as CP = W0 − WP (m2s−2), with P0 on the geoid and WP = W(P). Orthometric height, H (m) is the height above the geoid at point P measured along the local vertical or plumb line, and it is always perpendicular to the equipotential surfaces: H = CP/ğ, where ğ (ms−2) is the gravity mean value along the plumb line [24]. Any application in hydrology requires geopotential-based heights since they demonstrate the water’s natural flow. A resolution in defining and realising the International Height Reference System (IHRS) was issued by the International Association of Geodesy (IAG) in July 2015. The IHRS coordinates are defined in this resolution as potential differences with respect to the equipotential surface of the Earth’s gravity field, which is realised by the conventional value of W0 = 62 636 853.4 m2s−2 [25,26].
- A geometrical LVD option in which the selected horizontal surface (the geoid) must resemble the MSL surface in a certain way. In the context of the application where a vertical datum is required to provide heights in a consistent system for a particular nation or region, the geometrical option, i.e., the height above the local MSL datum or gravimetric geoid fitted to the local MSL is normally selected. The orthometric height, H, barely varies from the height measured along the normal to the reference ellipsoid (even for the extreme case of deflection of the vertical, ξ = 1 arcmin and H = 10,000 m, ΔH = H sin ξ tan ξ < 1 mm) [27]. Other error sources are more significant such as random errors in levelling, ellipsoidal height errors, and geoid modelling errors. The geoid undulation or geoid height (N), expressed as H = h − N − N0 is required to convert ellipsoidal heights (h) from coordinates in the geodetic reference system acquired from GNSS levelling to orthometric heights (H) in the vertical datum. N0 is a constant offset between the geoid and the vertical datum [28]. The general description of H is such that H = 0 is the geoid, H > 0 is for terrain heights above the geoid, and H < 0 is below the geoid (depth of the sea floor).
The following time-dependent surfaces must be considered when modernising the Peninsular Malaysia height reference system (referring to Figure 2):
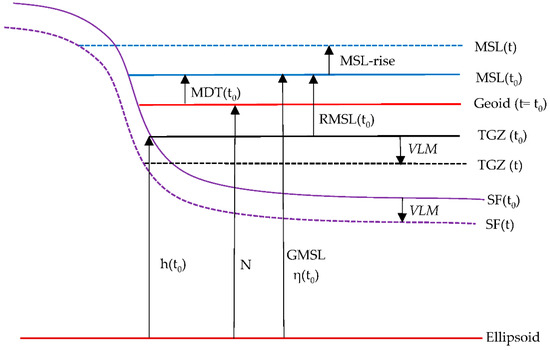
Figure 2.
The time-dependent relationship between surfaces and MSL at a reference epoch, t0 and epoch, t.
- Geodetic reference frame and reference ellipsoid. It is defined by the semi-kinematic geocentric datum GDM2020/ITRF2014@2020.0 and the GRS80/WGS84 as its ellipsoid of reference [21].
- Geoid surface (N). Is it the gravimetric geoid referenced to the local MSL at TG stations. Because temporal variations in geoid heights should be addressed only when defining geoid models with 1 cm accuracy, the geoid is defined as a static surface (N(t) = N(t0)) [29].
- Mean sea level (η, MSL) is the temporal average of the sea surface. The state of the sea level might be described by a time-mean long enough to exclude tidal influences (approximately 19 years). MSL is defined by its geodetic height (η) above the reference ellipsoid (negative if below) [30]. Epoch-based MSL at TGs (MSL) can be described using a linear expression technique defined as MSLTG(t) = MSLTG(t0) + (t − t0) MSLTG-trend, where the reference epoch is represented by t0 and MSLTG-trend, is the rate of sea level change in mm/year. However, MSL does not depict an equipotential surface because different height datums may refer to distinct equipotential surfaces, resulting in constant offsets between them.
- Mean dynamic ocean topography (MDT). MDT is defined as the difference between the averaged sea surface over time and the geoid, which is expressed as MDT(t) = η(t) − N(t) (see Figure 2). Every geoid slopes are ‘horizontal’. The strength of surface ‘geostrophic’ currents is measured by a tilt of the sea surface relative to the horizontal. The ‘steady-state’ circulation is observed by MDT from the long-term-averaged strength of ocean currents (https://gracejpl.nasa.gov, accessed on 3 August 2021).
- Vertical land motion (VLM). The level of the sea floor (SF) fluctuates over time owing to solid-Earth tides, accumulation of sediment, and VLM. VLM refers to either subsidence or uplift, and its sources include isostasy, elastic flexure of the lithosphere and plate tectonics in plate boundary zones. Some anthropogenic effects near coastal zones, such as extraction of groundwater and hydrocarbon, may cause subsidence and thus alter the coastline [30].
The change in local MSL per time that is referenced to the terrestrial frame or the reference ellipsoid is referred to as geocentric sea level (GMSLtrend). On the contrary, relative sea level change (RMSLtrend or MSLTG-trend) refers to the local MSL change with respect to the solid surface. Both MSL height η(t) and the sea floor height, h(t) of the tide gauge zero (TGZ) above the reference ellipsoid may change and thus alter relative MSL and hence can be expressed as epoch-based of RMSL(t) = η(t) − h(t), as shown in Figure 2. Taking the derivative relative to the time t yields ∂RMSL(t)/∂(t) = ∂η(t)/∂(t) − ∂h(t))/∂(t), which can be simplified as RMSLtrend = GMSLtrend − VLM, i.e., is the difference in mm/year between the geocentric sea level change rate and the rate of vertical land movement. Relative MSL rise (RMSLrise) is another name for relative MSL change. The quantity reported by a TG, which estimates the MSL relative to the solid surface to which it is connected, is the relative MSL change [30]. Conversion of relative sea level change to geocentric sea level (GMSLtrend = RMSLtrend + VLM) can be realised by subtracting the vertical land movement found in the TG record. To account for long-term MSL changes and minimise errors in computing MSL trends based on monthly MSL, RMSLtrend should be calculated using at least 30 years of TG data [16]. The long-term RMSLtrend at TG stations is approximately ±0.3 to ±0.5 mm/year [31]. Since relative sea level trends (RMSLtrend) reflect local sea level changes over time, it is one of the most important trends that account for changes in sea level, and it is thus important for many coastal applications such as coastal mapping, coastal engineering, coastal management, marine boundary delineation, and habitat restoration planning [15].
TGs, which provide point-by-point measurements of relative MSL, are the main source of coastal sea level data. In addition to recording ocean tides, TGs also record various types of sea level signals caused by changes in currents, melting of continental ice, atmospheric pressure, and vertical movement of land [31]. It is frequently found on the coast, at the intersection of the sea, atmosphere, and land. Absolute sea level variations, on the other hand, have been continuously observed by high-precision satellite altimeters (SALT) since 1992, in addition to being monitored by TG [32]. There are distinctions in the spatial and temporal sampling of TG and SALT. Radar altimeters observe sea level along satellite ground tracks at sampling rates ranging from 1 Hz (equivalent to every 6 km) to 20 Hz, with ground track distances ranging from 20 to 300 km (dependent on the altimeters number in the constellation) [32]. TGs, on the other hand, measure relative sea level at only one coastal point but with a temporal sampling of a few seconds or minutes. Users still can benefit from recent coastal altimetry processing advancements beyond 10 km from the shore, but obtaining precise absolute coastal sea levels in the 0–10 km range remains challenging [33]. As a result, to maximise the precision of information they can provide, the datasets are frequently merged to complement one another. Since TGs give relative sea level fluctuations relative to zero tide gauges, whereas SALT monitors absolute geocentric sea level with respect to reference ellipsoid, they must be standardised in terms of reference frame.
2.2. TGs Vertical Stability Analysis
2.2.1. ITRF2014 Geodetic Coordinates
The GPS levelling stations at the existing TGs (TG-GPSBM) have each been observed for at least two days with Trimble equipment (Trimble 5700 GPS receiver with Trimble TRM41249.00 antennae). GPS observations were only conducted at 11 TG-GPSBM as the TG station at JHB was unfortunately destroyed due to some harbour reconstructions. The recorded slant height measurements were converted to vertical heights (from the top of the TG benchmark). The dual frequency GPS data (in Hatanaka compressed Receiver Independent Exchange format (RINEX)) from the eleven TG-GPS benchmarks were processed along with GPS data from the following stations: (i) fifteen (15) Malaysia Real-Time Kinematic GNSS Network (MyRTKnet) on Peninsular Malaysia operated by DSMM; (ii) five (5) TUDelft stations (Thailand (2), Malaysia (1) and Sulawesi Indonesia (2)); and (iii) four (4) stations of International GNSS Service (IGS) in Southeast Asia (Figure 3). The incorporation of supplementary GPS data is optional. Nevertheless, by doing so, it improves ambiguity resolution of GPS data in TG stations, allows for inter-comparison of the daily GPS position outputs and assists further integration of the TG network with MyRTKnet.
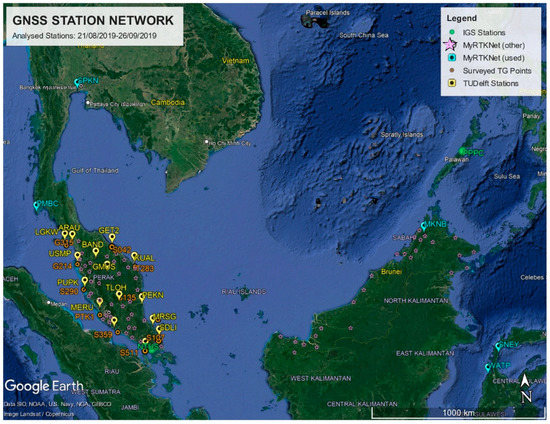
Figure 3.
Overview of the GNSS stations that were used in the data analysis. In total, GPS data from 35 locations were used, including 11 TG points (in red), 15 MyRTKNet stations in Peninsular Malaysia (yellow place markers), 5 TUDelft stations (orange place markers) in Thailand, Eastern-Malaysia, and Sulawesi Indonesia, and 4 IGS stations (green dots) in Thailand, Singapore, and the Philippines. The other MyRTKNet station locations in Malaysia are also shown (yellow star markers). Source of Image: Google Earth Pro.
GIPSY-OASIS II Software Version 6.4 was used to process GPS data [34] in the 2014 global reference frame solution derived from IGS14 [35], which is based on the International Terrestrial Reference Frame 2014 (ITRF2014) [36]. The Precise Point Positioning (PPP) technique was utilised to derive precise daily coordinate outputs in post-processing, as adopted by Zumberge et al. [37]. The Jet Propulsion Laboratory (JPL) provided precise satellite ephemeris as well as parameters of Earth rotation (non-fiducial style, IGS14), allowing stable derivation of very accurate daily absolute GPS positioning outputs. The parameters of daily transformation provided by JPL were then applied to the daily positions to align the solutions with the IGS14. These parameters are known as X-files, and more information on the processing setup can be accessed from Simons et al. [38].
The quality of the vertical position component (height) for the TG-GPSBM is crucial. This can be assessed by the formal errors of the multi-day averaged solutions (based on 2–4 daily solutions) or, more commonly, by the daily repeatability (Weighted Root Mean Square (WRMS) of the daily offsets relative to the average solutions). However, these (statistically estimated) height accuracies may not be sufficiently representative with only two days’ worth of observations. The GPS software packages utilised usually underestimate the formal errors of the TG (height) position (for example, non-systematic errors and the complete GNSS (satellite) position error budget may not be properly accounted for).
Therefore, a scale factor was estimated using the continuous stations included in the multi-day averaged solution (since they are available on each of the six (6) analysed days). The scale factor was determined by averaging the daily repeatability ratios and the formal error of the 6-day averaged solution for each station. The estimated coordinate accuracies using both methods for all eleven (11) TG benchmarks are shown in Figure 4. Both position error estimation methods indicated that the vertical component of the (absolute) TG benchmark positions in IGS14/ITRF2014 was defined within 1 cm for most stations (assuming no vertical antenna height measurement errors were made since the points were only observed in two successive sessions). The scaled standard deviations of the height were typically higher and can be considered as an upper margin. The coordinate standard deviation scaling method also revealed that the best results were obtained for stations that were observed twice during two successive days (the PTK1 and S135 points were occupied for four days). Alternative GPS data processing was also performed using the AUSPOS procedure [39]. Table 2 indicates the Root Mean Square (RMS) difference between GYPSY-OASIS II and AUSPOS latitude (φ), longitude (λ) and ellipsoidal height (h) coordinates of 0.1 cm, 1.2 cm, and 1.1 cm for Δφ, Δλ, and Δh, respectively. The RMS difference for all three components (3D) is 1.7 cm. The Bernese 5.2 (AUSPOS) and GYPSY-OASIS II solutions have been proven to provide consistent geodetic coordinate values.
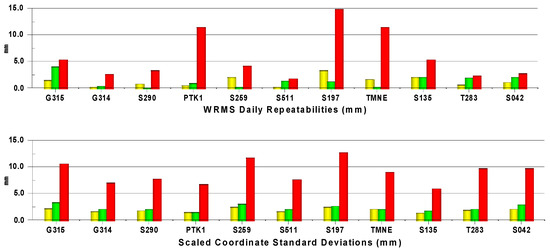
Figure 4.
Overview of the IGS14 position error estimates for eleven (11) TG benchmarks in the north (yellow), east (green), and vertical (red) directions. TG benchmarks. In the top panel, the WRMS of the daily offsets with respect to the 6-day averaged solutions are shown (the daily coordinate repeatability). The bottom panel shows scaled (by a factor of 1.67) standard deviations of the 6-day averaged solution for each TG benchmark.

Table 2.
Differences in ITRF201414/WGS84 geodetic coordinates at TG-GPSBM sites from AUSPOS (Bernese ver. 5.2) and GIPSY-OASIS II solutions (observation period: August–September 2019).
2.2.2. Vertical Land Motion (VLM)
The GPS position time series of twelve (12) MyRTKnet stations (1994–2021) were also analysed to gain a better understanding of the VLM near the twelve (12) TG locations in Peninsular Malaysia. MyRTKNet is the successor to the Malaysian Active GPS System (MASS), which was launched in 1999, and later on, most stations became part of the MyRTKNet. Referring to Figure 5, the nearest MyRTKNet stations to the TG (TG) stations are LGKW (Langkawi TG), USMP (Penang TG), PUPK (Lumut TG), MERU (Port Klang TG), JUML (Tanjung Keling TG), KUKP (Kukup TG), JHJY (Johor Bahru TG), SDLI (Sedeli TG), MRSG (Tioman TG), PEKN (Tanjung Gelang TG), KUAL (Cendering TG), and GET2 (Geting TG).
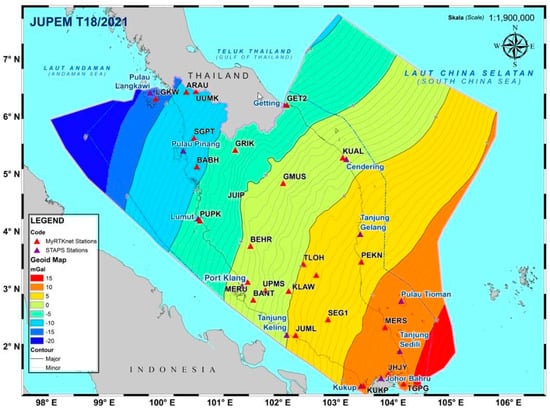
Figure 5.
Location of tide gauge stations (blue triangles) and selected MyRTKnet stations (red triangles) are shown on the gravimetric geoid of Peninsular Malaysia, illustrating the integrated approach adopted in the present height reference system analysis.
It is important to consider the VLM study of Phuket Island by Simons et al., as it covers Phuket tectonic motions study that spans over 25 years and encompasses inter-, co-, and post-seismic deformation phases [38]. Phuket is located (similar to the northwest of Peninsular Malaysia) at the edge of the plate boundary deformation zone between the Australian/Indian and Sundaland plates. Significant deformations are seen prior to, during, and after the 2004 megathrust earthquake. For instance, significant inter-seismic to post-seismic motion transitions are demonstrated by the Phuket combined GPS position time series following an almost instantaneous horizontal co-seismic position shift of 25 cm to the ESE during the moment magnitude (Mw) 9.2 earthquake. In addition, small co-seismic horizontal position jumps were also observed during the March 2005 Mw 8.6 Nias and April 2012 Mw 8.6/8.2 Indian Ocean earthquakes.
Despite the fact that none of these earthquake epochs revealed significant vertical co-seismic position jumps, the vertical motion trend of Phuket clearly begins to shift after the Mw 9.2 event. The post-seismic deformation phase begins immediately (about a month) after the Mw 9.2 earthquake and follows a (roughly) exponential decline pattern, whereas the inter-seismic motion seems quasi-linear. As a result, Phuket was positioned 7 ± 1 cm lower than before the earthquake, with a considerable short-term change in the vertical movement of the island. Therefore, Peninsular Malaysia could also be affected by the changes in vertical position (and related relative sea level) after 2004.
MASS and MyRTKNet GPS data were also processed by the GIPSY-OASIS software and the same daily solution processing procedure as previously described [38]. Following that, weekly averaged station positions were calculated to screen for outliers and improve the reliability of the coordinate solutions. The weekly averaged station coordinates’ daily repeatability (WRMS) from 1994 to 2021 (all in mm) are 1.1/1.2/4.4 (12 MASS + MyRTKNet stations) in the north, east, and vertical position components, respectively. The daily GPS positioning findings from MASS + MyRTKNet stations show that their VLM can be used to monitor the changes in the vertical motion at the nearby TGs at the mm level. These RMS values demonstrate the absolute accuracy of the daily station coordinates in the IGS14 global reference frame, given that all daily station locations were directly mapped in IGS14 using the X-file method. The velocity estimates for all stations were then computed from the weekly averaged coordinate solutions in the IGS14 by using a 3D-linear regression approach on the position time series, where station KUAL (Kuala Terengganu) has the longest total length of GPS observations (27.1 years, including the Geodynamics of South and South East Asia (GEODYSSEA) campaign type measurements between 1994 and 1998) [40]).
Figure 6 depicts the linear vertical velocity estimates for twelve (12) MyRTKNet stations. Position jumps caused by equipment changes (e.g., different antenna types and/or (wrong) antenna height) were removed from the vertical position time series and computed as 1D vertical position jumps at each incident in the position time series. Seasonal variations in vertical position solutions were modelled. The vertical time series was fitted with a seasonal variation according to Blewitt and Lavallee [41] and modelled using the equation A × sin(α) + B × cos(α), where α is 360°/365.25 days × (time in days from the beginning of data epoch). The linear regression function, as well as parameters A and B, were calculated. The technique by Simons et al. [42] (2 × WRMS/T) was used to compute velocity uncertainties, and employs the WRMS of the position deviants and the time, T of the data to estimate the maximum probable tilt of the trend line with a confidence level of 99.999%.
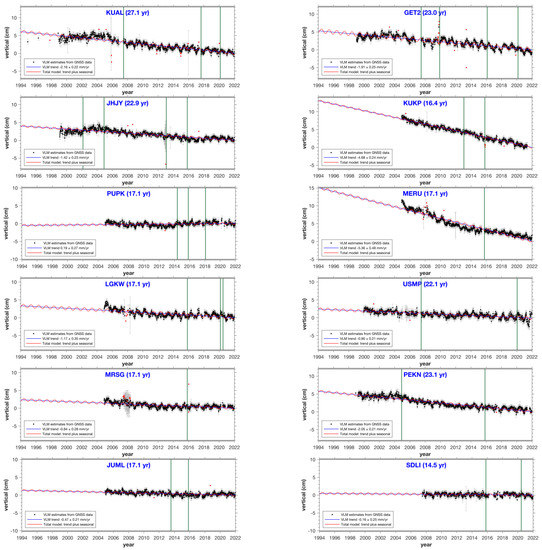
Figure 6.
VLM estimates from 12 MyRTKNet stations located near the TG stations in Peninsular Malaysia. The vertical position time series for each station, as well as the overall observation period, are provided. The vertical reference position is specified on 1 January 2002 (0 cm). The green vertical lines are the epochs at which a vertical position jump (due to antenna change or MASS to MyRTKNet transition) was estimated. The linear trend line is given in blue, with the modelled seasonal (annual) signal superimposed on it. The VLM estimates come from the linear regression through the weekly averaged positions (black dots). Weekly averaged position outliers are marked in red. The VLM estimate is given at a confidence level of 95% (1.96 sigmas).
Following the Mw 9.2 Sumatra–Andaman earthquake on 26 December 2004, the extended position time series for stations KUAL, GET2, JHY, and PEKN (1994–2021) confirm that the vertical position time series on Peninsular Malaysia have been affected correspondingly by a non-linear pattern change (post-seismic tectonic subsidence). Prior to this, the inter-seismic VLM results indicate a slight uplift at these stations. Most of the MyRTKNet stations exhibit an onset of subsidence that gradually decreases over the years. A few stations have a near-zero VLM, and two stations (KUKP in Kukup and MERU in Meru) show strong local subsidence rates of –4.68± 0.24 and –5.36 ± 0.48 mm/year, respectively. The latter is probably due to declining groundwater levels in urban and industrial areas. These rates may differ at the nearby TG stations, as the GNSS is not co-located, and the distances vary between 0 km (GET2 to Geting TG) and 54 km (PEKN to Port Kuantan TG). Furthermore, no detailed information is available on the monument depth and soil composition for both the GNSS and TG benchmarks.
The VLM change phenomenon requires attention when evaluating TG RMSL time series with the difference of geocentric MSL (GMSL) time series derived from SALT and VLM from GNSS. These should optimally be compared over the same periods (e.g., 1984–2005 and 2005–2021) since VLM on Peninsular Malaysia differs within these two periods (inter-seismic tectonic uplift vs. post-seismic tectonic subsidence) due to the Sundaland plate deformation in its boundary zone with the Indian and Australian plates. Nevertheless, for the purpose of this paper, we will make use of RMSL, and its linear trend estimates over the entire period.
2.3. MSL Determination and Trends Analysis
The hourly TG data from DSMM were reduced to monthly averaged RMSL by averaging hourly sea level data within a monthly period. This step allows for the filtering of the majority of tidal constituents (mainly diurnal and semi-diurnal) that should not end up in MSL. The actual number of hourly data available in a month is divided by the theoretical maximum number to improve reliability: a valid monthly value is acceptable when the ratio is 2/3 or higher. This is more stringent than the 15-day regulation imposed by the Permanent Service for Mean Sea Level (PSMSL). When a valid monthly value converges, the ratio is used as a weight criterion in our data model fit. We analyse the monthly averaged RMSL time series without any special editing or jumps and without applying inverted barometer correction. Since TG data exhibit both trends and periodic behaviour, we simultaneously fitted a bias, trend, as well as an annual and semi-annual cycle (6-parameter model): when the data span does not contain an integer number of these periods, the existence of periodic signals can affect the trend estimation.
Previous analyses indicate that the annual and semi-annual cycles are the most prominent. Another study by Simons et al. [38] shows that Peninsular Malaysia is affected by the seismic cycle of “nearby” megathrust Earthquakes due to the tectonic setting of the region. Some TGs exhibit unusual behaviour prior to and after the 9.2 Mw Andaman-Sumatra Earthquake on 26 December 2004, which occurred along the Sumatra Fault. This behaviour results in different VLM rates, which affect both GNSS and TG data. Therefore, we chose not to include this difference in this study to establish a long-term (30+ years) RMSL. We also decided not to average the data over the given time span, which results in MSL2022A, but rather to evaluate the linear part of our model at the epoch 1 January 2022, resulting in MSL2022B. Depending on the data time span, an average would not consider the secular sea level change; this would introduce differences in the averaging period as well as changes in the midpoint of these periods from one TG to the other, basically introducing differences in the treatment of the different TGs. We apply an iterative 3σ outlier criterion during fitting to filter out extremes, such as the 1997 low sea level event in the Indian Ocean brought on by the Indian Ocean Dipole (IOD). Since the glacial isostatic adjustment’s (GIA) impact is minimal, the results have not been adjusted for it. Additionally, it will exclude any cross-sectional comparisons between GPS, TG, and SALT. Figure 7 presents an example of this approach for the TG at Port Klang (PTK). The RMSL trend (blue line) is estimated at 2.40 mm/year. The red line represents the total model, which is trend plus periodic cycles, the black dots represent the underlying data, and the red dots with grey squares represent our monthly averages and outliers.
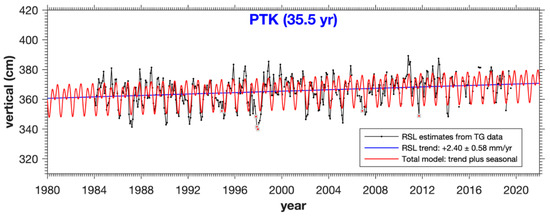
Figure 7.
Trend and annual and semi-annual estimates from the monthly tide gauge data at Port Klang station.
Table 3 shows the MSL for each of the 12 TG stations, as well as the difference between directly averaging the data (MSL2022A) and analysing the trend of our model fit on 1 January 2022. (MSL2022B). The RMS difference between these MSLs is 6.4 cm. Table 4 shows the overall result of our model fit for all TGs in Peninsular Malaysia. The station abbreviation, location, and data time span are given per station. It also includes the RMSLtrend and the relative sea level rise RMSLrise since 1 January 1993, which appears to be 9.2 cm on average. Meanwhile, Table 5 compares the RMSL values at PTK (vertical datum point) from sea level data analysis for the years 1984–1993 and 1984–2022. For the past 29 years, the observed and predicted RMSL-rise is 8.4 cm and 7.0 cm, respectively.

Table 3.
Differences in tide gauge relative mean sea level (RMSL) and its trends (RMSLtrend) between averaging and time-series techniques.

Table 4.
Relative mean sea level (RMSL), RMSL trends (RMSLtrend), and RMSL rise (RMSLrise) at the twelve tide gauges along the Peninsular Malaysia coastline.

Table 5.
Sea level rise at Port Klang vertical datum.
The height of GPSBMs above the new vertical datum MSL2022B is shown in Table 6. Nevertheless, the stability of the TG station is critical in order to obtain a reliable MSL value. Local VLM investigations were carried out at continuous GNSS active stations (MASS/MyRTKNet) located near the TG stations along the coast of Peninsular Malaysia. All sites near the stations show insignificant vertical land movement except for KUKP (near S5110/KUK) and MERU (about 20 km away from PTK1/PTK). Significant land subsidence is observed at the KUKP MyRTKNet station at a rate of –4.68 mm/year (see Figure 8). As a result, the height for S5110 above MSL2022B should reduce by –0.16 m (–4.68 mm/year × 34 years) to account for the subsidence over 34 years (1987–2021). The land subsidence at the Kukup TG has also been verified by the GPS levelling/PMGeoid2020, indicating about –15 cm subsidence. However, we were unable to detect any significant subsidence occurring at the Port Klang TG from the same analysis. A more detailed analysis of the subsidence at the Port Klang (PTK1) and Kukup (S5110) TGs using GPS levelling and the new PMGeoid2022 is provided in Section 4.2. Consequently, the resulting height of GPSBM S5110 above MSL2022B at Kukup TG is 1.715 m (1.875 m minus 0.16 m). The final geodetic coordinates and orthometric heights above PMGVD2000 and MSL2022B for eleven (11) TG stations in IGS14/WGS84 are shown in Table 7.

Table 6.
GPS benchmark (GPSBM) heights above the new vertical datum MSL2022B.
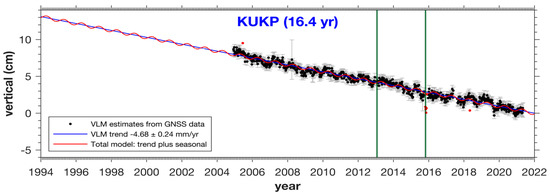
Figure 8.
Vertical land motion (VLM) estimates at Kukup GNSS station (KUKP) from 1994 to 2021.

Table 7.
Final GPS benchmark geodetic coordinates from GIPSY-OASIS II solution and orthometric heights above PMGVD2000 and MSL2022B at tide gauge stations.
2.4. Geoid Mapping
DSMM carried out airborne geoid mapping over Peninsular Malaysia and East Malaysia in 2002–2003 as part of the MyGeoid Project. Nevertheless, between 2014 and 2016, DSMM carried out another airborne geoid mapping task over the marine extent of East Malaysia as part of the Marine Geodetic Infrastructure Project (MAGIC). The Marine Geodetic Infrastructures in Malaysian Waters (MyMarineGI) Project was later on replaced by the MAGIC Project. DSMM embarked on yet another airborne geoid mapping survey in 2019–2022 over the marine area of Peninsular Malaysia, covering the South China Sea and the Malacca Strait. The survey was conducted to conclude the airborne geoid mapping project covering the whole territorial land and marine extent of Malaysia.
The primary purpose of these projects was to develop a seamless gravimetric geoid model over land/sea area for East Malaysia and the Peninsular. In 2017, the East Malaysian gravimetric geoid model, known as EMGeoid2017, was established using airborne gravity data [43]. The geoid has been fitted to six (6) TG stations along the Sabah and Sarawak coast with an estimated 3–5 cm level accuracy. The ultimate goal of having such a precise gravimetric geoid model is to develop new reference height datums for East Malaysia and Peninsular Malaysia. The following sub-section will focus on the airborne gravity surveys, followed by the procedure for computing a seamless, accurate gravimetric geoid model for the land/sea area of Peninsular Malaysia.
2.4.1. Data Sources
A combination of airborne datasets of land and maritime areas of Peninsular Malaysia is covered by a total of 68,200 km flight lines (refer to Figure 9 and Table 8). During the airborne data acquisitions over land and marine extent of the Peninsula, Antonov-38 and Beechcraft-BE200 aircraft were used, respectively. The details of the campaigns are presented in Table 8, in which a flight line spacing of 5 km was maintained over the land area for the MyGeoid Project (2002–2003). After flying more than 30,000-line km of flights, the 2022 survey supplemented the 2019 offshore survey of the South China Sea and the Malacca Strait, resulting in nearly complete coverage of the Peninsular Malaysia Exclusive Economic Zone (EEZ).
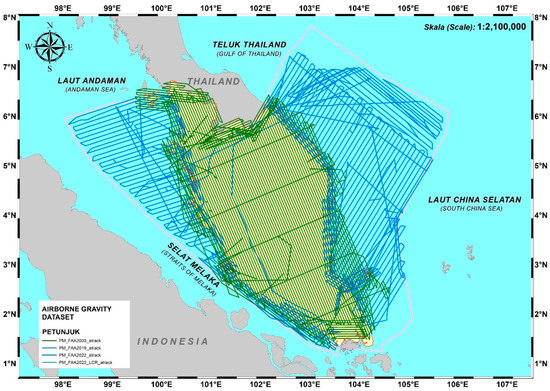
Figure 9.
Airborne gravity dataset (green lines are airborne gravity data on land while blue lines represent the marine airborne gravity data).

Table 8.
Campaigns for airborne gravity survey in Peninsular Malaysia.
The marine area was divided into two sections during the project, with 5 km spacing for up to 12 nautical miles (NM) from the shore and 10 km spacing for the area beyond 12 NM. Two sets of equipment have been used in the surveys: a LaCoste and Romberg (LC&R) air-sea conventional gravimeter, combined with strapdown inertial units (Honeywell H764G IMU or temperature-stabilised iMAR IMU’s, acting as auxiliary gravity sensors). In addition to the LC&R air-sea gravimeter, two iMAR-IMU gravimeter units, a Geometrics G-823A magnetometer, and two Javad “Delta” geodetic GPS receivers were installed in the aircraft. For ground references, a Javad “Maxor” GPS receiver and a Geometric G-856AX magnetometer were used.
Gravimeter readings were taken at the base station before and after each flight, every day, to control equipment drift and to tie airborne gravimeter readings with the existing terrestrial gravity network. The aerogravity flights were completed from the Subang, Johor Bahru, Kota Bharu, Langkawi, Ipoh, and Penang Airports. A Denmark Technical University (DTU) LC&R land gravimeter G-867 and a DSMM CG-6 gravimeter were used to measure the airport base gravity values required for processing the airborne gravity data. Gravity ties were established by connecting available DSMM gravity reference points to the Kuala Lumpur absolute gravity station.
Aircraft altitude during the marine data acquisitions was maintained at an approximate 1900 m level with a speed of about 300 km/h (land flights were higher sometimes). All data were downloaded routinely onto backup hard drives and were checked for quality control (QC) on a daily basis. The airborne gravity processing was performed using newly developed software at DTU and Technical University Darmstadt (TUD). The LC&R air-sea gravimeter data were then processed as a stand-alone sensor by a new DTU MATLAB-based software. The drift of the LC&R sensor indicated somewhat noisy base readings at the airport aprons, particularly in the early part of the campaign, but confirmed the excellent long-term stability of the LC&R.
Two iMAR units were onboard for the 2022 survey, and they were processed using completely different software and methods. The DTU processing of the iMAR RQH unit was performed using an 18-state Kalman Filter/Optimal smoother setup [44], with 3rd order Markov model parameters fitted on a daily base depending on flight conditions. The TUD processing, on the other hand, was performed using an independent pre-processing for precise positions, roll, pitch, and heading, followed by using the IMU accelerometer triad data as a gravity sensor, filtering it in a 120 s (full wavelength) filter, similar to standard LC&R processing [45]. Due to two different g-sensors and two different processing methods, each flight has two independent gravity anomaly results. Both the iMAR and the LC&R processing chains rely on the precise kinematic GNSS positioning performed in the NovAtel Waypoint software (version 8.90) (position-only for DTU, position and attitude for TUD). The AUSPOS service processed the ITRF2014 coordinates of the reference stations. However, many lines were ultimately processed by the Precise Point Positioning (PPP) technique, which is known to be superior for long-baseline flights.
The gravity disturbances δg (i.e., anomalies computed using ellipsoidal heights) were estimated for all three sensors, then converted to classical geodetic free-air anomalies Δg (based on orthometric heights) using the XGM2019 geoid (NXGM2019) and applying an altitude-dependent atmosphere correction (δgATM) as follows: Δg = δg − 0.3086 NXGM2019 + δgATM. The use of geodetic gravity anomalies Δg ensures consistency with the earlier airborne surveys of Peninsular Malaysia and with the surface gravimetry from DSMM (Figure 10). The final processed airborne gravity data were evaluated by crossover comparison, yielding an RMS crossover of around 2.2 mGal, corresponding to an estimated RMS error of 1.6–1.7 mGal, at a spatial solution of 5–6 km with the used filtering, which is a highly satisfactory result.
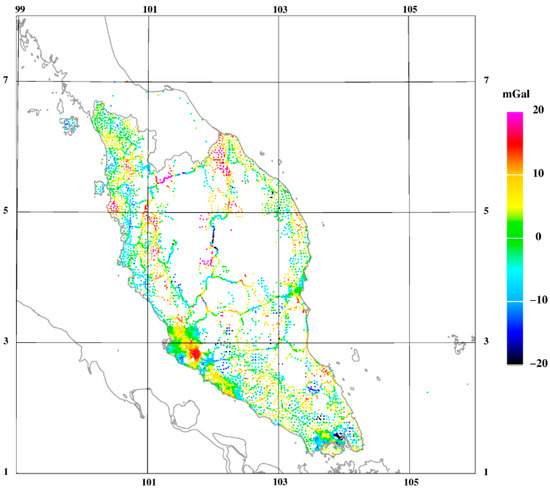
Figure 10.
Terrestrial gravity data after XGM2019 and RTM terrain reduction.
A least-squares collocation (LSC) technique was used for downward continuation of the airborne data to the terrain level [46]. The least squares collocation was done in a 1 × 1 degree block set-up, with a 0.5-degree border overlapped to neighbouring blocks. For the collocation procedure, the airborne and surface data were allocated a relatively conservative standard deviation of 2 mGal (due to potential biases). The covariance function was based on a planar logarithmic model with parameters √C0 = 9 mGal, D = 6 and T = 30 km, where C0 is the covariance, D and T analogous to the Bjerhammar sphere depth of the spherical collocation and a long-wavelength “compensating depth” attenuation factor, respectively [47].
The following local gravity data are available for the geoid computations in Peninsular Malaysia:
- 2019 and 2022 airborne gravity survey results (free-air anomalies at altitude).
- 2003 airborne gravity survey (5 km line spacing).
- Edited DSMM surface gravimetry data (as used in the 2019 geoid model).
- DSMM Height Modernization System (HMS) gravimetry data in the vicinity of Kuala Lumpur, Melaka, and Johor Bharu.
- Satellite altimetry gravity offshore was selected away from other data (DTU21).
Figure 11 shows the combined terrestrial, airborne and DTU21 satellite altimetry gravity datasets, whereas Table 9 summarises the statistics derived from several gravity data sources, as well as the residuals following the subtraction of XGM2019 and RTM terrain effects. Two terrestrial gravity data sources are edited DSMM gravimetry (unchanged since the 2016 geoid computation) and newer terrestrial gravity data from the DSMM-HMS project in the Kuala Lumpur, Melaka, and Johor Bahru area.
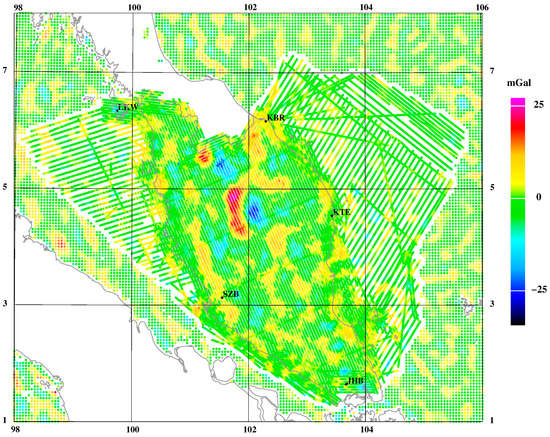
Figure 11.
XGM2019/RTM reduced airborne (2003–2022) and DTU21 data outside the airborne coverage.

Table 9.
Statistics for the gravity data and reductions from the XGM2019 and RTM (mGal).
2.4.2. Geoid Modelling Method
Gravimetric geoid computation is performed using a remove-compute-restore (RCR) method. This method necessitates the division of the anomalous gravity potential, T, into components of T = TEGM + TRTM + Tres, where TEGM represents the anomalous gravity potential from the XGM2019e global field [48], TRTM represents the anomalous gravity potential derived from residual terrain modelling (RTM), which is the topography’s high-frequency component, and Tres represents the residual of anomalous gravity potential, i.e., the potential corresponding to the unmodeled part of the residual gravity field. Likewise, the gravity anomaly Δg is also expressed in three components of Δg = ΔgEGM + ΔgRTM + Δgres. The height anomalies of quasi-geoid (ζ) are theoretically modelled by the RTM method as ζ = T(φ,λ,H)/γ(φ,H), where H is the orthometric height. According to Jamil et al. [43] and Forsberg et al. [49], the classical geoid (N) and the quasi-geoid (ζ) are deemed as the “geoid at sea level” and the “geoid at the topography level”, respectively. The following is the process for gravimetric geoid estimation, which is based on RCR steps techniques:
- Remove Step: The residual gravity anomaly field is calculated by subtracting the XGM2019e and RTM components from the total anomalies, resulting in Δgres = Δg − ΔgEGM − ΔgRTM. The free-air anomaly residual, Δgres, calculated here, remains in the gravity data after subtracting the residual terrain effect contributions ΔgRTM, and the global field ΔgEGM (Figure 12a).
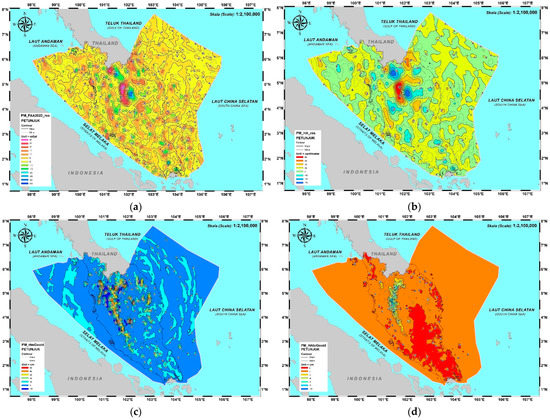 Figure 12. (a) Gridded downward continued residual of free-air anomalies, where the contour interval (CI) is 5 mGal; (b) Gridded residual height anomalies (CI = 10 cm); (c) Gridded geoid RTM correction (CI = 2 cm); (d) Gridded co-geoid to geoid correction (CI = 2 cm).
Figure 12. (a) Gridded downward continued residual of free-air anomalies, where the contour interval (CI) is 5 mGal; (b) Gridded residual height anomalies (CI = 10 cm); (c) Gridded geoid RTM correction (CI = 2 cm); (d) Gridded co-geoid to geoid correction (CI = 2 cm). - Compute Step: Spherical Fast Fourier Transform (FFT) with optimised kernels is utilised to determine the gravimetric geoid, a rather new variant to the classical geoid integral (Stokes’ integral), where a fitted weighting of the XGM2019e long wavelengths and the local gravity data shorter wavelengths is presented. The residual height anomaly (ζres) is computed mathematically by analysing convolution equations of the following form: ζres = Sref (Δφ, Δλ) × [Δgres (φ, λ)sinφ] = F−1 [F(Sref) F (Δgres sinφ)], where Sref, denotes a modified “Stokes” kernel and F denotes the operator of 2-dimensional Fourier Transform. The block-wise LSC using the planar logarithmic covariance model in 1° × 1° degree blocks with overlap has been employed to generate gridded data, taking into account the varied elevations of the airborne and surface gravimetry data. Forsberg et al. [50] or Forsberg et al. [51] and references therein provide more information on the geoid determination approach. Figure 12b illustrates the FFT method output, i.e., the gridded height anomalies.
- Restore Step: The contributions from XGM2019e and RTM (Figure 12c) are added back following the computation of the residual height anomaly (ζres) from Δgres to obtain total height anomalies (quasi geoid) resulting in ζ = ζEGM + ζRTM + ζres. The relationship between geoid (N) and quasi-geoid (ζ) is expressed as N − ζ = (ΔgB/γ)H [52], where ΔgB is the Bouguer anomaly and H is the orthometric height. This is readily implemented as a minor correction (typically <10 cm) to a final gravimetric geoid estimated from surface data. H = 0 is often found in the marine environment, and it also indicates that the quasi-geoid coincides with the geoid (N = ζ). In Peninsular Malaysia, the term, N − ζ is relatively minor, reaching an extreme value of only–11 cm in the highest mountains (see Figure 12d). Figure 13 displays the final computed gravimetric geoid (PMGeoid2022).
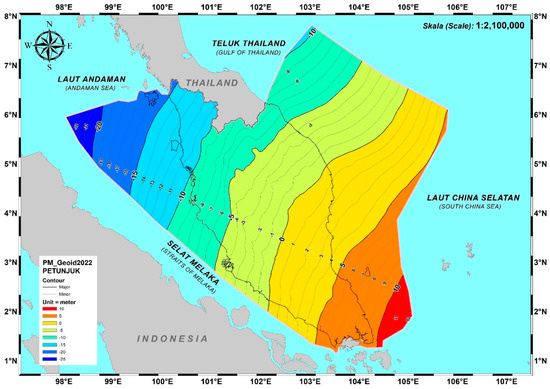 Figure 13. Gridded final gravimetric geoid for Peninsular Malaysia, PMGeoid2022 (CI = 1 m).
Figure 13. Gridded final gravimetric geoid for Peninsular Malaysia, PMGeoid2022 (CI = 1 m).
Two types of gravimetric geoids were computed for Peninsular Malaysia: (i) Gravimetric “airborne” geoid computed solely from airborne gravity data (Geoid1), and (ii) Gravimetric geoid computed from both airborne and terrestrial gravity data (Geoid2). The new gravimetric geoid models (Geoid1/Geoid2) outperform the previous gravimetric geoid model (PMGeoid2003) in comparison results. The differences between the new Geoid1 and Geoid2, with and without terrestrial data, are minor and most likely reflect spurious errors in the terrestrial data as well as a lack of data in the southern Thailand region (see Figure 10). The fit of the older GPS/levelling dataset to an airborne-only and combined geoid is summarised in Table 10. The fit to the 2008 GPS-levelling data in the Kuala Lumpur region is remarkably good, with only a 15 mm standard deviation, revealing that the 1 cm geoid in the Kuala Lumpur area could be available even with a simple fit process. The overall accuracy of the new gravimetric geoid model (Geoid2/PMGeoid2022) is estimated at 2–4 cm in RMS level across most of Peninsular Malaysia (the highest is in the mountain regions).

Table 10.
Fit of older GPS/levelling data to the airborne-only geoid and combined geoid (in meters).
3. Results
3.1. PMGeoid2022 Fitting to Local MSL
The remove–restore method generates a gravimetric geoid that refers to an implicit global height datum. The geoid fitted to GPS/TG control is required in determining the final geoid to fit the geoid to the local vertical datum and minimise probable long-wavelength geoid errors. The long-wavelength geoid errors and inherent datum variations can be addressed by incorporating geoid information from GPS-levelling. However, both levelling and GPS heights must be as error-free as possible during the computation of GPS geoid heights; otherwise, these errors will contaminate the geoid that has been “fitted”. Ionospheric biases, particularly antenna height inaccuracies, are common contributors to GPS height errors. The same can be said of levelling errors, which can be systematic, generally unknown, and heavily dependent on levelling practices. The fitted gravimetric geoid is sometimes referred to as a “combined gravimetric-geometric” model or a “hybrid geoid model” [12].
A fitted gravimetric geoid is typically given in grid form. To fit the gravimetric geoid to a set of GPS geoid heights, it is necessary to model the difference signal ε = NGPS − NGRAV and then applies the modelled ε-correction to the gravimetric geoid. As a result, a new geoid grid “tuned” to the specific levelling and GPS datum is generated.
For modelling the residuals, LSC in conjunction with bias estimation is preferable. The covariance function must be presumed for the residual geoid errors ε’ (after fitting of, e.g., bias or 4-parameter model) as a function of distance s, yielding C(s) = Cov (ε’, ε’). Such covariance function will have zero variance C0 and a correlation length s1/2 (the distance at which the covariance function attains half its maximum metric). This defines the fit degree and the interpolated geoid error smoothness. In most cases, a simple covariance model will suffice. GRAVSOFT’s GEOGRID Collocation Program [53,54] employs a second-order Markov model (which accurately simulates Kaula’s rule). The user has a wide range of options in selecting either a strong fit to the GPS data or a more relaxed fit in terms of correlation length and noise of observed errors, which consequently reduces the effect of any errors in the GPS levelling data. The correlation length should be selected as a general rule to be about equivalent to the station distance between the GPS-levelling points. For example, the GPFIT Function in the GRAVSOFT package can be used to estimate the empirical covariance function of ε’, if there are enough GPS points available.
3.2. Fitting to a Single TG at Port Klang
A fitted geoid model, PMGeoid2022_fit_PTK, was generated by first tying the gravimetric geoid to the TG at Port Klang (PTK). The orthometric height for the rest of the TG stations was then computed using HGPS Lev = hGPS − NPMGeoid2022_fit_PTK. The GPS levelling analysis on the PMGVD2000 and MSL2022B datums are shown in Table 11 and Table 12, respectively. From Table 11, it is revealed that the local vertical datum offsets at Langkawi (GPS315) and Pulau Pinang (GPS314) indicate a datum offset between LSD12 and PMGVD2000. Similarly, a datum offset between Tioman and PMGVD2000 is observed at GPSBM C0501. According to the VLM analysis, the significant difference of about–16 cm at Kukup (S5110) is caused by land subsidence. The variations at the other GPSBM stations could be attributed to levelling error propagation from the PMGVD2000 datum at PTK to the respective TG locations.

Table 11.
Result of GPS levelling by fitting PMGeoid2022 to PMGVD2000 datum at Port Klang tide gauge station, revealing local datum offsets, subsidence, and levelling error propagations.

Table 12.
GPS levelling result by fitting PMGeoid2022 to MSL2022B at Port Klang tide gauge station, revealing relative geodetic-MDT between MSL2022B at Port Klang and MSL2022B at other tide gauges.
Comparison between the PMGeoid2022 fitted at PTK and MSL2022 at the TGs GPSBM presented in Table 12 reveals datum bias or sea slopes or relative geodetic mean dynamic ocean topography (RMDTG) with respect to PTK datum, especially along the southern part of Malacca Strait and the South China Sea. The Malacca Strait connects the South China Sea and the Andaman Sea via the Singapore Strait and has a very intricate hydrodynamic system [55,56]. The Malacca Strait is funnel-shaped and is about 980 km long, 52 km wide in the south, and 445 km wide in the north, with sea depth ranging from 10 m to 200 m, as shown in Figure 1 [57]. Semi-diurnal tides are predominant in the Indian Ocean, whereas both diurnal and semi-diurnal tides dominate the South China Sea. The Malacca Strait’s southern end becomes a meeting point for tidal waves, particularly the semi-diurnal M2 tidal component generated at the Indian Ocean as well as mixed diurnal and semi-diurnal waves from the South China Sea, where it connects to Singapore Strait [58]. As a result, the distinct oceanographic surface geostrophic currents in the Malacca Strait and the South China Sea [59] may have caused significant MDT differences along the west and east coasts of Peninsular Malaysia. The MSL along the eastern coast of the Peninsular seems to be offset by about +16 cm relative to the MSL at PTK (on the west coast). This has caused the MSL along the southern part of Malacca Strait to shift upward to balance the MSL on the east coast.
The geodetic MDT (MDTG) at TG-GPSBM is expressed as MDTG = HGeoid − HMSL-TG = hGPS − N − HMSL-TG (see Figure 14a). Since the gravimetric geoid PMGeoid2022 has been fitted to the relative MSL2022B at PTK, the MDTG at TG-GPSBM PTK is equal to zero. Therefore, the differences in orthometric heights at a TG-GPSBM with respect to the fitted PMGeoid2022 at Port Klang TG (TGPTK) and to the local MSLTG provide the relative-MDTG (RMDTG) or sea slope between TGPTK and TGi: RMDTPTK-TG = MDTTG − MDTPTK = HPMGeoid22022_fit_PTK2022 − HMSL-TG (see Figure 14b).
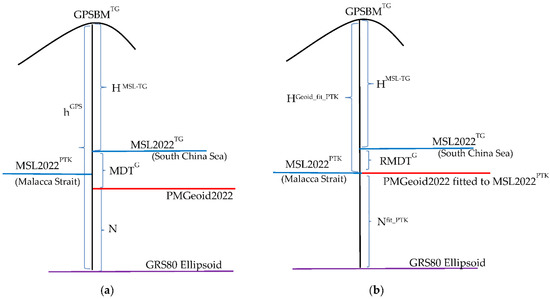
Figure 14.
(a) Absolute MDTG at TG-GPSBM: MDTG = hGPS − N − HMSL-TG; (b) Relative-MDTG between PTK (Malacca Strait) and GPSBMTG (South China Sea): RMDTPTK-TG= HGeoid_fit_PTK − HMSL-TG.
On the other hand, the unfitted geoid model PMGeoid2022 allows the marine MDT to be determined from the altimetry dataset as MDTSALT = MSS − N. MSS denotes the DTU21 mean sea surface height, which has been transformed from the TOPEX reference ellipsoid (used in the altimetry grids) to WGS84. Figure 15 shows a relatively smooth DTU21-derived MDTSALT signal, with an abrupt increase southward in the Malacca Strait. Other narrow straits connecting major world seas exhibit the same phenomenon. The features seen in the narrow channels around Singapore are most likely due to MSS errors, but they can also be due to geoid errors, as no gravity data is available for the Indonesian islands situated in the Malacca Strait. The MDTSALT on the east coast of Peninsular Malaysia appears to be higher than on the west coast. It shows that the value of MDT on the east coast is between 1.0 m and 1.1 m. Meanwhile, the MDT value on the west coast is between 0.75 m and 1.0 m. Figure 15 illustrates the RMDTG or sea slopes relative to TGPTK at each of the ten (10) TG-GPSBM locations. The negative values (RMDT < 0) indicate that the MSL2022TG are lower than MSL2022PTK, which is the case for the northern half of Malacca Strait. Meanwhile, positive values (RMDT > 0) indicate that the MSLTG are higher than MSLPTK in the southern half of Malacca Strait and the South China Sea.
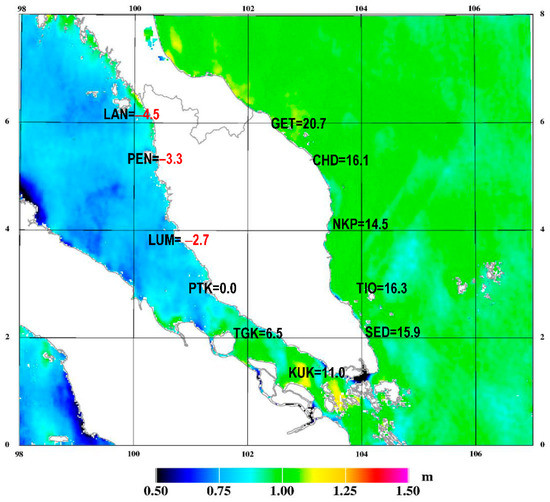
Figure 15.
The magnitude of sea slopes (RMDTG) in cm along the Malacca Strait and the South China Sea relative to Port Klang (PTK). The background map is the MDTSALT from the DTU21 altimetry dataset. The strong resemblance of sea slopes derived from TGs and DTU21 is observed.
3.3. Fitting to Eleven TGs
The final gravimetric geoid (Geoid2) was then fitted to all eleven (11) TG stations using MSL2022B datum at epoch 2022.0 and is known as PMGeoid2022-fit-11TG. Corrections to the gridded geoid heights ranged from 78 cm to 100 cm in the E-W direction to accommodate the MSL tilt between the Malacca Strait and the South China Sea (see Figure 16). The gridded geoid fitting correction incorporates MSL-rise at all TGs with an average of about 9 cm for the years 1993–2022. However, fitting to multiple TGs has caused the geoid to tilt in the E-W direction, as shown in Figure 16. Another option to account for the sea level tilt is to fit the PMGeoid2022 to the Port Klang datum point and to apply a datum bias correction in the vicinity of existing TG stations. Therefore, orthometric height can be determined from H = hGNSS–Nfit_PTK–NRMDT, where NRMDT is the datum bias between the fitted PMGeoid2022 at Port Klang and the local MSL2022 at the other ten TGs (refer to Table 12 and Figure 14b).
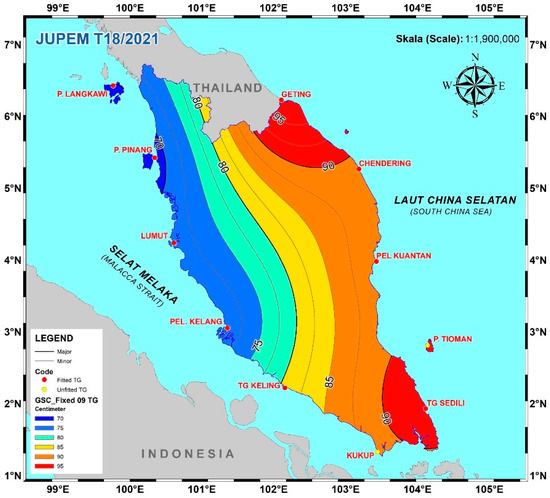
Figure 16.
Geoid corrector surface to PMGeoid2022-fit-11TG (CI = 1 cm).
4. Discussions
4.1. Peninsular Malaysia Geodetic Vertical Datum 2022: PMGVD2022
The defining parameters of the PMGVD2022 height datum are shown in Table 13. PMGVD2022 is determined from the PMGeoid2022 fitted to MSL2022B at PTK, and it is supplemented with corrections for the effect of sea slopes along the Peninsular Malaysia coast. These corrections are defined by the relative MDT at the ten (10) TG stations. Fitting the PMGeoid2022 to a single TG at PTK reduces the deformation and tilt. The new vertical datum meets the following desirable vertical datum characteristics: [60]:

Table 13.
PMGVD2022 defining parameters and extent.
- Semi-kinematic RMSL Model: RMSL(t) = RMSL(t0) + (t − t0) RMSLtrend.
- Unified within the Land Mass and Definitive: A single recognised vertical datum is provided by PMGVD2022 so that benchmarks may be issued with a single definitive height.
- Good Coverage: Access to the PMGVD2022 datum is available everywhere in the nation, even in new development zones. The GNSS levelling technique will allow users to easily generate heights for points no matter where they are.
- Consistent with Gravimetric Geoid Model: PMGVD2022 is consistent with the fitted PMGeoid2022 model, with an additional local datum bias correction, NRMDT: H = hGNSS − Nfit_PTK − NRMDT.
- Zero Height Close to Sea Level: PMGVD2022, which is based on MSL at eleven (11) TG stations, provides epoch-based sea level that accounts for sea level rise and tilts along Peninsular Malaysia’s coast.
- Applicable to Continental Shelf and Consistent with International Standards: PMGVD2022, together with the 3D geocentric datum of GDM2020/ITRF2014 [21], support the development of the Marine Geodetic Network (MGN) and other marine-related positioning in the Continental Shelf of Peninsular Malaysia.
4.2. Transformation from PMGVD2000 to PMGVD2022
The new height datum also defines relationship grids that enable heights to be transformed consistently from the PMGVD2000, LSD12 datum and TIOMAN datum to PMGVD2022. PMGVD2000 was constrained to a single TG at Port Klang. As a result, the height difference between PMGVD2022 and PMGVD2000 (ΔH) may include the effect of RMSLrise, RMDT, vertical datum offsets (VD offset), and levelling errors (LE) in the following relationship:
where ΔHRMSLrise(t) = (t − t0) RMSLtrend, t0 = 1993.0, t = 2022.0 (refer to Table 4); ΔHRMDT = HMSL2022 − HPMGeoid2022_fit_PTK_2022 (refer to Table 12, but with reverse positive–negative signs for RMDT from TG-GPSBM datum to PTK datum (RMDTTG-PTK = MDTPTK − MDTTG) and ΔH1LVD offset + LE = ΔH − ΔHRMSLrise − ΔHRMDT. By subtracting PMGVD2000 heights from PMGeoid2022 fitted at PTK, we also obtained the following equation:
ΔH = ΔHRMSLrise + ΔHRMDT + ΔH1LVD_offset + LE
ΔH2LVD_offset + LE = HPMGeoid2022_fit_PTK_2000− HPMGVD2000
Both ΔH1LVD_offset + LE and ΔH2LVD_offset + LE show consistent differences with an RMS of 9.7 cm and 9.9 cm, respectively (refer to Table 14). Figure 17 depicts the gridded correction for the transformation from PMGVD2000 to PMGVD2022 based on differences at the First Order Levelling Benchmarks. The differences between PMGVD2000 and PMGVD2022 range from about –8 cm to –40 cm, indicating that the old 2000 datum is lower than the new 2022 datum mainly due to MSL rise, sea slopes and land subsidence.

Table 14.
PMGVD2000 datum inconsistencies due to relative MSL rise, sea slopes (RMDT), local vertical datum offset (LVD-offset), and levelling error (LE).
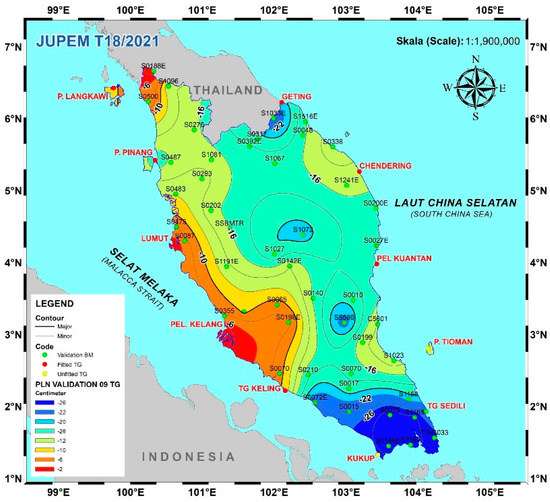
Figure 17.
Gridded correction (ΔH) for the transformation from PMGVD2000 to PMGVD2022 based on 45 Precise Levelling Network (PLN) benchmarks (CI = 2 cm) (HPMGVD2022 = HPMGVD2000 + ΔH).
Although the MyRTKnet station at MERU, near the PTK TG, exhibits significant subsidence (5.36 mm/year), we have not observed this at PTK1. Any significant subsidence at PTK1 will appear as systematic bias at all the other ten TGs because the gravimetric geoid (PMGeoid2022) was fitted to PTK1 in the analysis shown in Table 14. From Table 14, only the TG at Kukup shows significant subsidence of about –16 cm. The TG at PTK was built on a stable wharf at PTK and located about 20 km away from MERU MyRTKnet station. On the other hand, the TG at Kukup is located less than 5 km from KUKP MyRTKnet station. It has been observed that some industrial sites are being developed in the vicinity of MyRTKnet station at MERU, which may have caused a drop in groundwater level and subsequent land subsidence. Furthermore, the MERU MyRTKnet GPS pillar may not be planted deep enough into the bedrock compared to the PTK/PTK1 benchmarks, which are located on a stable wharf.
The new height values in PMGVD2022 can be derived from HPMGVD2022 = HPMGVD2000 + ΔH, where ΔH is obtained from the interpolation of the gridded correction surface. Additional work is required to further improve the gridded correction surface depicted in Figure 17. Orthometric heights in PMGVD2022 can be modelled as time-dependent quantities using H(t) = H(t0 = 2022.0) − (t − t0) MSLTG-trend + δVLC(t), where δVLC(t) is the vertical land changes (refers to either subsidence or uplift) at epoch t.
5. Conclusions
Despite no change in storm frequency or severity, higher sea levels can amplify the consequences of storm surges, high tides, coastal erosion, and wetlands loss [15]. In height-based analyses of sea level rise and coastal flooding exposure, vertical height uncertainty is an important aspect to take into account. The reference elevation data for Peninsular Malaysia relies on a large set of high-accuracy Precise Levelling Network (PLN) established by DSMM in the form of Standard Benchmarks (SBM) and Benchmarks (BM). However, orthometric heights at these SBMs and BMs are referenced to MSL at Port Klang (PTK), which is based on a tidal observation over 10 years between 1984 and 1993. The Peninsular Malaysia Geodetic Vertical Datum (PMGVD2000) inherited several deficiencies due to the following factors: (i) Datum offsets for Land Survey Datum 1912 (LSD12) and Tioman datum inconsistencies; (ii) Levelling error propagation emanating from the single PTK datum; (iii) Land subsidence; (iv) MSL rise from 1993–2022; and (v) MSL tilt relative to the PTK datum along the southern half of Malacca Strait on the west coast and the South China Sea in the east coast.
Based on a gravimetric geoid PMGeoid2022 fitted to MSL@2022.0 at PTK TG, a new epoch-based geodetic vertical datum PMGVD2022 has been developed to provide highly reliable vertical data information for elevation-based assessments of sea level rise and risk of coastal flooding via the use of a datum offset NRMDT between PTK datum and local MSL datum: H = hGNSS–Nfit_PTK–NRMDT. The new height reference system of Peninsular Malaysia PMGVD2022 comprises the following components:
- TGs MSL@2022.0—which consists of a network of eleven (11) TG Benchmarks (TGBM) with their height measured above RMSL derived from more than 30 years tidal observation. Time-dependent RMSL at epoch t can be expressed as RMSL(t) = RMSL(t0) + (t − t0) RMSLtrend, where t0 is the reference epoch, RMSLtrend is the relative sea level change in mm/year. VLM has also been calculated at the TG locations to convert relative RMSLtrend to geocentric GMSLtrend.
- Geodetic Relative Mean Dynamic Ocean Topography (RMDTG)—which consists of the RMDTG values at ten (10) TG stations along the Peninsular Malaysia coast relative to the TG at PTK (RMDTG = HPMGeoid2022_fit_PTK – HMSL2022B).
- Fitted Gravimetric Geoid Surface—which consists of a new MSL-geoid PMGeoid2022-fit-PTK and is referred to as a seamless height reference surface for the land and marine area of Peninsular Malaysia. The new reference height surface has been fitted with respect to the local MSL at PTK.
- Precise Levelling Network—which consists of a network SBMs and BMs from existing PLN of Peninsular Malaysia and then transformed to PMGVD2022. It is worth noting that any re-levelling and maintenance of the existing PLN-BM will be expensive and require more human labour. Orthometric heights in the PMGVD2022 system can be expressed as a semi-kinematic model of H(t) = H(t0) − (t − t0) MSLtrend + δVLC(t), which takes into account the sea level rise and vertical land changes (subsidence or uplift) at epoch t.
PMGVD2022 will become the single vertical datum for land and coastal/offshore of Peninsular Malaysia with an improved accuracy of less than ±3 cm on land and ±10 cm in the continental shelf area, respectively. PMGVD2022 applications on land and coastal zones seem to be a straightforward issue since the procedure of the migration to the new semi-kinematic vertical datum will be provided by DSMM. PMGVD2022 will provide an accurate translation of the reference from the ellipsoid to the “MSL geoid” for offshore positioning. By employing high-accuracy GNSS positioning techniques for vertical positioning of survey platforms, sea surface, and sea floor, Ellipsoidally Referenced Surveying is necessary for hydrographic surveying to deliver direct seabed measurement to the ellipsoid. [61].
The long-term stability of the vertical datum is impacted by the variation in MSL caused by global climate and regional tectonic plate deformation-induced changes, as well as the change in geoid in response to the continuously changing mass distribution within Earth [22,29,30,62]. Therefore, PMGVD2022 shall be revised every 20–25 years to account for the impact of the coastal sea level rise, VLMs and temporal gravity changes with a height change threshold of about 5–6 cm. The following recommendations may need to be considered:
- TG stations in Peninsular Malaysia should be appropriately maintained for continuous and up-to-date sea level data, which is critical for the analysis of the stability of the vertical datum and the impact of sea level rise. TG data is a valuable source of information for a wide variety of activities over a wide variety of time scales, including scientific research as well as for a variety of industrial applications [31]. The TGBM is also incredibly essential since it serves as the reference point for sea level data. It may be required to redefine the TGBM and TG-GPSBM to account for variations in orthometric and ellipsoidal heights caused by VLMs.
- Sea level rise influenced by global warming is reinforced by (negative) vertical land motion, and their impacts on coastal zone should be seriously considered (see Figure 18). Regarding its impact on shoreline changes, land subsidence has a shorter time span and more measurable magnitude compared to the influences of the tectonic setting [63]. Therefore, VLM detection and monitoring using GNSS observations co-located at all TGs must be performed religiously. GNSS reflection methods should be thoroughly researched as an alternative method for simultaneously monitoring sea level and VLM [64]. The integration of GNSS and InSAR techniques should also be considered to map VLM along the coasts.
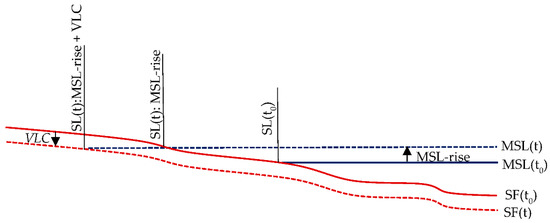 Figure 18. Shoreline (SL) retreat is either caused by sea level rise (HSL(t) = HSL(t0) − (t-t0)MSLtrend) or by a combination of sea level rise and land subsidence (HSL(t) = HSL(t0) − (t-t0)MSLtrend − δVLC(t)).
Figure 18. Shoreline (SL) retreat is either caused by sea level rise (HSL(t) = HSL(t0) − (t-t0)MSLtrend) or by a combination of sea level rise and land subsidence (HSL(t) = HSL(t0) − (t-t0)MSLtrend − δVLC(t)). - The existing PLN may be replaced by Malaysia Real-Time Kinematic GNSS Network (MyRTKnet) for heighting purposes. MyRTKnet stations should be used as reference stations for local height updates or densification either by traditional methods or by GPS levelling. PMGVD2022 geoid model and GPS levelling have been successfully used in detecting systematic errors in PMGVD2000 due to sea slopes, MSL rise, land subsidence and levelling error propagation. The future of levelling will be a mixture of traditional levelling and GNSS. Local precise survey work will continue to be performed using traditional methods, but less accurate survey work will be handled by GPS/GNSS levelling.
- Future GPS/GNSS campaigns on TGBMs will have a minimum duration of three days (24-h sessions). To ensure that the same satellite visibility and multipath environment are experienced during the re-occupations, the same antenna setup (type and height) must be maintained. Minimal obstruction for the satellite visibility by the antenna shall be maintained.
Author Contributions
Conceptualization, S.C. and M.K.; methodology, M.K.; airborne geoid mapping, R.F., T.J., F.J., H.T., H.Y., D.M., and F.M.; mean sea level and trends determination, M.N., A.H.D., and K.A.; vertical land motions, W.S., H.Y., A.A., and Z.I.; validation, M.K., S.N., A.Y., and W.S.; formal analysis, R.F., W.S., M.K., S.S., and A.Y.; writing—original draft preparation, M.K., S.C., R.F., M.N., and W.S.; writing—review and editing R.F., W.S., S.S., and A.Y.; supervision S.C. and N.Y. All authors have read and agreed to the published version of the manuscript.
Funding
Project funding was made available through the Department of Survey and Mapping Malaysia, Ministry of Energy and Natural Resources (DSMM Project Number: T9/2019 and T18/2021).
Data Availability Statement
Data is available upon request.
Acknowledgments
The authors would like to express their gratitude to the Director General, Department of Survey and Mapping Malaysia, for the support and guidance rendered during the implementation of the Geodetic Infrastructures in Malaysian Waters (MyMarineGI) Project (2019–2022), from which most of the geodetic data and results presented in this article were derived. The authors would also like to thank Ole Andersen at DTU Space and GFZ Data Services, who provided DTU21 Mean Sea Surface and the experimental gravity field model XGM2019e data accordingly. The GPS research activities were partly funded by grants from the Dutch NWO User Support Programme Space Research (2007–2023). The authors would like to thank the reviewers as well for taking the time and effort necessary to review the manuscript. Maps and diagrams throughout this work were created using ArcGIS® software by Esri. ArcGIS® and ArcMap™ are the intellectual property of ESRI and are used herein under license.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| DSMM | Department of Survey and Mapping Malaysia |
| DTU | Technical University of Denmark |
| FOLN67 | First Order Levelling Network 1967 |
| GDM | Geocentric Datum for Malaysia |
| GMSL | Geocentric Mean Sea Level |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| GPSBM | GPS benchmark |
| GRS80 | Geodetic Reference System 1980 |
| GVD | Global Vertical Datum |
| Hz | Hertz |
| IGS | International GNSS Service |
| IHRS | International Height Reference System |
| IMU | Inertial Measurement Unit |
| ITRF2014 | International Terrestrial Reference Frame 2014 |
| KMS | Kort & Matrikelstyrelsen, a Danish geodata agency. |
| LC&R | LaCoste and Romberg |
| LE | Levelling Errors |
| LSD12 | Land Survey Datum 1912 |
| LVD | Local vertical datum |
| MASS | Malaysian Active GPS System |
| MDT | Mean Dynamic Ocean Topography |
| MDTG | Geodetic MDT |
| mGal | milligal |
| MGN | Marine Geodetic Network |
| MGRF2020 | Malaysian Geodetic Reference Frame 2020 |
| MSL | Mean Sea Level |
| Mw | Magnitude |
| MyGeoid | Malaysian Gravimetric Geoid |
| MyMarineGI | Marine Geodetic Infrastructures in Malaysian Waters |
| MyRTKNet | Malaysia Real-Time Kinematic GNSS Network |
| NM | Nautical Miles |
| PLN | Precise Levelling Network |
| PMGVD | Peninsular Malaysia Geodetic Vertical Datum |
| PSMSL | Permanent Service for Mean Sea Level |
| PTK | Port Klang |
| RCR | Remove-Compute-Restore technique |
| RMDT | Relative Mean Dynamic Ocean Topography |
| RMDTG | Geodetic Relative Mean Dynamic Ocean Topography |
| RMS | Root Mean Square |
| RMSL | Relative Mean Sea Level |
| RMSLrise | Relative Mean Sea Level Rise |
| RTM | Residual Terrain Modelling |
| SALT | Satellite Altimeter |
| SBM | Standard Benchmarks |
| SF | Seafloor |
| SL | Shoreline |
| TG | Tide Gauge |
| TGBM | Tide Gauge Benchmark |
| TG-GPSBM | GPSBM at tide gauge locations |
| TGZ | Tide Gauge Zero |
| TON | Tidal Observation Network |
| TUD | Technical University Darmstadt, Germany |
| VLM | Vertical Land Motion |
| WGS84 | World Geodetic System 1984 |
| WRMS | Weighted Root Mean Square |
References
- Janssen, V.; McElroy, S. The Australian Height Datum Turns 50: Past, Present & Future. In APAS Webinar Series 2021 (AWS2021); APAS: Bathurst, Australia, 2021; pp. 3–27. [Google Scholar]
- Jamil, H. GNSS Heighting and Its Potential Use in Malaysia. In GNSS Processing and Analysis; GNSS: Marrakech, Morocco, 2011; pp. 1–19. [Google Scholar]
- Mohamed, A. An Investigation of the Vertical Control Network of Peninsular Malaysia Using a Combination of Levelling, Gravity, GPS and Tidal Data. Ph.D. Thesis, Universiti Teknologi Malaysia, Johor, Malaysia, 2003. [Google Scholar]
- Kadir, M.; Ses, S.; Hisam, A.; Abu, S. Current and Future Geodetic Activities in Malaysia; GNSS: Hong Kong, China, 2022; 19p. [Google Scholar]
- Matsuo, K.; Kuroishi, Y. Refinement of a Gravimetric Geoid Model for Japan Using GOCE and an Updated Regional Gravity Field Model. Earth Planets Space 2020, 72, 33. [Google Scholar] [CrossRef]
- Hwang, C.; Hsu, H.-J.; Featherstone, W.E.; Cheng, C.-C.; Yang, M.; Huang, W.; Wang, C.-Y.; Huang, J.-F.; Chen, K.-H.; Huang, C.-H.; et al. New Gravimetric-Only and Hybrid Geoid Models of Taiwan for Height Modernisation, Cross-Island Datum Connection and Airborne LiDAR Mapping. J. Geod. 2020, 94, 83. [Google Scholar] [CrossRef]
- Véronneau, M.; Duval, R.; Huang, J. A Gravimetric Geoid Model as a Vertical Datum in Canada. Geomatica 2006, 60, 165–172. [Google Scholar]
- Véronneau, M. The Canadian Geodetic Vertical Datum of 2013 (CGVD2013). Geomatica 2014, 60, 9–19. [Google Scholar] [CrossRef]
- Amos, M. Improving New Zealand’s Geoid Based Datum with Airborne Gravimetry. In Proceedings of the FIG Working Week 2016, Christchurch, New Zealand, 2–6 May 2016. [Google Scholar]
- Smith, D. The GRAV-D Project: Gravity for the Redefinition of the American Vertical Datum; National Oceanic and Atmosphoric Administration (NOAA)/National Geodetic Survey: Silver Spring, MD, USA, 2007; 40p. [Google Scholar]
- DSMM. Airborne Gravity Survey and Geoid Determination Project for Peninsular Malaysia, Sabah and Sarawak; Internal Report; Department of Survey and Mapping Malaysia, Geodetic Division: Kuala Lumpur, Malaysia, 2003. [Google Scholar]
- Brown, N.J.; McCubbine, J.C.; Featherstone, W.E.; Gowans, N.; Woods, A.; Baran, I. AUSGeoid2020 Combined Gravimetric–Geometric Model: Location-Specific Uncertainties and Baseline-Length-Dependent Error Decorrelation. J. Geod. 2018, 92, 1457–1465. [Google Scholar] [CrossRef]
- Ses, S.; Mohamed, A. The Second Precise Levelling Network of Peninsular Malaysia. Surv. Rev. 2009, 41, 384–394. [Google Scholar] [CrossRef]
- Hamid, A.I.A.; Din, A.H.M.; Hwang, C.; Khalid, N.; Tugi, A.; Omar, K. Contemporary Sea Level Rise Rates around Malaysia: Altimeter Data Optimization for Assessing Coastal Impact. J. Asian Earth Sci. 2018, 166, 247–259. [Google Scholar] [CrossRef]
- Sweet, W.V.; Hamlington, B.D.; Kopp, R.E.; Weaver, C.P.; Barnard, P.L.; Bekaert, D.; Brooks, W.; Craghan, M.; Dusek, G.; Frederikse, T.; et al. Global and Regional Sea Level Rise Scenarios for the United States: Updated Mean Projections and Extreme Water Level Probabilities Along U.S. Coastlines; NOAA Technical Report NOS 01; National Ocean Service: National Oceanic and Atmospheric Administration: Silver Spring, MD, USA, 2022; 111p. [Google Scholar]
- Woodworth, P.L.; Melet, A.; Marcos, M.; Ray, R.D.; Wöppelmann, G.; Sasaki, Y.N.; Cirano, M.; Hibbert, A.; Huthnance, J.M.; Monserrat, S.; et al. Forcing Factors Affecting Sea Level Changes at the Coast. Surv. Geophys. 2019, 40, 1351–1397. [Google Scholar] [CrossRef]
- Ehsan, S.; Ara Begum, R.; Ghani Md Nor, N.; Nizam Abdul Maulud, K. Current and Potential Impacts of Sea Level Rise in the Coastal Areas of Malaysia. IOP Conf. Ser. Earth Environ. Sci. 2019, 228, 012023. [Google Scholar] [CrossRef]
- NAHRIM. Impact of Climate Change to Sea Level Rise in Malaysia; NAHRIM: Seri Kembangan, Malaysia, 2019. [Google Scholar]
- Gesch, D.B. Best Practices for Elevation-Based Assessments of Sea-Level Rise and Coastal Flooding Exposure. Front. Earth Sci. 2018, 6, 230. [Google Scholar] [CrossRef]
- Durand, G.; van den Broeke, M.R.; Le Cozannet, G.; Edwards, T.L.; Holland, P.R.; Jourdain, N.C.; Marzeion, B.; Mottram, R.; Nicholls, R.J.; Pattyn, F.; et al. Sea-Level Rise: From Global Perspectives to Local Services. Front. Mar. Sci. 2022, 8, 709595. [Google Scholar] [CrossRef]
- Azhari, M.; Altamimi, Z.; Azman, G.; Kadir, M.; Simons, W.J.F.; Sohaime, R.; Yunus, M.Y.; Irwan, M.J.; Asyran, C.A.; Soeb, N.; et al. Semi-Kinematic Geodetic Reference Frame Based on the ITRF2014 for Malaysia. J. Geod. Sci. 2020, 10, 91–109. [Google Scholar] [CrossRef]
- Vaníček, P. Vertical Datum and the NAVD 88. Surv. Land Inf. Syst. 1990, 51, 83–86. [Google Scholar]
- Sjöberg, L. On the Definition and Realization of a Global Vertical Datum. J. Geod. Sci. 2011, 1, 154–157. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd ed.; corrected ed.; Springer: Wien, Austria; New York, NY, USA, 2006. [Google Scholar]
- Barzaghi, R.; De Gaetani, C.I.; Betti, B. The Worldwide Physical Height Datum Project. Rend. Fis. Acc. Lincei 2020, 31 (Suppl. S1), 27–34. [Google Scholar] [CrossRef]
- Sánchez, L.; Sideris, M.G. Vertical Datum Unification for the International Height Reference System (IHRS). Geophys. J. Int. 2017, 209, 570–586. [Google Scholar] [CrossRef]
- Jekeli, C. Heights, the Geopotential, and Vertical Datums; Ohio Sea Grant Development Program, NOAA; Technical Report 459; Ohio State University, Department of Civil and Environmental Engineering and Geodetic Science: Columbus, OH, USA, 2000; pp. 1–34. [Google Scholar]
- Jekeli, C.; Montenbruck, O. Time and Reference Systems. In Springer Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017; pp. 25–28. [Google Scholar]
- Godah, W.; Szelachowska, M.; Krynski, J. On the Analysis of Temporal Geoid Height Variations Obtained from GRACE-Based GGMs over the Area of Poland. Acta Geophys. 2017, 65, 713–725. [Google Scholar] [CrossRef]
- Gregory, J.M.; Griffies, S.M.; Hughes, C.W.; Lowe, J.A.; Church, J.A.; Fukimori, I.; Gomez, N.; Kopp, R.E.; Landerer, F.; Cozannet, G.L.; et al. Concepts and Terminology for Sea Level: Mean, Variability and Change, Both Local and Global. Surv. Geophys. 2019, 40, 1251–1289. [Google Scholar] [CrossRef]
- Wöppelmann, G.; Zerbini, S.; Marcos, M. TGs and Geodesy: A Secular Synergy Illustrated by Three Present-Day Case Studies. Comptes Rendus Geosci. 2006, 338, 980–991. [Google Scholar] [CrossRef]
- Marcos, M.; Wöppelmann, G.; Matthews, A.; Ponte, R.M.; Birol, F.; Ardhuin, F.; Coco, G.; Santamaría-Gómez, A.; Ballu, V.; Testut, L.; et al. Coastal Sea Level and Related Fields from Existing Observing Systems. Surv. Geophys. 2019, 40, 1293–1317. [Google Scholar] [CrossRef]
- Vignudelli, S.; Birol, F.; Benveniste, J.; Fu, L.-L.; Picot, N.; Raynal, M.; Roinard, H. Satellite Altimetry Measurements of Sea Level in the Coastal Zone. Surv. Geophys. 2019, 40, 1319–1349. [Google Scholar] [CrossRef]
- Jet Propulsion Laboratory. GNSS-Inferred Positioning System and Orbit Analysis Simulation Software (GIPSY-OASIS). Available online: https://gipsy-oasis.jpl.nasa.gov (accessed on 1 November 2019).
- Rebischung, P.; Schmid, R. IGS14/Igs14.Atx: A New Framework for the IGS Products. In Proceedings of the AGU Fall Meeting 2016, San Francisco, CA, USA, 12–16 December 2016. [Google Scholar]
- Altamimi, Z.; Rebischung, P.; Métivier, L.; Collilieux, X. ITRF2014: A New Release of the International Terrestrial Reference Frame Modeling Nonlinear Station Motions: ITRF2014. J. Geophys. Res. Solid Earth 2016, 121, 6109–6131. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Simons, W.J.F.; Naeije, M.C.; Brown, B.E.; Niemnil, S.; Pradit, S.; Thongtham, N.; Mustafar, M.A.; Towatana, P.; Darnsawasdi, R.; Yucharoen, M.; et al. Vertical Motion of Phuket Island (1994–2018) Due to the Sumatra-Andaman Mega-Thrust Earthquake Cycle: Impact on Sea-Level and Consequences for Coral Reefs. Mar. Geol. 2019, 414, 92–102. [Google Scholar] [CrossRef]
- Janssen, V.; McElroy, S. A Practical Guide to AUSPOS. In Proceedings of the 25th Association of Public Authority Surveyors Conference (APAS2022), Leura, Australia, 21–23 March 2022. [Google Scholar]
- Simons, W.J.F.; Ambrosius, B.A.C.; Noomen, R.; Angermann, D.; Wilson, P.; Becker, M.; Reinhart, E.; Walpersdorf, A.; Vigny, C. Observing Plate Motions in S.E. Asia: Geodetic Results of the GEODYSSEA Project. Geophys. Res. Lett. 1999, 26, 2081–2084. [Google Scholar] [CrossRef]
- Blewitt, G.; Lavallée, D. Effect of Annual Signals on Geodetic Velocity. J. Geophys. Res. 2002, 107, ETG 9-1–ETG 9-11. [Google Scholar] [CrossRef]
- Simons, W.J.F.; Socquet, A.; Vigny, C.; Ambrosius, B.A.C.; Haji Abu, S.; Promthong, C.; Subarya, C.; Sarsito, D.A.; Matheussen, S.; Morgan, P.; et al. A Decade of GPS in Southeast Asia: Resolving Sundaland Motion and Boundaries. J. Geophys. Res. 2007, 112, B06420. [Google Scholar] [CrossRef]
- Jamil, H.; Kadir, M.; Forsberg, R.; Olesen, A.; Isa, M.N.; Rasidi, S.; Mohamed, A.; Chihat, Z.; Nielsen, E.; Majid, F.; et al. Airborne Geoid Mapping of Land and Sea Areas of East Malaysia. J. Geod. Sci. 2017, 7, 84–93. [Google Scholar] [CrossRef]
- Jensen, T.E.; Olesen, A.V.; Forsberg, R.; Olsson, P.-A.; Josefsson, Ö. New Results from Strapdown Airborne Gravimetry Using Temperature Stabilisation. Remote Sens. 2019, 11, 2682. [Google Scholar] [CrossRef]
- Johann, F.; Becker, D.; Becker, M.; Ince, E.S. Multi-Scenario Evaluation of the Direct Method in Strapdown Airborne and Shipborne Gravimetry. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Forsberg, R. A New Covariance Model for Inertial Gravimetry and Gradiometry. J. Geophys. Res. Solid Earth 1987, 92, 1305–1310. [Google Scholar] [CrossRef]
- Forsberg, R. Local Covariance Functions and Density Distributions; Scientific Report No. 6; The Ohio State University: Columbus, OH, USA, 1984. [Google Scholar]
- Zingerle, P.; Pail, R.; Gruber, T.; Oikonomidou, X. The Combined Global Gravity Field Model XGM2019e. J. Geod. 2020, 94, 66. [Google Scholar] [CrossRef]
- Forsberg, R.; Ses, S.; Alshamsi, A.; Din, A.H. Coastal Geoid Improvement Using Airborne Gravimetric Data in the United Arab Emirates. Int. J. Phys. Sci. 2012, 7, 6012–6023. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.; Bastos, L.; Gidskehaug, A.; Meyer, U.; Timmen, L. Airborne Geoid Determination. Earth Planet Space 2000, 52, 863–866. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.V. Airborne Gravity Field Determination. In Sciences of Geodesy—I; Xu, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 83–104. [Google Scholar] [CrossRef]
- Tziavos, I.N.; Sideris, M.G. Topographic Reductions in Gravity and Geoid Modeling. In Geoid Determination; Sansò, F., Sideris, M.G., Eds.; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; Volume 110, pp. 337–400. [Google Scholar]
- Forsberg, R.; Tscherning, C.C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs, 2nd ed.; DTU Space: Kongens Lyngby, Denmark, 2008. [Google Scholar]
- Forsberg, R.; Tscherning, C.C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs, 3rd ed.; DTU Space: Kongens Lyngby, Denmark, 2014. [Google Scholar]
- Luu, Q.H.; Tkalich, P.; Tay, T.W. Sea Level Trend and Variability around Peninsular Malaysia. Ocean Sci. 2015, 11, 617–628. [Google Scholar] [CrossRef]
- Strassburg, M.W.; Hamlington, B.D.; Leben, R.R.; Manurung, P.; Lumban Gaol, J.; Nababan, B.; Vignudelli, S.; Kim, K.-Y. Sea Level Trends in Southeast Asian Seas. Clim. Past 2015, 11, 743–750. [Google Scholar] [CrossRef]
- Rizal, S.; Damm, P.; Wahid, M.A.; Sundermann, J.; Ilhamsyah, Y.; Iskandar, T.; Muhammad. General Circulation in the Malacca Strait and Andaman Sea: A Numerical Model Study. Am. J. Environ. Sci. 2012, 8, 479–488. [Google Scholar] [CrossRef]
- Haditiar, Y.; Putri, M.R.; Ismail, N.; Muchlisin, Z.A.; Ikhwan, M.; Rizal, S. Numerical Study of Tides in the Malacca Strait with a 3-D Model. Heliyon 2020, 6, e04828. [Google Scholar] [CrossRef]
- Mansor, K.N.A.A.K.; Pa’suya, M.F.; Abbas, M.A.; Ali, T.A.T.; Aziz, M.A.C.; Din, A.H.M. Ocean Surface Circulation in Strait of Malacca Using Satellite Altimeter and Low-Cost GPS-Tracked Drifting Buoys. In Proceedings of the 2016 7th IEEE Control and System Graduate Research Colloquium (ICSGRC), Shah Alam, Malaysia, 8 August 2016; pp. 175–180. [Google Scholar] [CrossRef]
- Grant, D.B.; Blick, G.H. A National Vertical Datum Independent of Local Mean Sea Level? In Vistas for Geodesy in the New Millennium: IAG 2001 Scientific Assembly; Józef, Á., Schwarz, K.P., Eds.; International Association of Geodesy Symposia; Springer: Budapest, Hungary, 2001; Volume 1. [Google Scholar]
- Mills, J.; Dodd, D. Ellipsoidally Referenced Surveying for Hydrography, 1st ed.; The International Federation of Surveyors (FIG): Frederiksberg, Denmark, 2014. [Google Scholar]
- Wu, F.; Zeng, A.; Ming, F. Analyzing the Long-Term Changes in China’s National Height Datum. Adv. Space Res. 2020, 66, 1342–1350. [Google Scholar] [CrossRef]
- Triana, K.; Wahyudi, A.J. Sea Level Rise in Indonesia: The Drivers and the Combined Impacts from Land Subsidence. ASEAN J. Sci. Technol. Dev. 2020, 37, 115–121. [Google Scholar] [CrossRef]
- Dewi, R.S.; Putra, A.A.; Widyantoro, B.T.; Meilano, I.; Safi’i, A.N. Sea-Level Variations from Co-Located TG and GNSS Stations Using GNSS-Reflectometry in Indonesia. IOP Conf. Ser. Earth Environ. Sci. 2021, 824, 012066. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).