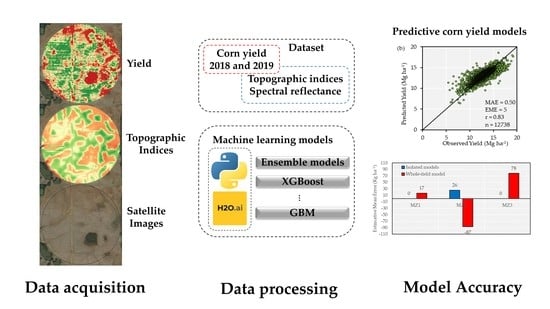
Training Machine Learning Algorithms Using Remote Sensing and Topographic Indices for Corn Yield Prediction
Abstract
1. Introduction
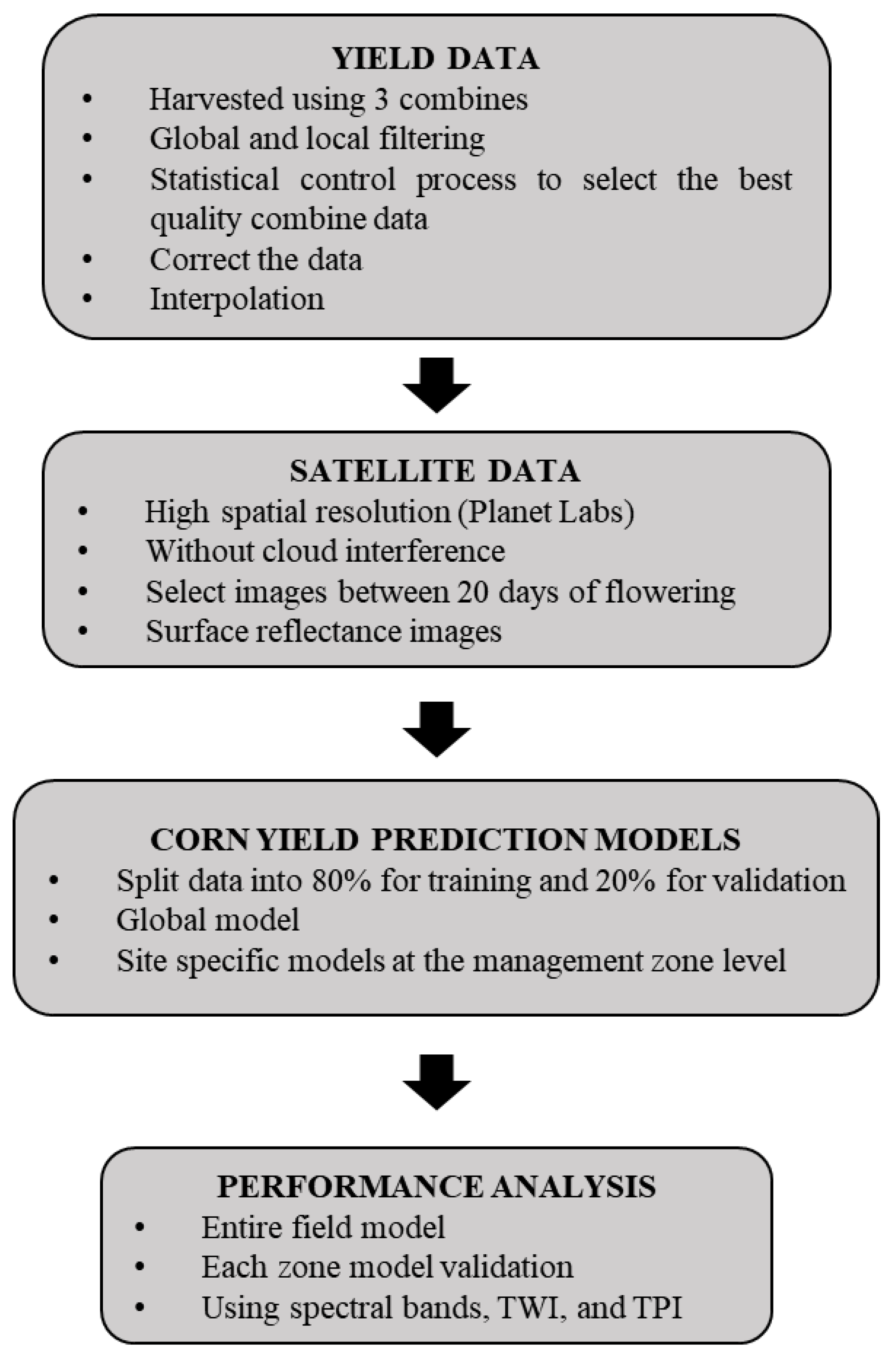
2. Materials and Methods
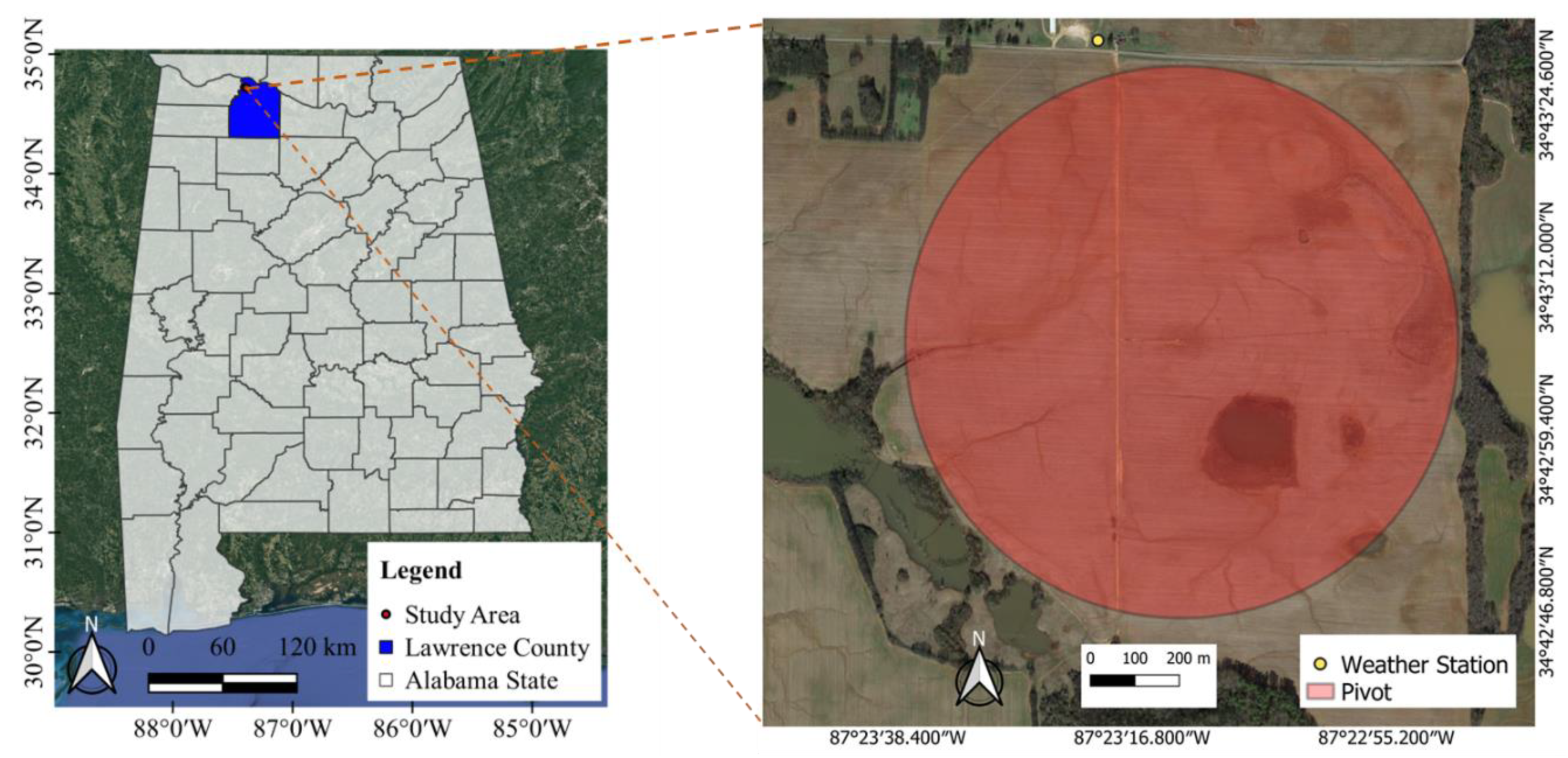
2.1. Study Area
2.2. Satellite Imagery
2.3. Data Processing and Building the Dataset
2.3.1. Yield Data
2.3.2. Topographical Data
2.3.3. Dataset Extraction and Feature Importance
2.4. Auto-ML
2.5. Model Performance Analysis
2.6. Theoretical Framework
3. Results
3.1. Descriptive Statistics of Corn Yield, Spectral Bands, TWI, and TPI
3.2. Feature Importance
3.3. Auto-ML for Predicting Corn Yield Using TWI, TPI, and Spectral Bands
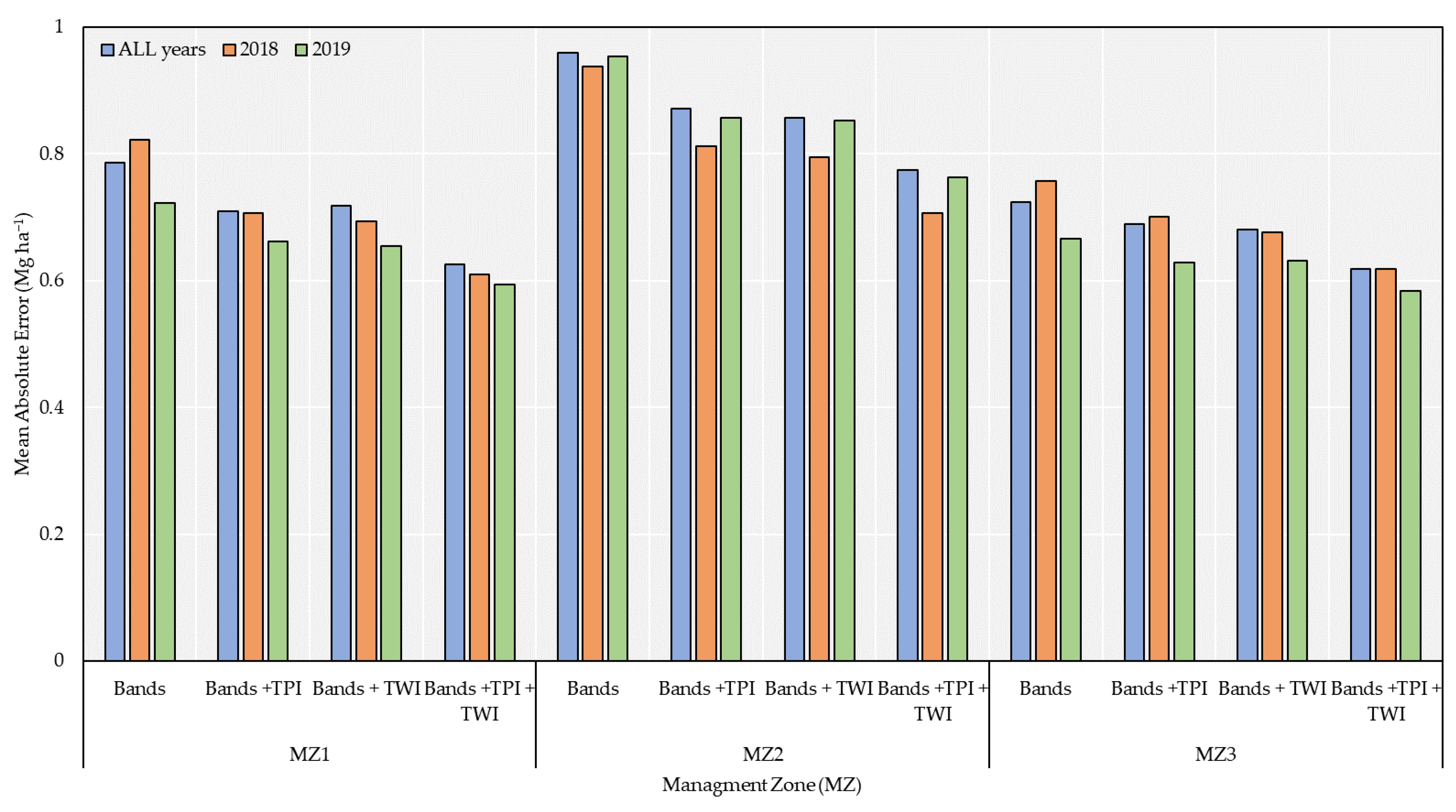
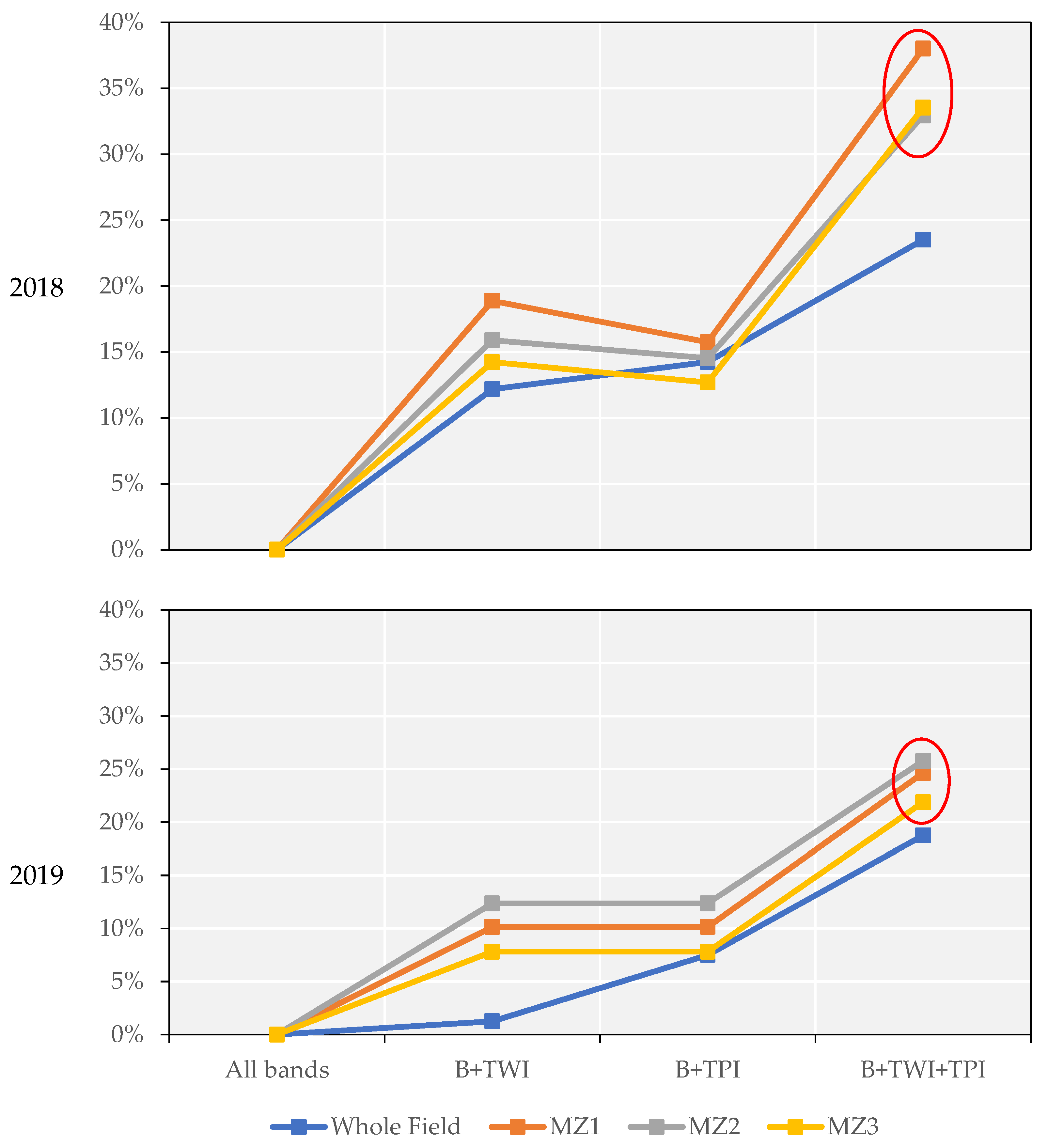
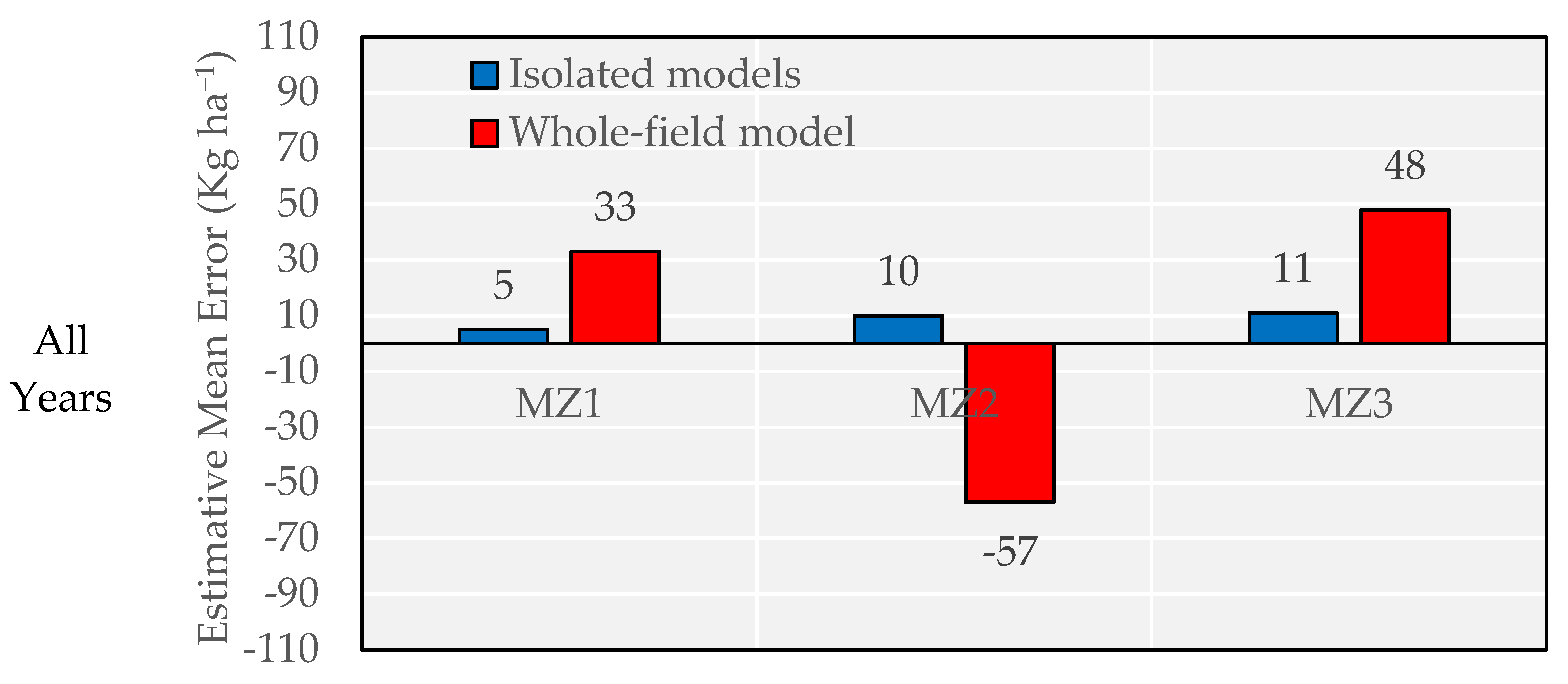
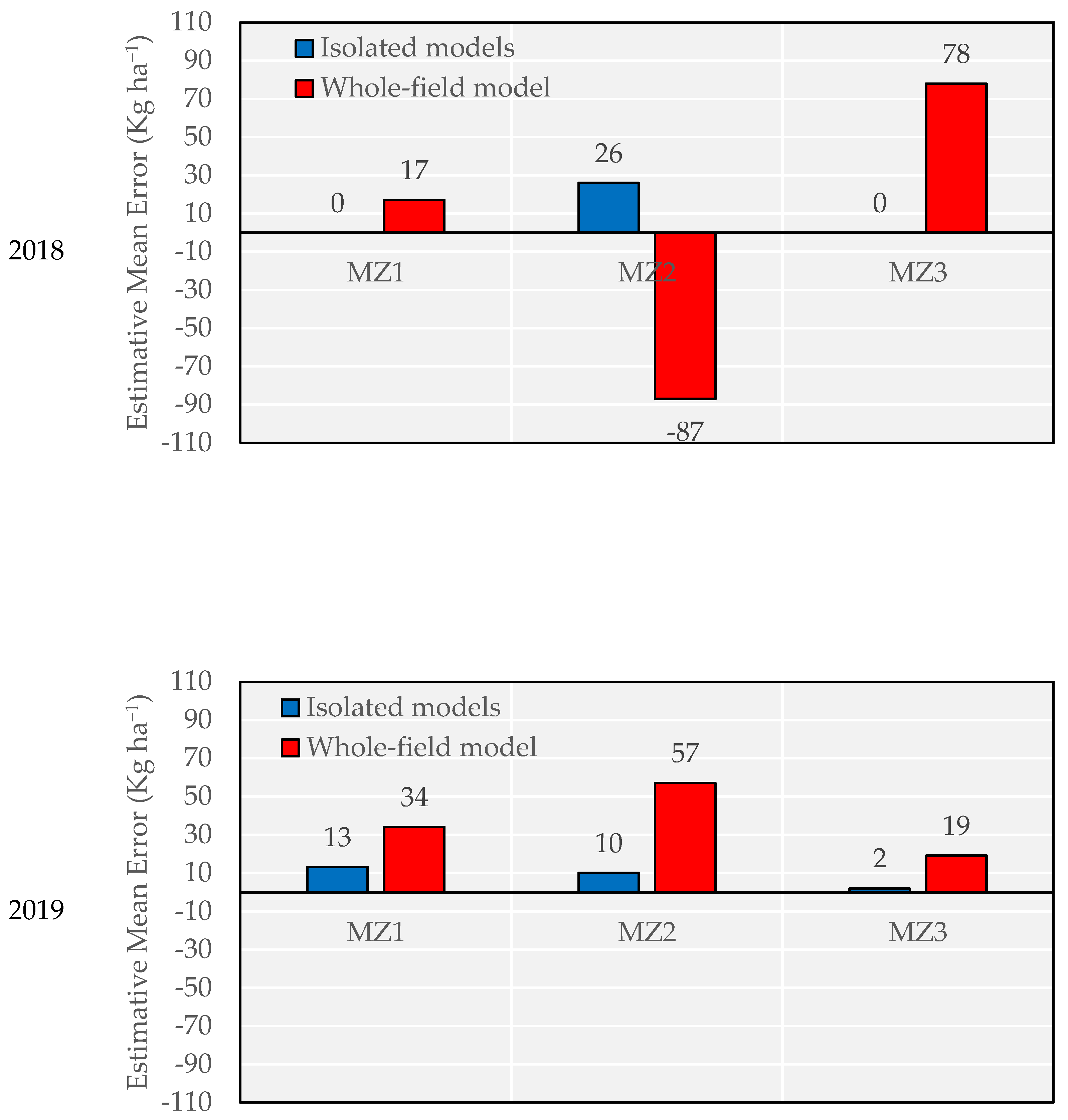
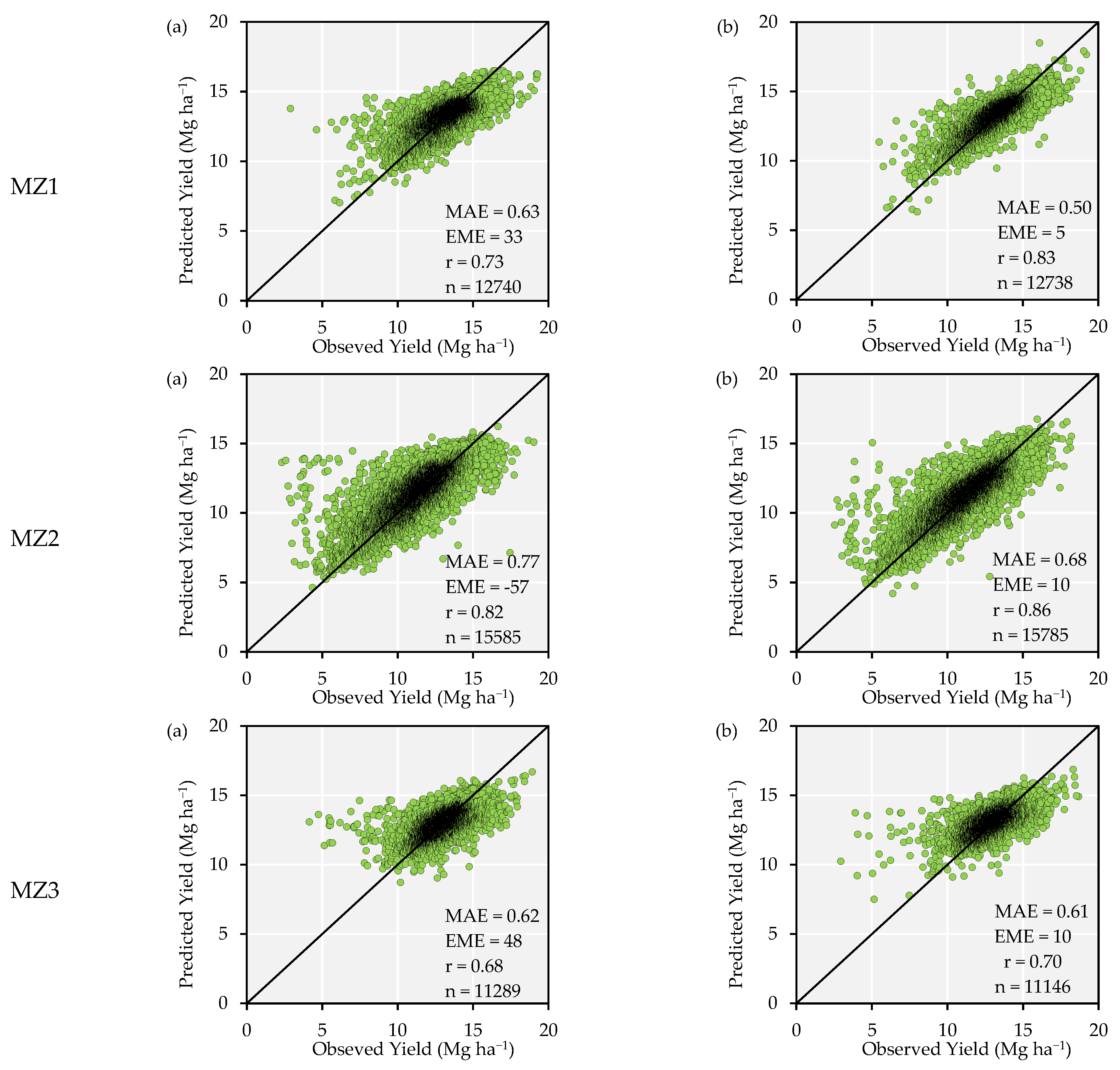
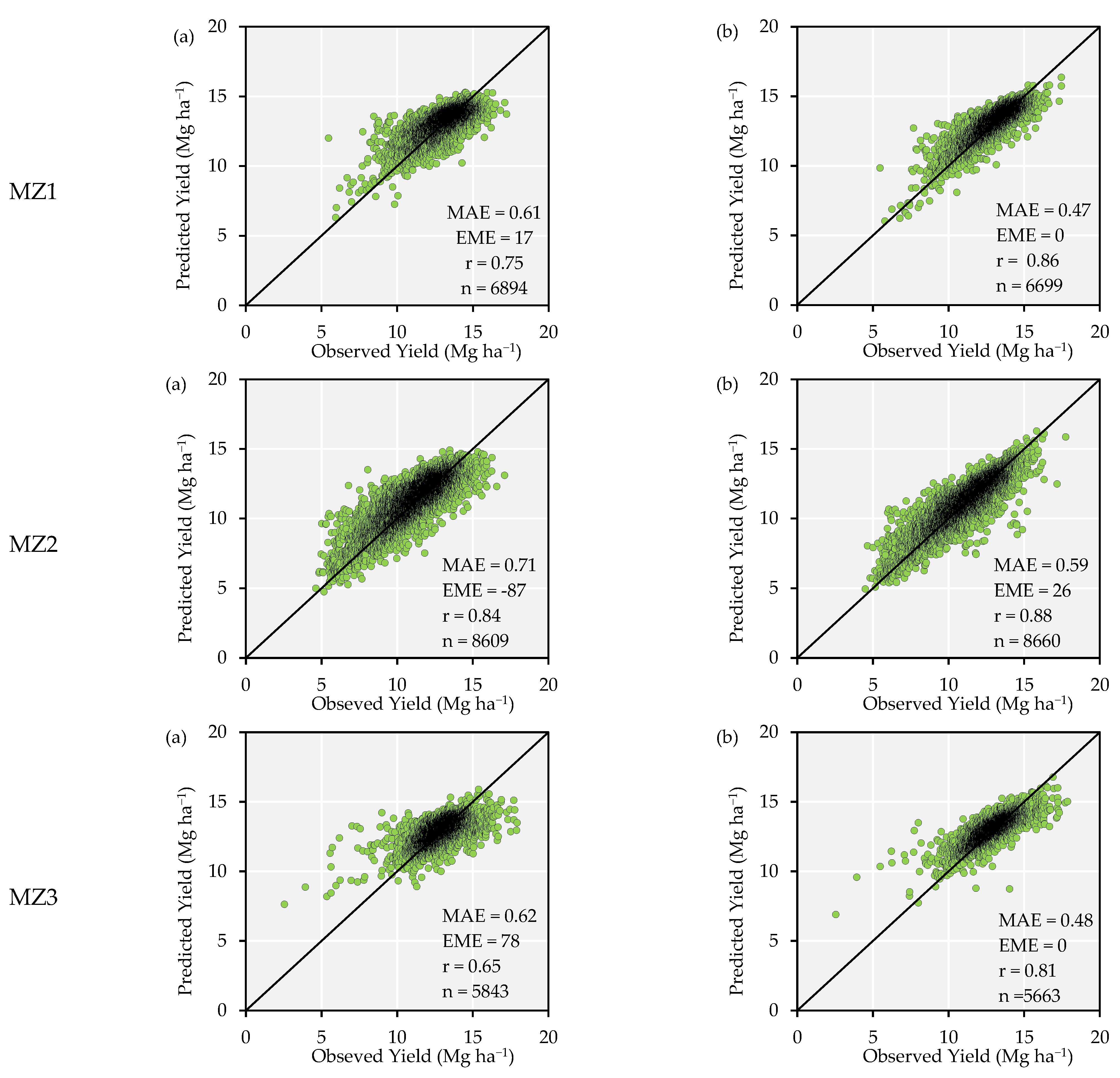
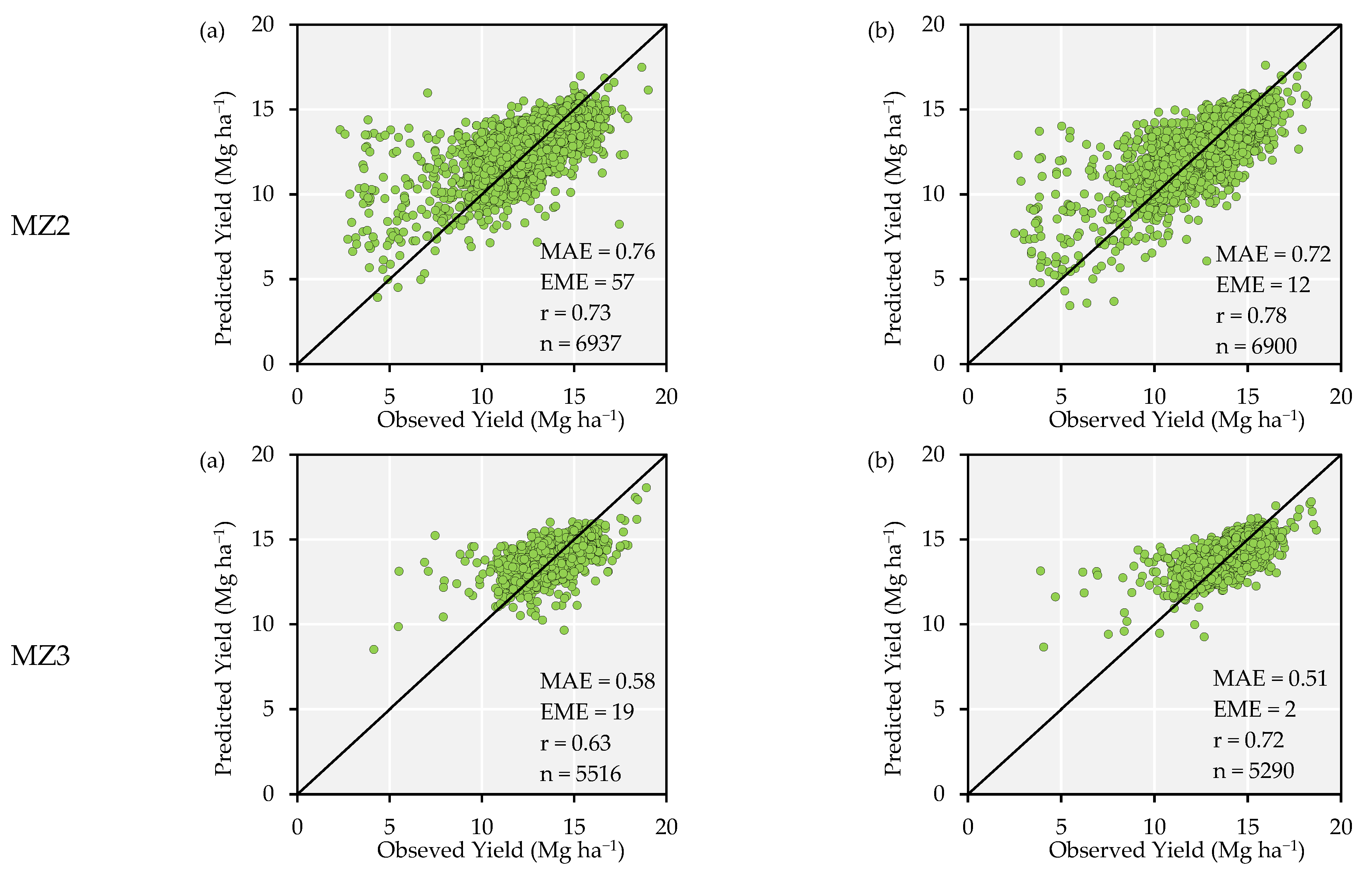
3.4. Comparison of Models Using Different Features in Three Scenarios in Terms of Accuracy, Relative Error, and Tendency
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Venancio, L.P.; Mantovani, E.C.; do Amaral, C.H.; Usher Neale, C.M.; Gonçalves, I.Z.; Filgueiras, R.; Campos, I. Forecasting corn yield at the farm level in Brazil based on the FAO-66 approach and soil-adjusted vegetation index (SAVI). Agric. Water Manag. 2019, 225, 105779. [Google Scholar] [CrossRef]
- Peralta, N.; Assefa, Y.; Du, J.; Barden, C.; Ciampitti, I. Mid-Season High-Resolution Satellite Imagery for Forecasting Site-Specific Corn Yield. Remote Sens. 2016, 8, 848. [Google Scholar] [CrossRef]
- Kayad, A.; Sozzi, M.; Gatto, S.; Marinello, F.; Pirotti, F. Monitoring Within-Field Variability of Corn Yield using Sentinel-2 and Machine Learning Techniques. Remote Sens. 2019, 11, 2873. [Google Scholar] [CrossRef]
- Al-Gaadi, K.A.; Hassaballa, A.A.; Tola, E.K.; Kayad, A.G.; Madugundu, R.; Assiri, F.; Alblewi, B. Characterization of the spatial variability of surface topography and moisture content and its influence on potato crop yield. Int. J. Remote Sens. 2018, 39, 8572–8590. [Google Scholar] [CrossRef]
- Yu, B.; Shang, S. Multi-year mapping of major crop yields in an irrigation district from high spatial and temporal resolution vegetation index. Sensors 2018, 18, 3787. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine learning approaches for crop yield prediction and nitrogen status estimation in precision agriculture: A review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Sørensen, R.; Zinko, U.; Seibert, J. On the calculation of the topographic wetness index: Evaluation of different methods based on field observations. Hydrol. Earth Syst. Sci. 2006, 10, 101–112. [Google Scholar] [CrossRef]
- Zinko, U.; Seibert, J.; Dynesius, M.; Nilsson, C. Plant species numbers predicted by a topography-based groundwater flow index. Ecosystems 2005, 8, 430–441. [Google Scholar] [CrossRef]
- McCann, B.L.; Pennock, D.J.; van Kessel, C.; Walley, F.L. The Development of Management Units for Site-Specific Farming. In Proceedings of the Third International Conference on Precision Agriculture, Minneapolis, MN, USA, 23–26 June 1996; Robert, P.C., Rust, R.H., Larson, W.E., Eds.; American Society of Agronomy: Madison, WI, USA; Crop Science Society of America: Fitchburg, WI, USA; Soil Science Society of America: Madison, WI, USA, 1996; pp. 295–302. [Google Scholar]
- Kaspar, T.C.; Colvin, T.S.; Jaynes, D.B.; Karlen, D.L.; James, D.E.; Meek, D.W.; Pulido, D.; Butler, H. Relationship between six years of corn yields and terrain attributes. Precis. Agric. 2003, 4, 87–101. [Google Scholar] [CrossRef]
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Burt, T.; Butcher, D. Stimulation from simulation? A teaching model of hillslope hydrology for use on microcomputers. J. Geogr. High. Educ. 1986, 10, 23–39. [Google Scholar] [CrossRef]
- Moore, I.D.; Gessler, P.E.; Nielsen, G.A.; Peterson, G.A. Soil Attribute Prediction Using Terrain Analysis. Soil Sci. Soc. Am. J. 1993, 57. [Google Scholar] [CrossRef]
- Qin, C.-Z.; Zhu, A.-X.; Pei, T.; Li, B.-L.; Scholten, T.; Behrens, T.; Zhou, C.-H. An approach to computing topographic wetness index based on maximum downslope gradient. Precis. Agric. 2011, 12, 32–43. [Google Scholar] [CrossRef]
- Silva, J.R.M.D.; Alexandre, C. Spatial Variability of Irrigated Corn Yield in Relation to Field Topography and Soil Chemical Characteristics. Precis. Agric. 2005, 6, 453–466. [Google Scholar] [CrossRef]
- Maestrini, B.; Basso, B. Drivers of within-field spatial and temporal variability of crop yield across the US Midwest. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Reu, J.D.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; Smedt, P.D.; Chu, W.; Antrop, M.; Maeyer, P.D.; Finke, P.; et al. Geomorphology Application of the topographic position index to heterogeneous landscapes. Geomorphology 2013, 186, 39–49. [Google Scholar] [CrossRef]
- Foster, T.; Gonçalves, I.Z.; Campos, I.; Neale, C.M.U.; Brozović, N. Assessing landscape scale heterogeneity in irrigation water use with remote sensing and in situ monitoring. Environ. Res. Lett. 2019, 14, 024004. [Google Scholar] [CrossRef]
- Battude, M.; Al Bitar, A.; Morin, D.; Cros, J.; Huc, M.; Marais Sicre, C.; Le Dantec, V.; Demarez, V. Estimating maize biomass and yield over large areas using high spatial and temporal resolution Sentinel-2 like remote sensing data. Remote Sens. Environ. 2016, 184, 668–681. [Google Scholar] [CrossRef]
- Veloso, A.; Mermoz, S.; Bouvet, A.; Le Toan, T.; Planells, M.; Dejoux, J.F.; Ceschia, E. Understanding the temporal behavior of crops using Sentinel-1 and Sentinel-2-like data for agricultural applications. Remote Sens. Environ. 2017, 199, 415–426. [Google Scholar] [CrossRef]
- Liu, J.; Pattey, E.; Miller, J.R.; McNairn, H.; Smith, A.; Hu, B. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model. Remote Sens. Environ. 2010, 114, 1167–1177. [Google Scholar] [CrossRef]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, P.; Bai, X.; Khan, J.; Zhang, S.; Li, L.; Wang, L. Assimilation of the leaf area index and vegetation temperature condition index for winter wheat yield estimation using Landsat imagery and the CERES-Wheat model. Agric. For. Meteorol. 2017, 246, 194–206. [Google Scholar] [CrossRef]
- Lopresti, M.F.; Di Bella, C.M.; Degioanni, A.J. Relationship between MODIS-NDVI data and wheat yield: A case study in Northern Buenos Aires province, Argentina. Inf. Process. Agric. 2015, 2, 73–84. [Google Scholar] [CrossRef]
- Lobell, D.B. The use of satellite data for crop yield gap analysis. F. Crop. Res. 2013, 143, 56–64. [Google Scholar] [CrossRef]
- Řezník, T.; Pavelka, T.; Herman, L.; Lukas, V.; Širůček, P.; Leitgeb, Š.; Leitner, F. Prediction of Yield Productivity Zones from Landsat 8 and Sentinel-2A/B and Their Evaluation Using Farm Machinery Measurements. Remote Sens. 2020, 12, 1917. [Google Scholar] [CrossRef]
- Zhao, Y.; Potgieter, A.B.; Zhang, M.; Wu, B.; Hammer, G.L. Predicting Wheat Yield at the Field Scale by Combining High-Resolution Sentinel-2 Satellite Imagery and Crop Modelling. Remote Sens. 2020, 12, 1024. [Google Scholar] [CrossRef]
- Mas, J.F.; Flores, J.J. The application of artificial neural networks to the analysis of remotely sensed data. Int. J. Remote Sens. 2008, 29, 617–663. [Google Scholar] [CrossRef]
- Yuan, H.; Yang, G.; Li, C.; Wang, Y.; Liu, J.; Yu, H.; Feng, H.; Xu, B.; Zhao, X.; Yang, X. Retrieving Soybean Leaf Area Index from Unmanned Aerial Vehicle Hyperspectral Remote Sensing: Analysis of RF, ANN, and SVM Regression Models. Remote Sens. 2017, 9, 309. [Google Scholar] [CrossRef]
- Stuart, R.; Peter, N. Artificial Intelligence—A Modern Approach, 3rd ed.; Pearson Education, Inc.: Berkeley, CA, USA, 2016. [Google Scholar]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of Machine Learning Approaches for Biomass and Soil Moisture Retrievals from Remote Sensing Data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef]
- Kaneko, A.; Kennedy, T.; Mei, L.; Sintek, C.; Burke, M.; Ermon, S.; Lobell, D. Deep Learning For Crop Yield Prediction in Africa. In Proceedings of the International Conference on Machine Learning AI for Social Good Workshop, Long Beach, CA, USA, 15 June 2019; pp. 1–5. [Google Scholar]
- Sun, J.; Lai, Z.; Di, L.; Sun, Z.; Tao, J.; Shen, Y. Multilevel Deep Learning Network for County-Level Corn Yield Estimation in the U.S. Corn Belt. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5048–5060. [Google Scholar] [CrossRef]
- Khaki, S.; Wang, L. Crop Yield Prediction Using Deep Neural Networks. Front. Plant Sci. 2019, 10, 1–10. [Google Scholar] [CrossRef]
- Schwalbert, R.A.; Amado, T.J.C.; Nieto, L.; Varela, S.; Corassa, G.M.; Horbe, T.A.N.; Rice, C.W.; Peralta, N.R.; Ciampitti, I.A. Forecasting maize yield at field scale based on high-resolution satellite imagery. Biosyst. Eng. 2018, 171, 179–192. [Google Scholar] [CrossRef]
- Aworka, R.; Cedric, L.S.; Adoni, W.Y.H.; Zoueu, J.T.; Mutombo, F.K.; Kimpolo, C.L.M.; Nahhal, T.; Krichen, M. Agricultural decision system based on advanced machine learning models for yield prediction: Case of East African countries. Smart Agric. Technol. 2022, 2, 100048. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, Y.; Che, X.; Chen, S.; Ying, Q.; Zheng, X.; Feng, A. Coupling Process-Based Crop Model and Extreme Climate Indicators with Machine Learning Can Improve the Predictions and Reduce Uncertainties of Global Soybean Yields. Agriculture 2022, 12, 1791. [Google Scholar] [CrossRef]
- Roy Choudhury, M.; Das, S.; Christopher, J.; Apan, A.; Chapman, S.; Menzies, N.W.; Dang, Y.P. Improving Biomass and Grain Yield Prediction of Wheat Genotypes on Sodic Soil Using Integrated High-Resolution Multispectral, Hyperspectral, 3D Point Cloud, and Machine Learning Techniques. Remote Sens. 2021, 13, 3482. [Google Scholar] [CrossRef]
- Duffera, M.; White, J.G.; Weisz, R. Spatial variability of Southeastern U.S. Coastal Plain soil physical properties: Implications for site-specific management. Geoderma 2007, 137, 327–339. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Z.; Wu, C.; Li, H.; Li, F. Determination of potential management zones from soil electrical conductivity, yield and crop data. J. Zhejiang Univ. Sci. B 2008, 9, 68–76. [Google Scholar] [CrossRef]
- Nawar, S.; Corstanje, R.; Halcro, G.; Mulla, D.; Mouazen, A.M. Delineation of Soil Management Zones for Variable-Rate Fertilization. In Advances in Agronomy; Elsevier Inc.: Amsterdam, The Netherlands, 2017; Volume 143, pp. 175–245. [Google Scholar]
- Morata, G.T. Evaluation of Deficit Irrigation Strategies and Management Zones Delineation for Corn Production in Alabama. Master’s Thesis, Auburn University, Auburn, AL, USA, 2020. [Google Scholar]
- Fridgen, J.J.; Kitchen, N.R.; Sudduth, K.A.; Drummond, S.T.; Wiebold, W.J.; Fraisse, C.W. Management Zone Analyst (MZA). Agron. J. 2004, 96, 100. [Google Scholar] [CrossRef]
- Lab, P. Planet Imagery Product Specification: Planetscope & Rapideye. Available online: https://www.planet.com/products/satellite-imagery/files/1610.06_SpecSheet_Combined_Imagery_Product_Letter_ENGv1.pdf (accessed on 20 July 2021).
- Johnson, D.M.; Mueller, R. The 2007 Cropland Data Layer. Photogramm. Eng. Remote Sens. 2010, 76, 1201–1205. [Google Scholar]
- Sakamoto, T.; Gitelson, A.A.; Arkebauer, T.J. Near real-time prediction of U.S. corn yields based on time-series MODIS data. Remote Sens. Environ. 2014, 147, 219–231. [Google Scholar] [CrossRef]
- Menezes, P.C.D.; Silva, R.P.d.; Carneiro, F.M.; Girio, L.A.d.S.; Oliveira, M.F.D.; Voltarelli, M.A. Can combine headers and travel speeds affect the quality of soybean harvesting operations? Rev. Bras. Eng. Agrícola Ambient. 2018, 22, 732–738. [Google Scholar] [CrossRef]
- Gírio, L.A.d.S.; Silva, R.P.; Menezes, P.C.; Carneiro, F.M.; Zerbato, C.; Ormond, A.T.S. Quality of multi-row harvesting in sugarcane plantations established from pre-sprouted seedlings and billets. Ind. Crops Prod. 2019, 142, 111831. [Google Scholar] [CrossRef]
- de Tavares, T.O.; de Borba, M.A.P.; de Oliveira, B.R.; da Silva, R.P.; Voltarelli, M.A.; Ormond, A.T.S. Effect of soil management practices on the sweeping operation during coffee harvest. Agron. J. 2018, 110, 1689–1696. [Google Scholar] [CrossRef]
- Zhao, J.; Karimzadeh, M.; Masjedi, A.; Wang, T.; Zhang, X.; Crawford, M.M.; Ebert, D.S. FeatureExplorer: Interactive Feature Selection and Exploration of Regression Models for Hyperspectral Images. In Proceedings of the 2019 IEEE Visualization Conference (VIS), Vancouver, BC, Canada, 20–25 October 2019; pp. 161–165. [Google Scholar]
- Moghimi, A.; Yang, C.; Marchetto, P.M. Ensemble Feature Selection for Plant Phenotyping: A Journey From Hyperspectral to Multispectral Imaging. IEEE Access 2018, 6, 56870–56884. [Google Scholar] [CrossRef]
- Feng, L.; Zhang, Z.; Ma, Y.; Du, Q.; Williams, P.; Drewry, J.; Luck, B. Alfalfa Yield Prediction Using UAV-Based Hyperspectral Imagery and Ensemble Learning. Remote Sens. 2020, 12, 2028. [Google Scholar] [CrossRef]
- Sylvester, E.V.A.; Bentzen, P.; Bradbury, I.R.; Clément, M.; Pearce, J.; Horne, J.; Beiko, R.G. Applications of random forest feature selection for fine-scale genetic population assignment. Evol. Appl. 2018, 11, 153–165. [Google Scholar] [CrossRef]
- Ilniyaz, O.; Kurban, A.; Du, Q. Leaf Area Index Estimation of Pergola-Trained Vineyards in Arid Regions Based on UAV RGB and Multispectral Data Using Machine Learning Methods. Remote Sens. 2022, 14, 415. [Google Scholar] [CrossRef]
- Hall, P.; Gill, N.; Kurka, M.; Phan, W.; Bartz, A. Machine Learning Interpretability with H2O Driverless AI: First Edition Machine Learning Interpretability with H2O Driverless AI. Available online: http://docs.h2o.ai (accessed on 6 August 2022).
- Kross, A.; Znoj, E.; Callegari, D.; Kaur, G.; Sunohara, M.; Lapen, D.R.; McNairn, H. Using artificial neural networks and remotely sensed data to evaluate the relative importance of variables for prediction of within-field corn and soybean yields. Remote Sens. 2020, 12, 2230. [Google Scholar] [CrossRef]
- Turpin, K.M.; Lapen, D.R.; Gregorich, E.G.; Topp, G.C.; Edwards, M.; McLaughlin, N.B.; Curnoe, W.E.; Robin, M.J.L. Using multivariate adaptive regression splines (MARS) to identify relationships between soil and corn (Zea mays L.) production properties. Can. J. Soil Sci. 2005, 85, 625–636. [Google Scholar] [CrossRef]
- Zhu, H.D.; Shi, Z.H.; Fang, N.F.; Wu, G.L.; Guo, Z.L.; Zhang, Y. Soil moisture response to environmental factors following precipitation events in a small catchment. Catena 2014, 120, 73–80. [Google Scholar] [CrossRef]
- Yang, M.; Wang, G.; Lazin, R.; Shen, X.; Anagnostou, E. Impact of planting time soil moisture on cereal crop yield in the Upper Blue Nile Basin: A novel insight towards agricultural water management. Agric. Water Manag. 2021, 243, 106430. [Google Scholar] [CrossRef]
- Szypuła, B. Quality assessment of DEM derived from topographic maps for geomorphometric purposes. Open Geosci. 2019, 11, 843–865. [Google Scholar] [CrossRef]
- Mieza, M.S.; Cravero, W.R.; Kovac, F.D.; Bargiano, P.G. Delineation of site-specific management units for operational applications using the topographic position index in La Pampa, Argentina. Comput. Electron. Agric. 2016, 127, 158–167. [Google Scholar] [CrossRef]
- Longchamps, L.; Khosla, R. Improving N Use Efficiency by Integrating Soil and Crop Properties for Variable Rate N Management, 15th ed.; Stafford, J.V., Ed.; Wageningen Academic Publishers: Wageningen, The Netherlands, 2015; ISBN 978-90-8686-267-2. [Google Scholar]





| ML Algorithm | Features | Reference | Model Level |
|---|---|---|---|
| Deep neural network | NDVI, EVI, and temperature | [32] | Country |
| Recurrent neural network and convolutional neural network | MODIS reflectance (MOD091A), Weather data and soil property data | [33] | County |
| Deep neural network | Genotype, weather, and soil | [34] | Hybrid locations |
| Ordinary least-square considering spatial correlation | NDRE, NDVI, and GDVI | [35] | Field |
| Year | ||
|---|---|---|
| 2018 | 2019 | |
| Sowing | 10 April | 27 March |
| Tasseling | 23 June | 9 June |
| Harvest | 3 September | 29 August |
| Corn hybrid | Dekalb® DKC 66-97 | Dekalb® DKC 66-97 |
| Row spacing | 0.76 m | 0.76 m |
| Plant population | 84,000 pl/ha−1 | 84,000 pl/ha−1 |
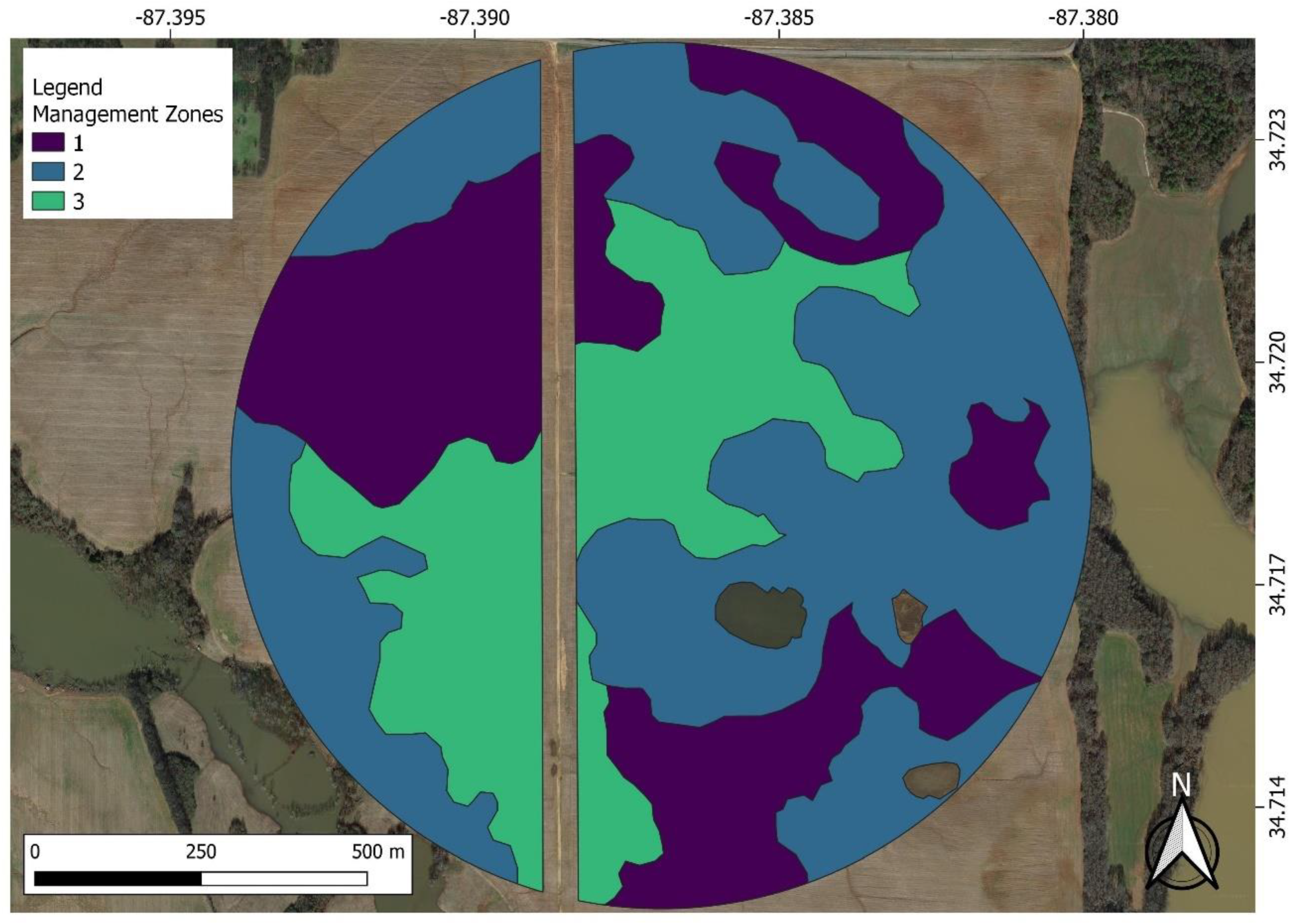
| Management Zone | Soil Type | Sand% | Silt% | Clay% |
|---|---|---|---|---|
| MZ1 1 | Silty clay | 13.07 | 40.13 | 46.80 |
| MZ2 2 | Clay loam | 23.20 | 45.47 | 31.33 |
| MZ3 3 | Clay loam | 34.40 | 31.60 | 34.00 |
| 2018 | 2019 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MZ1 | |||||||||||
| mean | Std | C.V(%) | min | max | mean | std | C.V(%) | min | max | ||
| Blue | 5509 | 72 | 1 | 5172 | 6189 | Blue | 499 | 27 | 5 | 410 | 723 |
| Green | 4773 | 58 | 1 | 4554 | 5398 | Green | 588 | 32 | 5 | 504 | 819 |
| Red | 3238 | 85 | 3 | 2959 | 4380 | Red | 557 | 52 | 9 | 443 | 909 |
| NIR | 11,441 | 290 | 3 | 8590 | 12,435 | NIR | 3721 | 159 | 4 | 2983 | 4210 |
| TWI | 6 | 1 | 20 | 2 | 10 | TWI | 6 | 1 | 18 | 2 | 10 |
| TPI | −1 | 1 | −158 | −5 | 5 | TPI | −1 | 1 | −151 | −5 | 5 |
| Yield | 13.25 | 1.28 | 9 | 5.31 | 17.49 | Yield | 14.19 | 1.14 | 8 | 2.89 | 19.77 |
| MZ2 | |||||||||||
| Blue | 5576 | 99 | 2 | 5231 | 6904 | Blue | 529 | 35 | 7 | 382 | 702 |
| Green | 4857 | 104 | 2 | 4567 | 5897 | Green | 626 | 42 | 7 | 473 | 818 |
| Red | 3368 | 168 | 5 | 3031 | 5101 | Red | 627 | 79 | 13 | 412 | 981 |
| NIR | 11,126 | 423 | 4 | 5476 | 12,717 | NIR | 3686 | 180 | 5 | 1962 | 4277 |
| TWI | 4 | 1 | 23 | 2 | 9 | TWI | 4 | 1 | 23 | 2 | 8 |
| TPI | 0 | 2 | 413 | −9 | 6 | TPI | 1 | 2 | 309 | −9 | 6 |
| Yield | 11.37 | 1.68 | 15 | 3.97 | 17.75 | Yield | 13.05 | 1.68 | 13 | 2.35 | 19.44 |
| MZ3 | |||||||||||
| Blue | 5513 | 79 | 1 | 5176 | 6965 | Blue | 510 | 26 | 5 | 431 | 696 |
| Green | 4784 | 68 | 1 | 4574 | 6136 | Green | 604 | 31 | 5 | 507 | 808 |
| Red | 3255 | 96 | 3 | 3005 | 5453 | Red | 579 | 50 | 9 | 453 | 979 |
| NIR | 11,366 | 273 | 2 | 9093 | 12,499 | NIR | 3715 | 121 | 3 | 3146 | 4210 |
| TWI | 6 | 1 | 15 | 1 | 9 | TWI | 6 | 1 | 15 | 1 | 9 |
| TPI | 0 | 1 | −2218 | −3 | 4 | TPI | 0 | 1 | −2081 | −3 | 4 |
| Yield | 13.05 | 1.14 | 9 | 1.41 | 17.96 | Yield | 13.99 | 1.08 | 8 | 3.23 | 19.17 |
| 2018 | 2019 | All Years | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Whole Field | |||||||||
| Model Type | Training | Test | Model Type | Training | Test | Model Type | Training | Test | |
| Bands | SE | 0.83 | 0.85 | XGBoost | 0.78 | 0.8 | SE | 0.81 | 0.84 |
| Bands + TWI | SE | 0.4 | 0.73 | SE | 0.47 | 0.73 | SE | 0.64 | 0.76 |
| Bands + TPI | SE | 0.44 | 0.75 | SE | 0.45 | 0.73 | SE | 0.63 | 0.77 |
| Bands + TPI + TWI | SE | 0.5 | 0.65 | SE | 0.42 | 0.66 | SE | 0.57 | 0.68 |
| MZ1 | |||||||||
| Bands | GBM | 0.73 | 0.76 | GBM | 0.67 | 0.69 | GBM | 0.7 | 0.74 |
| Bands + TWI | SE | 0.49 | 0.64 | SE | 0.39 | 0.62 | SE | 0.36 | 0.63 |
| Bands + TPI | SE | 0.19 | 0.62 | SE | 0.3 | 0.62 | XGBoost | 0.36 | 0.63 |
| Bands + TPI + TWI | SE | 0.1 | 0.47 | SE | 0.16 | 0.52 | SE | 0.19 | 0.5 |
| MZ2 | |||||||||
| Bands | SE | 0.83 | 0.88 | XGBoost | 0.91 | 0.97 | SE | 0.85 | 0.92 |
| Bands + TWI | SE | 0.38 | 0.75 | SE | 0.44 | 0.85 | SE | 0.45 | 0.79 |
| Bands + TPI | SE | 0.4 | 0.74 | SE | 0.41 | 0.85 | SE | 0.46 | 0.78 |
| Bands + TPI + TWI | SE | 0.15 | 0.59 | SE | 0.22 | 0.72 | SE | 0.45 | 0.68 |
| MZ3 | |||||||||
| Bands | GBM | 0.72 | 0.73 | GBM | 0.63 | 0.64 | GBM | 0.67 | 0.68 |
| Bands + TWI | XGBoost | 0.38 | 0.64 | XGBoost | 0.32 | 0.59 | XGBoost | 0.31 | 0.61 |
| Bands + TPI | SE | 0.25 | 0.62 | XGBoost | 0.33 | 0.59 | XGBoost | 0.32 | 0.6 |
| Bands + TPI + TWI | SE | 0.11 | 0.48 | XGBoost | 0.25 | 0.51 | SE | 0.19 | 0.49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, M.F.d.; Ortiz, B.V.; Morata, G.T.; Jiménez, A.-F.; Rolim, G.d.S.; Silva, R.P.d. Training Machine Learning Algorithms Using Remote Sensing and Topographic Indices for Corn Yield Prediction. Remote Sens. 2022, 14, 6171. https://doi.org/10.3390/rs14236171
Oliveira MFd, Ortiz BV, Morata GT, Jiménez A-F, Rolim GdS, Silva RPd. Training Machine Learning Algorithms Using Remote Sensing and Topographic Indices for Corn Yield Prediction. Remote Sensing. 2022; 14(23):6171. https://doi.org/10.3390/rs14236171
Chicago/Turabian StyleOliveira, Mailson Freire de, Brenda Valeska Ortiz, Guilherme Trimer Morata, Andrés-F Jiménez, Glauco de Souza Rolim, and Rouverson Pereira da Silva. 2022. "Training Machine Learning Algorithms Using Remote Sensing and Topographic Indices for Corn Yield Prediction" Remote Sensing 14, no. 23: 6171. https://doi.org/10.3390/rs14236171
APA StyleOliveira, M. F. d., Ortiz, B. V., Morata, G. T., Jiménez, A.-F., Rolim, G. d. S., & Silva, R. P. d. (2022). Training Machine Learning Algorithms Using Remote Sensing and Topographic Indices for Corn Yield Prediction. Remote Sensing, 14(23), 6171. https://doi.org/10.3390/rs14236171