Abstract
The Temperature–Vegetation–Precipitation–Drought Index (TVPDI) has a good performance in drought monitoring in China. However, different regions have different responses to droughts due to terrain differences. In southeastern Tibet, the drought monitoring capacity of some drought indices without soil information has to be assessed on account of the poor sensitivity between temperature and soil humidity. Therefore, soil moisture was added to calculate a new drought index based on TVPDI in southeastern Tibet, named the Temperature–Vegetation–Soil-Moisture–Precipitation–Drought Index (TVMPDI). Then, the TVMPDI was validated by using the Standardized Precipitation Evapotranspiration Index (SPEI) and other remote sensing drought indices, including the Vegetation Health Index (VHI) and Scale Drought Conditions Index (SDCI), during the growing seasons of 2003–2018. The Standardized Precipitation Index (SPI) and SPEI were used to represent meteorological drought and Gross Primary Productivity (GPP) was used to represent agricultural drought. The relation between TVMPDI and these drought indices was compared. Finally, the time trends of TVMPDI were also analyzed. The relation coefficients of TVMPDI and SPEI were above 0.5. The correlations between TVMPDI and drought indices, including the Vegetation Health Index (VHI) and Scale Drought Conditions Index (SDCI), also had a good performance. The correlation between the meteorological drought indices (SPI and SPEI) and TVMPDI were not as good as for the TVPDI, but the temporal correlation between the TVMPDI and GPP was greater than that between the TVPDI and GPP. This indicates that the TVMPDI is more suitable for monitoring agricultural drought than the TVPDI. In addition, historical drought monitoring had values that were consistent with those of the actual situation. The trend of the TVMPDI showed that drought in the study area was alleviated from 2003 to 2018. Furthermore, GPP was negatively correlated with SPEI (r = −0.4) and positively correlated with Soil Moisture (SM) drought index (TVMPDI, SMCI) (r = 0.4) in the eastern part of the study area, which suggests that SM, rather than precipitation, could promote the growth of vegetation in the region. A correct understanding of the role of soil information in drought comprehensive indices may monitor meteorological drought and agricultural drought more accurately.
1. Introduction
One of the worst and most prevalent natural catastrophes in the world is droughts. Over 35% of the world’s land surface is composed of arid and semiarid areas. More than 60 nations and areas throughout the world are at risk of drought, which has the Qinghai–Tibet Plateau (QTP) yearly economic impact of USD 6 to 8 billion, a cost that is significantly greater than that of other meteorological disasters [1,2]. Therefore, it is crucial for human civilization to accurately monitor the incidence of droughts.
Drought is mainly divided into four types, namely meteorological drought, agricultural drought, hydrological drought and socio-economic drought [3]. The first occurrence of a lack of rainfall that lasts for several months and reaches a specific threshold is meteorological drought. [4]. With the continuous evaporation of water and the continuous reduction in water resources, the shortage of soil water supply gradually leads to agricultural drought. Hydrological drought [5] results from river flows and [5] water storage in water bodies that are below long-term averages. Due to water shortages, there is an excessive demand for commercial goods, which has detrimental social, economic and environmental impacts [6,7]. Social and economic drought is the term used to describe the anomalous phenomena of a water scarcity brought on by an imbalance between the natural systems for precipitation, surface and subsurface water distribution, and human social water consumption and drainage [8].
In the early stage, traditional drought monitoring is mainly performed to conduct statistical analysis on the monitoring data of ground meteorological stations or hydrological stations, calculate the corresponding index and finally determine the drought index suitable for the region, to clarify the time, scope and degree of drought. Three of the most common drought indexes, including Palmer Drought Severity Index (PDSI) [9], SPI [10] and SPEI [11], based on one or more hydroclimatic factors, are widely used in meteorological drought monitoring. SPEI, combined with the characteristics of PDSI and SPI, can describe the impact of temperature change on drought assessment [12].
The assessment of agricultural drought is based on the lack of SM during the plant growth season. SM-based agricultural drought index mainly includes the Palmer Z index [13], CMI [6], Normalized Soil Moisture [14] and Soil Water Deficit Index (SWDI) [15]. In addition to indices based on soil moisture, vegetation-based indices have also been proposed to describe agricultural drought, such as Vegetation Condition Index (VCI), Normalized Difference Vegetation Index (NDVI) or GPP [16,17,18].
Droughts are generally affected by a variety of factors, such as precipitation, temperature and soil moisture. Many researchers have realized that using multiple variables or parameters can improve the accuracy of dryness assessment [19]. The common comprehensive remote sensing dryness index includes monitoring land surface temperature (LST), vegetation, precipitation, evapotranspiration and soil moisture [20,21]. In addition to these dryness indices, with the Temperature Vegetation Drought Index (TVDI) [22], it was found that the spatial relationship between NDVI and Ts was triangular when the range of vegetation cover change was large and the soil moisture change ranged from lack to sufficient. With the progress of related research, other normalized indicators, such as the Soil Moisture Condition Index (SMCI) [23] and Precipitation Condition Index (PCI) [24], were introduced to the comprehensive remote sensing dryness indices. The present paper assesses how to fairly balance each indicator in the composite index, including the Scaled Drought Condition Index (SDCI) and Synthesized Drought Index (SDI) [25,26]. The principal component analysis of SDI was calculated, and the first principal component was emphasized, while other useful drought information was ignored. Thus, the correlation between the two indices decreases [27]. TVPDI [28] is used to monitor wet and dry conditions in China. In addition to these drought indices, Abhishek and Kinouchi et al. [29] used GRACE gravity and PCR-GLOBWB model data to quantify the deficiencies of terrestrial water stocks (LWS) and groundwater stocks (GWS) in Peninsular India, providing new insights into the groundwater monitoring framework.
Natural habitats vary greatly throughout an area. Tibet, which is situated at a high altitude in the QTP, is significant as a “river source”. The principal rivers of China originate there. The environment of Tibet is very vulnerable because of its unique geological, geographical and meteorological factors [30]. As a result, natural calamities, including droughts, storms and frosts, frequently affect Tibet. Therefore, further studies are needed on the features of recent droughts in Tibet and how they relate to climatic variables.
Many research studies have contributed to drought resistance on the QTP. Fang et al. [31] established a PDSI reconstruction model from 1440 to 2007 in the southeastern QTP. They found that temperature changes in this region may be related to SST changes in the North Pacific and Atlantic oceans. Wang et al. assessed the candidacy of various probability functions for SPI and SPEI for more than 500 stations in China, including the QTP. Feng et al. analyzed the elevation dependence in SPEI index by using gauged-based time-series data of precipitation and temperature at 274 meteorological stations scattered over the QTP [32,33]. These meteorological drought indexes based on atmospheric precipitation and evapotranspiration can monitor droughts at a specific time better, but in some regions, soil moisture is not completely controlled by precipitation and evapotranspiration [34]. TVPDI contains factors that increase or decrease moisture in the atmosphere, but lacks information about moisture in the soil. Therefore, it is unknown whether TVPDI can keep track of the agricultural drought in southeastern Tibet. On the other hand, southeastern Tibet has a small and irregularly distributed number of weather stations. There may be uncertainties caused by large spatial variability, due of the restricted ground observations, considerable regional variability and demographics connected to drought [35].
In this paper, soil moisture was added to TVPDI, named Temperature–Vegetation–Soil-Moisture–Precipitation–Dryness Index (TVMPDI), based on multi-dimensional Euclidean distance, considering the influence of atmospheric, soil and vegetation moisture during agricultural drought. The objectives of the study are to evaluate the performance of TVMPDI in drought monitoring, and then analyze the spatial and temporal variation characteristics of TVMPDI in southeast Tibet. We also compare the monitoring effects of TVMPDI and TVPDI on meteorological drought and agricultural drought, respectively, and analyze the factors controlling agricultural drought in different regions.
2. Study Area and Materials
2.1. Study Area
The Tibet Autonomous Region (TAR) in China’s southwest frontier is the main body of the QTP. Due to the strong influence of westerly weather and warm and humid air currents over the Indian Ocean, there are obvious differences in the dry and wet seasons in Tibet. The unique hazard-formative environments, coupled with the vulnerability of regional carriers (social and economic systems), makes it the region where meteorological disasters occur most frequently in China. The five cities in the southeast of the TAR are the main agricultural areas in Tibet, as shown in Figure 1, and include more than 70 percent of the region’s weather stations [36,37,38].
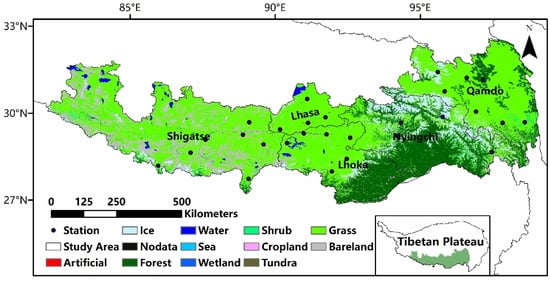
Figure 1.
Land-use types in southeastern Tibet.
Most areas in Tibet belong to arid and semi-arid areas. Affected by monsoon climate and geographical conditions, they suffer from seasonal drought, which lasts for a long time. A drought disaster usually lasts for one month or even several months. The frequent and sudden occurrence of meteorological disasters in the TAR makes the fragile agricultural ecological environment and infrastructure protection facilities more vulnerable to damage, causing serious losses to the work and life of the people, especially farmers and herdsmen.
2.2. Materials
The following are the three categories of datasets that we used: (1) meteorological datasets, including precipitation and temperature for SPEI calculation, and soil relative moisture data were obtained through NCDC (http://data.cma.cn/ (accessed on 18 March 2022)). These datasets were calculated for SPEI. (2) The datasets were utilized to assess the effectiveness of drought indices, such as SPI, SPEI and GPP, on the spatial distribution of meteorological drought and agricultural drought. (3) Input datasets were used for calculating drought index, including Precipitation, LST and Enhanced Vegetation Index (EVI) and SM. Details regarding these datasets are listed in Table 1.

Table 1.
The datasets used in the study.
2.2.1. Remote Sensing Data
The Tropical Rainfall Measuring Mission (TRMM) was a joint international project developed by National Aeronautics and Space Administration (NASA) and the Japan Aerospace Exploration Agency (JAXA) to study weather and precipitation [39]. TRMM3B43 monthly mean grid precipitation data are the precipitation product of the TRMM satellite, other satellites and ground observation. This dataset makes the best use of the existing detection data and provides an optimal estimate of precipitation per grid for each standard observation time, especially with a good suitable for mid-latitude areas. The alternate TRMM precipitation abstracts were accumulated monthly. Additionally, precipitation data were also used to calculate SPI.
The monthly SMC datasets were obtained from the National Tibetan Plateau Data Center. It is made from 3 passive microwave remote sensing data: Level 3 SM data from The Japan Aerospace Exploration Agency (JAXA), and soil moisture data for SMOS products developed by the French Institute of Agricultural Sciences (INRA) and the French Centre for Space Biosphere Research (CESBIO) [40]. The value of its spatial resolution was unified as 1km, and then we calculated the SMCI using the monthly soil moisture.
Terra MODIS LST (MOD11A2) and NDVI (MOD13A2) with a resolution of 1 km were obtained from NASA and EOSDIS, respectively. The TCI and VCI, which were used to construct the TVMPDI, were determined by using the cumulative monthly LST and Enhanced Vegetation Index (EVI), respectively.
These data also include SMC, SPEI and GPP, which are included in Table 1. SMC were normalized and again acclimated to account for TVMPDI. The SPEI and GPP as meteorological and agronomical aridity factors for appraising the achievement of aridity indices for both droughts.
2.2.2. Meteorological Data
The meteorological station data from the NCDC (http://data.cma.cn/ (accessed on 18 March 2022)) include precipitation, temperature and relative soil moisture, which were used to calculate the SPEI. These site data can be used as an auxiliary validation of meteorological drought and agricultural drought when spatial discrimination between SPEI Base datasets and GPP is insufficient. In addition, the precipitation and soil relative moisture data from these stations can be used to verify the downscaling of the TRMM and SM datasets.
In addition, the precipitation and soil relative humidity data of these stations can be used to verify the downscaling of TRMM and SM data: the spatial resolution of TRMM and SMC was reduced to 1 km by means of resampling. Then, correlation analysis was conducted between the precipitation and soil relative humidity data of 28 stations in the study area and the pixel values of the corresponding points after downscaling. The results show that the correlation coefficients of precipitation and soil moisture data with the data of corresponding stations were 0.87 and 0.88, respectively, and both passed the significance test at 0.01.
3. Methodology
Drought in agriculture has a major impact on the development and growth of crops. The majority of crops are at their height from April to October every year in TAR, and any drought that occurs during this time has a major negative impact on the agriculture sector and agricultural output. In addition, because of the special geographical conditions of Tibet, some remote sensing data records requirements cannot be met in winter. Therefore, the SPEI and the relative soil humidity of 28 stations in TAR from April to October from 2003 to 2018 were selected as the verifiable indicators, and the remote sensing image data of corresponding stations were taken to calculate the TVMPDI, including multiple drought factors (TRMM, LST, SM and EVI).
3.1. Drought Indices
3.1.1. SPEI and SPI
The SPI was created by first computing the precipitation distribution probability and then normalizing it from a continuous time series of precipitation at a certain time scale. The SPEI was constructed by introducing potential evapotranspiration on the basis of the SPI. The SPEI index integrates the advantages of the SPI index and PDSI, which can reflect regional drought situation more comprehensively. Therefore, it is widely used in drought monitoring [11]. The Thornthwaite technique was used to determine the probability distribution functions, which has a scroll probabilistic model.
3.1.2. Scaled Drought Indices
The variables used to calculate the TVMPDI include four kinds of scaled remote sensing drought indices, which were calculated from four raw variables (TRMM, LST, SM and EVI) by the normalization processing (Table 2). Additionally, they were scaled on a vertical ranging from 0 to 1, where 0 denotes dryness conditions and 1 denotes rainy conditions.

Table 2.
Formulas for the scaled variables.
The normalization method is applied by taking the difference between the maximum and minimum values of the pixel point for many years as the denominator and the difference between the pixel and minimum values of the month as the numerator (LST: the difference between the maximum and pixel values), and then using their ratio as the normalization value.
3.2. Dryness Index
The Euclidean ambit can admeasure the complete ambit amid credibility in a hyperspace, and in its simplest form, it can be defined as a straight line connecting two points A and B. Due to its objectivity, science and universality, the Euclidean ambit primarily acclimates to ecological boredom [28,41,42]. The Euclidean ambit is expressed as follows:
where n is the number of the multidimensional space’s dimension and D(x, y) is the shortest distance among endpoints X(x1, x2, x3, …, xn) and Y(y1, y2, y3, …, yn).
The dryness index based on Euclidean distance formula sets a reference point in the three-dimensional space, which represents the state point with the most severe drought in each dimension. The shorter the distance, the more severe the drought.
The TRMM, EVI and LST were integrated to establish a three-dimensional environment and measure dryness [28]. However, the formation of agricultural drought is a very complicated process. It is difficult to describe the whole information of drought with these three variables. Therefore, this study added an additional soil moisture variable on the basis of TVPDI to compare the difference between the two indexes in drought detection, and the formulas to calculate the two European dryness indices are as follows:
where PCIMIN, TCIMIN, SMCIMIN and VCIMIN represent the driest status. They are (0, 0, 0) and (0, 0, 0, 0), respectively. PCIi, TCIi, SMCIi and VCIi represent the normalized values at a point.
We also used several other drought indices in this study, including the VHI, SDCI and SMCI. They can help us to evaluate the monitoring ability of the TVMPDI more intuitively and analyze the dry and wet changes in different zones of the study area. The VHI and SDCI were calculated as follows:
3.3. Accuracy Assessment
In numerous earlier research, the Pearson correlation coefficient was utilized to assess the relationship between two variables [43,44]. Its calculation is as follows:
where xi is the simulation value; yi is the observed value; and are the average value of simulation value and observed value, respectively; m is the simple randomization; and i is the serial number of the observation month.
The TVMPDIs of 28 stations in the growing season were extracted and compared with the SPEI in the study area, calculated by the corresponding stations for accuracy verification. The examination of the temporal association between the TVMPDI and several drought monitoring indices was performed, including the VHI, SDCI, SMCI and TVPDI.
3.4. Classification of TVMPDI
In order to verify the consistency between the regional and chronological incidence of drought monitored by the TVMPDI and the actual drought events, the drought grade of the TVMPDI was divided according to the SPEI and SPI drought grade divided by Meteorological Drought Grade, combined with the correlation between the TVMPDI and SPI and SPEI and the frequency of each drought grade [45,46,47]. The TVMPDI calculated in this study was graded as shown in Table 3.

Table 3.
Drought classification.
This paper analyzed the spatial distribution of drought in typical dry years in study area using the TVMPDI to evaluate its performance in monitoring actual drought duration, according to the statistics yearbook of TAR.
3.5. Theil–Sen Median Trend Analysis and Mann–Kendall Test
In this paper, Theil–Sen median trend analysis and the Mann–Kendall method were employed to examine the properties of the geographical distribution, temporal variation characteristics and variation trend of the TVMPDI in southeastern Tibet. These two methods were combined by many studies to examine the trend of lengthy regression analysis [48,49,50].
The Theil–Sen median trend assay is an adjustment that could abate the access of abstract outliers [51]. The Theil–Sen median trend calculates the average abruptness of n(n − 1)/2 abstract portfolios (n is the arrangement length), and its blueprint is as follows:
indicates that the TVMPDI presents a growing trend; otherwise, the TVMPDI presents a degenerate trend.
The Mann–Kendall assay is a non-parametric statistical analysis adjustment that is acclimated to adjudicate the acceptation of trend. It is not all-important for samples to chase an assertive distribution, and it is not diminished by a few outliers [52]. The calculation formula is as follows:
First, set
where TVMPDIi and TVMPDIj represent the TVMPDI value of pixel years i and j; n is the duration; and sgn is the symbol operation. The statistic Z ranges from −∞ to +∞.
The mean TVMPDI of the five cities in the study area from 2003 to 2018 was statistically analyzed. When adding more hours to the TVMDI in the study area, it shows that drought intensifies; so, when the linear regression trend for timing (TVMPDI over time will increase), the drought trend becomes gradual over time, and when there is a yuan linear regression trend for negative, the TVMDI gradually decreases with time, with the drought increasing gradually over time.
These two methods were accumulated to reflect the spatial administration characteristics of the TVMPDI trends in southeastern Tibet from 2003 to 2018. Since there is basically no range, STVMPDI is equal to 0, with values between −0.0005 and 0.0005 classified as stable and values greater than or equal to 0.0005 classified as the advance area. STVMPDI values lower than −0.0005 are classified according to the absolute values of STVMPDI. The acceptation assay after-effects of the Mann–Kendall assay at 0.05 were divided into cogent change (Z > 1.96 or Z < −1.96) and bush change (−1.96 ≤ Z ≤ 1.96). Finally, the allocation after-effects of the Theil–Sen median trend assay and the allocation after-effects of the Mann–Kendall assay were superimposed to access the TMVPDI trend abstracts at the pixel scale, and the after-effects were divided into bristle change types (Table 4).

Table 4.
Statistics of the TVMPDI trend.
3.6. Cross-Validation of TVMPDI with Meteorological Drought and Agricultural Drought
In order to understand how the association changed over time in various research areas, we also assessed at the geographical correlation between each drought indicator and the GPP or meteorological drought indices. We calculated the Pearson correlation coefficient for each month from April to October from 2003 to 2018 using grid pixels from the index map, GPP and drought index for a climate system. This analysis shows the responses of the TVMPDI and other drought indices with soil moisture information to two kinds of drought, and the changes in the responses of different regions to agricultural drought in southeastern Tibet.
4. Result
4.1. Accuracy Evaluation of TVMPDI
The Pearson correlation coefficient and scatter plot of the TVMPDI and SPEI in the growing season are shown in Figure 2. In general, the correlation coefficient between the TVMPDI and SPEI was above 0.5 from April to October (p < 0.01). Among them, the correlation coefficients of April, May, September and October were all between 0.5 and 0.6, which indicates a moderate correlation. The correlation coefficients were between 0.6 and 0.7 in June, July and August, reaching a high correlation (p < 0.005).
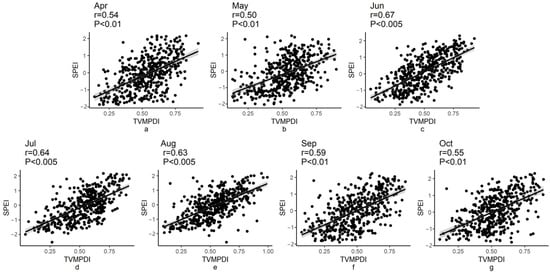
Figure 2.
Scatter plot of the TVMPDI and SPEI at the meteorological station from April to October: (a) April; (b) May; (c) June; (d) July; (e) August; (f) September; (g) October.
According to the theory behind each dryness indicator, the lower the VHI, SDCI, SM, TVPDI, and TVMPDI values are, the drier the area is. Therefore, the monitoring findings of the TVMPDI are consistent with these indices when VHI, SDCI, SMCI, and TVPDI are positively correlated with the TVMPDI; otherwise, the monitoring results are inconsistent.
The spatial distribution of the time-series correlation between the TVMPDI and remote sensing drought indices (VHI, SDCI, SMCI and TVPDI) are shown in Figure 3. The correlations of the TVMPDI with VHI and SDCI were above 0.8 (Figure 3a,b, respectively), which reached the level of extreme correlation, while the correlations of the TVMPDI with SMCI and TVPDI are different from those above. The correlation was slightly lower between the TVMPDI and TVPDI, especially in the western and central regions of the study area. In these areas the correlation remains around 0.6 (Figure 3d). Additionally, the correlation between the TVMPDI and SMCI in this region was only 0.3–0.6 (Figure 3c). These weakly correlated areas accounted for about 28%.
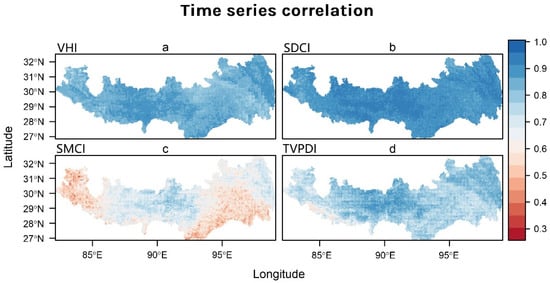
Figure 3.
Temporal correlation between TVMPDI and several remote sensing drought indices, including VHI (a), SDCI (b), SMCI (c) and TVPDI (d).
4.2. Historical Relationships between Drought Index and SPI, SPEI and GPP
Figure 4 depicts the spatial distribution of the correlation between the three indices and the meteorological drought indices (SPI and SPEI). The results show that the TVPDI has the best correlation with meteorological drought, followed by the SDCI and TVMPDI. The correlation of the TVMPDI with the SPI and SPEI was not as good as that with the SDCI and TVPDI (Figure 4), and the regions with low correlation were in the central and western regions of the study area (Figure 4a,b). The correlation of the TVPDI with the SPI and SPEI was the best in the whole region (Figure 4e,f).
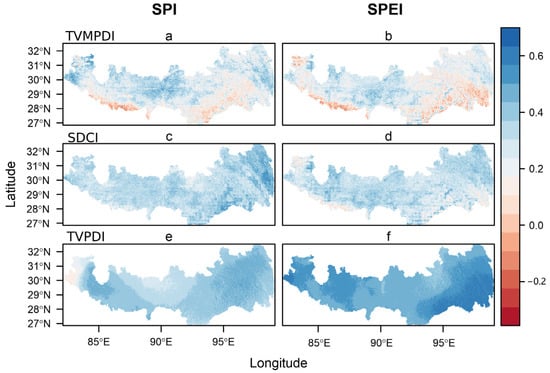
Figure 4.
Temporal correlation between the TVMPDI (a,b), SDCI (c,d) and TVPDI (e,f) with SPI and SPEI.
Figure 5 shows the correlation between GPP and the drought index. The area with a positive correlation between the TVMPDI and GPP accounts for 78.59%, and the significant area is mainly concentrated in the central and eastern part of the study area, which accounts for more than 20% (Figure 5e). In contrast, the area with a positive correlation between the TVPDI and GPP was only 47.5%, and the significant area accounts 5.7% (Figure 5f). The positive correlation area and significant area of the SDCI were not as high as that of the TVMPDI (Figure 5d). We also compared the correlation between the SMCI and GPP for cross-validation (Figure 5c).
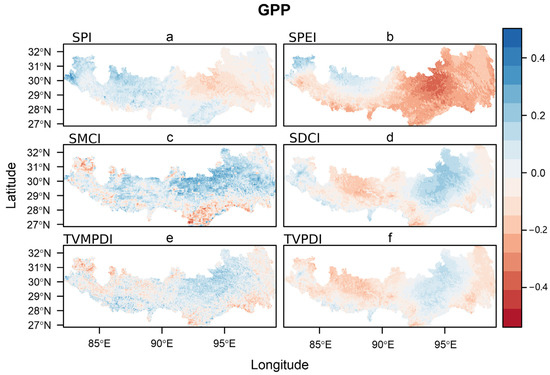
Figure 5.
Temporal correlation between GPP and dryness indices, including SPI (a), SPEI (b), SMCI (c), SDCI (d), TVMPDI (e) and TVPDI (f).
In addition, the relationship between GPP and drought indicators (SPI and SPEI) was negative in the middle of the study area (Figure 5a,b). In particular, the SPEI showed a strong negative correlation with GPP in areas where GPP and drought indices were positively correlated.
4.3. Spatial and Temporal Distribution of TVMPDI
The Theil–Sen median trend analysis values of the TVMPDI change are shown in Figure 6. In general, the slope of change in all five cities is positive. Except Lhasa, the other four districts are shown in Figure 6a (p < 0.05). The slope of the TVMPDI in March and December looks higher, which remains around 0.01 (Figure 6b,e, respectively), while the increase in the TVMPDI was insignificant in June and September (Figure 6c,d, respectively).
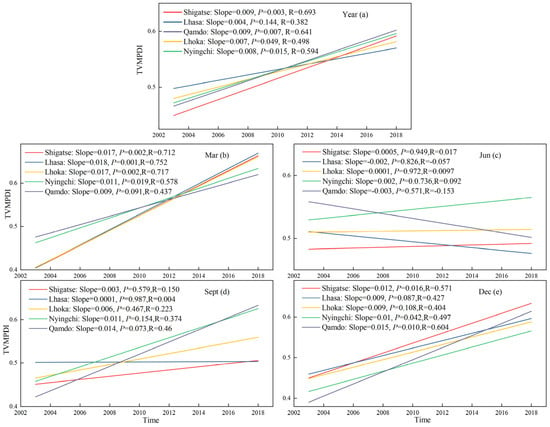
Figure 6.
Interannual variation of the TVMPDI in five regions of the study area: (a) interannual variation; (b) variation in March; (c) variation in June; (d) variation in September; (e) variation in December.
Figure 7a demonstrates that the annual mean value of the TVMPDI increased in the southeast of Tibet from 2003 to 2018, which indicates that the drought in this region was decreasing. The region behaved differently according to different seasons: Wet and slightly wet areas in the study area accounted for 93.05% in March (Figure 7b), while the value was just 48.21% in June (Figure 7c). The areas of gradual drying were concentrated on the east and west sides. This situation improved in September (Figure 7d), with only some western parts of the study area becoming slightly dry. In December, 55.86% was wet and 31.85% was slightly wet (Figure 7e).
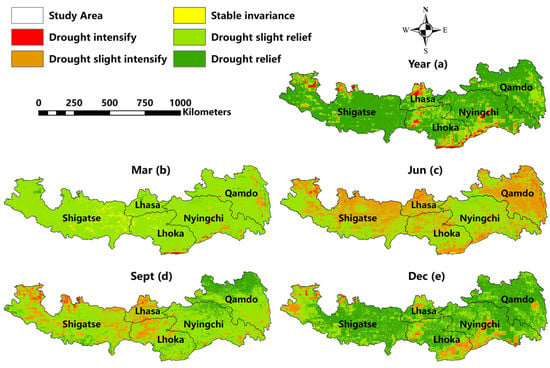
Figure 7.
Spatial distribution of the TVMPDI trend level from 2003 to 2018; (a) interannual variation; (b) variation in March; (c) variation in June; (d) variation in September; (e) variation in December.
4.4. The Effect of TVMPDI for Drought Monitoring
Figure 8 shows that, in 2009, a significant amount of drought affected the five cities in southeastern Tibet. Some mild drought occurred in Nyingchi, Lhoka and Qamdo in May 2009 (Figure 8a). In June and July 2009, large areas of extreme drought occurred in Lhasa, Lhoka and Shigatse (Figure 8b,c), while in May 2010, the drought hit the eastern city of Shigatse (Figure 8e). In June, the drought intensified, with extreme drought and severe drought accounting for about 48% (Figure 8f).
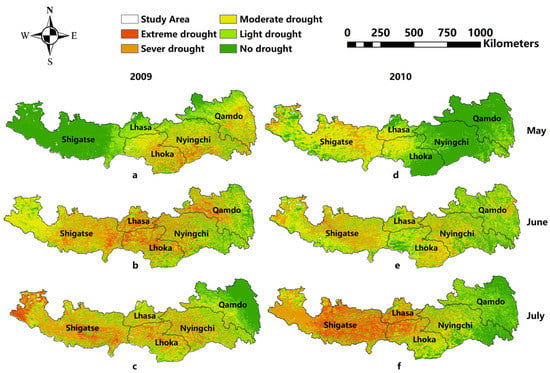
Figure 8.
Simulation drought distribution by three models from May to July 2009 and 2010: (a) drought simulation in May 2009; (b) drought simulation in June 2009; (c) drought simulation in July 2009; (d) drought simulation in May 2010; (e) drought simulation in June 2010; (f) drought simulation in July 2009.
5. Discussion
5.1. Drought Monitoring Capability of TVMPDI in Southeastern Tibet
In the southeast of TAR, the TVMPDI was moderately correlated with the SPEI, which was similar to the correlation between the TVPDI and SPEI [28]. When these drought indexes are positively correlated with the TVPDI, their monitoring results are consistent. This strong positive correlation implies that the TVMPDI can describe the dryness of the atmosphere in the study area. The authors of [18] showed that alternations between precipitation and evapotranspiration depend on the altitude blazon and the time of frondescence, becoming increasingly divided in the altered regions. However, drought conditions on the QTP, where the study area is located, are also affected by its altitude. Global warming is melting glaciers, which will increase groundwater at lower altitudes in the study area [33]. Glaciers are a different antecedent of drought-resistant water brought about by special terrain. They are lowering dry season resistance, and investigations on this phenomenon are still rare [53]. Therefore, the analysis of glaciers regarding drought in lower reach of regions could be included in future research plans, as it can help us to better understand the process of this drought pattern, and thus provide guidance for the development of drought resistance strategies.
In addition, the TVMPDI has a general correlation with the TVPDI and SMCI, which may be because the TVMPDI adds soil information on the basis of the TVPDI. Generally, agricultural drought index based on soil moisture can represent the available water for plants in the region. For example, SMCI believes that drought patterns are based on the available water content in the soil [54], but the TVMPDI adds atmospheric information, such as precipitation and temperature, which makes them less relevant than other drought indices.
Due to the complex reaction between soil and atmospheric moisture, it seems impossible to directly express plant water stress and atmospheric drought at the same time [5,55]. However, the TVMPDI, a new remote sensing index combined with SM, has a good correlation with other drought indexes. Due to the joint characteristics of soil and climate balance, the TVMPDI can capture the changes in SM and atmospheric dryness at the same time. This indicates that the TVMPDI is of great significance in delineating droughts.
In Figure 3c, the temporal correlation between drought and the SMCI shows an east–west gradient change, which is due to the different drought patterns in the east and west. The eastern part has more precipitation, which is generally attributed to the abnormal precipitation, while the western part is more affected by temperature. Both of these change soil moisture in the region and cause drought. Anderson et al. [56] compared the spatial correlation of various drought indices at different time scales and found that drought in arid and humid regions of the United States had similar east–west gradients.
As can be seen from Figure 5, the correlation between TVMPDI and meteorological drought index (SPI and SPI) was not as good as that between TVPDI and them, while the correlation between TVMPDI and GPP, which represents agricultural drought, was better than that between TVPDI and GPP. In addition, it is worth mentioning that in the eastern part of the study area, the monitoring effect of TVPDI, which has better correlation with meteorological index, was worse than that of TVMPDI for the areas with excess vegetation moisture. This is because precipitation inhibits vegetation growth and land-air coupling effect makes atmospheric composition unable to reflect soil moisture changes (this will be explained in more detail in Section 5.3). TVMPDI with adding soil moisture could better represent the changes, which can be verified by Figure 6c,e.
5.2. Variation Trend and Effect of Drought
The findings in Section 4.3 demonstrate a considerably higher trend for five regional TVMPDIs in the research area, suggesting that south-east Tibet from 2003 to 2018 gradually became moister. However, it is worth noting that the summer drought trend is not consistent with the overall trend, and the summer drought is becoming worse, which is consistent with other related studies [57]. They contend that there has been a notable yearly and seasonal trend toward increased precipitation in the Qinghai–Tibet Plateau, which is affected by the summertime intensification of the Indian Ocean monsoon. However, there are different results in other reports. The precipitation records of the Indian Ocean monsoon area in the past 60 years show that the Indian Ocean monsoon intensity is undergoing a weakening process [58]. Therefore, we believe that the intensification of summer drought in this study is influenced by the weakening of the Indian Ocean monsoon in summer, and the reason for the different results obtained in the above related studies is that the Tibetan Plateau is not only affected by the Indian Ocean monsoon, but also by the North Atlantic Oscillation. The study area is located in the southeast of the Tibetan Plateau. The various geographical settings influence the summer drought trend differently in various places.
According to China Weather Network, from April to the middle of June 2009 and 2010, the precipitation in eastern Tibet was the lowest in the same period in the past 10 years. Especially, the precipitation in the first and middle of June was the lowest in the history of the same period since 1956, resulting in a severe early summer drought.
It can be observed that the drought shown in Figure 8 is consistent with the actual drought situation. According to the record, in July 2009 and 2010 artificial rainfall was carried out in Lhasa, which alleviated the drought. The drought situation in Tibet in 2010 was similar to that in 2009, starting from the beginning of summer in May and abating in July as presented in Figure 8.
5.3. Regional Climate Characteristics
The correlation between the meteorological drought index and TVMPDI is about 0.4 in the middle and west of the study area and some eastern regions, because the dryness and humidity in Tibet are mainly affected by precipitation [35]. The Himalayan mountains to the southwest of the study region often block atmospheric moisture carried to Tibet by the dominant westerly winds [59]. Previous studies [60,61,62,63] also proposed that the decrease in potential evapotranspiration and insufficient precipitation in Tibet were the main reasons for the arid environment.
The relationship between GPP and drought indices varies from region to region, reflecting the different patterns of driving drought in different regions [64]. In the western part of southeastern Tibet, shown in Figure 6a,b, the meteorological drought index (SPI and SPEI) has a weak positive correlation with GPP. According to the study by [65], these locations are known as vegetation–water stress zones because the principal factor limiting seed germination is water availability, and GPP increases with wetness and decreases with dryness. However, there was a strong negative correlation in the east, which was considered as the vegetation water surplus area. Because vegetation growth is largely limited by other factors (e.g., solar radiation and anthropogenic influence), increasing levels of rainfall may, in turn, expose plants to waterlogging. However, low temperatures allow the atmosphere to hold less moisture from the air and the low evapotranspiration allows the soil to hold more water in southeastern Tibet [35], which is also the reason why the negative correlation in the east is stronger than the positive correlation in the west.
In Shigatse and other southern areas of the study area, the correlation decreased or was negative. In the dry environment, there is a vicious cycle between plant nutrition and SM supply due to land–air interaction [65]. In contrast, the relation coefficient was above 0.4 in the central areas. Instead of precipitation, SM in terms of the amount of accessible water influences ecosystem production (GPP), and a lack of SM can cause droughts in the agriculture sector [38,66,67].
The low and negative correlations of some areas may be caused by the complex topographical features and atmospheric conditions. Some studies [68] have shown that the precipitation difference in the Qinghai–Tibet Plateau is the main reason for the north Atlantic oscillation, and the north Atlantic Oscillation and Pacific interannual oscillations has a negative correlation, enhancing the La Niña phenomenon that influenced Indian monsoons. These convective systems and active water vapor transport jets are not alone in creating delays in precipitation and dryness over southern Tibet due to increased water vapor from the Bay of Bengal. Similar delays or decoupling have been reported in some studies in the Midwestern United States [69]. Due to the stronger mesoscale convective system in this region, land–air decoupling is more likely to occur. It is also worth mentioning that the gradual deterioration of the relationship between plant growth and water supply caused by this decoupling phenomenon has become more and more serious [70,71].
5.4. Limitations
Due to the limitations of the SM datasets and precipitation datasets, the study period only covered 16 years from 2003 to 2018. In the future, longer time spans and higher precision SM data will improve the application of soil moisture information in the remote sensing integrated drought index. The SPI constructed with precipitation data of long time series is also more reliable. This study did not assess the TVMPDI by land cover. We did not use the lag time of meteorological drought index, GPP and agricultural drought for analysis, which may be different in different land covers and needs further study.
In addition, the study did not take into account the influence of human activities on drought changes in the eastern and western parts of the study area. In future studies, we will assess the influence of human activities on the occurrence of drought and the response of the TVMPDI and the Land Water Storage (LWS).
6. Conclusions
An agricultural drought monitoring model was constructed based on the Euclidean distance method with the effects of multiple drought-causing factors in Tibet. The effects of soil moisture on agricultural drought monitoring models were included when generating the TVMPDI. Then, this model was constructed to monitor, analyze, evaluate and verify drought levels in Tibet, and the following main conclusions were obtained:
- (1)
- The relation coefficients between the TVMPDI and SPEI were all above 0.5, and the correlation between the TVMPDI and other remote sensing drought indices performed well. In addition, the TVMPDI monitored the drought conditions in summer and autumn from May to July 2009 and 2010, which were basically consistent with the actual drought conditions, and reflect better the drought distribution and drought conditions in Tibet.
- (2)
- The TVPDI based on atmospheric indices performs perfectly in delineating meteorological drought, but failed to recognize water availability in soil systems, which is critical for crop growth and agricultural drought delineation. The TVMPDI with soil moisture information was more suitable for agricultural drought monitoring than the TVPDI.
- (3)
- In the 16-year span from 2003 to 2018, the southeastern region of Tibet experienced a gradual wetting process. The gradual humidification in summer was not significant.
- (4)
- Various drought indices divided the study into arid and semi-arid areas in the west and humid areas in the east. In the western arid and semi-arid regions, soil wetting caused by precipitation promoted vegetation growth, while in the eastern humid regions, precipitation inhibited vegetation growth.
Author Contributions
Conceptualization, Z.W. (Ziyu Wang) and Z.W. (Zegen Wang); methodology, Z.W. (Ziyu Wang); software, Z.W. (Ziyu Wang); validation, Z.W. (Ziyu Wang), W.H. and X.W.; formal analysis, Z.W. (Ziyu Wang); investigation, Z.W. (Ziyu Wang); resources, Z.W. (Ziyu Wang); data curation, Z.W. (Ziyu Wang); writing—original draft preparation, Z.W. (Ziyu Wang); writing—review and editing, Z.W. (Zegen Wang), W.H. and Z.Y.; visualization, Z.W. (Ziyu Wang); supervision, W.H.; project administration, Z.W. (Zegen Wang) and J.X.; funding acquisition, J.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Key R & D project of Sichuan Science and Technology Department (Grant No. 2021YFQ0042), The Science and Technology Project of Xizang Autonomous Region (Grant No. XZ201901-GA-07), Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA20030302), National Key R&D Program of China (2020YFD1100701).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dai, A.; Trenberth, K.E.; Qian, T. A Global Dataset of Palmer Drought Severity Index for Relationship with Soil Moisture and Effects of Surface Warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Liu, X.; Wang, S.; Zhou, Y.; Wang, F.; Yang, G.; Liu, W. Spatial analysis of meteorological drought return periods in China using Copulas. Remote Sens. Environ. 2016, 80, 367–388. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts (Review). J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Carrão, H.; Singleton, A.; Naumann, G.; Barbosa, P.; Vogt, J.V. An Optimized System for the Classification of Meteorological Drought Intensity with Applications in Drought Frequency Analysis. J. Appl. Meteorol. Clim. 2014, 53, 1943–1960. [Google Scholar] [CrossRef]
- Keyantash, J.A.; Dracup, J.A. An aggregate drought index: Assessing drought severity based on fluctuations in the hydrologic cycle and surface water storage. Water. Resour. Res. 2004, 40, 333–341. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Loon, A.F.V. Hydrological drought explained. Wires. Water 2015, 2, 359–392. [Google Scholar] [CrossRef]
- Eklund, L.; Seaquist, J. Meteorological, agricultural and socioeconomic drought in the Duhok Governorate, Iraqi Kurdistan. Nat. Hazards 2015, 76, 421–441. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; Research Paper No.45; U.S. Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; pp. 45–58.
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Palmer, W. Keeping Track of Crop Moisture Conditions, Nationwide: The New Crop Moisture Index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Dutra, E.; Viterbo, P.; Miranda, P.M.A. ERA-40 reanalysis hydrological applications in the characterization of regional drought. Geophys. Res. Lett. 2008, 35, 116–122. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A. A soil water based index as a suitable agricultural drought indicator. J. Hydrol. 2015, 522, 265–273. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M.D. Examining the relationship between drought development and rapid changes in the evaporative stress index. J. Hydrometeorol. 2014, 15, 938–956. [Google Scholar] [CrossRef]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M.; Johnson, D.; Mueller, R.; Tadesse, T.; Wardlow, B.; Brown, J. Assessing the evolution of soil moisture and vegetation conditions during the 2012 United States flash drought. Agric. For. Meteorol. 2016, 218–219, 230–242. [Google Scholar] [CrossRef]
- Jiao, W.; Tian, C.; Chang, Q.; Novick, K.A.; Wang, L. A new multi-sensor integrated index for drought monitoring. J. Hydrol. 2019, 574, 74–85. [Google Scholar] [CrossRef]
- Um, M.J.; Kim, Y.; Park, D. Evaluation and modification of the Drought Severity Index (DSI) in East Asia. Remote Sens. Environ. 2018, 209, 66–76. [Google Scholar] [CrossRef]
- Eswar, R.; Das, N.N.; Poulsen, C.; Behrangi, A.; Swigart, J.; Svoboda, M.; Entekhabi, D.; Doorn, B.; Entin, J. SMAP Soil Moisture Change as an Indicator of Drought Conditions. Remote Sens. 2018, 10, 788. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Zhang, A.; Jia, G. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data. Remote Sens. Environ. 2013, 134, 12–23. [Google Scholar] [CrossRef]
- Du, L.; Tian, Q.; Huang, Y.; Liu, J. Drought monitoring based on TRMM data and its reliability validation in Shandong province(Article). Tran. CSAE 2012, 28, 121–126. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J.; Carbone, G.J. Monitoring agricultural drought for arid and humid regions using multi-sensor remote sensing data. Remote Sens. Environ. 2010, 114, 2875–2887. [Google Scholar] [CrossRef]
- Du, L.; Tian, Q.; Yu, T.; Meng, Q.; Jancso, T.; Udvardy, P.; Huang, Y. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int. J. Appl. Earth Obs. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Wei, W.; Pang, S.; Wang, X.; Zhou, L.; Li, C. Temperature Vegetation Precipitation Dryness Index (TVPDI)-based dryness-wetness monitoring in China. Remote Sens. Environ. 2020, 248, 111957. [Google Scholar] [CrossRef]
- Abhishek; Kinouchi, T. Multidecadal Land Water and Groundwater Drought Evaluation in Peninsular India. Remote Sens. 2022, 14, 1486. [Google Scholar] [CrossRef]
- Zhao, Y.; Zou, X.; Cheng, H.; Jia, H.; Wu, Y.; Wang, G.; Zhang, C.; Gao, S. Assessing the ecological security of the Tibetan plateau: Methodology and a case study for Lhaze County. J. Environ. Manag. 2006, 80, 120–131. [Google Scholar] [CrossRef]
- Fang, K.; Gou, X.; Chen, F.; Li, J.; D’Arrigo, R.; Cook, E.; Yang, T.; Davi, N. Reconstructed droughts for the southeastern Tibetan Plateau over the past 568 years and its linkages to the Pacific and Atlantic Ocean climate variability. Clim. Dyn. 2010, 35, 577–585. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Chen, Z.; Ren, Z. Assessment of candidate distributions for SPI/SPEI and sensitivity of drought to climatic variables in China. Int. J. Climatol. 2019, 39, 4392–4412. [Google Scholar] [CrossRef]
- Feng, W.; Lu, H.; Yao, T.; Yu, Q. Drought characteristics and its elevation dependence in the Qinghai–Tibet plateau during the last half-century. Sci. Rep. 2020, 10, 14323. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ali, Z.; Cui, T.; Qamar, S.; Ismail, M.; Nazeer, A.; Faisal, M. A comparative analysis of pre- and post-industrial spatiotemporal drought trends and patterns of Tibet Plateau using Sen slope estimator and steady-state probabilities of Markov Chain. Nat. Hazards 2022, 113, 547–576. [Google Scholar] [CrossRef]
- Li, S.; Yao, Z.; Liu, Z.; Wang, R.; Liu, M.; Adam, J. The spatio-temporal characteristics of drought across Tibet, China: Derived from meteorological and agricultural drought indexes. Theor. Appl. Climatol. 2019, 137, 2409–2424. [Google Scholar] [CrossRef]
- Yao, T.; Li, Z.; Yang, W.; Guo, X.; Zhu, L.; Kang, S.; Wu, Y.; Yu, W. Glacial distribution and mass balance in the Yarlung Zangbo River and its influence on lakes. Chin. Sci. Bull. 2010, 55, 2072–2078. [Google Scholar] [CrossRef]
- Li, F.; Xu, Z.; Feng, Y.; Liu, M.; Liu, W. Changes of land cover in the Yarlung Tsangpo River basin from 1985 to 2005. Environ. Earth Sci. 2013, 68, 181–188. [Google Scholar] [CrossRef]
- Li, H.; Liu, L.; Shan, B.; Xu, Z.; Niu, Q.; Cheng, L.; Liu, X.; Xu, Z. Spatiotemporal Variation of Drought and Associated Multi-Scale Response to Climate Change over the Yarlung Zangbo River Basin of Qinghai–Tibet Plateau, China. Remote Sens. 2020, 12, 19. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, L.; Guo, M.; Liu, X. Suitability analysis of TRMM satellite precipitation data in regional drought monitoring(Article). Tran. CSAE 2018, 34, 126–132. [Google Scholar] [CrossRef]
- Meng, X.; Mao, K.; Meng, F.; Shi, J.; Zeng, J.; Shen, X.; Cui, Y.; Jiang, L.; Guo, Z. A fine-resolution soil moisture dataset for China in 2002–2018. Earth Syst. Sci. Data 2021, 13, 3239–3261. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Masjedi, A.; Dehnavi, S. Temperature-Vegetation-soil Moisture Dryness Index (TVMDI). Remote Sens. Environ. 2017, 197, 1–14. [Google Scholar] [CrossRef]
- Mesquita, D.P.P.; Gomes, J.P.P.; Junior, A.H.S.; Nobre, J.S. Euclidean distance estimation in incomplete datasets. Neurocomputing 2017, 248, 11–18. [Google Scholar] [CrossRef]
- Sharmaa, T.C.; Panua, U.S. Predicting return periods of hydrological droughts using the Pearson 3 distribution: A case from rivers in the Canadian prairies. Hydrol. Sci. J. 2015, 60, 1783–1796. [Google Scholar] [CrossRef]
- Shi, H.; Zhou, Z.; Liu, L.; Liu, S. A global perspective on propagation from meteorological drought to hydrological drought during 1902–2014. Atmos. Res. 2022, 280, 106441. [Google Scholar] [CrossRef]
- Bhuiyan, C.; Singh, R.P.; Kogan, F.N. Monitoring drought dynamics in the Aravalli region (India) using different indices based on ground and remote sensing data. Int. J. Appl. Earth Obs. 2006, 8, 289–302. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Kimball, J.S.; Mcdowell, N.G.; Running, S.W. A Remotely Sensed Global Terrestrial Drought Severity Index. Bull. Am. Meteorol. Soc. 2013, 94, 83–98. [Google Scholar] [CrossRef]
- Li, X.; He, B.; Quan, X.; Liao, Z.; Bai, X. Use of the Standardized Precipitation Evapotranspiration Index (SPEI) to Characterize the Drying Trend in Southwest China from 1982-2012. Remote Sens. 2015, 7, 10917–10937. [Google Scholar] [CrossRef]
- Khavse, R.; Chaudhary, J.L.a. Trend assessment in climate variable by Mann Kendall test of Bastar district of Chhattisgarh. Mausam 2022, 73, 79–82. [Google Scholar] [CrossRef]
- Gao, H.; Jin, J. Analysis of Water Yield Changes from 1981 to 2018 Using an Improved Mann-Kendall Test. Remote Sens. 2022, 14, 2009. [Google Scholar] [CrossRef]
- Wang, J. Determining the most accurate program for the Mann-Kendall method in detecting climate mutation. Theor. Appl. Climatol. 2020, 142, 847–854. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379. [Google Scholar] [CrossRef]
- Tošić, I. Spatial and temporal variability of winter and summer precipitation over Serbia and Montenegro. Theor. Appl. Climatol. 2004, 77, 47–56. [Google Scholar] [CrossRef]
- Pritchard, H.D. Asia’s shrinking glaciers protect large populations from drought stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Bockheim, J.G.; Hartemink, A.E.; Huang, J. Distribution and properties of sandy soils in the conterminous USA—A conceptual thickness model, and taxonomic analysis. Catena 2020, 195, 104746. [Google Scholar] [CrossRef]
- Miralles, D.G.; Gentine, P.; Seneviratne, S.I.; Teuling, A.J. Land-atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 2019, 1436, 19–35. [Google Scholar] [CrossRef] [PubMed]
- Anderson, M.; Hain, C.; Wardlow, B.; Pimstein, A.; Mecikalski, J.; Kustas, W. Evaluation of Drought Indices Based on Thermal Remote Sensing of Evapotranspiration over the Continental United States. J. Clim. 2011, 24, 2025–2044. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Lai, C.; Zeng, Z.; Zhong, R.; Chen, X.; Zhou, X.; Wang, M. Does drought in China show a significant decreasing trend from 1961 to 2009? Sci. Total Environ. 2017, 579, 314–324. [Google Scholar] [CrossRef] [PubMed]
- Krishnan, R.; Sugi, M. Pacific decadal oscillation and variability of the Indian summer monsoon rainfall. Clim. Dyn. 2003, 21, 233–242. [Google Scholar] [CrossRef]
- Tian, L.; Yao, T.; Schuster, P.F.; White, J.W.C.; Ichiyanagi, K.; Pendall, E.; Pu, J.; Yu, W. Oxygen-18 concentrations in recent precipitation and ice cores on the Tibetan Plateau. J. Geophys. Res.-Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Zhou, W. Assessment of future drought in Southwest China based on CMIP5 multimodel projections. Adv. Atmos. Sci. 2014, 31, 1035–1050. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, C.; Tang, Y.; Yang, Y. Trends in pan evaporation and reference and actual evapotranspiration across the Tibetan Plateau. J. Geophys. Res.-Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Xu, Y.; Xu, Y.; Wang, Y.; Wu, L.; Li, G.; Song, S. Spatial and temporal trends of reference crop evapotranspiration and its influential variables in Yangtze River Delta, eastern China. Theor. Appl. Climatol. 2017, 130, 945–958. [Google Scholar] [CrossRef]
- Li, Z.; Chen, Y.; Yang, J.; Wang, Y. Potential evapotranspiration and its attribution over the past 50 years in the arid region of Northwest China. Hydrol. Process. 2014, 28, 1025–1031. [Google Scholar] [CrossRef]
- Chatterjee, S.; Desai, A.; Zhu, J.; Townsend, P.; Huang, J. Soil moisture as an essential component for delineating and forecasting agricultural rather than meteorological drought. Remote Sens. Environ. 2022, 269, 112833. [Google Scholar] [CrossRef]
- Jiao, W.; Wang, L.; Smith, W.K.; Chang, Q.; Wang, H.; D’Odorico, P. Observed increasing water constraint on vegetation growth over the last three decades. Nat. Commun. 2021, 12, 3777. [Google Scholar] [CrossRef] [PubMed]
- Krueger, E.S.; Ochsner, T.E.; Engle, D.M.; Carlson, J.D.; Twidwell, D.; Fuhlendorf, S.D. Soil Moisture Affects Growing-Season Wildfire Size in the Southern Great Plains. Remote Sens. Environ. 2015, 79, 1567–1576. [Google Scholar] [CrossRef]
- Huang, J.; Hartemink, A.E.; Kucharik, C.J. Soil-dependent responses of US crop yields to climate variability and depth to groundwater. Agric. Syst. 2021, 190, 103085. [Google Scholar] [CrossRef]
- Ye, Z.-X.; Cheng, W.-M.; Zhao, Z.-Q.; Guo, J.-Y.; Yang, Z.-X.; Wang, R.-B.; Wang, N. Spatio-Temporal Characteristics of Drought Events and Their Effects on Vegetation: A Case Study in Southern Tibet, China. Remote Sens. 2020, 12, 4174. [Google Scholar] [CrossRef]
- Gerken, T.; Ruddell, B.L.; Yu, R.; Stoy, P.C.; Drewry, D.T. Robust observations of land-to-atmosphere feedbacks using the information flows of FLUXNET. NPJ Clim. Atmos. Sci. 2019, 2, 37. [Google Scholar] [CrossRef]
- Maxwell, J.; Harley, G.; Robeson, S. On the declining relationship between tree growth and climate in the Midwest United States: The fading drought signal. Clim. Change 2016, 138, 127–142. [Google Scholar] [CrossRef]
- Ponce-Campos, G.E.; Moran, M.S.; Huete, A.; Zhang, Y.; Bresloff, C.; Huxman, T.E.; Eamus, D.; Bosch, D.D.; Buda, A.R.; Gunter, S.A.; et al. Ecosystem resilience despite large-scale altered hydroclimatic conditions. Nature 2013, 494, 349–352. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).