Assessments of the Above-Ocean Atmospheric CO2 Detection Capability of the GAS Instrument Onboard the Next-Generation FengYun-3H Satellite
Abstract
1. Introduction
2. GAS
2.1. Spectral Bands
2.2. Spectral Resolution
2.3. Spectrum Sampling Rate
3. Model
3.1. Radiative Transfer Model
3.2. Marine Aerosol Model
3.3. Sea-Surface Sun-Glint Model
3.4. Wind-Driven Rough-Sea-Surface Reflectivity Model
4. Detection Accuracy Evaluation
5. Results
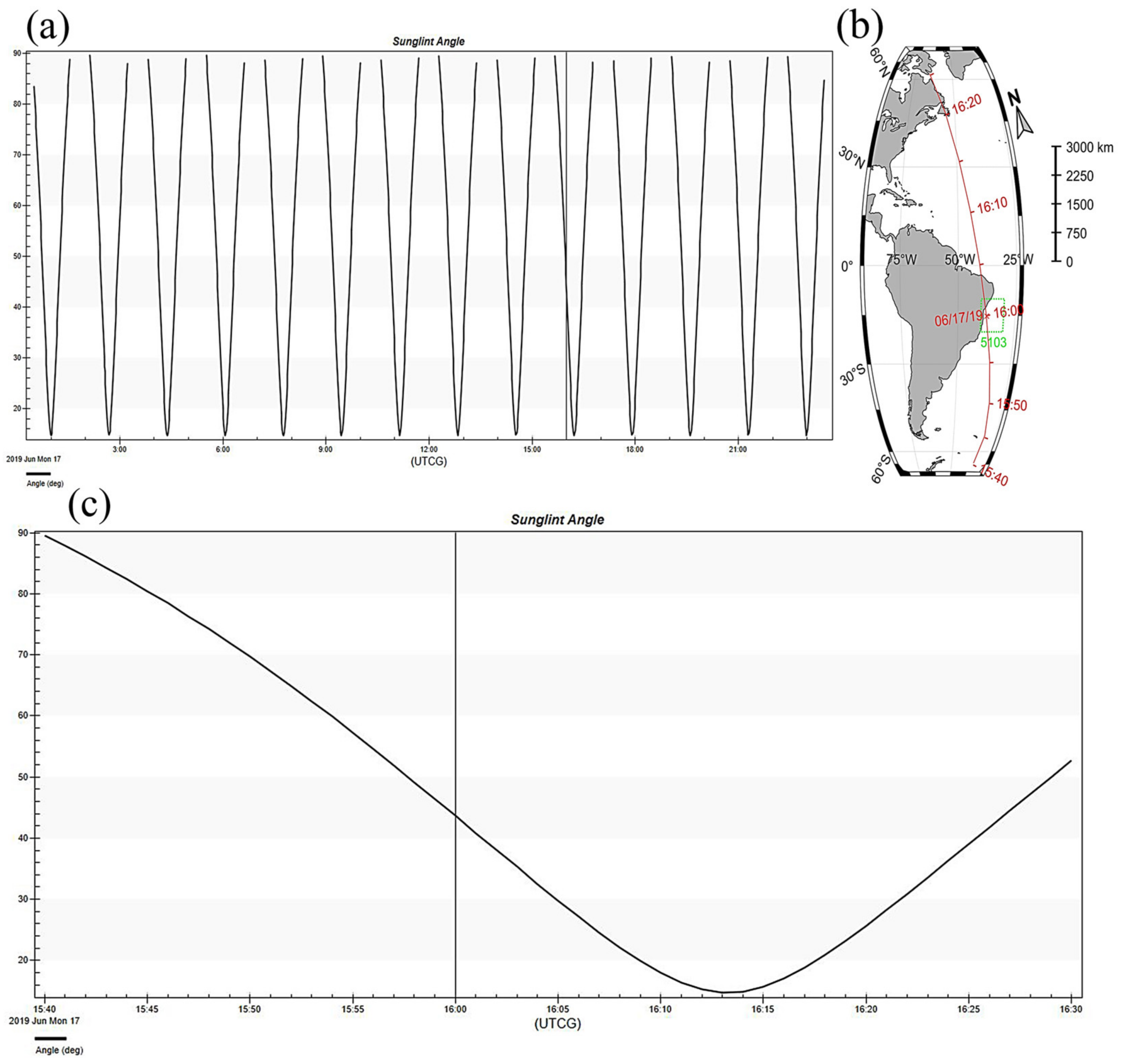
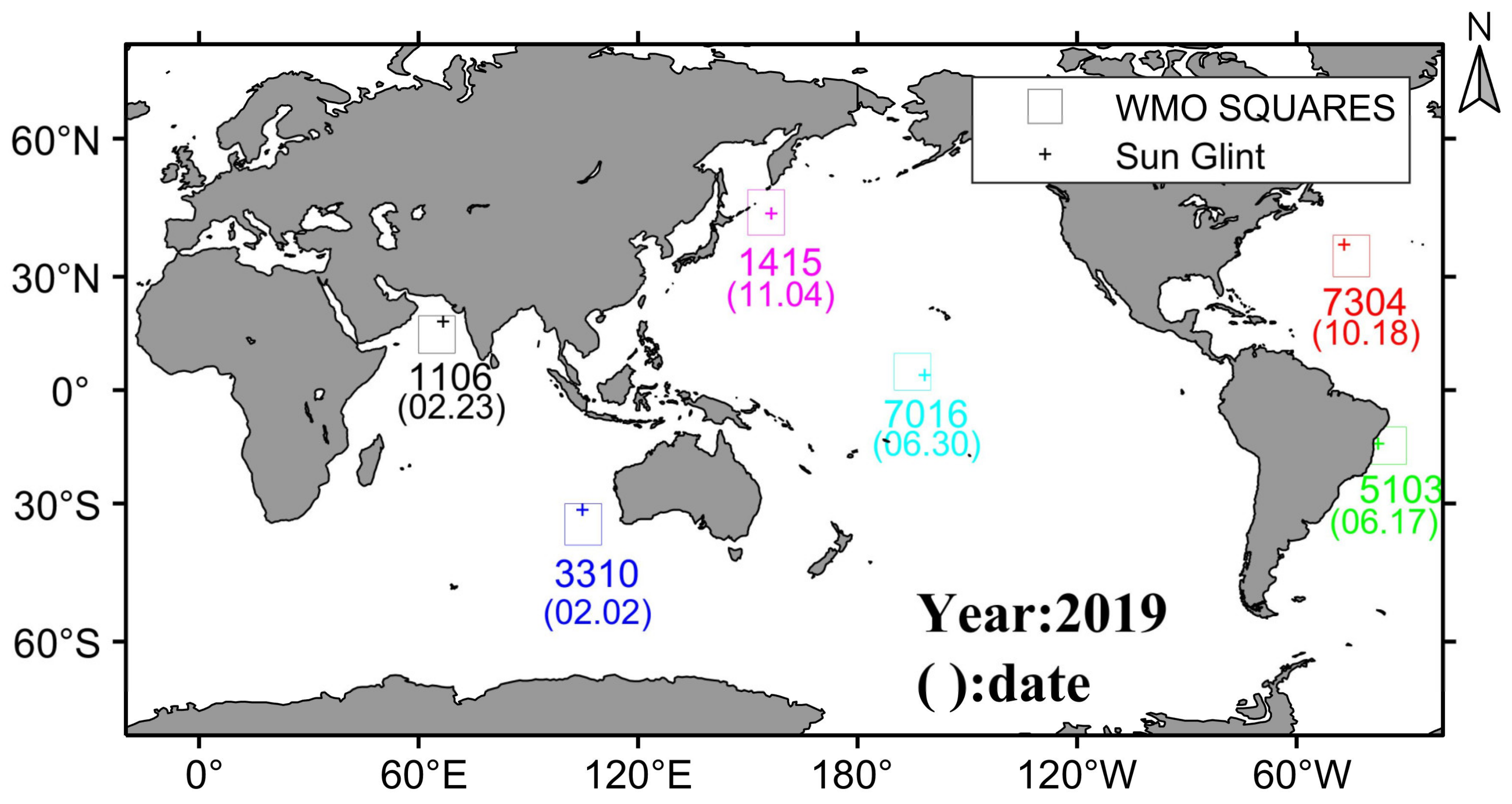
5.1. Simulation of Sun-Glint Locations and Zenith Angles
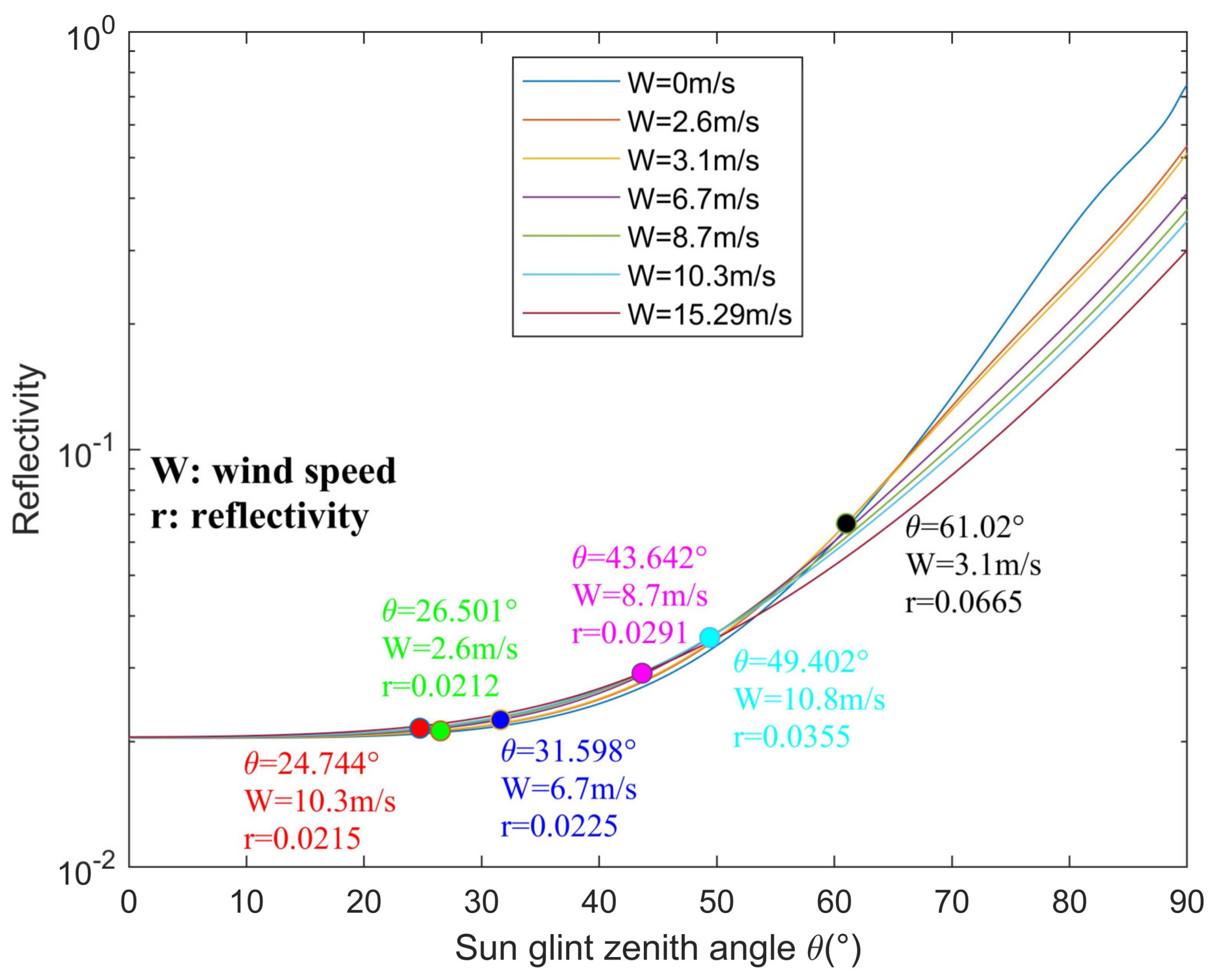
5.2. Simulation of Wind-Driven Rough-Sea-Surface Reflectivity
5.3. Simulations under Different Instrumental Parameters
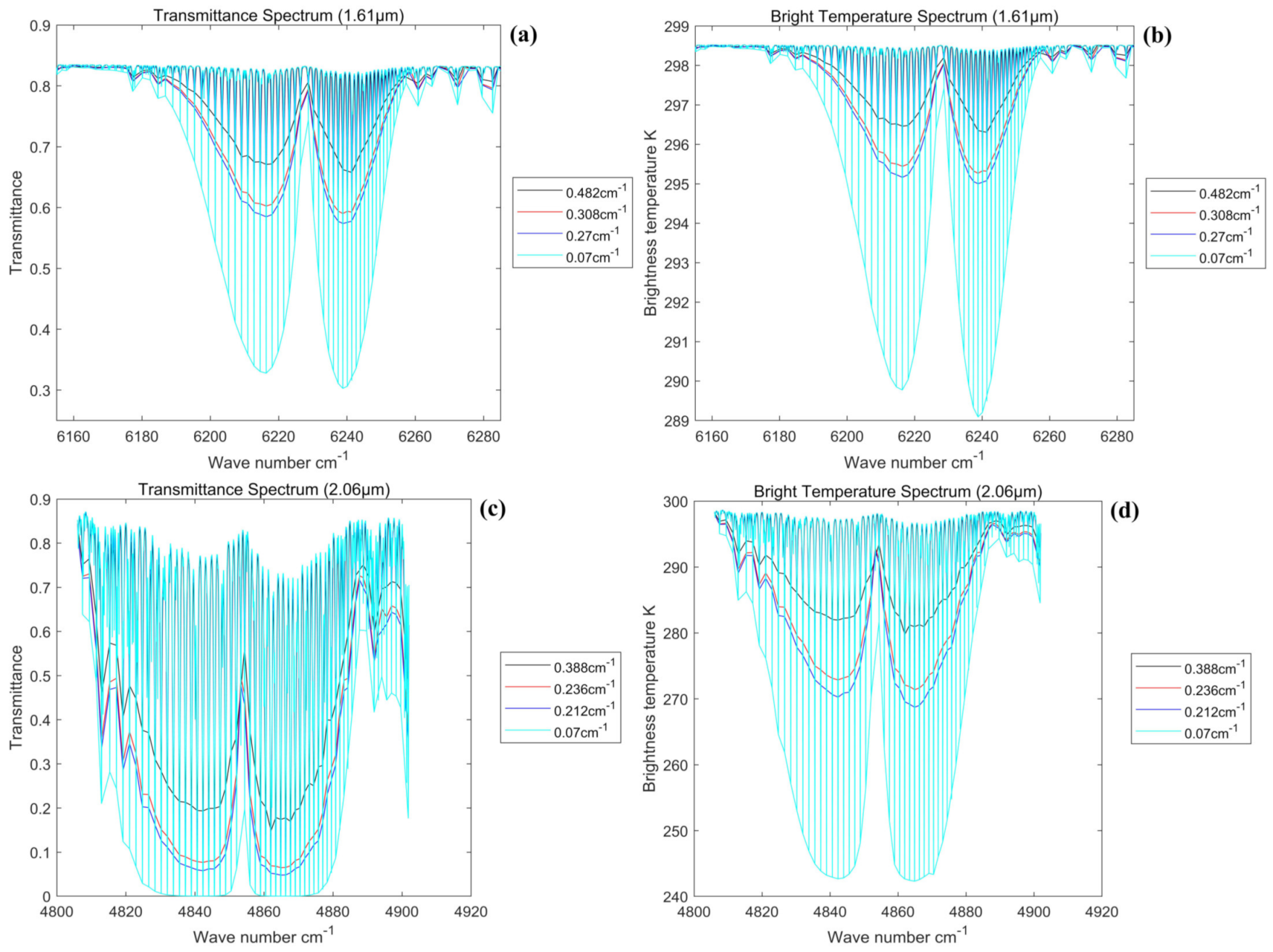
5.3.1. Spectral Resolution
5.3.2. Spectrum Sampling Rate
5.4. Simulations under Different Environmental Parameters
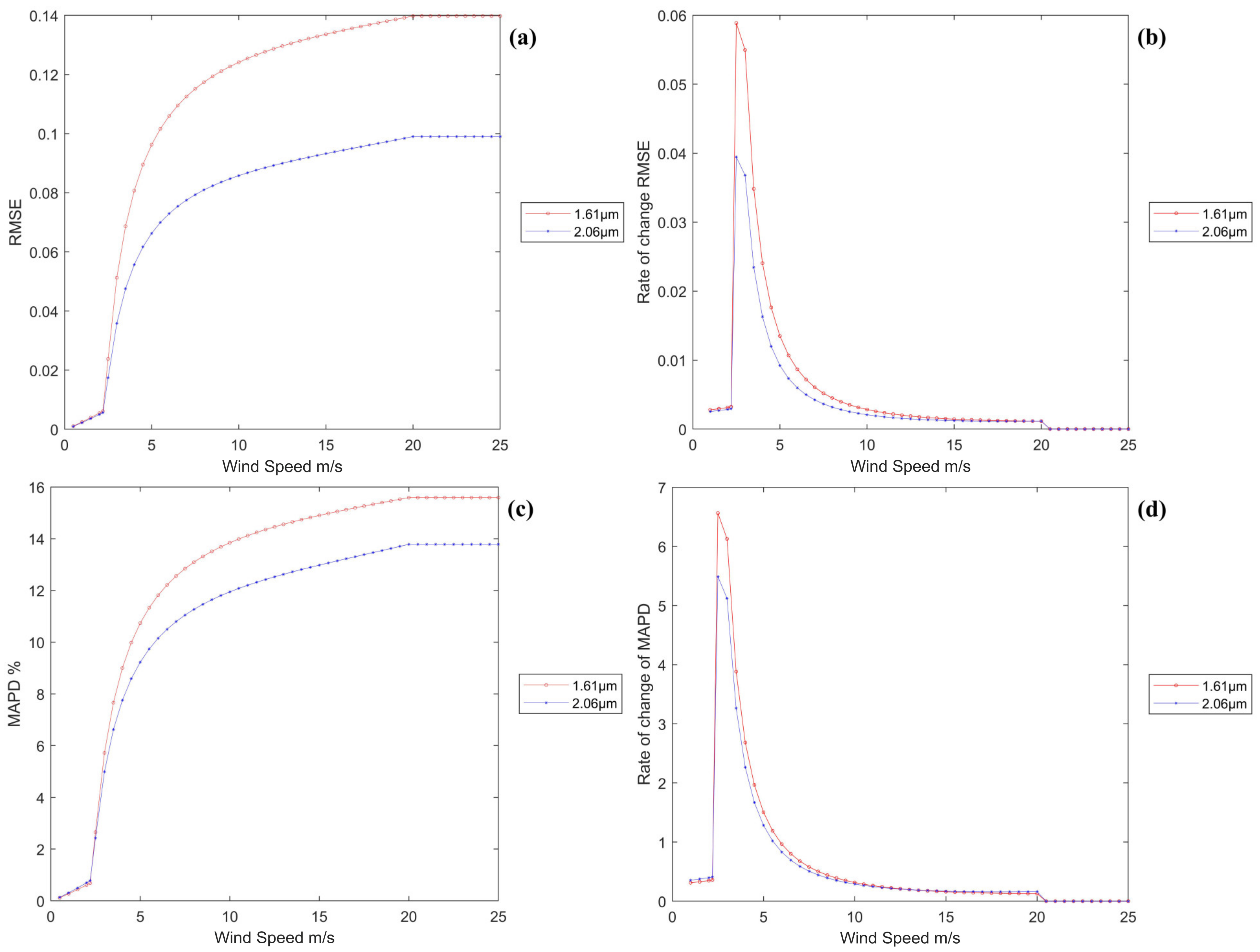
5.4.1. Different Wind Speeds and Visibilities
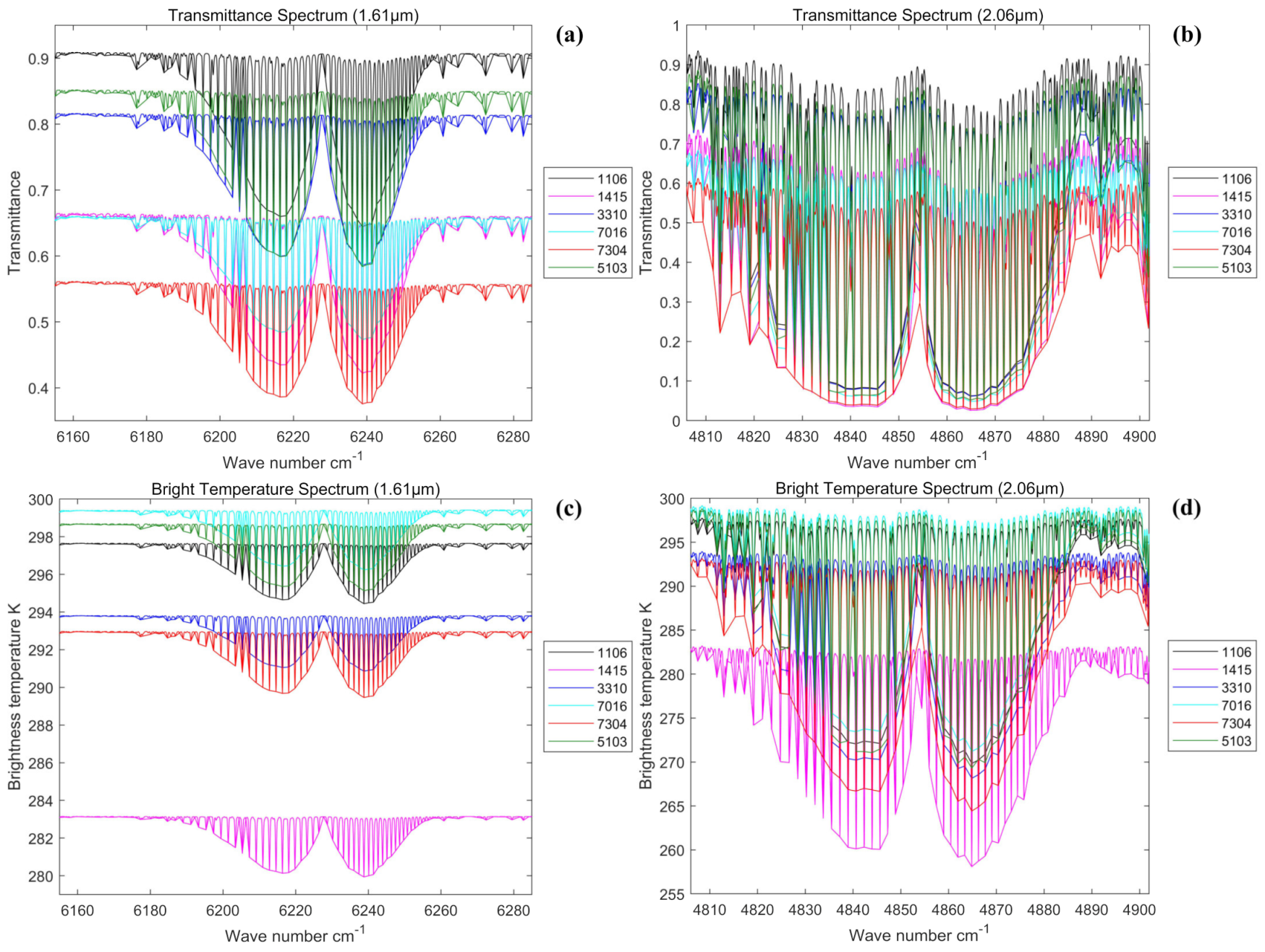
5.4.2. Different Sea Areas
5.4.3. Rough Sea Surface
6. Discussion
6.1. Evaluation of the Detection Accuracies at Different Spectral Resolutions
6.2. Evaluation of Detection Accuracies under Different Spectral Sampling Rates
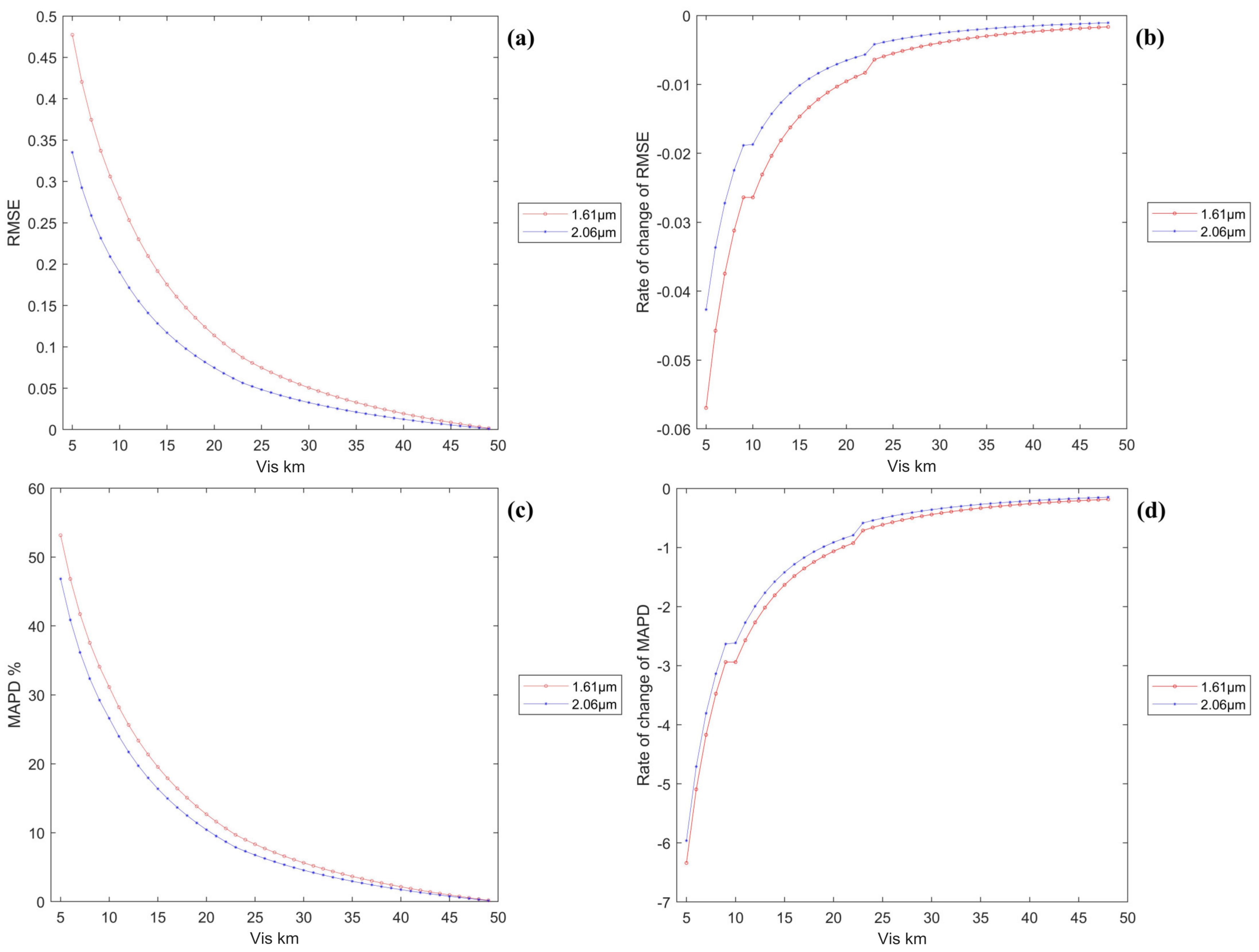
6.3. Evaluation of the Detection Accuracies Obtained under Different Wind Speeds and Visibility Levels within the Simulated Spectra
6.4. Evaluation of the Detection Accuracies Obtained under Different Rough-Sea-Surface Conditions
7. Conclusions
- (1)
- The higher the spectral resolution of an instrument is, the richer the received detection spectral information is, the lower the absolute deviation index is, the lower the RMSE is, and the closer the overall simulated spectral curve is to the real spectrum. The spectral resolution of the new-generation GAS instrument is at a leading level internationally, and the spectral deviation index values obtained for the 1.61 μm and 2.06 μm spectral bands are smallest among similar existing instruments;
- (2)
- The higher the spectral sampling rate of the instrument is, the smaller the absolute deviation of the detection spectrum and the lower the RMSE are. Compared to the effect of the spectral resolution, the impact of the spectral sampling rate on the accuracy of the detection spectrum is approximately an order of magnitude smaller. In the actual instrument design, the detector image element should prioritize ensuring that the instrumental spectral resolution can reach the design level before considering increasing the spectral sampling rate. Generally, a spectral sampling rate of 3 is appropriate;
- (3)
- The higher the wind speed of the sea-surface atmosphere is, the lower the overall instrument detection spectrum is. When the wind speed is less than 2 m/s, the effect of the transmittance spectrum introduced by the wind speed is less than 0.02% and can thus be ignored. When the wind speed is above 5 m/s, the difference in transmittance spectra is more obvious, and the spectral effects introduced by the wind speed must be considered in the simulations;
- (4)
- The greater the atmospheric visibility of the sea surface is, the lower the overall instrument detection spectrum is. The variation in transmittance is larger in the 5–10 km visibility range; at visibilities above 20 km, the variation in transmittance is relatively low. The overall transmittance trends in the 2.06 μm and 1.61 μm spectral bands were similar, and the former was relatively less affected by visibility;
- (5)
- Approximately 43% of the sun-glint zenith angles were > 60° during the study period. Under these conditions, it is important to consider the change in the reflectivity of the rough sea surface; otherwise, the CO2 detection accuracy will be seriously affected.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

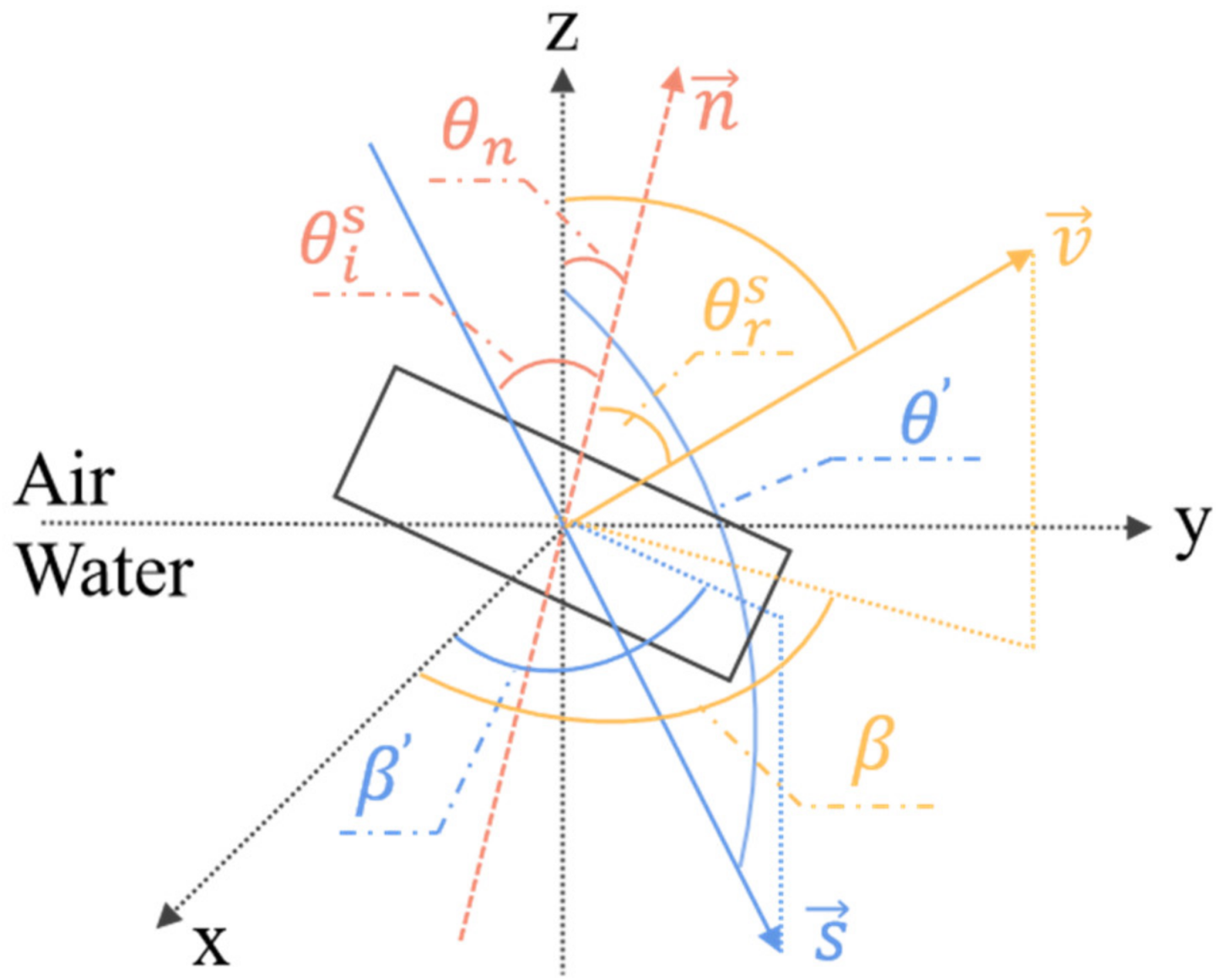
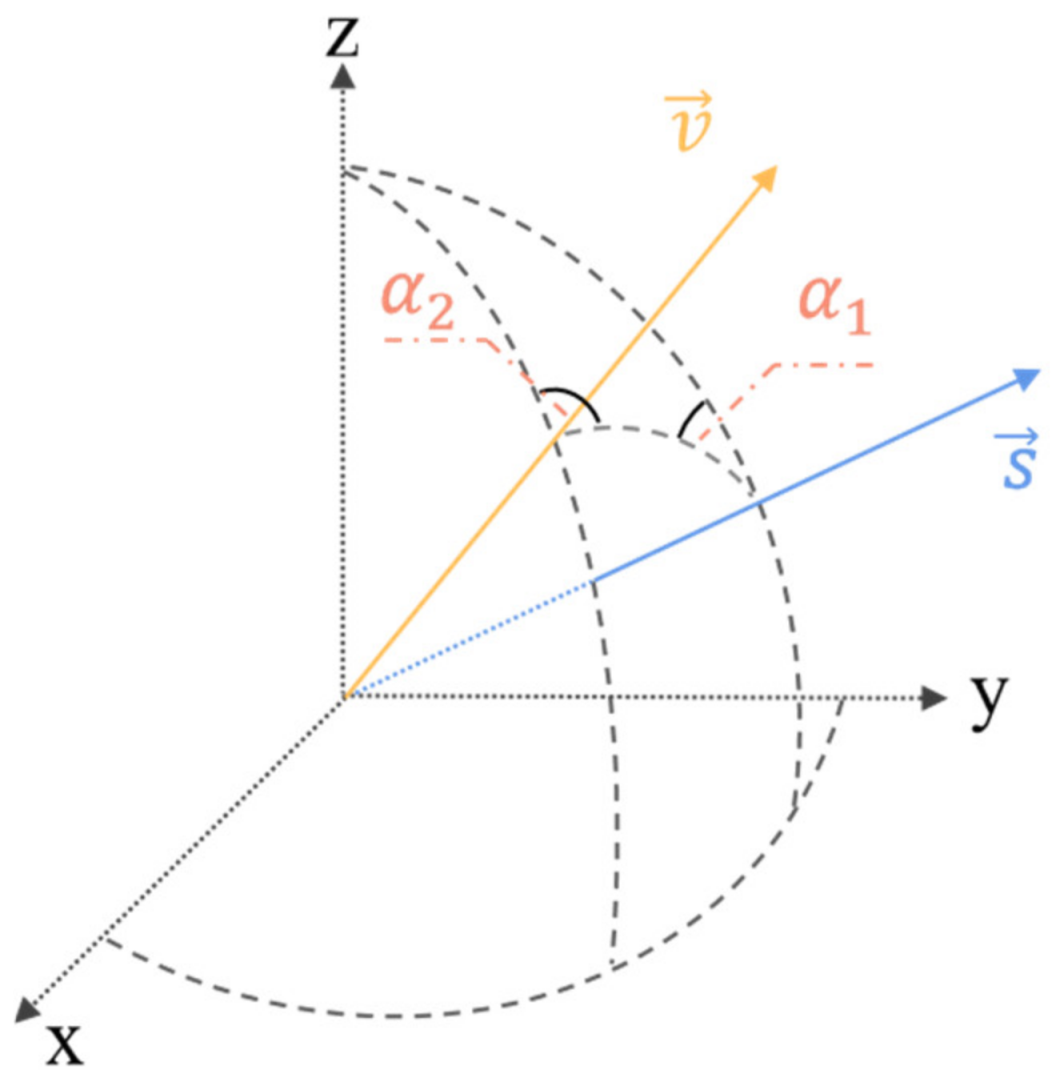
| Payload (Satellite) | TANSO-FTS (GOSAT) | OCO-3 | ACGS (TanSAT) | CO2M (Sentinel 7) | GAS (FY-3H) |
|---|---|---|---|---|---|
| Country of origin | Japan | USA | China | EU | China |
| Detection of component | O2, CO2, CH4, H2O | O2, CO2 | O2, CO2 | O2, CO2, N2, CO, aerosols | O2, CO2, CH4 |
| Waveband (μm) | 0.758–0.775 1.56–1.72 1.92–2.08 5.56–14.3 | 0.758~0.772 1.59~1.62 2.04~2.08 | 0.758~0.776 1.594~1.624 2.041~2.081 | 0.747~0.773 1.59~1.675 1.990~2.095 | 0.75–0.77 1.59–1.625 2.04–2.08 2.05–2.55 |
| Spectral resolution | 0.2 cm−1 | 0.693 cm−1 0.308 cm−1 0.236 cm−1 | 0.762 cm−1 0.482 cm−1 0.388 cm−1 | 2.077 cm−1 1.157 cm−1 0.825 cm−1 | 0.693 cm−1 0.27 cm−1 0.212 cm−1 |
| Simulation of Indicator | Parameter |
|---|---|
| Atmospheric model | U.S. Standard Atmosphere 1976 |
| Wavenumber range/cm−1 | 6150–6290; 4806–4902 |
| Aerosol type | Maritime |
| Real-time sea-surface wind speed | 8.7 m/s |
| 24 h average sea-surface wind speed | 7.29 m/s |
| ICSTL | 6 |
| Sea-surface temperature | 300.2 K |
| Sea-surface visibility | 20 km |
| Solar zenith angle of the observer | 142.358° |
| Solar zenith angle of the sun glint | 43.642° |
| Sea-surface reflectivity | 0.0291 |
| Payload | CO2 Absorption | GAS | OCO-3 | AGAS | |
|---|---|---|---|---|---|
| Spectral resolution | 0.07 cm−1 | 0.27 cm−1 | 0.308 cm−1 | 0.482 cm−1 | |
| Transmittance spectrum | P-branch Tmin (6216 cm−1) | 0.3279 | 0.5848 | 0.6025 | 0.6709 |
| R-branch Tmin (6239 cm−1) | 0.3028 | 0.5738 | 0.5897 | 0.6578 (6241 cm−1) | |
| Brightness temperature spectrum | P-branch BTmin (6216 cm−1) | 288.8 K | 295.1 K | 295.4 K | 296.5 K |
| R-branch BTmin (6239 cm−1) | 288.1 K | 295.0 K | 295.3 K | 296.3 K (6241 cm−1) | |
| Payload | CO2 Absorption | GAS | OCO-3 | AGAS | |
|---|---|---|---|---|---|
| Spectral resolution | 0.07 cm−1 | 0.212 cm−1 | 0.236 cm−1 | 0.388 cm−1 | |
| Transmittance spectrum | P-branch Tmin (4842 cm−1) | 0.00036 | 0.05783 | 0.07688 | 0.19353 |
| R-branch Tmin (4865 cm−1) | 0.00017 | 0.064857 | 0.040283 | 0.14792 (4862 cm−1) | |
| Brightness temperature spectrum | P-branch BTmin (4842 cm−1) | 242.7 K | 270.3 K | 272.9 K | 281.9 K |
| R-branch BTmin (4865 cm−1) | 242.3 K | 268.7 K | 271.4 K | 279.7 K | |
References
- Kuttippurath, J.; Peter, R.; Singh, A.; Raj, S. The increasing atmospheric CO2 over India: Comparison to global trends. Iscience 2022, 25, 104863. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Wang, J.; Yao, L.; Chen, X.; Cai, Z.; Yang, D.; Yin, Z.; Gu, S.; Tian, L.; Lu, N.; et al. The TanSat mission: Preliminary global observations. Sci. Bull. 2018, 63, 1200–1207. [Google Scholar] [CrossRef]
- Schwandner, F.M.; Gunson, M.R.; Miller, C.E.; Carn, S.A.; Eldering, A.; Krings, T.; Verhulst, K.R.; Schimel, D.S.; Nguyen, H.M.C.; David, O.; et al. Spaceborne detection of localized carbon dioxide sources. Science 2017, 358, eaam5782. [Google Scholar] [CrossRef] [PubMed]
- Kiehl, J.T. Satellite detection of effects due to increased atmospheric carbon dioxide. Science 1983, 222, 504–506. [Google Scholar] [CrossRef] [PubMed]
- Baker, D.F.; Boesch, H.; Doney, S.C.; O'Brien, D.; Schimel, D.S. Carbon source/sink information provided by column CO2 measurements from the Orbiting Carbon Observatory. Atmos. Chem. Phys. 2010, 10, 4145–4165. [Google Scholar] [CrossRef]
- Chatterjee, A.; Gierach, M.M.; Sutton, A.J.; Feely, R.A.; Crisp, D.; Eldering, A.; Gunson, M.R.; O’Dell, C.; Stephens, B.B.; Schimel, D.S. Influence of El Ni?o on atmospheric CO2 over the tropical Pacific Ocean: Findings from NASA’s OCO-2 mission. Science 2017, 358, eaam5776. [Google Scholar] [CrossRef]
- Miller, J.B.; Tans, P.P.; Gloor, M. Steps for success of OCO-2. Nat. Geosci. 2014, 7, 691. [Google Scholar] [CrossRef]
- Sun, Y.; Frankenberg, C.; Wood, J.D.; Schimel, D.S.; Jung, M.; Guanter, L.; Drewry, D.T.; Verma, M.; Porcar-Castell, A.; Griffis, T.J.; et al. OCO-2 advances photosynthesis observation from space via solar-induced chlorophyll fluorescence. Science 2017, 358, eaam5747. [Google Scholar] [CrossRef]
- Heffernan, O. NASA’s next challenge. Nat. Clim. Change 2009, 1, 28. [Google Scholar] [CrossRef][Green Version]
- Butz, A.; Guerlet, S.; Hasekamp, O.; Schepers, D.; Galli, A.; Aben, I.; Frankenberg, C.; Hartmann, J.M.; Tran, H.; Kuze, A. Toward accurate CO2 and CH4 observations from GOSAT. Geophys. Res. Lett. 2011, 38, L14812. [Google Scholar] [CrossRef]
- Guanter, L.; Frankenberg, C.; Dudhia, A.; Lewis, P.E.; Gómez-Dans, J.; Kuze, A.; Suto, H.; Grainger, R.G. Retrieval and global assessment of terrestrial chlorophyll fluorescence from GOSAT space measurements. Remote Sens. Environ. 2012, 121, 236–251. [Google Scholar] [CrossRef]
- Frankenberg, C.; Fisher, J.B.; Worden, J.; Badgley, G.; Saatchi, S.S.; Lee, J.E.; Toon, G.C.; Butz, A.; Jung, M.; Kuze, A. New global observations of the terrestrial carbon cycle from GOSAT: Patterns of plant fluorescence with gross primary productivity. Geophys. Res. Lett. 2011, 38, L17706. [Google Scholar] [CrossRef]
- Yang, D.; Boesch, H.; Liu, Y.; Somkuti, P.; Cai, Z.; Chen, X.; Di Noia, A.; Lin, C.; Lu, N.; Lyu, D. Toward high precision XCO2 retrievals from TanSat observations: Retrieval improvement and validation against TCCON measurements. J. Geophys. Res. Atmos. 2020, 125, e2020JD032794. [Google Scholar] [CrossRef] [PubMed]
- Hong, X.; Zhang, P.; Bi, Y.; Liu, C.; Sun, Y.; Wang, W.; Chen, Z.; Yin, H.; Zhang, C.; Tian, Y. Retrieval of global carbon dioxide from TanSat satellite and comprehensive validation with TCCON measurements and satellite observations. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X. TanSat: A new star in global carbon monitoring from China. Sci. Bull. 2019, 64, 284–285. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J.; Liu, Y.; Xu, X.; Cai, Z.; Yang, D.; Yan, C.-X.; Feng, L. Angular dependence of aerosol information content in CAPI/TanSat observation over land: Effect of polarization and synergy with A-train satellites. Remote Sens. Environ. 2017, 196, 163–177. [Google Scholar] [CrossRef]
- Krishnapriya, M.; Chandra, A.B.; Nayak, R.K.; Patel, N.R.; Rao, P.V.N.; Dadhwal, V.K. Seasonal and inter-annual variability of atmosphere CO2 based on NOAA Carbon Tracker analysis and satellite observations. J. Indian Soc. Remote Sens. 2018, 46, 309–320. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Bai, L.; Tao, J.; Chen, L.; Zou, M.; Han, Z.; Wang, Z. Retrieval of Carbon Dioxide Using Cross-Track Infrared Sounder (CrIS) on S-NPP. Remote Sens. 2021, 13, 1163. [Google Scholar] [CrossRef]
- Kuze, A.; Suto, H.; Nakajima, M.; Hamazaki, T. Thermal and near infrared sensor for carbon observation Fourier-transform spectrometer on the Greenhouse Gases Observing Satellite for greenhouse gases monitoring. Appl. Opt. 2009, 48, 6716–6733. [Google Scholar] [CrossRef]
- Wu, L.; Aan de Brugh, J.; Meijer, Y.; Sierk, B.; Hasekamp, O.; Butz, A.; Landgraf, J. XCO2 observations using satellite measurements with moderate spectral resolution: Investigation using GOSAT and OCO-2 measurements. Atmos. Meas. Tech. 2020, 13, 713–729. [Google Scholar] [CrossRef]
- Wang, Q.; Yang, Z.-D.; Bi, Y.-M. Spectral parameters and signal-to-noise ratio requirement for TANSAT hyper spectral sensor to measure atmospheric CO2. In Proceedings of the Conference on Remote Sensing of the Atmosphere, Clouds, and Precipitation V, Beijing, China, 13–15 October 2014. [Google Scholar]
- Nong, C.; Yin, Q.; Song, C.; Shu, J. Sensitivity analysis of the satellite infrared hyper-spectral atmospheric sounder GIIRS on FY-4A. J. Infrared Millim. Waves 2021, 40, 353–362. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Connor, B.; Boesch, H.; O’Brien, D.; Frankenberg, C.; Castano, R.; Christi, M.; Crisp, D.; Eldering, A.; Fisher, B.; et al. The ACOS CO2 retrieval algorithm-Part 1: Description and validation against synthetic observations. Atmos. Meas. Tech. 2012, 5, 99–121. [Google Scholar] [CrossRef]
- Crisp, D.; Fisher, B.M.; O’Dell, C.; Frankenberg, C.; Basilio, R.; Bösch, H.; Brown, L.R.; Castano, R.; Connor, B.; Deutscher, N.M.; et al. The ACOS CO2 retrieval algorithm-Part II: Global X CO2 data characterization. Atmos. Meas. Tech. 2012, 5, 687–707. [Google Scholar] [CrossRef]
- Bi, Y.; Yang, Z.; Lu, N.; Zhang, P.; Wang, Q. Channel Selection for Hyper Spectral CO_2 Measurement at the Near-infrared Band. J. Appl. Meteorolgical Sci. 2014, 25, 143–149. [Google Scholar]
- Liou, K.N. An Introduction to Atmospheric Radiation, 2nd ed.; Elsevier Science (USA): Alpharetta, GA, USA, 1980. [Google Scholar]
- Kuhlmann, G.; Broquet, G.; Marshall, J.; Clément, V.; Löscher, A.; Meijer, Y.; Brunner, D. Detectability of CO 2 emission plumes of cities and power plants with the Copernicus Anthropogenic CO 2 Monitoring (CO2M) mission. Atmos. Meas. Tech. 2019, 12, 6695–6719. [Google Scholar] [CrossRef]
- Sierk, B.; Fernandez, V.; Bézy, J.-L.; Meijer, Y.; Durand, Y.; Courrèges-Lacoste, G.B.; Pachot, C.; Löscher, A.; Nett, H.; Minoglou, K. The Copernicus CO2M mission for monitoring anthropogenic carbon dioxide emissions from space. In Proceedings of the International Conference on Space Optics—ICSO 2020, Oberpfaffenhofen, Germany, 30 March–2 April 2021; pp. 1563–1580. [Google Scholar]
- Eldering, A.; Taylor, T.E.; O’Dell, C.W.; Pavlick, R. The OCO-3 mission: Measurement objectives and expected performance based on 1 year of simulated data. Atmos. Meas. Tech. 2019, 12, 2341–2370. [Google Scholar] [CrossRef]
- Taylor, T.E.; Eldering, A.; Merrelli, A.; Kiel, M.; Somkuti, P.; Cheng, C.; Rosenberg, R.; Fisher, B.; Crisp, D.; Basilio, R. OCO-3 early mission operations and initial (vEarly) XCO2 and SIF retrievals. Remote Sens. Environ. 2020, 251, 112032. [Google Scholar] [CrossRef]
- Stanford, G. Information Theory; Prentice-Hall: New York, NY, USA, 1953. [Google Scholar]
- Liu, Y.; Cai, Z.; Yang, D.; Zheng, Y.; Duan, M.; Lu, D. Effects of spectral sampling rate and range of CO2 absorption bands on XCO2 retrieval from TanSat hyperspectral spectrometer. Chin. Sci. Bull. 2014, 59, 1485–1491. [Google Scholar] [CrossRef]
- Bingyan, Z. Preliminary Research on Optimization of Atmospheric Radiation Transfer Model LBLRTM and Near Space Atmospheric Temperature Inversion. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2020. [Google Scholar]
- Zhang, H.; Shi, G. A fast and efficient line-by-line calculation method for atmospheric absorption. Chin. J. Atmos. Sci. 2000, 24, 111–121. [Google Scholar]
- Clough, S.A.; Iacono, M.J. Line-by-line calculation of atmospheric fluxes and cooling rates: 2. Application to carbon dioxide, ozone, methane, nitrous oxide and the halocarbons. J. Geophys. Res. -Atmos. 1995, 100, 16519–16535. [Google Scholar] [CrossRef]
- Clough, S.A.; Iacono, M.J.; Moncet, J.-L. LBLRTM: Line-By-Line Radiative Transfer Model; Astrophysics Source Code Library, The SAO/NASA Astrophysics Data System (ADS): Cambridge, MA, USA, 2014; p. ascl:1405.1001. [Google Scholar]
- Kneizys, F.X.; Anderson, G.P.; Shettle, E.P.; Abreu, L.W.; Chetwynd, J.H., Jr.; Selby, J.E.A.; Gallery, W.O.; Clough, S.A. LOWTRAN 7: Status, review, and impact for short-to-long-wavelength infrared applications. In Proceedings of the Advisory Group for Aerospace Research and Development (AGARD), Paris, France, 1 March 1990. [Google Scholar]
- Kneizys, F.X.; Shettle, E.P.; Abreu, L.W.; Chetwynd, J.H. Users guide to LOWTRAN 7; United States Air Force: Hanscom AFB, MA, USA, 1988. [Google Scholar]
- Li, F.; Wu, B. A Review of Atmospheric Aerosol Model in the LOWTRAN Code. Remote Sens. Technol. Appl. 1995, 10, 48–55. [Google Scholar]
- Jiang, T.; Cao, Q.; Wen, Y. Study on Satellite Observation Mode and Simulation for Atmospheric CO_2 Remote Sensing Over Ocean. Aerosp. Shanghai 2015, 32, 47–50. [Google Scholar] [CrossRef]
- Wen, Y.; Yang, Y.; Dai, H.-S.; Li, Y.-D.; Sun, Y.-Z.; Jiang, G.-W. High Accuracy Solar Glint 2-dimension Pointing Algorithm. Infrared 2018, 39, 28–33. [Google Scholar]
- Yin, J.; Xu, P.; Hou, L.; Chen, L.; Cao, Q. Research on Sunglint Point Positioning Accuracy Based on Greenhouse Gas Detector. In Proceedings of the International Conference on Mechanical, Material and Aerospace Engineering (2MAE), Beijing, China, 12–14 May 2017. [Google Scholar]
- Harmel, T.; Chami, M. Estimation of the sunglint radiance field from optical satellite imagery over open ocean: Multidirectional approach and polarization aspects. J. Geophys. Res. Ocean. 2013, 118, 76–90. [Google Scholar] [CrossRef]
- Ren, H.; Liu, Y.; Chen, H. Calculation of routh sea surface reflection. Int. J. Infrared Millim. Waves 2006, 27, 1019–1026. [Google Scholar] [CrossRef]
- Orji, O.C.; Sollner, W.; Gelius, L.J. Sea Surface Reflection Coefficient Estimation. In Proceedings of the SEG Technical Program Expanded Abstracts, Society of Exploration Geophysicists, Houston, TX, USA, 19 August 2013; pp. 51–55. [Google Scholar]
- Zhang, Z.; Chen, P.; Mao, Z.; Pan, D. Polarization Properties of Reflection and Transmission for Oceanographic Lidar Propagating through Rough Sea Surfaces. Appl. Sci. Basel 2020, 10, 1030. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Measurement of the roughness of the sea surface from photographs of the sun’s glitter. J. Opt. Soc. Am. 1954, 44, 838–850. [Google Scholar] [CrossRef]
- Cox, C.; Munk, W. Statistics of the sea surface derived from sun glitter. J. Mar. Res. 1954, 13, 198–227. [Google Scholar]
- Sancer, M.I. Shadow-corrected electromagnetic scattering from a randomly rough surface. Ieee Trans. Antennas Propag. 1969, 17, 577–585. [Google Scholar] [CrossRef]
- Smith, B.G. Geometrical shadowing of a random rough surface. Ieee Trans. Antennas Propag. 1967, 15, 668–671. [Google Scholar] [CrossRef]
- Integrated Meteorological Dataset of Sea Surface. Service, N.M.D.a.I., Ed.; 2019. National Marine Data Center, National Science & Technology Resource Sharing Service Platform of China. Available online: http://mds.nmdis.org.cn/ (accessed on 19 September 2022).
- Atmosphere, U.S. US Standard Atmosphere; National Oceanic and Atmospheric Administration: Washington, DC, USA, 1976. [Google Scholar]
- Chen, X.; Wei, H.; Li, X.; Xu, C.; Xu, Q. Calculating model for aerosol extinction from visible to far infrared wavelength. High Power Laser Part. Beams 2009, 21, 183–189. [Google Scholar]
- World Meteorological Organization. Access to World Ocean Database 2005 Geographically Sorted Data. Available online: https://www.nodc.noaa.gov/OC5/WOD05/data05geo.html (accessed on 12 October 2022).
- World Meteorological Organization Squares. Available online: http://wiki.gis.com/wiki/index.php/World_Meteorological_Organization_squares (accessed on 12 October 2022).
- Chen, X.; Liu, Y.; Cai, Z. Review of Radiative Transfer Model in Retrieval of Atmospheric CO2 from Satellite Shortwave Infrared Measurements. Remote Sens. Technol. Appl. 2015, 30, 825–834. [Google Scholar]
- Junge, C.E. Atmospheric Chemistry; Academic Press: New York, NY, USA, 1958. [Google Scholar]
- Nakajima, M.; Suto, H.; Yotsumoto, K.; Shiomi, K.; Hirabayashi, T. Fourier transform spectrometer on GOSAT and GOSAT-2. In Proceedings of the International Conference on Space Optics (ICSO), Tenerife, Spain, 7–10 October 2014. [Google Scholar]






| Time (UTCG) | Detic Latitude (deg) | Detic Longitude (deg) | Solar Zenith Angle of the Sun Glint (°) | Solar Zenith Angle of the Observer (°) |
|---|---|---|---|---|
| 2019/6/17 15:42 | −60.492 | −32.266 | 86.097 | 118.385 |
| 2019/6/17 15:45 | −54.053 | −31.452 | 80.454 | 119.605 |
| 2019/6/17 15:50 | −42.249 | −32.475 | 69.69 | 124.232 |
| 2019/6/17 15:51 | −39.708 | −32.873 | 67.327 | 125.564 |
| 2019/6/17 15:52 | −37.108 | −33.313 | 64.898 | 127.027 |
| 2019/6/17 15:54 | −31.734 | −34.29 | 59.856 | 130.316 |
| 2019/6/17 15:56 | −26.15 | −35.363 | 54.6 | 134.038 |
| 2019/6/17 15:58 | −20.382 | −36.508 | 49.177 | 138.117 |
| 2019/6/17 15:59 | −17.438 | −37.102 | 46.42 | 140.265 |
| 2019/6/17 16:00 | −14.459 | −37.71 | 43.642 | 142.47 |
| 2019/6/17 16:01 | −11.45 | −38.329 | 40.852 | 144.721 |
| 2019/6/17 16:05 | 0.834 | −40.935 | 29.798 | 153.918 |
| 2019/6/17 16:08 | 10.217 | −43.054 | 22.146 | 160.478 |
| 2019/6/17 16:10 | 16.512 | −44.576 | 17.932 | 164.148 |
| 2019/6/17 16:15 | 32.237 | −48.988 | 15.674 | 166.247 |
| 2019/6/17 16:20 | 47.672 | −55.087 | 25.669 | 157.627 |
| WMO SQUARE | 7016 | 1106 | 1415 | 3310 | 7304 | 5103 |
|---|---|---|---|---|---|---|
| Longitude (°) | (160,170) W | (60,70) E | (150,160) E | (100,110) E | (40,50) W | (30,40) W |
| Latitude (°) | (0,10) N | (10,20) N | (40,50) N | (30,40) S | (30,40) N | (10,20) S |
| Time (UTCG) | 2019/6/30 0:06:00 | 2019/2/23 8:42:00 | 2019/11/4 1:58:00 | 2019/2/2 6:42:00 | 2019/10/18 15:50:00 | 2019/6/17 16:00:00 |
| Sun-glint position | (4.08°N, 161.59°W) | (18.534°N, 66.611°E) | (44.87°N, 156.438°E) | (31.567°S, 104.739°E) | (37.746°N, 47.067°W) | (14.459°S, 37.71°W) |
| AT (K) | 303.3 | 298.6 | 283.3 | 295.4 | 297.2 | 300.2 |
| WSS (m/s) | 2.6 | 6.7 | 3.1 | 10.3 | 10.8 | 8.7 |
| WHH (m/s) | 2.35 | 6.308 | 9.58 | 9.91 | 8.98 | 7.29 |
| VIS (km) | 10 | 20 | 10 | 20 | 10 | 20 |
| SZA of the sun glint (°) | 26.501 | 31.598 | 61.02 | 24.744 | 49.402 | 43.642 |
| Sea-surface reflectivity | 0.0212 | 0.0225 | 0.0665 | 0.0215 | 0.0355 | 0.0291 |
| SZA of the observer (°) | 156.730 | 152.471 | 129.452 | 158.370 | 137.947 | 142.470 |
| ICSTL | 1 | 9 | 7 | 3 | 2 | 6 |
| WSS (m/s) | 7 | 7 | 10 | 10 | 12 | 12 |
|---|---|---|---|---|---|---|
| SZA of the sun glint (°) | 60 | 65 | 65 | 70 | 75 | 80 |
| Reflectivity | 0.060 | 0.080 | 0.0745 | 0.0984 | 0.1246 | 0.1693 |
| Payload | SR (cm−1) | Nmp | RMSE | MAXAD | MAXAPD (%) | MAD | MAPD (%) | |
|---|---|---|---|---|---|---|---|---|
| Tr | GAS | 0.27 | 4119 | 0.0304 | 0.2644 | 85.45 | 0.0104 | 1.74 |
| OCO-3 | 0.308 | 3707 | 0.0329 | 0.2873 | 94.89 | 0.0114 | 1.90 | |
| ACGS | 0.482 | 2308 | 0.0422 | 0.3571 | 116.91 | 0.0160 | 2.62 | |
| BT | GAS | 0.27 | 4119 | 0.5251 K | 5.7100 K | 1.97 | 0.1507 K | 5.103 × 10−2 |
| OCO-3 | 0.308 | 3707 | 0.5620 K | 6.1735 K | 2.14 | 0.1638 K | 5.548 × 10−2 | |
| ACGS | 0.482 | 2308 | 0.6921 K | 7.1785 K | 2.48 | 0.2209 K | 7.475 × 10−2 |
| Payload | SR (cm−1) | Nmp | RMSE | MAXAD | MAXAPD (%) | MAD | MAPD (%) | |
|---|---|---|---|---|---|---|---|---|
| Tr | GAS | 0.212 | 3623 | 0.0469 | 0.2390 | 2.807 × 104 | 0.0320 | 111.37 |
| OCO-3 | 0.236 | 3254 | 0.0538 | 0.2740 | 2.531 × 104 | 0.0372 | 134.31 | |
| ACGS | 0.388 | 1979 | 0.0906 | 0.3800 | 5.332 × 104 | 0.0654 | 292.68 | |
| BT | GAS | 0.212 | 3623 | 4.3469 K | 28.501 K | 11.71 | 1.5292 K | 0.57 |
| OCO-3 | 0.236 | 3254 | 4.7765 K | 30.526 K | 12.54 | 1.7132 K | 0.64 | |
| ACGS | 0.388 | 1979 | 6.4635 K | 39.107 K | 16.07 | 2.5352 K | 0.94 |
| SSR | RMSE | MAXAD | MAXAPD (%) | MAD | MAPD (%) |
|---|---|---|---|---|---|
| 1.167 | 0.0086 | 0.0667 | 11.50 | 0.0035 | 0.49 |
| 1.63 | 0.0047 | 0.0409 | 6.98 | 0.0018 | 0.25 |
| 2.33 | 0.0024 | 0.0202 | 3.49 | 8.791 × 10−4 | 0.12 |
| 3.03 | 0.0014 | 0.0138 | 2.40 | 4.980 × 10−4 | 0.069 |
| 3.50 | 0.0010 | 0.0110 | 1.92 | 3.536 × 10−4 | 0.049 |
| SSR | RMSE | MAXAD | MAXAPD (%) | MAD | MAPD (%) |
|---|---|---|---|---|---|
| 1.125 | 0.0226 | 0.1157 | 150.24 | 0.0148 | 5.14 |
| 1.575 | 0.0121 | 0.0621 | 71.33 | 0.0078 | 2.71 |
| 2.25 | 0.0059 | 0.0295 | 36.09 | 0.0038 | 1.31 |
| 2.925 | 0.0034 | 0.0173 | 19.92 | 0.0022 | 0.74 |
| 3.375 | 0.0025 | 0.0133 | 14.84 | 0.0016 | 0.54 |
| WSS (m/s) | RMSE | MAXAD | MAXAPD (%) | MAD | MAPD (%) | |
|---|---|---|---|---|---|---|
| 1.61 μm spectral band | 0.1 | 0 | - | - | - | - |
| 2 | 0.0055 | 0.0057 | 0.6148 | 0.0055 | 0.6147 | |
| 3 | 0.0513 | 0.0528 | 5.7529 | 0.0512 | 5.7176 | |
| 5 | 0.0963 | 0.0993 | 10.8067 | 0.0961 | 10.7359 | |
| 7 | 0.1126 | 0.1161 | 12.6346 | 0.1124 | 12.5523 | |
| 15 | 0.1336 | 0.1377 | 14.9897 | 0.1334 | 14.8986 | |
| 2.06 μm spectrum band | 0.1 | 0 | - | - | - | - |
| 2 | 0.0050 | 0.0066 | 0.6997 | 0.0048 | 0.6978 | |
| 3 | 0.0358 | 0.0466 | 5.0370 | 0.0341 | 4.9873 | |
| 5 | 0.0663 | 0.0862 | 9.3265 | 0.0630 | 9.2277 | |
| 7 | 0.0775 | 0.1008 | 10.9082 | 0.0737 | 10.7931 | |
| 15 | 0.0932 | 0.1212 | 13.1070 | 0.0887 | 12.9781 |
| VIS (km) | RMSE | MAXAD | MAXAPD (%) | MAD | MAPD (%) | |
|---|---|---|---|---|---|---|
| 1.61 μm spectral band | 50 | 0 | - | - | - | - |
| 25 | 0.0747 | 0.0772 | 8.3902 | 0.0746 | 8.3173 | |
| 15 | 0.1754 | 0.1811 | 19.6810 | 0.1752 | 19.5339 | |
| 7 | 0.3746 | 0.3862 | 41.9733 | 0.3741 | 41.7112 | |
| 5 | 0.4773 | 0.4917 | 53.4362 | 0.4766 | 53.1544 | |
| 2.06 μm spectrum band | 50 | 0 | - | - | - | - |
| 25 | 0.0483 | 0.0628 | 6.8248 | 0.0460 | 6.7547 | |
| 15 | 0.1171 | 0.1522 | 16.5253 | 0.1114 | 16.3681 | |
| 7 | 0.2588 | 0.3358 | 36.4654 | 0.2461 | 36.1677 | |
| 5 | 0.3351 | 0.4350 | 47.1845 | 0.3187 | 46.8365 |
| WSS (m/s) | SZA of the sun glint (°) | Reflectivity | Spectral Band | RMSE (W·m−2sr−1 cm−1) | MAD (W·m−2sr−1 cm−1) | MAPD (%) |
|---|---|---|---|---|---|---|
| 7 | 60 | 0.0600 | 1.61 μm | 6.785 × 10−13 | 6.624 × 10−13 | 1.2762 |
| 2.06 μm | 4.150 ×10−10 | 3.757 × 10−10 | 1.7266 | |||
| 7 | 65 | 0.0800 | 1.61 μm | 2.320 × 10−12 | 2.268 × 10−12 | 4.5303 |
| 2.06 μm | 8.454 × 10−10 | 7.674 × 10−10 | 3.6585 | |||
| 10 | 65 | 0.0745 | 1.61 μm | 2.361 × 10−12 | 2.308 × 10−12 | 4.6148 |
| 2.06 μm | 8.637 × 10−10 | 7.864 × 10−10 | 3.7633 | |||
| 10 | 70 | 0.0984 | 1.61 μm | 5.233 × 10−12 | 5.116 × 10−12 | 10.8831 |
| 2.06 μm | 1.916 × 10−9 | 1.747 × 10−9 | 8.9576 | |||
| 12 | 75 | 0.1246 | 1.61 μm | 7.940 × 10−12 | 7.761 × 10−12 | 17.5713 |
| 2.06 μm | 2.890 × 10−9 | 2.628 × 10−9 | 14.3476 | |||
| 12 | 80 | 0.1693 | 1.61 μm | 1.519 × 10−11 | 1.485 × 10−12 | 40.2094 |
| 2.06 μm | 6.282 × 10−9 | 5.711 × 10−9 | 38.7185 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Chen, P.; Ding, L.; Pan, D. Assessments of the Above-Ocean Atmospheric CO2 Detection Capability of the GAS Instrument Onboard the Next-Generation FengYun-3H Satellite. Remote Sens. 2022, 14, 6032. https://doi.org/10.3390/rs14236032
Chen S, Chen P, Ding L, Pan D. Assessments of the Above-Ocean Atmospheric CO2 Detection Capability of the GAS Instrument Onboard the Next-Generation FengYun-3H Satellite. Remote Sensing. 2022; 14(23):6032. https://doi.org/10.3390/rs14236032
Chicago/Turabian StyleChen, Su, Peng Chen, Lei Ding, and Delu Pan. 2022. "Assessments of the Above-Ocean Atmospheric CO2 Detection Capability of the GAS Instrument Onboard the Next-Generation FengYun-3H Satellite" Remote Sensing 14, no. 23: 6032. https://doi.org/10.3390/rs14236032
APA StyleChen, S., Chen, P., Ding, L., & Pan, D. (2022). Assessments of the Above-Ocean Atmospheric CO2 Detection Capability of the GAS Instrument Onboard the Next-Generation FengYun-3H Satellite. Remote Sensing, 14(23), 6032. https://doi.org/10.3390/rs14236032






