Intersection Constraint Weighting (ICW) Method: High-Resolution Joint Magnetic Susceptibility Inversion of Aeromagnetic and Gradient Data
Abstract
1. Introduction
2. Methodology
2.1. Data Joint Inversion
2.2. Cross-Gradient Inversion
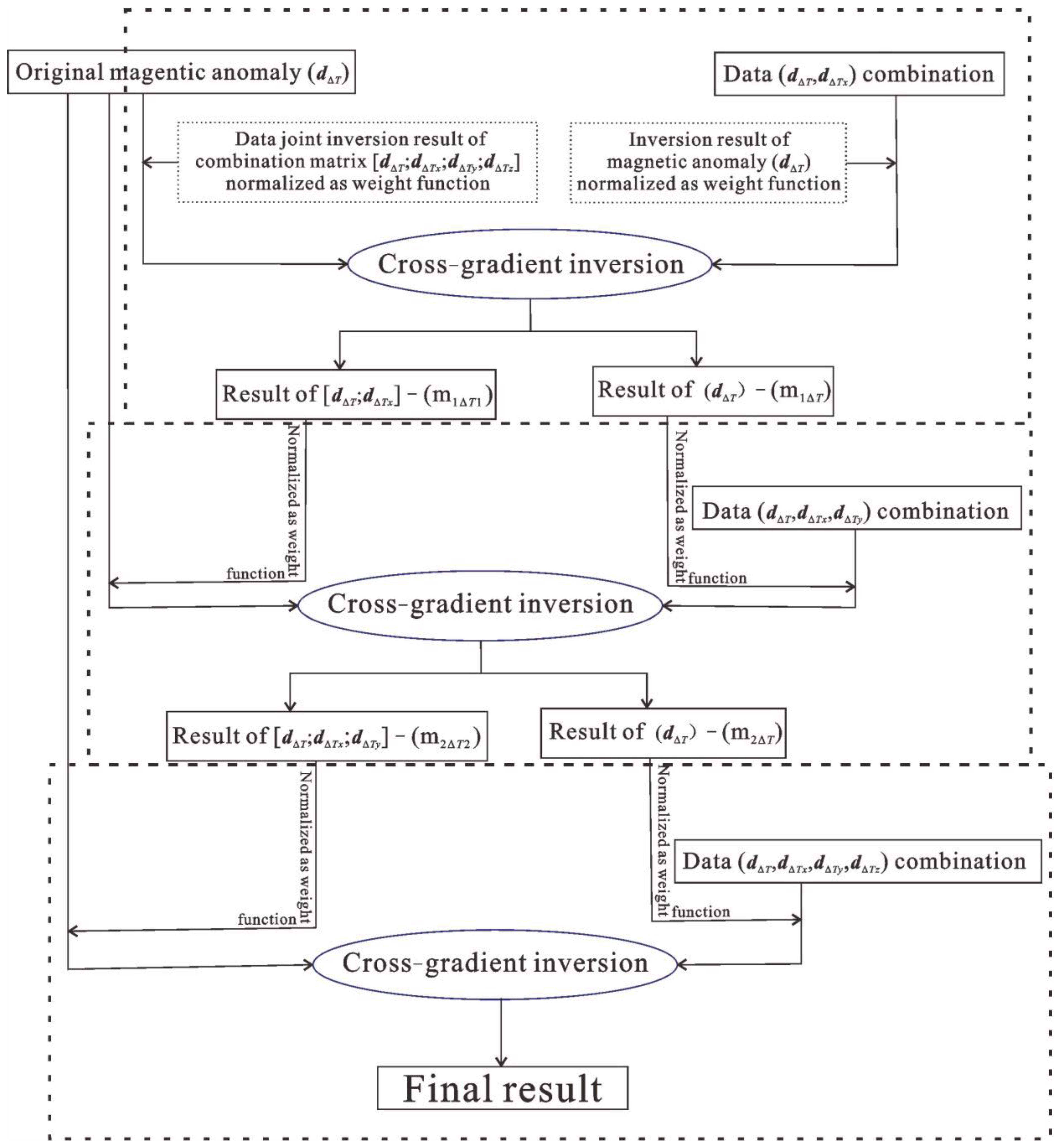
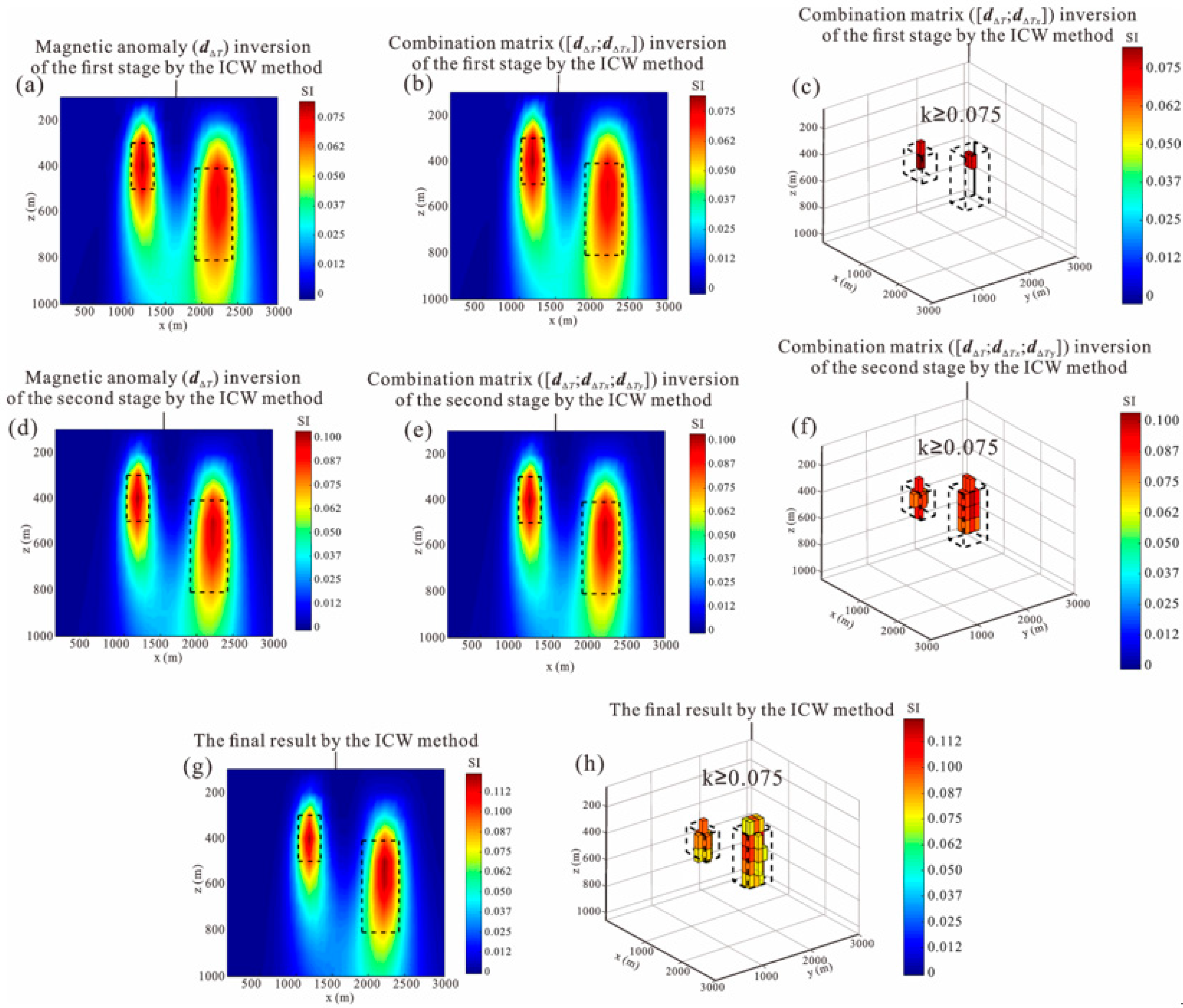
2.3. Intersection Constraint Weighting (ICW) Method
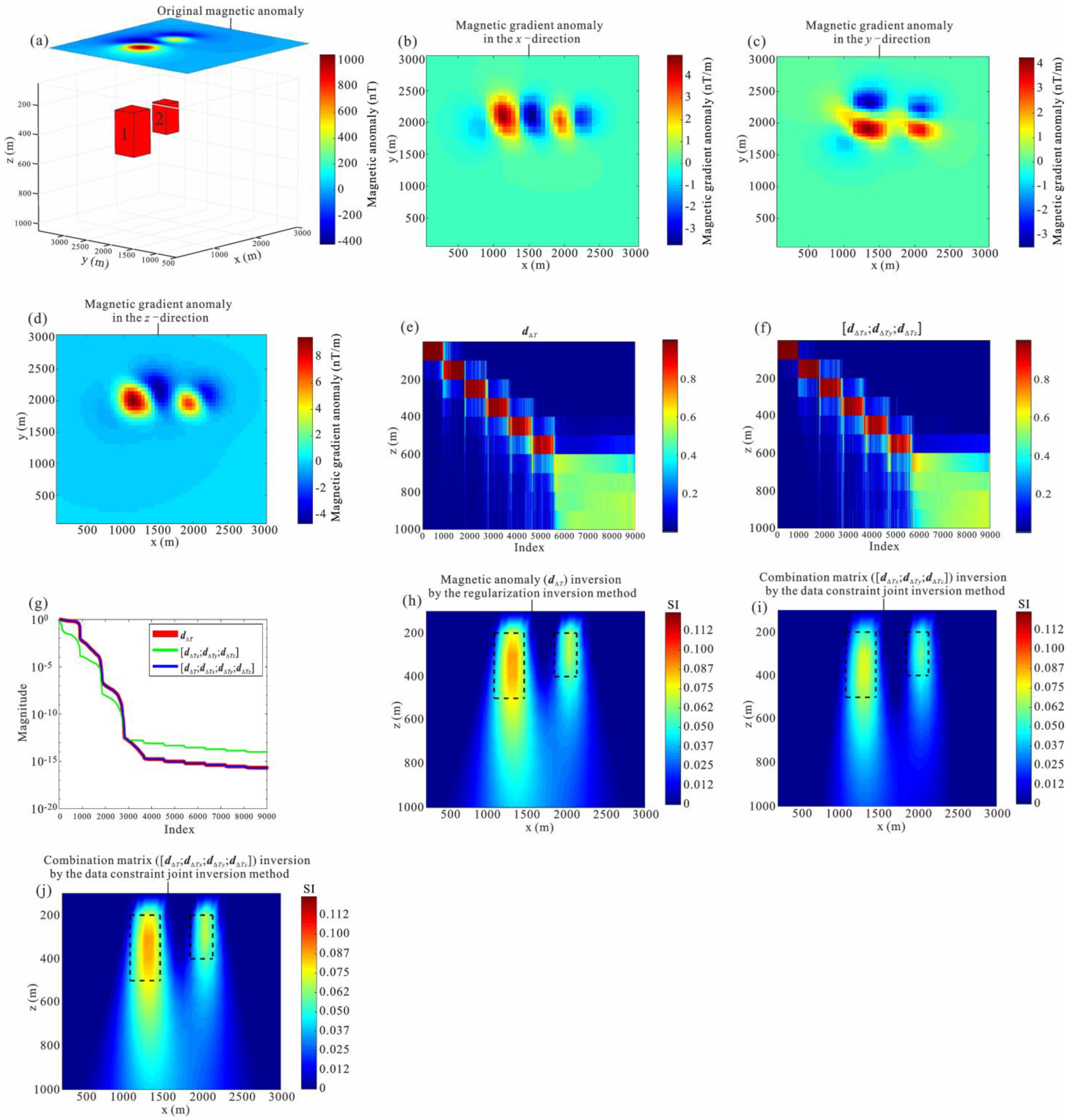
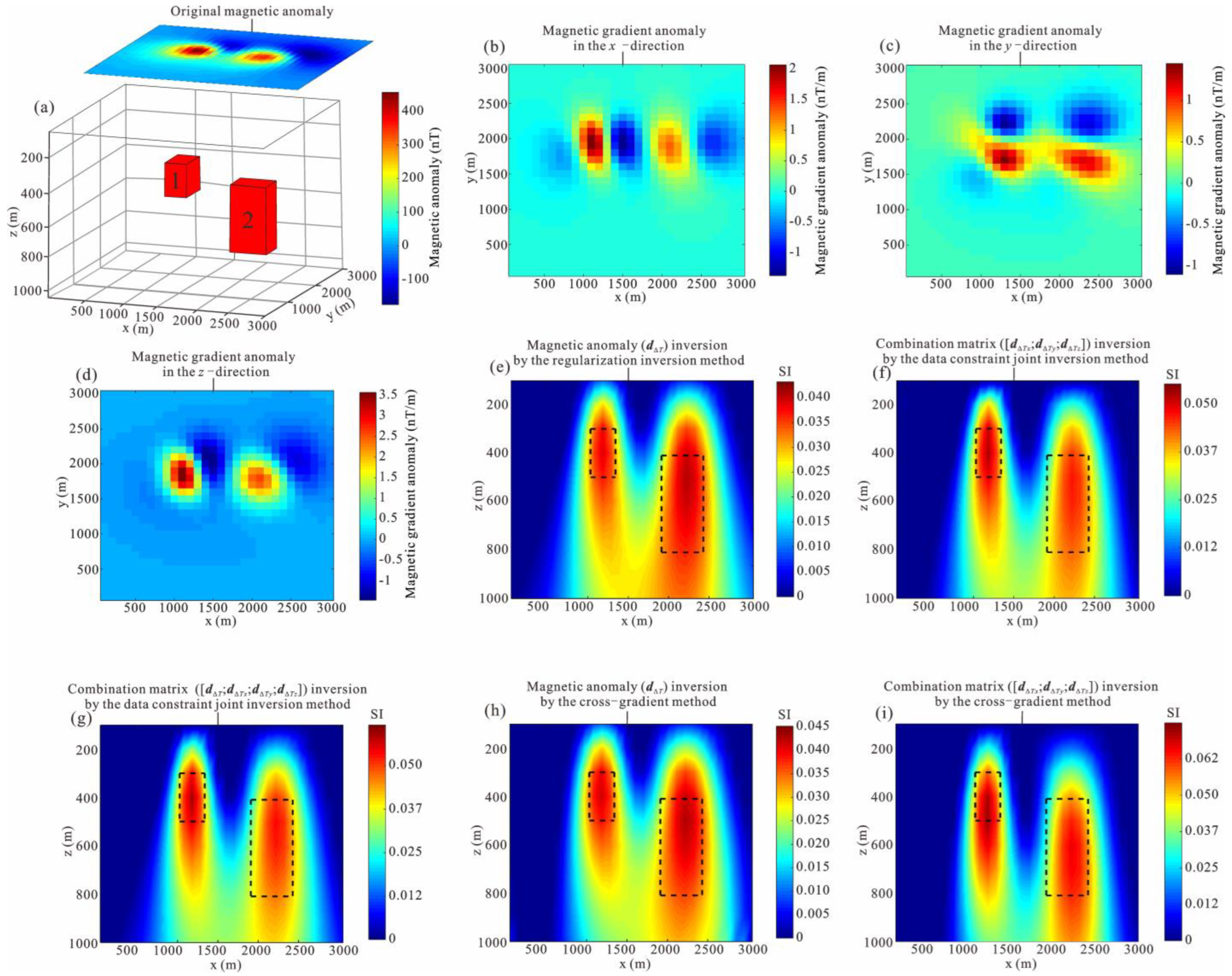
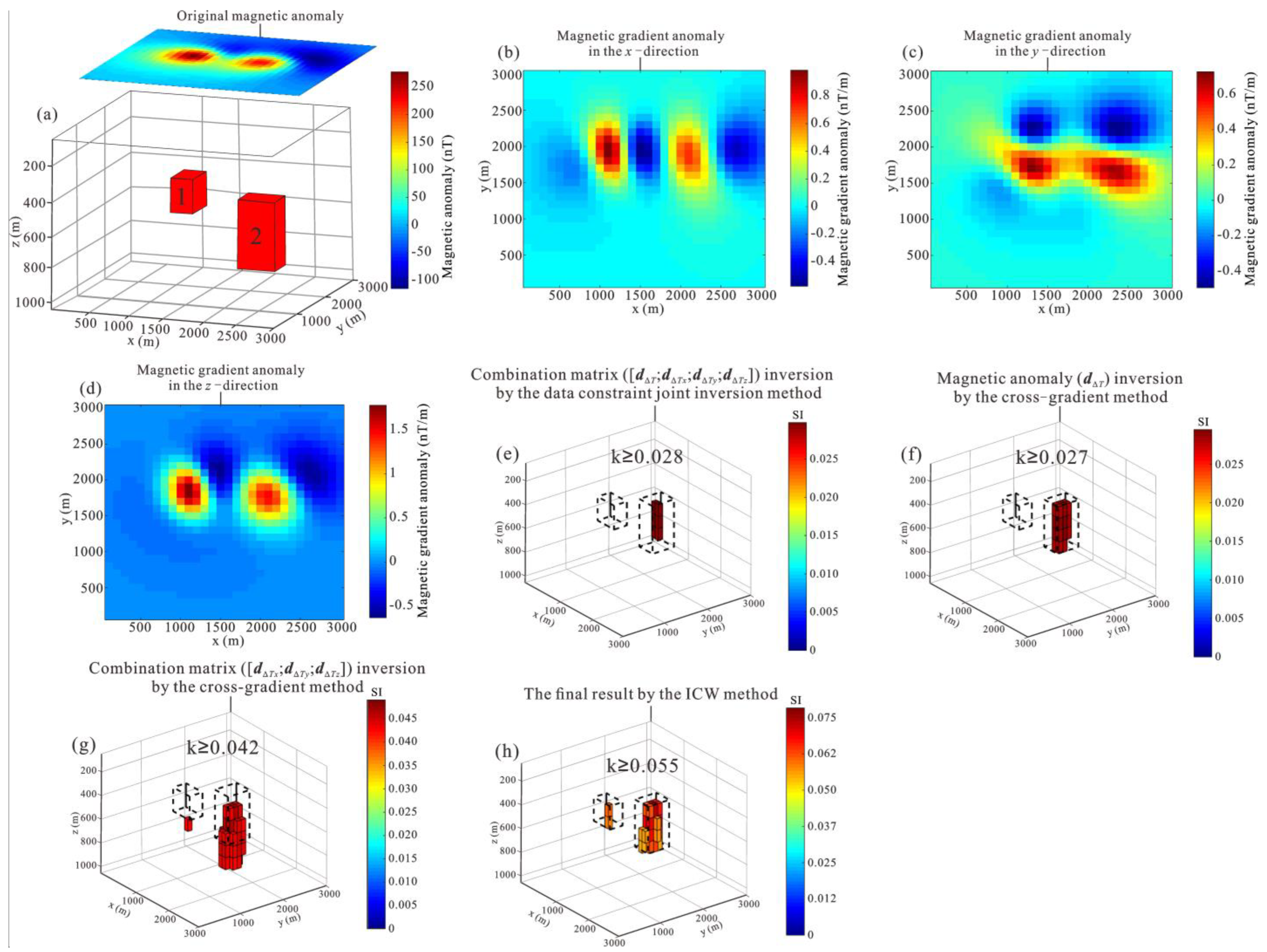
3. Theoretical Model Tests
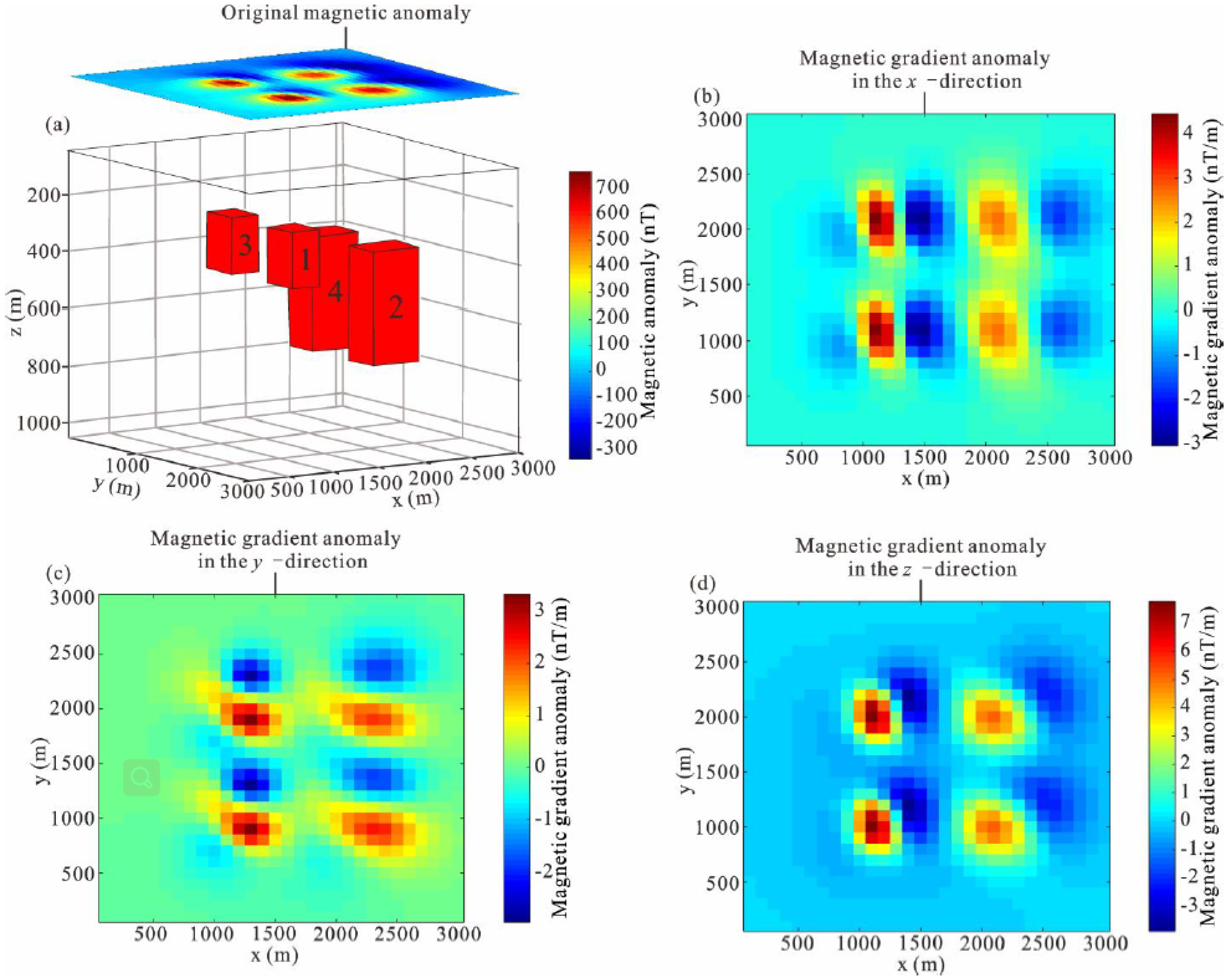
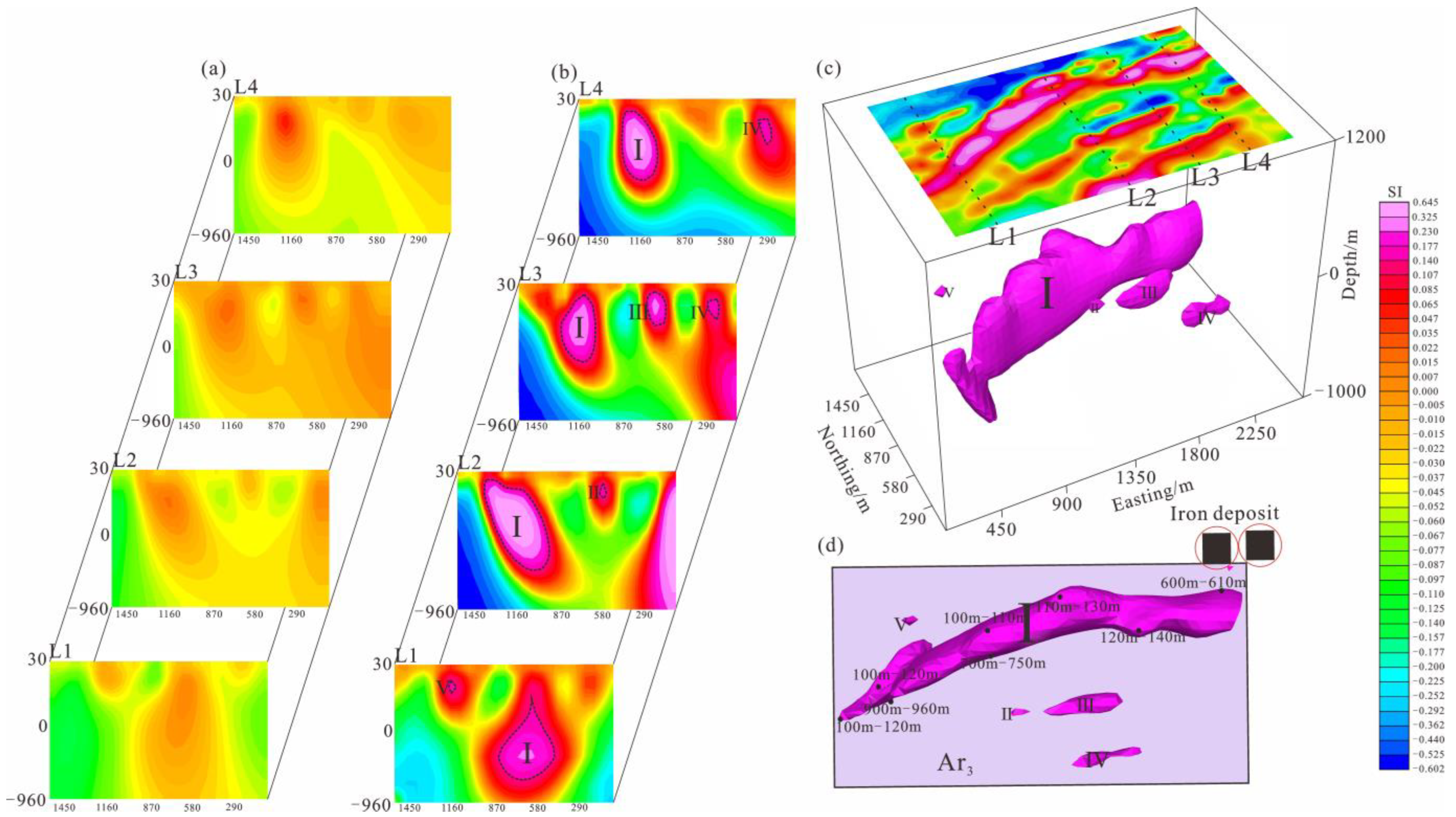
4. Real Data Application
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, J.; Meng, X.H. An aeromagnetic investigation of the Dapai deposit in Fujian Province, South China: Structural and mining implications. Ore Geol. Rev. 2019, 112, 103061. [Google Scholar] [CrossRef]
- Gao, X.H.; Xiong, S.Q.; Yu, C.C.; Zhang, D.H.; Wu, C.P. The estimation of magnetite prospective resources based on aeromagnetic data: A case study of Qihe Area, Shandong Province, China. Remote Sens. 2021, 13, 1216. [Google Scholar] [CrossRef]
- Wasilewski, P.; Fountain, D.W. The Ivrea Zone as a model for the distribution of magnetization in the continental crust. Geophys. Res. Lett. 1982, 9, 333–336. [Google Scholar] [CrossRef]
- Schnetzler, C.C. An estimation of continental crust magnetization and susceptibility from Magsat data for the conterminous United States. J. Geophys. Res.-Sol. Earth 1985, 90, 2617–2620. [Google Scholar] [CrossRef]
- Woodward, D.J. Inversion of aeromagnetic data using digital terrain models. Geophysics 1993, 58, 645–652. [Google Scholar] [CrossRef]
- Batista-Rodríguez, J.A.; Pérez-Flores, M.A.; Quiroga-Goode, G.; Gallardo, L.A. Geometry of ophiolites in eastern Cuba from 3D inversion of aeromagnetic data, constrained by surface geology. Geophysics 2007, 72, B81–B91. [Google Scholar] [CrossRef]
- Liu, S.; Hu, X.Y.; Liu, T.Y.; Feng, J.; Gao, W.L.; Qiu, L.Q. Magnetization vector imaging for borehole magnetic data based on magnitude magnetic anomaly. Geophysics 2013, 78, D429–D444. [Google Scholar] [CrossRef]
- Anderson, E.D.; Zhou, W.; Li, Y.G.; Hitzman, M.W.; Monecke, T.; Lang, J.R.; Kelley, K.D. Three-dimensional distribution of igneous rocks near the Pebble porphyry Cu−Au−Mo deposit in southwestern Alaska: Constraints from regional-scale aeromagnetic data. Geophysics 2014, 79, B63–B79. [Google Scholar] [CrossRef]
- Bott, M.H.P. Solution of the linear inverse problem in magnetic interpretation with application to oceanic magnetic anomalies. Geophys. J. Int. 1957, 13, 313–323. [Google Scholar] [CrossRef]
- Arkani-Hamed, J.; Strangway, D.W. Magnetic susceptibility anomalies of lithosphere beneath eastern Europe and the Middle East. Geophysics 1986, 51, 1711–1724. [Google Scholar] [CrossRef]
- Li, Y.G.; Oldenburg, D.W. 3-D inversion of magnetic data. Geophysics 1996, 61, 394–408. [Google Scholar] [CrossRef]
- Pilkington, M. 3-D magnetic imaging using conjugate gradients. Geophysics 1997, 62, 1132–1142. [Google Scholar] [CrossRef]
- Li, Y.G.; Oldenburg, D.W. Fast inversion of large-scale magnetic data using wavelet transforms and a logarithmic barrier method. Geophys. J. Int. 2003, 152, 251–265. [Google Scholar] [CrossRef]
- Pilkington, M. 3D magnetic data-space inversion with sparseness constraints. Geophysics 2009, 74, L7–L15. [Google Scholar] [CrossRef]
- Li, W.B.; Qian, J.L.; Li, Y.G. Joint inversion of surface and borehole magnetic data: A level-set approach. Geophysics 2020, 85, J15–J33. [Google Scholar] [CrossRef]
- Paoletti, V.; Fedi, M.; Italiano, F.; Florio, G.; Ialongo, S. Inversion of gravity gradient tensor data: Does it provide better resolution? Geophys. J. Int. 2016, 205, 192–202. [Google Scholar] [CrossRef]
- Zhdanov, M.S.; Robert, E.; Souvik, M. Three-dimensional regularized focusing inversion of gravity gradient tensor component data. Geophysics 2004, 69, 925–937. [Google Scholar] [CrossRef]
- Meng, Z.H. 3D inversion of full gravity gradient tensor data using SL0 sparse recovery. J. Appl. Geophys. 2016, 127, 112–128. [Google Scholar] [CrossRef]
- Qin, P.B.; Zhang, C.; Meng, Z.H.; Zhang, D.L.; Hou, Z.L. Three integrating methods for gravity and gravity gradient 3-D inversion and their comparison based on a new function of discrete stability. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Martinez, C.Y.; Li, Y. Inversion of regional gravity gradient data over the Vredefort Impact Structure, South Africa. In Proceedings of the 81st SEG Annual International Meeting, San Antonio, CA, USA, 18–23 September 2011; pp. 841–845. [Google Scholar]
- Capriotti, J.; Li, Y.; Krahenbuhl, R. Joint inversion of gravity and gravity gradient data using a binary formulation: GEM Chengdu 2015. In Proceedings of the International Workshop and Gravity, Electrical & Magnetic Methods and Their Applications, Chengdu, China, 19–22 April 2015; pp. 326–329. [Google Scholar]
- Qin, P.B.; Xiang, M.; Liang, X.; Hou, Z.L. A new method to integrate different gravity gradient components in reweighted regularized inversion with a minimum support constraint. Geophys. J. Int. 2019, 217, 1387–1412. [Google Scholar] [CrossRef]
- Hood, P. Gradient measurement in aeromagnetic survey. Geophysics 1965, 30, 891–902. [Google Scholar] [CrossRef]
- Barongo, J.O. Method for depth estimation on aeromagnetic vertical gradient anomalies. Geophysics 1985, 50, 963–968. [Google Scholar] [CrossRef]
- Oruç, B.; Keskinsezer, A. Detection of causative bodies by normalized full gradient of aeromagnetic anomalies from east Marmara region, NW Turkey. J. Appl. Geophys. 2008, 65, 39–49. [Google Scholar] [CrossRef]
- Beiki, M.; Clark, D.A.; Austin, J.R.; Foss, C.A. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data. Geophysics 2012, 77, J23–J37. [Google Scholar] [CrossRef]
- Li, L.; Guo, H.; Wang, P.; Jia, W.J. Research on RTP aeromagnetic gradient data and its applicability in different latitudes. Appl. Geophys. 2016, 13, 48–58. [Google Scholar] [CrossRef]
- Brahimi, S.; Maire, P.L.; Ghienne, J.F.; Munschy, M. Deciphering channel networks from aeromagnetic potential field data: The case of the North Sea Quaternary tunnel valleys. Geophys. J. Int. 2020, 220, 1447–1462. [Google Scholar] [CrossRef]
- Davis, K.; Li, Y.G. Joint processing of total-field and gradient magnetic data. Explor. Geophys. 2011, 42, 199–206. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Characterization of heterogeneous near-surface materials by joint 2D inversion of dc resistivity and seismic data. Geophys. Res. Lett. 2003, 30, 1658. [Google Scholar] [CrossRef]
- Gallardo, L.A.; Meju, M.A. Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints. J. Geophys. Res.-Sol. Earth 2004, 109, B03311. [Google Scholar] [CrossRef]
- Linde, N.; Binley, A.; Tryggvason, A.; Pedersen, L.B.; Revil, A. Improved hydrogeophysical characterization using joint inversion of cross-hole electrical resistance and ground-penetrating radar traveltime data. Water Resour. Res. 2006, 42, W12404. [Google Scholar] [CrossRef]
- Fregoso, E.; Gallardo, L.A. cross-gradients joint 3D inversion with applications to gravity and magnetic data. Geophysics 2009, 74, L31–L42. [Google Scholar] [CrossRef]
- Gross, L. Weighted cross-gradient function for joint inversion with the application to regional 3-D gravity and magnetic anomalies. Geophys. J. Int. 2019, 217, 2035–2046. [Google Scholar] [CrossRef]
- Vatankhah, S.; Liu, S.; Renaut, R.A.; Hu, X.Y. An efficient alternating algorithm for the Lp-norm cross-gradient joint inversion of gravity and magnetic data using the 2-D fast fourier transform. IEEE Trans. Geosci. Remote Sens. 2020, 60, 1–16. [Google Scholar] [CrossRef]
- Tavakoli, M.; Kalateh, A.N.; Rezaie, M.; Gross, L. Sequential joint inversion of gravity and magnetic data via the cross-gradient constraint. Geophys. Prospect. 2021, 69, 1542–1559. [Google Scholar] [CrossRef]
- Lawson, L.C.; Hanson, J.R. Solving Least-Squares Problems; Prentice-Hall: Englewood Cliffs, NJ, USA, 1974. [Google Scholar]
- Portniaguine, O.; Zhdanov, M.S. Focusing geophysical inversion images. Geophysics 1999, 64, 874–887. [Google Scholar] [CrossRef]
- Li, Y.G.; Oldenburg, D.W. Joint inversion of surface and Three-component borehole magnetic data. Geophysics 2000, 65, 540–552. [Google Scholar] [CrossRef]
- Paoletti, V.; Hansen, P.C.; Hansen, M.F.; Fedi, M. A computationally efficient tool for assessing the depth resolution in potential–field inversion. Geophysics 2014, 79, A33–A38. [Google Scholar] [CrossRef]
- Xiao, W.J.; Windley, B.F.; Hao, J.; Zhai, M.G. Accretion leading to collision and the Permian Solonker suture, Inner Mongolia, China: Termination of the central Asian orogenic belt. Tectonics 2003, 22, 1069–1089. [Google Scholar] [CrossRef]
- Jian, P.; Liu, D.; Kröner, A.; Windley, B.F.; Shi, Y.; Zhang, F.; Shi, G.; Miao, L.; Zhang, W.; Zhang, Q. Time scale of an early to mid-Paleozoic orogenic cycle of the long-lived Central Asian Orogenic Belt, Inner Mongolia of China: Implications for continental growth. Lithos 2008, 101, 233–259. [Google Scholar] [CrossRef]
- Jian, P.; Liu, D.Y.; Kroner, A.; Windley, B.F.; Shi, Y.R.; Zhang, W.; Zhang, F.Q.; Miao, L.C.; Zhang, L.Q.; Tomurhuu, D. Evolution of a Permian intraoceanic arc-trench system in the Solonker suture zone, Central Asian Orogenic Belt, China and Mongolia. Lithos 2010, 118, 169–190. [Google Scholar] [CrossRef]
- Sun, J.; Zhu, X.K.; Chen, Y.L.; Fang, N. Iron isotopic constraints on the genesis of Bayan Obo ore deposit, Inner Mongolia, China. Precambrian Res. 2013, 235, 88–106. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, J.; Ma, G.; Li, L. Intersection Constraint Weighting (ICW) Method: High-Resolution Joint Magnetic Susceptibility Inversion of Aeromagnetic and Gradient Data. Remote Sens. 2022, 14, 6029. https://doi.org/10.3390/rs14236029
Cai J, Ma G, Li L. Intersection Constraint Weighting (ICW) Method: High-Resolution Joint Magnetic Susceptibility Inversion of Aeromagnetic and Gradient Data. Remote Sensing. 2022; 14(23):6029. https://doi.org/10.3390/rs14236029
Chicago/Turabian StyleCai, Jin, Guoqing Ma, and Lili Li. 2022. "Intersection Constraint Weighting (ICW) Method: High-Resolution Joint Magnetic Susceptibility Inversion of Aeromagnetic and Gradient Data" Remote Sensing 14, no. 23: 6029. https://doi.org/10.3390/rs14236029
APA StyleCai, J., Ma, G., & Li, L. (2022). Intersection Constraint Weighting (ICW) Method: High-Resolution Joint Magnetic Susceptibility Inversion of Aeromagnetic and Gradient Data. Remote Sensing, 14(23), 6029. https://doi.org/10.3390/rs14236029






