Abstract
Loess landslides represent an important geohazard in relation to the deformation of unstable loess structures occurred on the slope of loess-covered area. It has become one of the important topics to accurately identify the distribution and activity of loess landslides and describe the spatio-temporal kinematics in the western-project construction in China. Interferometric synthetic aperture radar (InSAR) proves to be effective for landslides investigation. This study proposes an improved InSAR-based procedure for large-area landslide mapping in loess-hilly areas, including tropospheric-delay correction based on quadtree segmentation and automatic selection of interferograms based on minimum-error boundary. It is tested in Dingbian County in Shaanxi Province, China. More than 200 SAR images were processed and a total of 50 potential loess landslides were detected and mapped. Results show that the landslides are mainly distributed along the river basins and concentrated in areas with elevation ranging from 1450 m to 1650 m, and with slope angles of 10–40°. Then, a total of eight (16%) loess landslides are classified as active ones based on three parameters derived from InSAR-deformation rates: activity index (AI), mean deformation rate, and maximum deformation rate. Moreover, we characterize the segmentation of detected landslides and describe the discrepancy of local topography and deformation rates by coupling the peak in probability-density curves of deformation rates and profiles of the elevation and deformation rates. Finally, correlation between landslide deformation and rainfall is given through wavelet analysis.
1. Introduction
The Loess Plateau, covering an area of approximately 630,000 km2 in northwestern China, is located in the upper and middle reaches of the Yellow River, which occupies the most concentrated loess region in the world [1]. Statistically, one-third of the geohazards in China occurred in the Loess Plateau, including landslides, collapse, ground fissures, and land subsidence [2]. The frequency of landslides on the Loess Plateau is increasing with the influence of human activities and extreme weather conditions [3]. Field investigations revealed that about 12,000 landslides occurred in the Loess Plateau of Shaanxi province with an average density of over four per square kilometer [4]. Loess landslides, one of the severe geological hazards in Loess Plateau, have the special characteristics of small spatial extent, group occurrence, abruptness, and recurrence [5]. Loess mainly forms four types of geomorphological structures: platforms, ridges, dome, and gullies [2]. These structures with steep slopes on their sides make them prone to fall under the gravity and other favorable conditions, such as infiltration of rainfall, irrigation water, and engineering activities [6]. Evidently, fragile slopes are widely distributed on the Loess Plateau, and cause severe economic losses and human casualties. Therefore, it is of great importance to find effective ways of detecting and assessing the stability of loess slopes for disaster prevention and management.
In recent years, InSAR with its unique capability of large coverage and high sensitivity to ground-surface deformation has become an ideal tool for detecting potential landslides and monitoring its deformation history [7]. However, errors of various scales should be considered and corrected when the study area becomes much larger. The measurement accuracy is largely limited by atmospheric noise, especially the topography-correlated component in the mountainous area with large elevation variations, causing poor performance of landslide detection and low accuracy of deformation monitoring. At present, many atmospheric-delay correction methods have been proposed, including external-auxiliary data [8,9], spatio-temporal filtering methods [10], and empirical models between phase and elevation [11]. Therefore, it is essential to select and use the most appropriate method according to the real situation. As the study area is located in the transition zone between Loess Plateau and the southern edge of Mu Us desert, with great topographic differences, the area is subject to long-term denudation, erosion, and accumulation, forming a combination of loess beams, loess mounts, loess ditch, and loess-ravines landform units. So tropospheric-delay correction is one of key problems to obtain a highly accurate deformation result.
On the other hand, along with the development of SAR sensors and accumulation of SAR images, interferograms are generated by setting the maximum thresholds of spatio-temporal baselines. Usually, high-quality interferograms are determined visually in order to obtain reliable deformation results. However, it becomes more time-consuming and less reliable to select high-quality interferograms from thousands to even ten thousand interferograms [12]. Therefore, it is necessary to find an automatic way to determine the high-quality interferograms optimally.
Thirdly, monitoring landslide deformation can help us to better understand spatial zonation, temporal evolution, and possible diving factors [13]. Crippa et al. (2021) developed an automatic approach to characterize the kinematics of each landslide based on the combination of 2D decomposition of InSAR velocity vectors [14]. Some scholars used permanent scatterers (PSInSAR) and SqueeSAR techniques to analyze the activity based on statistical indicators for large landslides and deep-seated gravitational slope deformations (DSGSDs) [15]. Many studies have been conducted on the types and distribution of loess landslides over the whole or a part of the Loess Plateau [4,16,17,18], where InSAR deformation results are not fully considered for loess-landslide-activity assessment.
In this study, we firstly propose a complete InSAR procedure to detect and map potential loess landslides with emphasize on tropospheric-delay correction and automatic-interferograms selection. Then, the activity of all detected loess landslides is evaluated and classified at a regional scale by means of activity index, mean deformation rate, and maximum deformation rate. Finally, spatial kinematics of individual landslide are conducted in terms of the probability-density curves, the longitudinal-slope profiles, and the correlation between rainfall and landslide deformation that is interpreted by wavelet tools.
2. Study Area
Dingbian County, which is located in the northwest of Shaanxi province, China, bordering the Ningxia Hui Autonomous Region to the west, Gansu to the south and Inner Mongolia to the north, is chosen as the study area, as shown in Figure 1. The study area is also situated in the transition zone between Mu Us desert and Loess Plateau in northern Shaanxi. The terrain increases from the north to the south, with elevation varying from 1280 m to 1913 m. The main geomorphic types of the study area include loess platform, loess ridge, and loess knoll, as shown in Figure 1b. The natural landscape of gullies and fragmented terrain are prone to slide under the influence of rainfall and human activities.
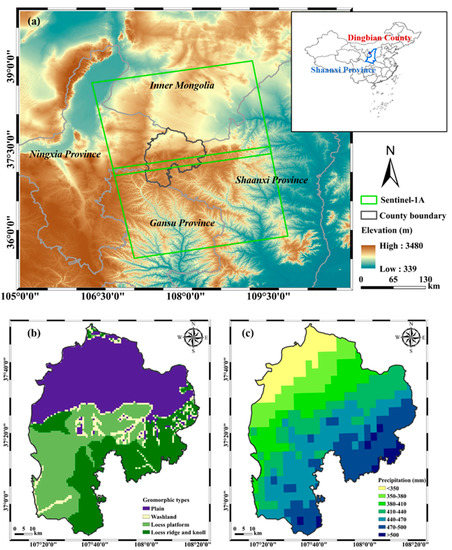
Figure 1.
(a) The study area and the coverage of ascending Sentinel-1A datasets. The background is obtained from the shuttle radar topography mission (SRTM) digital elevation model (DEM), with inset showing the location of the study area in China. (b) Typical geomorphic-types map and (c) annual-average precipitation map of the study area.
The annual average temperature in the study area is 9.3 °C, with a large temperature difference, which corresponds to the typical temperate, semi-arid, and continental monsoon climate. The spatial distribution of the precipitation is less in the north and more in the south, and the annual average precipitation from 2017 to 2020 is shown in Figure 1c. Besides, the annual average precipitation shows alternating changes with uneven temporal distribution within the year. Generally, maximum precipitation is in July and August, and precipitation decreases from September to December.
3. Datasets and Methodology
3.1. Datasets
In order to determine the distribution of potential landslides in Dingbian County and reveal their spatio-temporal characteristics, we used the free Sentinel-1A data of Interferometric Wide (IW) swath mode with spatial resolutions of 5 m in range and 20 m in azimuth. The datasets were acquired from frames 115 and 120 at track 84 with a total of 216 ascending single look complex (SLC) images from January 2018 to November 2021. The ground coverage of the SAR images is illustrated in Figure 1a. In addition, a one arc-second SRTM DEM was employed to generate the topographic factors and remove the topographic-phase components. The optimal-remote-sensing images covering the study area were mainly sourced from the Google Earth platform at spatial resolutions between 0.5 and 8 m.
3.2. Methodology
Figure 2 shows the flowchart of large-area landslides mapping and characterization with InSAR method. Section I is SBAS InSAR processing. All possible interferograms were automatically generated, filtered using an adaptive-filtering algorithm based on previously defined parameters (e.g., four looks in range and one look in azimuth, temporal and spatial baseline thresholds, size of the filter window, coherence index) [19]. Then, interferograms were unwrapped using the minimum cost flow (MCF) algorithm, and the component of stratified atmosphere was removed for each interferogram and the residual-orbital ramp was removed using refined baselines. After the significant phase error were removed, the strategy based on the relative-error boundary was applied to select high-quality interferogram for deformation results. Finally, the average deformation rate for each pixel was subsequently estimated by the weighted averaging of interferograms (i.e., the stacking interferograms method). Followed by the inversion of deformation time series through the least square (LS) criterion or singular value decomposition (SVD) [20], Section Ⅱ is the regional-potential-landslide activity analysis, where an inventory map of potential-loess landslides was generated by combining the deformation results, topographic factors, and optical-remote-sensing images. Then, the spatial distribution of the detected loess landslides was analyzed and the types of loess landslides were classified. Finally, the activity degree of the detected loess landslides was evaluated by three parameters, namely, active index, mean deformation rate, and maximum deformation rate. Followed by the landslide-activity analysis of the detected loess landslides. Section Ⅲ is the spatio-temporal, landslide-kinematics analysis, where the wavelet tools, namely, continuous wavelet transform (CWT), cross wavelet transform (XWT), and wavelet coherence (WTC) were applied to analyze the correlation between periodic kinematics of a landslide and its trigger factors. Additionally, probability curves were used to detect segmentation of typical landslides, and longitudinal slope profiles were applied to recognize the morphological characteristics of landslides.
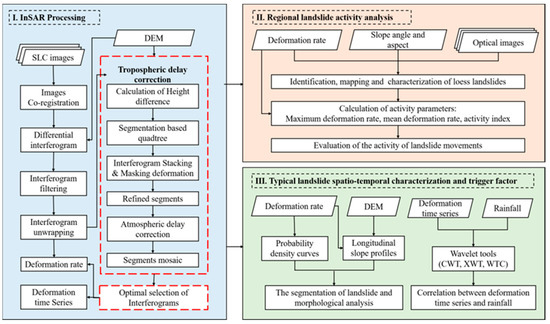
Figure 2.
Flowchart of large-area landslides mapping and characterization.
3.2.1. Tropospheric Delay Correction
It should be noted that two key steps—tropospheric-delay correction and selection of high-quality interferograms—were improved in this study in order to detect small-scale loess landslide over a large area.
In this study, in order to estimate the vertically stratified and tropospheric delay accurately, all the interferograms were segmented into small patches according to height gradient by a quadtree. Only the window with a large height difference, which is larger than a threshold, was divided into four windows. The segmentation process was repeated until the size of the segmented window was smaller than the set-window-size threshold. In this paper, we set the height difference threshold of 400 m and the window size threshold of 500 pixels. To maintain spatial consistency, we set an overlap of 25% window size between adjacent windows. More details about window segmentation can be found in [21,22]. Once window segmentation based on the quadtree was finished, tropospheric-delay correction and deformation inversion were executed for each segment as follows.
Firstly, a quadratic model was used to estimate the tropospheric delay for each segmented window [21]. In order to reduce the influence of decorrelation noise in the phase-based, tropospheric-delay estimation, the pixels of low coherence were masked. Secondly, the linear-deformation rate was preliminarily inverted through stacking-InSAR. Then, the unstable pixels and reference point in each segment were determined. Next, tropospheric delay was re-estimated based on the quadratic model and the pre-determined, unstable pixels were masked during this estimated process. Finally, the results of the segments were merged to form an entire-corrected-unwrapped interferogram. The phases were averaged to merge the overlapping parts of adjacent segments.
We firstly explored the performance of tropospheric-delay corrections on one interferogram of frame 120 from 11 January 2018 to 23 January 2018 in the transition zone with obvious height difference, which presents a spatially varying, elevation-related tropospheric delay, as shown in Figure 3a. The results of corrected tropospheric delay by three methods, namely, linear model (LM), linear model and de-trend method (LM-DT), and quadtree segmentation process (QT-SP), are shown in Figure 3. The standard deviation (STD) of residual-unwrapped phases corrected by LM, LM-DT, and QT-SP methods decreased from 2.033 rad to 1.258 rad, 0.852 rad, and 0.489 rad, respectively. The LM method applied a single-model parameter to the entire interferogram, which is a poor strategy to capture the spatially varying atmospheric states. Therefore, it failed to properly estimate the tropospheric delay and sometimes overfitted tropospheric delay in local areas, so did the LM-DT method. A statistical evaluation was then performed on all interferograms of frame 120 and frame 115. The STD values of all unwrapped phases before and after tropospheric-delay corrections were computed over all the points for each interferogram, as shown in Figure A1 and Table A1.
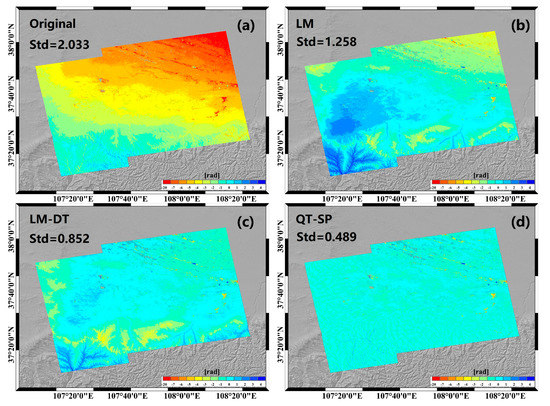
Figure 3.
The unwrapped phase of Sentinel−1A images acquired on 11 January 2018 and 23 January 2018 in the transition zone from southern mountain to northern desert. (a) Original unwrapped phase; (b) atmospheric phase correction by linear model (LM), (c) atmospheric phase correction by linear detrend method (LM−DT) and (d) atmospheric phase correction by quadtree segmentation process (QT−SP).
3.2.2. The Optimization of Interferograms Selection
In order to select high quality interferograms automatically, we applied the method based on relative error boundary theory [22]. After an atmospheric phase error, unwrapped phase error and DEM phase error were corrected from interferograms, and we estimated the time series deformation phases by using the Equation:
where A is the design matrix of the involved linear transformation that is known, X is the unknown vector of deformation rates between two adjacent SAR acquisitions, that is, , and is the vector of the unwrapped phases, which is acquired by the removal of atmospheric-phase error, unwrapped-phase error, and DEM-phase error.
Based on the theory introduced in [22], the relative error boundary of unknown parameter X can be derived from Equation (2):
where k(A) is the condition number of the design matrix A, is the relative error of the input vector of the unwrapped phases.
Decorrelation is the main factor affecting the application of InSAR. Coherence is commonly used to measure the decorrelation of interferograms. Besides, the relation between the variance of phase and coherence can be represented as Equation (3):
where L is the look number. The relative error of the unwrapped interferograms can be approximated with Equation (4):
where is the vector of the average-coherence value. By substituting Equation (4) into Equation (2), we can get:
where the term depends on the deformation norm and system parameters, which can be regarded as a constant. The term stands for the average coherence of the selected interferograms, which measures the quality of the interferograms. is the condition number of the small baseline-network matrix A, which evaluates the robustness of the interferogram network.
Automatic processing of optimal selection for interferograms is illustrated by taking the dataset of Frame 115 as an example, as shown in Figure 4. In addition, Figure A2 shows how the average coherence of interferograms changes with the spatio-temporal baseline. Finally, the result of interferograms optimal selection is presented in Figure 5.
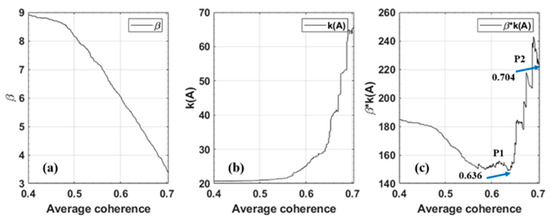
Figure 4.
The process for automatic selection of candidate interferograms. Plots of (a) average coherence β, (b) condition number, (c) upper-error bound vs. the interferometric-average-coherence threshold.
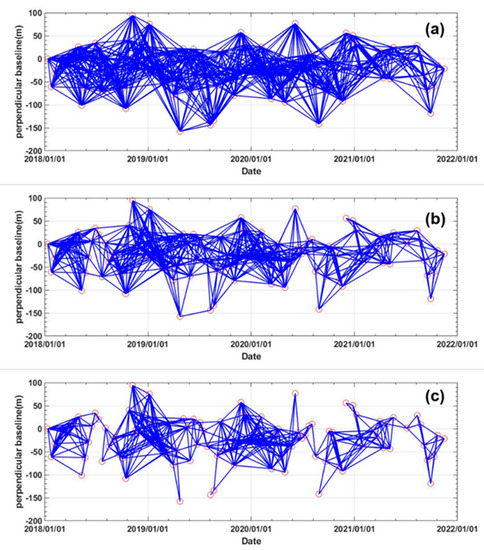
Figure 5.
Distribution of interferograms in a temporal/perpendicular baseline domain. (a) Set of available interferograms generated by setting a maximum temporal baseline separation of 150 days and spatial baseline of ±150 meters. (b) Optimal network of interferograms retrieved by applying the proposed InSAR automatic selection method. (c) Reduced network of interferograms at boundary condition where one single data pair exists that connects the group of interferograms to form a single set of data. Note that (b,c) refer to the condition on minimum average spatial coherence of selected interferograms of 0.636 (P1 in Figure 4) and 0.704 (P2 in Figure 4).
3.2.3. Evaluation of Landslide Activity
The evaluation of landslide activity mainly takes into account three statistical values: (1) activity index, which is defined as the proportion of active pixels for one landslide, i.e., the ratio between the number of active pixels (pixels with deformation rate larger than the given threshold; the absolute value of 20 mm/year) and the total number pixels for one landslide; (2) the mean deformation rate of all pixels for each landslide, which is used to preliminary identify the activeness of surface; and (3) the maximum value of all pixels for each landslide, which is used to estimate the maximum activeness of the landslide body.
Due to morphological structure and the deformation distribution of different failure surfaces, instability in landslides can evolve in different ways. To assess the spatial kinematics of the landslide, the probability density curves were used to demonstrate the deformation rate frequency distributions and spatial zonation, and longitudinal slope curves were used to interpret the segmented failure surface.
3.2.4. Correlation between Landslide Deformation and Rainfall
CWT was used to extract features from individual time series of periodic deformation and daily precipitation, in which positions with high values in the CWT representation presented significant time patterns at particular dates [23]. The relationship between periodic deformation and precipitation was analyzed by using the XWT and WTC tools to combine two individual CWTs. XWT can find regions in time-frequency space where the periodicity intensity of time series has large power, and the phase of the XWT indicates the time lag between two time series [24]. The WTC tool is defined as the coherence between the two CWTs, and it can find regions in time-frequency space where the time series has similar patterns [24].
Wavelet-power spectrum is the energy distribution of the time series for an objective wavelet scale and time domain [25]. The relative phase relationship is presented as within-phase arrows pointing right and anti-phase arrows pointing left [26]. Phase angle represents the phase shift between both time series and indicates the temporal delay, which can be calculated as [26]:
where T is the period of interest.
4. Results
4.1. The Identification of Potential Loess Landslides
The annual-deformation-rate maps in the line-of-sight (LOS) direction derived from the Sentinel-1A datasets of frames 120 and 115 over the study area are shown in Figure 6. Positive deformation rate represents a landslide moving toward the sensor and negative deformation rate indicates movements away from the sensor [27]. The detected loess-landslide zones are outlined with white rectangles in Figure 6, in which small scale, loess landslides are mainly distributed in the southern mountainous areas with deformation rates between −20 mm/year and −60 mm/year. Figure 7 shows the enlarged figures describing the annual deformation rate of four regions. A potential loess landslide inventory map for Dingbian County is generated from the deformation maps, topographic factors, and optical remote sensing images. A total of 50 potential loess landslides are detected and mapped, as shown by the polygons in Figure 6a. According to the unique geological settings of loess covered geomorphology and general landslide classification criteria, the 50 loess landslides are divided into five types: loess slide (54%), loess bedrock bedding slide (36%), loess bedrock interface slide (6%), loess collapse (2%), and loess surface mud flow (2%), as shown in Figure 6b.
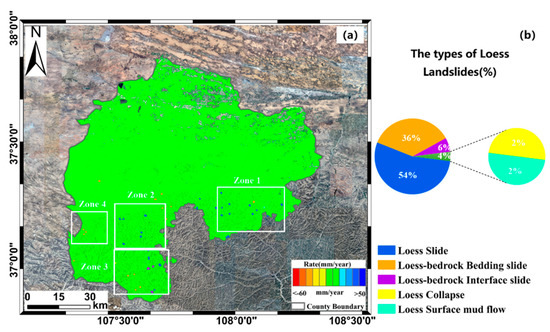
Figure 6.
Annual deformation rate map and the pie chart of loess landslides types in Dingbian County detected by the Sentinel-1A SAR images. The polygons indicate the detected active landslides. (a) The deformation rate map in the line-of-sight (LOS) direction, where white rectangles indicate the detected landslides zones. (b) The pie chart for the loess landslide types in the study area.
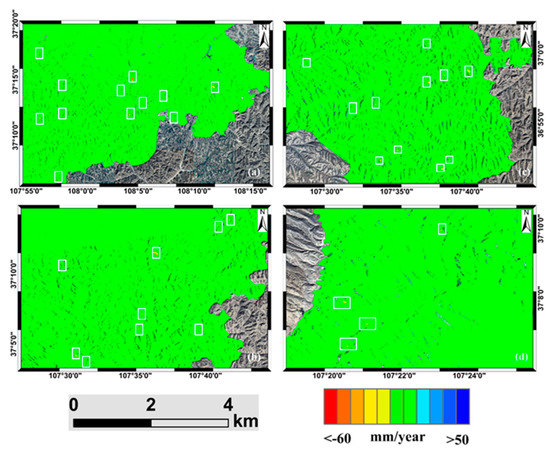
Figure 7.
Enlarged annual-deformation-rate maps of four regions: (a) Zone 1; (b) Zone 2; (c) Zone 3; (d) Zone 4 (marked in Figure 6), where the white rectangles indicate individual landslides.
Loess slide mainly occurr in the slip surface in a paleosol layer within the Malan loess, which are usually a fan-shaped accumulation at the foot of the slope, as shown in Figure 8b(13,14). It can be easily triggered at the sites where many cracks and vertical joints in loess are widely developed [28]. The slip surface of loess-bedrock-bedding slide is mainly composed of bedding planes of the subjacent bedrocks [28], as shown in Figure 8b(2,6). The slope angle is usually less than 45° with obvious scrapes on both sides and bulging at the foot of the slope, and they usually travel a short distance at a slow average velocity. The loess-bedrock interface slides generally develop on the surface with slopes of 10–20°. Loess mudflow generally develop at the edge of loess gullies cut by rivers, as shown in Figure 8b(10). Loess landslides are usually transformed into mudflow under the condition of continuous rain and heavy rainfall due to the loose structure of the Malan loess [29]. Loess collapse mostly occurs in steep slopes larger than 45°, where the vertical fissure of overlying loess is well developed.

Figure 8.
Typical loess landslides shown in deformation maps and optimal remote sensing images. (a) Enlarged deformation rate maps and (b) optical remote sensing images of 16 exemplary landslides. The white lines indicate the boundaries of the detected landslides. The optical-remote- sensing images were the perspectives of a Google Earth image.
4.2. Characteristics of the Detected Loess Landslides
To demonstrate the characteristics of the detected loess landslides, 16 typical loess landslides are highlighted together with the deformation-rate maps (Figure 8a) and the corresponding optical-remote-sensing images (Figure 8b). It can be seen that the surface deformation rates and the corresponding geomorphological features match very well, and the landslide boundary derived from optical-remote-sensing images are based on loess microtopography.
In this study, 50 detected loess landslides are used to reveal their spatial characteristics. The statistical results of topographical factors, including elevation, relative elevation, local topographic relief, and slope angle, are shown in Figure 9. It can be seen from Figure 9a that approximately 76% of the detected loess landslides are distributed at elevations ranging from 1450 m to 1550 m. More than 18% of the loess landslides occur above 1600 m. Moreover, it is obvious that the number of loess landslides increases with the elevation from 1400 m to 1550 m, while the number decreases with the elevation at values above 1550 m. The maximum landslide density should be located at elevations ranging from 1500 m to 1550 m. Figure 9b also indicates that almost all landslides detected (98%) are distributed in areas with a relative elevation of 400 m to 700 m, and the maximum frequency of landslide occurrence is located in the elevation difference of 400 m to 600 m. Figure 9c shows the variation in landslide frequency with a local topographic relief. It indicates that 89% of the detected loess landslides are distributed in areas with a topographic relief of 90 m to 150 m. The highest density of landslides (39%) occurs at reliefs of 120–150 m. The slope angle for the whole study area is divided into six categories. It can be seen from Figure 9d that 89% of the detected loess landslides are distributed in areas with slopes between 10° and 40°, while the maximum number of landslides is distributed in areas where slopes are 20–30°. Moreover, the number of the detected landslides increases alongside the slope angle up to 10–30°, and then decreases as the slope angle increases further.
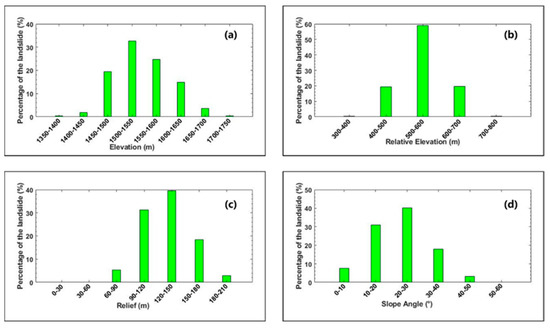
Figure 9.
Statistics of landslide distribution versus (a) elevation; (b) relative elevation; (c) local topographic relief; and (d) slope angle.
4.3. The Activity of Detected Loess Landslides
The activity of the detected loess landslides is comprehensively evaluated in terms of activity index (AI), mean deformation rate, and maximum deformation rate, as shown in Figure 10. Loess landslides showing a low activity index (AI) (smaller than 0.15) are widely distributed in the whole area with a significant proportion of 48% (Figure 10(a2)), while only five landslides (10%) have a high activity index with the values larger than 0.45. Besides, about 30% of the loess landslides show an AI with a value between 0.15 and 0.30, and 12% has an AI value of 0.30 to 0.45. As for the mean deformation rate, we observe that about 64% of the loess landslides show a negative deformation rate between −10 to −15 mm/year, and only 10% show a deformation rate smaller than −10 mm/year (Figure 10(b2)). The faster-moving loess landslides, which are characterized by an average deformation rate of less than −20 mm/year, have a higher activity index as well. Figure 10(c1) shows the spatial distribution of loess landslides classified by maximum deformation rate. As shown in Figure 10(c2), only two landslides (4%) have a maximum deformation rate of lower than −20 mm/year, while the maximum deformation rates of loess landslides in −40–−50 −50–−60, and greater than −60 mm/year account for 10%, 2%, and 4% of the loess landslides, respectively. It can also be seen that about 80% of the loess landslides have a maximum deformation rate between −20 mm/year and −40 mm/year. Finally, the combination of the absolute-mean deformation rate (greater than 20 mm/year), the absolute-maximum deformation rate (greater than 40 mm/year), and the activity index (greater than 0.45) can be considered as evaluation criteria. Accordingly, we draw the conclusion that, eight (16%) loess landslides are active ones and 42 (84%) are inactive ones (Figure 10(d2)).
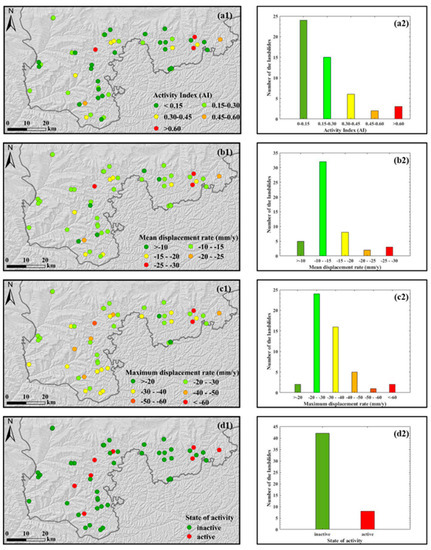
Figure 10.
The spatial distribution of all detected loess landslides is classified by (a1) Activity Index (AI); (b1) Mean deformation rate (mm/y); (c1) maximum deformation rate (mm/y) and (d1) the activity degree, which is evaluated by (a1,b1,c1). The right column, (a2,b2,c2,d2), represent the frequency distribution of the loess landslides.
5. Discussion
5.1. Landslide Spatial Kinematics Analysis
To further demonstrate the spatial kinematics of individual loess landslide, five typical landslides are selected as examples. The activity parameters are shown in Table 1 and the corresponding deformation characteristics are shown in Figure 11. It can be seen from the activity parameters of Table 1 that L1 and L2 can be considered as active landslides. However, the use of statistics derived from deformation rates is only a representative value, which is more suitable to evaluate the activity of landslides at a regional scale. In practice, slope deformation is often characterized by partial zones faster than the main body, resulting in deformation-rate differentiation in the space domain. Therefore, probability-density curves are applied to characterize the internal segmentation of each landslide. Generally, landslides with segmented activity are distinguished by multi-peak velocity distributions (Figure 11(a2,b2,c2)). Conversely, landslide bodies with little damage or lower deformation rates (Figure 11(d1)) exhibit homogeneous displacement fields and unimodal velocity distributions (Figure 11(d2)). In this study, peaks defined as local maxima represent the distribution of a specific cluster of deformation rates. Distinct peaks indicate the occurrence of clearly segmented domains, each characterized by a given rate value and dispersion. In other words, the number of peaks in the probability density curves minus one is the same as the number of active landslide partitions, which can be clearly seen in Figure 11.

Table 1.
Activity parameters of various loess landslides shown in Figure 8. (Unit: mm/year).
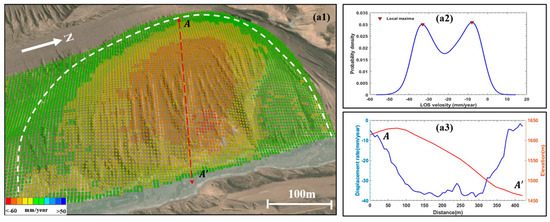
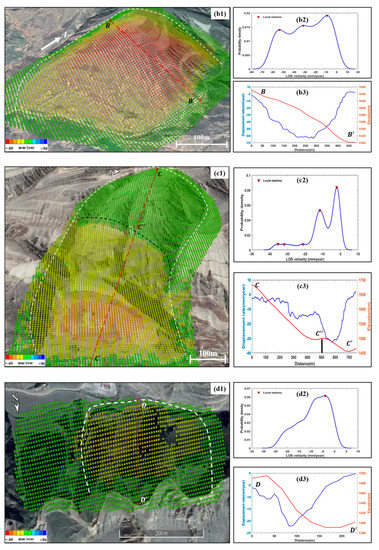
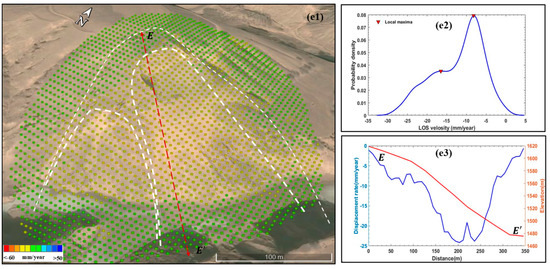
Figure 11.
The spatial distribution characteristics of deformation rates within the typical loess landslides detected (a1,b1,c1,d1,e1), performed by probability-density curves (a2,b2,c2,d2,e2), and slope profiles of deformation rate and elevation (a3,b3,c3,d3,e3). Note that peaks are identified as local maxima of the curves in (a2,b2,c2,d2,e2). The white dashed lines show the outline of the landslides and the red lines indicate the profile of the landslides.
In order to analyze the dynamic and morphological characteristics of landslides, the profile of deformation rate and topographic height along the longitudinal direction of landslide are generated [30], which is shown in the red lines in Figure 11(a1–a5). The longitudinal variation of deformation rate and topographic height within a landslide is basically the result of some different phenomena: the location of failure surface (Figure 11(a3–c3)); the variation of the deformation rate with respect to the LOS direction; the presence of secondary landslides (Figure 11(c3)); and the change of the topographic characteristic along the slope direction (Figure 11(a3–c3)) [31].
As is shown in Figure 11(a3), the main body of the landslide is moving at a steady rate greater than 30 mm/year, and the foot of landslide has a few active pixels with a deformation rate greater than 40 mm/year. It can also be seen that the landslide has a remarkable feature with an average slope of 42°, a width of 420 m, and a height of 176 m. The segmented variation in deformation rate and topography can be clearly seen in Figure 11(c3). The rupture surface of the landslide is located at Point C” in Figure 11(c1,c3). The whole active area of the landslide can be divided into three parts, according to the topography, and its location corresponds to the three dotted lines in Figure 11(c3). The deformation of L2 located on the loess knoll, where the foot of the slope moves slowly and the main body is relatively active, can be seen in Figure 11(b3). The slope of L4 is steeper with a slope angle greater than 50. The deformation rate varies rapidly along the down-slope direction, and there is a collapse phenomenon in the head of L4.
5.2. Landslide Temporal Kinematics Analysis
The relationship between monthly precipitation and landslide deformation is a key aspect for understanding landslide-temporal kinematics. Figure 12a shows the annual deformation rate calculated using the Sentinel-1A images from 11 January 2018 to November 15, 2021, and Figure 12b shows the time series of accumulative deformation, deformation gradient, and periodic deformation against monthly precipitation. It can be seen from Figure 12b that there is a clear cycle in rainfall time series from April to September each year along the whole observation period. The deformation gradient represents the rate of deformation change, where the rate changes abruptly when heavy rainfall occurs.
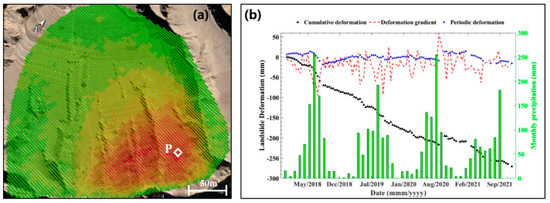
Figure 12.
Relationship between deformation time series and monthly precipitation. (a) Annual deformation rate map from 11 January 2018 to 15 November 2021; (b) the time series of cumulative deformation (in black), deformation gradient (in red), and periodic deformation (in blue) on Point P against monthly precipitation.
The result of wavelet analysis is presented to understand time patterns and the coherence between deformation time series and monthly precipitation, as shown in Figure 13. The CWT power spectra of monthly precipitation and periodic deformation (Figure 13a,b) present two regions of relatively high wavelet power with a period of about 10 months, corresponding to the time interval from April 2018 to December 2020. These regions of high wavelet power correspond to the periodic deformation triggered by seasonal rainfall. The results of XWT cross power spectra, and WTC for periodic deformation and monthly precipitation are shown in Figure 13c,d. Regions of high cross-wavelet spectral power and high coherence are evident in the period of 9 and 12 months. The phase shift indicates time lags from 1.1 to 3.0 months, between landslide deformation and monthly precipitation, in the period of January 2018 to September 2021.
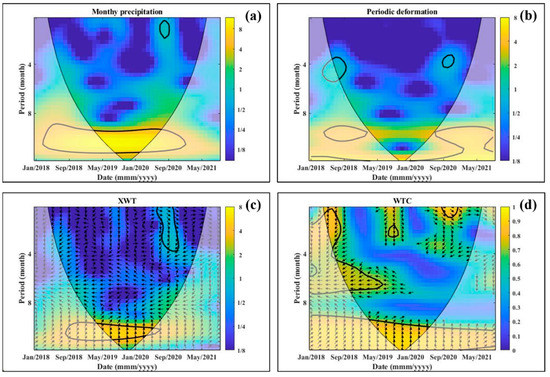
Figure 13.
The relationship between deformation and monthly precipitation. (a) continuous wavelet power (CWT) of monthly precipitation; (b) continuous wavelet power (CWT) of periodic deformation; (c) cross wavelet transform (XWT) and (d) wavelet coherence (WTC) of periodic deformation and monthly precipitation for point P (see Figure 12a). Note that the thick contour designates the 95% significance level and the arrows represent phase relationships.
Rainfall influence on landslide deformation is mainly through reducing the shear strength on the slip surface by increasing pore water and hydrodynamic pressure, and weakening loess-soil stickiness [32]. Rainfall often takes approximately several months to penetrate from the top surface to the saturated layer, which is useful to understand the fact that the accelerate time of landslide deformation often lags behind rainfall [33]. Additionally, the time lag of rainfall landslides is related to rainfall intensity, continuous rainfall, and the geomorphic characteristics of landslides. Therefore, time lag usually stays in a wide range of days and months.
6. Conclusions
This study conducts an early identification and spatio-temporal activity analysis of loess landslides over a wide area using SBAS-InSAR technology. We propose an improved InSAR-based procedure with an emphasis on tropospheric-delay correction based on quadtree segmentation and optimal selection of interferograms based on minimum error boundary. Firstly, we generate a complete-inventory map containing the types and distribution of 50 loess landslides in Dingbian County with Sentinel-1A images based on the proposed procedure. The landslides detected are mainly distributed along the river basins, mostly concentrated in areas with elevation ranging from 1450 m to 1650 m and slope angles of 10–40°.
Secondly, we use three indexes to assess the landslide activity to a certain degree of reliability, including mean deformation rate, maximum deformation rate, and activity index. Accordingly, a total of eight loess landslides are classified as active and the remaining ones are inactive. Additionally, spatial-kinematic behavior is interpreted by means of probability-density curves and slope profiles. Finally, we apply wavelet tools (CWT, XWT and WTC) to recognize the correlation between In SAR deformation and rainfall-triggering factor. This study can provide insights into landslide hazard zonation, and prediction and early warning of similar loess landslides.
Author Contributions
Z.J., C.Z., M.Y., B.W. and X.L. performed the experiments and produced the results. Z.J. drafted the manuscript and C.Z. finalized the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This study is funded by the National Natural Science Foundation of China (Nos. 41929001 and 41874005), this study also is supported by Chang’an University High Performance Computing Platform.
Data Availability Statement
The SAR images acquired by Sentinel-1A were downloaded from the Copernicus Open Access Hub and the NASA Distributed Active Archive Center at the Alaska Satellite Facility (https://earthdata.nasa.gov/eosdis/daacs/asf). The Shuttle Radar Topography Mission (SRTM) DEM with a resolution of about 30 m/pixel were downloaded from the National Aeronautics and Space Administration (https://data.nasa.gov).
Acknowledgments
The authors would like to thank all the reviewers for their valuable suggestions. The Sentinel-1 datasets were provided by the European Space Agency (ESA) freely.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
It is assumed that the phase errors such as orbit error, unwrapping phase error have been suitably corrected in the previous operation, and thus, the STD can be used to measure the effect of tropospheric delay correction. The STD values of the unwrapped phase are decreased by the three methods to different extents, as shown in Figure A1. As for the datasets of frame 120 and frame 115, the LM, LM−DT, QT−SP method had reduced the STD values for all interferograms. As a whole, the QT−SP method has the smallest STD for each interferogram among the three methods. The original STD of interferograms of frame 120 declined by more than 65% after corrections by QT−SP method, as demonstrated in Table A1. For the frame 115 datasets, we obtained similar results, as shown in Figure A1b and listed in Table A1. The original STD of the interferograms declined by more than 57% after corrections by the QT−SP method.
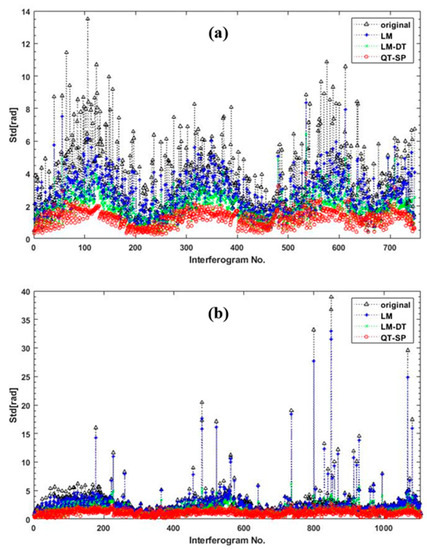
Figure A1.
The STD values of all original unwrapped phases and the ones corrected by three methods for (a) frame 120 and (b) frame 115 Sentinel−1A interferograms.

Table A1.
Statistical evaluation on tropospheric delay corrections of Sentinel−1A datasets from frame 120 and frame 115.
Table A1.
Statistical evaluation on tropospheric delay corrections of Sentinel−1A datasets from frame 120 and frame 115.
| Method | Individual Interferograms of Dataset from Frame 120 | Individual Interferograms of Dataset from Frame 115 | ||
|---|---|---|---|---|
| Number of Reduced Std | Std Mean [rad] | Number of Reduced Std | Std Mean [rad] | |
| No correction | 748 | 3.524 | 1105 | 2.629 |
| LM | 748 | 2.594 | 1105 | 2.319 |
| LM−DT | 748 | 1.840 | 1105 | 1.500 |
| QT−SP | 748 | 1.245 | 1105 | 1.138 |
Appendix B
In the process of interferograms optimal selection, we firstly calculated the corresponding coherence for every generated differential SAR interferogram. And then we did the statistics on how the average coherence of interferograms change with the spatio−temporal baseline, as shown in the Figure A2. Figure A2a shows that the average coherence of interferograms drops with the increase of the temporal baseline; however, the minimum coherence of the SAR data pairs in each time division point remains stable when the temporal baseline is greater than 50 days. Figure A2b shows that the average coherence of the interferograms decreases with the increase of perpendicular baseline. Moreover, we identified the optimal set of SAR interferograms by minimizing the error bound β∙K(A), which is shown as Figure 4. Figure 4a,b present the plots of β, K(A), respectively, versus the average spatial coherence threshold. Figure 4c plots the value of β∙K(A) versus the average coherence threshold. We noted that, the value of β has a small reduction with the increase of the applied threshold on the minimum average spatial coherence, however, the condition number of the design matrix becomes infinite when the number of interferograms is reduced to a certain degree. Finally, the optimal set of interferograms is identified by minimizing the product of β and K(A). As is shown in Figure 4c, it can be shown that there exist two cases, P1 and P2, which correspond to the optimal boundary of the interferogram network and the maximum coherence that can satisfy the connectivity of the interferogram network, respectively. In the case of point P1, an optimal network of 758 interferograms is determined in which P1 corresponds to the threshold of 0.636. Figure 5b shows the distribution of the selected optimal interferometric SAR data pairs in the spatio−temporal baseline domain. P2 highlights the limit case when only one single interferogram exists to connect the interferometric network. This case corresponds to the coherence threshold of 0.704 and a set of 539 differential SAR interferograms, which can be shown in Figure 5c.
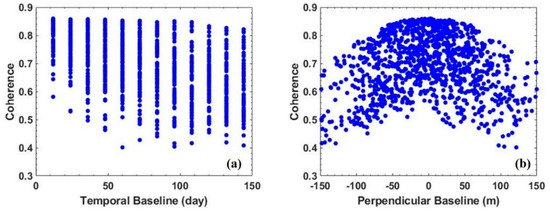
Figure A2.
Scatter plot of average coherence of candidate interferograms vs. their (a) temporal and (b) perpendicular baseline, respectively.
Appendix C
It can be seen from Table A1 that the LM method has the worst results for this study. Therefore, in the following analysis, we mainly compare the results of the deformation rates which obtained through QT−SP and LM−DT method. The resulting deformation rates of frame 120 and frame 115 using QT−SP and LM−DT method are shown in the left columns and right columns of Figure A3 and Figure A4, respectively. The standard deviation of deformation rate can be used as an index to measure the inner precision of linear deformation rate and the uncertainty of the measurement because many factors can lead to an increase in the standard deviation of deformation rate, such as nonlinear deformation, decorrelation noise and atmospheric delay. The original deformation rate is corrected to varying degrees by the above methods. It can be seen that the standard deviation of LS−DT is relatively larger in the areas over the valleys with significant topographic relief. The linear deformation rates from LS−DT method still have an obvious correlation with the topography in some areas. The phenomenon shows that it is difficult to accurately estimate the topography−related atmospheric delay using a phase−based correction model with a fixed parameters in a large−scale region.
The deformation rates are statistically evaluated. For the SAR dataset from frame 120, the standard deviation value of QT−SP method (mean of 0.8mm/year) is generally lower than that from LM−DT method (mean of 1.4mm/year). A smaller standard deviation value indicates a lower noise level, making it more reliable to find unstable slopes with small deformation. In addition, the two methods show similar results in Sentinel−1A datasets of frame 115 and the QT−SP method keeps the better performance, as shown in Figure A4. That is, QT−SP improves the average inner precision of the linear deformation rate by about 70% over LM−DT. The larger standard deviations are generally caused by the environmental characteristics in this study area. We enlarged the local area marked by the red pentacle in Figure A4a, b showing the effect of deformation rate before and after the tropospheric delay corrections. Theoretically, it is more favorable to identify landslides when most slope deformation rate is close to zero except for landslides.
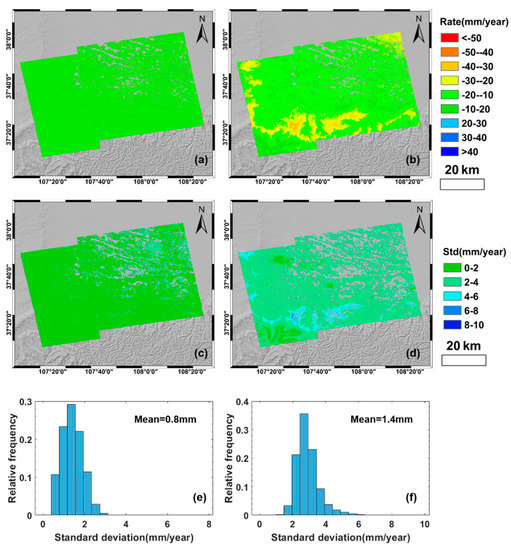
Figure A3.
A comparative results of SAR datasets from frame 120 for deformation rate (a,b), standard deviation of the deformation rate (c,d) and histogram of the standard deviation (e,f) for two processing methodologies: QT−SP and LM−DT. The left column shows QT−SP results; the right column shows LM−DT results. Note that the results in both columns are based on the corresponding interferogram network selected by the method proposed in Section 3.2.2.
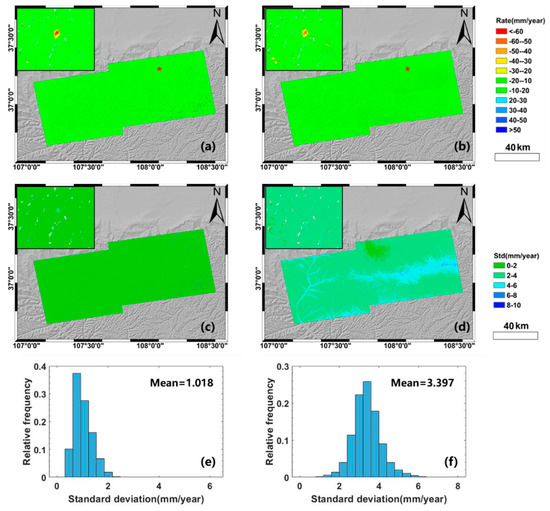
Figure A4.
A comparative results of SAR datasets from frame 115 for deformation rate (a,b), standard deviation of the deformation rate (c,d) and histogram of the standard deviation (e,f) for two processing methodologies: QT−SP and LM−DT. The left column shows QT−SP results; the right column shows LM−DT results. Note that the results in both columns are based on the corresponding interferogram network selected by point P1 in Figure 4, and the red pentacle indicates the enlarged area.
References
- Wang, L.; Shao, M.; Wang, Q.; Gale, W.J. Historical changes in the environment of the Chinese Loess Plateau. Environ. Sci. Policy 2006, 9, 675–684. [Google Scholar] [CrossRef]
- Zhuang, J.; Peng, J.; Wang, G.; Javed, I.; Wang, Y.; Li, W. Distribution and characteristics of landslide in Loess Plateau: A case study in Shaanxi province. Eng. Geol. 2018, 236, 89–96. [Google Scholar] [CrossRef]
- Derbyshire, E. Geological hazards in loess terrain, with particular reference to the loess regions of China. Earth-Sci. Rev. 2001, 54, 231–260. [Google Scholar] [CrossRef]
- Peng, J.; Wang, S.; Wang, Q.; Zhuang, J.; Huang, W.; Zhu, X.; Leng, Y.; Ma, P. Distribution and genetic types of loess landslides in China. J. Asian Earth Sci. 2019, 170, 329–350. [Google Scholar] [CrossRef]
- Duan, Z.; Cheng, W.-C.; Peng, J.-B.; Wang, Q.-Y.; Chen, W. Investigation into the triggering mechanism of loess landslides in the south Jingyang platform, Shaanxi province. Bull. Eng. Geol. Environ. 2018, 78, 4919–4930. [Google Scholar] [CrossRef]
- Li, T.; Wang, C.; Li, P. Loess Deposit and Loess Landslides on the Chinese Loess Plateau. In Progress of Geo-Disaster Mitigation Technology in Asia; Environmental Science and Engineering Book Series; Springer: Berlin/Heidelberg, Germany, 2013; pp. 235–261. [Google Scholar] [CrossRef]
- Shi, X.; Xu, Q.; Zhang, L.; Zhao, K.; Dong, J.; Jiang, H.; Liao, M. Surface displacements of the Heifangtai terrace in Northwest China measured by X and C-band InSAR observations. Eng. Geol. 2019, 259, 105181. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Onn, F.; Zebker, H.A. Correction for interferometric synthetic aperture radar atmospheric phase artifacts using time series of zenith wet delay observations from a GPS network. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, L.; Liao, M.; Gong, J. Improved correction of seasonal tropospheric delay in InSAR observations for landslide deformation monitoring. Remote Sens. Environ. 2019, 233, 111370. [Google Scholar] [CrossRef]
- Liao, M.; Jiang, H.; Wang, Y.; Wang, T.; Zhang, L. Improved topographic mapping through high-resolution SAR interferometry with atmospheric effect removal. ISPRS J. Photogramm. Remote Sens. 2013, 80, 72–79. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, Q.; Pepe, A.; Mastro, P.; Zhao, C.; Lu, Z.; Zhu, W.; Yang, C.; Zhang, J. Analysis of Groundwater Depletion/Inflation and Freeze–Thaw Cycles in the Northern Urumqi Region with the SBAS Technique and an Adjusted Network of Interferograms. Remote Sensing 2021, 13, 2144. [Google Scholar] [CrossRef]
- Meng, Q.; Xu, Q.; Wang, B.; Li, W.; Peng, Y.; Peng, D.; Qi, X.; Zhou, D. Monitoring the regional deformation of loess landslides on the Heifangtai terrace using the Sentinel-1 time series interferometry technique. Nat. Hazards 2019, 98, 485–505. [Google Scholar] [CrossRef]
- Crippa, C.; Valbuzzi, E.; Frattini, P.; Crosta, G.B.; Spreafico, M.C.; Agliardi, F. Semi-automated regional classification of the style of activity of slow rock-slope deformations using PS InSAR and SqueeSAR velocity data. Landslides 2021, 18, 2445–2463. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.B.; Rossini, M.; Allievi, J. Activity and kinematic behaviour of deep-seated landslides from PS-InSAR displacement rate measurements. Landslides 2018, 15, 1053–1070. [Google Scholar] [CrossRef]
- Meng, Q.; Confuorto, P.; Peng, Y.; Raspini, F.; Bianchini, S.; Han, S.; Liu, H.; Casagli, N. Regional Recognition and Classification of Active Loess Landslides Using Two-Dimensional Deformation Derived from Sentinel-1 Interferometric Radar Data. Remote Sens. 2020, 12, 1541. [Google Scholar] [CrossRef]
- Xu, Y.; Allen, M.B.; Zhang, W.; Li, W.; He, H. Landslide characteristics in the Loess Plateau, northern China. Geomorphology 2020, 359, 107150. [Google Scholar] [CrossRef]
- Li, Y.; Mo, P. A unified landslide classification system for loess slopes: A critical review. Geomorphology 2019, 340, 67–83. [Google Scholar] [CrossRef]
- Liang, J.; Dong, J.; Zhang, S.; Zhao, C.; Liu, B.; Yang, L.; Yan, S.; Ma, X. Discussion on InSAR Identification Effectivity of Potential Landslides and Factors That Influence the Effectivity. Remote Sens. 2022, 14, 1952. [Google Scholar] [CrossRef]
- Kang, Y.; Zhao, C.; Zhang, Q.; Lu, Z.; Li, B. Application of InSAR Techniques to an Analysis of the Guanling Landslide. Remote Sens. 2017, 9, 1046. [Google Scholar] [CrossRef]
- Kang, Y.; Lu, Z.; Zhao, C.; Xu, Y.; Kim, J.-w.; Gallegos, A.J. InSAR monitoring of creeping landslides in mountainous regions: A case study in Eldorado National Forest, California. Remote Sens. Environ. 2021, 258, 112400. [Google Scholar] [CrossRef]
- Pepe, A. Multi-Temporal Small Baseline Interferometric SAR Algorithms: Error Budget and Theoretical Performance. Remote Sens. 2021, 13, 557. [Google Scholar] [CrossRef]
- Tomás, R.; Li, Z.; Lopez-Sanchez, J.M.; Liu, P.; Singleton, A. Using wavelet tools to analyse seasonal variations from InSAR time-series data: A case study of the Huangtupo landslide. Landslides 2015, 13, 437–450. [Google Scholar] [CrossRef]
- Ikuemonisan, F.E.; Ozebo, V.C.; Olatinsu, O.B. Investigation of Sentinel-1-derived land subsidence using wavelet tools and triple exponential smoothing algorithm in Lagos, Nigeria. Environ. Earth Sci. 2021, 80, 722. [Google Scholar] [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Tomás, R.; Pastor, J.L.; Béjar-Pizarro, M.; Bonì, R.; Ezquerro, P.; Fernández-Merodo, J.A.; Guardiola-Albert, C.; Herrera, G.; Meisina, C.; Teatini, P.; et al. Wavelet analysis of land subsidence time-series: Madrid Tertiary aquifer case study. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 353–359. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Handwerger, A.L.; Agram, P.; Kirschbaum, D.B. InSAR-based detection method for mapping and monitoring slow-moving landslides in remote regions with steep and mountainous terrain: An application to Nepal. Remote Sens. Environ. 2020, 249, 111983. [Google Scholar] [CrossRef]
- Xu, L.; Dai, F.; Tu, X.; Tham, L.G.; Zhou, Y.; Iqbal, J. Landslides in a loess platform, North-West China. Landslides 2013, 11, 993–1005. [Google Scholar] [CrossRef]
- Wang, G.; Li, T.; Xing, X.; Zou, Y. Research on loess flow-slides induced by rainfall in July 2013 in Yan’an, NW China. Environ. Earth Sci. 2014, 73, 7933–7944. [Google Scholar] [CrossRef]
- Zhao, C.; Kang, Y.; Zhang, Q.; Lu, Z.; Li, B. Landslide Identification and Monitoring along the Jinsha River Catchment (Wudongde Reservoir Area), China, Using the InSAR Method. Remote Sens. 2018, 10, 993. [Google Scholar] [CrossRef]
- Li, L.; Lan, H.; Strom, A. Automatic generation of landslide profile for complementing landslide inventory. Geomat. Nat. Hazards Risk 2020, 11, 1000–1030. [Google Scholar] [CrossRef]
- Wang, H.; Sun, P.; Zhang, S.; Han, S.; Li, X.; Wang, T.; Guo, Q.; Xin, P. Rainfall-induced landslide in loess area, Northwest China: A case study of the Changhe landslide on September 14, 2019, in Gansu Province. Landslides 2020, 17, 2145–2160. [Google Scholar] [CrossRef]
- Gu, T.; Wang, J.; Lin, H.; Xue, Q.; Sun, B.; Kong, J.; Sun, J.; Wang, C.; Zhang, F.; Wang, X. The Spatiotemporal Relationship between Landslides and Mechanisms at the Heifangtai Terrace, Northwest China. Water 2021, 13, 3275. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).