DOA Estimation under GNSS Spoofing Attacks Using a Coprime Array: From a Sparse Reconstruction Viewpoint
Abstract
1. Introduction
- We suggest a coprime array-based method from a sparse reconstruction perspective to estimate the DOA of GNSS signals in the spoofing environment.
- The scheme combines virtual array interpolation with the proposed off-grid error compensation technology to provide better DOA estimation performance, which is beneficial to subsequent spoofing detection and suppression.
- Our approach not only does not need to know the number of incident GNSS signals in advance, but also can estimate the DOAs of spoofing and real signals before receiver despreading.
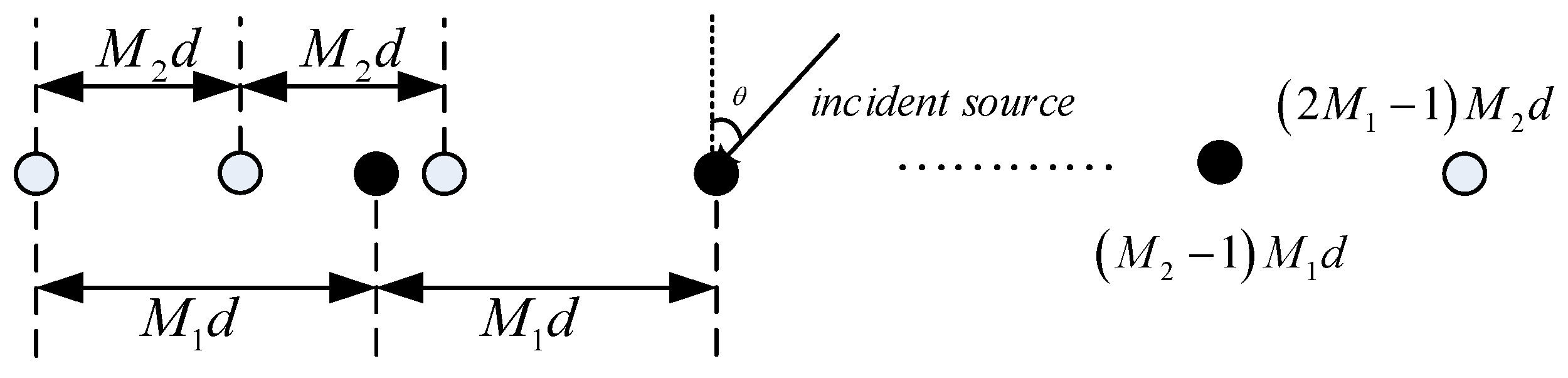
2. Signal Model
3. Proposed DOA Estimation Method under a Spoofing Attack
3.1. Noise Component Suppression
3.2. Array Interpolation and Matrix Recovery
3.3. Off-Grid DOA Estimation
3.4. Performance Analysis
4. Simulation Results
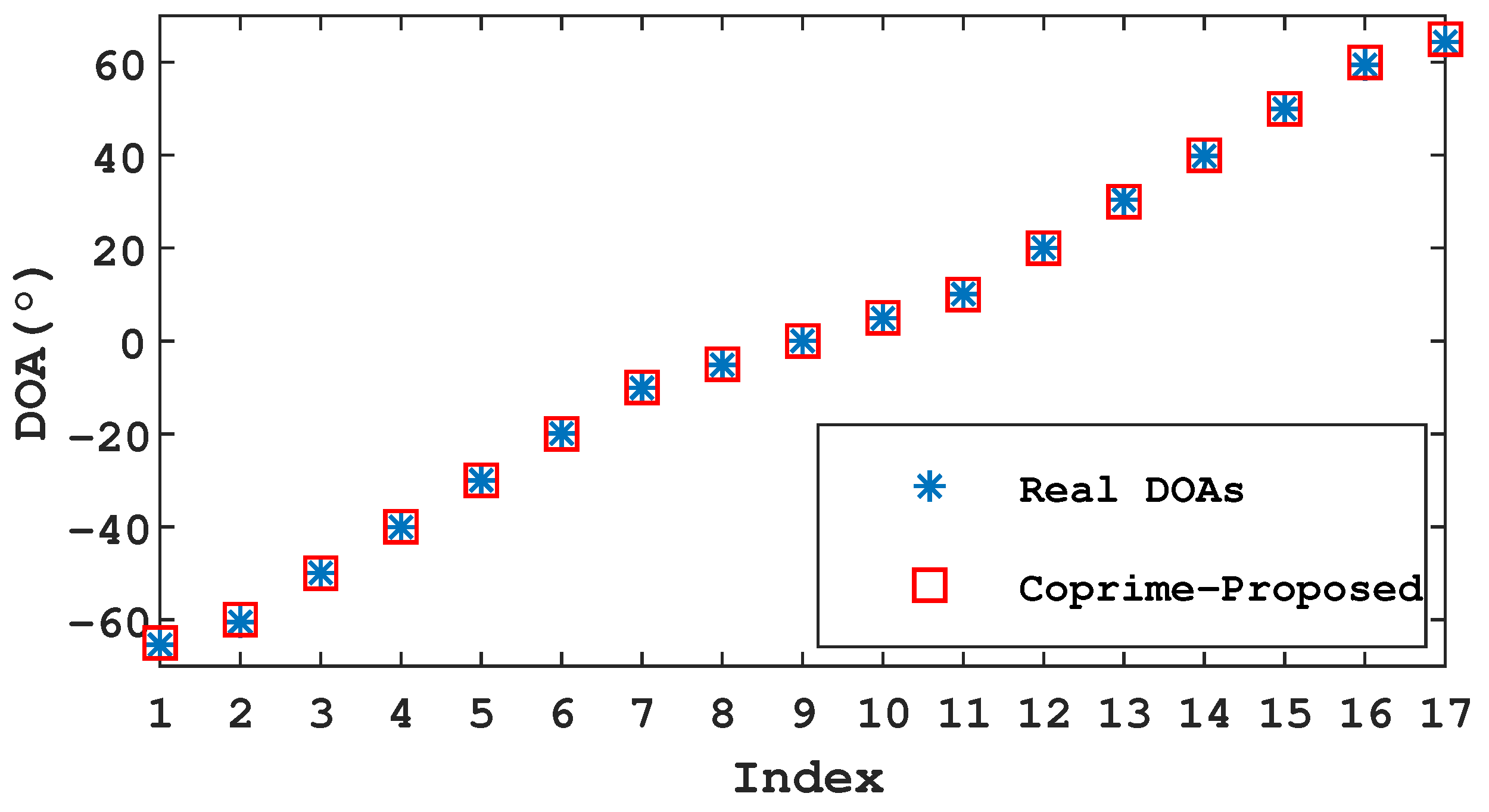
4.1. DOF Comparison
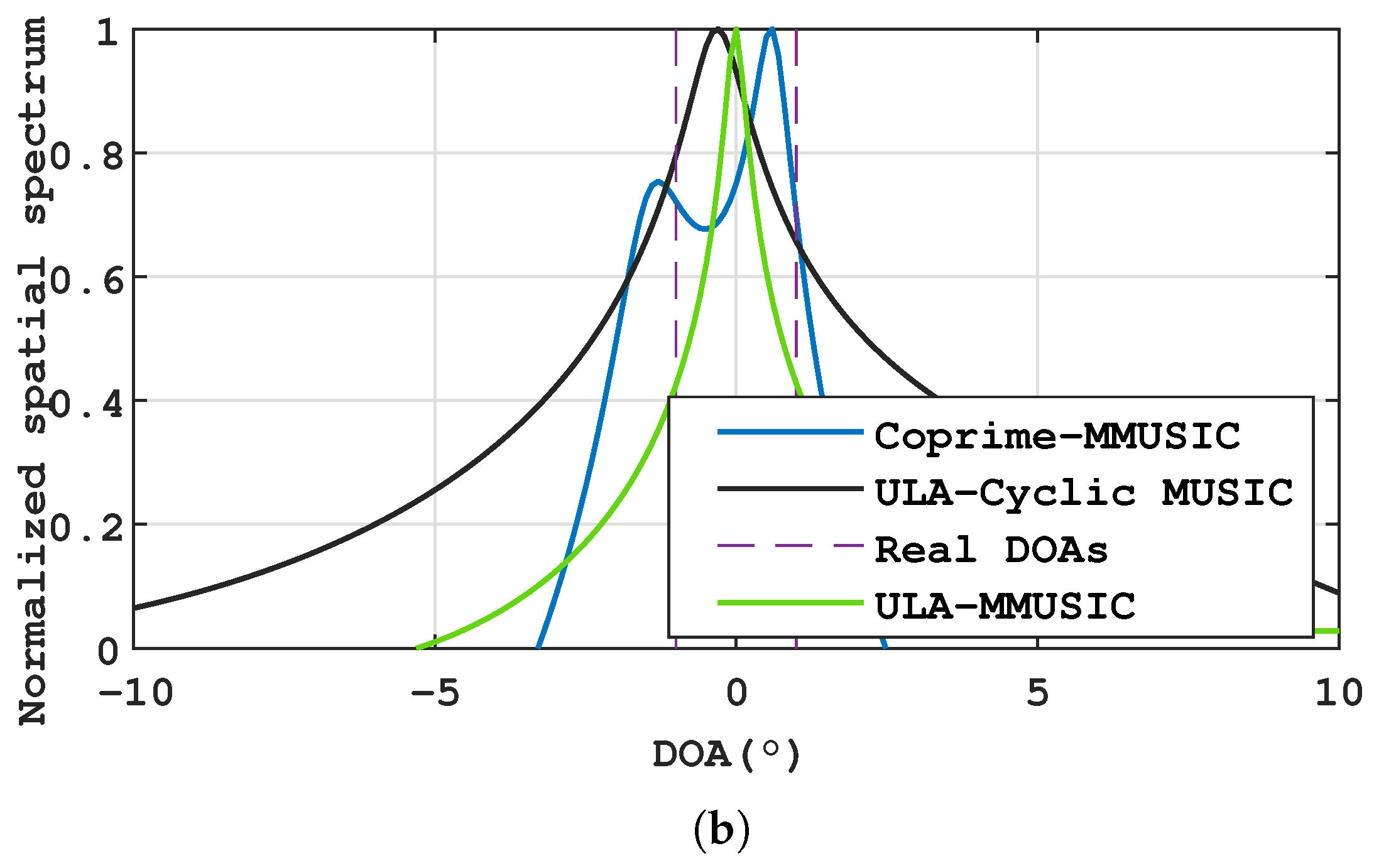
4.2. Resolution Comparison
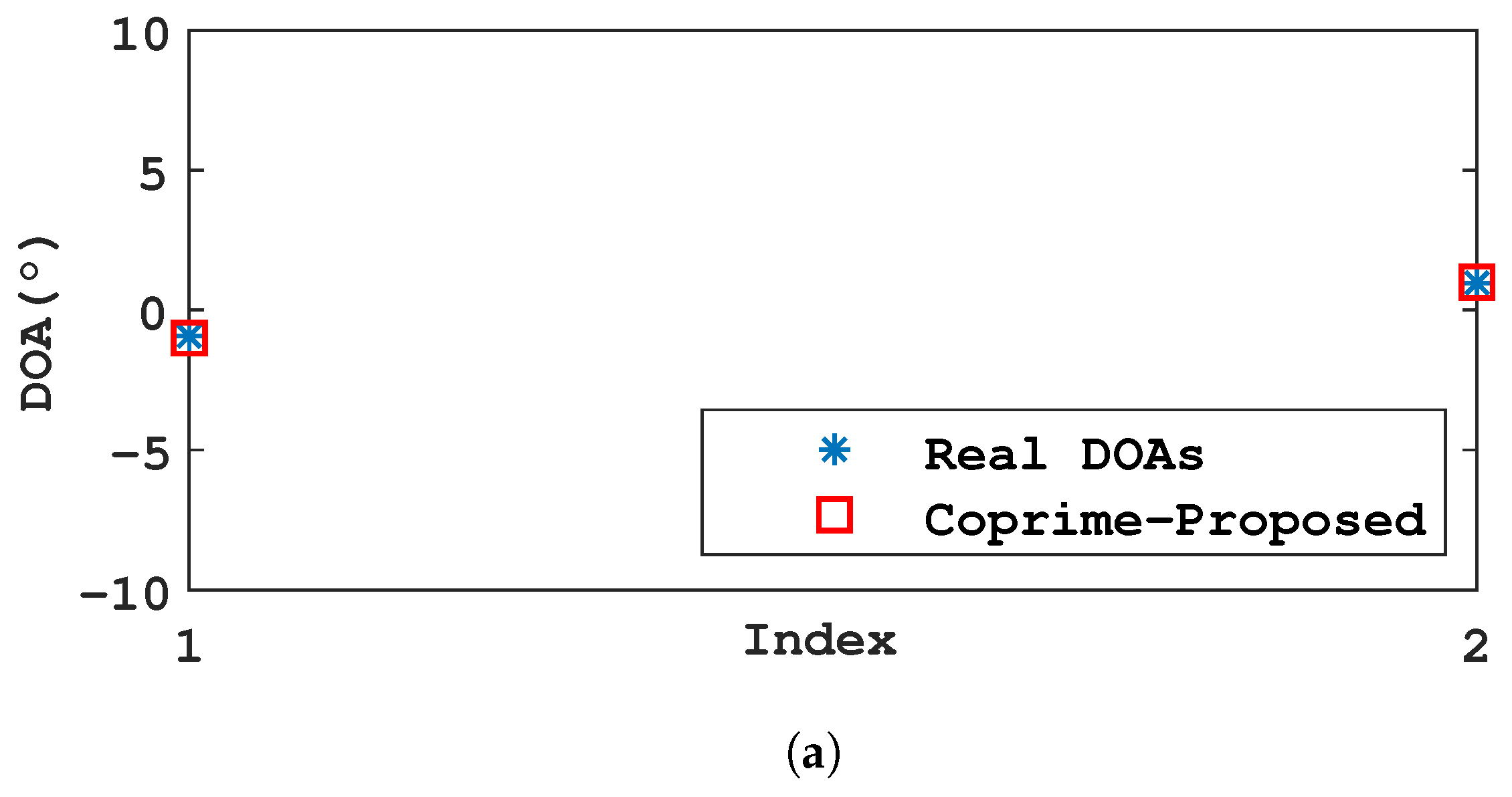
4.3. Accuracy Comparison
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wei, X.; Wang, Y.; Sun, C. PerDet: Machine-Learning-Based UAV GPS Spoofing Detection Using Perception Data. Remote Sens. 2022, 14, 4925. [Google Scholar] [CrossRef]
- Psiaki, M.L.; Humphreys, T.E. GNSS Spoofing and Detection. Proc. IEEE 2016, 104, 1258–1270. [Google Scholar] [CrossRef]
- Meng, L.; Yang, L.; Yang, W.; Zhang, L. A Survey of GNSS Spoofing and Anti-Spoofing Technology. Remote Sens. 2022, 14, 4826. [Google Scholar] [CrossRef]
- Broumandan, A.; Jafarnia-Jahromi, A.; Daneshmand, S.; Lachapelle, G. Overview of Spatial Processing Approaches for GNSS Structural Interference Detection and Mitigation. Proc. IEEE 2016, 104, 1246–1257. [Google Scholar] [CrossRef]
- Jain, H.; Lo, S.; Chen, Y.H.; Rothmaier, F.; Powell, J.D. Accommodating direction ambiguities in direction of arrival based gnss spoof detection. In Proceedings of the ION 2019 Pacific PNT Meeting, Honolulu, HI, USA, 8–11 April 2019; pp. 274–289. [Google Scholar]
- Zhang, J.; Cui, X.; Xu, H.; Lu, M. A two-stage interference suppression scheme based on antenna array for GNSS jamming and spoofing. Sensors 2019, 19, 3870. [Google Scholar] [CrossRef]
- Appel, M.; Konovaltsev, A.; Meurer, M. Robust spoofing detection and mitigation based on direction of arrival estimation. In Proceedings of the 28th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2015), Dana Point, CA, USA, 26–28 January 2015; pp. 3335–3344. [Google Scholar]
- Xu, G.; Shen, F.; Amin, M.; Wang, C. DOA classification and CCPM-PC based GNSS spoofing detection technique. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 389–396. [Google Scholar]
- Shi, J.; Wen, F.; Liu, Y.; Liu, Z.; Hu, P. Enhanced and Generalized Coprime Array for Direction of Arrival Estimation. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–12. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, H.; Wen, F.Q.; Shi, J.P. PARAFAC Estimators for Coherent Targets in EMVS-MIMO Radar with Arbitrary Geometry. Remote Sens. 2022, 14, 2905. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; He, J.; Truong, T.K. 2D-DOD and 2D-DOA Estimation Using Sparse L-Shaped EMVS-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–7. [Google Scholar] [CrossRef]
- Zhao, Y.; Shen, F.; Zhou, D. A Spoofing Detection Algorithm Based on Coprime Array for GNSS Receiver. In Proceedings of the China Satellite Navigation Conference (CSNC 2021) Proceedings, Nanchang, China, 22–25 May 2021; pp. 387–396. [Google Scholar]
- Pal, P.; Vaidyanathan, P.P. A Grid-Less Approach to Underdetermined Direction of Arrival Estimation via Low Rank Matrix Denoising. IEEE Signal Process. Lett. 2014, 21, 737–741. [Google Scholar] [CrossRef]
- Qi, B.; Wang, W.; Wang, B. Off-Grid Compressive Channel Estimation for mm-Wave Massive MIMO with Hybrid Precoding. IEEE Commun. Lett. 2019, 23, 108–111. [Google Scholar] [CrossRef]
- Amin, M.; Sun, W. A novel interference suppression scheme for global navigation satellite systems using antenna array. IEEE J. Sel. Areas Commun. 2005, 23, 999–1012. [Google Scholar] [CrossRef]
- Sun, W.; Amin, M.G. A self-coherence anti-jamming GPS receiver. IEEE Trans. Signal Process. 2005, 53, 3910–3915. [Google Scholar] [CrossRef]
- Kou, J.; Li, M.; Jiang, C. Robust Direction-of-Arrival Estimation for Coprime Array in the Presence of Miscalibrated Sensors. IEEE Access 2020, 8, 27152–27162. [Google Scholar] [CrossRef]
- Fan, X.; Zhou, C.; Gu, Y.; Shi, Z. Toeplitz Matrix Reconstruction of Interpolated Coprime Virtual Array for DOA Estimation. In Proceedings of the 2017 IEEE 85th Vehicular Technology Conference (VTC Spring), Sydney, Australia, 4–7 June 2017; pp. 1–5. [Google Scholar]
- Paik, J.W.; Hong, W.; Lee, J.H. Direction-of-Departure and Direction-of-Arrival Estimation Algorithm Based on Compressive Sensing: Data Fitting. Remote Sens. 2020, 12, 2773. [Google Scholar] [CrossRef]
- Luo, J.; Zhang, Y.; Yang, J.; Zhang, D.; Zhang, Y.; Zhang, Y.; Huang, Y.; Jakobsson, A. Online Sparse DOA Estimation Based on Sub–Aperture Recursive LASSO for TDM–MIMO Radar. Remote Sens. 2022, 14, 2133. [Google Scholar] [CrossRef]
- McCloud, M.; Scharf, L. A new subspace identification algorithm for high-resolution DOA estimation. IEEE Trans. Antennas Propag. 2002, 50, 1382–1390. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-Arrival Estimation for Coprime Array via Virtual Array Interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]


| Parameter | Setting |
|---|---|
| Intermediate frequency | MHz |
| Sampling frequency | MHz |
| Data length | 20 ms |
| Samples in each chip | 37 |
| SNRau | dB |
| Noise bandwidth | 2 MHz |
| Regularization parameter | 1 |
| Predefined grid interval | |
| Maximum iteration number | 1000 |
| Extended coprime array | , |
| Sat1 | Sat2 | Sat3 | Sat4 | Sat5 | Sat6 | Sat7 | Sat8 | Sat9 | Sat10 | Sat11 | Sat12 | Sat13 | Sat14 | Sat15 | Sat16 | Spoofing | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PRN | 2 | 3 | 5 | 6 | 8 | 10 | 12 | 13 | 15 | 16 | 18 | 19 | 21 | 22 | 26 | 29 | |
| DOA |
| Sat1 | Spoofing | |
|---|---|---|
| PRN | 1 | |
| DOA |
| Sat1 | Sat2 | Sat3 | Sat4 | Spoofing | |
|---|---|---|---|---|---|
| PRN | 2 | 5 | 8 | 19 | |
| DOA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Shen, F.; Qi, B.; Meng, Z. DOA Estimation under GNSS Spoofing Attacks Using a Coprime Array: From a Sparse Reconstruction Viewpoint. Remote Sens. 2022, 14, 5944. https://doi.org/10.3390/rs14235944
Zhao Y, Shen F, Qi B, Meng Z. DOA Estimation under GNSS Spoofing Attacks Using a Coprime Array: From a Sparse Reconstruction Viewpoint. Remote Sensing. 2022; 14(23):5944. https://doi.org/10.3390/rs14235944
Chicago/Turabian StyleZhao, Yuqing, Feng Shen, Biqing Qi, and Zhen Meng. 2022. "DOA Estimation under GNSS Spoofing Attacks Using a Coprime Array: From a Sparse Reconstruction Viewpoint" Remote Sensing 14, no. 23: 5944. https://doi.org/10.3390/rs14235944
APA StyleZhao, Y., Shen, F., Qi, B., & Meng, Z. (2022). DOA Estimation under GNSS Spoofing Attacks Using a Coprime Array: From a Sparse Reconstruction Viewpoint. Remote Sensing, 14(23), 5944. https://doi.org/10.3390/rs14235944








