Plant Density Estimation Using UAV Imagery and Deep Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Acquisition
2.1.1. Study Area
2.1.2. Field Sampling
2.1.3. UAV Flight Campaigns
2.2. Image Preparation and Postprocessing
2.2.1. Image Allocation
2.2.2. Image Splitting and Heatmap Assembling
2.2.3. Image Annotation
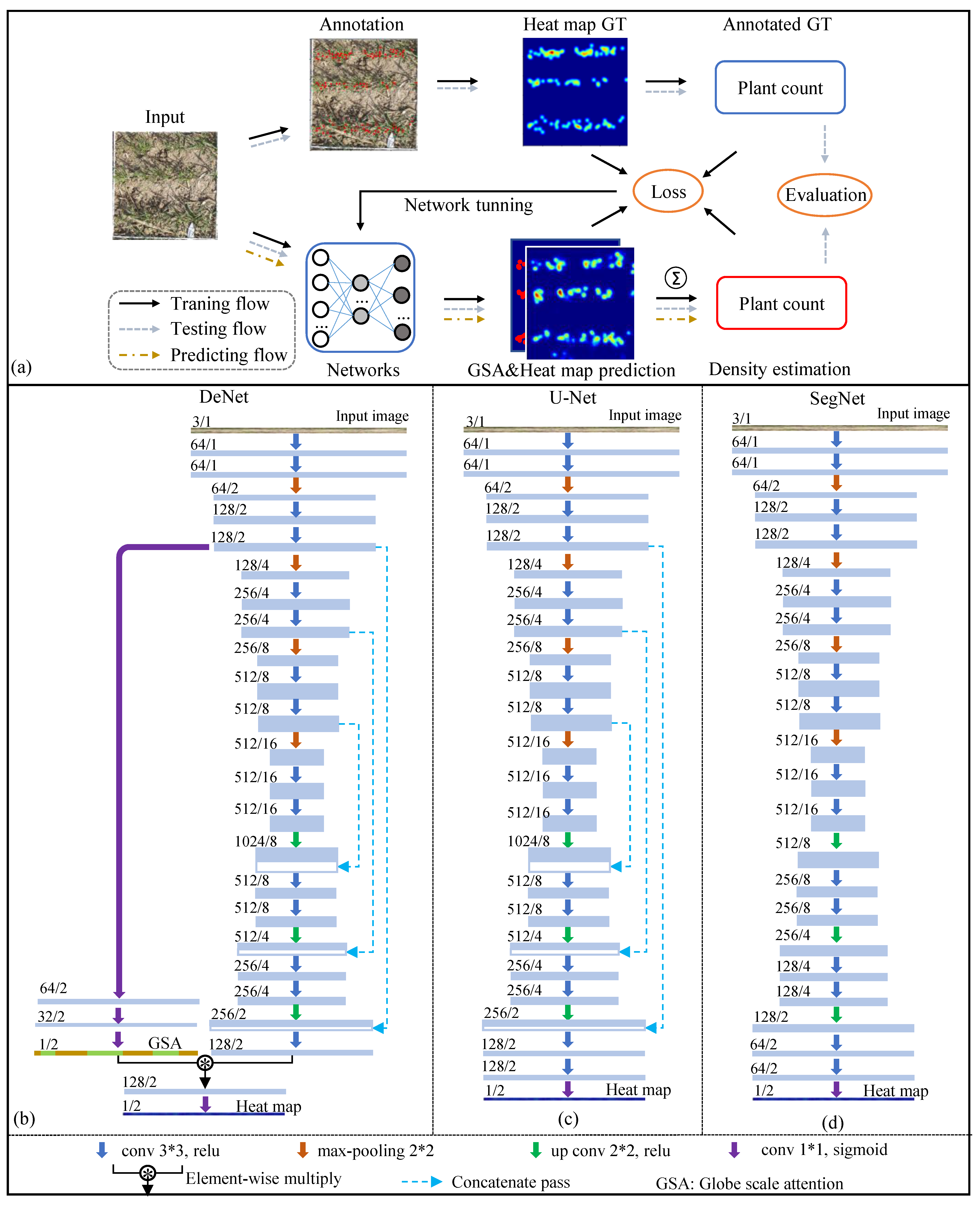
2.3. Deep Learning Models
2.3.1. Network Architecture
2.3.2. Gaussian Heatmap
2.3.3. Loss Function
2.3.4. Evaluation Criteria
2.3.5. Running Environment
3. Experiments and Results
3.1. Model Validation
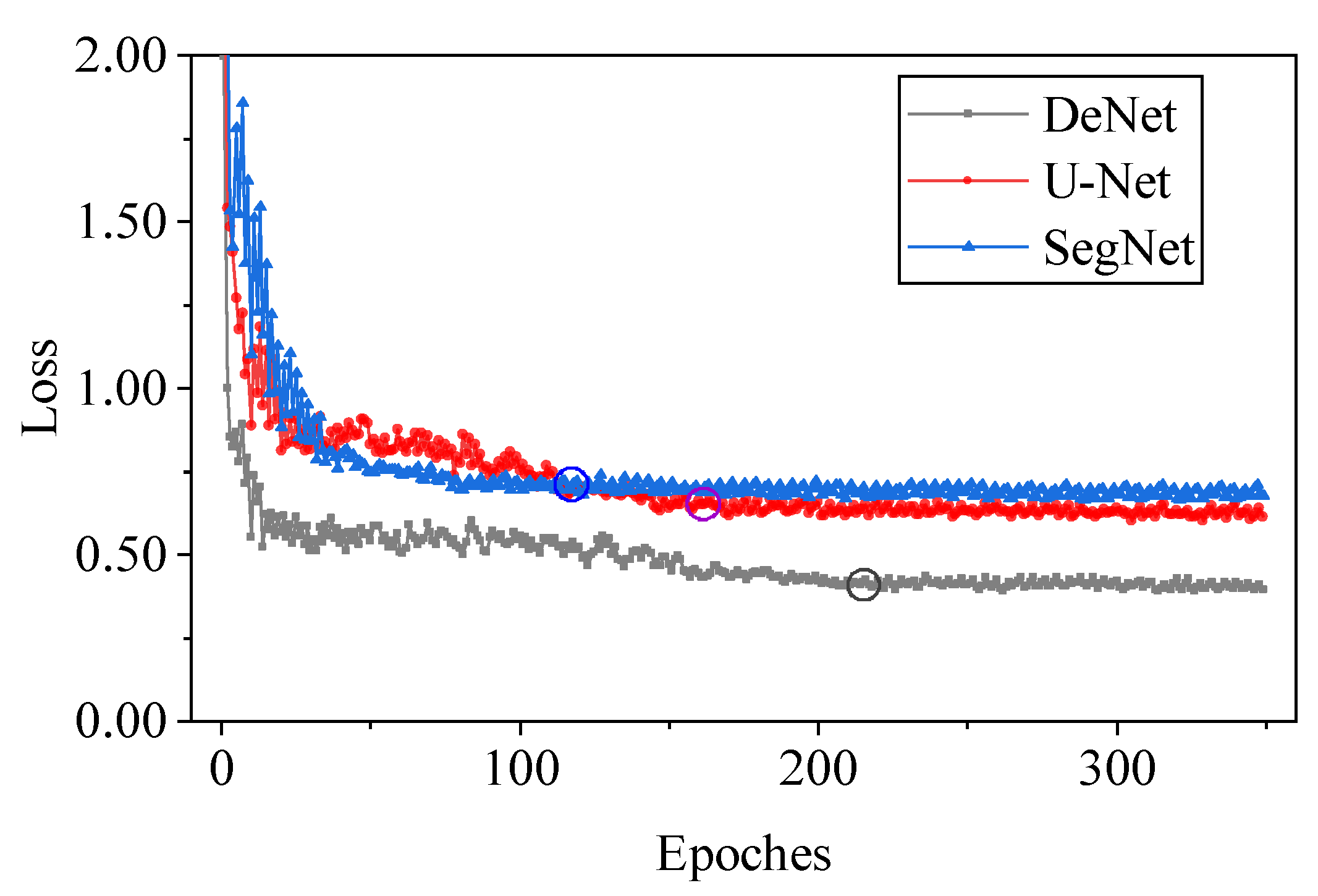
3.1.1. Comparison of Different Networks
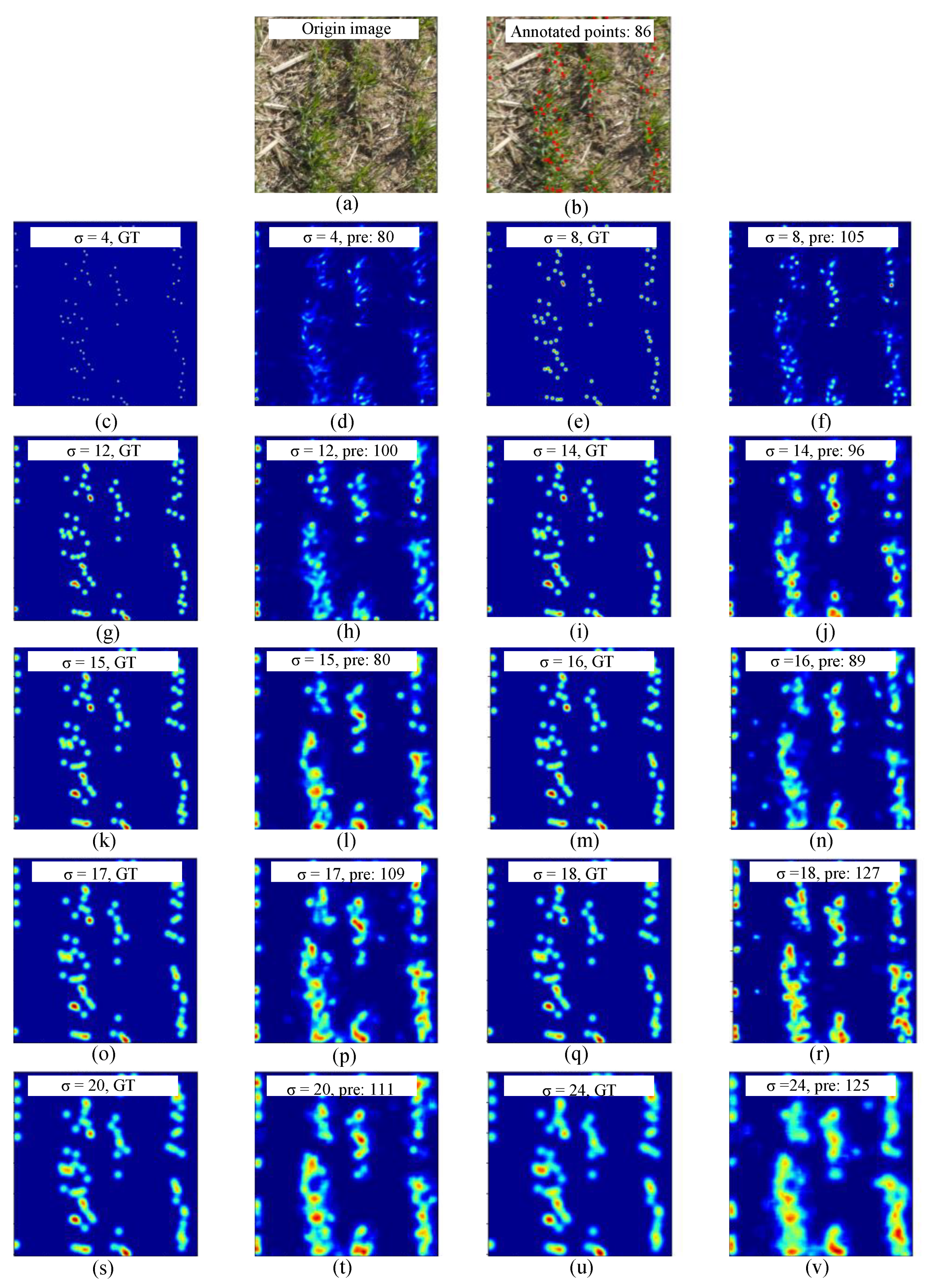
3.1.2. Sensitivity Analysis on Sigma
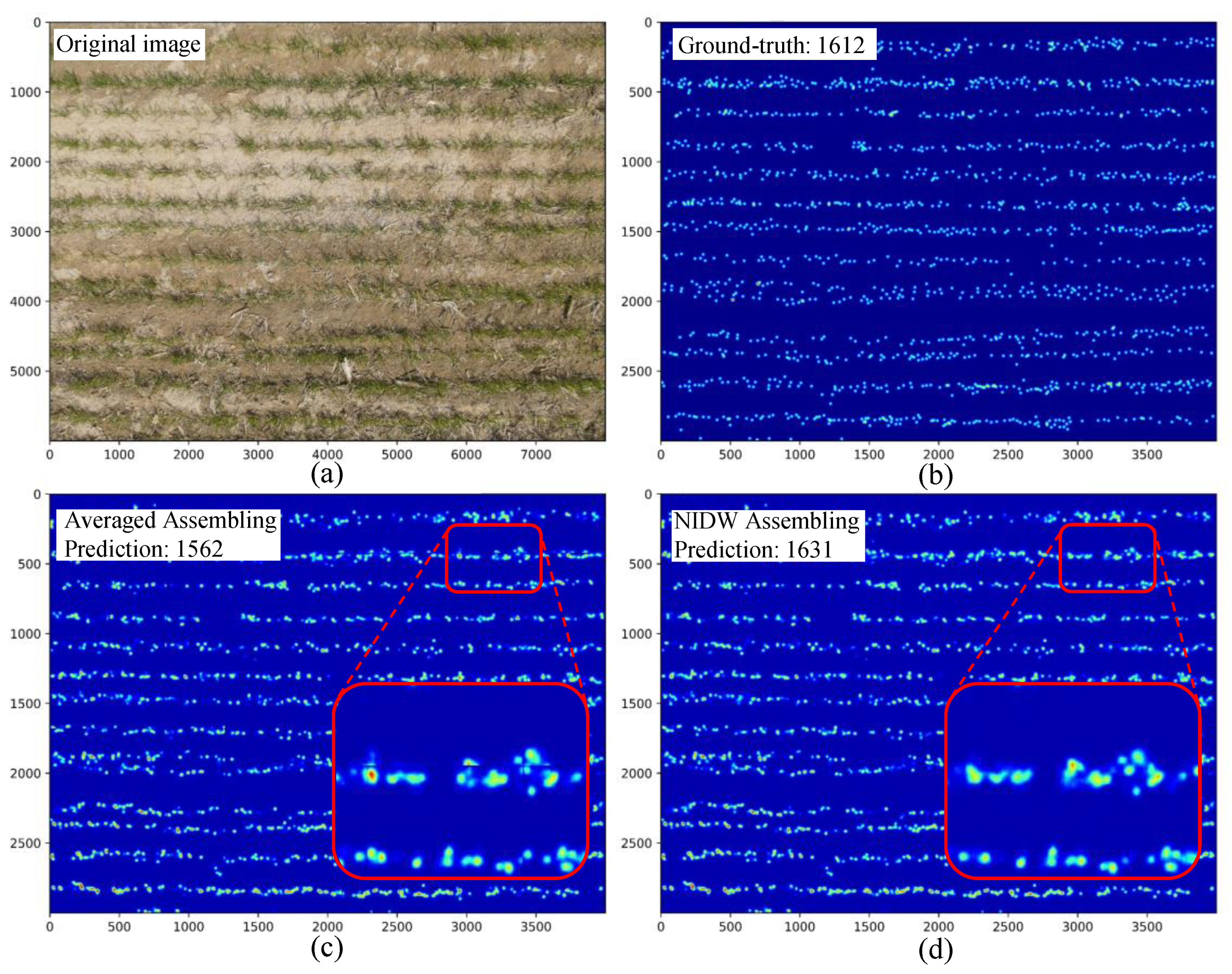
3.1.3. Heatmap Assembling
3.2. Model Test
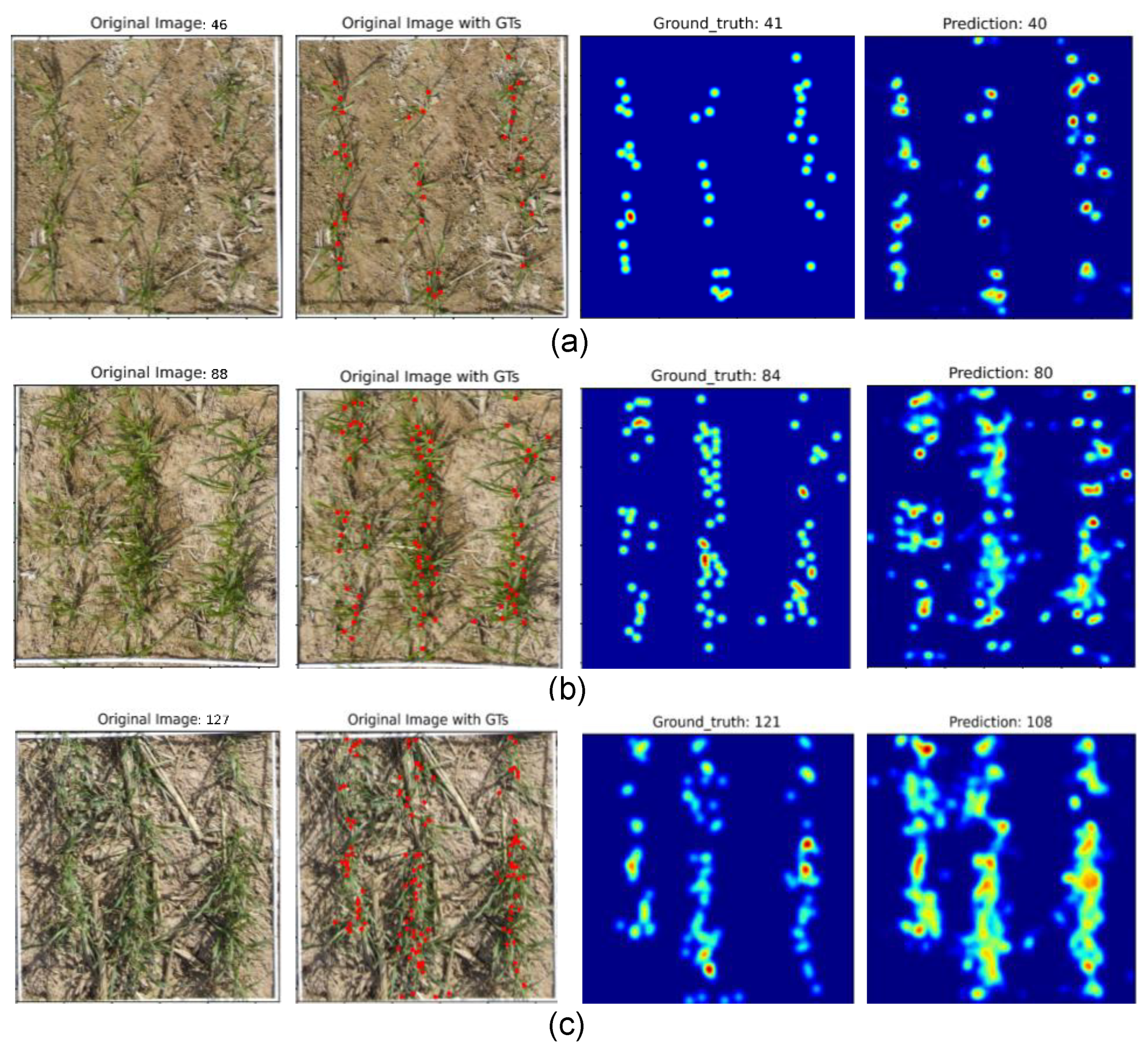
3.2.1. Field-Sampling-Based Plant Density Estimation
3.2.2. Density Level Impact on Model Performance
3.2.3. Impacts of Zenith Angle on Model Performance
4. Discussion
4.1. Research Contributions
4.2. Potential Future Works
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.; Baret, F.; Andrieu, B.; Burger, P.; Hemmerlé, M. Estimation of wheat plant density at early stages using high resolution imagery. Front. Plant Sci. 2017, 8, 739. [Google Scholar] [CrossRef]
- Liu, S.; Baret, F.; Allard, D.; Jin, X.; Andrieu, B.; Burger, P.; Hemmerlé, M.; Comar, A. A method to estimate plant density and plant spacing heterogeneity: Application to wheat crops. Plant Methods 2017, 13, 1–11. [Google Scholar] [CrossRef]
- Finch-Savage, W.E.; Bassel, G.W. Seed vigour and crop establishment: Extending performance beyond adaptation. J. Exp. Bot. 2016, 67, 567–591. [Google Scholar] [CrossRef]
- Karayel, D. Performance of a modified precision vacuum seeder for no-till sowing of maize and soybean. Soil Tillage Res. 2009, 104, 121–125. [Google Scholar] [CrossRef]
- Cowley, R.B.; Luckett, D.J.; Moroni, J.S.; Diffey, S. Use of remote sensing to determine the relationship of early vigour to grain yield in canola (Brassica napus L.) germplasm. Crop Pasture Sci. 2014, 65, 1288. [Google Scholar] [CrossRef]
- Zhang, D.; Luo, Z.; Liu, S.; Li, W.; Wei, T.; Dong, H. Effects of deficit irrigation and plant density on the growth, yield and fiber quality of irrigated cotton. F. Crop. Res. 2016, 197, 200–231. [Google Scholar] [CrossRef]
- Ren, T.; Liu, B.; Lu, J.; Deng, Z.; Li, X.; Cong, R. Optimal plant density and N fertilization to achieve higher seed yield and lower N surplus for winter oilseed rape (Brassica napus L.). F. Crop. Res. 2017, 204, 199–207. [Google Scholar] [CrossRef]
- Bai, Y.; Nie, C.; Wang, H.; Cheng, M.; Liu, S.; Yu, X.; Shao, M.; Wang, Z.; Wang, S.; Tuohuti, N.; et al. A fast and robust method for plant count in sunflower and maize at different seedling stages using high-resolution UAV RGB imagery. Precis. Agric. 2022, 23, 1720–1742. [Google Scholar] [CrossRef]
- Jin, X.; Zarco-Tejada, P.J.; Schmidhalter, U.; Reynolds, M.P.; Hawkesford, M.J.; Varshney, R.K.; Yang, T.; Nie, C.; Li, Z.; Ming, B.; et al. High-Throughput Estimation of Crop Traits: A Review of Ground and Aerial Phenotyping Platforms. IEEE Geosci. Remote Sens. Mag. 2021, 9, 200–231. [Google Scholar] [CrossRef]
- Mhango, J.K.; Harris, W.E.; Monaghan, J.M. Relationships between the spatio-temporal variation in reflectance data from the sentinel-2 satellite and potato (Solanum tuberosum l.) yield and stem density. Remote Sens. 2021, 13, 4371. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, C.; Paterson, A.H.; Robertson, J.S. DeepSeedling: Deep convolutional network and Kalman filter for plant seedling detection and counting in the field. Plant Methods 2019, 15, 141. [Google Scholar] [CrossRef]
- Lu, H.; Liu, L.; Li, Y.N.; Zhao, X.M.; Wang, X.Q.; Cao, Z.G. TasselNetV3: Explainable Plant Counting with Guided Upsampling and Background Suppression. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4700515. [Google Scholar] [CrossRef]
- Jin, X.; Liu, S.; Baret, F.; Hemerlé, M.; Comar, A. Estimates of plant density of wheat crops at emergence from very low altitude UAV imagery. Remote Sens. Environ. 2017, 198, 105–114. [Google Scholar] [CrossRef]
- Oh, S.; Chang, A.; Ashapure, A.; Jung, J.; Dube, N.; Maeda, M.; Gonzalez, D.; Landivar, J. Plant counting of cotton from UAS imagery using deep learning-based object detection framework. Remote Sens. 2020, 12, 2981. [Google Scholar] [CrossRef]
- Osco, L.P.; dos Santos de Arruda, M.; Gonçalves, D.N.; Dias, A.; Batistoti, J.; de Souza, M.; Gomes, F.D.G.; Ramos, A.P.M.; de Castro Jorge, L.A.; Liesenberg, V.; et al. A CNN approach to simultaneously count plants and detect plantation-rows from UAV imagery. ISPRS J. Photogramm. Remote Sens. 2021, 174, 1–17. [Google Scholar] [CrossRef]
- Mhango, J.K.; Harris, E.W.; Green, R.; Monaghan, J.M. Mapping potato plant density variation using aerial imagery and deep learning techniques for precision agriculture. Remote Sens. 2021, 13, 2705. [Google Scholar] [CrossRef]
- Valente, J.; Sari, B.; Kooistra, L.; Kramer, H.; Mücher, S. Automated crop plant counting from very high-resolution aerial imagery. Precis. Agric. 2020, 21, 1366–1384. [Google Scholar] [CrossRef]
- Shrestha, D.S.; Steward, B.L. Automatic corn plant population measurement using machine vision. Trans. Am. Soc. Agric. Eng. 2003, 46, 559–565. [Google Scholar] [CrossRef]
- Liu, T.; Wu, W.; Chen, W.; Sun, C.; Zhu, X.; Guo, W. Automated image-processing for counting seedlings in a wheat field. Precis. Agric. 2016, 17, 392–406. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, J.; Yang, C.; Zhou, G.; Ding, Y.; Shi, Y.; Zhang, D.; Xie, J.; Liao, Q. Rapeseed seedling stand counting and seeding performance evaluation at two early growth stages based on unmanned aerial vehicle imagery. Front. Plant Sci. 2018, 9, 1362. [Google Scholar] [CrossRef]
- Wu, F.; Wang, J.; Zhou, Y.; Song, X.; Ju, C.; Sun, C.; Liu, T. Estimation of Winter Wheat Tiller Number Based on Optimization of Gradient Vegetation Characteristics. Remote Sens. 2022, 14, 1338. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, C.; Song, H.; Hoffmann, W.C.; Zhang, D.; Zhang, G. Evaluation of an airborne remote sensing platform consisting of two consumer-grade cameras for crop identification. Remote Sens. 2016, 8, 257. [Google Scholar] [CrossRef]
- Banerjee, B.P.; Sharma, V.; Spangenberg, G.; Kant, S. Machine learning regression analysis for estimation of crop emergence using multispectral uav imagery. Remote Sens. 2021, 13, 2918. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Kitano, B.T.; Mendes, C.C.T.; Geus, A.R.; Oliveira, H.C.; Souza, J.R. Corn Plant Counting Using Deep Learning and UAV Images. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1–5. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Machefer, M.; Lemarchand, F.; Bonnefond, V.; Hitchins, A.; Sidiropoulos, P. Mask R-CNN refitting strategy for plant counting and sizing in uav imagery. Remote Sens. 2020, 12, 3015. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar] [CrossRef]
- Longnecker, N.; Kirby, E.J.M.; Robson, A. Leaf Emergence, Tiller Growth, and Apical Development of Nitrogen-Dificient Spring Wheat. Crop Sci. 1993, 33, 154–160. [Google Scholar] [CrossRef]
- Maas, E.V.; Lesch, S.M.; Francois, L.E.; Grieve, C.M. Tiller development in salt-stressed wheat. Crop Sci. 1994, 34, 1594–1603. [Google Scholar] [CrossRef]
- Rodríguez, D.; Andrade, F.H.; Goudriaan, J. Effects of phosphorus nutrition on tiller emergence in wheat. Plant Soil 1999, 209, 283–295. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, X.; Ma, Q.; Li, F.; Tao, R.; Zhu, M.; Li, C.; Zhu, X.; Guo, W.; Ding, J. Tiller fertility is critical for improving grain yield, photosynthesis and nitrogen efficiency in wheat. J. Integr. Agric. 2022, 21. [Google Scholar] [CrossRef]
- Bastos, L.M.; Carciochi, W.; Lollato, R.P.; Jaenisch, B.R.; Rezende, C.R.; Schwalbert, R.; Vara Prasad, P.V.; Zhang, G.; Fritz, A.K.; Foster, C.; et al. Winter Wheat Yield Response to Plant Density as a Function of Yield Environment and Tillering Potential: A Review and Field Studies. Front. Plant Sci. 2020, 11, 54. [Google Scholar] [CrossRef] [PubMed]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9351, pp. 234–241. ISBN 978-3-319-24573-7. [Google Scholar]
- Peterson, C.M.; Klepper, B.; Rickman, R.W. Tiller Development at the Coleoptilar Node in Winter Wheat 1. Agron. J. 1982, 74, 781–784. [Google Scholar] [CrossRef]
- NVIDIA Developer CUDA. Available online: https://developer.nvidia.com/cuda-toolkit (accessed on 5 September 2022).
- Peng, J.; Wang, D.; Liao, X.; Shao, Q.; Sun, Z.; Yue, H.; Ye, H. Wild animal survey using UAS imagery and deep learning: Modified Faster R-CNN for kiang detection in Tibetan Plateau. ISPRS J. Photogramm. Remote Sens. 2020, 169, 364–376. [Google Scholar] [CrossRef]
- Russell, B.C.; Torralba, A.; Murphy, K.P.; Freeman, W.T. LabelMe: A Database and Web-Based Tool for Image Annotation. Int. J. Comput. Vis. 2008, 77, 157–173. [Google Scholar] [CrossRef]
- Karen, S.; Andrew, Z. Very deep convolutional networks for large-scale image recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Hossain, M.A.; Hosseinzadeh, M.; Chanda, O.; Wang, Y. Crowd counting using scale-aware attention networks. In Proceedings of the 2019 IEEE winter conference on applications of computer vision (WACV), Waikoloa Village, HI, USA, 7–11 January 2019; pp. 1280–1288. [Google Scholar] [CrossRef]
- Sam, D.B.; Surya, S.; Babu, R.V. Switching convolutional neural network for crowd counting. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 4031–4039. [Google Scholar] [CrossRef]
- Sindagi, V.A.; Patel, V.M. Generating High-Quality Crowd Density Maps Using Contextual Pyramid CNNs. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1879–1888. [Google Scholar] [CrossRef]
- Bendali-Braham, M.; Weber, J.; Forestier, G.; Idoumghar, L.; Muller, P.-A. Recent trends in crowd analysis: A review. Mach. Learn. Appl. 2021, 4, 100023. [Google Scholar] [CrossRef]
- Munea, T.L.; Jembre, Y.Z.; Weldegebriel, H.T.; Chen, L.; Huang, C.; Yang, C. The Progress of Human Pose Estimation: A Survey and Taxonomy of Models Applied in 2D Human Pose Estimation. IEEE Access 2020, 8, 133330–133348. [Google Scholar] [CrossRef]
- Duan, K.; Bai, S.; Xie, L.; Qi, H.; Huang, Q.; Tian, Q. CenterNet: Keypoint triplets for object detection. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, South Korea, 27–28 October 2019; pp. 6568–6577. [Google Scholar] [CrossRef]
- Keras Google Group. Available online: https://keras.io/ (accessed on 8 September 2022).
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
- Fischer, R.A.; Moreno Ramos, O.H.; Ortiz Monasterio, I.; Sayre, K.D. Yield response to plant density, row spacing and raised beds in low latitude spring wheat with ample soil resources: An update. F. Crop. Res. 2019, 232, 95–105. [Google Scholar] [CrossRef]
- Liu, T.; Zhao, Y.; Wu, F.; Wang, J.; Chen, C.; Zhou, Y.; Ju, C.; Huo, Z.; Zhong, X.; Liu, S.; et al. The estimation of wheat tiller number based on UAV images and gradual change features (GCFs). Precis. Agric. 2022, 23, 1–22. [Google Scholar] [CrossRef]
- Che, Y.; Wang, Q.; Zhou, L.; Wang, X.; Li, B.; Ma, Y. The effect of growth stage and plant counting accuracy of maize inbred lines on LAI and biomass prediction. Precis. Agric. 2022, 23, 1–27. [Google Scholar] [CrossRef]
- Mills, S.; McLeod, P. Global seamline networks for orthomosaic generation via local search. ISPRS J. Photogramm. Remote Sens. 2013, 75, 101–111. [Google Scholar] [CrossRef]



| Dataset | Quadrat | Full Image | Patch | Patch Size | Usage |
|---|---|---|---|---|---|
| Training | No | 85 | 2550 | 1200 × 1200 | Model training |
| Validation | No | 15 | 945 | ~1200 × 1200 | Model validation |
| Test | Yes | 270 | 270 | ~1200 to 1300 | Model test |
| Model | Time | GT | PR | MAE | RMSE | R2 |
|---|---|---|---|---|---|---|
| SegNet | 8.8 | 35,435 | 30,386 | 18.28 | 21.12 | 0.72 |
| U-Net | 9.1 | 35,435 | 32,789 | 14.05 | 20.38 | 0.75 |
| DeNet | 9.5 | 35,435 | 35,961 | 12.63 | 17.25 | 0.79 |
| Round | Sigma Value | GT | PR | MAE | RMSE | R2 |
|---|---|---|---|---|---|---|
| First round | 4 | 35,435 | 27,699 | 21.94 | 26.88 | 0.73 |
| 8 | 35,435 | 28,429 | 20.26 | 25.30 | 0.76 | |
| 12 | 35,435 | 33,423 | 13.19 | 18.34 | 0.78 | |
| 16 | 35,435 | 35,387 | 12.11 | 16.21 | 0.82 | |
| 20 | 35,435 | 35,538 | 15.48 | 19.78 | 0.74 | |
| 24 | 35,435 | 39,621 | 17.67 | 22.74 | 0.72 | |
| Second round | 14 | 35,435 | 35,727 | 13.04 | 17.24 | 0.73 |
| 15 | 35,435 | 35,961 | 12.63 | 17.25 | 0.79 | |
| 17 | 35,435 | 35,592 | 12.34 | 16.78 | 0.78 | |
| 18 | 35,435 | 36,259 | 23.37 | 27.67 | 0.73 |
| Assembling Techniques | GT | PR | MAE | RMSE | R2 |
|---|---|---|---|---|---|
| Averaging | 26,582 | 26,512 | 11.87 | 16.13 | 0.82 |
| NIDW | 26,582 | 26,562 | 11.34 | 15.94 | 0.83 |
| Not assembled | 35,435 | 35,387 | 12.11 | 16.21 | 0.82 |
| Evaluation Matrix | Density Level | GT | PR | MAE | RMSE | R2 |
|---|---|---|---|---|---|---|
| Sampled GT | Low | 7002 | 6474 | 9.35 | 11.51 | 0.29 |
| Moderate | 6300 | 5190 | 12.68 | 14.93 | 0.25 | |
| High | 7749 | 7088 | 15.38 | 18.87 | 0.22 | |
| Annotated GT | Low | 6590 | 6474 | 9.40 | 11.50 | 0.33 |
| Moderate | 5758 | 5190 | 10.76 | 12.91 | 0.30 | |
| High | 6788 | 7088 | 11.85 | 18.87 | 0.17 |
| Evaluation Matrix | Quadrat Location | GT | PR | MAE | RMSE | R2 |
|---|---|---|---|---|---|---|
| Sampled GT | Z1 | 2339 | 2052 | 6.63 | 8.61 | 0.91 |
| Z2 | 4678 | 4356 | 12.50 | 13.15 | 0.86 | |
| Z3 | 4678 | 4324 | 14.80 | 17.89 | 0.84 | |
| Z4 | 9356 | 7786 | 19.13 | 22.39 | 0.74 | |
| Annotated GT | Z1 | 2047 | 2052 | 7.17 | 8.82 | 0.88 |
| Z2 | 4230 | 4356 | 10.10 | 11.88 | 0.86 | |
| Z3 | 4327 | 4558 | 14.13 | 18.36 | 0.83 | |
| Z4 | 8532 | 7786 | 18.23 | 21.05 | 0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Rezaei, E.E.; Zhu, W.; Wang, D.; Li, H.; Yang, B.; Sun, Z. Plant Density Estimation Using UAV Imagery and Deep Learning. Remote Sens. 2022, 14, 5923. https://doi.org/10.3390/rs14235923
Peng J, Rezaei EE, Zhu W, Wang D, Li H, Yang B, Sun Z. Plant Density Estimation Using UAV Imagery and Deep Learning. Remote Sensing. 2022; 14(23):5923. https://doi.org/10.3390/rs14235923
Chicago/Turabian StylePeng, Jinbang, Ehsan Eyshi Rezaei, Wanxue Zhu, Dongliang Wang, He Li, Bin Yang, and Zhigang Sun. 2022. "Plant Density Estimation Using UAV Imagery and Deep Learning" Remote Sensing 14, no. 23: 5923. https://doi.org/10.3390/rs14235923
APA StylePeng, J., Rezaei, E. E., Zhu, W., Wang, D., Li, H., Yang, B., & Sun, Z. (2022). Plant Density Estimation Using UAV Imagery and Deep Learning. Remote Sensing, 14(23), 5923. https://doi.org/10.3390/rs14235923









