A 3D Space-Time Non-Local Mean Filter (NLMF) for Land Changes Retrieval with Synthetic Aperture Radar Images
Abstract
1. Introduction
2. Method
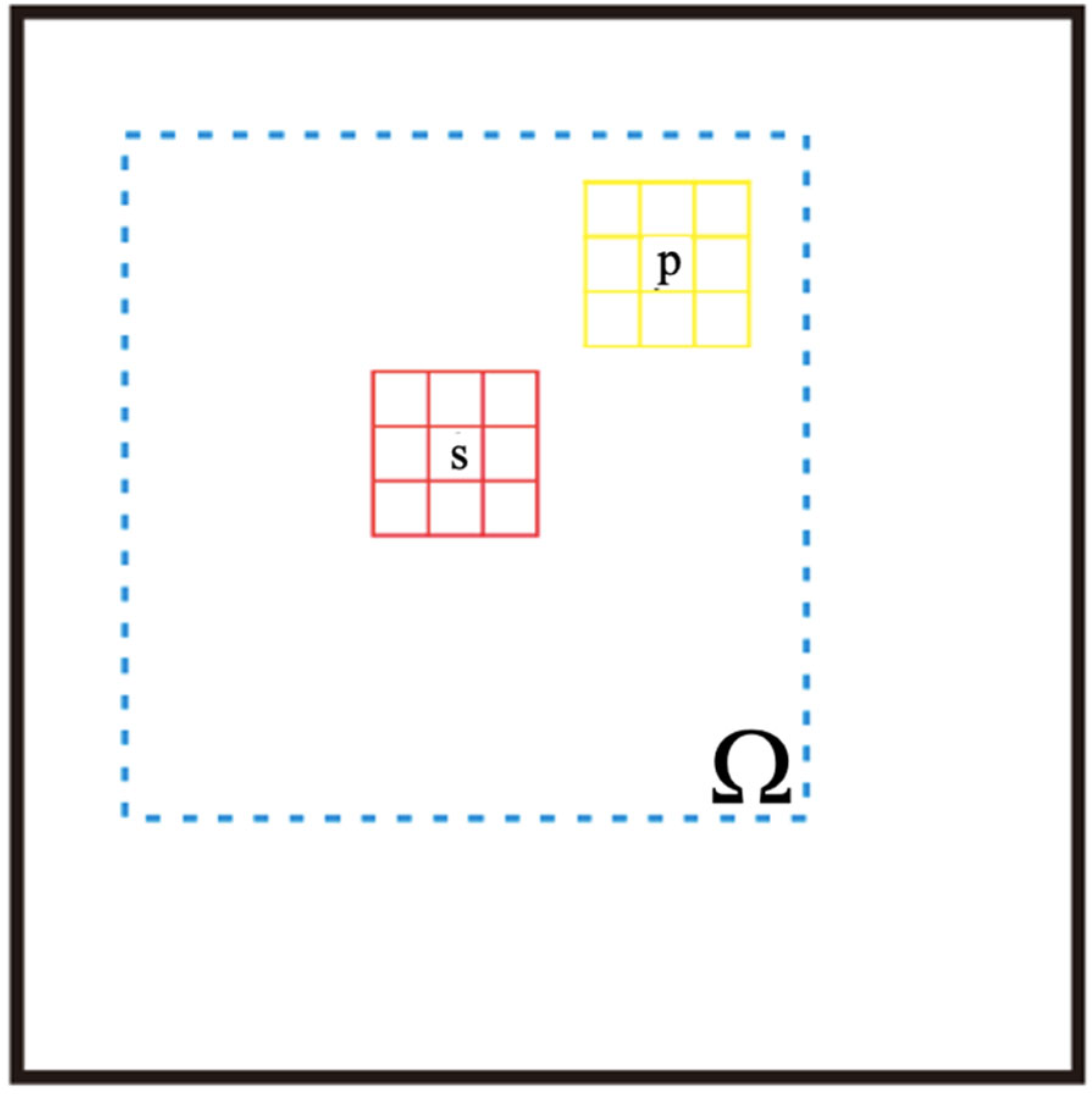
2.1. Spatial (2D) Non-Local Mean Filters for SAR Image De-Speckling
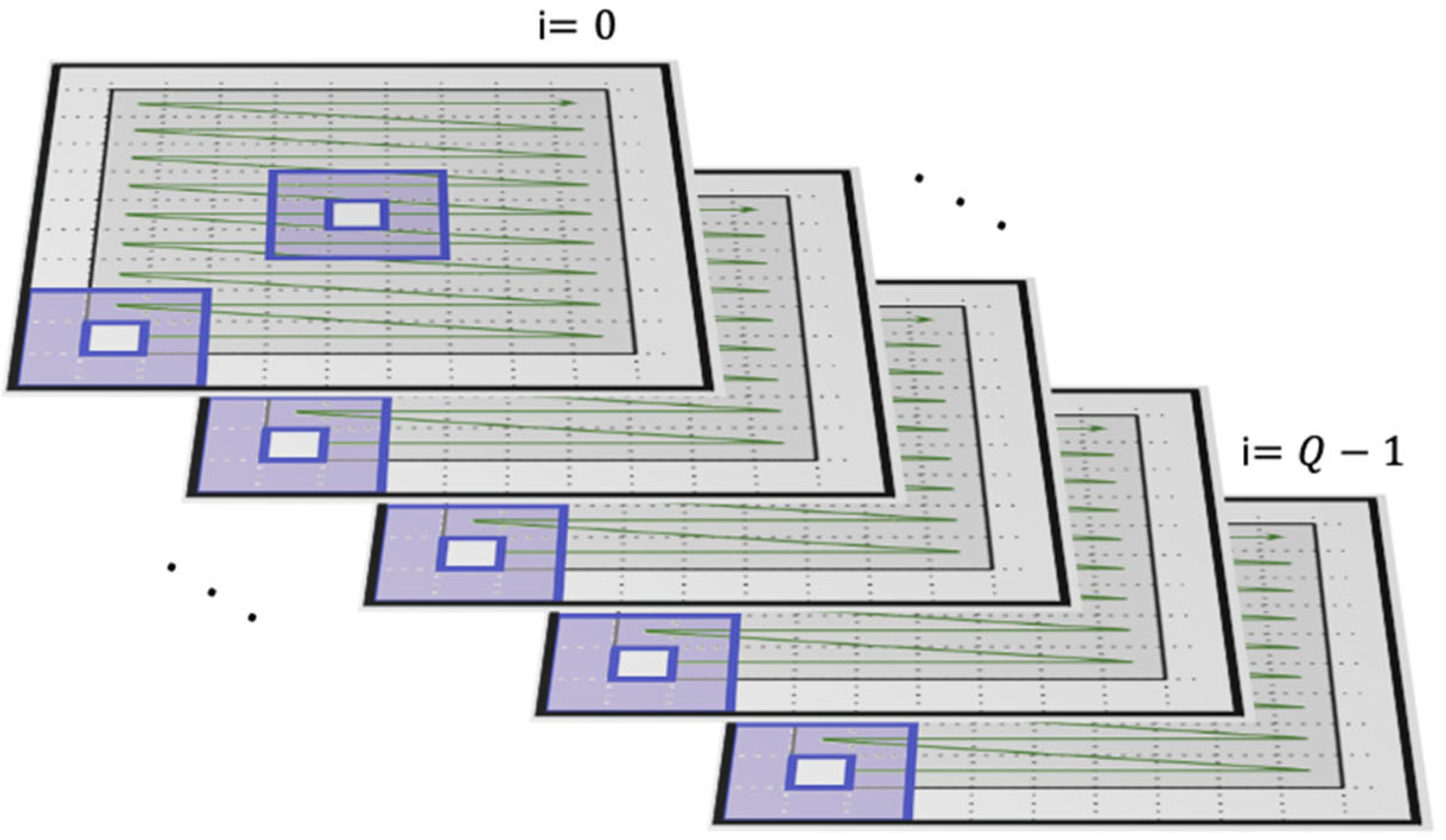
2.2. The Developed Space-Time (3D) NLMF
2.3. Key Performance of the Developed 3D NLMF De-Speckling Method
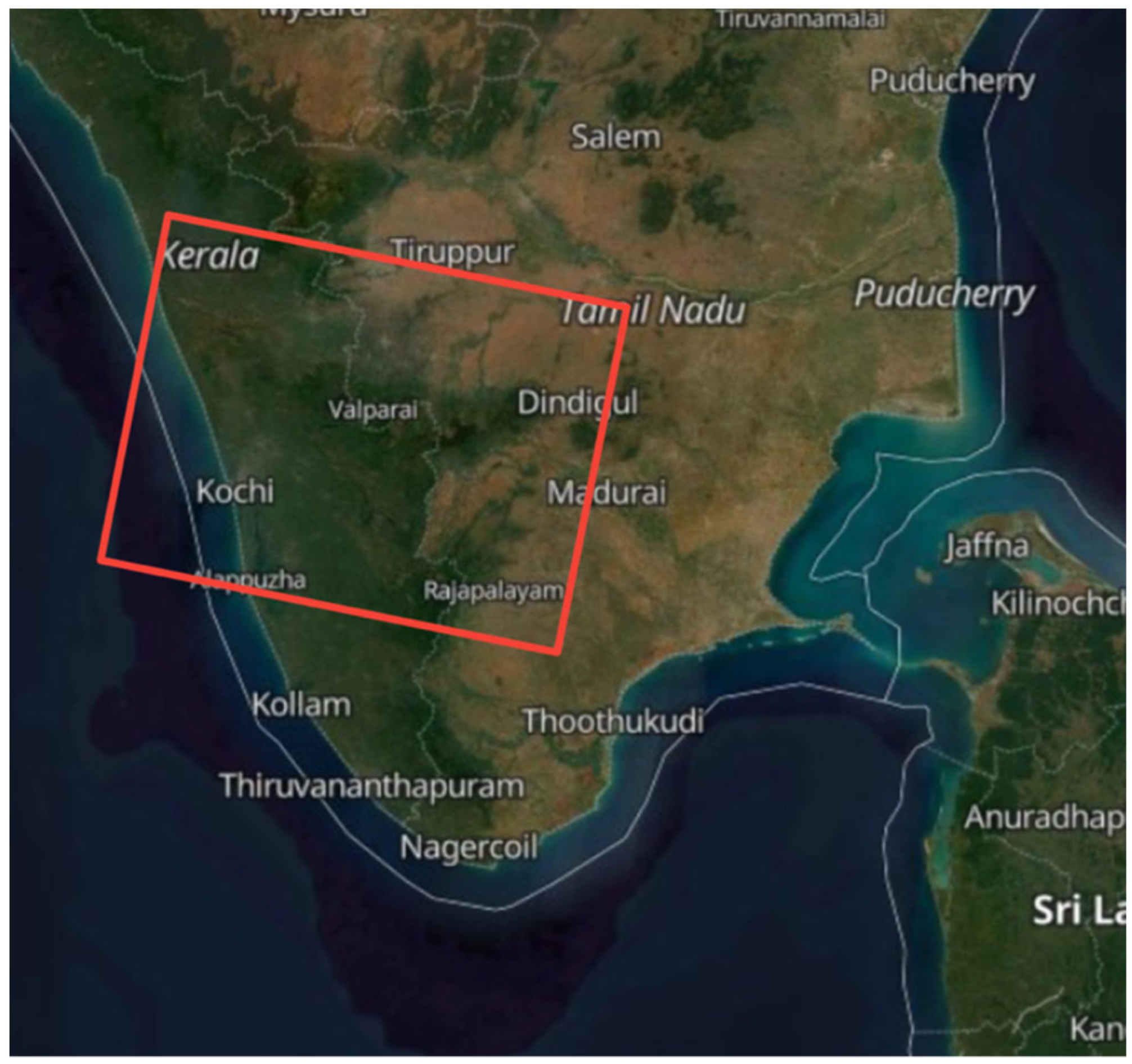
3. Material
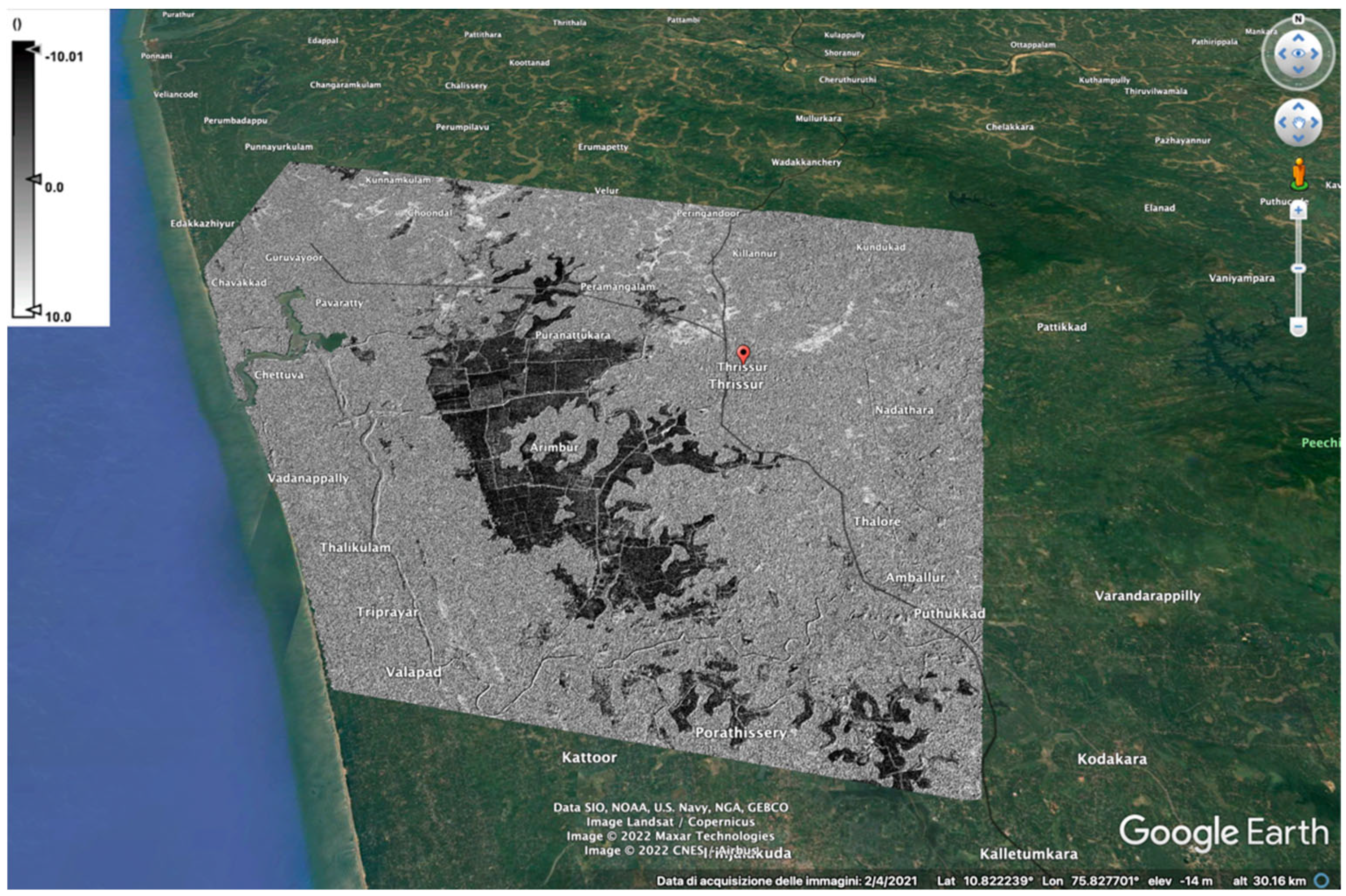
4. Experimental Results
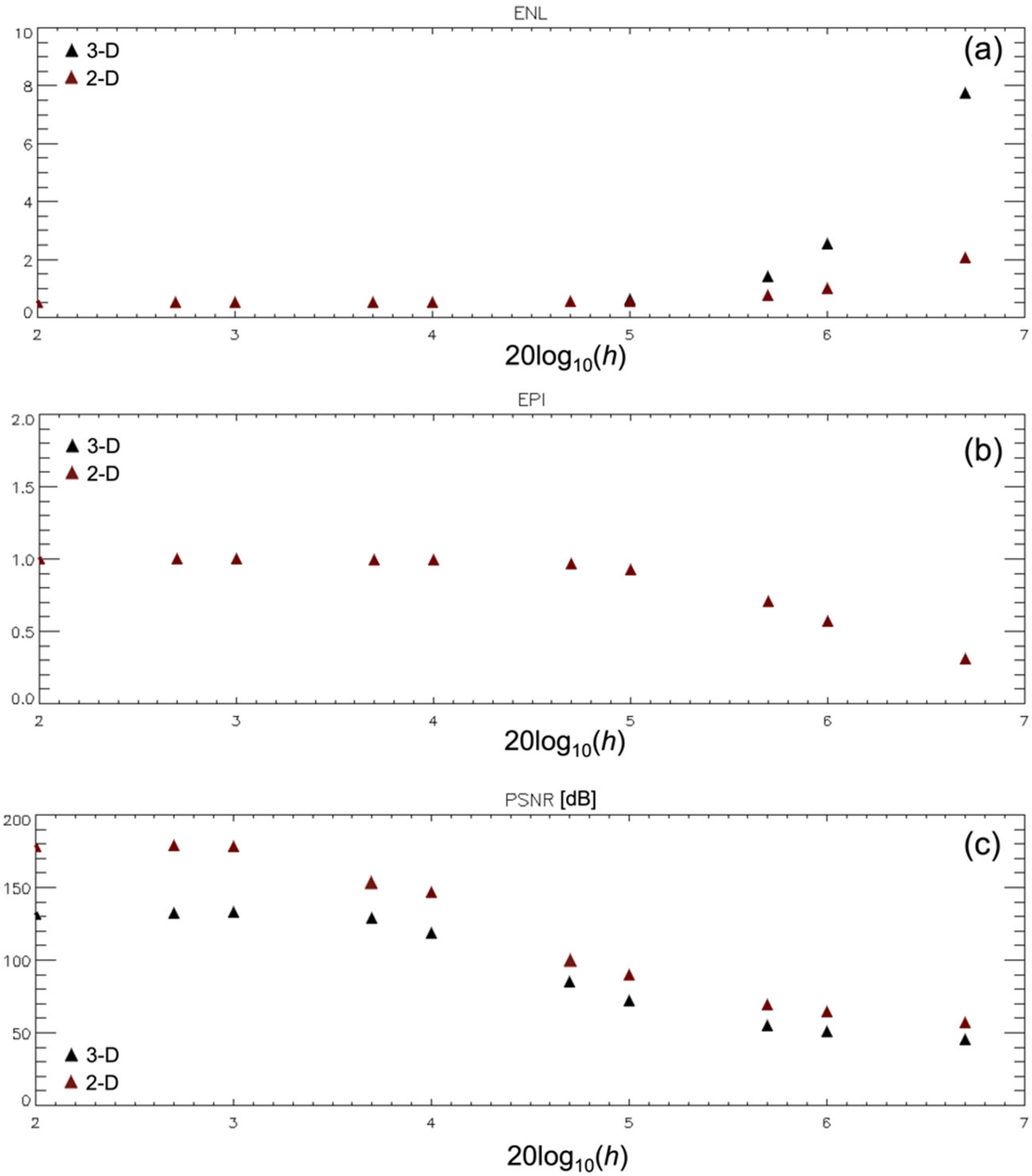
5. Key Performance of the Proposed Method
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wasowski, J.; Bovenga, F. Investigating Landslides and Unstable Slopes with Satellite Multi Temporal Interferometry: Current Issues and Future Perspectives. Eng. Geol. 2014, 174, 103–138. [Google Scholar] [CrossRef]
- Deledalle, C.-A.; Denis, L.; Tupin, F.; Reigber, A.; Jager, M. NL-SAR: A Unified Nonlocal Framework for Resolution-Preserving (Pol)(In)SAR Denoising. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2021–2038. [Google Scholar] [CrossRef]
- Zhu, X.X.; Bamler, R. Very High Resolution Spaceborne SAR Tomography in Urban Environment. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4296–4308. [Google Scholar] [CrossRef]
- Gong, M.; Zhou, Z.; Ma, J. Change Detection in Synthetic Aperture Radar Images Based on Image Fusion and Fuzzy Clustering. IEEE Trans. Image Process. 2012, 21, 2141–2151. [Google Scholar] [CrossRef] [PubMed]
- Strozzi, T.; Luckman, A.; Murray, T.; Wegmuller, U.; Werner, C.L. Glacier Motion Estimation Using SAR Offset-Tracking Procedures. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2384–2391. [Google Scholar] [CrossRef]
- Ding, J.; Chen, B.; Liu, H.; Huang, M. Convolutional Neural Network with Data Augmentation for SAR Target Recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [Google Scholar] [CrossRef]
- Hooper, A.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent Advances in SAR Interferometry Time Series Analysis for Measuring Crustal Deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Bazi, Y.; Bruzzone, L.; Melgani, F. An Unsupervised Approach Based on the Generalized Gaussian Model to Automatic Change Detection in Multitemporal SAR Images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 874–887. [Google Scholar] [CrossRef]
- Mora, O.; Mallorqui, J.J.; Broquetas, A. Linear and Nonlinear Terrain Deformation Maps from a Reduced Set of Interferometric Sar Images. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2243–2253. [Google Scholar] [CrossRef]
- Hooper, A.; Segall, P.; Zebker, H. Persistent Scatterer Interferometric Synthetic Aperture Radar for Crustal Deformation Analysis, with Application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Hooper, A. A Multi-Temporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-Component Scattering Model for Polarimetric SAR Image Decomposition. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1699–1706. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Yagüe-Martínez, N.; Prats-Iraola, P.; Rodríguez González, F.; Brcic, R.; Shau, R.; Geudtner, D.; Eineder, M.; Bamler, R. Interferometric Processing of Sentinel-1 TOPS Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2220–2234. [Google Scholar] [CrossRef]
- Galloway, D.L.; Hudnut, K.W.; Ingebritsen, S.E.; Phillips, S.P.; Peltzer, G.; Rogez, F.; Rosen, P.A. Detection of Aquifer System Compaction and Land Subsidence Using Interferometric Synthetic Aperture Radar, Antelope Valley, Mojave Desert, California. Water Resour. Res. 1998, 34, 2573–2585. [Google Scholar] [CrossRef]
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A Review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A New Algorithm for Processing Interferometric Data-Stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2202–2212. [Google Scholar] [CrossRef]
- Gong, M.; Cao, Y.; Wu, Q. A Neighborhood-Based Ratio Approach for Change Detection in SAR Images. IEEE Geosci. Remote Sens. Lett. 2012, 9, 307–311. [Google Scholar] [CrossRef]
- Gong, M.; Su, L.; Jia, M.; Chen, W. Fuzzy Clustering With a Modified MRF Energy Function for Change Detection in Synthetic Aperture Radar Images. IEEE Trans. Fuzzy Syst. 2014, 22, 98–109. [Google Scholar] [CrossRef]
- Giustarini, L.; Hostache, R.; Matgen, P.; Schumann, G.J.-P.; Bates, P.D.; Mason, D.C. A Change Detection Approach to Flood Mapping in Urban Areas Using TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2417–2430. [Google Scholar] [CrossRef]
- Matgen, P.; Hostache, R.; Schumann, G.; Pfister, L.; Hoffmann, L.; Savenije, H.H.G. Towards an Automated SAR-Based Flood Monitoring System: Lessons Learned from Two Case Studies. Phys. Chem. Earth Parts ABC 2011, 36, 241–252. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B. Generalized Minimum-Error Thresholding for Unsupervised Change Detection from SAR Amplitude Imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2972–2982. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L. A Detail-Preserving Scale-Driven Approach to Change Detection in Multitemporal SAR Images. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2963–2972. [Google Scholar] [CrossRef]
- Mastro, P.; Masiello, G.; Serio, C.; Pepe, A. Change Detection Techniques with Synthetic Aperture Radar Images: Experiments with Random Forests and Sentinel-1 Observations. Remote Sens. 2022, 14, 3323. [Google Scholar] [CrossRef]
- DeVries, B.; Huang, C.; Armston, J.; Huang, W.; Jones, J.W.; Lang, M.W. Rapid and Robust Monitoring of Flood Events Using Sentinel-1 and Landsat Data on the Google Earth Engine. Remote Sens. Environ. 2020, 240, 111664. [Google Scholar] [CrossRef]
- Sowter, A.; Amat, M.B.C.; Cigna, F.; Marsh, S.; Athab, A.; Alshammari, L. Mexico City Land Subsidence in 2014–2015 with Sentinel-1 IW TOPS: Results Using the Intermittent SBAS (ISBAS) Technique. Int. J. Appl. Earth Obs. Geoinform. 2016, 52, 230–242. [Google Scholar] [CrossRef]
- Dai, K.; Li, Z.; Tomás, R.; Liu, G.; Yu, B.; Wang, X.; Cheng, H.; Chen, J.; Stockamp, J. Monitoring Activity at the Daguangbao Mega-Landslide (China) Using Sentinel-1 TOPS Time Series Interferometry. Remote Sens. Environ. 2016, 186, 501–513. [Google Scholar] [CrossRef]
- Ndikumana, E.; Minh, D.H.T.; Baghdadi, N.; Courault, D.; Hossard, L. Deep Recurrent Neural Network for Agricultural Classification Using Multitemporal SAR Sentinel-1 for Camargue, France. Remote Sens. 2018, 10, 1217. [Google Scholar] [CrossRef]
- Nagler, T.; Rott, H.; Hetzenecker, M.; Wuite, J.; Potin, P. The Sentinel-1 Mission: New Opportunities for Ice Sheet Observations. Remote Sens. 2015, 7, 9371–9389. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Freeman, V.; Cao, S.; Paulik, C.; Schaufler, S.; Stachl, T.; Modanesi, S.; Massari, C.; Ciabatta, L.; Brocca, L.; et al. Toward Global Soil Moisture Monitoring With Sentinel-1: Harnessing Assets and Overcoming Obstacles. IEEE Trans. Geosci. Remote Sens. 2019, 57, 520–539. [Google Scholar] [CrossRef]
- Tian, X.; Ma, Z.-F.; Jiang, M. A Modification to Time-Series Coregistration for Sentinel-1 TOPS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1639–1648. [Google Scholar] [CrossRef]
- Ma, Z.-F.; Jiang, M.; Zhao, Y.; Malhotra, R.; Yong, B. Minimum Spanning Tree Co-Registration Approach for Time-Series Sentinel-1 TOPS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3004–3013. [Google Scholar] [CrossRef]
- Ma, Z.-F.; Jiang, M.; Huang, T. A Sequential Approach for Sentinel-1 TOPS Time-Series Co-Registration Over Low Coherence Scenarios. IEEE Trans. Geosci. Remote Sens. 2021, 59, 4818–4826. [Google Scholar] [CrossRef]
- Mastro, P.; Serio, C.; Masiello, G.; Pepe, A. The Multiple Aperture SAR Interferometry (MAI) Technique for the Detection of Large Ground Displacement Dynamics: An Overview. Remote Sens. 2020, 12, 1189. [Google Scholar] [CrossRef]
- Fusco, A.; Pepe, A.; Berardino, P.; De Luca, C.; Buonanno, S.; Lanari, R. A Phase-Preserving Focusing Technique for TOPS Mode SAR Raw Data Based on Conventional Processing Methods. Sensors 2019, 19, 3321. [Google Scholar] [CrossRef]
- Prats, P.; Scheiber, R.; Mittermayer, J.; Meta, A.; Moreira, A. Processing of Sliding Spotlight and TOPS SAR Data Using Baseband Azimuth Scaling. IEEE Trans. Geosci. Remote Sens. 2010, 48, 770–780. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Scheiber, R.; Marotti, L.; Wollstadt, S.; Reigber, A. TOPS Interferometry with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3179–3188. [Google Scholar] [CrossRef]
- De Zan, F.; Monti Guarnieri, A. TOPSAR: Terrain Observation by Progressive Scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Hoang, T.T.; Truong, V.T.; Hayashi, M.; Tadono, T.; Nasahara, K.N. New JAXA High-Resolution Land Use/Land Cover Map for Vietnam Aiming for Natural Forest and Plantation Forest Monitoring. Remote Sens. 2020, 12, 2707. [Google Scholar] [CrossRef]
- Çolak, E.; Chandra, M.; Sunar, F. The use of multi-temporal sentinel satellites in the analysis of land cover/land use changes caused by the nuclear power plant construction. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 23 August 2019; Copernicus GmbH: Göttingen, Germany, 2019; Volume XLII-3-W8, pp. 491–495. [Google Scholar]
- Aydöner, C.; Maktav, D. The Role of the Integration of Remote Sensing and GIS in Land Use/Land Cover Analysis after an Earthquake. Int. J. Remote Sens. 2009, 30, 1697–1717. [Google Scholar] [CrossRef]
- Zhang, R.; Tang, X.; You, S.; Duan, K.; Xiang, H.; Luo, H. A Novel Feature-Level Fusion Framework Using Optical and SAR Remote Sensing Images for Land Use/Land Cover (LULC) Classification in Cloudy Mountainous Area. Appl. Sci. 2020, 10, 2928. [Google Scholar] [CrossRef]
- Ohki, M.; Shimada, M. Large-Area Land Use and Land Cover Classification with Quad, Compact, and Dual Polarization SAR Data by PALSAR-2. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5550–5557. [Google Scholar] [CrossRef]
- Olen, S.; Bookhagen, B. Mapping Damage-Affected Areas after Natural Hazard Events Using Sentinel-1 Coherence Time Series. Remote Sens. 2018, 10, 1272. [Google Scholar] [CrossRef]
- Washaya, P.; Balz, T.; Mohamadi, B. Coherence Change-Detection with Sentinel-1 for Natural and Anthropogenic Disaster Monitoring in Urban Areas. Remote Sens. 2018, 10, 1026. [Google Scholar] [CrossRef]
- Liu, J.G.; Black, A.; Lee, H.; Hanaizumi, H.; Moore, J.M. Land surface change detection in a desert area in Algeria using multi-temporal ERS SAR coherence images. Int. J. Remote Sens. 2001, 22, 2463–2477. [Google Scholar] [CrossRef]
- Jung, J.; Kim, D.; Lavalle, M.; Yun, S.-H. Coherent Change Detection Using InSAR Temporal Decorrelation Model: A Case Study for Volcanic Ash Detection. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5765–5775. [Google Scholar] [CrossRef]
- Atwood, D.K.; Meyer, F.; Arendt, A. Using L-band SAR coherence to delineate glacier extent. Can. J. Remote Sens. 2010, 36, S186–S195. [Google Scholar] [CrossRef]
- Kim, S.-W.; Wdowinski, S.; Amelung, F.; Dixon, T.H.; Won, J.-S. Interferometric Coherence Analysis of the Everglades Wetlands, South Florida. IEEE Trans. Geosci. Remote Sens. 2013, 51, 5210–5224. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mahdianpari, M.; Brisco, B.; Motagh, M. Multi-Temporal, Multi-Frequency, and Multi-Polarization Coherence and SAR Backscatter Analysis of Wetlands. ISPRS J. Photogramm. Remote Sens. 2018, 142, 78–93. [Google Scholar] [CrossRef]
- Dekker, R.J. Speckle filtering in satellite SAR change detection imagery. Int. J. Remote Sens. 1998, 19, 1133–1146. [Google Scholar] [CrossRef]
- Torres, L.; Sant’Anna, S.J.; da Costa Freitas, C.; Frery, A. Speckle reduction in polarimetric SAR imagery with stochastic distances and nonlocal means. Pattern Recognit. 2014, 47, 141–157. [Google Scholar] [CrossRef]
- López-Martínez, C.; Fabregas, X. Modeling and Reduction of SAR Interferometric Phase Noise in the Wavelet Domain. Geosci. Remote Sens. IEEE Trans. 2003, 40, 2553–2566. [Google Scholar] [CrossRef]
- Feng, H.; Hou, B.; Gong, M. SAR Image Despeckling Based on Local Homogeneous-Region Segmentation by Using Pixel-Relativity Measurement. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2724–2737. [Google Scholar] [CrossRef]
- Sipos, D.; Gleich, D. Model-Based Information Extraction from SAR Images Using Deep Learning. IEEE Geosci. Remote Sens. Lett. 2020, 19, 4007005. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, H.; Patel, V.M. SAR Image Despeckling Using a Convolutional Neural Network. IEEE Signal Process. Lett. 2017, 24, 1763–1767. [Google Scholar] [CrossRef]
- Baran, I.; Stewart, M.P.; Kampes, B.M.; Perski, Z.; Lilly, P. A Modification to the Goldstein Radar Interferogram Filter. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2114–2118. [Google Scholar] [CrossRef]
- Geng, J.; Fan, J.; Wang, H.; Ma, X.; Li, B.; Chen, F. High-Resolution SAR Image Classification via Deep Convolutional Autoencoders. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2351–2355. [Google Scholar] [CrossRef]
- Lee, J.-S.; Papathanassiou, K.; Ainsworth, T.; Grunes, M.; Reigber, A. A new technique for noise filtering of SAR interferometric phase images. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1456–1465. [Google Scholar] [CrossRef]
- Touzi, R. A Review of Speckle Filtering in the Context of Estimation Theory. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2392–2404. [Google Scholar] [CrossRef]
- Xie, H.; Pierce, L.E.; Ulaby, F.T. SAR Speckle Reduction Using Wavelet Denoising and Markov Random Field Modeling. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2196–2212. [Google Scholar] [CrossRef]
- Lee, J.-S.; Wen, J.-H.; Ainsworth, T.L.; Chen, K.-S.; Chen, A.J. Improved Sigma Filter for Speckle Filtering of SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2009, 47, 202–213. [Google Scholar] [CrossRef]
- Deledalle, C.-A.; Denis, L.; Tupin, F. Iterative Weighted Maximum Likelihood Denoising with Probabilistic Patch-Based Weights. IEEE Trans. Image Process. 2009, 18, 2661–2672. [Google Scholar] [CrossRef]
- Aiazzi, B.; Alparone, L.; Baronti, S.; Garzelli, A. Coherence estimation from multilook incoherent sar imagery. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2531–2539. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, H.; Wang, C.; Wu, F. Change Detection of Multilook Polarimetric SAR Images Using Heterogeneous Clutter Models. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7483–7494. [Google Scholar] [CrossRef]
- Lee, J.-S.; Ainsworth, T.L.; Kelly, J.P.; Lopez-Martinez, C. Evaluation and Bias Removal of Multilook Effect on Entropy/Alpha/Anisotropy in Polarimetric SAR Decomposition. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3039–3052. [Google Scholar] [CrossRef]
- Touzi, R.; Lopes, A. Statistics of the Stokes Parameters and of the Complex Coherence Parameters in One-Look and Multilook Speckle Fields. IEEE Trans. Geosci. Remote Sens. 1996, 34, 519–531. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A Model for Radar Images and Its Application to Adaptive Digital Filtering of Multiplicative Noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, 4, 157–166. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.-S. Speckle Analysis and Smoothing of Synthetic Aperture Radar Images. Comput. Graph. Image Process. 1981, 17, 24–32. [Google Scholar] [CrossRef]
- Kuan, D.; Sawchuk, A.; Strand, T.; Chavel, P. Adaptive Restoration of Images with Speckle. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 373–383. [Google Scholar] [CrossRef]
- Baraldi, A.; Parmiggiani, F. A Refined Gamma MAP SAR Speckle Filter with Improved Geometrical Adaptivity. IEEE Trans. Geosci. Remote Sens. 1995, 33, 1245–1257. [Google Scholar] [CrossRef]
- Lee, J.-S. Statistical Modelling and Suppression of Speckle in Synthetic Aperture Radar Images. In Proceedings of the IGARSS’87-International Geoscience and Remote Sensing Symposium 1987, Ann Arbor, MI, USA, 18–21 May 1987; Volume 2, pp. 1331–1339. [Google Scholar]
- Gao, F.; Dong, J.; Li, B.; Xu, Q. Automatic Change Detection in Synthetic Aperture Radar Images Based on PCANet. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1792–1796. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Hou, B.; Liu, G. Using Combined Difference Image and K-Means Clustering for SAR Image Change Detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 691–695. [Google Scholar] [CrossRef]
- Lee, J.S.; Jurkevich, I.; Dewaele, P.; Wambacq, P.; Oosterlinck, A. Speckle filtering of synthetic aperture radar images: A review. Remote Sens. Rev. 1994, 8, 313–340. [Google Scholar] [CrossRef]
- Ajadi, O.A.; Meyer, F.J.; Webley, P.W. Change Detection in Synthetic Aperture Radar Images Using a Multiscale-Driven Approach. Remote Sens. 2016, 8, 482. [Google Scholar] [CrossRef]
- Smith, D.M. Speckle Reduction and Segmentation of Synthetic Aperture Radar Images. Int. J. Remote Sens. 1996, 17, 2043–2057. [Google Scholar] [CrossRef]
- Liu, Z.; Li, G.; Mercier, G.; He, Y.; Pan, Q. Change Detection in Heterogenous Remote Sensing Images via Homogeneous Pixel Transformation. IEEE Trans. Image Process. 2018, 27, 1822–1834. [Google Scholar] [CrossRef] [PubMed]
- Shamsoddini, A.; Trinder, J. Image Texture Preservation in Speckle Noise Suppression; IAPRS: Vienna, Austria, 2010. [Google Scholar]
- Penna, P.A.A.; Mascarenhas, N.D.A. (Non-) Homomorphic Approaches to Denoise Intensity SAR Images with Non-Local Means and Stochastic Distances. Comput. Geosci. 2018, 111, 127–138. [Google Scholar] [CrossRef]
- Jia, M.; Wang, L. Novel Class-Relativity Non-Local Means with Principal Component Analysis for Multitemporal SAR Image Change Detection. Int. J. Remote Sens. 2018, 39, 1068–1091. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.-M. A Non-Local Algorithm for Image Denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Deledalle, C.-A.; Tupin, F.; Denis, L. Polarimetric SAR Estimation Based on Non-Local Means. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2515–2518. [Google Scholar]
- Jojy, C.; Nair, M.S.; Subrahmanyam, G.R.K.S.; Riji, R. Discontinuity Adaptive Non-Local Means with Importance Sampling Unscented Kalman Filter for De-Speckling SAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 1964–1970. [Google Scholar] [CrossRef]
- A Novel Approach of Despeckling SAR Images Using Nonlocal Means Filtering|SpringerLink. Available online: https://link.springer.com/article/10.1007/s12524-016-0607-0 (accessed on 27 September 2022).
- Hu, J.; Guo, R.; Zhu, X.; Baier, G.; Wang, Y. Non-Local Means Filter For Polarimetric SAR Speckle Reuction Experiments Using TERRASAR-X Data. In Proceedings of the ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 11 March 2015; Copernicus GmbH: Göttingen, Germany, 2015; Volume II-3-W4, pp. 71–77. [Google Scholar]
- Zhong, H.; Li, Y.; Jiao, L. SAR Image Despeckling Using Bayesian Nonlocal Means Filter with Sigma Preselection. IEEE Geosci. Remote Sens. Lett. 2011, 8, 809–813. [Google Scholar] [CrossRef]
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A Nonlocal SAR Image Denoising Algorithm Based on LLMMSE Wavelet Shrinkage. IEEE Trans. Geosci. Remote Sens. 2012, 50, 606–616. [Google Scholar] [CrossRef]
- MuraliMohanBabu, Y.; Subramanyam, M.; GiriPrasad, M. A Modified BM3D Algorithm for SAR Image Despeckling. Procedia Comput. Sci. 2015, 70, 69–75. [Google Scholar] [CrossRef]
- Su, X.; Deledalle, C.-A.; Tupin, F.; Sun, H. Two-Step Multitemporal Nonlocal Means for Synthetic Aperture Radar Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6181–6196. [Google Scholar] [CrossRef]
- Zhao, W.; Deledalle, C.-A.; Denis, L.; Maitre, H.; Nicolas, J.-M.; Tupin, F. Ratio-Based Multitemporal SAR Images Denoising: RABASAR. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3552–3565. [Google Scholar] [CrossRef]
- Trouve, E.; Chambenoit, Y.; Classeau, N.; Bolon, P. Statistical and Operational Performance Assessment of Multitemporal SAR Image Filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2519–2530. [Google Scholar] [CrossRef]
- Ma, X.; Wu, P. Multitemporal SAR Image Despeckling Based on a Scattering Covariance Matrix of Image Patch. Sensors 2019, 19, 3057. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive/Volume II, Radar Remote Sensing and Surface Scattering and Emission Theory; Remote Sensing; Addison-Wesley: Reading, MA, USA, 1982; ISBN 978-0-201-10760-9. [Google Scholar]
- Chen, S.; Hou, J.; Zhang, H.; Da, B. De-Speckling Method Based on Non-Local Means and Coefficient Variation of SAR Image. Electron. Lett. 2014, 50, 1314–1316. [Google Scholar] [CrossRef]
- Wu, J.; Liu, F.; Hao, H.; Li, L.; Jiao, L.; Zhang, X. A Nonlocal Means for Speckle Reduction of SAR Image With Multiscale-Fusion-Based Steerable Kernel Function. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1646–1650. [Google Scholar] [CrossRef]
- Su, L.; Gong, M.; Sun, B. Change detection in synthetic aperture radar images based on non-local means with ratio similarity measurement. Int. J. Remote Sens. 2014, 35, 7673–7690. [Google Scholar] [CrossRef]
- Deledalle, C.-A.; Tupin, F.; Denis, L. A Non-Local Approach for SAR and Interferometric SAR Denoising. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; IEEE: Honolulu, HI, USA, 2010; pp. 714–717. [Google Scholar]
- Lee, J.S.; Hoppel, K. Noise Modeling and Estimation of Remotely-Sensed Images. In Proceedings of the 12th Canadian Symposium on Remote Sensing Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; Volume 2, pp. 1005–1008. [Google Scholar]
- Tong, D.; Yang, H.; Wu, J.; Yang, J. An Improved Non-Local Means Filter for Sar Image Despeckle Based on Heterogeneity Measurement. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2801–2804. [Google Scholar]
- Pepe, A. Use of Multi-Temporal SAR Non-Local Mean Filtering Operations for Change Detection Analyses. In Proceedings of the 2022 IEEE 21st Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 14–16 June 2022; pp. 616–620. [Google Scholar]
- Ma, W.; Xin, Z.; Liao, G.; Sun, Y.; Wang, Z.; Xuan, J. Sub-Region Non-Local Mean Denoising Algorithm of Synthetic Aperture Radar Images Based on Statistical Characteristics. IET Image Process. 2022, 16, 2665–2679. [Google Scholar] [CrossRef]
- Vanama, V.S.K.; Musthafa, M.; Khati, U.; Gowtham, R.; Singh, G.; Rao, Y.S. Inundation Mapping of Kerala Flood Event in 2018 Using ALOS-2 and Temporal Sentinel-1 SAR Images. Curr. Sci. 2021, 120, 11. [Google Scholar] [CrossRef]
- Vijaykumar, P.; Abhilash, S.; Sreenath, A.V.; Athira, U.N.; Mohanakumar, K.; Mapes, B.E.; Chakrapani, B.; Sahai, A.K.; Niyas, T.N.; Sreejith, O.P. Kerala Floods in Consecutive Years—Its Association with Mesoscale Cloudburst and Structural Changes in Monsoon Clouds over the West Coast of India. Weather Clim. Extrem. 2021, 33, 100339. [Google Scholar] [CrossRef]
- Sentinel Application Platform. Available online: https://eo4society.esa.int/resources/snap/ (accessed on 27 September 2022).
- Pepe, A.; Yang, Y.; Manzo, M.; Lanari, R. Improved EMCF-SBAS Processing Chain Based on Advanced Techniques for the Noise-Filtering and Selection of Small Baseline Multi-Look DInSAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4394–4417. [Google Scholar] [CrossRef]
- Pepe, A.; Mastro, P.; Jones, C.E. Adaptive Multilooking of Multitemporal Differential SAR Interferometric Data Stack Using Directional Statistics. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6706–6721. [Google Scholar] [CrossRef]
- Ansari, H.; De Zan, F.; Bamler, R. Efficient Phase Estimation for Interferogram Stacks. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4109–4125. [Google Scholar] [CrossRef]
- Massonnet, D.; Feigl, K.L. Radar Interferometry and Its Application to Changes in the Earth’s Surface. Rev. Geophys. 1998, 36, 441–500. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic Aperture Radar Interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]





| Year | Month | Day |
|---|---|---|
| 2018 | 03 | 06 |
| 2018 | 03 | 18 |
| 2018 | 03 | 30 |
| 2018 | 04 | 11 |
| 2018 | 04 | 23 |
| 2018 | 05 | 05 |
| 2018 | 05 | 17 |
| 2018 | 05 | 29 |
| 2018 | 06 | 10 |
| 2018 | 06 | 22 |
| 2018 | 07 | 04 |
| 2018 | 07 | 16 |
| 2018 | 07 | 28 |
| 2018 | 08 | 09 |
| 2018 | 08 | 21 |
| 2018 | 09 | 02 |
| 2018 | 09 | 14 |
| 2018 | 09 | 26 |
| 2018 | 10 | 08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pepe, A. A 3D Space-Time Non-Local Mean Filter (NLMF) for Land Changes Retrieval with Synthetic Aperture Radar Images. Remote Sens. 2022, 14, 5933. https://doi.org/10.3390/rs14235933
Pepe A. A 3D Space-Time Non-Local Mean Filter (NLMF) for Land Changes Retrieval with Synthetic Aperture Radar Images. Remote Sensing. 2022; 14(23):5933. https://doi.org/10.3390/rs14235933
Chicago/Turabian StylePepe, Antonio. 2022. "A 3D Space-Time Non-Local Mean Filter (NLMF) for Land Changes Retrieval with Synthetic Aperture Radar Images" Remote Sensing 14, no. 23: 5933. https://doi.org/10.3390/rs14235933
APA StylePepe, A. (2022). A 3D Space-Time Non-Local Mean Filter (NLMF) for Land Changes Retrieval with Synthetic Aperture Radar Images. Remote Sensing, 14(23), 5933. https://doi.org/10.3390/rs14235933








