SATNet: A Spatial Attention Based Network for Hyperspectral Image Classification
Abstract
1. Introduction
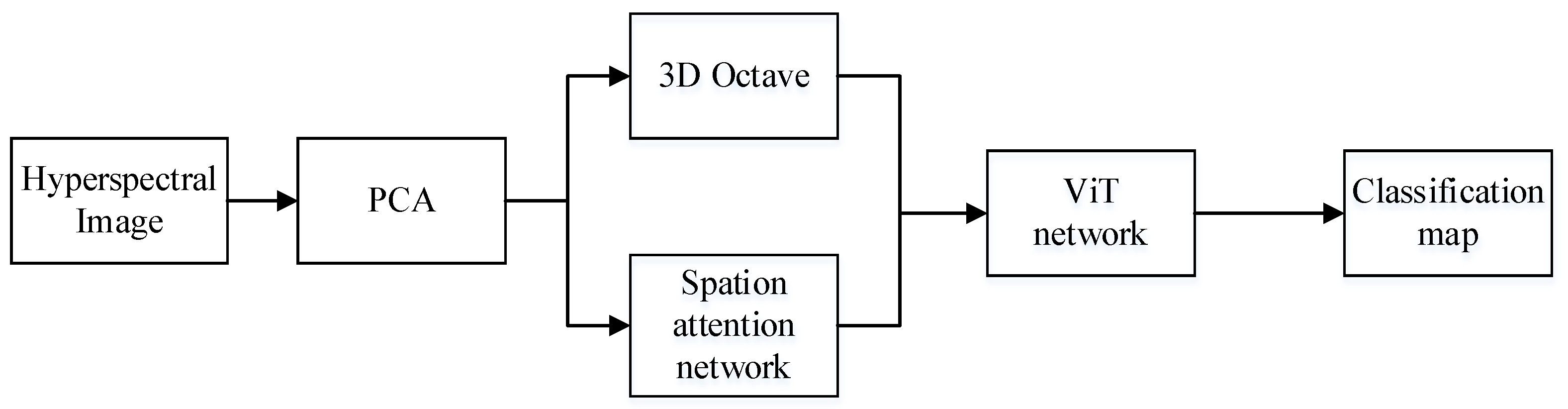
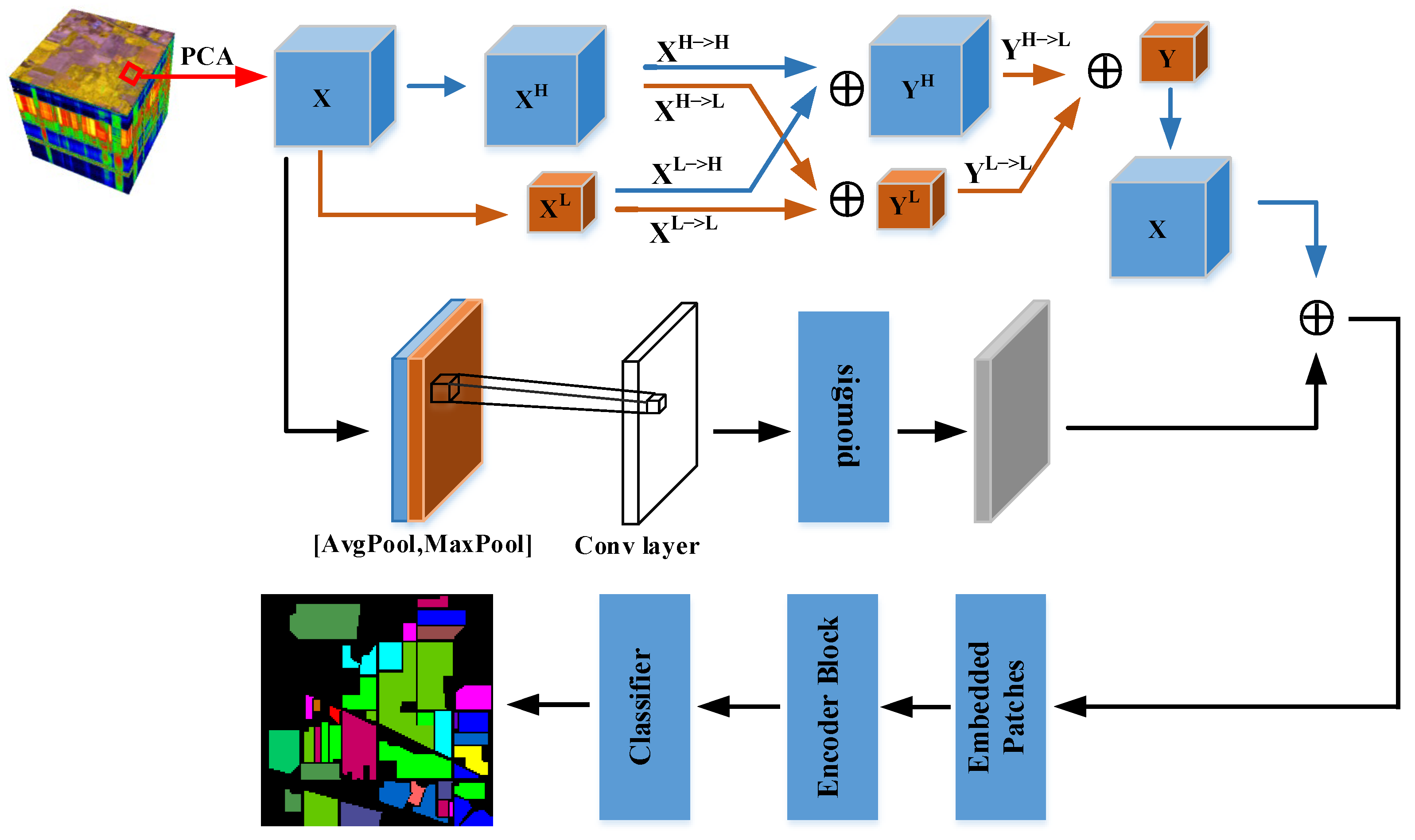
2. Related Work and Method
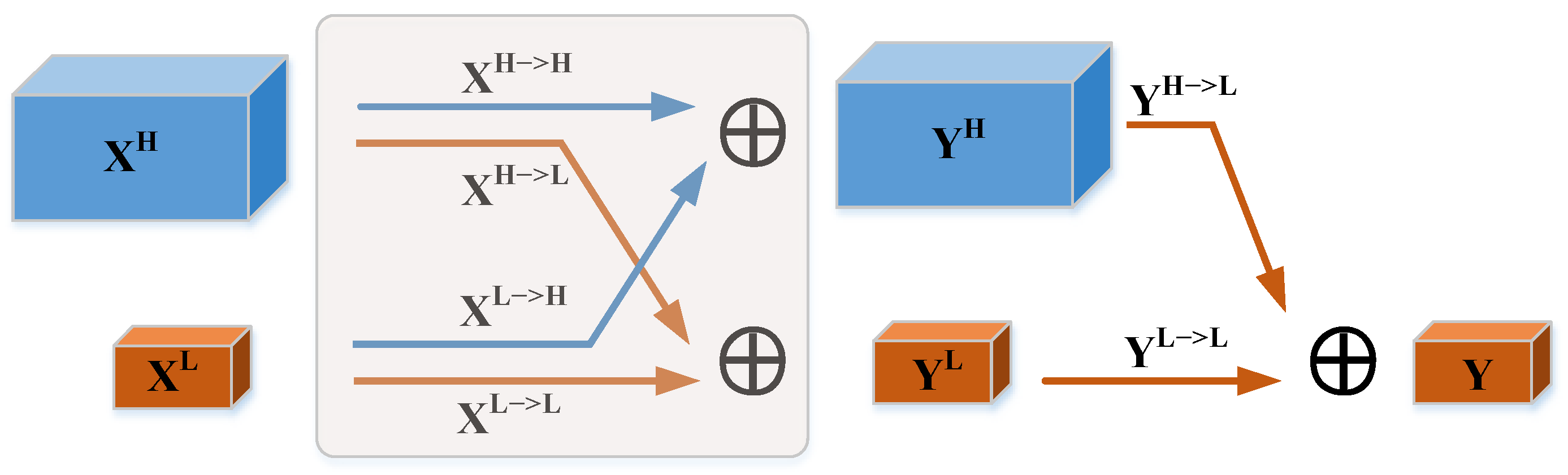
2.1. D OctConv Module
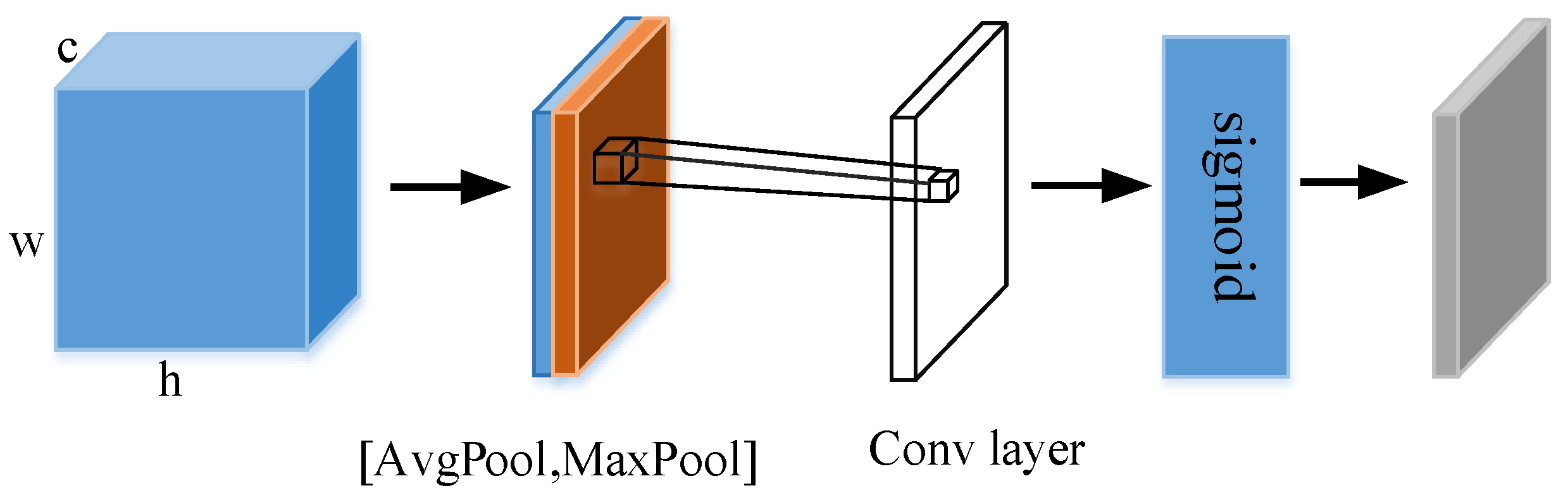
2.2. Spatial Attention Module
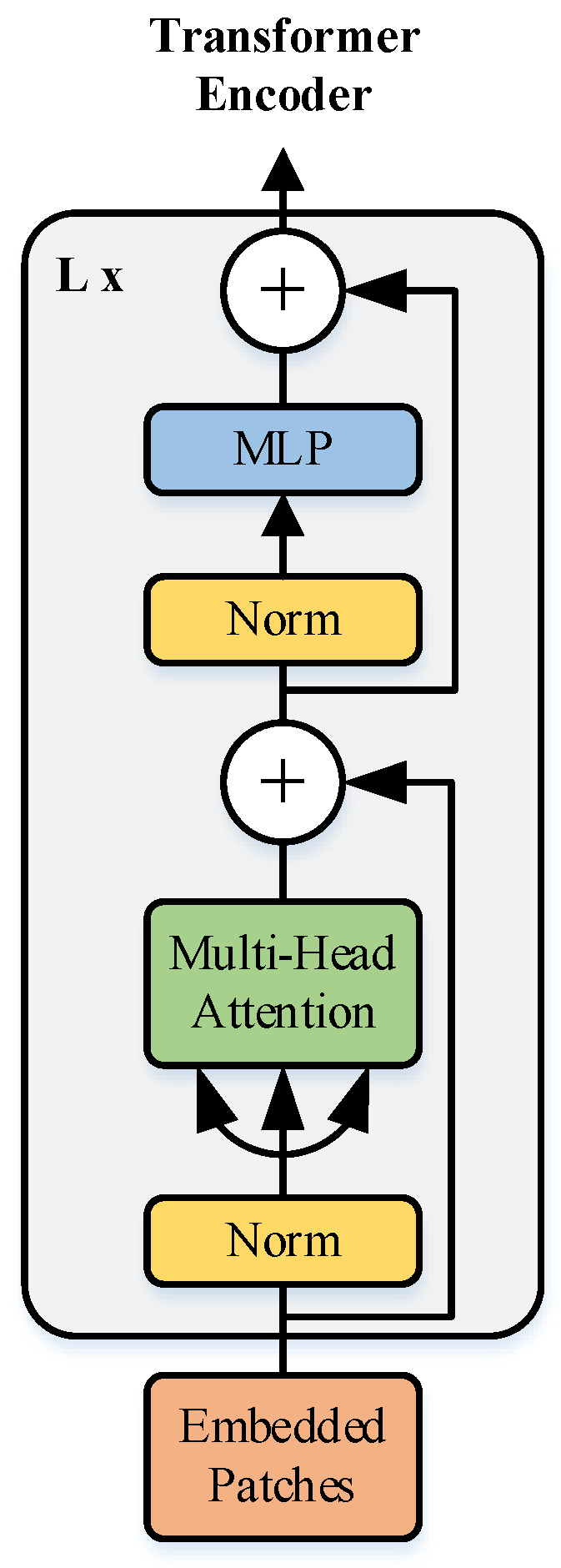
2.3. ViT Feature Extraction Module
- (i)
- Input sequence data , where (i = 1, …, t) denote the vector.
- (ii)
- The initial embedding is performed by embedding layer to get , , where W is the shared matrix.
- (iii)
- Multiplying each by three different matrices Wq, Wk and Wv, respectively, three vectors Query , Key and Value could be obtained.
- (iv)
- The attention score S is obtained by inner product of each Q and each K, for example. To make the gradient stable, the attention score is normalized. Such as , d is the dimension of or .
- (v)
- Performing the Softmax function on S, we get as . The Softmax function is defined as follows:
- (vi)
- Finally, an attention matrix , where . In summary, the multi-headed attention mechanism could be expressed as
| Algorithm 1 Self-Attention |
| Input: Input sequence |
| Output: Attention Matrix |
|
2.4. Method
3. Experiments
3.1. Data Description
- 1.
- India Pines (IP): It was taken by the airborne sensor AVIRIS in the agricultural area of northwestern Indiana, USA. The image has a spatial size of , a spatial resolution of roughly 20 m, and a wavelength range of 400–2500 nm. Additionally, there are 200 effective spectral bands, which were divided into 16 feature classes. During the experiment, 10% of the samples in each category were randomly selected as the training set, and the remaining samples were used as the test set. The detailed division results are shown in Table 1.
- 2.
- Pavia University (UP): It was acquired by the airborne sensor ROSIS in the area of the University of Pavia, Northern Italy. The image has a spatial size of , a spatial resolution of roughly 1.3 m, and a wavelength range of 430–860 nm. There are 103 effective spectral bands of the image, and it has 9 feature classes in total. During the experiment, 5% of the samples in each category were randomly selected as the training set, and the remaining samples were used as the test set. The detailed division results are shown in Table 2.
- 3.
- Salinas (SA): It was acquired by the airborne sensor AVIRIS in Salinas Valley, California, USA. The image has a spatial size of , a spatial resolution of roughly 3.7 m, and a wavelength range of 360–2500 nm. Additionally, there are 204 effective spectral bands, which were divided into 16 feature classes. During the experiment, 5% of the samples in each category were randomly selected as the training set, and the remaining samples were used as the test set. The detailed division results are shown in Table 3.
3.2. Parameter Setting
- 4.
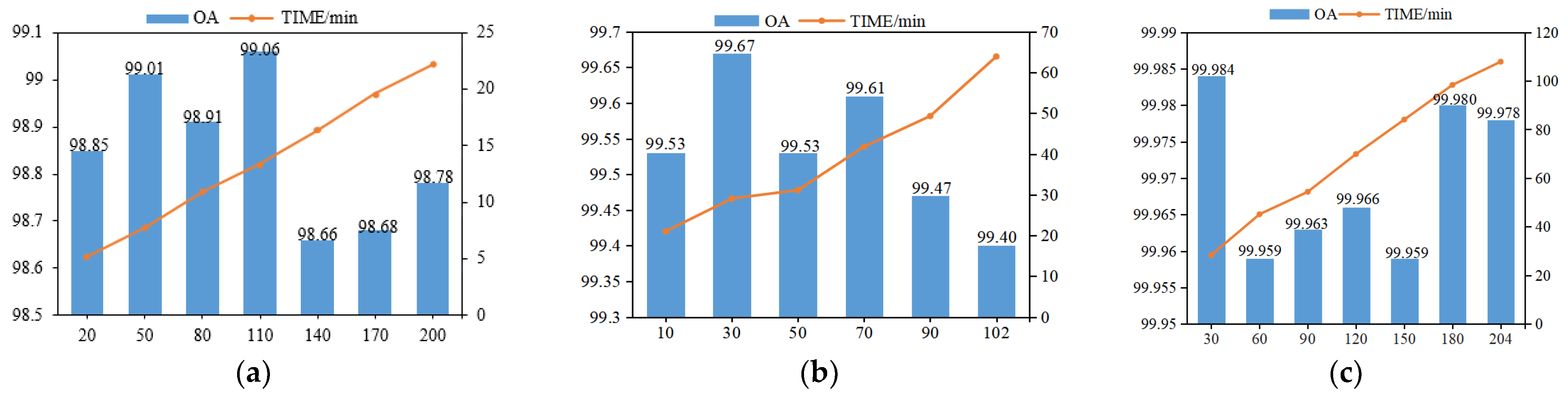
- The different values of dropout rate setting would affect the experimental results. After setting the dropout rate, some neurons would be stopped during training, but no neurons would be discarded during testing. Therefore, setting a reasonable dropout rate is helpful to improve the stability and robustness of the model and prevent overfitting. The range of values of dropout was [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0], and we compared different dropouts chosen for three data sets, respectively. The classification results of different dropout sizes were shown in Table 4. From Table 4, we could see that for the IP dataset, when the dropout value was set to 0.3, the OA was the maximum value, and the classification performance was the best. For the UP dataset, when the dropout value was set to 0.4, the OA was the maximum value, and the classification performance was the best. For the SA dataset, when the dropout value was set to 0.9, the OA was the maximum value, and the classification performance was the best.
- 5.
- The tuning of the learning rate has an important impact on the performance of the network model. If the learning rate is too large, it would cause the training cycle to oscillate and is likely to cross the optimal value. Conversely, the optimization efficiency may be too low, leading to a long time without convergence. In this paper, a grid search method was used to find the optimal learning rate from [0.01, 0.005, 0.001, 0.0005, 0.0001, 0.00005] for experiments. The classification results of different learning rate sizes were shown in Table 5. From Table 5, it could be seen that for the IP dataset, when the learning rate was set to 0.001, the OA at this time was the maximum value and the classification performance was the best. For the UP dataset, when the learning rate was set to 0.00005, the OA at this time was the maximum value and the classification performance was the best. For the SA dataset, when the learning rate was set to 0.0001, the OA at this time was the maximum value and the classification performance is the best.
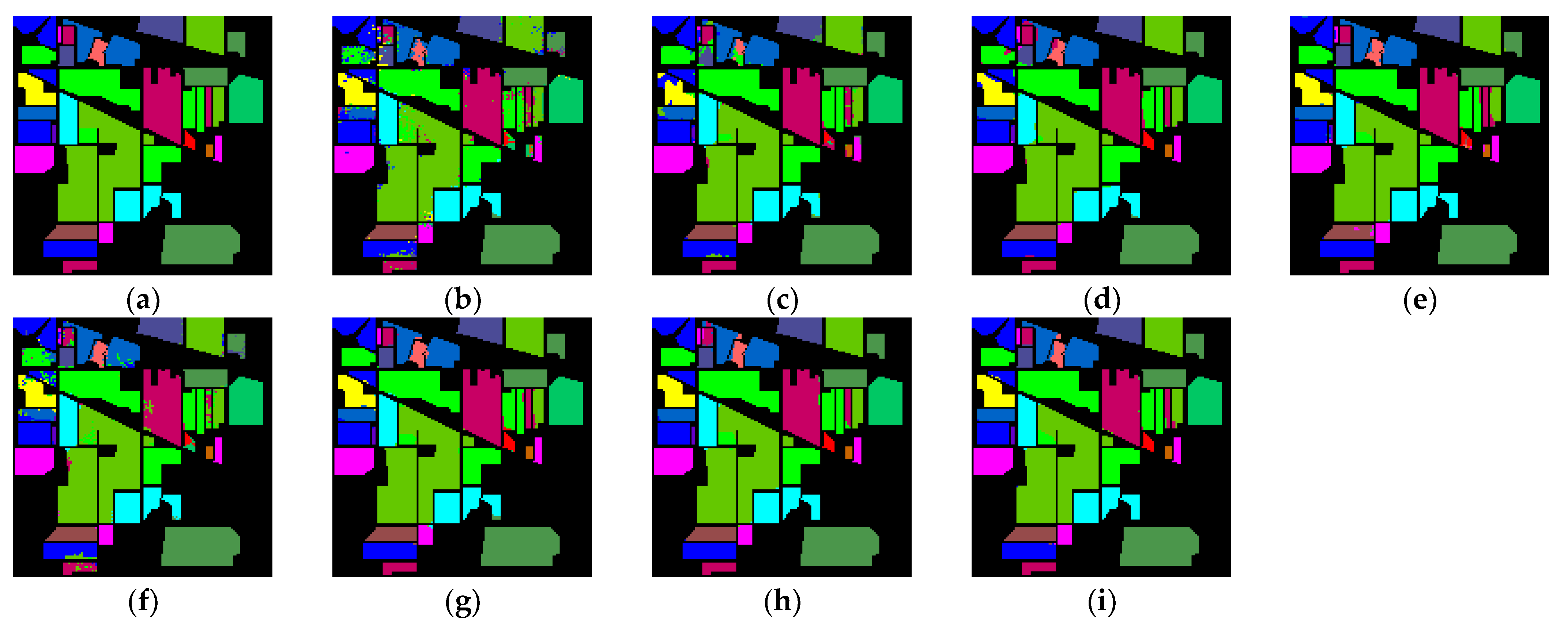
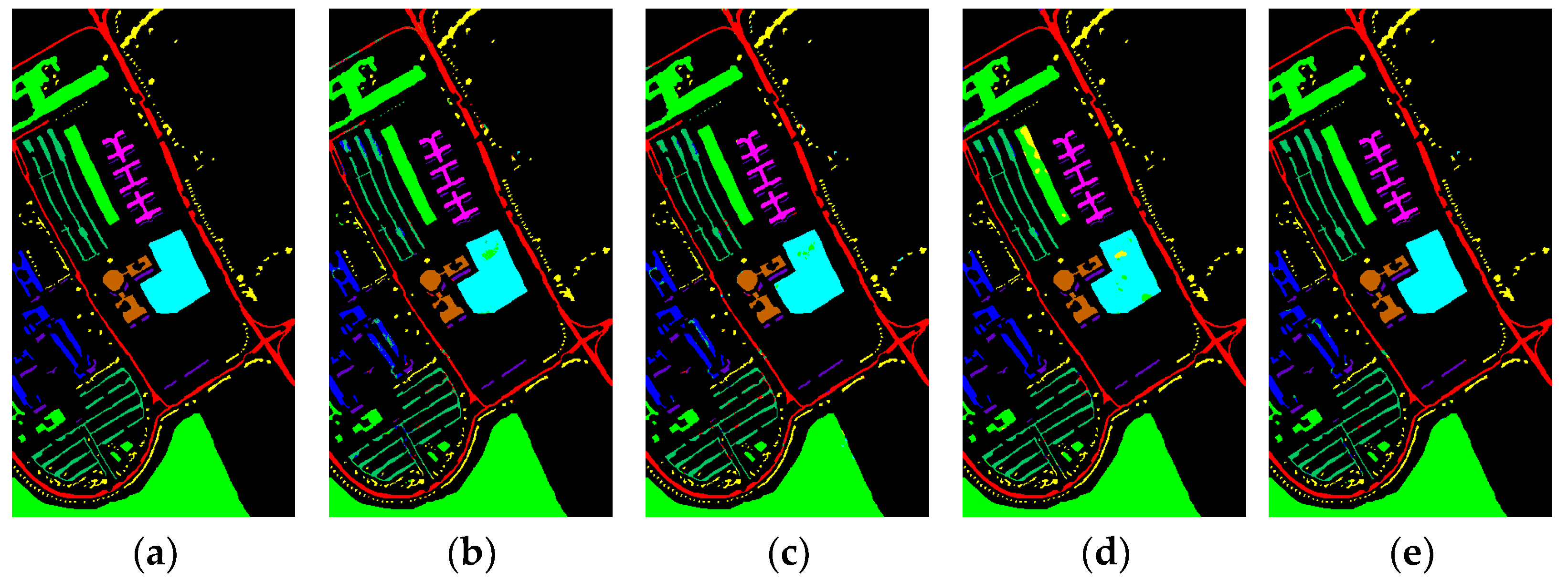
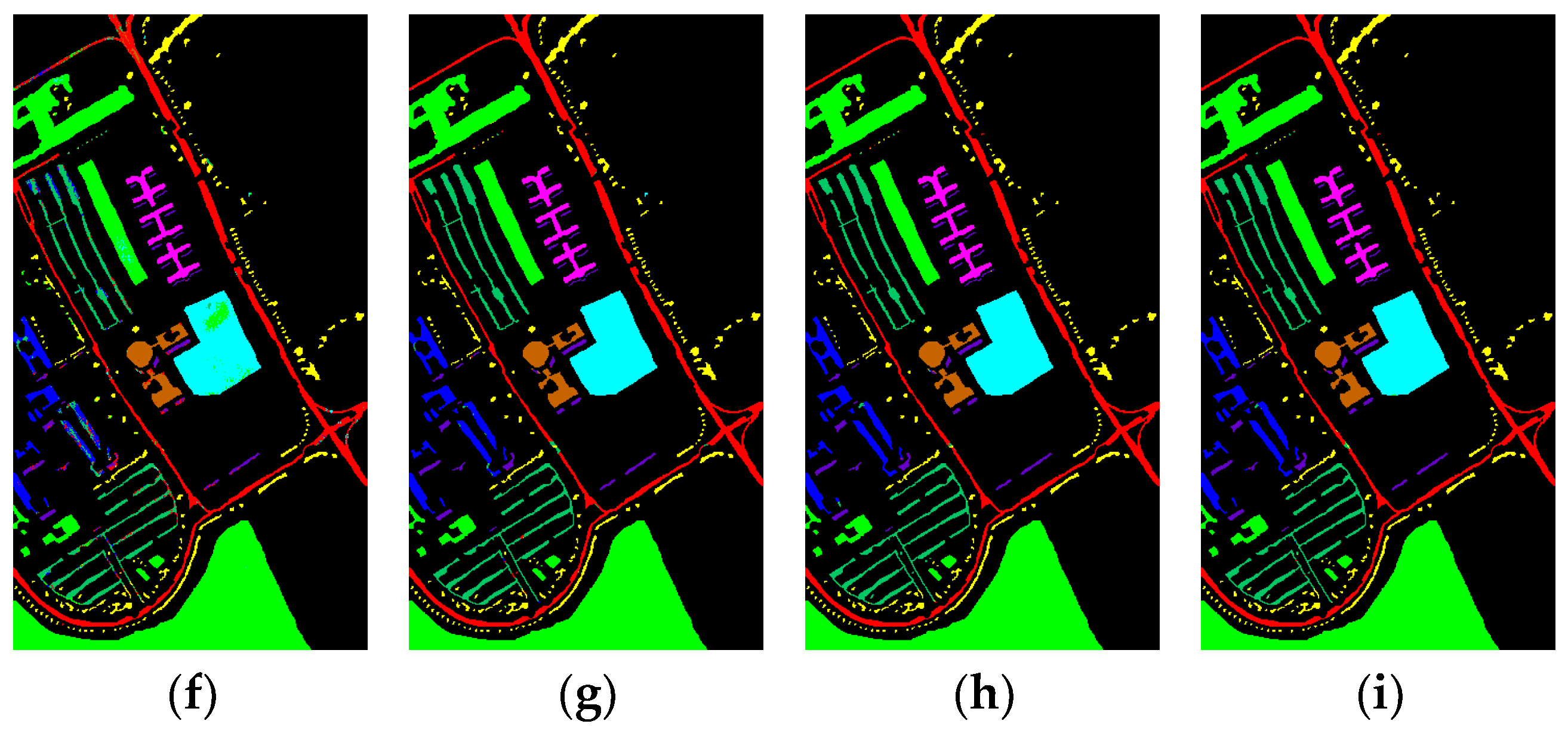
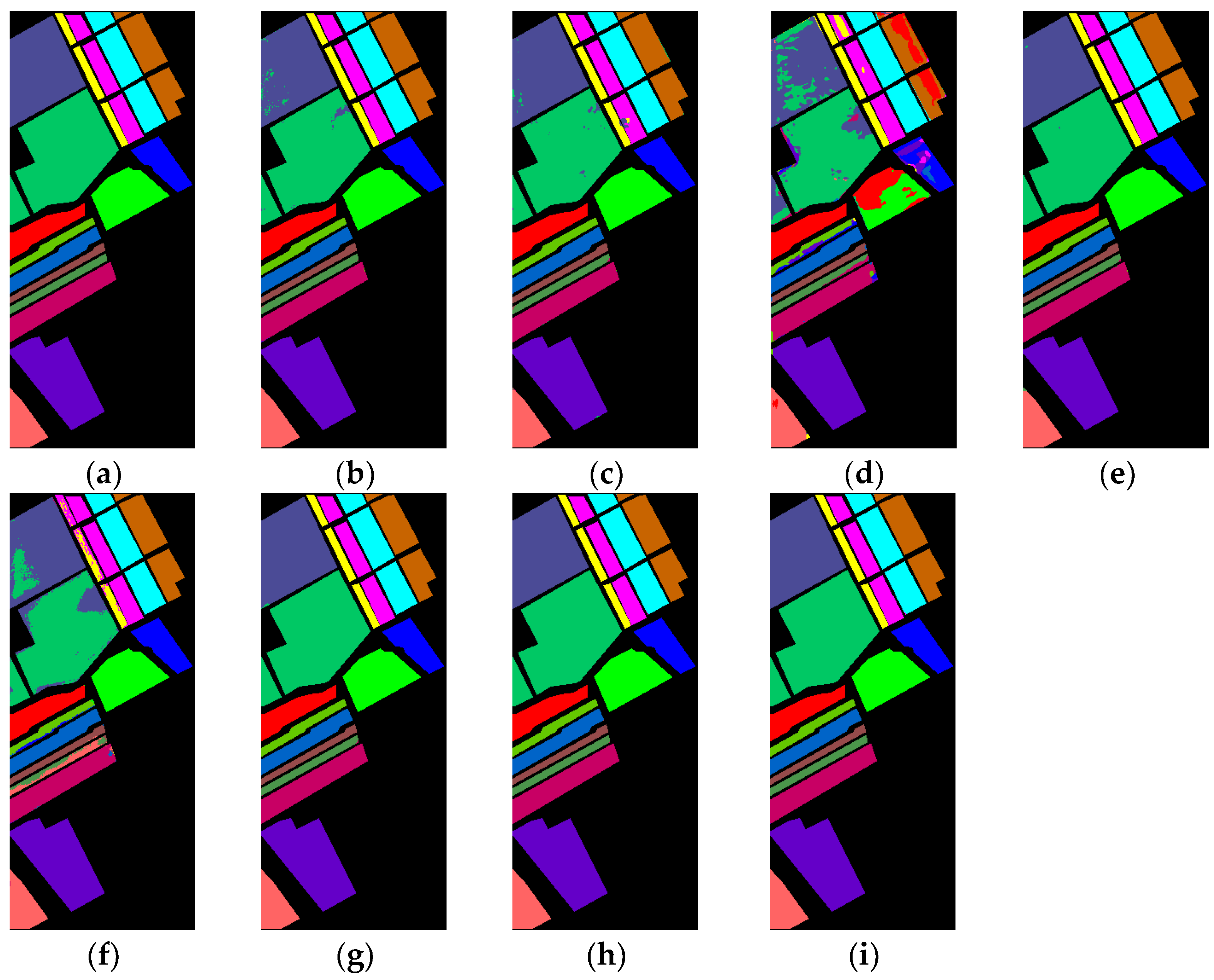
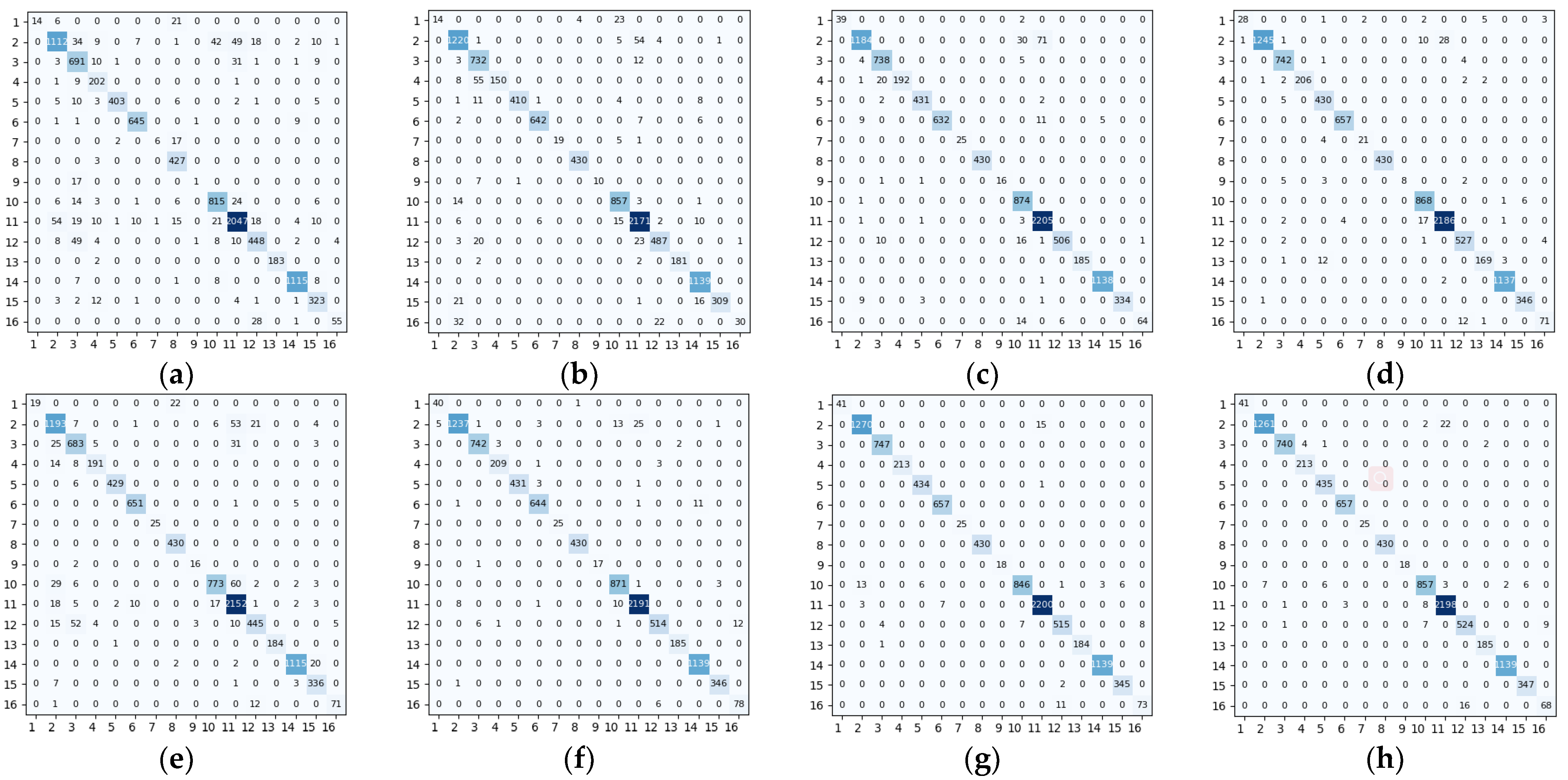
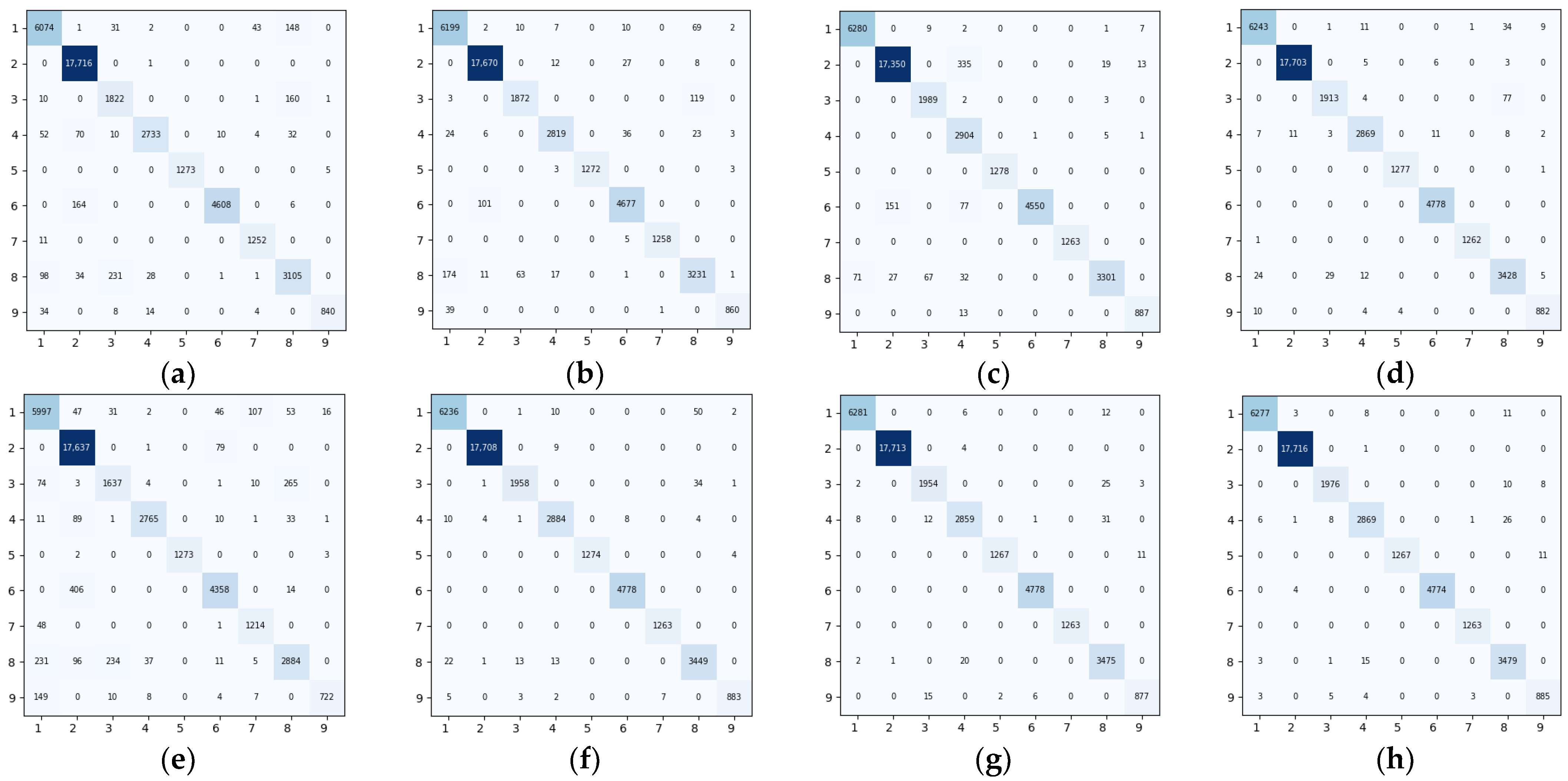
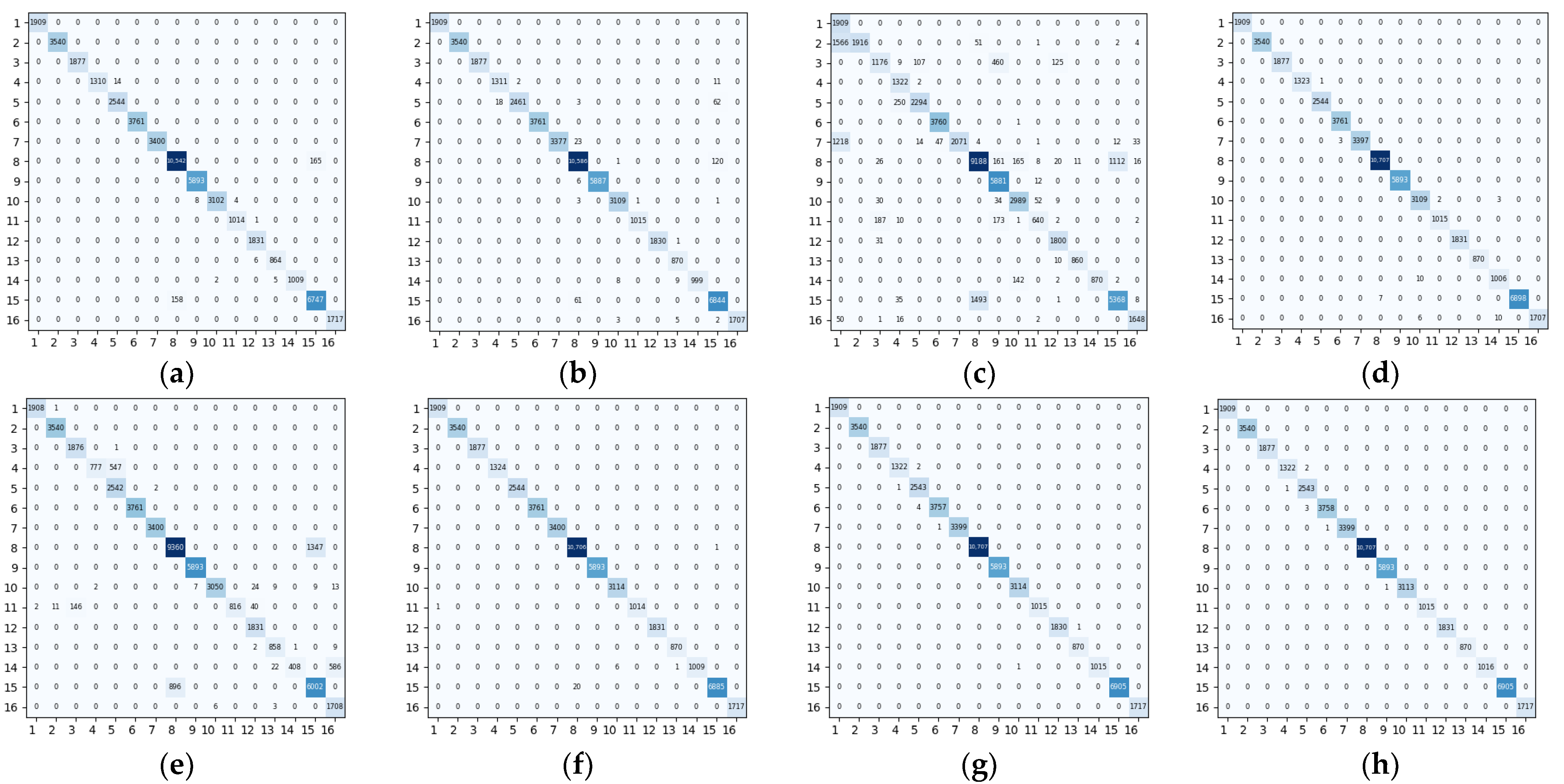
3.3. Performance Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mahlein, A.-K.; Oerke, E.-C.; Steiner, U.; Dehne, H.-W. Recent advances in sensing plant diseases for precision crop protection. Eur. J. Plant Pathol. 2012, 133, 197–209. [Google Scholar] [CrossRef]
- Murphy, R.J.; Schneider, S.; Monteiro, S.T. Consistency of Measurements of Wavelength Position from Hyperspectral Imagery: Use of the Ferric Iron Crystal Field Absorption at ~900 nm as an Indicator of Mineralogy. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2843–2857. [Google Scholar] [CrossRef]
- Su, H.; Yao, W.; Wu, Z.; Zheng, P.; Du, Q. Kernel low-rank representation with elastic net for China coastal wetland land cover classification using GF-5 hyperspectral imagery. ISPRS J. Photogramm. Remote Sens. 2021, 171, 238–252. [Google Scholar] [CrossRef]
- Erturk, A.; Iordache, M.-D.; Plaza, A. Sparse Unmixing-Based Change Detection for Multitemporal Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 708–719. [Google Scholar] [CrossRef]
- Hughes, G. On the Mean Accuracy of Statistical Pattern Recognizers. IEEE Trans. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Delalieux, S.; Somers, B.; Haest, B.; Spanhove, T.; Vanden Borre, J.; Mücher, C. Heathland conservation status mapping through integration of hyperspectral mixture analysis and decision tree classifiers. Remote Sens. Environ. 2012, 126, 222–231. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B.; Fu, P. Active Semi-Supervised Random Forest for Hyperspectral Image Classification. Remote Sens. 2019, 11, 2974. [Google Scholar] [CrossRef]
- Cui, B.; Cui, J.; Lu, Y.; Guo, N.; Gong, M. A Sparse Representation-Based Sample Pseudo-Labeling Method for Hyperspectral Image Classification. Remote Sens. 2020, 12, 664. [Google Scholar] [CrossRef]
- Cao, X.; Xu, Z.; Meng, D. Spectral-Spatial Hyperspectral Image Classification via Robust Low-Rank Feature Extraction and Markov Random Field. Remote Sens. 2019, 11, 1565. [Google Scholar] [CrossRef]
- Madani, H.; McIsaac, K. Distance Transform-Based Spectral-Spatial Feature Vector for Hyperspectral Image Classification with Stacked Autoencoder. Remote Sens. 2021, 13, 1732. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M. Adaptable Convolutional Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 3637. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, Z.; Jia, X.; Xu, Y.; Wei, Z. From Local to Global: Class Feature Fused Fully Convolutional Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 5043. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Yao, D.; Zhi-li, Z.; Xiao-feng, Z.; Wei, C.; Fang, H.; Yao-Ming, C.; Cai, W.-W. Deep hybrid: Multi-graph neural network collaboration for hyperspectral image classification. Def. Technol. 2022, in press. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N.; Zhan, Y. Semi-Supervised Locality Preserving Dense Graph Neural Network with ARMA Filters and Context-Aware Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511812. [Google Scholar] [CrossRef]
- Mughees, A.; Tao, L. Efficient Deep Auto-Encoder Learning for the Classification of Hyperspectral Images. In Proceedings of the 2016 International Conference on Virtual Reality and Visualization (ICVRV), Hangzhou, China, 24–26 September 2016; pp. 44–51. [Google Scholar]
- Wang, C.; Zhang, P.; Zhang, Y.; Zhang, L.; Wei, W. A multi-label Hyperspectral image classification method with deep learning features. In Proceedings of the Proceedings of the International Conference on Internet Multimedia Computing and Service, Xi’an, China, 19–21 August 2016; pp. 127–131. [Google Scholar]
- Chen, C.; Ma, Y.; Ren, G. Hyperspectral Classification Using Deep Belief Networks Based on Conjugate Gradient Update and Pixel-Centric Spectral Block Features. IEEE J. Sel. Appl. Earth Obs. Remote Sens. 2020, 13, 4060–4069. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2017, 55, 844–853. [Google Scholar] [CrossRef]
- Ding, C.; Li, Y.; Xia, Y.; Wei, W.; Zhang, L.; Zhang, Y. Convolutional Neural Networks Based Hyperspectral Image Classification Method with Adaptive Kernels. Remote Sens. 2017, 9, 618. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Li, J.; Plaza, A. Active Learning with Convolutional Neural Networks for Hyperspectral Image Classification Using a New Bayesian Approach. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6440–6461. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N. Graph Sample and Aggregate-Attention Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5504205. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, W.; Yang, N.; Hu, H.; Huang, X.; Cao, Y.; Cai, W. Unsupervised Self-Correlated Learning Smoothy Enhanced Locality Preserving Graph Convolution Embedding Clustering for Hyperspectral Images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536716. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, Y.; Li, S.; Deng, B.; Cai, W. Self-Supervised Locality Preserving Low-Pass Graph Convolutional Embedding for Large-Scale Hyperspectral Image Clustering. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5536016. [Google Scholar] [CrossRef]
- Chen, Y.; Fan, H.; Xu, B.; Yan, Z.; Kalantidis, Y.; Rohrbach, M.; Shuicheng, Y.; Feng, J. Drop an Octave: Reducing Spatial Redundancy in Convolutional Neural Networks with Octave Convolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3435–3444. [Google Scholar]
- Feng, Y.; Zheng, J.; Qin, M.; Bai, C.; Zhang, J. 3D Octave and 2D Vanilla Mixed Convolutional Neural Network for Hyperspectral Image Classification with Limited Samples. Remote Sens. 2021, 13, 4407. [Google Scholar] [CrossRef]
- Lian, L.; Jun, L.; Zhang, S. Hyperspectral Image Classification Method based on 3D Octave Convolution and Bi-RNN Ateention Network. Acta Photonica Sin. 2021, 50, 0910001. [Google Scholar]
- Hu, J.; Shen, L.; Albanie, S.; Sun, G.; Wu, E.H. Squeeze-and-Excitation Networks. arXiv 2008, arXiv:1709.01507v4. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Zhu, M.; Jiao, L.; Liu, F.; Yang, S.; Wang, J. Residual Spectral–Spatial Attention Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 449–462. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the Thirty-first Conference on Neural Information Processing Systems NIPS, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Zhao, Z.; Hu, D.; Wang, H.; Yu, X. Convolutional Transformer Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6009005. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking Hyperspectral Image Classification with Transformers. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Li, R.; Zheng, S.; Duan, C.; Yang, Y.; Wang, X. Classification of Hyperspectral Image Based on Double-Branch Dual-Attention Mechanism Network. Remote Sens. 2020, 12, 582. [Google Scholar] [CrossRef]
- Zhong, J.; Li, Z.; Chapman, M. Spectral-Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 2, 847–858. [Google Scholar] [CrossRef]
- Ben Hamida, A.; Benoit, A.; Lambert, P.; Ben Amar, C. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef]
- Ji, S.; Yang, M.; Yu, K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 221–231. [Google Scholar] [CrossRef] [PubMed]

| Number | Class Name | Train | Test | Total |
|---|---|---|---|---|
| 1 | Alfalfa | 5 | 41 | 46 |
| 2 | Corn-notill | 143 | 1285 | 1428 |
| 3 | Corn-min | 83 | 747 | 830 |
| 4 | Corn | 24 | 213 | 237 |
| 5 | Grass-pasture | 48 | 435 | 483 |
| 6 | Grass-trees | 73 | 657 | 730 |
| 7 | Grass-pasture-mowed | 3 | 25 | 28 |
| 8 | Hay-windrowed | 48 | 430 | 478 |
| 9 | Oats | 2 | 18 | 20 |
| 10 | Soybean-notill | 97 | 875 | 972 |
| 11 | Soybean-mintill | 245 | 2210 | 2455 |
| 12 | Soybean-clean | 59 | 534 | 593 |
| 13 | Wheat | 20 | 185 | 205 |
| 14 | Woods | 126 | 1139 | 1265 |
| 15 | Buildings-Grass-Trees | 39 | 347 | 386 |
| 16 | Stone-Steel-Tosers | 9 | 84 | 93 |
| Total Samples | 1024 | 9225 | 10,249 | |
| Number | Class Name | Train | Test | Total |
|---|---|---|---|---|
| 1 | Asphalt | 332 | 6299 | 6631 |
| 2 | Meadows | 932 | 17,717 | 18,649 |
| 3 | Gravel | 105 | 1994 | 2099 |
| 4 | Trees | 153 | 2911 | 3064 |
| 5 | Painted metal sheets | 67 | 1278 | 1345 |
| 6 | Bare soil | 251 | 4778 | 5029 |
| 7 | Bitumen | 67 | 1263 | 1330 |
| 8 | Self-Blocking bricks | 184 | 3499 | 3683 |
| 9 | Shadows | 47 | 900 | 947 |
| Total Samples | 2138 | 40,638 | 42,776 | |
| Number | Class Name | Train | Test | Total |
|---|---|---|---|---|
| 1 | Broccoli_green_weeds_1 | 100 | 1909 | 2009 |
| 2 | Broccoli_green_weeds_2 | 186 | 3540 | 3726 |
| 3 | Fallow | 99 | 1877 | 1976 |
| 4 | Fallow_rough_plow | 70 | 1324 | 1394 |
| 5 | Fallow_smooth | 134 | 2544 | 2678 |
| 6 | Stubble | 198 | 3761 | 3959 |
| 7 | Celery | 179 | 3400 | 3579 |
| 8 | Grapes_untrained | 564 | 10,707 | 11,271 |
| 9 | Soil_vinyard_develop | 310 | 5893 | 6203 |
| 10 | Com_senesces_green_weeds | 164 | 3114 | 3278 |
| 11 | Lettuce_romaine_4wk | 53 | 1015 | 1068 |
| 12 | Lettuce_romaine_5wk | 96 | 1831 | 1927 |
| 13 | Lettuce_romaine_6wk | 46 | 870 | 916 |
| 14 | Lettuce_romaine_7wk | 54 | 1016 | 1070 |
| 15 | Vinyard_untrained | 363 | 6905 | 7268 |
| 16 | Vinyard_untrained_trellis | 90 | 1717 | 1807 |
| Total Samples | 2706 | 51,423 | 54,129 | |
| Dropout Rate | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 |
|---|---|---|---|---|---|---|---|---|---|
| IP(OA/%) | 98.79 | 98.60 | 99.06 | 98.97 | 98.85 | 99.02 | 98.71 | 98.85 | 98.72 |
| UP(OA/%) | 99.65 | 99.59 | 99.52 | 99.67 | 99.57 | 99.45 | 99.62 | 99.58 | 98.64 |
| SA(OA/%) | 99.97 | 99.96 | 99.96 | 99.97 | 99.93 | 99.97 | 99.97 | 99.96 | 99.98 |
| Learning Rate | 0.01 | 0.005 | 0.001 | 0.0005 | 0.0001 | 0.00005 |
|---|---|---|---|---|---|---|
| IP(OA/%) | 92.325 | 98.569 | 99.06 | 98.785 | 98.916 | 98.959 |
| UP(OA/%) | 94.918 | 98.983 | 99.552 | 99.456 | 99.542 | 99.670 |
| SA(OA/%) | 53.866 | 86.684 | 99.928 | 99.945 | 99.984 | 99.929 |
| Class No. | Baseline | 3DCNN | SSRN | HybridSN | ViT | 3D_Octave | OctaveVit | SATNet |
|---|---|---|---|---|---|---|---|---|
| 1 | 100.00 | 100.00 | 100.00 | 96.55 | 100.00 | 88.89 | 100.00 | 100.00 |
| 2 | 92.74 | 93.13 | 97.93 | 99.84 | 91.63 | 99.20 | 98.76 | 99.45 |
| 3 | 81.01 | 88.41 | 95.72 | 97.63 | 88.82 | 98.93 | 99.34 | 99.73 |
| 4 | 78.29 | 100.00 | 100.00 | 100.00 | 95.50 | 98.12 | 100.00 | 98.16 |
| 5 | 99.02 | 97.76 | 98.85 | 95.34 | 99.31 | 100.00 | 98.64 | 99.77 |
| 6 | 97.14 | 98.92 | 100.00 | 99.39 | 98.34 | 98.77 | 98.95 | 99.55 |
| 7 | 85.71 | 100.00 | 100.00 | 91.30 | 100.00 | 100.00 | 100.00 | 100.00 |
| 8 | 86.44 | 99.88 | 100.00 | 100.00 | 94.71 | 99.77 | 100.00 | 100.00 |
| 9 | 33.33 | 100.00 | 100.00 | 100.00 | 84.21 | 100.00 | 100.00 | 100.00 |
| 10 | 91.16 | 94.28 | 94.58 | 96.66 | 97.11 | 97.32 | 99.18 | 98.85 |
| 11 | 94.42 | 95.47 | 96.20 | 98.65 | 93.16 | 98.74 | 99.28 | 98.88 |
| 12 | 86.99 | 94.56 | 98.83 | 96.34 | 92.52 | 98.28 | 97.35 | 97.04 |
| 13 | 100.00 | 100.00 | 100.00 | 95.48 | 100.00 | 98.93 | 100.00 | 98.93 |
| 14 | 98.24 | 96.53 | 99.56 | 99.56 | 98.94 | 99.04 | 99.74 | 99.82 |
| 15 | 87.06 | 99.68 | 100.00 | 98.30 | 91.06 | 98.86 | 98.29 | 98.30 |
| 16 | 91.67 | 96.77 | 98.46 | 91.03 | 93.42 | 86.67 | 90.12 | 88.31 |
| OA(%) | 92.00 | 95.64 | 97.48 | 98.33 | 93.89 | 98.63 | 99.04 | 99.06 |
| AA(%) | 78.29 | 90.23 | 95.44 | 91.30 | 82.50 | 98.14 | 98.56 | 98.35 |
| Kappa(%) | 90.89 | 95.01 | 97.12 | 98.09 | 93.01 | 98.44 | 98.91 | 98.92 |
| Class No. | Baseline | 3DCNN | SSRN | HybridSN | ViT | 3D_Octave | OctaveVit | SATNet |
|---|---|---|---|---|---|---|---|---|
| 1 | 96.74 | 96.27 | 98.88 | 99.33 | 92.12 | 99.41 | 99.81 | 99.81 |
| 2 | 98.50 | 99.33 | 98.98 | 99.94 | 96.48 | 99.97 | 99.99 | 99.95 |
| 3 | 86.68 | 96.25 | 96.32 | 98.30 | 85.57 | 99.09 | 99.39 | 99.30 |
| 4 | 98.38 | 98.64 | 86.30 | 98.76 | 98.15 | 98.83 | 98.45 | 99.30 |
| 5 | 100.00 | 100.00 | 100.00 | 99.69 | 100.00 | 100.00 | 100.00 | 100.00 |
| 6 | 99.76 | 98.34 | 99.98 | 99.65 | 96.63 | 98.83 | 99.94 | 100.00 |
| 7 | 95.94 | 99.92 | 100.00 | 99.92 | 90.33 | 99.45 | 99.53 | 99.68 |
| 8 | 89.97 | 93.65 | 99.16 | 96.56 | 88.77 | 97.51 | 98.08 | 98.67 |
| 9 | 99.29 | 98.96 | 97.69 | 98.11 | 97.30 | 99.21 | 98.43 | 97.68 |
| OA (%) | 97.01 | 98.08 | 97.94 | 99.30 | 94.70 | 99.49 | 99.60 | 99.67 |
| AA (%) | 95.43 | 97.09 | 98.36 | 98.81 | 91.27 | 99.17 | 99.14 | 99.33 |
| Kappa (%) | 96.02 | 97.45 | 97.28 | 99.08 | 92.93 | 99.33 | 99.47 | 99.56 |
| Class No. | Baseline | 3DCNN | SSRN | HybridSN | ViT | 3D_Octave | OctaveVit | SATNet |
|---|---|---|---|---|---|---|---|---|
| 1 | 100.00 | 100.00 | 40.25 | 100.00 | 99.90 | 99.95 | 100.00 | 100.00 |
| 2 | 100.00 | 100.00 | 100.00 | 100.00 | 99.66 | 100.00 | 100.00 | 100.00 |
| 3 | 100.00 | 100.00 | 81.05 | 100.00 | 92.78 | 100.00 | 100.00 | 100.00 |
| 4 | 100.00 | 98.65 | 80.51 | 100.00 | 99.74 | 100.00 | 99.92 | 99.92 |
| 5 | 99.45 | 99.92 | 94.91 | 99.96 | 82.27 | 100.00 | 99.76 | 99.80 |
| 6 | 100.00 | 100.00 | 98.77 | 99.92 | 100.00 | 100.00 | 99.97 | 99.80 |
| 7 | 100.00 | 100.00 | 100.00 | 100.00 | 99.94 | 100.00 | 100.00 | 99.97 |
| 8 | 98.52 | 99.10 | 85.58 | 99.93 | 91.26 | 99.81 | 100.00 | 100.00 |
| 9 | 99.86 | 100.00 | 87.66 | 100.00 | 99.88 | 100.00 | 100.00 | 100.00 |
| 10 | 99.94 | 99.62 | 90.63 | 99.68 | 99.58 | 99.81 | 99.97 | 99.98 |
| 11 | 99.61 | 99.90 | 89.39 | 99.80 | 100.00 | 100.00 | 100.00 | 100.00 |
| 12 | 99.62 | 100.00 | 91.42 | 100.00 | 96.52 | 100.00 | 100.00 | 100.00 |
| 13 | 99.42 | 98.31 | 98.74 | 100.00 | 96.19 | 99.89 | 99.89 | 100.00 |
| 14 | 100.00 | 100.00 | 100.00 | 98.72 | 99.76 | 100.00 | 100.00 | 100.00 |
| 15 | 97.61 | 97.22 | 82.64 | 99.90 | 81.57 | 99.99 | 100.00 | 100.00 |
| 16 | 100.00 | 100.00 | 96.32 | 100.00 | 73.75 | 100.00 | 100.00 | 100.00 |
| OA (%) | 99.29 | 99.33 | 84.97 | 99.91 | 92.81 | 99.94 | 99.980 | 99.984 |
| AA (%) | 99.57 | 99.40 | 85.55 | 99.87 | 90.58 | 99.93 | 99.970 | 99.979 |
| Kappa (%) | 99.21 | 99.26 | 83.28 | 99.90 | 92.00 | 99.94 | 99.978 | 99.982 |
| IP | UP | SA | ||||
|---|---|---|---|---|---|---|
| GFLOPs | Params | GFLOPs | Params | GFLOPs | Params | |
| Baseline | 2.16 | 67.5M | 0.98 | 30.6M | 0.98 | 30.6M |
| 3DCNN | 0.187 | 0.82M | 0.043 | 0.11M | 0.459 | 0.20M |
| SSRN | 14.19 | 0.34M | 7.29 | 0.19M | 14.47 | 0.35M |
| HybridSN | 8.88 | 2.67M | 1.70 | 1.19M | 1.70 | 1.19M |
| ViT | 0.0726 | 1.9M | 0.0357 | 0.8M | 0.0357 | 0.8M |
| 3D_Octave | 5.46 | 22.1M | 1.489 | 6.06M | 1.489 | 6.06M |
| OctaveVit | 6.81 | 2.41M | 2.10 | 0.93M | 2.10 | 0.93M |
| SATNet | 7.89 | 2.40M | 2.40 | 0.93M | 2.40 | 0.93M |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Q.; Zhong, X.; Chen, W.; Zhang, Z.; Li, B.; Sun, H.; Yang, T.; Tan, C. SATNet: A Spatial Attention Based Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 5902. https://doi.org/10.3390/rs14225902
Hong Q, Zhong X, Chen W, Zhang Z, Li B, Sun H, Yang T, Tan C. SATNet: A Spatial Attention Based Network for Hyperspectral Image Classification. Remote Sensing. 2022; 14(22):5902. https://doi.org/10.3390/rs14225902
Chicago/Turabian StyleHong, Qingqing, Xinyi Zhong, Weitong Chen, Zhenghua Zhang, Bin Li, Hao Sun, Tianbao Yang, and Changwei Tan. 2022. "SATNet: A Spatial Attention Based Network for Hyperspectral Image Classification" Remote Sensing 14, no. 22: 5902. https://doi.org/10.3390/rs14225902
APA StyleHong, Q., Zhong, X., Chen, W., Zhang, Z., Li, B., Sun, H., Yang, T., & Tan, C. (2022). SATNet: A Spatial Attention Based Network for Hyperspectral Image Classification. Remote Sensing, 14(22), 5902. https://doi.org/10.3390/rs14225902






