A Fast and Robust Heterologous Image Matching Method for Visual Geo-Localization of Low-Altitude UAVs
Abstract
1. Introduction
- A fast end-to-end feature-matching model is proposed. The model adopts the matching strategy from coarse to fine, and the minimum Euclidean distance is used to accelerate the coarse matching.
- The detector-free matching method and perspective transformation module are proposed to improve the matching robustness. In addition, a transformation criterion is added to ensure the efficiency of the algorithm.
- A complete visual geo-localization system is designed, including the image preprocessing module, the image matching module, and the localization module.
2. Materials and Methods
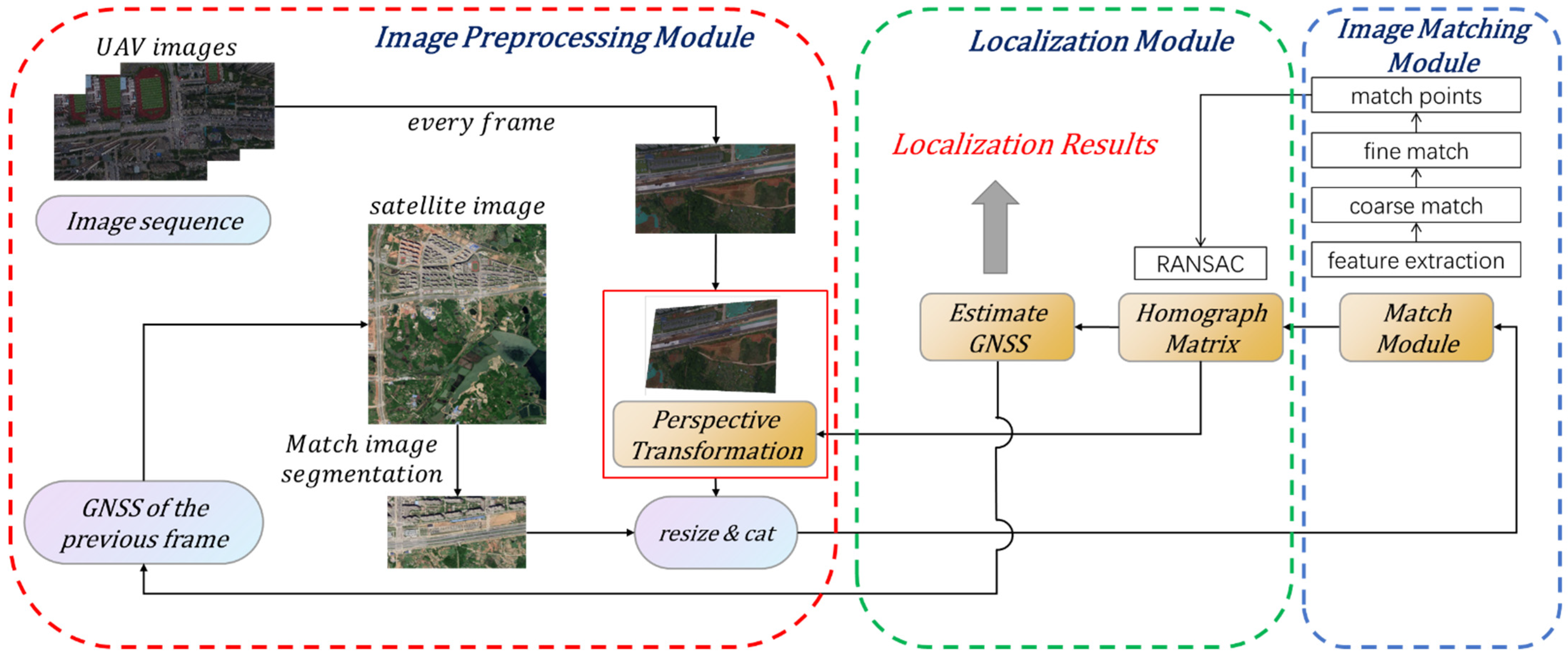
2.1. Overview
2.2. Image Preprocessing Module
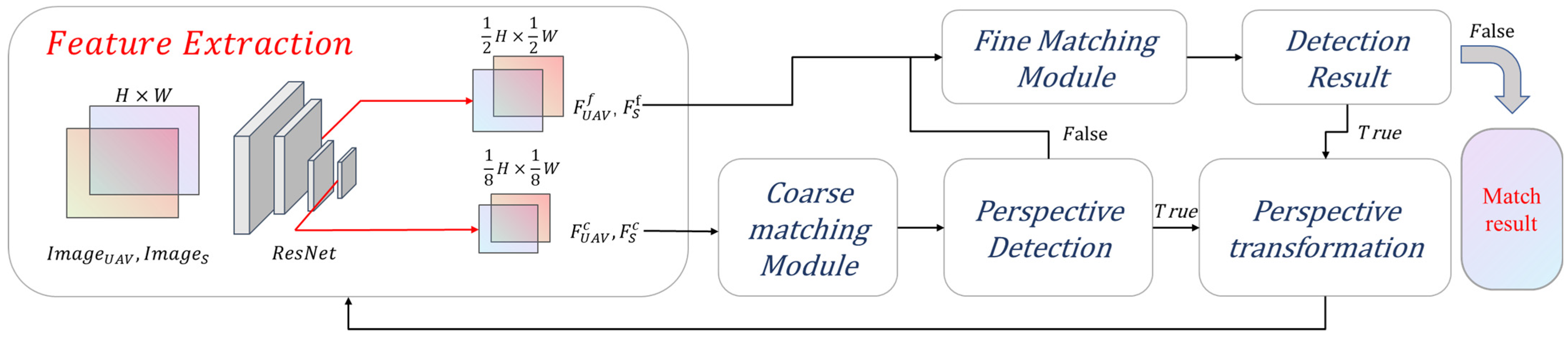
2.3. Image Matching Module
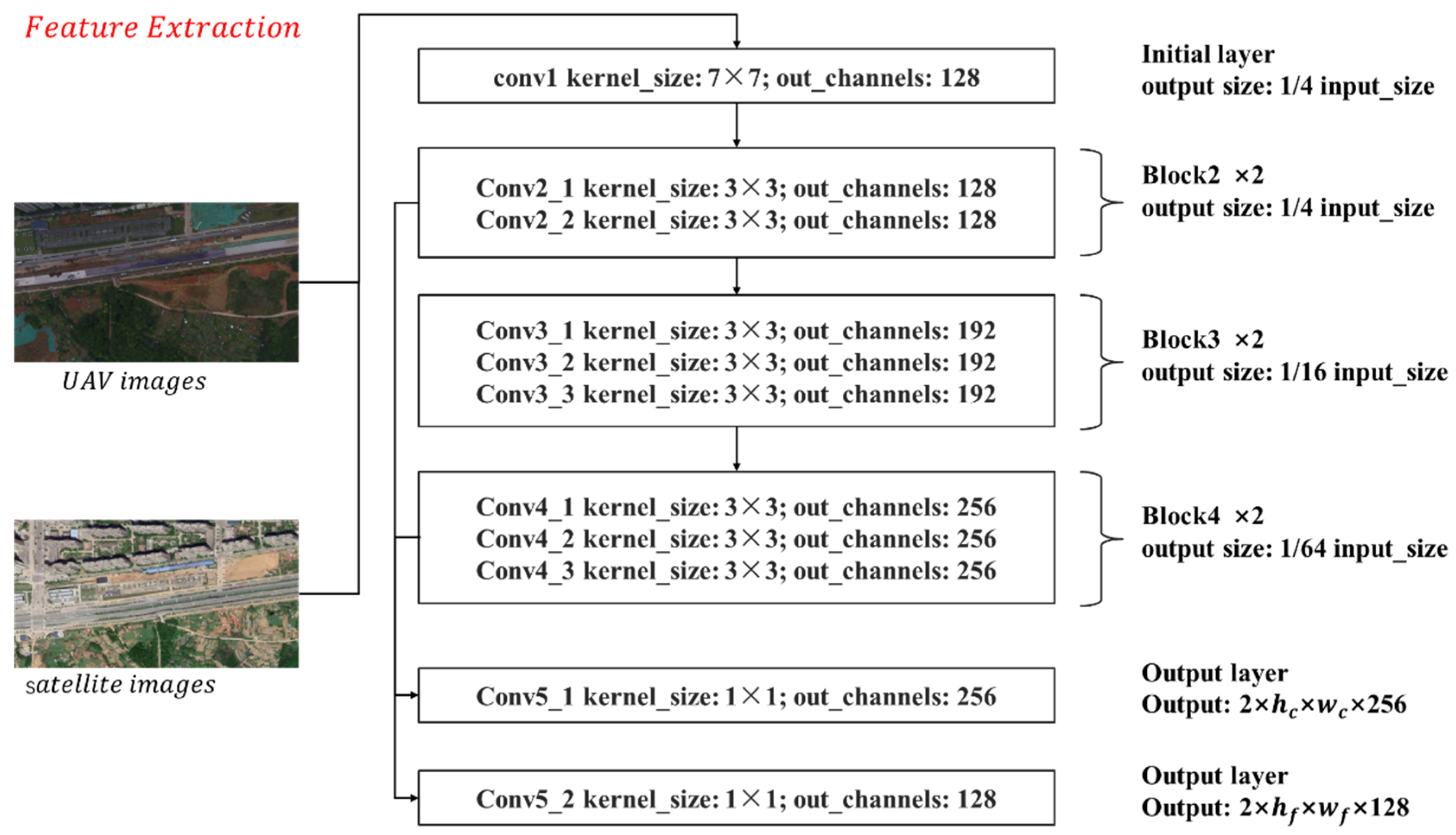
2.3.1. Feature Extraction Backbone
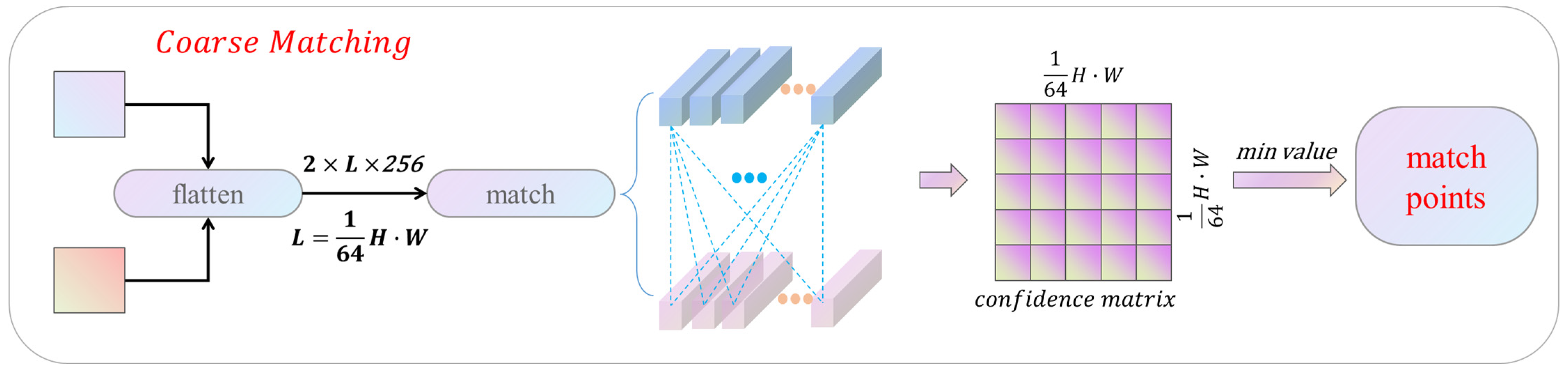
2.3.2. Coarse Matching Module
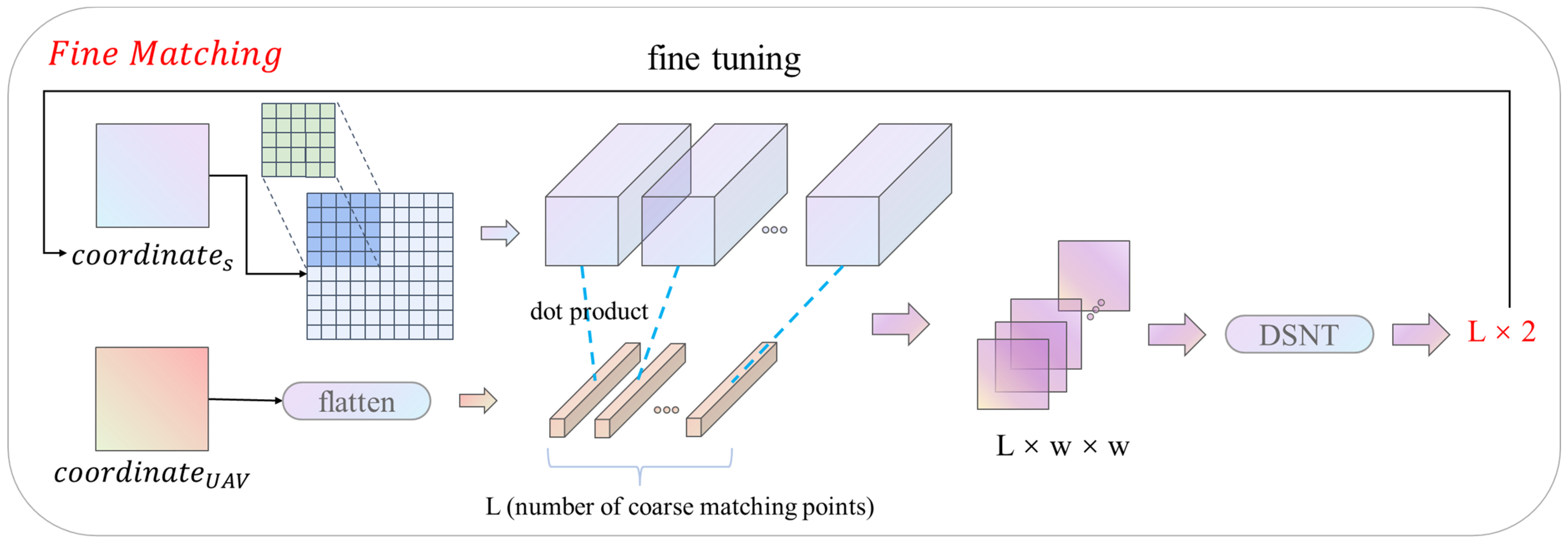
2.3.3. Fine Matching Module
2.3.4. Perspective Transformation Module
2.3.5. Training
2.4. Localization Module
3. Results
3.1. Datasets
3.2. Matching Performance Experiment
3.2.1. Matching Point Precision
3.2.2. Homography Matrix Precision
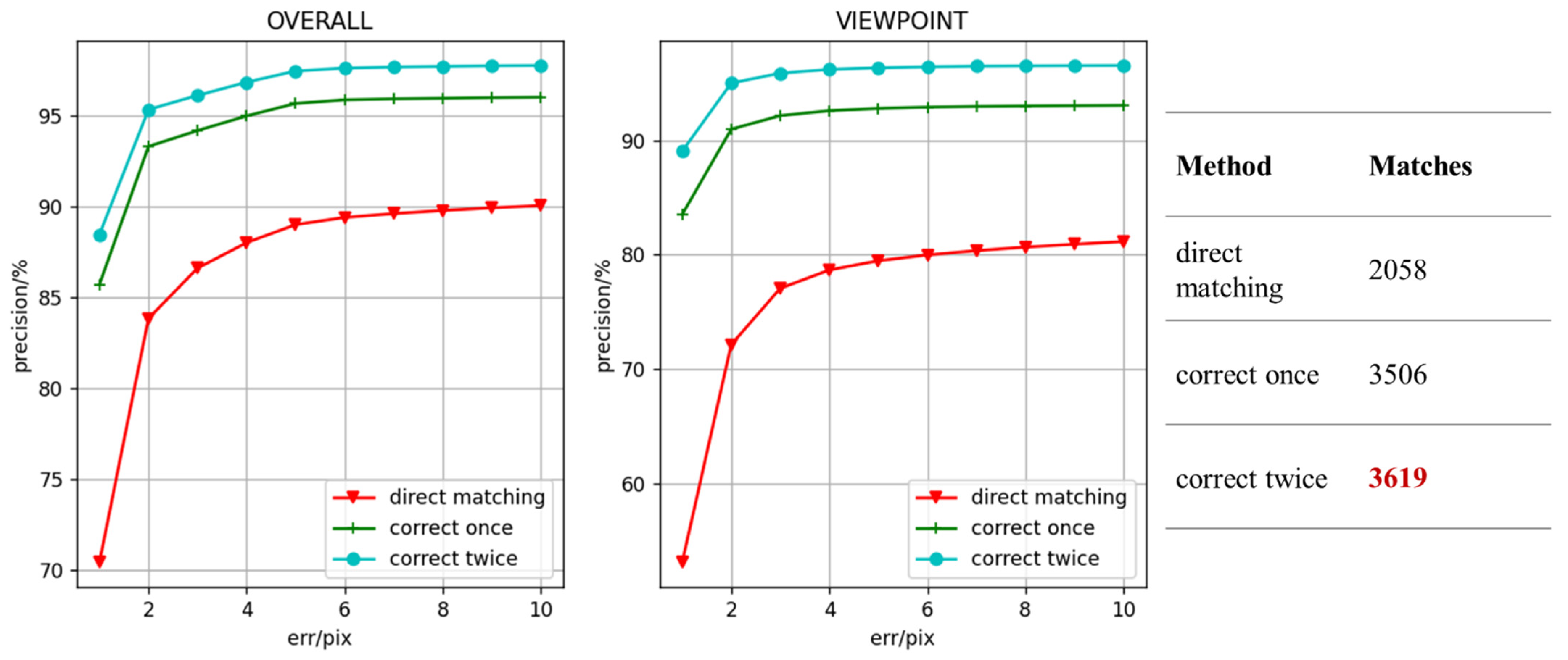
3.2.3. Ablation Experiment
3.3. Localization Precision
3.4. Efficiency
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kazerouni, I.A.; Fitzgerald, L.; Dooly, G.; Toal, D. A Survey of State-of-the-Art on Visual SLAM. Expert Syst. Appl. 2022, 205, 117734. [Google Scholar] [CrossRef]
- Gyagenda, N.; Hatilima, J.V.; Roth, H.; Zhmud, V. A review of GNSS-independent UAV navigation techniques. Robot. Auton. Syst. 2022, 152, 104069. [Google Scholar] [CrossRef]
- Couturier, A.; Akhloufi, M.A. A review on absolute visual localization for UAV. Robot. Auton. Syst. 2021, 135, 103666. [Google Scholar] [CrossRef]
- Alkendi, Y.; Seneviratne, L.; Zweiri, Y. State of the art in vision-based localization techniques for autonomous navigation systems. IEEE Access 2021, 9, 76847–76874. [Google Scholar] [CrossRef]
- Hu, K.; Wu, J.; Zheng, F.; Zhang, Y.; Chen, X. A survey of visual odometry. Nanjing Xinxi Gongcheng Daxue Xuebao 2021, 13, 269–280. [Google Scholar]
- Jin, Z.; Wang, X.; Moran, B.; Pan, Q.; Zhao, C. Multi-region scene matching based localisation for autonomous vision navigation of UAVs. J. Navig. 2016, 69, 1215–1233. [Google Scholar] [CrossRef]
- Yu, Q.; Shang, Y.; Liu, X.; Lei, Z.; Li, X.; Zhu, X.; Liu, X.; Yang, X.; Su, A.; Zhang, X.; et al. Full-parameter vision navigation based on scene matching for aircrafts. Sci. China Inf. Sci. 2014, 57, 1–10. [Google Scholar] [CrossRef][Green Version]
- Kaur, R.; Devendran, V. Image Matching Techniques: A Review. Inf. Commun. Technol. Compet. Strateg. 2021, 401, 785–795. [Google Scholar]
- Chen, L.; Heipke, C. Deep learning feature representation for image matching under large viewpoint and viewing direction change. ISPRS J. Photogramm. Remote Sens. 2022, 190, 94–112. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, J.; Xiao, G.; Shao, Z.; Guo, X. A review of multimodal image matching: Methods and applications. Inf. Fusion 2021, 73, 22–71. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, X.; Fan, A.; Jiang, J.; Yan, J. Image matching from handcrafted to deep features: A survey. Int. J. Comput. Vis. 2021, 129, 23–79. [Google Scholar] [CrossRef]
- Yao, G.; Yilmaz, A.; Meng, F.; Zhang, L. Review of Wide-Baseline Stereo Image Matching Based on Deep Learning. Remote Sens. 2021, 13, 3247. [Google Scholar] [CrossRef]
- Harris, C.; Stephens, M. A combined corner and edge detector. In Alvey Vision Conference; dblp: Saarland, Germany, 1988; Volume 15, pp. 10–5244. Available online: https://dblp.org/db/conf/bmvc/index.html (accessed on 3 October 2022).
- Trajković, M.; Hedley, M. Fast corner detection. Image Vis. Comput. 1998, 16, 75–87. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar]
- Calonder, M.; Lepetit, V.; Strecha, C.; Fua, P. Brief: Binary robust independent elementary features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2010; pp. 778–792. [Google Scholar]
- LOWE, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Tuytelaars, T.; Gool, L.V. Surf: Speeded up robust features. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2006; Volume 3951, pp. 404–417. [Google Scholar]
- Matas, J.; Chum, O.; Urban, M.; Pajdla, T. Robust wide-baseline stereo from maximally stable extremal regions. Image Vis. Comput. 2004, 22, 761–767. [Google Scholar] [CrossRef]
- Yi, K.M.; Trulls, E.; Lepetit, V.; Fua, P. Lift: Learned invariant feature transform. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; Volume 9910, pp. 467–483. [Google Scholar]
- Zhang, X.; Yu, F.; Karaman, S.; Chang, S. Learning discriminative and transformation covariant local feature detectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2017; pp. 6818–6826. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superpoint: Self-supervised interest point detection and description. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2017; pp. 224–236. [Google Scholar]
- Ono, Y.; Trulls, E.; Fua, P.; Yi, K.M. LF-Net: Learning local features from images. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; Volume 31. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-net: A trainable cnn for joint description and detection of local features. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2019; pp. 8092–8101. [Google Scholar]
- Chen, H.; Luo, Z.; Zhang, J.; Zhou, L.; Bai, X.; Hu, Z.; Tai, C.; Quan, L. Learning to match features with seeded graph matching network. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2021; pp. 6301–6310. [Google Scholar]
- Efe, U.; Ince, K.G.; Alatan, A. Dfm: A performance baseline for deep feature matching. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; IEEE Xplore: Washington, DC, USA, 2021; pp. 4284–4293. [Google Scholar]
- Revaud, J.; Leroy, V.; Weinzaepfel, P.; Chidlovskii, B. PUMP: Pyramidal and Uniqueness Matching Priors for Unsupervised Learning of Local Descriptors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2022; pp. 3926–3936. [Google Scholar]
- Liu, C.; Yuen, J.; Torralba, A. Sift flow: Dense correspondence across scenes and its applications. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 33, 978–994. [Google Scholar] [CrossRef]
- Choy, C.B.; Gwak, J.; Savarese, S.; Chandraker, M. Universal correspondence network. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; Volume 29. [Google Scholar]
- Schmidt, T.; Newcombe, R.; Fox, D. Self-supervised visual descriptor learning for dense correspon-dence. IEEE Robot. Autom. Lett. 2016, 2, 420–427. [Google Scholar] [CrossRef]
- Rocco, I.; Cimpoi, M.; Arandjelovi, R.; Torii, A.; Pajdla, T.; Sivic, J. Ncnet: Neighbourhood consensus networks for estimating image correspondences. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 1020–1034. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, X. DRC-NET: Densely Connected Recurrent Convolutional Neural Network for Speech Dereverberation. In Proceedings of the ICASSP 2022–2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 166–170. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; Volume 30. [Google Scholar]
- Sarlin, P.E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2020; pp. 4938–4947. [Google Scholar]
- Sun, J.; Shen, Z.; Wang, Y.; Bao, H.; Zhou, X. LoFTR: Detector-free local feature matching with transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2021; pp. 8922–8931. [Google Scholar]
- Wang, Q.; Zhang, J.; Yang, K.; Peng, K.; Stiefelhagen, R. MatchFormer: Interleaving Attention in Transformers for Feature Matching; Karlsruhe Institute of Technology: Karlsruhe, Germany, 2022; to be submitted. [Google Scholar]
- Liu, Y.; Tao, J.; Kong, D.; Zhang, Y.; Li, P. A Visual Compass Based on Point and Line Features for UA V High-Altitude Orientation Estimation. Remote Sens. 2022, 14, 1430. [Google Scholar] [CrossRef]
- Zhang, Y.; Ma, G.; Wu, J. Air-Ground Multi-Source Image Matching Based on High-Precision Reference Image. Remote Sens. 2022, 14, 588. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2016; pp. 770–778. [Google Scholar]
- Wen, K.; Chu, J.; Chen, J.; Chen, Y.; Cai, J. MO SiamRPN with Weight Adaptive Joint MIoU for UAV Visual Localization. Remote Sens. 2022, 14, 4467. [Google Scholar] [CrossRef]
- Wang, T.; Zheng, Z.; Yan, C.; Zhang, J.; Sun, Y.; Zheng, B.; Yang, Y. Each part matters: Local patterns facilitate cross-view geo-localization. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 867–879. [Google Scholar] [CrossRef]
- Zheng, Z.; Wei, Y.; Yang, Y. University-1652: A multi-view multi-source benchmark for drone-based geo-localization. In Proceedings of the 28th ACM International Conference on Multimedia; Association for Computing Machinery: New York, NY, USA, 2020; pp. 1395–1403. [Google Scholar]
- Ding, L.; Zhou, J.; Meng, L.; Long, Z. A practical cross-view image matching method between UAV and satellite for UAV-based geo-localization. Remote Sens. 2020, 13, 47. [Google Scholar] [CrossRef]
- Zhuang, J.; Dai, M.; Chen, X.; Zheng, E. A Faster and More Effective Cross-View Matching Method of UAV and Satellite Images for UAV Geolocalization. Remote Sens. 2021, 13, 3979. [Google Scholar] [CrossRef]
- Wang, G.; Zhao, Y.; Tang, C.; Luo, C.; Zeng, W. When Shift Operation Meets Vision Transformer: An Extremely Simple Alternative to Attention Mechanism; University of Science and Technology of China: Hefei, China, 2022; to be submitted. [Google Scholar]
- Lee-Thorp, J.; Ainslie, J.; Eckstein, I.; Ontanon, S. FNet: Mixing tokens with fourier transforms. In Proceedings of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL), Seattle, WA, USA, 10–15 July 2022. [Google Scholar]
- Yu, W.; Luo, M.; Zhou, P.; Si, C.; Zhou, Y.; Wang, X.; Feng, J.; Yan, S. Metaformer is actually what you need for vision. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition; IEEE Xplore: Washington, DC, USA, 2022; pp. 10819–10829. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Nibali, A.; He, Z.; Morgan, S.; Prendergast, L. Numerical Coordinate Regression with Convolutional Neural Networks; La Trobe University: Melbourne, Australia, 2018; to be submitted. [Google Scholar]
- Li, Z.; Snavely, N. Megadepth: Learning single-view depth prediction from internet photos. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2018; pp. 2041–2050. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Balntas, V.; Lenc, K.; Vedaldi, A.; Mikolajczyk, K. HPatches: A benchmark and evaluation of handcrafted and learned local descriptors. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2017; pp. 5173–5182. [Google Scholar]
- Zhou, Q.; Sattler, T.; Leal-Taixe, L. Patch2pix: Epipolar-guided pixel-level correspondences. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE Xplore: Washington, DC, USA, 2021; pp. 4669–4678. [Google Scholar]
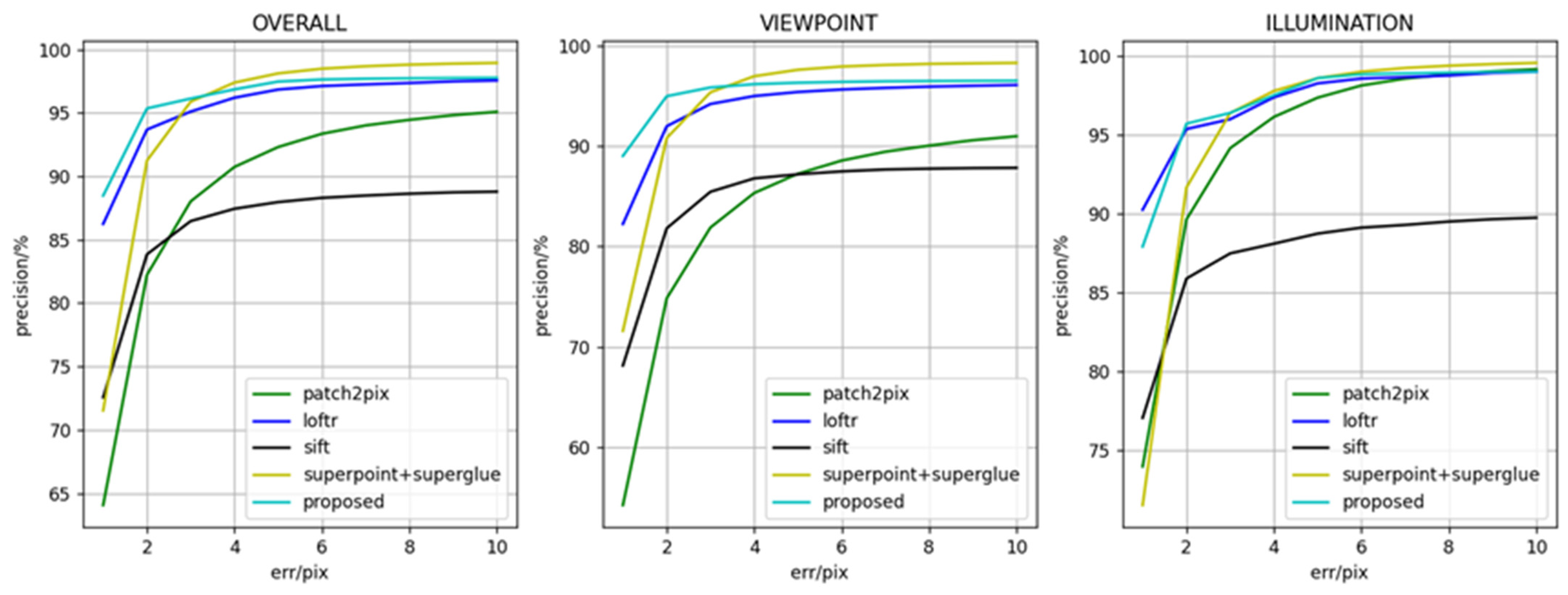



| Method | 1 px | 3 px | 5 px |
|---|---|---|---|
| LoFTR | 65.9 | 80.9 | 86.3 |
| SuperGlue | 51.3 | 83.6 | 89.1 |
| Patch2Pix | 51.0 | 79.2 | 86.4 |
| SIFT | 35.9 | 61.5 | 71.0 |
| Proposed | 66.5 | 84.5 | 90.1 |
| Method | 1 px | 3 px | 5 px |
|---|---|---|---|
| direct matching | 26.8 | 56.6 | 67.7 |
| correct once | 42.5 | 69.8 | 77.0 |
| correct twice | 50.3 | 77.3 | 84.4 |
| Method | Same Points | Correct Points | Precision | Time (CPU) |
|---|---|---|---|---|
| Euclidean Distance | 73.8(1486/2015) | 95.1(503/529) | 91.6(1845/2015) | 0.13 s |
| Pearson Correlation Coefficient | 74.3(1485/1997) | 94.5(484/512) | 92.1(1840/1997) | 2.1 s |
| Cosine Distance | 74.3(1483/1994) | 95.1(486/511) | 92.1(1839/1994) | 0.11 s |
| Transformer | 99.9(2157/2159) | 1.3 s |
| Method | Average Error | Max Error | Matches |
|---|---|---|---|
| LoFTR | 12.01 m/× | 24.61 m/× | 471/601 |
| SuperGlue | 11.14 m/9.84 m | 20.42 m/21.00 m | 601/601 |
| Patch2Pix | 11.16 m/9.81 m | 21.54 m/21.54 m | 601/601 |
| Proposed | 11.13 m/9.80 m | 20.14 m/20.72 m | 601/601 |
| Method | Average Error | Max Error | Matches |
|---|---|---|---|
| LoFTR | 3.31 m/× | 8.80 m/× | 432/792 |
| SuperGlue | 3.21 m/× | 8.50 m/× | 423/792 |
| Patch2Pix | 3.30 m/2.57 m | 8.60 m/14.48 m | 792/792 |
| Proposed | 3.17 m/2.24 m | 8.60 m/14.16 m | 792/792 |
| Method | Time |
|---|---|
| LoFTR | 1.84 s |
| SuperGlue | 0.80 s |
| Patch2Pix | 2.20 s |
| Proposed | 0.65 s/1.03 s/1.46 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sui, H.; Li, J.; Lei, J.; Liu, C.; Gou, G. A Fast and Robust Heterologous Image Matching Method for Visual Geo-Localization of Low-Altitude UAVs. Remote Sens. 2022, 14, 5879. https://doi.org/10.3390/rs14225879
Sui H, Li J, Lei J, Liu C, Gou G. A Fast and Robust Heterologous Image Matching Method for Visual Geo-Localization of Low-Altitude UAVs. Remote Sensing. 2022; 14(22):5879. https://doi.org/10.3390/rs14225879
Chicago/Turabian StyleSui, Haigang, Jiajie Li, Junfeng Lei, Chang Liu, and Guohua Gou. 2022. "A Fast and Robust Heterologous Image Matching Method for Visual Geo-Localization of Low-Altitude UAVs" Remote Sensing 14, no. 22: 5879. https://doi.org/10.3390/rs14225879
APA StyleSui, H., Li, J., Lei, J., Liu, C., & Gou, G. (2022). A Fast and Robust Heterologous Image Matching Method for Visual Geo-Localization of Low-Altitude UAVs. Remote Sensing, 14(22), 5879. https://doi.org/10.3390/rs14225879






