Computer Vision and Pattern Recognition for the Analysis of 2D/3D Remote Sensing Data in Geoscience: A Survey
Abstract
1. Introduction
2. Computer Vision and Pattern Recognition Approaches
2.1. Computer Vision and Pattern Recognition prior Deep Learning
2.1.1. Descriptors
2.1.2. Active Contours
2.1.3. Markov Random Fields
2.1.4. Superpixels
2.1.5. Clustering
2.1.6. Decision Trees and Random Forests
2.1.7. Support Vector Machines
2.1.8. Linear and Logistic Regression
2.1.9. Artificial Neural Networks
2.2. Deep Learning-Based Computer Vision and Pattern Recognition
2.2.1. Convolutional Neural Networks
2.2.2. Recurrent Neural Networks
2.2.3. Deep Generative Models and GANs
3. Geoscience-Related Applications of Computer Vision and Pattern Recognition
3.1. Land Cover Mapping
3.2. Target Detection
3.3. Pattern Mining in Geoscience Imaging Data
3.4. Boundary Extraction
3.5. Change Detection
3.6. Image Preprocessing
4. Discussion
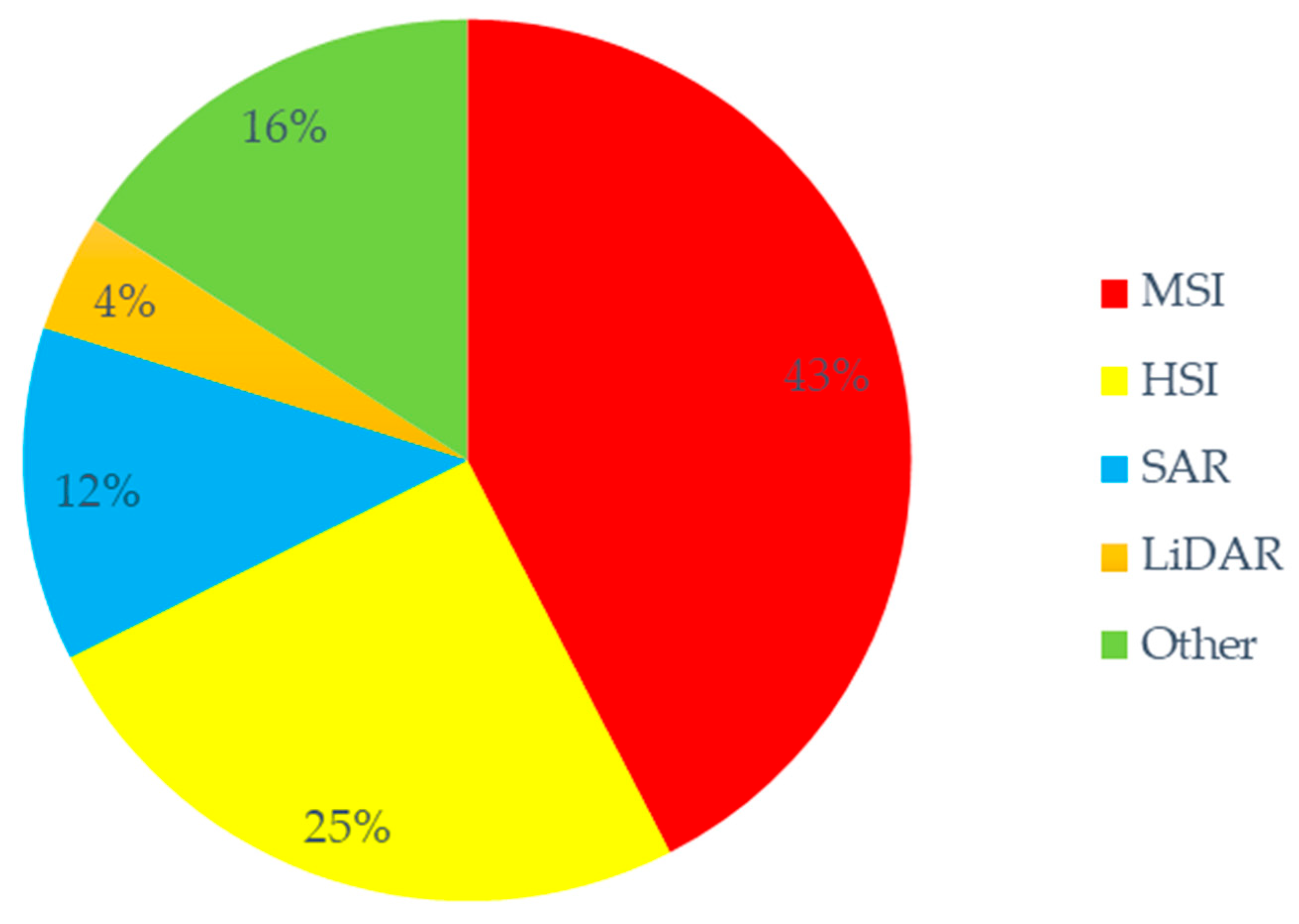
4.1. Geoscience-Related Imaging Data Availability
4.2. Inherent Issues in Geoscience Imaging Data
5. Conclusions
- -
- There are several widely adopted geoscience datasets. Still, most works involve model training or benchmarking with ad hoc subsets of these datasets. Aiming to cope with this issue, there is a number of organized efforts towards the standardization of geoscience datasets, including Microsoft’s effort for AI on Earth, Google Earth and various benchmarking platforms [11].
- -
- There are inherent difficulties in obtaining labelled geoscience data. Satellite observations are often limited, in both spatial and temporal dimensions, whereas ground truth labelling is often associated with the cost of high-quality measurements. For very complex systems, in which the exact state cannot be accurately inferred, ground truth is completely out of reach. In other cases, there are processes and events that occur rarely. This labelled data paucity can be partially addressed with standard data augmentation approaches, as well as with synthetic data generation by means of GANs. These neural network architectures provide a promising tool for synthetic data generation. In addition, some machine learning approaches, such as active learning or few shot learning, aid model training in cases of limited availability of labelled data. Still, active learning has not been widely adopted, whereas few shot learning has not been applied at all in geoscience.
- -
- Another issue related to data and label scarcity is the ‘curse of dimensionality’ or Hughes phenomenon, which ultimately leads to overfitting. This issue is even more intense in the case of HSIs, due to the large number of correlated spectral bands. A standard remedy for Hughes phenomenon is dimensionality reduction via feature extraction.
- -
- DL-based methods, especially CNNs and CNN-based architectures, are prevalent in recent developments. Still, the successful application of such approaches depends on labelled data availability. Standard pre-DL computer vision approaches remain relevant and often provide an alternative to bypass the aforementioned difficulties in data labelling, either as standalone approaches or in the context of hybrid methods that also employ learning-based components.
Author Contributions
Funding
Conflicts of Interest
References
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine learning for the geosciences: Challenges and op-portunities. IEEE Tran. Knowl. Dat. Eng. 2019, 31, 1544–1554. [Google Scholar] [CrossRef]
- NASA; USGS. Landsat Data Archive. Available online: https://landsat.gsfc.nasa.gov/data/ (accessed on 24 June 2022).
- Jafarbiglu, H.; Pourreza, A. A comprehensive review of remote sensing platforms, sensors, and applications in nut crops. Comput. Electron. Agric. 2022, 197, 106844. [Google Scholar] [CrossRef]
- Manfreda, S.; McCabe, M.F.; Miller, P.E.; Lucas, R.; Madrigal, V.P.; Mallinis, G.; Ben Dor, E.; Helman, D.; Estes, L.; Ciraolo, G.; et al. On the Use of Unmanned Aerial Systems for Environmental Monitoring. Remote Sens. 2018, 10, 641. [Google Scholar] [CrossRef]
- Peckham, S.D. The CSDMS standard names: Cross-domain naming conventions for describing process models, data sets and their associated variables. In Proceedings of the International Congress on Environmental Modelling and Software, San Diego, CA, USA, 15–19 June 2014. [Google Scholar]
- Microsoft, AI for Earth. Available online: https://www.microsoft.com/en-us/ai/ai-for-earth (accessed on 24 June 2022).
- Gorelick, Ν.; Hancher, Μ.; Dixon, Μ.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Env. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Brown, C.F.; Brumby, S.P.; Guzder-Williams, B.; Birch, T.; Hyde, S.B.; Mazzariello, J.; Czerwinski, W.; Pasquarella, V.J.; Haertel, R.; Ilyushchenko, S.; et al. Dynamic World, near real-time global 10 m land use land cover mapping. Sci. Data 2022, 9, 251. [Google Scholar] [CrossRef]
- O’Connor, J.; Smith, M.J.; James, M.R. Cameras and settings for aerial surveys in the geosciences. Prog. Phys. Geogr. Earth Environ. 2017, 41, 325–344. [Google Scholar] [CrossRef]
- Eismann, M.T. Hyperspectral Remote Sensing; SPIE Press: Bellingham, WA, USA, 2012. [Google Scholar]
- Gewali, U.B.; Monteiro, S.T.; Saber, E. Machine learning based hyperspectral image analysis: A survey. arXiv 2018, arXiv:1802.08701. [Google Scholar]
- Yan, W.Y.; Shaker, A.; El-Ashmawy, N. Urban land cover classification using airborne LiDAR data: A review. Remote Sens. Environ. 2015, 158, 295–310. [Google Scholar] [CrossRef]
- Li, W.; Chen, C.; Su, H.; Du, Q. Local Binary Patterns and Extreme Learning Machine for Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3681–3693. [Google Scholar] [CrossRef]
- Hsu, P.-H. Feature extraction of hyperspectral images using wavelet and matching pursuit. ISPRS J. Photogramm. Remote Sens. 2007, 62, 78–92. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Villa, A.; Benediktsson, J.A.; Chanussot, J.; Bruzzone, L. Classification of hyperspectral images by using ex-tended morphological attribute profiles and independent component analysis. IEEE Geosci. Remote Sens. Lett. 2010, 8, 542–546. [Google Scholar] [CrossRef]
- Azar, S.G.; Meshgini, S.; Rezaii, T.Y.; Beheshti, S. Hyperspectral image classification based on sparse modeling of spectral blocks. Neurocomputing 2020, 407, 12–23. [Google Scholar] [CrossRef]
- Johnson, A.; Hebert, M. Using spin images for efficient object recognition in cluttered 3D scenes. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 433–449. [Google Scholar] [CrossRef]
- Rusu, R.B.; Blodow, N.; Marton, Z.C.; Beetz, M. Aligning point cloud views using persistent feature histograms. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3384–3391. [Google Scholar]
- Tombari, F.; Salti, S.; Stefano, L.D. Unique signatures of histograms for local surface description. In Proceedings of the European Conference on Computer Vision, Heraklion, Crete, Greece, 5–11 September 2010; pp. 356–369. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef]
- Csurka, G.; Dance, C.; Fan, L.; Willamowski, J.; Bray, C. Visual categorization with bags of keypoints. In Proceedings of the European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 1–22. [Google Scholar]
- Hu, F.; Xia, G.-S.; Wang, Z.; Huang, X.; Zhang, L.; Sun, H. Unsupervised feature learning via spectral clustering of multidimensional patches for remotely sensed scene classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2015–2030. [Google Scholar] [CrossRef]
- van Gemert, J.C.; Veenman, C.J.; Smeulders, A.W.; Geusebroek, J.-M. Visual Word Ambiguity. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 1271–1283. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Blake, A.; Kohli, P.; Rother, C. Markov Random Fields for Vision and Image Processing; The MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Stutz, D.; Hermans, A.; Leibe, B. Superpixels: An evaluation of the state-of-the-art. Comput. Vis. Image Underst. 2018, 166, 1–27. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. In Proceedings of the International Conference on Neural Information Processing Systems, Lake Tahoe, CA, USA, 3–8 December 2012. [Google Scholar]
- Le Cun, Y.; Boser, B.; Denker, J.; Henderson, D.; Howard, R.; Hubbard, W.; Jackel, L. Handwritten digit recognition with a back-propagation network. In Proceedings of the International Conference on Neural Information Processing Systems, Denver, CO, USA, 27–30 November 1989. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Schmidhuber, J. Network Architectures, Objective Functions, and Chain Rule; Institut fur Informatik, Technische Universitat Munchen: Munich, Germany, 1993. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neur. Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational Bayes. In Proceedings of the International Conference on Learning Representations, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Bergen, K.J.; Johnson, P.A.; de Hoop, M.V.; Beroza, G.C. Machine learning for data-driven discovery in solid Earth geoscience. Science 2019, 363, eaau0323. [Google Scholar] [CrossRef]
- Lary, D.J.; Alavi, A.H.; Gandomi, A.H.; Walker, A.L. Machine learning in geosciences and remote sensing. Geosci. Front. 2016, 7, 3–10. [Google Scholar] [CrossRef]
- Ioannidou, A.; Chatzilari, E.; Nikolopoulos, S.; Kompatsiaris, I. Deep learning advances in computer vision with 3D data: A survey. ACM Comp. Surv. 2018, 50, 1–38. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, L.; Du, B. Deep learning for remote sensing data: A technical tutorial on the state of the art. IEEE Geosci. Remote Sens. Mag. 2016, 4, 22–40. [Google Scholar] [CrossRef]
- Zhang, L.; Xia, G.-S.; Wu, T.; Lin, L.; Tai, X.-C. Deep Learning for Remote Sensing Image Understanding. J. Sens. 2016, 2016, 7954154. [Google Scholar] [CrossRef]
- Beroza, G.C.; Segou, M.; Mousavi, S.M. Machine learning and earthquake forecasting—Next steps. Nat. Commun. 2021, 12, 4761. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural Features for Image Classification. IEEE Trans. Syst. Man Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Ojala, T.; Pietikainen, M.; Maenpaa, T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 971–987. [Google Scholar] [CrossRef]
- Shen, L.; Jia, S. Three-Dimensional Gabor Wavelets for Pixel-Based Hyperspectral Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2011, 49, 5039–5046. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comp. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Frome, A.; Huber, D.; Kolluri, R.; Bülow, T.; Malik, J. Recognizing Objects in Range Data Using Regional Point Descriptors. In Proceedings of the 8th European Conference on Computer Vision, Prague, Czech Republic, 11–14 May 2004; pp. 224–237. [Google Scholar]
- Rusu, R.B.; Bradski, G.; Thibaux, R.; Hsu, J. Fast 3D recognition and pose using the viewpoint feature histogram. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Chicago, IL, USA, 14–18 September 2014. [Google Scholar]
- Sivic, J.; Zisserman, A. Video Google: A text retrieval approach to object matching in videos. In Proceedings of the IEEE International Conference on Computer Vision, Nice, France, 14–18 October 2004. [Google Scholar]
- Jegou, H.; Perronnin, F.; Douze, M.; Sanchez, J.; Perez, P.; Schmid, C. Aggregating Local Image Descriptors into Compact Codes. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 1704–1716. [Google Scholar] [CrossRef]
- Perronnin, F.; Liu, Y.; Sanchez, J.; Poirier, H. Large-scale image retrieval with compressed Fisher vectors. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Wu, Q.; An, J. An Active Contour Model Based on Texture Distribution for Extracting Inhomogeneous Insulators From Aerial Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3613–3626. [Google Scholar] [CrossRef]
- Osher, S.; Sethian, J.A. Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formula-tions. J. Comp. Phys. 1988, 79, 12–49. [Google Scholar] [CrossRef]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Fauvel, M.; Chanussot, J.; Benediktsson, J.A. SVM- and MRF-based method for accurate classification of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 736–740. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Hyperspectral Image Classification via Multitask Joint Sparse Representation and Stepwise MRF Optimization. IEEE Trans. Cybern. 2016, 46, 2966–2977. [Google Scholar] [CrossRef]
- Solberg, A.; Taxt, T.; Jain, A. A Markov random field model for classification of multisource satellite imagery. IEEE Trans. Geosci. Remote Sens. 1996, 34, 100–113. [Google Scholar] [CrossRef]
- Wang, C.; Komodakis, N.; Paragios, N. Markov Random Field modeling, inference & learning in computer vision & image understanding: A survey. Comput. Vis. Image Underst. 2013, 117, 1610–1627. [Google Scholar] [CrossRef]
- Kolmogorov, V.; Zabin, R. What energy functions can be minimized via graph cuts? IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 147–159. [Google Scholar] [CrossRef]
- Golipour, M.; Ghassemian, H.; Mirzapour, F. Integrating Hierarchical Segmentation Maps with MRF Prior for Classification of Hyperspectral Images in a Bayesian Framework. IEEE Trans. Geosci. Remote Sens. 2016, 54, 805–816. [Google Scholar] [CrossRef]
- Moser, G.; Serpico, S.B.; Benediktsson, J.A. Land-Cover Mapping by Markov Modeling of Spatial–Contextual Information in Very-High-Resolution Remote Sensing Images. Proc. IEEE 2013, 101, 631–651. [Google Scholar] [CrossRef]
- Neubert, P.; Protzel, P. Superpixel Benchmark and Comparison; Karlsruher Instituts für Technologie (KIT) Scientific Publishing: Karlsruhe, Germany, 2012. [Google Scholar]
- Csillik, O. Fast Segmentation and Classification of Very High Resolution Remote Sensing Data Using SLIC Superpixels. Remote Sens. 2017, 9, 243. [Google Scholar] [CrossRef]
- Achanta, R.; Shaji, A.; Smith, K.; Lucchi, A.; Fua, P.; Süsstrunk, S. SLIC Superpixels Compared to State-of-the-Art Superpixel Methods. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2274–2282. [Google Scholar] [CrossRef] [PubMed]
- Moore, A.P.; Prince, J.; Warrell, J.; Mohammed, U.; Jones, G. Superpixel lattices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, AK, USA, 23–28 June 2008. [Google Scholar]
- Levinshtein, A.; Stere, A.; Kutulakos, K.N.; Fleet, D.J.; Dickinson, S.J.; Siddiqi, K. TurboPixels: Fast Superpixels Using Geometric Flows. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2290–2297. [Google Scholar] [CrossRef] [PubMed]
- Vedaldi, A.; Soatto, S. Quick shift and kernel methods for mode seeking. In Proceedings of the European Conference on Computer Vision, Marseille, France, 12–18 October 2008. [Google Scholar]
- Webb, A.R.; Copsey, K.D. Statistical Pattern Recognition, 3rd ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neur. Net. 2005, 16, 645–678. [Google Scholar] [CrossRef]
- Jain, A.K.; Duin, R.P.W.; Mao, J. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comp. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Madhulatha, T.S. An Overview on Clustering Methods. IOSR J. Eng. 2012, 2, 719–725. [Google Scholar] [CrossRef]
- Fahad, A.; Alshatri, N.; Tari, Z.; Alamri, A.; Khalil, I.; Zomaya, A.Y.; Foufou, S.; Bouras, A. A Survey of Clustering Algorithms for Big Data: Taxonomy and Empirical Analysis. IEEE Trans. Emerg. Top. Comput. 2014, 2, 267–279. [Google Scholar] [CrossRef]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview. WIREs Data Min. Knowl. Discov. 2012, 2, 86–97. [Google Scholar] [CrossRef]
- Murtagh, F.; Contreras, P. Algorithms for hierarchical clustering: An overview, II. WIREs Data Min. Knowl. Discov. 2017, 7, e1219. [Google Scholar] [CrossRef]
- Baraldi, A.; Blonda, P. A survey of fuzzy clustering algorithms for pattern recognition. I. IEEE Trans. Sys. Man Cybern. Part B (Cybern.) 1999, 29, 778–785. [Google Scholar] [CrossRef]
- Chiou, Y.-C.; Lan, L.W. Genetic clustering algorithms. Eur. J. Oper. Res. 2001, 135, 413–427. [Google Scholar] [CrossRef]
- Yang, M.-S.; Wu, K.-L. Unsupervised possibilistic clustering. Pattern Recognit. 2006, 39, 5–21. [Google Scholar] [CrossRef]
- Kriegel, H.-P.; Kröger, P.; Sander, J.; Zimek, A. Density-based clustering. WIREs Dat. Min. Knowl. Disc. 2011, 1, 231–240. [Google Scholar] [CrossRef]
- Vidal, R. Subspace Clustering. IEEE Sig. Proc. Mag. 2011, 28, 52–68. [Google Scholar] [CrossRef]
- Lloyd, S.P. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Gustafson, D.E.; Kessel, W.C. Fuzzy clustering with a fuzzy covariance matrix. In Proceedings of the IEEE Conference on Decision and Control including the 17th Symposium on Adaptive Processes, San Diego, CA, USA, 10–12 January 1979. [Google Scholar]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD’96), Portland, Oregon, 2–4 August 1996. [Google Scholar]
- Fukunaga, K.; Hostetler, L. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Trans. Inf. Theory 1975, 21, 32–40. [Google Scholar] [CrossRef]
- Ankerst, M.; Breunig, M.M.; Kriegel, H.-P.; Sander, J. OPTICS: Ordering points to identify the clustering structure. SIGMOD Rec. 1999, 28, 49–60. [Google Scholar] [CrossRef]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: An efficient data clustering method for very large databases. In Proceedings of the 1996 ACM SIGMOD international conference on Management of Data—SIGMOD’96, Montreal, QC, Canada, 4–6 June 1996. [Google Scholar]
- Vidal, R.; Ma, Y.; Sastry, S. Generalized principal component analysis (GPCA). IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1945–1959. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedan, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition, 4th ed.; Academic Press, Inc.: Cambridge, MA, USA, 2008. [Google Scholar]
- Dietterich, T.G.; Bakiri, G. Solving multi-class learning problems via error-correcting output codes. J. Art. Intell. Res. 1995, 2, 263–286. [Google Scholar]
- Theodoridis, S. Machine Learning, a Bayesian and Optimization Perspective; Academic Press: New York, NY, USA, 2015. [Google Scholar]
- Chong, E.K.P.; Zak, S.H. An Introduction to Optimization; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Hassoun, M.H.; Intrator, N.; McKay, S.; Christian, W. Fundamentals of Artificial Neural Networks. Comput. Phys. 1995, 10, 137. [Google Scholar] [CrossRef]
- Gurney, K. An Introduction to Neural Networks; Taylor & Francis, Inc.: Florence, KY, USA, 1997. [Google Scholar]
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef]
- Svozil, D.; Kvasnicka, V.; Pospichal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- Mcculloch, W.S.; Pitts, W.H. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Chung, J.; Cho, C.G.K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar]
- Cho, K.; van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder–decoder approaches. In Proceedings of the Workshop on Syntax, Semantics and Structure in Statistical Translation, Doha, Qatar, 25 October 2014. [Google Scholar]
- Graves, A.; Mohamed, A.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural machine translation by jointly learning to align and translate. arXiv 2016, arXiv:1409.0473. [Google Scholar]
- Savelonas, M.; Vernikos, I.; Mantzekis, D.; Spyrou, E.; Tsakiri, A.; Karkanis, S. Hybrid Representation of Sensor Data for the Classification of Driving Behaviour. Appl. Sci. 2021, 11, 8574. [Google Scholar] [CrossRef]
- Khan, S.; Naseer, M.; Hayat, M.; Zamir, S.W.; Khan, F.S.; Shah, M. Transformers in Vision: A Survey. ACM Comput. Surv. 2022, 54, 1–41. [Google Scholar] [CrossRef]
- Han, K.; Wang, Y.; Chen, H.; Chen, X.; Guo, J.; Liu, Z.; Tang, Y.; Xiao, A.; Xu, C.; Xu, Y.; et al. A Survey on Vision Transformer. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 1. [Google Scholar] [CrossRef]
- Aleissaee, A.A.; Kumar, A.; Anwer, R.M.; Khan, S.; Cholakkal, H.; Xia, G.-S.; Khan, F.S. Transformers in remote sensing: A survey. arXiv 2022, arXiv:2209.01206. [Google Scholar]
- Metz, L.; Poole, B.; Pfau, D.; Sohl-Dickstein, J. Unrolled generative adversarial networks. arXiv 2016, arXiv:1611.02163. [Google Scholar]
- Arjovsky, M.; Chintala, S.; Bottou, L. Wasserstein GAN. arXiv 2017, arXiv:1701.07875. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable representation learning by information maximizing generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. Progressive growing of GANs for improved quality, stability, and variation. arXiv 2017, arXiv:1710.10196. [Google Scholar]
- Isola, P.; Zhu, J.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Xia, G.-S.; Liu, G.; Yang, W.; Zhang, L. Meaningful object segmentation from SAR images via a multiscale nonlocal active contour model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1860–1873. [Google Scholar] [CrossRef]
- Li, Z.; Shi, W.; Myint, S.W.; Lu, P.; Wang, Q. Semi-automated landslide inventory mapping from bitemporal aerial photographs using change detection and level set method. Remote Sens. Env. 2016, 175, 215–230. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Duan, W.; Ren, J.; Benediktsson, J.A. Classification of hyperspectral images by exploiting spectral–spatial in-formation of superpixel via multiple kernels. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6663–6674. [Google Scholar] [CrossRef]
- Fang, L.; Li, S.; Kang, X.; Benediktsson, J.A. Spectral–Spatial Classification of Hyperspectral Images with a Superpixel-Based Discriminative Sparse Model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4186–4201. [Google Scholar] [CrossRef]
- Shi, C.; Pun, C.-M. Superpixel-based 3D deep neural networks for hyperspectral image classification. Pattern Recognit. 2018, 74, 600–616. [Google Scholar] [CrossRef]
- Maulik, U.; Saha, I. Automatic fuzzy clustering using modified differential evolution for image classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3503–3510. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Qin, F.; Guo, J.; Lang, F. Superpixel Segmentation for Polarimetric SAR Imagery Using Local Iterative Clustering. IEEE Geosci. Remote Sens. Lett. 2015, 12, 13–17. [Google Scholar] [CrossRef]
- Zhang, H.; Zhai, H.; Zhang, L.; Li, P. Spectral–Spatial Sparse Subspace Clustering for Hyperspectral Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3672–3684. [Google Scholar] [CrossRef]
- Wang, S.; Azzari, G.; Lobell, D.B. Crop type mapping without field-level labels: Random forest transfer and unsupervised clustering techniques. Remote Sens. Environ. 2019, 222, 303–317. [Google Scholar] [CrossRef]
- Reza, N.; Na, I.S.; Baek, S.W.; Lee, K.-H. Rice yield estimation based on K-means clustering with graph-cut segmentation using low-altitude UAV images. Biosyst. Eng. 2019, 177, 109–121. [Google Scholar] [CrossRef]
- Jia, S.; Tang, G.; Zhu, J.; Li, Q. A Novel Ranking-Based Clustering Approach for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 88–102. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef]
- Yuan, Y.; Lin, J.; Wang, Q. Dual-Clustering-Based Hyperspectral Band Selection by Contextual Analysis. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1431–1445. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, F.; Li, X. Optimal Clustering Framework for Hyperspectral Band Selection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5910–5922. [Google Scholar] [CrossRef]
- Zhai, H.; Zhang, H.; Zhang, L.; Li, P. Laplacian-regularized low-rank subspace clustering for hyperspectral image band se-lection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1723–1740. [Google Scholar] [CrossRef]
- Afonso, M.V.; Bioucas-Dias, J.M.; Figueiredo, M.A.T. An Augmented Lagrangian Approach to the Constrained Optimization Formulation of Imaging Inverse Problems. IEEE Trans. Image Process. 2011, 20, 681–695. [Google Scholar] [CrossRef]
- Ham, J.; Chen, Y.; Crawford, M.M.; Ghosh, J. Investigation of the random forest framework for classification of hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 492–501. [Google Scholar] [CrossRef]
- Morgan, J.T.; Henneguelle, A.; Ham, J.; Ghosh, J.; Crawford, M.M. Adaptive feature spaces for land cover classification with limited ground truth. Int. J. Pattern Recognit. Art. Intell. 2004, 18, 777–799. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-oriented mapping of landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Eisavi, V.; Homayouni, S.; Yazdi, A.M.; Alimohammadi, A. Land cover mapping based on random forest classification of multitemporal spectral and thermal images. Environ. Monit. Assess. 2015, 187, 291. [Google Scholar] [CrossRef] [PubMed]
- Peerbhay, K.Y.; Mutanga, O.; Ismail, R. Random Forests Unsupervised Classification: The Detection and Mapping of Solanum mauritianum Infestations in Plantation Forestry Using Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3107–3122. [Google Scholar] [CrossRef]
- Scott, G.L.; Longuet-Higgins, H.C. Feature grouping by relocalisation of eigenvectors of proximity matrix. In Proceedings of the British Machine Vision Conference, Oxford, UK, September 1990. [Google Scholar]
- Anselin, L. The Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Sun, L.; Schulz, K. The Improvement of Land Cover Classification by Thermal Remote Sensing. Remote Sens. 2015, 7, 8368–8390. [Google Scholar] [CrossRef]
- Kalantar, B.; Mansor, S.B.; Sameen, M.I.; Pradhan, B.; Shafri, H.Z.M. Drone-based land-cover mapping using a fuzzy unordered rule induction al-gorithm integrated into object-based image analysis. Int. J. Remote Sens. 2017, 38, 2535–2556. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F. Toward an Optimal SVM Classification System for Hyperspectral Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3374–3385. [Google Scholar] [CrossRef]
- Mantero, P.; Moser, G.; Serpico, S.B. Partially Supervised classification of remote sensing images through SVM-based probability density estimation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 559–570. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. Toward intelligent training of supervised image classifications: Directing training data acquisition for SVM classification. Remote Sens. Environ. 2004, 93, 107–117. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. The use of small training sets containing mixed pixels for accurate hard image classification: Training on mixed spectral responses for classification by a SVM. Remote Sens. Environ. 2006, 103, 179–189. [Google Scholar] [CrossRef]
- Mathur, A.; Foody, G.M. Multiclass and Binary SVM Classification: Implications for Training and Classification Users. IEEE Geosci. Remote Sens. Lett. 2008, 5, 241–245. [Google Scholar] [CrossRef]
- Marconcini, M.; Camps-Valls, G.; Bruzzone, L. A Composite Semisupervised SVM for Classification of Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2009, 6, 234–238. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L. An SVM Ensemble Approach Combining Spectral, Structural, and Semantic Features for the Classification of High-Resolution Remotely Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2013, 51, 257–272. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. WIREs Comp. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Fauvel, M.; Benediktsson, J.A.; Chanussot, J.; Sveinsson, J.R. Spectral and Spatial Classification of Hyperspectral Data Using SVMs and Morphological Profiles. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3804–3814. [Google Scholar] [CrossRef]
- Chini, M.; Pacifici, F.; Emery, W.J. Morphological operators applied to X-band SAR for urban land use classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009. [Google Scholar]
- Yoo, H.Y.; Lee, K.; Kwon, B.-D. Quantitative indices based on 3D discrete wavelet transform for urban complexity estimation using remotely sensed imagery. Int. J. Remote Sens. 2009, 30, 6219–6239. [Google Scholar] [CrossRef]
- Xu, S.; Fang, T.; Li, D.; Wang, S. Object Classification of Aerial Images with Bag-of-Visual Words. IEEE Geosci. Remote Sens. Lett. 2010, 7, 366–370. [Google Scholar] [CrossRef]
- Pasolli, E.; Melgani, F.; Tuia, D.; Pacifici, F.; Emery, W.J. SVM Active Learning Approach for Image Classification Using Spatial Information. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2217–2233. [Google Scholar] [CrossRef]
- Cheng, Q.; Varshney, P.K.; Arora, M.K. Logistic Regression for Feature Selection and Soft Classification of Remote Sensing Data. IEEE Geosci. Remote Sens. Lett. 2006, 3, 491–494. [Google Scholar] [CrossRef]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Semisupervised Hyperspectral Image Segmentation Using Multinomial Logistic Regression with Active Learning. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4085–4098. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. Royal Stat. Soc. Series B (Methodol.) 1977, 39, 1–38. [Google Scholar]
- Li, J.; Bioucas-Dias, J.M.; Plaza, A. Spectral–Spatial Hyperspectral Image Segmentation Using Subspace Multinomial Logistic Regression and Markov Random Fields. IEEE Trans. Geosci. Remote Sens. 2012, 50, 809–823. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F.; Serpico, S.B. A neural-statistical approach to multitemporal and multisource remote-sensing image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1350–1359. [Google Scholar] [CrossRef]
- Hu, X.; Weng, Q. Estimating impervious surfaces from medium spatial resolution imagery using the self-organizing map and multi-layer perceptron neural networks. Remote Sens. Environ. 2009, 113, 2089–2102. [Google Scholar] [CrossRef]
- D’Alimonte, D.; Zibordi, G. Phytoplankton determination in an optically complex coastal region using a multilayer perceptron neural network. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2861–2868. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep Convolutional Neural Networks for Hyperspectral Image Classification. J. Sensors 2015, 2015, 258619. [Google Scholar] [CrossRef]
- Maggiori, E.; Tarabalka, Y.; Charpiat, G.; Alliez, P. Convolutional neural networks for large-scale remote-sensing image classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 645–657. [Google Scholar] [CrossRef]
- Volpi, M.; Tuia, D. Dense Semantic Labeling of Subdecimeter Resolution Images with Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 55, 881–893. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.-Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Scott, G.J.; England, M.R.; Starms, W.A.; Marcum, R.A.; Davis, C.H. Training Deep Convolutional Neural Networks for Land–Cover Classification of High-Resolution Imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 549–553. [Google Scholar] [CrossRef]
- Jia, Y.; Shelhamer, E.; Donahue, J.; Karayev, S.; Long, J.; Girshick, R.; Guadarrama, S.; Darrell, T. Caffe: Convolutional architecture for fast feature embedding. In Proceedings of the 22nd ACM International Conference on Multimedia, Orlando, FL, USA, 3–7 November 2014. [Google Scholar]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource Remote Sensing Data Classification Based on Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2017, 56, 937–949. [Google Scholar] [CrossRef]
- Li, E.; Xia, J.; Du, P.; Lin, C.; Samat, A. Integrating Multilayer Features of Convolutional Neural Networks for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5653–5665. [Google Scholar] [CrossRef]
- Cai, D.; He, X.; Han, J. SRDA: An Efficient Algorithm for Large-Scale Discriminant Analysis. IEEE Trans. Knowl. Data Eng. 2007, 20, 1–12. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep Learning-Based Classification of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, K.; Zhu, L.; He, X.; Ghamisi, P.; Benediktsson, J.A. Automatic Design of Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7048–7066. [Google Scholar] [CrossRef]
- Cao, X.; Yao, J.; Xu, Z.; Meng, D. Hyperspectral Image Classification with Convolutional Neural Network and Active Learning. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4604–4616. [Google Scholar] [CrossRef]
- Wu, X.; Hong, D.; Chanussot, J. Convolutional Neural Networks for Multimodal Remote Sensing Data Classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5517010. [Google Scholar] [CrossRef]
- Mei, S.; Chen, X.; Zhang, Y.; Li, J.; Plaza, A. Accelerating convolutional neural network-based hyperspectral image classifica-tion by step activation quantization. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5502012. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageΝet classification using binary convolutional neural networks. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Lin, J.; Mou, L.; Zhu, X.X.; Ji, X.; Wang, Z.J. Attention-Aware Pseudo-3-D Convolutional Neural Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 7790–7802. [Google Scholar] [CrossRef]
- Dong, Y.; Liu, Q.; Du, B.; Zhang, L. Weighted Feature Fusion of Convolutional Neural Network and Graph Attention Network for Hyperspectral Image Classification. IEEE Trans. Image Process. 2022, 31, 1559–1572. [Google Scholar] [CrossRef] [PubMed]
- Lu, Z.; Liang, S.; Yang, Q.; Du, B. Evolving block-based convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5525921. [Google Scholar] [CrossRef]
- Ienco, D.; Gaetano, R.; Dupaquier, C.; Maurel, P. Land Cover Classification via Multitemporal Spatial Data by Deep Recurrent Neural Networks. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1685–1689. [Google Scholar] [CrossRef]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef]
- Maggiori, E.; Charpiat, G.; Tarabalka, Y.; Alliez, P. Recurrent Neural Networks to Correct Satellite Image Classification Maps. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4962–4971. [Google Scholar] [CrossRef]
- Rußwurm, M.; Körner, M. Multi-Temporal Land Cover Classification with Sequential Recurrent Encoders. ISPRS Int. J. Geo-Inf. 2018, 7, 129. [Google Scholar] [CrossRef]
- Ndikumana, E.; Minh, D.H.T.; Baghdadi, N.; Courault, D.; Hossard, L. Deep Recurrent Neural Network for Agricultural Classification using multitemporal SAR Sentinel-1 for Camargue, France. Remote Sens. 2018, 10, 1217. [Google Scholar] [CrossRef]
- Ho Tong Minh, D.; Lalande, N.; Ndikumana, E.; Osman, F.; Maurel, P. Deep recurrent neural networks for winter vegetation quality mapping via multitemporal SAR Sen-tinel-1. IEEE Geosci. Remote Sens. Lett. 2018, 15, 464–468. [Google Scholar] [CrossRef]
- Hang, R.; Liu, Q.; Hong, D.; Ghamisi, P. Cascaded Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5384–5394. [Google Scholar] [CrossRef]
- Lee, H.; Slatton, K.C.; Roth, B.E.; Cropper, W.P., Jr. Adaptive clustering of airborne LiDAR data to segment individual tree crowns in managed pine forests. Int. J. Remote Sens. 2010, 31, 117–139. [Google Scholar] [CrossRef]
- Beucher, S.; Lantuéjoul, C. Use of watersheds in contour detection. In Proceedings of the International Workshop on Image Processing: Real-Time Edge and Motion Detection/Estimation, Rennes, France, 17–21 September 1979. [Google Scholar]
- Kim, Y.; Ling, H. Human Activity Classification Based on Micro-Doppler Signatures Using a Support Vector Machine. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1328–1337. [Google Scholar] [CrossRef]
- Kim, Y.J.; Nam, B.H.; Youn, H. Sinkhole detection and characterization using LiDAR-derived DEM with logistic regression. Remote Sens. 2019, 11, 1592. [Google Scholar] [CrossRef]
- Martorella, M.; Giusti, E.; Capria, A.; Berizzi, F.; Bates, B. Automatic Target Recognition by Means of Polarimetric ISAR Images and Neural Networks. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3786–3794. [Google Scholar] [CrossRef]
- Cameron, W.L.; Rais, H. Conservative polarimetric scatterers and their role in incorrect extensions of the Cameron decomposition. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3506–3516. [Google Scholar] [CrossRef]
- Taravat, A.; Proud, S.; Peronaci, S.; Del Frate, F.; Oppelt, N. Multilayer Perceptron Neural Networks Model for Meteosat Second Generation SEVIRI Daytime Cloud Masking. Remote Sens. 2015, 7, 1529–1539. [Google Scholar] [CrossRef]
- Chen, X.; Xiang, S.; Liu, C.L.; Pan, C.H. Vehicle detection in satellite images by hybrid deep convolutional neural networks. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1797–1801. [Google Scholar] [CrossRef]
- Cheng, G.; Zhou, P.; Han, J. Learning Rotation-Invariant Convolutional Neural Networks for Object Detection in VHR Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7405–7415. [Google Scholar] [CrossRef]
- Ding, J.; Chen, B.; Liu, H.; Huang, M. Convolutional Neural Network with Data Augmentation for SAR Target Recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [Google Scholar] [CrossRef]
- Long, Y.; Gong, Y.; Xiao, Z.; Liu, Q. Accurate Object Localization in Remote Sensing Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2486–2498. [Google Scholar] [CrossRef]
- Uijlings, J.R.R.; van de Sande, K.E.A.; Gevers, T.; Smeulders, A.W.M. Selective Search for Object Recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Cheng, G.; Wang, Y.; Xu, S.; Wang, H.; Xiang, S.; Pan, C. Automatic Road Detection and Centerline Extraction via Cascaded End-to-End Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3322–3337. [Google Scholar] [CrossRef]
- Shao, Z.; Pan, Y.; Diao, C.; Cai, J. Cloud Detection in Remote Sensing Images Based on Multiscale Features-Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4062–4076. [Google Scholar] [CrossRef]
- Hsieh, M.R.; Lin, Y.L.; Hsu, W.H. Drone-based object counting by spatially regularized regional proposal network. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Kellenberger, B.; Marcos, D.; Tuia, D. Detecting mammals in UAV images: Best practices to address a substantially imbalanced dataset with deep learning. Remote Sens. Environ. 2018, 216, 139–153. [Google Scholar] [CrossRef]
- Bengio, Y.; Louradour, J.; Collobert, R.; Weston, J. Curriculum learning. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 14–18 June 2009. [Google Scholar]
- Shrivastava, A.; Gupta, A.; Girshick, R. Training region-based object detectors with online hard example mining. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhang, H.; Wang, G.; Lei, Z.; Hwang, J.N. Eye in the sky: Drone-based object tracking and 3D localization. In Proceedings of the ACM International Conference on Multimedia, Nice, France, 21–25 October 2019. [Google Scholar]
- Wang, G.; Wang, Y.; Zhang, J.N.; Gu, R.; Hwang, J.N. Exploit the connectivity: Multi-object tracking with TrackletNet. In Proceedings of the ACM International Conference on Multimedia, Nice, France, 21–25 October 2019. [Google Scholar]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A comparison and evaluation of multi-view stereo reconstruction algorithms. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Zhang, C.; Zuo, R.; Xiong, Y. Detection of the multivariate geochemical anomalies associated with mineralization using a deep convolutional neural network and a pixel-pair feature method. Appl. Geochem. 2021, 130, 104994. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral Image Classification Using Deep Pixel-Pair Features. IEEE Trans. Geosci. Remote Sens. 2016, 55, 844–853. [Google Scholar] [CrossRef]
- Xu, D.; Wu, Y. MRFF-YOLO: A Multi-Receptive Fields Fusion Network for Remote Sensing Target Detection. Remote Sens. 2020, 12, 3118. [Google Scholar] [CrossRef]
- Redmon, J.; Farhadi, A. YOLOv3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Xu, D.; Wu, Y. FE-YOLO: A Feature Enhancement Network for Remote Sensing Target Detection. Remote Sens. 2021, 13, 1311. [Google Scholar] [CrossRef]
- Qing, Y.; Liu, W.; Feng, L.; Gao, W. Improved YOLO Network for Free-Angle Remote Sensing Target Detection. Remote Sens. 2021, 13, 2171. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, X.; Ma, N.; Han, J.; Ding, G.; Sun, J. RepVGG: Making VGG-style convnets great again. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021. [Google Scholar]
- Wang, C.; Wang, Q.; Wu, H.; Zhao, C.; Teng, G.; Li, J. Low-Altitude Remote Sensing Opium Poppy Image Detection Based on Modified YOLOv3. Remote Sens. 2021, 13, 2130. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollár, P. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2014, arXiv:1412.7062. [Google Scholar]
- Zakria, Z.; Deng, J.; Kumar, R.; Khokhar, M.S.; Cai, J.; Kumar, J. Multiscale and Direction Target Detecting in Remote Sensing Images via Modified YOLO-v4. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1039–1048. [Google Scholar] [CrossRef]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. YOLOv4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Ke, X.; Zhang, X.; Zhang, T. GCBANet: A Global Context Boundary-Aware Network for SAR Ship Instance Segmentation. Remote Sens. 2022, 14, 2165. [Google Scholar] [CrossRef]
- Li, Q.; Chen, Y.; Zeng, Y. Transformer with Transfer CNN for Remote-Sensing-Image Object Detection. Remote Sens. 2022, 14, 984. [Google Scholar] [CrossRef]
- Xiao, X.; Guo, W.; Chen, R.; Hui, Y.; Wang, J.; Zhao, H. A Swin Transformer-Based Encoding Booster Integrated in U-Shaped Network for Building Extraction. Remote Sens. 2022, 14, 2611. [Google Scholar] [CrossRef]
- Chen, X.; Qiu, C.; Guo, W.; Yu, A.; Tong, X.; Schmitt, M. Multiscale Feature Learning by Transformer for Building Extraction From Satellite Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2503605. [Google Scholar] [CrossRef]
- Zhu, Q.; Liao, C.; Hu, H.; Mei, X.; Li, H. MAP-Net: Multiple Attending Path Neural Network for Building Footprint Extraction From Remote Sensed Imagery. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6169–6181. [Google Scholar] [CrossRef]
- Joseph, M.; Wang, L.; Wang, F. Using Landsat Imagery and Census Data for Urban Population Density Modeling in Port-au-Prince, Haiti. GIScience Remote Sens. 2012, 49, 228–250. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Kempen, B.; Leenaars, J.G.B.; Walsh, M.G.; Shepherd, K.D.; Sila, A.; MacMillan, R.A.; de Jesus, J.M.; Tamene, L.; et al. Mapping soil properties of Africa at 250 m resolution: Random forests significantly improve current predictions. PLoS ONE 2015, 10, e0125814. [Google Scholar] [CrossRef]
- Odeh, I.O.A.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Heterotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Stevens, F.R.; Gaughan, A.E.; Linard, C.; Tatem, A.J. Disaggregating Census Data for Population Mapping Using Random Forests with Remotely-Sensed and Ancillary Data. PLoS ONE 2015, 10, e0107042. [Google Scholar] [CrossRef] [PubMed]
- Georganos, S.; Grippa, T.; Gadiaga, A.N.; Linard, C.; Lennert, M.; VanHuysse, S.; Mboga, N.; Wolff, E.; Kalogirou, S. Geographical random forests: A spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int. 2021, 36, 121–136. [Google Scholar] [CrossRef]
- Sun, D.; Li, Y.; Wang, Q. A Unified Model for Remotely Estimating Chlorophyll a in Lake Taihu, China, Based on SVM and In Situ Hyperspectral Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2957–2965. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N. Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression. Remote Sens. Env. 1999, 67, 267–287. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Lee, S. Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int. J. Remote Sens. 2005, 26, 1477–1491. [Google Scholar] [CrossRef]
- Dardel, C.; Kergoat, L.; Hiernaux, P.; Mougin, E.; Grippa, M.; Tucker, C.J. Re-greening Sahel: 30years of remote sensing data and field observations (Mali, Niger). Remote Sens. Environ. 2014, 140, 350–364. [Google Scholar] [CrossRef]
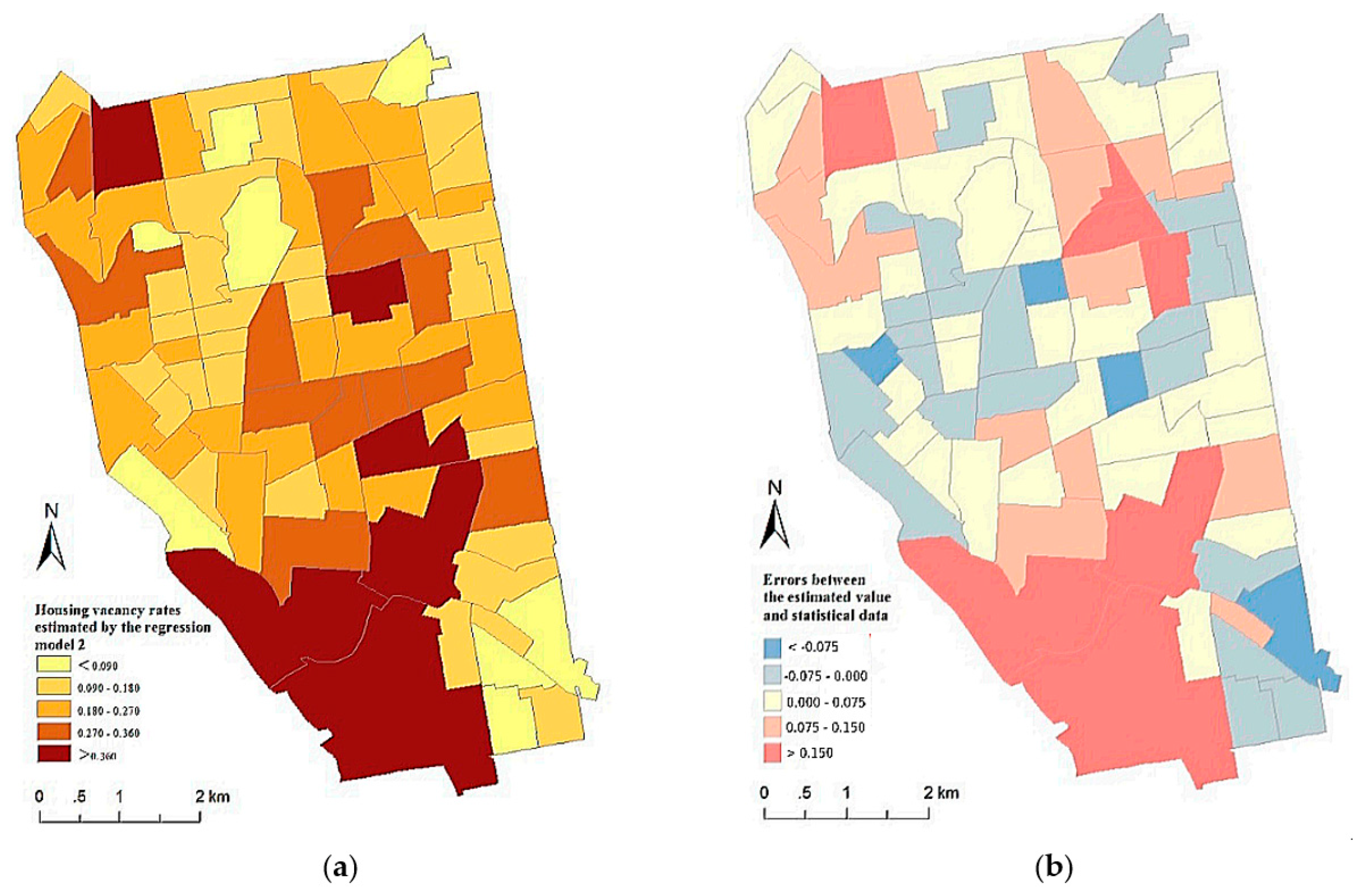
- Du, M.; Wang, L.; Zou, S.; Shi, C. Modeling the Census Tract Level Housing Vacancy Rate with the Jilin1-03 Satellite and Other Geospatial Data. Remote Sens. 2018, 10, 1920. [Google Scholar] [CrossRef]
- Tien Bui, D.; Khosravi, K.; Shahabi, H.; Daggupati, P.; Adamowski, J.F.; Melesse, A.M.; Pham, B.T.; Pourghasemi, H.R.; Mahmoudi, M.; Bahrami, S.; et al. Flood spatial modeling in northern Iran using remote sensing and gis: A com-parison between evidential belief functions and its ensemble with a multivariate logistic regression model. Remote Sens. 2019, 11, 1589. [Google Scholar] [CrossRef]
- Corsini, G.; Diani, M.; Grasso, R.; De Martino, M.; Mantero, P.; Serpico, S. Radial Basis Function and Multilayer Perceptron neural networks for sea water optically active parameter estimation in case II waters: A comparison. Int. J. Remote Sens. 2003, 24, 3917–3931. [Google Scholar] [CrossRef]
- Ozturk, D. Urban Growth Simulation of Atakum (Samsun, Turkey) Using Cellular Automata-Markov Chain and Multi-Layer Perceptron-Markov Chain Models. Remote Sens. 2015, 7, 5918–5950. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.; Pradhan, B. Spatial landslide susceptibility assessment using machine learning techniques assisted by additional data created with generative adversarial networks. Geosci. Front. 2021, 12, 625–637. [Google Scholar] [CrossRef]
- Sukcharoenpong, A.; Yilmaz, A.; Li, R. An Integrated Active Contour Approach to Shoreline Mapping Using HSI and DEM. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1586–1597. [Google Scholar] [CrossRef]
- Liu, C.; Xiao, Y.; Yang, J. A Coastline Detection Method in Polarimetric SAR Images Mixing the Region-Based and Edge-Based Active Contour Models. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3735–3747. [Google Scholar] [CrossRef]
- Modava, M.; Akbarizadeh, G. Coastline extraction from SAR images using spatial fuzzy clustering and the active contour method. Int. J. Remote Sens. 2017, 38, 355–370. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, X.; Zhao, X.; Xin, Q. Extracting Building Boundaries from High Resolution Optical Images and LiDAR Data by Integrating the Convolutional Neural Network and the Active Contour Model. Remote Sens. 2018, 10, 1459. [Google Scholar] [CrossRef]
- Bovolo, F.; Bruzzone, L.; Marconcini, M. A Novel Approach to Unsupervised Change Detection Based on a Semisupervised SVM and a Similarity Measure. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2070–2082. [Google Scholar] [CrossRef]
- Bazi, Y.; Melgani, F.; Al-Sharari, H.D. Unsupervised Change Detection in Multispectral Remotely Sensed Imagery with Level Set Methods. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3178–3187. [Google Scholar] [CrossRef]
- Gong, M.; Su, L.; Jia, M.; Chen, W. Fuzzy Clustering with a Modified MRF Energy Function for Change Detection in Synthetic Aperture Radar Images. IEEE Trans. Fuzzy Syst. 2014, 22, 98–109. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Hou, B.; Liu, G. Using combined difference image and k-means clustering for SAR image change detection. IEEE Geosci. Remote Sens. Lett. 2014, 11, 691–695. [Google Scholar] [CrossRef]
- Deledalle, C.-A.; Denis, L.; Tupin, F. Iterative Weighted Maximum Likelihood Denoising with Probabilistic Patch-Based Weights. IEEE Trans. Image Process. 2009, 18, 2661–2672. [Google Scholar] [CrossRef]
- Ghosh, A.; Mishra, N.S.; Ghosh, S. Fuzzy clustering algorithms for unsupervised change detection in remote sensing images. Inf. Sci. 2011, 181, 699–715. [Google Scholar] [CrossRef]
- Leichtle, T.; Geiß, C.; Wurm, M.; Lakes, T.; Taubenböck, H. Unsupervised change detection in VHR remote sensing imagery—An object-based clustering approach in a dynamic urban environment. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 15–27. [Google Scholar] [CrossRef]
- Singh, A. Review Article Digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Khurshid, H.; Khan, M.F. Segmentation and Classification Using Logistic Regression in Remote Sensing Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 224–232. [Google Scholar] [CrossRef]
- Tan, K.; Jin, X.; Plaza, A.; Wang, X.; Xiao, L.; Du, P. Automatic Change Detection in High-Resolution Remote Sensing Images by Using a Multiple Classifier System and Spectral–Spatial Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 3439–3451. [Google Scholar] [CrossRef]
- Molin, R.D.; Rosa, R.A.S.; Bayer, F.M.; Pettersson, M.I.; Machado, R. A change detection algorithm for SAR images based on logistic regression. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Pacifici, F.; Del Frate, F. Automatic Change Detection in Very High Resolution Images with Pulse-Coupled Neural Networks. IEEE Geosci. Remote Sens. Lett. 2009, 7, 58–62. [Google Scholar] [CrossRef][Green Version]
- Salmon, B.P.; Olivier, J.C.; Kleynhans, W.; Wessels, K.J.; Van den Bergh, F.; Steenkamp, K.C. The use of a multilayer perceptron for detecting new human settlements from a time series of MODIS images. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 873–883. [Google Scholar] [CrossRef]
- Roy, M.; Routaray, D.; Ghosh, S.; Ghosh, A. Ensemble of Multilayer Perceptrons for Change Detection in Remotely Sensed Images. IEEE Geosci. Remote Sens. Lett. 2014, 11, 49–53. [Google Scholar] [CrossRef]
- Zhao, B.; Zhong, Y.; Xia, G.-S.; Zhang, L. Dirichlet-Derived Multiple Topic Scene Classification Model for High Spatial Resolution Remote Sensing Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 54, 2108–2123. [Google Scholar] [CrossRef]
- Lyu, H.; Lu, H.; Mou, L. Learning a Transferable Change Rule from a Recurrent Neural Network for Land Cover Change Detection. Remote Sens. 2016, 8, 506. [Google Scholar] [CrossRef]
- Mou, L.; Bruzzone, L.; Zhu, X.X. Learning Spectral-Spatial-Temporal Features via a Recurrent Convolutional Neural Network for Change Detection in Multispectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 57, 924–935. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral Image Denoising Employing a Spatial–Spectral Deep Residual Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1205–1218. [Google Scholar] [CrossRef]
- Li, T.; Zuo, R.; Xiong, Y.; Peng, Y. Random-drop data augmentation of deep convolutional neural network for mineral pro-spectivity mapping. Nat. Res. Res. 2021, 30, 27–38. [Google Scholar] [CrossRef]
- Zuo, R.; Wang, Z. Effects of Random Negative Training Samples on Mineral Prospectivity Mapping. Nat. Resour. Res. 2020, 29, 3443–3455. [Google Scholar] [CrossRef]
- Nykänen, V.; Lahti, I.; Niiranen, T.; Korhonen, K. Receiver operating characteristics (ROC) as validation tool for prospectivity models—A magmatic Ni–Cu case study from the Central Lapland Greenstone Belt, Northern Finland. Ore Geol. Rev. 2015, 71, 853–860. [Google Scholar] [CrossRef]
- Molini, A.B.; Valsesia, D.; Fracastoro, G.; Magli, E. Speckle2Void: Deep Self-Supervised SAR Despeckling with Blind-Spot Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Laine, S.; Karras, T.; Lehtinen, J.; Aila, T. High-quality self-supervised deep image denoising. In Proceedings of the International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Liu, Q.; Zhou, H.; Xu, Q.; Liu, X.; Wang, Y. PSGAN: A Generative Adversarial Network for Remote Sensing Image Pan-Sharpening. IEEE Trans. Geosci. Remote Sens. 2020, 59, 10227–10242. [Google Scholar] [CrossRef]
- Pan, H. Cloud removal for remote sensing imagery via spatial attention generative adversarial network. arXiv 2020, arXiv:2009.13015. [Google Scholar]
- Spot. Available online: https://earth.esa.int/eogateway/missions/spot (accessed on 27 September 2022).
- ERS. Available online: https://earth.esa.int/eogateway/missions/ers (accessed on 27 September 2022).
- RADARSAT. Available online: https://earth.esa.int/eogateway/missions/radarsat (accessed on 27 September 2022).
- IRS. Available online: https://earth.esa.int/eogateway/missions/irs-1d (accessed on 27 September 2022).
- WorldView. Available online: https://earth.esa.int/eogateway/missions/worldview-3 (accessed on 27 September 2022).
- QuickBird. Available online: https://earth.esa.int/eogateway/catalog/quickbird-full-archive (accessed on 27 September 2022).
- Pleiades. Available online: https://earth.esa.int/eogateway/catalog/pleiades-esa-archive (accessed on 27 September 2022).
- AVIRIS. Available online: https://aviris.jpl.nasa.gov/data/free_data.html (accessed on 27 September 2022).
- Basu, S.; Ganguly, S.; Mukhopadhyay, S.; DiBiano, R.; Karki, M.; Nemani, R. DeepSat: A learning framework for satellite imagery. In Proceedings of the SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, DC, USA, 3–6 November 2015. [Google Scholar]
- Demir, I.; Koperski, K.; Lindenbaum, D.; Pang, G.; Huang, J.; Basu, S.; Hughes, F.; Tuia, D.; Raskar, R. DeepGlobe 2018: A challenge to parse the earth through satellite images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Helber, P.; Bischke, B.; Dengel, A.; Borth, D. EuroSAT: A Novel Dataset and Deep Learning Benchmark for Land Use and Land Cover Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2217–2226. [Google Scholar] [CrossRef]
- Sumbul, G.; Charfuelan, M.; Demir, B.U.M.; Markl, V. Big Earth Net: A large-scale benchmark archive for remote sensing image understanding. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Schmitt, M.; Hughes, L.H.; Qiu, C.; Zhu, X.X. SEN12MS—A curated dataset of georeferenced multi-spectral Sentinel-1/2 im-agery for deep learning and data fusion. arXiv 2019, arXiv:1906.07789. [Google Scholar]
- Xu, G.; Fang, Y.; Deng, M.; Sun, G.; Chen, J. Remote Sensing Mapping of Build-Up Land with Noisy Label via Fault-Tolerant Learning. Remote Sens. 2022, 14, 2263. [Google Scholar] [CrossRef]
- ESA World Cover 10 m 2020 v100. Available online: https://doi.org/10.5281/zenodo.5571936 (accessed on 27 September 2022).
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use/land cover with Sentinel 2 and deep learning. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Gong, P.; Liu, H.; Zhang, M.; Li, C.; Wang, J.; Huang, H.; Clinton, N.; Ji, L.; Li, W.; Bai, Y.; et al. Stable classification with limited sample: Transferring a 30-m resolution sample set collected in 2015 to mapping 10-m resolution global land cover in 2017. Sci. Bull. 2019, 64, 370–373. [Google Scholar] [CrossRef]
- Jun, C.; Ban, Y.; Li, S. Open access to Earth land-cover map. Nature 2014, 514, 434. [Google Scholar] [CrossRef]
- Dell’ Acqua, F.; Iannelli, G.C.; Kerekes, J.; Moser, G.; Pierce, L.; Goldoni, E. The IEEE GRSS data and algorithm standard evaluation (DASE) website: Incrementally building a standardized assessment for algorithm performance. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- IEEE GRSS Data Fusion Contest. Available online: https://www.grss-ieee.org/community/technical-committees/2022-ieee-grss-data-fusion-contest/ (accessed on 5 September 2022).
- Target Detection Blind Test. Available online: http://dirsapps.cis.rit.edu/blindtest/ (accessed on 5 September 2022).
- Abady, L.; Barni, M.; Garzelli, A.; Tondi, B. GAN generation of synthetic multispectral satellite images. In Proceedings of the SPIE 11533, Image and Signal Processing for Remote Sensing XXVI, Online, 21–25 September 2020. [Google Scholar]
- Copernicus Open Access Hub. Available online: https://scihub.copernicus.eu/dhus/#/home (accessed on 5 September 2022).
- Jiang, K.; Wang, Z.; Yi, P.; Wang, G.; Lu, T.; Jiang, J. Edge-Enhanced GAN for Remote Sensing Image Superresolution. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5799–5812. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Q.; Kwok, J.; Ni, L.N. Generalizing from a few examples: A survey on few-shot learning. arXiv 2019, arXiv:1904.05046. [Google Scholar] [CrossRef]
- Sellami, A.; Ben Abbes, A.; Barra, V.; Farah, I.R. Fused 3-D spectral-spatial deep neural networks and spectral clustering for hyperspectral image classification. Pattern Recognit. Lett. 2020, 138, 594–600. [Google Scholar] [CrossRef]
- Thyagharajan, K.K.; Vignesh, T. Soft Computing Techniques for Land Use and Land Cover Monitoring with Multispectral Remote Sensing Images: A Review. Arch. Comput. Methods Eng. 2019, 26, 275–301. [Google Scholar] [CrossRef]
- Kwan, C. Methods and challenges using multispectral and hyperspectral images for practical change detection applications. Information 2019, 10, 353. [Google Scholar] [CrossRef]
- Singh, P.; Diwakar, M.; Shankar, A.; Shree, R.; Kumar, M. A Review on SAR Image and its Despeckling. Arch. Comput. Methods Eng. 2021, 28, 4633–4653. [Google Scholar] [CrossRef]
- Liu, S.; Wu, G.; Zhang, X.; Zhang, K.; Wang, P.; Li, Y. SAR despeckling via classification-based nonlocal and local sparse representation. Neurocomputing 2017, 219, 174–185. [Google Scholar] [CrossRef]
- Wang, G.; Bo, F.; Chen, X.; Lu, W.; Hu, S.; Fang, J. A collaborative despeckling method for SAR images based on texture classification. Remote Sens. 2022, 14, 1465. [Google Scholar] [CrossRef]
- Choi, H.; Jeong, J. Speckle Noise Reduction Technique for SAR Images Using Statistical Characteristics of Speckle Noise and Discrete Wavelet Transform. Remote Sens. 2019, 11, 1184. [Google Scholar] [CrossRef]
- Dalsasso, E.; Yang, X.; Denis, L.; Tupin, F.; Yang, W. SAR Image Despeckling by Deep Neural Networks: From a Pre-Trained Model to an End-to-End Training Strategy. Remote Sens. 2020, 12, 2636. [Google Scholar] [CrossRef]
- Mullissa, A.G.; Marcos, D.; Tuia, D.; Herold, M.; Reiche, J. DeSpeckNet: Generalizing deep learning-based SAR image despeckling. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5200315. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, J.G.; Zhang, B.; Hong, W.; Wu, Y.-R. Adaptive Total Variation Regularization Based SAR Image Despeckling and Despeckling Evaluation Index. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2765–2774. [Google Scholar] [CrossRef]
- Muhadi, N.A.; Abdullah, A.F.; Bejo, S.K.; Mahadi, M.R.; Mijic, A. The use of LiDAR-derived DEM in flood applications: A Review. Remote Sens. 2020, 12, 2308. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P.; Plaza, J.; Plaza, A. Fusion of hyperspectral and LiDAR data using sparse and low-rank component analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6354–6365. [Google Scholar] [CrossRef]
- Zhou, L.; Geng, J.; Jiang, W. Joint classification of hyperspectral and LiDAR data based on position-channel cooperative at-tention network. Remote Sens. 2022, 14, 3247. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Zeng, H.; Li, D.; Xia, S.; Wang, P. Fusion of airborne discrete-return LiDAR and hyperspectral data for land cover classification. Remote Sens. 2016, 8, 3. [Google Scholar] [CrossRef]
- Millard, K.; Richardson, M. Wetland mapping with LiDAR derivatives, SAR polarimetric decompositions, and LiDAR–SAR fusion using a random forest classifier. Can. J. Remote Sens. 2013, 39, 290–307. [Google Scholar] [CrossRef]
- Pourshamsi, M.; Garcia, M.; Lavalle, M.; Balzter, H. A Machine-Learning Approach to PolInSAR and LiDAR Data Fusion for Improved Tropical Forest Canopy Height Estimation Using NASA AfriSAR Campaign Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3453–3463. [Google Scholar] [CrossRef]
- Seo, D.K.; Kim, Y.H.; Eo, Y.D.; Lee, M.H.; Park, W.Y. Fusion of SAR and Multispectral Images Using Random Forest Regression for Change Detection. ISPRS Int. J. Geo-Inf. 2018, 7, 401. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, H.; Yuan, Q.; Guan, X. Multispectral and SAR image fusion based on Laplacian pyramid and sparse representation. Remote Sens. 2022, 14, 870. [Google Scholar] [CrossRef]
- Hu, J.; Hong, D.; Wang, Y.; Zhu, X.X. A Comparative Review of Manifold Learning Techniques for Hyperspectral and Polarimetric SAR Image Fusion. Remote Sens. 2019, 11, 681. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and Hyperspectral Image Fusion Using a 3-D-Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 639–643. [Google Scholar] [CrossRef]
- Sun, W.; Ren, K.; Meng, X.; Xiao, C.; Yang, G.; Peng, J. A Band Divide-and-Conquer Multispectral and Hyperspectral Image Fusion Method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.M.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.M.; Anders, K.; Gloaguen, R.; et al. Multisource and multitemporal data fusion in remote sensing a comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef]
- Dalla Mura, M.; Prasad, S.; Pacifici, F.; Gamba, P.; Chanussot, J.; Benediktsson, J.A. Challenges and opportunities of multi-modality and data fusion in remote sensing. Proc. IEEE 2015, 103, 1585–1601. [Google Scholar] [CrossRef]
- Kahraman, S.; Bacher, R. A comprehensive review of hyperspectral data fusion with LiDAR and SAR data. Ann. Rev. Contr. 2021, 51, 236–253. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Mura, M.D.; Garzelli, A.; Licciardi, G.A.; Restaino, R.; Wald, L. A Critical Comparison Among Pansharpening Algorithms. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2565–2586. [Google Scholar] [CrossRef]
- Kawale, J.; Liess, S.; Kumar, A.; Steinbach, M.; Snyder, P.; Kumar, V.; Ganguly, A.R.; Samatova, N.F.; Semazzi, F. A graph-based approach to find teleconnections in climate data. Stat. Anal. Data Min. ASA Data Sci. J. 2013, 6, 158–179. [Google Scholar] [CrossRef]
- Yang, L.; Shami, A. On hyperparameter optimization of machine learning algorithms: Theory and practice. Neurocomputing 2020, 415, 295–316. [Google Scholar] [CrossRef]
- Yu, T.; Zhu, H. Hyper-parameter optimization: A review of algorithms and applications. arXiv 2020, arXiv:2003.05689. [Google Scholar]
- Hernández, A.M.; Nieuwenhuyse, I.V.; Rojas-Gonzalez, S. A survey on multi-objective hyperparameter optimization algo-rithms for machine learning. arXiv 2021, arXiv:2111.13755. [Google Scholar]
- Kakogeorgiou, I.; Karantzalos, K. Evaluating explainable artificial intelligence methods for multi-label deep learning classification tasks in remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2021, 103, 102520. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European Conference of Computer Vision, Zurich, Switzerland, 5–12 September 2014. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar]
- Abdollahi, A.; Pradhan, B. Urban Vegetation Mapping from Aerial Imagery Using Explainable AI (XAI). Sensors 2021, 21, 4738. [Google Scholar] [CrossRef]
- Temenos, A.; Tzortzis, I.N.; Kaselimi, M.; Rallis, I.; Doulamis, A.; Doulamis, N. Novel Insights in Spatial Epidemiology Utilizing Explainable AI (XAI) and Remote Sensing. Remote Sens. 2022, 14, 3074. [Google Scholar] [CrossRef]
- Gevaert, C.M. Explainable AI for earth observation: A review including societal and regulatory perspectives. Int. J. Appl. Earth Obs. Geoinf. ITC J. 2022, 112, 102869. [Google Scholar] [CrossRef]
- Vassilakis, E.; Konsolaki, A. Quantification of cave geomorphological characteristics based on multi source point cloud data interoperability. Zeitschr. Geomorphol. 2022, 63, 265–277. [Google Scholar] [CrossRef]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep learning on point sets for 3D classification and segmentation. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Aoki, Y.; Goforth, H.; Srivatsan, R.A.; Lucey, S. PointNetLK: Robust & efficient point cloud registration using PointNet. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Ding, L.; Cai, Y.; Zhang, J.; Gao, Y.; Wang, J.; Zheng, C.; Lei, L.; Ma, A. PointNet: Learning point representation for high-resolution remote sensing imagery land-cover classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Hong, D.; Gao, L.; Yokoya, N.; Yao, J.; Chanussot, J.; Du, Q.; Zhang, B. More Diverse Means Better: Multimodal Deep Learning Meets Remote-Sensing Imagery Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 4340–4354. [Google Scholar] [CrossRef]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Beyond RGB: Very high resolution urban remote sensing with multimodal deep networks. ISPRS J. Photogramm. Remote Sens. 2018, 140, 20–32. [Google Scholar] [CrossRef]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. SegNet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef]
- Hazirbas, C.; Ma, L.; Domokos, C.; Cremers, D. FuseNet: Incorporating depth into semantic segmentation via fusion-based cnn architecture. In Proceedings of the Asian Conference on Computer Vision, Taipei, Taiwan, 20–24 November 2016. [Google Scholar]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, M.; Chen, T.; Sun, Z.; Ma, Y.; Yu, B. Recent advances in convolutional neural network acceleration. Neurocomputing 2019, 323, 37–51. [Google Scholar] [CrossRef]
- Mathieu, M.; Henaff, M.; Le Cun, Y. Fast training of convolutional networks through FFTs. arXiv 2013, arXiv:1312.5851. [Google Scholar]
- Jaderberg, M.; Vedaldi, A.; Zisserman, A. Speeding up convolutional neural networks with low rank expansions. arXiv 2014, arXiv:1405.3866. [Google Scholar]




| Application | Article | Core Methodology | Data Type | Supervision Type | DL-Based |
|---|---|---|---|---|---|
| Land Cover Mapping | [117,118] | AC | MSI: [118] SAR: [117] | Unsupervised | No |
| [57,61] | MRF | HSI: [55,59] | Supervised | No | |
| [54,62,119,121,124,126,173,183,187] | SVM/MRF: [54] SVM/Superpixels: [119] RF/Superpixels: [62] CNN/Superpixels: [183] CNN/RNN/Superpixels: [121] Clustering/Superpixels: [124] RF/Clustering: [126] SVM/CNN: [173] CNN/RNN: [187] | MSI: [62,126,173,187] HSI: [54,119,121,183] SAR: [124] | Supervised: [54,62,119,121,173,183,187] Unsupervised: [124] Supervised & Unsupervised: [126] | No: [54,62,119,124,126] Yes: [122,174,184,188] | |
| [120] | Superpixels | HIS | Supervised | No | |
| [122,125,127,128,130,131,132] | Clustering | MSI: [122,127] HSI: [125,128,130,131,132] | Unsupervised | No | |
| [134,137,138,139,140,143,144] | RF | MSI: [137,138,139,143,144] HSI: [134,140] Other: [137,138,139,143] | Supervised | No | |
| [145,146,147,148,149,150,151,156,157] | SVM | MSI: [146,148,149,156,157] HSI: [145,147,150,151] Other: [151] | Semisupervised: [150] Supervised: [145,146,147,148,149,150,151,156,157] | No | |
| [158,159,161] | LR | MSI: [158] HSI: [158,159,161] | Supervised | No | |
| [162,163,164] | MLP | MSI: [162,163] SAR: [162] Other: [164] | Supervised | No | |
| [165,166,167,168,169,170,172,175,177,178,179,180,181,182,184] | CNN | MSI: [168,170,172,181] HSI: [165,166,172,175,177,178,179,180,182,184] SAR: [169,179] LiDAR: [172,179] Other: [167] | Supervised | Yes | |
| [185,186,188,189,190,191] | RNN | MSI: [185,188] HSI: [186,191] SAR: [189,190] | Supervised | Yes | |
| Target Detection | [192] | Clustering | LiDAR | Supervised | No |
| [194] | SVM | Other | Supervised | No | |
| [195] | LR | LiDAR, Other | Supervised | No | |
| [196,198] | MLP | SAR: [196] Other: [198] | Supervised | No | |
| [199,200,201,202,204,205,206,208,211,214,216,218,219,221,224,226,227,228,229] | CNN | MSI: [199,200,202,204,205,206,208,211,214,216,218,219,221,224,227,228,229] SAR: [201,226] | Supervised | Yes | |
| Pattern Mining | [232,235,236] | RF | Other | Supervised | No |
| [237] | SVM | Other | Supervised | No | |
| [238,240,241,242,243] | LR | MSI: [242] Other: [238,240,241,243] | Supervised | No | |
| [164,244,245] | MLP | MSI: [245] Other: [164,244,245] | Supervised | No | |
| [246] | GAN | Other | Supervised | Yes | |
| Boundary Extraction | [247,248] | AC | HSI: [247] SAR: [248] LiDAR: [247] | Supervised: [247] Unsupervised: [248] | No |
| [249,251,254,266,268] | Multiple: Clustering/AC: [249] CNN/AC: [251] Clustering/MRF: [254] CNN/RNN: [266,268] | MSI: [251,266,268] SAR: [249,254] LiDAR: [251] | Supervised: [251] Unsupervised: [249] | No: [249,254] Yes: [251,266,268] | |
| Change Detection | [253] | AC | MSI | Unsupervised | No |
| [255,257,258] | Clustering | MSI: [263] SAR: [255,257] | Unsupervised | No | |
| [252] | SVM | MSI | Semisupervised | No | |
| [260,261,262] | LR | MSI: [260,261] SAR: [262] | Supervised | No | |
| [263,264,265] | MLP | MSI | Supervised | No | |
| [267] | RNN | MSI | Supervised | Yes | |
| Image Preprocessing | [269,270,273] | CNN | HSI: [269] SAR: [273] Other: [270] | Supervised | Yes |
| [275,276] | GAN | MSI: [275,276] | Supervised | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Savelonas, M.A.; Veinidis, C.N.; Bartsokas, T.K. Computer Vision and Pattern Recognition for the Analysis of 2D/3D Remote Sensing Data in Geoscience: A Survey. Remote Sens. 2022, 14, 6017. https://doi.org/10.3390/rs14236017
Savelonas MA, Veinidis CN, Bartsokas TK. Computer Vision and Pattern Recognition for the Analysis of 2D/3D Remote Sensing Data in Geoscience: A Survey. Remote Sensing. 2022; 14(23):6017. https://doi.org/10.3390/rs14236017
Chicago/Turabian StyleSavelonas, Michalis A., Christos N. Veinidis, and Theodoros K. Bartsokas. 2022. "Computer Vision and Pattern Recognition for the Analysis of 2D/3D Remote Sensing Data in Geoscience: A Survey" Remote Sensing 14, no. 23: 6017. https://doi.org/10.3390/rs14236017
APA StyleSavelonas, M. A., Veinidis, C. N., & Bartsokas, T. K. (2022). Computer Vision and Pattern Recognition for the Analysis of 2D/3D Remote Sensing Data in Geoscience: A Survey. Remote Sensing, 14(23), 6017. https://doi.org/10.3390/rs14236017






