A Sequential Student’s t-Based Robust Kalman Filter for Multi-GNSS PPP/INS Tightly Coupled Model in the Urban Environment
Abstract
1. Introduction
2. Multi-GNSS PPP/INS Tightly Coupled Model
2.1. Multi-GNSS PPP/INS Tightly Coupled Observation Model
2.2. North-Oriented INS State Model
3. PPP/INS Observation Noise Distributional Characteristic Analysis
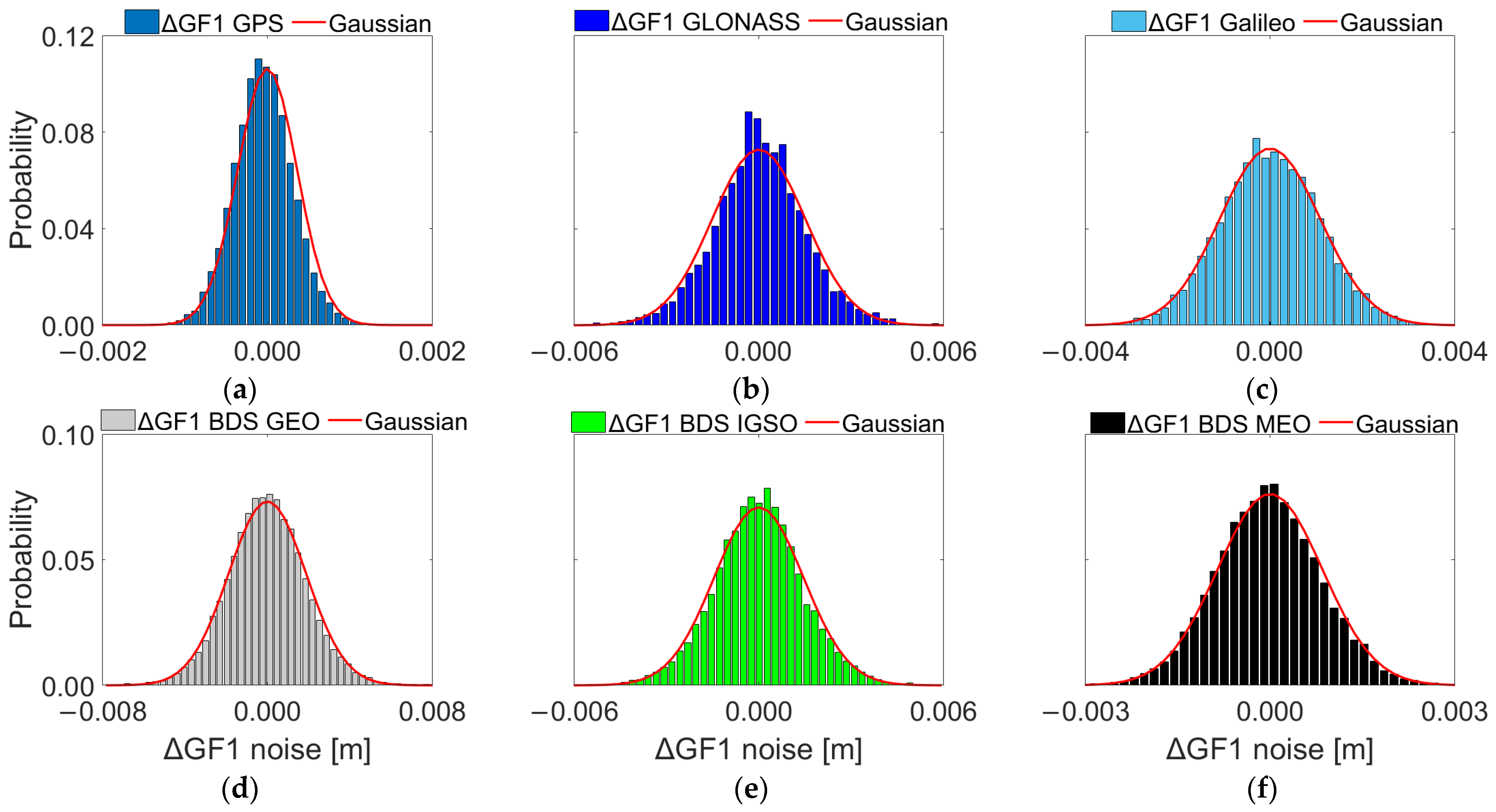
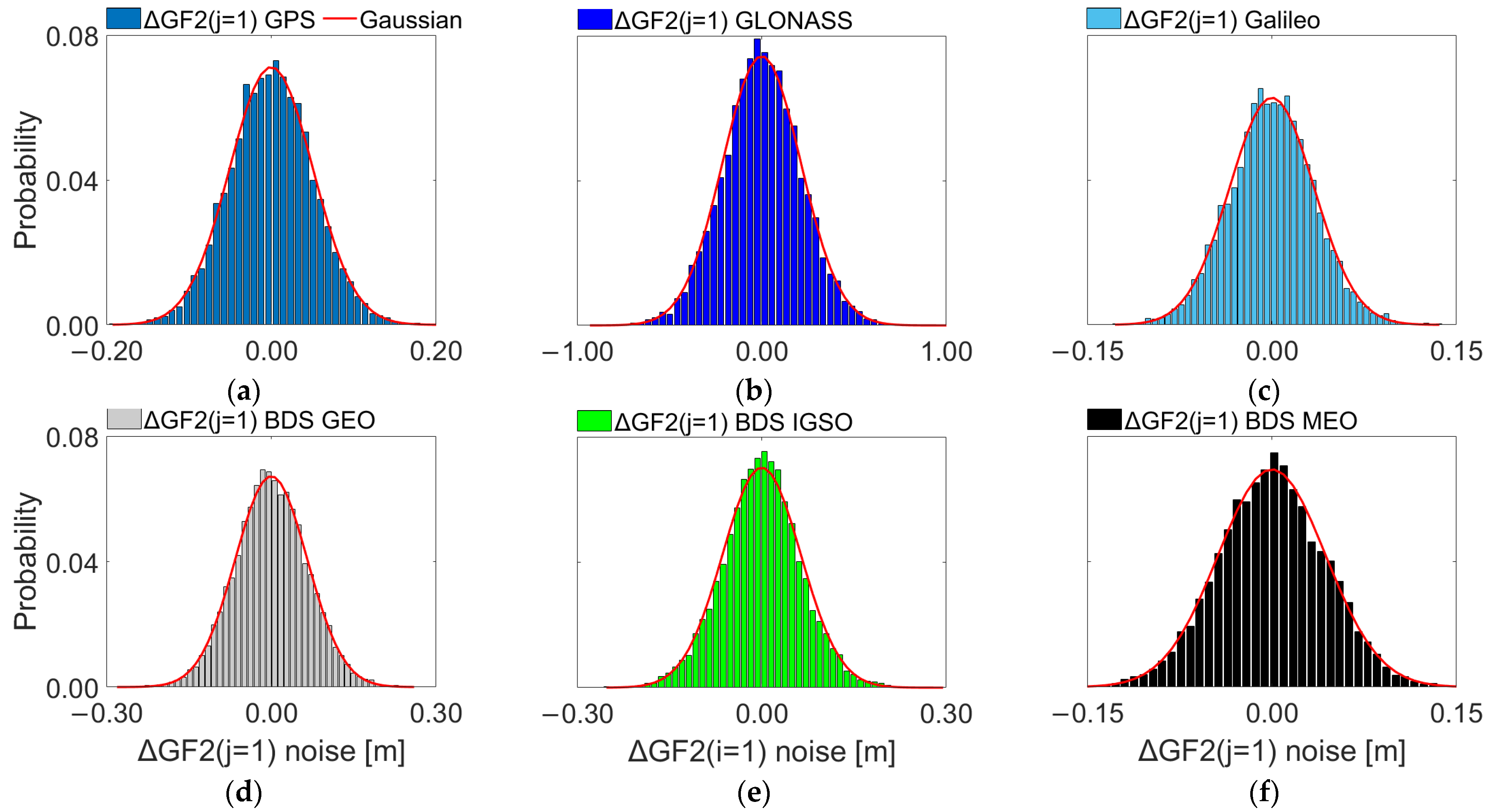
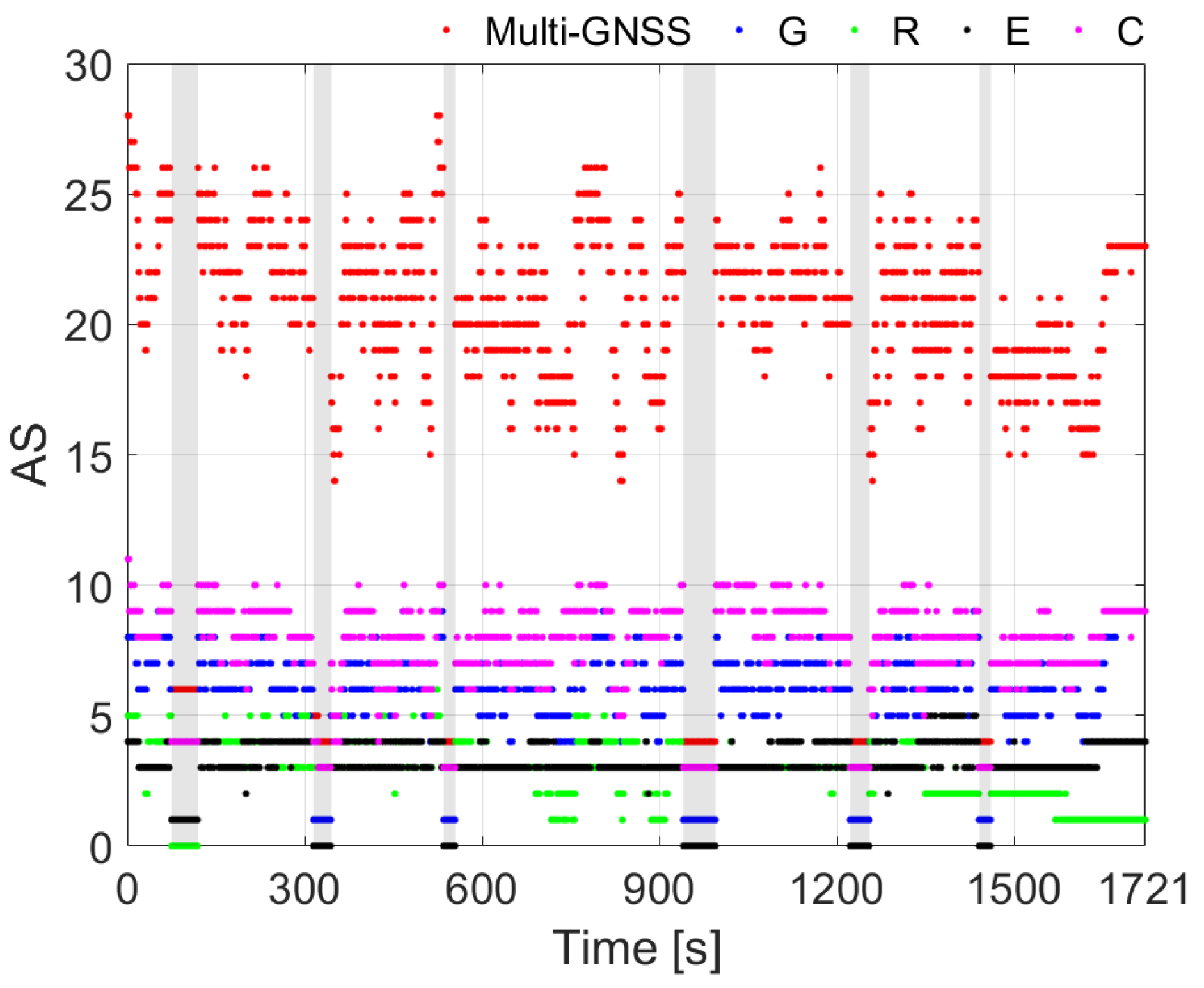
3.1. Multi-GNSS Observation Noise Extraction
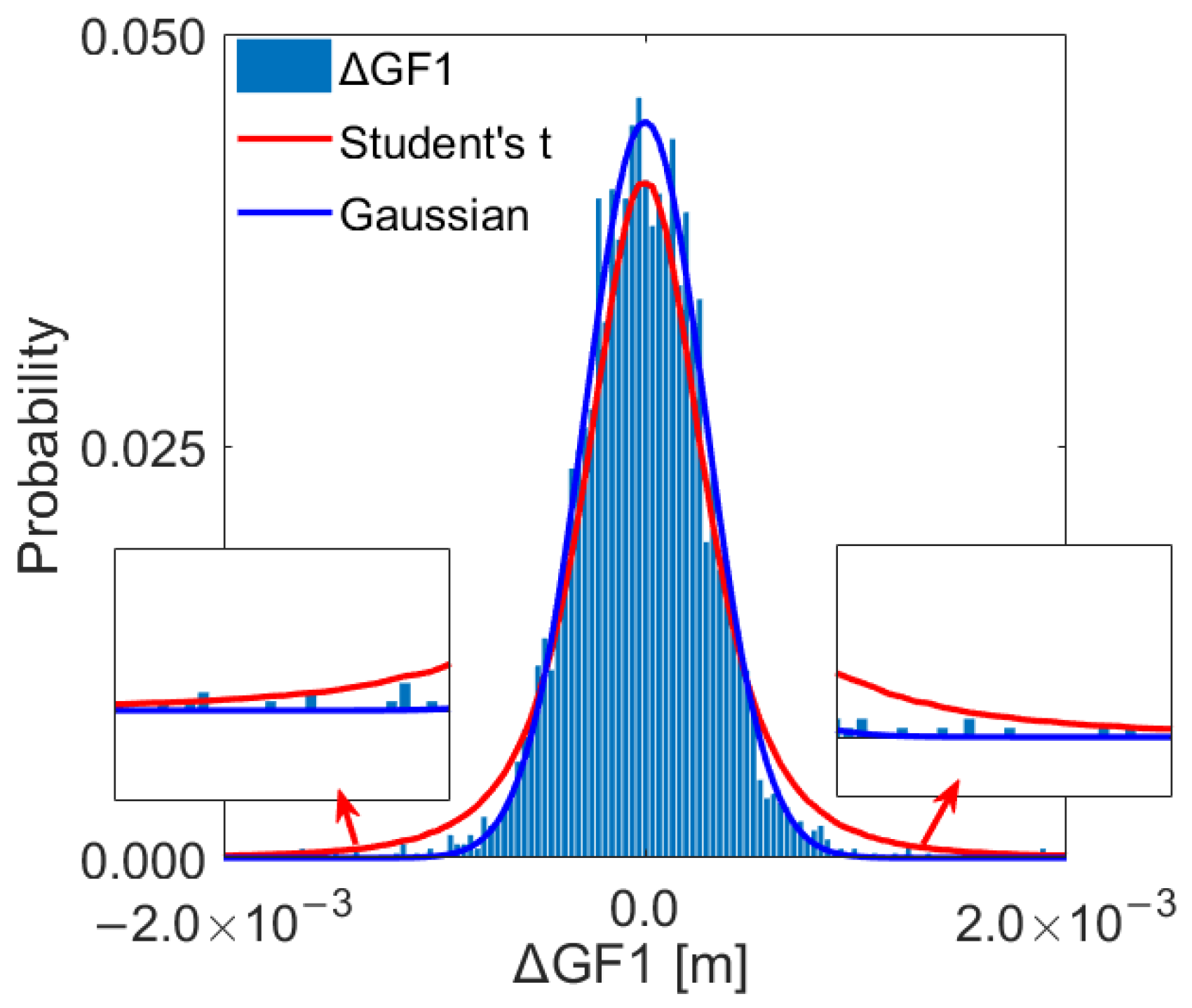
3.2. Distributional Characteristic Analysis on Gross-Error-Contaminated Observation Noise
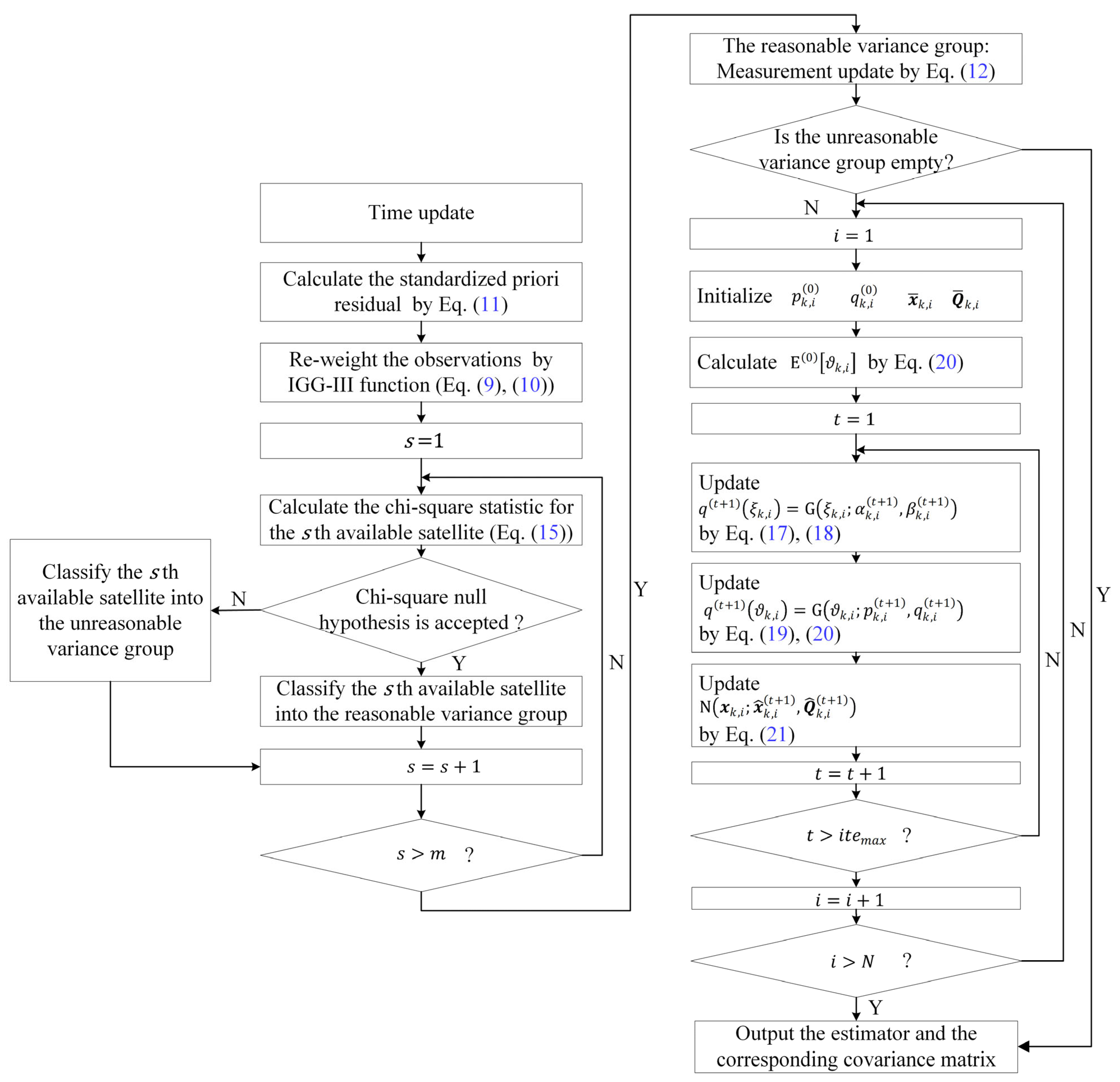
4. Sequential Student’s t-Based Robust Kalman Filter
4.1. Robust Kalman Filter Based on IGG-III Function
4.2. Student’s t-Based Kalman Filter
4.3. Sequential Student’s t-Based Robust Kalman Filter
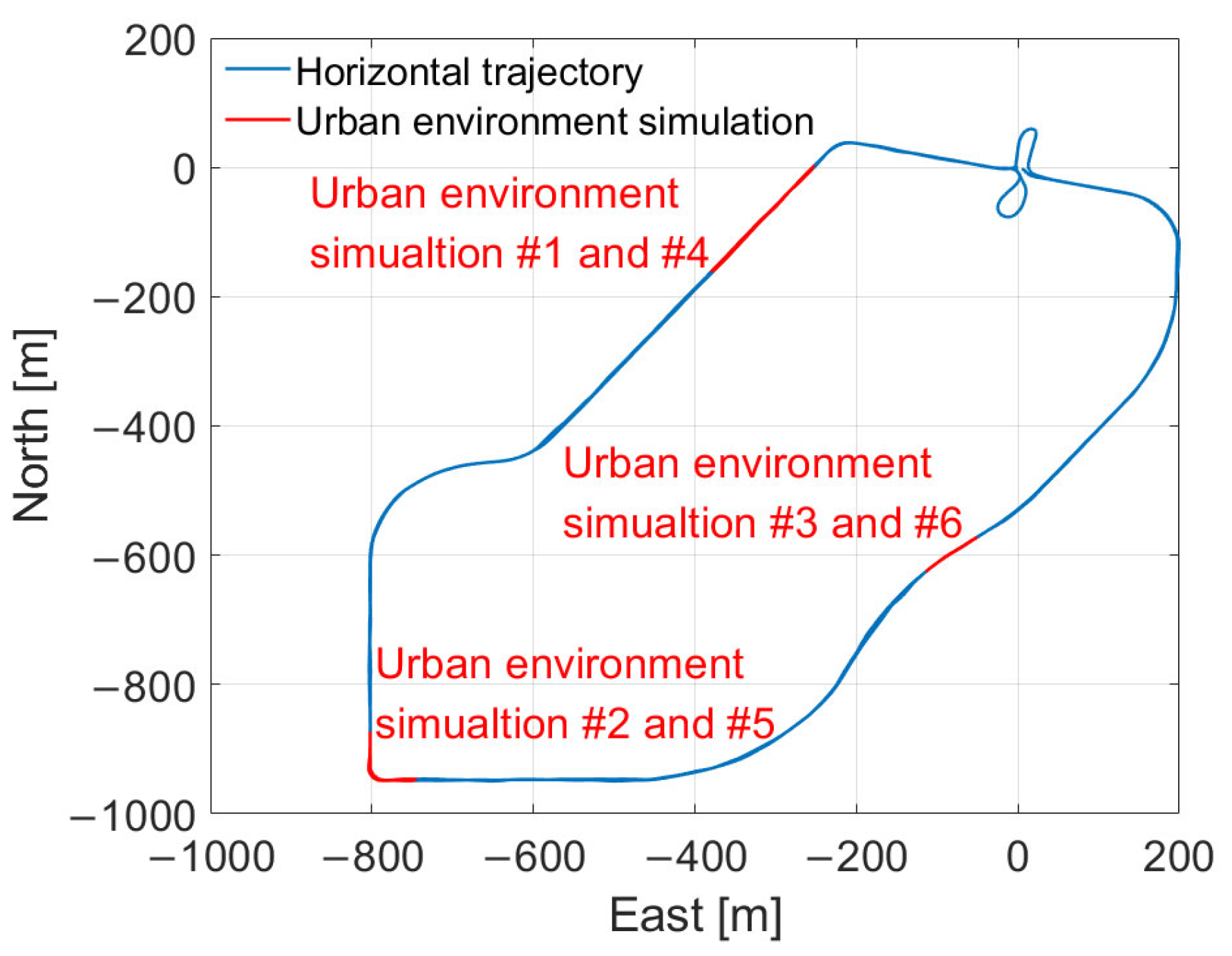
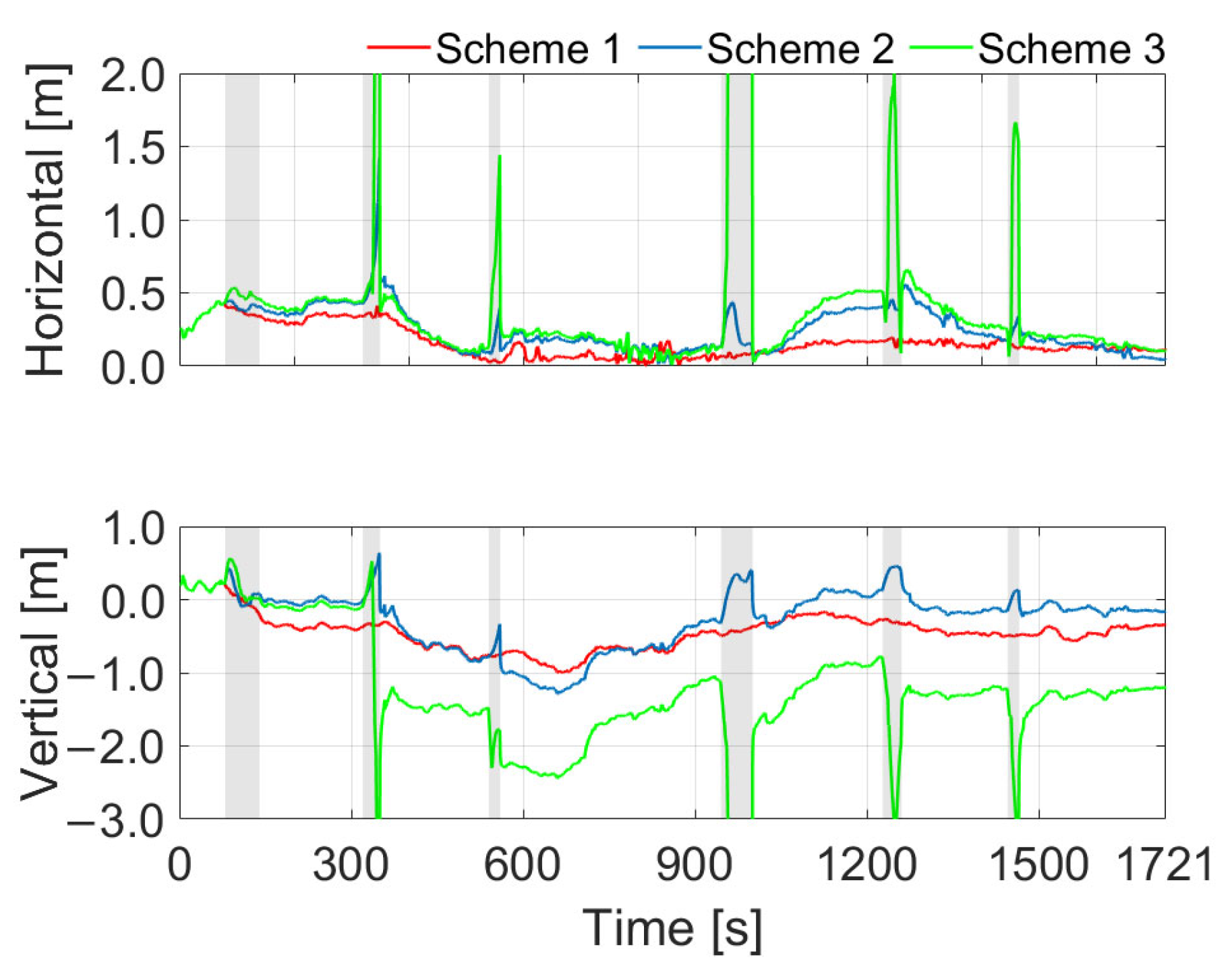
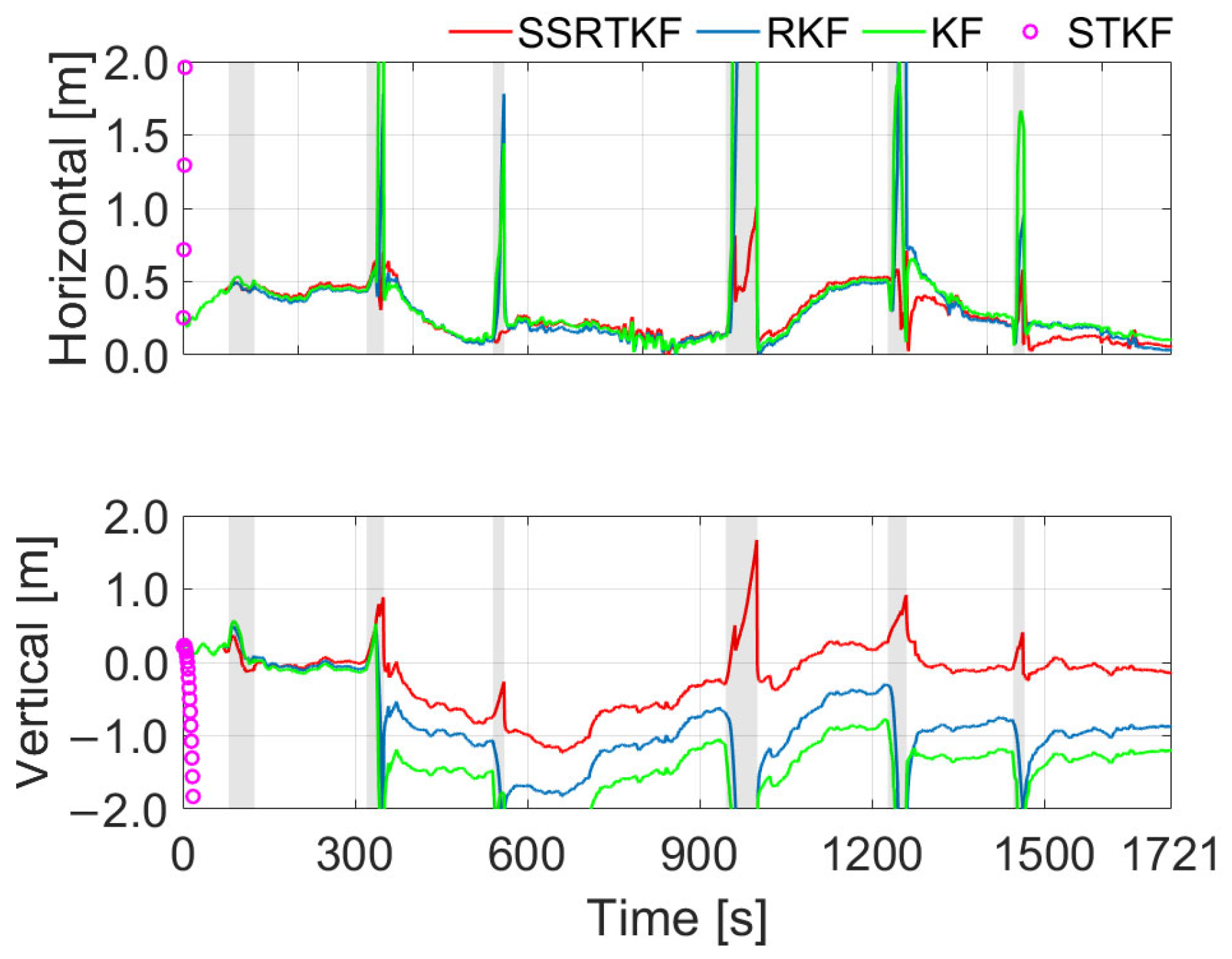
5. Experiments and Discussions
6. Conclusions
- The GNSS phase and code observation noise obey the Gaussian assumption in the absence of the LOS multipath and NLOS reception errors. Moreover, the Student’s t distribution can fit the heavy tails of the gross-error-contaminated observation noise.
- The proposed SSTRKF can adjust the IGG-III function-derived unreasonable variances through the chi-square test and the sequential Student’s t-based Kalman filter, respectively.
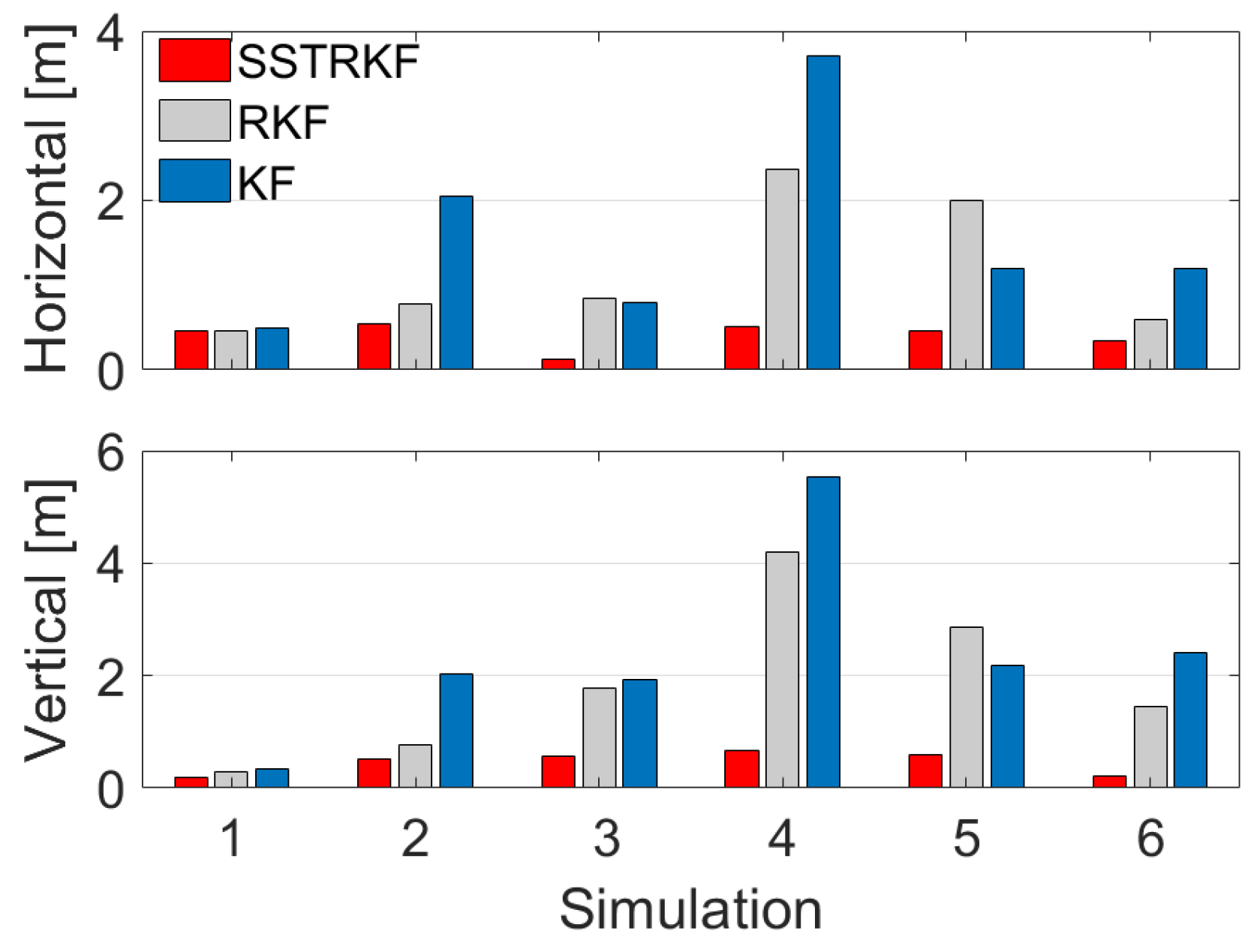
- The numerical comparisons have validated our proposed SSTRKF for the gross-error-contaminated observations. Compared with the RKF, the proposed SSTRKF improves the horizontal and vertical positioning precisions by 57.5% and 62.0% on average during the urban environment simulations. Consequently, the proposed SSTRKF is superior to the KF and the RKF in the urban environment.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, X.; Yu, J.M.; Yu, W.; Truong, T.K. GPS L1CA/BDS B1I Multipath Channel Measurements and Modeling for Dynamic Land Vehicle in Shanghai Dense Urban Area. IEEE Trans. Veh. Technol. 2020, 69, 14247–14263. [Google Scholar] [CrossRef]
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; Wiley: New York, NY, USA, 2015. [Google Scholar]
- Tang, W.; Wang, Y.; Zou, X.; Li, Y.; Deng, C.; Cui, J. Visualization of GNSS multipath effects and its potential application in IGS data processing. J. Geod. 2021, 95, 103. [Google Scholar] [CrossRef]
- Spangenberg, M.; Calmettes, V.; Julien, O.; Tourneret, J.Y.; Duchâteau, G. Detection of variance changes and mean value jumps in measurement noise for multipath mitigation in urban navigation. Navigation 2010, 57, 35–52. [Google Scholar] [CrossRef]
- Brodin, G.; Daly, P. GNSS code and carrier tracking in the presence of multipath. Int. J. Satell. Commun. 1997, 15, 25–34. [Google Scholar] [CrossRef]
- Hsu, L.T.; Jan, S.S.; Groves, P.D.; Kubo, N. Multipath mitigation and NLOS detection using vector tracking in urban environments. GPS Solut. 2015, 19, 249–262. [Google Scholar] [CrossRef]
- Groves, P.D.; Jiang, Z.; Rudi, M.; Strode, P. A portfolio approach to NLOS and multipath mitigation in dense Urban areas. In Proceedings of the ION-GNSS+−2013, Nashville, TN, USA, 16–20 September 2013; pp. 3231–3247. [Google Scholar]
- Ng, H.F.; Zhang, G.; Hsu, L.T. A computation effective range-based 3D mapping aided GNSS with NLOS correction method. J. Navig. 2020, 73, 1202–1222. [Google Scholar] [CrossRef]
- Wen, W.; Zhang, G.; Hsu, L.T. GNSS NLOS exclusion based on dynamic object detection using LiDAR point cloud. IEEE Trans. Intell. Transp. 2019, 22, 853–862. [Google Scholar] [CrossRef]
- Hsu, L.T. Analysis and modeling GPS NLOS effect in highly urbanized area. GPS Solut. 2018, 22, 7. [Google Scholar] [CrossRef]
- Atkins, C.; Ziebart, M. Effectiveness of observation-domain sidereal filtering for GPS precise point positioning. GPS Solut. 2016, 20, 111–122. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Luo, X.; Knöpfler, A.; Mayer, M. Generating statistically robust multipath stacking maps using congruent cells. GPS Solut. 2015, 19, 83–92. [Google Scholar] [CrossRef]
- Chang, G. Robust Kalman filtering based on Mahalanobis distance as outlier judging criterion. J. Geod. 2014, 88, 391–401. [Google Scholar] [CrossRef]
- Cheng, C.; Tourneret, J.Y.; Pan, Q.; Calmettes, V. Detecting, estimating and correcting multipath biases affecting GNSS signals using a marginalized likelihood ratio-based method. Signal Process. 2016, 118, 221–234. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, X. Adaptive robust Kalman filtering for precise point positioning. Meas. Sci. Technol. 2014, 25, 105011. [Google Scholar] [CrossRef]
- Gao, Z.; Li, Y.; Zhuang, Y.; Yang, H.; Pan, Y.; Zhang, H. Robust Kalman filter aided GEO/IGSO/GPS raw-PPP/INS tight integration. Sensors 2019, 19, 417. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhang, Y.; Li, N.; Wu, Z.; Chambers, J.A. A novel robust Student’s t-based Kalman filter. IEEE Trans. Aero. Elec. Sys. 2017, 53, 1545–1554. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y. A New Process Uncertainty Robust Student’s t based Kalman Filter for SINS/GPS Integration. IEEE Access 2017, 5, 14391–14404. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, T.; Jin, B.; Zhu, Y.; Tong, J. Student’s t-based robust Kalman filter for a SINS/USBL integration navigation strategy. IEEE Sens. J. 2020, 20, 5540–5553. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, P.; Zha, J.; Liu, T. Integer-estimable FDMA model as an enabler of GLONASS PPP-RTK. J. Geod. 2021, 95, 91. [Google Scholar] [CrossRef]
- Zhang, B.; Hou, P.; Zha, J.; Liu, T. PPP–RTK functional models formulated with undiferenced and uncombined GNSS observations. Satell. Navig. 2022, 3, 3. [Google Scholar] [CrossRef]
- Zang, N.; Li, B.; Nie, L.; Shen, Y. Inter-system and inter-frequency code biases: Simultaneous estimation, daily stability and applications in multi-GNSS single-frequency precise point positioning. GPS Solut. 2019, 24, 18. [Google Scholar] [CrossRef]
- Yan, G.; Weng, J. Strapdown Inertial Navigation Algorithm and Integrated Navigation Theory, 1st ed.; NPU Press: Xi’an, China, 2019. [Google Scholar]
- Zhang, Z.; Li, B.; Shen, Y.; Yang, L. A noise analysis method for GNSS signals of a standalone receiver. Acta. Geod. Geophys. 2017, 52, 301–316. [Google Scholar] [CrossRef]
- De Bakker, P.F.; Van Der Marel, H.; Tiberius, C.C.J.M. Geometry-free undifferenced, single and double differenced analysis of single frequency GPS, EGNOS and GIOVE-A/B measurements. GPS Solut. 2009, 13, 305–314. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X. Instantaneous re-initialization in real-time kinematic PPP with cycle slip fixing. GPS Solut. 2012, 16, 315–327. [Google Scholar]
- Blewitt, G. An automatic editing algorithm for GPS data. Geophys. Res. Lett. 1990, 17, 199–202. [Google Scholar] [CrossRef]
- Liu, Z. A new automated cycle slip detection and repair method for a single dual-frequency GPS receiver. J. Geod. 2011, 85, 171–183. [Google Scholar] [CrossRef]
- Li, B.; Qin, Y.; Liu, T. Geometry-based cycle slip and data gap repair for multi-GNSS and multi-frequency observations. J. Geod. 2019, 93, 399–417. [Google Scholar] [CrossRef]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]
- Chen, K.; Chang, G.; Chen, C. GINav: A MATLAB-based software for the data processing and analysis of a GNSS/INS integrated navigation system. GPS Solut. 2021, 25, 108. [Google Scholar] [CrossRef]

| Simulation Number | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| LOS multipath error | Lifetime | 10 s | 10 s | 0 s | 0 s | 20 s | 10 s |
| Model | |||||||
| NLOS reception error | Lifetime | 45 s | 30 s | 20 s | 55 s | 23 s | 20 s |
| Model | |||||||
| The LOS Multipath and NLOS Reception Errors | Blockage Environment | |
|---|---|---|
| Scheme 1 | No | No |
| Scheme 2 | No | Yes |
| Scheme 3 | Yes | Yes |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Cheng, J.; Zang, N.; Zhang, Z.; Chen, S. A Sequential Student’s t-Based Robust Kalman Filter for Multi-GNSS PPP/INS Tightly Coupled Model in the Urban Environment. Remote Sens. 2022, 14, 5878. https://doi.org/10.3390/rs14225878
Cheng S, Cheng J, Zang N, Zhang Z, Chen S. A Sequential Student’s t-Based Robust Kalman Filter for Multi-GNSS PPP/INS Tightly Coupled Model in the Urban Environment. Remote Sensing. 2022; 14(22):5878. https://doi.org/10.3390/rs14225878
Chicago/Turabian StyleCheng, Sixiang, Jianhua Cheng, Nan Zang, Zhetao Zhang, and Sicheng Chen. 2022. "A Sequential Student’s t-Based Robust Kalman Filter for Multi-GNSS PPP/INS Tightly Coupled Model in the Urban Environment" Remote Sensing 14, no. 22: 5878. https://doi.org/10.3390/rs14225878
APA StyleCheng, S., Cheng, J., Zang, N., Zhang, Z., & Chen, S. (2022). A Sequential Student’s t-Based Robust Kalman Filter for Multi-GNSS PPP/INS Tightly Coupled Model in the Urban Environment. Remote Sensing, 14(22), 5878. https://doi.org/10.3390/rs14225878






