Abstract
Ballistic target recognition is of great significance for space attack and defense. The micro-motion features, which contain spatial and motion information, can be regarded as the foundation of the recognition of ballistic targets. To take full advantage of the micro-motion information of ballistic targets, this paper proposes a method based on feature fusion to recognize ballistic targets. The proposed method takes two types of data as input: the time–range (TR) map and the time–frequency (TF) spectrum. An improved feature extraction module based on 1D convolution and time self-attention is applied first to extract the multi-level features at each time instant and the global temporal information. Then, to efficiently fuse the features extracted from the TR map and TF spectrum, deep generalized canonical correlation analysis with center loss (DGCCA-CL) is proposed to transform the extracted features into a hidden space. The proposed DGCCA-CL possesses better performance in two aspects: small intra-class distance and compact representation, which is crucial to the fusion of multi-modality data. At last, the attention mechanism-based classifier which can adaptively focus on the important features is employed to give the target types. Experiment results show that the proposed method outperforms other network-based recognition methods.
1. Introduction
Space target defense is an important aspect of modern combat. Ballistic targets (such as warheads, decoys, etc.) pose a significant threat to homeland security, and ballistic target recognition becomes the key to missile defense [1,2]. The common radar signatures used for ballistic target recognition include radar cross-section (RCS) [3], inverse synthetic aperture radar (ISAR) image [4], high-resolution range profile (HRRP) map [5], and so on. By analyzing these radar feature data, parameters such as the structure size, motion trajectory, and flight speed of the targets can be obtained, and the identification and classification of the targets can be further realized. However, with the development of target feature control technology, the decoys released during the flight of ballistic missiles are very close to the warhead in terms of geometry, flight speed, RCS, etc., which decreases the recognition performance based on traditional radar features. Additionally, the mining and identification of the fine features of ballistic targets have become the focus of research.
Micro-motion refers to the small reciprocating motion of the target or its components in addition to the translation of the main body [6]. Affected by dynamics, ballistic targets experience micro-motion such as spin, coning, nutation, and tumbling outside of high-speed translation [7]. Compared with traditional characteristics of ballistic targets, the micro-motion feature reflects the unique structural information and motion characteristics of the ballistic targets, which can be regarded as an important basis for the recognition of ballistic targets [8,9]. Micro-motion causes subtle changes in the range and frequency of the targets—or scattering center movement—which are known as micro-range and micro-Doppler [10]. Micro-range is generally represented as HRRP sequence and TR map, while micro-Doppler is mainly represented as TF spectrum and cadence velocity diagram (CVD) map [11]. Currently, ballistic target recognition based on micro-range and micro-Doppler features has become a major research direction [12,13].
The current ballistic target recognition methods can be mainly divided into two categories: methods based on manual feature extraction and methods based on neural network feature extraction. The first category extracts physical features (e.g., target shape, structure, and motion) for recognition [10,14,15,16]. Ai et al. proposed a method named genetic algorithm-general parameterized time–frequency transform (GA-GPTF) to extract the micro-Doppler curve and estimate parameters accurately, which provided an additional method for ballistic target recognition [10]. Authors in [15] achieved the classification of warheads and decoys by computing seven features such as mean, standard deviation, etc., in the CVD map. Persico et al. proposed a new method based on the inverse Radon transform of the target signatures to classify different ballistic targets, which was represented by the feature of micro-range obtained in a whole period of the coning of ballistic targets [16]. However, the methods based on manual feature extraction require features designed by experts and their performance is limited when the scenario changes.
The second category designs deep neural networks, which automatically learn features from the training data and achieve recognition. Compared with the methods based on manual feature extraction, deep networks could automatically draw significant features of the targets and avoid the impact of human errors on the results, and have been studied by many scholars [13,17,18,19,20,21]. Kim and Moon creatively used convolutional neural networks (CNNs) to recognize space targets with the micro-Doppler spectrum [21]. Authors in [13] used truncated singular value decomposition (SVD) to compress the TF dataset and further enhance the recognition accuracy of inertia characteristics of the targets by their designed network. Wang et al. inputted a processed TR map into the designed CNN for recognition, and the recognition rate of five micro-motion forms under the signal-to-noise ratio (SNR) of −10 dB reached 80% [20]. However, the above methods use a single feature image of the micro-motion target for classification, which can cause the unstable performance of the classifier because the characteristics of targets and the observation parameters of radar may change.
To improve the stability and robustness of ballistic target recognition, fusion-based recognition methods are recently proposed, which are mainly divided into the decision-level fusion method and the feature-level fusion method [22]. The decision-level fusion method makes decisions by weighted fusion of classification results of different features [22,23]. However, this kind of fusion method loses a large amount of detailed information. Compared with decision-level fusion, feature-level fusion retains the details of different forms of data and has a stronger expressive ability [24,25,26]. The feature maps obtained by feeding the CVD map and TF spectrogram are spliced along the same dimension to achieve the classification of spatial targets [24,25]. By splicing the targets’ macro-motion and micro-motion features after weighting, Choi et al. effectively identified targets and decoys [26].
The feature-level fusion method retains the details of different forms of data and has a strong expressive ability, which is widely used in various fields. Tang et al. proposed a novel cognitive attention network (CAN) for visual commonsense reasoning to achieve interpretable visual understanding, which was based on a designed image–text fusion module to fuse information from images and text collectively and a novel inference module to encode commonsense among image, query, and response [27]. Authors in [28] proposed a novel expansion–squeeze–excitation fusion network (ESE-FN) to realize human activity recognition, which learned modal and channel-wise attention for attentively fusing the multiple features in the modal and channel-wise ways. To realize audiovisual cross-modal retrieval, Zhang et al. constructed a joint embedding subspace for the input audio data and visual data, in which the mutuality of audiovisual information was reinforced and the cross-modal discrepancy from inter-modal information was simultaneously eliminated. In addition, the proposed architecture was verified appreciably better than the existing cross-modal retrieval methods by experiments [29]. No research has yet proved that these fusion methods can be applied to the field of ballistic target recognition.
In conclusion, the current ballistic target recognition methods have the following two problems: (1) Most of the micro-motion target recognition methods based on deep networks are directly migrated from the field of optical image target recognition, ignoring the characteristics of micro-motion feature data. Not only is the interpretability poor, but there is still improvement needed in the optimization and extraction of features. (2) Current fusion recognition methods for micro-motion targets possess the problem of losing a large amount of target detail information or ignoring the intrinsic relationship among feature vectors, and the recognition performance and robustness are poor.
To solve the above problems and make good use of the micro-motion information of the ballistic targets, we propose a feature fusion-based ballistic target recognition method which contains the feature extraction module, DGCCA-CL module, and the attention mechanism-based classifier. Specifically, we treat the TR map and TF spectrogram as a high-dimensional time series, and the one-dimensional range sequence and frequency sequence are obtained at each time instant, respectively. Then, we use the designed feature extraction module to extract the features of the TR and TF time series, respectively, which outputs a two-channel range and frequency features. The feature extraction module firstly extracts the multi-level features of range and frequency, respectively, through the designed module named one-dimensional multi-level features fusion (1D-MFF), and then uses the time self-attention (TSA) module to extract their global temporal information. The DGCCA-CL module enhances the correlation of the output features of the two channels by mapping them into a shared hidden subspace, and reduces the variance of features within classes by penalizing the distance between the deep features and their corresponding class centers. The attention mechanism-based classifier, which can adaptively select the important features of the two-channel range and frequency features, is employed to provide the final classification results. Our main contributions are as follows:
- For the inputted TR map and TF spectrogram, we propose a novel feature extraction module based on 1D convolution and the TSA module. The former is used to extract the multi-level features of range and frequency and the latter is used to obtain the global temporal information of range sequence and frequency sequence.
- We propose a novel optimization method named DGCCA-CL—a method to learn nonlinear transformations and minimize the intra-class distances of the deep features of multi-modality data, such that the resulting transformations are maximally informative of each other.
- A novel recognition method of ballistic targets by fusing micro-motion features is proposed and the validity and robustness of our method are verified through a series of simulation results.
The paper is organized as follows. Section 2 introduces the related work. Section 3 establishes the micro-motion model and signal model of ballistic targets. Section 4 introduces the proposed method in detail. Section 5 establishes a simulation dataset and verifies the validity of the proposed method through multiple groups of experiments. Section 6 discusses and analyzes the experimental results. Section 7 presents the conclusion.
2. Related Work
We survey some works related to micro-motion feature extraction based on network and features fusion recognition.
- A.
- micro-motion feature extraction based on network
Compared with manual feature extraction, feature extraction methods based on neural networks can automatically extract significant features of the targets and avoid the impact of human errors on the results, which has become the main manner of feature extraction in micro-motion target recognition methods. Current micro-motion feature extraction methods based on neural networks are mostly performed by CNN [19,20,21,22,23,24,25,26,30,31]. Wang et al. performed feature extraction on the TR map based on the designed CNN [20], and Kim et al. used Googlenet to perform feature extraction on the CVD map of the targets [19]. However, these methods are directly migrated from the field of optical image target recognition, ignoring the unique feature information of radar images, and the interpretability is poor. To solve the problem, Wang et al. combined the advantages of CNN and recurrent neural network (RNN), which can simultaneously extract range-Doppler features and time series features of gesture motion repressively [32]. Authors in [33] used long short-term memory (LSTM) to extract time sequential features of HRRP sequences. Han et al. used a one-dimensional convolutional neural network to extract the features of the frequency, and then used LSTM to extract the time series features among frequencies, which achieves better results compared to other classic CNNs [34].
In this work, the TF spectrogram and TR map that reflect the change of micro-motion speed and micro-motion range of the targets are used for recognition. It is important to extract the temporal features and select the most significant information. Though existing networks can process this type of data to some extent, they are not well-designed, leading to redundant parameters or low recognition performance. In view of this, we first design a novel feature extraction module based on 1D convolution and the time self-attention (TSA) module. The 1D convolution is used to extract the multi-level features of range and frequency, respectively, and then the TSA module is used to extract their global temporal information.
- B.
- features fusion recognition
Because feature fusion can combine and utilize the detailed information of multiple modalities, it is widely used in visual understanding, cross-modal retrieval, emotion analysis, target recognition, and other fields [27,28,29,35,36,37,38,39]. As one of the important applications, recognition based on feature fusion has attracted more and more scholars’ attention and research. Some works [25,40,41] fused and recognized the features extracted from different modal data through simple splicing, which easily lead to data redundancy. Zhou et al. added an attention mechanism to highlight the weight of different modal features on classification when splicing features [41]. However, the above methods do not consider the relevant information between modal features and ignore the internal relationship among eigenvectors. To use the relevant information between different modal features, Zadeh et al. calculated the correlation between elements of different modalities through the tensor outer product between modalities for feature fusion [38]. Hou et al. proposed a feature fusion method named polynomial tensor pool block (PTP), which multiplied each tensor connection by order P and then performed low-order decomposition. It could describe the local and global correlation between multimodal data at the fine-grained level [42]. However, the above matrix methods greatly increased the dimension of the feature vector, causing the models to be too large and difficult to train.
The fusion recognition methods based on typical correlation analysis (CCA) extract the relevant features of different modal feature data by maximizing their correlation in subspace. Qiu et al. adopted deep canonical correlation analysis (DCCA) for multimodal emotion recognition and obtained significant performance improvement with respect to three emotion recognition tasks [43]. However, DCCA can only maximize the correlation between two different modalities due to the limitation of the CCA constraint. To extend DCCA from two modalities to arbitrarily numerous modalities, Lin et al. introduce deep generalized correlation constraints analysis (DGCCA) to ISAR image classification [44]. However, DGCCA-based fusion methods ignore the role of label information in supervised classification. To utilize the label information of the data and enhance the clustering effect in supervised classification, in this paper, we propose the DGCCA-CL module, which introduces center loss on the basis of DGCCA. At the same time, we design an attention-based classifier to achieve the effective classification of ballistic targets by adaptively assigning weights to different modalities.
3. Model
3.1. Micro-Motion Model
The micro-motion forms of space ballistic targets include spin, coning, nutation, and tumbling. Radar targets can generally be represented by multiple scattering centers. In the local coordinate system of target, we make represent the initial position of the lth scattering center, represents the direction vector of radar line of sight (LOS), and represents the motion-dependent rotation matrix. Then, the time-varying position vector can be represented as . The instantaneous slant range is the inner product between and , i.e.,:
where represents the inner product [3].
3.2. Signal Model
According to [45], after range compression, we can obtain the radar echoes as:
where is the back-scattering coefficient of the lth scattering center, and the rest depends on the autocorrelation or other filtering of the waveform, is the signal bandwidth, c is the light speed, is the slant range between the lth scattering center and the distance of the reference point, is the wavelength of the transmitted signal, and is the carrier frequency. By summing the echoes along the range bin, the target echoes of narrowband radar can be generated as:
As an effective time–frequency transform method, short-time Fourier transform (STFT) is usually applied to the radar echo to obtain the time–frequency spectrogram. The main idea is that a window function is used to extract the signal in a small time interval, and then a fast Fourier transform (FFT) is used to analyze the signal frequency in each time interval. By applying STFT to the radar echo , the time–frequency distribution can be represented as:
where and represent the time and Doppler variables, respectively.
4. Method
The overall network architecture of the proposed method can be shown in Figure 1, which includes the feature extraction module based on 1D convolution and TSA, the DGCCA-CL module, and the attention mechanism-based classifier. For the input TR map and TF spectrogram, firstly they are divided into the range sequence and frequency sequence in the time dimension, respectively, and then the multi-level features of range and frequency are extracted and further fused in the 1D-MFF module, and their temporal relationships are extracted by the TSA module, respectively. The DGCCA-CL module maps the output features of the two channels into a shared hidden subspace for unified representation and reduces the differences in intra-class features at the same time. In the attention mechanism-based classifier module, the adaptive feature fusion is carried out on the features of two channels by using the attention mechanism, and the classification is achieved with the softmax function.
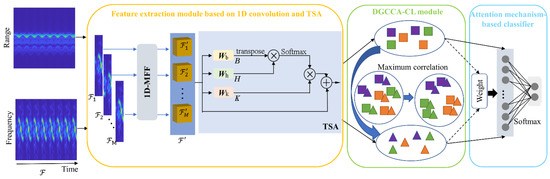
Figure 1.
The overall network structure of the proposed method ( and represent matrix multiplication and element-wise addition, respectively).
4.1. Feature Extraction Module Based on 1D Convolution and TSA
Unlike the popular 2D convolution used in computer vision, we would like to use 1D convolution to extract the feature data of micro-motion at each instant. Furthermore, the temporal correlation information can be preserved for subsequent processing. In this paper, we treat the TR map and the TF spectrogram as a high-dimensional time series, i.e., at each time instant, we have a one-dimensional range sequence and frequency sequence. The feature extraction module includes the 1D-MFF module and the TSA module. The 1D-MFF module is used to extract and fuse the range and frequency features at different levels, respectively. In addition, the TSA module extracts the global temporal information among 1D feature map sequence of range and frequency, respectively. In the previous image recognition networks, the convolutional layer often adopts a two-dimensional structure and ignores the temporal correlation among the range sequence and frequency sequence, which is related to the motion of targets.
Taking the input TF spectrogram as an example, firstly, the input TF spectrogram is divided into one-dimensional sequence along the time dimension, where F and N represent the height and width of the input TF spectrogram, respectively. For each one-dimensional feature map , the 1D-MFF module is used to extract and fuse its features of different levels to acquire feature maps . Then we concatenate the obtained feature maps along the time dimension and the output feature sequence is , which is obtained by:
Then, the TSA module is used to exploit the relation of one-dimensional sequence to capture the global temporal cue:
In the same way, the feature can be obtained by taking the TR map as input.
4.1.1. D-MFF Module
Deep learning has successfully played a significant role in the domain of object recognition. As a method of deep learning, CNN transforms original data into more abstract features via a nonlinear model. Many scholars have designed CNNs with different structures to achieve target classification, such as Alexnet [46], VGG-19 [47], Googlenet [48], and Resnet-34 [49].
Unfortunately, these networks perform classification by extracting deep features through a deep frame structure that ignores details contained in shallow features and does not reflect frequency change information over time. In order to utilize the shallow and deep features of the original image, we introduce one-dimensional multi-level features fusion (1D-MFF).
Figure 2 shows the structure of the 1D-MFF module, in which the input one-dimensional feature map proceeds sequentially through four one-dimensional convolution layers, extracting features at different depth levels to obtain feature maps , , , and . The feature maps obtained by different layers of convolution layers contain features with different details and semantic information. , , , and are converted into feature maps , , , and through the adaptive global average pooling. Then, , , , and are spliced along the channel dimension and, finally, are fused and compressed through 1 × 1 convolution.
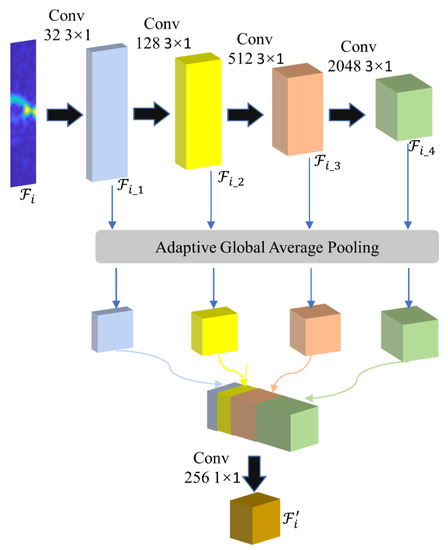
Figure 2.
The structure of the 1D-MFF module.
4.1.2. TSA Module
Inspired by the good performance of the self-attention mechanism [50] in spatial context modeling, we generalize it to capture the context–temporal relation among the 1D feature sequence. Based on the relation, we can further obtain the global temporal cue.
1D feature sequence is linearly mapped with two parameter matrices and with the same dimension to obtain feature maps B and H. The transpose of B and H are multiplied and the result is normalized by the softmax function to obtain the attention mask M, which stores the contextual relation among all the frequency features. The process can be represented as:
Finally, M is applied to re-weight K to embed extra global temporal cue, where K is obtained by multiplying the parameter matrix and . At the same time, the residual structure is introduced to add supplementary information to the original feature point by point, and accelerate the training of network. The calculation formula is as follows:
4.2. DGCCA-CL Module
Multi-modal data of the same target often possess a large difference in low-level features, but have a strong correlation in high-level semantic space. Based on this idea, subspace learning can be generated from a shared hidden space by assuming high-level correlated features of multi-modal data. The shared hidden space composes the high-level semantic representations. In addition, we can better handle the redundancy of data and complementarity of multi-source information based on a unified representation in the shared hidden space.
As a typical subspace learning method, canonical correlation analysis (CCA) was first proposed in 1936 [51]. The main idea is to find the paired projection for different views to maximize the correlation between them. There are currently many improvements and applications based on CCA. To overcome the limitation that CCA can only compute the correlation between two views, generalized canonical correlation analysis (GCCA) [52] extracts correlated features by projecting features from multiple views into a shared subspace. However, in many practical applications, the true relationship between views may be nonlinear. Deep canonical correlation analysis (DCCA) [53] and deep generalized canonical correlation analysis (DGCCA) [54] use the neural network to draw nonlinear features of different view data for projection on the basis of CCA and GCCA, respectively. However, in the above methods, the application of labels in supervised classification is ignored.
To utilize the label information of the data and enhance the clustering effect in supervised classification, we propose the DGCCA-CL module, which introduces center loss on the basis of DGCCA. For the samples of each class, center loss studies a center of the deep features and penalizes the distance between the deep features of the samples’ data in the same modality and their corresponding class centers. DGCCA-CL enhances the intra-class correlation and reduces the variance of features within classes on the basis of DGCCA.
Let represent the input data of m modalities and () indicate the instance for the modality. n is the number of instances and d represents the dimensions of extracted features. represents the output feature that goes through the feature extraction module and is the output feature of instance in (in this paper, m is equal to 2, and represents the output features of the TR map and TF spectrogram though the feature extraction module, respectively). The DGCCA-CL function can be represented as:
where represents the shared representation, represents a linear transformation of the modality, r represents the size of the projection to the subspace dimension, and represents the class center of deep features.
According to [54], we can solve the solution of by solving an eigenvalue problem. Specifically, a scaled empirical covariance matrix of the network output can be defined as ; is the corresponding projection matrix. It is easy to determine that is symmetric and idempotent. Because is positive semidefinite, is also positive semidefinite. It is obvious that the rows of are the top r (orthonormal) eigenvectors of , and . Then, the objective function can be written as:
By taking the derivative of with respect to , we obtain the following:
And the gradients of with respect to and update equation of are computed as:
where if the condition is satisfied, and if not.
For the gradient of , the gradient is the difference between the r-dimensional auxiliary representation G embedded into the subspace spanned by the columns of (the first term) and the projection of the actual data in onto the subspace mentioned above (the second term). Intuitively, if the auxiliary representation G is far away from the modal-specific representation , then the network weights will receive a large update. For the gradient of , if the extracted features are far from the center point of the class, it will also receive a larger update.
4.3. Attention Mechanism-Based Classifier
In recent years, the neural networks based on the attention mechanism have been applied successfully in multiple domains such as text translation, object recognition, etc. [55]. We propose an attention mechanism-based classifier for multi-modality ballistic target classification. The purpose of the attention mechanism-based classifier is to adaptively select the important features of the two-channel range and frequency features, and to provide a more efficient fuse recognition result.
Let represent a matrix consisting of the instance of each output layer , where is the output features of modality. The joint representation of all the qth instances is formed by the weighted sum of the vectors in :
where is the trained parameter vector and is the transpose of . The dimensions of α and are m and o, respectively.
In this model, a softmax classifier is used to predict the label for the fusion-extracted features:
The model is trained using cross entropy, which can be defined as follows:
In Algorithm 1, we sum up the learning details of our method.
| Algorithm 1: Training the proposed model |
| Input: Training dataset regularization rate learning rate , and number of iterations T Output: Projection matrices , parameters of , parameter of the attention mechanism-based classifier t = 1 while: Validation loss does not converge or t ≦ T Step 1. Calculate ← Step 2. Training and using Step 3. Training and using t ← t + 1 end while |
5. Experiment Setup and Dataset
Because it is hard to acquire the real measurement data of the ballistic targets, and the traditional radar cross-section measurement method in the darkroom requires the installation of expensive sensors and supporting facilities and environment, which is uneconomical and difficult to implement [56], we use the electromagnetic calculation tool to acquire the dynamic RCS echo of the targets, and then process the data set according to the method in Section 3. Finally, we design multiple sets of experiments to confirm the validity of our method for micro-motion target recognition.
5.1. Dataset Generation
In the experiment, we construct 3D models of three typical warheads and three common decoys with the same surface material, and set their micro-motion parameters according to the existing literature [14]. Figure 3 shows the 3D models of six targets, named warhead 1, warhead 2, warhead 3, decoy 1 (conical decoy), decoy 2 (cylindrical decoy), and decoy 3 (spherical decoy). The specific micro-motion parameters of the six targets can be shown in Table 1, in which warhead 1 and warhead 2 perform nutation motion, warhead 3 and decoy 1 perform coning motion, and decoy 2 and decoy 3 perform tumbling motion. We obtained 14,700 examples altogether.
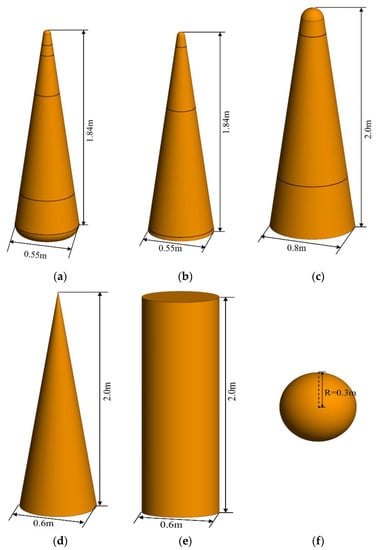
Figure 3.
The geometric models of the six targets. (a) Warhead 1; (b) warhead 2; (c) warhead 3; (d) decoy 1; (e) decoy 2; (f) decoy 3.

Table 1.
Setting of the micro-motion parameters.
Since the six targets are rotationally symmetric and axisymmetric, the azimuth of the target can be fixed as 0 degrees; the radar LOS is changed from 0 degrees to 360 degrees. In addition, the interval is 0.2 degrees of the local coordinate system. Moreover, the operating frequency of the radar is set to X band (8–12 GHz), which can detect centimeter-level displacement changes when the targets move [57]. The physical optics method was used to calculate the static RCS data of the six targets. The static RCS (dB) of six targets with the radar frequency of 10Ghz is shown in Figure 4. Figure 5 shows the variation of six targets’ wideband HRRPs with the elevation angle.
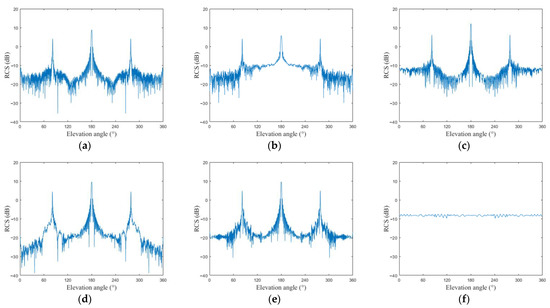
Figure 4.
Variation of the static RCS (dB) of six targets with the elevation angle. (a) Warhead 1; (b) warhead 2; (c) warhead 3; (d) decoy 1; (e) decoy 2; (f) decoy 3.
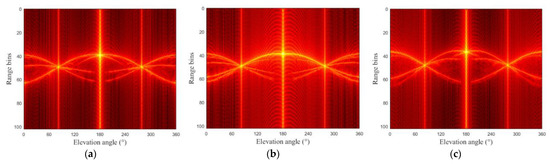
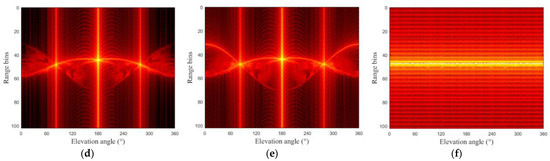
Figure 5.
Variation of the HRRPs of the six targets with the elevation angle. (a) Warhead 1; (b) warhead 2; (c) warhead 3; (d) decoy 1; (e) decoy 2; (f) decoy 3.
In order to obtain the dynamic RCS sequence when the targets move, we adopt the correlation angle method with short time-consumption and high accuracy for symmetric structural targets [25]. This method is not concerned with turning the target in the actual direction. Specifically, for all possible incident angles, a lookup table is used to configure the RCS value of a fixed-direction target and the relative angle between the incident angle; the direction of the object is used as an input parameter. To avoid Doppler ambiguity, the PRF is 600 and the observation time is 2 s.
By calculating the equivalent elevation angle (that is, the angle between the radar LOS and the target rotational symmetry axis) [58], the corresponding broadband range static data is obtained, and the dynamic echo matrix is generated. Finally, the dynamic data matrix is processed to obtain the TR maps and TF spectrums of the six targets, as shown in Figure 6 and Figure 7.
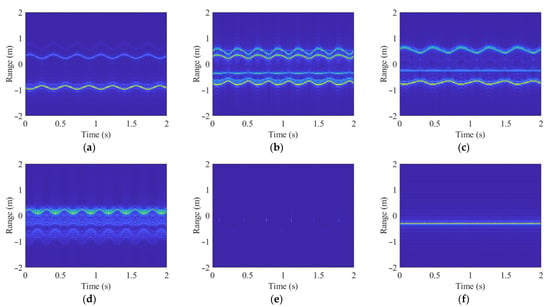
Figure 6.
TR maps of the six targets. (a) Warhead 1; (b) warhead 2; (c) warhead 3; (d) decoy 1; (e) decoy 2; (f) decoy 3.
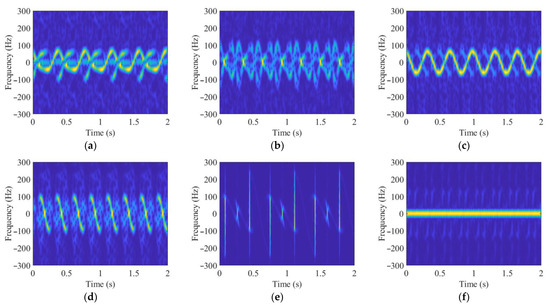
Figure 7.
TF spectrums of the six targets. (a) Warhead 1; (b) warhead 2; (c) warhead 3; (d) decoy 1; (e) decoy 2; (f) decoy 3.
5.2. Simulation Results
To verify the effectiveness of the proposed method, we randomly divide the TR map and TF spectrogram data set into the training set and test set with a ratio of 7:3. The training set and test set contain 10,290 and 4410 samples, respectively. Four classic signal channel CNNs are selected for comparison: Alexnet, VGG-19, Googlenet, and Resnet-34. We select ballistic target recognition methods that include one-dimensional parallel network (1D-PNet) [33] and dual-channel residual neural network (DCRNN) [40]. At the same time, we select three kinds of multi-view fusion methods that include the multi-view harmonized bilinear network (MHBN) [59], the multi-view convolutional neural networks (MVCNN) [60], multimodal transfer module (MMTM) [61], cross-modal fusion network based on self-attention and residual structure (CFN-SR) [62] and the method in [44] that is based on attention and DGCCA. Table 2 shows the results of the experiment.

Table 2.
Performance comparison of various methods.
From Table 2, we can see that in terms of the single-channel neural networks, the proposed feature extraction module 1D-MFF+TSA has the least number of parameters. The accuracy of the single-channel network is higher when the TF spectrum is the input than the TR map is used as the input, which can be seen that the features of the TF spectrum for the classification of targets are more separable.
At the same time, we can see that the accuracy of dual-channel networks is higher than the signal channel networks due to the fusion of the features of the TR map and TF spectrum in the dual channel, which proves the fundamental advantage of multi-feature fusion recognition. Increasing the feature information and achieving effective fusion is conducive for improving the recognition accuracy. In addition, compared with the advanced micro-motion target recognition methods and multi-modal fusion recognition methods, the proposed method still has advantages in parameters and recognition accuracy.
To explore the influence of different modules in the proposed method on recognition, we conduct ablation contrast experiments for the feature extraction module and DGCCA-CL module, respectively.
Figure 8 shows the recognition results of different network structures used for feature extraction. Due to the fusion of multi-level features and the extraction of the global temporal cues for the range feature sequence and frequency feature sequence, the proposed method can achieve a recognition rate of 98.91%.
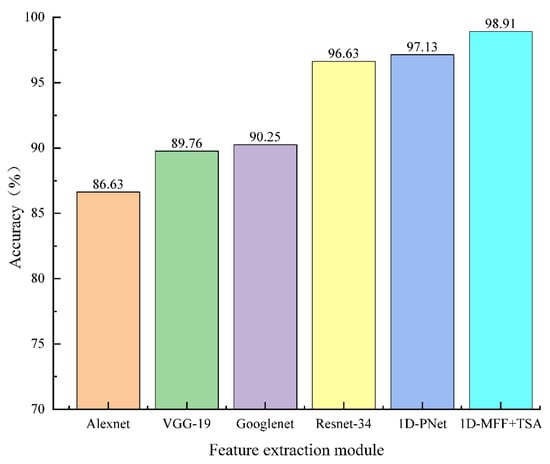
Figure 8.
Recognition rate of different networks as feature extraction module.
Moreover, we research the way that the DGCCA-CL module affects the distribution of the fused features and recognition. In addition, we use the T-SNE algorithm [63], which is one of the best feature downscaling and visualization methods to visualize the distribution of fused features. Figure 9 shows the visualization results with different methods after optimization.
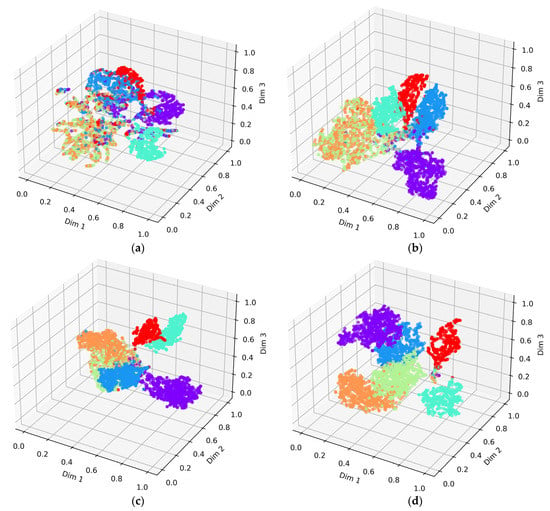
Figure 9.
Feature distributions for different optimization methods. (a) CrossEntropy loss (); (b) + DCCA; (c) + DGCCA; (d) + DGCCA-CL. ● Warhead 1 ● Warhead 2 ● Warhead 3 ● Decoy 1 ● Decoy 2 ● Decoy 3.
It can be seen that the addition of the canonical correlation analysis makes the features among classes become more distinguishing than the cross-entropy loss. In addition, compared with the DCCA and DGCCA, DGCCA-CL can reduce the distance of intra-class features and enhance the discriminative power of deep features significantly.
Figure 10 shows the variation of the recognition rate of different optimization methods with the number of iterations. We can see that the addition of CCA can not only accelerate the convergence of the network, but also improve the accuracy of the network. Moreover, the network optimized by DGCCA-CL has the fastest convergence rate among the contrasting subspace methods, and its accuracy increases by about 3% compared with DGCCA.
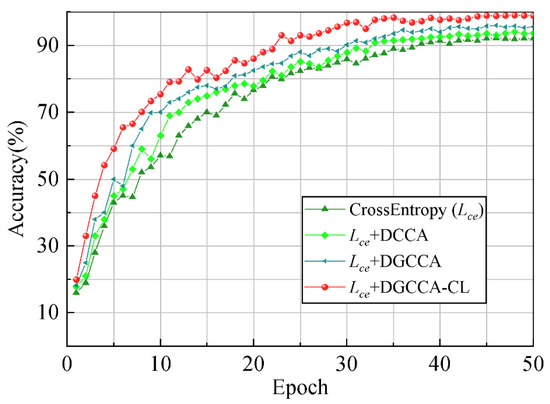
Figure 10.
Recognition results of different optimization methods.
For space ballistic target recognition, the SNR is a significant factor affecting the recognition accuracy. Therefore, to evaluate the robustness of the proposed method to noise, we add Gaussian noise to raw echoes and obtain five SNRs, i.e., −10 dB, −5 dB, 0 dB, 5 dB, and 10 dB. Finally, we obtain the TR map and TF spectrogram data set with different SNRs. In addition, the training set and test set with different SNRs are divided in the same manner as the original data set. Figure 11 shows the specific recognition results.
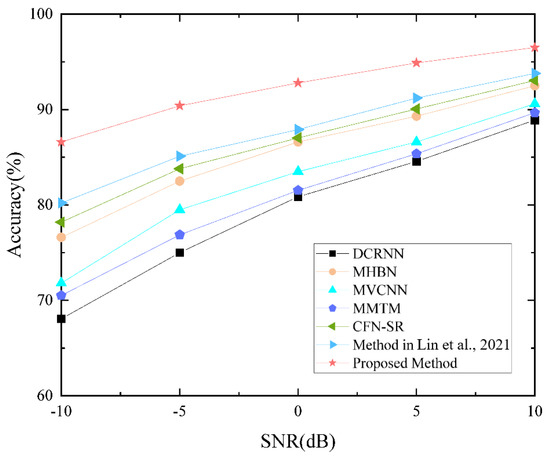
Figure 11.
Variation curve of recognition rate changing with SNR for different networks [44].
As can be seen from Figure 11, the larger the SNR is, the higher the recognition accuracy of the networks is. When the SNR is in the range of −10~10 dB, the accuracy of the proposed method for ballistic targets is always higher than in other networks. In addition, the accuracy of the proposed network for ballistic targets is still higher than 85% with the SNR of −10 dB. At the same time, we can see that since that DGCCA-CL extracts TF spectrum features and target-related information from the RT map and discards noises, the corresponding recognition rate declines more gently when the SNR decreases.
Figure 12 shows the confusion matrix of our method for six targets with the SNR of −10 dB, which shows the classification effect of our method more clearly. We can see that it is easier to distinguish decoy 2 and decoy 3 than other targets because the tumbling motion shows obvious features. Moreover, because of the similarity of coning and nutation and the similarity of shapes, misclassification mostly happens among warhead 1, warhead 2, warhead 3, and decoy1.
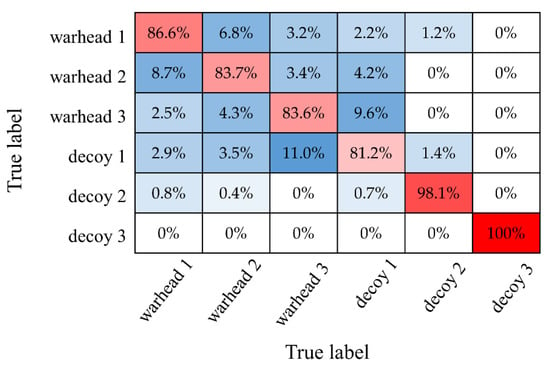
Figure 12.
Confusion matrix of our method with the SNR of −10 dB.
6. Discussion
For the input TR map and TF spectrum, this paper first proposes a feature extraction module based on 1D convolution and time self-attention. Compared with the popular 2D convolution used in target recognition, the proposed feature extraction module uses 1D convolution to extract the feature of micro-motion and further uses time self-attention to extract the temporal correlation information, which is more explanatory. Experiment results show that the proposed feature extraction module possesses a lower number of parameters and higher accuracy than other popular 2D CNNs.
The dual-channel networks possess higher accuracy than the single-channel networks due to the fusion of the features of the TR map and TF spectrum in the dual channel, which proves the fundamental advantage of multi-feature fusion recognition. Increasing the target feature information and achieving effective fusion helps to completely describe the movement of the target and is conducive to improving the accuracy of recognition.
The addition of CCA can not only accelerate the convergence of the network, but also improve the recognition rate of the network. The proposed DGCCA-CL module combines the advantages of CCA and center loss. Because it can extract the relevant deep features of the two channels and reduce the intra-class instance of instances at the same time, it presents greater advantages than other methods based on CCA at the convergence speed of the network and recognition.
Moreover, based on the above advantages, the proposed method has better robustness under low SNR, which makes it more applicable in the field of ballistic target recognition.
7. Conclusions
In this paper, we propose a recognition method for ballistic targets based on micro-motion feature fusion. The proposed method takes the TR map and TF spectrum as input. The multi-level features with respect to time are extracted through an improved feature extraction module based on 1D convolution and time self-attention. Then, in order to combine the TR and TF features efficiently, deep canonical correlation analysis enhanced with center loss (DGCCA-CL) is proposed to transform the extracted features into a hidden space. The proposed DGCCA-CL module possesses better performance for multi-modality feature fusion in two aspects: small intra-class distance and compact representation. Furthermore, an attention mechanism-based classifier is used to adaptively select the important features for target recognition.
Compared with previous target recognition methods, it can extract more distinguishable micro-motion information from the TR map and the TF spectrum, and further fuse the features extracted from the two channels, with a higher recognition rate and robustness. Finally, experiment results show that our method outperforms other network-based recognition methods. The proposed method demonstrates good recognition performance with the SNR of −10~10 dB, but the recognition rate at low SNR still needs to be improved, which will become the major work of our next research.
Author Contributions
Conceptualization, L.Y. and W.Z.; methodology, L.Y.; software, W.J.; validation, L.Y. and W.Z.; formal analysis, W.J.; investigation, L.Y.; resources, L.Y.; data curation, W.Z.; writing—original draft preparation, L.Y.; writing—review and editing, W.Z.; visualization, W.J.; supervision, W.J.; project administration, W.J.; funding acquisition, W.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China under Grant 61901487, 61871384, and 61921001, and the Natural Science Foundation of Hunan Province under Grant 2021JJ40699. Project funded by China Postdoctoral Science Foundation under Grant 2021TQ0084.
Data Availability Statement
Not applicable.
Acknowledgments
All authors would like to thank the editors and reviewers for their helpful suggestions.
Conflicts of Interest
There is no conflict of interest in the submission of this manuscript. All authors approve the publication of the manuscript.
References
- Luo, Y.; Zhang, Q.; Yuan, N.; Zhu, F.; Gu, F. Three-Dimensional Precession Feature Extraction of Space Targets. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1313–1329. [Google Scholar] [CrossRef]
- Bai, X.; Xing, M.; Zhou, F.; Bao, Z. High-Resolution Three-Dimensional Imaging of Spinning Space Debris. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2352–2362. [Google Scholar] [CrossRef]
- Chen, J.; Xu, S.; Chen, Z. Convolutional neural network for classifying space target of the same shape by using RCS time series. IET Radar Sonar Navig. 2018, 12, 1268–1275. [Google Scholar] [CrossRef]
- Mai, Y.; Zhang, S.; Jiang, W.; Zhang, C.; Liu, Y.; Li, X. ISAR Imaging of Target Exhibiting Micro-Motion with Sparse Aperture via Model-Driven Deep Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Lundén, J.; Koivunen, V. Deep learning for HRRP-based target recognition in multistatic radar systems. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Chen, V.; Li, F.; Ho, S.-S.; Wechsler, H. Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Q.; Qiu, C.; Liang, X.; Li, K. Micro-Doppler Effect Analysis and Feature Extraction in ISAR Imaging with Stepped-Frequency Chirp Signals. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2087–2098. [Google Scholar] [CrossRef]
- Zhao, M.-M.; Zhang, Q.; Luo, Y.; Sun, L. Micromotion Feature Extraction and Distinguishing of Space Group Targets. IEEE Geosci. Remote Sens. Lett. 2017, 14, 174–178. [Google Scholar] [CrossRef]
- Ai, X.; Xu, Z.; Wu, Q.; Liu, X.; Xiao, S. Parametric Representation and Application of Micro-Doppler Characteristics for Cone-Shaped Space Targets. IEEE Sens. J. 2019, 19, 11839–11849. [Google Scholar] [CrossRef]
- Hanif, A.; Muaz, M.; Hasan, A.; Adeel, M. Micro-Doppler Based Target Recognition with Radars: A Review. IEEE Sens. J. 2022, 22, 2948–2961. [Google Scholar] [CrossRef]
- Guo, X.; Ng, C.S.; de Jong, E.; Smits, A.B. Micro-Doppler based mini-UAV detection with low-cost distributed radar in dense urban environment. In Proceedings of the 2019 16th European Radar Conference (EuRAD), Paris, France, 2–4 October 2019; pp. 189–192. [Google Scholar]
- Xia, S.; Jiang, H.; Cai, W.; Yang, J.; Zhang, C.; Chen, W. Research on Micro-motion Modeling and Feature Extraction of Passive Bistatic Radar Based on CMMB Signal. J. Phys. Conf. Ser. 2022, 2213, 012013. [Google Scholar] [CrossRef]
- Wang, S.; Li, M.; Yang, T.; Ai, X.; Liu, J.; Andriulli, F.P.; Ding, D. Cone-Shaped Space Target Inertia Characteristics Identification by Deep Learning with Compressed Dataset. IEEE Trans. Antennas Propag. 2022, 70, 5217–5226. [Google Scholar] [CrossRef]
- Choi, I.-O.; Park, S.-H.; Kim, M.; Kang, K.-B.; Kim, K.-T. Efficient discrimination of ballistic targets with micromotions. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1243–1261. [Google Scholar] [CrossRef]
- Persico, A.R.; Clemente, C.; Gaglione, D.; Ilioudis, C.V.; Cao, J.; Pallotta, L.; De Maio, A.; Proudler, I.; Soraghan, J.J. On model, algorithms, and experiment for micro-Doppler-based recognition of ballistic targets. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1088–1108. [Google Scholar] [CrossRef]
- Persico, A.R.; Ilioudis, C.V.; Clemente, C.; Soraghan, J.J. Novel Classification Algorithm for Ballistic Target Based on HRRP Frame. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 3168–3189. [Google Scholar] [CrossRef]
- Zhang, R.; Li, G.; Clemente, C.; Soraghan, J.J. Multi-aspect micro-Doppler signatures for attitude-independent L/N quotient estimation and its application to helicopter classification. IET Radar Sonar Navig. 2017, 11, 701–708. [Google Scholar] [CrossRef]
- Zhang, W.; Li, G. Detection of multiple micro-drones via cadence velocity diagram analysis. Electron. Lett. 2018, 54, 441–443. [Google Scholar] [CrossRef]
- Kim, B.K.; Kang, H.S.; Park, S.O. Drone classification using convolutional neural networks with merged Doppler images. IEEE Geosci. Remote Sens. Lett. 2016, 14, 38–42. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, C.; Hu, X.; Zhang, Y. Classification of Space Micromotion Targets with Similar Shapes at Low SNR. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Kim, Y.; Moon, T. Human Detection and Activity Classification Based on Micro-Doppler Signatures Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 8–12. [Google Scholar] [CrossRef]
- Wei, N.; Zhang, L.; Zhang, X. A Weighted Decision-Level Fusion Architecture for Ballistic Target Classification in Midcourse. Phase. Sens. 2022, 22, 6649. [Google Scholar] [CrossRef]
- Tian, X.; Bai, X.; Xue, R.; Qin, R.; Zhou, F. Fusion Recognition of Space Targets with Micromotion. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3116–3125. [Google Scholar] [CrossRef]
- Lee, J.I.; Kim, N.; Min, S.; Kim, J.; Jeong, D.K.; Seo, D.W. Space Target Classification Improvement by Generating Micro-Doppler Signatures Considering Incident Angle. Sensors 2022, 22, 1653. [Google Scholar] [CrossRef]
- Jung, K.; Lee, J.-I.; Kim, N.; Oh, S.; Seo, D.-W. Classification of Space Objects by Using Deep Learning with Micro-Doppler Signature Images. Sensors 2021, 21, 4365. [Google Scholar] [CrossRef] [PubMed]
- Choi, I.O.; Kim, S.H.; Jung, J.H.; Kim, K.T.; Park, S.H. Efficient recognition method for ballistic warheads by the fusion of feature vectors based on flight phase. J. Korean Inst. Electromagn. Eng. Sci. 2019, 30, 487–497. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, W.; Yu, Y.; Turner, K.; Derr, T.; Wang, M.; Ntoutsi, E. Interpretable visual understanding with cognitive attention network. In International Conference on Artificial Neural Networks; Springer: Cham, Switzerland, 2021; pp. 555–568. [Google Scholar]
- Shu, X.; Yang, J.; Yan, R.; Song, Y. Expansion-squeeze-excitation fusion network for elderly activity recognition. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 5281–5292. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, Y.; Tang, S.; Wu, J.; Li, W. Variational Autoencoder with CCA for Audio-Visual Cross-Modal Retrieval. arXiv 2021, arXiv:2112.02601. [Google Scholar]
- Tahmoush, D. Micro-range micro-Doppler for classification. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–4. [Google Scholar]
- Wang, S.; Song, J.; Lien, J.; Poupyrev, I.; Hilliges, O. Interacting with soli: Exploring fine-grained dynamic gesture recognition in the radio-frequency spectrum. In Proceedings of the 29th Annual Symposium on User Interface Software and Technology, Tokyo, Japan, 16–19 October 2016; pp. 851–860. [Google Scholar]
- Liu, Q.; Zhang, X.; Liu, Y. Hierarchical Sequential Feature Extraction Network for Radar Target Recognition Based on HRRP. In Proceedings of the 7th International Conference on Signal and Image Processing (ICSIP), Suzhou, China, 20–22 July 2022; pp. 167–171. [Google Scholar]
- Han, L.; Feng, C. Micro-Doppler-based space target recognition with a one-dimensional parallel network. Int. J. Antennas Propag. 2020, 128–135. [Google Scholar] [CrossRef]
- Lei, P.; Wang, J.; Guo, P.; Cai, D. Automatic classification of radar targets with micro-motions using entropy segmentation and time-frequency features. AEU-Int. J. Electron. Commun. 2011, 65, 806–813. [Google Scholar] [CrossRef]
- Liu, W.; Qiu, J.L.; Zheng, W.L.; Lu, B.L. Comparing recognition performance and robustness of multimodal deep learning models for multimodal emotion recognition. IEEE Trans. Cogn. Dev. Syst. 2022, 14, 715–729. [Google Scholar] [CrossRef]
- Liu, Y.; Miao, C.; Ji, J.; Li, X. MMF: A Multi-scale MobileNet based fusion method for infrared and visible image. Infrared Phys. Technol. 2021, 119, 103894. [Google Scholar] [CrossRef]
- Liang, T.; Lin, G.; Feng, L.; Zhang, Y.; Lv, F. Attention is not Enough: Mitigating the Distribution Discrepancy in Asynchronous Multimodal Sequence Fusion. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 8148–8156. [Google Scholar]
- Hou, M.; Tang, J.; Zhang, J.; Kong, W.; Zhao, Q. Deep multimodal multilinear fusion with high-order polynomial pooling. In Proceedings of the Advances in Neural Information Processing Systems 32 (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32, pp. 12136–12145. [Google Scholar]
- Nguyen, D.K.; Okatani, T. Improved fusion of visual and language representations by dense symmetric co-attention for visual question answering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–21 October 2018; pp. 6087–6096. [Google Scholar]
- An, B.; Zhang, W.; Liu, Y. Hand gesture recognition method based on dual-channel convolutional neural network. In Proceedings of the 6th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 9–11 April 2021; pp. 529–533. [Google Scholar]
- Zhou, P.; Yang, W.; Chen, W.; Wang, Y.; Jia, J. Modality attention for end-to-end audio-visual speech recognition. In Proceedings of the ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 6565–6569. [Google Scholar]
- Zadeh, A.; Chen, M.; Poria, S.; Cambria, E.; Morency, L.-P. Tensor fusion network for multimodal sentiment analysis. arXiv 2017, arXiv:1707.07250. [Google Scholar]
- Qiu, J.-L.; Liu, W.; Lu, B.-L. Multi-view emotion recognition using deep canonical correlation analysis. In International Conference on Neural Information Processing; Springer: Cham, Switzerland, 2018; pp. 221–231. [Google Scholar]
- Lin, W.; Gao, X. Feature fusion for inverse synthetic aperture radar image classification via learning shared hidden space. Electron. Lett. 2021, 57, 986–988. [Google Scholar] [CrossRef]
- Bai, X.; Zhang, Y.; Zhou, F. High-Resolution Radar Imaging in Complex Environments Based on Bayesian Learning with Mixture Models. IEEE Trans. Geosci. Remote Sens. 2019, 57, 972–984. [Google Scholar] [CrossRef]
- Han, X.; Zhong, Y.; Cao, L.; Zhang, L. Pre-trained AlexNetarchitecture with pyramid pooling and supervision for highspatial resolution remote sensing image scene classification. Remote Sens. 2017, 9, 848. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, H.; Hu, Z. Statistics of Visual Responses to Image Object Stimuli from Primate AIT Neurons to DNN Neurons. Neural Comput. 2018, 30, 447–476. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going Deeper with Convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Hotelling, H. Relations Between Two Sets of Variates. Breakthr. Stat. 1992, 162–190. [Google Scholar] [CrossRef]
- Horst, P. Generalized Canonical Correlations and Their Applications to Experimental Data. J. Clin. Psychol. 1961, 17, 331–347. [Google Scholar] [CrossRef]
- Andrew, G.; Arora, R.; Bilmes, J.; Livescu, K. Deep canonical correlation analysis. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; pp. 1247–1255. [Google Scholar]
- Benton, A.; Khayrallah, H.; Gujral, B.; Reisinger, D.A.; Zhang, S.; Arora, R. Deep Generalized Canonical Correlation Analysis. In Proceedings of the 4th Workshop on Representation Learning for NLP (RepL4NLP-2019), Florence, Italy, 15 January 2019; Association for Computational Linguistics: Florence, Italy, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- de Santana Correia, A.; Colombini, E.L. Attention, please! A survey of neural attention models in deep learning. Artif. Intell. Rev. 2022, 1–88. [Google Scholar] [CrossRef]
- Tang, W.; Yu, L.; Wei, Y.; Tong, P. Radar Target Recognition of Ballistic Missile in Complex Scene. In Proceedings of the 2019 IEEE International Conference on Signal, Information and Data Processing (ICSIDP), Chongqing, China, 11–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Dai, J.; Wang, J. Recognition of Warheads Based on Features of Range Profiles in Ballistic Missile Defense. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Bai, X.; Bao, Z. Imaging of Rotation-Symmetric Space Targets Based on Electromagnetic Modeling. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1680–1689. [Google Scholar] [CrossRef]
- Yu, T.; Meng, J.; Yuan, J. Multi-View Harmonized Bilinear Network for 3D Object Recognition. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 186–194. [Google Scholar] [CrossRef]
- Su, H.; Maji, S.; Kalogerakis, E.; Learned-Miller, E. Multi-View Convolutional Neural Networks for 3D Shape Recognition. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 945–953. [Google Scholar] [CrossRef]
- Joze HR, V.; Shaban, A.; Iuzzolino, M.L.; Koishida, K. MMTM: Multimodal transfer module for CNN fusion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 13289–13299. [Google Scholar]
- Fu, Z.; Liu, F.; Wang, H.; Qi, J.; Fu, X.; Zhou, A.; Li, Z. A cross-modal fusion network based on self-attention and residual structure for multimodal emotion recognition. arXiv 2022, arXiv:2111.02172. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).