A Comparison of Machine Learning and Geostatistical Approaches for Mapping Forest Canopy Height over the Southeastern US Using ICESat-2
Abstract
1. Introduction
2. Materials and Methods
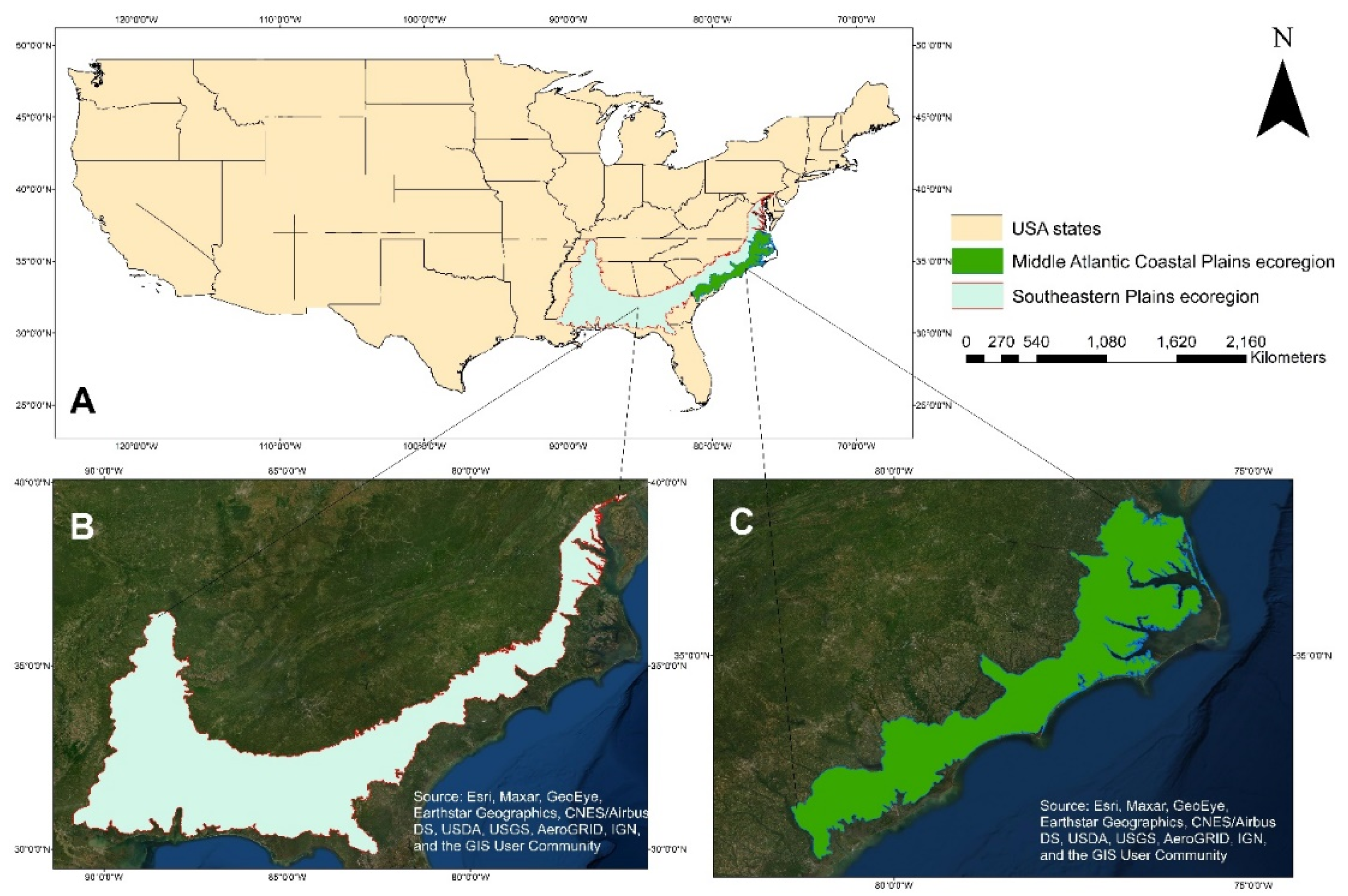
2.1. Study Area
2.2. Data
2.2.1. ICESat-2 ATL08 Data
2.2.2. Landsat-8 Data
2.2.3. Ancillary Data
- i.
- Land Cover data:
- ii.
- Canopy Cover (CC) data:
- iii.
- Digital Elevation Model (DEM):
2.2.4. Airborne Lidar Data
2.3. Data Processing
2.4. Data Analysis
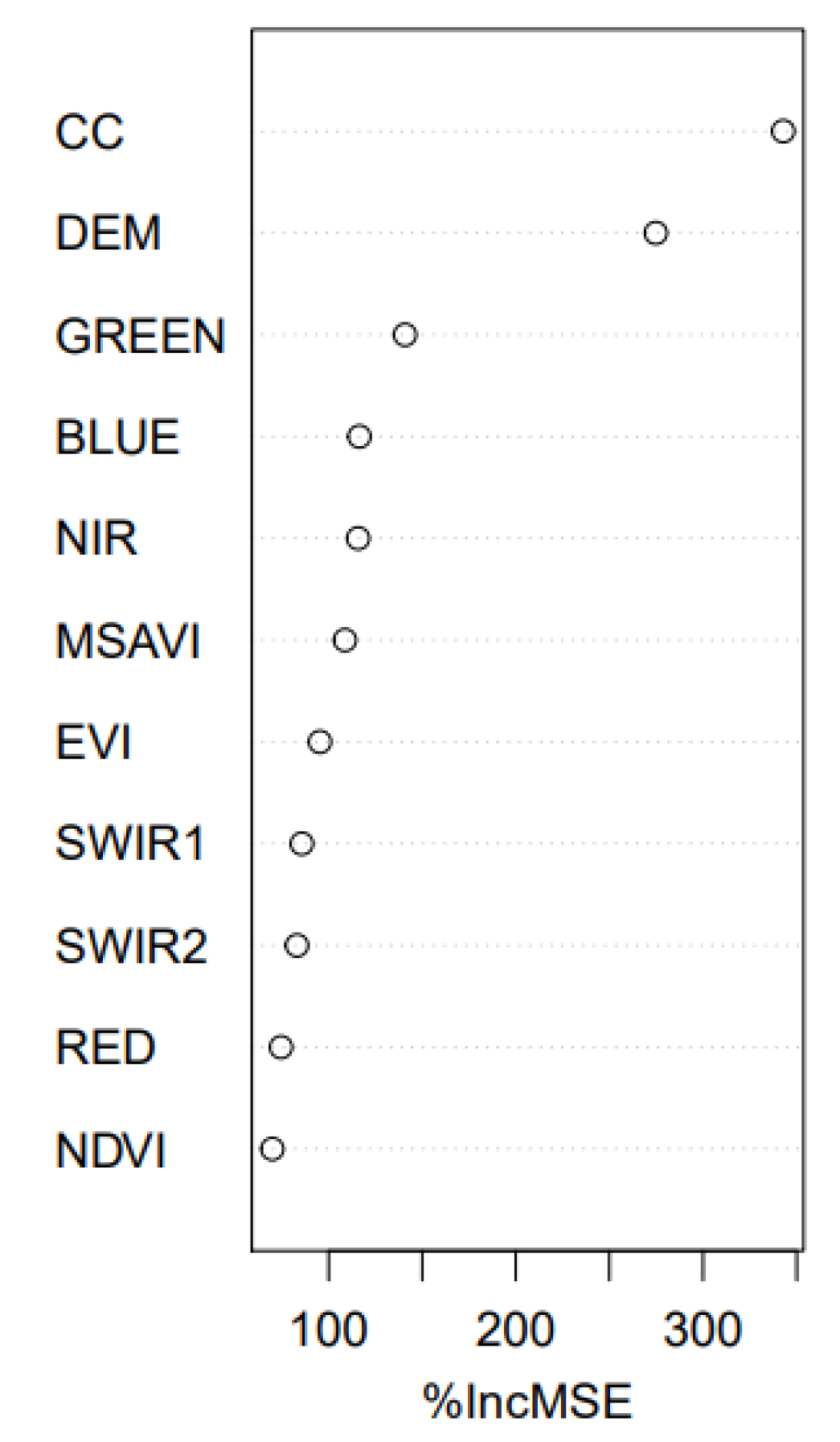
2.4.1. Canopy Height Mapping Using Random Forest
2.4.2. Canopy Height Mapping by Regression Kriging
2.5. Accuracy Assessment
3. Results
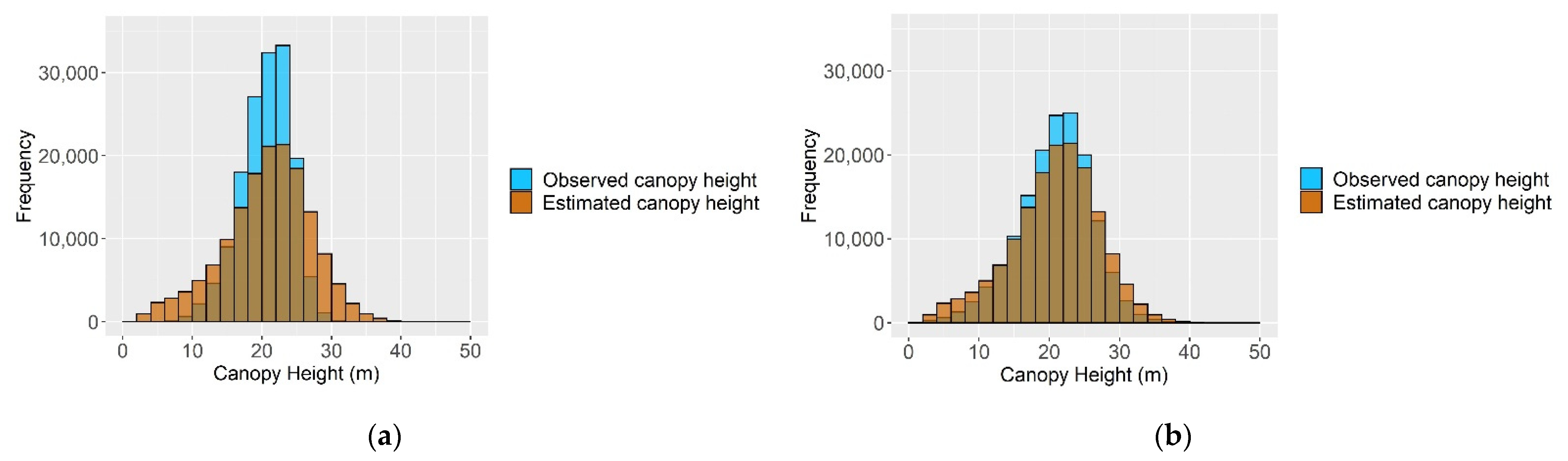
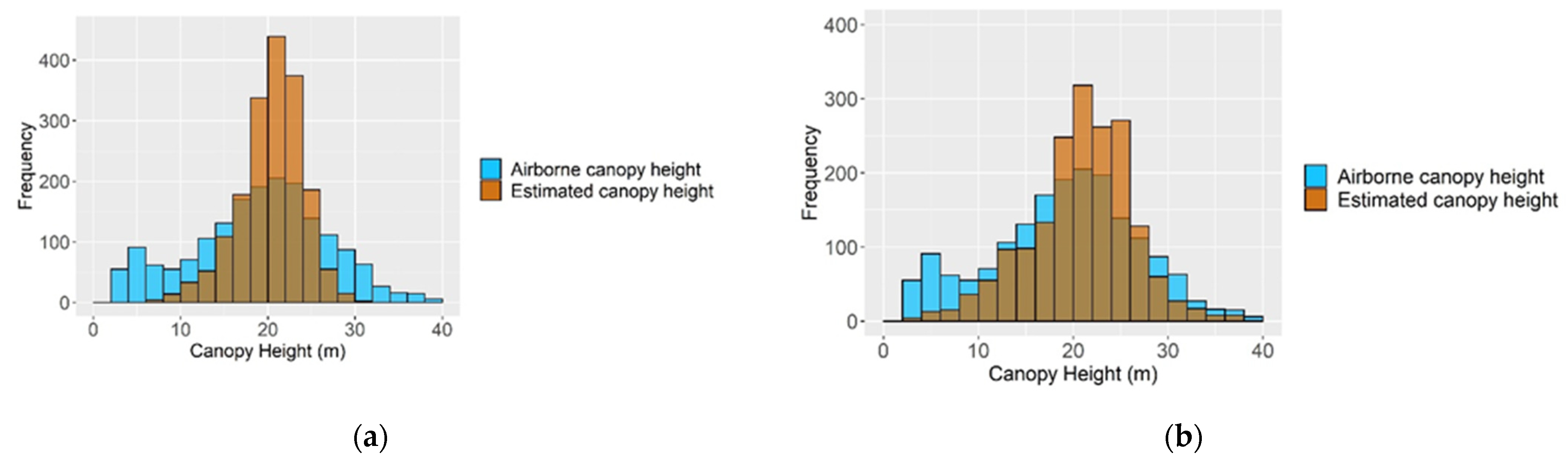
3.1. Canopy Height Mapping
3.2. Comparison of Canopy Height Estimated by RF and RK with Airborne Lidar Canopy Height Data
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef]
- Arneth, A.; Harrison, S.P.; Zaehle, S.; Tsigaridis, K.; Menon, S.; Bartlein, P.; Feichter, J.; Korhola, A.; Kulmala, M.; O’donnell, D. Terrestrial biogeochemical feedbacks in the climate system. Nat. Geosci. 2010, 3, 525–532. [Google Scholar] [CrossRef]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote sensing for biodiversity science and conservation. Trends Ecol. Evol. 2003, 18, 306–314. [Google Scholar] [CrossRef]
- Wear, D.N.; Greis, J.G. Southern Forest Resource Assessment; Southern Research Station: Asheville, NC, USA, 2002; Volume 53. [Google Scholar]
- Birdsey, R.A. Carbon Storage and Accumulation in United States Forest Ecosystems; US Department of Agriculture, Forest Service: Washington, DC, USA, 1992; Volume 59. [Google Scholar]
- McNulty, S.; Caldwell, P.; Doyle, T.W.; Johnsen, K.; Liu, Y.; Mohan, J.; Prestemon, J.; Sun, G. Forests and Climate Change in the Southeast USA. In Climate of the Southeast United States: Variability, Change, Impacts, and Vulnerability; Ingram, K., Dow, K., Carter, L., Anderson, J., Eds.; Island Press: Washington, DC, USA, 2013; pp. 161–183, 165–189. [Google Scholar]
- Ghosh, S.M.; Behera, M.D.; Paramanik, S. Canopy height estimation using sentinel series images through machine learning models in a mangrove forest. Remote Sens. 2020, 12, 1519. [Google Scholar] [CrossRef]
- Liu, M.; Cao, C.; Dang, Y.; Ni, X. Mapping forest canopy height in mountainous areas using ZiYuan-3 stereo images and Landsat data. Forests 2019, 10, 105. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Li, R.; Ren, X.; Ni, W.; Fu, A. Estimation of forest aboveground biomass in Changbai Mountain region using ICESat/GLAS and Landsat/TM data. Remote Sens. 2017, 9, 707. [Google Scholar] [CrossRef]
- Carreiras, J.; Melo, J.B.; Vasconcelos, M.J. Estimating the above-ground biomass in miombo savanna woodlands (Mozambique, East Africa) using L-band synthetic aperture radar data. Remote Sens. 2013, 5, 1524–1548. [Google Scholar] [CrossRef]
- Selkowitz, D.J.; Green, G.; Peterson, B.; Wylie, B. A multi-sensor lidar, multi-spectral and multi-angular approach for mapping canopy height in boreal forest regions. Remote Sens. Environ. 2012, 121, 458–471. [Google Scholar] [CrossRef]
- Zhang, G.; Ganguly, S.; Nemani, R.R.; White, M.A.; Milesi, C.; Hashimoto, H.; Wang, W.; Saatchi, S.; Yu, Y.; Myneni, R.B. Estimation of forest aboveground biomass in California using canopy height and leaf area index estimated from satellite data. Remote Sens. Environ. 2014, 151, 44–56. [Google Scholar] [CrossRef]
- Lin, X.; Xu, M.; Cao, C.; Dang, Y.; Bashir, B.; Xie, B.; Huang, Z. Estimates of forest canopy height using a combination of ICESat-2/ATLAS data and stereo-photogrammetry. Remote Sens. 2020, 12, 3649. [Google Scholar] [CrossRef]
- Baltsavias, E.P. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Akay, A.E.; Oğuz, H.; Karas, I.R.; Aruga, K. Using LiDAR technology in forestry activities. Environ. Monit. Assess. 2009, 151, 117–125. [Google Scholar] [CrossRef]
- Ma, Q.; Su, Y.; Guo, Q. Comparison of canopy cover estimations from airborne LiDAR, aerial imagery, and satellite imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4225–4236. [Google Scholar] [CrossRef]
- Coops, N.C.; Tompalski, P.; Goodbody, T.R.; Queinnec, M.; Luther, J.E.; Bolton, D.K.; White, J.C.; Wulder, M.A.; van Lier, O.R.; Hermosilla, T. Modelling lidar-derived estimates of forest attributes over space and time: A review of approaches and future trends. Remote Sens. Environ. 2021, 260, 112477. [Google Scholar] [CrossRef]
- Dassot, M.; Constant, T.; Fournier, M. The use of terrestrial LiDAR technology in forest science: Application fields, benefits and challenges. Ann. For. Sci. 2011, 68, 959–974. [Google Scholar] [CrossRef]
- Yao, T.; Yang, X.; Zhao, F.; Wang, Z.; Zhang, Q.; Jupp, D.; Lovell, J.; Culvenor, D.; Newnham, G.; Ni-Meister, W. Measuring forest structure and biomass in New England forest stands using Echidna ground-based lidar. Remote Sens. Environ. 2011, 115, 2965–2974. [Google Scholar] [CrossRef]
- Khosravipour, A.; Skidmore, A.K.; Isenburg, M.; Wang, T.; Hussin, Y.A. Generating pit-free canopy height models from airborne lidar. Photogramm. Eng. Remote Sens. 2014, 80, 863–872. [Google Scholar] [CrossRef]
- Anderson, J.; Martin, M.; Smith, M.; Dubayah, R.; Hofton, M.; Hyde, P.; Peterson, B.; Blair, J.; Knox, R. The use of waveform lidar to measure northern temperate mixed conifer and deciduous forest structure in New Hampshire. Remote Sens. Environ. 2006, 105, 248–261. [Google Scholar] [CrossRef]
- Baccini, A.; Friedl, M.; Woodcock, C.; Warbington, R. Forest biomass estimation over regional scales using multisource data. Geophys. Res. Lett. 2004, 31, L10501. [Google Scholar] [CrossRef]
- Wang, M.; Sun, R.; Xiao, Z. Estimation of forest canopy height and aboveground biomass from spaceborne LiDAR and Landsat imageries in Maryland. Remote Sens. 2018, 10, 344. [Google Scholar] [CrossRef]
- Fouladinejad, F.; Matkan, A.; Hajeb, M.; Brakhasi, F. History and Applications of Space-Borne Lidars; International Archives of the Photogrammetry, Remote Sensing & Spatial Information Sciences: Karaj, Iran, 2019. [Google Scholar]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Del Bom Espirito-Santo, F.; Hunter, M.O.; de Oliveira, R., Jr. Estimates of forest canopy height and aboveground biomass using ICESat. Geophys. Res. Lett. 2005, 32, L22S02. [Google Scholar] [CrossRef]
- Simard, M.; Pinto, N.; Fisher, J.B.; Baccini, A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosciences 2011, 116, G04021. [Google Scholar] [CrossRef]
- Hu, T.; Su, Y.; Xue, B.; Liu, J.; Zhao, X.; Fang, J.; Guo, Q. Mapping global forest aboveground biomass with spaceborne LiDAR, optical imagery, and forest inventory data. Remote Sens. 2016, 8, 565. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Wang, Y.; Li, G.; Ding, J.; Guo, Z.; Tang, S.; Wang, C.; Huang, Q.; Liu, R.; Chen, J.M. A combined GLAS and MODIS estimation of the global distribution of mean forest canopy height. Remote Sens. Environ. 2016, 174, 24–43. [Google Scholar] [CrossRef]
- Nandy, S.; Srinet, R.; Padalia, H. Mapping forest height and aboveground biomass by integrating ICESat-2, Sentinel-1 and Sentinel-2 data using Random Forest algorithm in northwest Himalayan foothills of India. Geophys. Res. Lett. 2021, 48, e2021GL093799. [Google Scholar] [CrossRef]
- Yin, J.; Feng, Q.; Liang, T.; Meng, B.; Yang, S.; Gao, J.; Ge, J.; Hou, M.; Liu, J.; Wang, W. Estimation of grassland height based on the random forest algorithm and remote sensing in the Tibetan Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 13, 178–186. [Google Scholar] [CrossRef]
- Xi, Z.; Xu, H.; Xing, Y.; Gong, W.; Chen, G.; Yang, S. Forest Canopy Height Mapping by Synergizing ICESat-2, Sentinel-1, Sentinel-2 and Topographic Information Based on Machine Learning Methods. Remote Sens. 2022, 14, 364. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.C.; Malambo, L. Using ICESat-2 to estimate and map forest aboveground biomass: A first example. Remote Sens. 2020, 12, 1824. [Google Scholar] [CrossRef]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ. 2002, 82, 397–416. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bailly, J.-S.; Barbier, N.; Gond, V.; Hérault, B.; El Hajj, M.; Fabre, F.; Perrin, J. Regional scale rain-forest height mapping using regression-kriging of spaceborne and airborne LiDAR data: Application on French Guiana. Remote Sens. 2016, 8, 240. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Huang, N.; Wang, C.; Gao, S.; Wu, C. Airborne LiDAR technique for estimating biomass components of maize: A case study in Zhangye City, Northwest China. Ecol. Indic. 2015, 57, 486–496. [Google Scholar] [CrossRef]
- Schirrmann, M.; Hamdorf, A.; Giebel, A.; Gleiniger, F.; Pflanz, M.; Dammer, K.-H. Regression kriging for improving crop height models fusing ultra-sonic sensing with UAV imagery. Remote Sens. 2017, 9, 665. [Google Scholar] [CrossRef]
- Griffith, G. Level III North American Terrestrial Ecoregions: United States Descriptions; North American Commission for Environmental Cooperation: Montreal, QC, Canada, 2010; pp. 1–64. [Google Scholar]
- Wiken, E.; Nava, F.J.; Griffith, G. North American Terrestrial Ecoregions—Level III; Commission for Environmental Cooperation: Montreal, QC, Canada, 2011; 149p. [Google Scholar]
- Neuenschwander, A.L.; Pitts, K.L.; Jelley, B.P.; Robbins, J.; Klotz, B.; Popescu, S.C.; Nelson, R.F.; Harding, D.; Pederson, D.; Sheridan, R. ATLAS/ICESat-2 L3A Land and Vegetation Height, Version 4. Boulder, Colorado USA. NASA National Snow and Ice Data Center Distributed Active Archive Center. 2021. Available online: https://doi.org/10.5067/ATLAS/ATL08.004 (accessed on 10 May 2021).
- Malambo, L.; Popescu, S.C. Assessing the agreement of ICESat-2 terrain and canopy height with airborne lidar over US ecozones. Remote Sens. Environ. 2021, 266, 112711. [Google Scholar] [CrossRef]
- Zhu, X.; Nie, S.; Wang, C.; Xi, X. The Performance of ICESat-2’s Strong and Weak Beams in Estimating Ground Elevation and Forest Height. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020. [Google Scholar]
- Loveland, T.R.; Irons, J.R. Landsat 8: The plans, the reality, and the legacy. Remote Sens. Environ. 2016, 185, 1–6. [Google Scholar] [CrossRef]
- U.S. Geological Survey. Landsat 8. Available online: https://www.usgs.gov/landsat-missions/landsat-8 (accessed on 10 March 2021).
- Staben, G.; Lucieer, A.; Scarth, P. Modelling LiDAR derived tree canopy height from Landsat TM, ETM+ and OLI satellite imagery—A machine learning approach. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 666–681. [Google Scholar] [CrossRef]
- Shah, S.A.A.; Manzoor, M.A.; Bais, A. Canopy height estimation at Landsat resolution using convolutional neural networks. Mach. Learn. Knowl. Extr. 2020, 2, 23–36. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Third Earth Reserves Technology Satellite Symposium, Washington, DC, USA, 10–14 December 1973; NASA SP-351. NASA: Greenbelt, MD, USA, 1973. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Liu, H.Q.; Huete, A. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens. 1995, 33, 457–465. [Google Scholar] [CrossRef]
- Dewitz, J. National Land Cover Database (NLCD) 2019 Products [Dataset]; US Geological Survey: Sioux Falls, SD, USA, 2021. [Google Scholar]
- Wickham, J.; Stehman, S.V.; Sorenson, D.G.; Gass, L.; Dewitz, J.A. Thematic accuracy assessment of the NLCD 2016 land cover for the conterminous United States. Remote Sens. Environ. 2021, 257, 112357. [Google Scholar] [CrossRef]
- MRLC. NLCD 2016 USFS Tree Canopy Cover (CONUS). 2016. Available online: https://www.mrlc.gov/data/nlcd-2016-usfs-tree-canopy-cover-conus (accessed on 15 April 2021).
- Balasubramanian, A.; Duraisamy, K.; Thirumalaisamy, S.; Krishnaraj, S.; Yatheendradasan, R.K. Prioritization of subwatersheds based on quantitative morphometric analysis in lower Bhavani basin, Tamil Nadu, India using DEM and GIS techniques. Arab. J. Geosci. 2017, 10, 552. [Google Scholar] [CrossRef]
- Sugarbaker, L.; Constance, E.W.; Heidemann, H.K.; Jason, A.L.; Lucas, V.; Saghy, D.; Stoker, J.M. The 3D Elevation Program Initiative: A Call for Action; US Geological Survey: Reston, VA, USA, 2014. [Google Scholar] [CrossRef]
- U.S. Geological Survey. 3D Elevation Program. 2021. Available online: https://www.usgs.gov/core-science-systems/ngp/3dep (accessed on 19 February 2021).
- United States Environmental Protection Agency. Ecoregion Download Files by Region. 2021. Available online: https://www.epa.gov/eco-research/ecoregion-download-files-region (accessed on 23 February 2021).
- Landfire. Forest Canopy Height. 2021. Available online: https://landfire.gov/ch.php (accessed on 14 June 2021).
- Li, L.; Guo, Q.; Tao, S.; Kelly, M.; Xu, G. Lidar with multi-temporal MODIS provide a means to upscale predictions of forest biomass. ISPRS J. Photogramm. Remote Sens. 2015, 102, 198–208. [Google Scholar] [CrossRef]
- Narine, L.; Malambo, L.; Popescu, S. Characterizing canopy cover with ICESat-2: A case study of southern forests in Texas and Alabama, USA. Remote Sens. Environ. 2022, 281, 113242. [Google Scholar] [CrossRef]
- Esri Inc. ArcGIS Pro (Version 2.7.0). 2021. Available online: https://www.esri.com/en-us/arcgis/products/arcgis-pro/overview (accessed on 25 January 2021).
- Gupta, R.; Sharma, L.K. Mixed tropical forests canopy height mapping from spaceborne LiDAR GEDI and multisensor imagery using machine learning models. Remote Sens. Appl. Soc. Environ. 2022, 27, 100817. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bailly, J.-S.; Barbier, N.; Gond, V.; El Hajj, M.; Fabre, F.; Bourgine, B. Canopy height estimation in French Guiana with LiDAR ICESat/GLAS data using principal component analysis and random forest regressions. Remote Sens. 2014, 6, 11883–11914. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing stand-level forest canopy cover and height using Landsat time series, samples of airborne LiDAR, and the Random Forest algorithm. ISPRS J. Photogramm. Remote Sens. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Gao, S.; Hu, T.; Liu, J.; Guo, Q. The transferability of Random Forest in canopy height estimation from multi-source remote sensing data. Remote Sens. 2018, 10, 1183. [Google Scholar] [CrossRef]
- Mutanga, O.; Adam, E.; Cho, M.A. High density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Motagh, M. Random forest wetland classification using ALOS-2 L-band, RADARSAT-2 C-band, and TerraSAR-X imagery. ISPRS J. Photogramm. Remote Sens. 2017, 130, 13–31. [Google Scholar] [CrossRef]
- Dong, J.; Xiao, X.; Sheldon, S.; Biradar, C.; Duong, N.D.; Hazarika, M. A comparison of forest cover maps in Mainland Southeast Asia from multiple sources: PALSAR, MERIS, MODIS and FRA. Remote Sens. Environ. 2012, 127, 60–73. [Google Scholar] [CrossRef]
- Tian, S.; Zhang, X.; Tian, J.; Sun, Q. Random forest classification of wetland landcovers from multi-sensor data in the arid region of Xinjiang, China. Remote Sens. 2016, 8, 954. [Google Scholar] [CrossRef]
- Freeman, E.A.; Frescino, T.S.; Moisen, G.G. ModelMap: An R package for model creation and map production. R Package Version 2018, 4, 6–12. [Google Scholar]
- Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef]
- Isaaks, E.H.; Srivastava, M.R. Applied Geostatistics; No. 551.72 ISA; Oxford University Press: New York.
- Ou, Y.; Rousseau, A.N.; Wang, L.; Yan, B. Spatio-temporal patterns of soil organic carbon and pH in relation to environmental factors—A case study of the Black Soil Region of Northeastern China. Agric. Ecosyst. Environ. 2017, 245, 22–31. [Google Scholar] [CrossRef]
- Neuenschwander, A.L.; Magruder, L.A. Canopy and terrain height retrievals with ICESat-2: A first look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Jiang, F.; Zhao, F.; Ma, K.; Li, D.; Sun, H. Mapping the forest canopy height in Northern China by synergizing ICESat-2 with Sentinel-2 using a stacking algorithm. Remote Sens. 2021, 13, 1535. [Google Scholar] [CrossRef]
- Narine, L.L.; Popescu, S.; Zhou, T.; Srinivasan, S.; Harbeck, K. Mapping forest aboveground biomass with a simulated ICESat-2 vegetation canopy product and Landsat data. Ann. For. Res. 2019, 62, 69–86. [Google Scholar] [CrossRef]
- Stojanova, D.; Panov, P.; Gjorgjioski, V.; Kobler, A.; Džeroski, S. Estimating vegetation height and canopy cover from remotely sensed data with machine learning. Ecol. Inform. 2010, 5, 256–266. [Google Scholar] [CrossRef]
- Dickinson, Y.; Zenner, E.K.; Miller, D. Examining the effect of diverse management strategies on landscape scale patterns of forest structure in Pennsylvania using novel remote sensing techniques. Can. J. For. Res. 2014, 44, 301–312. [Google Scholar] [CrossRef]
- Snavely, R.A.; Uyeda, K.A.; Stow, D.A.; O’Leary, J.F.; Lambert, J. Mapping vegetation community types in a highly disturbed landscape: Integrating hierarchical object-based image analysis with lidar-derived canopy height data. Int. J. Remote Sens. 2019, 40, 4384–4400. [Google Scholar] [CrossRef]
- Lovell, J.; Jupp, D.; Newnham, G.; Coops, N.; Culvenor, D. Simulation study for finding optimal lidar acquisition parameters for forest height retrieval. For. Ecol. Manag. 2005, 214, 398–412. [Google Scholar] [CrossRef]
- Noordermeer, L.; Gobakken, T.; Næsset, E.; Bollandsås, O.M. Predicting and mapping site index in operational forest inventories using bitemporal airborne laser scanner data. For. Ecol. Manag. 2020, 457, 117768. [Google Scholar] [CrossRef]
- Dubayah, R.; Blair, J.B.; Goetz, S.; Fatoyinbo, L.; Hansen, M.; Healey, S.; Hofton, M.; Hurtt, G.; Kellner, J.; Luthcke, S. The Global Ecosystem Dynamics Investigation: High-resolution laser ranging of the Earth’s forests and topography. Sci. Remote Sens. 2020, 1, 100002. [Google Scholar] [CrossRef]
- Wang, C.; Elmore, A.J.; Numata, I.; Cochrane, M.A.; Shaogang, L.; Huang, J.; Zhao, Y.; Li, Y. Factors affecting relative height and ground elevation estimations of GEDI among forest types across the conterminous USA. GIScience Remote Sens. 2022, 59, 975–999. [Google Scholar] [CrossRef]
- Liu, X.; Su, Y.; Hu, T.; Yang, Q.; Liu, B.; Deng, Y.; Tang, H.; Tang, Z.; Fang, J.; Guo, Q. Neural network guided interpolation for mapping canopy height of China’s forests by integrating GEDI and ICESat-2 data. Remote Sens. Environ. 2022, 269, 112844. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tiwari, K.; Narine, L.L. A Comparison of Machine Learning and Geostatistical Approaches for Mapping Forest Canopy Height over the Southeastern US Using ICESat-2. Remote Sens. 2022, 14, 5651. https://doi.org/10.3390/rs14225651
Tiwari K, Narine LL. A Comparison of Machine Learning and Geostatistical Approaches for Mapping Forest Canopy Height over the Southeastern US Using ICESat-2. Remote Sensing. 2022; 14(22):5651. https://doi.org/10.3390/rs14225651
Chicago/Turabian StyleTiwari, Kasip, and Lana L. Narine. 2022. "A Comparison of Machine Learning and Geostatistical Approaches for Mapping Forest Canopy Height over the Southeastern US Using ICESat-2" Remote Sensing 14, no. 22: 5651. https://doi.org/10.3390/rs14225651
APA StyleTiwari, K., & Narine, L. L. (2022). A Comparison of Machine Learning and Geostatistical Approaches for Mapping Forest Canopy Height over the Southeastern US Using ICESat-2. Remote Sensing, 14(22), 5651. https://doi.org/10.3390/rs14225651






