Abstract
The objective of this work is to analyze the behavior of short temporal baseline interferometric coherence in forested areas for L-band spaceborne SAR data. Hence, an exploratory assessment of the impacts of temporal and spatial baselines on coherence, with emphasis on how these effects vary between SAOCOM-1 L-band and Sentinel-1 C-band data is presented. The interferometric coherence is analyzed according to different imaging parameters. In the case of SAOCOM-1, the impacts of the variation of the incidence angle and the ascending and descending orbits over forested areas are also assessed. Finally, short-term 8-day interferometric coherence maps derived from SAOCOM-1 are especially addressed, since this is the first L-band spaceborne mission that allows us to acquire SAR images with such a short temporal span. The analysis is reported over two forest-production areas in Argentina, one of which is part of the most important region in terms of forest plantations at the national level. In the case of SAOCOM, interferometric configurations are characterized by a lack of control on the spatial baseline, so a zero-baseline orbital tube cannot be guaranteed. Nevertheless, this spatial baseline variability is crucial to exploit volume decorrelation for forest monitoring. The results from this exploratory analysis demonstrates that SAOCOM-1 short temporal baseline interferograms, 8 to 16 days, must be considered in order to mitigate temporal decorrelation effects and to be able to experiment with different spatial baseline configurations, in order to allow appropriate forest monitoring.
1. Introduction
Synthetic Aperture Radar interferometry (InSAR) has been widely used for topographic and surface mapping [1]. The technique has evolved significantly since its beginnings, leading to the possibility of generating global DEMs, such as SRTM [2] or TanDEM-X DEMs [3]. In the case of forestry, the generation of digital surface models is a key input for the estimation of forest canopy height, as it may represent the initial step to the calculation of forest biomass or forest productivity [4,5]. Additionally, Polarimetric SAR Interferometry (PolInSAR) is an InSAR-based technique that exploits the phase and amplitude observations at different polarization states to estimate forest parameters by using a radar scattering model [6,7]. PolInSAR has been applied with special emphasis on forest canopy height estimation [8,9,10,11,12,13,14].
Under both approaches—InSAR and PolInSAR—the main observable is the interferometric coherence, a complex magnitude that measures the correlation between two SAR images. For volumetric scatters, such as forests, canopy height information can be estimated from the volume decorrelation term, providing a suitable physical separation between the SAR acquisitions [15,16,17]. Nevertheless, when considering repeat-pass InSAR configurations, another decorrelation source that arises is the temporal one. In general, as more time passes between two SAR acquisitions, more changes may occur in the target’s properties, or even in its location, which in turn degrades the accuracy of forest canopy height measurements [18,19]. Besides, temporal decorrelation increases generally with frequency in forests, as electromagnetic waves increase sensitivity with frequency to smaller components, such as branches or leaves, which are more affected by weather effects, such as wind, for instance. Thus, proper InSAR and PolInSAR forest mapping faces a compromise among (i) the InSAR geometric configuration in terms of the physical separation between the SAR acquisitions or spatial baseline, (ii) the temporal separation of the SAR acquisitions or temporal baseline and (iii) the imaging frequency, as it determines the penetration capabilities into the forest volume.
Temporal decorrelation studies for repeat-pass interferometry have been widely addressed in airborne SAR missions as these systems offer the flexibility of experimenting with different temporal baselines and there is full control on the spatial baseline [20,21,22,23,24]. In spaceborne systems, the conditions are quite different. First, satellite platforms have a pre-defined revisit cycle which can be too long in terms of temporal decorrelation. Second, because not all spaceborne systems have a stable orbital tube over the platform’s position. This implies that there might be high variability in the spatial baseline, which may not always be the most appropriate for an InSAR configuration [25] focused on forest monitoring. As for the first constraint, satellite missions in X-band such as TerraSAR-X/TanDEM-X/PAZ and COSMO-SkyMed have offered the possibility of developing InSAR case studies with very short temporal separation [26,27], limiting temporal decorrelation, but where forest canopy penetration capabilities are reduced, compared to L- or C-bands.
With the launch of C-band ESA’s constellation Sentinel-1 research has been focused on the study of temporal series of the interferometric coherence for different application fields, taking advantage of the mission’s short revisit time of 6 to 12 days [28,29,30,31]. For lower frequencies, there has been a number of studies on the InSAR capabilities of JAXA’s ALOS-PALSAR mission to map vegetation or forest canopy height considering the temporal decorrelation with a revisit time from 23 to 46 days [25,32,33], but no studies have considered coherence at shorter revisit times for L-band orbital data. The Argentinian L-band SAOCOM system fills this gap, thanks to the capability to generate 8-day interferograms. Regarding future missions, ESA is planning to launch the ROSE-L system as part of its Copernicus Programme [34], and the United States and India Space Agencies (NASA & ISRO) are working on the NISAR mission, scheduled for 2023 [35]. Both platforms will carry an L-band SAR instrument designed to acquire InSAR data. Among their applications, forest mapping, and characterization will be one of the most important ones.
The purpose of this paper is to contribute to the existing knowledge on InSAR analysis for forestry monitoring, with an emphasis on the analysis and characterization of the interferometric coherence for short temporal baseline L-band spaceborne systems. The analyses presented in this work refer to the amplitude of the InSAR coherence only, namely . To achieve this goal, this work presents an assessment of the InSAR coherence over forests based on the analysis of data from the L-band Argentinian SAOCOM-1 and the C-band European Sentinel-1 constellations, as a first step towards understanding the suitability of SAOCOM-1 data for forest monitoring and mapping. It is worth noting that since November 2021, the SAOCOM-1B satellite is in operation, allowing us to form 8-day InSAR pairs in combination with SAOCOM-1A images. This work presents, for the first time, the analysis of these 8-day temporal baselines, L-band, orbital interferograms, with its focus on forest monitoring. In addition, collocated GEDI data is considered to perform a preliminary analysis of the InSAR coherence dependency on forest canopy height. All these analyses are intended to generate a proper basis and criteria for interferometric pairs selection in future research involving forest canopy height retrieval.
The article is organized as follows. Section 2 introduces the basics of InSAR, and, in particular, the concepts of interferometric coherence and coherence decorrelation, as well as the study sites and the data sources considered in this study. Section 3 refers to the processing results, and presents a detailed assessment of the InSAR coherence, considering different acquisition parameters and target characteristics. Section 4 presents further analyses of the results to understand the advantages and limitations of the proposed approach, and Section 5 concludes the article.
2. Materials and Methods
2.1. Interferometric SAR Principles
The principle of the InSAR technique relies on the measurement of the phase difference between two or more SAR images, acquired from different positions and/or at different times [36,37]. The interferometric phase, related to any point seen within the illumination footprint, is expressed as
where and are the sensor-target distance for the reference and secondary acquisitions, respectively, is the radar wavelength, and B, , and are the spatial baseline, the incidence look angle, and the tilt angle, respectively.
The spatial baseline is very important in any InSAR application. As depicted in Figure 1, B represents the spatial separation between the two acquisitions, which can be decomposed into parallel baselines and perpendicular baselines , which are respectively highlighted in green and blue. is an important factor because it defines the system sensitivity for elevation or topographic mapping. In the InSAR literature it is common to measure the interferometric performance for elevation mapping by means of the Height of Ambiguity, and it can be derived from Equation (1)
where R is the slant range distance, which can be either or from Equation (1). In the PolInSAR literature, the system sensitivity to height is usually defined as vertical wavenumber , which expresses the ratio of change in the interferometric phase with the variation of the target height [15]
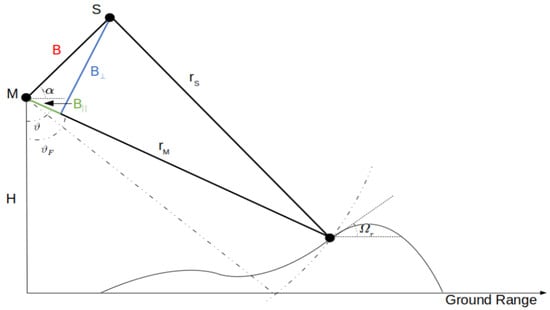
Figure 1.
InSAR acquisition geometry (Source: [5]).
Regardless of the metric used to measure the interferometric sensitivity, or , it is important to work with the appropriate according to the range of elevation values to map. In spaceborne systems there is little possibility of selecting or controlling the spatial baseline, unlike airborne systems that can acquire in more experimental and flexible contexts. This is a constraint that needs to be accounted for when estimating canopy height from spaceborne instruments.
Finally, when working with interferometric pairs, it is very important to know what is the critical baseline of the system, which is normally defined as
is the value of beyond which the spectral shift between two acquisitions is higher than the system range bandwidth , leading to a zero geometric decorrelation. is the terrain slope, but normally a good approximation of can be obtained by using the incidence angle only.
2.2. Interferometric Coherence
Let and be two SAR images acquired with a given spatial and temporal baseline, see Figure 1, at a given polarization assumed to be the same for both images [6,15,38]. The interferometric coherence is defined as
where represents the speckle filtering [39], is a complex magnitude, whose modulus indicates the correlation between the images and its angle denotes the interferometric phase. This work focuses on , as it is a good indicator of how different decorrelation sources affect the coherence. Due to the polarimetric capabilities of SAOCOM-1 and Sentinel-1, , , , will refer to the InSAR coherences at the different polarization combinations for transmission and reception, where H and V denote the linear horizontal and vertical wave polarization states, respectively.
The coherence suffers from different decorrelation processes, and according to [15,40] it can be written as
For volumetric scatterers such as trees, appears due to the different scattering processes that occur at different heights within a resolution cell [6]. It is a term that has a high dependence on frequency, as a variation in the wavelength implies different interactions with the scatterers. However, it does also depend on . For forested targets, if an exponential decrease of the scattering power is assumed within the canopy, can be modeled as [18,19]
where h is the volume height, and is the attenuation coefficient, which is normally expressed in dB/m and is also known as the extinction parameter in the PolInSAR literature. An important outcome of Equation (7) is that plays a relevant role on the value of . Indeed, with higher values of and , see Equation (3), will decrease more rapidly with an increase in the volume height. Satellite constellations such as Sentinel-1 have stringent orbit control. Orbit positioning control is defined using an orbital Earth fixed tube which is approximately 50 m wide in radius around the nominal operation path. Therefore, values for Sentinel-1 are normally within a range of −200 to 200 m, which mitigates the potential effect of volume decorrelation [41].
comprises a wide range of decorrelation effects caused by the SAR system configuration and processing aspects, that include contributions induced by additive noise, range and azimuth ambiguities, quantization, and other effects [15]. One of the most important components is the geometric term , which is function of and [42]
Hence, if , becomes 0, causing a total loss of correlation.
Finally, represents the temporal decorrelation, and it is originated by geometric and/or dielectric changes in the scatterers within the temporal window that separates SAR acquisitions. Generally, the larger the temporal baseline, the lower the . This term is critical when working with repeat-pass InSAR, and it is present even when working with almost-zero temporal separation between the images [16]. The decay of as a function of time or the temporal baseline between images can be estimated through several models. One of them is the exponential one [43]
where and represent the long-term coherence and the rate of coherence decay, respectively, which can be approximated by fitting Equation (9) to the coherence measurements in a temporal series.
2.3. Study Areas
This work considers two areas of analysis. The first one corresponds to a sector in the northeast of Corrientes province, Argentina, near its border with the neighboring Misiones province, see Figure 2a. Corrientes is amongst the most important areas in terms of forest production in Argentina, with pine and eucalyptus as the main planted species. This is the main reason for choosing this region, only surpassed by Misiones [44]. In this sense, the retrieval of forest plantations’ height, which is directly linked to their productivity, is very relevant both for local producers and government agencies [5]. As can be seen in the zoomed area of the same figure, three sub-regions were selected for the analysis performed on this site. Region C forms part of a forest field, from which in-field inventories were available. Region A corresponds to a forested area which, according to GEDI measurements, see Section 2.5, presented lower tree heights than region C. Region B, finally, covers a bare-soil area, used to compare the behavior of coherence between the land covers in Section 3.1.
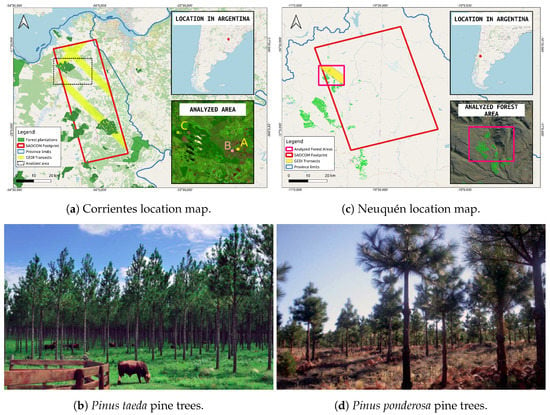
Figure 2.
Study-areas in Corrientes and Neuquén provinces, Argentina.
The main planted species of pine in the Corrientes site corresponds to Pinus taeda, spanning a surface of over 250,000 ha for the whole province [45]. According to field measurements provided by local producers, the analyzed forest stands of region C have an age of around 18 to 20 years, with a mean average canopy height of 24 m, obtained from ground campaigns. As indicated by [46], the Pinus taeda trees in Corrientes reach heights of around 23 m at the age of 20, which is in agreement with the given figures.
The second area of analysis is located near the Domuyo Volcano, in the Neuquén province, Argentina, see Figure 2c, which is much less important than Corrientes in terms of forest production. This area was included to assess the InSAR coherence in a different environment, where trees generally reach lower heights in contrast with the northeast of the country. This comparison based on forest height will be addressed in Section 3.4.
The tree plantations in the second area correspond to pines of the Pinus ponderosa species, which is one of the most important in the Patagonian Andes of Argentina, with a total surface of 56,000 ha [47]. The analyzed forest stands have an age of around 30 years, with a mean average canopy height of 15 m, obtained from ground campaigns. In this case too, these numbers are in agreement with previous studies that developed growth models for Pinus ponderosa in the region [48].
2.4. SAR Data
In this study, SAR data acquired by the SAOCOM-1 and Sentinel-1 systems are considered. SAOCOM-1 is a two-satellite constellation launched by CONAE, in 2018 and 2020. Sentinel-1 is also a two-platform constellation launched in April 2016 and operated by ESA. The SAR instruments on board these spaceborne platforms work at L-band ( 23 cm) for SAOCOM-1 and C-band ( 5.6 cm) for Sentinel-1. Their use in forestry applications is of great interest due to the way in which microwaves interact with trees [5].
For this study, we selected different temporal series of SAOCOM-1A&B and Sentinel-1B images, covering the period from August to December 2021 in the case of the Corrientes site, and from February to August 2020 in the case of Neuquén site. In the former (Corrientes), a shorter dataset of SAOCOM-1 images with descending orbit was also considered in order to assess the InSAR coherence changes according to the orbit direction, see Section 3.2. Table 1 summarizes the image datasets used in this work, where A and D indicate ascending and descending orbits, respectively, refers to the approximate mid-range incidence angle, N indicates the number of images of the temporal series, Pol. refers to the polarization, QP for fully-polarimetric data and VV/VH for dual-pol data and, finally, is the critical perpendicular baseline. Section 3.1, Section 3.2 and Section 3.3 refer to data processed in the Corrientes site, while Section 3.4 makes use of both sites to compare the variation of InSAR coherence according to forest canopy height.

Table 1.
Temporal SAR datasets. Site 1 is Corrientes, Site 2 is Neuquén.
Finally, it is worth noting that, since 20 November 2021, the first SAOCOM-1B images started to be acquired over the Corrientes site, allowing us to form 8-day InSAR pairs with the combination with the SAOCOM-1A images. At the moment, the amount of SAOCOM-1B images is not long enough to make a long temporal analysis, but these shorter term orbital L-band interferograms have been included in this work, and are specifically addressed and analyzed in Section 3.3.
The temporal baseline between the SAOCOM-1A images is 16-day, which is equivalent to the platform’s nominal revisit time. This temporal cycle can be reduced to 8 days if images are acquired by the SAOCOM-1A&B constellation. Regarding the C-band dataset, the Sentinel-1B images used for this work are separated by a 12-day temporal baseline. Figure 3a,b depicts the perpendicular spatial and temporal separation between the scenes for the datasets used in the Corrientes and Neuquén sites. The spatial baselines refer to the interferograms created by considering the first images of the series as reference images and the rest as secondary images. As expected, Sentinel-1 spatial baselines tend to be stable since the mission has a narrow orbital tube, which is suitable for instance for Differential SAR Interferometry [49]. On the other hand, SAOCOM-1 does not have control over the orbital tube, and hence the perpendicular spatial baseline shows much more variability. While having larger perpendicular baselines may be better for topography or forest canopy mapping, this is a factor that is not equal between both SAOCOM-1 and Sentinel-1, and will be considered when assessing the temporal decorrelation.
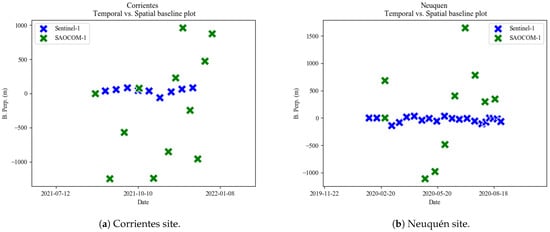
Figure 3.
Spatial and temporal distribution of SAOCOM-1 and Sentinel-1 acquisitions.
As indicated previously, InSAR coherence needs to be estimated from data, see Equation (5), by using a speckle filter. In this work, we will use a -pixel multi-look filter. The use of these dimensions is justified to limit the coherence estimation bias at low coherences, especially for C-band data. Additionally, the number of Equivalent Number of Looks (ENL) has been computed on different homogeneous areas, mainly forest sites. For Single Look Complex images, SAOCOM-1 data presents an average of , whereas Sentinel-1 presents an average of . These values can be explained as forested areas in the analyzed regions are not totally homogeneous. For filtered data, SAOCOM-1 data presents an average , whereas Sentinel-1 presents an average .
2.5. GEDI Data
To assess how the InSAR coherence varies according to tree heights, we selected a number of points with measurements of the GEDI instrument. GEDI produces high-resolution laser-ranging observations of the 3-dimensional structure of the Earth. It was launched on 5 December 2018, as a joint project between the University of Maryland and NASA. The GEDI instrument consists of 3 lasers producing a total of 8-beam ground transects [50], some of which cover partially the studied sites, as showed in yellow in the Figure 2a,c. Most of the GEDI measurements used for this work correspond to the years 2020 and 2021, which makes them relatively contemporary to the SAR data temporal series. The processed product was GEDI Level 2B, which contains information about the canopy height.
3. Results
3.1. Coherence Maps
In the Corrientes site, co-located SAOCOM-1 and Sentinel-1 interferometric pairs were formed and processed with the Free Open-Source Software GMTSAR. Range spectral filtering has been applied to SAOCOM-1 images to mitigate the baseline spatial decorrelation effect. The time series of SAOCOM-1 consisted of 12 scenes with 66 interferometric pairs, with a minimum temporal baseline of 8 days and a maximum temporal span of 128 days, at a nominal incidence angle of 32°. On the other hand, the Sentinel-1 time series comprised 10 images and 45 interferograms, with a minimum temporal baseline of 12 days and a maximum of 108 days, at a nominal incidence angle of 40°. A similar processing was carried out in the Neuquén site, but this section will focus on the first study site.
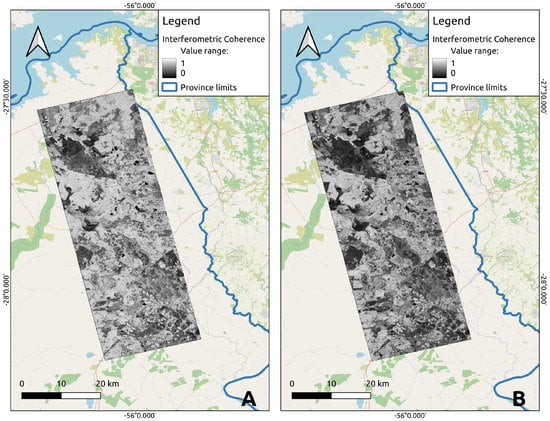
The visual comparison of the obtained VV InSAR coherence maps can be observed in Figure 4, for two different temporal baselines, to observe the effect of the temporal baseline at the minimum time span for each times series, 16 days in the case of SAOCOM-1A and 12 days in the case of Sentinel-1, and then taking a longer one that is coincident in both cases, being 48 days.
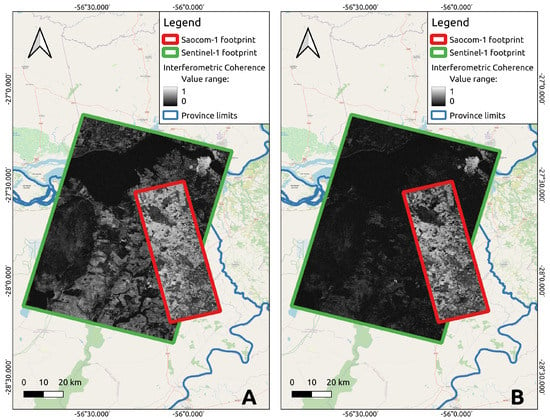
Figure 4.
Comparison of the for SAOCOM-1 (red) and Sentinel-1 (green). (A) SAOCOM-1 16-day (September) interferogram and a Sentinel-1 12-day (September). (B) 48-day interferogram for both systems (September–October).
To see the detailed effect of the temporal decorrelation at the two frequencies, for the previous temporal series of SAR data for SAOCOM-1 and Sentinel-1, the complete InSAR coherence matrices were calculated for the forested area indicated as region C on Figure 2a. Figure 5a,b show the values of for the pixels of this region. For comparison purposes, the complete InSAR coherence matrices for bare soil pixels, region B on Figure 2b, were also derived. As expected, on bare or short vegetation-covered surfaces volumetric decorrelation, in general, tends to be lower than in vegetated pixels, see Figure 6a,b. A comparison of the four orbital InSAR coherence matrices shows that InSAR coherence is lower for vegetated areas, if compared with bare areas, independently of the working frequency, but that L-band coherences are larger than C-band coherences, independently of the observed type of target. This has a relation with the different wavelengths at which each instrument operates, but there is also an important influence of the perpendicular baseline, which is further discussed in Section 4.1.
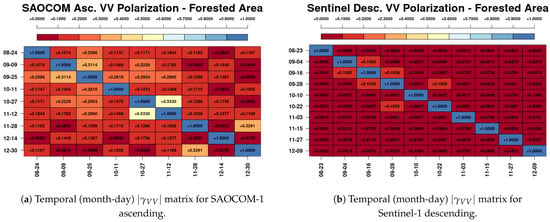
Figure 5.
Forested-area, Corrientes site.
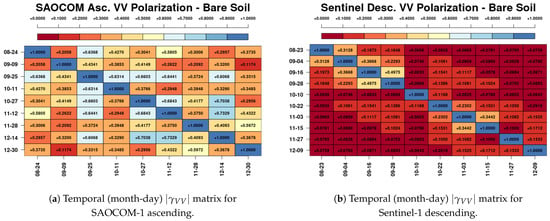
Figure 6.
Bare-soil area, Corrientes site.
3.2. Ascending/Descending Orbits
According to Table 1, SAOCOM-1A images with both ascending and descending orbits are available at the Corrientes site, comprising the period from September to December 2021. Nevertheless, the descending orbit presents a lower number of images as some images were not acquired due to conflicts with higher priority acquisitions. It is important to highlight that the ascending orbit had an incidence angle of 32°, whereas the incidence angle of the descending pass was 19°. The approximate footprint of this pass can be observed in Figure 7. As performed previously, we computed the temporal coherence matrices for the descending pass over region C, and compared them to the matrices of the ascending pass, see Figure 8a,b.
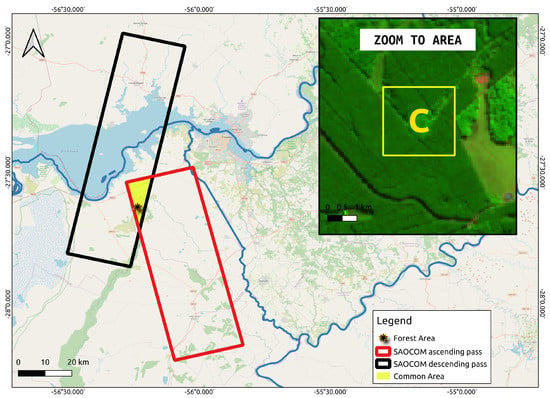
Figure 7.
Area common to the ascending and descending passes used to compare the interferometric coherence (highlighted in yellow). The zoom shows the forested pixels, region C, which is also indicated on Figure 2a.
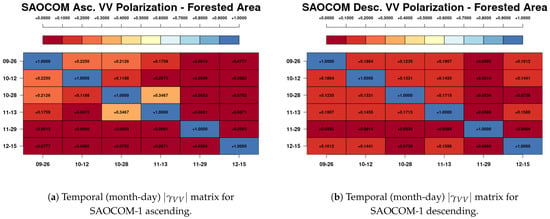
Figure 8.
Forested area, Corrientes site.
3.3. SAOCOM-1 8-Day Coherence
As indicated in Section 2.4, three SAOCOM-1B images were acquired over the Corrientes site to form 8-day L-band interferograms and thus evaluate the effect of reducing the temporal baseline on the coherence, with respect to the 16-day nominal revisit time of the SAOCOM-1A images. Table 2 details the interferometric pairs formed and compared to assess , with their corresponding values. In this sense, it is important to note that the perpendicular baselines have high variability in these subsets of interferometric pairs, and in some cases its effect might compensate for an expected improvement of due to using a shorter temporal baseline. Figure 9 reflects this issue, where we have compared 8 and 16-day contemporary pairs whose are very different. In all these cases, the effect of the perpendicular spatial baseline is determinant. To limit this dependency, Figure 10 presents the coherence for pairs 3 and 4 in Table 2 with the most similar values of . In this case, decorrelation is mainly governed by temporal decorrelation. The detailed difference is analyzed in Section 4.4.

Table 2.
8 and 16-day interferometric pairs used to compare formed with the SAO1-A and SAO1-B ascending images.
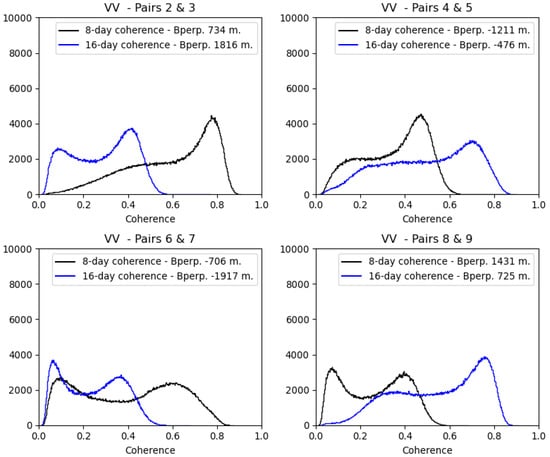
Figure 9.
histograms for SAOCOM-1 8-day and 16-day pairs chosen from Table 2.
3.4. Forest Canopy Height
Due to the volumetric decorrelation term indicated in Section 2.2, forest canopy height can be interpreted from the InSAR data. Based on the forest canopy height measurements provided by the GEDI instrument, this section assesses the behavior of with the variation of height in both the Corrientes and the Neuquén sites, see Figure 11. The analysis is divided into two parts to account for the temporal decorrelation term by selecting two long temporal baselines, i.e., 48-day, SAOCOM-1 interferograms for each site with HH polarization and short temporal baseline SAOCOM-1 interferograms, i.e., 8 and 16-day. As a complement, Sentinel-1 VV interferograms are also considered since VV polarization is more similar in terms of behavior to the HH one, see Section 4.2.
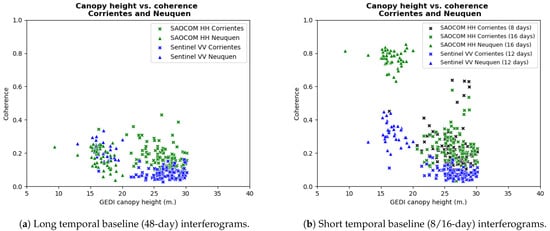
Figure 11.
vs. GEDI canopy height for forests in Corrientes and Neuquén sites.
4. Discussion
4.1. Spatial and Temporal Baselines
As presented in Section 2.2, decreases with larger temporal baselines due to temporal decorrelation. For the case of SAOCOM-1 seems to follow an exponential pattern, as suggested by Equation (9), see Figure 12a, where the parameters day and are considered. In particular, the latter is selected in such a way as to account for the coherence estimation bias for zero coherence. There are, however, some points that do not seem to fit totally with this exponential model. This is because this temporal series does also have high variability in the spatial baseline in comparison to Sentinel-1, and Figure 12a,b depicts this situation more clearly. Both scatter plots are based on the same pixels of the forested area in Figure 2a and considered for the interferometric coherence matrices, but in this case is compared with the value of the temporal baselines and . These graphs show that large values seem to have a negative impact on the interferometric coherence, regardless of the temporal separation between the images and the range spectral filtering applied to mitigate the spatial decorrelation. This might be explained by the volumetric decorrelation term, which is baseline-dependent as indicated by Equation (7). Another interesting observation is that in the case of Sentinel-1, seems to have a strong influence on the coherence values, as temporal decorrelation is larger at C-band despite the much smaller variation and values of , see Figure 13a,b.
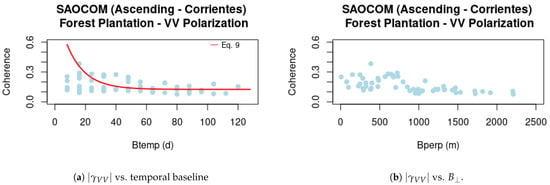
Figure 12.
SAOCOM-1 vs. baselines.
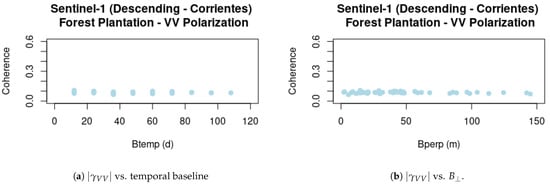
Figure 13.
Sentinel-1 vs. baselines.
4.2. Polarimetry
The results presented previously comprise the VV polarization only, which is a channel present both in SAOCOM-1 and Sentinel-1. In order to understand if the polarization state for transmission and reception is a determinant factor on the coherence behavior, we considered also the coherence for SAOCOM-1 in a similar way to Figure 12b, but for all the polarimetric channels, always referring to the Corrientes site, where the full polarimetric images are available.
Figure 14 and Figure 15 confirm that the influence of on is very strong and it is an important factor to be considered in this analysis. However, polarization has an effect on the coherence, as it can be seen in the same figure, where co-polarized channels have higher coherence values than the cross-polarized ones.
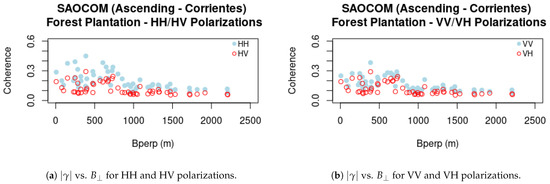
Figure 14.
SAOCOM-1 , , & vs. (cross-polarized coherences in red).
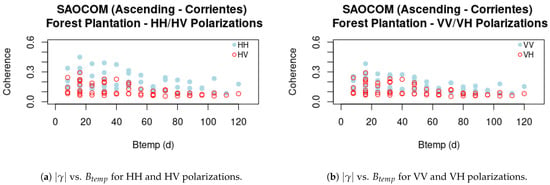
Figure 15.
SAOCOM-1 , , & vs. (cross-polarized coherences in red).
4.3. Orbits Analysis
From the matrices of Section 3.2, no clear difference can be inferred in the temporal behavior of between the ascending and descending passes. Therefore, we also plotted the scatterplots of and vs. the coherence, see Figure 16. Due to the particular distribution of values in this dataset, Figure 16a needs to be analyzed together with Figure 16b, since many of the longer temporal baseline pairs have a small perpendicular baseline. As a consequence, no clear pattern can be inferred from Figure 16a, in contrast to Figure 12a.
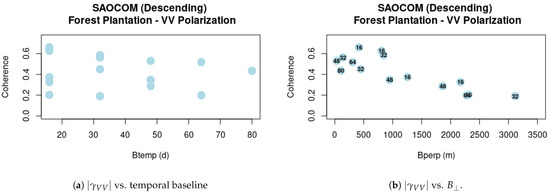
Figure 16.
Scatter plot of and vs. for SAOCOM-1 for region C, Figure 7. The points are labeled with the temporal baseline value to illustrate the effect of .
4.4. Short Temporal Baselines
To compensate for the effect of presented in Section 3.3, pairs 3 and 4 were selected based on Table 2, since their baseline values were much closer than in the pairs showed in Figure 9, and they were also contemporary in time. Figure 10 shows the coherence maps for these two pairs. We computed the histograms over region C, see Figure 2a, to specifically assess the effect on forested pixels. The coherence values are lower than the average for the whole image. Nevertheless, the positive effect of the reduction of the temporal baseline can still be observed, especially in the cross-polarized channels, see Figure 17a,b. This low coherence might be related to the volumetric decorrelation term as the mean forest canopy height of these pixels, according to the GEDI points, is around 24 m. In Section 4.5, we compare these histograms with region A, see Figure 2a, where trees present a lower height of around 14 m.
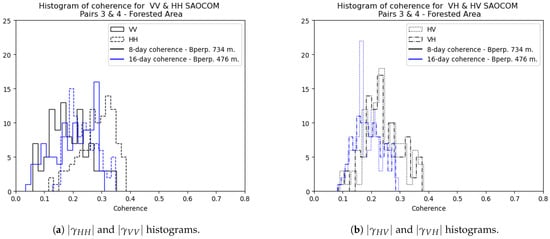
Figure 17.
Histograms of for SAOCOM-1 at 8 and 16 days separation in region C, Figure 2a.
4.5. Forest Canopy Height
The results shown in Figure 11a suggest that with a temporal span of 48 days, at L-band seems to suffer from large temporal decorrelation, as indicated in Section 2.1, and this applies both to Corrientes and Neuquén sites. However, when selecting shorter temporal baselines for both instruments and sites, things look quite different. Figure 11b shows scatter plots for 12-day interferograms in the case of Sentinel-1, and 8 to 16 days in the case of SAOCOM-1. While for Sentinel-1 the variation of the coherence with respect to the forest height is limited, in the case of SAOCOM-1 the system seems to be much more sensitive to this variable. In the Neuquén site, where the average height measured by GEDI is around 16.5 m, the coherence is higher than in Corrientes, where the mean canopy height is 24.5 m. The forest canopy height does not only vary between the two sites, but also within the Corrientes one. If we observe the histograms shown in Figure 17a,b of Section 4.4, the coherence values correspond to region C zoomed in Figure 2a, which has a mean canopy height of 24 m. According to the GEDI data, the other forested area analyzed in this work, region A in Figure 2a, has a mean canopy height of 14 m, and the histograms of coherence show higher values than the C one, as can be seen on Figure 18a,b.
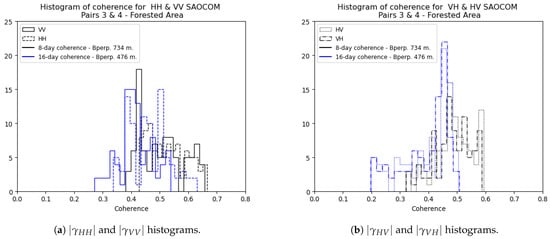
Figure 18.
Histograms of for SAOCOM-1 at 8 and 16 days separation in region A, Figure 2a.
Following the analysis proposed in [51], we plotted a scatter plot comprising the relation between all the observed coherence values coming from 8 and 16-day interferometric pairs, and the ratio between GEDI canopy height and the Height of Ambiguity, namely , see Figure 19. The reason for using this metric is that the variability introduced by different spatial baselines is mitigated when using this ratio rather than the height itself. On the same Figure, we have included a curve corresponding to the RVoG volumetric decorrelation model, also introduced in [51], taking the mean value for all the pairs. When fitting this curve, we also compensated for the temporal decorrelation that affects these observations, by applying Equation (9).
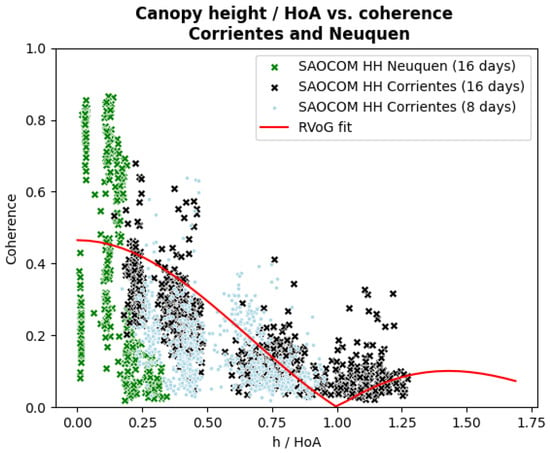
Figure 19.
Ratio of GEDI Canopy Height and () vs. in Corrientes and Neuquen Sites.
The observed result is quite interesting, since although the values do not cover the full numeric range needed to fit a model-based curve such as the RVoG one, the scatter plot effectively accounts for a non-linear negative relation between the ratio and . Bearing in mind that we are working with an orbital mono-static SAR system—unlike a bi-static one like the data set presented by [51], this relation deserves further analysis with a longer and more baseline-heterogeneous InSAR time series.
These results are relevant as they indicate that SAOCOM-1 L-band coherence is related to the canopy height, which is essential for the implementation of inversion models such as the RVoG considered in PolInSAR [7,14]. It is also important since it proves that working at L-band with short temporal baselines is critical for this type of application. Further analysis needs to be performed regarding this point, especially assessing whether the volumetric coherence estimated by the RVoG model fits the distribution of the observed data. However, this requires all data points to come from the same pair and the same interferometric configuration, and this is not the case of Figure 11b. An alternative to this constraint could be to adopt a multi-baseline approach such as the one proposed by [17], in order to exploit the variability in baselines and choose the one that best fits each target’s height.
5. Conclusions
This work presents an assessment of the interferometric coherence with two different spaceborne SAR instruments: the L-band SAOCOM-1 and the C-band Sentinel-1, focusing on the study of forested areas. In both cases, this assessment has considered different parameters such as the spatial baseline, the temporal baseline, and the forest canopy height. In particular, this study has considered the analysis of short temporal baseline spaceborne, L-band interferograms.
The results presented in this work show that the SAOCOM-1 L-band instrument appears to be more suitable than the Sentinel-1 C-band system for forest studies, due to the fact that interferometric data shows higher coherence values and data are also less sensitive to the temporal decorrelation. Additionally, SAOCOM-1 presents the possibility of acquiring fully polarimetric data, unlike Sentinel-1. These factors are critical for the feasibility of mapping forest canopy height by means of the InSAR or PolInSAR techniques. On the other hand, Sentinel-1 showed not only very low coherence values in both sites, but also little variation in relation to the analyzed parameters. This is probably explained by the fact that C-Band data present fewer penetration capabilities and are much more affected by temporal decorrelation than L-band data in forested areas.
The high variability of the perpendicular baseline in SAOCOM-1, compared to Sentinel-1, has a strong influence on the interferometric coherence and, as already exposed in Section 2.1, it is also an important factor to define the system sensitivity to forest canopy height. In this assessment, we have had to account for the effect of this variable, since in many cases it determines the difference in the coherence between different pairs, making it difficult to achieve good or ideal experimental conditions. In the future, this may lead to better or worse scenarios for forest canopy height mapping, either with InSAR only or PolInSAR techniques. Nevertheless, as discussed in Section 4.5, this might allow experimenting with multiple baseline values in places with high heterogeneity in forest stand heights.
Regardless of the limitations that need to be considered, this work demonstrates that the Argentinean constellation SAOCOM-1 yields a promising scenario for forest mapping, especially considering that it operates a spaceborne L-band SAR system, which can provide images every 8 days; something that had not been achieved before with other orbital SAR L-band missions. The exploratory assessment carried out in this work is a starting point for the development of case studies where PolInSAR is applied to invert forest canopy height from SAOCOM data, going beyond the traditional InSAR technique that has been assessed for the Argentinean constellation in [5].
Finally, it is important to mention that we have considered two forest areas in Argentina comprising essentially managed forests, where ground-truth data were available, demonstrating the potential of SAOCOM-1 for forest studies based on InSAR and PolInSAR techniques. The generalisation of these results to other types of forests, such as boreal, tropical, or Mediterranean forests, is a foremost task, especially regarding the future L-band SAR missions ROSE-L and NISAR. We are confident that very similar performances can be expected in these types of forests.
Author Contributions
Conceptualization, S.A.S. and C.L.-M.; methodology, S.A.S. and C.L.-M.; software, S.A.S.; validation, S.A.S.; formal analysis, S.A.S. and C.L.-M.; investigation, S.A.S. and C.L.-M.; resources, S.A.S. and M.J.J.; data curation, S.A.S. and M.J.J.; writing—original draft preparation, S.A.S. and C.L.-M.; writing—review and editing, S.A.S. and C.L.-M.; visualization, S.A.S. and C.L.-M.; supervision, C.L.-M.; project administration, C.L.-M.; funding acquisition, C.L.-M.. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the project INTERACT PID2020-114623RB-C32 funded by the Spanish MCIN/AEI/10.13039/501100011033. (Corresponding author: S. Seppi).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data policy of the SAOCOM system is determined by the Argentinian Government and its collaboration with the Italian Space Agency ASI. In essence, this system has a double nature. On one hand, it was launched to support monitoring and control activities of the Argentinian Government. On the other hand, the SAOCOM system is also commercial, where the commercialization of data is done under the agreement CONAE has with ASI in the case of Europe, and with other partners in the rest of the world. Plase contact atencion.usuario@conae.gov.ar for further information.
Acknowledgments
The authors thank the local companies Bosques del Plata S.A. (Corrientes) and Asociación de Fomento Rural (AFR) Manzano Amargo y Pichi (Neuquén) for providing with field measurements used to support the assessment performed in this article. The authors are also grateful to the Argentinean Space Agency (CONAE) for granting access to the SAOCOM-1 images and Rubén Iglesias for the discussions concerning geometric decorrelation.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ALOS-PALSAR | Advanced Land Observing Satellite-Phased Array type L-band SAR |
| CONAE | Comisión Nacional de Actividades Espaciales |
| COSMO-SkyMed | COnstellation of Satellites for the Mediterranean basin Observation |
| DEM | Digital Elevation Models |
| ESA | European Space Agency |
| GEDI | Global Ecosystem Dynamics Investigation |
| InSAR | SAR Interferometry |
| ISRO | Indian Space Research Organisation |
| JAXA | Japan Aerospace Exploration Agency |
| NASA | National Aeronautics and Space Administration |
| NISAR | NASA-ISRO SAR |
| PolInSAR | Polarimetric SAR Interferometry |
| ROSE-L | Radar Observing System for Europe at L-band |
| RVoG | Random Volume over Ground |
| SAOCOM | Satélite Argentino de Observación con Microondas |
| SAR | Synthetic Aperture Radar |
| SRTM | Shuttle Radar Topography Mission |
| TanDEM | TerraSAR-X add-on for Digital Elevation Measurement |
References
- Zebker, H.A.; Goldstein, R.M. Topographic mapping from interferometric synthetic aperture radar observations. J. Geophys. Res. Solid Earth 1986, 91, 4993–4999. [Google Scholar] [CrossRef]
- Rodriguez, E.; Morris, C.; Belz, J. A global assessment of the SRTM performance. Photogramm. Eng. Remote Sens. 2006, 72, 249–260. [Google Scholar] [CrossRef]
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy assessment of the global TanDEM-X Digital Elevation Model with GPS data. ISPRS J. Photogramm. Remote Sens. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- Soja, M.J.; Persson, H.; Ulander, L.M. Estimation of forest height and canopy density from a single InSAR correlation coefficient. IEEE Geosci. Remote. Sens. Lett. 2014, 12, 646–650. [Google Scholar] [CrossRef]
- Seppi, S.; Solarte, A.; Roa, Y.; Euillades, L.; Gaute, M. On the Feasibility of Applying Orbital Corrections to SAOCOM-1 Data with Free Open Source Software (FOSS) to Generate Digital Surface Models: A Case Study in Argentina. ISPRS J. Photogramm. Remote Sens. 2021, 46, 167–174. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Cloude, S.; Papathanassiou, K. Three-stage inversion process for polarimetric SAR interferometry. Radar Sonar Navig. IEE Proc. 2003, 150, 125–134. [Google Scholar] [CrossRef]
- Garestier, F.; Le Toan, T.; Dubois-Fernandez, P. Forest height estimation using P-band Pol-InSAR data. In Proceedings of the 3rd International Workshop on Science and Applications of SAR Polarimetry and Polarimetric Interferometry, Noordwijk, The Netherlands, March 2007. [Google Scholar]
- López-Sánchez, J.M.; Vicente-Guijalba, F.; Erten, E.; Campos-Taberner, M.; Garcia-Haro, F.J. Retrieval of vegetation height in rice fields using polarimetric SAR interferometry with TanDEM-X data. Remote Sens. Environ. 2017, 192, 30–44. [Google Scholar] [CrossRef]
- Lee, S.K. Forest parameter estimation using polarimetric SAR interferometry techniques at low frequencies. Doctoral Dissertation, ETH Zurich, Zurich, Switzerland, 2012. [Google Scholar]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.; Hajnsek, I. Polarimetric SAR interferometry for forest application at P-band: Potentials and challenges. IEEE IGARSS 2009, 4, 4–13. [Google Scholar]
- Simard, M.; Denbina, M. An assessment of temporal decorrelation using the uninhabited aerial vehicle synthetic aperture radar over forested landscapes. IEEE J.-STARS 2017, 11, 95–111. [Google Scholar]
- Denbina, M.; Simard, M.; Riel, B.V.; Hawkins, B.P.; Pinto, N. AfriSAR: Rainforest Canopy Height Derived from PolInSAR and Lidar Data, Gabon; ORNL DAAC: Oak Ridge, TN, USA, 2018. [Google Scholar]
- López-Martínez, C.; Papathanassiou, K. Cancellation of Scattering Mechanisms in PolInSAR: Application to Underlying Topography Estimation. IEEE Trans. Geosci. Remote Sens. 2013, 51, 953–965. [Google Scholar] [CrossRef]
- Kugler, F.; Lee, S.K.; Hajnsek, I.; Papathanassiou, K.P. Forest height estimation by means of Pol-InSAR data inversion: The role of the vertical wavenumber. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5294–5311. [Google Scholar] [CrossRef]
- Simard, M.; Denbina, M. An assessment of temporal decorrelation compensation methods for forest canopy height estimation using airborne L-band same-day repeat-pass polarimetric SAR interferometry. IEEE J.-STARS 2017, 11, 95–111. [Google Scholar] [CrossRef]
- Denbina, M.; Simard, M.; Hawkins, B. Forest height estimation using multibaseline PolInSAR and sparse lidar data fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3415–3433. [Google Scholar] [CrossRef]
- Askne, J.; Smith, G. Forest InSAR decorrelation and classification properties. ERS SAR Interferom. 1997, 406, 95. [Google Scholar]
- Askne, J.; Santoro, M.; Smith, G.; Fransson, J.E. Multitemporal repeatpass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens. 2003, 47, 1540–1550. [Google Scholar] [CrossRef]
- Simard, M.; Hensley, S.; Lavalle, M.; Dubayah, R.; Pinto, N.; Hofton, M. An empirical assessment of temporal decorrelation using the uninhabited aerial vehicle synthetic aperture radar over forested landscapes. Remote Sens. 2012, 4, 975–986. [Google Scholar] [CrossRef]
- Lavalle, M.; Simard, M.; Hensley, S. A temporal decorrelation model for polarimetric radar interferometers. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2880–2888. [Google Scholar] [CrossRef]
- Li, W.; Chen, E.; Li, Z.; Zhang, W.; Li, H. Temporal decorrelation on airborne repeat pass P-, L-band T-SAR in boreal forest. IEEE IGARSS 2016, 50, 5–8. [Google Scholar]
- Denbina, M.; Simard, M. The effects of temporal and topographic decorrelation on forest height retrieval using airborne repeat-pass L-Band polarimetric SAR interferometry. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium, Beijing, China, 10–15 July 2016. [Google Scholar]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I. Quantification of temporal decorrelation effects at L-band for polarimetric SAR interferometry applications. IEEE J.-STARS 2013, 6, 1351–1367. [Google Scholar] [CrossRef]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.; Moreira, A. Forest Height Estimation by means of Pol-InSAR. K&C Science Report–Phase 1. 2009. Available online: https://www.researchgate.net/publication/224990685_Forest_Height_Estimation_by_means_of_Pol-InSAR_Limitations_posed_by_Temporal_Decorrelation (accessed on 10 September 2022).
- Deutscher, J.; Perko, R.; Gutjahr, K.; Hirschmugl, M.; Schardt, M. Mapping tropical rainforest canopy disturbances in 3D by COSMO-SkyMed spotlight InSAR-stereo data to detect areas of forest degradation. Remote Sens. 2013, 5, 648–663. [Google Scholar] [CrossRef]
- Sefercik, U.G.; Buyuksalih, G. and Atalay, C. DSM generation with bistatic TanDEM-X InSAR pairs and quality validation in inclined topographies and various land cover classes. Arab. J. Geosci. 2020, 13, 1–15. [Google Scholar] [CrossRef]
- Jacob, A.W.; Vicente-Guijalba, F.; López-Martínez, C.; López-Sánchez, J.M.; Litzinger, M.; Kristen, H. Sentinel-1 InSAR coherence for land cover mapping: A comparison of multiple feature-based classifiers. IEEE J.-STARS 2020, 13, 535–552. [Google Scholar] [CrossRef]
- Conde, V.; Nico, G.; Mateus, P.; Catalão, J.; Kontu, A.; Maria, G. On the estimation of temporal changes of snow water equivalent by spaceborne SAR interferometry: A new application for the Sentinel-1 mission. J. Hydrol. Hydromech. 2019, 67, 535–552. [Google Scholar] [CrossRef]
- Pulella, A.; Aragão Santos, R.; Sica, F.; Posovszky, P.; Rizzoli, P. Multi-temporal Sentinel-1 backscatter and coherence for rainforest mapping. Remote Sens. 2020, 12, 847. [Google Scholar] [CrossRef]
- Nico, G.; Mira, N.; Masci, O.; Catalão, J.; Panidi, E. Remote Sensing for Agriculture, Ecosystems, and Hydrology XXI; SPIE: Bellingham, WA, USA, 2019; Volume 11149. [Google Scholar]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I. The Impact of Temporal Decorrelation over Forest Terrain in Polarimetric SAR Interferometry. In Proceedings of the International Workshop on Applications of Polarimetry and Polarimetric Interferometry (Pol-InSAR) 2009. Available online: https://elib.dlr.de/58408/1/S.-K.Lee.pdf (accessed on 10 September 2022).
- Khati, U.; Singh, G.; Kumar, S. Potential of space-borne PolInSAR for forest canopy height estimation over India—A case study using fully polarimetric L-, C-, and X-band SAR data. IEEE J.-STARS 2018, 11, 2406–2416. [Google Scholar] [CrossRef]
- Davidson, M.W.; Furnell, R. ROSE-L: Copernicus L-Band SAR Mission. In Proceedings of the IEEE IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 872–873. [Google Scholar]
- Kellogg, K.; Hoffman, P.; Standley, S.; Shaffer, S.; Rosen, P.; Edelstein, W.; Sarma, C.V.H.S. NASA-ISRO synthetic aperture radar (NISAR) mission. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–21. [Google Scholar]
- Pepe, A.; Calò, F. A review of interferometric synthetic aperture RADAR (InSAR) multi-track approaches for the retrieval of Earth’s surface displacements. Appl. Sci. 2017, 7, 1264. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Lee, J.; Pottier, E. Polarimetric Radar Imaging: From Basics to Applications; Optical Science and Engineering; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Foucher, S.; López-Martínez, C. Analysis, evaluation, and comparison of polarimetric SAR speckle filtering techniques. IEEE Trans. Image Process. 2014, 23, 1751–1764. [Google Scholar] [CrossRef] [PubMed]
- Zebker, H.; Villasenor, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens. 1992, 30, 950–959. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Cartus, O.; Lavalle, M.; Magnard, C.; Milillo, P.; Oveisgharan, S.; Wegmüller, U. Global seasonal Sentinel-1 interferometric coherence and backscatter data set. Sci. Data 2022, 9, 1–16. [Google Scholar] [CrossRef]
- Hanssen, R. Radar interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: New York, NY, USA, 2002. [Google Scholar]
- Sica, F.; Pulella, A.; Nannini, M.; Pinheiro, M.; Rizzoli, P. Repeat-pass SAR interferometry for land cover classification: A methodology using Sentinel-1 Short-Time-Series. Remote Sens. Environ. 2019, 232, 111277. [Google Scholar] [CrossRef]
- Arturi, M.F.; Goya, J.F.; Sandoval López, D.M.; Cellini, J.M. Inventario Nacional de Plantaciones Forestales. 2017. Available online: http://sedici.unlp.edu.ar/handle/10915/70444 (accessed on 10 September 2022).
- Elizondo, M.H. Primer Inventario Forestal de la provincia de Corrientes; Consejo Federal de Inversiones: Buenos Aires, Argentina, 2009. [Google Scholar]
- Caniza, F.J.; Torres, C.G. Funciones de Índice de Sitio para Pinus Taeda en las Planicies Arenosas de Corrientes. 2019. Available online: https://inta.gob.ar/sites/default/files/inta_funciones_de_calidad_de_sitio_para_pinus_taeda_en_las_planicies_arenosas_de_corrientes_2019.pdf (accessed on 10 September 2022).
- Chauchard, L.M. Esquemas silvícolas para plantaciones de Pino ponderosa en el noroeste de la Patagonia, Argentina. Rev. Prod. For. 2012, 4, 7–12. [Google Scholar]
- Andenmatten, E.; Letourneau, F. Curvas de índice de Sitio para Pinus ponderosa (Dougl.) Law de aplicación en la región Andino Patagónica de Chubut y Río Negro, Argentina. Bosque 1997, 18, 13–18. [Google Scholar] [CrossRef]
- Braun, A. Retrieval of digital elevation models from Sentinel-1 radar data–open applications, techniques, and limitations. Open Geosci. 2021, 13, 532–569. [Google Scholar] [CrossRef]
- Tang, H.; Armston, J.; Dubayah, R. Algorithm Theoretical Basis Document (ATBD) for GEDI L2B Footprint Canopy Cover and Vertical Profile Metrics; Goddard Space Flight Center: Greenbelt, MD, USA, 2019. [Google Scholar]
- Olesk, A.; Praks, J.; Antropov, O.; Zalite, K.; Arumäe, T.; Voormansik, K. Interferometric SAR coherence models for characterization of hemiboreal forests using TanDEM-X data. Remote Sens. 2016, 8, 700. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).